1 Introduction

By interconnection of power systems, the stability of a large-scale power system becomes more important and challenging. Usually, the electric power stations and sources are far away from the load centers [1]. In a power system, power generation (turbines, generators) and loads (consumption) are interconnected through a network, of various power equipment and transmission lines (AC as well as DC lines). Power system is continually exposed to instabilities, such as fluctuations of load and line breakdown. It happens due to different reasons like low- or ultra-low-frequency oscillations (LFO and ULFO, respectively, 0.1–2.0 Hz is LFO, below 0.1 Hz is ULFO). Hydropower has an important role in the safe, stable, and efficient operation of the electric power system. Supply of stable and balanced electric power during such instabilities, proper operations of a controller, such as an excitation system or a governor are required. In sizeable power systems, wide-ranging low-frequency oscillation (LFO) threatens the operational stability. So exact assessment and suppression of the dominant oscillation mode are some of the important factors for the steady and stable operation of the system. In the power system, oscillation occurs generally in low and ultra-low-frequency ranges [2,3,4].

In recent years, with the widespread applications of huge-capacity, long-distance DC transmission technologies in real power grids, some ultra-low-frequency oscillation phenomena with oscillation frequencies below 0.1 Hz have arisen [5,6,7,8,9,10]. As ULFO is not a relative oscillation between the generator rotors, but the frequency oscillation in the primary frequency modulation process triggered by small system disturbances, it is a power system frequency stability issue [11]. Hydropower units in the Yunnan power grid contribute about 71–75% of the total output. When a power disturbance occurs, the water hammer effect of the hydropower turbine increases the active power imbalance, which leads to instability of grid frequency. In April 2016, when an asynchronous connection test was performed to connect the Yunnan power grid to China Southern Power Grid (main grid), a ULFO arose in the Yunnan power grid with an oscillation frequency of 0.05 Hz and amplitude of 0.1 Hz. The interconnection of regional power grids is becoming more and more compact. As the grid operates in a variety of ways, the occurrence of low-frequency oscillations will have a serious impact on the grid. As the primary frequency regulation function of a significant power plant ended, the oscillation gradually vanished [12,13,14]. To ensure the secure and steady operation of power system grids, it is of huge value to analyze the oscillation characteristics and the suppression measures of ULFOs arising in the system.

In Refs. [15, 16], the Nyquist curve of the primary frequency modulation model was used to expose the mechanism of ULFO. The influence of governor PID parameters on system stability was analyzed with the Routh–Hurwitz criterion. The stability analysis of the hydropower units has also been performed. In Refs. [17, 18], the proportional-integral-derivative (PID) controller is widely used in the power system with the characteristics of a simple structure and strong robustness. Reference [19] describes that the hydraulic turbine governing system (HTGS) is the main controlling system of hydropower production units. References [11, 20] introduced the dynamic characteristics of the hydropower governor in detail. References [21, 22] pointed out that the governor system’s control method is ULFO mode, with the damping ratio often affected by the PID parameters. The ULFO was a non-electromechanical oscillation mode in the Yunnan power grid. Optimizing the governor’s PID parameters could effectively increase the system stability. In Ref. [23], a relevant coefficient index (RCI) was proposed to screen the generator units with high sensitivity to ULFO. The governor’s PID parameters of the sensitive generators were optimized to suppress ULFO. Reference [24] proposed a method to optimize the governor’s parameters, where the optimization’s constraint was the damping torque of the prime mover in the entire oscillation frequency range. The optimization objective was the integral of the time-weighted-absolute-error (ITAE) of prime mover’s step response under different load conditions. The optimized parameters effectively ensured the system stability under different conditions. Right now, at most the ULFO is suppressed by tuning the PID parameters of the governor control system. But the effect is subject to system operating conditions as well as the specific PID parameter optimization method itself. At the same time, tuning the PID parameters of the governor control system may hurt some low-frequency oscillation modes. Reference [25] describes that a PID governor controller design based on the particular operational conditions does not always ensure the provision of acceptable performance over a wide-range of conditions. In Ref. [26], a field test was performed on the hydropower units, with governor power system stabilizer (GPSS) to verify that GPSS could increase the stability of the units. In Ref. [27], the power system experiences persistent low-frequency oscillation in the transmission lines after being troubled due to the lack of damping. In recent years, many research results of damping control strategies are available. Reference [28] to analyze small-signal dynamics damping torque analysis is an imperative technique. Reference [25] states that an appropriate tuning of governor offers an enhanced damping of the system oscillations along with increased system robustness. References [29, 30] analyzed the damping characteristics of large and small disturbances under the additional damping control of GPSS. It is completely performed in a single-machine infinity system as well as a multi-machine system. The results showed the efficacy of GPSS for both large and small disturbances. Reference [31] proposed an adaptive governor power system stabilizer (AGPSS) with multi-machine decoupling characteristics, which could suppress low-frequency oscillation in the single-machine infinite system as well as a multi-machine system.

Keeping in view the previous works, in this paper, at first the ULFO mode was solved based on the linearized state-space model of the multi-machine system that contains hydropower and steam turbine governor control systems before the ULFO was analyzed in the 4-machine 2-area system according to the participation factor and the root locus. The damping characteristics of the PID-type governor control system were then analyzed using the damping torque analysis method and a GPSS design method to suppress ULFO based on the phase compensation principle.

Finally, the suggested method is verified by the simulations with a single-machine, single-load system and the 13 main hydropower plants of the Yunnan power grid with large rated capacities. The mechanical damping provided by GPSS is not affected by the operating mode and conditions on the grid side. On top of the advantages of simple design, easy debug and calculation, GPSS damping has no negative impact on low-frequency oscillation mode in the system. Therefore, it could be of great value to guarantee the safe and stable operation of power system grids.

In this paper, the model linearization is established in Sect. 2. Section 3 is a description of GPSS design based on the phase compensation principle, where the principle of ULFO suppression and parameter tunings of the single- and multi-machine systems are stated. Section 4 presents analysis and verification of state-space model, analysis of the mechanical damping torque coefficient, Sensitivity analysis of ULFO mode, Influence of governor system model parameters on eigenvalues and ULFO in the actual power grid are explained. Finally, in Sect. 5 some conclusions are drawn.

2 Model linearization including hydrogenerator and steam turbine generator

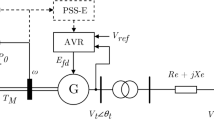
A linearized state-space model for multi-machine systems is established here. Considering the saliency pole effect of the generator and the excitation system dynamic, a practical third-order model is adopted for the generator, and the static excitation system is represented with a first-order inertial element. The small disturbance models of the generator and excitation system are

$$ \left\{ {\begin{array}{*{20}l} {\Delta \dot{\delta } = \omega_{0} \Delta \omega } \hfill \\ {M\Delta \dot{\omega } = \Delta P_{\text{m}} - \Delta P_{\text{e}} - D\Delta \omega } \hfill \\ {T^{\prime}_{\text{d0}} \Delta \dot{E^{\prime}}_{\text{q}} = \Delta E^{\prime}_{\text{fd}} - \Delta E_{\text{q}} } \hfill \\ {T_{\text{A}} \Delta \dot{E^{\prime}}_{\text{fd}} = - \Delta E^{\prime}_{\text{fd}} - K{\text{A}}\Delta V} \hfill \\ \end{array} } \right. $$
(1)

where ∆δ is the rotor angular increment of the generator; ∆ω is the angular speed increment of the generator; ω0 is the reference angular frequency of the system; M is the inertia time constant of the generator; D is the damping coefficient of the generator; ∆Pm is the mechanical power increment of the generator; ∆Pe is the electromagnetic power increment of the generator; \( T^{\prime}_{\text{d0}} \) is the time constant of the exciting winding itself; ∆Eq is the idle electromotive force increment of the actual exciting current; \( \Delta E^{\prime}_{\text{q}} \) is the quadrature-axis transient electromotive force increment of the generator; \( \Delta E^{\prime}_{\text{fd}} \) is the output voltage increment of the excitation system; KA and TA are the gain and the time constant of the excitation system, respectively; ∆V is the actual terminal voltage increment of the generator.

  1. (a)

    Model of hydrogenerator units

To study ULFO, a relatively complicated hydropower governor control system model is selected, which consists of the governor system model (GM\GM+), the electro-hydraulic servo system model (GA) and the prime mover model (TW) in PSD-BPA software. In actual operation and control of power system, the differential and integral coefficients of the PID governor of hydrosystem hardly affect its dynamic characteristics. For the sake of simplicity, usually their values are set to 0. Such a linearized model of the hydroturbine and governing system is shown in Fig. 1 where KW is the gain of the frequency deviation; BP is the permanent speed droop; KP1 is the proportional gain of the governor system; KI1 is the integral gain of the governor system; KP2 is the proportional gain of the servo system; TCO is the closing or opening time constant of the hydraulic servo-motor; T2 is the time constant of the feedback element of the hydraulic servo-motor; and TW is the time constant of the water hammer effect.

Fig. 1
figure 1

Linearized model of a hydropower governor control system

Full size image

According to the linearized model shown in Fig. 1, the transfer function of the hydropower system is

$$ G_{\text{ht}} (s) = \frac{{1 - T_{\text{W}} s}}{{1 + 0.5T_{\text{W}} s}} $$
(2)

Opening feedback element of the servo system almost does not participate in the ULFO, and its time constant does not affect the characteristics of ULFO, for simplicity, T2 = 0. Now the transfer function of the governor system is

$$ G_{\text{hg}} (s) = \frac{{K_{\text{W}} (K_{\text{P1}} + K_{\text{I1}} /s)}}{{1 + K_{\text{I1}} B_{\text{P}} /s}}\frac{1}{{1 + T_{\text{CO}} s /K_{\text{P2}} }} $$
(3)

According to Eqs. (2) and (3), the transfer function of the hydroturbine prime mover system is

$$ G_{\text{hm}} (s) = G_{\text{hg}} (s)G_{\text{ht}} (s) $$
(4)

Taking the state variables of the integral element output of governor system as ∆x1, the opening feedback element output of the servo system as ∆x2, the governor valve opening as ∆Phg, and the mechanical power as ∆Phm, the small disturbance models of the hydroturbine and the governor system are

$$ \left\{ {\begin{array}{*{20}l} {\Delta \dot{P}_{\text{hm}} = \frac{{2K_{\text{W}} K_{\text{P1}} K_{\text{P2}} }}{{T_{\text{CO}} }}\Delta \omega - \frac{2}{{T_{\text{W}} }}\Delta P_{\text{hm}} + \frac{2}{{T_{\text{W}} }}\Delta P_{\text{hg}} }\\ \quad {- \frac{{2K_{\text{P2}} }}{{T_{\text{CO}} }}\Delta x_{1} + \frac{{2K_{\text{P2}} }}{{T_{\text{CO}} }}\Delta x_{2} } \hfill \\ {\Delta \dot{P}_{\text{hg}} = \frac{{K_{\text{W}} K_{\text{P1}} K_{\text{P2}} }}{{T_{\text{CO}} }}\Delta \omega + \frac{{K_{\text{P2}} }}{{T_{\text{CO}} }}\Delta x_{1} - \frac{{K_{\text{P2}} }}{{T_{\text{CO}} }}\Delta x_{2} } \hfill \\ {\Delta \dot{x}_{1} = (B_{\text{P}} K_{\text{W}} K_{\text{P1}} K_{\text{I1}} - K_{\text{W}} K_{\text{I1}} )\Delta \omega - B_{\text{P}} K_{\text{I1}} \Delta x_{1} } \hfill \\ {\Delta \dot{x}_{2} = \frac{1}{{T_{2} }}\Delta P_{\text{hg}} - \frac{1}{{T_{2} }}\Delta x_{2} } \hfill \\ \end{array} } \right. $$
(5)
  1. (b)

    Model of steam turbine generator units

The selected steam turbine governor control system model consists of a governor model (GS) and a prime mover model (TB). The linearized model is shown in Fig. 2, R is the permanent speed droop; TC is the servo time constant; TCH, TRH, and TCO are the time constants of the steam chest, reheater, and crossover duct, respectively; FHP, FIP, and FLP are the power ratio coefficients of the high-, medium-, and low-pressure cylinders, respectively.

Fig. 2
figure 2

Linearized model of steam turbine governor control system

Full size image

Setting FLP = 0, the transfer function of the steam turbine primary system is obtained.

$$ G_{\text{sm}} (s) = \frac{1}{R}\frac{1}{{1 + T_{\text{C}} s}}\frac{{1 + F_{\text{HP}} T_{\text{RH}} s}}{{(1 + T_{\text{CH}} s)(1 + T_{\text{RH}} s)}} $$
(6)

Take the state variables as ∆y1, ∆y2, ∆Psg, and ∆Psm, the small disturbance models of the steam turbine and the governor system are

$$ \left\{ {\begin{array}{*{20}l} {\Delta \dot{P}_{\text{sm}} = F_{\text{HP}} \Delta y_{1} + F_{\text{IP}} \Delta y_{2} } \hfill \\ {\Delta \dot{P}_{\text{sg}} = - \frac{1}{{RT_{\text{C}} }}\Delta \omega - \frac{1}{{T_{\text{C}} }}\Delta P_{\text{sg}} } \hfill \\ {\Delta \dot{y}_{1} = \frac{1}{{T_{\text{CH}} }}\Delta P_{\text{sg}} - \frac{1}{{T_{\text{CH}} }}\Delta y_{1} } \hfill \\ {\Delta \dot{y}_{2} = \frac{1}{{T_{\text{RH}} }}\Delta y_{1} - \frac{1}{{T_{\text{RH}} }}\Delta y_{2} } \hfill \\ \end{array} } \right. . $$
(7)

Including multiple hydrogenerator and steam turbine generator models, according to the linearized models of the generator–excitation system, the load–governor control system and taking the derivation process of the linearized model of multi-machine system as a reference, keep the state variables ∆δ, ∆ω, \( \Delta E^{\prime}_{\text{q}} \), \( \Delta E^{\prime}_{\text{fd}} \), ∆Phm, ∆Psg, ∆Psm, ∆Phg, ∆x1, ∆x2, ∆y1, and ∆y2, but use state variables to represent ∆Pe, ∆Eq, and ∆V. The linearized state-space equation of the multi-machine system is

$$ \left[ \begin{aligned} \Delta \dot{\delta } \hfill \\ \Delta \dot{\omega } \hfill \\ \Delta \dot{E^{\prime}}_{\text{q}} \hfill \\ \Delta \dot{E^{\prime}}_{\text{fd}} \hfill \\ \Delta \dot{P}_{\text{hm}} \hfill \\ \Delta \dot{P}_{\text{sm}} \hfill \\ \Delta \dot{P}_{\text{hg}} \hfill \\ \Delta \dot{P}_{\text{sg}} \hfill \\ \Delta \dot{x}_{1} \hfill \\ \Delta \dot{x}_{2} \hfill \\ \Delta \dot{y}_{1} \hfill \\ \Delta \dot{y}_{2} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} 0 & {A_{12} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {A_{21} } & {A_{22} } & {A_{23} } & 0 & {M_{\text{h}}^{ - 1} } & {M_{\text{s}}^{ - 1} } & 0 & 0 & 0 & 0 & 0 & 0 \\ {A_{31} } & 0 & {A_{33} } & {A_{34} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {A_{41} } & 0 & {A_{43} } & {A_{44} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {2X_{1} } & 0 & 0 & { - 2X_{2} } & 0 & {2X_{2} } & 0 & { - 2X_{3} } & {2X_{3} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {F_{\text{HP}} } & {F_{\text{IP}} } \\ 0 & { - X_{1} } & 0 & 0 & 0 & 0 & 0 & 0 & {X_{3} } & { - X_{3} } & 0 & 0 \\ 0 & {Y_{1} } & 0 & 0 & 0 & 0 & 0 & {Y_{2} } & 0 & 0 & 0 & 0 \\ 0 & {X_{4} } & 0 & 0 & 0 & 0 & 0 & 0 & {X_{5} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {X_{6} } & 0 & 0 & { - X_{6} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {Y_{3} } & 0 & 0 & { - Y_{3} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {Y_{4} } & { - Y_{4} } \\ \end{array} } \right]\left[ \begin{aligned} \Delta \delta \hfill \\ \Delta \omega \hfill \\ \Delta E^{\prime}_{\text{q}} \hfill \\ \Delta E^{\prime}_{\text{fd}} \hfill \\ \Delta P_{\text{hm}} \hfill \\ \Delta P_{\text{sm}} \hfill \\ \Delta P_{\text{hg}} \hfill \\ \Delta P_{\text{sg}} \hfill \\ \Delta x_{1} \hfill \\ \Delta x_{2} \hfill \\ \Delta y_{1} \hfill \\ \Delta y_{2} \hfill \\ \end{aligned} \right] $$
(8)

where

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} 0 & {A_{12} } & 0 & 0 \\ {A_{21} } & {A_{22} } & {A_{23} } & 0 \\ {A_{31} } & 0 & {A_{33} } & {A_{34} } \\ {A_{41} } & 0 & {A_{43} } & {A_{44} } \\ \end{array} } \right] \\ &\quad = \left[ {\begin{array}{*{20}c} 0 & {\omega_{0} I} & 0 & 0 \\ { - M^{ - 1} K_{1} } & { - M^{ - 1} D} & { - M^{ - 1} K_{2} } & 0 \\ { - T\prime_{\text{d0}}^{ - 1} K_{4} } & 0 & { - T\prime_{\text{d0}}^{ - 1} K_{3} } & {T\prime_{\text{d0}}^{ - 1} } \\ { - T_{\text{A}}^{ - 1} K_{\text{A}} K_{5} } & 0 & { - T_{\text{A}}^{ - 1} K_{\text{A}} K_{6} } & { - T_{\text{A}}^{ - 1} } \\ \end{array} } \right] \end{aligned} $$

and K1–K6 are the coefficient matrices reflecting the component parameters, grid structure, load characteristics, and operating conditions; X1–X6 and Y1–Y4 are the system matrices under the governor control system, and \( X_{1} = {\text{diag}}(K_{\text{W}} K_{\text{P1}} K_{{{\text{P}}2}} /T_{\text{CO}} ) \), \( X_{2} = {\text{diag}}(1 /T_{\text{W}} ) \), \( X_{3} = {\text{diag}}(K_{{{\text{P}}2}} /T_{\text{CO}} ) \), \( X_{4} = {\text{diag}}(B_{\text{P}} K_{\text{W}} K_{\text{P1}} K_{{{\text{I}}1}} - K_{\text{W}} K_{{{\text{I}}1}} ) \), \( X_{5} = {\text{diag}}( - B_{\text{P}} K_{{{\text{I}}1}} ) \), \( X_{6} = {\text{diag}}(1 /T_{ 2} ) \), \( Y_{1} = {\text{diag}}( - 1 /RT_{\text{C}} ) \), \( Y_{2} = {\text{diag}}( - 1 /T_{\text{C}} ) \), \( Y_{3} = {\text{diag}}( - 1 /T_{\text{CH}} ) \), and \( Y_{4} = {\text{diag}}( - 1 /T_{\text{RH}} ) \), respectively.

The eigenvalues of the ULFO mode appear in the form of conjugate pairs, i.e.,

$$ \lambda = \sigma \pm {\text{j}}\omega $$
(9)

The oscillation frequency is

$$ f = \frac{\omega }{{2\uppi}} $$
(10)

The damping ratio is

$$ \zeta = - \frac{\sigma }{{\sqrt {\sigma^{2} + \omega^{2} } }} . $$
(11)

Based on the linearized state-space model of a multi-machine system, the eigenvalues of the ULFO mode are calculated. The oscillation frequency ωS and the damping ratio ζS can be obtained according to Eqs. (9)–(11).

3 GPSS design based on the phase compensation principle

3.1 Principle of ULFO suppression by GPSS

The high hydropower proportion can lead to ULFOs in the system. Therefore, in this section, a frequency regulation model of a hydropower governor control system is established in Fig. 3, based on which the principle of ULFO suppression by GPSS is analyzed using the damping torque method.

Fig. 3
figure 3

Frequency regulation model of the governor control system

Full size image

Since the system rotational speed changes little during the transient process, i.e., \( \omega \approx 1\,{\text{p}} . {\text{u}} . \), \( \Delta P_{\text{m}} \approx \Delta T_{\text{m}} \) and \( \Delta P_{\text{e}} \approx \Delta T_{\text{e}} \). The incremental equations of the rotor motion of the generator can be expressed with the first two equations of Eq. (1). When the angular frequency of the system oscillation is ωs, the first equation of Eq. (1) is written as

$$ \Delta \omega = {\text{j}}\frac{{\omega_{\text{S}} }}{{\omega_{0} }}\Delta \delta . $$
(12)

When the angular frequency of the mechanical oscillation is ωS, the mechanical power increment ∆Phm of the hydropower governor control system is;

$$ \begin{aligned} & - \Delta P_{\text{hm}} = \bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )\Delta \omega \\ &\quad = \text{Re} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]\Delta \omega + {\text{jIm}} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]\Delta \omega {\kern 1pt} {\kern 1pt} \\ &\quad = \text{Re} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]\Delta \omega - \frac{{\omega_{\text{S}} }}{{\omega_{0} }}\text{Im} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]\Delta \delta \\ &\quad = K_{\text{D}} \Delta \omega + K_{\text{S}} \Delta \delta \\ \end{aligned} $$
(13)

where KD is the mechanical damping torque coefficient and KS is the mechanical synchronous torque coefficient.

The relationship between ULFO damping ratio ζS and total mechanical damping torque KD satisfies [11]

$$ \zeta_{\text{S}} = \frac{{D + K_{\text{D}} }}{{2M\omega_{\text{n}} }} = \frac{{D + K_{\text{D}} }}{{2\sqrt {K_{\text{S}} M\omega_{0} } }} $$
(14)

where ωn is the angular frequency of the undamped natural oscillation.

In the \( \Delta \delta - \Delta \omega \) coordinate system, the vector diagram of mechanical torque is drawn in Fig. 4. When \( - \Delta P_{\text{hm}} \) falls in the first quadrant, KD > 0, and the positive damping torque provided by the governor system is shown in Fig. 4a. When \( - \Delta P_{\text{hm}} \) falls in the 4th quadrant, KD < 0, and the negative damping torque provided by the governor system is shown in Fig. 4b. In the hydropower governor system, \( G_{\text{hg}} (s) \) and \( G_{\text{ht}} (s) \) are both lag elements, which make \( - \Delta P_{\text{hm}} \) lag behind \( \Delta \omega \) in phase. When a ULFO occurs in the system, the hydropower governor control system provides negative damping, so that \( - \Delta P_{\text{hm}} \) falls in the 4th quadrant.

Fig. 4
figure 4

Vector diagram of mechanical torque

Full size image

In this paper, a GPSS that has a similar structure and transfer function to a power system stabilizer (PSS) is introduced into the governor control system. The transfer function is

$$ G_{\text{GPSS}} (s) = K_{\text{GPSS}} \frac{{1 + sT_{2} }}{{1 + sT_{1} }}\frac{{1 + sT_{4} }}{{1 + sT_{3} }} $$
(15)

where \( T_{2} > T_{1} > 0 \), \( T_{4} > T_{3} > 0 \), and \( K_{\text{GPSS}} > 0 \).

In the governor control model with GPSS as shown in Fig. 5, the GPSS generates the leading phase to reduce the phase lag \( - \Delta P_{\text{hm}} \) concerning ∆ω. As a result, the mechanical damping torque coefficient of the governor control system and the system damping ratio both increase to help suppress ULFO.

Fig. 5
figure 5

Block diagram of the governor control system with GPSS

Full size image

3.2 GPSS parameters tuning

3.2.1 GPSS parameter tunings in a single-machine system

Using the phase compensation method to tune the GPSS parameters in a single-machine system is straightforward, easy to debug and involves fewer calculations. From Fig. 5, the mechanical torque provided by GPSS is

$$ \Delta T_{\text{GPSS}} = - G_{\text{GPSS}} (s)G_{\text{hm}} (s)\Delta \omega $$
(16)

The mechanical torque provided by GPSS under the angular frequency ωs can be decomposed as follows:

$$ \begin{aligned} \Delta T_{\text{GPSS}} = & - \bar{G}_{\text{GPSS}} ({\text{j}}\omega_{\text{S}} )\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )\Delta \omega \\ = & - \text{Re} [\bar{G}_{\text{GPSS}} ({\text{j}}\omega_{\text{S}} )\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]\Delta \omega \\ &\quad + \frac{{\omega_{\text{S}} }}{{\omega_{0} }}\text{Im} [\bar{G}_{\text{GPSS}} ({\text{j}}\omega_{\text{S}} )\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]\Delta \delta \\ = & T_{\text{GPSSD}} \Delta \omega + T_{\text{GPSSS}} \Delta \delta \\ \end{aligned} $$
(17)

where TGPSSD and TGPSSS are the damping torque coefficient and the synchronous torque coefficient, respectively. For an efficient design, GPSS should ideally provide only positive damping torque, i.e.,

$$ \Delta T_{\text{GPSS}} = D_{\text{GPSS}} \Delta \omega ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D_{\text{GPSS}} < 0 $$
(18)

where DGPSS is the desired damping torque coefficient provided by GPSS. From Eqs. (17) and (18), DGPSS should satisfy

$$ D_{\text{GPSS}} { = } - \text{Re} [\bar{G}_{\text{GPSS}} ({\text{j}}\omega_{\text{S}} )\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )] . $$
(19)

According to Eq. (19), the phase angle of GPSS should be set to cancel out the forward path phase angle \( \bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} ) \). The objective of the GPSS parameter tuning is to compensate for the phase lag of the forward path, ensuring a positive net damping torque. Equation (19) represents the phase-compensation-based GPSS parameters tuning method. Only if

$$ \left\{ {\begin{array}{*{20}l} {\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} ) = \left| {G_{\text{hm}} } \right|\angle \phi } \hfill \\ {\bar{G}_{\text{GPSS}} ({\text{j}}\omega_{\text{S}} ) = \left| {G_{\text{GPSS}} } \right|\angle \gamma } \hfill \\ \end{array} } \right. $$
(20)

where

$$ \left\{ {\begin{array}{*{20}l} {\left| {G_{\text{hm}} } \right| = \sqrt {(\text{Re} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )])^{2} + (\text{Im} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )])^{2} } } \hfill \\ {\phi = \arctan \frac{{\text{Im} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]}}{{\text{Re} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )]}}} \hfill \\ \end{array} } \right. $$
(21)

Substituting \( s = {\text{j}}\omega_{\text{S}} \) into Eq. (4) yields

$$ \left\{ {\begin{array}{*{20}l} {\text{Re} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )] = A(a_{1} \omega_{\text{S}}^{4} + a_{2} \omega_{\text{S}}^{2} + a_{3} )} \hfill \\ {\text{Im} [\bar{G}_{\text{hm}} ({\text{j}}\omega_{\text{S}} )] = A(b_{1} \omega_{\text{S}}^{5} + b_{2} \omega_{\text{S}}^{3} + b_{3} \omega_{\text{S}} )} \hfill \\ {A = [(\omega_{\text{S}}^{2} + K_{\text{I1}}^{2} B_{\text{P}}^{2} )(1 + T_{\text{CO}}^{2} \omega_{\text{S}}^{2} /K_{\text{P2}}^{2} )(1 + 0.25T_{\text{W}}^{2} \omega_{\text{S}}^{2} )]^{ - 1} } \hfill \\ \end{array} } \right. $$
(22)

where

$$ \left\{ {\begin{array}{*{20}l} \begin{aligned} a_{1} = & - 0.5K_{\text{W}} K_{\text{P1}} T_{\text{W}}^{2} - 1.5K_{\text{W}} K_{\text{P1}} T_{\text{W}} T_{\text{CO}} /K_{\text{P2}} \\ & \quad - 0.5(K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} )T_{\text{W}}^{2} T_{\text{CO}} /K_{\text{P2}} \\ \end{aligned} \hfill \\ \begin{aligned} a_{2} = & K_{\text{W}} K_{\text{P1}} + 1.5(K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} )T_{\text{W}} \\ & \quad - 0.5K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}}^{2} B_{\text{P}} T_{\text{W}}^{2} \\ & \quad + (K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} )T_{\text{CO}} /K_{\text{P2}} \\ & \quad - 1.5K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}}^{2} B_{\text{P}} T_{\text{CO}} T_{\text{W}} /K_{\text{P2}} \\ \end{aligned} \hfill \\ {a_{3} = K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}}^{2} B_{\text{P}} } \hfill \\ {b_{1} = 0.5K_{\text{W}} K_{\text{P1}} T_{\text{W}}^{2} T_{\text{CO}} /K_{\text{P2}} } \hfill \\ \begin{aligned} b_{2} = & - 0.5(K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} )T_{\text{W}}^{2} \\ & \quad - K_{\text{W}} K_{\text{P1}} T_{\text{CO}} /K_{\text{P2}} \\ & \quad - 0.5(K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} )T_{\text{W}}^{2} \\ & \quad + 0.5K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}}^{2} B_{\text{P}} T_{\text{CO}} T_{\text{W}}^{2} /K_{\text{P2}} \\ & \quad - 1.5(K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} )T_{\text{W}} T_{\text{CO}} /K_{\text{P2}} \\ \end{aligned} \hfill \\ {b_{3} = (K_{\text{W}} K_{\text{P1}} K_{\text{I1}} B_{\text{P}} - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}} ) - 1.5K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}}^{2} B_{\text{P}} T_{\text{W}} }\\ \quad { - K_{\text{W}}^{2} K_{\text{P1}} K_{\text{I1}}^{2} B_{\text{P}} T_{\text{CO}} /K_{\text{P2}} } \hfill \\ \end{array} } \right. $$

According to the phase compensation method, the following equations should be satisfied.

$$ \left\{ {\begin{array}{*{20}l} {T_{\text{GPSSD}} = \left| {G_{\text{GPSS}} G_{\text{hm}} } \right|\cos (\phi + \gamma ) = D_{\text{GPSS}} } \hfill \\ {T_{\text{GPSSS}} = \left| {G_{\text{GPSS}} G_{\text{hm}} } \right|\sin (\phi + \gamma ) = 0} \hfill \\ \end{array} } \right. $$
(23)

It can be set that

$$ \gamma = - \phi ,\quad \left| {G_{\text{GPSS}} } \right| = \frac{{D_{\text{GPSS}} }}{{\left| {G_{\text{hm}} } \right|}} . $$
(24)

According to Eq. (15), the transfer function of GPSS can be written as

$$ G_{\text{GPSS}} (s) = K_{\text{GPSS1}} \frac{{1 + sT_{2} }}{{1 + sT_{1} }}K_{\text{GPSS2}} \frac{{1 + sT_{4} }}{{1 + sT_{3} }} $$
(25)

where \( K_{\text{GPSS}} = K_{\text{GPSS1}} K_{\text{GPSS2}} \). The GPSS parameters need to satisfy

$$ \left\{ {\begin{array}{*{20}l} {K_{\text{GPSS1}} \frac{{1 + {\text{j}}\omega_{\text{S}} T_{2} }}{{1 + {\text{j}}\omega_{\text{S}} T_{1} }} = \left| {G_{\text{GPSS}} } \right|\angle - \frac{\phi }{2}} \hfill \\ {K_{\text{GPSS2}} \frac{{1 + {\text{j}}\omega_{\text{S}} T_{4} }}{{1 + {\text{j}}\omega_{\text{S}} T_{3} }} = 1.0\angle - \frac{\phi }{2}} \hfill \\ \end{array} } \right. $$
(26)

i.e.,

$$ \left\{ {\begin{array}{*{20}l} {K_{\text{GPSS}} = \left| {G_{\text{GPSS}} } \right|\frac{{\sqrt {1 + T_{1}^{2} } }}{{\sqrt {1 + T_{2}^{2} } }}\frac{{\sqrt {1 + T_{3}^{2} } }}{{\sqrt {1 + T_{4}^{2} } }}} \hfill \\ {\arctan (\omega_{\text{S}} T_{2} ) }\\ \quad {- \arctan (\omega_{\text{S}} T_{1} ) = \arctan (\omega_{\text{S}} T_{4} ) - \arctan (\omega_{\text{S}} T_{3} ) = - \frac{\phi }{2}} \hfill \\ \end{array} } \right. $$
(27)

which allows the GPSS to provide a positive damping torque. Since the connection between the governor system and the power grid is weak, the mechanical damping provided by the GPSS is not affected by the grid operating modes and conditions.

3.2.2 GPSS parameters tuning in multi-machine system

Due to the decoupled operation of the GPSS in the multi-machine system, the phase-compensation-based GPSS parameters tuning method in a single-machine system can be extended to the multi-machine system. The specific steps are as follows:

  1. 1.

    Based on the linearized state-space model of the multi-machine system in Eq. (8), together with Eqs. (9)–(11), the oscillation frequency ωS in ULFO mode and the damping ratio ζS can be calculated;

  2. 2.

    With the given oscillation frequency ωS, the amplitude \( \left| {G_{\text{hm}} } \right| \) and phase angle \( \phi \) can be calculated from the system parameters and the oscillation frequency, according to Eqs. (21) and (22);

  3. 3.

    GPSS needs to provide a positive damping torque. According to the phase compensation principle, the GPSS design should satisfy Eq. (19), and parameter tuning should satisfy Eq. (24);

  4. 4.

    Given the desired damping torque coefficient DGPSS from GPSS, which satisfies DGPSS > \( \left| {\zeta_{\text{S}} } \right| \), the transfer function of GPSS is rewritten as Eq. (25). At the same time, the time constants are set to \( T_{1} = T_{3} \) and \( T_{2} = T_{4} \);

  5. 5.

    According to Eq. (27), all the GPSS parameters can be calculated.

4 Analysis and examples

4.1 ULFO characteristics

According to the actual operating parameters of the 4-machine 2-area system, and based on the linearized state-space equation, the characteristic analysis method is used to study the ULFO problem.

4.1.1 Verification of the linearized state-space model

The structure and steady-state data of the 4-machine 2-area system in Fig. 6 are derived from Ref. [11]. In the system, G1 and G2 are the hydropower units with GPSS, G3 and G4 are steam turbine units. GM\GM+, GA, and TW models are adopted for the hydropower governor control systems, while GS and TB models are used for the steam turbine governor control systems. The MG, FG, and constant power load models are adopted for the third-order generator, first-order excitation system, and the load, respectively. The dynamic parameter values for the MG models and the governor control system models of the four generators are shown in Table 1.

Fig. 6
figure 6

4-machine 2-area system

Full size image
Table 1 Model parameters
Full size table

The PSD-BPA software is used to simulate the 4-machine 2-area system. The simulation time is set to 100 s. At t = 10 s, a 3-phase short-circuit fault, which lasts for 0.1 s, occurs between lines 4 and 5. The simulations obtain the oscillations of the angular speed deviation of the generator before and after GPSS participation in Fig. 7.

Fig. 7
figure 7

Oscillation of angular speed deviation in the 4-machine 2-area system

Full size image

In Fig. 7, the ULFO occurs in 10 s, and the 4 oscillation curves of the angular speed deviations are in phase completely. Prony is used to analyze the curves in Fig. 7. At the same time, based on the linearized state-space model of the multi-machine system, the oscillation frequency and damping ratio of the ULFO mode in the 4-machine 2-area system are calculated. The results are compared in Table 2. The consistent results endorse the linearized state-space model of the multi-machine system as an effective tool to analyze the oscillation characteristics of ULFO.

Table 2 Identification results of Prony analysis and calculation results of the state-space model
Full size table

4.1.2 Analysis of the mechanical damping torque coefficient

Based on Eqs. (4) and (6), the phase–frequency curves of the hydropower and steam turbine governor control systems of the 4-machine 2-area system can be obtained (Fig. 8). The phase angle variations of \( - \Delta P_{\text{hm}} \) and \( - \Delta P_{\text{sm}} \) concerning ∆ω are presented, respectively.

Fig. 8
figure 8

Phase–frequency curves of governor control system

Full size image

From the phase–frequency curves shown in Fig. 8, when the oscillation frequency is 0.01–0.1 Hz (corresponding angular frequency 0.0628–0.628 rad/s), the governor control systems of hydropower units G1 and G2 have larger phase lags than those of steam turbine units G3 and G4. Without GPSS for G1 and G2, the ULFO mode has λ1,2 = \( - 0.002 \pm {\text{j}}0.286 \), the oscillation frequency is 0.046 Hz, and the phase lags of \( - \Delta P_{\text{hm}} \) in G1 and G2 and \( - \Delta P_{\text{sm}} \) in G3 and G4 concerning ∆ω are 102°, 124°, 45°, and 46.7°, respectively. Therefore, when ULFO occurs, ∆ω falls in the first quadrant, and the steam turbine governor control systems provide positive damping; but \( - \Delta P_{\text{hm}} \) falls in the 4th quadrant, and the hydropower governor control systems provide negative damping. With GPSS added to G1 and G2, the ULFO mode has \( \lambda_{1,2} = - 0.021 \pm {\text{j}}0.297 \), the oscillation frequency is still 0.046 Hz, and the phase lags of \( - \Delta P_{\text{hm}} \) in G1 and G2 concerning ∆ω are, respectively, 93° and 118°, which are lower than those without GPSS. Before and after the GPSS, the values of the mechanical damping torque coefficients of G1–G4 are shown in Table 3, which shows an increase in the mechanical damping torque coefficients after the GPSS involvement.

Table 3 Mechanical damping torque coefficients of G1–G4
Full size table

Equation (14) shows that the damping ratio ζS of ULFO increases with the increase of the mechanical damping torque coefficient. Therefore, ULFO is mainly due to the negative mechanical damping torque coefficient of the hydropower governor control system in ultra-low-frequency range, which reduces ζS to impair the system damping. The addition of GPSS in the hydropower governor control system can generate a leading phase to reduce the phase lag of \( - \Delta P_{\text{hm}} \) with respect to ∆ω, so that the increased mechanical damping torque coefficient of the governor control system as well as the system damping ratio could be helpful to suppress ULFO.

4.1.3 Sensitivity analysis of ULFO mode

The participation factor reflects each state variable’s relative degree of involvement in the oscillation mode. A pair of conjugate eigenvalues of the ULFO mode is calculated with the linearized state-space model of the multi-machine system: \( \lambda_{1,2} = - 0.010 \pm {\text{j}}0.290 \). Based on the left and right eigenvectors, the participation factors of the system model in ULFO are calculated (Table 4).

Table 4 Participation factors of system models
Full size table

In Table 4, the MG, GM, GA, and TW models of hydropower units G1 and G2, and the MG, GS, and TB models of steam turbine units G3 and G4 all take part in ULFO, while the FG models of the 4 generators hardly participate. For a constant power load, the state variable of the excitation system is completely decoupled from ULFO. The excitation system has a participation factor of 0 and does not participate in ULFO.

4.1.4 Influence of governor system model parameters on eigenvalues

Now, turn to the proportional gain (KP1) and integral gain (KI1) of the hydropower governor system model, for which reasonable value ranges are set, as shown in Table 5.

Table 5 Some parameters and its value ranges
Full size table

One of the parameters is made to increase monotonically within the range in Table 5, while other parameters and the operating mode are kept unchanged. The corresponding eigenvalues calculated by the linearized state-space model of the multi-machine system are plotted in Fig. 9.

Fig. 9
figure 9

Root locus curves with different parameters

Full size image

From Fig. 9 and Eq. (11), the change of the damping ratio in response to an increase in a certain parameter is calculated and shown in Table 6. The PID parameters could be tuned within a reasonable range to raise the system damping ratio for ULFO suppression.

Table 6 Change of damping ratio
Full size table

4.2 Simulation verification of ULFO suppression by GPSS

4.2.1 Single-machine single-load system

In the single-machine single-load system, the system parameters are set as M = 10.0 s, KW = 1.5, KP1 = 3.8, KI1 = 0.53, BP = 0.05, KP2 = 3, TCO = 20 s, T2 = 0 s, and TW = 1.0 s. The simulation time is set to 100 s. At t = 2 s, the system has a 3-phase short-circuit fault, which lasts for 0.2 s. The simulation obtains the oscillations of angular speed deviation and mechanical power deviation, shown in Fig. 10. The calculated eigenvalues of the system are 0.0000 ± j0.3082. A ULFO with an angular speed oscillation period of 20.384 s and oscillation amplitude \( 0.1\;{\text{Hz}} \) is generated in the system.

Fig. 10
figure 10

Oscillations of angular speed deviation and mechanical power deviation

Full size image

From Eqs. (21) and (22), \( \left| {G_{\text{m}} } \right| = 1.004 \) and \( \phi = 109.6^\circ \), that is, \( \Delta P_{\text{m}} \) lags \( - \Delta \omega \) by \( 109.6^\circ \). If the GPSS is added to the governor control system to increase the system mechanical power damping by 0.142, one should set DGPSS = − 0.142. The calculated parameters of the designed GPSS are KGPSS = 0.7766, T1 = T3 = 0.592 s, and T2 = T4 = 7.0 s. Using these parameter values, the oscillation curves of the angular speed deviation with and without the GPSS are obtained, as shown in Fig. 11.

Fig. 11
figure 11

Oscillations of angular speed deviation in the single-machine single-load system

Full size image

After calculation, the eigenvalues of the system with GPSS are λ1,2 = − 0.0442 ± j0.3082. From Fig. 11, without GPSS, the system is zero-damping with a ULFO of constant amplitude, as the negative damping provided by the governor control system and the positive damping in the system cancel out each other. With GPSS added, GPSS reduces the negative damping by the governor control system to pull the system into a positive damping state, so that the ULFO gradually dies out.

4.2.2 Actual power grid

When ULFO occurs in a system, all the generator units oscillate synchronously. To study the close relationship between the hydropower units and ULFO in the Yunnan power grid, the frequency regulation effect of the thermal power units and the minor hydropower plants is neglected. Based on the offline simulation result of Yunnan power grid in 2017, 13 large capacity hydropower plants are selected as concerned objects: Xiaowan (XW), Jinanqiao (JAQ), Xiluodu (XLD), Zhazadu (NZD), Manwan (MW), Dachaoshan (DCS), Gongguoqiao (GGQ), Jinghong (JH), Longkou (LKK), Ahhai (AH), Ludila (LDL), Liyuan (LY), and Guanyinyan (GYY). The simulation is to verify the effectiveness of GPSS for ULFO suppression. When a constant amplitude ULFO occurs, the main parameters of the governor systems of 13 main hydropower plants are shown in Table 7, in which Ki is the ratio of the rated capacity of the ith hydropower plant over the total capacity of the 13 main hydropower plants.

Table 7 Main parameters of the governor systems of 13 main hydropower plants
Full size table

During the GPSS parameter setup for the Yunnan power grid simulation system, each of the 13 main hydropower plants is equipped with a GPSS that is supposedly providing the same damping torque coefficient. The GPSS parameters are designed with the phase compensation method. The simulation time is set to 100 s. At 1 s, there is a three-phase short-circuit fault, which lasts for 0.2 s. The oscillation curves of the angular speed deviation with and without the GPSS are obtained by the simulation (Fig. 12). Prony analysis is performed on these curves, and a comparison is given in Table 8.

Fig. 12
figure 12

Oscillations of angular speed deviation in the actual power grid

Full size image
Table 8 Comparison of oscillation modes
Full size table

It can be seen from Fig. 12 and Table 8 that after GPSS is added, the oscillation amplitude of the angular speed deviation is gradually attenuated, and the damping ratio is raised by 0.105. Therefore, adding GPSS to a multi-machine system can effectively suppress ULFO in the system.

5 Conclusions

In this paper, by establishing the linearized state-space model of a multi-machine system with PID-type governors, the characteristic analysis method is used to study characteristics and suppression measures of hydropower-unit-induced ULFO with the participation factors and root locus. The conclusions are as follows:

  1. 1.

    The governor control system model places a part in ULFO, while the excitation system model does not. In Table 4, the MG, GM, GA, and TW models of hydropower units G1 and G2, as well as the MG, GS, and TB models of steam turbine units G3 and G4 in the 4-machine 2-area system all have large participation factors, while the participation factor of the excitation system is 0.

  2. 2.

    With the increase in proportional gain KP1 and integral gain KI1 of the PID-type governor system, the system damping ratio is gradually reduced. In Fig. 4 with the increase of KP1 and KI1 in the 4-machine 2-area system, the real part of the eigenvalues of the ULFO mode gradually increases, and the system damping ratio gradually deteriorates.

  3. 3.

    The GPSS with leading phase element is added on the governor side, and the GPSS transfer function is divided into leading and lag elements–both with gains. By properly setting the parameters in each part, the phase lag generated by the complicated hydropower governor system can be compensated, and the desired positive damping torque achieved, to suppress ULFO in the system.