Keywords

1 Introduction

Microgrid (MG) plays a vital role for reliable and economic operation of a power system. The reliability includes stabilising voltage and frequency. When a MG is connected to a grid, there are several challenges for a system operator out of which an important issue is the dynamical interaction of low inertia MG with the conventional grid. The MG may be of AC, DC or hybrid type and may include synchronous generation, induction generation or generation based on different power electronics converters. For the dynamic stability study of MG a linearized model of MG along with other power system components is needed. The linear modelling of various power systems has been reported by different researchers [1,2,3]. The low frequency Heffron Phillips modelling of the power system has been employed in many research studies for linear modelling [4,5,6,7]. In [8], a generalised modelling of MG has been reported and in [9] KVL and KCL have been employed for MG modelling. But estimating the MG and control action parameters are reported [10, 11]. The equivalent model of MG has been reported in many research studies including black box theory as in [12,13,14] or using mathematical modelling as in [15]. A linear equivalent model of MG connected to the grid has been presented in [16] which has been considered in this work with optimal tuning of the governor parameters for the synchronous generator of MG. An important issue is selection of proper gains for creating an effective damping torque and for which a suitable algorithm can be applied. In [5] a modification of the GWO algorithm called random walk GWO is proposed as a challenging technique in contrast to prevailing algorithms. This algorithm is proposed here to tune governor gains and has been compared with PSO and GWO algorithms for justification of tuning efficacy.

2 Low Frequency Model of Micro Grid

2.1 Synchronous Generator-Based MG Modelling

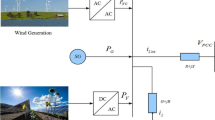
The low frequency MG model considered here is based on modification of the small signal Heffron Phillips model [5] including the governor and excitation system. Figure 1 represents the single line diagram of MG connected to an infinite bus. Figure 2 shows the IEEE ST6B excitation system considered in this work and Fig. 3 depicts the equivalent turbine governor model. Equations describing the MG are presented by [16]

$$\begin{gathered} \frac{dw}{{dt}} = \frac{1}{2H}\left( {T_m - T_e - T_D } \right) \hfill \\ \hfill \\ \end{gathered}$$
$$\frac{d\delta }{{dt}} = \omega_b \left( {\omega - 1} \right)$$
$$\frac{{de^{\prime}_q }}{{dt}} = \frac{1}{{T^{\prime}_{d0} }}\left[ {E_{fd} - e^{\prime}_q - \left( {X_d - X^{\prime}_d } \right)i_d } \right]$$
(1)
$$i = i_d + ji_q$$
$$v_t = v_d + jv_q$$
$$V_{pcc} = v_{pcc} \left( {\sin \delta + j\cos \delta } \right)$$
$$Z = R + jX\, Y = G + jB$$
$$C_1 + jC_2 = 1 + ZY$$
$$R_1 = R - C_2 X_d^{\prime} , \, R_2 = R - C_2 X_q$$
$$X_1 = X + C_1 X_q , \, R_2 = R - C_2 X_q$$
$$X_1 = X + C_1 X_q , \, X_2 = X - C_1 X^{\prime}_d$$
$$Z_e^2 = R_1 R_2 + X_1 X_2$$
$$Y_d = \left( {C_1 X_1 - C_2 R_2 } \right)/Z_e^2$$
$$Y_q = {{\left( {C_1 R_1 - C_2 X_2 } \right)} / {Z_e^2 }}$$
(2)
$$v_{do} = P_o v_{t0} \left[ {P_0^2 + \left( {{{Q_0^2 + v_{t0}^2 } / {X_q }}} \right)^2 } \right]^{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt}\!\lower0.7ex\hbox{$2$}}}$$
$$V_{q0} = \left( {V_{t0}^2 - V_d^2 } \right)^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt}\!\lower0.7ex\hbox{$2$}}}$$
$$i_{q0} = \frac{vd0}{{X_q }}i_{d0} = {{\left( {P_0 - i_{q0} v_{q0} } \right)} / {v_{d0} }}$$
$$e_{q0}^{\prime} = v_{q0} + X_d^{\prime} i_{d0}$$
$$v_{pccd0} = C_1 v_{d0} - C_2 v_{q0} - Ri_{d0} + Xi_{q0}$$
$$v_{pccq0} = C_2 v_{d0} + C_1 v_{q0} - Xi_{d0} - Ri_{q0}$$
$$\delta_0 = \tan^{ - 1} \left( {\frac{{v_{pccd0} }}{{v_{pccq0} }}} \right)$$
$$i_{Ld0} = Gv_{d0} - Bv_{q0} \, i_{Lq0} = Gv_{q0} + Bv_{d0}$$
$$i_{Lined0} = i_{d0} - i_{Ld0} i_{Lineq0} = i_{q0} - i_{Lq0}$$
(3)
Fig. 1
figure 1

SG with SPV and wind source connected to infinite bus

Full size image
Fig. 2
figure 2

IEEE-ST6B excitation system

Full size image
Fig. 3
figure 3

Equivalent turbine governor modelling

Full size image

By Kirchoff’s voltage law the parameters are presented as:

$$Zi = \left( {1 + ZY} \right)v_t - v_{pcc}$$
$$\left[ {\begin{array}{*{20}c} R & { - X} \\ X & R \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_d } \\ {i_q } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C_1 } & { - C_2 } \\ {C_2 } & {C_1 } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_d } \\ {v_q } \\ \end{array} } \right] - v_{pcc} \left[ {\begin{array}{*{20}c} {\sin \delta } \\ {\cos \delta } \\ \end{array} } \right]$$
(4)

As per the voltage and currents in d and q axis are stated as:

$$\left[ {\begin{array}{*{20}c} {v_d } \\ {v_q } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]e_q^{\prime} - \left[ {\begin{array}{*{20}c} 0 & { - X_q } \\ {X_d^{\prime} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_d } \\ {i_q } \\ \end{array} } \right]$$
(5)

By combining Eqs. (4) and (5) the equations are presented as

$$\left[ {\begin{array}{*{20}c} {i_d } \\ {i_q } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Y_d } \\ {Y_q } \\ \end{array} } \right]e_q^{\prime} - \frac{{v_{pcc} }}{Z_e^2 }\left[ {\begin{array}{*{20}c} {R_2 } & {X_1 } \\ { - X_2 } & {R_1 } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sin \delta } \\ {\cos \delta } \\ \end{array} } \right]$$
(6)

And which can be linearized as

$$\left[ {\begin{array}{*{20}c} {\Delta i_d } \\ {\Delta i_q } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Y_d } \\ {Y_q } \\ \end{array} } \right]\Delta e_q^{\prime} + \left[ {\begin{array}{*{20}c} {F_d } \\ {F_q } \\ \end{array} } \right]\Delta \delta$$
(7)

For which

$$\left[ {\begin{array}{*{20}c} {F_d } \\ {F_q } \\ \end{array} } \right] = \frac{{v_{pcc} }}{Z_e^2 }\left[ {\begin{array}{*{20}c} { - R_2 } & {X_1 } \\ {X_2 } & {R_1 } \\ \end{array} } \right]\left[ {\frac{\cos \delta_0 }{{\sin \delta_0 }}} \right]\Delta e_q^{\prime}$$
(8)

In the Heffron–Phillips model, the input signals have relations with the variables by the K-constants. So the torque and real powers are presented as:

$$T_e = p = i_d v_d + i_q v_q$$
$$\Delta T_e = K_1 \Delta \delta + K_2 \Delta e_q^{\prime}$$
$$\left[ {\begin{array}{*{20}c} {K_1 } \\ {K_2 } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {i_{q0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {F_d } & {F_q } \\ {Y_d } & {Y_q } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left( {X_q - X_d } \right)i_{q0} } \\ {e_{qo}^{\prime} + \left( {X_q - X_d^{\prime} } \right)i_{d0} } \\ \end{array} } \right]$$
(9)

The equation of internal voltage in Eq. (1) is linearized as

$$\left( {1 + sT_{d0}^{\prime} } \right)\Delta e_q^{\prime} = \Delta E_{fd} - \left( {X_d - X_d^{\prime} } \right)\Delta i_d$$
(10)

And using Eq. (7) we can write Eq. (11) as:

$$\left( {1 + sT_{d0}^{\prime} } \right)\Delta e_q^{\prime} = K_3 \left[ {\Delta E_{fd} - K_4 \Delta \delta } \right]$$
$$K_3 = {1 / {\left[ {1 + \left( {X_d - X_d^{\prime} } \right)Y_d } \right]}}$$
$$K_4 = \left( {X_d - X_d^{\prime} } \right)F_d$$
(11)

The state variables can be linked with output reactive power as Eq. (12).

$$Q = i_d v_q - i_q v_d$$
$$\Delta Q = K_5 \Delta \delta Z + K_6 \Delta e_q^{\prime}$$
$$\left[ {\begin{array}{*{20}c} {K_5 } \\ {K_6 } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {i_{d0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {F_d } & {F_q } \\ {Y_d } & {Y_q } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {e_{q0}^{\prime} - 2X_d i_{d0} } \\ { - 2X_q i_{q0} } \\ \end{array} } \right]$$
(12)

K1 to K5 are constants for small signal model of the generator. The equivalent model of grid integrated MG can be formed by Eqs. (9), (11) and (12). The small signal model of MG is presented in Fig. 4 where the governor parameters are to be set optimally to provide adequate damping torque. Here the SPV and wind sources are integrated. Kv, Tv are gain and time constants for the SPV system, Kwg, Twg are gain and time constants for the wind energy conversion system.

Fig. 4
figure 4

Small signal MG modelling

Full size image

The active and reactive powers at PCC are given by Eqs. (13) and (14):

$$P_{pcc} = v_{pcc} i_{Lined} + v_{pccq} i_{Lineq}$$
$$Q_{pcc} = v_{pcc} i_{Lined} - v_{pccd} i_{Lineq}$$
(13)
$$\Delta P_{pcc} = \Delta v_{pcc} i_{Lined0} + v_{pccd0} \Delta i_{Lined} + \Delta v_{pccq} i_{Lined} + v_{pccq0} \Delta i_{Lineq}$$
$$\Delta Q_{pcc} = \Delta v_{pccq} i_{Lined0} + v_{pccq0} \Delta i_{Lined} - \Delta v_{pccd} i_{Lineq0} - v_{pccd0} \Delta i_{Lineq}$$
(14)

3 Governor Control Action and Objective Function

In the small signal model of Fig. 4, the governor parameters are Kg, t1g, t2g, t3g and t4g that represent the governor control action and these parameters are to be tuned by the RWGO algorithm. The flow chart of the proposed control scheme is presented in Fig. 5. The objective of the present work is to damp out the electromechanical oscillations followed by disturbances. So, an ITAE based objective function is chosen here.

$$J = \int\limits_0^{tsim} {t\left| {\Delta \omega } \right|} dt$$
(15)
Fig. 5
figure 5

Flow chart of proposed control scheme

Full size image

Subject to constraint

$${\text{K}}_{{\text{pg}}}^{{\text{min}} } \le {\text{ K}}_{{\text{pg}}} \le {\text{ K}}_{{\text{pg}}}^{{\text{max}}} ,$$
$${\text{t}}_{{\text{1g}}}^{{\text{min}}} \le {\text{ t}}_{{\text{1g}} } \le {\text{ t}}_{{\text{1g}}}^{{\text{max}}} ,{\text{ t}}_{{\text{2g}}}^{{\text{min}}} \le {\text{ t}}_{{\text{2g}}} \le {\text{ t}}_{{\text{2g}}}^{{\text{max}}}$$
$${\text{t}}_{{\text{3g}}}^{{\text{min}}} \le {\text{ t}}_{{\text{3g}}} \le {\text{ t}}_{{\text{3g}}}^{{\text{max}}}$$

4 Random Grey Wolf Optimiser Algorithm

GWO has been implemented by many researchers in different areas of applications which involve around 5–11 wolves in a group which are divided as per their participation in the hunting process. There are certain merits and demerits of GWO. The demerit is that the decision regarding the group which will guide the positions of the alpha group because this group dominates the wolf pack and also the problem is whether the alpha group takes the guidance of the guidance of the lower group or not. Due to this, for each iteration in the GWO, the position of different individual wolf packs needs updation, hence premature convergence may occur in GWO. To avoid this, certain changes may be implemented in the leader pack of GWO. Also, to avoid stagnation in local optimum, in [5] the leaders explore the searching space by random walk known as Random path Grey Wolf Optimisation (RGWO) followed by finally omega wolves being presented as:

$$W_N = \sum_{i = 1}^N {S_i }$$
(16)

Si being a random step can be obtained by random distributions.

Two consecutive random wolves are related as

$$W_N = \sum_{i = 1}^N {S_i } = \sum_{i = 1}^{N - 1} {S_i + X_N = W_{N - 1} + S_N }$$
(17)

Initiation point of wolf denoted as x0 & final as xN, so the random wolves are represented as: -

$$x_n = x_0 + \alpha_1 S_1 + \alpha_2 S_2 +\cdots + \alpha_N S_N = x_0 + \sum_{i = 1}^N {\alpha_i S_i }$$
(18)

where αi > 0 is a condition controlling step size Si.

The algorithm RW-GWO step size is taken from Cauchy distribution. As the variance of Cauchy distribution is infinity, it might take longer jump sometimes which is very effective at the time of stagnation and very useful from the leader wolves exploring the search space for getting the prey and guiding other wolves. Pseudcode for RGWO is given in Table 1.

Table 1 Pseudo code of RGWO
Full size table

5 Result and Analysis

Different case studies have been conducted in the present work to justify the optimal governor actions for power oscillation damping. These case studies include sudden and discrete variations in solar and wind generations. RWGO has been implemented to set the governor parameters optimally. The initial stage of synchronous generators is set at 0.8 pu and 0.17 pu for real and reactive power generations, respectively. In case 1, solar generation is a step raised by 0.3 pu and the system response is presented in Fig. 6. Bode plot is presented in Fig. 7 with the RGWO algorithm. Also, in case-1 wind source is varied suddenly by 0.4 pu and eigen values depicted in Table 2. Table 3 depicts optimal governor parameters with fixed PID excitation gains. The performance of RWGO has been compared with PSO, GWO techniques. In case 2, the solar and wind powers are varied discretely as per the pattern shown in Fig. 8. The system response has been represented in Figs. 9 and 10. From the results obtained in discrete variations of solar and wind penetrations, it has been observed that the parameters of the governor when tuned by RGWO provide better damping efficacy as compared to PSO, and GWO. Also the capability of the governor can be significantly improved by properly tuning of its parameters.

Fig. 6
figure 6

Angular frequency variations

Full size image
Fig. 7
figure 7

Bode plot for case-1

Full size image
Table 2 Prominent system eigen values with SPV/wind variations
Full size table
Table 3 Optimized parameters
Full size table
Fig. 8
figure 8

SPV/wind power random variations

Full size image
Fig. 9
figure 9

Angular speed variations for case-2 for varying wind source

Full size image
Fig. 10
figure 10

Angular speed variations for case-2 for varying SPV source

Full size image

6 Conclusion

In a micro-grid, the oscillations brought by uncertain solar and wind penetrations create challenge for maintaining oscillatory stability, which has been presented in this work. The variations in solar and wind sources are executed with step and random pattern for a micro-grid integrated with grid, and subject to this the governor gains are set optimally by the RWGO algorithm in contrast with PSO and GWO algorithms. A random walk being incorporated with GWO makes it more robust for the optimization problem and the additional lead compensation brought by governor action can provide a better damping torque to enhance oscillatory stability of the micro-grid system. System eigen analysis and frequency response plots are obtained for sudden variations in solar and wind generations. It has been concluded that synchronous generator’s governor can improve oscillatory stability if its parameters are efficiently tuned by a suitable algorithm. This work was further extended with more renewable penetrations using the 33-bus micro-grid system.