The role of colleges within the higher education sector

Abstract

Over the past decades, the (private) college sectors in the higher education systems of several European countries have expanded their capacities massively. This happened even though colleges have been at a competitive disadvantage with universities which are publicly subsidized, while colleges must self-finance through tuition fees. The question arises how, in equilibrium, a diverse student population is allocated between these institutions and which factors may account for the college expansion over time. Moreover, the efficiency properties of the resulting human capital accumulation process are of special interest. Our paper explores these questions within an information-based theoretical framework. Individuals are screened for their (unobservable) innate abilities, and the precision of the screening mechanism, which is endogenous, balances demand and supply of educational services. We find that in the short term, when the college capacity is fixed, the introduction of college subsidies is not desirable in most cases. In the long term, the college sector may expand excessively, thereby establishing inefficiently low screening standards in the admission process to higher education.

1 Introduction

Since the early 1950s of the twentieth century, the higher education (HE) systems in Israel and in much of Western Europe were confronted with the phenomenon of continually increasing demand. Soon, the rising demand exceeded the capacity of the existing HE systems which, at the time, consisted mainly of public high-cost research universities. This situation built up political pressure leading to the emergence of a less expensive type of private HE institutions, called “colleges” in this paper. Typically, (private) colleges have lower reputation as they operate on weaker scientific profiles and less ambitious curricula than (public) research universities.¹ The lower reputation of college education translates into lower incomes of college graduates. The colleges are also more flexible in adapting enrollment capacities over time, because college staff members tend to hold non-tenured positions. Finally and most importantly, the colleges charge tuition fees to cover their operating costs, while the universities are, to a large extent, funded by the government. As a consequence, university students pay significantly lower tuition fees.²

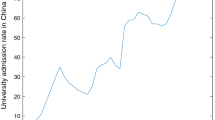
During the last several decades, the college sectors in large parts of Europe, in Israel, and also in the BRIC countries (Brazil, Russia, India, China) have expanded their capacities massively. In Israel, for instance, colleges were established in 1990 when less than 100,000 students were enrolled in universities (see Fig. 1).³ Since then, the capacity of the university sector has remained more or less constant, while the college sector expanded continually and has now an enrollment capacity of more than 200,000 students. Over the same time span, college expansions of a similar magnitude took place in the BRIC countries (see Carnoy et al. 2013).

Fig. 1

Expansion of college sector in Israel

The coexistence of universities and colleges with different educational profiles and cost structures raises the question how, in equilibrium, students are allocated between these institutions and to what extent this allocation supports efficiency of the aggregate human capital accumulation process. Particularly, striking is the observation that in the above-mentioned countries the college sector, which receives no public funding, has expanded steadily over time relative to the heavily subsidized university sector. This paper tries to answer these questions within a theoretical model of a HE system consisting of universities and colleges. Universities are modeled as public institutions, while colleges are private institutions of HE. Students who apply for HE will be tested, or screened, for their (unobservable) abilities. The precision of the tests, called screening intensity, constitutes the equilibrium mechanism which balances demand and supply of educational services. More precisely, in equilibrium the HE sector responds to an expanded demand for access to HE by adjusting the screening intensity in the admission process. Thus, when the demand for HE changes, colleges and universities become choosier or less choosy in the admission process so as to fill up their capacities.

In our model, colleges and universities differ in their educational technologies which convert a student’s ability into human capital, hence into income. The high-cost universities perform this conversion more effectively than the low-cost colleges. Moreover, university education is heavily subsidized by the government, while colleges charge cost-covering tuition fees. As a consequence, universities are first choice for obtaining HE. Access to university is restricted, however. Only individuals who performed well in the screening process, thus possessing sufficiently high “potential,” are admitted to university. All other agents face a choice between attending college and remaining uneducated. Agents with very poor test results have low potentials. These individuals may be better off remaining uneducated, because the college tuition fee outweighs their expected income gains from college education. By contrast, agents with sufficiently high potential will apply for college education if they are rejected by the university sector. In equilibrium, the screening intensity used in the admission process balances demand and supply of higher educational services. This implies that, among all individuals admitted to college, the students with the lowest potential are just indifferent between attending college and remaining uneducated.

This paper analyzes the role of the college sector for human capital production in HE under a short-term perspective as well as under a long-term perspective. By assumption, the capacity of the university sector is fixed throughout the analysis. In the short term, the capacity of the college sector is also fixed. Since, due to technical reasons, the range of the screening intensity is restricted to the unit interval, the screening mechanism achieves equilibrium in HE only for certain capacity constellations of universities and colleges. The set of all capacity constellations for which an equilibrium screening intensity exists is called the “admissible region.” In the long term, the college capacity is a choice variable of the college sector. The college sector understands how college capacity interacts with equilibrium screening and, based on this knowledge, chooses the college capacity optimally within the admissible region.

In the short term, colleges are at a competitive disadvantage to universities, because universities receive public subsidies, while colleges must rely on cost-covering tuition fees. This raises the question of tuition subsidies for college students in order to ease access to college education. We find that in most cases college subsidies are not desirable. Indeed, if college education is relatively expensive, a tuition subsidy reduces aggregate human capital production in both sectors of HE. The reason for this adverse effect is that the subsidy reduces the equilibrium screening intensity which, in turn, lowers the quality of the student bodies at colleges and universities. Only if college education is relatively cheap may a college tuition subsidy be advisable. In that case, the subsidy strengthens screening in HE, thus causing a gain in aggregate human capital production. Moreover, provided the college sector is small enough, this effect turns out to be sufficiently strong such that the gain outweighs the cost of the subsidy.

In the long term, the capacity of the college sector becomes an endogenous choice variable which maximizes the net value of college human capital production. If the college operating costs are sufficiently high, we find that the long-term college capacity shrinks to minimal size within the admissible region. At the same time, equilibrium screening is most intense and the process of human capital production in HE is efficient. By contrast, if college education is cheap enough, then the long-term college capacity expands to maximum size, effectively absorbing all agents who were rejected by universities. In such equilibrium, the process of human capital production is inefficient. Indeed, the college sector admits too many students, thereby establishing inefficiently low screening standards in HE.

The literature attributes the empirical phenomenon of college expansion over the past decades mostly to exogenous public policies such as various financial aid programs in European countries and in Israel.⁴ Our paper offers a different endogenous explanation: If the size of the university sector is fixed, and if screening for individual ability acts as an equilibrium mechanism in HE, then excessive capacity expansion may, in fact, constitute an optimal long-term strategy for the college sector.

Relation to literature This paper is related to an extensive literature on human capital production in HE. Part of this literature links the returns to education to the capacity of the college sector. Using empirical evidence from Russia, Belskaya et al. (2014) showed that college expansion reduces the average college wage premium, i.e., the wage differential between college educated workers and uneducated workers. These findings are consistent with earlier studies by Moffitt (2008) and Carneiro et al. (2011) which, however, build on different databases. Our work also predicts that college expansion draws students with lower potentials to college. Yet, this theoretical relationship is caused by endogenous changes of the screening intensity in HE rather than by changes in the college premium.

The return to education in our model can be affected by public subsidies. The role of tuition subsidies for human capital formation has been studied by Viaene and Zilcha (2013) within an OLG model, by Bevia and Iturbe-Ormaetxe (2002) in the presence of externalities, and by Garcia-Penalosa and Wälde (2000) in combination with tax-financing schemes. Eckwert and Zilcha (2014) used an information-based dynamic setting and compared tuition subsidies with student loan subsidies. They find that these two types of subsidies affect human capital formation in different ways.

Our paper is also related to the literature on competition between HE institutions. Most of this literature assumes that all institutions use the same curriculum (e.g., Epple et al. 2006). An exception is the work by Kaganovich and Su (2018). They allow HE institutions to differentiate themselves horizontally by setting curricular standards. In equilibrium, higher ability students enroll in institutions with more demanding curricula.

Finally, our work is related to the broad literature aimed at ordering information systems. The screening technologies considered in this study form a parametrized family of information systems.⁵ The screening technologies can be ranked by precision. The ranking is consistent with the Blackwell (1951) information order, with the more restrictive Lehmann (1988) and Persico (2000) information orders, and even with the information order suggested by Brandt et al. (2014, 2017) which allows for variable priors.

Building on this literature, the contribution of the present paper is to analyze how, in equilibrium, a heterogeneous student population is allocated between private and public educational institutions and how the equilibrium mechanism works in such HE system. We argue that the equilibrium mechanism is governed by the screening intensity in the admission process rather than by tuition costs levied on the students. This is an important and, we believe, realistic feature of our model.

2 Theoretical framework

Our model of the higher education (HE) sector is populated by risk-neutral students who differ with regard to their innate abilities. Let $\nu (a)$ denote the density of students with ability a and assume that individual abilities are uniformly distributed on the unit interval, i.e., $\nu (a)=1\quad \forall ~a\in [0,1]$. The students may obtain HE either at a public university with capacity $U<\frac{1}{2}$ (measure of students admitted) or at a private college with capacity C, $U+C\le 1$. HE is of better quality at the university than at the college. More precisely, the human capital of a student with ability a is $h_{u}(a)=a$, if he studies at the university, and $h_{c}(a)=\alpha a$, $\alpha \in (0,1)$, if he goes to college. Agents who attend neither a university nor a college remain uneducated. The human capital of uneducated individuals is normalized to zero. At the time when education decisions are made, an individual’s ability is not known. The students learn their abilities only afterward, i.e., during the process of HE.

The operating costs per student are $k_{u}$ for the university and $k_{c}$ for the college, $k_{u}>k_{c}$.⁶ The budgets of the university sector and the college sector are both partially funded by the government. The university receives a public subsidy, $B_u>0$, and finances the remaining costs through tuition payments, $t_u$, by its students. The university’s financing constraint is

$$\begin{aligned} B_u+(t_u-k_u)U=0. \end{aligned}$$

(1)

Similarly, the college receives a subsidy, $B_c$, from the government. We think of the college subsidy as being a small number close (or equal) to zero. The remaining costs are financed through tuition payments, $t_c$, by the college students. The college’s financing constraint reads

$$\begin{aligned} B_{c}+(t_{c}-k_{c})~C=0. \end{aligned}$$

(2)

The university receives a higher subsidy per student than the college. More precisely, we assume that

$$\begin{aligned} k_u-\frac{B_u}{U}\le \min \left\{ k_c-\frac{B_c}{C},\frac{w}{2(1+r)}\right\} . \end{aligned}$$

(3)

w denotes the wage earned per unit of human capital, and r is the interest rate. $k_u-\frac{B_u}{U}\le k_c-\frac{B_c}{C}$ implies $t_c\ge t_u$. Thus, university students pay a lower tuition fee than college students, while, at the same time, $\alpha <1$ implies that the HE provided by the university is of better quality than that provided by the college. Therefore, students always prefer the university over the college. $k_u-\frac{B_u}{U}\le \frac{w}{2(1+r)}$ implies that at least half of the student population applies for admission to university and, hence, the university capacity $U<\frac{1}{2}$ will always be exhausted. We further elaborate on this aspect below.

Access to the university is restricted. At the outset of an academic year, all prospective students are tested for their abilities. A measure U of students with the best test results will be admitted to university where they pay the tuition fee, $t_u$. Everybody else has the option either to go to college and pay the tuition fee, $t_c$, or remain uneducated.⁷

The test consists of a Farlie–Gumble–Morgenstern information technology which assigns a signal $y^{i}\in [0,1]$ to each student i. Thus, the signals assigned to students with ability a are distributed according to the density (see Brandt et al. (2014))

$$\begin{aligned} f_{\theta }(y|a)=1+\theta (1-2y)(1-2a);\quad \theta \in [0,1]. \end{aligned}$$

(4)

It is easily verified that the marginal signal distribution is uniform, i.e., $f_{\theta }(y)=1~\forall ~y\in [0,1]$, which implies $\nu _{\theta }(a|y)=f_{\theta }(y|a)=f_{\theta }(y,a)$. $\theta$ measures the precision of the test according to the Blackwell information order (Blackwell 1951). This precision variable, called screening intensity, can be endogenously adjusted in equilibrium to ensure that the capacities in the HE sector are fully used. $y=\frac{1}{2}$ is the neutral signal, i.e., the posterior ability distribution for $y=\frac{1}{2}$, $\nu _\theta (a,\frac{1}{2})$, coincides with the prior distribution, $\nu (a)$. Signal realizations larger (smaller) than the neutral signal constitute good news (bad news) in the sense of Milgrom (1981).

In our model, due to centralized administration, the screening intensity adjusts for the HE system as a whole. The screening intensity captures the level of selectivity, or choosiness, of HE institutions. Note, however, that more selective institutions do not set higher standards or admit fewer students. The university, for instance, always admits a fixed measure U of applicants. Rather, being more selective means that the HE institutions identify the students’ abilities more precisely in the admission process.

The updated expected ability of a student with test outcome y, called the student’s potential, can be calculated as

$$\begin{aligned} {} E_{\theta }[{\tilde{a}}|y]=\int ^{1}_{0}a\nu _{\theta }(a|y) \text{ d }a=\frac{1}{2}+\frac{\theta }{6}(2y-1). \end{aligned}$$

(5)

Note that a student’s potential is increasing in the signal, i.e., higher signals constitute better test outcomes. Students with signals higher than $\frac{1}{2}$ (the neutral signal) have above-average potential, and those with signals less than $\frac{1}{2}$ have below-average potential. Moreover, the potential of a student with signal y increases (decreases) under more precise screening if $y{\mathop {>}\limits ^{(<)}}\frac{1}{2}$, i.e., if the signal constitutes good news (bad news). Indeed, good news, $y>\frac{1}{2}$, raise a student’s potential above-average ability in the population, and this upgrade becomes stronger if the signal is more reliable, i.e., if $\theta$ is higher. Likewise, bad news, $y<\frac{1}{2}$, reduce the potential below-average ability and, again, the downgrade becomes stronger under more precise screening.

Also note that due to the Bayesian nature of our framework conditionally expected abilities are biased toward the middle, i.e., toward $E_\theta [{{\tilde{a}}}]=\frac{1}{2}$. By this, we mean that expected ability based on signals of an agent with above-average ability is less than his true ability. And expected ability of an agent with below-average ability is higher than his true ability. Formally,

$$\begin{aligned} \int ^1_0E_\theta [{{\tilde{a}}}|y]f_\theta (y|a_0)\,\text{ d }y{\mathop {\ge }\limits ^{(\le )}}a_0, \text{ if } a_0{\mathop {\le }\limits ^{(\ge )}}\frac{1}{2}. \end{aligned}$$

The above inequality can be verified easily using Eqs. (4) and (5).

In a first step, students with the highest potential are admitted to university until the university’s capacity is exhausted. Thus, since the marginal signal distribution is uniform, all students with signals larger or equal to $y_{u}:=1-U$ are admitted to university. These students accept the offer, because

$$\begin{aligned} (1+r)t_u{\mathop {\le }\limits ^{(3)}} \frac{w}{2}\le wE_\theta [{{\tilde{a}}}|y] \end{aligned}$$

(6)

for $y\ge y_u$. The income of uneducated individuals does not depend on innate ability and is normalized to zero. Recalling that r is the interest rate and w denotes the wage earned per unit of human capital, Eq. (6) says that the increase in expected wage income due to university education outweighs the tuition cost. Being risk neutral, in that case the individual opts for university education rather than remaining uneducated.

Agents who have not been admitted to university face a choice between attending college or remaining uneducated. An agent with signal $y<y_{u}$ goes to college if

$$\begin{aligned} {} w\alpha E_{\theta }[{\tilde{a}}|y]\ge (1+r)t_c \end{aligned}$$

(7)

and remains uneducated otherwise. Equation (7) says that the increase in expected wage income due to college education outweighs the tuition cost.⁸ Combining Eqs. (5) and (7), the cutoff signal, $y^\prime$, at which an agent is indifferent between attending college and abstaining from HE satisfies

$$\begin{aligned} {} \alpha w \left[ \frac{1}{2}+\frac{\theta }{6}\left( 2y^{\prime }-1\right) \right] =\left( 1+r\right) t_c~. \end{aligned}$$

(8)

Remark: dropout risk

The model outlined above does not take into account the dropout risk of students who enter HE. This is an important omission. In fact, using US data, Hendricks and Leukhina (2017) and Castex (2017) have shown that dropout risks can be substantial and vary across different institutions of HE as they tend to be correlated with school selectivity. These risks may be higher at the more selective universities, thereby affecting their relative attractiveness as compared to colleges. In our information-based framework, a higher dropout risk can have complex and ambiguous implications. Suppose, for instance, that the university (college) chooses a curriculum which requires an ability level $a_u$, or higher ($a_c$, or higher), for graduation. Failure to graduate leaves the individual uneducated and results in zero income. Higher $a_u$ (resp. $a_c$) thus implies a higher dropout risk. The expected income of a student with signal y is

$$\begin{aligned} {} \left( 1-\Gamma _\theta (a_u|y)\right) wE_\theta \left[ {{\tilde{a}}}|y,{{\tilde{a}}}\ge a_u\right] =\frac{w}{2}\left[ 1-a_u^2 +\theta (1-2y)\left( 1-a_u^2-\frac{4}{3}\left( 1-a_u^3\right) \right) \right] ,\nonumber \\ \end{aligned}$$

(9)

if he attends university, and

$$\begin{aligned} \left( 1-\Gamma _\theta (a_c|y)\right) w\alpha E_\theta [{{\tilde{a}}}|y,{{\tilde{a}}}\ge a_c]=\frac{\alpha w}{2}\left[ 1-a_c^2+\theta (1-2y)\left( 1-a_c^2-\frac{4}{3}(1-a_c^3)\right) \right] ,\nonumber \\ \end{aligned}$$

(10)

if he goes to college, where $\Gamma _\theta$ denotes the cdf of $\nu _\theta$. Observe that the difference between the expected incomes from university education in Eq. (9) and college education in Eq. (10) is not necessarily increasing in the signal. Thus, even when a student with signal $y_u$ (weakly) prefers university education over college education, this may not be true for all students with signals larger than $y_u$. A similar ambiguity applies when individuals weigh a college education against the option of remaining uneducated. This ambiguous impact of the signal on the relative attractiveness of college and university education adds massively to the complexity of our analysis. In order to preserve the tractability of our information-based framework, we are leaving a detailed analysis of dropout risks in HE and their implications for school choices and screening for future research.

2.1 The higher education sector in the short run

Throughout our analysis, we consider the size of the university sector, U, to be fixed. By contrast, capacity adjustments in the college sector are possible and occur over time, helped by the fact that employees in this sector do not hold tenured positions. Thus, the size of the college sector, C, will be endogenous in the long run. Such modeling specification seems broadly consistent with the HE systems in Israel, Germany, and several other European countries. In the short run, however, $C>0$ is also fixed. Combining Eqs. (8) and (2) and using the equilibrium condition for the college sector, $y^{\prime }=y_{c}:=y_{u}-C$ (see Fig. 2),

Fig. 2

Structure of HE sector

we obtain

$$\begin{aligned} {} \left( k_{c}-\frac{\alpha w}{1+r}\left[ \frac{1}{2}+\frac{\theta ^*}{6}(2y_{c}-1)\right] \right) (y_{u}-y_{c})=B_c. \end{aligned}$$

(11)

Equation (11) determines the equilibrium screening intensity, $\theta ^{*}$, which ensures that the capacity of the college sector is fully used. Note, however, that the range for the screening intensity is the unit interval. For $\theta$-values outside the unit interval, $f_{\theta }(y|a)$ in Eq. (4) fails to be a density. There may thus exist restrictions on the $(y_c,y_u)$-constellations of the higher education sector for which equilibrium screening is possible. The set of all constellations which are compatible with equilibrium screening is called the admissible region of the HE sector. Below we derive and illustrate graphically the admissible region for the case that (initially) the college subsidy is zero.

Admissible region ($B_c=0$)

We determine the admissible region in the absence of a college subsidy, i.e., we identify those $(y_{c},y_{u})$-combinations, $y_{c}<y_{u}$, for which an equilibrium screening intensity $\theta ^*\in [0,1]$ exists. For $B_{c}=0$ and $y_{u}>y_{c}$, Eq. (11) can be rewritten as

$$\begin{aligned} \theta ^*=\frac{6\kappa }{2y_{c}-1}~, \end{aligned}$$

(12)

where

$$\begin{aligned} {} \kappa :=\frac{(1+r)k_{c}}{\alpha w} -\frac{1}{2}~~. \end{aligned}$$

(13)

$\kappa$ is an (inverse) measure of the profitability of college education. Since abilities are uniformly distributed on the unit interval, average individual potential is equal to $\frac{1}{2}$. For a student with average potential, expected income from college education is equal to $\frac{1}{2}\alpha w$, while college tuition costs are $(1+r)k_c$. Thus, this person’s expected net return from obtaining college education is positive (negative) iff $\kappa {\mathop {<}\limits ^{(>)}}0$.

The equilibrium screening intensity in Eq. (12) is increasing (decreasing) in $\kappa$, if $y_c{\mathop {>}\limits ^{(<)}}\frac{1}{2}$. To intuitively understand this relationship, consider an agent with signal $y_c$. In equilibrium, this agent is indifferent between attending college and remaining uneducated. Now suppose that $\kappa$ increases. This will reduce the profitability of college education. Therefore, in order to keep the agent with signal $y_c$ indifferent, his potential must increase, because agents with higher potential benefit more from college education. Yet, according to Eq. (5), the agent’s potential increases with better screening if $y_c>\frac{1}{2}$, i.e., if the signal constitutes good news, and the agent’s potential increases with less screening if $y_c<\frac{1}{2}$, i.e., if the signal conveys bad news. In conclusion, an increase in $\kappa$ raises (lowers) the equilibrium screening intensity, if the cutoff signal $y_c$ is larger (smaller) than $\frac{1}{2}$ and thus indicates above (below) average potential.

In the sequel, we ignore the case $\kappa =0$ which involves some unenlightening technical difficulties. $\kappa =0$ implies $\theta ^*=0$ according to Eq. (12), i.e., equilibrium screening is uninformative. This is a very special non-generic case in which all individuals are indifferent between attending college and remaining uneducated.

We assume $0\not =\kappa \in [-\frac{1}{6},\frac{1}{6})$.⁹ For $\kappa \in [-\frac{1}{6},0)$, the admissible region

$$\begin{aligned} A(\kappa ):=\left\{ (y_c,y_u)\in [0,1]^2\big |y_c<y_u\in \big ({\textstyle \frac{1}{2}},1\big ],\theta ^*=\frac{6\kappa }{2y_c-1}\in [0,1]\right\} \end{aligned}$$

(14)

is characterized by the restrictions $y_{u}\in (\frac{1}{2},1],~y_{c}\in [0,\frac{1}{2}+3\kappa ]$ (Fig. 3).

Fig. 3

Admissible region for $\kappa \in [-\frac{1}{6},0)$

A negative value of $\kappa$ means that college education is profitable for an agent with average potential. This implies that uninformative screening, $\theta =0$, leads to excess demand for college education. Moreover, the excess demand is decreasing in $\theta$ according to Eqs. (5) and (7). For given $y_u$, therefore, the college sector must be sufficiently large, namely larger than $y_u-(\frac{1}{2}+3\kappa )$. Otherwise, the demand for college education exceeds the capacity of the college sector even at the highest possible screening intensity $\theta =1$.

For $\kappa \in (0,\frac{1}{6})$, the admissible region in Eq. (14) is characterized by the restrictions $y_{u}\in (\frac{1}{2},1]$, $y_{c}\in [\frac{1}{2}+3\kappa ,y_{u})$. This region is graphically illustrated in Fig. 4. A positive value of $\kappa$ means that agents with average potential find college education unprofitable. Thus, only agents who receive a sufficiently strong upgrade of their expected ability (potential) in the screening process will apply for college education. As a consequence, uninformative screening, $\theta =0$, leads to excess capacity of the college sector. Moreover, the excess capacity is decreasing in $\theta$ according to Eqs. (5) and (7). For given $y_u$, therefore, the college sector must be sufficiently small, namely smaller than $y_u-(\frac{1}{2}+3\kappa )$. Otherwise, the college sector exhibits excess capacity even at the highest possible screening intensity $\theta =1$.

Fig. 4

Admissible region for $\kappa \in (0,\frac{1}{6})$

College subsidy and human capital production

The screening intensity constitutes an equilibrium mechanism which ensures that the capacity of the HE sector is fully used. However, screening also affects the ability distribution of students admitted to HE and, hence, has implications for human capital production in the economy. In the sequel, we focus on this particular feature of the equilibrium screening process. More precisely, we analyze the impact of a (marginal) college subsidy on the production of human capital in the higher education sector. The subsidy may be paid with the political intent to strengthen the competitiveness of the college sector relative to the university sector. Starting out from $B_{c}=0$, we study the implications of a marginal increase in the subsidy.

Lemma 1

The subsidy affects the screening intensity according to

$$\begin{aligned} {} \frac{\text{ d }\theta ^*}{\text{ d }B_{c}}\overset{(<)}{>}~0~{ for } y_{c}\overset{(>)}{<}\frac{1}{2}~. \end{aligned}$$

(15)

Proof

See “Appendix.” $\square$

According to Lemma 1, the subsidy strengthens (weakens) the screening intensity if more (less) than half the population receives higher education. To intuitively understand this result, observe that a higher subsidy reduces the college tuition on the RHS of Eq. (8). In order to keep a student with signal $y_{c}$ indifferent between attending college and remaining uneducated, his updated expected ability must decline. For $y_{c}<\frac{1}{2}$, this happens if screening intensifies: A signal smaller than $\frac{1}{2}$ constitutes “bad news” in the sense of Milgrom (1981), which gets even worse if the signal becomes more reliable. Similarly, for $y_{c}>\frac{1}{2}$ noisier screening is needed in order to reduce expected ability.

The result in Eq. (15) can also be interpreted in terms of the bias toward the middle mechanism. Suppose, for instance, that $y_c>\frac{1}{2}$, i.e., the college is only interested in students with expected abilities sufficiently above average. The subsidy reduces tuition costs which makes college education more attractive. Due to the bias toward the middle feature, therefore, laxer testing is required in order to discourage some students from applying.

Human capital production in the university sector increases with better screening:

$$\begin{aligned} {} H^{u}:= & {} \int ^{1}_{y_{u}}E_{\theta }[{\tilde{a}}|y] \text{ d }y=\int ^{1}_{y_{u}}\left[ \frac{1}{2}+\frac{\theta }{6}(2{y}-1) \right] \text{ d }y\nonumber \\= & {} \frac{1}{2}(1-y_{u})+\frac{\theta }{6}\varphi (y_{u}), \end{aligned}$$

(16)

where

$$\begin{aligned} {} \varphi (y):=y-y^{2}\ge 0~. \end{aligned}$$

(17)

Differentiating Eq. (16) yields

$$\begin{aligned} {} \frac{\text{ d }H^{u}}{\text{ d }\theta }=\frac{\varphi (y_{u})}{6}\ge 0,\quad y_{u}\in (\textstyle \frac{1}{2},1]. \end{aligned}$$

(18)

The university accepts a mass $1-y_{u}$ of students with the best test results. Average ability and, hence, aggregate human capital of the accepted students increase if the tests become more reliable.

Human capital production in the college sector,

$$\begin{aligned} {} H^{c}:=\alpha \int ^{y_{u}}_{y_{c}}E_{_\theta }[{\tilde{a}}|y]\text{ d }y=\alpha \int ^{y_{u}}_{y_{c}}\frac{1}{2}+\frac{\theta }{6}(2y-1)\text{ d }y, \end{aligned}$$

(19)

may increase or decrease with better screening.

Lemma 2

Better screening affects human capital production in the college sector according to

$$\begin{aligned} {} \frac{\text{ d }H^{c}}{\text{ d }\theta }\left\{ \begin{array}{cc} \ge 0~; &{}\quad y_{c}\in [1-y_{u},y_{u})\\ <0~;&{}\quad y_{c}\in [0,1-y_{u})\end{array}\right. . \end{aligned}$$

(20)

Proof

See “Appendix.” $\square$

For $\kappa \in (0,\frac{1}{6})$, we have $y_{c}>1-y_{u}$ in the entire feasible region (see Fig. 4). Thus, better screening increases human capital production in the college sector according to Eq. (20). For $\kappa \in [-\frac{1}{6},0)$, the impact of better screening on college human capital production can be positive or negative in the feasible region. Better screening increases college human capital production if $y_{c}>1-y_{u}$, i.e., if the uneducated individuals outnumber the university graduates. Conversely, human capital production in the college sector declines with better screening if more students attend the university than remain uneducated (Fig. 5).

Fig. 5

Impact of screening for $\kappa \in [-\frac{1}{6},0)$

Better screening affects college human capital production through two channels. On the one hand, the college sector loses some high-ability students to the university sector when the signal reflects individual ability more reliably. At the same time, however, the college can screen the remaining applicants who were rejected by the university more effectively. The first effect decreases, and the second effect increases average ability of the college student body. The first effect increases with the capacity of the university sector, and the second effect increases with the mass of uneducated individuals. Depending on which effect dominates, better screening may have a favorable or adverse impact on college human capital production. If the mass of university students equals the mass of uneducated individuals, the two effects cancel out, thus leaving college human capital production unchanged under better screening.

Now we are ready to assess the impact of a college subsidy in the admissible region $A(\kappa ),0\not =\kappa \in [-\frac{1}{6},\frac{1}{6})$.

For $\kappa \in [-\frac{1}{6},0)$, we have $y_{c}<\frac{1}{2}$ in $A(\kappa )$. From Eq. (15), we conclude $\text{ d }\theta ^*/\text{ d }B_{c}>0$. Equations (18) and (20) then imply

$$\begin{aligned} {} \kappa \in [-{\textstyle \frac{1}{6},0)}\Longrightarrow ~~~~ \frac{\text{ d }H^{u}}{\text{ d }B_{c}}>0,\quad \frac{\text{ d }H^{c}}{\text{ d }B_{c}}\left\{ \begin{array}{ll}\ge 0~;&{}y_{c}\in [1-y_u,y_u)\\ <0;&{}y_{c}\in [0,1-y_u) \end{array} \right. ~. \end{aligned}$$

(21)

For $\kappa \in (0,\frac{1}{6})$, we have $y_{c}>\frac{1}{2}>1-y_{u}$ in $A(\kappa )$, hence $\text{ d }\theta ^*/\text{ d }B_{c}<0$ by Eq. (15). From Eqs. (18) and (20), we conclude

$$\begin{aligned} {} \kappa \in (0,{\textstyle \frac{1}{6})}\Longrightarrow ~~~~\frac{\text{ d }H^{u}}{\text{ d }B_{c}}<0,\quad \frac{\text{ d }H^{c}}{\text{ d }B_{c}}<0~. \end{aligned}$$

(22)

Even though the subsidy is financed from an outside source, it can reduce human capital production in both sectors. This happens for $\kappa \in (0,\frac{1}{6})$ where the subsidy leads to less efficient screening. Also observe that for $\kappa \in [-\frac{1}{6},0)$ the subsidy benefits the university sector and hurts the college sector in terms of human capital production if $y_{c}<1-y_{u}$, i.e., when more students attend the university than remain uneducated. This happens even though the subsidy may be paid to the college sector with the political intent to strengthen its competitiveness relative to the university sector.

The counterintuitive effect of the college subsidy for negative $\kappa$ has a straightforward and rather simple explanation: The subsidy raises the equilibrium screening intensity. Due to better screening, the college sector gains additional student potential at its lower end $y=y_c$. This positive effect is stronger the more agents remain uneducated. At the same time, however, the college sector looses student potential at its upper end $y=y_u$, because potentials are now better identified and students with the highest potentials go to university. This negative effect is stronger when the university has larger capacity. By Eq. (21), the second effect dominates the first effect if and only if the mass of university graduates exceeds the mass of uneducated agents.

We finally examine the question how the college subsidy affects total human capital production, $H:=H^u+H^c$. A marginal increase of the subsidy is desirable, iff the following criterion is satisfied:

$$\begin{aligned} {} \gamma :=\frac{w}{1+r}~\frac{\text{ d }H}{\text{ d }\theta }\bigg |_{\,\theta =\theta ^*}~\frac{\text{ d }\theta ^*}{\text{ d }B_c}>1~. \end{aligned}$$

(23)

In Eq. (23), $(1+r)$ denotes the opportunity cost of the subsidy. $\text{ d }\theta ^*/\text{ d }B_{c}$ has been determined in Eq. (15). To make use of Eq. (23), we calculate $\text{ d }H/\text{ d }\theta$:

$$\begin{aligned} H= & {} \alpha \int ^{y_{u}}_{y_{c}}E_{\theta }[{\tilde{a}}|y]\text{ d }{y}+\int ^{1}_{y_{u}}E_\theta [{\tilde{a}}|y]\text{ d }y\nonumber \\= & {} \alpha \int ^{y_{u}}_{y_{c}}\frac{1}{2}+\frac{\theta }{6}(2y-1)\text{ d }{y}+\int ^{1}_{y_u}\frac{1}{2}+\frac{\theta }{6}(2y-1)\text{ d }y{}\end{aligned}$$

(24)

$$\begin{aligned} \frac{\text{ d }H}{\text{ d }\theta }= & {} \frac{1}{6}\left[ (1-\alpha )\varphi (y_{u})+\alpha \varphi (y_{c})\right] \ge 0 {} \end{aligned}$$

(25)

Next, combine Eq. (25) with Eqs. (23) and (15) to obtain

$$\begin{aligned} {} \gamma (y_{c},y_{u})= & {} \frac{(1-\alpha )\varphi (y_{u})+\alpha \varphi (y_c)}{\alpha (1-2y_{c})(y_{u}-y_{c})}~. \end{aligned}$$

(26)

For $\kappa \in (0,\frac{1}{6})$, we have $y_{c}>\frac{1}{2}$ in the admissible region $A(\kappa )$ which implies $\gamma <0$. Hence, a college subsidy is not desirable in that case. Indeed, the subsidy reduces not only aggregate human capital, H, but also human capital production in both sectors of higher education [see Eq. (22)]. We summarize this finding in

Proposition 1

Consider a (marginal) college subsidy $\text{ d }B_c>0$. Under the criterion (23), such policy is not desirable for $\kappa \in (0,\frac{1}{6})$—i.e., when college education is unprofitable for students with below-average potential.

For $\kappa \in [-\frac{1}{6},0)$, the situation turns out to be more complex. We first state a lemma which facilitates the subsequent analysis.

Lemma 3

For any $y_{u}>\frac{1}{2}$, there exists a unique $y^*_{c}(y_u)\in [0,\frac{1}{2})$ such that $\gamma (y_{c},y_{u})\ge 1$ iff $y_{c}\ge y^*_{c}(y_u)$ .

Moreover, $y^{*}_{c}(\cdot )$ is increasing on $(\frac{1}{2},1]$ and satisfies $y^*_{c}(1)<\frac{1}{2}$.

Proof

See “Appendix.” $\square$

The above lemma implies that the subsidy region $B(\kappa )$, $\kappa \in [-\frac{1}{6},0)$, of $(y_{c},y_{u})$-constellations for which a college subsidy pays off is given by

$$\begin{aligned} B(\kappa ):=\left\{ (y_{c},y_{u})\in A(\kappa )|y_{c}\ge y_{c}^{*}(y_{u})\right\} ~. \end{aligned}$$

(27)

Fig. 6

Subsidy region for $\kappa \in [-\frac{1}{6},0)$

For negative $\kappa$, the subsidy region consists of those constellations for which the mass of uneducated individuals, $y_c$, and the mass of university students, $1-y_u$, are both sufficiently large (Fig. 6). Or, in other words, the college capacity, $y_u-y_c$, must be sufficiently small in the subsidy region. To intuitively understand this result, notice that total human capital production in the higher education sector always increases with better screening according to Eq. (25). Moreover, in the admissible region $A(\kappa )$, $\kappa \in [-\frac{1}{6},0)$, the subsidy strengthens screening according to Eq. (15). Thus, combining these two effects, the subsidy causes a gain in total human capital production via better screening. Yet, only when the subsidy-induced screening effect is sufficiently strong will this gain outweigh the cost of the subsidy. In order to jump this hurdle, a combination of sufficiently high $y_c$ (large mass of uneducated people) and low $y_{u}$ (large mass of university students) is needed, because the subsidy-induced screening effect is increasing in $y_c$ and decreasing in $y_{u}$ [see Eq. (15)].

We summarize this finding in

Proposition 2

Assume that the mass of uneducated individuals and the mass of university graduates are both sufficiently large (hence, the college capacity is sufficiently small). Consider a (marginal) college subsidy $\text{ d }B_c>0$. Under the criterion (23), such policy is desirable for $\kappa \in [-\frac{1}{6},0)$—i.e., when college education is profitable for at least some students with below-average potential.

2.2 The higher education sector in the long run

In this section, we analyze the structure of the higher education sector from a longer term perspective. The college sector receives no subsidies, $B_{c}=0$. Moreover, the capacity of the university sector remains fixed, while the college sector may adjust its capacity over time through recruitment or suspension of staff.¹⁰ The size of the college sector, C, therefore, becomes an endogenous choice variable. Under this long-term perspective, the college sector maximizes, by choice of $y_{c}$, the net value of college human capital production

$$\begin{aligned} {} \eta _{c}:=wH^{c}-(1+r)k_{c}(y_{u}-y_{c}), \end{aligned}$$

(28)

where $H^{c}$ has been defined in Eq. (19) and $\theta ^*$ satisfies Eq. (12). Differentiating $\eta _{c}$ and using Eq. (36) yields

$$\begin{aligned} {} \frac{\text{ d }\eta _{c}}{\text{ d }y_{c}}= & {} w\left[ \frac{\partial H^{c}}{\partial y_{c}}+\frac{\partial H^{c}}{\partial \theta }\bigg |_{\,\theta =\theta ^*}\frac{\text{ d }\theta ^*}{\text{ d }y_{c}}\right] +(1+r)k_{c}\nonumber \\= & {} -\frac{2\alpha w \kappa }{(2y_{c}-1)^{2}}\left[ \varphi (y_{c})-\varphi (y_{u})\right] ~ . \end{aligned}$$

(29)

We analyze the optimal college size and aggregate human capital production in the admissible regions for $\kappa \in (0,\frac{1}{6})$ and $\kappa \in [-\frac{1}{6},0)$.

$Case 1: \kappa \in (0,\frac{1}{6})$

For $\kappa$-values in this range, all $(y_{c},y_{u})$-combinations in the admissible region $A(\kappa )$ satisfy (see Figs. 4, 7)

$$\begin{aligned} {} y_{u}\ge y_{c}\ge \frac{1}{2}+3\kappa \ge \frac{1}{2}~,\quad \varphi (y_{c})\ge \varphi (y_{u})~. \end{aligned}$$

(30)

Thus, $\text{ d }\eta _{c}/\text{ d }y_{c}$ in Eq. (29) is negative and $\eta _{c}$ assumes its maximum in the admissible region at $y_{c}=\frac{1}{2}+3\kappa$, the lowest $y_{c}$-value in the admissible region $A(\kappa )$. Since the equilibrium screening intensity is decreasing in $y_{c}$ according to Eq. (12), screening is also maximal at $y_{c}=\frac{1}{2}+3\kappa$, i.e., $\theta ^*=1$ . Therefore, the net value of university human capital production

$$\begin{aligned} {} \eta _{u}:=wH^{u}-(1+r)k_u(1-y_{u}) \end{aligned}$$

(31)

and, hence, the net value of total human capital production

$$\begin{aligned} {} \eta :=\eta _{c}+\eta _{u} \end{aligned}$$

(32)

are maximal at $y_{c}=\frac{1}{2}+3\kappa$. We summarize these findings in

Proposition 3

For $\kappa \in (0,\frac{1}{6})$, the net value of total human capital production and the net value of human capital production in the college sector and in the university sector are all maximal in the admissible region $A(\kappa )$ for $y_{c}=\frac{1}{2}+3\kappa$. The optimal college size is $y_{u}-\frac{1}{2}-3\kappa$, and the equilibrium screening intensity at the optimum is $\theta ^*=1$.

$Case 2: \kappa \in [-\frac{1}{6}, 0)$

For $\kappa$-values in this range, the admissible $(y_{c},y_{u})$-combinations satisfy (see Figs. 3, 7)

$$\begin{aligned} {} y_{c}\le \frac{1}{2}+3\kappa<\frac{1}{2},~\varphi (y_{c})\overset{(<)}{>}\varphi (y_{u})~\text { for }~ y_{c}\overset{(<)}{>}1-y_{u}. \end{aligned}$$

(33)

Moreover, the equilibrium screening intensity is increasing in $y_{c}$ according to Eq. (12). Combining Eqs. (29) and (33), we get

$$\begin{aligned} {} \frac{\text{ d }\eta _{c}}{\text{ d }y_{c}}\overset{(<)}{>}0~\text { for }~y_{c}\overset{(<)}{>}(1-y_{u}),~~(y_{c},y_{u})\in A(\kappa ). \end{aligned}$$

(34)

Thus, in the admissible region $A(\kappa ),~\eta _{c}$ assumes its unique (interior) minimum at $y_{c}=1-y_{u}$ and its maximum in one of the two boundary points $y_{c}=0$ or $y_{c}=\frac{1}{2}+3\kappa$. To determine the maximum, we analyze the difference between $\eta _{c}(y_{c}=0)$ and $\eta _{c}(y_{c}=\frac{1}{2}+3\kappa )$. Define

$$\begin{aligned} {} \Phi (\kappa ):=\eta _{c}(0)-\eta _{c}(\textstyle \frac{1}{2}+3\kappa ). \end{aligned}$$

(35)

For given $\kappa \in [-\frac{1}{6},0)$, the college sector chooses $y_{c}=0$ if $\Phi (\kappa )>0$, and $y_{c}=\frac{1}{2}+3\kappa$ if $\Phi (\kappa )<0$.

Lemma 4

There exists a unique $\kappa ^{*} \in (-\frac{1}{6},0)$ such that $\Phi (\kappa )\overset{(\le )}{\ge }0$ for $\kappa \overset{(\ge )}{\le }\kappa ^{*},$ $\kappa \in [-\frac{1}{6},0)$.

Proof

See “Appendix.” $\square$

Lemma 4 implies that the result stated in Proposition 3 can be extended to the range $0\not =\kappa \in [\kappa ^{*},\frac{1}{6})$: For $\kappa \ge \kappa ^{*}$, the optimal college size in the admissible region, $A(\kappa )$, is $y_u-\frac{1}{2}-3\kappa$ and the equilibrium screening intensity is maximal, i.e., $\theta ^*=1$. In particular, the decision $y_{c}=\frac{1}{2}+3\kappa$ taken by the college sector maximizes not only the net value of college human capital production but also the net value of university human capital production. For $\kappa <\kappa ^*$, Lemma 4 implies $y_c=0$, i.e., the college sector expands to its maximum size, and Eq. (12) yields $\theta ^*=-6\kappa$. We summarize our finding in

Proposition 4

For $\kappa \in [\kappa ^{*},\frac{1}{6})$, the college sector chooses $y_{c}=\frac{1}{2}+3\kappa$. The implied college size, $y_{u}-\frac{1}{2}-3\kappa$, maximizes the net values of human capital production in both sectors and is therefore optimal for the whole economy in the admissible region $A(\kappa )$. For $\kappa <\kappa ^{*}$, the college sector expands to maximum size absorbing all individuals who are rejected by the university, i.e., $y_{c}=0$ and $\theta ^*=-6\kappa$.

If $\kappa <\kappa ^{*}$, the decision taken by the college sector no longer maximizes the net value of university human capital production. Indeed, it minimizes this value, because the decision $y_c=0$ leads to the lowest possible screening intensity $\theta ^*=-6\kappa$. The efficiency property of equilibria with $\kappa \ge \kappa ^*$ stated in Proposition 4 may therefore break down in situations where $\kappa <\kappa ^*$ holds. Our next proposition shows that this is in fact the case.

Proposition 5

For $\kappa \in [-\frac{1}{6},\kappa ^*)$, the long-run equilibrium of the higher education sector is inefficient.

Proof

See “Appendix.” $\square$

By marginally raising $y_c$ above zero and, thus, reducing the capacity of the college sector, a social planner can increase net total human capital production in the HE sector. This can be achieved without interference into the equilibrium screening mechanism. With $\kappa <0$, a smaller college sector induces two effects: The first effect is a reduction in net college human capital production according to Eq. (29) and Fig. 7, and the second effect consists of a higher screening intensity $\theta ^*$. Better screening leads to higher (net) total human capital production according to Eq. (25). The second effect is dominant, if and only if $\kappa <\kappa ^*$, i.e., when the cost of college education is very low. In that case, the college sector admits too many students, thereby establishing inefficiently low screening standards which adversely affect human capital production in the university sector.

In conclusion: as a main takeaway of our analysis, we note that the profitability of college education is a critical factor determining the efficiency properties of equilibria in the short and long run. Both short-run equilibria and long-run equilibria tend to be inefficient if college education is highly profitable (propositions 2 and 5). In the short term, such inefficiency can be mitigated through a college subsidy. In the long term, lower profitability of college education (higher tuition cost) may restore efficiency through higher equilibrium screening standards.

3 Conclusion

We have developed the model of a higher education (HE) system which allocates a diverse student population between private colleges and public (research) universities. Colleges are at a double disadvantage in comparison with universities. First, they employ educational technologies which are inferior to those of universities. And second, colleges must self-finance through tuition fees, while universities receive public subsidies. On the other hand, colleges are more flexible than universities in adapting enrollment capacities over time. Applicants to HE are screened for their unobservable abilities. Students with sufficiently high potentials are admitted to university; all others are rejected, but may still apply for college admission. These specifications, we believe, capture some essential characteristics of the HE systems in Israel and throughout much of Europe.

The university sector thus absorbs the students with the highest potentials which strengthens the human capital production process there. Yet, how large this advantage depends on the intensity of screening in the admission process. And the screening intensity is endogenous in our model as it balances the demand and supply of educational services. The processes of human capital production at universities and colleges therefore interact through the equilibrium intensity of screening in admission to HE.

We have identified the “admissible region” which is the set of all short-term capacity constellations of universities and colleges for which screening in admission to HE functions as an equilibrium mechanism. In this region, college subsidies are likely to be counterproductive as they weaken, in most cases, the process of human capital production in HE.¹¹ In the long term when the college size is endogenous, inefficiently low equilibrium screening standards in HE may prompt the college sector to admit too many students, thereby causing efficiency losses for the economy. This result seems broadly consistent with the empirical phenomenon of college expansion in Israel and in much of Europe since the beginning of the 1990s.

The most salient characteristic which distinguishes our model from the existing literature is the screening mechanism in the admission process to HE. The screening intensity, rather than prices such as the level of tuition fees, functions as an equilibrium mechanism which ensures that the capacities in HE are fully used. Thus, colleges and universities become choosier, or less choosy, when the demand for HE changes. While this specification of the equilibrium mechanism in HE is novel and may be debatable, we do believe that it constitutes a reasonably realistic feature of our model.

Appendix

In this “Appendix,” we prove lemmas 1–4 and Proposition 5.

Proof of Lemma 1

Differentiating Eq. (11) yields

$$\begin{aligned} \frac{\text{ d }\theta ^*}{\text{ d }B_{c}}=\frac{1}{\frac{\alpha w(1-2y_{c})}{6(1+r)}(y_{u}-y_{c})}~, \end{aligned}$$

from which the claim in the lemma follows immediately. $\square$

Proof of Lemma 2

Differentiating Eq. (19), we obtain

$$\begin{aligned} \frac{\text{ d }H^{c}}{\text{ d }\theta }=\frac{\alpha }{6}\left[ \varphi (y_{c})-\varphi (y_{u})\right] . \end{aligned}$$

(36)

$\varphi :[0,1]\rightarrow [0,\frac{1}{4}]$ has been defined in Eq. (17). It is a strictly concave function that satisfies

$$\begin{aligned} \varphi (y)=\varphi (1-y),\quad y\in [0,1]~. \end{aligned}$$

(37)

Fig. 7

$\varphi$ strictly concave and symmetric around $y=\frac{1}{2}$

Equations (36) and (37) in combination with Fig. 7 imply the claim in the lemma. $\square$

Proof of Lemma 3

Define $y^*_{c}(y_{u}):={\text {inf }}\{y_{c}\in [0,\frac{1}{2})|\gamma (y_{c},y_{u})\ge 1 \}$. Note that $y_{c}^{*}(y_{u})$ is well defined since $\underset{y_{c}\rightarrow \frac{1}{2}}{\lim }\gamma (y_{c},y_{u})=\infty ,y_{u}\in (\frac{1}{2},1]$. Since $\gamma (y_{c},y_u)$ is strictly increasing in $y_c$ and strictly decreasing in $y_{u}$ for $(y_{c},y_{u})\in [0,\frac{1}{2}) \times (\frac{1}{2},1]$, the properties claimed in the lemma follow immediately. $\square$

Proof of Lemma 4

Using Eqs. (12) and (19) in Eq. (28) we find

$$\begin{aligned} \eta _{c}(0)= & {} -\alpha w\kappa y_{u}^{2} \end{aligned}$$

(38)

$$\begin{aligned} \eta _{c}\left( \textstyle \frac{1}{2}+3\kappa \right)= & {} -\alpha w \kappa \left( y_{u}-{\textstyle \frac{1}{2}}-3\kappa \right) -\frac{\alpha w}{6}\int ^{y_{u}}_{\frac{1}{2}+3\kappa }(1-2y)\text{ d }y \end{aligned}$$

(39)

Substituting Eqs. (38) and (39) into Eq. (35) yields after some rearrangements

$$\begin{aligned} {} \frac{6}{\alpha w}\Phi (\kappa )= & {} (y_{u}-y_{u}^{2}-{\textstyle \frac{1}{2}})(1-6\kappa )+\frac{1}{4}-9\kappa ^{2}~. \end{aligned}$$

(40)

Fig. 8

Curvature of $\Phi$-function

The RHS of Eq. (40) is strictly increasing in $\kappa$ for $\kappa =-\frac{1}{6}$ and strictly concave for $\kappa \in [-\frac{1}{6},0)$. Moreover, direct substitution into Eq. (40) yields $\frac{6}{\alpha w}\Phi (-\frac{1}{6})=0$ and $\frac{6}{\alpha w}\Phi (0)<0.$ The claim in the lemma now follows immediately from the curvature in the graph of Fig. 8. $\square$

Proof of Proposition 5

We show that under the restriction of the proposition the net value of human capital production in higher education, $\eta =\eta _{c}+\eta _{u}$, is not maximal in the long-run equilibrium. For $\kappa \in [-\frac{1}{6},\kappa ^{*})$, the college sector chooses $y_{c}=0$ according to Proposition 4. We prove the proposition by showing that $\partial \eta /\partial y_{c}|_{y_{c}=0}>0$.

Using Eqs. (12), (16), (19), (28), (31), (32), we calculate $\eta$ as

$$\begin{aligned} \eta= & {} \eta _{c}+\eta _u=wH^{c}-(1+r)k_{c}(y_{u}-y_{c})+wH^{u}-(1+r)k_u(1-y_{u})\\= & {} \alpha w \left[ \frac{y_{u}-y_{c}}{2}-\frac{\kappa [\varphi (y_{u})-\varphi (y_{c})]}{2y_{c}-1}\right] +w\left[ \frac{1-y_{u}}{2}+\frac{\kappa \varphi (y_{u})}{2y_{c}-1}\right] \\- & {} (1+r)\left[ k_{c}(y_{u}-y_{c})+k_u(1-y_{u})\right] . \end{aligned}$$

Differentiating $\eta$ with respect to $y_{c}$, we obtain after some rearrangements

$$\begin{aligned} \frac{\partial \eta }{\partial y_{c}}\bigg |_{\,y_{c}=0}=2w \kappa \varphi (y_{u})(\alpha -1). \end{aligned}$$

(41)

Since $\kappa <0$ and $\alpha <1$, the expression in (41) is positive. $\square$