Motivating informed decisions

Abstract

This paper studies a principal-agent model where a risk-neutral principal delegates to a risk-neutral agent the decision of whether to pursue a risky project or a safe one. The return from the risky project is unknown and the agent can acquire costly unobservable information about it before taking the decision. The problem has features of moral hazard and hidden information since the acquisition of information and its content is unobservable to the principal. The optimal contract suggests that the principal should only reward the agent for outcomes that are significantly better than the safe return. It is also optimal to distort the project choice in favor of the risky one as a mechanism to induce the direct revelation of the uncertain state. In a managerial context, the findings explain why options induce better decision-making from CEOs, as well as why excessive risk taking might be optimal.

1 Introduction

It has been suggested that option-type contracts cause excessive risk taking from CEOs and that such risk taking is misaligned with shareholders interests (see, for example, Dong et al. 2010). On the other hand, Low (2009) shows that after an exogenous increase in takeover protection, CEOs lowered the firm risk. Since this risk reduction decreased the value of the firm, firms responded by providing managers with incentives to increase risk taking through equity-based compensation. This paper seeks to contribute to the debate from a theoretical point of view. We propose a model of delegated expertise to explain why stock options are optimal forms of compensation when a CEO has to be motivated to take informed decisions. It also provides an explanation of why excessive risk taking is optimal from a shareholder perspective, where excessive risk taking is understood here as pursuing a risky project even though it is ex-ante inefficient.

In the proposed model, a principal can hire an agent to decide between a risky project and a safe project. Before taking the decision, the agent can acquire information about the risky project by exerting costly effort. However, both the effort and the acquired information are unobservable to the principal. Hence, this framework shares features of moral hazard and hidden information, and incentives must be used to motivate both information acquisition and the (partial) revelation of the obtained information.

Incentives in this scenario are potentially different than the ones in standard moral hazard problems since effort does not generate greater expected returns directly. In contrast, the unobservable action taken by the agent generates a privately observed signal that improves the decision-making. The studied setup is quite general, and the only restriction imposed is that signals can be ordered in the likelihood ratio order (Milgrom 1981). Under risk neutrality, limited liability and payoff monotonicity for the principal, optimal wages are option-like with a strike price greater than the safe return. Moreover, it is optimal to distort the project choice in favor of the risky project as a strategy to reveal the uncertainty directly.

The intuition why the contract rewards the agent only for extreme good outcomes has two components whose main instrument is the probability of adopting the risky project given the observed return. The first one is a likelihood ratio that unravels the moral hazard concerns. It suggests that we should reward the agent when the probability of choosing the risky project was greater when effort was exerted rather than when no information was acquired. Since such probability is increasing in the risky return when effort was exerted and constant when that was not the case, the moral hazard incentives must be monotone increasing.

There is a second component associated with the hidden information problem and is summarized by a hazard rate. The principal must provide incentives for the agent to choose the risky project whenever he observes a sufficiently high signal. Since the distribution of signals is assumed to be continuous, there exists a unique cutoff signal where an agent is indifferent between the safe project and the risky project. Higher signals will induce the choice of the risky project. This implies that, in the limit, the principal wants to penalize agents that chose the risky project when the cutoff signal was observed. Given the ordering of the signals, the probability of being at the cutoff signal given that the risky project was chosen (the hazard rate) is decreasing in the risky return. Therefore, this effect also suggests that compensation should be increasing in the risky return.

The intuition for the project choice distortion relies on the idea that the principal has two mechanisms to induce the revelation of the unknown return. The first one is through risky wages as discussed before. The second one is through the safe wage, which is equivalent to picking the cutoff signal. Instead of paying the agent more to reveal the uncertainty imperfectly (the signal), the principal can also decrease the safe wage to induce the choice of the risky project and have the uncertainty revealed directly.

The model applies to a variety of situations. The model is tightly connected to the optimal compensation of CEOs who must be motivated by the shareholders to undertake risky projects that could potentially lead to higher returns. In this scenario, the effort exerted by the CEO in learning about the portfolio of projects, and the learned information, is usually never observed by the shareholders, only the project chosen and the realized returns are observed. In this environment, the optimal contract can be implemented using an option with strike price greater than the return of the safe project.

The conclusions derived from the model explain why options and restricted stock are so widely used in this context. It also suggests that it is the best form of compensation to align the interests of shareholders and CEOs. Moreover, the optimal distortion on the project choice suggests that it is on the shareholders interest to have a CEO taking excessive risks. Letting a CEO pursue risky projects that are not ex-ante profitable would help the shareholders to ameliorate the information problems.

The model also represents the strategic interaction between a principal and an expert, e.g., a consultant. The paper shows, by means of the revelation principle, that the solution to the delegation problem is equivalent to the solution to a problem where an agent suggests a project to the principal, and the principal follows such suggestion. Again, the effort exerted and the gathered information are privately observed by the consultant; thus, the firm seeking advice must design a contract that motivates effort and the (partial) revelation of the information. In line with the predictions of our model, it has been observed that start-ups use stock options to pay consultants when they face liquidity constraints (akin to limited liability).¹

The acquisition of information in a principal-agent environment has been studied by Manso (2011), who relies on a bandit framework. In this context, an agent can learn about the return of a project by undertaking it; however, this learning structure implies that signals are perfectly informative and are observable, which is not the case in our paper. Interestingly, his result of “tolerance for early failure” is connected to the project choice distortion found here, since the principal encourages the agent to choose the risky project even though is ex-ante inefficient. Chade and Kovrijnykh (2011) also study the motivation of information acquisition when the acquired information is also observable, whereas Rosenberg et al. (2007), Hopenhayn and Squintani (2011), and Murto and Valimaki (2011) study problems where actions chosen by agents are observed and outcomes are unobserved.

Our analysis uses a so-called delegated expertise model. These models were first proposed by Lambert (1986), who used a environment with two possible risky outcomes and a risk averse agent. He focuses on characterizing optimal distortions of project selection, but is unable to characterize its interaction with optimal wages given the simplified environment. Similar models were later developed as in Demski and Sappington (1987), Feess and Walzl (2004) and Gromb and Martimort (2007). These papers are concerned on how to implement efficient choices using payments contingent on such discrete returns. Zermeno (2012) also uses a similar model with a binary state and characterizes optimal distortions with menu contracts and without them. In contrast, we allow for a continuum of outcomes and signals, which permits a complete characterization of optimal contracts and the project choice distortion. Moreover, instead of imposing the mechanism, we characterize the optimal one, thus generalizing his results.

Malcomson (2009) allows for a continuum of outcomes, a continuum of decisions, and risk aversion. He characterizes situations where there are optimal distortions from the efficient decision as a mechanism to encourage more information acquisition given a wage schedule. However, he does not characterize optimal wages and it is not concerned about information revelation since these only depend on the final return. The information structure used in this paper is also similar to the one used in Szalay (2009) and Persico (2000). However, the first model is used in a procurement environment where the acquired information is induced to be completely revealed; this is not the case in this paper. In the second one, the agents acquire information to learn about their value for an object, not the value for a principal as in our model.

The optimal contract obtained here is also obtained under other setups. In particular, our analysis yields the same debt contract found by Innes (1990) and Poblete and Spulber (2012) in a principal-agent scenario. However, in their setup, the principal is willing to pay the agent for high outcomes for the standard moral hazard argument where more effort increases directly the probability of higher outcomes. Here, the returns are determined ex-ante, but are unknown; thus, effort cannot directly increase the expected returns. A debt contract is also commonly obtained under financial contracting where the agent has private information over the final return (see Hellwig 2001). On the other hand, the overinvestment result on risky projects also arises in models where there are career concerns, and the agent has private information over her ability, see Chen (2015) for the closest case and for a review of similar papers. However, in these models the agent cares about the return and the signal about the project is costless.

The next section introduces the setup, the third section solves for the first best, while the fourth section solves for the optimal contract when moral hazard and hidden knowledge exist. The fifth section evaluates extensions to the model such as risk aversion and explains the role of the monotone payoffs to the principal. The next section discusses how to implement the contract and the empirical evidence that supports our results. In the last section, we conclude.

2 Setup

Consider the problem where a risk-neutral principal (she) can delegate to a risk-neutral agent (he) the decision of whether to pursue a safe project with known returns or a risky project with unknown returns.² Before taking the decision, the agent can acquire information about the risky project by exerting costly effort. The effort and the information gathered by the agent (if any) are unobservable to the principal. The only observable variable is the final return. Therefore, the optimal contract designed by the principal must induce effort and the (partial) revelation of the information using the observed return.

It is assumed that the agent has limited liability and that payments for the principal must be monotone nondecreasing as in Innes (1990).³ The latter assumption is somehow natural since the principal is the owner of the project and may observe the returns before the agent. Thus, if her payoff is not monotone, she will have an incentive to sabotage profits once the return has been observed.⁴ We explore in Sect. 5.2 the role of such monotonicity in the results.

We assume the two available projects cannot be pursued simultaneously. The safe project has a known net return $y_{s}\in \left( 0,1\right)$.⁵ The risky one has an unknown return $y_{r}\in \left[ 0,1\right]$. Let both individuals have the same nondegenerate prior belief $g\left( y_r \right)$ over the unknown return with finite mean $\mu _{0}$.

Before taking the decision, the agent can exert effort and generate information about the risky project by acquiring a signal $x\in \mathbb {R}$ at a cost c. This cost can be associated with the cost of running trials or the disutility of effort. In a context of bandit problems, where signals are the same returns of the risky project, the fixed cost can also be thought as the ex-ante expected return of the risky project, $\mu _0$, and reflects the fact that individuals are initially pessimistic about it (as in Manso 2011). The agent can also shirk, in which case no signal is generated and there will be no cost.

Let the conditional pdf and cdf of the signal x be denoted by $f\left( x|y_r\right)$ and $F\left( x|y_r\right)$, respectively. Assume these are differentiable with respect to x. Similarly, the unconditional pdf and cdf will be denoted by $f\left( x\right)$ and $F\left( x\right)$, respectively. Let the signals be ordered in the likelihood ratio sense: A signal x is more favorable than signal $x'$ if the posterior distribution $g\left( y_r|x\right)$ first order stochastically dominates the posterior distribution $g\left( y_r|x'\right)$.⁶ These type of problems are known as monotone ones and were first studied by Karlin and Rubin (1956). Since signals are ordered, the posterior mean will be a monotone increasing transformation of the signal. Thus, the distribution of the posterior mean will be a transformation of the distribution of the signal. Without loss of generality, let $x\equiv \mathbb {E}_{y_r}\left[ y_{r}|x \right] \$ be the posterior mean of the risky project. Hence, the support of x is $\left[ 0,1\right]$.⁷

The acquisition of the signal and its content is privately known by the agent. The only observable variable for the principal is the final return of the chosen project $y_s$ or $y_r$. Following the revelation principle, instead of designing an indirect mechanism where the agent chooses the project and the principal commits to pay a wage conditional on such choice and the observed return, a principal can use a direct mechanism where the agent reports truthfully its private information and the principal chooses the project and the wage to be paid to the agent.

The most general contract in this context, $w\left( \hat{x},y\right)$, is a function of the observed returns y and the reported signal $\hat{x}$. Given that a project j is chosen, a signal has been reported and a return is realized, the payoff for the principal is given by $y_{j}-w\left( \hat{x},y_{j}\right)$ and the payoff for an agent who acquired information is $w\left( \hat{x},y_{j}\right) -c$. It will be assumed that the agent has a limited liability constraint, and that payments for the principal must be monotone nondecreasing:

$$\begin{aligned} 0\le w\left( \hat{x},y_{j}\right) \text {for all}\quad \hat{x}, y_j\;\hbox {and}\;j=r,s \end{aligned}$$

(LL)

$$\begin{aligned} \frac{\partial w\left( \hat{x},y_{j}\right) }{\partial y_j}\le 1 \text { for all}\quad \hat{x}, y_j\;\hbox {and}\;j=r,s \end{aligned}$$

(Mon)

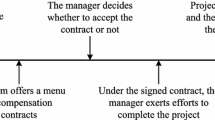
The direct mechanism game consists of three stages. In the first stage, the principal designs a payment schedule and makes a take it or leave it offer to the agent. The agent accepts or rejects the contract. If she accepts the contract, she decides whether to acquire or not a signal, which is privately observed by her. In the second stage, the agent will report a signal $\hat{x}$, and the principal will update her beliefs and choose a project j to pursue. In the third stage, a return y is realized and the principal pays to the agent the contracted wage $w_j\left( \hat{x},y\right)$.

3 First best

As a benchmark, we will first focus on the case where there are no information asymmetries. We will assume that the effort exerted by the agent to acquire a signal is observed, as well as the content of the acquired information. Since the acquired information by the agent is observed by the principal, we have that $w\left( \hat{x},y\right) =w\left( x,y\right)$. If the principal decides to hire the agent, she will face the following problem:

$$\begin{aligned} \max _{w\left( x,y_{r}\right) ,w\left( x,y_{s}\right) }\mathbb {E}_{x}\left[ \max _{j\left( x\right) \in \left\{ s,r\right\} }\mathbb {E}_{y_{j\left( x\right) }}\left[ y_{j\left( x\right) }-w\left( x,y_{j\left( x\right) }\right) |x\right] \right] \end{aligned}$$

$$\begin{aligned} \text {s.t } \mathbb {E}_{x}\left[ \mathbb {E}_{y_{j\left( x\right) }}\left[ w\left( x,y_{j\left( x\right) }\right) |x \right] \right] -c\ge \underline{u} \end{aligned}$$

(IR)

where $j\left( x\right)$ is the project chosen when x is realized. The constraint (IR) assures the agent will accept the contract by making sure his expected utility is greater than or equal to an outside option $\underline{u}$. The first best can be obtained by a constant payment from the principal to the agent that covers his cost and his outside option, $w\left( x,y_{j\left( x\right) }\right) =c+\underline{u}$ for all ${x},y\in \left[ 0,1\right]$. This optimal wage leads us to the following maximization problem when the agent is hired:

$$\begin{aligned} \mathbb {E}_{x}\left[ \max _{j\left( x\right) \in \left\{ s,r\right\} }\mathbb {E}_{y_{j\left( x\right) }}\left[ y_{j\left( x\right) }|x \right] \right] -c-\underline{u} \end{aligned}$$

Since there are two stages, we proceed to solve the individual’s problem using backward induction. That is, I will first determine which project is going to be chosen given the information acquired. Then, I will characterize when the principal decides to hire an agent as a function of $y_s$ and c.

In the last stage, the principal will choose the risky project if $x>y_s$; thus, the payoff of the second period is given by $\max \left\{ x;y_s\right\}$. Note this is a convex function of x, see Fig. 1. Going one stage backward, the value of experimentation is defined as the ex-ante expectation of the utility in the second stage: $U\left( y_s\right) =\mathbb {E}_{x}\left[ \max \left\{ x;y_s\right\} \right]$.

Fig. 1

Utility in second period

Lemma 1

The value of experimentation $U\left( y_s\right)$ is strictly increasing and convex in $y_s$, and strictly greater than $\max \left\{ \mu _0; y_s\right\}$.

The result states that information is always valuable in this setup. However, since information is costly, the principal may not want to hire the agent to acquire information. At the beginning of the first period, a principal will choose to hire an agent if and only if $c\le \hat{c}$, where $\hat{c}$ is defined by

$$\begin{aligned} U\left( \mu _0\right) - \hat{c}-\underline{u} =\mu _{0} \end{aligned}$$

(1)

Let the maximized objective function of the principal be denoted by $V\left( y_s,c\right) =\max \left\{ U\left( y_s\right) -c-\underline{u}; y_s;\mu _{0}\right\}$. This function is also strictly increasing and convex in $y_s$. The next proposition characterizes when the principal decides to hire an agent as a function of $y_s$.

Lemma 2

The principal decides to hire the agent when $y_s\in \left( a_c,b_c\right) \subseteq \left( 0,1\right)$, where $\mu _0\in \left( a_c,b_c\right)$. Moreover, such interval is decreasing in c, that is $\left( a_c,b_c\right) \subset \left( a_{c'},b_{c'}\right)$ for any $c'<c<\hat{c}$, with $\left( a_0,b_0\right) =\left( 0,1\right)$ and $a_{\hat{c}}=\mu _0=b_{\hat{c}}$.

Even if beliefs are relatively pessimistic, the individual decides to acquire information because of the potential gain represented by the value of experimentation. The lower is the fixed cost c, the greater is the interval over which the principal decides to hire the agent. Furthermore, if there is no fixed cost, the principal will always decide to hire an agent to collect information.

4 Constrained efficiency

Now suppose the principal does not observe the effort of the agent, nor the information gathered by the individual. In this context, a fixed wage will not induce any effort from the agent. Therefore, the principal must provide incentives to the agent by imposing more risk in her payoff, and by distorting the choice of the best project. This distortion indicates that the first best will never be attained.

4.1 Optimal contract

The constrained efficient problem for a principal who decides to hire an agent is the following:

$$\begin{aligned} \max _{w\left( \hat{x},y_{r}\right) ,w\left( \hat{x},y_{s}\right) }\mathbb {E}_{x}\left[ \max _{j\left( x\right) \in \left\{ s,r\right\} }\mathbb {E}_{y_{j\left( x\right) }}\left[ y_{j\left( x\right) }-w\left( \hat{x},y_{j\left( x\right) }\right) |x \right] \right] \end{aligned}$$

(P)

$$\begin{aligned} \hbox {subject\;to} \end{aligned}$$

$$\begin{aligned} \mathbb {E}_{x}\left[ \mathbb {E}_{y_{j\left( x\right) }}\left[ w\left( \hat{x},y_{j\left( x\right) }\right) |x \right] \right] -c\ge \max _{j\in \left\{ s,r\right\} }\left\{ \mathbb {E}_{y_j}\left[ w\left( \hat{x},y_{j}\right) \right] \right\} \text {for all}~~\hat{x} \end{aligned}$$

(IC1)

$$\begin{aligned} x=\arg \max _{\hat{x}\in \left[ 0,1\right] }\mathbb {E}_{y_{j\left( \hat{x}\right) }}\left[ w\left( \hat{x},y_{j\left( \hat{x}\right) }\right) |x \right] \text {for all}~~x \end{aligned}$$

(IC2)

(IR), (LL) and (Mon)

Equation (IC1) is the incentive compatibility constraint that ensures the agent will exert effort. It states that the agent’s utility when he exerts effort is greater than the expected utility when he does not, in which case he picks the project that gives her the greatest ex-ante expected wage. Equation (IC2) is another incentive compatibility constraint to make sure the agent reports truthfully the information he gathered.

This problem is hard to solve because the second incentive compatibility constraint involves a continuum of restrictions for each possible realization of the signal. Nevertheless, it is shown in the next lemma that optimal wages are not a function of the reported signal, and they are just a function of the suggested project by the signal and the observed return.

Lemma 3

The optimal wage schedule $w\left( \hat{x},y_{j}\right)$ is not a function of the reported $\hat{x}$ and thus can be simplified to $w\left( y_{r}\right)$ and $w\left( y_{s}\right) =w_s$.

Since the reported signal is used by the principal to choose a project, all signals suggesting the same project create the same value for the principal. Therefore, in order to avoid unnecessary rents to be paid to the agent, the principal will only make the contract contingent on the chosen project (not the reported signal) and the return. In other words, instead of providing incentives for the agent to report truthfully the realization of the signal, the principal must provide incentives to the agents to report truthfully which project to choose. This is the reason why the optimal solution to the problem of delegating the decision to an agent with private information is equivalent to the optimal solution to a problem where the agent with private information suggests the principal which project to choose. Constraint (IC2) can thus be replaced by:

$$\begin{aligned} \mathbb {E}_{y_{j\left( x\right) }}\left[ w\left( y_{j\left( x\right) }\right) |x \right] \ge \mathbb {E}_{y_{-j\left( x\right) }}\left[ w\left( y_{-j\left( x\right) }\right) |x \right] \text {for all}~~x, \end{aligned}$$

(2)

where $-j\left( x\right)$ denotes the project not preferred by the principal given realized signal x. Equation (2) implies that such constraint is binding only when the agent is indifferent between the two projects. It is still a complex problem since this could potentially happen for several values of x. The next lemma establishes that indifference only happens for a unique signal and that the decision problem is monotone nondecreasing.

Lemma 4

If the agent is hired, then there exists a threshold $x_e\in \left( 0,1\right)$ such that the principal (and the agent) is indifferent between the safe project and the risky project; moreover, for any $x>(<)x_e$ the risky (safe) is weakly preferred.

Therefore, at signal $x_e$ the expected wage when the risky project is chosen is equal to the safe wage. Formally, there exists a unique cutoff $x_e$ such that:

$$\begin{aligned} \int _0^{1} w\left( y_{r}\right) g\left( y_r|x_e\right) \mathrm{d}y_r= w_s \end{aligned}$$

Any more (less) favorable signal than $x_e$ implies the agent will choose the risky (safe) project and that constraint (2) will not be binding. Therefore, by choosing $w\left( y_r\right)$ and $w_s$, the principal is implicitly defining $x_e$. However, this also implies that by choosing $w\left( y_r\right)$ and $x_e$, the principal is implicitly defining $w_s$. Hence, we assume from now on that the principal chooses the latter approach to provide more intuition on the solution. Using the indifference condition, the ex-ante agent’s utility can be rewritten as:

$$\begin{aligned} \int _{x_e}^{1}\int _0^{1}w\left( y_{r}\right) f\left( x|y_r\right) g\left( y_r\right) \mathrm{d}y_rdx +w_sF\left( x_e\right) -c \end{aligned}$$

By integrating the possible signal values when they are higher than the cutoff, we obtain the relevant object to provide incentives: $1-F\left( x_e|y_r\right)$. This is the conditional probability that the agent chose the risky project when he exerted effort, given the observed outcome. The problem can be reexpressed as:

$$\begin{aligned} \max _{w\left( y_{r}\right) ,x_e}\int _{0}^{1} \left( y_{r}-w\left( y_{r}\right) \right) \left( 1-F\left( x_e|y_r\right) \right) g\left( y_r\right) \mathrm{d}y_r +\left( y_s-w_s\right) F\left( x_e\right) \end{aligned}$$

(P*)

$$\begin{aligned} \hbox {subject\;to} \end{aligned}$$

$$\begin{aligned} \int _0^{1}w\left( y_{r}\right) \left( 1-F\left( x_e|y_r\right) \right) g\left( y_r\right) \mathrm{d}y_r +w_sF\left( x_e\right) -c\ge \underline{u} \end{aligned}$$

(IR*)

$$\begin{aligned} \int _0^{1}w\left( y_{r}\right) \left( 1-F\left( x_e|y_r\right) \right) g\left( y_r\right) \mathrm{d}y_r +w_sF\left( x_e\right) -c\ge \max \left\{ \mathbb {E}_{y}\left[ w\left( y_{r}\right) \right] ,w_s\right\} \end{aligned}$$

(IC1*)

$$\begin{aligned} \int _0^{1} w\left( y_{r}\right) \frac{f\left( x_e|y_r\right) g\left( y_r\right) }{f\left( x_e\right) }\mathrm{d}y_r= w_s \end{aligned}$$

(IC2*)

$$\begin{aligned} 0\le w\left( y_{j}\right) \text {for all} y_j\;\hbox {and}\; j=r,s \end{aligned}$$

(LL)

$$\begin{aligned} w^{\prime }\left( y_{r}\right) \le 1 \quad \text { for all}\quad y_r \end{aligned}$$

(Mon)

Let $\lambda$, $\delta _r$, $\delta _s$, and $\phi$ be the Lagrange multipliers for the first three constraints. The distinction between $\delta _r$ and $\delta _s$ arises because the expected wage from the risky project does not need to be necessarily equal to the safe wage. Since the problem is linear on the wages, the optimal wages are determined by a bang-bang solution that is bounded by the limited liability constraint and the monotonicity constraint. After rearranging the derivative with respect to wages, we obtain

$$\begin{aligned} -1+\lambda +\left( \delta _r+\delta _s\right) \left( 1-\frac{\frac{\delta _r}{\delta _r+\delta _s}}{1-F\left( x_e|y_r\right) }\right) -\phi \frac{f\left( x_e|y_r\right) }{\left( 1-F\left( x_e|y_r\right) \right) f\left( x_e\right) } \end{aligned}$$

(3)

Whenever this condition is positive, the wage will be set to the upper bound given by the monotonicity constraint and the agent will appropriate all the marginal return; if it is negative, then the optimal wage is bounded by the limited liability constraint. Using the structure of the signals and the latter equation, we can prove that the optimal wage is an option. Figure 2 illustrates the contract.

Proposition 1

If $f\left( x|y_r\right)$ satisfies the likelihood ratio order, then the optimal risky wage is a debt contract $w\left( y_r\right) =\max \left\{ 0,y_r-z\right\}$ such that $z>y_s$.

Fig. 2

Optimal monotone contract: $y_s=0.5$, $z=0.7$. a Payment to agent and b payment to principal

Condition (3) has four elements, the first two of them independent of $y_r$. The first one is the marginal cost to the principal of increasing the wage. The second one is the benefit from relaxing the IR constraint which might be 0 if such constraint is not binding. This case arises when the agent gets information rents for the private information.

As it is common in moral hazard problems, the third term is related to a likelihood ratio. It is related to the probability of having undertaken the risky project when no information was acquired relative to that same probability when the information was acquired. Whereas the first one is independent of $y_r$, the second one is increasing in $y_r$ since the likelihood ratio order induces first-order stochastic dominance.

There are three possible cases. If $w_s$ is greater than $\mathbb {E}_{y}\left[ w\left( y_{r}\right) \right]$, implying that $\delta _r=0$, then it would become obvious that the agent exerted effort whenever the risky project is chosen. In this case, the problem simplifies to one of just hidden information where incentives must be given to encourage the adoption of the risky project. Conversely, if $w_s<\mathbb {E}_{y}\left[ w\left( y_{r}\right) \right]$ and the agent chose the safe project, it is also an indicative that he acquired information. Thus, there will always be a punishment for choosing the risky project, but such punishment will decrease the greater is the return. When $y_r$ approaches to 1, there will be no punishment.

When $w_s=\mathbb {E}_{y}\left[ w\left( y_{r}\right) \right]$, the principal is minimizing the cost of inducing acquisition of information. To see this, note the similar structure of restriction (IC1) with equation (1) and its subsequent properties. In this case, the agent will be indifferent between the safe project and the risky project when he does not acquire information and it will appear as if he randomizes his decision and chooses the risky project with probability $\frac{\delta _r}{\delta _r+\delta _s}$. Then, the principal can reward the agent for risky returns that induced a greater probability of choosing the risky project when the information was acquired; otherwise, the agent will be punished. As argued before, such likelihood ratio will be monotone increasing as it is shown in Fig. 3.

Fig. 3

Likelihood ratio

The final component is associated with the hidden information problem and is represented by the hazard rate $\frac{f\left( x_e|y_r\right) }{1-F\left( x_e|y_r\right) }$. The hazard rate in this context is interpreted as the probability of having observed the cutoff signal given that the risky project was chosen. Intuitively, the principal wants to make sure the right project is chosen, which implies that, in the limit, she wants to penalize agents who chose the risky project when they just observed the cutoff signal. Given the MLRP condition of the signals with respect to the return, this hazard ratio is monotone decreasing with respect to the return (see Athey 2002 and Fig. 4 for an example). In other words, a lower observed return increases the chances that the agent observed the cutoff signal. Therefore, this effect also suggests that compensation should be increasing in $y_r$.

Fig. 4

Negative hazard rate

In sum, a monotone contract encourages information acquisition and the partial revelation of information. On the one hand, paying more for higher outcomes induces the acquisition of information since this increases the probability of choosing the best project. On the other hand, paying more for higher outcomes induces the agent to choose the best project once the information has been revealed since a higher signal is associated with a higher return. Hence, the optimal wage schedule creates the incentive for the agent to adopt the risky technology after observing favorable signals.

Finally, note that z must be greater than $y_s$. If this is not the case, then the principal will never want to hire the agent since she is better off by pursuing the safe project. This result suggests that the agent should be rewarded for pursuing the risky project only when its return is significantly better than the safe return, not just marginally better.

Now that risky wages have been characterized, and the safe wage must be set according to constraint (IC2*). As noted before, choosing $w_s$ is equivalent to choosing $x_e$. The first-order condition with respect to $x_e$ is simplified to:

$$\begin{aligned} f\left( x_e\right) \left( y_s-x_e\right) -\phi \frac{\partial \mathbb {E}\left[ w\left( y_r\right) |x_e\right] }{\partial x_e}=0 \end{aligned}$$

(4)

Raising the threshold will yield a marginal benefit of $y_s$ since the safe project will be pursued more often. However, it also generates a cost of $x_e=\mathbb {E}\left[ y_r|x_e\right]$, the return of the risky project at the threshold, and a cost of increasing the expected wage when such threshold increases. The last cost arises because the safe wage must increase to generate the appropriate incentives to the agent to choose the desired project.⁸

Lemma 5

When the agent is hired, it is optimal to distort the project choice in favor of the risky project, formally $x_e<y_s$

This distortion is purely generated by the hidden information problem. Note that constraints (IR*) and (IC1*) remained constant after a change on $x_e$ precisely because of constraint (IC2*). Since it is costly for the principal to induce the agent to reveal the information through the risky wage, she favors the decision that reveals the uncertain state. This distortion also suggests that the first best is never attained. To avoid the distortion, the risky wage should be constant. Although the hidden information would be solved in this case, the moral hazard will persist since information will have no value to the agent. The first best is also never attained because the principal will hire the agent only for c strictly lower than $\hat{c}$, where $\hat{c}$ was defined in equation (1). To see this, just note that the value of experimentation decreases for the principal since she will only appropriate risky returns lower than z; thus, her payoff is no longer convex.

4.2 Debt contracts

An optimal debt contract was first obtained by Innes (1990) using a principal-agent setup. In his paper, the argument relies on the standard assumption that a greater effort generates better distributions of profits in the likelihood ratio sense.⁹ Therefore, an optimal contract rewards the agent for higher profits and punishes him otherwise. To obtain the debt contract, he restricted payments to both the principal and the agent to be monotone nondecreasing. As argued by Innes (1990), a nonmonotone payoff could be manipulated by either the principal or the agent if any of them can affect the return before the contract is paid. For example, the principal would have an incentive to sabotage the risky project by burning profits in excess of the threshold. Similarly, the agent would have an incentive to inflate profits by borrowing money and “revealing” a higher apparent profit to the principal.

The difference with our setup is that effort does not lead to such ordering on the distribution of returns. In fact, effort does not directly influence the observed returns. The returns for either project are given ex-ante, and the problem is that individuals are uncertain about the risky return. Effort in our context lets the agent take a more informed decision, and that is why the agent is rewarded for good outcomes. Moreover, we do not restrict the analysis to monotone wages, and the result arises because it is profitable to take monotone decisions, which require monotone payments to align the incentives.

5 Extensions

5.1 Risk aversion

Now suppose that the agent is risk averse, and its utility is represented by a monotone increasing and concave function $u\left( \cdot \right)$. The first-order condition with respect to $w\left( y_r\right)$ for this case is given by:

$$\begin{aligned} \frac{1}{u^\prime \left( w\left( y_r\right) \right) }=\lambda +\left( \delta _r+\delta _s\right) \left( 1-\frac{\frac{\delta _r}{\delta _r+\delta _s}}{1-F\left( x_e|y_r\right) }\right) -\phi \frac{f\left( x_e|y_r\right) }{\left( 1-F\left( x_e|y_r\right) \right) f\left( x_e\right) } \end{aligned}$$

(5)

Therefore, the optimal wage will continue to be monotone increasing and the intuition will be the same as before. However, it is no longer true that it will be necessarily convex, and this will depend on the degree of risk aversion. For example, if the agent is sufficiently risk averse, insurance concerns will be more important than incentives for information acquisition, and the wage will no longer be convex.

For similar reasons, there is not necessarily a distortion in favor of the risk project when the agent is sufficiently risk averse. The first-order condition (FOC) with respect to $x_e$ is:

$$\begin{aligned} f\left( x_e\right) \left( y_s-x_e+\mathbb {E}\left[ w\left( y_r\right) |x_e\right] -w_s\right) -\phi \frac{\partial \mathbb {E}\left[ u\left( w\left( y_r\right) \right) |x_e\right] }{\partial x_e}=0 \end{aligned}$$

(6)

The last term plays a similar role that in Equation (4): Given the monotonicity of the wage and the utility function, it suggests that project choice should be distorted in favor of the risky one. However, risk aversion implies that $\mathbb {E}\left[ w\left( y_r\right) |x_e\right] >w_s$ to make the agent indifferent between the risky project and the safe project when $x_e$ is observed. Therefore, it is more costly for the principal to implement the indifference for the agent and thus will expect a higher return when choosing a risky project, which generates incentives to distort project choice in favor of the safe one.

This last result when the agent is risk averse is in line with the results obtained by Lambert (1986) and Malcomson (2009), who also assume risk aversion. However, the monotonicity property of the contract derived in this paper was not obtained by them. On the one hand, Lambert (1986) uses a model with two possible risky outcomes, and thus, different contracts can implement the second best project distortion. In his model, project distortion will depend on how the posterior is compared to the prior. On the other hand, Malcomson (2009) allows for a continuum of outcomes but also for a continuum of decisions, which does not allow him to characterize optimal contracts; instead, he fixes wages and derives results on project choice distortion given such wages.

5.2 The role of the monotone payments to the principal

The monotonicity imposed for both the principal’s and agent’s payment has been assumed in the literature motivated by the possible manipulation of the returns by both individuals (see, for example, Innes 1990; Poblete and Spulber 2012 ). In this paper, we weaken the assumption of monotonicity for the agent and rather obtain it as a result for the optimal contract. However, we maintain the monotonicity assumption for the principal since wages cannot be characterized without it. This subsection aims to explain the role of such assumption for the solution.

A project choice is implementable if it is monotone; that is, if a given signal x induces the risky choice, then a higher signal $x^\prime >x$ induces also the risky choice. This condition is satisfied if both the agent and the principal have incentives to choose a monotone decision rule. In the first case, the agent has an incentive to implement the monotone decision if and only if $\mathbb {E}\left[ w\left( y_r\right) |x\right] \ge w_s$ for all $x>x_e$. In the second case, it is sufficient to show that the problem for the principal is quasiconcave in $x_e$. That is, the FOC with respect to $x_e$ is equal to 0 and is negative (positive) if it is evaluated in $x>(<)x_e$. That FOC is given by

$$\begin{aligned} f\left( x_e\right) \left\{ -x_e+\mathbb {E}\left[ w\left( y_r\right) |x_e\right] +y_s-w_s\right\} -\phi \frac{\partial \mathbb {E}\left[ w\left( y_r\right) |x_e\right] }{\partial x_e}=0 \end{aligned}$$

(7)

Note that a sufficient condition to obtain quasiconcavity is that both the term in curly brackets and the last term are nonincreasing with respect to $x_e$. Integrating by parts the expected wage and then deriving the term in parenthesis with respect to $x_e$, we obtain:

$$\begin{aligned} -\int _0^1{w^\prime \left( y_r \right) F_x\left( y|x\right) \mathrm{d}y\le 1} \end{aligned}$$

Note that $\int _0^1{\left( 1-F\left( y|x\right) \right) \mathrm{d}y=x}$, and hence $-F_x\left( y|x\right)$ is a probability distribution. Therefore, the monotonicity assumption for the principal payments $w^\prime \left( y_r\right) \le 1$ is sufficient to show that the term in the curly brackets of equation (7) is nonincreasing in $x_e$. It is also sufficient to have a nonincreasing last term of the same equation since the analysis throughout the paper showed that the expected optimal wage is convex for the agent. The analysis also showed that the wage is monotone nondecreasing, and therefore, the agent also has the incentives to choose a monotone rule.

However, the monotonicity of the principal payments is, certainly, not a necessary condition to obtain implementability. In particular, one may replace it by requiring the whole FOC to be nonincreasing with respect to $x_e$ (not term by term, which is stronger) and the expected wage of the agent to be greater than $w_s$ for $x> x_e$. This weakened restrictions may result in nonmonotone wages with respect to $y_r$. However, this possible nonmonotonicity depends on the (conditional) distribution of the returns and its characterization is difficult to obtain.

6 Implementation

The studied setup closely resembles the interaction between a CEO and the shareholders of a firm. The shareholders hire a CEO to take decisions concerning the future of the company. It is usually the case that the CEO has more expertise than the shareholders in making such decisions, or at least is more efficient at gathering information related to such decisions. Decisions can range from acquisitions to the marketing of new products, whose main characteristic is the uncertainty of their return. Such uncertain returns will be reflected in the value of the firm and thus affect the shareholders payoff. The effort exerted by the CEO to acquire information is not observable. It is also common that if information has been acquired by the CEO, it is not (completely) observed by the shareholders.

The optimal debt contract derived here, where the agent is paid the whole marginal return of the risky project when returns are higher than a threshold, suggests that stock options are optimal ways to motivate the acquisition of information and its revelation. Stock option programs give workers the right to buy company’s shares at a fixed price for a given period of time. These will only be exercised if the market price is higher than the strike price originally agreed to. Stock options are thus used as a long- term motivator and the employee is constrained on exercising the option only after their performance has been (partially) observed. To implement the suggested contract, the firm has to set the strike price significantly higher than the actual value of the company.

The constrained efficient solution also explains why it is optimal to pursue risky projects even when the information suggests the safe project is better. This feature is in close connection to the debate on excessive risk taking of CEOs. Although this is inefficient ex-ante, it is a valuable strategy because it helps to reveal the uncertain state of nature. This is also related to the result obtained by Manso (2011) where early failure is not punished and long-term success is rewarded.

The model also resembles the interaction between a firm and a consultant in charge of advising decision-making. The consultant offers advice to the firm about the project to be selected and the firm decides whether to follow the advice and how much to pay the consultant. Again, the effort exerted by the consultant is unobserved as well as the interpretation of the information he has gathered. The revelation principle suggests that the delegation problem is equivalent to this advice problem where the agent advices truthfully the principal which project to choose. Indeed, it has been observed that start-ups use stock options to reward consultants given their liquidity constraints to pay for the services. Such constraints are represented here by the limited liability that faces the principal who cannot pay at front to the consultant and has to offer stock options to reward him.

7 Concluding remarks

This paper studies the problem faced by a risk-neutral principal who can hire a risk-neutral agent to seek advice before deciding between a risky project and a safe one. The agent can acquire costly information about the risky project before suggesting a project to the principal. The acquisition of information and its content is unobservable to the principal; thus, the problem features moral hazard and hidden information frictions. The main result is that the wage schedule when the risky project is pursued must be monotone increasing. The agent will be rewarded if the return is significantly better than the safe return; otherwise, he will be paid nothing. Thus, the risk of the decision is imposed to the agent. It has been also shown that decision-making is distorted in favor of the risky project as a strategy to reveal uncertainty directly. The optimal contract resembles stock options with a strike price greater than the safe return in an environment where shareholders hire a CEO to delegate decision-making or situations where a liquidity constrained firm hires a consultant to obtain advice. The model also provides an explanation as to why excessive risk taking is optimal.

A Appendix

Proof (Lemma 1)

To show that $U\left( y_s\right) >\max \left\{ \mu _0,y_s\right\}$ integrate by parts the value of experimentation to obtain

$$\begin{aligned} U\left( y_s\right)= & {} y_s+\int _{y_s}^{1}\left( 1-F\left( x\right) \right) \mathrm{d}x \nonumber \\= & {} y_s+\int _0^{1}\left( 1-F\left( x\right) \right) \mathrm{d}x-\int _0^{y_s}\left( 1-F\left( x\right) \right) \mathrm{d}x \nonumber \\= & {} \mu _0+\int _0^{y_s}F\left( x\right) \mathrm{d}x \end{aligned}$$

(8)

Also note that

$$\begin{aligned} \frac{\partial U\left( y_s\right) }{\partial y_s}=F\left( y_s\right) >0 \end{aligned}$$

where the strict inequality comes from footnote 7. Convexity is also easily obtained since the second derivative is the probability of having a signal equal to $y_s$.

Proof (Lemma 2)

First note that $U\left( 0\right) =\mu _0$ and $U\left( 1\right) =y_s$. Therefore, $U\left( y_s\right) -c$ will cross at most once each of the outside options. It could cross once the constant $\mu _0$ from below since it is increasing in $y_s$. It could cross once $y_s$ from above since its first derivative with respect to $y_s$ is between 0 and 1. This in turn implies that $U\left( y_s\right)$ is farther from $\max \left\{ \mu _0;y_s\right\}$ precisely when $\mu _0=y_s$.

Since $U\left( y_s\right) -c$ is linear in c, there exists a $\hat{c}$ such that $U\left( y_s\right) -c=\mu _0=y_s$. Thus, for any $c<\hat{c}$, there exists $a_c,b_c\in \left( 0,1\right)$ such that $U\left( y_s\right) -c>\mu _0$ for any $y_s>a_c$, and $U\left( y_s\right) -c>y_s$ for any $y_s<b_c$. Obviously it must be the case that $\mu _0\in \left( a_c,b_c\right)$. Note that $a_c$ and $b_c$ are increasing and decreasing in c, respectively, precisely because the function crosses from below and above each of the corresponding outside options. Finally, for any $c>\hat{c}$, the interval is empty and the principal never experiments.

Proof (Lemma 3)

The principal is interested in obtaining a truthful report from the agent in order to take a decision between the safe project and the risky project. Let the set of signals that lead the principal to choose the risky project be denoted by R and the corresponding set that lead her to choose the safe project be denoted by S. Lets consider first the case when $x\in S$ and suppose the paid wage is $w\left( \hat{x},y_s\right)$. Since x is unrelated to $y_s$, the expected safe wage will not depend on x, only on $\hat{x}$. Thus, the agent will always prefer to report a $\hat{x}$ that maximizes $w\left( \hat{x},y_s\right)$, regardless of the observed x. Therefore, in order to have truthful revelation, the safe wage must not depend on $\hat{x}$ and can be expressed as $w_s$ given that $y_s$ is constant.

Now, consider the case where $x\in R$. Lets first consider any deviation from the agent such that $\hat{x}\in R$. Since $j\left( x\right) =r=j\left( \hat{x}\right)$, the principal is only interested in paying the agent the least possible as long as he reports a signal that leads her to choose the risky project. Formally, the principal solves the following problem:

$$\begin{aligned}&\min _{w\left( x,y_r\right) }\mathbb E\left[ w\left( x,y_r\right) |x\right] \\&\text {subject\;to } \mathbb E\left[ w\left( x,y_r\right) |x\right] \ge \mathbb E\left[ w\left( \hat{x},y_r\right) |x\right] \text { for all } \hat{x},x\in R\\&\text {and } \mathbb E\left[ w\left( x,y_r\right) |x\right] \ge w_s \text { for all }x\in R \end{aligned}$$

The solution to this program is to set $w\left( x,y_r\right) =w\left( y_r\right)$; thus, the first constraint will be always binding and the principal will not have to pay unnecessary informational rents.

Proof ( Lemma 4)

If the agent is hired, it must be the case that there exist signals $x_s$ and $x_r$ such that the safe project and the risky project are chosen, respectively. If this is not the case, and either project is always chosen, then the principal would not hire the agent since its information has no value. The existence of $x_e$ is therefore obtained using the intermediate value theorem given the continuity of the problem on x. Since payments for the principal are monotone nondecreasing, she wishes to implement a monotone decision. Such monotone decision can be implemented using expected monotone nondecreasing payments in x for the agent $\mathbb E\left[ w\left( y_r\right) |x\right]$, since an increase in x would benefit both individuals and the IR and IC constraints would continue to be satisfied. Those expected monotone nondecreasing payments exist and can be obtained through monotone nondecreasing payments, a consequence of the likelihood ratio order.

Proof (Proposition 1)

The problem and the constraints are linear in $w\left( y_r\right)$ and the Slater’s Condition is satisfied by the constraints. Therefore, Condition (3) is necessary and sufficient to obtain a maximum. We proceed in two steps. First we show that wages must be monotone nondecreasing. Since payments to the principal are also monotone nondecreasing, then optimal wages are option-like as suggested in the proposition. Finally, we prove that $z>y_s$.

For the first step it is sufficient to prove that Condition (3) is monotone increasing in $y_r$. The first two terms are independent of $y_r$. The third term is increasing in $y_r$ since the multipliers $\delta _r$ and $\delta _s$ are nonnegative, and the probability $1-F\left( x_e|y_r\right)$ is increasing in $y_r$ because the monotone likelihood ratio order induces first-order stochastic dominance. On the other hand, the hazard rate $\frac{f\left( x_e|y_r\right) }{1-F\left( x_e|y_r\right) }$ is decreasing in $y_r$ because the monotone likelihood ratio order induces log supermodularity (Athey 2002). Hence, it remains to prove that $\phi$ is nonnegative.

Suppose $\phi$ is negative and the wages are not monotone nondecreasing. Then there exists $y_L<y_H$ such that $w\left( y_L\right) >w\left( y_H\right)$. Consider a decrease of $w\left( y_L\right)$, denoted by $\Delta w_L<0$, compensated by an increase in $w\left( y_H\right)$, denoted by $\Delta w_H$, such that the total ex-ante utility of the agent does not change, and therefore, the IR constraint remains unaffected, as well as the objective function of the principal. Formally, it must be the case that:

$$\begin{aligned} \Delta w_L\left( 1-F\left( x_e|y_L\right) \right) g\left( y_L\right) +\Delta w_H\left( 1-F\left( x_e|y_H\right) \right) g\left( y_H\right) =0 \end{aligned}$$

This change continues to satisfy the IC1 constraint since $w_s$ does not change and $\mathbb E\left[ w\left( y_r\right) \right]$ decreases by

$$\begin{aligned} \Delta w_Lg\left( y_L\right) +\Delta w_Lg\left( y_H\right) =\Delta w_Hg\left( y_H\right) \left[ -\frac{1-F\left( x_e|y_H\right) }{1-F\left( x_e|y_L\right) }+1\right] <0 \end{aligned}$$

This reallocation also decreases $\mathbb E\left[ w\left( y_r\right) |x_e\right]$ by

$$\begin{aligned} \Delta w_Hf\left( y_H|x_e\right) \left( -\frac{\frac{f\left( y_L|x_e\right) }{1-F\left( y_L|x_e\right) }}{\frac{f\left( y_H|x_e\right) }{1-F\left( y_H|x_e\right) }}+1\right) <0 \end{aligned}$$

Moreover, for any x, the change on $\mathbb E\left[ w\left( y_r\right) |x\right]$ is given by

$$\begin{aligned} \Delta w_Hf\left( y_H|x\right) \left( -\frac{\frac{f\left( y_L|x_e\right) }{1-F\left( y_L|x_e\right) }}{\frac{f\left( y_H|x_e\right) }{1-F\left( y_H|x_e\right) }}\frac{\frac{f\left( y_L|x\right) }{f\left( y_h|x\right) }}{\frac{f\left( y_L|x_e\right) }{f\left( y_h|x_e\right) }}+1\right) \end{aligned}$$

where the term inside the brackets is increasing in x. Therefore, this reallocation leads to a minimization of the expected payments conditional on the signal, while maintaining to induce a monotone decision. Therefore, it must be the case that wages are monotone nondecreasing and that $\phi >0$. Given the monotonicity condition for the principal’s payoff, wages are option-like and it is also optimal for the principal to implement such monotone decision.

Finally, the cutoff z is given by the value of $y_r$ such that condition (3) is equal to zero. It must be greater than $y_s$, otherwise the principal prefers not to hire the agent and pursue the safe project since her net benefit from choosing the risky project would be $y_r- w\left( y_r\right) =\min \left\{ y_r,z\right\} <w_s$.

Proof (Lemma 5)

The first-order condition with respect to $x_e$ is given by:

$$\begin{aligned} f\left( x_e\right) \left( -x_e+\mathbb {E}\left[ w\left( y_r\right) |x_e\right] +y_s-w_s\right) -\phi \frac{\partial \mathbb {E}\left[ w\left( y_r\right) |x_e\right] }{\partial x_e}=0 \end{aligned}$$

Given the payment monotonicity for the principal and the agent, such condition becomes negative (positive) for any $x>(<)x_e$. Therefore, the problem is quasiconcave on $x_e$ and condition (4), which is obtained after using Condition (IC2*), characterizes a global maximum.