Why uncertainty matters: discounting under intertemporal risk aversion and ambiguity

Abstract

Uncertainty has an almost negligible impact on project value in the standard economic model. I show that a comprehensive evaluation of uncertainty and uncertainty attitude changes this picture fundamentally. The illustration of this result relies on the discount rate, which is the crucial determinant in balancing immediate costs against future benefits, and the single most important determinant of optimal mitigation policies in the integrated assessment of climate change. First, the paper removes an implicit assumption of (intertemporal or intrinsic) risk neutrality from the standard economic model. Second, the paper introduces aversion to non-risk uncertainty (ambiguity). I show a close formal similarity between the model of intertemporal risk aversion, which is a reformulation of the widespread Epstein–Zin–Weil model, and a recent model of smooth ambiguity aversion. I merge the models, achieving a threefold disentanglement between risk aversion, ambiguity aversion, and the propensity to smooth consumption over time.

1 Introduction

1.1 Overview

The paper makes three contributions to theory and shows how these contributions affect policy analysis. First, I show a close formal similarity between a model disentangling risk aversion from a decision maker’s propensity to smooth consumption over time, and a model disentangling risk attitude from ambiguity attitude. Second, I merge the two models into a framework that achieves a threefold disentanglement of Arrow–Pratt risk aversion, intertemporal substitutability, and smooth ambiguity aversion. Third, in an analytically tractable setting, I derive the resulting consumption discount rates. I show that the formal similarity between the models translates into two fully symmetric effects on the discount rate. The applied contribution of the paper illustrates the importance of a comprehensive uncertainty attitude in long-term evaluation. In the standard discounted expected utility model, uncertainty has an almost negligible impact on project value. I show how a model of comprehensive risk and uncertainty attitude changes this result. I contribute to the social discounting debate and provide simple analytic discounting formulas that pay particular attention to the correlation between growth uncertainty and project payoff.

I disentangle intertemporal consumption smoothing and risk attitude in a reformulated version of the Epstein–Zin–Weil model (Epstein and Zin 1989; Weil 1990). The reformulation builds on Traeger’s (2010a, 2012) measure of intertemporal risk attitude. Risk aversion has two effects on evaluation. First, stochasticity generates wiggles in the consumption path. Agents with a propensity to smooth consumption over time dislike these wiggles. Second, agents intrinsically dislike risk because it creates uncertainty over the future. Intertemporal risk aversion measures this second effect. In comparison, Arrow–Pratt risk aversion in the Epstein–Zin–Weil model measures both risk effects jointly. Expressing the Epstein–Zin–Weil model in terms of intertemporal risk aversion reveals its formal similarity to the smooth ambiguity model by Klibanoff et al. (2005). Ambiguity models capture the distinction between uncertainty that is characterized by a unique probability distribution (risk), and more general uncertainty, usually referred to as ambiguity, hard uncertainty, deep uncertainty, or Knightian uncertainty. The similarity between the reformulated Epstein–Zin model and the smooth ambiguity model translates into equivalent terms in the consumption discount rate. These terms are proportional to intertemporal risk aversion in the Epstein–Zin setting, and proportional to ambiguity aversion in the smooth ambiguity model.

The consumption discount rate determines the optimal trade-off between current investment costs and future investment payoffs. In the context of public projects, this consumption discount rate is known as the social discount rate. The UK and France have explicitly adapted their discounting schemes for the evaluation of legislation and long-term projects to recognize uncertainty. The US Environmental Protection Agency is currently preparing a similar proposal to the Office of Management and Budget. The economic insights underlying these political reforms are based on the standard economic model. However, it is well known that this standard model gives rise to a variety of puzzles in asset pricing under uncertainty, including the equity premium and the risk-free rate puzzles. These puzzles are easily explained using more comprehensive uncertainty models (Bansal and Yaron 2004). In particular, the finance literature shows and exploits the fact that agents are more Arrow–Pratt risk averse than they are averse to consumption substitution in the time dimension: they are intertemporal risk averse. I illustrate the importance of modeling general uncertainty attitude when incorporating uncertainty into public evaluation.

My derivation and discussion of the discount rate pays special attention to the correlation between growth uncertainty and project payoffs. This contribution has important implications for long-term evaluation. Examples of large-scale projects (or legislation) with uncertain payoffs include investments into basic research, national defense, development of new energy technologies, or climate change adaptation and mitigation. I focus on the climate policy example, where the social discount rate is currently hotly debated (Stern 2007; Nordhaus 2007; Weitzman 2007, 2009; Dasgupta 2009; Heal 2009). The social discount rate is the single most important explanatory variable, when comparing the policy recommendations resulting from different integrated assessments of climate change (Nordhaus 2007). For example, a social discount rate of $1.4\,\%$, as chosen in the Stern (2007) review, implies an optimal present day carbon tax that is 10 times higher than using a rate of $5.5\,\%$, as chosen by Nordhaus (2008).¹ First, I illustrate that thin-tailed growth risk easily results in adjustments of the social discount rate in the same order of magnitude as the difference between the rates chosen by Nordhaus and Stern. This finding contributes to a recent discussion on the importance of uncertainty in climate change evaluation (Weitzman 2009; Pindyck 2009; Nordhaus 2012). Second, in the climate context, there is support for positive, for negative, and for no correlation between mitigation payoffs and economic growth. I illustrate the major relevance of this correlation for climate policy evaluation. Thus, the paper calls for a more careful analysis of the correlation channels in the climate–economy interaction.

1.2 Related Literature

The disentanglement of risk aversion from the propensity to smooth consumption over time goes back to Selden (1978), Kreps and Porteus (1978), Epstein and Zin (1989), and Weil (1990). Traeger (2010a, 2012) extends the Epstein–Zin–Weil disentanglement to a multi-commodity setting. For this purpose, he introduces the concept of intertemporal risk aversion. Intertemporal risk aversion directly measures intrinsic aversion to risk, which is not captured in the standard model. Thus, discounting contributions proportional to intertemporal risk aversion measure the deviations from the discount rate in the standard model. As I point out in this paper, smooth ambiguity aversion by Klibanoff et al. (2005, 2009) similarly captures a form of intrinsic aversion to ambiguity. I show that the measure of smooth ambiguity aversion is an analogue to the measure of intertemporal risk aversion, applied to ambiguous settings.

Gollier (2002) discusses the socially optimal discount rate for public investment projects in a model that disentangles risk aversion from intertemporal consumption smoothing. He identifies a sufficient condition for discount rates to be lower under uncertainty than under certainty: the disentangled Arrow–Pratt measure of absolute risk aversion has to decrease in consumption. This finding closely relates to Leland’s (1968) finding in the standard model: savings increase under uncertainty if entangled Arrow–Pratt risk aversion decreases in consumption. This condition is widely believed to hold and, in particular, it is satisfied in case of isoelastic preferences employed in the current paper’s application. Apart from adding ambiguity, the present paper complements and extends Gollier’s (2002) analysis in several ways. First, I derive an exact formula that differs from Gollier’s approximate formula for the social discount rate under isoelastic preferences. Second, I use quantitative estimates from the asset pricing literature to discuss the magnitude of the various contributions to the social discount rate. Third, my formulation extracts the difference in discounting between the general and the standard economic model into a single simple-to-interpret adjustment of the discount rate, proportional to intertemporal risk aversion. Fourth, this reformulation in terms of intertemporal risk aversion shows that Epstein–Zin preferences and smooth ambiguity aversion imply largely equivalent adjustments of the discount rate. Fifth, I extend the setting to account for the important correlation between project payoffs and baseline uncertainty.

Paralleling the current research, Gierlinger and Gollier (2008) analyze the social discount rate in Klibanoff et al.’s (2005) smooth ambiguity framework. Whereas I focus on the analytic extension of the Ramsey formula and discuss the magnitude and relevance of individual terms, Gierlinger and Gollier (2008) focus on general ambiguity attitude and qualitative characterizations of the impact of uncertainty and ambiguity aversion. In comparison with their paper, first, I sacrifice generality of functional forms for the sake of analytic tractability. Second, the present paper adds stochasticity of the investment projects and shows how general uncertainty attitude amplifies the importance of the correlation between economic baseline growth and the stochastic payoffs of the project. Third, Klibanoff et al. (2005) and, thus, Gierlinger and Gollier (2008) conflate the disentanglement between the propensity to smooth consumption over time versus risk states with aversion to ambiguity.² In contrast, I provide a clear threefold disentanglement of all three preference dimensions. Finally, a minor difference is that my derivation of the social discount rate does not rely on the assumption of a rational and efficient equilibrium. An efficient Lucas (1987) tree equilibrium as described in Gierlinger and Gollier (2008) is highly interesting from the intellectual viewpoint, however, in the climate change context, mitigation efforts are far from efficient and complete future markets do not even come close to the time horizons necessary for evaluating these long-run public investments.

Weitzman (2007, 2009) argues that uncertainty gives rise to a low social discount rate in climate change assessment. Weitzman reaches this conclusion by following a Bayesian approach to modeling structural uncertainty. His analysis delivers a fat-tailed posterior over damages that translates into a high willingness to pay for a (certain) transfer into the future. Instead of following Weitzman’s path of augmenting uncertainty to a questionable level,³ I follow the decision theoretic developments that treat uncertainty attitude more comprehensively. Finally, following the original working paper version of this paper, Ju and Miao (2012) calibrated a version of the threefold disentangling model I present here.⁴ A motivation of general risk and uncertainty attitude on the basis of observed behavior can raise a concern regarding the applicability of the current analysis to public decision making.⁵ In response to this criticism, Traeger (2010b) provides a normative axiomatic foundation to decision making under intertemporal risk aversion and under smooth ambiguity version. Moreover, Traeger (2011) shows that the basic isoelastic discounting formulas derived here carry over to the multi-period setting.

In its relevance for climate change policy and environmental cost-benefit analysis, the paper closely relates to the special issue of this journal on “Economic theory and the global environment” edited by Chichilnisky (2012). The present paper shows how risk and uncertainty affect the discount rate and discusses implications for climate change evaluation. A set of papers in the special issue develop axiomatic, normative approaches for evaluating the future with discussion of the climate change context (Lauwers 2012; Figuiéres and Tidball 2012; Asheim et al. 2012). Climate change is caused by greenhouse gas emissions, which are a global negative externality. Karp and Zhang (2012) discuss the advantages and disadvantages of a taxes versus a cap and trade system to regulate such externalities. Their endogenization of abatement costs extends earlier work on taxes versus quantities for stock pollutants (Hoel and Karp 2001, 2002; Newell and Pizer 2003; Kelly 2005; Karp and Zhang 2006; Heutel 2011). Rezai et al. (2012) point out that an intertemporal externality component of the greenhouse gas emission problem can be addressed by shifting produced capital into climate capital, avoiding intergenerational redistribution. Finally, Karp (2005) discusses hyperbolic discounting in the climate change context.

Section 2 provides the background to the paper. It discusses the consumption discount rate in the standard model and introduces the concept of intertemporal risk aversion. Section 3 extends the discounting formula to intertemporal risk aversion and stochastic projects. It shows that, in a model of comprehensive risk attitude, even minor growth risk can reduce the social discount rate to the level of pure time preference. Section 4 incorporates smooth ambiguity aversion. It applies the model to second-order uncertainty over expected growth and over the correlation between project payoff and baseline uncertainty. Section 5 concludes.

2 Background

2.1 Discounting the future under uncertain growth

The consumption or social discount rate characterizes how the value of consumption develops over time. This section lays out the basic setting and summarizes important aspects of the recent debate over the correct social discount rate (Stern 2007; Nordhaus 2007; Weitzman 2007, 2009; Dasgupta 2009; Plambeck et al. 1997). First-period consumption $x_1\in X$ is certain, whereas second-period consumption is captured by the probability measure $p$ over $X$.⁶ In the standard model, a decision maker evaluates utility for every period and for every state of the world by a utility function $u$ and sums over states and over time to arrive at

$$\begin{aligned} U^s(x_1,p)=u(x_1)+ e^{-\delta } {\hbox {E}}_{p} u(x_2). \end{aligned}$$

(1)

The utility discount rate $\delta$ is known as the rate of pure time preference.

The decision maker faces a trade-off between aggregate consumption in the present and in the future. Growth is stochastic and his utility is $u(x)=\frac{x^{1-\eta }}{1-\eta },\,\eta \!>\! 0, \eta \!\ne \! 1$. Given $x_1$, the consumption growth rate $g=\ln \frac{x_2}{x_1}$ is normally distributed with $g\sim N(\mu ,\sigma ^2)$. The risk-free social or consumption discount rate $r= \ln \frac{\mathrm{d}x_2}{-\mathrm{d}x_1}|_{\bar{U}}$ characterizes a marginal, certain trade-off between the future ($\mathrm{d}x_2$) and the present ($\mathrm{d}x_1$) that leaves overall welfare unchanged:⁷

$$\begin{aligned} r = \delta + \eta \mu - \eta ^2 \frac{{\sigma }^2}{2}. \end{aligned}$$

(2)

The formula is a well-known extension of the classic Ramsey (1928) formula that makes growth stochastic. More precisely, the consumption or social discount rate equals the right-hand side of the Ramsey equation. Given incomplete markets, externalities, and transaction costs, this right-hand side is a preferred measure for optimality of trade-offs characterizing long-term projects and legislation that affect consumption. I emphasize the risk-free nature of the trade-off characterized by the consumption (or social) discount rate. The rate evaluates deterministic projects in an uncertain growth scenario. Frequently, this rate in Eq. (2) is also applied to evaluate certainty-equivalent project payoffs. However, Sect. 3.2 discusses why the stochastic discount rate should be used instead for evaluating stochastic projects. The first term characterizing the discount rate in Eq. (2) reflects pure impatience. The second term is a consequence of economic growth. The consumption elasticity of marginal utility $\eta$ characterizes the percentage decrease in marginal utility from a percentage increase in consumption. Together with the expected growth rate $\mu$, the term $\eta \mu$ equals the decrease in marginal utility because of expected consumption growth. The parameter $\eta$ captures aversion to intertemporal consumption changes. Apart from expected growth, these changes include expected wiggles that are caused by stochastic fluctuations. The decision maker’s aversion to these wiggles is captured in the term $\mu \frac{{\sigma }^2}{2}$. This aversion to wiggles in the consumption path is the only risk contribution in the standard model and $\eta$ is simultaneously interpreted as a measure of risk aversion. For the annual discount rate, the parameters $\delta ,\mu ,$ and ${\sigma }$ are in the order of percent, whereas $\eta$ is in the unit order. Therefore, ${\sigma }^2$ makes the third term $10\hbox {--}100$ times smaller than the others, and risk can be neglected in discounting.⁸

The parameter choices of Stern (2007) can be approximated by $\delta =0.1\,\%,\,\eta =1$, and $\mu =1.3\,\%$ delivering $r=1.4\,\%$ under certainty. Whereas Stern’s team argues from a normative perspective for these choices, the majority of integrated assessment modelers reject that standpoint.⁹ A representative of this positive school is Nordhaus, creator of the widely used open-source integrated assessment model DICE. His parameter choices in DICE-2007 (Nordhaus 2008) are $\delta =1.5\,\%,\,\eta =2$, and $\mu =2\,\%$ ¹⁰ delivering $r=5.5\,\%$ (again under certainty). This difference in the social discount rate implies a factor 10 difference in the resulting optimal carbon tax. Introducing uncertainty with a standard deviation of ${\sigma }=2\,\%\,(4\,\%$) results in an adjustment of the risk-free rate by $0.02\,\%\,(0.08\,\%$) in the case of Stern and $0.08\,\%\,(0.3\,\%$) in the case of Nordhaus. The lower standard deviation of ${\sigma }=2\,\%$ is used by Weitzman (2009) to approximate the volatility of economic growth without climate change and catastrophic risks. The high standard deviation of ${\sigma }=4\,\%$ is the rounded estimate of historic consumption fluctuations by Kocherlakota (1996).¹¹ The magnitude of the resulting adjustments for the low standard deviation are negligible, whereas the high standard deviation results in minimal adjustments.

2.2 Intertemporal risk aversion

The standard model of the previous section implicitly assumes that a decision maker’s aversion to risk coincides with his aversion to intertemporal variation. Epstein and Zin (1989) and Weil (1990) derive an alternative setting that disentangles these two a priori quite different characteristics of preference. Traeger (2010a) extends their framework to a multi-commodity setting, introducing a new measure of intertemporal risk aversion that measures the difference between Arrow–Pratt risk aversion and the propensity to smooth consumption over time. The current section motivates the Epstein–Zin generalization of risk attitude along the lines of intertemporal risk aversion. Later sections use the intertemporal risk aversion measure to give a more compact characterization of the social discount rate adjustment under general risk attitude and to show and exploit its similarity to the smooth ambiguity measure in the case of general uncertainty. From the perspective of intertemporal risk aversion, the standard model is risk neutral. It only generates aversion to stochasticity because of the resulting wiggles in the consumption path and a decision maker’s propensity to smooth consumption over time, not because of intrinsic aversion to being uncertain about the future. As a consequence, expressing the social discount rate in terms of intertemporal risk aversion splits its constituents cleanly into those contributions arising in the standard model and those additional contributions that are due to intrinsic risk aversion.

The curvature of the utility function $u$ in Eq. (1) captures both aversion to risk and aversion to intertemporal variation. A priori, however, risk aversion and the propensity to smooth consumption over time are two distinct concepts. More generally, welfare is characterized by two independent functions corresponding to these two distinct preference characteristics

$$\begin{aligned} U(x_1,p)=u(x_1)+e^{-\delta } f^{-1} \left[ {\hbox {E}}_p f\circ u(x_2) \right] . \end{aligned}$$

(3)

Under certainty, the $f$-functions cancel. Therefore, utility $u$ is a measure for the appreciation of consumption that derives from the willingness to trade over time. The concavity of $u$ captures the aversion to intertemporal consumption variation. The curvature of $f$ describes intertemporal risk aversion, which can be interpreted as aversion with respect to utility gains and losses. Note that the curvature of $f$ is a one-dimensional risk measure even in a multi-commodity world.¹² Contrary to a widespread belief, Eq. (3)—not Eq. (1)—is the general representation of preferences satisfying the Neumann and Morgenstern (1944) axioms, additive separability over certain consumption paths, time consistency, and (finite time) stationarity (Traeger 2012).¹³

A representation-free, i.e., choice-based characterization of, intertemporal risk aversion, motivates why the standard model generally falls short of capturing risk attitude comprehensively. The general definition is provided in Traeger (2010a). It requires at least two uncertain periods. Here, I give a simplified characterization that requires the absence of pure time preference.¹⁴ Let $\succeq$ characterize preferences on $X\times P$ represented by Eq. (3) with $\delta =0$. A decision maker is called (weakly)¹⁵ intertemporal risk averse, if and only if for all $x^*,x_1,x_2 \in X$

$$\begin{aligned} (x^*,x^*) \sim (x_1,x_2) \quad \Rightarrow \quad (x^*,x^*) \;\; \succeq \;\; \left( x^*,\left( \frac{1}{2},x_1;\frac{1}{2},x_2\right) \right) , \end{aligned}$$

(4)

where the term $(\frac{1}{2},x_1;\frac{1}{2},x_2)$ denotes a fair coin flip returning either $x_1$ or $x_2$. The premise in Eq. (4) states that a decision maker is indifferent between a certain constant consumption path delivering the same outcome $x^*$ in both periods and another certain consumption path that delivers outcome $x_1$ in the first and outcome $x_2$ in the second period. For example, $x_1$ can be an inferior outcome with respect to $x^*$. Then, $x_2$ is a superior outcome with respect to $x^*$. On the right-hand side of Eq. (4), the decision maker receives $x^*$ in the first period, independent of his choice. For the second period, he has a choice between the certain outcome $x^*$ or a lottery that returns with equal probability either the superior or the inferior outcome. The decision maker is called (weakly) intertemporal risk averse if he prefers the certain outcome $x^*$ in the second period over the lottery.¹⁶ I show in Proposition 5 in “Appendix 2” that a decision maker (with $\delta =0$) is intertemporal risk averse in the sense of Eq. (4) if and only if the function $f$ in the representation (3) is concave.

In the two-period setting, the intertemporally additive reformulation of Epstein and Zin (1989, 1991) infinite horizon recursive utility model is¹⁷

$$\begin{aligned} U(x_1,p)=\frac{x_1^{1-\eta }}{1-\eta } + e^{-\delta } \frac{1}{1-\eta } \left[ {\hbox {E}}_{p} x_2^{1-{{\mathrm{RRA}}}} \right] ^{\frac{1-\eta }{1-{{\mathrm{RRA}}}}}, \end{aligned}$$

(5)

where ${{\mathrm{RRA}}}$ is the coefficient of Arrow–Pratt risk aversion. It is easily verified that Eq. (5) results from Eq. (3) using the intertemporal risk aversion function

$$\begin{aligned} f(z)=\big ((1-\eta ) z\big )^{\frac{1-{{\mathrm{RRA}}}}{1-\eta }}. \end{aligned}$$

(6)

Instead of Arrow–Pratt risk aversion, I will make frequent use of the measure of relative intertemporal risk aversion

$$\begin{aligned} {{\mathrm{RIRA}}}(z)=-\frac{f'' (z)}{f'(z)} \, |z| = \left\{ \begin{aligned} 1-\frac{1-{{\mathrm{RRA}}}}{1-\eta }\quad \text{ if } \eta <1 \;\\ \frac{1-{{\mathrm{RRA}}}}{1-\eta }-1 \quad \text{ if } \eta >1. \end{aligned}\right. \end{aligned}$$

(7)

The measure ${{\mathrm{RIRA}}}(z)$ depends on the choice of zero in the definition of the utility function $u$. This normalization dependence is the analog to, e.g., the wealth level dependence of the Arrow–Pratt measure of relative risk aversion.¹⁸ $^{,}$ ¹⁹ Traeger (2010a) further elaborates that $f$ and ${{\mathrm{RIRA}}}$ can be interpreted as a measure for the difference between Arrow–Pratt risk aversion and the willingness to smooth consumption over time.

2.3 Quantification of parameters

For my quantitative analysis, I focus on the case of risk, where parametric estimates have converged to a more reliable quantification of general attitude than for ambiguity. However, I show that the formal adjustments of the discount rate to include ambiguity attitude are almost identical to the adjustment in the case of intertemporal risk aversion. Thus, the quantitative illustration in the case of risk translates immediately into an illustration of the quantitative effects under ambiguity aversion. Estimates of the generalized isoelastic model usually build on Epstein and Zin (1991) and Campbell’s (1996) log-linearizing the Euler equations. The estimation of the isoelastic model is significantly more challenging than in the case of the standard model.²⁰ However, over the recent years, a somewhat reliable set of parameters emerges to be $\eta =\frac{2}{3}$ and ${{\mathrm{RRA}}}\in [8,10]$, explaining well asset prices and related puzzles (Vissing-Jørgensen and Attanasio 2003; Bansal and Yaron 2004; Basal et al. 2010). The message of these estimates and calibration results is that agents tend to have a higher aversion to risk than to intertemporal substitution. I denote the corresponding preference scenario by “D” for “disentangled model” and use the values $\eta =\frac{2}{3}$ and ${{\mathrm{RRA}}}=9.5$ that are emphasized by Vissing-Jørgensen and Attanasio (2003). These estimates imply a coefficient of relative intertemporal risk aversion of ${{\mathrm{RIRA}}}=27$. The standard model does not allow the decision maker to distinguish between risk and intertemporal smoothing attitude. In consequence, the joint, entangled estimate usually falls somewhere inbetween the disentangled estimates of Arrow–Pratt risk aversion and the propensity to smooth consumption over time. For my quantitative analysis, I use the entangled standard model with $\eta =2$ as scenario “N”. The value of 2 is widespread and, in particular, employed in Nordhaus’s (2008) integrated assessment of climate change. The standard model implies zero intertemporal risk aversion. Depending on the assessment, I also provide sensitivity scenarios or vary parameters on a continuum.

3 Discounting under intertemporal risk aversion

3.1 Risk-free projects

Intertemporal risk aversion results in the following adjustment of the risk-free rate.

Proposition 1

The risk-free social/consumption discount rate in the isoelastic setting with intertemporal risk aversion is

$$\begin{aligned} r = \delta + \eta \mu - \eta ^2 \frac{\sigma ^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma ^2}{2}. \end{aligned}$$

(8)

In the presence of growth uncertainty, a decision maker exhibiting positive intertemporal risk aversion ${{\mathrm{RIRA}}}>0$ discounts the future payoffs at a lower rate. In consequence, a certain project with a relatively low productivity can still improve the welfare of an intertemporal risk averse decision maker, even if an evaluation based on the standard model rejects the project.

In Eq. (8), the parameter $\eta$ reflects only aversion to intertemporal fluctuations. Therefore, the term $\eta ^2 \frac{\sigma ^2}{2}$ is interpreted as the cost of expected fluctuations triggered by the aversion to non-smooth intertemporal consumption paths. I refer to the expression as “the standard risk term,” as it is the only expression capturing risk in an analysis based on the standard model. In the case of fully disentangled preferences (scenario D, see Sect. 2.3), the magnitude of the intertemporal risk aversion contribution is

$$\begin{aligned} \frac{{{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma ^2}{2}}{\eta ^2 \frac{\sigma ^2}{2}} \approx 33, \end{aligned}$$

times that of the standard risk contribution. Figure 1 depicts the different discounting contributions as a function of $\eta$. The graph sets ${{\mathrm{RRA}}}=9.5,\,\mu _t=2\,\%$ and $\sigma _t=4\,\%$.

Fig. 1

Depicts the different contributions of the discount rate as well as the total discount rate net of pure time preference $r-\delta$. The terms are drawn as a function of aversion to intertemporal fluctuations $\eta$, keeping relative Arrow–Pratt risk aversion fixed at ${{\mathrm{RRA}}}=9.5$ and using $\mu _t=2\,\%$ and $\sigma _t=4\,\%$. A minus sign in the bracket implies that the term is negative and subtracted from the positive growth term. The abbreviation ira denotes the contribution from intertemporal risk aversion

The positive growth term (brown, dash-dotted) dominates for reasonably high values of $\eta$. The intertemporal risk aversion term (blue, dashed) defines the main reduction. The standard risk term (black, dotted) plays a very minor role in determining the overall discount rate net of pure time preference (green, solid). Note that the intertemporal risk aversion contribution is continuous at $\eta =1$. Keeping ${{\mathrm{RRA}}}$ fixed, ${{\mathrm{RIRA}}}$ is itself a function of $\eta$ as it measures the difference between Arrow–Pratt risk aversion and aversion to intertemporal substitution.²¹ Moving from the standard model with ${{\mathrm{RRA}}}=\eta =2$ to the disentangled model with $\eta =\frac{2}{3}$ implies two changes in the discount rate. First, the growth effect is significantly reduced once $\eta$ captures only the attitude to intertemporal substitution (brown dash-dotted line is evaluated further to the left). This first effect is an indirect effect of disentanglement. It merely corrects the estimate of the growth term in the standard Ramsey equation. Second, intertemporal risk aversion reduces the discount rate (blue dashed line is now subtracted from the brown dashed line). This second effect is the direct effect of intertemporal risk aversion. When moving in Fig. 1 from $\eta =2$ all the way to $\eta =\frac{2}{3}$, the indirect effect implies an even larger reduction in the discount rate than the direct effect.

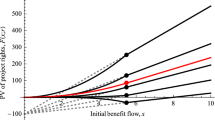
Figure 2 illustrates the crucial difference between the standard model and a model of general risk attitude in terms of the resulting discount rates. The standard model confines ${{\mathrm{RRA}}}=\eta$. The thick colored line moving upwards from the origin depicts the discount rate net of pure time preference $r-\delta$ in the standard model. The yellow region of the otherwise red line reflects the most common preference specifications, $\eta \in [1,2]$. Accounting for higher risk aversion in the standard model moves $r-\delta$ up along the ${{\mathrm{RRA}}}=\eta$ line and significantly increases the discount rate. In contrast, higher risk aversion in the disentangled model decreases the discount rate. The thin black lines going from right to left increase risk aversion while keeping $\eta =\frac{2}{3}$ (D) and $\eta =2$ (N). The thin black lines moving up increase $\eta$ while fixing ${{\mathrm{RRA}}}$ at 5 and 10. All of the cited estimates of the disentangled model imply discount rates in the lowest corner of the shaded area between these lines. In contrast, an attempt to accommodate observed risk aversion of ${{\mathrm{RRA}}}\in [5,10]$ in the standard model would imply discount rates far above the $7\,\%$ bound of the graph (plus pure time preference).

Fig. 2

Depicts the total discount rate net of pure time preference $r-\delta$ as a function of $\eta$ and ${{\mathrm{RRA}}}$. Moving along the thick (red and yellow) line keeps ${{\mathrm{RRA}}}=\eta$, representing the only movement possible in the standard model. The yellow part of the line marks the most common parameterization $\eta \in [1,2]$. Increasing risk aversion along this line necessarily leads to high discount rates. In contrast, increasing risk aversion in the disentangled model corresponds to a movement to the left and reduces the discount rate. The two thin black lines $a$ and $a'$ from right to left hold $\eta$ fix at $\frac{2}{3}$ (as in D) and 2 (as in N), while increasing risk aversion. The two thin lines $b$ and $b'$ moving up hold ${{\mathrm{RRA}}}$ fix at 5 and 10, while increasing $\eta$. The cited estimates of the disentangled model all imply rates in the lowest left corner of the shaded area between the thin black lines. It is $\mu _t=2\,\%$ and $\sigma _t=4\,\%$ (color figure online)

Gollier (2002) derives a social discount rate that closely relates to the rate characterized in Eq. (8). It differs in two respects. First, only Eq. (8) decomposes the discount rate into terms that resemble the rate in the standard model, and a term capturing the deviation from the standard model. The term capturing this deviation, which is proportional to intertemporal risk aversion, fleshes out the magnitude of the difference between employing the standard model and the comprehensive model. Moreover, the term will be crucial in drawing the parallel to discounting under smooth ambiguity aversion. Second, his derivation of the isoelastic special case of his model is an approximation and assumes that the support of the growth rate is a small neighborhood around zero. In contrast, the normal growth distribution assumed here has infinite support. Contrary to a seemingly widespread belief, Gollier’s equation neither holds for normal growth, nor does he claim so. For normal growth, equation (14) in Gollier (2002) misses a term $\eta \frac{\sigma ^2}{2}$. Gollier’s derivation starts with the Arrow–Pratt approximation of the certainty equivalent. The Arrow–Pratt approximation is globally exact for normally distributed risk and CARA utility, i.e., for utility or risk aversion functions that capture constant absolute aversion rather than constant relative aversion as assumed by isoelastic preferences. For short-time horizons, low-growth, and low-variance, Gollier’s approximation is good in the case of a normal growth distribution and CARA aggregators. I discuss these results in “Appendix 3.”

3.2 Stochastic projects

In the preceding section, uncertainty is about economic growth. Many long-term investment projects, however, are characterized by uncertain payoffs. Greenhouse gas mitigation and climate change adaptation projects are important examples. Once stochasticity of the project is introduced, the correlation between project payoff and uncertain economic growth becomes crucial for valuation. Lind (1982) argues for full positive correlation between project payoffs and economic baseline growth. Weitzman (2007) points out that this standard approach to cost-benefit analysis does not apply to climate change projects. The major areas impacted by climate change would be “ ‘outdoor’ aspects (broadly defined) like agriculture, coastal recreational areas, and natural landscapes,” which are little correlated with technological progress. Moreover, some of these impacts directly affect utility rather than production. Various economists used related arguments to promote the use of the risk-free rate for the assessment of climate change projects. Indeed, the risk-free rate coincides with the discount rate for an uncorrelated stochastic project (see below).

Some common integrated assessment models imply a different correlation mechanism. Nordhaus (2008) notes that a high growth realization implies more production and, thus, more emissions. Then, damages and abatement payoff are both high. The resulting positive correlation between growth (or wealth) and project payoff is driven by the production–emissions–damage link. I add a third consideration driving correlation in the climate change context. The causal chain pointed out by Nordhaus (2008) and captured in his integrated assessment model DICE relies on the exogenous growth rate affecting emissions. However, if climate change turns out to have severe economic impact, then it is likely to affect the economic growth rate (Pindyck 2011). A possible transmission channel from climate change to economic growth is the mere straining of resources that would otherwise lead to technological progress. Another channel could divert general technological progress into adaptation technology that merely serves to maintain the status quo. Dell et al. (2012) find evidence that a similar channel indeed affects the growth rates in developing economies even at the moderate levels of climate change experienced in the past. A further transmission channel can be a distributional tension caused by fresh water scarcity, droughts, and agricultural impacts in some regions of the world, triggering social conflict within a society as well as international conflicts. In general, all three correlation arguments (Weitman’s, Nordhaus’, and the one added here) apply to the evaluation of climate change related projects and the integrated assessment of climate change under uncertainty.

This section derives the discounting formula for projects that are correlated with economic baseline growth. I show that general risk attitude creates a much more important role for correlation than in the standard model. For stochastic projects, the decision maker no longer trades a deterministic unit of consumption between the present and the future. Formally, she trades a marginal unit $\mathrm{d}x_1$ of her current certain consumption $x_1$ against a marginal fraction $\mathrm{d}\epsilon$ of a stochastic project $y$ with expected unit payoff, i.e., ${\hbox {E}}y=1$. The future payoff $y$ is correlated with uncertain future baseline consumption $x_2$. The stochastic discount rate is characterized as $r=\ln \frac{\mathrm{d}\epsilon }{-\mathrm{d}x_1}$ for an intertemporal trade-off that leaves overall welfare constant:

$$\begin{aligned} 0 = \frac{\mathrm{d}}{\mathrm{d}x_1}u(x_1)\mathrm{d}x_1+\beta \frac{\mathrm{d}}{\mathrm{d}\epsilon } \left. f^{-1} \left[ {\hbox {E}}_{p(x_2,y)} f\circ u(x_2+\epsilon y) \right] \right| _{\epsilon =0}\mathrm{d}\epsilon . \end{aligned}$$

(9)

I briefly comment on this extension of the social discounting model. First, for a certain project, the marginal payoff $\epsilon y$ is certain and corresponds to $\mathrm{d}x_2$ in the usual derivation of the risk-free social discount rate.²² Second, marginality in the trade-off that defines the discount rate plays the same role as in any other economic price concept. The analytic formula for the discount rate will characterize (in rates) the present value willingness to pay for a marginal unit of the stochastic project. This willingness to pay depends on correlation. Third, I formalize a trade-off between a marginal current unit and the first marginal part of a finite stochastic unit project $y$.²³ Fourth, observe that the derivation does not rely on an optimal allocation of an adaptation–mitigation portfolio. Such an optimality assumption would be inadequate in the climate change application that I discuss.

I assume that the uncertain productivity of the project $\ln y$ and the stochastic economic consumption growth rate $g$ are jointly normally distributed with standard deviations $\sigma _y,\,\sigma _g$, and correlation $\kappa$. The expected growth rate is denoted as $\mu _g$ and the condition ${\hbox {E}}y=1$ determines the remaining parameter of the distribution.²⁴

Proposition 2

The stochastic social discount rate in the isoelastic setting with intertemporal risk aversion is

$$\begin{aligned} r&= \delta + \eta \mu _g - \eta ^2 \frac{\sigma _g^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _g^2}{2}\nonumber \\&+ \eta \kappa \ \sigma _g \sigma _y + |1-\eta | {{\mathrm{RIRA}}}\kappa \ \sigma _g \sigma _y. \end{aligned}$$

(10)

The second line distinguishes the stochastic social discount rate from its risk-free relative of the previous section. In the case of certainty about the project, this second line vanishes ($\sigma _y= 0$). The same is true if the risk of the project and the baseline scenario are uncorrelated ($\kappa =0$). The discount rate characterizes a marginal shift between current consumption and uncertain future consumption. Therefore, risk aversion with respect to the marginal project itself is a second-order effect that does not find its way into the discount rate. Stochasticity of the small project only contributes through its interaction with baseline uncertainty. The second term in the second line of Eq. (10) distinguishes the correlation contribution in a model including intertemporal risk aversion from the correlation contribution in the standard model.

I assess the magnitude of the correlation contribution in the same growth scenario as before with $\mu =2\,\%$ and $\sigma _y=\sigma _g=4\,\%$. I discuss and relax the assumption that the standard deviation of the project payoff equals that of the growth process in the next section. The correlation multiplier in scenario N, the standard model with Nordhaus’ preferences, is $\eta \sigma _g \sigma _y = 0.3\,\%$. In contrast, scenario D (disentangling $\eta =\frac{2}{3}$ from ${{\mathrm{RRA}}}=9.5$) reduces the standard multiplier of the correlation coefficient to $\eta \sigma _g \sigma _y = 0.1\,\%$, but adds an intertemporal risk aversion multiplier of $|1-\eta |{{\mathrm{RIRA}}}\sigma _g\sigma _y= 1.4\,\%$. The correlation contributions to the social discount rate are proportional to these multipliers and the correlation coefficient. For example, a correlation of $\kappa =\pm 0.5$ increases the social discount rate in the disentangled scenario by $\pm 0.8\,\%$ to an overall rate of $2.4\,\%$ and $0.9\,\%$, respectively (for $\delta =1.5\,\%$). Thus, under intertemporal risk aversion, the correlation between the project payoff and economic growth is of first-order importance for the discount rate. Figure 1 shows the dominant correlation multiplier caused by intertemporal risk aversion as a function of $\eta$ in light gray. It is the amount added (subtracted) from the risk-free rate when accounting for full positive (negative) correlation and comprehensive risk attitude.

3.3 The relevance of future risk

How relevant is uncertainty for the evaluation of long-term projects? Weitzman (2009) emphasizes the importance of uncertainty about climate sensitivity and economic damages for the assessment of climate change policies. His analysis builds crucially on generating fat tails in a standard expected utility model. His interesting findings have been criticized in a series of papers for their assumptions about the climate system as well as for stretching a too simple economic trade-off model beyond the domain where it is meaningful (Horowitz and Lange 2009; Pindyck 2009; Nordhaus 2009; Millner 2011). The current paper opens up a very different perspective on how uncertainty affects climate change evaluation. Even without uncertainty about the climate system itself, uncertainty about economic growth has a major impact on optimal climate policy. Including uncertainty about the climate system, the interaction and correlation between growth and project payoffs becomes a major ingredient for evaluating climate change and pricing carbon. The section analyzes the relevance of growth and project uncertainty in the model of comprehensive risk attitude.

The previous sections have shown that growth uncertainty reduces the discount rate. The two-period model of those sections is equivalent to a simple iid growth model. However, once uncertainty becomes persistent, it is well known that uncertainty not only changes the level of the discount rate, but also its term structure (Weitzman 1998; Azfar 1999). Making the time step explicit in Eq. (8) results in

$$\begin{aligned} r_T = \delta T + \eta \mu _T - \eta ^2 \frac{\sigma _T^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _T^2}{2}, \end{aligned}$$

where variables indexed by $T$ depend on the time horizon (payoff period). For an iid process like a Brownian motion, the variance grows linearly in futurity $T$. Then, if expected growth is constant ($\mu _T=T \mu$), payoffs in period $T$ are simply discounted at $T$ times the constant rate stated in Eq. (8). However, with persistent uncertainty, the variance grows faster and the term structure of the discount rate falls: payoffs in the distant future are discounted at a relatively lower (annual average) discount rate than payoffs in the close future.

In the following, I analyze the importance of uncertainty for the evaluation of climate change, comparing the models with and without a comprehensive representation of risk attitude. The analysis relies on the primordial importance of the discount rate for climate change evaluation, impressively documented in Nordhaus’s (2007) simulation discussed in the introduction. I build the analysis around the following question: At what level of riskiness do uncertainty effects cancel the growth effect in the social discount rate? Growth discounting is the main economic driver of discounting. If uncertainty effects cancel the growth effect, then future costs and benefits are solely discounted with the pure rate of time preference $\delta$. I compare the necessary risk level between the standard and the disentangled model, and I analyze how this risk depends on the correlation between growth and project payoffs. A major advantage of approaching the uncertainty comparison in this way is that the uncertainty analysis is independent of pure time preference—a parameter whose magnitude is most contested in the debate.

The analysis uses a time horizon (or period) of 50 years. I now discuss long-term growth uncertainty, a highly intertemporally correlated event, instead of discussing a representative year in an iid growth scenario. I keep the assumption of an expected $2\,\%$ annual growth rate of consumption. In 50 years, climate change is going to affect our planet severely under almost any forecast. It will affect economic activities directly as well as non-produced consumption. Some events such as changes in precipitation patterns (or land loss) can also cause social unrest or war.²⁵ I will measure uncertainty in terms of the variance of the growth process (and the project payoff) and translate it into the probability of being worse off tomorrow than today.

Corollary 1

The discount rate reduces to pure time preference, i.e., $r_{T}= \delta T$, if and only if

• 1. in the case of the risk-free rate

  $$\begin{aligned} \sigma _T = \left( \frac{1}{2}\Big ( \eta +\frac{|1-\eta ^2|}{\eta } {{\mathrm{RIRA}}}\Big )\right) ^{-\frac{1}{2}} \ {\mu _T}^{\frac{1}{2}}. \end{aligned}$$

  (11)

• 2. in the case of a risky project with $\sigma _T=\sigma _{g_T}=\sigma _{y_T}$

  $$\begin{aligned} \sigma _T = \left( \frac{1}{2}\Big ( \eta +\frac{|1-\eta ^2|}{\eta } {{\mathrm{RIRA}}}\Big ) -\kappa \Big (1+\frac{|1-\eta |}{\eta } {{\mathrm{RIRA}}}\Big ) \right) ^{-\frac{1}{2}} \ {\mu _T}^{\frac{1}{2}}. \end{aligned}$$

  (12)

• 3. in the case of a general risky project

  $$\begin{aligned} \sigma _{y_T} = \frac{\left( \eta ^2+|1-\eta ^2|{{\mathrm{RIRA}}}\right) \sigma _{g_T} - 2 \eta \frac{ \mu _T}{\sigma _{g_T}}}{2\kappa \left( \eta +|1-\eta |{{\mathrm{RIRA}}}\right) }. \end{aligned}$$

The conditions for eliminating the growth effect are identical for the risk-free rate and for the case of a risky project whose payoffs are uncorrelated to overall growth. More uncertainty is required, if the risk terms are to cancel the growth term, for a project whose payoffs are positively correlated to growth uncertainty. If the expected growth rate is simply $\mu _T=\mu T$, with a constant annual expectation of $\mu$, then Eqs. (11) and (12) show that (only) a standard deviation that evolves proportional to $\sqrt{T}$ leaves the annual discount rate constant (at pure time preference). This fact illustrates once again that the term structure of the discount rate is flat only for iid uncertainty where $\sigma _T \propto \sqrt{T}$.

I analyze Corollary 1 using concrete probabilistic events. By $p^\star \equiv P(x_{50}\le x_{1})$, I denote the probability that anything including climate change causes society to be worse off in $T=50$ years than today. It is the probability mass in the thin left tail of the growth distribution that implies a non-increasing standard of living between today and in 50 years. For the subsequent simulations, I keep expected consumption growth at a annual rate of $2\,\%$ and $T=50$, which implies $\mu _T=1$. Table 1 summarizes the numerical results for the different preference representations and for differing degrees of correlation. The table follows part 2 of Corollary 1 assuming $\sigma _{g_{T=50}}=\sigma _{y_{T=50}}$ (relaxed further below). In scenario N, the intertemporally expected utility standard model, a standard deviation of unity is necessary to eliminate growth discounting from the risk-free discount rate ($\kappa =0$). This standard deviation translates into the large probability of $p^\star =16\,\%$ that society is equal or worse off in 50 years. In contrast, the disentangled scenario D with a comprehensive treatment of risk attitude implies ${\sigma }=0.3$ and $p^\star =0.04\,\%$. A chance of 4 in 10,000 that we might not be better off in 50 years than today seems quite reasonable. Then, we should not discount the future for growth in the disentangled model. The probability necessary in the standard model is 400 times larger. The sensitivity scenario $S1$ in the table leaves relative Arrow–Pratt risk aversion ${{\mathrm{RRA}}}$ at the estimate of $9.5$, but increases aversion to intertemporal substitution $\eta$ to Nordhaus’ value of 2. This change reduces intertemporal risk aversion, but still results in a probability $p^\star$ necessary to reduce discounting to pure time preference that is only a 30th of the probability needed in scenario N. Sensitivity scenario $S2$ further reduces intertemporal risk aversion by also lowering the Arrow–Pratt coefficient of risk aversion to 5. Then, $p^\star$ is about a fifth of the corresponding probability in scenario N.

Table 1 Risk that reduces the social discount rate to pure time preference

The table also shows the important role played by the correlation between project payoff and growth uncertainty in the disentangled approach: correlation can change the probability $p^\star$ by several orders of magnitude. With disentangled preferences and a correlation coefficient $\kappa =-.5$, a probability of $p^\star =0.0009\,\%$ is sufficient to make the risk terms cancel the growth effect, yielding a social discount rate that is equivalent to pure time preference. In contrast, with a correlation coefficient $\kappa =+.5$, a probability of $p^\star =2\,\%$ would be needed. Under standard preferences, these probabilities would be $11\,\%$ and $24\,\%$, respectively. The stochasticity of the project with expected unit payoff can be characterized as follows. Let $p_y=P(y<0.5 \vee y>2)$ denote the probability that the project pays less than half or more than double of the expected unit. The interval $\sigma _y\in [0.2,0.3]$ found for a non-positive correlation in the disentangled approach translates into $p_y\in [0.1\,\%,2.2\,\%]$, whereas the corresponding interval $\sigma _y\in [.7,1]$ in the N scenario translates into $p_y\in [35\,\%,54\,\%]$. For perfect positive correlation $\kappa =1$, the risk effects can only cancel the growth effect if the standard deviation of baseline growth exceeds that of the stochastic project. Thus, condition (12) has no solution.²⁶

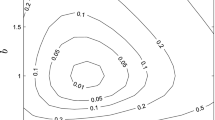
Disentangling the two different risks yields further insight. The left graph in Fig. 3 depicts combinations of standard deviations that reduce the social discount rate to pure time preference. The right graph translates these standard deviations into the probabilities $p^\star$ that society is equal or worse off in 50 years under the expected annual growth rate of $2\,\%$ (growth uncertainty) and into the probability $p_y$ that the project pays out less than half or more than double the expected unit.²⁷ The dashed lines correspond to disentangled preferences (D), whereas the solid lines correspond to Nordhaus preferences (N). The graphs demonstrate that more uncertainty of the stochastic project decreases the baseline risk necessary for a reduction in the discount rate, if and only if the correlation is negative. For a positive correlation, higher project uncertainty also requires a higher volatility of baseline growth if risk effects are to cancel the growth effect. The graphs clearly show the importance of the correlation coefficient already for low levels of the project’s payoff uncertainty $p_y$. Moreover, the graphs reiterate the order of magnitude difference resulting from entangled versus disentangled preferences.

4 Ambiguity aversion and second-order uncertainty

4.1 Ambiguity

A different shortcoming of the intertemporally additive expected utility standard model is its assumption that uncertainty can be described by a unique probability measure. In many real-world applications, these probability distributions or risks are unknown. Different strands of literature capture non-risk uncertainty under the names deep uncertainty, hard uncertainty, or ambiguity. In this paper, I employ and extend Klibanoff et al.’s (2005) model of smooth ambiguity aversion (KMM) and show how ambiguity affects the discount rate. In contrast to many models of ambiguity and deep uncertainty, the KMM model satisfies normative desiderata including time consistency and other rationality constraints. I show the close similarity of this ambiguity model to the model of intertemporal risk aversion. The KMM model captures uncertainty about the correct objective probability distribution in terms of second-order uncertainty: a subjective probability distribution over objective probability distributions or risk. The model is particularly interesting and applicable in the context of climate change and long-term economic growth: in both situations, we face too little data and insufficient knowledge about the underlying model to derive confident probabilistic estimates governing the future.

The basic structure of the model is similar to a Bayesian prior model. The Bayesian prior is interpreted as ambiguous second-order uncertainty. The crucial distinction between the smooth ambiguity and the standard Bayesian model lies once more in the preference representation that accompanies the uncertainty model. In a standard Bayesian expected utility model, a decision maker evaluates objective first-order probabilities and subjective second-order probabilities with the same risk aversion function (simultaneously capturing aversion to intertemporal substitution). In contrast, the KMM model incorporates the finding that individuals generally prefer objective risk to subjective risk. For this purpose, the model introduces a new measure of risk aversion for ambiguous lotteries, i.e., the subjective second-order probability distributions. I will explain that this measure of ambiguity is a close analog to the measure of intertemporal risk aversion. The original KMM model does not disentangle attitudes in the case of objective risk. By introducing ambiguity aversion, the model introduces intertemporal risk aversion only to subjective lotteries, while keeping intertemporal risk neutrality for objective lotteries. I extend the model to capture both, disentangled aversion to subjective and to objective risk. I show that the resulting social discounting model is a clone of the model discussed in the previous sections.

The decision-theoretic literature has developed a range of different approaches to capture situations of ambiguity. I briefly survey the most important ones in the remainder of this section. One way to characterize non-risk uncertainty is by extending the concept of probabilities to more general set functions called “capacities.” These set functions weigh possible events but are not necessarily additive in the union of disjoint events. Because of this non-additivity, the standard measure integral has to be exchanged for the more general Choquet integral in order to calculate expected utility, giving rise to the name “Choquet expected utility.” A second approach defines an evaluation function that expresses beliefs in the form of sets of probability distributions rather than unique probability distributions. The first and simplest such representation goes back to Gilboa and Schmeidler (1989). Here, a decision maker evaluates a scenario by taking expected values with respect to every probability distribution deemed possible and then identifies the scenario with the minimal expected value in this set.²⁸ A more general representation of this type is given by Ghirardato et al. (2004), Maccheroni et al. (2006a), and, in an intertemporal framework, Maccheroni et al. (2006b). There are several equivalence results between the Choquet approach and that of multiple priors as well as rank-dependent utility theory where a decision maker uses distorted probabilities in an expected utility approach increasing the weights given to small probability events. In the climate change context, the main advantage of the smooth ambiguity model over these alternatives is its normative attractiveness achieved by maintaining time consistency and the essence of the independence axiom. Just as importantly for my purposes, I want to show that the KMM model is closely related to the model of intertemporal risk aversion and yields similar discounting results. Finally, its similarity to the Bayesian framework makes the model not only easy to interpret, but also allows me to relate to Weitzman’s (2009) discourse on structural uncertainty.

4.2 The generalized model of smooth ambiguity aversion

The section introduces the smooth ambiguity aversion model by Klibanoff et al. (2005) and, in the intertemporal setting, by Klibanoff et al. (2009). It represents ambiguity (non-risk uncertainty) as second-order probability distributions, i.e., probabilities over probabilities. The model introduces a different attitude for evaluating second-order uncertainty as compared to first-order risk. For the purpose of my paper, this model has two advantages over the other approaches cited above. First, the model is time consistent, making it suitable not only for a descriptive but also for a normative decision framework. Translated into the simple setting of this paper, the generally recursive evaluation of the future writes as

$$\begin{aligned} V(x_1,p,\pi )=u(x_1) + \beta \varPhi ^{-1} \left\{ \int \limits _\varTheta \varPhi \left[ {\hbox {E}}_{p_\theta (x_2)} u(x_2) \right] \mathrm{d}\pi (\theta ) \right\} . \end{aligned}$$

For a given parameter $\theta$, the probability measure $p_\theta$ on the consumption space $X$ denotes first-order or “objective” probabilities over consumption. The expectation operator takes expectations with respect to $p_\theta$. However, the parameter $\theta$ and, thus, the correct objective probability distribution are unknown. The probability measure $\pi$ denotes the prior over the parameter $\theta \in \varTheta$.²⁹

In Klibanoff et al.’s setting, the utility function $u$ corresponds to the utility function of the standard model. It jointly captures aversion to intertemporal substitutability and “objective” or first-order risk. The function $\varPhi$ captures additional aversion with respect to second-order uncertainty, which they call ambiguity aversion. For $\varPhi$ linear, the model collapses to the standard Bayesian model. The coefficient describing relative ambiguity aversion is defined as

$$\begin{aligned} {{\mathrm{RAA}}}=\frac{\varPhi ''(z)}{\varPhi '(z)}|z|. \end{aligned}$$

A different perspective on ambiguity aversion in the KMM model is as follows. The utility function captures aversion to intertemporal substitution. Aversion to objective risk is only captured to the degree that risk generates intertemporal fluctuations in the consumption path. In contrast, the evaluation of the subjective prior incorporates intrinsic aversion to ambiguity, just as intertemporal risk aversion incorporated intrinsic aversion to risk. I noted that intrinsic aversion is, e.g., able to explain asset pricing puzzles. However, the current model only picks up intrinsic aversion to ambiguity, not to risk. Thus, it remains unclear what part of the ambiguity aversion effects are driven by additional aversion to subjective as opposed to objective risk, and what effects that are labeled ambiguity aversion are merely driven by uncertainty aversion dominating the propensity to smooth consumption over time.

In this paper, I combine Klibanoff et al.’s model of ambiguity aversion with my model of intertemporal risk aversion, leading to a welfare representation of the form

$$\begin{aligned} V(x_1,p,\pi )=u(x_1) + \beta \varPhi ^{-1} \left\{ \int \limits _\varTheta \varPhi \left[ f^{-1}{\hbox {E}}_{p_\theta (x_2)} f\circ u(x_2) \right] \mathrm{d}\pi (\theta ) \right\} . \end{aligned}$$

(13)

In this generalization, $u$ characterizes aversion to intertemporal substitution only, $f$ characterizes intertemporal risk aversion, and $\varPhi$ characterizes ambiguity aversion.³⁰ In the representation of Eq. (13), ambiguity aversion characterizes attitude with respect to second-order uncertainty similar to the way that intertemporal risk aversion characterizes attitude with respect to first-order risk. This parallel is a fundamental insight into the smooth ambiguity model and will also emerge in the expression for the discount rate. The current generalized framework permits a threefold disentanglement of risk aversion, ambiguity aversion, and aversion to intertemporal substitution. To enable an analytic derivation of the social discount rate, I will once more revert to the isoelastic setting. In addition to the earlier assumptions of Sect. 2.2 and Eq. (6), I assume $\varPhi (z)=(\rho z)^\varphi$, which yields a coefficient of relative ambiguity aversion

$$\begin{aligned} {{\mathrm{RAA}}}= \left\{ \begin{aligned} 1-\varphi \quad \text{ if } \rho >0&\\ \varphi -1 \quad \text{ if } \rho <0&. \end{aligned} \right. \end{aligned}$$

4.3 The social discount rate and ambiguity about growth

In the context of climate change, Weitzman (2009) recently argued that the parameters of the distribution governing economic growth are unknown. Like Weitzman, I adopt a Bayesian setting to capture such second-order uncertainty. However, Weitzman sticks with the standard risk model underlying Eq. (2), in contrast, I introduce ambiguity attitude as formulated by Klibanoff et al. (2005, 2009) as well as intertemporal risk aversion. Taking the simplest example of Bayesian second-order uncertainty, I assume that expected growth is itself a normally distributed parameter $\theta$ with expectation $\mu$ and variance $\tau ^2$. Formally, first-order uncertainty $p_\theta$ is once more a joint normal distribution over economic growth and project payoff (see Sect. 3.2). However, the expected growth rate is unknown, and I assume ${\hbox {E}}(g|\theta )\sim N(\theta ,\sigma ^2)$ and $\theta \sim N(\mu ,\tau ^2)$, preserving the interpretation of $\mu$ as the overall expectation of the growth trend. The special case of Proposition 3 for ${{\mathrm{RIRA}}}=0$ and $\kappa =0$ has independently been derived by Gierlinger and Gollier (2008).

Proposition 3

The stochastic social discount rate in the isoelastic setting with intertemporal risk aversion and ambiguity about expected growth is

$$\begin{aligned} r&= \delta + \eta \mu _g - \eta ^2 \frac{\sigma _g^2+\tau ^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _g^2}{2} \nonumber \\&+ \ \eta \, \kappa \ \sigma _g \sigma _y + |1-\eta | {{\mathrm{RIRA}}}\ \kappa \ \sigma _g \sigma _y \nonumber \\&- {{\mathrm{RAA}}}|1-\eta ^2| \frac{\tau ^2}{2}. \end{aligned}$$

(14)

The first two terms on the right-hand side reflect, once more, the discount rate in the standard Ramsey equation under certainty. The third term $-\eta ^2 \frac{\sigma ^2+\tau ^2}{2}$ reflects the well-known extension for risk. Note that the overall variance of the growth process is now $\sigma ^2+\tau ^2$ because of the additional layer of uncertainty characterized by the second-order variance $\tau ^2$. The second line gives the corrections if the project is stochastic. This correction remains as in the previous section. The third line characterizes the new contribution to intertemporal value development due to ambiguity aversion. The term is proportional to second-order variance $\tau ^2$, relative ambiguity aversion ${{\mathrm{RAA}}}$, and the term $|1-\eta ^2|$ already encountered in the correction of the social discount rate for intertemporal risk aversion. In fact, the contribution of ambiguity aversion is formally equivalent to the contribution of intertemporal risk aversion, replacing first by second-order variance and ${{\mathrm{RIRA}}}$ by ${{\mathrm{RAA}}}$. Proposition 3 provides a full disentanglement between the contributions already present under certainty, those arising under risk only reflecting aversion to intertemporal fluctuations, the contributions driven by intrinsic risk aversion, and those brought about by aversion to ambiguity.

Quantitatively, a decision maker who is more averse to ambiguity than to risk will lower the discount rate more for second-order variance (ambiguity) than for first-order variance (risk). Otherwise, the discussion from Sect. 3 stays qualitatively the same. In general, an ambiguity averse decision maker will employ a lower (risk-free or stochastic) discount rate when the baseline scenario is ambiguous. He is willing to invest in a certain or stochastic project with relatively lower productivity than is a decision maker who is ambiguity neutral or just faces (first order) risk.

Relating my result to Weitzman (2009), I ignore everything, but the first three terms on the right of Eq. (14). The only difference between these remaining terms and the standard equation (2) is the additional variance $\tau ^2$ in the third term (standard risk term). This additional variance is a straightforward consequence of making the growth process more uncertain by introducing a prior over some parameter of the growth process. In the case of the normal distributions adopted here, the variance simply adds up. From the given example, it is difficult to see how adding a Bayesian prior would bring the standard risk term back into the order of magnitude comparable to the other terms of the social discount rate. Instead of a doubling, a factor of $10\hbox {--}100$ is needed. The only way to reach this result is by sufficiently increasing the variance of the prior. Effectively, this is what Weitzman (2009) does in deriving what he calls a dismal theorem. He introduces a fat tailed (improper) prior whose moments do not exist. Consequently, the risk-free social discount rate in Eq. (14) goes to minus infinity implying an infinite willingness to transfer (the first unit of certain) consumption into the future. Weitzman limits this willingness by the value of a (or society’s) statistical life.³¹ Instead of augmenting uncertainty, the above proposition introduces ambiguity aversion, i.e., the term ${{\mathrm{RAA}}}|1-\eta ^2| \frac{\tau ^2}{2}$, into social discounting, reflecting experimental evidence that economic agents tend to be more afraid of unknown probabilities than they are of known probabilities (most famously, Ellsberg 1961).

Observe that intertemporal risk aversion affects the correlation terms, whereas ambiguity aversion does not. Uncertainty aversion enters the stage if the corresponding uncertainty affects overall welfare. If uncertainty only affects the payoff of the marginal project, then aversion is a second-order effect absent from the social discount rate. Thus, growth variance $\sigma _g^2$ directly interacts with intertemporal risk aversion, and uncertainty over the expected growth rate, captured by $\tau ^2$, directly interacts with ambiguity aversion. Moreover, correlation between overall economic growth and the project payoff interacts growth uncertainty and the marginal project payoff. This interaction results in the correlation terms captured in Eqs. (10)–(14). Intertemporal risk aversion in these terms captures how intertemporal risk aversion with respect to correlated overall growth affects the value of the marginal project. In contrast, the ambiguous second-order distribution is not directly correlated with the project payoff and, thus, ambiguity aversion only interacts directly with the variance of the expected economic growth.

Current estimates of the parameter ${{\mathrm{RAA}}}$ in the KMM model are significantly less reliable than in the intertemporal risk aversion framework, and I refrain from a numerical analysis. Moreover, these models do not simultaneously estimate aversion to risk, ambiguity, and intertemporal substitution.³² However, the similarity of the ambiguity aversion effect to the direct effect of intertemporal risk aversion gives a good feeling for the magnitude, by which a given degree of relative ambiguity aversion changes the social discount rate. Instead of redoing these simulations for ambiguity aversion, I will explore the effects of ambiguity about correlation between project payoffs and economic growth.

4.4 The social discount rate and uncertainty about correlation

In Sect. 3.2, I discussed different arguments in favor of positive, negative, and no correlation between climate change related project payoffs and baseline growth risk. In this subsection, I introduce uncertainty about correlation. Taking the opposite extreme of a perfectly known correlation, I assume an uniform prior over the correlation coefficient, which permits an analytic solution. I am particularly interested in the difference between complete ignorance about the correlation and a known absence of correlation. The first-order distribution capturing risk is a joint normal over project productivity and economic growth as in the previous sections. I assume that the correlation $\kappa$, between project productivity $\ln y$ and economic growth $g$, is uniformly distributed on $[-1,1]$.

Proposition 4

The stochastic social discount rate in the isoelastic setting with intertemporal risk aversion and a uniform prior over correlation is

$$\begin{aligned} r&= \delta + \eta \mu _g - \eta ^2 \frac{\sigma _g^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _g^2}{2} \nonumber \\&-\ln \left[ \frac{\sinh \left\{ \eta \ \sigma _g \sigma _y + |1-\eta | {{\mathrm{RIRA}}}\ \sigma _g \sigma _y \right\} }{\eta \ \sigma _g \sigma _y + |1-\eta | {{\mathrm{RIRA}}}\ \sigma _g \sigma _y} \right] \!. \end{aligned}$$

(15)

The terms in the first line resemble the risk-free social discount rate under intertemporal risk aversion derived in Sect. 3. The second line captures the effect of uncertainty about the project and its correlation with baseline growth. This additional component is of the form $h(z)=\ln \left[ \frac{\sinh \left\{ z\right\} }{z}\right]$, non-negative, and always reduces the discount rate as long as $z=\left( \eta + |1-\eta | {{\mathrm{RIRA}}}\right) \sigma _g \sigma _y\ne 0$. This latter condition, $z\ne 0$, is satisfied as long as the project and the baseline are stochastic and preferences do not simultaneously satisfy $\eta =0$ and ${{\mathrm{RIRA}}}=0$. The function $h$ can be expanded into $h(z)=\frac{z^2}{6}-\frac{z^4}{180}+\frac{z^6}{2835}+O[z^{7}]$, where the first term already gives a good approximation for the magnitude relevant for the annual discount rate. In the setting with annual iid growth uncertainty in Sect. 3.2, I found that $z$ was below one percent in all scenarios, which makes $h(z)$ negligible. Observe that ambiguity aversion does not affect the social discount rate in Eq. (15). Only the first-order probability distribution (risk) affects overall growth, and only aversion the overall growth uncertainty finds its way into the social discount rate, valuing a marginal project. Ambiguity over the correlation coefficient merely affects the project payoff in second order and has no effect on overall economic growth. Therefore, ambiguity aversion has no impact on the social discount rate in the case of an ambiguous correlation parameter.

In the 50-year scenario, ignorance about correlation still only implies a small deviation from the case of no correlation. I adopt a pure time preference of $\delta =1.5\,\%$ and the growth scenario introduced in Sect. 3.3. I assume a probability of $p^\star =0.1\,\%$ that society will be worse off in 50 years than today. Then, in the disentangled scenario D, ignorance over correlation reduces the average discount rate from an uncorrelated $1.3\,\%$ to $1.2\,\%$.³³ In the first sensitivity scenario (S1), where ${{\mathrm{RRA}}}=9.5$ and $\eta =2$, it reduces the average discount rate from $2.7\,\%$ to $2.6\,\%$. The differences in the second sensitivity scenario (average rate of $4.1\,\%$) and in Nordhaus’s scenario (average rate of $5.1\,\%$) are negligible. The difference between the assumptions of ignorance over correlation and no correlation grows as the risk increases. For $p^\star =0.5\,\%$, ignorance as opposed to being uncorrelated reduces the average rate from $0.6\,\%$ to $0.4\,\%$ in the disentangled D scenario, and from $1.5\,\%$ to $1.3\,\%$ in the S1 scenario, still leaving the last digit unchanged in the S2 and the N scenarions (with average rates of $3.5\,\%$ (S2) and $4.9\,\%$ (N), respectively). Thus, for moderate growth risk, the intertemporal evaluation of uncorrelated stochastic projects and projects with ignorance over the correlation coefficient are both well approximated by the risk-free social discount rate. Then, only a reasonably well-founded estimate of a non-trivial correlation will have a major impact on the evaluation. For larger growth risk, the function $h(z)$ captures a small precautionary reduction in the growth rate when correlation is unknown.

5 Conclusions

The paper shows a close similarity between the recent smooth ambiguity model and a reformulated version of the well-known Epstein–Zin–Weil model. Both models disentangle uncertainty attitude from the propensity to smooth consumption over time. The smooth ambiguity model does so by capturing an additional intrinsic uncertainty aversion when evaluating subjective second-order uncertainty. Analogously, intertemporal risk aversion captures an additional intrinsic aversion to risk in the reformulated Kreps–Porteus–Epstein–Zin–Weil model. I combined the models, obtaining a threefold disentanglement between risk aversion, intertemporal consumption smoothing, and ambiguity aversion. The original version of the intertemporal smooth ambiguity model, in contrast, entangles whether ambiguity aversion captures a difference from risk attitude or a difference from consumption smoothing attitude. I showed how the similarity of the two models and their unification translates into the resulting discount rates.

Long-term investment projects are subject to major uncertainties. The assessment of climate change is an important example. The recent discussion following the Stern review has shown the primordial importance of the discount rate. This discussion is framed almost exclusively in the standard intertemporally additive expected utility setting. I pointed out several omitted contributions, three of which already arise in settings of pure risk. First, decoupling Arrow–Pratt risk aversion from intertemporal substitutability lowers the growth effect in the social discount rate. This increase in future weight is a consequence of the empirical finding that the aversion to intertemporal consumption change is overestimated when the parameter simultaneously has to capture the generally stronger aversion to risk. Second, decoupling risk aversion from the a priori independent preference for consumption smoothing also removes an implicit assumption of intrinsic or intertemporal risk neutrality. I showed that a term proportional to the coefficient of relative intertemporal risk aversion further reduces the risk-free social discount rate. The third contribution is for stochastic projects, where payoffs are correlated to the economic baseline. I showed that, for moderate risks, ignorance about correlation only implies a small precautionary effect reducing the discount rate. However, well understood correlation has a major influence on cost-benefit analysis and intertemporal evaluation. I showed that, under general uncertainty attitude, a small intertemporally correlated risk suffices to cut the discount rate back to pure time preference, eliminating the major growth effect in discounting. The application focused on analytic extensions on the Ramsey rule with simple tractable solutions. These formulas invite back of the envelope calculations determining the relative importance of the different discounting contributions. Accounting for uncertainty in large-scale economic models is usually computationally expensive. The derived formulas can guide a cost-benefit analysis of incorporating uncertainty into integrated assessment models.

Appendices

Appendix 1

Notation: The calculations in the appendix make frequent use of the abbreviations $\rho =1-\eta$ and $\alpha =1-{{\mathrm{RRA}}}$, characterizing the exponents of the isoelastic aggregators.

Proof of Proposition 1

The first part of the proof calculates the marginal value of an additional certain unit of consumption in the second period ($\mathrm{d}x_2$), expressed in terms of marginal first-period consumption units ($\mathrm{d}x_1$). This value derives from the marginal trade-off that leaves aggregate welfare

$$\begin{aligned} U(x_1,p)=\frac{x_1^\rho }{\rho } + \beta \frac{1}{\rho } \left[ {\hbox {E}}_{p} x_2^\alpha \, \right] ^{\frac{\rho }{\alpha }} \end{aligned}$$

unchanged:

$$\begin{aligned} d U(x_1,p)&= x_1^{\rho -1} \mathrm{d}x_1 + \beta \frac{1}{\alpha } \left[ {\hbox {E}}_{p} x_2^{\alpha } \right] ^{\frac{\rho }{\alpha }-1} \, {\hbox {E}}_{p} \alpha x_2^{\alpha -1} \mathrm{d}x_2 \mathop {=}\limits ^{!} 0\\&\Rightarrow x_1^{\rho -1} \mathrm{d}x_1 = - \beta \left[ {\hbox {E}}_{p} x_2^{\alpha } \, \right] ^{\frac{\rho }{\alpha }-1} \, {\hbox {E}}_{p} x_2^{\alpha -1} \mathrm{d}x_2\\&\Rightarrow \frac{\mathrm{d}x_1}{\mathrm{d}x_2} = - \beta \left[ {\hbox {E}}_{p} \left( \frac{x_2}{x_1}\right) ^{\alpha } \, \right] ^{\frac{\rho }{\alpha }-1} \, {\hbox {E}}_{p} \left( \frac{x_2}{x_1}\right) ^{\alpha -1}\\&\Rightarrow \frac{\mathrm{d}x_1}{\mathrm{d}x_2} = - \beta \left[ {\hbox {E}}_{p} e^{\alpha \ln {\frac{x_2}{x_1}}} \, \right] ^{\frac{\rho }{\alpha }-1} \, {\hbox {E}}_{p} e^{(\alpha -1)\ln {\frac{x_2}{x_1}}}\\&\Rightarrow \frac{\mathrm{d}x_1}{\mathrm{d}x_2} = - \beta \left[ e^{\alpha \mu + \alpha ^2 \frac{\sigma ^2}{2}} \, \right] ^{\frac{\rho }{\alpha }-1} \, e^{(\alpha -1)\mu + (1-\alpha )^2\frac{\sigma ^2}{2}}\\&\Rightarrow \frac{\mathrm{d}x_1}{\mathrm{d}x_2} = - \beta e^{\rho \mu + \alpha \rho \frac{\sigma ^2}{2} -\alpha \mu - \alpha ^2 \frac{\sigma ^2}{2}} \, e^{(\alpha -1)\mu + (1-\alpha )^2\frac{\sigma ^2}{2}}\\&\Rightarrow \frac{\mathrm{d}x_1}{\mathrm{d}x_2} = - \beta e^{(\rho -1) \mu + (\alpha \rho + 1-2\alpha ) \frac{\sigma ^2}{2}}\\&\Rightarrow \frac{\mathrm{d}x_1}{\mathrm{d}x_2} = - \beta e^{(\rho -1) \mu + (\alpha \rho + 1-2\alpha ) \frac{\sigma ^2}{2}}. \end{aligned}$$

The second part of the proof translates the relation into rates by defining the social discount rate $r=-\ln \frac{\mathrm{d}x_1}{-\mathrm{d}x_2}\,\left( =-\ln \frac{\mathrm{d}x_2}{-\mathrm{d}x_1}|_{\bar{U}}\right)$, the rate of pure time preference $\delta =-\ln \beta$, and $\eta =1-\rho \,\left( =\frac{1}{\sigma }\right)$. Further below, I make use of the relation $1=\frac{1-\eta }{\rho }$.

$$\begin{aligned}&\Rightarrow r = \delta + \left( 1-\rho \right) \mu - \left( \alpha \left( \rho -1\right) + 1-\alpha \right) \frac{\sigma ^2}{2} \end{aligned}$$

(16)

$$\begin{aligned}&\Rightarrow r = \delta + \eta \mu - \eta ^2 \frac{\sigma ^2}{2} + \left( \eta ^2 + \alpha \left( \eta +1\right) - 1 \right) \frac{\sigma ^2}{2} \nonumber \\&\Rightarrow r = \delta + \eta \mu - \eta ^2 \frac{\sigma ^2}{2} + \left( \eta ^2 + \frac{\alpha }{\rho }\left( 1-\eta \right) \left( \eta +1\right) - 1 \right) \frac{\sigma ^2}{2} \nonumber \\&\Rightarrow r = \delta + \eta \mu - \eta ^2 \frac{\sigma ^2}{2} + \left( \eta ^2 + \frac{\alpha }{\rho }\left( 1-\eta ^2\right) - 1 \right) \frac{\sigma ^2}{2}\nonumber \\&\Rightarrow r = \delta + \eta \mu - \eta ^2 \frac{\sigma ^2}{2} - \left( 1-\frac{\alpha }{\rho }\right) \left( 1-\eta ^2\right) \frac{\sigma ^2}{2}\nonumber \\&\Rightarrow r = \delta + \eta \mu - \eta ^2 \frac{\sigma ^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma ^2}{2}. \end{aligned}$$

(17)

$\square$

Proof of Proposition 2

For the isoelastic specification and with the definition,

$$\begin{aligned} U_2(\epsilon ) = f^{-1} \left[ {\hbox {E}}_{p(x_2,y)} f\circ u(x_2+\epsilon y) \right] =\frac{1}{\rho } \left[ {\hbox {E}}_{p(x_2,y)} (x_2+\epsilon y)^\alpha \, \right] ^{\frac{\rho }{\alpha }} \end{aligned}$$

Eq. (9) translates into

$$\begin{aligned} x_1^{\rho -1} \, \mathrm{d}x_1+\beta \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2(\epsilon ) \right| _{\epsilon =0}\mathrm{d}\epsilon \mathop {=}\limits ^{!} 0 \end{aligned}$$

(18)

In order to calculate $\left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2(\epsilon ) \right| _{\epsilon =0}\mathrm{d}\epsilon$ the following definition is useful.

$$\begin{aligned} V_\epsilon (a,b)= {\hbox {E}}_{p(x_2,y)} (x_2+\epsilon y)^a y^b. \end{aligned}$$

(19)

Then,

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2(\epsilon ) \right| _{\epsilon =0}&= \left. \frac{1}{\alpha }V_\epsilon (\alpha ,0)^{\frac{\rho }{\alpha }-1} \alpha V_\epsilon (\alpha -1,1) \right| _{\epsilon =0}\nonumber \\&= V_0(\alpha ,0)^{\frac{\rho }{\alpha }-1} V_0(\alpha -1,1) \end{aligned}$$

(20)

where equality between the first and the second lines follow from Lebesgue’s dominated convergence theorem. Analogously to step 1 in the proof of Proposition 1, I calculate with $z=\ln y$

$$\begin{aligned} V_0(\alpha ,0)&= x_1^{\alpha } \, {\hbox {E}}_{p(x_2,y)} \Big (\frac{x_2}{x_1}\Big )^\alpha =x_1^{\alpha } \, {\hbox {E}}_{p(g,z)} e^{\alpha g}\nonumber \\&= x_1^{\alpha } \, \int \limits _{-\infty }^{\infty } \int \limits _{-\infty }^{\infty } e^{\alpha g} \frac{e^{-\frac{1}{2(1-\kappa ^2)} \left[ \left( \frac{g-\mu _g}{\sigma _g}\right) ^2 + \left( \frac{z-\mu _y}{\sigma _y}\right) ^2 - 2\kappa \left( \frac{g-\mu _g}{\sigma _g}\right) \left( \frac{z-\mu _y}{\sigma _y}\right) \right] }}{ 2 \pi \sigma _g \sigma _y \sqrt{1-\rho ^2}} \mathrm{d}g \ \mathrm{d}z\qquad \quad \end{aligned}$$

(21)

$$\begin{aligned}&= x_1^{\alpha } \, e^{\alpha \mu _g+ \alpha ^2 \frac{\sigma _g^2}{2}}. \end{aligned}$$

(22)

Similarly,

$$\begin{aligned} V_0(\alpha -1,1)&= x_1^{\alpha -1} \, {\hbox {E}}_{p(x,y)} \Big (\frac{x_2}{x_1}\Big )^{\alpha -1} y = x_1^{\alpha -1} \, {\hbox {E}}_{p(g,z)} e^{(\alpha -1)g+z}\\&= x_1^{\alpha -1} \, e^{-(1-\alpha ) \left[ \mu _g - (1-\alpha ) \frac{\sigma _g^2}{2} + \kappa \sigma _g\sigma _y \right] +\mu _y +\frac{\sigma _y^2}{2}} \end{aligned}$$

so that

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2(\epsilon ) \right| _{\epsilon =0}&= x_1^{\rho -\alpha +\alpha -1} e^{(\alpha \mu _g+ \alpha ^2 \frac{\sigma _g^2}{2})({\frac{\rho }{\alpha }-1})} e^{-(1-\alpha ) \left[ \mu _g - (1-\alpha ) \frac{\sigma _g^2}{2} + \kappa \sigma _g\sigma _y \right] +\mu _y +\frac{\sigma _y^2}{2}}\nonumber \\&= x_1^{\rho -1} e^{(\rho -1) \mu _g+ \left[ \alpha (\rho -1)+(1-\alpha )\right] \frac{\sigma _g^2}{2} -(1-\alpha ) \kappa \sigma _g\sigma _y +\mu _y +\frac{\sigma _y^2}{2}}. \end{aligned}$$

(23)

Substituting the result into Eq. (18) and solving for the discount rate yields

$$\begin{aligned} r = \ln \frac{\mathrm{d}\epsilon }{-\mathrm{d}x_1}&= \delta + (1-\rho ) \mu _g - [\alpha (\rho -1) + 1-\alpha ] \frac{\sigma ^2}{2}\\&+ (1-\alpha ) \kappa \sigma _g\sigma _y - \left( \mu _y +\frac{\sigma _y^2}{2}\right) . \end{aligned}$$

The first line corresponds to Eq. (16) and, thus, Eq. (17), yielding the risk-free discount rate under intertemporal risk aversion. Moreover, the random variable $y$ was assumed to yield an expected value (project payoff) of unity, which implies

$$\begin{aligned} {\hbox {E}}_{p(x,y)} y = e^{\mu _y +\frac{\sigma _y^2}{2}} \mathop {=}\limits ^{!} 1 \qquad \Rightarrow \quad \mu _y + \frac{\sigma _y^2}{2}=0, \end{aligned}$$

eliminating the last bracket. Finally, $1-\alpha$ has to be expressed in terms of $\eta$ (capturing the effects of the standard model) and ${{\mathrm{RIRA}}}$ (capturing the additional effects of intertemporal risk averison). I find for $\rho >0$ that

$$\begin{aligned} 1-\alpha = 1-(1-\eta )(1-{{\mathrm{RIRA}}}) = \eta + (1-\eta ) {{\mathrm{RIRA}}}\end{aligned}$$

and for $\rho <0$ that

$$\begin{aligned} 1-\alpha = 1-(1-\eta )(1+{{\mathrm{RIRA}}}) = \eta - (1-\eta ) {{\mathrm{RIRA}}}. \end{aligned}$$

In both cases, this yields

$$\begin{aligned} 1-\alpha = \eta + |1-\eta | {{\mathrm{RIRA}}}, \end{aligned}$$

(24)

which gives rise to the form stated in the proposition.

Proof of Corollary 1

In case 1 of the risk-free discount rate, Eq. (8) translates $r_{50} = 50 \delta$ into the condition $\eta \, 50\mu \mathop {=}\limits ^{!} \eta ^2 \frac{\sigma ^2}{2} + {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma ^2}{2}$, which results in the stated equation for $\sigma$. Similarly in case 2, Eq. (10), $\sigma =\sigma _g=\sigma _y$, and $\eta \, 50\mu _g \mathop {=}\limits ^{!} \eta ^2 \frac{\sigma _g^2}{2} + {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _g^2}{2}- \eta \kappa \ \sigma _g \sigma _y - |1-\eta | {{\mathrm{RIRA}}}\kappa \ \sigma _g \sigma _y$ yield the result. Without the condition $\sigma =\sigma _g=\sigma _y$, the same reasoning gives statement 3 of the corollary.

Proof of Proposition 3

Define for the isoelastic specification

$$\begin{aligned} U_2^a(\epsilon )&= \varPhi ^{-1} \left\{ \int \limits _\varTheta \varPhi \left[ f^{-1}{\hbox {E}}_{p_\theta (x_2,y)} f\circ u(x_2+\epsilon y) \right] \mathrm{d}\pi (\theta ) \right\} \\&= \frac{1}{\rho }\left\{ \int \limits _\varTheta \left[ {\hbox {E}}_{p_\theta (x_2,y)} (x_2+\epsilon y)^\alpha \right] ^{\frac{\rho }{\alpha }\varphi } \mathrm{d}\pi (\theta ) \right\} ^{\frac{1}{\varphi }}. \end{aligned}$$

I have to solve once more the equation

$$\begin{aligned} \mathrm{d}V(x_1,p,\pi )= x_1^{\rho -1} \, \mathrm{d}x_1+\beta \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U^a_2(\epsilon ) \right| _{\epsilon =0}\mathrm{d}\epsilon \mathop {=}\limits ^{!} 0 \end{aligned}$$

(25)

for $r=\ln \frac{\mathrm{d}\epsilon }{-\mathrm{d}x_1}$. Making once more use of the definition

$$\begin{aligned} V_\epsilon (a,b)= {\hbox {E}}_{p_\theta (x_2,y)} (x_2+\epsilon y)^a y^b \,, \end{aligned}$$

where $\theta$ replaces $\mu _g$ in $p_{(x,y)}$ of Eqs. (19) and (21), I find

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2^a(\epsilon ) \right| _{\epsilon =0}&= \frac{1}{\rho }\frac{1}{\varphi }\left\{ \int \limits _\varTheta V_\epsilon (\alpha ,0)^{\frac{\rho }{\alpha }\varphi } \mathrm{d}\pi (\theta ) \right\} ^{\frac{1}{\varphi }-1}\nonumber \\&\left. \left\{ \int \limits _\varTheta {\frac{\rho }{\alpha }\varphi } V_\epsilon (\alpha ,0)^{\frac{\rho }{\alpha }\varphi -1} \alpha V_\epsilon (\alpha -1,1) \mathrm{d}\pi (\theta ) \right\} \right| _{\epsilon =0}\nonumber \\&= \left\{ \int \limits _\varTheta V_0(\alpha ,0)^{\frac{\rho \varphi }{\alpha }} \mathrm{d}\pi (\theta ) \right\} ^{\frac{1}{\varphi }-1}\nonumber \\&\int \limits _\varTheta V_0(\alpha ,0)^{\frac{\rho \varphi }{\alpha }-1} V_0(\alpha -1,1) \mathrm{d}\pi (\theta ). \end{aligned}$$

(26)

With the help of Eq. (22), the expression $\{ \cdot \}$ calculates to

$$\begin{aligned} \int \limits _\varTheta x_1^{\alpha (\frac{\rho \varphi }{\alpha })} \, e^{(\alpha \theta + \alpha ^2 \frac{\sigma _g^2}{2})(\frac{\rho \varphi }{\alpha })} \mathrm{d}\pi (\theta )&= x_1^{\rho \varphi } e^{\rho \varphi \alpha \frac{\sigma _g^2}{2}}\int \limits _\varTheta e^{\rho \varphi \theta } \frac{e^{-\frac{1}{2} \left( \frac{\theta -\mu _g}{\sigma _g}\right) ^2}}{ \sqrt{2 \pi } \sigma _g } \mathrm{d}\theta \\&= x_1^{\rho \varphi } e^{\rho \varphi \alpha \frac{\sigma _g^2}{2}} e^{\rho \varphi \mu _g+\rho ^2\varphi ^2\frac{\tau _g^2}{2}}. \end{aligned}$$

Acknowledging the equality of Eqs. (20) and (23) and their similarity to the second integrand in Eq. (26) (for $\rho \leftrightarrow \rho \varphi$), this second integral becomes

$$\begin{aligned}&\int \limits _\varTheta V_0(\alpha ,0)^{\frac{\rho \varphi }{\alpha }-1} V_0(\alpha -1,1) \mathrm{d}\pi (\theta ) \\&\quad =\int \limits _\varTheta x_1^{\rho \varphi -1} e^{(\rho \varphi -1) \theta + \left[ \alpha (\rho \varphi -1)+(1-\alpha )\right] \frac{\sigma _g^2}{2} -(1-\alpha ) \kappa \sigma _g\sigma _y +\mu _y +\frac{\sigma _y^2}{2}} \mathrm{d}\pi (\theta ) \\&\quad =x_1^{\rho \varphi -1} e^{\left[ \alpha (\rho \varphi -1)+(1-\alpha )\right] \frac{\sigma _g^2}{2} -(1-\alpha ) \kappa \sigma _g\sigma _y +\mu _y +\frac{\sigma _y^2}{2}} \int \limits _\varTheta e^{(\rho \varphi -1) \theta } \mathrm{d}\pi (\theta ) \\&\quad =x_1^{\rho \varphi -1} e^{\left[ \alpha (\rho \varphi -1)+(1-\alpha )\right] \frac{\sigma _g^2}{2} -(1-\alpha ) \kappa \sigma _g\sigma _y +\mu _y +\frac{\sigma _y^2}{2}} e^{(\rho \varphi -1)\mu _g + (\rho \varphi -1)^2\frac{\tau _g^2}{2}}. \end{aligned}$$

Substituting these results back into Eq. (26) delivers

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2^a\left( \epsilon \right) \right| _{\epsilon =0}&= x_1^{\rho \varphi \left( \frac{1}{\varphi }-1\right) } e^{\left( \rho \varphi \alpha \frac{\sigma _g^2}{2}\right) \left( \frac{1}{\varphi }-1\right) } e^{\left( \rho \varphi \mu _g+\rho ^2\varphi ^2\frac{\tau _g^2}{2}\right) \left( \frac{1}{\varphi }-1\right) }\\&x_1^{\rho \varphi -1} e^{\left[ \alpha \left( \rho \varphi -1\right) +\left( 1-\alpha \right) \right] \frac{\sigma _g^2}{2} -\left( 1-\alpha \right) \kappa \sigma _g\sigma _y +\mu _y +\frac{\sigma _y^2}{2}} e^{\left( \rho \varphi -1\right) \mu _g + \left( \rho \varphi -1\right) ^2\frac{\tau _g^2}{2}}\\&= x_1^{\rho -1} e^{\left[ \alpha \left( \rho -1\right) +\left( 1-\alpha \right) \right] \frac{\sigma _g^2}{2}+\left( \rho -1\right) \mu _g +\left[ \rho \varphi \left( \rho -1\right) +1-\rho \varphi \right] \frac{\tau _g^2}{2}-\left( 1-\alpha \right) \kappa \sigma _g\sigma _y +\mu _y +\frac{\sigma _y^2}{2}}. \end{aligned}$$

Substituting this result into Eq. (25) and solving for $r=\ln \frac{\mathrm{d}\epsilon }{-\mathrm{d}x_1}$ yields analogously to the proof of Proposition 2, the discount rate

$$\begin{aligned} r&= \delta + \eta \mu _g - \eta ^2 \frac{\sigma _g^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _g^2}{2} + \ \eta \, \kappa \ \sigma _g \sigma _y \\&+ |1-\eta | {{\mathrm{RIRA}}}\ \kappa \ \sigma _g \sigma _y - [1-2\rho \varphi +\rho ^2\varphi ]\frac{\tau _g^2}{2}. \end{aligned}$$

The last term can be rearranged to the form

$$\begin{aligned}{}[1-2\rho \varphi +\rho ^2\varphi ]\frac{\tau _g^2}{2}&= [(1-\varphi )+\varphi (1-\rho )-\varphi \rho (1-\rho )]\frac{\tau _g^2}{2}\\&= [(1-\varphi )+(1-\rho )^2+(\varphi -1)(1-\rho )^2]\frac{\tau _g^2}{2}\\&= [\eta ^2+(1-\varphi )(1-\eta ^2)]\frac{\tau _g^2}{2} =\eta ^2 \frac{\tau _g^2}{2} + {{\mathrm{RAA}}}|1-\eta ^2| \frac{\tau _g^2}{2}, \end{aligned}$$

completing the proof. $\square$

Proof of Proposition 4

Up to Eq. (26), the proof is identical to that of Proposition 3. In the next step, in $V_0(\alpha ,0)^{\frac{\rho \varphi }{\alpha }}$ the ambiguity parameter $\theta$ replaces $\kappa$ instead of $\mu _g$. Thus, the first integral in Eq. (26) becomes

$$\begin{aligned} \int \limits _\varTheta x_1^{\alpha (\frac{\rho \varphi }{\alpha })} \, e^{(\alpha \mu _g+ \alpha ^2 \frac{\sigma _g^2}{2})(\frac{\rho \varphi }{\alpha })} \mathrm{d}\pi (\theta )&= x_1^{\rho \varphi } e^{\rho \varphi \mu _g+\rho \varphi \alpha \frac{\sigma _g^2}{2}} \int \limits _{-1}^{1} \frac{1}{2} \mathrm{d}\theta \\&= x_1^{\rho \varphi } e^{\rho \varphi \mu _g+\rho \varphi \alpha \frac{\sigma _g^2}{2}}. \end{aligned}$$

For the integrand of the second integral in Eq. (26), I find

$$\begin{aligned} V_0(\alpha -1,1)= x_1^{\alpha -1} e^{(\alpha -1) \mu _g+(\alpha -1)^2 \frac{\sigma _g^2}{2}+(\alpha -1) \theta \sigma _g \sigma _y+\mu _y+\frac{\sigma _y^2}{2}} \end{aligned}$$

delivering the integral

$$\begin{aligned}&\int \limits _\varTheta V_0(\alpha ,0)^{\frac{\rho \varphi }{\alpha }-1} V_0(\alpha -1,1) \mathrm{d}\pi (\theta ) \\&\quad =\int \limits _\varTheta x_1^{\rho \varphi -\alpha } e^{\rho \varphi \mu _g+\rho \varphi \alpha \frac{\sigma _g^2}{2}-\alpha \mu _g-\alpha ^2 \frac{\sigma _g^2}{2}}\\&\quad x_1^{\alpha -1} e^{(\alpha -1) \mu _g+(\alpha -1)^2 \frac{\sigma _g^2}{2}+(\alpha -1) \theta \sigma _g \sigma _y+\mu _y+\frac{\sigma _y^2}{2}} \mathrm{d}\pi (\theta ) \\&\quad =x_1^{\rho \varphi -1} e^{(\rho \varphi -1) \mu _g+(\rho \varphi \alpha -2\alpha -1) \frac{\sigma _g^2}{2} +\mu _y+\frac{\sigma _y^2}{2}} \int \limits _{-1}^{1} e^{(\alpha -1) \theta \sigma _g \sigma _y} \frac{1}{2} \mathrm{d}\theta \\&\quad =x_1^{\rho \varphi -1} e^{(\rho \varphi -1) \mu _g+(\rho \varphi \alpha -2\alpha -1) \frac{\sigma _g^2}{2} +\mu _y+\frac{\sigma _y^2}{2}} \quad \frac{\sinh [(\alpha -1) \sigma _g \sigma _y]}{(\alpha -1)\sigma _g\sigma _y}. \end{aligned}$$

Substituting these results back into Eq. (26) returns the second-period welfare change in $\epsilon$:

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}\epsilon } U_2^a(\epsilon )\right| _{\epsilon =0}&= x_1^{\rho \varphi \left( \frac{1}{\varphi }-1\right) } e^{\left( \rho \varphi \mu _g+\rho \varphi \alpha \frac{\sigma _g^2}{2}\right) \left( \frac{1}{\varphi }-1\right) }\\&x_1^{\rho \varphi -1} e^{(\rho \varphi -1) \mu _g+(\rho \varphi \alpha -2\alpha -1) \frac{\sigma _g^2}{2} +\mu _y+\frac{\sigma _y^2}{2}} \quad \frac{\sinh [(\alpha -1) \sigma _g \sigma _y]}{(\alpha -1)\sigma _g\sigma _y}\\&= x_1^{\rho -1} e^{(\rho -1) \mu _g +(\rho \alpha -2\alpha -1) \frac{\sigma _g^2}{2} +\mu _y+\frac{\sigma _y^2}{2}} \quad \frac{\sinh [(\alpha -1) \sigma _g \sigma _y]}{(\alpha -1)\sigma _g\sigma _y}. \end{aligned}$$

Substituting this result into Eq. (25) and solving for $r=\ln \frac{\mathrm{d}\epsilon }{-\mathrm{d}x_1}$ yields analogously to the proof of Proposition 2, the discount rate

$$\begin{aligned} r =&\delta + \eta \mu _g - \eta ^2 \frac{\sigma _g^2}{2} - {{\mathrm{RIRA}}}\, |1-\eta ^2| \frac{\sigma _g^2}{2} - \ln \left[ \frac{\sinh [(\alpha -1) \sigma _g \sigma _y]}{(\alpha -1)\sigma _g\sigma _y} \right] . \end{aligned}$$

By symmetry of the hyperbolic sine, the sign of $(\alpha -1)$ can be flipped simultaneously in the numerator and the denominator. Using Eq. (24) to substitute for $(1-\alpha )$ then yields the result stated in the proposition. $\square$

Appendix 2

The following proposition formalizes how intertemporal risk aversion, defined in the sense of Eq. (4), translates into the curvature of the function $f$ in a preference representation of the form (3).³⁴

Proposition 5

Let preferences over $X\times P$ be represented by Eq. (3) with a continuous function $u:X\rightarrow {\mathbb R}$ and a strictly increasing and continuous function $f:U\rightarrow {\mathbb R}$, where $U=u(X)$ and $\beta =1$.

• (a) The corresponding decision maker is (weakly) intertemporal risk averse [loving], if and only if the function $f$ is concave [convex].

• (b) The corresponding decision maker is intertemporal risk neutral, if and only if there exist $a,b \in {\mathbb R}$ such that $f(z)=a z + b$. An intertemporal risk neutral decision maker maximizes intertemporally additive expected utility (Eq. (1)).

Proof of Proposition 5

(a) Sufficiency of axiom (4): The premise of axiom (4) translates with $\beta =1$ into the representation (3) as

$$\begin{aligned} \displaystyle \left( x^*,x^*\right)&\sim \displaystyle \left( x_1,x_2\right) \nonumber \\ \Leftrightarrow \displaystyle u(x^*) + u(x^*)&= \displaystyle u(x_1) + u(x_2)\\ \Leftrightarrow \displaystyle u(x^*)&= \displaystyle \frac{1}{2} u(x_1) + \frac{1}{2} u(x_2)\nonumber \end{aligned}$$

(27)

Writing the implication of the axiom in terms of representation (3) yields

$$\begin{aligned} \begin{array}{llll} &{} (x^*,x^*) &{} \succ &{} \displaystyle \left( x^*,\frac{1}{2} x_1 + \frac{1}{2} x_2\right) \\ \Leftrightarrow &{} u(x^*) + &{} \ge &{} \displaystyle f^{-1} \left( \frac{1}{2} f\circ u(x_1) + \frac{1}{2} f\circ u(x_2)\right) . \end{array} \end{aligned}$$

(28)

Combining Eqs. (27) and (28) returns

$$\begin{aligned} \begin{array}{lccc}&\displaystyle \frac{1}{2} u(x_1) + \frac{1}{2} u(x_2)&\ge \displaystyle f^{-1} \left( \frac{1}{2} f\circ u(x_1) + \frac{1}{2} f\circ u(x_2)\right) , \end{array} \end{aligned}$$

(29)

which for an increasing [decreasing] version of $f$ is equivalent to

$$\begin{aligned} \begin{array}{lccc} \Leftrightarrow&\displaystyle f \left( \frac{1}{2} u(x_1) + \frac{1}{2} u(x_2) \right)&>\; [<]\;&\displaystyle \frac{1}{2} f\circ u(x_1) + \frac{1}{2} f\circ u(x_2). \end{array} \end{aligned}$$

Defining $z_i=u(x_i)$, the equation becomes

$$\begin{aligned} \begin{array}{lccc} \Leftrightarrow&\displaystyle f \left( \frac{1}{2} z_1 + \frac{1}{2} z_2 \right)&\ge \; [\le ]\;&\displaystyle \frac{1}{2} f (z_1) + \frac{1}{2} f (z_2). \end{array} \end{aligned}$$

(30)

Because preferences are assumed to be representable in the form (3), there exists a certainty equivalent $x^*$ to all lotteries $\frac{1}{2} x_1 + \frac{1}{2} x_2$ with $x_1,x_2 \in X$. Taking $x^*$ to be the certainty equivalent, the premise and, thus, Eq. (30) have to hold for all $z_1,z_2 \in u(X)$. Therefore, $f$ has to be concave [convex] on $U(x)$ ((Hardy et al. 1964, 75)).

Necessity of axiom 4 The necessity is seen to hold by going backward through the proof of sufficiency above. Strict concavity [convexity] of $f$ with $f$ increasing [decreasing] implies that Eq. (30) and, thus, Eq. (29) have to hold for $z_1,z_2 \in u(X)$. The premise corresponding to (27) guarantees that Eq. (29) implies Eq. (28) which yields the implication in condition (4). Replacing $\succeq$ by $\preceq$ and $\ge$ by $\le$ in the proof above implies that the decision maker is intertemporal risk averse, if and only if $f$ is convex [for an increasing version of $f$ and concave for $f$ decreasing].

(b) The decision maker is intertemporal risk neutral, if and only if $f$ is concave and convex on $u(X)$, which is equivalent to $f$ being linear.³⁵ However, a linear function $f$ cancels out in representation (3) and makes it identical to the intertemporally additive expected utility standard representation (1).

Appendix 3

1.1 Relation to Proposition 1 and Gollier (2002)

Equation (14) in Gollier (2002) is

$$\begin{aligned} r=\delta + \eta \ {\hbox {E}}\ \tilde{g} - {{\mathrm{RRA}}}(1+\eta ) \frac{\text{ Var }(\tilde{g})}{2} \ , \end{aligned}$$

where $\delta =\frac{1}{\beta }-1,\,\tilde{g}=\frac{\tilde{x}_2}{x_1}-1$, and $\beta$ denotes Gollier’s utility discount factor. The tilde ($\tilde{}$) marks random variables. In contrast, Eq. (16) for the isoelastic normal case translates into

$$\begin{aligned} r = \delta + \eta \mu - ((1-{{\mathrm{RRA}}}) (-\eta ) + {{\mathrm{RRA}}}) \frac{\sigma ^2}{2} = \delta + \eta \mu - {{\mathrm{RRA}}}(1+\eta ) \frac{\sigma ^2}{2} + \eta \frac{\sigma ^2}{2}. \end{aligned}$$

Thus, Gollier’s approximate formula underestimates the social discount rate by the term $\eta \frac{\sigma ^2}{2}$. Much of the difference can be traced back to the first step of his derivation, where the Arrow–Pratt approximation of the certainty equivalent (or equivalently the certainty-equivalent growth rate) loses a term proportional to $\frac{\sigma ^2}{2}$ in a setting with isoelastic preferences and a normal growth rate.

In a setting with CARA utility and a normal distribution of the growth rate Gollier’s approximation does better. I assume that Gollier’s growth rate $\tilde{g}=\frac{\tilde{x}_2}{x_1}-1\sim N(\mu ,\sigma ^2)$, which is equivalent to a distribution of second-period consumption $\tilde{x}_2 \sim N\big (x_1(1+\mu ),x_1^2\sigma ^2\big ) \equiv N(\mu _x,\sigma _x^2)$. Moreover, the assumption of CARA aggregators translates into $u(x)=-\frac{\exp (-A_u x)}{A_u}$ for utility and $v(x)=-\frac{\exp (-A_v x)}{A_v}$ for Arrow–Pratt risk aversion, adopting Gollier’s notation where $A_u$ is absolute aversion to intertemporal substitution and $A_v$ is absolute aversion to risk in the Arrow–Pratt sense. Then, the resulting exact discount rate becomes

$$\begin{aligned} r&= \frac{1}{\beta } \exp \left( A_u \left[ \mu _x - x_1 - A_v \frac{\sigma _x^2}{2} \right] \right) \end{aligned}$$

(31)

$$\begin{aligned}&\approx \delta + A_u \ (\mu _x - x_1) - A_u \ A_v \frac{\sigma _x^2}{2} = \delta + A_u \ x_1 \ \mu - A_u \ A_v \ x_1^2 \frac{\sigma ^2}{2}. \end{aligned}$$

(32)

The second line is equivalent to Gollier’s equation (12), before replacing his absolute aversion measures with relative aversion measures. Thus, in the CARA-normal case, the quality of his approximation is given by the quality of the approximation going from Eqs. (31) to (32). For this approximation to hold, risk has to be moderate and expected absolute growth has to be small. Small absolute growth is equivalent to a low expected growth rate or a low present consumption level.