On the location of public bads: strategy-proofness under two-dimensional single-dipped preferences

Abstract

In a model with finitely many agents who have single-dipped Euclidean preferences on a polytope in the Euclidean plane, a rule assigns to each profile of reported dips a point of the polytope. A point $x$ of the polytope is called single-best if there is a point $y$ of the polytope such that $x$ is the unique point of the polytope at maximal distance from $y$. It is proved that if the polytope does not have either exactly two single-best points or exactly four single-best points which form the vertices of a rectangle, then any Pareto optimal and strategy-proof rule is dictatorial. If the polytope has exactly two single-best points, then there are non-dictatorial strategy-proof and Pareto optimal rules, which can be described by committee voting (simple games) between the two single-best points. This also holds if there are exactly four single-best points which form the vertices of a rectangle, but in that case, we limit ourselves to describing an example of such a rule. The framework under consideration models situations where public bads such as garbage dumping grounds or nuclear plants have to be located within a confined region.

1 Introduction

Consider the problem of locating a windmill park, garbage dumping ground, heavy industry, or nuclear plant within a confined area, such as a city, province, or country. These are examples of public bads: People agree on their usefulness or even necessity but typically do not want them in their backyards. In this paper, we assume that the public bad is to be located within a given region—a subset of the plane—and that the location is determined by voting among a set of agents (for instance, inhabitants of the region or political representatives). Each agent is characterized by a Euclidean single-dipped preference: There is a worst point, the dip, which is a specific point of the region, and preference increases with the Euclidean distance from this dip. A vote then consists of reporting one’s dip. Typically, what an agent regards to be his dip is private knowledge: It could coincide with his residence, the school of his children, an important natural resource, etc. Also, the location of a public bad is typically decided for a longer period, whereas an agent’s future situation is subject to change, only possibly known to the agent. So a central planner may not have full information about the true preferences of the agents. Therefore, in order for the location of the public bad to be based on the right information about the agents’ preferences, the (voting) rule should be strategy-proof: No agent should be able to achieve a location farther away from his true dip by not reporting truthfully. Additionally, we will require the rule to be Pareto optimal: It should not assign a location for which there is another location at least as distant for all and strictly farther away for some agents, given the reported dips.

In this paper, we assume that the region is a two-dimensional polytope $A$, i.e., the convex hull of at least three but finitely many points, which are the extreme points of the polytope. An important concept is that of a single-best point, i.e., a point of $A$ that is the unique point at maximal distance from some other point of $A$. Single-best points are always extreme points, although not every extreme point is necessarily a single-best point. For instance, if the boundary of $A$ is a triangle with vertices $a,\,b$, and $c$, then these three points are the single-best points if the triangle is acute. However, if the angle at $a$ is right, then $a$ can be a best point, but it is not a single-best point, and if this angle is obtuse, then $a$ is not even a best point.

We assume that there are $n \ge 2$ agents; a profile is a vector of $n$ points of $A$—interpreted as a vector of reported dips—and a rule assigns a point of $A$ to each profile. Our main results are as follows. If $A$ does not have exactly two single-best points and if $A$ does not have exactly four single-best points which form the vertices of a rectangle, then a strategy-proof and Pareto optimal rule must be dictatorial: There is a fixed agent $d$ such that the rule always assigns a point at maximal distance from $d$’s dip. This result is obtained by proving that the set of decisive coalitions is an ultrafilter and, in particular, closed under taking intersections. The last property does not hold if $A$ has exactly two single-best points or exactly four single-best points which are the vertices of a rectangle. For the case that $A$ has exactly two single-best points $a$ and $b$—which means, roughly, that $A$ is sufficiently flat with $a$ and $b$ as ‘end points’—we characterize all strategy-proof and Pareto optimal rules under a few mild additional (tie-breaking) assumptions: Such rules are described by committee (simple game) voting between $a$ and $b$. Similarly, for the case where $A$ has exactly four single-best points which are the vertices of a rectangle, we can obtain strategy-proof and Pareto optimal rules by committee voting between the upper and lower and between the left and right vertices of the rectangle; for this case, we content ourselves by giving an example.

The message of the paper is therefore that dictatorship can be avoided only if the region is sufficiently flat (in terms of width) or if we can identify four locations which are the vertices of a rectangle and which are the only single-best points. The lesson to be learnt from these results is that in order to make strategy-proof and Pareto optimal (e.g.) majority voting possible, one has to restrict the range of potential locations for the public bad accordingly. Although there is certainly some hindsight intuition for these results—like a small induced preference domain in the flat case and separability of preferences along axes in the rectangular case—the proofs are far from trivial. In particular, it is far from straightforward to show that the mentioned cases are the only ones in which dictatorship can be avoided.

Since some parts of the proof rely on the finiteness of the set of extreme points of a region $A$, extension of our results to general compact convex set does not seem straightforward. In a companion note (Öztürk et al. 2013), we show that dictatorship continues to hold when $A$ is a disk (a circle and its inside), but this needs a separate proof.

Related literature To the dictatorship part of our results, the classical work of Gibbard (1973) and Satterthwaite (1975) does not directly apply since we do not have full preference domains. An exception is the acute triangle: If we know that the rule assigns a vertex, then in this case dictatorship follows from Gibbard-Satterthwaite, since single-dipped preferences generate the full domain of six (strict) preferences over the vertices (see the end of Sect. 3).

In one dimension, single-dipped and single-peaked preferences are both special cases of value restriction (Inada 1964), but it is well known that the consequences for Pareto optimal and strategy-proof rules are quite different. Also in spatial models like ours, this is the case. In particular, under single-dipped preferences, strategy-proofness and Pareto optimality force the outcome of the rule to be on the boundary of the region under consideration—which is also why the restriction to compact sets is natural in the present framework. As a result, under single-dipped preferences much is going to depend on the shape of the boundary of the region. Typically, also, continuity of a rule is not a condition that can be imposed since even a dictatorial rule is not continuous: A small change in the preference (dip) of the dictator may cause the outcome to swap to the opposite side of the region; the same happens with committee voting between two points or between the four corner points of a rectangle. Thus, adding continuity as a requirement would lead to genuine impossibility. Generally speaking, single peakedness of preferences seems to allow for more possibilities and to lead less frequently to dictatorship (Black 1948; Moulin 1980; Border and Jordan 1983).

In spite of its apparent relevance, existing work on collective decision making in the presence of single-dipped preferences is relatively limited. As far as we know ours is the first paper to study strategy-proofness under single-dipped preferences in two-dimensional space. The one-dimensional case has been studied before. Peremans and Storcken (1999) characterize all strategy-proof rules for the case that $A$ is an arbitrary subset of the real line, and preferences are single-dipped (and not necessarily symmetric). An implication of their work is that individual and coalitional strategy-proofness are equivalent in this model. Also Barbera et al. (2012) reach this conclusion and sharpen the bounds on the range of strategy-proof rules, depending on different subclasses of single-dipped preferences. Manjunath (2009) specifically studies unanimous (instead of Pareto optimal) and strategy-proof rules defined on a real interval, i.e., a one-dimensional polytope, for a larger class of single-dipped preferences, i.e., not only Euclidean preferences—see the concluding section for a discussion about related extensions within our framework. Typically, in this one-dimensional case, strategy-proof and unanimous rules can be characterized as committee voting between the end points of the interval, comparable to our case with two single-best points. Thus, all these works concern the location of a public bad where the region $A$ is one-dimensional.

The private good case with single-dipped preferences is considered in Klaus et al. (1997), which deals with the division of a perfectly divisible commodity. Klaus (2001) considers the case where this commodity is an indivisible object and has to be allocated to one of the agents. Ehlers (2002) considers the probabilistic allocation of an indivisible object.

The line of reasoning in the proof of the dictatorship result, based on decisive coalitions and ultrafilters, has been used before, see Kirman and Sondermann (1972) and Hansson (1976).

Finally, there is a—more extensive—literature on mechanism design for the location of public bads (obnoxious facilities) when monetary transfers are allowed, see for instance Kunreuther and Kleindorfer (1986) or, more recently, Lescop (2007) or Besfamille and Lozachmeur (2010). Sakai (2012) considers the location of a public bad as a pricing problem, where locations differ in cost. Berliant et al. (2013) presents an equilibrium model to determine the location of polluting firms.

Organization of the paper Section 2 starts with notations, the basic model, and some preliminary results. In Sect. 3 we derive the dictatorship result, and in Sect. 4 we consider the non-dictatorship cases. Section 5 concludes. Some auxiliary results and some of the proofs are delegated to the Appendix.

2 Notations, basic model, and preliminaries

We start by fixing some notations to be used throughout the paper.

2.1 Notations

For a subset $X$ of ${\mathbb {R}}^{2}$ (endowed with the usual topology), we denote by $\partial X$ its boundary, by $X^{\circ }$ its interior, and by $\overline{X}$ its closure.

Some of the following notions are illustrated in Figure 1.

Fig. 1

Illustrating some notions of Sect. 2.1

Let $a,b,c\in {\mathbb {R}}^{2}$ be three different points. Then $[a,b]$ denotes the closed line segment between points $a$ and $b,\,]a,b[$ the (relatively) open line segment between $a$ and $b$, and $[a,b[$ and $]a,b]$ the two half open line segments. The midpoint of $[a,b]$ is denoted by $m_{a,b}$ and its perpendicular bisector by $\ell _{a,b}$. For $x\in {\mathbb {R}}^2$, we denote by $\sigma _{a,b}(x)$ the reflection of $x$ in the line $\ell _{a,b}$, i.e., $\ell _{a,b}$ is the perpendicular bisector of $[x,\sigma _{a,b}(x)]$.

If $a,\,b$, and $c$ are non-collinear, we denote $m_{a,b,c} = \ell _{a,b} \cap \ell _{b,c} \cap \ell _{a,c}$ (and regard $m_{a,b,c}$ as a point rather than a set). Further, $\ell (a,b)$ denotes the straight line through the points $a$ and $b$.

The Euclidean distance between $a$ and $b$ is denoted by $||a-b||$. A straight line $\ell$ divides the plane ${\mathbb {R}}^{2}$ into two half-planes. For $a\notin \ell ,\,H(\ell ,a)$ indicates the closed half-plane containing $a$; we write $H^\circ (\ell ,a)$ for the open half-plane, thus $H^\circ (\ell ,a)=H(\ell ,a)^\circ$. The circle with center $a$ and radius $r\ge 0$ is denoted by $\odot (a,r)$, hence $\odot (a,r)=\{x\in {\mathbb {R}} ^{2}:||a-x||\,=r\}$. For $x,y \in {\mathbb {R}}^2$ on the same circle with center $a \in {\mathbb {R}}^2$, we write $[a;x \!\!\smallfrown \!\!y]$ for the arc between $x$ and $y$, that is, $[a;x\!\!\smallfrown \!\!y] = \odot (a,||a-x||)\backslash H^\circ (\ell (x,y),a)$ if $a$ is not on $\ell (x,y)$, otherwise $[a;x\!\!\smallfrown \!\!y] = \odot (a,||a-x||)$.

For an arbitrary set $D$, we denote by $|D|$ its cardinality.

2.2 The basic model

We next formulate the basic model. There is a finite set $N=\{1,\ldots , n\}\,(n \ge 2)$ of agents and a compact subset $A \subseteq {\mathbb {R}}^{2}$ of alternatives or simply points.¹ Each agent is endowed with a (Euclidean single-dipped) preference $R_{x},\,x\in A$, defined as follows: for all $y,z \in A,\,(y,z) \in R_x$ if $||x-y|| \ge ||x-z||$. The point $x$ is the dip of preference $R_x$. Clearly, preference $R_{x}$ is completely determined by its dip; therefore, if convenient, we will denote a preference by its dip. An element $p=(p(1),\ldots , p(n)) \in A^N$, where $p(i)$ is the dip of agent $i$, is called a profile (of single-dipped preferences). A social choice function or simply rule is a map $\varphi :A^{N}\rightarrow A$. We are interested in rules that satisfy the following two properties. Rule $\varphi$ is called

• [PO] Pareto optimal if for every profile $p\in A^{N}$, every agent $i\in N$, and every point $a\in A$ with $||p(i)-a|| > ||p(i)-\varphi (p)||$ there is an agent $j\in N$ such that $||p(j)-a|| < ||p(j)-\varphi (p)||$;

• [SP] strategy-proof if for every agent $i$ in $N$ and all profiles $p,q \in A^{N}$, with $q(j)=p(j)$ for all $j\in N\backslash \{i\}$, we have $||p(i)-\varphi (p)|| \ge ||p(i)-\varphi (q)||$.

The interpretation of Pareto optimality is as usual, and strategy-proofness (also as usual) implies that no agent can improve the outcome by misreporting his preference.

A subset of $N$ is called a coalition. Strategy-proofness is equivalent to the following condition (see Lemma 6.1 in the Appendix for a proof). Rule $\varphi$ is called

• [ISP] intermediate strategy-proof if for every coalition $S\subseteq N$ and all profiles $p,q \in A^{N}$ such that $p(j)=q(j)$ for all $j\in N\backslash S$ and there is a point $a$ with $p(i)=a$ for all $i\in S$, we have $||a-\varphi (p)|| \ge ||a-\varphi (q)||$.

Intermediate strategy-proofness says that if all agents of a coalition $S$ in some profile $p$ have the same preference, and these agents simultaneously misrepresent their preferences in possibly different ways, resulting in a profile $q$, then no agent of $S$ benefits if the rule $\varphi$ is applied. Observe that this is weaker than what is usually called ‘coalitional strategy-proofness,’ since in ISP it is assumed that the true preferences of the agents of a coalition $S$ are identical.

Often ISP will be used instead of SP without explicit mentioning.

2.3 Preliminary results

Let $S\subseteq N$ be a coalition and let $a,b \in A$. By $(a^S,b^{N\setminus S})\in A^N$, we denote the profile $p$ with $p(i)=a$ for all $i\in S$ and $p(i)=b$ for all $i\in N\setminus S$. (If $S=N$ we usually write $a^N$ instead of $(a^N,b^\emptyset )$.) To such a two-dipped profile, a Pareto optimal rule always assigns a boundary point, as the following lemma shows.

Lemma 2.1

Let $a,b\in A,\,S\subseteq N$, and $p=(a^S,b^{N \setminus S})$. Let $\varphi :A^{N}\rightarrow A$ be a Pareto optimal rule. Then $\varphi (p)\in \partial A$.

Proof

Let $\ell = \ell (a,b)$ if $a\ne b$ and let $\ell$ be an arbitrary straight line through $a$ if $a=b$. Let $x$ be the intersection of $\ell$ and the line $\ell '$ through $\varphi (p)$ perpendicular to $\ell$. Now for points $c$ on $\ell '$ such that $\varphi (p)\in \; ]c,x]$, it follows that $||a-c|| > ||a-\varphi (p)||$ and $||b-c||>||b-\varphi (p)||$. Hence, by Pareto optimality, we must have $c \notin A$, so that $\varphi (p)$ cannot be an interior point of $A$. Hence $\varphi (p)\in \partial A$. $\square$

Observe that the proof of this lemma does not use the compactness of the set $A$. Thus, the lemma justifies our restriction to compact sets: If $A$ is not bounded, then a Pareto optimal rule does not exist, and if $A$ is not closed, it may also fail to exist.

For a preference $R_a$, the set of best points is denoted by $\mathfrak {b}(R_a)$ or by $\mathfrak {b}(a)$, i.e., $\mathfrak {b}(R_{a})=\mathfrak {b}(a)=\{y\in A : ||a-y||\,\ge ||a-z||$ for all $z\in A\}$. A coalition $S\subseteq N$ is decisive (given a rule $\varphi$) if $\varphi (p)\in \mathfrak {b}(R_{a})$ for all $a\in A$ and all $p\in A^{N}$ with $p(i)=a$ for all $i\in S$. Clearly, if $S$ is decisive and $S\subseteq T\subseteq N$, then $T$ is decisive. A rule $\varphi$ is dictatorial if there is a dictator, i.e., an agent $d\in N$ such that $\{d\}$ is decisive.

A collection ${\mathcal {W}}$ of subsets of $N$ is called an ultrafilter on $N$ if for all subsets $S,T \subseteq N$ we have (i) $\emptyset \notin {\mathcal {W}}$, (ii) if $S,T\in {\mathcal {W}}$, then $S\cap T\in {\mathcal {W}}$, and (iii) $S\in {\mathcal {W}}$ or $N\setminus S\in {\mathcal {W}}$. We have the following familiar property, of which we include the simple proof for completeness. For more information on ultrafilters, see for instance Aliprantis and Border (2006).

Lemma 2.2

Let ${\mathcal {W}}$ be an ultrafilter on $N$. Then there exists a unique $d\in N$ such that $\{d\}\in {\mathcal {W}}$.

Proof

By properties (i) and (ii) of an ultrafilter, there can be at most one such $d$. If $N \setminus \{i\} \in {\mathcal {W}}$ for all $i\in N$ then $\cap _{i\in N} N \setminus \{i\} \in {\mathcal {W}}$ by (ii), but this violates (i) since $\cap _{i\in N} N \setminus \{i\} =\emptyset$. Hence, there must be a $d\in N$ with $N \setminus \{d\} \notin {\mathcal {W}}$, so by (iii) we have $\{d\} \in {\mathcal {W}}$. $\square$

3 Dictatorship

Throughout this section, the set $A$ is a polytope with non-empty interior, i.e., the convex hull of a finite set $C =\{c_{1},c_{2},\ldots , c_{k}\} \subseteq {\mathbb {R}}^2$ with $k \ge 3$ where all points in $C$ are extreme points of $A$. Further, $\varphi : A^N \rightarrow A$ is a strategy-proof and Pareto optimal rule.

The main purpose of the section is to identify those cases where $\varphi$ is a dictatorship, culminating in Theorem 3.10. First we give an outline of the proof.

3.1 Outline of the proof

We first show that, if $\varphi$ always assigns a boundary point, then this must always be an extreme point, i.e., an element of $C$ (Lemma 3.1). Together with Lemma 2.1, which stated that $\varphi$ always assigns boundary points to two-dipped profiles (this followed from Pareto optimality alone), we obtain that $\varphi$ always assigns extreme points to two-dipped profiles (Lemma 3.2).

Next, we formally introduce the concept of a single-best point: This is a point which is the unique best point for at least one element of $A$. The auxiliary Lemmas 3.3 and 3.4 prove some geometrical facts about single-best points.

Lemma 3.5 shows that, if the two dips in a two-dipped profile have unique best points—so these points are single-best points—then the rule $\varphi$ must assign one of these single-best points to such a profile. Suppose this is the single-best point for a coalition $S$. Then Lemma 3.6 shows that, in every two-dipped profile between $S$ and $N \setminus S$, the rule must assign the single-best point for coalition $S$, under the additional assumption that there are at least three single-best points in $A$. In that case, coalition $S$ is called quasi-decisive; thus, Lemma 3.6 shows that for every coalition $S$, either $S$ or $N \setminus S$ is quasi-decisive, provided that there are at least three single-best points. In Lemma 3.7, we take this a step further and show that, again under the condition that there are at least three single-best points, for each coalition $S$, either $S$ or $N\setminus S$ is decisive; recall that this means that $S$ gets a best point whenever all the agents of $S$ have the same preference (dip).

Lemma 3.8 shows that, if there are at least three single-best points and an additional condition holds, then the set of decisive coalitions is closed under intersection. Lemmas 6.3 and 3.9 show that this additional condition is equivalent to the set of single-best points being non-rectangular; a finite set in ${\mathbb {R}}^2$ is rectangular if it consists of four points which are the vertices of a rectangle. Hence, so far we have proved that if the set of single-best points contains at least three points and is not rectangular, then the set of decisive coalitions is an ultrafilter. So by Lemma 2.2, there must be a decisive single agent, hence a dictator (Theorem 3.10).

We repeat that this line of argument is familiar in social choice (e.g., Kirman and Sondermann 1972; Hansson 1976).

The cases where we do not necessarily have dictatorship are treated in Sect. 4.

3.2 Proof of the main result

We start by showing that only extreme points can be boundary outcomes of $\varphi$.

Lemma 3.1

Let $p\in A^N$ and $\varphi (p)\in \partial A$. Then $\varphi (p)\in C$.

Proof

Some of the main ideas of the proof can be explained by considering a regular polygon (cf. Remark 3.11). So we let $A$ be a regular 5-polygon (see Figure 2, which also illustrates the rest of the proof) and we let $p$ be a two-dipped profile, say $p=(a^S,b^{N\setminus S})$. The proof of the general case (which is considerably more complicated) is in the Appendix.

Fig. 2

Illustrating the proof of Lemma 3.1 for $A$ a regular 5-polygon

We argue from contradiction. If the boundary point $\varphi (p)$ is not an element of $C$, then it is contained in a line segment between adjacent vertices $c$ and $c'$. Let the perpendicular bisectors $\ell _{c,\varphi (p)}$ and $\ell _{c',\varphi (p)}$ of $[c,\varphi (p)]$ and $[c',\varphi (p)]$ intersect the opposite boundary of $A$ in the points $\bar{a}$ and $\bar{b}$, respectively. By Pareto optimality, it follows that neither $a$ nor $b$ can be located between those bisectors, so say that $a$ is to the left of $\ell _{c,\varphi (p)}$ and $b$ is to the right of $\ell _{c',\varphi (p)}$.

Consider the profile $(\bar{a}^S,b^{N\setminus S})$. By (I)SP, we have $||a-\varphi (\bar{a}^S,b^{N\setminus S})|| \le ||a-\varphi (p)||$ and $||\bar{a}-\varphi (p)|| \le ||\bar{a}-\varphi (\bar{a}^S,b^{N\setminus S})||$. Hence, $\varphi (\bar{a}^S,b^{N\setminus S}) \in \{c,\varphi (p)\}$. By PO, this implies $\varphi (\bar{a}^S,b^{N\setminus S}) = c$. Again by SP, $||\bar{b}-\varphi (\bar{a}^S,\bar{b}^{N\setminus S})|| \ge ||\bar{b}-\varphi (\bar{a}^S,b^{N\setminus S})|| = ||\bar{b}-c||$, but this implies $\varphi (\bar{a}^S,\bar{b}^{N\setminus S})=c$ since $c$ is at maximal distance from $\bar{b}$ in $A$.

By an analogous argument, now starting by moving the agents in $N\setminus S$ from $b$ to $\bar{b}$, we obtain $\varphi (\bar{a}^S,\bar{b}^{N\setminus S})=c'$. This contradiction completes the proof for this case. $\square$

The next lemma follows by combining Lemmas 2.1 and 3.1.

Lemma 3.2

Let $a,b\in A$ and $S\subseteq N$. Then $\varphi (a^{S},b^{N\setminus S})\in C$.

For a subset $B$ of $A$, let $A_{B}$ denote the set of dips for which $B$ is exactly the set of best points, i.e.,

$$\begin{aligned} A_B = \{ x \in A : \mathfrak {b}(x) = B\}. \end{aligned}$$

For a singleton $\{a\}$, we write $A_{a}$ instead of $A_{\{a\}}$. We can make the following observations. If $B\subseteq A$ and $B\not \subseteq C$, then $A_B = \emptyset$. If $B = \{a,b\}$ for some distinct $a,b \in C$ then $A_B \subseteq \ell _{a,b}$ and if $B = \{a,b,c\}$ for some distinct $a,b,c \in C$ then $A_B \subseteq \ell _{a,b} \cap \ell _{b,c}$. Moreover, if $A_a \ne \emptyset$ for some $a \in C$ then $A_a$ is convex. This can be seen as follows. Let $x,y \in A_a$ and let $b \in A \setminus \{a\}$, then $x,y \in H^\circ (\ell _{a,b},b)$, hence $z \in H^\circ (\ell _{a,b},b)$ for any convex combination $z$ of $x$ and $y$, so $b \notin \mathfrak {b}(z)$. Since $b$ was arbitrary and $\mathfrak {b}(z) \ne \emptyset$, this implies that $z \in A_a$. Let

$$\begin{aligned} \mathcal {B}= \{ a\in A : A_a \ne \emptyset \}. \end{aligned}$$

Elements of $\mathcal {B}$ are called single-best points. Hence, a point of $A$ is a single-best point if there is some preference for which this point is the unique best point. Combining our observations, we see that for each $a\in \mathcal {B}$ the set $A_a$ is a convex polygon which is open relative to $A$ and that $A=\cup _{x \in \mathcal {B}} \overline{A}_x$.

The following two lemmas establish further facts about points in $\mathcal {B}$. Their proofs are delegated to the Appendix.

Lemma 3.3

Let $a,\,b$, and $c$ be three distinct points in $\mathcal {B}$. Then $m_{a,b,c}$ exists and $m_{a,b,c}\in A^{\circ }$.

Lemma 3.4

Let $a\in \mathcal {B}$. Then $A^{\circ }\setminus \overline{A}_a$ is connected.

In what follows we often use a notation like $R=\ldots x\ldots yz\ldots \,(x,y,z \in C)$ to express that, in the preference $R,\,x$ is strictly preferred to $y$ and $y$ to $z$ such that other points in $C$ are either above $y$ or below $z$ in preference.

The next result can be interpreted as saying that $\varphi$ leaves no room for compromising at two-dipped profiles. It says, more precisely, that at such a profile, if the two preferences have unique best points, then the rule must assign one of those. Its proof is delegated to the Appendix.

Lemma 3.5

Let $S \subseteq N,\,a,b\in \mathcal {B},\,x\in A_a,\,y\in A_b$, and $p=(x^S,y^{N\setminus S}) \in A^N$. Then $\varphi (p)\in \{a,b\}$.

Call a coalition $S \subseteq N$ quasi-decisive (given $\varphi$) if $\varphi (p)=a$ for all $a,b \in \mathcal {B}$ and every profile $p=(x^S,y^{N\setminus S})$ with $x\in A_a$ and $y\in A_b$. Recall that $S$ is decisive if $\varphi (p)=a$ whenever $p(i)=a$ for all $i\in S$; so quasi-decisiveness is a weakening of decisiveness. We now first show that, if there are at least three single-best points, then, for every coalition, either that coalition or its complement is quasi-decisive. Next, we will show that this remains true for decisiveness instead of quasi-decisiveness.

Lemma 3.6

Let $|\mathcal {B}| \ge 3$. Then for every $S\subseteq N$, either $S$ or $N\setminus S$ is quasi-decisive.

Proof

Let $S\subseteq N$. If $S=N$ or $S=\emptyset$ then we are done by Pareto optimality. So assume $S \ne \emptyset , N$. Clearly, $S$ and $N \setminus S$ cannot both be quasi-decisive. Let $a,b$ be two different elements of $\mathcal {B}$, and let $x\in A_a,\,y\in A_b$, and $p=(x^S,y^{N\setminus S})$. By Lemma 3.5, $\varphi (p) \in \{a,b\}$. Without loss of generality assume that $\varphi (p)=a$. Take $c,d \in \mathcal {B},\,v\in A_c$ and $w\in A_d$ arbitrary, and let $q=(v^S,w^{N\setminus S})$. It is sufficient to prove that $\varphi (q)=c$. By Pareto optimality, we may assume that $c\ne d$. Lemma 3.5 implies $\varphi (q)\in \{c,d\}$. We proceed in four steps.

Step 1 Assume $v=x$.

Then, since $v=x$ we have $c=a$. If also $b=d$, then $\varphi (q)=c =a$ otherwise coalition $N\setminus S$ could manipulate from $p$ to $q$ and obtain $d= b$. So assume $b \ne d$. By Lemma 3.4 there is a path² from $y$ to $w$ disjoint from $\overline{A}_{a}$. Along this path, we can find points $y=u_{1}, u_2,\ldots , u_k=w\,(k\ge 2)$ such that $u_t \in A_{f_t},\,f_t\in \mathcal {B}$, for $t=1,\ldots ,k$ (so $f_1=b,\,f_k=d$) and such that for every $t=1,\ldots ,k-1$ we have ${R_{u_t}}_{|\mathcal {B}}=f_t f_{t+1}\ldots$ and ${R_{u_{t+1}}}_{|\mathcal {B}}=f_{t+1} f_t\ldots$ ³ For every $t=1,\ldots ,k$ let $p^t=(x^S,u_t^{N\setminus S})$. Thus, $p^1=p$ and $p^k=q$. Since $\varphi (p^1)=a,\,f_1, f_2 \ne a,\,{R_{u_2}}_{|\mathcal {B}}=f_2 f_1\ldots$, and $\varphi (p^2) \in \{a,f_2\}$ by Lemma 3.5, we have by strategy-proofness that $\varphi (p^{2})=a$, since otherwise coalition $N\setminus S$ could manipulate from $p^1=p$ to $p^2$, obtaining $f_2$ instead of $a$. Similarly, it follows that $\varphi (p^{3})=a,\,\varphi (p^{4})=a$, etc., so that $\varphi (q) = \varphi (p^{k})= a$, hence $\varphi (q) = c$.

Step 2 Assume $v\ne x$ and $d\ne a$.

Consider $p'=(x^S,w^{N\setminus S})$. Then Step 1 implies $\varphi (p')=a$. By Step 1 applied to $p'$ and $q$, if $\varphi (q)=d$ then $\varphi (p')=d$, a contradiction since $d \ne a$. Hence $\varphi (q)=c$.

Step 3 Assume $y=v,\,w=x$.

Let $e \in \mathcal {B}\setminus \{a,b\}$ (recall that $|\mathcal {B}| \ge 3$) and $u \in A_e$. Then $\varphi (p)= \varphi (x^S,y^{N\setminus S}) = a$ implies by Step 1 that $\varphi (x^S,u^{N\setminus S}) = a$. In turn, by Step 2, this implies that $\varphi (y^S,u^{N\setminus S})=b$, which by Step 1 again yields $\varphi (q)=\varphi (y^S,x^{N\setminus S})=b$. Since $y=v$, we have $b=c$, so $\varphi (q)=c$.

Step 4 Assume $v \ne x,\,d=a$.

Then $\varphi (p)= \varphi (x^S,y^{N\setminus S}) = a$ implies by Step 3 that $\varphi (y^S,x^{N\setminus S}) = b$, hence by Step 1 we obtain $\varphi (y^S,w^{N\setminus S}) = b$. If $y=v$, hence $b=c$, we have $\varphi (q)=\varphi (v^S,w^{N\setminus S})=\varphi (y^S,w^{N\setminus S})=b=c$. If $y\ne v$, then $d=a\ne b$ and Step 2 imply $\varphi (q)=\varphi (v^S,w^{N\setminus S})=c$.

Since the case $v=x$ is covered in Step 1, the case $v\ne x$ and $d\ne a$ in Step 2, and the case $v\ne x$ and $d=a$ in Step 4, all cases are covered, so the proof is complete. $\square$

Lemma 3.7

Let $|\mathcal {B}| \ge 3$. Then for every $S\subseteq N$, either $S$ or $N\setminus S$ is decisive.

Proof

Let $S\subseteq N$. Clearly, $S$ and $N\setminus S$ cannot both be decisive. By Lemma 3.6, either $S$ or $N\setminus S$ is quasi-decisive. Assume that $S$ is quasi-decisive, the other case is analogous.

First, consider a profile $p$ with $p(i)=x$ for all $i \in S$ such that $x \in A_a$ for some $a\in \mathcal {B}$. We prove that $\varphi (p)=a$. Take a $d \in \mathcal {B}$ such that $a \in \partial A_d$, and take a $v \in A_d$. Let $r=(x^S,v^{N\setminus S})$. Quasi-decisiveness of $S$ implies that $\varphi (r)=a$. By applying intermediate strategy-proofness to the profiles $r$ and $p$, we obtain $||v-a|| \ge ||v-\varphi (p)||$. Since we can take $v$ as close to $a$ as desired (since $a \in \partial A_d$), this implies $\varphi (p)=a$.

Finally, let $q$ be a profile with $q(i)=y \in A$ for all $i\in S$. We show that $\varphi (q) \in \mathfrak {b}(y)$. Suppose this were not the case. Then take $b \in \mathfrak {b}(y) \cap \mathcal {B}$ (this is possible since $A=\cup \{\overline{A}_x : x \in \mathcal {B}\}$) and $z\in A$ such that $z \in A_b$. By the first part of the proof, $\varphi (q')=b$ where $q'(i)=z$ for all $i\in S$ and $q'(i)=q(i)$ for all $i \in N\setminus S$. Then $S$ can manipulate from $q$ to $q'$, violating (intermediate) SP. $\square$

In what follows we pin down those polytopes $A$ for which the intersection of two decisive coalitions is again decisive. Call a finite subset of ${\mathbb {R}}^2$ rectangular, if it consists of exactly four points which are the vertices of one and the same rectangle.

Lemma 3.8

Let the following conditions hold:

• (i) $|\mathcal {B}| \ge 3$.

• (ii) There are distinct $a,b,c \in \mathcal {B}$ such that $m_{a,b,c} \in \partial A_{a} \cap A^{\circ }$ and such that there is no $x\in \mathcal {B}$ for which $\{a,b,c,x\}$ is rectangular.⁴

Let $S, T\subseteq N$ be both decisive. Then $S\cap T$ is decisive.

Proof

Suppose, to the contrary (cf. Lemma 3.7), that $N\backslash (S\cap T)$ is decisive. Then we have a partition $X=S\cap T,\,Y=S\setminus T$ and $Z=N\setminus S$ of $N$ such that $X,\,Y$ and $Z$ are not decisive. Hence, any union of two of these sets, being the complement of the third one, is decisive. We will derive a contradiction.

Let $a,\,b$ and $c$ be as in (ii) in the statement of the lemma. We choose (see Fig. 3(a)) $\widetilde{a}\in A^\circ$ close to $a$ and $\overline{b}, \overline{c}, \overline{a}_b, \overline{a}_c \in A^\circ$ close to $m: = m_{a,b,c}$ such that

$$\begin{aligned} R_{\overline{b}}&= ba\ldots c\ldots \\ R_{\overline{c}}&= ca\ldots b\ldots \\ R_{\overline{a}_b}&= ab\ldots c\ldots \\ R_{\overline{a}_c}&= ac\ldots b\ldots \\ R_{\widetilde{a}}&= \ldots c\ldots b\ldots a \end{aligned}$$

and such that all these preferences (restricted to $C$) are strict. Moreover, we choose $\overline{b} \in A_b$ and $\overline{c} \in A_c$. (These choices are possible since $m_{a,b,c} \in \partial A_a \cap A^\circ$; in particular, this implies that $m$ is the center of the circle through $a,\,b$, and $c$ such that the set $A$ is inside this circle, which enables the choices $\overline{b} \in A_b$ and $\overline{c} \in A_c$.) If $\widetilde{a}$ cannot be chosen this way, then we choose it such that $R_{\widetilde{a}} = \ldots b\ldots c\ldots a$ and proceed analogously.) By choosing all these points close enough to $a$ and $m$, respectively, we have that for any profile $q$ with dips at these points, any point in $A^{\circ }$ is Pareto dominated by some boundary point. Hence, by Lemma 3.1, $\varphi (q)\in C$ for such profiles $q$. In particular, $\varphi$ assigns a point in $C$ to any of the following profiles:

$$\begin{aligned} p&= (\widetilde{a}^X, \overline{b}^Y, \overline{c}^Z) \\ p^{\overline{a}_{b}}&= (\widetilde{a}^X,\overline{a}_b^Y,\overline{c}^Z)\\ p^{\overline{a}_{c}}&= (\widetilde{a}^X,\overline{b}^Y,\overline{a}_c^Z)\\ r&= (\widetilde{a}^X,\overline{a}_b^Y,\overline{a}_c^Z)\;. \end{aligned}$$

We first prove the following claim.

Claim $\varphi (p) \in \{a,b,c\}$.

To prove this claim, let $\varphi (p)=x,\,\varphi (p^{\overline{a}_{b}})=y$ and $\varphi (p^{\overline{a}_{c}})=z$. Since $Y \cup Z$ is decisive and since $\overline{a}_b,\overline{a}_c \in A_a$, we have by strategy-proofness that $\varphi (r)=a$.

First consider $r$ and $p^{\overline{a}_{b}}$. If $\overline{a}_c$ and $\overline{c}$ are chosen sufficiently close, then by Lemma 6.2 it follows that the first change, starting from below, in the preferences $R_{\overline{a}_c}$ and $R_{\overline{c}}$ must be a swap between $\varphi (r)$ and $\varphi (p^{\overline{a}_{b}})$. Since $\varphi (r)=a$, this implies that either (i.a) $y=a$ or (i.b) $y=c$.

Similarly, comparing $r$ and $p^{\overline{a}_{c}}$ yields either (ii.a) $z=a$ or (ii.b) $z=b$.

We next compare $p$ and $p^{\overline{a}_{b}}$. These profiles differ for the agents in $Y$, who have dips $\overline{b}$ in $p$ and dips $\overline{a}_b$ in $p^{\overline{a}_{b}}$. By going from $\overline{b}$ to $\overline{a}_b$, only the perpendicular bisector $\ell _{a,b}$ is crossed. By Lemma 6.2, as before the first change in preference from below must be a swap between $\varphi (p)=x$ and $\varphi (p^{\overline{a}_{b}})=y$, but this implies that $\ell _{x,y}$ coincides with $\ell _{a,b}$. This implies that, if $x \ne y$, then $x$ is the mirror image of $y$ with respect to the perpendicular bisector of $[a,b]$. Therefore, we have either (iii.a) $x=y$ or (iii.b) $x\ne y$ and $\sigma _{a,b}(x)=y$.

Similarly, comparing $p$ and $p^{\overline{a}_{c}}$ yields either (iv.a) $x=z$ or (iv.b) $x\ne z$ and $\sigma _{a,c}(x)=z$.

Fig. 3

Illustrating the proof of Lemma 3.8

If $x=y$ or $x=z$, then (i.a) and (i.b) or (ii.a) and (ii.b) imply that $x\in \{a,b,c\}$. Let $x\ne y,\,x\ne z$. Then $\sigma _{a,b}(x)=y$ and $\sigma _{a,c}(x)=z$ by (iii.b) and (iv.b). Since $a,b,c$ are distinct and thus $\ell _{a,b}\ne \ell _{a,c}$ it follows that $z\ne y$. If $y=a$ or $z=a$, then $\sigma _{a,b}(x)=y$ and $\sigma _{a,c}(x)=z$ imply $x=b$ or $x=c$, hence we are done again. So, assume $y\ne a$ and $z\ne a$, then $y=c$ by (i.b) and $z=b$ by (ii.b). Then by (iii.b) and (iv.b) we have $\sigma _{a,b}(x)=y=c$ and $\sigma _{a,c}(x)=z=b$. We now assume $a \ne x$ and derive a contradiction, which will complete the proof of the Claim. Since $\sigma _{a,c}(a)=c$ and $\sigma _{a,b}(a)=b$ the assumption $a\ne x$ implies that $a,\,b,\,c$ and $x$ are vertices of a rectangle. (See Fig. 3(b).) To derive the contradiction it is, in view of condition (ii) in the lemma, sufficient to prove that $x\in \mathcal {B}$. Let $d\in \mathfrak {b}(R_{a})$, hence $d \notin \{a,b,c\}$, with $d\ne x$. We will show that $m \in \ell _{x,d}$. Since $m=m_{a,x}$, this implies that $a,\,x$, and $d$ are on the same circle with center $m$. Since $a$ and $x$ are on the same diameter in this circle, we have that $||d-a|| < ||x-a||$, contradicting $d \in \mathfrak {b}(R_a)$. So $a \in A_x$, hence $x \in \mathcal {B}$.

We are left to show that $m \in \ell _{x,d}$. Suppose, to the contrary, that $m\notin \ell _{x,d}$. Since $d \in \mathfrak {b}(R_a)$ we have $a\in H(\ell _{x,d},x)$, hence $m\in H^\circ (\ell _{x,d},x)$ and therefore $\overline{b},\overline{c} \in H^\circ (\ell _{x,d},x)$ by the choice of these points (note that these points can be chosen close enough to $m$ to achieve this, given that there are only finitely many candidates for the points $x$ and $d$). By the choice of $\widetilde{a}$, also $\widetilde{a} \in H^\circ (\ell _{x,d},x)$. But this implies that $d$ Pareto dominates $x$ at profile $p$, contradicting $\varphi (p)=x$. This completes the proof of the Claim.

Consider the profile $p'=(\overline{c}^X,\overline{b}^Y,\overline{c}^Z)$. Since $X \cup Z$ is decisive and $\overline{c} \in A_c$ we have that $\varphi (p')=c$. Strategy-proofness and the Claim now imply that $x=\varphi (p)=c$.

Let $p''=(\overline{b}^X,\overline{b}^Y,\overline{a}_c^Z )$. Since $X \cup Y$ is decisive and $\overline{b} \in A_b$ we have $\varphi (p'')=b$. We have already seen in the proof of the Claim that $z = \varphi (p^{\overline{a}_c}) \in \{a,b\}$. So strategy-proofness implies $\varphi (p^{\overline{a}_{c}})=b$. Since $\varphi (p)=c$, coalition $Z$ can manipulate from $p^{\overline{a}_{c}}$ to $p$, violating strategy-proofness. $\square$

Before continuing with the main result of this section, a consideration of the polytopes to which the preceding lemmas apply is in order. First, let $|C|=3$, i.e., $A$ is a triangle including its interior. If this triangle is acute, then $\mathcal {B}=C$, hence $|\mathcal {B}| =3$ and also condition (ii) of Lemma 3.8 is trivially satisfied. If this triangle is not acute, however, then $|\mathcal {B}|=2$ and this case will be studied in the next section. Second, let $|C|>3$. If $|\mathcal {B}|=2$, which means, roughly, that the polytope $A$ is rather flat—an exact characterization is given by Lemma 4.1, then again the results in the next section apply. For cases where $|\mathcal {B}| \ge 3$ the following lemma provides an exact characterization of those polytopes where condition (ii) of Lemma 3.8 is not satisfied. The proof is in the Appendix.

Lemma 3.9

Let $|\mathcal {B}| \ge 3$. Then condition $(ii)$ in Lemma 3.8 does not hold if and only if $\mathcal {B}$ is rectangular.

We can now formulate the main result of this section. Call $\varphi$ dictatorial if there is a dictator, i.e., an agent $d\in N$ such that $\varphi (p) \in \mathfrak {b}(p(d))$ for all $p\in A^N$.

Theorem 3.10

If $|\mathcal {B}| \ge 3$ and ${\mathcal {B}}$ is not rectangular, then $\varphi$ is dictatorial.

Proof

By Lemmas 3.7, 3.8, and 3.9 the set of decisive coalitions is an ultrafilter. Hence, by Lemma 2.2, there is a $d\in N$ such that $d$ is decisive. So $\varphi$ is dictatorial with dictator $d$. $\square$

We conclude this section with two remarks. The first remark is about regular polytopes.

Remark 3.11

Call a polytope $A$ in ${\mathbb {R}}^2$ regular if its extreme points—the elements of the set $C$—are the vertices of a regular polygon (equilateral triangle, square, etc.). For such a regular polytope, Theorem 3.10 implies that $\varphi$ is dictatorial if and only if $|C| \ne 4$. Thus, on regular polytopes $A$, a strategy-proof and Pareto optimal rule is dictatorial unless $A$ is a square including its inside.

The second remark concerns a relation between the results of Gibbard (1973) and Satterthwaite (1975) and Theorem 3.10.

Remark 3.12

Let $C=\{a,b,c\}$ such that $a,\,b$, and $c$ are the vertices of an acute triangle. By Theorem 3.10, any strategy-proof and Pareto optimal rule on $A$ must be a dictatorship. An alternative proof of this fact could work as follows. Let $\varphi$ be such a rule and first prove that $\varphi (p) \in C$ for every $p \in A^N$. Then, effectively, $\varphi$ is a strategy-proof and Pareto optimal social choice function on the set $C$ of points, with full domain of preferences, as can be seen in Fig. 4(a), where the perpendicular bisectors of the edges are drawn. Hence, $\varphi$ must be a dictatorship according to the Gibbard-Satterthwaite theorem. If the triangle is not acute, then only four strict preferences are generated (Fig. 4(b)), and thus, the Gibbard-Satterthwaite theorem does not apply. Indeed, in this case, if the right or obtuse angle is at $c$, then $a$ and $b$ are the only single-best points, and for instance, majority voting between $a$ and $b$ is a strategy-proof and Pareto optimal rule (see Sect. 4.1).

Fig. 4

Remark 3.12

4 Non-dictatorship

In this section, we study the two cases excluded in Theorem 3.10, namely the case $|\mathcal {B}|=2$ and the case where $\mathcal {B}$ is rectangular. The main result in the first case—two single-best points—is Theorem 4.5, which characterizes all Pareto optimal and strategy-proof rules for this case. In the second case—where there are exactly four single-best points, forming the vertices of a rectangle—we content ourselves by giving an example of a non-dictatorial Pareto optimal and strategy-proof rule.

4.1 $|\mathcal {B}|=2$

According to Theorem 3.10, dictatorship is implied by Pareto optimality and strategy-proofness under two conditions on the set $\mathcal {B}$ of single-best points in $C$. In this section, we consider the case where the first one of these conditions does not hold. The following lemma reveals a consequence of this assumption. It says that, if $a$ and $b$ are the only single-best points, then the center of the circle $m_{a,b,c}$ through $a,\,b$, and any other point $c \in A \setminus [a,b]$ cannot be an interior point of $A$. Also the converse holds: If $a$ and $b$ are single-best points and $m_{a,b,c}$ is not an interior point of $A$ for every $c \in A \setminus [a,b]$, then $a$ and $b$ are the only single-best points.

Lemma 4.1

Let $a,b$ be distinct single-best points. Then $\{a,b\}=\mathcal {B}$ if and only if $m_{a,b,c} \notin A^\circ$ for every $c \in A \setminus [a,b]$.

Proof

For the only if part, suppose $\{a,b\}=\mathcal {B}$. First observe that for any $B \subseteq C$ with $|B| \ge 2$, we have that $A_B$, if not empty, consists of a line segment (which may happen if $|B|=2$) or a single point. Since $A_x = \emptyset$ for all $x \in A \setminus \{a,b\}$, this implies that any open subset of $A^\circ$ has a non-empty intersection with $A_a$ or $A_b$. Now let $c \in A \setminus [a,b]$ and suppose $m_{a,b,c} \in A^\circ$. Then (see Fig. 5) the set $(V_{cab}^\circ \cup V_{cba}^\circ ) \cap A^\circ$, where $V_{cab} = \{ x\in A : (c,a), (a,b) \in R_x \}$ and $V_{cba} = \{ x\in A : (c,b), (b,a) \in R_x \}$, is an open subset of $A^\circ$. However, $A_a \cap (V_{cab}^\circ \cup V_{cba}^\circ ) \cap A^\circ = \emptyset$ and $A_b \cap (V_{cab}^\circ \cup V_{cba})^\circ \cap A^\circ = \emptyset$. This contradicts that any open subset of $A^\circ$ has a non-empty intersection with $A_a$ or $A_b$. Hence, $m_{a,b,c} \notin A^\circ$.

Fig. 5

Illustrating the proof of Lemma 4.1

For the if part, suppose that $c \in \mathcal {B}$ for some $c \in A \setminus \{a,b\}$. Clearly, $c \notin [a,b]$, hence $m_{a,b,c}$ exists and, by assumption, $m_{a,b,c} \notin A^\circ$. Let $x \in A$ be a point for which $c$ is the unique best point. Then (with notations as before) we must have $x \in V_{cab}^\circ \cup V_{cba}^\circ$, but this implies that $m_{a,b,c}$ is an interior point of the convex hull of $a,\,b$, and $x$, and thus of $A$. This contradiction completes the proof of the if part. $\square$

For the remainder of this section, we assume that $\mathcal {B}=\{a,b\}$ and that $\varphi$ is a Pareto optimal and strategy-proof rule. We first show that in almost all cases, we have $\varphi (p) \in \{a,b\}$.

Lemma 4.2

Let $p\in A^N,\,p\ne m_{a,b,c}^{N}$ for all $c\in C\backslash \{a,b\}$. Then $\varphi (p)\in \{a,b\}$.

Proof

To the contrary suppose $\varphi (p) \notin \{a,b\}$. We write $m$ for $m_{a,b,\varphi (p)}$ if $a,\,b$, and $\varphi (p)$ are not collinear; otherwise, $\varphi (p) \in \; ]a,b[$ and we take $m=\varphi (p)$. (Below it will follow that $\varphi (p)\in \partial A$, so that in view of Lemma 3.1 the latter case will actually not occur.) By Lemma 4.1, $m \notin A^\circ$, which implies that $||x-\varphi (p)||\le ||x-a||$ or $||x-\varphi (p)||\le ||x-b||$ for all $x \in A$ (since otherwise $m$ would be an interior point of the triangle with vertices $a,b,x$ for some $x\in A$, hence an interior point of $A$). In particular, we have for every $i\in N$ with $p(i)\notin \{a,b,m\}$ that $||p(i)-\varphi (p)||<||p(i)-a||$ or $||p(i)-\varphi (p)||<||p(i)-b||$. If $||p(i)-\varphi (p)||<||p(i)-a||$ for some $i\in N$, then consider the profile $p'$ with $p'(i)=b$ and $p'(j)=p(j)$ for all $j\ne i$. If $\varphi (p')=b$ then agent $i$ would manipulate from $p'$ to $p$ since $\varphi (p)\ne b$, and if $\varphi (p')=a$ then agent $i$ would manipulate from $p$ to $p'$. Hence, strategy-proofness implies $\varphi (p') \notin \{a,b\}$. If $||p(i)-\varphi (p)||<||p(i)-b||$ for some $i\in N$ then we consider the profile $p''$ with $p''(i)=a$ and $p''(j)=p(j)$ for all $j \ne i$ and similarly derive that $\varphi (p'') \notin \{a,b\}$. Therefore, we may assume that $p(N)\subseteq \{a,b,m\}$. Since $p(N)\subseteq \{a,b\}$ would imply $\varphi (p) \in \{a,b\}$ by Lemma 3.5, contrary to our assumption, we may further assume that $p$ is of the form $p=(a^S,b^T,m^V)$ for some coalitions $S,\,T$, and $V=N\setminus (S\cup T) \ne \emptyset$. By Pareto optimality, we have that either $S$ and $T$ are non-empty or $V=N$.

Suppose that $\varphi (p) \in A^\circ$. Then there are points of $A$ on the straight line through $\varphi (p)$ perpendicular to $\ell (a,b)$ that Pareto dominate $\varphi (p)$ given the profile $p$, contradicting Pareto optimality of $\varphi$. Hence, $\varphi (p) \in \partial A$, so that $\varphi (p)\in C$ by Lemma 3.1. Thus, by the condition on $p$ in the lemma, $V \ne N$, so that $S,T,V \ne \emptyset$.

Next, let $\overline{a}=m_{a,\varphi (p)}$ and consider profile $p^{a}=(\overline{a}^S,b^T,m^V)$. We prove that $\varphi (p^{a})=a$. (See Fig. 6 for an illustration of this part of the argument.) By comparing $p$ and $p^a$, strategy-proofness implies that $||\varphi (p^{a})-\overline{a}|| \ge ||\varphi (p)-\overline{a} || = ||a-\overline{a}||$ and $||\varphi (p)-a||\ge ||\varphi (p^{a})-a||$. Consider the profile $q=(\overline{a}^S,b^{T\cup V})$. Note that $b \in A_a$; also, since by Lemma 4.1, $m_{a,b,c}\notin A^\circ$ and $m_{a,b,c}\in \ell _{a,b}$ for all $c \in A\setminus \{a,b\}$, it follows that $\overline{a} \in A_b$. Now Lemma 3.5 implies $\varphi (q)\in \{a,b\}$, hence strategy-proofness yields $||m-a|| = ||m-b|| \le ||m-\varphi (p^{a})||$. This means that $\varphi (p^a)$ is not inside the circle with center $m$ through the points $a,\,b$ and $\varphi (p)$, but then $\varphi (p^a)$ must be on this circle since there are no points of $A$ outside this circle (since otherwise we could find a point in $\mathcal {B}$ different from $a$ and $b$, a contradiction). Hence, $||m-a|| = || m-\varphi (p^{a})||$. Since $||\varphi (p)-a||\ge ||\varphi (p^{a})-a||,\,||\varphi (p^{a})-\overline{a}|| \ge ||a-\overline{a}||$ and $||m-a||=||m -\varphi (p^{a})||$ it follows that either $\varphi (p^{a}) = \varphi (p)$ or $\varphi (p^{a})$ is on the circle with center $m$ through $a$ and $\varphi (p)$ on the arc between $a$ and $b$ not containing $\varphi (p)$. The latter case, however, implies $\varphi (p^a)=a$ since there cannot be points of $C$ on this arc other than $a$ or $b$. Hence, $\varphi (p^a) \in \{a,\varphi (p)\}$. But $\varphi (p)$ is Pareto dominated by $a$ at the profile $p^a$. So, $\varphi (p^{a})=a$.

Now let $\overline{b}=m_{b,\varphi (p)}$ and consider the profile $p^{ab}=(\overline{a}^S,\overline{b}^T,m^V)$. Note that $\overline{b} \in {\mathcal {H}}^\circ (\ell _{a,b},b)$. Similarly as above we have $\overline{b} \in A_a$. Therefore, $\varphi (p^{ab})=a$ by strategy-proofness.

By an analogous argument but now starting with the profile $p^b=(a^S,\overline{b}^T,m^V)$, we obtain $\varphi (p^{ab})=b$, a contradiction which completes the proof. $\square$

Fig. 6

Illustrating the proof of Lemma 4.2

In order to characterize all strategy-proof and Pareto optimal rules while avoiding technicalities due to preference indifferences, we make the following additional assumptions. The first assumption takes care of the cases not covered by Lemma 4.2. More precisely, suppose $m_{a,b,c} \in A$ for some $c\in C \setminus \{a,b\}$. Then by Lemma 4.1 we must have $m_{a,b,c} \in \{\underline{m},\overline{m}\}$, where $\{\underline{m},\overline{m}\} = \partial A \cap \ell _{a,b}$.

Assumption 4.3

$\varphi (p) \in \{a,b\}$ for $p=\underline{m}^N$ and $p=\overline{m}^N$.

The second assumption, which is a version of the familiar non-bossiness condition, guarantees that indifferent agents cannot change the assigned point.

Assumption 4.4

For all $i\in N$ and $p,q \in A^N$ such that $p(j)=q(j)$ for all $j\in N\setminus \{i\}$, if $||p(i)-a|| = ||p(i)-b||$ and $||q(i)-a|| = ||q(i)-b||$, then $\varphi (p)=\varphi (q)$.

With these additional assumptions, it is straightforward to verify that (a strategy-proof and Pareto optimal rule) $\varphi$ depends only on the individual preferences between $a$ and $b$ and not on the exact location of the dips. We will now develop a precise description of $\varphi$.

Let ${\mathcal {W}}_{a}^{\varphi }$ be the set of pairs $(S,U)\in N\times N$ with $S\cap U=\emptyset$ and such that $\varphi (p)=a$ for all profiles $p$ with $a$ single-best for all agents in $S$ and both $a$ and $b$ best for all agents in $U$. Let ${\mathcal {W}}_{b}^{\varphi }$ be defined analogously. Since $\varphi$ depends only on the individual preferences between $a$ and $b$ we have that the pair $({\mathcal {W}}_{a}^{\varphi },{\mathcal {W}}_{b}^{\varphi })$ is both proper and strong, i.e., either $(S,U)\in {\mathcal {W}}_{a}^{\varphi }$ or $(T,U)\in {\mathcal {W}}_{b}^{\varphi }$ for all pairwise disjoint sets $S,\,U$ and $T$ with $S\cup T\cup U=N$. Pareto optimality of $\varphi$ implies that the pair $({\mathcal {W}}_{a}^{\varphi }, {\mathcal {W}}_{b}^{\varphi })$ is Pareto optimal, i.e., $(S,U)\in {\mathcal {W}}_{a}^{\varphi }$ if $S\ne \emptyset$ and $S\cup U=N$, and $(T,U)\in {\mathcal {W}}_{b}^{\varphi }$ if $T\ne \emptyset$ and $T\cup U=N$. Furthermore, strategy-proofness of $\varphi$ implies that the pair $({\mathcal {W}} _{a}^{\varphi },{\mathcal {W}}_{b}^{\varphi })$ is monotone, i.e., $(S^{\prime },U^{\prime })\in {\mathcal {W}}_{a}^{\varphi }$ whenever $(S,U)\in {\mathcal {W}}_{a}^{\varphi }$ and $S\subseteq S^{\prime }$ and $S\cup U\subseteq S^{\prime }\cup U^{\prime }$ and $(T^{\prime },U^{\prime })\in {\mathcal {W}}_{b}^{\varphi }$ whenever $(T,U)\in {\mathcal {W}}_{b}^{\varphi }$ and $T\subseteq T^{\prime }$ and $T\cup U\subseteq T^{\prime }\cup U^{\prime }$. It is straightforward to check that any proper and strong, Pareto optimal and monotone pair $({\mathcal {W}}_{a},{\mathcal {W}}_{b})$ defines a Pareto optimal and strategy-proof rule $\varphi$, satisfying Assumptions 4.3 and 4.4, with $({\mathcal {W}}_{a}^\varphi ,{\mathcal {W}}_{b}^\varphi )=({\mathcal {W}}_{a}, {\mathcal {W}}_{b})$. We summarize these findings in the following theorem.

Theorem 4.5

Let $\mathcal {B}= \{a,b\}$ with $a \ne b$. Then

• (i) If $\varphi$ is strategy-proof, Pareto optimal, and satisfies Assumptions 4.3 and 4.4, then $({\mathcal {W}}_{a}^\varphi ,{\mathcal {W}}_{b}^\varphi )$ is proper and strong, Pareto optimal and monotone.

• (ii) If $({\mathcal {W}}_{a},{\mathcal {W}}_{b})$ is proper and strong, Pareto optimal and monotone, then there is a strategy-proof, and Pareto optimal rule $\varphi$, satisfying Assumptions 4.3 and 4.4, such that ${\mathcal {W}}_{a} = {\mathcal {W}}_{a}^\varphi$ and ${\mathcal {W}}_{b} = {\mathcal {W}}_{b}^\varphi$.

4.2 $\mathcal {B}$ is rectangular

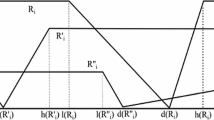
In this section, we consider the case where $\mathcal {B}$ is rectangular. Thus, we assume that $\mathcal {B}=\{a,b,c,d\}$ and that $[a,b],\,[b,c],\,[c,d]$, and $[d,a]$ are the edges of a rectangle. Rather than attempting to describe all strategy-proof and Pareto efficient rules for this case—which becomes a very technical exercise mainly due to many tie-breaking decisions that have to be made—we content ourselves with giving a typical example of a rule.

Example 4.6

(Cf. Fig 7.) Let $h$ be the common perpendicular bisector of $[a,d]$ and $[b,c]$ and let $v$ be the common perpendicular bisector of $[a,b]$ and $[c,d]$. For every profile $p$ define $\varphi (p)$ as follows. If $|\{i\in N : p(i) \in H(h,a)\}| \ge |\{i\in N : p(i) \in H(h,d)\}|$ then $\varphi (p) \in \{c,d\}$ and if $|\{i\in N : p(i) \in H(h,a)\}| < |\{i\in N : p(i) \in H(h,d)\}|$ then $\varphi (p) \in \{a,b\}$. If $|\{i\in N : p(i) \in H(v,a)\}| \ge |\{i\in N : p(i) \in H(v,b)\}|$ then $\varphi (p) \in \{b,c\}$ and if $|\{i\in N : p(i) \in H(v,a)\}| < |\{i\in N : p(i) \in H(v,b)\}|$ then $\varphi (p) \in \{a,d\}$. In words, we let majority voting decide between $\{a,b\}$ and $\{c,d\}$, on the one hand, and between $\{a,d\}$ and $\{b,c\}$, on the other. It can be proved (left to the reader) that this rule is strategy-proof and Pareto optimal.

Fig. 7

Illustrating Example 4.6

5 Concluding remarks

The preceding sections naturally lead to the question if the obtained results can be extended to other regions, such as general compact convex sets. Since some of the proofs seem to rely heavily on the finiteness of the set of extreme points, this question does not appear to have a straightforward answer. In a companion note (Öztürk et al. 2013), we show that the dictatorship result extends to the disk (circle and its inside) in ${\mathbb {R}}^2$. This result may not come as a surprise in view of the fact that the disk can be seen as the ‘limit’ of polytopes for which Theorem 3.10 implies dictatorship, but nevertheless we need a separate proof to show this.

Another issue is the domain of preferences. One may expect the dictatorship result to carry over to larger preference domains. Indeed, consider a polytope $A$ with set of extreme points $C$ for which the dictatorship result holds under Euclidean single-dipped preferences. Consider a larger domain of single-dipped preferences, including the Euclidean ones, such that each best point of a preference in this domain is still an element of $C$, and each element of $C$ is the unique best point of some Euclidean single-dipped preference (this holds, for instance, if $A$ is a regular polygon with $|C| \ne 4$, and if all preferences have strictly convex lower contour sets). Let $\psi$ be a Pareto optimal and strategy-proof rule. Then the restriction of $\psi$ to profiles of single-dipped Euclidean preferences must be a dictatorial rule $\varphi$, say with dictator $d$. For an arbitrary profile $p$, we show that $\psi (p) \in \mathfrak {b}(p(d))$, so that $\psi$ is dictatorial on the whole domain. To the contrary, suppose that $\psi (p) \notin \mathfrak {b}(p(d))$. Take $a \in \mathfrak {b}(p(d))$, hence by assumption $a \in C$. Let $q$ be the profile of Euclidean single-dipped preferences with $\mathfrak {b}(q(d)) = \{a\}$ and $q(j)=a$ for all $j \in N \setminus \{d\}$. Then $\psi (q) = \varphi (q) = a$. Then, by intermediate strategy-proofness, it follows that $\psi (r)=a$, where $r$ is the profile with $r(d)=q(d)$ and $r(j)=p(j)$ for all $j \in N \setminus \{d\}$. It follows that $d$ can manipulate from $p$ to $r$, contradicting strategy-proofness.

Also, by enlarging the domain of preferences, a non-dictatorship result may turn into a dictatorship result. For instance, let $C$ be the set $\{(-1,0),(1,0),(0,1)\}$. Then Theorem 4.5 applies, so there are non-dictatorial strategy-proof and Pareto optimal rules. If we extend the domain of preferences by allowing for all distance functions $d_\varepsilon (x,y) = \sqrt{(x_1-y_1)^2 + \varepsilon (x_2-y_2)^2}$ for $1 \le \varepsilon \le \varepsilon _0$ for some $\varepsilon _0 > 1$—so some elliptic preferences are allowed—then one can still prove that a strategy-proof and Pareto optimal rule assigns to each profile a point of $C$, but now all possible orders over the three points in $C$ are possible: for $\varepsilon > 1$ an agent with dip at the interior point $(0,(\varepsilon -1)/2\varepsilon )$ of $A$ is indifferent between the three extreme points, as is straightforward to compute. Thus, by the Gibbard-Satterthwaite Theorem, the rule must be a dictatorship. Observe that allowing asymmetric preferences in the one-dimensional case does not have this impact (cf. Manjunath 2009).

The non-dictatorship result for rectangles (Sect. 4.2) seems to be more robust and continues to hold if we allow for a larger domain of elliptic (separable quadratic) single-dipped preferences, as long as the axes are parallel to the edges of the rectangle. This non-dictatorship results also easily extends to higher dimensions.

Finally, we mention that it at least under some assumptions, Pareto optimality can be weakened to unanimity. Call a rule $\varphi$ unanimous if $\varphi (p) \in \mathfrak {b}(p(1))$ whenever $p$ is a profile with $p(i) = p(1)$ for all $i \in N$. Suppose we would know that for each profile $p$, if $\varphi (p)$ is not Pareto optimal, then there is a single-best point Pareto dominating $\varphi (p)$. Now let $\varphi$ be unanimous and strategy-proof. Suppose $\varphi (p)$ were not Pareto optimal for some profile $p$. Then take a single-best point $a\in A$ Pareto dominating $\varphi (p)$, and take $b \in A_a$. Let $q$ be the profile with $q(i)=b$ for all $i\in N$, then by unanimity, $\varphi (q)=a$. Then $\varphi (p)=a$ by (intermediate) strategy-proofness, a contradiction. So $\varphi$ is Pareto optimal. This argument applies, for instance, if $A$ is a regular polygon and we have that $\varphi$ always assigns an extreme point. But it is not clear whether the latter follows from unanimity and strategy-proofness alone. Note that in the one-dimensional case (Manjunath 2009), unanimity and Pareto optimality are equivalent within the same framework.

Appendix: A remaining proofs

We start by proving the claim in Sect. 2.2 that strategy-proofness and intermediate strategy-proofness are equivalent.

Lemma 6.1

Let $\varphi : A^N \rightarrow A$ be a rule. Then $\varphi$ satisfies SP if and only if it satisfies ISP.

Proof

Clearly, ISP implies SP. Now let $\varphi$ satisfy SP, let $S \subseteq N$, and let $a \in A$ and $p,q \in A^N$ such that $p(i)=a$ for all $i\in S$ and $p(i)=q(i)$ for all $i \in N \setminus S$. Without loss of generality suppose $S=\{1,\ldots , s\}$. Define $p^0,p^1,\ldots ,p^s \in A^N$ by $p^0=p,\,p^s=q$ and for each $i=1,\ldots , s-1$: $p^i(j)=q(j)$ for $j=1,\ldots , i$ and $p^i(j)=p(j)$ for $j=i+1,\ldots , n$. By SP we have $||p(i)-\varphi (p^{i-1})|| \ge ||p(i) - \varphi (p^i)||$ for every $i=1,\ldots , s$. Hence, $||a-\varphi (p)|| = ||p(1)-\varphi (p^0)|| \ge \ldots \ge ||p(s)-\varphi (p^s)|| = ||a-\varphi (q)||$. So $\varphi$ satisfies ISP. $\square$

We continue with the proof of Lemma 3.1. (The proof in the main text is for the case where $A$ is a regular 5-polygon.)

Proof of Lemma 3.1

Let $\varphi (p)=c$. To the contrary suppose that $c\notin C$. Then $c\in \, ]\widetilde{c}_{L},\widetilde{c}_{R}[\,\subseteq \partial A$ for some $\widetilde{c}_{L},\widetilde{c}_{R}\in C$. Let $\ell$ be the line through $c$ perpendicular to $]\widetilde{c}_{L}, \widetilde{c}_{R}[$. Line $\ell$ divides $A$ in a left part and a right part, which we denote by ${\mathcal {L}}$ and ${\mathcal {R}}$, respectively, more precisely, ${\mathcal {L}}=H^\circ (\ell ,\widetilde{c} _{L})\cap A$ and ${\mathcal {R}}=H^\circ (\ell ,\widetilde{c }_{R})\cap A$. For $x$ in $\partial A \cap {\mathcal {L}}$ consider the perpendicular bisector $\ell _{x,c}$ of $[x,c]$. If $x\notin [\widetilde{c}_{L},c]$, let $d_{x}$ be the point of intersection of $\ell _{x,c}$ and $\partial A$ which is not in $H^\circ (\ell (x,c),\widetilde{c}_{L})$ (i.e., not in the open half-plane bounded by the straight line through $x$ and $c$ and containing the point $\widetilde{c}_{L}$); if $x \in [\widetilde{c}_{L},c]$, let $d_{x}$ be the point of intersection of $\ell _{x,c}$ and $\partial A$ which is not in $[\widetilde{c}_{L},c]$.

Consider the set $Z$ of points $z \in C \cap {\mathcal {L}}$ such that $d_z$ is in between $d_{z'}$ and $c$ for all $z' \in C \cap {\mathcal {L}}$ on the path along the boundary of $A$ passing $\widetilde{c}_L$ before $c$. If $Z$ consists of a unique point then call this point $c_L$; otherwise, let $c_L$ be the point of $Z$ such that $z$ is in between $c_L$ and $c$ for all other points $z\in Z$.⁵ We write $d_L$ instead of $d_{c_L}$. Clearly, $d_L \in \partial A \cap {\mathcal {L}}$ since $d_{\widetilde{c}_L} \in \partial A \cap {\mathcal {L}}$. Now the choice of $c_L$ implies that $d_L \in H(\ell _{z,c},z)$ for all $z \in C \cap {\mathcal {L}}$, hence that $||d_L-z|| \le ||d_L-c||$ for all $z \in C \cap {\mathcal {L}}$. In turn, this implies $||d_L-x|| \le ||d_L-c||$ for all $x \in \overline{{\mathcal {L}}}$.

Let $S_L = \{ i \in N : p(i) \in H^\circ (\ell _{c_L,c},c_L) \}$. Since $||d_L-\widetilde{c}_L|| \le ||d_L-c||$ and $\ell _{\widetilde{c}_L,c} \cap A \subseteq {\mathcal {L}}$ it follows that $\ell _{c_{L},c}\cap A\subseteq {\mathcal {L}}$. Pareto optimality of $\varphi$ implies that either $S_{L}$ is non-empty or $p(i) \in \ell _{c_{L},c}\cap A$ for all $i \in N$ (since otherwise $c_L$ would Pareto dominate $c=\varphi (p)$). Now similarly we can define $c_{R},\,d_{R}$ and $S_{R}$ for the right part of $A$ and have by Pareto optimality that either $S_{R}$ is non-empty or $p(i) \in \ell _{c_{R},c}\cap A$ for all $i \in N$. Since ${\mathcal {L}} \cap {\mathcal {R}}= \emptyset$ we have that $\ell _{c_{L},c}\cap A$ and $\ell _{c_{R},c}\cap A$ are disjoint. This implies that both $S_{L}$ and $S_{R}$ are non-empty.

Now consider the profile $q_{L}$ with $q_L(i) = p(i)$ for all $i \notin S_L$ and $q_{L}(i)=d_{L}$ for all $i \in S_L$. With the aid of the following claim we will prove that $\varphi (q_{L})=c_{L}$.

Claim Let $v,w \!\in \! A^N,\,i\!\in \! S_L$, and $a \!\in \! H^\circ (\ell _{c_{L},c},c_{L})$ with $v(i)\!=\!a,\,w(i)\!=\!d_L,\,v(j)\!=\!w(j)$ for all $j \!\in \! N \setminus \{i\}$, and $\varphi (v)\!\in \! [d_L; c_{L} \!\!\smallfrown \!\!\, c]$. Then $\varphi (w) \in [d_L; c_{L} \!\!\smallfrown \!\!\,c]$.

To prove this, first note that $||a-x|| \le ||a-c||$ for all $x\in [d_{L}; c_{L} \!\!\smallfrown \!\!\, c]$; this is so since $a \in H(\ell (c,d_L),c_L)$ because $c, d_L \in \partial A$, and therefore $a \in H(\ell _{x,c},x)$ for all $x\in [d_{L}; c_{L} \!\!\smallfrown \!\!\, c]$. (See Fig. 8(a).) Hence SP of $\varphi$ implies $||a-c|| \ge ||a-\varphi (w)||$ otherwise agent $i$ could manipulate from $v$ to $w$. Again by strategy-proofness we have $||d_{L}-\varphi (w)|| \ge ||d_{L}-c||$ otherwise agent $i$ could manipulate from $w$ to $v$. Suppose that $||d_{L}-\varphi (w)|| > ||d_{L}-c||$. Then, since $c_L \in Z$, we have $\varphi (w)\in {\mathcal {R}}$. Since $d_{L}$ and $c$ are both in $H(\ell _{c,\varphi (w)},c)$ we have $A \cap H(\ell (d_{L},c),\widetilde{c}_{L})\subseteq H (\ell _{c,\varphi (w)},c)$. Since $a\in A\cap H^\circ (\ell (d_{L},c), \widetilde{c}_{L})$ it follows that $a\in H^\circ (\ell _{c,\varphi (w)},c)$, contradicting $||a-c|| \ge ||a-\varphi (w)||$. (See Fig. 8(b).) Therefore, we must have $||d_{L}-\varphi (w)|| = ||d_{L}-c||$.

Fig. 8

Illustrating the proof of Lemma 3.1

Now the two circles $\odot (d_{L},||d_{L}-c||)$ and $\odot (a,||a-c||)$ intersect in $c$ and say $c'$. Since $||a-c|| \ge ||a-\varphi (w)||$ and $||d_{L}-\varphi (w)|| = ||d_{L}-c||$ it follows that $\varphi (w)\in [d_{L}; c' \!\!\smallfrown \!\!\, c]$. But by the choice of $c_{L}$, we have $[d_{L}; c' \!\!\smallfrown \!\!\, c] \cap A = [d_{L}; c_{L} \!\!\smallfrown \!\!\, c] \cap A$. Therefore, $\varphi (w)\in [d_{L}; c_{L} \!\!\smallfrown \!\!\, c]$, which completes the proof of the Claim.

Repeated application of the Claim yields that $\varphi (q_{L})\in [d_{L};c_{L} \!\!\smallfrown \!\!\, c]$. For all $x\in [d_{L};c_{L} \!\!\smallfrown \!\!\, c]$, we have by construction that $H(\ell _{c_{L},x},c_{L})\cap A$ is a subset of $H(\ell _{c_{L},c},c_{L}) \cap A$ and therefore contains no dips of the profile $q_L$ other than $d_L$. Since $S_R \ne \emptyset$, it follows that for profile $q_L$ the point $c_{L}$ Pareto dominates all $x\in [d_{L};c_{L} \!\!\smallfrown \!\!\, c]$ with $x \ne c_L$. Hence, $\varphi (q_{L})=c_{L}$.

Next consider the profile $r$ with $r(i)=d_{R}$ for all $i \in S_R$ and $r(i) = q_L(i)$ for all $i \notin S_R$. SP of $\varphi$ implies that $||d_{R}-\varphi (r)|| \ge ||d_{R}-c_{L}||$. But clearly $d_{R}\in H^\circ (\ell _{c_{L},c},c)$ and therefore $||d_{R}-c|| <||d_{R}-c_{L}||$. Hence, $||d_{R}-\varphi (r)|| > ||d_{R}-c||$ and by the definition of $d_R$ (similar to $d_L$ above) $||d_{R}-c|| \ge ||d_{R}-x||$ for all $x\in \overline{{\mathcal {R}}}$. This implies $\varphi (r)\in {\mathcal {L}}$. By a completely analogous argument, now starting on the right part of $A$ with a profile $q_R$, we can show that $\varphi (r)\in {\mathcal {R}}$. Since ${\mathcal {L}} \cap {\mathcal {R}} = \emptyset$, we have a contradiction, which completes the proof of the lemma. $\square$

Next, we prove Lemmas 3.3 and 3.4.

Proof of Lemma 3.3

Since $a, b, c \in C$ they are not collinear and thus $m_{a,b,c}$ exists. The straight lines $\ell _{a,b},\ell _{a,c}$, and $\ell _{b,c}$ intersect at $m_{a,b,c}$ and determine six open non-empty regions which divide $A^{\circ }\setminus (\ell _{a,b}\cup \ell _{a,c}\cup \ell _{b,c})$ into disjoint sets. A single-dipped preference $R_x$ is constant over $a,\,b$, and $c$ as long as $x$ stays in one of these regions. Call these regions $V_{abc},V_{bac},V_{bca},V_{cba},V_{cab}$ and $V_{acb}$; for $x \in V_{abc}$ we have that $a$ is (strictly) preferred over $b$ and $b$ over $c$ according to $R_x$ and similarly for the other five regions. Now $A_a \subseteq (V_{abc}\cup V_{acb}\cup \ell _{b,c})^{\circ }\cap A$. Since $A_{a}$ is non-empty we have that $(V_{abc}\cup V_{acb}\cup \ell _{b,c})^{\circ }\cap A$ is non-empty and therefore $(V_{abc}\cup V_{acb}\cup \ell _{b,c})^{\circ }\cap A^{\circ }$ is non-empty. Similarly $(V_{bca}\cup V_{bac}\cup \ell _{a,c})^{\circ }\cap A^{\circ }$ and $(V_{cab}\cup V_{cba}\cup \ell _{a,b})^{\circ }\cap A^{\circ }$ are non-empty. Take points $x_a, x_b, x_c$ in these respective regions, then $m_{a,b,c}$ is in the convex hull of these three points and is therefore an interior point of $A$. $\square$

Proof of Lemma 3.4

If $A^{\circ }\setminus \overline{A}_a=A_{b}$ for some $b\in \mathcal {B}$, then we are done since $A_{b}$ is convex and therefore connected. Therefore, let $y,z \in A^\circ$ with $y\in A_{b}$ and $z\in A_{c}$ for some distinct $b,c\in \mathcal {B}\setminus \{a\}$. Since $A^{\circ }\subseteq \cup \{\overline{A}_x : x\in \mathcal {B}\}$ it is sufficient to prove that there is a path in $A^{\circ }\setminus \overline{A}_a$ connecting $y$ and $z$. Lemma 3.3 implies that $m_{a,b,c} \in A^{\circ }$. Convexity of $A$ implies that $A^{\circ }$ is convex. Hence, $[y,m_{a,b,c}] \subseteq A^\circ$ and $[z,m_{a,b,c}] \subseteq A^\circ$. With notations as in the proof of Lemma 3.3, we may further conclude that $[y,m_{a,b,c }[\; \subseteq (V_{bca}\cup V_{bac}\cup \ell _{a,c})^{\circ }$ and $[z,m_{a,b,c}[\; \subseteq (V_{cab}\cup V_{cba}\cup \ell _{a,b})^{\circ }$. Since $A_{a}\subseteq (V_{abc}\cup V_{acb}\cup \ell _{b,c})^{\circ }\cap A$ and $(V_{abc}\cup V_{acb}\cup \ell _{b,c})^{\circ }$ is disjoint from both $(V_{bca}\cup V_{bac}\cup \ell _{a,c})^{\circ }$ and $(V_{cab}\cup V_{cba}\cup \ell _{a,b})^{\circ }$ it follows that we can construct a path from $y$ to $z$ in $A^{\circ }\setminus \overline{A}_a$, as follows. (See Fig. 9.) Choose points $y' \in [y,m_{a,b,c}[$ and $z' \in \; ] m_{a,b,c},z]$ close enough to $m_{a,b,c}$ such that there is a path $P$ from $y'$ to $z'$ in $A^\circ$ disjoint from $\overline{A}_a$; then the desired path is $[y,y'] \cup P \cup [z',z]$. $\square$

Fig. 9

Illustrating the proof of Lemma 3.4: path between $y$ and $z$; $m=m_{a,b,c}$

The following lemma is a consequence of (intermediate) strategy-proofness. It will be used in the proof of Lemma 3.5 below. The lemma says that if an agent’s preference changes by swapping two alternatives in $C$ while not changing the (strict) order between other alternatives in $C$, and if therefore the alternative assigned by the rule changes, then the two swapped alternatives must be the alternatives assigned by the rule.⁶

Lemma 6.2

Let $\emptyset \ne S \subseteq N,\,p,q \in A^N$ and $x,y\in C$ with $x \ne y$ such that $(i)\,p(j)=q(j)$ for all $j \in N \setminus S$; $(ii)\,p(i)=p(j)$ and $q(i)=q(j)$ for all $i,j \in S$; $(iii)$ for all $i\in S,\,p(i)$ and $q(i)$ order the alternatives of $C$ strictly and coincide on $C$ except for a swap between $x$ and $y$: $p(i)=\ldots xy\ldots ,\,q(i)=\ldots yx\ldots$; and $(iv)\,\varphi (p), \varphi (q) \in C,\,\varphi (p) \ne \varphi (q)$. Then $x=\varphi (p)$ and $y=\varphi (q)$.

Proof

By ISP, we may assume that $S$ consists of a single agent, say $i$. By SP, we must have $p(i) = \ldots \varphi (p)\ldots \varphi (q)\ldots$ and $q(i)= \ldots \varphi (q)\ldots \varphi (p)\ldots$. Therefore, by the assumptions on the profiles $p$ and $q$, we must have that $x=\varphi (p)$ and $y=\varphi (q)$. $\square$

Proof of Lemma 3.5

If $a=b$ then the claim in the lemma follows from Pareto optimality. Thus, let $a\ne b$ and suppose that $\varphi (p)=c \notin \{a,b\}$. We derive a contradiction. Pareto optimality implies $R_x=a\ldots c\ldots b\ldots x$ and $R_y=b\ldots c\ldots a\ldots y$ We take a path from $x$ to $c$ with the following properties (see below for a formal description): (i) along this path, $c$ can only become worse compared to other elements of $C$; (ii) along this path the preference over elements of $C$ changes by swaps of at most two alternatives at the same time; and (iii) along this path preferences over $C$ are strict except at swaps as in (ii). Formally, this path is the graph of a continuous function $\pi$ from $[0,1]$ to $A$ with $\pi (0)=x$ and $\pi (1)=c$ such that (i) for all $t_1 < t_2$ and $z \in C$, if $(z,c) \in R_{\pi (t_1)}$ then $(z,c) \in R_{\pi (t_2)}$ and $(c,z) \notin R_{\pi (t_2)}$; (ii) for all $t \in [0,1]$ there are no distinct $z,z',z'' \in C$ such that $\pi (t) \in \ell _{z,z'} \cap \ell _{z,z''}$; and (iii) there are at most finitely many $t$ for which $\pi (t) \in \ell _{z,z'}$ for some $z,z'\in C$. We call a pair $R_{\pi (t_1)},\,R_{\pi (t_2)}$ an ‘elementary change’ if the latter preference arises from the former after swapping two adjacent alternatives in $C$.

Let $p^{t}=(\pi (t)^S,y^{N\setminus S})$. Then $\varphi (p^{1})\ne c$ since $c$ is not Pareto optimal at $p^1$ (it is dominated by $b$). Thus, there must be a first elementary change such that $\varphi (p^{t_{1}})=c$ and $\varphi (p^{t_{2}})=d\ne c$. By Lemma 6.2, this implies that $R_{\pi (t_1)}=\ldots cd\ldots$ whereas $R_{\pi (t_2)}=\ldots dc\ldots$

Now there are two cases.

Case 1 $R_y = b\ldots d\ldots c\ldots a\ldots y$ (so $d$ is preferred to $c$ at $R_y$).

Then in the same way as above we can find a path $\rho$ from $y$ to $c$, profiles $q^{t}=(\pi (t_{1})^{S}, \rho (t)^{N\setminus S})$ and $t_3$ and $t_4$ such that $\varphi (q^{t_{3}})=c,\,\varphi (q^{t_{4}})=e \ne c$ and $R_{\rho (t_3)}$ and $R_{\rho (t_4)}$ form an elementary change swapping $c$ and $e$. Consider $r=(\pi (t_{2})^{S}, \rho (t_{4})^{N\setminus S})$ and $u^{t}=(\pi (t)^{S}, \rho (t_{3})^{N\setminus S})$ for $t\in [t_{1},t_{2}]$. So, $u^{t_1}=q^{t_3}$ and hence $\varphi (u^{t_{1}})=\varphi (q^{t_{3}})=c$. Let $\varphi (r)=f$. Note that $R_{\rho (t_{3})}=\ldots d\ldots ce\ldots$ and $R_{\rho (t_{4})}=\ldots d\ldots ec\ldots$. Since $\varphi (u^{t_{1}})=c$ it follows by Pareto optimality and Lemma 6.2 that $\varphi (u^{t_{2}})=d$. Summarizing we have:

	$u^{t_{1}}=q^{t_{3}}$	$q^{t_{4}}$
$i \in S$	$u^{t_{1}}(i) = R_{\pi (t_{1})} = \ldots cd\ldots$	$q^{t_4}(i) = R_{\pi (t_{1})} = \ldots cd\ldots$
$i \in N \setminus S$	$u^{t_{1}}(i) = R_{\rho (t_{3})} = \ldots d\ldots ce\ldots$	$q^{t_4}(i) = R_{\rho (t_{4})} = \ldots d\ldots ec\ldots$
	$\varphi (u^{t_{1}})=c$	$\varphi (q^{t_{4}})=e$
	$u^{t_{2}}$	$r$
$i\in S$	$u^{t_{2}}(i) = R_{\pi (t_{2})} = \ldots dc\ldots$	$r(i) = R_{\pi (t_{2})} = \ldots dc\ldots$
$i \in N\setminus S$	$u^{t_{2}}(i) = R_{\rho (t_{3})} = \ldots d\ldots ce\ldots$	$r(i) = R_{\rho (t_{4})} = \ldots d\ldots ec\ldots$
	$\varphi (u^{t_{2}})=d$	$\varphi (r)=f$

There are two subcases.

Subcase $d\ne f$. Comparing $u^{t_{2}}$ and $r$, Lemma 6.2 implies $R_{\rho (t_{3})}=\ldots df\ldots ce\ldots$ and $R_{\rho (t_{4})}=\ldots fd\ldots ec\ldots$ So $c,\,d,\,e$, and $f$ are all different. Comparing $q^{t_{4}}$ and $r$, Lemma 6.2 implies (i) $R_{\pi (t_{1})} = \ldots ef\ldots cd\ldots$ and $R_{\pi (t_{2})} = \ldots fe\ldots dc\ldots$ or (ii) $R_{\pi (t_{1})} = \ldots cd\ldots ef\ldots$ and $R_{\pi (t_{2})} = \ldots dc\ldots fe\ldots$ But (i) implies that $\varphi (u^{t_{1}})=c$ is Pareto dominated by $f$ at $u^{t_{1}}$, a contradiction; and (ii) implies that $\varphi (q^{t_{4}})=e$ is Pareto dominated by $d$ at $q^{t_{4}}$, likewise a contradiction. So this subcase cannot occur.

Subcase $d=f$. Comparing $q^{t_{4}}$ and $r$, Lemma 6.2 implies $R_{\pi (t_{1})} = \ldots ed\ldots$ and $R_{\pi (t_{2})} =\ldots de\ldots$ This implies the contradiction $c=e$ and therefore also this subcase cannot occur. This ends the proof of Case 1.

Case 2 $R_y = b\ldots c\ldots d\ldots a\ldots y$ (so $c$ is preferred to $d$ at $R_y$).

By interchanging the roles of $c$ and $d$ and thus those of $R_{\pi (t_{1})}$ and $R_{\pi (t_{2})}$, and then proceeding like in Case 1, we derive a similar contradiction. $\square$

The following lemma will be used in the proof of Lemma 3.9. It states that we can always find $a,b,c \in \mathcal {B}$ satisfying the first part of the condition in (ii) of Lemma 3.8.

Lemma 6.3

Let $|\mathcal {B}| \ge 3$ and let $a \in \mathcal {B}$. Then there are distinct $b,c \in \mathcal {B}\setminus \{a\}$ such that $m_{a,b,c} \in A^\circ \cap \partial A_a$.

Proof

For any two distinct points $x,y \in \mathcal {B}\setminus \{a\}$, we have $m_{a,x,y}\in A^\circ$ by Lemma 3.3. Now, since ${\mathcal {B}}$ is finite there must be distinct $b,c \in {\mathcal {B}} \setminus \{a\}$ such that the set $H^\circ (\ell _{a,b},b) \cap H^\circ (\ell _{a,c},b)$ contains no point of the form $m_{a,x,y}$ for distinct $x,y \in {\mathcal {B}}\setminus \{a\}$.⁷ We claim that $H^\circ (\ell _{a,b},b) \cap H^\circ (\ell _{a,c},c) \cap A$ also has empty intersection with $\ell _{a,x}$ for any $x\in C \setminus {\mathcal {B}}$. If not, then there is such an $x$ and a point $x_a \in H^\circ (\ell _{a,b},b) \cap H^\circ (\ell _{a,c},b) \cap H^\circ (\ell _{a,x},x) \cap A$ with $R_{x_a} = ax\ldots$ and such that $R_{\sigma _{a,x}(x_a)}=xa\ldots$ But then $\sigma _{a,x}(x_a) \in A_x$, so $x\in {\mathcal {B}}$, a contradiction. It follows that $H^\circ (\ell _{a,b},b) \cap H^\circ (\ell _{a,c},b) \cap A \subseteq A_a$. Since $m_{a,b,c} = \ell _{a,b} \cap \ell _{a,c}$ this implies that $m_{a,b,c} \in \overline{A}_a$. Since, clearly, $m_{a,b,c} \notin A_a$ we have $m_{a,b,c} \in \partial A_a$. $\square$

Proof of Lemma 3.9

For the only if direction, assume that condition $(ii)$ in Lemma 3.8 does not hold. We show that $\mathcal {B}$ is rectangular. The proof of this fact proceeds in a few steps. We start with stating (without proof) the following useful fact.

Step 1 A set $Q \subseteq {\mathbb {R}}^2$ is an orthant if it is of the form $Q = \{ p+\lambda _1 x^1 + \lambda _2 x^2 \mid \lambda _1, \lambda _2 \ge 0 \}$ for some $p\in {\mathbb {R}}^2$ and some perpendicular vectors $x^1,x^2 \in {\mathbb {R}}^2 \setminus \{0\}$. Denote $p(Q) = p$. Let $X$ be a compact and convex subset of ${\mathbb {R}}^2$ with non-empty interior, and suppose $X$ can be written as $X = \bigcup _{i\in I} (Q^i \cap X)$ where $I$ is some index set, $Q^i$ is an orthant with $p(Q^i) \in X^\circ$ for each $i\in I$, and $(Q^j \cap X)^\circ \cap (Q^k \cap X)^\circ = \emptyset$ for all distinct $j,k \in I$. Then $|I|=4$.

Step 2 Let $a \in \mathcal {B}$ and let $b,c \in \mathcal {B}\setminus \{a\},\,b \ne c$, such that $m_{a,b,c} \in A^\circ \cap \partial A_a$. Since condition $(ii)$ in Lemma 3.8 does not hold, there is an $x \in \mathcal {B}$ such that $\{a,b,c,x\}$ is rectangular. Without loss of generality assume that $\ell (a,b)$ and $\ell (c,x)$, as well as $\ell (a,c)$ and $\ell (b,x)$ are parallel. (See Fig. 10 for an illustration of the proof of this step.) Denote $Q = H(\ell _{a,b},x) \cap H(\ell _{a,c},x)$. Then: $A_a = Q^\circ \cap A$.

Fig. 10

Illustrating the proof of Lemma 3.9, Step 2

In order to prove this, we first observe the following. Let $y$ be any point of $\overline{A}_a$ and let $\ell$ be the line through $a$ and $y$. Then $y' \in A_a$ for any point $y'\in A$ on $\ell$ on the other side of $y$ than $a$. Therefore, to prove our claim, it is sufficient to prove that $y \in \partial A_a$ for every $y \in \partial Q \cap A$. Suppose this were not true, without loss of generality suppose there is some point in $\ell _{a,b} \cap Q \cap A$ which is not in $\partial A_a$. Then, since $m_{a,b,c} \in \partial A_a$ and since $A_a$ is convex there is a $\widehat{y} \in \ell _{a,b} \cap Q \cap A$ such that $[m_{a,b,c},\widehat{y}] \subseteq \partial A_a$ and such that $(\ell _{a,b} \cap Q) \setminus [m_{a,b,c},\widehat{y}] \ne \emptyset$ but $(\ell _{a,b} \cap Q) \setminus [m_{a,b,c},\widehat{y}] \cap \overline{A}_a = \emptyset$. Then there must be a $z \in \mathcal {B}$ such that $\ell _{a,z}$ intersects $\ell _{a,b}$ at the point $\widehat{y}$. Since, clearly, $\widehat{y} \in \partial A_a \cap A^\circ$ and condition $(ii)$ in Lemma 3.8 does not hold, there must be a $v \in \mathcal {B}$ such that the set $\{a,z,b,v\}$ is rectangular. This implies in particular that $\ell _{a,z}$ and $\ell _{a,b}$ are perpendicular. But then $y \notin A_a$ for all $y$ in $Q^\circ \cap A$ on the straight line $\ell '$ through $a$ and $\widehat{y}$. This is a contradiction with the observation at the beginning of the proof, since $\widehat{y}\in \partial A_a$. This completes the proof of the claim in Step 2.

Step 3 Let $a \in \mathcal {B}$. Then the set $\overline{A}_a$ is the intersection of $A$ with an orthant $Q_a$ with $p(Q_a) \in A^\circ$.

To prove this, just note that by Lemma 6.3, there are $b,c$ as in Step 2. The claim of Step 3 now follows from Step 2.

We can now complete the proof of the only if direction. By Step 3, for each $a \in \mathcal {B}$, the set $\overline{A}_a$ is the intersection of $A$ with an orthant $Q_a$ with $p(Q_a) \in A^\circ$. Moreover, $A = \bigcup _{a\in \mathcal {B}} \overline{A}_a = \bigcup _{a\in \mathcal {B}} (Q_a \cap A)$. Hence by Step 1, $|\mathcal {B}|=4$, in particular $\mathcal {B}= \{a,b,c,x\}$ with $a,b,c,x$ as in Step 2. Thus, $\mathcal {B}$ is rectangular.

For the if direction, let $\mathcal {B}$ be rectangular with $\mathcal {B}= \{v,w,y,z\}$. Clearly, among any three distinct points in $\{v,w,y,z\}$, there is a point $a$ such that $m_{a,b,c} \in \partial A_a \cap A^\circ$, where $b$ and $c$ are the other two points, but together with the fourth point they form the rectangular set $\mathcal {B}$. Hence, condition (ii) does not hold. $\square$