A never-decisive and anonymous criterion for optimal growth models

Abstract

We address in this paper the question of the existence of a Social Welfare Function that would be sustainable and would allow us to obtain solutions to optimal growth models. We define sustainability by two new axioms called Never-decisiveness of the present and Never-decisiveness of the future. We first show that a SWF which has Never-decisiveness properties cannot be defined on a ball of $l_{\infty }^{+}$. We must (i) restrict to the set of utility streams for which the value of the SWF is finite and (ii) introduce additional assumptions in order to obtain the Never-decisiveness properties. Our main result in this paper is therefore to show that the undiscounted utilitarian criterion is an anonymous and never-decisive criterion for optimal growth models. We consider the set of utilities of consumptions which are generated by a specific technology, namely a technology with decreasing returns for high levels of capital, and restrict ourselves to good programs, i.e., any program for which intertemporal utility is well defined.

1 Introduction

Optimal growth theory is largely built around the discounted utilitarian approach, but the debate between authors subscribing to discounted utilitarianism and authors rejecting it has always been vivid. Ramsey (1928) himself, in a much-cited statement, held that “discount later enjoyments in comparison with earlier ones [is] a practice which is ethically indefensible and arises merely from the weakness of imagination.” This debate is particularly passionate when the sustainability of growth is concerned, because the process of discounting forces a fundamental asymmetry between present and future generations, particularly those in the distant future, and so appears to be in contradiction with the intergenerational equity concern underlying the search for sustainability.

Several alternative social welfare functions (SWFs) have been proposed in the optimal growth literature. The Rawlsian or maximin criterion (Rawls 1971; Solow 1974) maximizes the utility of the least well-off generation. The undiscounted utilitarian criterion (Ramsey 1928; Koopmans 1965) maximizes the infinite sum of the (negative) differences between actual utilities and their upper bound (the bliss), with a zero-utility discount rate. With the overtaking criterion (Gale 1967), one utility stream is said to be better than another if from some date on, the first one is greater than the second one. Whereas the usual discounted utilitarian criterion assumes a constant discount rate, criteria with nonconstant and declining discount rates, hyperbolic for instance, have also been used (see, e.g., Heal 1998).

In the context of each particular growth model, the shape of the optimal growth paths obtained under these various criteria is intimately dependent on the properties of each criterion. For instance, in the canonical Dasgupta–Heal–Solow model of growth with exhaustible resources, optimal consumption asymptotically vanishes with the discounted utilitarian criterion, whereas it grows forever with the undiscounted utilitarian criterion, and remains constant with the maximin criterion (see, e.g., Dasgupta and Heal 1979). The properties leading to these different paths are related to discounting, but also to the degree of intertemporal substitutability of utilities embodied in the criterion; more deeply, these properties are consubstantial with the axiomatic foundations of the criteria, as we have been knowing since Koopmans (1960).

The axiomatic approach founding social welfare criteria considers the set of intertemporal utility streams generated by a general set of bounded consumptions and defines a preference relation between them. This relation is ideally required to satisfy two main axioms, the Pareto axiom and the Anonymity axiom. Pareto guarantees efficiency. Broadly speaking, it demands that the preference relation is sensitive to the well-being of each generation. Anonymity guarantees equity, which is an equal treatment of all generations, in the sense that any finite permutation of utilities does not change the evaluation of the utility stream. Besides, preferences are often required to be independent¹ and to satisfy some continuity, transitivity and completeness properties. Unfortunately, Basu and Mitra (2003) show that when the social welfare criterion is represented by a function, it cannot satisfy simultaneously the Pareto and Anonymity axioms when instantaneous utilities are uniformly bounded: It is impossible to represent by a numerical function a preference relation embodying both the efficiency and equity requirements.

For practical purposes then, the point is to determine which axiom(s) we are ready to drop, depending on the context. Obviously, the discounted utilitarian criterion does not satisfy Anonymity. It seems very counterintuitive to drop Anonymity as far as sustainability is concerned. The undiscounted utilitarian criterion does not satisfy completeness: It is not a well-defined, real-valued function on all $l_{\infty }$ ² and cannot therefore define a complete order on $l_{\infty }$. The overtaking criterion also is not a well-defined function of $l_{\infty }$, since it cannot rank a pair of utility streams of $l_{\infty }$ for which neither the first overtakes the second, nor the second overtakes the first. This criterion does not also satisfy the axiom of “Strong Relative Anonymity,” introduced by Asheim et al. (2010), where “strong” reflects that all infinite permutations are considered. The maximin criterion does not satisfy the independence property. Nevertheless, neither completeness nor independence seem crucial for sustainability.

Chichilnisky (1996) drops the Anonymity axiom. But her purpose is to capture the idea of sustainable growth, and so she proposes a weaker concept of equity embodied in two new axioms: No-dictatorship of the present and No-dictatorship of the future. A social welfare function is said to give a dictatorial role to the present if it disregards the utilities of all generations from some generations on. Conversely, a social welfare function gives a dictatorial role to the future if it is only sensitive to the utilities of the generations coming after some generations. She exhibits, for the set of uniformly bounded consumptions, a social welfare criterion satisfying, besides the Pareto and independence requirements, these two axioms for sustainability. It is a mixed criterion, composed of one discounted utilitarian part taking into account the interests of the present and a part taking into account only the interests of the future.

This approach is very appealing. But its drawback is that most of the time the Chichilnisky’s criterion does not allow us to obtain explicit optimal growth paths with optimal control techniques. Chichilnisky (1996) does not apply her criterion to growth models but confines herself to the axiomatic approach. Applications are presented in Chichilnisky (1997) and Heal (1998), in the framework of canonical optimal growth models with exhaustible or renewable resources. When the discounted utilitarian part of the criterion embodies a constant discount rate, they claim that they obtain, using nonstandard techniques, a solution in the case of exhaustible resources, but they show that no solution exists in the model with renewable resources. Only when the discount rate is decreasing are they able to obtain a solution to the renewable resource model. Figuières and Tidball (2012) focus on the inexistence result of the case with a constant discount rate and show that they can find in the model with renewable resources “near-optimal” growth paths.

More recently, Alvarez-Cuadrado and Long (2009) have proposed another mixed criterion named the mixed Bentham–Rawls criterion, weighted average of a discounted utilitarian part as in Chichilnisky’s criterion, and a maximin part. They show that Chichilnisky does not obtain this criterion because it does not satisfy the independence property she imposes, property that they do not find compelling.

We address in this paper the question of the existence of a continuous SWF which is sustainable, in the sense that this continuous SWF is anonymous, Pareto and independent and allows us to obtain solutions to optimal growth models. We introduce a new concept of sustainability embodied in two new axioms, we call Never-decisiveness of the present and Never-decisiveness of the future. These axioms are inspired by the No-dictatorship axioms. We show that in the set of utilities bounded uniformly by a constant, there exists, up to a positive scalar, a unique SWF which is continuous, anonymous, Pareto and independent. This SWF satisfies our two Never-decisiveness axioms. Moreover, we can use this SWF to solve the discrete time version of the original Ramsey model (Ramsey 1928). Actually, the two Never-decisiveness axioms give another axiomatic foundation to the Gale’s overtaking criterion (Gale 1967). More precisely, we show that, under the assumptions introduced above and some others (see below), the overtaking criterion for optimal growth models satisfies Anonymity, Pareto axioms and the two Never-decisiveness axioms for sustainability.

We come back to the seminal definition of SWF through the Yosida theorem. We consider the SWF, W, which are restrictions to $l_{\infty }^{+}$ of continuous, linear functions on $l_{\infty }$. From the Yosida theorem, such a SWF has a unique decomposition: $W(\mathbf{x})=\sum _{t=0}^{\infty }a_{t}x_{t}+\phi (\mathbf{x})$, where $\mathbf{x}\in X$ , a set of infinite sequences, $\sum _{t=0}^{\infty }\left| a_{t}\right| <\infty$, and $\phi$ is purely finitely additive. This SWF satisfies the No-dictatorship axioms introduced by Chichilnisky (1996) for sequences of utility streams. We show that, in $l_{\infty }$, a continuous and independent SWF satisfies the No-dictatorship axioms if, and only if, it satisfies the Never-decisiveness axioms. Notice that this criterion is a nonconstructible criterion (see Lauwers 2012).

Now consider optimal growth models with decreasing returns. In these models, the feasible consumption paths are uniformly bounded by the same quantity. So, without any lost of generality, we can assume that the set of sequences X is $\left[ 0,1\right] ^{\infty }$. With this restriction, we show that there exists no SWF W (as defined above) from X into $\mathbb R _{+}$, with $a_{t}>0,\,\forall t,\,\sum _{t=0}^{\infty }a_{t}=1,\,\phi$ purely finitely additive, which satisfies the two Never-decisiveness axioms. This result comes from the assumption $\sum _{t=0}^{\infty }a_{t}=1$. We therefore remove it and assume $\sum _{t=0}^{\infty }a_{t}=+\infty$.³ The criterion is not complete anymore. Then, we easily show that the SWF W satisfies the two Never-decisiveness axioms on the set of utility sequences for which the value of the social welfare function is finite.

Asheim et al. (2012) and Asheim and Mitra (2010) propose the sustainable discounted utilitarianism. As Chichilnisky does, they drop the Anonymity axiom. They propose to replace it by the axiom of Hammond equity for the future introduced by Asheim and Tungodden (2004), which entails that the social welfare is sensitive to the interests of the present generation only when the present is worse off than the future. It may not be the case with our criterion (see example in “Appendix 1”).

Basu and Mitra (2007) propose and characterize a set of new social welfare criteria called the overtaking social welfare relations, allowing us to ensure an equal treatment of all generations. They show that the overtaking SWRs can be characterized in terms of four axioms. Moreover, in a one-dimensional Ramsey growth model, they actually show that the optimal path for the Gale overtaking criterion coincides with the optimal path for overtaking SWRs. From Dana and Le Van (1990), one can see that this path is actually the optimal path for the SWF obtained from Anonymity, Pareto axioms and our Never-decisiveness axioms. Observe that Asheim et al. (2010) show that Basu and Mitra welfare criterion is also incomplete. In other words, it may be effective in the sense of selecting a small set of optimal or maximal elements for a given class of feasible infinite utility streams. They establish a result that generalizes the time-invariant overtaking criterion to satisfy stationarity and an Anonymity criterion called Strong Relative Anonymity.

To sum up, for the issue of sustainability and intergenerational equity, our main result is to show that the undiscounted utilitarian criterion is a nondictatorial and anonymous criterion for optimal growth models. It is also upper-semicontinuous for the product topology, under a set of assumptions which can be summarized as follows: Instead of $l_{\infty }^{+}$ as set of utilities, we just consider the set of utilities of consumptions which are generated by a specific technology, namely a technology with decreasing returns for high levels of capital; by doing so, we restrict ourselves to good programs in the sense of Gale (1967), Brock (1970), Arkin and Evstigneev (1987), and Dana and Le Van (1990), Dana and Le Van (1993), when the state variables are in a finite dimension, and Zaslvaski (2007) when these variables belong to an abstract compact metric space, i.e., any program for which intertemporal utility is well defined.⁴

The paper is organized as follows. In Sect. 2 we present the Never-decisiveness criteria when the state space is, respectively, $l_{\infty }^{+}$ or $[0,1]^{\infty }$. We show that for an optimal growth model with decreasing returns for high value of capital stock where the utilities of the streams of consumptions typically belong to $[0,1]^{\infty }$, there exists no SWF which is never-decisive. We then restrict the state space to the sets of utilities for which the value of the SWF is finite. In Sect. 3, we show that, actually, the Gale’s overtaking criterion, restricted to the set of good programs, is anonymous and never-decisive.⁵ Section 4 shows that using the overtaking criterion, one can obtain optimal solutions to growth models. Some examples of models are also presented in this section. In particular, we present an economy with a convex–concave production function (see Dechert and Nishimura 1983). In Dechert and Nishimura (1983), the proof of existence of a poverty trap is given, but its precise value is not easy to compute. As a by-product, we obtain here the explicit value of this poverty trap. We also use our criterion to solve two growth models, respectively, with exhaustible and renewable resources.

2 Never-decisiveness criterion

We introduce here a new concept, called Never-decisiveness, based on Chichilnisky (1996) concept of No-dictatorship. We show that the two concepts are equivalent in $l_{\infty }$. As we are interested in finding solutions of optimal growth models, we restrict ourselves to the space of uniformly bounded consumptions. Then we know that the Chichilnisky criterion may not allow us to obtain solutions. We show how our criterion overcomes this problem.

2.1 Preliminaries

We first recall the concepts of No-dictatorship of the present and No-dictatorship of the future given by Chichilnisky (1996).

Let X denote a set of infinite sequences. A criterion W is a nondecreasing function from X into $\mathbb{R }$.

A criterion $W$ exhibits No-dictatorship of the present if there exist $\mathbf{x}\in X,\;\mathbf{y}\in X$ which satisfy $W(\mathbf{x})>W(\mathbf{y})$, and for any $N$, there exist $k\ge N,\, (z_{t})_{t\ge k+1},\;(s_{t})_{t\ge k+1}$ such that

$$\begin{aligned} W(x_{0},\ldots ,x_{k},z_{k+1},\ldots ,z_{k+t},\ldots )\le W(y_{0},\ldots ,y_{k},s_{k+1},\ldots ,s_{k+t},\ldots ). \end{aligned}$$

A criterion $W$ exhibits No-dictatorship of the future if there exist $\mathbf{x}\in X,\;\mathbf{y}\in X$ which satisfy $W(\mathbf{x})>W(\mathbf{y})$, and for any $N$, there exist $k\ge N,\, (z_{t})_{t=0,\ldots ,k}, \;(s_{t})_{t=0,\ldots ,k}$ such that

$$\begin{aligned} W(z_{0},\ldots ,z_{k},x_{k+1},\ldots ,x_{k+t},\ldots )\le W(s_{0},\ldots ,s_{k},y_{k+1},\ldots ,y_{k+t},\ldots ). \end{aligned}$$

We now define the concepts of Never-decisiveness of the present and Never-decisiveness of the future.

A criterion $W$ exhibits Never-decisiveness of the present if for any $\mathbf{x}\in X,\;\mathbf{y}\in X$ which satisfy $W(\mathbf{x})>W( \mathbf{y})$, then, for any $N$, there exist $k\ge N,\, (z_{t})_{t\ge k+1},\;(s_{t})_{t\ge k+1}$ such that

$$\begin{aligned} W(x_{0},\ldots ,x_{k},z_{k+1},\ldots ,z_{k+t},\ldots )\le W(y_{0},\ldots ,y_{k},s_{k+1},\ldots ,s_{k+t},\ldots ). \end{aligned}$$

A criterion $W$ exhibits Never-decisiveness of the future if for any $\mathbf{x}\in X,\;\mathbf{y}\in X$ which satisfy $W(\mathbf{x})>W(\mathbf{y})$, then, for any $N$, there exist $k\ge N,\, (z_{t})_{t=0,\ldots ,k},\;(s_{t})_{t=0,\ldots ,k}$ such that

$$\begin{aligned} W(z_{0},\ldots ,z_{k},x_{k+1},\ldots ,x_{k+t},\ldots )\le W(s_{0},\ldots ,s_{k},y_{k+1},\ldots ,y_{k+t},\ldots ). \end{aligned}$$

The following definition generalizes Definition 7 in Chichilnisky (1996), p. 251:

Definition 1

Let X be a nonempty subset of $l_\infty$ and W be a criterion from X into $\mathbb R$. The criterion W is independent if there exists a linear function l on $l_\infty$ such that for any $\mathbf{x} \in l_\infty$, any $\mathbf{y} \in l_\infty ,\, W(\mathbf{x}) = W (\mathbf{y}) \Leftrightarrow l(\mathbf{x}-\mathbf{y})=0$.

From Chichilnisky (1996), p. 251, when $X=l_\infty , W$ can be represented by a linear function on $l_{\infty }$. Now, when X is a subset of $l_\infty$, we say that W is independent if it is affine.

We say that the SWF W is sustainable if it is complete (i.e., well defined on the whole space $l_{\infty }^{+}$), increasing and satisfies the two No-dictatorship axioms.

We consider the SWFs which are restrictions to $l_{\infty }^{+}$ of continuous, linear functions on $l_{\infty }$. From Yosida theorem, such a SWF W has a unique decomposition

$$\begin{aligned} W(\mathbf{x})=\sum _{t=0}^{\infty }a_{t}x_{t}+\phi (\mathbf{x}) \end{aligned}$$

where $\sum _{t=0}^{\infty }\left| a_{t}\right| <\infty$ and $\phi$ is purely finitely additive. If W is increasing, then $a_{t}>0$ for all t and $\phi$ is increasing.

In the following Proposition, when $X=l_{\infty }$, sustainability is equivalent to Never-decisiveness:

Proposition 1

Let W be a continuous independent SWF from $l_{\infty }$ into $\mathbb R _{+}$. Then W is sustainable if, and only if, it satisfies Never-decisiveness of the future and Never-decisiveness of the present.

Proof

• 1. From Chichilnisky (1996), Theorem 2, if W is sustainable, then it has the decomposition:

  $$\begin{aligned} W(\mathbf{x})=\sum _{t=0}^{\infty }a_{t}x_{t}+\phi (\mathbf{x}) \end{aligned}$$

  (1)

  where $\sum _{t=0}^{\infty }\left| a_{t}\right| <\infty$ and $\phi$ is purely finitely additive. Moreover, $a_t>0,\forall t$ and $\phi \ne 0$. We can assume $\sum _{t=0}^\infty a_t =1$ and $\phi (1, 1, \ldots , 1, \ldots )>0$.⁶

• 2. Let us consider a SWF W as in (1). We will prove that it is never-decisive.

  • (a) Never-decisiveness of the present Let $W(\mathbf{x})>W(\mathbf{y})$ with $\mathbf{x}\in \ell _{\infty }, \mathbf{y}\in \ell _{\infty }$. Choose $\lambda >0$ large enough s.t. $\phi (\lambda , \lambda , \ldots )=\lambda \phi (1, 1, \ldots )>\sum _{t=0}^{\infty } a_{t}x_{t}-\sum _{t=0}^{\infty } a_{t}y_{t}$ and $\lambda >\sup _{t}\vert y_{t}\vert$. For any $N$ large enough, we have $\phi (\lambda , \lambda , \ldots )=\lambda \phi (1, 1, \ldots )>\sum _{t=0}^{N}a_{t}x_{t}-\sum _{t=0}^{\infty }a_{t} y_{t}$. Take such an N. For any $k\ge N$, define $z_{t}=0,\,\forall t\ge k+1,\, z_{t}^{\prime }=\lambda , \forall t\ge k+1$. Then $\phi (y_{0},\ldots y_{k},z_{k+1}^{\prime }, \ldots )=\phi (\lambda , \lambda , \ldots )=\lambda \phi (1, 1, \ldots )$. Then

    $$\begin{aligned} W(x_{0},\ldots ,x_{k},z_{k+1},\ldots )&= \sum _{t=0}^{k}a_{t}x_{t} < \sum _{t=0}^{\infty }a_{t}y_{t}+\lambda \phi (1,1, \ldots ) \\&< \sum _{t=0}^{k}a_{t}y_{t}+\sum _{t=k+1}^{\infty }a_{t} z_{t}^{\prime }+\phi (y_{0},\ldots y_{k},z_{k+1}^{\prime },\ldots ) \\&= W(y_{0}, \ldots y_{k}, z_{k+1}^{\prime }, \ldots ). \end{aligned}$$

  • (b) Never-decisiveness of the future Let $W(\mathbf{x})>W(\mathbf{y})$ with $\mathbf{x}\in \ell _{\infty }, \mathbf{y}\in \ell _{\infty }$. Let $\lambda >0$ satisfy $\lambda +\phi (\mathbf{y}) >\phi (\mathbf{x})$. There exists $N$ s.t. for any $k\ge N,\, \lambda \sum _{t=0}^{k}a_{t} +\phi (\mathbf{y})>\phi (\mathbf{x})+\sum _{t=k+1}^{\infty }a_{t}x_{t}$, since $\sum _{t=0}^{\infty } a_{t}=1$ and $\sum _{t=T}^{\infty }a_{t}x_{t}\rightarrow 0$, when $T\rightarrow +\infty$. For any $k\ge N$, define $z_{t}=0$ for $t=0,\ldots k,\,z_{t}^{\prime }=\lambda$ for $t=0,\ldots k$. Then

    $$\begin{aligned} W(z_{0},\ldots ,z_{k},x_{k+1},\ldots )&= \sum _{t=k+1}^{\infty } a_{t}x_{t}+\phi (\mathbf{x})<\lambda \sum _{t=0}^{k}a_{t} +\phi (\mathbf{y}) \\&= \sum _{t=0}^{k}a_{t}z_{t}^{\prime }+\phi (\mathbf{y}) = W(z_{0}^{\prime },\ldots z_{k}^{\prime },y_{k+1},\ldots ). \end{aligned}$$

  • 3. Obviously, if W is a Never-decisive social welfare function, then it is sustainable. $\square$

2.2 The case where $X\subseteq \left[ 0,1\right] ^{\infty }$

We mentioned at the beginning of the paper that in optimal growth models with decreasing returns, the feasible consumption paths are uniformly bounded. So, without loss of generality, we can first assume $X=\left[ 0,1\right] ^{\infty }$.

Proposition 2

The SWF W from X into $\mathbb{R }_{+}$:

$$\begin{aligned} W(\mathbf{x})=\sum _{t=0}^{\infty }a_{t}x_{t}+\phi (\mathbf{x}) \end{aligned}$$

with $a_{t}>0, \forall t, \sum _{t=0}^{\infty } a_{t}=1, \phi$ positive, purely finitely additive, which satisfies the two No dictatorship properties.⁷

Proof

• (a) No-dictatorship of the present Let $\mathbf{x}$ satisfy $x_t=\zeta$ for any t with $\zeta < \min \{1, \phi (1, 1, \ldots )\}$. Let $y_t=0,\forall t$. Take ${\gamma }= \mathbf{0}$ and $\sigma _t =1,\forall t$. Then, for any K,

  $$\begin{aligned} W(x_0,\ldots , x_K,\gamma _{K+1},\ldots ,)&= \zeta \sum _{t=0}^K a_t +\phi (x_0,\ldots , x_K, 0,\ldots , 0,\ldots ) \\&= \zeta \sum _{t=0}^K a_t +\phi (\mathbf{0})=\zeta \sum _{t=0}^K a_t \\&< \zeta < \sum _{K+1}^\infty a_t \sigma _t +\phi (1, 1, \ldots ) \\&= W(y_0, \ldots , y_K, \sigma _{K+1},\ldots ) \end{aligned}$$

• (b) No-dictatorship of the future Let $x_{0}=1,\, x_{t}=0$ for $t\ge 1$, and let all components of $\mathbf{y},\mathbf{z}$ and $\mathbf{s}$ be equal to 0. Then, since $a_{0}>0$ and $x_{0}=1>0=y_{0},\, W(\mathbf{x} )>W(\mathbf{y})$, but

  $$\begin{aligned} W(z_{0},z_{1},\ldots ,z_{K},y_{K+1},\ldots )=W(s_{0},\ldots , s_{K},x_{K+1},\ldots ) \end{aligned}$$

  for all $K\ge 0$. Essentially, the property that $W$ is increasing in all components implies No-dictatorship of the future. $\square$

However, in “Appendix 2,” we show that the basic one sector Ramsey model with a criterion defined by (1), where $x_{t}$ is the utility at period $t$ of the representative consumer, has no solution if the marginal productivity at the origin of the production function is larger than 1. When this marginal productivity is less than one, the criterion defined by (1) and the one defined by the discounted sum of utilities give the same solution to the Ramsey model.

The following proposition shows that there exists no independent, continuous (for the $l_{\infty }$ topology) SWF which is never-decisive in $[0,1]^{\infty }$.

Proposition 3

There exists no continuous independent SWF W from X into $\mathbb{R }_{+}$:

$$\begin{aligned} W(\mathbf{x})=\sum _{t=0}^{\infty }a_{t}x_{t}+\phi (\mathbf{x}) \end{aligned}$$

with $a_{t}> 0, \forall t, \sum _{t=0}^{\infty }a_{t}=1, \phi$ positive, purely finitely additive, which satisfies the two Never-decisiveness properties.

Proof

• Claim 1 If $\phi (1, 1, \ldots )\ge 1$, then W does not satisfy the Never-decisiveness of the future axiom. Indeed, let $W(\mathbf{x})>W(\mathbf{y})$ where $x_{t}=1,\,\forall t$ and $y_{t}=0,\,\forall t$. Let N be the first index s.t. $a_{N}>0$. Then $\forall k\ge N,\,\forall (z_{0},\ldots ,z_{k})\in [0,\; 1]^{k},\,\forall (z_{0}^{\prime },\ldots ,z_{k}^{\prime })\in [0,\; 1]^{k}$,

  $$\begin{aligned} W(z_{0},\ldots ,z_{k},x_{k+1},\ldots x_{k+t})&= \sum _{t=0}^{k}a_{t}z_{t}+\sum _{t=k+1}^{\infty }a_{t}x_{t}+\phi (1, 1, \ldots ) \\&\ge \phi (1, 1, \ldots ) \\&\ge \sum _{t=0}^{\infty }a_{t} \\&\ge \sum _{t=0}^{k}a_{t}z_{t}^{\prime }+\sum _{t=k+1}^{\infty }a_{t}y_{t}+\phi (0, 0, \ldots ) \\&= W(z_{0}^{\prime },\ldots ,z_{k}^{\prime },y_{k+1},\ldots ). \end{aligned}$$

• Claim 2  If $0<\phi (1, 1, \ldots )<1$, then W does not satisfy the Never-decisiveness of the present property. To prove that, let $\varepsilon >0$ satisfy $1-\varepsilon >\phi (1, 1, \ldots )$ and let $x_{t}=1,\,\forall t$ and $y_{t}=0,\,\forall t$. Hence, $W( \mathbf{x})>W(\mathbf{y})$. There exists N s.t. $\forall k\ge N,\, \sum _{t=0}^{k}a_{t}x_{t}=\sum _{t=0}^{k}a_{t}>\phi (1, 1, \ldots )+\sum _{t=k+1}^{\infty }a_{t}$. Then, for any $k\ge N$, for any $(z_{k+1},\ldots )\in \left[ 0,1\right] ^{\infty }$, any $(z ^\prime _{k+1},\ldots )\in \left[ 0,1\right] ^{\infty }$, we have

  $$\begin{aligned} W(y_{0},\ldots ,y_{k},z_{k+1}^{\prime },\ldots )&= \sum _{t=k+1}^{\infty }a_{t}z_{t}^{\prime }+\phi (y_{0},\ldots ,y_{k},z_{k+1}^{\prime },\ldots ) \\&\le \phi (1, 1, \ldots )+\sum _{t=k+1}^{\infty }a_{t} \\&\le \sum _{t=0}^{k}a_{t}x_{t}+\sum _{t=k+1}^{\infty }a_{t}z_{t}+\phi (x_{0},\ldots ,x_{k},z_{k+1},\ldots ) \\&= W(x_{0},\ldots ,x_{k},z_{k+1},\ldots ). \end{aligned}$$

The proof of the proposition is over. $\square$

We now extend the Never-decisiveness axioms to a SWF defined only on a subset of $[0,1]^{\infty }$. In view of Proposition 3, we now assume $\sum _{t=0}^{\infty }a_{t}=+\infty$ and impose a domain restriction.

We consider a sequence $\mathbf{a}$ which satisfies $a_{t}>0,\;\forall t\ge 0\,\sum _{t=0}^{\infty }a_{t}=+\infty ,\,0<\underline{a}\le a_{t}\le \overline{a},\,\forall t$. Let U be a subset of $[0,1]^{\infty }$, and let $\overline{x} \in [0, 1]$. Define

$$\begin{aligned} X(\mathbf{a}, \overline{x}) =\left\{ \mathbf{x}\in U:\sum _{t=0}^{\infty }a_{t}(x_{t}-\overline{x}) \text{ exists } \text{ in } \mathbb R \right\} \end{aligned}$$

We make the following assumption on $X(\mathbf a , \overline{x})$:

Assumption 1

• $(\fancyscript{T}_0)$: for any $\mathbf{x}\in X(\mathbf a , \overline{x})$, we have $x_t \rightarrow \overline{x}$ when $t\rightarrow +\infty$ and there exists a neighborhood $\fancyscript{V}(\overline{x})$ of $\overline{x}$ which satisfies:

• $(\fancyscript{T}_{1})$: there exists $x\in \fancyscript{V}(\overline{x}),\,x\ne \overline{x}$ such that for any $t$, if $x_{t}\in \fancyscript{V}( \overline{x})\cap [0,1]$, then there exist $s\in \fancyscript{V}(\overline{ x})\cap [0,1],\, s^{\prime }\in \fancyscript{V}(\overline{x})\cap [0,1],\, K$ such that for any $k\ge K$, the sequence $\mathbf{x^{\prime }}$ defined by $x_{i}^{\prime }=x_{i},\;i=1,\ldots ,t,\, x_{t+1}^{\prime }=s,\, x_{t+i+1}^{\prime }=x,\;\forall i=1,\ldots ,K,\, x_{t+2+K}^{\prime }=s^{\prime },\,x_{i}^{\prime }=\overline{x},\;i>t+2+K$ is in $X(\mathbf a , \overline{x})$.

• $(\fancyscript{T}_{2})$: there exist $x\in \fancyscript{V}(\overline{x} )\cap [0,\;1],x\ne \overline{x},\, K$ such that for any $k\ge K$, there exists $s\in \fancyscript{V}(\overline{x})\cap [0,1]$, and the sequence $\mathbf{x^{\prime }}$ defined by $x_{i}^{\prime }=x,\;i=1,\ldots ,k ,\, x_{k+1}^{\prime }=s,\,x_{k+i+1}^{\prime }=x_{k+i+1},\;\forall i>0$, is in $X(\mathbf a , \overline{x})$.

Let $W(\mathbf{x}; \mathbf a , \overline{x})=\sum _{t=0}^{\infty }a_t(x_{t}-\overline{x})+\phi (\mathbf{x})$ for any $\mathbf{x}\in X(\mathbf a , \overline{x})$. Since $x_t \rightarrow \overline{x}$, we have $\phi (\mathbf{x})=\phi (\overline{\mathbf{x}})$. Thus, we can take $W(\mathbf{x}; \mathbf{a }, {\overline{x}})=\sum _{t=0}^{\infty } a_t(x_{t}-{\overline{x}})$.

Proposition 4

Suppose $(\fancyscript{T}_{0}), (\fancyscript{T}_{1})\, and \, (\fancyscript{T}_{2})$ hold. Then the social welfare function $W(\cdot ; \mathbf a , \overline{x})$ satisfies the two Never-decisiveness axioms on $X(\mathbf a , \overline{x})$.

Proof

• (a) Never-decisiveness of the present Let $W(\mathbf{x}; \mathbf a , \overline{x})>W(\mathbf{y}; \mathbf a , \overline{x})$ with $\mathbf{x}\in X(\mathbf a , \overline{x}),\,\mathbf{y}\in X(\mathbf a , \overline{x})$. From $(\fancyscript{T}_0),\, (\fancyscript{T}_1)$, since $x_t \rightarrow \overline{x} ,\, y_t \rightarrow \overline{x}$ when $t\rightarrow +\infty$, one can find $\hat{x} , s, s^\prime$, close to $\overline{x}$, and $\tau$, s.t. for any $T\ge \tau$, for any $k$, when $\hat{x} > \overline{x}$, the sequence $\mathbf{y}^k= (y_0, y_1,\ldots , y_T, s, z_{T+2},\ldots , z_{T+1+k}, s^\prime , \overline{x}, \overline{x}, \ldots )$, with $z_{T+1+i}=\hat{x},\; i=1,\ldots , k$ , is in $X(\mathbf a , \overline{x})$ and when $\hat{x} <\overline{x}$, the sequence $\mathbf{x}^k= (x_0, x_1, \ldots , x_T,\,s, z_{T+2},\ldots , z_{T+1+k}, s^\prime , \overline{x}, \overline{x}, \ldots )$ with $z_{T+1+i}=\hat{x},\; i=1,\ldots , k$, is in $X(\mathbf a , \overline{x})$. When $\hat{x} >\overline{x}$, we have

  $$\begin{aligned} W(\mathbf{y}^k; \mathbf a , \overline{x})\!=\! \sum _{t=0} ^T a_t (y_t \!-\!\overline{x}) \!+\! a_{T+1} (s-\overline{x})\!+\! (\hat{x} -\overline{x}) \sum _{T+2} ^{T+1+k} a_t \!+\! a_{T+2+k} (s^\prime -\overline{x}) \end{aligned}$$

  Then $W(\mathbf{y}^k; \mathbf a , \overline{x}) \rightarrow +\infty$. Therefore, $W(\mathbf{y}^k; \mathbf a , \overline{x})>W(\mathbf{x}; \mathbf a , \overline{x})$ for k large enough. When $\hat{x} <\overline{x}$, we have

  $$\begin{aligned} W(\mathbf{x}^k; \mathbf a , \overline{x})\!=\! \!\sum _{t=0} ^T a_t (x_t \!-\!\overline{x}) +a_{T+1} (s-\overline{x})+ (\hat{x} \!-\!\overline{x}) \sum _{T+2} ^{T+1+k} a_t + a_{T+2+k}(s^\prime \!-\!\overline{x}) \end{aligned}$$

  then $W(\mathbf{x}^k; \mathbf a , \overline{x}) \rightarrow -\infty$. Therefore, $W(\mathbf{x}^k; \mathbf a , \overline{x})<W( \mathbf{y}; \mathbf a , \overline{x})$ for k large enough.

• (b) Never-decisiveness of the future Again, let $W(\mathbf{x}; \mathbf a , \overline{x})>W(\mathbf{y}; \mathbf a , \overline{x})$ with $\mathbf{x}\in X(\mathbf a , \overline{x}),\,\mathbf{y} \in X(\mathbf a , \overline{x})$. From $(\fancyscript{T}_0),\, (\fancyscript{T}_2)$, since $x_t \rightarrow \overline{x},\, y_t \rightarrow \overline{x}$ when $t\rightarrow +\infty$, one can find $\hat{x}$, close to $\overline{x}$, and $\tau$, s.t. for any $T\ge \tau$, there exists $s$ and when $\hat{x} > \overline{x}$, the sequence $\mathbf{y}^T= (\hat{x}, \hat{x},\ldots , \hat{x}, s, y_{T+2}, y_{T+3}, \ldots )$ is in $X(\mathbf a , \overline{x})$ and when $\hat{x} <\overline{x}$, the sequence $\mathbf{x}^T= (\hat{x}, \hat{x},\ldots , \hat{x}, s, x_{T+2}, z_{T+3}, \ldots )$ is in $X(\mathbf a , \overline{x})$. We have

  $$\begin{aligned} W(\mathbf{y}^T; \mathbf a , \overline{x})= \sum _{t=0} ^T a_t (\hat{x} -\overline{x}) + a_{T+1}(s-\overline{x}) + \sum _{T+2} ^{+\infty } a_t (y_t -\overline{x}). \end{aligned}$$

  When $T\rightarrow +\infty ,\, \sum _{t=0} ^T a_t (\hat{x} -\overline{x})\rightarrow +\infty ,\, \vert a_{T+1}(z-\overline{x})\vert \le 2\overline{a}$ and $\sum _{T+2} ^{+\infty } a_t (y_t -\overline{x}) \rightarrow 0$. Hence, $W(\mathbf{y}^T; \mathbf a , \overline{x})> W(\mathbf{x}; \mathbf a , \overline{x})$ for T large enough. We also have

  $$\begin{aligned} W(\mathbf{x}^T; \mathbf a , \overline{x})= \sum _{t=0} ^T a_t (\hat{x} -\overline{x}) + a_{T+1}(s -\overline{x}) + \sum _{T+2} ^{+\infty } a_t (x_t -\overline{x}). \end{aligned}$$

  When $T\rightarrow +\infty ,\, \sum _{t=0} ^T a_t (\hat{x} -\overline{x}) + a_{T+1}(z -\overline{x}) + \sum _{T+2} ^{+\infty } a_t (x_t -\overline{x}) \rightarrow -\infty$. Hence, $W(\mathbf{x}^T; \mathbf a , \overline{x})<W(\mathbf{y}; \mathbf a , \overline{x})$ for $T$ large enough. $\square$

Corollary 1

Let $(a_{t})$ satisfy

• (i) $\forall t,\,0<\underline{a}\le a_{t}\le \overline{a}$

• (ii) $\sum _{t=0}^{\infty }a_{t}=+\infty$.

Let $X(\mathbf a , 0) =\left\{ \mathbf{x}\in [0,1]^\infty :\sum _{t=0}^{\infty }a_{t}x_{t}<+\infty \right\}$, and $W(\mathbf{x}; \mathbf a , 0)=\sum _{t=0}^{\infty }a_{t}x_{t}$ for $\mathbf{x}\in X(\mathbf a , 0)$.

Then $X(\mathbf a , 0)$ satisfies $(\fancyscript{T}_0), (\fancyscript{T}_1), (\fancyscript{T}_2)$ and $W(.; \mathbf a , 0)$ satisfies the two Never-decisiveness axioms on $X$.

Proof

We just have to check that $X(\mathbf a , 0)$ satisfies $(\fancyscript{T}_{0}),(\fancyscript{T}_{1})$ and $(\fancyscript{T}_{2})$.

$\fancyscript{T}_0$ is obviously true since $x_t \rightarrow 0$ for any $\mathbf x \in X(\mathbf a , 0)$. $\fancyscript{T}_1$ is satisfied with any $x > 0,\, s = 0,\, s^\prime = 0$. $\fancyscript{T}_2$ is satisfied with any $x > 0,\, s = 0$. $\square$

Definition 2

A social welfare function $V$ is anonymous if $V(\mathbf{x})=V(\mathbf{y})$ when, for any $i,j,\, i\ne j,\, y_{t}=x_{t},\forall t\ne i,j$, and $y_{i}=x_{j},y_{j}=x_{i}$.

It is immediate that there exists no affine SWF defined on $[0,1]^{\infty }$ which is anonymous, excepting the purely finitely additive up to affine transformation. Unfortunately, no purely finitely additive SWF satisfies the Never-decisiveness of the future axiom. Indeed, let $V(x_{0},x_{1},\ldots )>V(y_{0},y_{1},\ldots )$. For any finite change $(x_{0}^{\prime },\ldots ,x_{T}^{\prime }),(y_{0}^{\prime },\ldots ,y_{T}^{\prime })$ of the present, we always have

$$\begin{aligned} V(x_{0}^{\prime },\!\ldots \! ,\!x_{T}^{\prime },x_{T+1},\!\ldots \! )\!=\!V(x_{0},x_{1},\ldots )>V(y_{0},y_{1},\ldots )\!=\!V(y_{0}^{\prime },\!\ldots \! ,\!y_{T}^{\prime },y_{T+1},\ldots ) \end{aligned}$$

For any $\overline{x} \in [0, 1]$, any $\overline{a} > 0$, define

$$\begin{aligned} X(\overline{a}, \overline{x}) = \{ \mathbf x \in [0,1]^\infty : \; \overline{a} \sum _{t=0}^\infty (x_ t - \overline{x}) \in \mathbb R \}. \end{aligned}$$

Let $\fancyscript{X}$ be the collection of $X(\overline{a}, \overline{x})$ which satisfy $(\fancyscript{T}_{0}),(\fancyscript{T}_{1})$ and $(\fancyscript{T}_{2})$. We have the following Theorem.

Theorem 1

There is a set of domains in $2^{[0,1]^\infty } \setminus \{\emptyset \}$ such that, for each of these domains, there exists a SWF which is independent, anonymous and Pareto. Moreover, for each of these domains, the SWF satisfies the two Never-decisiveness properties.

Proof

Consider $\fancyscript{X}$. Define $W(.; \overline{a}, \overline{x})$ by: for any $X(\overline{a}, \overline{x}) \in \fancyscript{X}$, any $\mathbf x \in X(\overline{a}, \overline{x})$,

$$\begin{aligned} W(\mathbf x ; \overline{a}, \overline{x}) = \overline{a} \sum _{t=0}^\infty (x_t - \overline{x}). \end{aligned}$$

From Definition 1, it is independent. Obviously, $W(.; \overline{a}, \overline{x})$ is anonymous and Pareto. From Proposition 4, it satisfies the two Never-decisiveness properties. $\square$

Corollary 2

Let $\overline{a} > 0$ and

$$\begin{aligned} X(\overline{a}, 0) = \{ \mathbf x \in [0,1]^\infty : \overline{a} \sum _{t=0}^\infty x_t < + \infty \}. \end{aligned}$$

Then $X(\overline{a}, 0) \in \fancyscript{X}$. The SWF $W(.; \overline{a}, 0)$ defined by

$$\begin{aligned} \forall \mathbf x \in X(\overline{a}, 0), W(\mathbf x ; \overline{a}, 0) = \overline{a} \sum _{t=0}^\infty x_ t \end{aligned}$$

is anonymous, independent and Pareto.

Proof

From Corollary 1, $X(\overline{a}, 0) \in \fancyscript{X}$. Then apply Theorem 1. $\square$

3 The overtaking criterion as an anonymous and never-decisive criterion for optimal growth models

The difficulty is to exhibit a criterion which satisfies assumptions $( \fancyscript{T}_{0}), (\fancyscript{T}_{1})\, and \,(\fancyscript{T}_{2})$ on some set $X$ of sequences. We will show that the overtaking criterion introduced by Gale (1967) for optimal growth models actually induces an anonymous and never-decisive SWF on the set of utilities of good programs of an intertemporal economy.

First, we construct the subset X on which the SWF (the overtaking criterion) is defined. It will be the set of the utilities yielded by good programs. We have the property that any good program converges, and therefore, the utilities yielded by good programs converge too (assumption $(\fancyscript{T}_{0})$ above is satisfied). Second, we prove that under the assumptions on the economy presented below, the utilities of good programs satisfy $(\fancyscript{T}_{1})$ and $(\fancyscript{T}_{2})$.

We consider an intertemporal economy where the instantaneous utility of the representative consumer depends on $\kappa _{t}$, the capital stock on hand at date t, and on $\kappa _{t+1}$, the capital stock for date $t+1$. Given $\kappa _{t}$, the set of feasible capital stocks for the next period $t+1$ is $\varGamma (\kappa _{t})$. We assume that at any period t the feasible capital stock on hand belongs to $A$, a subset of $\mathbb R _{+}^{n}$. More explicitly, we make the following assumptions.⁸

Assumptions

• H1: $A$ is a compact, convex set of $\mathbb R _+ ^n$ with nonempty interior.

• H2: $\varGamma$ is a continuous correspondence with nonempty images. It satisfies $\varGamma (A)\subseteq A$. Its graph is the set graph $\varGamma =\left\{ \left( \kappa , \chi \right) \in A\times A:\chi \in \varGamma (\kappa )\right\}$.

• H3: intgraph$\varGamma$, the interior of the graph of $\varGamma$, is nonempty. We will denote by cograph$\varGamma$ the convex hull of graph$\varGamma$.

• H4: The instantaneous utility function $u:$ cograph$\varGamma \rightarrow \mathbb R _+$ is strictly concave and continuous. It is increasing with respect to the first variable and decreasing with respect to the second variable. For the simplicity of our presentation, we also assume the following.

• H5: The function $u$ is differentiable in the interior of cograph $\varGamma$.

• H6: The set $I(A)=\left\{ \kappa \in A:(\kappa ,\kappa )\in \text{ graph }\varGamma \right\}$ is nonempty.

Remark 1

• 1. Dana and Le Van (1990) show that the following assumptions imply intgraph$\varGamma \ne \emptyset$.

  • Free disposal assumption: If $\chi \in \varGamma (\kappa ),\, \kappa ^{\prime }\,\ge \kappa ,\, \chi ^{\prime }\le \chi ,\,\kappa ^{\prime }\in A,\;\chi ^{\prime }\in A$, then $\chi ^{\prime }\in \varGamma (\kappa ^{\prime })$.

  • Existence of expansible capital stocks: There exists $(\kappa ,\chi )\in graph\varGamma$, with $\chi >>\kappa$, i.e., $\chi _{i}>\kappa _{i},\, \forall i\in \{1,\ldots ,n\}$.

• 2. If $\varGamma$ is continuous and satisfies the condition: There exists a number $a$ such that $\{\Vert \kappa \Vert \ge a,\; \chi \in \varGamma (\kappa ) \} \Rightarrow \Vert \chi \Vert < \Vert \kappa \Vert$, then $I(A)$ is compact.

• 3. An example where H1–H2 and H5 are satisfied. Let $\varGamma (\kappa )=\left\{ \chi \in \mathbb R _{+}:\chi \in [0,\right. \left. f(\kappa )]\right\}$, where f is a continuous increasing function which satisfies $f(0)=0,\;f(1)=1,\;f(\kappa )<\kappa ,\;\forall \kappa >1$. Take $A=[0,a]$ with $a>1$.

A sequence $\kappa$ is feasible from $\kappa _{0}\in X$ if, $\forall t\ge 0,\, \kappa _{t+1}\in \varGamma (\kappa _{t})$. We denote by $\varPi (\kappa _{0})$ the set of feasible sequences from $\kappa _{0}$. Following Gale (1967), a program from $\kappa _{0}$ is a feasible sequence from $\kappa _{0}$. The set of programs is denoted by $\varPi$, i.e., $\varPi =\cup _{\kappa \in A}\varPi (\kappa )$.

Lemma 1

Assume H1–H2. Then $\varPi (\kappa _0)$ is compact for the product topology.

Proof

See, e.g., Le Van and Dana (2003), chapter 4. $\square$

3.1 Good programs

Definition 3

A stationary point $(\overline{\kappa },\overline{\kappa })$ satisfies

$$\begin{aligned} \overline{x}=u(\overline{\kappa },\overline{\kappa })=\max \left\{ u(\kappa ,\kappa ):(\kappa ,\kappa )\in graph\varGamma \right\} . \end{aligned}$$

Proposition 5

There exists a stationary point $(\overline{\kappa }, \overline{\kappa })$ which satisfies

• (i) $\overline{x}=u(\overline{\kappa },\overline{\kappa })=\max \left\{ u(\kappa ,\kappa ):(\kappa ,\kappa )\in graph\varGamma \right\} ;$

• (ii) if $(\overline{\kappa },\overline{\kappa })\in$ intgraph$\varGamma$, then

  $$\begin{aligned} u(\kappa ,\chi )+u_{1}(\overline{\kappa },\overline{\kappa })\chi -u_{1}( \overline{\kappa },\overline{\kappa })\kappa \le u(\overline{\kappa }, \overline{\kappa }),\;\forall (\kappa ,\chi )\in {graph}\varGamma , \end{aligned}$$

  where $u_{1}(\kappa ,\chi )=\partial u(\kappa ,\chi )/\partial \kappa$ and $u_{2}(\kappa ,\chi )=\partial u(\kappa ,\chi )/\partial \chi$.

Proof

• (i) Since $I(A)$ is compact, the proof of the existence of $(\overline{\kappa },\overline{\kappa })$ is obvious.

• (ii) If $(\overline{\kappa },\overline{\kappa })$ is interior, then $u_{1}(\overline{\kappa },\overline{\kappa })+u_{2}(\overline{\kappa }, \overline{ \kappa })=0$. Since $u$ is concave, for any $(\kappa ,\chi )\in graph\varGamma$, we have

  $$\begin{aligned} u(\overline{\kappa },\overline{\kappa })-u(\kappa ,\chi )\ge u_{1}(\overline{ \kappa },\overline{\kappa })(\overline{\kappa }-\kappa ) +u_{2}(\overline{\kappa }, \overline{\kappa })(\overline{\kappa }-\chi ) =u_{1}(\overline{\kappa },\overline{ \kappa })\chi -u_{1}(\overline{\kappa },\overline{\kappa })\kappa . \end{aligned}$$

$\square$

We now add another assumption.

H7: $(\overline{\kappa },\overline{\kappa })\in$ intgraph$\varGamma$.

Assumption H7 is not very restrictive, since in the one-dimensional Ramsey model it implies that consumption is strictly positive at the Golden Rule. Indeed, if $\varGamma (\kappa )=\left\{ \chi :0\le \chi \le f(\kappa )\right\}$ where $f$ is the production function, then $\overline{ \kappa }$ satisfies $\overline{x}=\max _{\kappa }u(f(\kappa )-\kappa )$.

Let $\bar{p}=u_{1}(\overline{\kappa },\overline{\kappa })$.

Proposition 6

Under H1–H7, $(\overline{\kappa },\overline{ \kappa })$ is the unique solution to problem

$$\begin{aligned} \max \left\{ u(\kappa ,\chi )+\bar{p}\chi -\bar{p}\kappa :(\kappa ,\chi )\in \text{ graph }\varGamma \right\} . \end{aligned}$$

The proof is in “Appendix 3.”

Theorem 2

Assume H1–H7. For any program ${\kappa }$ , either

• (i) $\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})-\bar{x}\right]$ exists in $\mathbb R$ and $\kappa _{t}\rightarrow \overline{\kappa }$, or

• (ii) $\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})-\bar{x}\right] =-\infty$.

The proof is in “Appendix 3.”

Definition 4

A program ${\kappa }\,\in \varPi (\kappa _{0})$ is good if $\lim _{T\rightarrow \infty }\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})-u(\overline{\kappa },\overline{\kappa })\right]$ exists in $\mathbb R$.

Definition 5

The set of the good programs ${\kappa }\,\in \varPi (\kappa _{0})$ is denoted $G(\kappa _{0})$.

From Theorem 2 one gets:

Corollary 3

Assume H1–H7. If ${\kappa }\,\in G(\kappa _{0})$ , then $\kappa _{t}\rightarrow \overline{\kappa }$.

3.2 Never-decisiveness and anonymous criteria

Since A is compact, there exists a number $a>0$ such that for any program ${\kappa }$ we have $u(\kappa _t, \kappa _{t+1} )\in [0,\; a],\; \forall t$. We define

$$\begin{aligned} U=\{ (x_t)_t : \forall t, x_t =u(\kappa _t, \kappa _{t+1}),\; {\kappa } \in \varPi \} \end{aligned}$$

and

$$\begin{aligned} X= \{\mathbf{x} \in U: \sum _{t=0} ^{\infty } (x_t - \overline{x}) \in \mathbb R \} \end{aligned}$$

Observe that we have $X=\cup _\kappa G(\kappa )$.

Let

$$\begin{aligned} W(\mathbf{x})=\sum _{t=0} ^{\infty } (x_t - \overline{x}) \end{aligned}$$

and

$$\begin{aligned} \fancyscript{W}({\kappa }) = \sum _{t=0}^\infty [u(\kappa _t, \kappa _{t+1}) - \overline{x}]. \end{aligned}$$

Proposition 7

The social welfare function W is anonymous and satisfies the Never-decisiveness properties on X.

Proof

Anonymity is obvious. To prove that this SWF satisfies the Never-decisiveness properties, we apply Proposition 4. We prove that assumptions $(\fancyscript{T}_{0}), (\fancyscript{T}_{1}) and (\fancyscript{T}_{2})$ are satisfied.

Assumption $(\fancyscript{T}_0)$ comes from Corollary 3.

To check $(\fancyscript{T}_1):$ Since $(\overline{\kappa },\overline{\kappa })\in$ intgraph$\varGamma$, there exists an open ball $B((\overline{\kappa },\overline{\kappa }),\varepsilon )\subset$graph $\varGamma$ which satisfies the following properties:

• (i) There exists $(\hat{\kappa },\hat{\kappa })\in B((\overline{\kappa },\overline{\kappa }),\varepsilon )$ with $\hat{\kappa }\ne \overline{\kappa }$,

• (ii) $(\hat{\kappa }, \overline{\kappa }) \in B((\overline{\kappa },\overline{\kappa }),\varepsilon )$,

• (iii) For any y close enough to $\overline{\kappa }$, we have $(y,\hat{\kappa }) \in B((\overline{\kappa },\overline{\kappa }),\varepsilon )$.

Since $\kappa _t$ converges to $\overline{\kappa }$, there exists $N$ such that for any $T \ge N$ we have $(\kappa _{T-1}, \kappa _T) \in B((\overline{\kappa },\overline{\kappa }),\varepsilon )$ and $(\kappa _T,\hat{\kappa }) \in B((\overline{\kappa },\overline{\kappa }),\varepsilon )$.

Define $s=u(\kappa _T, \hat{\kappa }),\; \hat{x} = u(\hat{\kappa }, \hat{\kappa }), s^\prime =u( \hat{\kappa }, \overline{\kappa })$. Observe that $\hat{x} < \overline{x}$.

To check $(\fancyscript{T}_2)$: take $\hat{x} = u(\hat{\kappa }, \hat{\kappa })<\overline{x}$ and for any $T$ large enough $s=u(\hat{\kappa }, \kappa _{T+1})$. $\square$

4 Solving optimal growth models with the overtaking criterion

We want to solve an optimal growth model with the SWF defined above. We first have:

Proposition 8

Assume H1–H7. Then $\fancyscript{W}$ is upper-semicontinuous for the product topology.

Proof

See Dana and Le Van (1990). $\square$

We then obtain

Theorem 3

Assume H1–H7. If $G(\kappa _{0})\ne \emptyset$, then there exists an optimal path. It is unique if graph$\varGamma$ is convex.

Proof

From Proposition 8 and Lemma 1, for the product topology, $\fancyscript{W}$ is upper-semicontinuous and $\varPi (\kappa _{0})$ is compact. Therefore, an optimal path exists, since the problem is to maximize $\fancyscript{W}( {\kappa })$ with ${\kappa }\in \varPi (\kappa _{0})$. This optimal path is unique when graph$\varGamma$ is convex since $u$ is assumed strictly concave. $\square$

4.1 Applications

We now give examples of models which satisfy H1–H7 and for which X is nonempty.

4.1.1 Convex technology

Assume graph$\varGamma$ is convex. Now, let $A=[0,1],\, \varGamma (\kappa )=[0,\;f(\kappa )]$ where f is strictly concave, increasing and differentiable with $f^{\prime }(0)>1,\, f(0)=0,\, f(1)=1$, and $u(\kappa ,\chi )=v(f(\kappa )-\chi )$, where v is real-valued, defined on $\mathbb R _{+}$, increasing, strictly concave and differentiable. It is easy to check H1–H6. Observe that the stationary point $\overline{\kappa }$ is defined by $f^{\prime }(\overline{\kappa })=1$. It is therefore unique. Obviously, $0<\overline{\kappa }<f(\overline{\kappa })<1$. In other words, H7 is satisfied. We claim that $G(\kappa _{0})\ne 0,\;\forall \kappa _{0}>0$. Indeed, since $f^{t}(\kappa _{0})\rightarrow 1$ when $t\rightarrow +\infty$, there exists $T$ such that $f^{T}(\kappa _{0})\le f( \overline{\kappa })$ and $f^{T+1}(\kappa _{0})>f(\overline{\kappa })$. The sequence $(\kappa _{0},f(\kappa _{0}),\ldots ,f^{T}(\kappa _{0}),\overline{\kappa }, \overline{\kappa },\ldots ,\overline{\kappa },\ldots )\in G(\kappa _{0})$.

4.1.2 Economy with a convex–concave production function

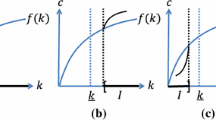
Let $A=[0,1],\, \varGamma (\kappa )=[0,\;f(\kappa )]$. Here we suppose that $f$ is increasing, continuously differentiable, $f(0)=0,\, f(1)=1$, strictly convex between 0 and $\kappa _{I}<1$ and strictly concave in $[\kappa _{I},\;+\infty [{}$. The function $u$ is as before $u(\kappa ,\chi )=v(f(\kappa )-\chi )$, where $v$ is real-valued, defined on $\mathbb R _{+}$, increasing, strictly concave and differentiable.

Let $a=\max _{\kappa \in A}\left\{ {\frac{{f(\kappa )}}{\kappa }}\right\}$ and $\kappa _{a}\in A$ satisfy $a=\left\{ {\frac{{f(\kappa _{a})}}{\kappa _{a}}} \right\}$. Let $F$ be defined as follows: $F(\kappa )=a\kappa ,\;\forall \kappa \le \kappa _{a};\;F(\kappa )=f(\kappa ),\;\kappa \ge \kappa _{a}$. Then $F$ is concave and $\left\{ (\kappa ,\chi )\in A\times A:\chi \le F(\kappa )\right\}$ is cograph$\,\varGamma$.

When $f^{\prime }(0)>1$, there exists a unique $\overline{\kappa }\in (\kappa _{I},\;1)$ such that $f^{\prime }(\overline{\kappa })=1$. One can check that $0<\overline{\kappa }<f(\overline{\kappa })<1$, i.e., $(\overline{ \kappa },\overline{\kappa })\in$ int graph$\,\varGamma$. Assumptions H1–H7 are satisfied. Again $G(0)=\emptyset$ and $G(\kappa _{0})\ne \emptyset$ if $\kappa _{0}>0$.

Now assume $f^{\prime }(0)<1<\frac{f(\kappa _{a})}{\kappa _{a}}$ and $f^{\prime }(\kappa _{I})>1$ (see Fig. 1). There are two points $\underline{\kappa },\, \overline{\kappa }$ such that $f^{\prime }(\underline{ \kappa })=f^{\prime }(\overline{\kappa })=1$. But $f(\underline{\kappa })- \underline{\kappa }<0$, i.e., $(\underline{\kappa },\underline{\kappa } )\notin$ graph$\,\varGamma$. We have a unique stationary point $\overline{ \kappa }$. It satisfies $0<\overline{\kappa }<f(\overline{\kappa })<1$, i.e., $(\overline{\kappa },\overline{\kappa })\in$ int graph$\,\varGamma$. Again, H1–H7 are satisfied.

Let $\tilde{\kappa }$ satisfy $f(\tilde{\kappa })=\tilde{\kappa }$. Then $\tilde{\kappa }\in (0,\;1)$. Moreover, $\kappa <\tilde{\kappa }\Rightarrow f(\kappa )<\kappa$ and $1>\kappa >\tilde{\kappa }\Rightarrow f(\kappa )>\kappa$. That implies:

• (i) any feasible path from $\kappa _{0}<\tilde{\kappa }$ will converge to 0. Hence, $G(\kappa _{0})=\emptyset$ for any $\kappa _{0}\le \tilde{\kappa }$.

• (ii) for any $\kappa _{0}>\tilde{\kappa },\, f^{t}(\kappa _{0}) \rightarrow 1$. Hence, one can find $T$ such that $f^{T}(\kappa _{0})\le \overline{\kappa }$ and $f^{T+1}(\kappa _{0})>f(\overline{\kappa })$. The sequence $(\kappa _{0},f(\kappa _{0}),\ldots ,f^{T}(\kappa _{0}),\overline{\kappa }, \overline{\kappa },\ldots ,\overline{\kappa },\ldots )\in G(\kappa _{0})$. Thus, $G(\kappa _{0})\ne \emptyset$ for any $\kappa _{0}>\tilde{\kappa }$.

One concludes that $\tilde{\kappa }$ is the poverty trap.

Fig. 1

The convex–concave technology

4.1.3 Growth and exhaustible resources

We consider the model in Le Van et al. (2010). The country possesses a stock of a nonrenewable natural resource ${S_{0}}$. This resource is extracted at a rate $\mathbb R _{t}$ and then sold abroad at a price $P_{t}$, in terms of the numeraire, which is the domestic single consumption good. The inverse demand function for the resource is $P(R_{t})$. The revenue from the sale of the natural resource, $\phi (R_{t})=P(R_{t})R_{t}$, is used to buy a foreign good, which is supposed to be a perfect substitute of the domestic good, used for consumption and capital accumulation. The domestic production function is $F(k_{t})$, where $k_{t}$ is physical capital. The depreciation rate is $\delta$. We define the function $f(k_{t})=F(k_{t})+(1-\delta )k_{t}$, and we name it for simplicity the technology. The constraints of the economy are:

$$\begin{aligned} \forall t,c_{t}&\ge 0, k_{t}\ge 0, R_{t}\ge 0, \\ c_{t}+k_{t+1}&\le f(k_{t})+\phi (R_{t}), \\ \sum \limits _{t=0}^{+\infty }R_{t}&\le {S_{0}}, \\ {S_{0}}&> 0, k_{0}\ge 0 \text{ are } \text{ given }, \end{aligned}$$

where $c_{t}$ is consumption. We assume that f is strictly concave, $f(0)=0,\;f^{\prime }(+\infty )<1,\;f^{\prime }(0)>1$. Let $\tilde{k}$ satisfy $\tilde{k}=f(\tilde{k})+\phi (S_{0})$. Such a $\tilde{k}$ is unique. Take $A=[0,\;\tilde{k}]\times [0,\;S_{0}]$. Let $\kappa =(k,R)$. Define $\varGamma (\kappa )=\left\{ \chi =(y,R):\;0\le y\le f(k)+\phi (R)\right\}$. One can check that $\varGamma$ is continuous and maps A into A. Observe that any feasible sequence $\{R_{t}\}$ will converge to zero. We also assume $\phi ^{\prime }(0)<+\infty$. The representative consumer has an instantaneous utility function $u$ which is increasing, strictly concave and satisfies $u(0)=0$. We show that the methodology of Sects. 2, 3, and 4 may be used for the present model.

Let $\bar{k}$ satisfy

$$\begin{aligned} u(f(\bar{k})-\bar{k})&= \max \left\{ u(f(k)-k):\;0\le k\le f(k)\right\} \\&= \max \left\{ u(f(k)-k):\;0\le k\le f(k)+\phi (S_{0})\right\} \end{aligned}$$

Such a $\bar{k}$ is unique and satisfies $0<\bar{k}<f(\bar{k})$ and $f^{\prime }(\bar{k})=1$. Let $\bar{p}=u^{\prime }(f(\bar{k})-\bar{k})$. We let to the reader to prove the following claim (see the Proofs of Propositions 5, 6).

Claim 1

$(\bar{k},\bar{k},0)$ is the unique solution to the problem

$$\begin{aligned} \max \left\{ u(f(k)-y+\phi (R))+\bar{p}y-\bar{p}k-\bar{p}\phi ^{\prime }(0)R:\left( (k,R),(y,R)\right) \in \text{ graph }\varGamma \right\} . \end{aligned}$$

Let $\bar{x}=u(f(\bar{k})-\bar{k})$.

Claim 2

For any program $(\mathbf{k,R})$, either

• (i) $\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(f(k_{t})-k_{t+1}+\phi (R_{t}))-\bar{x}\right]$ exists in $\mathbb R$ and $k_{t}\rightarrow \bar{k},\, R_{t}\rightarrow 0$, or

• (ii) $\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(f(k_{t})-k_{t+1}+\phi (R_{t}))-\bar{x}\right] =-\infty$

Proof of Claim 2

(i) and (ii): Observe that

$$\begin{aligned}&\sum _{t=0}^{T}\left[ u(f(k_{t})-k_{t+1}+\phi (R_{t}))+\bar{p}k_{t+1}-\bar{p }k_{t}-\bar{p}\phi ^{\prime }(0)R_{t}-\bar{x}\right] \\&\quad =\sum _{t=0}^{T}\left[ u(f(k_{t})-k_{t+1}+\phi (R_{t}))-\bar{x}\right] + \bar{p}(k_{T+1}-k_{0})-\bar{p}\phi ^{\prime }(0)\sum _{t=0}^{T}R_{t}. \end{aligned}$$

Since $\sum _{t=0}^{T}R_{t}$ converges, use Claim 1 and the proof of Theorem 2 to conclude. $\square$

A program $\{(\mathbf{k},\mathbf{R})\}$ is good if $\sum _{t=0}^{+\infty }\left[ u(f(k_{t})-k_{t+1}+\phi (R_{t}))-\bar{x}\right] \in \mathbb R$.

Now define

$$\begin{aligned} W(\mathbf{k},\mathbf{R})=\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(f(k_{t})-k_{t+1}+\phi (R_{t}))-\bar{x}\right] . \end{aligned}$$

$W$ is upper-semicontinuous, and one can check that it is never-decisive. The optimal solution $(\mathbf{k}^{*},\mathbf{R}^{*})$ to

$$\begin{aligned} \max _{(\mathbf{k},\mathbf{R})}W(\mathbf{k},\mathbf{R}) \end{aligned}$$

under the constraints

$$\begin{aligned} \forall t,\;0\le k_{t+1}&\le f(k_{t})+\phi (R_{t}),\;k_{0} \text{ is } \text{ given } \\ \sum _{t=0}^{+\infty }R_{t}&\le S_{0}, \end{aligned}$$

will converge to $(\bar{k},0)$.

4.1.4 Growth and renewable resources

We study the canonical model of growth with a renewable resource.⁹ The economy possesses a stock of a renewable natural resource ${S_{0}}$. This resource is extracted at a rate $R_{t}$. The domestic production function is $F(k_{t},R_{t})$. $k_{t}$ is the stock of physical capital. The depreciation rate is $\delta$. The natural growth of the renewable resource is $S_{t+1}-S_{t}=H(S_{t})$. The function $H$ is strictly concave, differentiable and satisfies $H(0)=0,\, H( \hat{S})=0$, with $\hat{S}>0$. There is a representative consumer with a utility function $u$ depending on her consumption $c$. The technological constraints for each period $t$ are as follows:

$$\begin{aligned} c_{t}+k_{t+1}&\le F(k_{t},R_{t})+(1-\delta )k_{t} \\ S_{t+1}&\le S_{t}+H(S_{t})-R_{t}. \end{aligned}$$

Let $\psi (S)=S+H(S)$. The function $\psi$ is strictly concave, $\psi (0)=0,\;\psi ^{\prime }(+\infty )<1, \text{ since } H^{\prime }(+\infty )<0$. We define the function $f(k_{t},R_{t})=F(k_{t},R_{t})+(1-\delta )k_{t}$, and we name it for simplicity the technology. We assume that F is strictly concave, $F(0,R)=F(k,0)=0,\;F_{1}(+\infty ,\psi (\hat{S}))<\delta ,\;F_{1}(0,\psi (\hat{S}))>\delta$. The constraints become

$$\begin{aligned} 0\le k_{t+1}&\le f(k_{t},R_{t}) \\ 0\le S_{t+1}&\le \psi (S_{t})-R_{t}. \end{aligned}$$

Let $\hat{k}$ satisfy $\hat{k}=f(\hat{k},\psi (\hat{S}))$. Let $A=[0,\;\hat{k }]\times [0,\;\hat{S}]$ and for $\kappa =(k,S)$ define

$$\begin{aligned} \varGamma (\kappa )=\left\{ \chi = (k^{\prime },S^{\prime }):0\le k^{\prime }\le f(k,\psi (S)-S^{\prime }),\;0\le S^{\prime }\le \psi (S)\right\} \end{aligned}$$

$\varGamma$ is continuous and maps A into A. Its graph is convex. There exists a unique $\bar{\kappa }=(\bar{k},\bar{S})$ such that $(\bar{\kappa }, \bar{\kappa })$ is in the interior of graph$\varGamma$ and solves

$$\begin{aligned} \max \left\{ u(f(k,\psi (S)-S)-k):\left( (k,S),(k,S)\right) \in \text{ graph } \varGamma \right\} . \end{aligned}$$

Namely, $f_{1}(\bar{k},\psi (\bar{S})-\bar{S})=1,\;\psi ^{\prime }(\bar{S} )=1$. This model satisfies assumptions H1–H7. Hence, one can define

$$\begin{aligned} W(\kappa _0, \kappa _1, \ldots ) = W(\mathbf{k},\mathbf{S})=\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u\left( f(k_{t},\psi (S_{t})-S_{t+1})-k_{t+1}\right) -\bar{x}\right] \end{aligned}$$

where $\overline{x}=u\left( f(\overline{k},\psi (\overline{S})-\overline{S} )- \overline{k}\right)$. The optimal solution to

$$\begin{aligned} \max _{\{\kappa _1,\kappa _2, \ldots \}} W(\kappa _0, \kappa _1, \ldots ) =\max _{( \mathbf{k},\mathbf{S})}W(\mathbf{k},\mathbf{S}) \end{aligned}$$

under the constraints

$$\begin{aligned} \forall t,\;0\le k_{t+1}&\le f(k_{t},\psi (S_{t})-S_{t+1}), \\ 0\le S_{t+1}&\le \psi (S_{t}),\;\;\;(k_{0},S_{0}) \text{ are } \text{ given } \end{aligned}$$

will converges to $(\bar{k},\bar{S})$ if there exists a good program from $(k_{0},S_{0})$.

Appendices

Appendix 1

We give a simple example where a SWF which satisfies our Never-decisiveness axioms does not satisfy the axiom of Hammond Equity for the future. First, our criterion is not complete on $[0,1]^{\infty }$. Now, consider $\mathbf{x} ,\mathbf{y}$ defined by $x_{0}>0,\, x_{t}=0,\forall t\ge 1,\, y_{0}={\frac{{ x_{0}}}{{2}}},y_{t}=({\frac{{1}}{{8}}}\times {\frac{{1}}{{2^{t-1}}}})x_{0}$, for $t\ge 1$. These sequences satisfy: $x_{0}>y_{0}>y_{t}>x_{t}$ for any $t\ge 1$. However, we have $\sum _{t=0}^{\infty }x_{t}=x_{0}>\sum _{t=0}^{\infty }y_{t}={\frac{{3}}{{4}}}x_{0}$.

Appendix 2

Consider two problems:

$$\begin{aligned}&\fancyscript{R}:\;\max \sum _{t=0}^{\infty }\beta ^{t}u(c_{t})\\&\fancyscript{C}:\;\max \sum _{t=0}^{\infty }\beta ^{t}u(c_{t})+\phi (u(c_{1}),u(c_{2}),\ldots ) \end{aligned}$$

under the constraint $c_{t}+k_{t+1}\le f(k_{t})$ for all t, with $k_{0}>0$ given.

Let $\varPi (k_{0})$ denote the set of feasible capital stocks. We make the following assumptions.

• H0 $0<\beta <1$.

• H1 The function $u:\mathbb R \rightarrow \mathbb R$ is twice continuously differentiable and satisfies $u(0)=0$. Moreover, its derivatives satisfy $u^{\prime }>0$ (strictly increasing) and $u^{\prime \prime }<0$ (strictly concave).

• H2 Inada condition $u^{\prime }(0)=+\infty$.

• H3 The function $f:\mathbb R \rightarrow \mathbb R$ is twice continuously differentiable and satisfies $f(0)=0$. Its derivatives satisfy $f^{\prime }>0$ (strictly increasing), $f^{\prime \prime }<0$, strictly concave, $\lim _{x\rightarrow \infty }f^{\prime }(x)<1$.

• H4 $\phi$ is purely finitely additive, continuous for the $l_{\infty }$-topology, homogeneous of degree 1, nondecreasing, $\phi (0)=0,\;\phi (\mathbf{1})>0$.

Lemma 2

Let $\mathbf{x} \in l_\infty$ be such that $\lim _{t \rightarrow \infty } x_t = \overline{x}$, then

$$\begin{aligned} \phi (\mathbf{x}) = \phi (\overline{x}, \overline{x}, \ldots ) \end{aligned}$$

Proof

Denote $\overline{\mathbf{x}}=(\overline{x}, \overline{x}, \ldots )$. Construct $\mathbf{x}^n$ as:

$$\begin{aligned} x^n_t&= \overline{x} \quad \text{ for } 0 \le t \le n \\ x^n_t&= x_t \quad \text{ for } t > n \end{aligned}$$

Since $\phi$ is purely finitely additive, for all $n,\, \phi (\mathbf{x} ^n)=\phi (\mathbf{x})$. On the other hand, $\Vert \mathbf{x}^n-\overline{ \mathbf{x}} \Vert =\sup _{t > n} \vert x_t - \overline{ {x}} \vert \, \Rightarrow \lim _{n \rightarrow \infty } \Vert \mathbf{x}^n - \overline{ \mathbf{x}} \Vert =0$, then

$$\begin{aligned} \phi (\mathbf{x})&= \lim _{n \rightarrow \infty } \phi (\mathbf{x}^n) \\&= \phi (\overline{\mathbf{x}}) \end{aligned}$$

$\square$

For each $\mathbf{k} \in \varPi (k_0)$, define:

$$\begin{aligned} \begin{aligned} \varPhi (\mathbf{k})&=\sum _{t=0}^\infty \beta ^t u(f(k_t)-k_{t+1}) +\phi (u(f(k_0)-k_1), u(f(k_1)-k_2), \ldots ), \\ W(\mathbf{k})&=\sum _{t=0}^\infty \beta ^t u(f(k_t)-k_{t+1})\\ \varphi (\mathbf{k})&= \phi (u(f(k_0) - k_1), u(f(k_1) - k_2), \ldots ). \end{aligned} \end{aligned}$$

(2)

Lemma 3

We have

$$\begin{aligned} \sup _{\mathbf{k} \in \varPi (k_0)} \varPhi (\mathbf{k}) \ge \sup _{\mathbf{k} \in \varPi (k_0)} W(\mathbf{k}) + \sup _{\mathbf{k} \in \varPi (k_0)} \varphi (\mathbf{k}). \end{aligned}$$

(3)

Proof

Take any $\epsilon > 0$ satisfying $\epsilon < \sup _{\mathbf{k} \in \varPi (k_0)} \varphi (\mathbf{k})$. Fix T big enough such that for all $\mathbf{k} \in \varPi (k_0)$, we have

$$\begin{aligned} \sum _{t=T+1}^\infty \beta ^t u(f(k_t) - k_{t+1}) < \epsilon . \end{aligned}$$

Denote by $\mathbf{k}^*$ the solution to Ramsey problem. Take $\mathbf{k} ^\prime$ feasible, such that

$$\begin{aligned} \varphi (\mathbf{k}^\prime ) > \sup _{\mathbf{k} \in \varPi (k_0)} \varphi (\mathbf{k }) - \epsilon > 0. \end{aligned}$$

Define $f^t(k) = f(f(\ldots (k)\ldots ),\, t$ times. We will prove that there exists $\tau$ satisfying $k^\prime _{T+\tau } < f^{\tau }(k^*_T)$.

Indeed, suppose the contrary $f^{\tau }(k^*_T) \le k^\prime _{T+\tau }$ for all $\tau$. Denote by $\overline{k}$ the solution to the equation $f(k) = k$. We can verify easily that $f^t(k) \rightarrow \overline{k}$ when $t \rightarrow \infty$, for all $k > 0$.

We have:

$$\begin{aligned} f^{\tau }(k^*_T) \le k^\prime _{T+\tau } \le f^{T+\tau }(k_0). \end{aligned}$$

From this inequality, we have $k^\prime _t \rightarrow \overline{k}$ when $t$ tends to infinity. Hence, $f(k_t) - k_{t+1} \rightarrow 0$ when $t \rightarrow \infty$. This implies, by using the Lemma 2, $\varphi (\mathbf{k}^\prime ) = 0$, a contradiction.

Now take $\tau$ such that $k^\prime _{T+\tau } < f^{\tau }(k^*_T)$. Define $\mathbf{k}^{\prime \prime }$ as

$$\begin{aligned} k^{\prime \prime } = (k_0, k^*_1, k^*_2, \ldots , k^*_T, f(k^*_T), f^2(k^*_T), \ldots , f^{\tau -1}(k^*_T), k^\prime _{T+\tau }, k^\prime _{T+\tau +1}, \ldots ). \end{aligned}$$

Since $k^\prime _{T+\tau } < f^{\tau }(k^*_T)$, the sequence $\mathbf{k} ^{\prime \prime }$ is feasible. Observe that $\varphi (\mathbf{k}^{\prime \prime }) = \varphi (\mathbf{k}^{\prime })$. We have

$$\begin{aligned} \varPhi (\mathbf{k}^{\prime \prime })&= W(\mathbf{k}^{\prime \prime }) + \varphi (\mathbf{k}^{\prime \prime }) \\&> \sum _{t=0}^T \beta ^t u(f(k^*_t) - k^*_{t+1}) + \varphi (\mathbf{k} ^{\prime }) \\&> \sup _{\mathbf{k} \in \varPi (k_0)} W(\mathbf{k}) + \sup _{\mathbf{k} \in \varPi (k_0)} \varphi (\mathbf{k}) - 2 \epsilon . \end{aligned}$$

This inequality is true for all $\epsilon$ small enough. Let $\epsilon \rightarrow 0$, we obtain (3). $\square$

Claim

• (1) Suppose that $f^\prime (0) > 1$. Then problem $\fancyscript{C}$ has no solution.

• (2) Suppose $f^\prime (0) \le 1$. Then problems $\fancyscript{C}$ and $\fancyscript{R}$ have the same solution.

Proof

• (1) Suppose that $\fancyscript{C}$ has a solution $\overline{\mathbf{k}}$. From the Lemma 3, we have $\overline{\mathbf{k}}$ is a solution to Ramsey problem and also a solution to problem

  $$\begin{aligned} \max _{\mathbf{k} \in \varPi (k_0)} \varphi (\mathbf{k}). \end{aligned}$$

  Since $\overline{\mathbf{k}}$ is solution to Ramsey problem, we have $\overline{k}_t \rightarrow k^s$, solution to $f^\prime (k) = \frac{1}{\beta }$, if $f^\prime (0 )> {\frac{{1}}{{\beta }}}$ and $k^s =0$ if $f^\prime (0 )\le {\frac{{1}}{{\beta }}}$. Denote by $\tilde{k}$ the solution to $f^\prime (k) = 1$. Observe that $f(k^s) - k^s < f(\tilde{k}) - \tilde{k}$. Since $\tilde{k} < \overline{k}$, there exists $T$ big enough such that $f^T(k_0) > \tilde{k}$. This implies the sequence

  $$\begin{aligned} k^{\prime \prime \prime } = (k_0, f(k_0), \ldots , f^T(k_0), \tilde{k}, \tilde{k}, \ldots ) \end{aligned}$$

  is feasible. Since $f(k^s) - k^s < f(\tilde{k}) - \tilde{k}$, and by using the Lemma 2, we have

  $$\begin{aligned} \varphi (\overline{\mathbf{k}}) < \varphi (k^{\prime \prime \prime }) , \end{aligned}$$

  a contradiction.

• (2) The proof is trivial since in this case any feasible sequence ${\mathbf{k }}$ converges to 0 and hence $\varphi ({\mathbf{k}})=0$. $\square$

Appendix 3

Proof of Proposition 6

Let $(\hat{\kappa },\hat{\chi })$ be another solution. Then

$$\begin{aligned} u(\hat{\kappa },\hat{\chi })+\bar{p}\hat{\chi }-\bar{p}\hat{\kappa } =u(\bar{ \kappa },\bar{\kappa }). \end{aligned}$$

(4)

Since $(\overline{\kappa },\overline{\kappa })\in$ intgraph $\varGamma$, for $\lambda \in (0,1)$, close enough to 1, we have

$$\begin{aligned} (\lambda \overline{\kappa }+(1-\lambda )\hat{\kappa },\lambda \overline{ \kappa }+(1-\lambda )\hat{\chi })\in \text{ graph }\,\varGamma . \end{aligned}$$

Denote $\kappa _{\lambda }=\lambda \overline{\kappa }+(1-\lambda ) \hat{\kappa },\, \chi _{\lambda }=\lambda \overline{\kappa }+(1-\lambda )\hat{ \chi }$. Then

$$\begin{aligned} \lambda u(\overline{\kappa },\overline{\kappa })+(1-\lambda )u(\hat{\kappa }, \hat{\chi })+\bar{p}\chi _{\lambda }-\bar{p}\kappa _{\lambda }<u(\kappa _{\lambda },\chi _{\lambda })+\bar{p}\chi _{\lambda }-\bar{p}\kappa _{\lambda }\le u(\overline{\kappa },\overline{\kappa }), \end{aligned}$$

and then

$$\begin{aligned} \lambda u(\overline{\kappa },\overline{\kappa })+(1-\lambda )\left[ u(\hat{ \kappa },\hat{\chi })+\bar{p}\hat{\chi }-\bar{p}\hat{\kappa }\right] <u( \overline{\kappa },\overline{\kappa }) \end{aligned}$$

or equivalently

$$\begin{aligned} u(\hat{\kappa },\hat{\chi })+\bar{p}\hat{\chi }-\bar{p}\hat{\kappa } <u(\overline{ \kappa },\overline{\kappa }), \end{aligned}$$

in contradiction with (4). $\square$

Proof of Theorem 2

Theorem 2 is identical to Proposition 1.3.1 and Corollary 1.3.2. in Le Van and Dana (2003). But we have to modify the proof since graph$\varGamma$ is not assumed to be convex. Consider $\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p}\kappa _{t}-\bar{x}\right]$ which exists in $\mathbb R _{-}\cup \{-\infty \}$ since $\forall t,\;u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p}\kappa _{t}-\bar{x}\le 0$. We have

$$\begin{aligned} \sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p }\kappa _{t}-\bar{x}\right] \!=\!\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})-\bar{x}\right] -\bar{p}(\kappa _{0}-\kappa _{T+1}).\qquad \end{aligned}$$

(5)

If $\lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p}\kappa _{t}-\bar{x}\right] \in \mathbb R _{-}$, then $u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p}\kappa _{t}\rightarrow \bar{x}$. Let $(\hat{\kappa },\hat{\chi })$ be a cluster point of $\{(\kappa _{t},\kappa _{t+1})\}$. Then $u(\hat{\kappa },\hat{\chi })+\bar{p }\hat{\chi }-\bar{p}\hat{\kappa }=\bar{x}$. From Proposition 6 , $(\hat{\kappa },\hat{\chi })=(\overline{\kappa },\overline{\kappa })$. Therefore, the sequence $(\kappa _{t})$ converges to $\overline{\kappa }$. From (5), $\sum _{t=0}^{\infty }\left[ u(\kappa _{t},\kappa _{t+1})-\bar{x}\right] \in \mathbb R$.

Relation (5) implies

$$\begin{aligned} \sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})-\bar{x}\right] \le \sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p }\kappa _{t}-\bar{x}\right] +|\bar{p}.\kappa _{0}|+|\bar{p}.\kappa _{T+1}|. \end{aligned}$$

Hence, if

$$\begin{aligned} \lim _{T\rightarrow +\infty }\sum _{t=0}^{T}\left[ u(\kappa _{t},\kappa _{t+1})+\bar{p}\kappa _{t+1}-\bar{p}\kappa _{t}-\bar{x}\right] =-\infty , \end{aligned}$$

then $\lim _{T\rightarrow +\infty }\sum _{t=0}^{\infty }\left[ u(\kappa _{t},\kappa _{t+1})-\bar{x}\right] =-\infty$, since the sequence $(\kappa _{T+1})$ is bounded. $\square$