Inductive reasoning about unawareness

Abstract

We develop a model of games with awareness that allows for differential levels of awareness. We show that, for the standard modal-logical interpretations of belief and awareness, a player cannot believe there exist propositions of which he is unaware. Nevertheless, we argue that a boundedly rational individual may regard the possibility that there exist propositions of which she is unaware as being supported by inductive reasoning, based on past experience and consideration of the limited awareness of others. In this paper, we provide a formal representation of inductive reasoning in the context of a dynamic game with differential awareness. We show that, given differential awareness over time and between players, individuals can derive inductive support for propositions expressing their own unawareness. We consider the ecological rationality of heuristics to guide decisions in problems involving differential awareness.

1 Introduction

As former US Secretary Rumsfeld (2002) famously observed, the problem of unknown unknowns (things we do not know we do not know) is one of the most difficult facing any decision maker. In standard decision-theoretic frameworks, the set of possible states of nature is known at the beginning of the problem. Learning consists of observing signals that restrict the set of possible states. Probabilities are then updated according to Bayes’ rule. In reality, however, decision makers are frequently presented with “surprises,” that is, events they had not previously considered. So, a realistic model of choice under uncertainty must incorporate the fact that individuals are unaware of some relevant possibilities. Similarly, in a game-theoretic context, at any given stage in an extensive-form game, some players may be unaware of possible moves of which other players are aware. Furthermore, sophisticated individuals will understand that there may be possibilities of which they are unaware, even though they cannot express this understanding within the state-space model of the world available to them.

The argument of this paper is twofold. First, we show that, even when standard game-theoretic and decision-theoretic models are extended to include unawareness and differential unawareness, these standard concepts of belief, knowledge and awareness cannot encompass the idea that individuals understand their own bounded awareness. This lack of self-awareness persists even in a dynamic and interactive setting, where individuals are aware of both their own past unawareness and the bounded awareness of other individuals. We conclude that a reasonable model of individuals with a sophisticated understanding of their own bounded awareness must incorporate modes of reasoning other than deductive inference based on a fully specified state space or dynamic game tree.

Second, we argue that, in a dynamic interactive setting, it is natural to employ inductive reasoning to justify inferences about one’s own awareness and unawareness. In particular, since everyone has the experience of becoming aware of propositions and possibilities they have not previously considered, standard principles of historical induction suggest that similar experiences will occur in the future and therefore that there exist propositions of which we are currently unaware. Similarly, in a game with awareness, described by a syntactic structure, individuals believe that others are unaware of at least some possible histories and the associated propositions. Inductive reasoning suggests that the same will be true of all individuals, including the person drawing the inference.

It follows that reasonable, but boundedly rational, individuals should not rely solely on standard Bayes-Nash reasoning to guide their decisions, whether these decisions involve games with Nature or interactions with other individuals. Rather, individuals may improve their welfare by adopting inductively justified heuristics that are, in the terminology of Goldstein and Gigerenzer (2002), ecologically rational.

The paper is organized as follows:

Section 2 presents semantic and syntactic representations of differential awareness in terms of extensive games. The syntactic representation is constructed by associating with any given extensive-form game a propositional language rich enough to specify all histories and sets of histories that arise in that game. The crucial idea in our representation of games with awareness is that players may be unaware of some possible histories of the game and may therefore have access only to a restricted version of the game. This leads to an important modification of the standard modal-logical approach, in which a proposition is known to be true by a player if it is true in all histories considered possible by that player, given the information she has observed. In a game with awareness, a proposition may be false in the actual history, but true in all histories considered possible by a player, given their limited awareness. From the perspective of the full game (or, more generally, from the perspective of a player with greater awareness), it makes sense to characterize the player’s attitude to such propositions as “belief” rather than “knowledge.” We show how knowledge and belief operators may be defined in a game with differential awareness, in a way that allows for false belief but not false knowledge. These ideas are illustrated with reference to an example first presented by Heifetz et al. (2006).

In Sect. 3 we consider the question of how individuals can reason about their own awareness and unawareness. First, the language is extended to include existential propositions of the general form “there exists a proposition $q$, such that $\ldots$.” This development enables us to consider the process of reasoning about awareness and unawareness. Within the model of games with awareness developed in Sect. , we show that an individual cannot believe that there exist propositions of which he is unaware. Nevertheless, this proposition can be formulated in the richer language we consider. Moreover, in the context of games with awareness, it will be true, in general, that there exist propositions of which players are unaware. Furthermore, players in games will, in general, experience the discovery of propositions of which they were previously unaware and observe the bounded awareness of other players.

These observations lead us to consider modes of reasoning other than the Bayesian inference that characterizes standard extensive-form games. We show how inductive modes of reasoning may be used by individuals to assess existential propositions about awareness. Inductive support may be derived from past experience or from the observation of others. We say that a proposition is supported by historical induction if it has been (believed) true in the past and never been (believed) false. In particular, since everyone has the experience of becoming aware of propositions and possibilities they have not previously considered, the proposition that they will continue to do so is supported by historical induction. Similarly, a proposition that holds true for at least some individuals and is not false for any individual is supported by induction over individuals. In a game with awareness, players believe that others are unaware of at least some propositions. Inductive reasoning suggests that the same will be true for all players, including the person undertaking the induction.

Finally, we consider the implications of inductive reasoning about unawareness of decisions, represented in general by the choice of strategy in an extensive-form game. In Sect. 5, we argue that decision makers may reasonably choose strategies subject to heuristic constraints that rule out actions if the proposition that these actions will have unforeseen consequences is supported by induction. We provide criteria under which the adoption of heuristic constraints may be ecologically rational from the perspective of the full game. The analysis is illustrated by a no-trade result for the speculative trade example developed previously. We discuss possible applications to decisions regarding research and discovery and to the precautionary principle, often advocated as a basis for regulatory decisions regarding environmental risks.

Finally, we offer some concluding comments.

2 Games with awareness

2.1 Extensive-form games and languages: notation

In this section, we describe the notation for games and the associated languages. We will use the term “semantic” to refer to the representation of the problem in terms of possible game histories, and “syntactic” to refer to the language associated with the game in terms of the truth values of propositions. We begin with a(n almost) standard definition of an extensive-form game, as in Osborne and Rubinstein (1994).

Definition 1

A finite extensive game is $\Gamma =(N\cup \{c\},A,H,P,f^{c},\mathcal I ,\{v^{i}:i\in N\})$ where:

• G1 (Player Set): $N=\{1,\ldots ,n\}$ is a finite set of players, and $c$ denotes Nature (the ‘chance’ player);

• G2 (Actions):$A$ is a finite non-empty set of actions;

• G3 (Histories): $H$ is a set of histories, defined as sequences of actions undertaken by the players. $H$ is partially ordered by the subhistory relationship $\preceq .$ The set of terminal histories is denoted by $Z$. The set of actions available at $h$ is denoted by $A\left( h\right) \subseteq A.$

• G4 (Player Function): $P:H\rightarrow N\cup \{c\}$ assigns to each history a player making a decision after that history;

• G5 (Chance Assignment): $f^{c}$ associates with every history $h$ such that $P(h)=c$ a probability distribution over $A$ drawn from some set $\Delta$, and with support $A\left( h\right).$

• G6 $\mathcal I :H\rightarrow 2^{H}$ is the information set assignment function whose range forms a partition of $H$ and exhibits the properties that $h\in \mathcal I \left( h\right)$ for all $h\in H$, and for any $h^{\prime }\in \mathcal I \left( h\right)$, $P\left( h\right) =P\left( h^{\prime }\right)$ and $A\left( h\right) =A\left( h^{\prime }\right)$.

• G7 (Payoffs): For each player $i\in N$, $v^{i}:Z\rightarrow \mathbb R$ is the payoff function for player $i$, representing expected-utility preferences for lotteries over $Z$.

So, the set of histories $h$ is the set of all sequences of the form $\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{k}\rangle$, where $\alpha _{j}\in A\left( \langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{j-1}\rangle \right)$, $j=1,\ldots ,k$, including the trivial sequence $\langle \cdot \rangle$. The extensive structure of the game $\Gamma$ is represented by the subhistory relationship $\langle \alpha _{1},\ldots ,\alpha _{k}\rangle \preceq$ $\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{k},..,\alpha _{l}\rangle$. If $h=\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{k}\rangle$, we denote $h\cdot \alpha _{k+1}=\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{k},\alpha _{k+1}\rangle$ and observe $h\preceq h\cdot \alpha _{k+1}$.

The process of Bayesian learning in an extensive-form game works by exclusion. That is, as the game is played out, players learn that some histories in the game are no longer possible and update their probabilities on the remaining possible histories using Bayes’ rule. The information set $\mathcal I \left( h\right)$ describes the set of histories that have not been ruled out by the information available to player $P\left( h\right)$ at $h.$

Following Osborne and Rubinstein (1994) we denote by $X_{P\left( h\right) }\left( h\right)$ the record of player $P\left( h\right)$’s experience along the history $h$, that is, the sequence consisting of the information sets she encountered in the history $h$ and the actions that she took at them, in the order they were encountered. Formally, for any history $h=\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{k}\rangle$, let $i=P\left( h\right)$, let $h^{0}=\langle \cdot \rangle$ (the trivial sequence), let $h^{r}=\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{r}\rangle$, for $r\in \{1,\ldots ,k-1\}$ and let $R\left( i\right) =\{r:P\left( h^{r}\right) =i\}$. Then $X_{i}\left( h\right) =\left( \mathcal I \left( h^{r_{1}}\right),a_{r_{1}+1},\ldots ,\mathcal I \left( h^{r_{\ell }}\right),a_{r_{\ell }+1}\right)$, where $r_{j}$ is the $j$th smallest member of $R\left( i\right)$ and $\ell =\left|R\left( i\right) \right|$.

We restrict attention to games of perfect recall.

Definition 2

A finite extensive game $\Gamma =(N\cup \{c\},A,H,P,f^{c},\mathcal I ,\{v^{i}:i\in N\})$ exhibits perfect recall if for each history $h$ in $H$, $X_{P\left( h\right) }\left( h\right) =X_{P\left( h\right) }\left( h^{\prime }\right)$, for all $h^{\prime }\in \mathcal I \left( h\right)$.

A behavioral strategy $\beta ^{i}$ for player $i$ is a collection of independent probability measures $\left( \beta ^{i}\left( h\right) :P\left( h\right) =i\right)$ where the support of each such $\beta ^{i}\left( h\right)$ is a subset of $A\left( h\right)$, and where for any $h^{\prime }\in \mathcal I \left( h\right)$, $\beta ^{i}\left( h^{\prime }\right) =\beta ^{i}\left( h\right)$. That is, there is an independent probability measure over actions specified for each history at which player $i$ is called upon to play, and this probability measure is the same for all histories residing in the same information set. A behavioral strategy profile $\beta$ is a set of behavioral strategies, one for each $i$.

We define a subjective probability $\mu ^{i}=\left( \mu ^{i}\left( h\right) :P\left( h\right) =i\right)$ for player $i$ to be an assignment to each history $h$ in $H$ for which $P\left( h\right) =i$, a probability measure on the set of histories in $\mathcal I \left( h\right)$ in which for any $h^{\prime }\in \mathcal I \left( h\right)$, $\mu ^{i}\left( h^{\prime }\right) =\mu ^{i}\left( h\right)$.¹ A subjective probability system $\mu$ is a set of subjective measures, one for each $i$. An assessment is a pair $\left( \beta ,\mu \right)$, where $\beta$ is a behavioral strategy profile and $\mu$ is a subjective probability system.

Given a strategy profile $\beta$, for each $h$ in $H$ we denote by $\tau \left( \beta |h\right)$ the probability distribution over terminal histories induced by $\beta$, conditional on history $h$ having been reached. Let $\tau \left( \beta \right)$ denote the unconditional probability distribution over terminal histories induced by $\beta$.

Hence, given the assessment $\left( \beta ,\mu \right)$, the continuation value of player $i=P\left( h\right)$ at $h$ (i.e., the continuation value conditional on information set $\mathcal I \left( h\right)$ having been reached) is

$$\begin{aligned} V_{\Gamma }^{i}\left( h;\beta ,\mu \right) =\sum \limits _{h^{\prime }\in \mathcal I \left( h\right) }\mu ^{i}\left( h\right) \left[ h^{\prime }\right] \left( \sum _{h^{\prime \prime }\in Z}\tau \left( \beta |h^{\prime }\right) \left[ h^{\prime \prime }\right] v^{i}\left( h^{\prime \prime }\right) \right) \text{,} \end{aligned}$$

and we denote the expected value of the (entire) game for player $i$ by $V_{\Gamma }^{i}\left( \beta \right) =\sum _{h\in Z}\tau \left( \beta \right) \left[ h\right] v^{i}\left( h\right)$.

An assessment $\left( \beta ,\mu \right)$ is sequentially rational if each player’s strategy is a best response at every information set at which she is called upon to play. That is, we require, for each player $i\in N$ and every $h$, such that $P\left( h\right) =i$,

$$\begin{aligned} V_{\Gamma }^{i}\left( h;\beta ,\mu \right) \ge V_{\Gamma }^{i}\left( h;\left( \hat{\beta }^{i},\beta ^{-i}\right),\mu \right), \quad \text{ for} \text{ every} \text{ strategy} \hat{\beta }^{i} \text{ of} \text{ player} i\text{.} \end{aligned}$$

We refer to a behavioral strategy profile that assigns positive probability to every information set as completely mixed. An assessment is consistent if it is the limit of a sequence $\left( \left( \beta _{m},\mu _{m}\right) \right) _{m=1}^{\infty }$ in which each strategy profile $\beta _{m}$ is completely mixed and each belief system $\mu _{m}$ is derived from $\beta _{m}$ using Bayes’ rule. A sequential equilibrium is a consistent and sequentially rational assessment. As in Osborne and Rubinstein, it is straightforward to demonstrate for a finite extensive-form game with perfect recall the existence of a sequential equilibrium.

We now consider a syntactic rendition of the same structure. With each game $\Gamma$, we associate a language $\mathcal L _{\Gamma }$. The language must be rich enough to encompass the sequential structure of $H$, the information in $\mathcal I$ and the valuations $v^{i}$. The relationship between the properties of the language $\mathcal L _{\Gamma }$ and of the game $\Gamma$ may be formalized using the semantic approach to modal logic first presented by Kripke (1963) and developed in relation to the logic of knowledge by Fagin and Halpern (1988).

Space does not permit a detailed exposition here, but a brief outline will be useful. The central idea is to use properties of the game $\Gamma$ to define (in Kripke’s terminology) accessibility relations between histories $h\in H$. More precisely, the property of common membership of an information set defines an equivalence relation, while the temporal structure defines a partial ordering. These relations define a class of Kripke frames for which an appropriate axiomatization of the language $\mathcal L _{\Gamma }$ can be shown to be complete (permitting derivation of all theorems applicable to games $\Gamma$) and sound (ensuring that every proposition derivable in $\mathcal L _{\Gamma }$ is valid in $\Gamma$).

Definition 3

For a game $\Gamma$, the game language $\mathcal L _{\Gamma }$ is a set of sentences closed under the logical operators $\wedge$ and $\lnot$ and derived from:

• L1 (Player terms): Terms $\mathcal N =\{p_{i}:i\in N\}$ representing players, with $c$ denoting Nature (the “chance” player), where $p_{i}$ is read as “$i$ is a player in the game”;

• L2 (Actions): A set of elementary propositions $\mathcal A =\left\{ :\alpha \in A\right\}$ where $p_{\alpha }$ is read as “action $\alpha$ has just been taken”;

• L3 (Histories): A set of elementary propositions $\mathcal H =\left\{ p_{h}:h\in H\right\}$ read as “the current history is $h$”;

• L4 (Player Assignment) A set of elementary propositions $\mathcal P =\left\{ p_{h,i}:h\in H,i\in N\right\}$ where $p_{h,i}$ is read as “player $i$ moves at $h$”;

• L5 (Knowledge operators): $\left\{ k_{i}p:i\in N\right\}$ read as “$i$ knows $p$”;

• L6 (Payoffs): For each player $i\in N$, and each feasible payoff $v$ for player $i$ in the game $\Gamma$, an elementary proposition $p_{v,i}$ is read as “player $i$ receives payoff $v$”$.$ We will assume, without details, that the language is rich enough to allow players to do standard arithmetic, for example, to express propositions like “my expected payoff is less than $v$”;

• L7 (Temporal structure) The temporal structure of the game is given by an operator $w$ (where $wp$ is read as “$p$ was true in the past”).

Given an appropriate semantic interpretation, the language $\mathcal L _{\Gamma }$ represents a syntactic rendition of a class of games including $\Gamma$. That is, for any given play of a game from this class,² the truth value of any proposition $p\in \mathcal L _{\Gamma }$ can be inferred.

The semantic interpretation works as follows. For any $p\in \mathcal L _{\Gamma }$, the statement “$p$ is true at $h$” is written $h\models _{\Gamma }p$. Conversely, the truth set $\mathfrak I \left( p\right) =\left\{ h:h\models _{\Gamma }p\right\}$ is the set of histories at which $p$ is true. The relation $\models _{\Gamma }$ can be derived using the standard rules of logic and the interpretation rules given below:

Definition 4

A semantic-syntactic game representation $\left( \Gamma ,\mathcal L _{\Gamma },\models _{\Gamma }\right)$ consists of an extensive-form game $\Gamma$, the associated language $\mathcal L _{\Gamma }$ and a relation $\models _{\Gamma }$ such that for all $p,h,$ either $h\models _{\Gamma }p$ or $h\models _{\Gamma }\lnot p,$ and:

• S1 (Players):$h\models _{\Gamma }p_{i},\forall h\in H,i\in N$

• S2 (Actions):$h\models _{\Gamma }p_{\alpha }\Leftrightarrow \exists h^{\prime },$ s.t. $h=h^{\prime }\cdot \alpha$

• S3 (History):$\forall h,h^{\prime }\in H$, (i) $h\models _{\Gamma }p_{h}$, (ii) $h^{\prime }\ne h\Leftrightarrow h^{\prime }\models _{\Gamma }\lnot p_{h}$, (iii) $h$ $\models _{\Gamma }wp_{h^{\prime }}\Leftrightarrow h^{\prime }\preceq h$

• S4 (Player Assignment) $h\models _{\Gamma }p_{h,i}\Leftrightarrow P\left(h\right) =i$

• S5 (Knowledge ): $h\models _{\Gamma }k_{i}p,$ if and only if $P\left( h\right) =i$ and $h^{\prime }$ $\models _{\Gamma }p$ for all $h^{\prime }\in \mathcal I \left( h\right);$

• S6 (Payoffs )): $h\models _{\Gamma }p_{v,i}\Leftrightarrow h\in Z\wedge v^{i}\left( h\right)=v$

• S7 (Temporal structure) $h\models _{\Gamma }wp\Leftrightarrow \exists h^{\prime }\prec h,h^{\prime }\models _{\Gamma }p$

Of these rules, S6 (which deals with the knowledge operator $k_{i}$) is the only one that requires special attention. It states that, at the history $h$ in the game, player $i$ knows the proposition $p$ is true if and only if $p$ is true in all histories considered possible by player $i$ at $h$. Thus, the semantic interpretation of the language relates knowledge directly to the information sets of players in the game.

It is straightforward to show that the knowledge operator satisfies the standard set of axioms referred to in the literature on modal logic as S5. The most important of these are Distribution $k_{i}\left( p\Rightarrow q\right) \Rightarrow \left( k_{i}p\Rightarrow k_{i}q\right)$, commonly denoted by K, Truth ($k_{i}p\Rightarrow p)$, commonly denoted by T, Positive Introspection ($k_{i}p\Rightarrow k_{i}k_{i}p)$, commonly denoted by 4, negative introspection ($\lnot k_{i}p\Rightarrow k_{i}\lnot k_{i}p)$, commonly denoted by 5, and Knowledge Generalization, which requires that if $p$ is true in all states, we can infer $k_{i}p$. Fagin et al. (1995) (p. 56) show that, in a “possible worlds” representation of knowledge, S5 is a complete and sound axiomatization for the knowledge operator defined as above (see also Halpern 2003, pp. 249–250). However, this result does not encompass the temporal structure of knowledge in an extensive-form game, where the notion corresponding to the set of worlds is the set of partial histories at which a given player is to move. In particular, we do not address issues that may arise in the absence of perfect recall.

We can now consider syntactic notions of awareness and unawareness. The standard definition of awareness is that an individual is aware of a proposition if they know its truth value or know that they do not know its truth value. That is, $a_{i}p\Leftrightarrow k_{i}p\vee k_{i}\lnot p\vee k_{i}\left( \lnot k_{i}p\wedge \lnot k_{i}\lnot p\right)$ with unawareness being the negation of awareness, that is, $u_{i}p$ is a synonym for $\lnot a_{i}p$. (Notice that $k_{i}p\vee k_{i}\lnot p\vee k_{i}\left( \lnot k_{i}p\wedge \lnot k_{i}\lnot p\right)$ may be stated more compactly as $k_{i}p\vee k_{i}\left( \lnot k_{i}p\right)$.)

As observed by Modica and Rustichini (1994), for a partitional information structure (which we have assumed), $a_{i}p$ is true for all $p\in \mathcal L _{\Gamma }$. Also, we have $a_{j}a_{i}p$ and so forth. Because of this property, we refer to a standard extensive-form game as a game of full common awareness. Since $u_{i}p$ is trivially false in a game of full common awareness, we will not use the definition above, but will define awareness and unawareness in the context of a game with awareness, which we now construct.

2.2 Restrictions

Under the standard assumptions of unbounded rationality and common knowledge, all players in a game are aware of the structure of the game, of each other’s awareness, of others’ awareness of their own awareness, and so on. With boundedly rational players, however, it is necessary to consider the possibility that, at some given history $h$, player $i=P\left( h\right)$, who must choose an action, may not be aware of all possible histories in the game. For example, player $i$ may be unaware of possible future moves available to other players, to the chance player or to herself. Player $i$ may even be unaware of the existence of some other players. We formalize the less than full awareness of the player $P\left( h\right)$ at $h$ by ascribing to her a game that is a restriction of the full awareness game. Essentially, the restriction is obtained by deleting some of the terminal histories and all partial histories of those terminal histories of the original game and then constructing the restricted game to be consistent with the original game in terms of its information structure.

Definition 5

Fix a game $\Gamma =(N\cup \{c\},A,H,P,f^{c},\mathcal I ,\{v^{i}:i\in N\})$, where $Z\subset H$ denotes the set of terminal histories in $\Gamma$. A non-empty subset of terminal histories $\tilde{Z}\subset Z$ is deemed admissible, if $\Gamma _{ \tilde{Z}}=(N_{\tilde{Z}}\cup \{c\},A_{\tilde{Z}},H_{\tilde{Z}},P_{\tilde{Z} },f_{\tilde{Z}}^{c},\mathcal I _{\tilde{Z}},\{v_{\tilde{Z}}^{i}:i\in N_{ \tilde{Z}}\})$ constitutes a restriction of the game $\Gamma$ in which:

$$\begin{aligned} H_{\tilde{Z}}&= \left\{ h\in H:\exists z\in \tilde{Z},h\preceq z\right\} \text{;} \\ N_{\tilde{Z}}&= \left\{ n\in N:\exists h\in H_{\tilde{Z}},P\left( h\right) =n\right\} \text{;} \\ \text{ for} \text{ each}\, h&\in H_{\tilde{Z}}\text{:} \\&\mathcal I _{\tilde{Z}}\left( h\right) =H_{\tilde{Z}}\cap \mathcal I \left( h\right) \text{;} \\&A_{\tilde{Z}}\left( h\right) =\{a\in A\left( h\right) :h\cdot a\in H_{ \tilde{Z}}\}\text{;} \\&P_{\tilde{Z}}\left( h\right) =P\left( h\right) \text{;} \\&f_{\tilde{Z}}^{c}\left( h\right) \left( a\right) =\frac{ f^{c}\left( h\right) \left( a\right) }{\sum \nolimits _{\tilde{a}\in A_{\tilde{Z }}\left( h\right) }f^{c}\left( h\right) \left( \tilde{a}\right) }\text{,} \\&\text{ and,} \\ \text{ for} \text{ each}\, i&\in N_{\tilde{Z}}\, \text{ and} \,z\in \tilde{Z}, v_{ \tilde{Z}}^{i}\left( z\right) =v^{i}\left( z\right). \end{aligned}$$

We denote the relation that $\Gamma _{\tilde{Z}}$ is a restriction of the game $\Gamma$ by $\Gamma _{\tilde{Z}}\sqsubseteq \Gamma$.

Furthermore, in a slight abuse of notation, we shall also extend the domains of $A_{\tilde{Z}}$, $P_{\tilde{Z}}$, $f_{\tilde{Z}}^{c}$, $\mathcal I _{ \tilde{Z}}$ to $H$, by setting for each $h$ in $H-H_{\tilde{Z}}$:

$$\begin{aligned}&\mathcal I _{\tilde{Z}}\left( h\right) :=H_{\tilde{Z}}\cap \mathcal I \left( h\right) \text{;} \quad A_{\tilde{Z}}\left( h\right) :=\left\{ a\in A\left( h\right) :\exists h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right) \text{ s.t.} h^{\prime }\cdot a\in H_{\tilde{Z}}\right\} \text{;} \\&\qquad P_{ \tilde{Z}}\left( h\right) :=P\left( h\right) \text{;} \text{ and,} \\&\quad f_{\tilde{Z}}^{c}\left( h\right) \left( a\right) :=\left\{ \begin{array}{ll} f^{c}\left( h\right) \left( a\right) \left.\sum \nolimits _{\tilde{a}\in A_{\tilde{Z} }\left( h\right)}\right. f^{c}\left( h\right) \left( \tilde{a}\right)&\quad \text{ if} A_{\tilde{Z}}\left( h\right) \ne \varnothing \\ 0&\quad \text{ if}\, A_{\tilde{Z}}\left( h\right) =\varnothing \end{array} \right. \text{.} \end{aligned}$$

By construction, the subhistories and the subhistory ordering are preserved in the sense that, for any $h,\tilde{h}\in H$, such that $\tilde{h}\preceq _{\Gamma }h$, if $h$ is in the restricted set of histories $H_{\tilde{Z}}$ then $\tilde{h}$ must also be in $H_{\tilde{Z}}$  and furthermore, we retain $\tilde{h}\preceq _{\Gamma _{\tilde{Z}}}h$ in the restricted game. In addition, no new terminal nodes are created in the restricted game, allowing us to obtain the payoff function from the restriction of $v^{i}$ to $\tilde{Z}$. The definition of the chance assignment function $f_{\tilde{Z}}^{c}$ ensures that if an action by nature is excluded from consideration at $h$, the relative probabilities of the remaining actions $\alpha \in A_{\tilde{Z}}\left( h\right)$ are unchanged. Notice it also follows from the definition that a restricted game does not add information or lose information with respect to the histories in the restricted game. Moreover, if the original game is one of perfect recall, then this property is inherited by the restricted game.

Lemma 1

Fix a game $\Gamma$ with perfect recall and an admissible subset of terminal histories $\tilde{Z} \subseteq Z$. The associated restricted game $\Gamma _{\tilde{Z}}$ satisfies perfect recall.

Proof

Recall perfect recall for $\Gamma$ requires for any history $h$ in $H$, $X_{P\left( h\right) }\left( h\right) =X_{P\left( h\right) }\left( h^{\prime }\right)$, for all $h^{\prime }\in \mathcal I \left( h\right)$. Now suppose $h=\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{r}\rangle$ is in $H_{\tilde{Z}}$, and denote by $\tilde{X}_{P\left( h\right) }\left( h\right)$ the record of player $P\left( h\right)$’s experience along the history $h$ in the restricted game $\Gamma _{\tilde{Z}}$. Let $h^{r}=\langle \alpha _{1},\alpha _{2},\ldots ,\alpha _{r}\rangle$ for $r\in \{1,\ldots ,k-1\}$ and let $R\left( i\right) =\{r:P\left( h^{r}\right) =i\}$. By construction $\tilde{X}_{P\left( h\right) }\left( h\right) =\left( \mathcal I \left( h^{r_{1}}\right) \cap H_{\tilde{Z}},a_{r_{1}+1},\ldots , \mathcal I \left( h^{r_{\ell }}\right)\right.$ $\left.\cap H_{\tilde{Z}},a_{r_{\ell }+1}\right) =\tilde{X}_{P\left( h\right) }\left( h^{\prime }\right)$, for all $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right) =\mathcal I \left( h\right) \cap H_{\tilde{Z}}$. $\square$

The partial relation of set inclusion for terminal histories generates a partial ordering over the set of restricted games that can be generated from a given extensive-form game.

Definition 6

The relation $\sqsubseteq$ is a partial ordering on the set of games, corresponding to the subset ordering on sets of terminal histories. In particular, if $\widetilde{\widetilde{Z}}\subseteq \tilde{Z} \subseteq Z$, then $\Gamma _{\widetilde{\widetilde{Z}}}\sqsubseteq \Gamma _{ \tilde{Z}}\sqsubseteq \Gamma$.

A parallel definition applies to the associated language $\mathcal L _{\Gamma }$ and to the interpretation $\models _{\Gamma }$. If $\Gamma _{ \tilde{Z}}\sqsubseteq \Gamma$, then $\mathcal L _{\Gamma _{\tilde{Z} }}\sqsubseteq \mathcal L _{\Gamma }$. For elementary propositions $p\in \mathcal L _{\Gamma _{\tilde{Z}}}$ (those incorporating only terms about players, actions and histories in the restricted game $\Gamma _{\tilde{Z}}$ ), we have, whenever $h\in \tilde{H}\subseteq H$, $h\models _{\Gamma _{ \tilde{Z}}}p$ if and only if $h\models _{\Gamma }p$. Things are different when we come to consider knowledge and belief. It is possible to have a situation where $h^{\prime }\models _{\Gamma _{\tilde{Z}}}p$ for all $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right)$, but nevertheless, $h\models _{\Gamma }\lnot p$. That is, $p$ is true for all the histories considered possible by player $i=P\left( h\right)$ at $\mathcal I _{\tilde{Z}}\left( h\right)$in the restricted game $\Gamma _{\tilde{Z}}$, but that the restricted information set does not include the actual history $h$, at which $p$ is false.

Thus, in a restricted game, players may hold false beliefs about propositions $p$. More generally, what appears to the player as reliable knowledge about a proposition $p$ may be an unreliable belief if there are histories $h^{\prime \prime }$ that cannot be ruled out on the basis of the information available at $h$, of which the player is unaware and at which $p$ is false. We write “$b_{i}p$” read as “$i$ believes $p$” and define what it means, from the viewpoint of the unrestricted game, for a player to believe a proposition is true in the game they perceive themselves to be playing.

Definition 7

Fix a game $\Gamma$ and an admissible subset of terminal histories $\tilde{Z}\subseteq Z$ with associated restricted game $\Gamma _{ \tilde{Z}}\sqsubseteq \Gamma$. For any proposition $p\in \mathcal L _{\Gamma _{\tilde{Z}}}$, any history $h\in H$ and $i=P\left( h\right)$, $h\models _{\Gamma ,\tilde{Z}}b_{i}p$ iff $h^{\prime }\models _{\Gamma _{ \tilde{Z}}}p$ for all $h^{\prime }\in \mathcal I _{\tilde{Z} }\left( h\right).$

Remark 1

Since the restricted game $\Gamma _{\tilde{Z}}$ is itself a game, it remains true that, for any $h^{\prime }\in H_{\tilde{Z}}, j= P_{\tilde{Z}}\left( h^{\prime }\right)$, and any $p\in \mathcal L _{\Gamma _{\tilde{Z}}}$, $h^{\prime }\models _{\Gamma _{\tilde{Z}}}k_{j}p$ if and only if $h^{\prime \prime }\models _{\Gamma _{\tilde{Z}}}p$ for all $h^{\prime \prime }\in \mathcal I _{\tilde{Z}}\left( h^{\prime }\right)$. That is, within any game, the knowledge operator is defined as usual. However, when considering a restriction of a game from the viewpoint of that game, we use the belief operator $b_{i}$. To sum this up

$$\begin{aligned} h\models _{\Gamma ,\tilde{Z}}b_{i}p\Leftrightarrow h^{\prime }\models _{\Gamma _{\tilde{Z}}}k_{i}p \quad \text{ for} \text{ any} \text{(and} \text{ hence} \text{ all)} h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right) \text{.} \end{aligned}$$

Note that $b_{i}p$ is a proposition in $\Gamma$ referring to the restriction $\Gamma _{\tilde{Z}}$, while the proposition $k_{i}p$ is well defined within each of $\Gamma$ and $\Gamma _{\tilde{Z}},$ but has different meanings. In particular, it is possible that $h\models _{\Gamma }\lnot k_{i}p$ while $h^{\prime }\models _{\Gamma _{\tilde{Z}}}k_{i}p$ for all $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right)$ (and in the latter case if $h\notin \mathcal I _{\tilde{Z}}\left( h\right)$ it may be, but need not be, true that $h\models _{\Gamma }\lnot p)$. That is, from the perspective of $\Gamma$ “knowledge” in $\Gamma _{\tilde{Z}}$ may be unreliable or false, which is why we call it belief. Only if $\mathcal I _{ \tilde{Z}}\left( h\right) =\mathcal I \left( h\right)$ will knowledge and belief coincide.

It follows from the above remark that the belief operator does not satisfy the Truth Axiom T. Even more importantly, the belief operator does not satisfy negative introspection (Axiom 5 in S5). Consider any history $h^{\prime }\in \mathcal I \left( h\right)$, such that $h^{\prime }\notin H_{ \tilde{Z}}$ and therefore $h^{\prime }\notin \mathcal I _{\tilde{Z}}(h)$. Then, $h\models _{\Gamma ,\tilde{Z}}\lnot b_{i}p_{h}$ but also (since $\lnot p_{h}$ is not a proposition in $\mathcal{L _\Gamma }_{\tilde{Z}}$) $h\vDash \!\!\!\!\!/\, _{\Gamma ,\tilde{Z}}b_{i}\lnot p_{h}$ and $h\vDash \!\!\!\!\!/\, _{\Gamma , \tilde{Z}}b_{i}b_{i}\lnot p_{h}$.

The remaining properties of S5 are satisfied by the belief operator as is shown in the following lemma.

Lemma 2

The belief operator satisfies the properties of the system KD4, namely:

• Distribution (K) $b_{i}\left( p\Rightarrow q\right) \Rightarrow \left( b_{i}p\Rightarrow b_{i}q\right)$;

• Consistency (D) $\lnot b_{i}false$; and,

• Positive Introspection (4) $b_{i}p\Rightarrow b_{i}b_{i}p$.

Proof

(K) If $h\models _{\Gamma _{\tilde{Z}}} b_{i}\left( p\Rightarrow q\right)$, then $\forall$ $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right)$, $h^{\prime }\models _{\Gamma _{\tilde{Z}}}\lnot p\vee q$. Now suppose $\forall$ $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right),\ h^{\prime }\models _{\Gamma _{\tilde{Z}}}p$ (i.e., $h\models _{\Gamma _{ \tilde{Z}}}b_{i}p$), then it follows $\forall$ $h^{\prime }\in \mathcal I _{ \tilde{Z}}\left( h\right)$ $h^{\prime }\models _{\Gamma _{\tilde{Z}}}q$, that is, $h\models _{\Gamma _{\tilde{Z}}}b_{i}q$, as required.

(D) Choose some $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right)$. Since $\ h^{\prime }\not \models _{\Gamma _{\tilde{Z}}}false$, it follows $h\not \models _{\Gamma _{\tilde{Z}}}b_{i}false$, as required.

(4) Suppose $\forall h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right)$, $h^{\prime }\models _{\Gamma _{\tilde{Z}}}p$, then also $\forall$ $h^{\prime }\in \mathcal I _{\tilde{Z}}\left( h\right)$, $h^{\prime }\models _{\Gamma _{\tilde{Z}}}b_{i}p$, so $h\models _{\Gamma _{\tilde{Z} }}b_{i}b_{i}p$, as required. $\square$

The absence of negative introspection means that the belief operator displays non-trivial unawareness. We write $a_{i}p$, read as “$i$ is aware of $p$,” and write $u_{i}p$, read as “$i$ is unaware of $p$,” and define what it means, from the viewpoint of the unrestricted game, for a player to be aware (respectively, unaware) of a proposition in the game they perceive themselves to be playing.

Definition 8

Fix a game $\Gamma$ and an admissible subset of terminal histories $\tilde{Z}\subseteq Z$, with associated restricted game $\Gamma _{\tilde{Z}}\sqsubseteq \Gamma$. For any proposition $p\in \mathcal L _{\Gamma }$, any history $h\in H$ and $i=P\left( h\right)$,

• (i) $h\models _{\Gamma ,\tilde{Z}}a_{i}p$ iff $h\models _{\Gamma ,\tilde{Z}}b_{i}p\vee b_{i}\left( \lnot k_{i}p\right)$

• (ii) $h\models _{\Gamma ,\tilde{Z}}u_{i}p$ iff $h\models _{\Gamma ,\tilde{Z} }\lnot a_{i}p$

In words, we say at a history $h$ in the game $\Gamma$, player $i=P\left( h\right)$ who perceives to be playing the game $\Gamma _{\tilde{Z}}$, is aware of a proposition if from the perspective of the unrestricted game $\Gamma$, he either believes the proposition is true or believes he does not know the proposition is true.

The fact that the belief operator does not satisfy negative introspection has the important consequence that, for any given proposition $p$, the fact that player $i$ is unaware of $p$ does not imply that she believes she is unaware of $p$. Indeed, the opposite is true.

Lemma 3

For any proposition $p\in \mathcal{L _{\Gamma }}$, any history $h\in H$ and $i=P(h)$,

$$\begin{aligned} h\vDash \!\!\!\!\!/\, _{\Gamma ,\tilde{Z}}b_{i}u_{i}p \end{aligned}$$

Proof

Notice either

• (i) $p\in \mathcal L _{\Gamma _{\tilde{Z}(h)}}$ in which case $h\models _{\Gamma ,\tilde{Z}}a_{i}p$, and hence $h\models _{\Gamma ,\tilde{Z} }b_{i}a_{i}p\Leftrightarrow h\models _{\Gamma ,\tilde{Z}}b_{i}\lnot u_{i}p$

• (ii) $p\notin \mathcal L _{\Gamma _{\tilde{Z}(h)}}$ in which case $u_{i}p\notin \mathcal L _{\Gamma _{\tilde{Z}(h)}}$ and hence $h\vDash \!\!\!\!\!/\,_{\Gamma ,\tilde{Z}}b_{i}u_{i}p$ $\square$

2.3 Perception mapping

We are concerned with games with awareness, in which players, at any given history where they are called on to play, may be unaware of some possible histories. To represent this, we need to relate the game actually being played to the game as perceived by the players. We shall define the evolution of awareness of the players through the game by the perception mapping:

Definition 9

Fix a game $\Gamma$. A perception mapping is a function $\tilde{Z}:H\rightarrow 2^{Z}\backslash \varnothing$, where with each history $h\in H$, the set $\tilde{Z}\left( h\right) \subseteq Z$ is an admissible set of terminal histories considered by player $P\left( h\right)$ at history $h$. Denote by

$$\begin{aligned} \Gamma _{\tilde{Z}\left( h\right) }=\left(N_{\tilde{Z}\left( h\right) }\cup \{c\},A_{\tilde{Z}\left( h\right) },H_{\tilde{Z}\left( h\right) },P_{\tilde{Z }\left( h\right) },f_{\tilde{Z}\left( h\right) }^{c},\mathcal I _{\tilde{Z} \left( h\right) }, \left\{ v_{\tilde{Z}\left( h\right) }^{i}:i\in N_{\tilde{Z} \left( h\right) }\right\} \right)\text{,} \end{aligned}$$

the restricted game associated with the set of terminal histories $\tilde{Z} \left( h\right)$ that is imputed to player $P\left( h\right)$ at $h$.

We impose the following requirements on the perception mapping.

IN: (Information Neutrality): For all $h$, $h^{\prime }$ in $H$, $h^{\prime }\in \mathcal I \left( h\right) \Rightarrow$ $\tilde{Z}\left( h^{\prime }\right) =\tilde{Z}\left( h\right).$

IA: (Increasing Awareness): If $h^{\prime }\preceq h$ and $P\left( h\right) =P\left( h^{\prime }\right)$ then $\tilde{Z}\left( h^{\prime }\right) \subseteq$ $\tilde{Z}\left( h\right)$.

NI: (No Impossibility): For all $h$, $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right) \ne \varnothing$.

The Information Neutrality property requires a player’s level of awareness be congruent with the information structure of the full awareness game. More precisely, at any two histories in the same information set, the player’s knowledge, beliefs and awareness are the same. This is consistent with the standard treatment of information sets in decision theory and game theory.

The Increasing Awareness property ensures that once a player considers a (terminal) history, she does not forget it. We will say the game displays non-trivial increasing awareness for $i$ at $h$ if there exists some $h^{\prime }\preceq h$ such that the inclusion is strict, that is, $\tilde{Z}\left( h^{\prime }\right) \subset$ $\tilde{Z}\left( h\right).$

The No Impossibility property ensures that the player who is to move always considers some history possible.

For interactive awareness, we suppose for any pair of histories $h$ and $h^{\prime }$ in $H$, such that there exists $h^{\prime \prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ for which $h^{\prime \prime }\preceq h^{\prime }$, and with $i=P\left( h\right)$ and $j=P\left( h^{\prime }\right)$, we can define the second-order imputation in which $i$ at $h$ imputes to $j$ at $h^{\prime }$ consideration of the set of terminal histories $\tilde{Z}\left( h\right) \cap \tilde{Z}\left( h^{\prime }\right)$. That is, player $i$ at $h$ cannot impute to $j$ at $h^{\prime }$ consideration of histories which $i$ at $h$ herself has not also considered. On the other hand, there is no reason to suppose that player $i$ at $h$ should incorrectly impute to $j$ at $h^{\prime }$ failure to consider histories that are in fact considered by both $i$ at $h$ and $j$ at $h^{\prime }$.

Higher-order imputations may be similarly constructed. However, given the properties of the perception mapping defined above, it turns out we need only consider second-order imputations.

To avoid the possibility that a player at the end of a second-order imputation is perceived to have reached an empty information set, we extend the No Impossibility condition as follows.³

NI $^{*}$:(No impossibility): For any for any pair of histories $h$ and $h^{\prime }$ in $H$, such that there exists $h^{\prime \prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ for which $h^{\prime \prime }\preceq h^{\prime }$, and with $i=P\left( h\right)$ and $j=P\left( h^{\prime }\right)$, the set of histories $\mathcal I _{\tilde{Z}\left( h\right) }\left( h^{\prime }\right) \cap \mathcal I _{\tilde{Z}\left( h^{\prime }\right) }\left( h^{\prime }\right)$ is not empty.

The concept of a second-order imputation is also useful in considering a player’s anticipation of her own future awareness. If $P\left( h\right) =P\left( h^{\prime }\right)$, then it follows that the awareness imputed by player $P\left( h\right)$ at $h$ to herself at $h^{\prime }$ is given by $\tilde{Z}\left( h\right) \cap \tilde{Z}\left( h^{\prime }\right)$. By properties IN (Information Neutrality) and IA (increasing awareness) of the perception mapping, $h\preceq h^{\prime }\Rightarrow \tilde{Z}\left( h\right) \cap \tilde{Z}\left( h^{\prime }\right) =\tilde{Z}\left( h\right)$. That is, a player cannot anticipate her own future increasing awareness.

We now have all the elements needed to define a game with awareness.

Definition 10

A game with awareness $\mathcal G$ is characterized by the tuple $\left( \Gamma ,\tilde{Z} \left( \cdot \right) \right)$ where $\Gamma =(N\cup \{c\},A,H,P,f^{c}, \mathcal I ,\{v^{i}:i\in N\})$ is the full (maximally aware) extensive-form game the players with perfect recall are actually playing and $\tilde{Z} \left( \cdot \right)$ is the associated perception mapping to admissible sets of terminal histories, that satisfies IN, IA and NI $^{*}$ and encodes the evolution of interactive awareness of the players $i$ in $N$. That is, for each history $h$ in $H$, player $P\left( h\right)$ is aware of the game $\Gamma _{\tilde{Z}\left( h\right) }$. Furthermore, for any pair of histories $h$ and $h^{\prime }$ in $H$, such that there exists $h^{\prime \prime }\in \mathcal I _{ \tilde{Z}\left( h\right) }\left( h\right)$ for which $h^{\prime \prime }\preceq h^{\prime }$, and with $i=P\left( h\right)$ and $j=P\left( h^{\prime }\right)$, $i$ at $h$ imputes to $j$ at $h^{\prime }$ consideration of the set of terminal histories $\tilde{Z}\left( h\right) \cap \tilde{Z}\left( h^{\prime }\right)$.

In a game with awareness $\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$, at the actual history $h$ in the “play” of the game $\Gamma$, player $P\left( h\right)$ is aware of the game $\Gamma _{\tilde{Z} \left( h\right) }$. Her information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ is determined by the set of terminal histories of which she is aware, and which have not been ruled out by the information available to her at $h$. In a standard extensive-form game, the set of terminal histories consistent with available information grows monotonically smaller until a unique terminal history is reached. By contrast, in a game with awareness, players may become aware of new possibilities. Nevertheless, it follows from Lemma  that the game a player perceives herself to be playing at each of her information sets is one of perfect recall, even though becoming aware of new possibilities will in general require her to revise what she had thought was the record of her experience.⁴ Ultimately, the information set must contract as the game approaches the terminal history.

This treatment of differential awareness may be compared to the standard common knowledge assumptions in a game of full awareness. In this case, $\tilde{Z}\left( h\right) =Z$ for all $h$, and the associated game $\Gamma =\Gamma _{\tilde{Z}\left( h\right) }$, for all $h$ in $H$, is a standard extensive-form game. Obviously, this assumption greatly simplifies the analysis for the external modeler and the computational problem facing the players. However, the assumption of common knowledge of the game is exceptionally strong. The approach adopted here represents the most limited possible modification of the full awareness case.

Remark 2

In a slight abuse of notation, for any proposition $p$ and history $h$, and where $i=P\left( h\right)$, we will write $h\models _{\Gamma }b_{i}p$ instead of $h\models _{\Gamma .\tilde{Z}\left( h\right) }b_{i}p$. This simplification reflects the fact that since the restriction $\tilde{Z}\left( h\right)$ applicable at $\,h$ in $\Gamma$ is entirely determined by $h$ and $\mathcal G$, it is redundant to spell it out.

2.4 Behavior rules, strategies, subjective probabilities and equilibrium in games with awareness

In a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$, at each history $h$ in the game, the player $P\left( h\right)$ who is called upon to play at that history selects a randomization defined over $A_{\tilde{Z}\left( h\right) }\left( h\right)$, the actions she thinks are available. A collection of these randomizations constitutes a “rule” for determining the “play” of the game $\Gamma$.⁵

Definition 11

Let $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ be a game with awareness. A behavioral rule $r$ for the players in the game $\Gamma$ is a collection of randomizations over actions $\left( r\left( h\right) :h\in H\text{,} \text{ s.t.} P\left( h\right) \ne c\right)$, where each $r\left( h\right)$ is a probability distribution whose support is a subset of $A_{\tilde{Z}\left( h\right) }\left( h\right)$, the set of actions player $P\left( h\right)$ perceives to be available at her information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$. Denote by $\tau \left( r\right)$ the probability distribution over terminal histories induced by $r$ and the chance assignment $f^{c}$ of nature. The (ex ante) expected value for player $i$ of the play of the game $\Gamma$ associated with the rule $r$ is given by:

$$\begin{aligned} V_{\Gamma }^{i}\left( r\right) =\sum _{h\in Z}\tau \left( r\right) \left[ h \right] v^{i}\left( h\right) \text{.} \end{aligned}$$

(1)

To determine at each history $h$ in the game $\Gamma$ what the player $P\left( h\right)$ will select, we shall impute to that player a “theory” of how she thinks the game will be played, in the form of a strategy profile for the continuation of the game she perceives she is playing at that history. We assume her theory of how the game is being played at that history is the same for any player at any history that goes through that information set who perceives himself to be playing the same game. In particular, this implies that the strategy profile ascribed to a player remains unchanged if her level of awareness at a subsequent information set is unchanged. In addition, we require the strategy a player’s theory ascribes to another player must be consistent with the awareness imputed to that player. Formally, we define a strategy profile for a game with awareness as follows.

Definition 12

Let $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ be a game with awareness. A strategy profile ${\varvec{\beta }}=\left( \beta _{h}:h\in H\right)$ for $\mathcal G$ assigns to each history $h$ a behavioral strategy profile $\beta _{h}$ for the continuation of the game $\Gamma _{\tilde{Z}\left( h\right) }$ from the information set $\mathcal I _{\tilde{Z}\left( h\right) }$ with the consistency properties: for any history $h^{\prime }\in \mathcal I _{\tilde{Z }\left( h\right) }\left( h\right)$ and any history $h^{\prime \prime }$ for which $h^{\prime }\preceq h^{\prime \prime }$:

• 1. if $\tilde{Z}\left( h^{\prime }\right) =\tilde{Z} \left( h^{\prime \prime }\right)$, then the continuation of $\beta _{h^{\prime }}$ from $\mathcal I _{\tilde{Z}\left( h^{\prime }\right) }\left( h^{\prime \prime }\right)$ coincides with $\beta _{h^{\prime \prime }}$;

• 2. for player $P\left( h^{\prime \prime }\right) =j$, the support of $\beta _{h}\left( \mathcal I _{\tilde{Z}\left( h\right) }\left( h^{\prime \prime }\right) \right)$ is a subset of $A_{\tilde{Z} \left( h\right) }\left( h^{\prime \prime }\right) \cap A_{\tilde{Z}\left( h^{\prime \prime }\right) }\left( h^{\prime \prime }\right)$.

Remark 3

Recall the property NI $^{*}$ (No impossibility) of the perception mapping ensures that a player at the end of any second-order imputation is not imputed to have reached an empty information set. Hence, it is always possible for a player to ascribe how another player is playing in a way that is consistent with the game she imputes to her opponent. The property IN (Information Neutrality) in conjunction with the first part of the consistency property for a strategy profile ensures that the “theory” a player holds about how the game is being played at a particular history is the same for all other histories in the same information set.

For a game of common awareness, the strategy profile conforming to the consistency property defines a strategy profile for a standard game. Conversely, any standard behavioral strategy profile for a standard game defines a behavioral strategy profile for the associated game of common awareness.

Next consider a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z} \left( \cdot \right) \right)$, in which, for each $h$ in $H$, either $\tilde{Z}\left( h\right) =Z$ or $\tilde{Z}\left( h\right) =\tilde{Z}\subset Z$, and with $\Gamma _{\tilde{Z}}$ a game of common awareness. Then, whenever $\tilde{Z}\left( h\right) =Z$, the strategy profile defines at information set $\mathcal I \left( h\right)$ a probability measure on $A\left( h\right)$. On the other hand, if $\tilde{Z}\left( h\right) =\tilde{Z }$ with $\Gamma _{\tilde{Z}}$ a game of common awareness, then $\beta _{h}$ is a strategy profile for the continuation of the standard game $\Gamma _{ \tilde{Z}}$ and therefore for each $h^{\prime }$ in $H_{\tilde{Z}}$ that follows from $\mathcal I _{\tilde{Z}}\left( h\right)$, $\beta _{h}\left( \mathcal I \left( h^{\prime }\right) \right)$ defines a probability measure on $A_{\tilde{Z}}\left( h\right) \ \subseteq$ $\ A\left( h\right)$. That is, the randomization over actions imputed by player $P\left( h\right)$ at history $h$ to another player $P\left( h^{\prime }\right)$ at his information set $\mathcal I \left( h^{\prime }\right)$ must be consistent with the game $\Gamma _{\tilde{Z}}$ that the game with awareness at $h$ imputes that player $P\left( h\right)$ imputes to player $P\left( h^{\prime }\right)$ at history $h^{\prime }$.

More generally, in any game with awareness $\mathcal G =\left( \Gamma , \tilde{Z}\left( \cdot \right) \right)$, any strategy profile ${\varvec{\beta } }=\left( \beta _{h}:h\in H\right)$ generates a behavioral rule $r$ for the game $\Gamma$ given by $r\left( h\right) =\beta _{h}\left( \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right) \right)$.

Analogous to standard games (i.e., games of common awareness), given a strategy profile, in order for a player to be able to evaluate her expected continuation payoff from an information set that she would be called upon to play, we also need to specify her subjective beliefs about where in her information set she thinks she is. Thus, we extend the definition of a subjective probability system for a game with awareness as follows.

Definition 13

Let $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ be a game with awareness. A subjective probability system ${\varvec{\mu }}=\left( \mu _{h}:h\in H\right)$ for $\mathcal G$ assigns to each history $h$ in $H$, a probability measure on the set of histories in $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ with the consistency property: for any $h^{\prime },h^{\prime \prime }$ in $H$, if $h^{\prime \prime }\in \mathcal I \left( h^{\prime }\right)$ then $\mu _{h^{\prime }}=\mu _{h^{\prime \prime }}$.

The interpretation of the subjective probability measure $\mu _{h}$ is that at history $h$, the probability that player $i=P\left( h\right)$ assigns to being at the history $h^{\prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ is $\mu _{h}\left( h\right)$. Thus, the consistency condition ensures that subjective probabilities are common across all elements of an information set.

Definition 14

Let $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ be a game with awareness. An assessment for $\mathcal G$ is a pair $\left( {\varvec{\beta },\varvec{\mu } }\right)$ where ${\varvec{\beta }}$ is strategy profile for $\mathcal G$ and ${\varvec{\mu }}$ is a belief system for $\mathcal G$.

Given a strategy profile ${\varvec{\beta }}$ for $\mathcal G$, for each $h$ in $H$ and each $h^{\prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ denote by $\tau _{\Gamma _{\tilde{Z}\left( h\right) }}\left( \beta _{h}|h^{\prime }\right)$ the probability distribution over terminal histories induced by the strategy profile $\beta _{h}$, conditional on being at history $h^{\prime }$ in the information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$. Given the assessment $\left( {\varvec{\beta },\varvec{\mu }}\right)$, we thus have at each $h$ in $H$, player $i=P\left( h\right)$ to whom the perception mapping imputes the game $\Gamma _{\tilde{Z}\left( h\right) }$ perceives the continuation value from her information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ from the play of the game according to the continuation strategy profile $\beta _{h}$ to be:

$$\begin{aligned} V_{\Gamma _{\tilde{Z}\left( h\right) }}^{i}\left( \beta _{h},\mu _{h}\right) =\sum \limits _{h^{\prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right) }\mu _{h}\left[ h^{\prime }\right] \left( \sum _{h^{\prime \prime }\in \tilde{Z}\left( h\right) }\tau _{\Gamma _{\tilde{Z}\left( h^{\prime }\right) }}\left( \beta _{h}|h^{\prime }\right) \left[ h^{\prime \prime } \right] v^{i}\left( h^{\prime \prime }\right) \right) \end{aligned}$$

(2)

Definition 15

Let $\mathcal G$ be a game with awareness. An assessment $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ is sequentially rational for player $i$, if $i$ is playing a “best response” at each of her information sets. That is, for every $h$ in $H$, such that $i=P\left( h\right) :$

$$\begin{aligned} V_{\Gamma _{\tilde{Z}\left( h\right) }}^{i}\left( \beta _{h},\mu _{h}\right) \ge V_{\Gamma _{\tilde{Z}\left( h\right) }}^{i}\left( \left( \hat{\beta } _{h}^{i},\beta _{h}^{-i}\right),\mu _{h}\right), \end{aligned}$$

for every continuation strategy $\hat{\beta }_{h}^{i}$ of $i$ in the continuation of the game $\Gamma _{\tilde{Z}\left( h\right) }$ from the information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$.

The assessment $\left( \varvec{\beta }, \varvec{\mu } \right)$ is sequentially rational if it is sequentially rational for all $i$.

We shall refer to a behavioral strategy profile ${\varvec{\beta }}$ for the game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ as being completely mixed as can be done consistently if for any three histories $h$, $h^{\prime }$ and $h^{\prime \prime }$, such that $h^{\prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ and $h^{\prime }\preceq h^{\prime \prime }$, $\beta _{h}\left( \mathcal I _{\tilde{Z}\left( h\right) }\left( h^{\prime }\right) \right)$ assigns positive probability to every action in $A_{\tilde{Z}\left( h\right) }\left( h^{\prime \prime }\right) \cap A_{\tilde{Z}\left( h^{\prime \prime }\right) }\left( h^{\prime \prime }\right)$. That is, if player $P\left( h\right)$ at $h$ perceives herself to be at the information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ in the game $\Gamma _{\tilde{Z }\left( h\right) }$ and imputes to player $P\left( h^{\prime \prime }\right)$ at his information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h^{\prime \prime }\right)$ in that game that he will perceive himself to be at the information set $\mathcal I _{\tilde{Z}\left( h\right) \cap \tilde{Z} \left( h^{\prime \prime }\right) }\left( h^{\prime \prime }\right)$ in the game $\Gamma _{\tilde{Z}\left( h\right) \cap \tilde{Z}\left( h^{\prime \prime }\right) }$, then each action available in the game $\Gamma _{\tilde{Z }\left( h\right) \cap \tilde{Z}\left( h^{\prime \prime }\right) }$ at the information set $\mathcal I _{\tilde{Z}\left( h\right) \cap \tilde{Z}\left( h^{\prime \prime }\right) }\left( h^{\prime \prime }\right)$ (i.e., each action in $A_{\tilde{Z}\left( h\right) }\left( h^{\prime \prime }\right) \cap A_{\tilde{Z}\left( h^{\prime \prime }\right) }\left( h^{\prime \prime }\right)$) is assigned strictly positive weight by the strategy profile.

Definition 16

Let $\mathcal G$ be a game with awareness. An assessment $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ is consistent if there exists a sequence of $\left( \left( {\varvec{\beta }}^{n}, {\varvec{\mu }}^{n}\right) \right) _{n=1}^{\infty }$ that converges pointwise to $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ and has the property that each strategy profile $\beta ^{n}$ is as completely mixed as can be done consistently and that each belief system $\mu ^{n}$ is derived from $\beta ^{n}$ using Bayes’ rule.

Thus, we have all the elements to extend the concept of a sequential equilibrium to a game with awareness.

Definition 17

Let $\mathcal G$ be a game with awareness. An assessment $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ is a sequential equilibrium if it is sequentially rational and consistent.

We prove in the Appendix the following.

Proposition 1

A sequential equilibrium exists for any game with awareness.

Sequential equilibrium is not the only equilibrium concept that might be considered for games with awareness. However, we view it as is a sensible choice because in a game with awareness players will, in general, have the experience of reaching information sets that they previously considered as off-equilibrium. This experience can arise because other players were acting on the basis of a different perception of the game from the one imputed to them. It therefore makes sense for players to confine attention to strategies that prescribe reasonable behavior at every information set at which they may move, and not merely at those that occur with positive probability in the equilibrium of the game they perceive themselves to be playing.

Proposition 1 demonstrates existence, but not uniqueness of sequential equilibrium. This limitation is not specific to games with awareness. To the best of our knowledge, there is no general characterization of uniqueness conditions for sequential equilibrium. For simplicity, however, we will confine our attention to the case of games in which there exists a unique equilibrium for the maximal game $\Gamma$ and for all restrictions of $\Gamma$.

2.5 Example

To illustrate the structure of a game with awareness, we adapt the speculative trade example of Heifetz et al. (2006). In this example, a buyer (player 1) and an owner (player 2) may contract the sale of the owner’s firm at a price of $1$. The value of the firm depends on two contingencies: the possibility of a lawsuit which would reduce the value by $L$ and a business opportunity which would increase the value by $G$. If neither occurs, the value remains unchanged at $1$. We represent the maximal game $\Gamma$ as follows. Nature has two initial moves determining whether the lawsuit and business opportunity arise. Before learning about Nature’s moves, the buyer chooses whether to make an offer of $1$. If an offer is made, the owner chooses whether to accept it, also before learning about Nature’s moves. At the terminal nodes, players receive their net payoffs, and Nature’s moves are revealed.

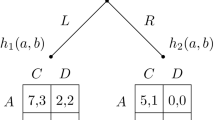
We first describe the full or maximal awareness game. The initial history is $\left\langle {}\right\rangle$. Nature’s first move is a choice from the set $\left\{ \alpha _{n},\alpha _{0}\right\}$ (innovation or null action). Let $p\in \left( 0,1\right)$ denote the probability Nature chooses $\alpha _{n}$. Nature’s second move is a choice from the set $\left\{ \alpha _{\ell },\alpha _{0}\right\}$ (lawsuit or null action). Let $q\in \left( 0,1\right)$ denote the probability Nature chooses $\alpha _{\ell }$. There are now four histories $\left\langle \alpha _{n},\alpha _{\ell }\right\rangle$, $\left\langle \alpha _{n},\alpha _{0}\right\rangle$, $\left\langle \alpha _{0},\alpha _{\ell }\right\rangle$, $\left\langle \alpha _{0},\alpha _{0}\right\rangle$, forming an information set which we shall denote $\mathbf{{I}}_{1}.$ At $\mathbf{{I}}_{1}$, player 1 chooses from the set $\left\{ \alpha _{1},\alpha _{0}\right\}$ (offer 1 or null action). If 1 chooses $\alpha _{0}$, the game terminates. If 1 chooses $\alpha _{1}$ the information set becomes $\mathbf{{I}}_{2}=\left\{ \left\langle \alpha _{n},\alpha _{\ell },\alpha _{1}\right\rangle ,\left\langle \alpha _{n},\alpha _{0},\alpha _{1}\right\rangle ,\left\langle \alpha _{0},\alpha _{\ell },\alpha _{1}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{1}\right\rangle \right\}$ and 2 chooses from the set $\left\{ \alpha _{A},\alpha _{R}\right\}$ (accept or reject the offer). The maximal game is illustrated in Fig. 1.

Fig. 1

The maximal game $\Gamma$ which starts at the chance node in the center

As in Heifetz et al. (2006), we suppose that the buyer is unaware of the possibility of a lawsuit while the seller is unaware of the possibility of an innovation. Thus, at each history $h$ in $\mathbf{{I}}_{1}$, the buyer only considers the terminal histories in which the lawsuit does not arise. That is,

$$\begin{aligned} \tilde{Z}\left( h\right)&= \tilde{Z}_{1}=\left\{ \left\langle \alpha _{n},\alpha _{0},\alpha _{0}\right\rangle ,\left\langle \alpha _{n},\alpha _{0},\alpha _{1},\alpha _{A}\right\rangle ,\left\langle \alpha _{n},\alpha _{0},\alpha _{1},\alpha _{R}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{0}\right\rangle ,\right.\\&\left.\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{A}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{R}\right\rangle \right\} \text{,} \end{aligned}$$

for all $h$ in $\mathbf{{I}}_{1}$.

Denoting the game of which the buyer is aware at any history $h$ in $\mathbf{{I}}_{1}$ by $\Gamma ^{1}$, we see that it is obtained from the fully aware game $\Gamma$ by deleting all histories containing nature’s second move $\alpha _{\ell }$.

Similarly, at each history $h$ in $\mathbf{{I}}_{2}$, the owner only considers the terminal histories in which the business opportunity does not arise. That is,

$$\begin{aligned} \tilde{Z}\left( h\right)&= \tilde{Z}_{2}=\left\{ \left\langle \alpha _{0},\alpha _{\ell },\alpha _{0}\right\rangle ,\left\langle \alpha _{0},\alpha _{\ell },\alpha _{1},\alpha _{A}\right\rangle ,\left\langle \alpha _{0},\alpha _{\ell },\alpha _{1},\alpha _{R}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{0}\right\rangle ,\right.\\&\left.\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{A}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{R}\right\rangle \right\} , \end{aligned}$$

for all $h$ in $\mathbf{{I}}_{2}$.

Denoting the game of which the owner is aware at any history $h$ in $\mathbf{{I}}_{2}$ by $\Gamma ^{2}$, we see that it is obtained from the fully aware game $\Gamma$ by deleting all histories containing nature’s first move $\alpha _{n}$. The games are illustrated in Figs. 2 and 3, respectively.

Fig. 2

$\Gamma ^{1},$ the game the buyer perceives he is playing, which starts at the chance node in the middle

Fig. 3

$\Gamma ^{2},$ the game the owner perceives she is playing, which starts at the chance node on the left

Both parties impute to the other a restriction of their own game. The buyer is unaware of the possible lawsuit and assumes the owner to be unaware of the possible innovation (at all non-terminal histories), while the converse is true for the owner. Hence, each imputes the other only considers the terminal histories

$$\begin{aligned} \tilde{Z}_{1}\cap \tilde{Z}_{2}=\left\{ \left\langle \alpha _{0},\alpha _{0},\alpha _{0}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{A}\right\rangle ,\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{R}\right\rangle \right\} \text{.} \end{aligned}$$

These lead to the same game $\Gamma ^{3}$, as illustrated in Fig. 4 and which is a game of common awareness.

Fig. 4

$\Gamma ^{3}$, the game of common awareness for the two players, which starts at the chance node on the left

Heifetz et al. (2006) propose a dominance principle that is sufficient to ensure that trade takes place in this model. In our model this corresponds to a sequential equilibrium $\left( {\varvec{\beta } }^{*}, {\varvec{\mu }}^{*}\right)$, in which

$$\begin{aligned} \beta _{\,<>}^{*}\left( \mathbf{{I}}_{1}\right) \left[ \alpha _{1}\right]&= 1\text{,} \quad \beta _{\,<>}^{*}\left( \mathbf{{I}}_{2}\right) \left[ \alpha _{A}\right] =1 \\ \beta _{h}^{*}\left( \mathbf{{I}}_{1}^{1}\right) \left[ \alpha _{1}\right]&= 1\text{,} \quad \beta _{h}^{*}\left( \mathbf{{I}}_{2}^{1}\right) \left[ \alpha _{A}\right] =1, \text{for all}\, h \text{ in} \, \mathbf{{I}}_{1} \\ \beta _{h}^{*}\left( \mathbf{{I}}_{2}^{2}\right) \left[ \alpha _{A}\right]&= 1, \text{for all}\, h\, \text{ in} \,\mathbf{{I}}_{2}\text{.} \end{aligned}$$

$$\begin{aligned}&\mu _{<>}^{*}[<>]=1 \\&\mu _{h}^{*}\left[ \left\langle \alpha _{n},\alpha _{0}\right\rangle \right] =p\text{,} \mu _{h}^{*}\left[ \left\langle \alpha _{0},\alpha _{0}\right\rangle \right] =1-p\text{,} \text{ for} \text{ all} h \text{ in} \mathbf{{I}}_{1} \\&\mu _{h}^{*}\left[ \left\langle \alpha _{0},\alpha _{\ell }\right\rangle \right] =q\text{,} \mu _{h}^{*}\left[ \left\langle \alpha _{0},\alpha _{0}\right\rangle \right] =1-q\text{,} \text{ for} \text{ all} h \text{ in} \mathbf{{I}}_{2} \end{aligned}$$

To check sequential rationality, notice that at $\mathbf{{I}}_{1}^{1}=\mathbf{{I}}_{1}\cap H_{\Gamma ^{1}}$ (in $\Gamma ^{1}$) the action $\alpha _{0}$ (no offer) leads to a payoff of zero for the buyer in all histories. The action $\alpha _{1}$ yields a net payoff of $G$ in the history $\left\langle \alpha _{n},\alpha _{0},\alpha _{1},\alpha _{A}\right\rangle$ and a net payoff of zero in all other histories (those where the innovation is not realized or the owner rejects the offer).

For the owner at $\mathbf{{I}}_{2}^{2}=\mathbf{{I}}_{2}\cap H_{\Gamma ^{2}}$ (in $\Gamma ^{2}$) the action $\alpha _{A}$ yields a sure net payoff of $0$, while $\alpha _{R}$ yields a net payoff of $-L$ for the history $\left\langle \alpha _{0},\alpha _{\ell },\alpha _{1},\alpha _{R}\right\rangle$ and $0$ for $\left\langle \alpha _{0},\alpha _{0},\alpha _{1},\alpha _{R}\right\rangle$.⁶

3 Inductive reasoning about unawareness

We now address the central question for any account of limited awareness: In what sense can an individual reason, from experience or observation, about the proposition that there exist propositions of which she is unaware?

We begin by extending the language to include existential propositions of the general form “there exists a proposition $p$ with property $\theta$.” Our primary interest is on existential propositions related to awareness, most notably, “there exists a proposition $p$ of which I am unaware.” Our first result, Proposition 2, is negative. We show that, within the modal-logical representation of knowledge developed above, an individual can never believe that there exist propositions of which she is unaware. In view of Proposition 2, we must consider whether a boundedly rational, but nevertheless sophisticated, individual might be able to reason about their own limited awareness, using methods outside the scope of the modal-logical framework considered thus far.

As we have argued above, an individual’s understanding of their own unawareness cannot be represented within the context of a semantic-syntactic game representation, even when the game itself is extended to allow for differential awareness. The kind of reasoning that can be represented in such a context may broadly be described as “deductive.” That is, an initial set of premises (the game tree and prior probabilities in the semantic rendition, the set of known propositions, tautologies and implications in the syntactic rendition) is combined with new information (signals in the semantic rendition, learning about the truth values of propositions in the syntactic rendition) to yield a new and improved model. Given sufficient information, the realized history of the game and the truth value of all propositions in the associated language may be determined.

The deductive mode of reasoning associated with games of common awareness and the associated modal logic of knowledge appear to offer the logical certainty of conclusions derived, in accordance with stated axiomatic properties, from known premises. In a game with awareness, however, this certainty is spurious. As we have seen, a proposition may be true in all states an individual considers possible, but nevertheless false in reality. Decision procedures that presume that logical certainty can be attained are likely to yield poor outcomes.

To address this problem, we need to answer two questions.

• *   First, how can, or should, individuals reason about their own unawareness?

• *   Second, if this reasoning supports the conclusion that the individual is unaware of some relevant contingencies, how should she act?

To address the first question, we need to consider how an individual might reach either a positive or a negative answer to the question: “Do there exist relevant propositions of which I am unaware?” One answer (though not the only one) is to consider inductive reasoning, based on generalization of past experience.

Consider first the situation of an individual who is to move in an extensive-form game with awareness. Under the assumption of increasing awareness (and assuming it holds non-trivially), the individual’s previous experience includes a number of “surprises,” that is, discoveries of possible terminal histories of the game she had previously not considered. Inductive reasoning supports the judgement “if I have been surprised in the past, I may be surprised in the future.”

Taken to an extreme, such reasoning could be paralyzing (a point made by critics of the precautionary principle, discussed below). Since decisions cannot be avoided, decision makers must adopt some combination of heuristics and formal rules to guide their choices.

In particular, individuals may use inductive criteria for identifying a “small world,” in which it is reasonable for players to disregard the possible existence of relevant unconsidered contingencies, and act on the basis of Bayesian decision theory applied to the game they perceive.

Inductive reasoning about games with awareness may therefore lead individuals to conjecture that either they are or they are not aware of all relevant contingencies. As will be shown by Proposition 2 below, such reasoning cannot be encompassed by the usual modal logic of awareness, if unawareness is represented, as it is here, by a failure to consider some possible histories of the game.

However, it can be represented using a more general syntactic-semantic framework, such as that put forward by Walker (2012), with precisely this kind of reasoning in mind. Walker suggests a two-stage evaluation framework for propositions, with the first “subjective” stage incorporating the decision maker’s inductively derived conjectures about their awareness and the second “objective” stage, incorporating the objective evaluation of an external observer.

Walker develops this approach with reference to the Fagin and Halpern (1988) approach in which unawareness is modelled in terms of a distinction between implicit and explicit awareness, so that a decision maker may not be (explicitly) aware of a proposition even though they are aware of semantically equivalent propositions. However, no changes to the central idea are required to apply the idea in the present context. The main difference is that whereas Walker’s syntax, developed in a static setting, includes only the single string corresponding to the sentence “I am aware of all propositions,” our dynamic, extensive-form approach would require subjective evaluation of a larger class of sentences of the general form “at my current position (in the game) I am aware of all relevant propositions.”

4 The existential quantifier, existential propositions and unawareness

The representation of differential awareness developed thus far is fairly standard. The central unresolved issue in the literature is how to deal with the fact that players may be conscious of their own bounded awareness, and of the possibility that others may be aware of histories (or propositions) of which they themselves are unaware. We note that from the definition of the belief operator for the restricted game a player has access to, that player cannot believe that they are unaware of particular propositions $p$. On the other hand, players may believe (in fact, know) that other players are unaware of some particular propositions and might conjecture that the same is true for themselves. Thus, we must consider interpretations of the statement “there exist propositions/histories of which I am unaware” that lie outside the syntactic-semantic framework developed so far.

In a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z} \left( \cdot \right) \right)$ although the language $\mathcal L _{\Gamma _{ \tilde{Z}\left( h\right) }}$ available to player $P\left( h\right)$ at the history $h$ is sufficiently expressive to describe the restricted game $\Gamma _{\tilde{Z}\left( h\right) }$ she perceives to be playing, it is inadequate to describe propositions she might reasonably entertain about the full awareness game $\Gamma$ and its associated language $\mathcal L _{\Gamma }$. The approach adopted here begins by extending the languages $\{ \mathcal{L }_{\Gamma _{{\tilde{Z}}\left( h\right) }}:h\in H\}$ to allow for reasoning about the existence of propositions as follows. We include an existential quantifier $\exists$, used in conjunction with a formula for substitution to produce propositions of the form

$$\begin{aligned} \exists q\in \mathcal L _{\Gamma } \text{ such} \text{ that} \left( \theta \left( q\right) \right) \text{,} \end{aligned}$$

(3)

where $\theta \left( q\right)$is a Boolean combination of the free proposition $q$ and propositions in $\mathcal L _{\Gamma }$. We denote by $\theta \left( q|p\right)$ the proposition obtained by replacing all instances of $q$ with $p$. For compactness, in the formal analysis to follow, the existential proposition in (3) will be denoted by $q_{\exists }\theta$. Then $h\models _{\Gamma }q_{\exists }\theta$ if and only if there is some $p\in \mathcal L _{\Gamma }$ such that $h\models _{\Gamma }\theta \left( q|p\right)$.

As is standard, we will define the derived universal operator $\forall$ by

$$\begin{aligned} p_{\forall }\theta \Leftrightarrow \lnot q_{\exists }\lnot \theta \end{aligned}$$

That is, property $\theta$ holds for all $p$ if there does not exist $q$ such that $\lnot \theta \left( q\right)$ holds.

Example 1

As an illustration, fix a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ and consider a history $h$, for which $\tilde{Z}\left( h\right) \subset \tilde{Z}$. For a given $p\in \mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}$, the extended language contains such propositions as,

$$\begin{aligned} \exists q\in \mathcal L _{\Gamma } \text{ such} \text{ that} \left( \left( q\Rightarrow p\right) \wedge \lnot \left( p\Rightarrow q\right) \right) \end{aligned}$$

which we may interpret as saying that there is some (non-equivalent) proposition $q$ in the richer language $\mathcal L _{\Gamma }$ that implies $p$. For example, in a criminal investigation, the fact that a person is classed as a suspect typically means that if some additional evidence were obtained, that person’s guilt could be inferred. However, investigators will not, in general, know the exact nature of the evidence they are looking for. The evidence could be either propositional ($X$ was at the scene of the crime) or epistemological ($X$ knew that the gun was loaded).

We may therefore examine a players’ beliefs about her own awareness by considering the proposition $b_{i}\left( q_{\exists }u_{i}q\right)$, read as “player $i$ believes there exists a proposition of which she is unaware.”

Proposition 2

Fix a game with awareness $\mathcal G =\left( \Gamma , \tilde{Z}\left( \cdot \right) \right)$. For all $h\in H$, and $i=P(h)$,

$$\begin{aligned} h\vDash \!\!\!\!\!/\, _{\Gamma ,\tilde{Z}}b_{i}\left( q_{\exists }u_{i}q\right) \end{aligned}$$

That is, players can never believe they are unaware of anything.

Proof

By Lemma 3, for any particular choice of $p\in \mathcal L _{\Gamma },h\vDash \!\!\!\!\!/\, _{\Gamma ,\tilde{Z}}b_{i}u_{i}p$

Observe that

$$\begin{aligned} q_{\exists }u_{i}q\Leftrightarrow \bigvee \limits _{p\in \mathcal L _{\Gamma }}u_{i}p \end{aligned}$$

Since the set $\mathcal L _{\Gamma }$ is countable, it may be placed in 1–1 correspondence with the natural numbers $p_{1},\ldots , p_{n}\ldots$. Define

$$\begin{aligned} \left( q_{\exists }u_{i}q\right) _{N}\equiv \bigvee \limits _{n=1..N}u_{i}p_{n} \end{aligned}$$

and observe by induction on $N$ that

$$\begin{aligned} h\vDash \!\!\!\!\!/\,_{\Gamma ,\tilde{Z}}b_{i}\left( q_{\exists }u_{i}q\right) _{N} \end{aligned}$$

Since

$$\begin{aligned} q_{\exists }u_{i}q\Leftrightarrow \bigvee \limits _{N}\left( q_{\exists }u_{i}q\right) _{N} \end{aligned}$$

the desired result follows. $\square$

Proposition 2 shows that given the specification of $\mathcal L _{\Gamma _{\tilde{Z}(h) }}$, including the existential quantifier $\exists$ which generates the set of existential propositions, the richer language $\mathcal L _{\Gamma }$ is not expressive enough to allow valid statements of the form “player $i$ believes that there exists some proposition $q\in \mathcal L _{\Gamma }$ of which he is currently unaware.” This is not surprising. To say that a player believes that there exist events of which he is unaware suggests, in some sense, that he is aware of those events, which might be seen as violating the spirit of what it means to be unaware of something.⁷ On the other hand, to the extent that players understand the structure of a game with awareness, that understanding must encompass the possibility that their own awareness is incomplete. This apparent contradiction suggests the need to consider modes of reasoning going beyond the semantic-syntactic model considered thus far. We argue below that the deductive reasoning characteristic of the semantic-syntactic model must be combined with inductive reasoning about the structure of the model itself.

4.1 Historical induction and induction over players

The most commonly used alternative to deductive reasoning is reasoning based on induction from experience or observation. The general principle of induction considered in the philosophical literature states that observations of members of some set $S$, all of which satisfy some property $\phi$, provide inductive support for the proposition “All members of set $S$ satisfy property $\phi$.” For example, if a number of ravens are observed to be black, and none are observed to be any other color, we derive inductive support for the proposition “All ravens are black.”

As the famous example of black swans shows, inductive reasoning is never conclusive. It is easy to define propositions that have always been true, but will cease to be true at some point in the future, either because they inherently involve time dating (person $i$, now aged 20, has always been younger than 21) or because the properties to which they refer change over time (US population has always been less than 320 million). Moreover, it is possible to derive inductive support for two or more propositions that may be logically inconsistent. For example, it is common to use inductive arguments to predict the outcomes of Presidential elections (e.g., that no incumbent president has been reelected if his approval rating is below $x$, or that incumbents are always reelected if the economy has improved during their term of office). It will often be the case that two such inductive arguments will point in opposite directions.

Under conditions of bounded rationality, however, no system of reasoning is absolutely reliable. Moreover, a judgement that it is appropriate to use deductive reasoning in some particular context must be based on some prior process of reasoning that is not itself deductive. So, boundedly rational players may find it appropriate to employ a mixture of inductive and deductive reasoning.

We begin by considering reasoning based on induction from experience (historical induction). Informally, the principle of historical (or temporal) induction states that if a proposition has been found to be true in many past instances, this fact provides support for belief that it will hold true in the future. For example, the fact that the proposition “the sun will rise tomorrow” was true yesterday, the day before and the day before that and so on provides inductive support for the belief that the same proposition is true today.

Formally, we state it as follows.

Definition 18

(support by historical induction) Fix a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ and a history $h$, and let $i=P\left( h\right)$. Suppose that for some proposition $p\in \mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}$,

$$\begin{aligned} h\models _{\Gamma }b_{i}wp\wedge \lnot b_{i}w\lnot p \end{aligned}$$

then $h\models _{\Gamma }t_{i}p$ [read as “at $h$ player $i$ regards $p$ as supported by historical induction”].

That is, suppose at history $h$ that player $i$ believes $p$ to have been true at some past history and does not believe $p$ to have been false for any past history, then $i$ regards $p$ as supported by historical induction.

In interactive games, the principle of induction may also be applied to reasoning about other players. In the application here, the sets to which induction is to be applied will consist of the set of players $N$. If player $i$ believes that some proposition is true for all other players, then induction suggests that the same proposition is true for $i$.

To formalize this idea in our notation, we define the following.

Definition 19

(support by induction over others) Fix a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ and a history $h$, and let $i=P\left( h\right)$. Let $\theta \left( \tilde{j} \right)$ be a Boolean combination of propositions in $\mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}$ and a free variable $\tilde{j}$, defined as an element of the set of players $N$, such that $\theta \left( \tilde{j}\right)$ is the proposition in which each instance of $\tilde{j}$ in $\theta \left( \cdot \right)$ is replaced by $j$. Suppose that, for all $j\ne i$

$$\begin{aligned} h\models _{\Gamma }b_{i}\theta \left( j\right) \end{aligned}$$

Then, $h\models _{\Gamma }n_{i}\theta \left( i\right)$ [read as “at $h$ player $i$ regards $\theta \left( i\right)$ as supported by induction over the set of players $N-\{i\}$”]

Thus, players can use their observations of others to draw conclusions about themselves that cannot necessarily be reached by deductive reasoning.

4.2 Inductive reasoning, awareness and unawareness

Our account of historical inductive reasoning about unawareness has a structure similar to that of more familiar examples of historical induction. Over time, players become aware of propositions that, previously, they have not considered. Thus, at any history $h$, players know that there exist propositions of which they were unaware at some previous information set. That is, they know that the existential proposition “there exists a proposition of which I am unaware” was true at a previous information set. Indeed, they know that this existential proposition has been true at all past histories, except perhaps recent histories in a period in which no new propositions have been discovered. Hence, the proposition that the future, like the past, will be characterized by the discovery of new propositions is supported by induction.⁸

On the other hand, players also learn positive lessons about their ability to understand particular subproblems in larger decision problems. So, they may become confident, when they perceive a particular problem to be of limited complexity, that they will not be surprised by becoming aware of unconsidered propositions relevant to their decision. The most important case, for our purposes, will be the choice of a strategy in the continuation of a game from some information set.

Suppose that for $h^{\prime }\prec h$, player $i$ becomes aware of previously unconsidered propositions in the course of the partial history from $h^{\prime }$ to $h$, so that $\mathcal L _{\Gamma _{\tilde{Z}\left( h^{\prime }\right) }}\subset \mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}$ where the inclusion $\subset$ is strict. Then for propositions $q$ $\in \mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}-\mathcal L _{\Gamma _{ \tilde{Z}\left( h^{\prime }\right) }}$ we have $h^{\prime }\models _{\Gamma }u_{i}q$ and $h\models _{\Gamma }a_{i}q$, so that $h\models _{\Gamma }wu_{i}q$. Further, these evaluations hold for any $\tilde{h}\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$, so that $h\models _{\Gamma }b_{i}a_{i}q$ and $h\models _{\Gamma }b_{i}wu_{i}q$. That is, at history $h$, the player (correctly) believes that there exist propositions of which she is now aware, but was unaware in the past.

We have established that player $i$ at $h$ cannot express and therefore cannot believe (in the modal-logical sense of $b_{i}$) propositions of the form $\exists q\in \mathcal L _{\Gamma }:u_{i}q$. Nevertheless, given past experience of discovery, it seems reasonable to suppose that the player may judge such propositions to be an appropriate basis for actions and decisions. Given the dynamic temporal structure of the model developed here, it is natural to consider whether historical/temporal induction can be used as a basis for such judgements. Our next result provides a positive answer to this question.

Proposition 3

Fix a game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ that displays non-trivial increasing awareness for $i$ at $h$. Then $h\models _{\Gamma }t_{i}\left( q_{\exists }u_{i}q\right)$.

Proof

By non-trivial increasing awareness for $i$ at $h$, there exists $h^{\prime }\prec h$, in which $\mathcal L _{\Gamma _{\tilde{Z}\left( h^{\prime }\right) }}\subset \mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}$. Hence, for a proposition $p$ $\in \mathcal L _{\Gamma _{\tilde{Z}\left( h\right) }}-\mathcal L _{\Gamma _{\tilde{Z}\left( h^{\prime }\right) }}$  we have $h\models _{\Gamma }a_{i}p$ and $h^{\prime }\models _{\Gamma }u_{i}p$, so that $h\models _{\Gamma }wu_{i}p$. By IN (information neutrality) these evaluations hold for all $\tilde{h}\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$, so that $h\models _{\Gamma }b_{i}\left( q_{\exists }u_{i}q\right)$ holds. From proposition 2 it follows that $q_{\exists }u_{i}q$ can never known to be false at any $h^{\prime }\prec h$; hence, $h\models _{\Gamma }\lnot b_{i}w\left( \lnot \left( q_{\exists }u_{i}q\right) \right)$ holds as well, implying $h\models _{\Gamma }t_{i}\left( q_{\exists }u_{i}q\right)$ as required. $\square$

Informally, given non-trivial increasing awareness, the player believes at $h$ that, for at least some past history, the proposition $q_{\exists }u_{i}q$ was true. On the other hand, this proposition can never be known false. Hence, the player judges the proposition that her awareness is incomplete is supported by historical induction.

Proposition 4

Fix a two-player game with awareness $\mathcal G =\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$ such that the restricted game $\Gamma _{\tilde{Z} \left( h\right) }$ is not a game of common awareness. Then $h\models _{\Gamma }n_{i}\left( q_{\exists }u_{i}q\right)$

Proof

Let $i=P\left( h\right)$, and denote the other player by $j$. Since $\Gamma _{\tilde{Z}\left( h\right) }$ is not a game of common awareness, $\exists h^{\prime }\in H_{\tilde{Z}\left( h\right) }$, with $P\left( h^{\prime }\right) =j$, such that $\Gamma _{\tilde{Z}\left( h^{\prime }\right) \cap \tilde{Z}\left( h\right) }\sqsubset \Gamma _{\tilde{Z}\left( h\right) }$. Hence, $h\models _{\Gamma }n_{i}\left( q_{\exists }u_{j}q\right)$. But as there are only two players, this means that $h\models _{\Gamma }n_{i}\left( q_{\exists }u_{k}q\right)$ holds for (all) $k\ne i$ which in turn implies $h\models _{\Gamma }n_{i}\left( q_{\exists }u_{i}q\right)$ as required. $\quad \square$

Proposition 4 is similar in its structure to Proposition 3. Given the belief on the part of $i$ that $j$ is unaware of some propositions, inductive reasoning supports the proposition that $i$ is also unaware of some propositions.

If the future and past selves are considered as other agents, there is a natural linkage between this idea and that of historical induction. The games perceived by the player $P\left( h\right)$ in the past were restrictions of the game she currently perceives to be playing, and this is known to her at $h$. Similarly, other players from player $P\left( h\right)$ ’s perspective at $h$ must be imputed to perceive games that are restrictions of $\Gamma _{\tilde{Z}\left( h\right) }$.

In summary, although the representation of a game with awareness presented here does not allow for knowledge of unawareness in the standard modal logical, inductive reasoning and symmetry arguments can provide a basis for a judgement that there exist unconsidered possibilities of which other players may be aware.

On the other hand, in a finite extensive game, players eventually reach a terminal history, at which point they are aware of the full history of the game, at least insofar as it is relevant to the payoff they receive. The fact that the game includes unrealized histories of which the player may remain unaware is no longer relevant.

This point may be extended to suggest an inductive basis for identifying a “small world,” in which it is reasonable for players to disregard the possible existence of unconsidered contingencies, and acts on the basis of Bayesian decision theory applied to the game they perceive. The crucial requirement for a small world is not that the decision maker should be aware of all possible contingencies (this requirement can never be met) but that she should be aware of all contingencies relevant to the outcome of a particular decision. This condition is trivially (but unhelpfully) satisfied at any terminal history of a game, since this is the point at which the outcome is actually realized and players receive their payoffs.

More generally, given that unawareness arises from bounded rationality, it seems reasonable to suppose that the more complex the game, the more likely it is that there exist unconsidered contingencies. Further, for a history $h$, the more complex the continuation of the game from the information set the player perceives to be in at $h$, the more likely it is that there exist unconsidered contingencies. Since games that have reached a terminal history are minimally complex in this sense, it seems plausible to argue that as a game (as perceived by the player) “approaches the end,” it becomes easier for the player to consider all payoff-relevant contingencies.

Based on their past experience of the game (or, not modelled here, drawing on experience of similar games), players may reason inductively as follows:

“In the past, I have found myself able to consider all relevant possibilities that might arise in the next $n$ moves. That is, previously unforeseen contingencies have come to my attention at least $n$ moves before they were actually realized. Hence, if the continuation of the game I now perceive as relevant to my choices will end in no more than $n$ moves, induction supports the conclusion that I am aware of all relevant contingencies.”

We begin by defining a proposition $p$ as relevant (denoted $\rho _{i}p)$ at some information set $\mathcal I \left( h\right)$ if the truth or falsity of $p$ affects the continuation value of the game at $\mathcal I \left( h\right)$. We can now formalize the proposition that player $i$ is aware of all relevant propositions at $h$ as

$$\begin{aligned} \forall p\left( \rho _{i}p\Rightarrow a_{i}p\right) \end{aligned}$$

(4)

If 4 holds at $\mathcal I \left( h\right),$ the continuation of the game at $\mathcal I \left( h\right)$ may be regarded as a “small world” in the sense of Savage.

Next we need a measure of the complexity of the continuation of the game. There is a large literature on the complexity of games, and a variety of measures have been proposed (state-space complexity, game tree size, decision complexity and so on). These measures are developed for games of full awareness (and mostly for games of perfect information). Fortunately for our purposes, we require only that the complexity measure should satisfy some elementary properties.

We will use $\xi _{\Gamma }\left( \mathcal I \right)$ to describe a complexity measure of the continuation of the game $\Gamma$ from the information set $\mathcal I$ and impose the properties:

C.1. Zero property: The measure should take the value zero at terminal histories.

C.2. Declining with learning: For any pair of information sets $\mathcal I$ and $\mathcal I ^{\prime }$ in $\Gamma$, $\mathcal I \ne \mathcal I ^{\prime }$, and $P\left( h\right) =P\left( h^{\prime }\right) =i$ for all $h\in \mathcal I$, all $h^{\prime }\in \mathcal I ^{\prime }$ and some $i\in N$, if there exists $h\in \mathcal I$ and $h\in \mathcal I ^{\prime }$ such that $h\preceq h^{\prime }$ then $\xi _{\Gamma }\left( \mathcal I \right) >\xi _{\Gamma }\left( \mathcal I ^{\prime }\right)$.

C3. Increasing with awareness. If $\Gamma \sqsubseteq \Gamma ^{\prime }$, then $\xi _{\Gamma ^{\prime }}\left( \mathcal I ^{\prime }\right) \ge \xi _{\Gamma }\left( \mathcal I \right)$ for any $\mathcal I \subseteq \mathcal I ^{\prime }$.

Property C.1 requires that all terminal histories are of equal and minimal complexity. Within a given game, property C.2 entails that the complexity of the continuation game must decline whenever a player makes a move (thereby eliminating some possible histories for that player). Property C.3, on the other hand, requires that increasing awareness will, in general, increase the complexity of the game.

We propose the following rule, which may be justified by historical induction over previous games.

Consider the following inductive principle

Small World Principle: Treat the proposition $\forall p\left( \rho _{i}p\Rightarrow a_{i}p\right)$ as inductively justified whenever $\xi _{\Gamma _{\tilde{Z}\left( h\right) }}\left( \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right) \right) \le \xi ^{*}$ for some constant $\xi ^{*}$.

The Small World Principle cannot be guaranteed to avoid surprises. Sophisticated players will understand this by virtue of Proposition 3 on inductive justification of unawareness. Nevertheless, use of the Small World Principle for appropriate choices of $\xi ^{*}$ may lead to the adoption of ecologically rational heuristics, in a sense that will be made precise below.

A related approach may be applied to reasoning about the awareness of other players. In general, considerations of symmetry justify the conclusion that if $i$ is aware of possibilities of which $j$ is unaware, the converse is also true. In the language of complexity, we have no general reason to suppose that $\xi _{i}^{*}$ is either greater than or less than $\xi _{j}^{*}.$ But in specific cases, $i$ may indeed be more capable of reasoning about the problem at hand, so that $\xi _{i}^{*}>\xi _{j}^{*}.$ In this case, $i$ may conclude that she is aware of all relevant possibilities even though $j$ is not.

4.3 Syntax and semantics of inductive reasoning about awareness

Space does not permit a full syntactic rendition of the model described above, in which players hold inductively justified beliefs about their own awareness or lack of it. Such a rendition has been developed by Walker (2012). In Walker’s rendition, the agent’s beliefs about whether or not she is fully aware in any state (or history) depend on a conjecture about awareness that does not require a comparison between her actual awareness and the domain of “things to be aware of.” As Walker observes, a process of inductive reasoning such as that developed here provides a natural basis for beliefs about whether or not the agent is fully aware of all relevant propositions, leaving beliefs about particular propositions to be determined by the standard process of deduction from what is true in states that are deemed possible given the available information set.

Walker develops this two-stage structure in detail and derives a semantic structure corresponding to a language in which the string (in our notation) $q_{\forall }a_{i}q$ stands for the claim “the agent is fully aware.”⁹ Walker shows that appropriate axiomatizations for this language are sound and complete for semantic structures in which agents’ beliefs about their awareness may be supposed to be derived from inductively justified conjectures.

Walker’s approach may be adapted to the extensive-form setting of the present problem. In the context of an extensive-form game, what matters is not awareness of all propositions, but awareness of all relevant propositions, as defined above. As shown above, player $i$ can reach a subjective judgement, based on inductive reasoning, as to whether they are, or are not, aware of all relevant contingencies at any history $h$ where $P\left( h\right) =i$, that is, whether $h\models \forall p\left( \rho _{i}p\Rightarrow a_{i}p\right)$. This enables us to define a semantic structure incorporating reasoning about awareness.

Now following the approach of Walker (2012) (but with a change of notation to fit our extensive-form game model), we define the subjective interpretation relation $\models _{\Gamma }^{*}$ which coincides with the objective relation $\models _{\Gamma }$ except for propositions regarding beliefs about awareness. The critical change is that the interpretation relation $h\models _{\Gamma }^{*}b_{i}\left( \forall p\left( \rho _{i}p\Rightarrow a_{i}p\right) \right)$ holds if and only if the proposition $\forall p\left( \rho _{i}p\Rightarrow a_{i}p\right)$ is supported by inductive judgement for $i$ at $h$, and more importantly, $h\models _{\Gamma }^{*}b_{i}\lnot \left( \forall p\left( \rho _{i}p\Rightarrow a_{i}p\right) \right)$ if the proposition $\lnot \left( \forall p\left( \rho _{i}p\Rightarrow a_{i}p\right) \right)$ is supported by inductive judgement for $i$ at $h$.

Following Walker (2012) it would be possible to construct a characterization of the semantic structures consistent with this interpretation relation. However, this is beyond the scope of the present paper. Instead, our focus will be on the way in which inductively derived subjective beliefs about awareness and unawareness may be used to guide player decisions and strategic choices. The key idea is that of heuristics.

5 Games subject to heuristic constraints

We now develop a basis for making decisions that depend upon judgements about propositions that cannot be expressed explicitly in the language of the game available to that player but are nonetheless supported either on historical inductive grounds or by induction over players. We refer to these as heuristic constraints. Conversely, we consider heuristics that may be applied to justify the adoption of a best response for the continuation of the game from an information set. Combining these heuristics, we obtain a definition for a game subject to heuristic constraints.

A heuristic constraint for a particular player associated with the game they perceive to be playing is an admissibility rule precluding the adoption by that player and her opponents of certain strategies whenever a certain proposition that involves the player or her opponents taking that action is supported either on historical inductive grounds or by induction over players. For example, in the speculative trade example of Heifetz et al. (2006), we can construct a heuristic constraint based on the proposition, “my opponent is aware of something that I am not, and whatever it is, may result in me incurring a loss from trading with him.” The corresponding heuristic constraint is not to engage in trade if the aforementioned proposition is supported either on historical inductive grounds or by induction over players.

Formally, we define a game with awareness subject to heuristic constraints as follows.

Definition 20

Fix a game with awareness $\mathcal G$. An awareness-based heuristic $\mathcal H$ for the game $\mathcal G$ is an admissibility rule such that, for each $h$ in $H$ in which $P\left( h\right) \ne c$, $\mathcal H \left( h\right) \subseteq \tilde{Z}\left( h\right)$ is a subset of the terminal histories available in the game $\Gamma _{\tilde{Z}\left( h\right) }$ from the information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$. The restriction $\mathcal H \left( h\right)$ depends only on the perceived game $\Gamma _{ \tilde{Z}\left( h\right) }$ and on the judgement of the player at $h$ as to whether she and/or her opponents are aware of all relevant possibilities and generates a restricted game $\Gamma _\mathcal{H \left( h\right) }\sqsubseteq \Gamma _{\tilde{Z}\left( h\right) }$. We denote by $\left( \mathcal G ,\mathcal H \right)$the game with awareness $\mathcal G$ that is subject to the heuristic constraints $\mathcal H .$ We denote by $\mathcal H _{i}$ the restriction of $\mathcal H$ to the set of histories $\left\{ h:P\left( h\right) =i\right\} .$

Imposing heuristic constraints on a game with differential awareness means that the perceived game in which the heuristic constraints may apply is modified by removing all histories that contain any actions that are precluded by the heuristic constraints. As the modified game is a restriction of the original game, this means that its set of terminal histories are a subset of those from the original game. This in turn implies that at any information set in the original game for which a heuristic constraint precludes the choice of at least one action, there is at least one other available action that is not precluded by any of the heuristic constraints that may apply.

We revise the definition of a strategy profile, so that in the game with awareness $\mathcal G$ subject to the heuristic $\mathcal H$, at each $h$ the continuation behavioral strategy profile is defined for the game $\Gamma _\mathcal{H \left( h\right) }$.

The definitions of subjective probabilities, assessments and sequential rationality from Sect.  can be modified accordingly with each instance of the game $\Gamma _{\tilde{Z }\left( h\right) }$ for history $h$, being replaced by the (in general even more restricted) game $\Gamma _\mathcal{H \left( h\right) }$ that excludes all histories that are precluded by the adoption of the heuristic constraints. Thus, we can extend the definition of a sequential equilibrium to apply to games with awareness subject to heuristic constraints. This definition requires that players, at each information set where they are called on to move, adopt a best response to the equilibrium strategies of the continuation game they perceive at that information set, excluding histories that are precluded by the adoption of their own heuristic constraints and those of other players. This is a natural generalization of the standard assumption of common knowledge of rationality, which applies to the game $\mathcal G$.

As an immediate corollary to Proposition 1 we have:

Corollary 1

A sequential equilibrium exists for any game with differential awareness subject to heuristic constraints.

As discussed above, we will confine attention here to the case when the equilibrium is unique.

5.1 Ecological rationality

A variety of criteria have been suggested for the adoption and evaluation of decision heuristics. Goldstein and Gigerenzer (2002) propose a concept of ecological rationality for heuristics, explained as “the capacity of the heuristic to exploit the structure of the information in natural environments.” As an example, they consider the “recognition heuristic” illustrated by the idea that a decision maker asked to estimate which of two cities has a larger population should choose one they have heard of in preference to one they have not heard of. In an environment where mentions of cities are positively correlated with their population, this heuristic is ecologically rational.

In a game with awareness, the concept of ecological rationality may be seen as the way a heuristic adopted by players with bounded awareness would be evaluated from the perspective of a more aware player, or an external modeler aware of the maximal game. In a game with increasing awareness, a player may evaluate the ecological rationality of their own heuristics, applied early in the game, from the more aware perspective available later in the game.

It is not necessary to confine attention to the actual outcome realized subsequent to the adoption of a heuristic. From the perspective of a more aware player (or from the perspective of a player considering their own earlier state of awareness), it is possible to compare the decision recommended by a heuristic to the optimal decision recommended by Bayesian decision theory for the full game, and also to the “naive” Bayesian decision derived for the restricted game. Even if, by virtue of an unlucky draw by nature, the heuristic yields a bad outcome in a particular play of the game, it may nonetheless be judged to be superior, in expected payoff terms, to the naïve Bayesian decision.

Consider a game with awareness $\mathcal G= \left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$, subject to heuristic constraints $\mathcal H$. Let $\mathcal H ^{-i}$ be the heuristic obtained from $\mathcal H$ by removing any constraints for information sets controlled by player $i$. That is, $\mathcal H ^{-i}\left( h\right) =\mathcal H \left( h\right)$, if $P\left( h\right) \ne i$ and $\mathcal H ^{-i}\left( h\right) =\tilde{Z}\left( h\right)$, if $P\left( h\right) =i$. We adopt the following definition.

Definition 21

Consider a game with awareness $\mathcal G= \left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$, subject to heuristic constraints $\mathcal H$. The heuristic constraints $\mathcal H$ are ecologically rational for player $i$ if

$$\begin{aligned} V_{\Gamma }^{i}\left( r^{\prime }\right) \ge V_{\Gamma }^{i}\left( r\right) \end{aligned}$$

where $r$ (respectively, $r^{\prime }$) is the behavioral rule generated by the sequential equilibrium $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ for $( \mathcal G ,\mathcal H )$ (respectively, sequential equilibrium $\left( {\varvec{\beta }}^{\prime }, {\varvec{\mu }}^{\prime }\right)$ for $(\mathcal G , \mathcal H ^{-i})$).

It is important to note that the ecological rationality of $\mathcal H$ cannot be determined from within the $\Gamma _{\tilde{Z}\left( h\right) }$ available to player $i=P\left( h\right)$ at a particular history $h$. Ecological rationality can be determined, however, by an unboundedly rational external modeler with access to the full awareness game $\Gamma$. More relevantly from the perspective of actual players, the belief that a particular heuristic is ecologically rational in a given setting may be justified inductively on the basis of its past performance in similar settings.

5.2 Example Part 2:

We now return to the speculative trade example of Heifetz et al. (2006). By Proposition 4, for each party $i=1,2$, the proposition $\exists q\in \mathcal L _{\Gamma }:\left( u_{j}q\wedge a_{i}q\right)$ is true for $j\ne i$. Moreover, in the given example, the proposition can be extended to

$$\begin{aligned} \theta \left( q_{\alpha ^{j}}\right) \equiv \exists q\in \mathcal L _{\Gamma }\left( u_{j}q\wedge a_{i}q\wedge \left( q\Rightarrow q_\mathrm{loss}^{j}\right) \right) \text{,} \end{aligned}$$

(5)

where $\alpha ^{j}$ is the action necessary for $j$ to take in order to transact with $i$ and $q_\mathrm{loss}^{j}$ is the proposition the transaction produces a loss for $j$.¹⁰

Now let party $i$ consider the proposition $\exists q\in \mathcal L _{\Gamma }:\left( u_{i}q\wedge a_{j}q\right)$, that is, that there exists a proposition of which she is unaware, but the other party is aware. As shown above, inductive reasoning, embodying the idea of symmetry, provides support by induction over the set of players for the existential proposition $\exists q\in \mathcal L _{\Gamma }:\left( u_{i}q\wedge a_{j}q\wedge \left( q\Rightarrow q_\mathrm{loss}^{i}\right) \right)$, so we have for both $h^{1}=\left\langle \alpha _{0},\alpha _{0}\right\rangle$ and $h^{2}=\left\langle \alpha _{0},\alpha _{0},\alpha _{1}\right\rangle$,

$$\begin{aligned} h^{i}\models _{\Gamma }n_{i}\theta \left( q_{\alpha ^{i}}\right) \text{.} \end{aligned}$$

Let us take $\mathcal R \left( h\right) \subseteq$ $\tilde{Z}\left( h\right)$ to be the set of terminal histories in the game $\Gamma _{\tilde{Z }\left( h\right) }$ that passes through $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ and that includes an action $\hat{\alpha }^{i}\in A_{\tilde{Z}\left( h\right) }$ that leads to a loss in the event that some unforeseen proposition $q$ holds. We can then define the heuristic $\mathcal H ^{i}\left( h\right) =\tilde{Z}\left( h\right) -\mathcal R \left( h\right) \$that precludes the adoption of $\hat{\alpha }^{i}$ by party $i$. If either the buyer adopts the heuristic $\mathcal H ^{1}$ or the owner adopts the heuristic $\mathcal H ^{2}$, then the transaction will not take place.

Now compare the dominance principle proposed by Heifetz et al. (2006). Heifetz et al. propose that if (i) in all histories $h^{\prime }$ an agent considers possible at $h$, action $\alpha$ leads to at least as good an outcome as $\alpha ^{\prime }$, and (ii) in some possible history, action $\alpha$ leads to a better outcome, then the agent should choose $\alpha$. As shown above, this principle leads the players to engage in trade, even though in the minimal game of common awareness the trade generates zero surplus. Each party’s own perceived game with awareness suggests a strictly positive surplus from trade for the player concerned, coming at the expense of the other party.

In the given example, this principle does not appear compelling. Even though this condition is satisfied for the modal-logical interpretation of “considers possible” (namely $h^{\prime }\in \mathcal I ^{i}\left( h\right) )$, observation of the limited awareness of other players, combined with principles of symmetry between players, provides inductive support for the proposition in expression (5). Notice that, evaluated in the fully aware game, (5) is in fact true for both players.

A potential problem with this analysis is that it might lead to the conclusion that players should never trade in the presence of differential awareness. However, this conclusion only arises in the case where there are no gains from trade, as in the given example. If both parties evaluate the transaction as mutually beneficial on the basis of their own awareness, there is, in general, no reason for them to conclude that this mutual benefit would not persist under full awareness. In particular, the fact that party 2 is willing to engage in trade does not imply that she must be aware of a contingency that would make the trade less appealing to party 1.

6 Applications

In this section, we sketch two applications, in which heuristics may be used as a way of responding to unawareness. Both applications deal with problems that may be addressed in terms of individual decisions (i.e., one-person games with Nature) or in a multi-player context. For ease of exposition, we will focus here on the case of individual decision.

6.1 Research and discovery

In some circumstances, unforeseen possibilities are both desirable and essential. The allocation of funds for research and development (R&D) provides an example. As discussed in Grant and Quiggin (2006), (Sect. 2.2), it is inherent in the concept of pure research that investigators cannot predict what they may discover. By contrast, the uncertainties associated with the development phase of R&D are well understood in most cases and may reasonably be modelled in a Bayesian framework. The contrast between research and development raises obvious difficulties in the allocation of funds. A common response is to require research proposals which purport to contain accurate predictions of the path of research for which funding is supported.¹¹ However, this does not appear to be a satisfactory solution.

This problem may be addressed by modeling the situation as a game with awareness. For simplicity, we will abstract from the interactive aspects of the problem and consider a decision maker playing a one-person game against nature with awareness. Let $\left( {\varvec{\beta }}^{0},{\varvec{\mu }} ^{0}\right)$denote her (unique) sequentially rational and consistent assessment, and let $r_{0}$ denote the associated behavioral rule generated by ${\varvec{\beta }}^{0}$.

At some history $h$ she is considering whether to allocate funds to one of a set of research projects, and if so which one. The alternative is to allocate the funds to a development project, where we assume there are no unconsidered outcomes. For ease of exposition (and without essential loss of generality), assume that $\mathcal I \left( h\right) = \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right) =\{h\}$. That is, the decision maker believes she is at history $h$ (and from the perspective of the fully aware game she actually is at history $h$).

At $h$, the decision maker faces the set of available actions $A\left( h\right) =\left\{ a_{0},a_{1},\ldots ,a_{K}\right\}$, leading to the set of histories $\left\{ h_{0},h_{1},\ldots ,h_{K}\right\}$, where $h_{k}=\langle h\cdot a_{k}\rangle$. Here $a_{0}$ denotes the choice of the development project, while $a_{k}$, $k=1,\ldots ,K$ are research projects. We assume that the complexity of the subgame starting at $h_{0}$ is less than $\xi$, while for $k>0$, the complexity of the subgame starting at $h_{k}$ is greater than $\xi .$

In the absence of unconsidered contingencies, let us suppose her unique best continuation strategy $\beta _{h}^{0}$ from the subgame starting at $h$ entails selecting the development option at $h$, that is, $\beta _{h}^{0}\left( h\right) =a_{0}$. We normalize by setting $V_{\tilde{\Gamma } _{Z\left( h\right) }}\left( \beta _{h}^{0}\right) =V_{\Gamma }\left( r_{0}\right) =0$. That is, resources used for any project are evaluated in terms of the opportunity cost associated with the development option.

For each $k=1,\ldots ,K$, let $\beta _{k}$ denote the continuation strategy that agrees with $\beta _{h}^{0}$ at every information set in the subgame starting at $h$, except initially where $\beta _{k}\left( h\right)$ is equal to $a_{k}$. And let $\left( {\varvec{\beta }}_{-h}^{0},\beta _{k}\right)$ denote the corresponding modified strategy profile for the entire game with awareness.

Since $\beta _{h}^{0}$ is the unique best option for the subgame starting at $h$, it follows that $V_{\tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right) <0$, for all $k=1,\ldots ,K$. That is, based on current awareness, the development project yields higher expected returns than any of the research projects. Hence, the unconstrained heuristic $\mathcal H ^{-i}$ (which may also be denoted by $\mathcal H ^{0}$ in the context of individual decision) will lead to the choice of $a_{0}$ at $h$.

Now suppose she has sufficient experience to provide inductive support for some proposition of the form:

For problems of complexity greater than $\xi$, there may exist contingencies of which I am unaware.

Hence, the decision maker believes herself to be aware of all contingencies relevant after a choice of $a_{0}$ but not for any choice $a_{k}$, $k>0$.

Then, given a “research budget” of $B$, we may consider the heuristic $\mathcal H ^{B}$:

Exclude $a_{0}$ from consideration unless $V_{\tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right) < -B$, for all $k=1,\ldots ,K$.

This leads to the behavioral rule that at $h$ prescribes the following: “Choose $a_{k}$ (that is, undertake the research project $k$) that maximizes $V_{\tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right)$ , provided $V_{\tilde{\Gamma } _{Z\left( h\right) }}^{i}\left( \beta _{k}\right) \ge$ $-B$. Otherwise choose $a_{0}.$”

The heuristic allows for the choice of a research project rather than the “safe” development option whenever the expected net cost, based on the possibilities already under consideration, is less than the research budget $B$. The quantity $B$ might be considered as a value at risk constraint.

In addition to the benefits that may be evaluated in advance, the research project may generate valuable discoveries, associated with awareness of previously unconsidered possibilities. If we denote by $r_{k}$ the behavioral rule generated by the strategy profile $\left( {\varvec{\beta }} _{-h}^{0},\beta _{k}\right)$, then the full value of a project, which may be estimated by a fully aware outside observer, but not by the decision maker, is $V_{\Gamma }\left( r_{k}\right).$ In this context, we assume that, for all $k$, the benefits of discovery are nonnegative, so that $V_{\Gamma }^{i}\left( r_{k}\right) \ge V_{\tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right)$.

Proposition 5

The following conditions are sufficient for $\mathcal H ^{B}$ to be ecologically rational:

• (a) $\frac{1}{K}\sum _{k=1}^{K}\left( V_{\Gamma }^{i}\left( r_{k}\right) -V_{ \tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right) \right) \ge B;$ and

• (b) $\left( V_{\Gamma }^{i}\left( r_{k}\right) -V_{\tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right) \right)$ is positively correlated with $V_{\tilde{\Gamma }_{Z\left( h\right) }}^{i}\left( \beta _{k}\right)$.

The first condition states that on average, the value of unanticipated discoveries exceeds the research budget $B$. Given this condition, the second condition ensures that the expected return from choosing the project with maximal expected net value (as perceived by the decision maker) will exceed $B$ and therefore be preferable to the development option.

As already noted, a crucial feature of ecological rationality is that it cannot be evaluated within the perspective available to a decision maker at $h$ who perceives the game $\Gamma _{\tilde{Z}\left( h\right) }$. Conversely, the heuristic $\mathcal H ^{B}$ which may be judged as ecologically rational by an outside observer under the given conditions can be implemented by the decision maker without requiring awareness of the full game $\Gamma$.

Thus, one interpretation of the heuristic is that it represents the advice that would be given by an unboundedly aware expert to a decision maker who must make decisions under conditions of bounded awareness.

6.2 The precautionary principle

The precautionary principle, presented as a guide to environmental policy decisions in the presence of uncertainty, has been the subject of vigorous debate (Wingspread 1998). However, discussion of the principle as a decision-theoretic rule has mostly relied on the (normally implicit) assumption that decision makers are unboundedly rational and aware of all possible contingencies. In this context, the precautionary principle has been criticized as involving inconsistency (Marchant and Mossman 2005; Sunstein 2005) or excessive risk aversion (Miller and Conko 2005) and defended as a way of capturing option value (Gollier et al. 2000). It is evident, however, that in a fully specified decision-theoretic model, with all contingencies taken into account, and an appropriately specified objective function, there should be no need for additional heuristic rules such as those of the precautionary principle.

When the limited awareness of participants in decision processes is taken into account, however, the precautionary principle seems more appealing. Given the bounded rationality of human agents, it is impossible to enumerate all relevant possibilities. This point is sometimes expressed with reference to “unknown unknowns,” that is, relevant possibilities of which we are unaware.

The case for the precautionary principle arises when a decision maker, such as a regulator, is faced with a choice between alternatives, one of which leads to consequences for which the relevant elements of the state space are well understood and the other which leads to consequences that depend to a significant extent on “unknown unknowns.” If most surprises are unpleasant, a risk analysis based only on known risks will underestimate the costs of choices of the second kind. That is, standard risk analysis leads to a bias in favor of taking chances on poorly understood risks. The precautionary principle may be seen as a rule designed to offset such biases.

Grant and Quiggin (2012) consider the case of a decision maker, faced with an uncertain choice, who has available a “safe option,” yielding a return that can be normalized to zero, and conditional on which the decision maker judges (by induction) that there are no relevant propositions of which she is unaware. Grant and Quiggin say that a behavioral rule other than the safe option is “subject to unfavorable surprises,” and there exist unconsidered moves by Nature, against which the payoff from the behavioral rule $r$ is less than zero. They define the Strong Form of the Precautionary Principle as the heuristic that excludes behavioral rules subject to unfavorable surprises and show that the Strong Version of the Precautionary Principle is ecologically rational if and only if $V\left( r_{0}\right) <0$, where $r_{0}$ is the behavioral rule associated with the unconstrained heuristic $\mathcal H ^{-i}$ (which, in the context of individual decision, may be denoted by $\mathcal H ^{0}$). Grant and Quiggin also define a weaker form of the Precautionary Principle and derive conditions for ecological rationality.

In a multi-agent context, regulatory decisions typically involved assessment of proposed actions seen as raising possible risks. In this context, the precautionary principle may be understood, as a procedural constraint, putting the burden of proof on to proponents of decisions involving poorly understood risks. If the proponent can provide sufficient information to satisfy the regulator that all relevant contingencies have been considered, standard principles of decision analysis may be applied to justify a proposal. If not, the regulator may choose to apply the precautionary principle and reject the project even in the absence of a negative benefit–cost evaluation.

7 Concluding comments

The model presented in this paper has incorporated the minimal deviations from the standard case of an extensive-form game necessary to allow a representation of inductive reasoning about differential awareness and to model possible behavioral responses. The analysis presented here could be extended in a number of ways.

First, the model presented here allows players to become aware of previously unconsidered possibilities, but not to forget about possibilities they have previously considered. To the extent that unawareness reflects bounded rationality, this seems unreasonable, since the model accessible to players becomes steadily more complex. A desirable property for a representation of bounded awareness is that the bound should be determined by limits on reasoning capacity which should be constant over time or at least should not increase monotonically

It would be desirable, therefore, to extend the analysis to allow for imperfect recall. The simplest version of imperfect recall is to suppose that individual $i$ at (perceived) information set $\mathcal I _{\tilde{Z} \left( h\right) }\left( h\right)$ forgets about some or all histories that do not pass through $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right),$ since these histories involve actions (by player $i,$ some other player $j,$ or Nature) known by $i$ not to have been taken. In the context of individual decision, such histories are strictly irrelevant, but in a game-theoretic context, the fact that they have not been chosen may inform reasoning about the other players. More generally, individuals may forget the details of their past history.

In the present paper, the perception mapping is taken to be exogenous, subject only to the restriction that players must always consider some history possible. A natural extension would be to consider games in which awareness is derived naturally from the tree structure of the game. For example, we might impose the requirement that players are always aware of actions when they become available.

Finally, the relationship between equilibrium and awareness could be explored further. As we have argued, differential awareness means that players will, in general, arrive at information sets they previously regarded as being off-equilibrium. This would appear to rule out equilibrium concepts that admit arbitrary actions at off-equilibrium information sets and therefore to mitigate the problem of multiplicity of equilibria. On the other hand, since changes in awareness imply, in general, changes in the perceived set of equilibria, difficulties may arise for notions such as forward induction, to the extent that they rely on the use of apparent deviations from equilibrium to make inferences about other players.

Much work remains to be done. However, the model presented in this paper allows for a coherent account of behavior in games where players are not, in general, aware of all possibilities and understand this fact. This seems likely to yield a more plausible account of actual behavior than a framework based on the assumption that all players are unboundedly rational and that this is a matter of common awareness.

Appendix A

Proof of Proposition 1

By standard arguments (e.g., Osborne & Rubinstein [1994, p 227]), it follows that an assessment in a game of perfect recall is sequentially rational $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ if and only if it satisfies the one-shot deviation property. That is, at each $h$, for the behavioral strategy $\beta _{h}^{P\left( h\right) }$ of player $P\left( h\right)$ in the continuation of the game $\Gamma _{\tilde{Z}\left( h\right) }$, there is no subsequent information set $\mathcal I _{\tilde{Z} \left( h\right) }\left( h^{\prime }\right)$, with $P\left( h^{\prime }\right) =P\left( h\right)$ in the continuation of the game at which a change in $\beta _{h}^{P\left( h\right) }\left( h^{\prime }\right)$ increases his payoff conditional on reaching $\mathcal I _{\tilde{Z}\left( h\right) }\left( h^{\prime }\right)$.

Therefore, we will first establish the existence of a trembling-hand equilibrium for the agent-normal form of $\mathcal G$, which by the one-shot deviation property also constitutes a trembling-hand equilibrium of $\mathcal G$. It will then suffice to show that for any trembling-hand equilibrium strategy profile ${\varvec{\beta }}$, there exists a subjective probability system ${\varvec{\mu }}$ such that $\left( {\varvec{\beta }, \varvec{\mu }}\right)$ is a sequential equilibrium.

We take the agent-normal form of the game with awareness $\left( \Gamma ,\tilde{Z}\left( \cdot \right) \right)$, to be the game with awareness $\left( \Gamma ^{an},\tilde{Z}\left( \cdot \right) \right)$, where $\Gamma ^{an}$ is the agent-normal form $\Gamma$, in which there is one player for each information set in the extensive-form game and where player $h$ is imputed to be playing $\Gamma _{\tilde{Z}\left( h\right) }^{an}$ the agent-normal form of $\Gamma _{\tilde{Z}\left( h\right) }$. For each $h$, denote the perturbation of the game $\Gamma _{\tilde{Z}\left( h\right) }^{an}$ by first fixing the strategies of all players $h^{\prime \prime }$, such that there exists $h^{\prime }\in \mathcal I _{\tilde{Z} \left( h\right) }\left( h\right)$ and $h^{\prime \prime }\preceq h^{\prime }$ and $h^{\prime \prime }\ne h^{\prime }$ (i.e., player $h^{\prime \prime }$ is a player has already moved by the time the game reaches the information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$) and then letting the set of actions of each player $h^{\prime \prime }$, such that there exists history $h^{\prime }\in \mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$ and $h^{\prime }\preceq h^{\prime \prime }$ (i.e., player $h^{\prime \prime }$ is a player who moves in the continuation of the game $\Gamma _{\tilde{Z}\left( h\right) }^{an}$ after information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h\right)$) be the set of mixed strategies in $A_{\tilde{Z}\left( h\right) }\left( h^{\prime \prime }\right) \cap A_{\tilde{Z}\left( h^{\prime \prime }\right) }\left( h^{\prime \prime }\right)$ that assign probability of at least $\varepsilon _{h^{\prime \prime }}^{a}\left( h\right)$ to each action that player $h$ (at $h$) imputes to player $h^{\prime \prime }$ at her information set $\mathcal I _{\tilde{Z}\left( h\right) }\left( h^{\prime \prime }\right)$. That is, this constrains $h$ and every player who follows $h$ to use every strategy $h$ imputes that they have available with some minimal probability. Consider a sequence of such perturbed games in which $\varepsilon _{h^{\prime \prime }}^{a}\left( h\right) \rightarrow 0$, for all $h$, for all $h^{\prime \prime }$ and $a$; by the compactness of the set of strategy profiles, some sequence of selections $\left( {\varvec{\beta }}^{k}\right)$ from the sets of strategy profiles that are sequentially rational for all $i$, of the games $\{\Gamma _{\tilde{Z}\left( h\right) }^{an}:h\in H\}$ converges to say ${\varvec{\beta }}$. It is straightforward to show from its construction that ${\varvec{\beta }}$ corresponds to a trembling-hand perfect equilibrium of the game with awareness.

Now, take the sequence $\left( {\varvec{\beta }}^{k}\right)$. At each information set $\mathcal I \left( h\right)$ define the belief $\mu _{h^{\prime }}$ for each $h^{\prime }$ in $\mathcal I \left( h\right)$, to be the limit of the beliefs defined from $\left( {\varvec{\beta }}^{k}\right)$ using Bayes rule. The assessment $\left({\varvec{\beta },{ \mu } }\right)$ is then by construction consistent. Since the strategies are completely mixed as can be done consistently, each information set consistent with each player’s level of awareness is reached with positive probability and each agent’s strategy is a best response when the beliefs at each information set are defined by ${\varvec{\mu }}$. Thus, $\left( {\varvec{\beta },\varvec{\mu }}\right)$ is a sequential equilibrium. $\square$