Numerical simulations of the early stages of high-speed droplet breakup

Abstract

Experiments reported in the literature are reproduced using numerical simulations to investigate the early stages of the breakup of water cylinders in the flow behind normal shocks. Qualitative features of breakup observed in the numerical results, such as the initial streamwise flattening of the cylinder and the formation of tips at its periphery, support previous experimental observations of stripping breakup. Additionally, the presence of a transitory recirculation region at the cylinder’s equator and a persistent upstream jet in the wake is noted and discussed. Within the uncertainties inherent to the different methods used to extract measurements from experimental and numerical results, comparisons with experimental data of various cylinder deformation metrics show good agreement. To study the effects of the transition between subsonic and supersonic post-shock flow, we extend the range of incident shock Mach numbers beyond those investigated by the experiments. Supersonic post-shock flow velocities are not observed to significantly alter the cylinder’s behavior, i.e., we are able to effectively collapse the drift, acceleration, and drag curves for all simulated shock Mach numbers. Using a new method that minimizes noise errors, the cylinder’s acceleration is calculated; acceleration curves for all shock Mach numbers are subsequently collapsed by scaling with the pressure ratio across the incident shock. Furthermore, we find that accounting for the cylinder’s deformed diameter in the calculation of its unsteady drag coefficient allows the drag coefficient to be approximated as a constant over the initial breakup period.

1 Introduction

The study of droplet breakup has applications in the combustion and detonation of multiphase mixtures, liquid jet atomization, and rain erosion damage. The primary motivation for the current work lies in geothermal waste heat recovery applications. Within variable phase turbines (VPTs), multiphase nozzles are used to flash evaporate and accelerate the working fluid into a high-speed two-phase jet composed mainly of gas with disperse liquid droplets. Experimental testing has shown that larger droplets tend to coalesce on the rotor blades to form a thin film that adversely impacts momentum transfer from droplet impacts [44]. On the other hand, smaller droplets are more likely to run off the rotor blade, while still imparting momentum during impact. A more complete understanding of the breakup process within the multiphase nozzle, so as to predict a final droplet size distribution, would allow for optimized nozzle design.

Much of the earlier literature on droplet breakup consists of experimental work performed in shock tubes and wind tunnels. Normal shock waves, by themselves, have little effect on the droplet. However, they have proven to be a reliable and repeatable technique to generate a high-speed flow around the droplet, which is responsible for the deformation and disintegration [12, 31]. Earlier studies focused on droplets of Newtonian fluids in subsonic streams, and attempted to characterize various breakup modes and mechanisms [6, 12, 15–17, 25, 31, 32]. Breakup has, classically, been separated into five distinct regimes (delineated by the Weber number, $We$): vibrational, bag, bag-and-stamen, shear or sheet stripping, and catastrophic. Descriptions of each regime and their corresponding Weber numbers can be found in the reviews of Pilch and Erdman [28] and Guildenbecher et al. [9]. More recently, Theofanous and Li [39] proposed a re-classification into two primary breakup regimes: Rayleigh–Taylor piercing and shear-induced entrainment. In this new classification, the shear-induced entrainment regime is the terminal regime for $We > 10^3$. The classical catastrophic regime was argued to be an artifact of low-resolution shadowgraph visualizations [39]. Earlier experimental studies noted the formation of a mist or spray in the wake of the disintegrating droplet [31–33]. In her investigation, Engel [6] concluded that the most likely explanation was a combination of breaking wave crests at the droplet’s equator and the stripping of water by vortices in the airflow. In addition to varying droplet size and shock Mach number, $M_S$, [6], studies have also calculated characteristic breakup times [7, 15, 31, 32], and attempted to quantify the dependence of breakup on parameters such as the density and viscosity ratios of the fluids [7, 12, 14, 15, 40].

Historically, the drag of a deforming droplet has been a quantity of keen interest for numerous applications. Various attempts have been made to determine accurate droplet velocities and accelerations. Experimental studies often fit a polynomial to the drift measurements from their visualizations, and then differentiate to approximate the acceleration [6, 24, 31, 33, 36, 37]. Empirical correlations exist in the literature to predict the drag coefficient of a droplet based on various non-dimensional groupings (commonly, the Weber, Ohnesorge, $Oh$, and Reynolds, $Re$, numbers) [26].

Due to the high computational cost of three-dimensional simulations, numerical droplet breakup studies often invoke two-dimensional [3, 18–20] or axisymmetric [1, 10, 11] approximations. Quan and Schmidt [29] studied breakup for incompressible fluids using three-dimensional simulations. Their computations were initialized by first simulating flow over a solid sphere. The steady-state velocity field around the sphere was then used as the initial flow condition around the droplet. The axisymmetric simulations [1, 10, 11] also solved the incompressible Navier–Stokes equations, and initialized droplet breakup by subjecting the droplet to either a body force [10] or a step change to a divergence-free velocity field [1, 11]. The two-dimensional simulations of Igra and Takayama [18–20] were limited by their numerical method, which was suitable only for the very early stages of breakup, and could not capture the majority of the deformation and breakup. The two-dimensional numerical work of Chen [3] also tried to duplicate the experiments of Igra and Takayama. The simulation results therein provide a, albeit limited, basis of comparison for the present work.

The goals of the present work are to perform high-fidelity simulations of the breakup of a water column in the flow behind a normal shock wave to understand the flow features associated with breakup, and extract accurate measurements of the cylinder’s acceleration and unsteady drag coefficient. Solving the multicomponent, compressible Euler equations allows our simulations to match the experimental setup of Igra and Takayama [20], and comparisons can be made with their data. We are also able to accurately calculate the cylinder’s center-of-mass velocity, acceleration, and unsteady drag coefficient. The present work is organized as follows. In Sect. 2, we present the physical model and relevant simulation flow parameters. Section 3 briefly describes the employed numerical method and the calculation of various flow quantities used in the analysis. Analysis of the computational results and a discussion of their implications follows in Sect. 4. The major conclusions are summarized in Sect. 5.

2 Physical modeling

2.1 Problem description

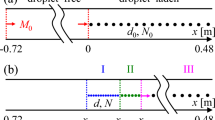
Droplet breakup is studied in two dimensions by simulating the breakup of a water cylinder in the high-speed flow behind a normal shock wave. We initially focus on the experiments of Igra and Takayama [20], and then extend the range of simulated shock Mach numbers to include supersonic post-shock gas velocities. The values of incident shock Mach numbers and their corresponding post-shock Mach numbers, $M_2$, are shown in Table 1. The Weber and Reynolds numbers, respectively, characterize the relative importance of inertial-to-capillary and inertial-to-viscous forces:

Table 1 Post-shock Mach numbers, $M_2$, in the shock-stationary (SS) and shock-moving (SM) reference frames

$$\begin{aligned} We&= \frac{\rho _g u_g^2 d_0}{\sigma },\end{aligned}$$

(1)

$$\begin{aligned} Re&= \frac{\rho _g u_g d_0}{\mu _g}, \end{aligned}$$

(2)

where the density, $\rho _g$, and velocity, $u_g$, are those of the shocked gas, $\sigma$ is the surface tension coefficient, $\mu _g$ is the dynamic viscosity of the gas, and the characteristic length scale is the initial cylinder diameter, $d_0$. Using the experimental parameters for a water cylinder in air, the approximate Weber numbers corresponding to the four weaker shocks range between 940–19,300. The Reynolds numbers corresponding to the same shock Mach numbers range between 39,900 and 237,600. These Weber and Reynolds numbers suggest that the physical mechanisms of breakup are primarily driven by inertia, and that a reasonable first approximation can be made by neglecting the effects of surface tension and viscosity. With these simplifications, we do not capture all the physics of the breakup process. For example, the absence of surface tension restricts our capability to simulate the breakup of the thin liquid filaments that are stripped off the edge of the cylinder. However, for the early stages of breakup where the cylinder remains, for the most part, a coherent body, the roles of viscosity and surface tension are expected to be relatively minor compared to that of inertia. Future work will restore these physical effects back into the model.

The breakup of the water cylinder is simulated using the computational setup shown in Fig. 1. In addition to the limitations imposed by the absence of viscous and capillary effects, our analysis is also restricted to the early stages of breakup since the flow is assumed to be symmetric across the cylinder’s centerline. Experimental visualizations of both cylinder and droplet breakup show no significant asymmetries during the early stages of breakup. We employ a symmetric boundary condition along the bottom of the computational domain, and enforce non-reflecting characteristic boundary conditions along the three remaining boundaries. Implemented following Thompson [41, 42], these characteristic boundary conditions do not contaminate the solution through the reflection of outgoing waves. The water cylinder and the air in front of the planar shock are initially at rest ($\rho _g = 1.204\,\hbox {kg/m}^3, \rho _l = 1,\!000\,\hbox {kg/m}^3$, and $p_g = p_l = 1$ atm). At the start of the simulation, the shock is set in motion towards the water cylinder and establishes a steady freestream flow field.

Fig. 1

Computational domain setup

2.2 Equations of motion

In the absence of surface tension and viscosity, the flow is governed by the multicomponent, compressible Euler equations. In addition to being compressible and inviscid, each fluid is considered immiscible and does not undergo phase change. In the absence of mass transfer and surface tension, material interfaces are simply advected by the local flow velocity. Following the five-equation model of Allaire et al. [2], interfaces are modeled using volume fractions, $\alpha$. The governing equations consist of two continuity equations, (3) and (4), a mixture momentum equation, (5), a mixture energy equation, (6), and a volume fraction advection equation, (7).

$$\begin{aligned} \frac{\partial (\alpha _g \rho _g)}{\partial t} + \nabla \cdot (\alpha _g \rho _g \mathbf {u})&= 0,\end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial (\alpha _l \rho _l)}{\partial t} + \nabla \cdot (\alpha _l \rho _l \mathbf {u})&= 0,\end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial (\rho \mathbf {u})}{\partial t} + \nabla \cdot (\rho \mathbf {u} \otimes \mathbf {u}+p {\mathsf {I}})&= \mathbf {0},\end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial E}{\partial t} + \nabla \cdot \big [(E + p) \mathbf {u}\big ]&= 0,\end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial \alpha _g}{\partial t} + \mathbf {u} \cdot \nabla \alpha _g&= 0, \end{aligned}$$

(7)

where the subscripts $l$ and $g$ denote, respectively, the liquid and gas phases. Since phasic continuity equations are solved, individual fluid masses (and, therefore, total mass) are conserved by the numerical method. As a consequence of the shock-capturing nature of the numerical scheme, interfaces are diffuse (smeared over several grid cells) and a smooth transition of volume fractions exists in a mixture region between the two constitutive fluids. These mixture regions are not indicative of molecular mixing (since the component fluids are immiscible), but are inherently unphysical and an artifact of numerical diffusion. The interface model of Allaire et al. [2] tends to the Euler equations in each of the pure fluids, and recovers the correct sharp interface properties in the limit of infinite grid resolution.

Non-dimensionalization of all physical flow variables is accomplished using the original cylinder diameter, and the nominal density and sound speed of water ($c_l = 1,\!450$ m/s). Time is non-dimensionalized using a scaling, found in the literature, characteristic of breakup by Rayleigh–Taylor or Kelvin–Helmholtz instabilities [28, 31, 33]. The resultant non-dimensional time is given by

$$\begin{aligned} t^* = t \frac{u_g}{d_0}\sqrt{\frac{\rho _g}{\rho _l}}, \end{aligned}$$

(8)

where $t$ is the dimensional time, and the gas velocity, $u_g$, and fluid densities, $\rho _g$ and $\rho _l$, refer to post-shock conditions.

2.3 Equation of state

The stiffened gas equation of state [13] is used to close the system of equations, and models both gases and liquids in the flow solver.

$$\begin{aligned} \varGamma p + \Pi _\infty = E - \frac{1}{2} \rho \mathbf {u} \cdot \mathbf {u}, \end{aligned}$$

(9)

where

$$\begin{aligned} \varGamma = \frac{1}{\gamma -1} = \sum _{i=1}^2 \alpha _i \bigg ( \frac{1}{\gamma _i -1} \bigg ), \end{aligned}$$

(10)

and

$$\begin{aligned} \varPi _\infty = \frac{\gamma P_\infty }{\gamma -1} = \sum _{i=1}^2 \alpha _i \bigg ( \frac{\gamma _i P_{\infty ,i}}{\gamma _i -1} \bigg ), \end{aligned}$$

(11)

are the mixture properties in the diffuse interface region [2]. For air, $\gamma = 1.4$ is the ratio of specific heats, $P_\infty = 0$, and the stiffened gas equation of state reduces to the ideal gas equation. The parameters $\gamma$ and $P_\infty$ for water are empirically determined from shock Hugoniot data. Following Gojani et al. [8], the properties for water are taken to be $\gamma = 6.12$ and $P_\infty = 343.44$ MPa.

3 Numerical methods

3.1 Spatial and temporal discretization

The numerical method is based on the work of Johnsen and Colonius [23], which was shown to be both interface- and shock-capturing. The original work has since been extended to three dimensions and includes the effects of viscosity and nonuniform grids [5]; it has been used to model the shock-induced collapse of bubbles [4]. Verification of the algorithm via benchmark test cases (e.g., isolated interface advection, shock–interface interaction, gas–liquid Riemann problem) is shown by Coralic and Colonius [5] and is not reproduced here.

The numerical method is based on a finite-volume framework. Spatial reconstruction is accomplished with a third-order, weighted, essentially non-oscillatory (WENO) scheme coupled with the Harten–Lax–van Leer Contact (HLLC) approximate Riemann solver [43]. The equations are advanced in time using a total-variation-diminishing (TVD) Runge–Kutta scheme. Since the time marching scheme is explicit, the time step is chosen to limit the Courant–Friedrichs–Lewy (CFL) condition to ${\mathrm {CFL}}\,{\approx \!0.25}$. For the production runs, a Cartesian grid of $1,\!200 \times 600$ cells is stretched near the boundaries using a hyperbolic tangent function. The most refined portion of the grid is located near the initial position of the cylinder and in the region of the near-field wake. In this region, the nominal grid resolution is 100 cells per cylinder diameter. The numerical diffusion of an initially discontinuous interface can result in unphysical mixture regions that are particularly vulnerable to computational failure and affect code stability. Therefore, in order to avoid such a discontinuous interface, a smoothing function is applied to the cylindrical geometry as it is initially laid out on the Cartesian grid.

Without the presence of molecular viscosity to regularize the smallest scales, ever finer flow features are obtained in the simulation as spatial resolution is improved. Therefore, traditional grid convergence or independence of the computational results cannot be definitively shown; this is a known issue associated with “inviscid” calculations using shock- and interface-capturing methods. A grid resolution study doubling the number of cells in each direction, while resolving finer flow features, showed little difference in measurements of cylinder deformation and center-of-mass properties. Further details of this study can be found in Appendix A. We believe that the present spatial resolution is able to capture the salient features in the flow without being computationally cumbersome.

3.2 Numerical viscosity

Since our numerical method is both shock- and interface-capturing, numerical viscosity is present in the simulation. Preliminary viscous simulations have been performed in an attempt to find an approximate lower bound for the “apparent” Reynolds number corresponding to the numerical viscosity associated with the present $1,\!200 \times 600$ grid resolution. A description of the implementation of viscosity into our solver can be found in Coralic and Colonius [5], which is based on the work of Perigaud and Saurel [27]. Our approach involved running a series of viscous simulations, holding grid resolution constant, while successively decreasing Reynolds numbers. At a critical Reynolds number, $Re_c$, the molecular viscosity becomes sufficient to influence the flow physics, and causes a significant deviation from the “inviscid” simulation results. The analysis is complicated by the fact that physical flow quantities exhibit varying degrees of sensitivity to changes in viscosity. For brevity, only representative results are shown here. Figures 2 and 3 show the results of a series of runs, at the same $1,\!200 \times 600$ grid resolution, varying the Reynolds number between $Re = 15$ and $Re = 5,\!000$. Note that time and energy in both figures have been non-dimensionalized using the original cylinder diameter, and the nominal density and sound speed of water. As the incident shock wave moves through the domain, the energy increases in a linear manner. When the shock exits, at a non-dimensional time of approximately 50, the energy in the domain begins to slowly decrease due to a net flux of energy out of the domain. In Fig. 2, the curves for $Re \ge 500$ match the inviscid curve indicating that the magnitude of the molecular viscosity is less than that of the numerical viscosity, which is responsible for the behavior of the curves. For Reynolds numbers $15 < Re < 150$, the magnitude of the molecular viscosity surpasses that of numerical viscosity, and changes the overall behavior of the curves. In Fig. 3, a smaller range of values for the Reynolds number is plotted, but it can be seen that the curves for $Re \ge 500$ are almost indistinguishable from the inviscid curve. Based on these viscous simulations, the apparent Reynolds number associated with the numerical viscosity is believed to be no less than $Re_c = 500$ at the level of resolution used in the present results. For a Mach 1.47 shock wave, this corresponds to a physical droplet diameter of approximately 18 $\upmu$m.

Fig. 2

Kinetic energy in the domain as a function of Reynolds number

Fig. 3

Total energy in the domain as a function of Reynolds number

3.3 Center-of-mass calculations

The accurate calculation of the cylinder’s center-of-mass acceleration is a necessary step towards estimating the cylinder’s unsteady drag. Experimental studies have often extracted acceleration data by differentiating a polynomial fit of the cylinder’s trajectory. The measurement of the cylinder’s drift from the forward stagnation point is often a necessary simplification for extracting meaningful data from photographic evidence, and has been used in previous experimental work [6, 33]. However, acceleration calculations following this methodology are subject to additional error since the drift of the cylinder front does not accurately represent the center-of-mass drift. As noted by Theofanous [38] and shown in our results, the leading edge drift first overestimates, then underestimates, the center-of-mass drift.

In our results, the location of the center of mass (denoted by an overbar) of the deforming cylinder is calculated using

$$\begin{aligned} \bar{\mathbf {x}} = \frac{\int \alpha _l \rho _l \mathbf {x} \, {\mathrm {dV}}}{\int \alpha _l \rho _l \, {\mathrm {dV}}}, \end{aligned}$$

(12)

where the integrated volume (area in 2D) is that of the entire computational domain. The liquid partial density, $\alpha _l \rho _l$, in (12) is then the parameter that restricts the integration to cells with non-zero liquid volume fractions. Once the center-of-mass location is calculated, a few options exist for calculating the velocity and acceleration. Perhaps the simplest method is to differentiate the discrete displacement data using finite difference approximations. However, this introduces significant noise error into the calculations, and makes it difficult to determine which oscillations (particularly in the acceleration and drag histories) are physical and which are noise-driven. Following the experiments, we could use a polynomial fit to the drift data, and then differentiate the fitted curve to obtain velocity and acceleration curves. Although preferable over the finite difference method, this strategy also has its drawbacks. Experimental data have shown that the drift history of the cylinders is well approximated by a quadratic polynomial. Fitting the drift data with a quadratic (or even cubic) polynomial then restricts the acceleration to, at best, a linear function. Of course, higher order polynomial fits are possible, but they are still unable to capture the high-frequency oscillations that end up characterizing the acceleration. Taking advantage of the type of quantitative analysis allowed by numerical simulations, we derive integral expressions for the center-of-mass velocity and acceleration, which minimize unnecessary noise error in the calculation. Assuming constant liquid mass in the computational domain (zero mass flux across volume boundaries), usage of the continuity equation and the divergence theorem allow simplification of the time derivatives of (12). Taking a derivative with respect to time through the integral in the numerator of (12) and simplifying yields the following expression for the center-of-mass velocity:

$$\begin{aligned} \bar{\mathbf {u}} = \frac{\int \alpha _l \rho _l \mathbf {u} \, {\mathrm {dV}}}{\int \alpha _l \rho _l \, {\mathrm {dV}}}. \end{aligned}$$

(13)

Note that the integrals in the denominators of (12) and (13) represent the total liquid mass in the domain, and can be treated as constants with respect to time under the given assumptions. Taking a time derivative of (13) then yields the following for the acceleration of the center of mass:

$$\begin{aligned} \bar{\mathbf {a}} = \frac{\frac{d}{dt} \int \alpha _l \rho _l \mathbf {u} \, {\mathrm {dV}}}{\int \alpha _l \rho _l \, {\mathrm {dV}}} = \frac{\int \frac{\partial }{\partial t} (\alpha _l \rho _l \mathbf {u}) \, {\mathrm {dV}}}{\int \alpha _l \rho _l \, {\mathrm {dV}}}. \end{aligned}$$

(14)

This can be directly calculated from our solver since $\alpha _l \rho _l \mathbf {u}$ is known everywhere in the domain at each timestep. It can be shown that (14) is equivalent to

$$\begin{aligned} \bar{\mathbf {a}} = \frac{\int \alpha _l \rho _l \mathbf {a} \, {\mathrm {dV}}}{\int \alpha _l \rho _l \, {\mathrm {dV}}}, \qquad \mathbf {a} = \frac{{\mathrm {D}} \mathbf {u}}{{\mathrm {D}}t} = \frac{\partial \mathbf {u}}{\partial t} + \mathbf {u} \cdot \nabla \mathbf {u}, \end{aligned}$$

(15)

under the same assumptions. Mathematically, (14) and (15) are equivalent. However, from a computational standpoint, it is preferable to use (14) since it involves only a finite difference approximation in time, whereas (15) requires finite difference approximations in both time and space. The integral expressions (13) and (14) allow us to calculate accurate time histories of the center-of-mass velocity and acceleration, while minimizing the amount of noise error in the calculation. Once liquid mass is lost through the volume boundaries, (13) and (14) do not hold, and we terminate their calculation.

4 Results and discussion

4.1 Qualitative features of breakup

Similar qualitative flow features of the breakup process are observed over the range of simulated shock Mach numbers, with the only differences arising when quantifying relevant length and time scales. Therefore, in describing the flow features, we will, in this section, focus solely on the Mach 1.47 case. A time history of the breakup process is shown in Fig. 4, where the shock (and subsequent flow) is moving from left to right. The incident shock and the subsequent wave system in the wake of the deforming cylinder are visualized using a numerical schlieren function¹ As previously mentioned, the actual traversal of the shock wave over the cylinder does little in terms of cylinder deformation. The shock’s influence, or lack of it, on the cylinder is attributed to the fact that the time scale of the shock is smaller than the relaxation time of the cylinder [1]. In fact, during the very early stages, the cylinder can be approximated as a rigid cylinder. The original shock and reflected wave are seen in Fig. 4b. Behind the reflected wave, there is a high pressure region associated with the forward stagnation point. At a critical angle preceding the equator of the cylinder, the shock reflection transitions from a regular reflection to a Mach reflection shown in Fig. 4c. This transition marks the peak drag experienced by the cylinder. This phenomenon has been studied in the literature for rigid cylinders and spheres [34, 35]. The convergence of the Mach stems behind the cylinder results in a secondary wave system (Fig. 4d) that generates high pressures at the rear stagnation point. The non-uniform pressure field around the cylinder results in an initial flattening that is reinforced by the pulling of material away from the equator by the surrounding flow. It has been suggested that the early time flattening is independent of viscosity or material type at large Weber numbers [24]. In conjunction with the lateral elongation, tips are observed to form on the cylinder’s periphery (Fig. 4e–g), which are thought to be the onset of the stripping process [3]. In time, these tips are drawn downstream into thin filaments. Though not captured in these simulations (due to the absence of surface tension), the rise of capillary instabilities in these filaments causes them to break up downstream. Behind the cylinder, unsteady vortex shedding drives the formation of a complex wake. Initially, the wake consists of a single large vortex seen in Fig. 4d–f. As more vortices are shed, the wake becomes increasingly chaotic. This vortical structure is observed to entrain downstream fluid and jet it upstream to impinge on the back of the cylinder. This upstream jet persists for the duration of the simulation. Within the wake, a standing shock can also be observed (Fig.4e–g), which is associated with the turning of the locally supersonic flow.

Fig. 4

Numerical schlieren images (top) and filled pressure contours (bottom) of the breakup of a 4.8 mm cylinder at $t^*=$ a 0.000 b 0.008 c 0.017 d 0.090 e 0.171 f 0.262 g 0.444 h 0.626 i 0.808 j 1.036 behind a Mach 1.47 shock wave (top to bottom, left to right). Isocontours are shown for $\alpha _l \ge 0.9$

An interesting flow feature to note is the existence of recirculation regions near the equator of the deforming cylinder, which, as far as we are aware, has not been noted before in the literature. Consider for now the top half of the water cylinder. As the normal shock passes over the hemisphere, negative vorticity is generated by the baroclinic vorticity term, $\frac{1}{\rho ^2} \nabla \rho \times \nabla p$, which is transported downstream by the surrounding flow. This stream of negative vorticity is the source of vortex shedding that creates the wake behind the deforming cylinder. Along the back side of the cylinder, positive vorticity is generated again by the baroclinic term. The large vortex in the cylinder’s wake transports this positive vorticity up along the flattened back of the cylinder until it runs perpendicularly into the stream of negative vorticity coming off the front of the cylinder. These two streams of opposite vorticity interact to form the recirculation region seen in Fig. 5. The recirculation region is composed of two counter-rotating vortices that are trapped by the two vorticity streams and the cylinder body. This recirculation region persists through the early deformation times of the cylinder, and appears to contribute to the stripping mechanism at the edge of the cylinder. This would support Engel’s theory that stripping of water by vortices contributes to the formation of mist in the wake [6]. In time, as pressure forces flatten the cylinder, the two vorticity streams are bent parallel to the flow, and the recirculation region disappears.

Fig. 5

Positive (red) and negative (blue) vorticity streams interacting to form a recirculation region at $t^* = 0.171$

Another interesting flow feature observed in the numerical simulations is the aforementioned upstream jet in the wake behind the cylinder. It is a possibility that the jet is an artifact of assuming symmetry in the simulation. It is well known that for a large range of Reynolds numbers ($45 < Re < 10^5$), flow around a rigid cylinder will generate a von Kármán vortex street. The symmetry assumption is acceptable for early times since a finite time is required to establish the vortex street. For the Reynolds numbers corresponding to the simulations, it is conceivable that, if the symmetry assumption were to be relaxed, a vortex street may develop in the wake of the deforming water cylinder. If, indeed, a vortex street is established, the upstream jet may decrease in strength, or cease to exist altogether. Finally, we note that the jet would most likely change in three-dimensional simulations of a deforming spherical droplet due to the “flow-relieving effect” of the third dimension.

4.2 Comparison with experimental visualizations

Qualitative comparisons with experimental visualizations of the breakup process are shown in Fig. 6 for the passage of a Mach 1.47 shock over a 4.8 mm diameter cylinder. At these early times in the breakup process, it is hard to make any comparisons regarding the cylinder’s deformation. Instead, one can compare the primary and secondary wave systems that are generated as the shock interacts with the water cylinder. The locations of the primary wave system, consisting of the incident and reflected shock, coincide between the experiment and the numerical simulations for both time instances shown. The secondary wave system, generated when the Mach stems on both sides of the cylinder converge on the rear stagnation point, looks qualitatively similar between the experiment and simulation. A closer comparison reveals that the secondary waves in the simulation are slower than those of the experiment; pending further analysis, the exact cause of this discrepancy is difficult to identify.

Fig. 6

Holographic interferograms (left) [19] and numerical schlieren images (right) at $t=$ a 16.18$\,\upmu$s b 32.14$\,\upmu$s. Note that the values of time have been adjusted from the original work as described in Appendix B. Reprinted from [19] with permission from Springer

4.3 Comparison of subsonic and supersonic post-shock gas velocities

Numerical schlieren images of the breakup of the water cylinders behind Mach 1.30 and Mach 2.50 shocks are shown in Fig. 7. The supersonic gas velocity behind the Mach 2.50 shock is evidenced by the detached bow shock preceding the deforming water cylinder. Cylinder wakes for supersonic post-shock flow appear to be narrower than their subsonic counterparts, and standing shocks are visible along the length of the wake.

Fig. 7

Numerical schlieren images of the breakup behind Mach 1.30 (top) and Mach 2.50 (bottom) shock waves at $t^* =$ a 0.3543 b 0.5117 c 0.7479 d 0.9053

4.4 Deformation

Using holographic interferograms, Igra and Takayama [20] quantified the cylinder’s deformation by measuring its spanwise diameter, $d$, centerline width, $w$, and coherent body area, $A$. In the following plots, we compare our numerical results with the experimental measurements for the above deformation metrics. There exists, in our comparison, an inherent uncertainty associated with the methodology or criteria used to define the boundary of the deforming body. The first part of the uncertainty arises from the experimental data itself. From Igra and Takayama’s discussion, it is not possible to unambiguously identify the criteria they used to determine the boundaries of the deforming body. Furthermore, they provide no quantification of the error associated with their measurements of deformation.

Additional uncertainty in the comparison stems from our numerical method, which has diffuse interfaces in finite grid resolution. To define a nominal interface location, we choose a threshold liquid volume fraction, $\alpha _T$, to bound the cylinder, i.e., any computational cell with a liquid volume fraction $\alpha _l \ge \alpha _T$ is considered part of the cylinder. Because of the uncertainty in the experimental measurements, it is unclear what value $\alpha _T$ should take to best match the data. Therefore, instead of specifying a single value, a range is chosen in an attempt to bound the experimental data. This is demonstrated in Fig. 8, which plots the cylinder’s centerline width for the $M_S = 1.47$ case (the stepped nature of the curves is an artifact of approximating to the nearest grid cell). The curves in the plot represent four distinct values of $\alpha _T$ that range between $0.25 \le \alpha _T \le 0.99$. Since the following comparison plots will show a range of shock Mach numbers, which are differentiated by color, only two $\alpha _T$ curves will be plotted for each $M_S$.

Fig. 8

Centerline width of the deforming water cylinder for various $\alpha _T$. The inset contour plot shows the cylinder boundary as defined by the values of $\alpha _T$ at $t^* = 0.810$

Figures 9, 10, and 11 show, respectively, the centerline width, spanwise diameter, and coherent body area for four $M_S$ cases. After the passage of the shock wave, the cylinder’s deformation is characterized by flattening in the streamwise direction, which is quantified here as an increase in spanwise diameter and decrease in centerline width. As material is stripped off the cylinder’s periphery by the surrounding high-speed flow, the area of the cylinder monotonically decreases. Additional comparison data from the numerical work of Chen [3] are shown in Fig. 11. Though not a rigorous validation of our solver due to the aforementioned ambiguities, comparison with the experimental data provides confidence in the accuracy of the numerical results.

Fig. 9

Cylinder centerline width from Igra and Takayama’s [20] experiments (discrete), and our simulations (continuous). The arrow indicates the direction of increasing $\alpha _T$

Fig. 10

Cylinder spanwise diameter from Igra and Takayama’s [20] experiments (discrete), and our simulations (continuous). The arrow indicates the direction of increasing $\alpha _T$

Fig. 11

Cylinder coherent body area from Igra and Takayama’s [20] experiments (discrete), and our simulations (continuous). The arrow indicates the direction of increasing $\alpha _T$. The numerical results of Chen [3] (dashed) are shown for $\alpha _T = 0.9$

4.5 Cylinder drift and velocity

Before analyzing the unsteady acceleration and drag of the deforming cylinder, it is informative to first look at the detailed drift and velocity histories of the cylinder. The cylinder’s drift, as measured off the forward stagnation point, is shown in Fig. 12. For shock Mach numbers up to $M_S = 1.47$, our numerical results coincide well with the experimental measurements, falling within the error bounds, and show a slight improvement over the results from Chen [3]. For reasons not yet understood, our comparison appears to deteriorate with increasing shock Mach number (as evidenced by the discrepancy in the $M_S = 1.73$ case).

Fig. 12

Cylinder leading edge drift from Igra and Takayama’s [20] experiments (discrete), and our simulations (continuous). The arrow indicates the direction of increasing $\alpha _T$. The numerical results of Chen [3] (inverted filled triangle) are shown for $\alpha _T = 0.9$

As noted by Theofanous [38], the stagnation point drift of the cylinder is an inaccurate representation of the center-of-mass drift. To evaluate the significance of the error, we compute both the location of the cylinder’s center of mass [using (12)] and its leading edge (using $\alpha _T = 0.50$), and plot both in Fig. 13 for the full range of simulated shock Mach numbers. The intersection of the center-of-mass and leading edge curves can be seen for the $M_S = 2.00$ and $M_S = 2.50$ cases. Although both sets of drift curves exhibit similar overall behavior, it is obvious to see that significant errors are incurred in the acceleration calculation if the fitted polynomial is based on the leading edge trajectory. It is noted that the appropriate non-dimensionalization of time using the characteristic breakup time shown in (8) appears to collapse the cylinder trajectories across all simulated $M_S$.

Fig. 13

Drift as measured from the center of mass (solid) and forward stagnation point (dashed), and normalized by the original diameter

The cylinder’s streamwise center-of-mass velocity, $\bar{u}$, is computed using (13) and shown in Fig. 14. Though scaled using the same characteristic breakup time, $t^*$, as the drift curves, the velocity curves do not appear to collapse, and clearly show that stronger shocks induce higher cylinder velocities. This is expected since, in the shock-moving reference frame, post-shock air velocity increases with shock Mach number. From these velocity curves, it can also be seen that the transition from subsonic to supersonic freestream flow does not seem to significantly alter the cylinder’s behavior.

Fig. 14

Center-of-mass velocity normalized by the post-shock air velocity

4.6 Unsteady acceleration and drag coefficient

The unsteady acceleration of a droplet suddenly exposed to a high-speed flow, and specifically, its unsteady drag coefficient, is of interest in many applications. For example, when modeling flows with particle or droplet clouds, the drag coefficient is often the parameter used to model the dynamics of the disperse phase. Attempts to calculate the drag coefficient of a deforming body have often assumed constant acceleration [21, 31, 33]. Indeed, the acceleration data reported by Chen [3] are derived from the drift data under this assumption. Despite the ubiquity of this simplification in the literature, our numerical results lead us to believe that this is not an accurate representation of the underlying physics. For this reason, we do not make comparisons with Chen [3] for the cylinder acceleration and drag coefficient.

Using (14), we compute the acceleration in the streamwise direction experienced by the cylinder’s center of mass, $\bar{a}$. The results are plotted in Fig. 15, where acceleration has been non-dimensionalized by the original cylinder diameter and post-shock air velocity. The initial spike in acceleration is the passage of the shock wave over the cylinder. As mentioned in Sect. 4.1, the maximum acceleration occurs when the shock reflection on the cylinder’s surface transitions from a regular reflection to a Mach reflection. Once the shock has passed, the surrounding high-speed air begins to accelerate the cylinder. The oscillations in the acceleration curves are believed to be related to the vortex shedding process in the cylinder’s wake. It is observed that oscillation frequency and amplitude increase and decrease, respectively, as the incident shock Mach number is increased. These changes in frequency and amplitude can be attributed to differences in the development of the wake behind the deforming cylinder.

Fig. 15

Center-of-mass acceleration normalized by the original diameter and the post-shock air velocity

In the course of our numerical analysis, we found that scaling the non-dimensional acceleration by the pressure ratio across the incident shock wave resulted in collapse of the acceleration curves across all simulated shock Mach numbers. As far as we are aware, this has not been noted before in the literature. The rescaled non-dimensional acceleration, plotted in Fig. 16, is given by

$$\begin{aligned} \bar{a}^* = \bar{a} \bigg ( \frac{d_0}{u_g^2} \bigg ) \bigg ( \frac{p_1}{p_2} \bigg ), \end{aligned}$$

(16)

where $\frac{p_2}{p_1}$ is the pressure ratio across the incident shock.

Fig. 16

Center-of-mass acceleration rescaled by the pressure ratio across the incident shock

Now that we have an accurate acceleration history for the deforming cylinder, we can calculate its unsteady drag coefficient. The drag coefficient is defined as:

$$\begin{aligned} C_D = \frac{D}{\frac{1}{2}\rho u^2 S} = \frac{m\bar{a}}{\frac{1}{2}\rho _g (u_g-\bar{u})^2d}, \end{aligned}$$

(17)

where $\rho _g$ and $u_g$ are the post-shock air density and velocity, $\bar{u}$ and $\bar{a}$ are the velocity and acceleration of the cylinder’s center of mass calculated using (13) and (14), $m$ is the constant liquid mass in the computational domain, and $d$ is a characteristic spanwise diameter. If we take the characteristic spanwise diameter to be the original cylinder diameter, $d_0$, the computed drag coefficients, shown in Fig. 17, collapse across the range of simulated $M_S$, and all exhibit an upward trend.

Fig. 17

Unsteady drag coefficient based on the original diameter

Though a time-dependent drag coefficient can be used to model the dynamics of particles or droplets, an improvement can be made by realizing that the drag coefficient calculation should account for the changing spanwise diameter of the deforming cylinder. If we re-calculate the drag coefficient using the cylinder’s deformed diameter, $d_{\mathrm {def}}$, it is found that the resultant $C_D$, shown in Fig. 18, can be reasonably approximated as a constant over the initial breakup period. It is notable that wave drag (in the case of supersonic post-shock flow) does not significantly alter the drag coefficient (as would be expected in the rigid body case). Not only is this drag coefficient more physically correct than the one based on the original cylinder diameter, it also simplifies the modeling of particle and drop dynamics since it can be approximated as a constant for the early times of breakup.

Fig. 18

Unsteady drag coefficient based on the deformed diameter

5 Conclusions

The breakup of water cylinders in the flow behind normal shock waves has been simulated and is compared to published experimental and numerical data. Our results support previous experimental observations regarding the stripping breakup of the cylinders. Specifically, the water cylinder is initially compressed in the streamwise direction and extended in its spanwise dimension. Tips are formed at the cylinder’s periphery, which are drawn downstream by the surrounding flow. The stripping of material at the cylinder periphery is partly attributed to the presence of a recirculation region at the equator. The recirculation regions, not noted before in the literature, are observed to result from the interaction of two streams of opposite vorticity generated by baroclinic torque on the cylinder surface. Engel [6] hypothesized the existence of such vortices in the flow, which would contribute to the formation of mist in the wake. An upstream jet in the wake of the deforming cylinder is also observed to persist for long times. The strength of this jet is expected to be mitigated if either the symmetry assumption or the two-dimensional approximation is relaxed.

Comparison with experimental data for metrics of the cylinder’s deformation is hampered by uncertainties associated with the experimental measurements and the numerical method. However, reasonable agreement is shown to the extent that the numerical results are able to bound, and exhibit similar behavior to, the experimental results. The transition from subsonic to supersonic freestream flow does not alter the similarity of the solutions, and collapse is shown for the unsteady acceleration and drag coefficients for the range of simulated shock Mach numbers. The acceleration time histories of the deforming cylinders for different incident shock Mach numbers are shown to scale with the pressure ratio across the incident shock wave. Furthermore, the unsteady drag coefficient is seen to increase with time when computed using the constant original cylinder diameter. However, when computed using the cylinder’s deformed diameter, the unsteady drag coefficient can be approximated as a constant over the initial breakup period. Three-dimensional simulations and the inclusion of viscous and capillary effects in future simulations will facilitate comparison with droplet experiments, and capture even more of the multiscale and multiphase flow physics present in the breakup process.

Appendices

Appendix A: Grid resolution

As part of the grid resolution study, we simulated the Mach 1.47 shock wave case at three different resolutions. A time history of these simulations is shown in Fig. 19. Though the wake structure becomes more detailed as the grid is refined, the overall qualitative features of the breakup process remain similar. Features characteristic of stripping breakup, such as the initial flattening of the cylinder and the formation of tips at the cylinder’s periphery, are present at all three grid resolutions. The recirculation regions at the cylinder’s equator and the presence of an upstream jet in the wake are also observable at all levels of grid refinement. Quantitative measurements of cylinder deformation and center-of-mass properties, used in the comparison with experimental data, do not show significant differences between the original and doubled resolution. As an example, Fig. 20 plots the center-of-mass drift calculated at the three different grid resolutions, and shows negligible differences between the two finest grid sizes.

Fig. 19

Numerical schlieren images (top) and filled pressure contours (bottom) of the breakup of a 4.8 mm cylinder at $t^*=$ a 0.017 b 0.171 c 0.262 d 0.444 e 0.626 f 0.808 g 1.036 behind a Mach 1.47 shock. Isocontours are shown for $\alpha _l \ge 0.9$. Grid resolutions correspond to 600x300 (left), $1,\!200 \times 600$ (middle), and $2,\!400 \times 1,\!200$ (right) cells

Fig. 20

Center-of-mass drift measurements at three grid resolutions

Appendix B: Experimental visualization comparison

The holographic interferograms of [19] used in Fig. 6 were originally stated to be at $t = 23\,\upmu$s and $t = 43\,\upmu$s after “the interaction between the incident shock wave and the water column” [19]. We interpret this to mean the time after the shock reaches the leading edge of the water cylinder. A comparison of the experimental interferograms and the numerical schlieren images from our simulations at these times is shown in Fig. 21. It is clear from the figure that any comparison is difficult to make since the images appear to be taken at different times. In an attempt to reconcile the discrepancy, digital measurements of the distance traversed by the incident shock were taken from the interferograms. Our measurements indicate that the times should perhaps be closer to 16 and 32 $\upmu$s, respectively. Numerical schlieren images at these modified times are compared to the experimental interferograms in Fig. 6, and are seen to match the incident and reflected shock locations. There is an inherent uncertainty in the exact location of the boundary of the water cylinder, owing to the thick ring on the holographic interferograms. Measurements to obtain times of 16 and 32 $\upmu$s were taken by assuming the boundary to be located in the middle of the thick ring. Measurements taken from the edge of the ring resulted in alternate times of approximately 22 and 42 $\upmu$s, respectively, which are closer to the reported times in [19]. It is unclear whether this discrepancy in time is a result of a reporting error in the original work, or a misinterpretation, on our part, of what is meant by “the interaction between the incident shock wave and the water column” [19].

Fig. 21

Holographic interferograms (left) [19] and numerical schlieren images (right) at $t=$ a 23$\,\upmu$s b 43$\,\upmu$s. Reprinted from [19] with permission from Springer