1 Introduction

The earlier GPS satellites provide signals on two frequencies so that the users can form dual-frequency combination to remove first-order effects of ionospheric delay based on its dispersive nature. With GPS modernization, the new-generation GPS satellites, namely Block IIF satellites, transmit a third civilian signal L5 besides the legacy signals L1 and L2. In addition, other new-generation global navigation satellite system (GNSS) satellites are also capable of operating with three or more frequency bands, including Galileo satellites, BeiDou navigation satellite system (BDS) satellites, part of GLONASS-M satellites and all satellites of GLONASS-K series. More optimal linear combinations for carrier phase and code observations can be formed using the additional frequencies. Therefore, the benefits from the extra signal for the precise processing of GNSS data in terms of cycle slip detection and repair (Zhao et al. 2015), carrier phase multipath extraction (Simsky 2006) and especially ambiguity resolution (AR) in precise relative positioning (Feng 2008) can be expected.

Although the joint use of multi-frequency signals can bring great benefits, there still exist difficulties in multi-frequency integrated PPP. Montenbruck et al. (2010) first identified the presence of time-, signal- and satellite-dependent line biases in carrier phase observations based on a geometry-free and ionospheric-free (GFIF) carrier phase combination, namely the difference between L1/L2 and L1/L5 ionospheric-free (IF) combined carrier phase observations. In precise clock estimation (PCE), the time-varying phase biases will be grouped with satellite clock offset parameters. The satellite clock estimates will be different when using different observations, and the disagreement among them is defined as inter-frequency clock bias (IFCB). Hence, it is not appropriate to employ a set of precise satellite clock products for PPP processing across all frequency bands since the current GNSS satellite clock products are generated based on specific measurements, such as L1/L2 IF combined observations for GPS. Many efforts have been made to investigate the IFCB characteristics. For GPS Block IIF satellites, the peak-to-peak amplitude of single-day IFCB variations between L1/L5 and L1/L2 IF satellite clocks ranged from 2 to 27 cm during a whole year (Pan et al. 2017a), while the regional BDS (BDS-2) satellites showed significantly smaller time-varying IFCBs with a peak amplitude of approximately 4 cm (Zhao et al. 2016; Montenbruck et al. 2013). On the contrary, the consistency of different IF satellite clocks could be ensured and the marginal IFCB variations could be neglected for the Galileo satellites (Cai et al. 2016), quasi-zenith satellite system (QZSS) satellites (Steigenberger et al. 2013) and global BDS (BDS-3) satellites (Pan et al. 2017b). A harmonic analysis was conducted to obtain the exact periods of IFCB series, and then, they were used to model the IFCB. The IFCB modeling accuracy was about 10 and 20 mm for GPS Block IIF satellites and BDS-2 geostationary orbit (GEO) satellites, respectively (Li et al. 2013; Montenbruck et al. 2012). The IFCB models can be further employed to carry out real-time triple-frequency PPP through prediction.

The effects of IFCB on PPP have been analyzed by several researchers. Zhao et al. (2017) implemented the B1/B3-based BDS PPP. Their results indicated that the positioning accuracy of B1/B3 PPP degraded by several millimeters without IFCB corrections, and it could achieve comparable positioning performance with the traditional B1/B2 ones in both kinematic and static modes after applying IFCB corrections. Without careful IFCB consideration, the convergence time was lengthened by 7.5, 8.0 and 2.5 min in east, north and up directions, respectively, and the positioning accuracy was reduced by 2, 0 and 10 mm in the three directions, respectively, even if B1/B3 IF combined observables were further introduced into B1/B2 PPP processing (Pan et al. 2017b). Therefore, the IFCB issue must be carefully taken into account when users adopt different observations from satellite clock providers.

There are currently three methods to solve the IFCB issue. The first one is satellite clock determination (Guo and Geng 2017). The traditional dual-frequency IF model is expanded by adding the uncombined (UC) L5 observations so that two sets of satellite clock products, namely L5 UC satellite clocks and legacy L1/L2 IF satellite clocks, can be obtained. The L1/L5 IF satellite clocks can be derived by combining L5 UC and L1/L2 IF satellite clocks. The second one is the least-squares adjustment based on pass-by-pass time series of GFIF carrier phase combinations (Montenbruck et al. 2012). The last one is the epoch-differenced (ED) strategy (Li et al. 2016), in which the GFIF combinations are also employed, but the invariable phase ambiguities are removed by between-epoch single-difference. The latter two methods focused on the IFCB estimation rather than the satellite clock determination. All the three methods can be used to conduct triple-frequency PPP processing with L1/L5 and L1/L2 IF combinations as well as L1/L5-based dual-frequency PPP processing. Only the first one can be adopted to carry out triple-frequency PPP processing using UC observations. The last one outperforms the other two methods in terms of computational efficiency because the complicated handing of phase ambiguities is absent, but it is not compatible with the UC triple-frequency PPP. The computational efficiency is very important for real-time applications. The huge additional computational burden coming with the estimation of IFCBs or the second satellite clocks will increase the latency of real-time streams with satellite clock corrections, which may degrade the performance of real-time PPP. Therefore, an efficient estimation approach of IFCB for UC triple-frequency PPP is required.

The above three methods can be expanded to estimate the IFCBs or satellite clocks for the triple-frequency observations integrated into a single IF combination. However, there is an infinite number of triple-frequency IF combinations with only two conditions, namely removing the first-order ionospheric delay and keeping the geometric distance unchanged. According to different requirements of users, an additional criterion, such as integer ambiguities and minimum noises, should be added to uniquely determine the three combination coefficients. To obtain the desired various L1/L2/L5 IF IFCBs or satellite clocks, the three methods should be modified from time to time, which complicates the triple-frequency PPP processing with a single IF combination. A unified IFCB estimation approach, which can be applied to various triple-frequency IF combinations, is needed.

Theoretically, the satellite clock determination (Guo and Geng 2017) and the IFCB estimation (Montenbruck et al. 2012) are equivalent. However, the IFCB estimation approach is more compatible with the international GNSS service (IGS) since only a set of satellite clocks are provided by the IGS at present. If the IGS still insists to only provide L1/L2 IF satellite clocks in the future, the approach of satellite clock determination will be inconvenient for the multi-frequency users. For example, the users can only use either L1/L2 IF satellite clocks from IGS and L5 UC satellite clocks from other organizations, or two sets of satellite clocks from a single organization to implement UC triple-frequency PPP. Nevertheless, both ways may degrade PPP performance because of incompatibility or lower accuracy of satellite clock products. In contrast, the IFCB estimation approach is always compatible with IGS by combining IGS satellite clocks with IFCBs directly derived from observations. In addition, the satellite clocks cannot be predicted with a high accuracy due to their short-term fluctuations. On the contrary, the high-accuracy IFCB modeling and prediction can be realized, which simplifies the triple-frequency PPP processing in real-time situations. Therefore, we also focus on the IFCB estimation approaches rather than satellite clock determination. To conduct triple-frequency PPP processing based on L1/L2 and L1/L5 IF combined observations, UC observations, or various L1/L2/L5 IF combined observations, the L1/L5 IF, L5 UC or various L1/L2/L5 IF IFCBs should be estimated, respectively. If we can know the relationship among them, all of them may be derived by converting only a set of estimated IFCBs, such as L1/L5 IF IFCBs, and the multi-frequency integration will be easy. We will rigorously derive the mathematical conversion formula in this contribution.

In this study, we concentrate on the IFCB estimation approaches for triple-frequency PPP based on UC observations and IF combined observations within a single arbitrary combination. The structure of the paper is given as follows. Section 2 formulates the mathematical models of IFCB corrections and triple-frequency PPP. Section 3 presents the practicability of our IFCB estimation approaches and investigates the benefits from the third frequency through the comparison with dual-frequency PPP solutions. Section 4 summarizes the conclusions.

2 Methods

We first describe the IFCB estimation approaches for triple-frequency PPP based on UC observations and IF combined observations, respectively. Subsequently, the UC and IF triple-frequency PPP models are successively developed.

2.1 Estimation of IFCB for UC triple-frequency PPP

The code and carrier phase observations on a single frequency can be shown as follows:

$$ P_{i} = \rho + c{\text{d}}t_{r} - c{\text{d}}t + I \cdot \gamma_{i} + T + d_{r,i} + d_{i} $$
(1)
$$ \varPhi_{i} = \rho + c{\text{d}}t_{r} - c{\text{d}}t - I \cdot \gamma_{i} + T + N_{i} + b_{r,i} + b_{c,i} + b_{v,i} $$
(2)

with \( \gamma_{i} = {{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {f_{i}^{2} }}} \right. \kern-0pt} {f_{i}^{2} }} \) and i = (1, 2, 5) where f denotes the carrier frequency, P denotes the measured code, Φ denotes the measured carrier phase, ρ denotes geometric distance, cdt and cdtr denote the frequency-independent physical clock errors of the satellite and receiver, respectively, I denotes first-order slant ionospheric delay on L1 frequency, T denotes slant tropospheric delay, N denotes the integer ambiguity, dr and d denote the code-specific hardware delay at the receiver and satellite, respectively, br denotes the receiver-dependent phase hardware delay, and bc and bv denote the time-invariant and time-varying parts of satellite-dependent phase hardware delay, respectively. The triple-frequency GFIF carrier phase combinations, which are a linear combination of phase hardware delays at both satellite and receiver ends as well as the constant phase ambiguities, show consistent variations for the stations located in different areas and equipped with different types of receivers and antennas. Thus, the time-varying parts of phase-specific hardware delay at the receiver can be neglected (Pan et al. 2017a), and they are not shown in Eq. (2). As to the time-varying parts of code-specific hardware delay, they are also not shown in Eq. (1). In view that the weights of code observations are usually much smaller than those of carrier phase observations, the time-varying biases in code observations can be safely neglected (Guo and Geng 2017).

The hardware delay within code and carrier phase observations differs. However, we usually assume common clock in both carrier phase and code observation equations. Consequently, the constant code-specific hardware delay and time-varying parts of phase-specific hardware delay of the satellite will be absorbed by satellite clock parameters in the process of PCE. The current GPS precise satellite clocks provided by IGS are generated using L1/L2 IF combined carrier phase and code observations, and they can be written below:

$$ \begin{aligned} c{\text{d}}t_{{{\text{IF}},12}} &= c{\text{d}}t - (a_{12,1} \cdot d_{1} + a_{12,2} \cdot d_{2} ) \\ &\quad\, - (a_{12,1} \cdot b_{v,1} + a_{12,2} \cdot b_{v,2} ) \\ \end{aligned} $$
(3)

with \( a_{12,1} = {{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {(f_{1}^{2} - f_{2}^{2} )}}} \right. \kern-0pt} {(f_{1}^{2} - f_{2}^{2} )}} \) and \( a_{12,2} = {{ - f_{2}^{2} } \mathord{\left/ {\vphantom {{ - f_{2}^{2} } {(f_{1}^{2} - f_{2}^{2} )}}} \right. \kern-0pt} {(f_{1}^{2} - f_{2}^{2} )}} \) where cdtIF,12 is the L1/L2 IF satellite clocks.

The satellite clocks on a single frequency do not coincide with the L1/L2 IF satellite clocks due to the different hardware delays lumped into satellite clock offset estimates. For the purpose of solving this problem, the IFCB should be estimated, and then the L1/L2 IF satellite clocks can be converted into UC satellite clocks by combining them with estimated IFCBs. The conversion equations can be expressed as:

$$ \left\{ {\begin{array}{l} {c{\text{d}}t_{{{\text{UC}},1}} = c{\text{d}}t_{{{\text{IF}},12}} + \beta_{{{\text{UC}},1}} + \delta_{{{\text{UC}},1}} \;} \\ {c{\text{d}}t_{{{\text{UC}},2}} = c{\text{d}}t_{{{\text{IF}},12}} + \beta_{{{\text{UC}},2}} + \delta_{{{\text{UC}},2}} } \\ {c{\text{d}}t_{{{\text{UC}},5}} = c{\text{d}}t_{{{\text{IF}},12}} + \beta_{{{\text{UC}},5}} + \delta_{{{\text{UC}},5}} } \\ \end{array} } \right. $$
(4)

with

$$ \left\{ {\begin{array}{l} {\beta_{{{\text{UC}},1}} = - a_{12,2} \cdot {\text{DCB}}(P_{1} ,P_{2} )\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ {\beta_{{{\text{UC}},2}} = a_{12,1} \cdot {\text{DCB}}(P_{1} ,P_{2} )\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ {\beta_{{{\text{UC}},5}} = - a_{12,2} \cdot {\text{DCB}}(P_{1} ,P_{2} ) + {\text{DCB}}(P_{1} ,P_{5} )} \\ {\begin{array}{l} {\delta_{{{\text{UC}},1}} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ {\delta_{{{\text{UC}},2}} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ \end{array} } \\ \end{array} } \right. $$
(5)
$$ \left\{ {\begin{array}{l} {{\text{DCB}}(P_{1} ,P_{2} ) = d_{1} - d_{2} } \\ {{\text{DCB}}(P_{1} ,P_{5} ) = d_{1} - d_{5} } \\ \end{array} } \right. $$
(6)

where β is the code-specific IFCB (CIFCB), δ is the phase-specific IFCB (PIFCB), and cdtUC,1, cdtUC,2 and cdtUC,5 are the L1, L2 and L5 UC satellite clocks, respectively. The differential code bias (DCB) products can be provided by German Space Operations Center (DLR/GSOC) (Montenbruck et al. 2014). Since the ionospheric delay estimates will absorb the signal-dependent time-varying phase biases, the L1 and L2 UC PIFCBs are equal to zero. In other words, the PIFCB is not a problem for UC dual-frequency PPP. The L1 and L2 observations share the same ionospheric delay parameters with L5 observations, but the time-varying phase biases on L5 frequency are different from those on legacy frequencies. Therefore, an additional consideration of L5 UC PIFCB δUC,5 is necessary.

After the fully measured code and carrier phase are corrected using the L1, L2 and L5 UC satellite clocks shown in Eq. (4), the corresponding satellite clock parameters in Eqs. (1) and (2) will be vanished. The UC triple-frequency PPP observation equations can be described below:

$$ \left\{ {\begin{array}{l} \overline{P}_{1} = \rho + c{\text{d}}t_{r,E} + I_{E} + T\; \hfill \\ \;\;\;\;\;\;\; + [ - (a_{12,1} - a_{12,2} ) \cdot b_{v,1} - 2 \cdot a_{12,2} \cdot b_{v,2} ] \hfill \\ \overline{P}_{2} = \rho + c{\text{d}}t_{r,E} + I_{E} \cdot \gamma_{2} \hfill \\ \;\;\;\;\;\;\; + T + [ - 2 \cdot a_{12,1} \cdot b_{v,1} + (a_{12,1} - a_{12,2} ) \cdot b_{v,2} ] \hfill \\ \overline{P}_{5} = \rho + c{\text{d}}t_{r,E} + I_{E} \cdot \gamma_{5} \hfill \\ \;\;\;\;\;\;\; + T + g_{\text{UC}} + [a_{12,2} \cdot (\gamma_{2} + \gamma_{5} ) \cdot b_{v,1} \hfill \\ \;\;\;\;\;\;\; + a_{12,2} \cdot (1 - \gamma_{5} ) \cdot b_{v,2} + \delta_{{{\text{UC}},5}} ] \hfill \\ {\overline{\varPhi }_{1} = \rho + c{\text{d}}t_{r,E} - I_{E} + T + N_{1,E} } \hfill \\ {\overline{\varPhi }_{2} = \rho + c{\text{d}}t_{r,E} - I_{E} \cdot \gamma_{2} + T + N_{2,E} } \hfill \\ {\overline{\varPhi }_{5} = \rho + c{\text{d}}t_{r,E} - I_{E} \cdot \gamma_{5} + T + N_{5,E} + \delta_{{{\text{UC}},5}} } \hfill \\ \end{array} } \right. $$
(7)

with

$$ \left\{ {\begin{array}{l} {c{\text{d}}t_{r,E} = c{\text{d}}t_{r} + a_{12,1} \cdot d_{r,1} + a_{12,2} \cdot d_{r,2} } \hfill \\ {I_{E} = I - a_{12,2} \cdot (d_{r,2} - d_{r,1} ) + a_{12,2} \cdot (b_{v,2} - b_{v,1} )} \hfill \\ \begin{aligned} g_{\text{UC}} = ( - \gamma_{5} \cdot a_{12,2} - a_{12,1} ) \cdot d_{r,1} - a_{12,2} \cdot (1 - \gamma_{5} ) \hfill \\ \;\;\;\;\;\; \cdot d_{r,2} + d_{r,5} \hfill \\ \end{aligned} \hfill \\ \begin{aligned} N_{1,E} = N_{1} + b_{r,1} + b_{c,1} - d_{1} - (a_{12,1} - a_{12,2} ) \hfill \\ \;\;\;\;\;\; \cdot d_{r,1} - 2 \cdot a_{12,2} \cdot d_{r,2} \hfill \\ \end{aligned} \hfill \\ \begin{aligned} N_{2,E} = N_{2} + b_{r,2} + b_{c,2} - d_{2} - (a_{12,1} - \gamma_{2} \cdot a_{12,2} ) \hfill \\ \;\;\;\;\;\; \cdot d_{r,1} - a_{12,2} \cdot (1 + \gamma_{2} ) \cdot d_{r,2} \hfill \\ \end{aligned} \hfill \\ \begin{aligned} N_{5,E} = N_{5} + b_{r,5} + b_{c,5} - d_{5} - (a_{12,1} - \gamma_{5} \cdot a_{12,2} ) \hfill \\ \;\;\;\;\;\; \cdot d_{r,1} - a_{12,2} \cdot (1 + \gamma_{5} ) \cdot d_{r,2} \hfill \\ \end{aligned} \hfill \\ \end{array} } \right. $$
(8)

where \( g_{\text{UC}} \) denotes the receiver inter-frequency bias (IFB). The receiver clock estimates are equal to those of classic IF dual-frequency PPP. As the receiver code hardware delay differs among all three frequency bands, it could not be compensated by employing only a receiver clock parameter. To account for this, a common IFB parameter for all Block IIF satellites is introduced into L5 code observations. In addition to the time-varying phase biases, the receiver code hardware delays are also lumped into ionospheric delay estimates. The ambiguity estimates are non-integers because of the presence of hardware delays. The brackets in Eq. (7) describe the effects of time-varying phase biases that come with satellite clock correction on code observations. Since the effects may be smaller than those of code measurement noises, they are ignored in the following equations. \( \overline{P} \) and \( \overline{\varPhi } \) denote the corrected code and carrier phase observations, respectively, and are different from those in Eqs. (1) and (2) because they are corrected using the satellite clocks.

According to Eqs. (7) and (8), we can straightforwardly formulate the L5 UC PIFCB, that is:

$$ \begin{aligned} \delta_{{{\text{UC}},5}} & = a_{12,1} \cdot (1 - {{\gamma_{5} } \mathord{\left/ {\vphantom {{\gamma_{5} } {\gamma_{2} }}} \right. \kern-0pt} {\gamma_{2} }}) \cdot b_{v,1} - a_{12,2} \\ & \; \cdot (\gamma_{5} - 1) \cdot b_{v,2} - b_{v,5} \\ \end{aligned} $$
(9)

It is obvious that the L5 UC PIFCB is a linear combination of time-varying phase biases across all frequency bands.

The PIFCBs between L1/L5 and L1/L2 IF satellite clocks can be efficiently estimated with the ED strategy based on the triple-frequency GFIF carrier phase combinations (Li et al. 2016). The correctness and feasibility of L1/L5 IF PIFCBs have been validated by implementation of triple-frequency PPP with L1/L5 and L1/L2 IF combinations (Pan et al. 2017a). The L1/L5 IF PIFCB δIF,15 can be formulated as:

$$ \begin{aligned} \delta_{{{\text{IF}},15}} &= \left( {a_{12,1} \cdot b_{v,1} + a_{12,2} \cdot b_{v,2} } \right) - \left( {a_{15,1} \cdot b_{v,1} + a_{15,2} \cdot b_{v,5} } \right) \hfill \\ &= (a_{12,1} - a_{15,1} ) \cdot b_{v,1} + a_{12,2} \cdot b_{v,2} - a_{15,2} \cdot b_{v,5} \hfill \\ \end{aligned} $$
(10)

with \( a_{15,1} = {{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {(f_{1}^{2} - f_{5}^{2} )}}} \right. \kern-0pt} {(f_{1}^{2} - f_{5}^{2} )}} \) and \( a_{15,2} = - {{f_{5}^{2} } \mathord{\left/ {\vphantom {{f_{5}^{2} } {(f_{1}^{2} - f_{5}^{2} )}}} \right. \kern-0pt} {(f_{1}^{2} - f_{5}^{2} )}} \).

If we multiply both sides of Eq. (9) by a scaling factor \( a_{15,2} \), the following equation can be derived:

$$ \begin{aligned} \delta_{{{\text{UC}},5}} \cdot a_{15,2} &= (a_{12,1} - a_{15,1} ) \cdot b_{v,1} \\ &\quad\; + a_{12,2} \cdot b_{v,2} - a_{15,2} \cdot b_{v,5} = \delta_{{{\text{IF}},15}} \\ \end{aligned} $$
(11)

As a result of Eq. (11), the following equation can be obtained:

$$ \delta_{{{\text{UC}},5}} = {{\delta_{{{\text{IF}},15}} } \mathord{\left/ {\vphantom {{\delta_{{{\text{IF}},15}} } {a_{15,2} }}} \right. \kern-0pt} {a_{15,2} }} $$
(12)

Therefore, the estimated L1/L5 IF PIFCBs divided by a constant \( a_{15,2} \) can be directly converted into L5 UC PIFCBs.

2.2 Estimation of IFCB for triple-frequency PPP with a single arbitrary IF combination

As discussed in the previous sections, the IFCB issue has been well solved for triple-frequency PPP based on two dual-frequency IF combinations L1/L5 and L1/L2. We only focus on the IFCB estimation approach for PPP directly integrating the triple-frequency observations into an IF combination in this study. To cancel first-order ionospheric delay and keep geometric range unchanged, the combination coefficients for each triple-frequency IF combination must fulfill the following two conditions:

$$ \left\{ {\begin{array}{l} {e_{1} + e_{2} + e_{5} = 1\;\;\;\;\;\;\;\;\;\;} \\ {e_{1} + e_{2} \cdot \gamma_{2} + e_{5} \cdot \gamma_{5} = 0} \\ \end{array} } \right. $$
(13)

where \( e_{1} \), \( e_{2} \) and \( e_{5} \) are the combination coefficients of L1, L2 and L5 signals, respectively. Note that the three unknown coefficients cannot be solved with such two conditions, and they are various according to different further criteria, for example, long wave length, integer ambiguities and minimum noises.

Similar to the L1/L2 IF satellite clocks shown in Eq. (3), the satellite clock estimates based on a triple-frequency IF combination \( (e_{1} ,e_{2} ,e_{5} ) \) can be theoretically formulated as:

$$ \begin{aligned} c{\text{d}}t_{{{\text{IF}},125}} &= c{\text{d}}t - (e_{1} \cdot d_{1} + e_{2} \cdot d_{2} + e_{5} \cdot d_{5} ) \\ &\quad\; - (e_{1} \cdot b_{v,1} + e_{2} \cdot b_{v,2} + e_{5} \cdot b_{v,5} ) \\ \end{aligned} $$
(14)

where cdtIF,125 denotes the L1/L2/L5 IF satellite clocks. In conjunction with Eq. (3), the hardware delays lumped into the two kinds of satellite clocks are different.

To compensate the different effects of hardware delays on L1/L2/L5 and L1/L2 IF satellite clocks, the similar IFCBs between them are also introduced, as given below:

$$ c{\text{d}}t_{{{\text{IF}},125}} = c{\text{d}}t_{{{\text{IF}},12}} + \beta_{{{\text{IF}},125}} + \delta_{{{\text{IF}},125}} $$
(15)

where βIF,125 and δIF,125 denote the L1/L2/L5 IF CIFCB and PIFCB, respectively. It is expected that the current GPS precise satellite clocks can also be converted into L1/L2/L5 IF satellite clocks through the high-accuracy IFCB estimation.

The L1, L2 and L5 UC CIFCB obtained using DCB products as given by Eq. (5) can be used to calculate the L1/L2/L5 IF CIFCB through a simple linear transformation, that is:

$$ \begin{aligned} \beta_{{{\text{IF}},125}} & = (a_{12,1} \cdot d_{1} + a_{12,2} \cdot d_{2} ) \\ & \quad - (e_{1} \cdot d_{1} + e_{2} \cdot d_{2} + e_{5} \cdot d_{5} ) \\ & = e_{1} \cdot \beta_{UC,1} + e_{2} \cdot \beta_{UC,2} + e_{5} \cdot \beta_{UC,5} \\ \end{aligned} $$
(16)

As to the L1/L2/L5 IF PIFCB, it can be formulated as:

$$ \begin{aligned} \delta_{{{\text{IF}},125}} & = \left( {a_{12,1} \cdot b_{v,1} + a_{12,2} \cdot b_{v,2} } \right) \\ & \quad - \left( {e_{1} \cdot b_{v,1} + e_{2} \cdot b_{v,2} + e_{5} \cdot b_{v,5} } \right) \\ & = c_{1} \cdot b_{v,1} + c_{2} \cdot b_{v,2} + c_{5} \cdot b_{v,5} \\ \end{aligned} $$
(17)

with

$$ \left\{ {\begin{array}{l} {c_{1} = a_{12,1} - e_{1} \;} \\ {c_{2} = a_{12,2} - e_{2} } \\ {c_{5} = - e_{5} \;\;\;\;\;\;\;} \\ \end{array} } \right. $$
(18)

where \( c_{1} \), \( c_{2} \) and \( c_{5} \) are the combination coefficients of time-varying phase biases in L1/L2/L5 IF PIFCB.

According to Eq. (13), the following two criteria should be satisfied for the three combination coefficients \( c_{1} \), \( c_{2} \) and \( c_{5} \), that is:

$$ \left\{ {\begin{array}{l} {c_{1} + c_{2} + c_{5} = 0\;\;\;\;\;\;\;\;\;\;} \\ {c_{1} + c_{2} \cdot \gamma_{2} + c_{5} \cdot \gamma_{5} = 0} \\ \end{array} } \right. $$
(19)

With Eq. (19), the coefficients \( c_{1} \) and \( c_{2} \) can be both expressed as a function of \( c_{5} \):

$$ \left\{ {\begin{array}{l} {c_{1} = \frac{{\gamma_{5} - \gamma_{2} }}{{\gamma_{2} - 1}} \cdot c_{5} } \\ {c_{2} = \frac{{1 - \gamma_{5} }}{{\gamma_{2} - 1}} \cdot c_{5} \;} \\ \end{array} } \right. $$
(20)

Inserting Eq. (20) into Eq. (17), we can obtain:

$$ \begin{aligned} \delta_{{{\text{IF}},125}} & = \frac{{\gamma_{5} - \gamma_{2} }}{{\gamma_{2} - 1}} \cdot c_{5} \cdot b_{v,1} + \frac{{1 - \gamma_{5} }}{{\gamma_{2} - 1}} \cdot c_{5} \cdot b_{v,2} + c_{5} \cdot b_{v,5} \\ \;\;\;\;\;\;\;\; & = \left( {\frac{{\gamma_{5} - \gamma_{2} }}{{\gamma_{2} - 1}} \cdot b_{v,1} + \frac{{1 - \gamma_{5} }}{{\gamma_{2} - 1}} \cdot b_{v,2} + b_{v,5} } \right) \cdot c_{5} \\ \;\;\;\;\;\;\;\; & = \left( {\frac{{\gamma_{5} - \gamma_{2} }}{{\gamma_{2} - 1}} \cdot b_{v,1} + \frac{{1 - \gamma_{5} }}{{\gamma_{2} - 1}} \cdot b_{v,2} + b_{v,5} } \right) \cdot \left( { - e_{5} } \right) \\ \end{aligned} $$
(21)

Since both \( \gamma_{2} \) and \( \gamma_{5} \) are constants, the L1/L2/L5 IF PIFCBs for different triple-frequency IF combinations are proportionally correlated with each other.

Actually, the L1/L5 IF combination is a special case of triple-frequency IF combination in case of a combination coefficient setting of zero for L2 signal. Combining Eqs. (10) and (21), the following relationship between L1/L2/L5 IF PIFCBs and L1/L5 IF PIFCBs can be derived:

$$ \delta_{{{\text{IF}},125}} = {{\delta_{{{\text{IF}},15}} \cdot e_{5} } \mathord{\left/ {\vphantom {{\delta_{{{\text{IF}},15}} \cdot e_{5} } {a_{15,2} }}} \right. \kern-0pt} {a_{15,2} }} $$
(22)

Therefore, the estimated L1/L5 IF PIFCBs can also be directly converted into L1/L2/L5 IF PIFCBs if scaled by \( {{e_{5} } \mathord{\left/ {\vphantom {{e_{5} } {a_{15,2} }}} \right. \kern-0pt} {a_{15,2} }} \).

The PIFCB estimation approach proposed here provides a concise conversion of L1/L5 IF PIFCBs derived from the traditional ED strategy. In other words, our approach is also based on the traditional ED strategy. It should be noted that the traditional ED strategy adopting the differences between L1/L2 and L1/L5 IF combinations can only be used to estimate the L1/L5 IF PIFCBs rather than the L1/L2/L5 IF PIFCBs or L5 UC PIFCBs. Actually, the traditional ED strategy can be expanded to estimate the L1/L2/L5 IF PIFCBs by using the differences between L1/L2 and L1/L2/L5 IF combinations. There will be slight differences between the converted L1/L2/L5 IF PIFCBs using the estimated L1/L5 IF PIFCBs shown in Eq. (22) and the estimated L1/L2/L5 IF PIFCBs using the expanded ED strategy due to the different effects of phase multipath and noise errors as well as the errors from the accumulation of respective ED PIFCBs. The scale factor shown in Eq. (22) may also affect the differences between the two sets of L1/L2/L5 IF PIFCBs because it can enlarge or reduce the above effects. However, a scale factor of larger than 1 does not mean that the approach proposed here will achieve worse L1/L2/L5 IF PIFCB estimates than the expanded ED strategy. A scale factor of larger than 1 only means that the accuracy of the converted L1/L2/L5 IF PIFCBs is worse than that of the estimated L1/L5 IF PIFCBs derived from the traditional ED strategy rather than the estimated L1/L2/L5 IF PIFCBs derived from the expanded ED strategy. If the scale factor \( {{e_{5} } \mathord{\left/ {\vphantom {{e_{5} } {a_{15,2} }}} \right. \kern-0pt} {a_{15,2} }} \) is relatively larger, the triple-frequency combination coefficient \( e_{5} \) must be larger, resulting in larger noise amplification factor when using the expanded ED strategy to estimate the L1/L2/L5 IF PIFCBs. Consequently, the accuracy of the estimated L1/L2/L5 IF PIFCBs also degrades. Theoretically, the accuracy of the converted L1/L2/L5 IF PIFCBs is comparable to that of the estimated L1/L2/L5 IF PIFCBs. According to Eq. (22), the accuracy of the converted L1/L2/L5 IF PIFCBs is only related to the magnitude of the combination coefficient \( e_{5} \). To achieve better converted L1/L2/L5 IF PIFCBs, the coefficient \( e_{5} \) should be relatively small. We suggest that the coefficient \( e_{5} \) should be preferably smaller than 2.

According to Eqs. (4), (5), (12), (15), (16) and (22), it is important to note that the satellite clocks for triple-frequency PPP based on UC observations or any triple-frequency IF combined observations can be derived by combining the current precise satellite clock products with DCB products as well as a set of L1/L5 IF PIFCB corrections. This will minimize the workload of satellite clock providers and multi-frequency PPP users.

2.3 UC triple-frequency PPP model

The slant tropospheric delays can be split into wet and dry parts, and the individual zenith delays and mapping functions can be used to model them. The wet part is estimated as unknown parameters from observations, while the dry part is usually corrected with a priori model. With L5 UC PIFCB corrections and precise satellite orbits, the corresponding terms in Eq. (7) can be removed. The linearized observation model for UC triple-frequency PPP can be written as:

$$ \left\{ {\begin{array}{l} {p_{1} = \mu \cdot X + c{\text{d}}t_{r,E} + I_{E} + m \cdot Z\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ {p_{2} = \mu \cdot X + c{\text{d}}t_{r,E} + I_{E} \cdot \gamma_{2} + m \cdot Z\;\;\;\;\;\;\;\;\;\;\;} \\ {p_{5} = \mu \cdot X + c{\text{d}}t_{r,E} + I_{E} \cdot \gamma_{5} + m \cdot Z + g_{\text{UC}} \;\;\;} \\ {\begin{array}{l} {\varphi_{1} = \mu \cdot X + c{\text{d}}t_{r,E} - I_{E} + m \cdot Z + N_{1,E} \;\;\;\;\;\;\;} \\ {\varphi_{2} = \mu \cdot X + c{\text{d}}t_{r,E} - I_{E} \cdot \gamma_{2} + m \cdot Z + N_{2,E} \;\;} \\ {\varphi_{5} = \mu \cdot X + c{\text{d}}t_{r,E} - I_{E} \cdot \gamma_{5} + m \cdot Z + N_{5,E} \;\;} \\ \end{array} } \\ \end{array} } \right. $$
(23)

where \( p \) and \( \varphi \) denote code and phase OMC (observed minus computed) observables, respectively, \( \mu \) denotes vector of line of sight direction, X denotes receiver coordinates in three dimensions, m denotes wet mapping function, and Z denotes tropospheric zenith wet delay (ZWD). Although the Earth tides, relativistic effects, phase center offset (PCO) and variation (PCV), and phase windup effects are not included in Eq. (23), they should be mitigated with corresponding models (Petit and Luzum 2010; Kouba 2009). Currently, there are no PCO and PCV corrections for L5 frequency. It is simply assumed that the L2 frequency shares the same corrections as those on L5 frequency due to the small differences between the two frequencies.

The estimated parameters include receiver positions, receiver clocks, slant ionospheric delays, ZWD, IFB and float ambiguities, and can be expressed as:

$$ S_{\text{UC}} = \left[ {X,c{\text{d}}t_{r,E} ,I_{E} ,Z,g_{\text{UC}} ,N_{1,E} ,N_{2,E} ,N_{5,E} } \right]^{\text{T}} $$
(24)

where \( S_{\text{UC}} \) denotes estimates vector.

The determination of proper stochastic models is also a key factor to improve triple-frequency PPP performance. Since the observations with low elevations are more susceptible to atmospheric refractions, multipath errors and measurement noises than those attaining high elevations, the elevation-dependent weighting scheme is adopted in this study (Gerdan 1995). Assuming that the three signals have the same a priori noises, and the observations from different satellites of different types or on different frequencies are uncorrelated, the covariance matrix of UC observations reads:

$$ Q_{\text{UC}} = {\text{diag}}\left( {\sigma_{P}^{2} ,\sigma_{P}^{2} ,\sigma_{P}^{2} ,\sigma_{\varPhi }^{2} ,\sigma_{\varPhi }^{2} ,\sigma_{\varPhi }^{2} } \right) $$
(25)

with \( \sigma_{P} = {{k_{1} } \mathord{\left/ {\vphantom {{k_{1} } {\sin (el)}}} \right. \kern-0pt} {\sin (el)}} \) and \( \sigma_{\varPhi } = {{k_{2} } \mathord{\left/ {\vphantom {{k_{2} } {\sin (el)}}} \right. \kern-0pt} {\sin (el)}} \) where both k1 and k2 are constants, which are usually set to 0.3 m and 0.003 m for code and phase observations, respectively, and el denotes satellite elevation angles.

2.4 Triple-frequency PPP model based on a single IF combination

We adopt the minimum noises as an additional condition to uniquely determine the three combination coefficients \( e_{1} \), \( e_{2} \) and \( e_{5} \) in this contribution. The optimal estimates for the three coefficients can be obtained by the Lagrangian equation \( R(e_{1} ,e_{2} ,e_{5} ,\kappa_{1} ,\kappa_{2} ) = e_{1}^{2} + e_{2}^{2} + e_{5}^{2} + \kappa_{1} \cdot (e_{1} + e_{2} + e_{5} - 1) + \kappa_{2} \cdot (e_{1} + e_{2} \cdot \gamma_{2} + e_{5} \cdot \gamma_{5} ) = \hbox{min} \). The partial derivatives of \( R \) with respect to each estimate (\( e_{1} \), \( e_{2} \), \( e_{5} \), \( \kappa_{1} \) and \( \kappa_{2} \)) are first taken, and the coefficients can then be obtained by letting the derivatives be zeroes. The triple-frequency IF combination for code and carrier phase observations can be formed as follows:

$$ \left\{ {\begin{array}{l} {P_{{{\text{IF}},125}} = e_{1} \cdot P_{1} + e_{2} \cdot P_{2} + e_{5} \cdot P_{5} \;\;} \\ {\varPhi_{{{\text{IF}},125}} = e_{1} \cdot \varPhi_{1} + e_{2} \cdot \varPhi_{2} + e_{5} \cdot \varPhi_{5} } \\ \end{array} } \right. $$
(26)

with

$$ \left\{ {\begin{array}{l} {e_{1} = \frac{{\gamma_{2}^{2} + \gamma_{5}^{2} - \gamma_{2} - \gamma_{5} }}{{2 \cdot (\gamma_{2}^{2} + \gamma_{5}^{2} - \gamma_{2} \cdot \gamma_{5} - \gamma_{2} - \gamma_{5} + 1)}}} \\ {e_{2} = \frac{{\gamma_{5}^{2} - \gamma_{2} \cdot \gamma_{5} - \gamma_{2} + 1}}{{2 \cdot (\gamma_{2}^{2} + \gamma_{5}^{2} - \gamma_{2} \cdot \gamma_{5} - \gamma_{2} - \gamma_{5} + 1)}}} \\ {e_{5} = \frac{{\gamma_{2}^{2} - \gamma_{2} \cdot \gamma_{5} - \gamma_{5} + 1}}{{2 \cdot (\gamma_{2}^{2} + \gamma_{5}^{2} - \gamma_{2} \cdot \gamma_{5} - \gamma_{2} - \gamma_{5} + 1)}}} \\ \end{array} } \right. $$
(27)

Using Eq. (27), the numerical values of the coefficients \( e_{1} \), \( e_{2} \) and \( e_{5} \) are 2.3269, − 0.3596 and − 0.9673, respectively.

Currently, only 12 GPS satellites, namely all the Block IIF satellites, have the capability of L5 emitting. It is impossible to carry out the PPP processing with L1/L2/L5 IF combined observations alone. Therefore, the L1/L2 IF combined observations from other GPS satellites are also introduced into the processing so that reliable PPP solutions can be achieved. The L1/L2 IF combination for code and carrier phase observations can be described below:

$$ \left\{ {\begin{array}{l} {P_{{{\text{IF}},12}} = a_{12,1} \cdot P_{1} + a_{12,2} \cdot P_{2} \;} \\ {\varPhi_{{{\text{IF}},12}} = a_{12,1} \cdot \varPhi_{1} + a_{12,2} \cdot \varPhi_{2} } \\ \end{array} } \right. $$
(28)

The numerical values of the coefficients \( a_{12,1} \) and \( a_{12,2} \) are 2.5457 and −1.5457, respectively.

After applying the precise satellite orbits and clocks, the linearized observation equations of Block IIF satellites [Eq. (29)] and other GPS satellites [Eq. (30)] for triple-frequency PPP based on a single IF combination can be written as:

$$ \left\{ {\begin{array}{l} {p_{{{\text{IF}},125}} = \mu \cdot X + c{\text{d}}t_{r,E} + m \cdot Z + g_{\text{IF}} \;\;\;} \\ {\varphi_{{{\text{IF}},125}} = \mu \cdot X + c{\text{d}}t_{r,E} + m \cdot Z + N_{125,E} } \\ \end{array} } \right. $$
(29)
$$ \left\{ {\begin{array}{l} {p_{IF,12} = \mu \cdot X + c{\text{d}}t_{r,E} + m \cdot Z\;\;\;\;\;\;\;\;\;\;} \\ {\varphi_{IF,12} = \mu \cdot X + c{\text{d}}t_{r,E} + m \cdot Z + N_{12,E} } \\ \end{array} } \right. $$
(30)

with

$$ \begin{array}{l} {c{\text{d}}t_{r,E} = c{\text{d}}t_{r} + a_{12,1} \cdot d_{r,1} + a_{12,2} \cdot d_{r,2} } \hfill \\ {g_{\text{IF}} = (e_{1} - a_{12,1} ) \cdot d_{r,1} + (e_{2} - a_{12,2} ) \cdot d_{r,2} + e_{5} \cdot d_{r,5} } \hfill \\ \begin{aligned} N_{12,E} = a_{12,1} \cdot (N_{1} + b_{r,1} + b_{c,1} - d_{r,1} - d_{1} ) \hfill \\ \;\;\;\;\;\;\;\;\; +\, a_{12,2} \cdot (N_{2} + b_{r,2} + b_{c,2} - d_{r,2} - d_{2} ) \hfill \\ \end{aligned} \hfill \\ \begin{aligned} N_{125,E} = e_{1} \cdot (N_{1} + b_{r,1} + b_{c,1} - d_{1} ) + e_{2} \cdot (N_{2} + b_{r,2} + b_{c,2} - d_{2} ) \hfill \\ \;\;\;\;\;\;\;\;\; +\, e_{5} \cdot (N_{5} + b_{r,5} + b_{c,5} - d_{5} ) - a_{12,1} \cdot d_{r,1} - a_{12,2} \cdot d_{r,2} \hfill \\ \end{aligned} \hfill \\ {} \hfill \\ \end{array} $$
(31)

where \( p_{{{\text{IF}},125}} \) and \( p_{{{\text{IF}},12}} \) denote the code OMC observables for Block IIF satellites and other GPS satellites, respectively, while \( \varphi_{{{\text{IF}},125}} \) and \( \varphi_{{{\text{IF}},12}} \) denote the corresponding phase OMC observables. The IF triple-frequency PPP also shares the same receiver clock estimates as those in traditional IF dual-frequency PPP. In order to mitigate the inconsistency of receiver code hardware delays between L1/L2/L5 and L1/L2 IF combinations, a constant IFB parameter \( g_{\text{IF}} \) is estimated besides receiver clocks. Comparing Eq. (31) with Eq. (8), it is noted that the IFB estimates are different in IF and UC triple-frequency PPP models, although we design the same parameters for them.

The unknown parameters including receiver positions, receiver clocks, ZWD, IFB and float ambiguities need to be estimated, that is:

$$ S_{\text{IF}} = \left[ {X,c{\text{d}}t_{r,E} ,Z,g_{\text{IF}} ,N_{12,E} ,N_{125,E} } \right]^{\text{T}} $$
(32)

where \( S_{IF} \) denotes estimates vector for IF triple-frequency PPP.

As to the stochastic models, they can be obtained by using error propagation law. The covariance matrices of measurements from GPS satellites with L1/L2/L5 transmitting (QIF,125) and GPS satellites with L1/L2 transmitting (QIF,12) read:

$$ Q_{{{\text{IF}},125}} = \left[ {\begin{array}{*{20}l} {(e_{1}^{2} + e_{2}^{2} + e_{5}^{2} ) \cdot \sigma _{P}^{2} } \hfill &\quad 0 \hfill \\ 0 \hfill &\quad {(e_{1}^{2} + e_{2}^{2} + e_{5}^{2} ) \cdot \sigma _{\Phi }^{2} } \hfill \\ \end{array} } \right] $$
(33)
$$ Q_{{{\text{IF}},12}} = \left[ {\begin{array}{*{20}l} {(a_{{12,1}}^{2} + a_{{12,2}}^{2} ) \cdot \sigma _{P}^{2} } \hfill &\quad 0 \hfill \\ 0 \hfill &\quad {(a_{{12,1}}^{2} + a_{{12,2}}^{2} ) \cdot \sigma _{\Phi }^{2} } \hfill \\ \end{array} } \right] $$
(34)

With Eqs. (33) and (34), the noise amplification factor is 2.546 and 2.978 for L1/L2/L5 and L1/L2 IF combinations, respectively, suggesting that the triple-frequency IF combination has smaller combination noises than conventional dual-frequency IF combination.

2.5 Accuracy of PIFCB estimates

Both L5 UC PIFCBs and L1/L2/L5 IF PIFCBs can be obtained by a concise conversion of L1/L5 IF PIFCBs. Following the law of random error propagation, the accuracy of L5 UC and L1/L2/L5 IF PIFCB estimates can be evaluated provided that the accuracy of L1/L5 IF PIFCB estimates is known. We use the traditional ED strategy to efficiently estimate the L1/L5 IF PIFCBs based on the triple-frequency GFIF carrier phase combinations, which can be expressed as:

$$ \begin{aligned} {\text{GFIF}} & = (a_{12,1} \cdot \varPhi_{1} + a_{12,2} \cdot \varPhi_{2} ) \\ & \quad - (a_{15,1} \cdot \varPhi_{1} + a_{15,2} \cdot \varPhi_{5} ) \\ & = \delta_{IF,15} + N_{\text{GFIF}} + b_{{r,{\text{GFIF}}}} + b_{{c,{\text{GFIF}}}} \\ \end{aligned} $$
(35)

where \( N_{\text{GFIF}} \) is the phase ambiguity of GFIF combination and \( b_{{r,{\text{GFIF}}}} \) and \( b_{{c,{\text{GFIF}}}} \) are the linear combination of constant phase hardware delays of the receiver and the satellite, respectively.

With Eq. (35), the L1/L5 IF PIFCB can be described below:

$$ \delta_{{{\text{IF}},15}} = {\text{GFIF}} - (N_{\text{GFIF}} + b_{{r,{\text{GFIF}}}} + b_{{c,{\text{GFIF}}}} ) $$
(36)

If no cycle slips occur between two adjacent epochs, the invariable phase ambiguity terms and the constant phase hardware delay terms in Eq. (36) can be eliminated by differencing the GFIF combinations at the two epochs. The ED L1/L5 IF PIFCB for satellite s at station r between epochs t and t − 1 can be computed as:

$$ \Delta \delta_{{{\text{IF}},15,r}}^{s} (t,t - 1) = {\text{GFIF}}_{r}^{s} (t) - {\text{GFIF}}_{r}^{s} (t - 1) $$
(37)

It is assumed that there are a total of n stations at which the satellite s is successfully tracked for the two adjacent epochs t and t − 1 in the global reference network. A weighted average of the solutions over the entire network can be used to calculate the final ED L1/L5 IF PIFCB estimates for satellite s between epochs t and t − 1, that is:

$$ \begin{aligned} & \Delta \delta_{{{\text{IF}},15}}^{s} (t,t - 1) \\ & \;\; = {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {\Delta \delta_{{{\text{IF}},15,r}}^{s} (t,t - 1) \cdot w_{r}^{s} (t,t - 1)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {\Delta \delta_{{{\text{IF}},15,r}}^{s} (t,t - 1) \cdot w_{r}^{s} (t,t - 1)} } \right]} {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]}}} \right. \kern-0pt}\\ &\qquad\; {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]} \\ \end{aligned} $$
(38)

where w is the elevation-dependent weight (Pan et al. 2017a).

The L1/L5 IF PIFCB estimate at epoch t can be computed through an accumulation of the obtained ED L1/L5 IF PIFCB estimates, that is:

$$ \delta_{{{\text{IF}},15}}^{s} (t) = \delta_{{{\text{IF}},15}}^{s} (t_{0} ) + \sum\limits_{{j = t_{0} + 1}}^{t} {\Delta \delta_{{{\text{IF}},15}}^{s} (j,j - 1)} $$
(39)

where \( \delta_{{{\text{IF}},15}}^{s} (t_{0} ) \) is the L1/L5 IF PIFCB at the first epoch of each day, namely \( t_{0} \), and its value is set to zero, resulting in a common bias for the L1/L5 IF PIFCB estimates at all epochs during a day. Since the phase ambiguity parameter will absorb this common bias in parameter estimation process, the ambiguity-float PPP solutions are free of its effects.

Applying Eq. (37) into Eq. (38), Eq. (38) can then be rewritten as:

$$ \begin{aligned} & \Delta \delta_{{{\text{IF}},15}}^{s} (t,t - 1) \\ & \;\; = {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {({\text{GFIF}}_{r}^{s} (t) - {\text{GFIF}}_{r}^{s} (t - 1)) \cdot w_{r}^{s} (t,t - 1)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {({\text{GFIF}}_{r}^{s} (t) - {\text{GFIF}}_{r}^{s} (t - 1)) \cdot w_{r}^{s} (t,t - 1)} } \right]} {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]}}} \right. \kern-0pt}\\ &\qquad\; {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]} \\ \end{aligned} $$
(40)

Similarly, the ED L1/L5 IF PIFCB estimates for satellite s between epochs t − 1 and t − 2 can be computed as:

$$ \begin{aligned} & \Delta \delta_{{{\text{IF}},15}}^{s} (t - 1,t - 2) \\ & \;\; = {\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {({\text{GFIF}}_{r}^{s} (t - 1) - {\text{GFIF}}_{r}^{s} (t - 2)) \cdot w_{r}^{s} (t - 1,t - 2)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {({\text{GFIF}}_{r}^{s} (t - 1) - {\text{GFIF}}_{r}^{s} (t - 2)) \cdot w_{r}^{s} (t - 1,t - 2)} } \right]} {\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {w_{r}^{s} (t - 1,t - 2)} } \right]}}} \right. \kern-0pt}\\ &\qquad\; {\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {w_{r}^{s} (t - 1,t - 2)} } \right]} \\ \end{aligned} $$
(41)

It is assumed that the weights and the stations that are used to estimate the ED L1/L5 IF PIFCB between epochs t and t − 1 are approximately equal to those between epochs t − 1 and t − 2. Combining Eqs. (40) and (41), we can obtain:

$$ \begin{aligned} & \Delta \delta_{{{\text{IF}},15}}^{s} (t,t - 1) + \Delta \delta_{{{\text{IF}},15}}^{s} (t - 1,t - 2) \\ & \;\; \approx {{\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {{\text{GFIF}}_{r}^{s} (t) \cdot w_{r}^{s} (t,t - 1)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {{\text{GFIF}}_{r}^{s} (t) \cdot w_{r}^{s} (t,t - 1)} } \right]} {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]}}} \right. \kern-0pt} {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]}} \\ & \;\;\; - {\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {{\text{GFIF}}_{r}^{s} (t - 2) \cdot w_{r}^{s} (t - 1,t - 2)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {{\text{GFIF}}_{r}^{s} (t - 2) \cdot w_{r}^{s} (t - 1,t - 2)} } \right]} {\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {w_{r}^{s} (t - 1,t - 2)} } \right]}}} \right. \kern-0pt} \\ &\qquad\; {\left[ {\sum\limits_{r = 1}^{n(t - 1,t - 2)} {w_{r}^{s} (t - 1,t - 2)} } \right]} \\ \end{aligned} $$
(42)

According to Eq. (42), Eq. (39) can be rewritten as:

$$ \begin{aligned} \delta_{{{\text{IF}},15}}^{s} (t) &\approx \delta_{{{\text{IF}},15}}^{s} (t_{0} ) + {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {{\text{GFIF}}_{r}^{s} (t) \cdot w_{r}^{s} (t,t - 1)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {{\text{GFIF}}_{r}^{s} (t) \cdot w_{r}^{s} (t,t - 1)} } \right]} {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]}}} \right. \kern-0pt}\\ &\qquad\; {\left[ {\sum\limits_{r = 1}^{n(t,t - 1)} {w_{r}^{s} (t,t - 1)} } \right]} \\ & \;\; - {\left[ {\sum\limits_{r = 1}^{{n(t_{0} + 1,t_{0} )}} {{\text{GFIF}}_{r}^{s} (t_{0} ) \cdot w_{r}^{s} (t_{0} + 1,t_{0} )} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{r = 1}^{{n(t_{0} + 1,t_{0} )}} {{\text{GFIF}}_{r}^{s} (t_{0} ) \cdot w_{r}^{s} (t_{0} + 1,t_{0} )} } \right]} {\left[ {\sum\limits_{r = 1}^{{n(t_{0} + 1,t_{0} )}} {w_{r}^{s} (t_{0} + 1,t_{0} )} } \right]}}} \right. \kern-0pt}\\ &\qquad\; {\left[ {\sum\limits_{r = 1}^{{n(t_{0} + 1,t_{0} )}} {w_{r}^{s} (t_{0} + 1,t_{0} )} } \right]} \\ \end{aligned} $$
(43)

Therefore, the standard deviation (STD) of the L1/L5 IF PIFCB estimates does not increase with the accumulation of ED L1/L5 IF PIFCBs. It is assumed that there is no correlation between the measurements on different frequencies or at different epochs. The STD of the GPS phase observations is set to 3 mm in this study. The sum of weights for two consecutive epochs shown in Eq. (43) ranges from 8.725 to 73.771 during the analysis period. It is assumed that all weights are equal to 1. After applying the error propagation law to Eq. (43), the STD of the L1/L5 IF PIFCB estimates is obtained and found to be approximately 1.0–2.9 mm. Since the weights with elevation angles lower than 40° are smaller than 1 (Pan et al. 2017a), the STD of the L1/L5 IF PIFCB estimates is usually smaller than the obtained values.

According to Eq. (12), the STD of the L5 UC PIFCB estimates can be computed by applying the law of random error propagation and varies in a range of 0.8–2.3 mm. Similarity, we can obtain the STD of the L1/L2/L5 IF PIFCB estimates, and it ranges from \( 0.8 \times \sqrt {(e_{5} )^{2} } \) to \( 2.3 \times \sqrt {(e_{5} )^{2} } \) mm. When adopting the minimum noises as an additional condition to uniquely determine the three combination coefficients for a single IF combination, the STD of the L1/L2/L5 IF PIFCB estimates is 0.8–2.2 mm.

3 Results and discussion

The validity of our IFCB estimation approaches for both UC and IF triple-frequency PPP is verified after a short description of data acquisition and processing strategies. Next, we compute and compare the PIFCB estimates derived from the approach proposed here and the expanded ED strategy for another arbitrary triple-frequency IF combination. Finally, we investigate the benefits from the third frequency by comparing the UC triple-frequency PPP solutions with UC dual-frequency PPP solutions.

3.1 Datasets and processing strategies

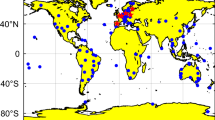
A week of datasets from 171 Multi-GNSS Experiment (MGEX) stations with a geographical distribution shown in Fig. 1 are chosen for analysis. All stations are able to track the triple-frequency signals of GPS. The analysis period spans days 92–98 of 2017. To test our IFCB estimation approaches, all datasets are first used for PIFCB estimation and then employed to carry out triple-frequency PPP processing together with the DCB products and estimated PIFCBs. Table 1 details the processing strategies of triple-frequency PPP.

Fig. 1
figure 1

Distribution of selected MGEX stations

Full size image
Table 1 Triple-frequency PPP processing strategies
Full size table

3.2 Effects of PIFCB on UC triple-frequency PPP

When using different observations from the satellite clock providers, the correction of CIFCBs has been widely noted through the DCB transformation (Li et al. 2012; Guo et al. 2015). Hence, we focus on the effects of PIFCBs on UC triple-frequency PPP. For comparison, two different situations are employed. One is the UC triple-frequency PPP ignoring PIFCB effects, and the other one is the UC triple-frequency PPP considering PIFCB corrections.

Figure 2 provides the statistical results of the two different cases. All 24-h UC triple-frequency PPP solutions from all the selected days and stations at common epochs are used to calculate the epoch-wise root-mean-square (RMS) statistics. Due to the smaller magnitude of PIFCBs and the larger positioning errors in the converging stage, the positioning accuracy of the two triple-frequency PPP cases is at the same level in the first 20 min. The positioning accuracy is significantly improved after applying PIFCB corrections since then. After an observation time of about 24 h, the UC triple-frequency PPP with PIFCB corrections can achieve a positioning accuracy of 5, 4 and 9 mm in east, north and up directions, respectively. For the case neglecting PIFCB corrections, the corresponding positioning accuracy degrades to 8, 6 and 13 mm in the three directions, respectively. The accuracy improvement in daily solutions for the UC triple-frequency PPP with PIFCB corrections over the case neglecting PIFCB corrections is 38, 33 and 31% in the three directions, respectively, suggesting the feasibility of our IFCB estimation approach for UC triple-frequency PPP.

Fig. 2
figure 2

Epoch-wise RMS values of UC triple-frequency PPP positioning errors without and with PIFCB consideration for different observational lengths

Full size image

In addition to measurement noises, some unmodeled errors such as PIFCB can also be identified by observation residuals. The phase observation residuals on L5 frequency in the UC triple-frequency PPP without PIFCB corrections at stations AJAC and CEBR on April 2, 2017, are illustrated in Fig. 3. Each color is associated with a specific Block IIF satellite. We can note dramatic systematic errors in L5 phase observation residuals at the two stations. For comparison, Fig. 3 also shows the phase observation residuals on L1, L2 and L5 frequencies in the UC triple-frequency PPP with PIFCB corrections. It is important to notice that the L1 and L2 phase residuals come from all GPS satellites. The RMS values of phase residuals are computed and given in each sub-figure. After considering the PIFCB, the systematic errors in L5 phase residuals disappear, and the RMS residuals are reduced from 6.2 and 6.3 mm to 1.7 and 1.9 mm at stations AJAC and CEBR, respectively. The phase residuals on the three frequencies vary in a similar range of −0.01 to 0.01 m. The L2 phase observations have the smallest RMS residuals of 1.5 and 1.8 mm at the two stations. L1 phase residuals are the largest with values of 2.3 and 2.8 mm at the two stations. The residual analysis further validates the correctness of our IFCB estimation approach for triple-frequency PPP based on UC observations.

Fig. 3
figure 3

Phase observation residuals for UC triple-frequency PPP at stations AJAC and CEBR on April 2, 2017

Full size image

3.3 Effects of PIFCB on triple-frequency PPP with a single IF combination

In order to test our IFCB estimation approach for triple-frequency PPP with a single IF combination, two different situations are also employed, namely the IF triple-frequency PPP without and with PIFCB corrections. Figure 4 shows the epoch-wise RMS statistics of positioning errors of the two different cases for different observation time. After taking the PIFCB into account, the positioning accuracy is significantly improved, especially for the east and up directions. After 24-h observation, an accuracy of 8, 5 and 13 mm for the IF triple-frequency PPP ignoring PIFCB corrections in east, north and up directions can be achieved, respectively, while the corresponding accuracy can be improved by 50, 40 and 23% to 4, 3 and 10 mm in the three directions for the case considering PIFCB corrections, respectively. The effectiveness of our IFCB estimation approach for IF triple-frequency PPP is manifested by the accuracy improvement.

Fig. 4
figure 4

Epoch-wise RMS statistics of IF triple-frequency PPP positioning errors without and with consideration of PIFCB for different observation time

Full size image

Figure 5 presents the phase observation residuals of L1/L2/L5 IF combination from 12 Block IIF satellites in the IF triple-frequency PPP without consideration of PIFCB at stations AJAC and CEBR on April 2, 2017. Different colors are chosen to identify different satellites. The longer-term changes of L1/L2/L5 phase residuals, namely systematic errors, can be observed. For the purpose of comparison, Fig. 5 also exhibits the L1/L2/L5 phase residuals from Block IIF satellites as well as L1/L2 phase residuals from other GPS satellites in the IF triple-frequency PPP with PIFCB consideration. In contrast, there are no significant systematic errors in these L1/L2/L5 phase residuals. Most of the phase observation residuals for L1/L2/L5 and L1/L2 IF combinations range from −0.02 to 0.02 m. The RMSs of phase residuals are also given in each sub-figure. After a consideration of PIFCB, the RMS residuals for L1/L2/L5 IF combination are reduced from 10.2 and 11.6 mm to 6.5 and 7.8 mm at stations AJAC and CEBR, respectively. The L1/L2/L5 IF combination has smaller RMS residuals than L1/L2 IF combination due to the smaller noise amplification factor. The ratio between RMS residuals of L1/L2/L5 and L1/L2 IF combinations is 0.844 and 0.848 at stations AJAC and CEBR, respectively. The above ratio roughly coincides with the ratio between noise amplification factor of L1/L2/L5 and L1/L2 IF combinations, which is 0.855. The validity of our IFCB estimation approach for triple-frequency PPP with a single IF combination is further confirmed according to the residual analysis.

Fig. 5
figure 5

Phase observation residuals for triple-frequency PPP with a single IF combination at stations AJAC and CEBR on April 2, 2017

Full size image

3.4 Benefits from the third frequency

For the purpose of investigating the benefits from the L5 frequency for precise positioning, the UC triple-frequency PPP solutions taking PIFCB into account are compared with the dual-frequency PPP solutions on the basis of UC observations. For completeness, the UC triple-frequency PPP solutions ignoring PIFCB effects are also provided. In theory, the joint use of multi-frequency signals should not be overly expected to improve PPP performance because of unenhanced satellite geometry. However, the contribution of better constraints of ionospheric delay parameters using an additional frequency to UC data processing cannot be neglected.

The differences between dual-frequency PPP solutions and triple-frequency PPP solutions with PIFCB consideration decrease with time. For clarity, Fig. 6 depicts the epoch-wise RMS statistical values of dual- and triple-frequency PPP positioning errors with different observational lengths in the first 5 min. The positioning accuracy of triple-frequency PPP considering PIFCB is slightly improved compared with dual-frequency PPP, and the accuracy improvement at the first epoch is 4.8, 6.5 and 9.3 cm in east, north and up directions, respectively. As to the triple-frequency PPP without PIFCB corrections, its positioning accuracy is also slightly better than that of dual-frequency PPP in the first 5 min and is almost the same as that of triple-frequency PPP with PIFCB corrections. The green curves are almost completely covered by the blue ones. This is because the magnitude of PIFCB is relatively small, and its effects are not significant in the converging stage. The positioning accuracy of daily solutions for dual-frequency PPP is comparable to that of triple-frequency PPP in consideration of PIFCB, which are 5, 3 and 9 mm, and 5, 4 and 9 mm in the three directions, respectively. The above accuracy is significantly better than the accuracy of triple-frequency PPP neglecting PIFCB, which are 8, 6 and 13 mm in the three directions, respectively.

Fig. 6
figure 6

Epoch-wise RMS values of dual- and triple-frequency PPP positioning errors based on UC observations with different observational lengths in the first 5 min

Full size image

The distribution of convergence time for all 24-h PPP solutions is plotted in Fig. 7. The convergence time is defined as the time span from the first epoch to the epoch, since which the positioning errors keep within 10 cm. The bars near the 120 min in Fig. 7 refer to the percentages of the cases with convergence time larger than 120 min. The convergence time of shorter than 10 min accounts for 36, 73 and 28% for triple-frequency PPP with PIFCB corrections in east, north and up directions, respectively, while the corresponding percentages are 34, 70 and 27% for dual-frequency PPP in the three directions, respectively. The average convergence time for all 24-h sessions is also shown in each panel. On the basis of average values, the improvement in triple-frequency PPP considering PIFCB on convergence time is 7, 4 and 2% over dual-frequency PPP in the three directions, respectively. At present, there are only 12 GPS satellites that can transmit triple-frequency signals. Greater benefits can be expected when more GPS satellites with capability of L1/L2/L5 emitting are available. As to the triple-frequency PPP without PIFCB corrections, its convergence time is lengthened by 12 and 25% in the east and up directions, respectively, but slightly reduced by 2% in the north direction, in comparison to the dual-frequency PPP. The triple-frequency PPP considering PIFCB improves the convergence time by 17, 1 and 22% over the triple-frequency PPP neglecting PIFCB in the three directions, respectively.

Fig. 7
figure 7

Distribution of convergence time for 24-h dual- and triple-frequency PPP solutions in UC model

Full size image

4 Conclusions

All the new-generation GNSS satellites are designed to transmit signals on three or more frequencies. The optimal integration of multi-frequency signals attracts increasing attention from GNSS community. The time-varying phase hardware delays and time-invariant code hardware delays at the satellite are correlated with satellite clocks, and thus, they are estimated as a lumped term in PCE. Since these hardware delays are frequency dependent, the satellite clock estimates will be different when using different observations, and the difference between them is defined as IFCB. The IFCB estimation approaches for triple-frequency PPP based on UC observations or IF combined observations within an arbitrary triple-frequency IF combination are proposed in this study. The key feature of the IFCB estimation approaches is that only a set of PIFCBs between L1/L5 and L1/L2 IF satellite clocks should be estimated, and the obtained L1/L5 IF PIFCBs can be directly converted into the L5 UC PIFCBs and L1/L2/L5 IF PIFCBs if scaled by individual constants, which will minimize the workload of satellite clock providers as well as multi-frequency PPP users. We rigorously derive the mathematical conversion formula among different types of PIFCBs. In addition, the UC and IF triple-frequency PPP models are developed.

With a week of data from 171 MGEX stations, we demonstrate the practicability of our IFCB estimation approaches. After a careful PIFCB consideration, the positioning accuracy of daily solutions for UC triple-frequency PPP is improved by 38, 33 and 31% from 8, 6 and 13 mm to 5, 4 and 9 mm in east, north and up directions, respectively, while the corresponding positioning accuracy of IF triple-frequency PPP is improved by 50, 40 and 23% from 8, 5 and 13 mm to 4, 3 and 10 mm in the three directions, respectively. After applying the PIFCB corrections, the convergence time of UC triple-frequency PPP is improved by 17, 1 and 22% in the three directions, respectively. In addition, the systematic errors in L5 and L1/L2/L5 phase observation residuals are found to be disappeared after applying PIFCB corrections. For the purpose of investigating the benefits from the additional frequency, the UC triple-frequency PPP solutions are compared with the UC dual-frequency PPP solutions. With the use of an extra frequency, the improvement is 7, 4 and 2% on convergence time in the three directions, respectively. The positioning accuracy of daily solutions for UC triple-frequency PPP is at the same level as that for UC dual-frequency PPP.