Multivariate analysis of GPS position time series of JPL second reprocessing campaign

Abstract

The second reprocessing of all GPS data gathered by the Analysis Centers of IGS was conducted in late 2013 using the latest models and methodologies. Improved models of antenna phase center variations and solar radiation pressure in JPL’s reanalysis are expected to significantly reduce errors. In an earlier work, JPL estimates of position time series, termed first reprocessing campaign, were examined in terms of their spatial and temporal correlation, power spectra, and draconitic signal. Similar analyses are applied to GPS time series at 89 and 66 sites of the second reanalysis with the time span of 7 and 21 years, respectively, to study possible improvements. Our results indicate that the spatial correlations are reduced on average by a factor of 1.25. While the white and flicker noise amplitudes for all components are reduced by 29–56 %, the random walk amplitude is enlarged. The white, flicker, and random walk noise amount to rate errors of, respectively, 0.01, 0.12, and 0.09 mm/yr in the horizontal and 0.04, 0.41 and 0.3 mm/yr in the vertical. Signals reported previously, such as those with periods of 13.63, 14.76, 5.5, and 351.4 / n for $n=1,2,{\ldots },8$ days, are identified in multivariate spectra of both data sets. The oscillation of the draconitic signal is reduced by factors of 1.87, 1.87, and 1.68 in the east, north and up components, respectively. Two other signals with Chandlerian period and a period of 380 days can also be detected.

1 Introduction

Continuous global positioning system (CGPS) time series have been widely used to study several geophysical phenomena (Segall and Davis 1997). These studies include inferring motion of the Earth’s surface due to plate tectonics (Thatcher 2003; Argus et al. 2010; Kreemer et al. 2014), post-glacial rebound (Johansson et al. 2002; King et al. 2010; Peltier et al. 2015), and hydrological loading (van Dam et al. 2001; Rajner and Liwosz 2012; Argus et al. 2014). Moreover, strain accumulation (Argus et al. 2005; d’Alessio et al. 2005; Serpelloni et al. 2005; Craig and Calais 2014), sea-level variation (Wöppelmann et al. 2007), volcanic deformation (Bonforte and Puglisi 2006; Cervelli et al. 2006), and subsidence studies (Lü et al. 2008; Bock et al. 2012) can be conducted.

To effectively apply GPS time series to geophysical phenomena, appropriate functional and stochastic models are required. The functional model takes into consideration the deterministic effects—a linear trend, offsets, and potential periodicities—to name a few. The stochastic model identifies and determines the remaining unmodeled effects—white noise and power-law noise for instance. Deterministic effects, if left undetected in the functional model, may mistakenly mimic flicker noise and random walk noise (Williams et al. 2004; Amiri-Simkooei et al. 2007).

A proper stochastic model provides the best linear unbiased estimator (BLUE) of unknown parameters. It can also provide a realistic description of the parameters’ precision. The parameter estimation in a stochastic model is referred to as variance component estimation (VCE). VCE can be conducted using various methods. The least-squares variance component estimation (LS-VCE), which was originally developed by Teunissen (1988), is used in the present contribution. For its geodetic and geophysical applications, we may refer to Amiri-Simkooei et al. (2007, 2009, 2013), Amiri-Simkooei (2007, 2009, 2013a, b), and Khodabandeh et al. (2012).

Proper analysis of GPS time series is a prerequisite for an appropriate geophysical interpretation. The VCE method based on the maximum likelihood estimation (MLE) has also been widely used to assess the noise structure of GPS time series. The differences between LS-VCE and MLE are explained by Amiri-Simkooei et al. (2007). Zhang et al. (1997) used MLE and found that the noise structure is a combination of white noise and flicker noise. Similar results have been drawn by Bock et al. (2000), Calais (1999), Langbein and Bock (2004), Mao et al. (1999), Williams et al. (2004). The presence of random walk noise or a combination of other noise components has been acknowledged by several scholars including Johnson and Agnew (2000), King and Williams (2009), Langbein (2008, 2012), Langbein and Bock (2004).

Cross-correlation among different series is an important issue. Errors in satellite orbits, Earth orientation parameters, and errors in daily and long-term geodetic reference frame are causes of regionally correlated errors (Wdowinski et al. 1997). Moreover, large-scale atmosphere errors, receiver and satellite antenna phase center variations (Dong et al. 2006), and atmospheric and hydrospheric water loading effects (van Dam et al. 2001) are also candidates for common-mode errors (CMEs). Williams et al. (2004) found that in the regional GPS solutions in which CMEs have been removed, the noise is significantly lower compared to the global solutions. CMEs can be estimated with regional spatial filtering methods. We refer to the stacking approach, which was first utilized by Wdowinski et al. (1997). Nikolaidis (2002) removed CMEs from daily GPS solutions by computing the daily weighted mean of residual noise from a few regional fiducial stations. Teferle et al. (2002) deployed a filtering technique to reduce the annual signal effect on site velocity estimates using a network of 9 stations. Teferle et al. (2006) used the weighted stacking method (WSM) to remove CMEs through analysis of a network consisting 6 permanent stations. Using the WSM, Bogusz et al. (2015) calculated CMEs for the ASG-EUPOS permanent stations.

As the regional networks expands, the magnitude of daily CMEs is reduced (Márquez-Azúa and DeMets 2003), and hence the application of the WSM becomes limited. Dong et al. (2006) presented a spatiotemporal filtering method based on principal component analysis (PCA) and Karhunen–Loeve expansion. Unlike the WSM, this method allows data to reveal the spatial distribution of CMEs by disregarding the assumption of spatially uniform distribution of these errors. Because the stations we utilized are globally distributed, the concept of CMEs has lost its meaning (Dong et al. 2006). The cross-correlation (i.e. spatial correlation) among time series is thus investigated (see Williams et al. 2004; Amiri-Simkooei 2009).

The GPS draconitic year (351.4 days) is the revolution period of the GPS constellation in inertial space with respect to the Sun. Harmonics of this periodic pattern have been observed in GPS-derived geodetic products. Ray et al. (2008) analyzed the time series of 167 IGS stations using the stacked Lomb–Scargle periodogram. They identified up to the sixth harmonic of GPS draconitic year in the east, north, and up components. Collilieux et al. (2007) found significant signals near the frequencies 2.08, 3.12, and 4.16 cpy in the up component. Amiri-Simkooei et al. (2007) computed the stacked least squares power spectra of 71 permanent GPS stations. They identified up to the eighth harmonic of the GPS draconitic signal. Amiri-Simkooei (2013a) identified ten harmonics of the draconitic signal by calculating the multivariate least-squares power spectrum of 350 permanent GPS stations. For more information on the harmonics of the GPS draconitic signal, we refer to the studies of King and Watson (2010), Rodriguez-Solano et al. (2012, 2014), Ostini (2012) and Santamaría-Gómez et al. (2011).

2 Second reprocessing campaign strategies

In 2008, the Analysis Centers (ACs) of the international GNSS service (IGS) initiated the reprocessing of the all GPS data gathered by the IGS global network since 1994 employing the latest methods upon that time in an entirely consistent manner. This was the first reprocessing campaign, and it was anticipated that as further analysis and improvements were made, undoubtedly, more reprocessing campaigns will be required. Thus, the 2nd reanalysis of all IGS data using the improved methods begun by the late 2013. Table 1 compares different aspects of the two processing campaigns.

Table 1 Setup of the first and second reanalysis campaign

Also, there are other modifications and changes in the models used within the 2nd reanalysis, which are explained in “Appendix 1”.

The new models used within the second reanalysis along with the studies conducted by Hugentobler et al. (2009) and Rodriguez-Solano et al. (2012), who emphasized the orbit mismodeling deficiencies and their effects on peculiar signals observed in GPS-derived products, motivated us to study the reprocessed daily position time series. We have suspected that since these models have been incorporated within the new reprocessing campaign, it is highly likely to observe significant improvements. Improvements expected include the reduction in the range of variations of the periodic pattern of GPS draconitic year, the amplitude of different noise components, the spatial correlation of GPS position time series (Rodriguez-Solano et al. 2012). Rebischung et al. (2016) have recently shown that the noise characteristics of GPS position time series for JPL second reprocessing deviate from the common white plus flicker noise toward an only flicker background noise.

This contribution is a follow-up to the work carried out by Amiri-Simkooei (2013a) in which the daily position of many permanent GPS stations was analyzed. In the present contribution, the daily position time series of 66 and 89 permanent GPS stations of the length 21 and 7 years are derived from the 2nd reprocessing campaign (Fig. 1). They are referred to as data set #1 and data set #2, respectively, which are freely available in ftp://sideshow.jpl.nasa.gov/pub/JPL_GPS_Timeseries/repro2011b/post/point/. The time series with 89 GPS stations (data set #2) are also derived from the 1st reprocessing campaign to make comparisons. Therefore, for the data set #2 we have two kinds of data (Repro1 and Repro2) with the same length, time span, and time instants.

Fig. 1

World distribution of 66 GPS stations with time span of 21 years (top: Repro2), 89 GPS stations with time span of 7 years (bottom: Repro1 and Repro2)

All formulas and methodologies, used in the subsequent sections, are based on those presented by Amiri-Simkooei (2013a) who used a multivariate time series analysis. This method is superior over univariate analysis because many weak signals and small noise amplitudes which cannot be detected in univariate analysis can be detected if we simultaneously analyze multiple time series. This holds, for example, when estimating the random walk amplitude, which has a high chance to be masked in the univariate analysis, but has a higher chance to be detected in the multivariate analysis. However, a drawback of this multivariate analysis is that it can only provide a kind of network-based random walk and hence such errors cannot necessarily be attributed to the individual time series. For further information, we may refer to Amiri-Simkooei (2013a).

3 Results and discussion

The multivariate method is used to study the GPS position time series of daily global solutions. These time series have been obtained using the precise point positioning (PPP) method in the GIPSY-OASIS software (Zumberge et al. 1997). The process has been carried out in an analysis center at JPL (Beutler et al. 1999).

Prior to the analysis, a multivariate offset detection method was used to identify and remove offsets in the series (Hoseini-Asl et al. 2013). Although the manual offset detection method is still more reliable than the existing methods (see Gazeaux et al. 2013), we used an automatic offset detection method having a few characteristics. This method assumes similar offsets in the three coordinate components. It also takes into account appropriate functional and stochastic models. For example, prior to offset detection, LS-VCE is applied to estimate the white and flicker noise amplitudes. Comparing the offset detection results with those in the JPL website indicates that our method detects all offsets reported by JPL. In addition, a few smaller offsets, which are likely due to other causes like small earthquakes, have been detected.

The initial functional model consists of a linear trend along with the three harmonics of the annual signal; the tri-annual signal was included because the power spectrum showed a signal near 122 days. Equation (8) in Amiri-Simkooei (2013a) is utilized to obtain the multivariate power spectrum (MPS) of multiple series. The analysis requires matrices ${\Sigma }$ and Q, which can be estimated using a multivariate method (see Amiri-Simkooei 2009, algorithm in Fig. 1). The nonnegative least-squares variance component estimation method (NNLS-VCE) (Amiri-Simkooei 2016, algorithm in Fig. 1) has been employed to avoid nonnegative variance factors for white noise, flicker noise, and random walk noise. While the matrix ${\Sigma }$ explains the spatial correlation among the series, Q considers the temporal correlation among observables within each series. For the flicker noise, the Hosking structure introduced by Williams (2003a) and Langbein (2004) has been employed.

Multivariate analysis requires simultaneous time series. This indicates that if there is a gap or outlier in a (couple of) series, the observations of other series should be removed to have simultaneous time instants for all series. However, if the data were available in 95 % of the series (missed in 5 % of the series), the observations for the gaps (missed) were reconstructed using the above functional model, and then a normally distributed noise based on the estimated stochastic model was added to reconstruct the data. For the data set # 2, 89 GPS stations were analyzed. Therefore, the total number of series is $r=267$. Matrix ${\Sigma }$, which expresses the spatial correlation, is of size $267\times 267$. Matrix Q is of size $m\times m$, where m is the number of observables in each series; for the multivariate analysis, m is identical for all time series. While the three $89\times 89$ block diagonals of the ${\Sigma }$ form the spatial correlation of each coordinate component (i.e. east-east (EE), north-north (NN), and up-up (UU)), the other three $89\times 89$ off-diagonals represent the cross-correlation of the components (i.e. between north-east (NE), north-up (NU), and east-up (EU)).

The VCE methods can computationally be an expensive process. Some researchers have contributed to reduce the computational burden of the VCE methods. We may refer to excellent studies by Bos et al. (2008, 2012) in which the computational burden of MLE is drastically reduced. One feature of our multivariate noise assessment method is also that its computational burden is similar to that of the univariate analysis (see Amiri-Simkooei 2009).

Fig. 2

Six kinds of spatial correlation estimated for position time series with the time span of 7 years as a function of angular distance (deg); (left) individual components NN, EE, and UU; (right) cross components NE, NU, and EU. Indicated in the plots also mean correlation curves for the second (blue) and first (black) reprocessing campaigns using a moving average

3.1 Spatial correlation

GPS position time series have been shown to have a significant spatial correlation (Williams et al. 2004; Amiri-Simkooei 2009, 2013a). The spatial (cross) correlation results for the data set with 89 GPS station are illustrated in Fig. 2. Derived from ${\Sigma }$, this figure shows the spatial correlation among NN, EE, UU, NE, NU, and EU components. Significant spatial correlations for NN, EE, and UU are observed over an angular range of $0{^{\circ }}$ to $30{^{\circ }}$, implying the presence of regionally correlated errors. No effort has been put forward to reduce CMEs here, and thus, as expected, the spatial correlation among stations which are close to each other (about 3000 km apart) is significant. This spatial correlation directly propagates into the correlation between site velocities, and hence it should be taken into consideration in the covariance matrix of the site velocities (Williams et al. 2004). Over larger distances, the correlations of individual components experience a significant decline, in agreement with the findings of Amiri-Simkooei (2013a) and Williams et al. (2004). This indicates that the CME noise is significant only over nearby stations. The component EE experiences higher correlations compared with the NN and UU components.

The spatial cross-correlations between components (NE, NU, and EU) are negligible. The cross-correlation curve is less than 0.1 which is owing to a good GPS geometry stemming from simultaneous processing of all observations. To fairly compare the average spatial (cross) correlations derived from the 1st and 2nd reprocessing campaign, the 1st reprocessing campaign time series for the data set with 89 stations have been processed as well. The results are presented in Table 2. The spatial correlations of individual components have been reduced compared to those computed for the Repro1 data except for the EE component, which shows a (small) increase from 0.57 to 0.62 in the second reprocessing. The reduction is the result of improvement in the models used within the new campaign. It could also be due to an improved alignment of the daily terrestrial frames, which makes it difficult to separate it from the impact of new models used in the analysis. The spatial correlation matrix ${\Sigma }$, estimated for the latest processing campaign, is to be taken into consideration in the estimation of the multivariate power spectrum.

Table 2 Average spatial correlation over the angular distance of $30^{\circ }$ for the first and second reprocessing campaign using 89 GPS stations

Fig. 3

Estimated amplitudes of white (left), flicker (middle), and random walk (right) noise for the data set with the time span of 7 years; top frame (north), middle frame (east), bottom frame (up)

In this contribution, we considered the correlation among the east, north and up components. In principle, by applying the error propagation law, these correlations can be propagated into the coordinate differences of X, Y, and Z in an earth-centered earth-fixed coordinate system using an appropriate coordinate transformation.

3.2 Temporal correlation and noise assessment

The amplitudes of white noise, flicker noise, and random walk noise can be obtained using matrices ${\Sigma }$ and Q. Noise characteristics of GPS time series have been expressed as a combination of white plus spatially correlated flicker noise (Zhang et al. 1997; Mao et al. 1999; Calais 1999; Nikolaidis et al. 2001; Williams et al. 2004; Amiri-Simkooei et al. 2007, 2009). The presence of random walk noise in GPS time series is due to monument instability (Williams et al. 2004) or the presence of nonlinear deformation behavior, for example in areas with active deformation or when the offsets remain in the data series (Williams 2003b). The presence of postseismic deformation or volcanic events could also increase the apparent amplitude of random walk noise. The reason for masking the (small) values of the random walk noise is the short time spans of the data series or the existence of dominant flicker noise (Williams et al. 2004).

The amplitudes of white noise, flicker noise, and random walk noise can simply be provided from the Kronecker structure ${\Sigma }\otimes Q$. The diagonal entries of the matrices $s_w {\Sigma },s_f {\Sigma }$ and $s_{rw} {\Sigma }$ represent the variances of white, flicker and random walk noise for each series. To compare the amplitudes of the three noise components for the two reprocessing campaigns, the data sets with the time span of 7 years (89 GPS stations) of the two campaigns have been processed. For the second reanalysis, the time correlation results of these stations are shown in Fig. 3. The average amplitudes of white, flicker, and random walk noise components along with their estimated standard deviations for both campaigns are presented in Table 3. A few observations are highlighted.

Table 3 Average amplitudes of white noise, flicker noise, and random walk noise along with their estimated standard deviations for permanent GPS stations of 1st and 2nd processing campaigns

• The amplitudes of all noise components of the vertical is larger than those of the horizontal by a factor of 3, consistent with the previously published results (Williams et al. 2004; Amiri-Simkooei 2013a; Dmitrieva et al. 2015).

• Amiri-Simkooei (2013a) published flicker noise variances for the repro1 series about 4 times smaller than those reported here. Unfortunately, there was a mistake in presenting flicker noise results in Amiri-Simkooei (2013a). There, the unit was mistakenly $\hbox {mm}/\hbox {day}^{1/4}$ (and not $\hbox {mm}/\hbox {year}^{1/4}$) for the flicker noise component. This indicates that a scaling factor of $\root 4 \of {365.25}=4.37$ should be applied to his flicker noise amplitudes.

• In contrast to the values obtained from the first reanalysis, the noise amplitudes of the north and east components are nearly identical in the second reanalysis.

• The amplitudes of flicker and random walk noise over different stations are multiples of the white noise amplitudes. In reality, however, this should not indicate all stations contain random walk noise, because the estimated values are an average value (over all stations) due to the special structure used (see Amiri-Simkooei et al. 2013). Therefore, the multivariate approach implemented in the present contribution can resolve only a single network-wide random walk value rather than a station specific one.

• When the values obtained from the latest reanalysis are compared to their older counterpart, the amplitudes of white and flicker noise of all components have been reduced by factors ranging from 1.40 to 2.33. This highlights that the new models used in the second reanalysis have significantly reduced the amplitude of these two noise components.

• While the amplitudes of both white and flicker noise have significantly reduced in this contribution, Rebischung et al. (2016) reported reduction in only white noise. This, however, was only speculated by explaining their power spectra and hence was not based on a real estimation of the noise amplitudes.

• The random walk noise amplitudes estimated in the second reanalysis are substantially larger than those of the first campaign. This further confirms the findings of King and Williams (2009), Dmitrieva et al. (2015) and Amiri-Simkooei et al. (2013), who identified significant random walk noise in GPS time series. As a non-stationary noise process, the variance increases over time under a random walk process. The zero amplitude of random walk in the first reprocessing campaign is likely because this noise process is being masked (or underestimated) in the ‘processing’ noise due to the lack of the new appropriate models and strategies used in the second reprocessing campaign.

• To further support the statement of the previous point, we present the detrended data (i.e. the mean residuals) of all 89 stations for these two reprocessing campaigns (Fig. 4). In contrast to the series derived from the first reanalysis, the noise of the new time series has not significantly changed over time as the latest models were used in the second reprocessing. Having a uniform ‘processing’ noise over time allows one to efficiently detect the possible non-stationary random walk noise process due to monument instability (see also Santamaría-Gómez et al. 2011).

Fig. 4

Mean residuals (for the data set with the time span of 7 years) of time series for north, east, and up components after removing a linear trend, 3 harmonics of annual signal and 10 draconitic harmonics; (left) first reprocessing campaign; (right) second reprocessing campaign

Table 4 White flicker and random walk noise rate errors using three types of formulas; left: this contribution with white ($Q=s_\mathrm{w} Q_\mathrm{w}$), flicker ($Q=s_\mathrm{f} Q_\mathrm{f}$) and random walk noise ($Q=s_{\mathrm{rw}} Q_{\mathrm{rw}}$) and those obtained using all noise components $\left( {Q=s_\mathrm{w} Q_\mathrm{w} +s_\mathrm{f} Q_\mathrm{f} +s_{\mathrm{rw}} Q_{\mathrm{rw}}} \right)$; middle: Bos et al. (2008); right: Argus (2012)

To estimate rate errors induced by white, flicker, and random walk noise in the multivariate model, we employ a method described in “Appendix 2”. Using Eqs. (7)–(9), the rate errors of different noise structures have been estimated for the north, east, and up components (Table 4); the rate errors are determined for the data set with the time span of 7 years. It is observed that random walk rate error is larger than those of white and flicker noise. These results are in good agreement with those obtained using Eqs. (30)–(31) of Bos et al. (2008) (see Table 4). We may also employ Eqs. (1)–(3) of Argus (2012), originated from Williams (2003a) and Bos et al. (2012), to calculate the rate errors (substitute $T=7\,\hbox {years}$ and $f=365$). Rate errors determined by employing these equations are also shown in Table 4. The last row of Table 4 presents the rate errors using the combination of all noise components.

The (large) amplitude of the random walk compared to those reported by King and Williams (2009) and Dmitrieva et al. (2015) can be explained as follows. It has been shown that white and flicker noise have nearly identical spatial correlation (Amiri-Simkooei 2009). However, random walk noise does not show such a significant correlation because this noise depends on site-related effects such as monument instability, etc. The Kronecker structure used in Amiri-Simkooei (2013a) will induce also significant spatial correlation for random walk. A sub-optimal stochastic model can bias (i.e. overestimates or underestimate) the estimated variance components (Amiri-Simkooei et al. 2009, see Eq. 33). This highlights again that the estimated random walk amplitudes of the multivariate analysis provide only a general indication of a single network-based random walk value.

Fig. 5

Multivariate least-squares power spectrum for the data set with the time span of 7 years. Vertical axes are normalized with respect to spectral values of bottom frame to provide the maximum power of one; (top) full structure of ${\Sigma }\otimes Q$ is taken into consideration, and (bottom) ${\Sigma }$ is considered to be diagonal

Fig. 6

Multivariate least-squares power spectrum on all coordinate components. Vertical axes are normalized to provide the maximum power of one; (top frame) data set with the time span of 7 years, (bottom frame) data set with the time span of 21 years

Fig. 7

Multivariate least-squares power spectrum analysis on individual components. Vertical axes are normalized to provide the maximum power of one; (right frame) data set with the time span of 7 years, (left frame) data set with the time span of 21 years

3.3 Multivariate power spectrum

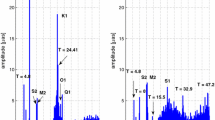
The multivariate power spectra (MPS), illustrated in Figs. 6, 7, 8 and the top frame of Fig. 5, are obtained using Eq. (8) of Amiri-Simkooei (2013a). The power spectrum would be flat if: (1) there were only white noise in the series, or, (2) the correct stochastic model ${\Sigma }\otimes Q$ were used. Both spectra shown in Fig. 5 are obtained when taking the temporal correlation of the series (estimated Q) into consideration. The spectrum at the top is derived assuming the series are spatially correlated (correct ${\Sigma }\otimes Q$), while the bottom frame is derived assuming that the spatial correlation is absent, i.e. ${\Sigma }=\hbox {diag}\left( {\sigma _{11} ,\ldots ,\sigma _{rr} } \right)$ is a diagonal matrix. The bottom frame is similar to the weighted power spectrum in the studies of Amiri-Simkooei et al. (2007) and Ray et al. (2008, 2013), but differs in that it is based on the correct Q, rather than stationery white noise. Therefore, in contrast to their spectra, our spectra is nearly flat. This indicates that the matrix Q, which compensates for the temporal correlation of the series, affects the flatness of the spectrum, whereas the spatial correlation (matrix ${\Sigma }$) affects the scale of the spectrum. Therefore, a mature stochastic model is crucial for the correct detection of signals. When employing an immature stochastic model, one takes the risk of not detecting peaks at higher frequencies (see Fig. 5); cluster of periods between 5 and 6 days, present in the top frame, are absent in the bottom frame.

The MPS in Fig. 6 shows signals with periods of 13.63 days (direct tides) and 14.76 days (direct 14.77 days tide or 24-h alias of M2). These signals are also detected in the MPS on individual components for both data sets (Fig. 7). It can be seen that the former signal is sharper in the bottom frame of Fig. 6 and the left frame of Fig. 7. The 14.76-day signal was not clearly observed in the up component of the data set with 66 stations. The signals detected for the east and north components are in good agreements with those reported by Ray et al. (2013). They, however, found that fortnightly signals are much less distinct in the up components. Our observations show that this holds indeed only for the 14.76-day signal.

The vertical dashed lines in Figs. 5, 6, 7, 8 illustrate harmonics of the GPS draconitic signal with the periods of 351.4/N days (1.04N cpy) for $\hbox {N}=1,\ldots ,8$. The peaks match nearly all of the frequencies. The aliasing signal can contribute to parts of this draconitic signal. Errors in GPS satellite orbit are considered to be the origin for the harmonics because the GPS draconitic year is intrinsic to the satellite orbits, and hence they provide a mechanism for the generation of harmonic modulations. As an example, Rodriguez-Solano et al. (2011) slightly reduced the level of the sixth draconitic harmonic by taking earth albedo and thermal effects on GPS orbits into consideration. For more information, we refer to Ray et al. (2008), Tregoning and Watson (2009), King and Watson (2010), and Griffiths and Ray (2013). Amiri-Simkooei (2013a) shows that a similar behavior of the draconitic pattern at adjacent stations implies that the dominant draconitic effect is not likely dependent on the station-related local effects—multipath for instance. Because the GPS orbit modeling has been improved in latest reanalysis campaign using the new models for Earth radiation pressure and Earth albedo radiation, the reduction in the draconitic signal is expected. This issue will be considered later in Sect. 3.5.

Fig. 8

Multivariate least-squares power spectrum after removing Chandlerian, annual, semiannual, tri-annual, and 8 harmonics of GPS draconitic year for the data set consisting 66 GPS stations (21 years of data). Vertical axes are normalized to provide the maximum power of one

Amiri-Simkooei (2013a) found, contrary to expected, that the first draconitic harmonic in Figs. 5, 6, 7, 8 does not have the largest and sharpest peak, owing to leakage. According to the Rayleigh criterion (Godin 1972), in order to clearly distinguish between two signals with the periods of $T_1$ and $T_2$, the time spans of the series should be at least equal to $\frac{T_1 T_2 }{T_2 -T_1 }.$ Applying this formula to the annual and draconitic signals with the periods of 365.25 and 351.4 days, respectively, we find that the minimum length of the time series should be equal to 25.4 years. This holds only in theory, but in reality longer time series are required because the above signals are (much) messier that the pure sinusoidal waves. If the time series are not long enough, the annual signal is leaked into the draconitic signal and prohibits it from having the largest and sharpest peak. This is, however, not the case for the higher harmonics of this periodic pattern as the length of the time series exceeds that of the minimum time span required. A sharper peak of the first harmonic in the bottom frame of Fig. 6 and the left frame of Fig. 7 in which longer data span (21 years) have been used verifies the above statement. Compared to Amiri-Simkooei (2013a), the number of draconitic harmonics detected has been reduced from 10 to 8.

The multivariate analysis is applied both to the individual components (Fig. 7) and simultaneously to the three components (Fig. 6). Both spectra show a cluster of periods around 5.5 days. Using daily time series of 306 IGS stations, Ray et al. (2013) detected a signal with this period in the north and up residuals, but barely visible in the east residuals. We also observe a cluster of periods around 2.75 days (likely the second harmonics of 5.5 days) in the data set with 89 stations (Fig. 6, top frame and Fig. 7, right), and to a lesser extent in the data set with 66 stations (Fig. 6, bottom frame). These findings are in agreement with those of Ray et al. (2013). We do not offer an explanation for the origin of these two signals.

Selle et al. (2014) reprocessed six stations in which a large 5.5 days feature has been found. They used the same orbit, clock product and GIPSY software as the JPL GPS PPP time series, but with a different processing strategy which results in a significant reduction in the strength of the 5.5 days feature. Their result suggested that this signal is both station dependent and probably related to parts of PPP processing strategy other than orbit and clock products or the GIPSY-OASIS software. Therefore, further research is needed for investigation into the origin of the 5.5 days feature in the JPL time series.

Apart from the detected signals discussed earlier, a signal with a period of 432.5 days referred to as Chandler wobble period has been found (Fig. 6, bottom frame). The amplitude of the Chandlerian signal (averaged over 66 stations) for the east, north, and up components are 0.2, 0.2, and 0.4 mm, respectively (Table 5), and the maximum amplitude of this signal for the up and east components reaches nearly 1.2 mm. Nikolaidis (2002) identified a signal with a period of $439\pm 15$ days in the power spectrum of the GPS position time series residuals derived from the SOPAC network. It was attributed to the unmodeled pole tide. Moreover, the amplitude of the first Chandlerian harmonics obtained by Bogusz and Klos (2016) was nearly 1 mm for the up component. Collilieux et al. (2007) identified a broad range of frequencies between 0.75 and 0.9 cpy in SLR height residuals from the ITRF2005 solution. The existence of this signal may indicate mismodeling of the Chandler period and its modulations (Bogusz and Klos 2016) on GPS time series. As the minimum time span needed for the identification of Chenlerian signal is 12 years, the signal has not been detected in the data set with the time span of 7 years. The Chandlerian signal, which is likely related to International Earth Rotation Service’s (IERS) pole tide model (Wahr 1985; King and Watson 2014), has not been reported in any of the IGS AC stacked spectra (including JPL) by Rebischung et al. (2016).

We would intuitively expect the spectrum not to show any peak around the annual signal if we were to remove 8 harmonics of the GPS draconitic year signal and the first harmonic of the Chandler wobble in addition to 3 harmonics of the annual signal. To examine our hypothesis, these signals are added to the functional model and the noise assessment was carried out and the correct matrices ${\Sigma }\otimes Q$ were estimated. The spectral values were then computed. Figure 8 shows the MPS for 66 stations after removing the signals mentioned above. Although the spectral values of 8 harmonics of the draconitic signals have been reduced compared to the bottom frame of Fig. 6, they are not totally removed. This indicates that the draconitic pattern is not completely of periodic nature. Moreover, a signal with a period of around 380 days has been detected, which was not previously observed. This signal is statistically significant because its spectral value (i.e. 412.56) is much larger than the critical value of ${\chi }_{0.99, 2\times 66}^2 =172.71$. We do not have an explanation for this. But it may correspond to the findings of Griffiths and Ray (2013), who computed the Doodson number 165.545 with the period of 23.9379816 h aliases into the period of 385.98 days when the 1-day sampling is used. As expected, this signal has not been observed in the data set with the time span of 7 years as the minimum length of the time series required for distinguishing between this signal and draconitic is 12.7 years (to clearly detect this signal and the annual signal at least 25.7 years of data is needed). The variations of the signal observed for the east, north, and up components of the 66 GPS stations are 0.3, 0.3, and 0.6 mm, respectively (Table 5). The variation of this signal is larger than those of the Chandlerian, tri-annual, and the third draconitic harmonics. The maximum variations of this signal for the up components is larger than those of the first draconitic and the semiannual signal (Table 5).

Fig. 9

Multivariate least-squares power spectrum for the data set with the time span of 7 years for first reprocessing (red) and second reprocessing (blue) campaign. Vertical axes are normalized with respect to the spectral values of the first reprocessing campaign (dashed red) to have the maximum power of one

Table 5 The mean and maximum range of variations of the 3 annual harmonics, the 3 draconitic harmonics separately, the 8 draconitic harmonics, the Chandlerian signal and the signal with a period of 383 days for the north, east and up components of the data set with 66 permanent GPS stations of the second reprocessing campaign

3.4 Draconitic periodic pattern

This section investigates the GPS draconitic year signal. Following Amiri-Simkooei (2013a), in the linear model $y=Ax$, one can partition A and x as $\left[ {A_1 A_2 } \right]$ and $\left[ {x_1^T x_2^T } \right] ^{t}$, respectively, where $x_1$ is the unknown parameters of linear term plus annual, semiannual, and tri-annual signals and $x_2$ is the unknowns of the 8 harmonics of draconitic year signal. Using $y_2 =A_2 x_2$, one can investigate the signal estimated for the draconitic signal. Assume we have r time series. All estimated $y_2$ vectors of individual time series can be collected in an $m\times r$ matrix $Y_2 =A_2 X_2$, where m is number of observations in the time series.

An investigation on $Y_2$ (for the data set consisting 89 GPS stations with the time span of 7 years) indicates that the mean range of variations of the draconitic signal reaches −1.91–1.91 , −1.75-1.73 and −4.72–4.72 mm for the north, east, and up components, respectively. They are the amplitudes (average of all minima and maxima over all GPS stations) of the draconitic signal. Compared to the first reprocessing campaign, the mean range of variations for the north, east, and up components are reduced by factors of 1.87, 1.87, and 1.68, respectively.

This reduction stems from the combined effect of the new models used. As an example, Rodriguez-Solano et al. (2012) found that the inclusion of the Earth radiation pressure model causes a change in the north component position estimates at a submillimeter level. The effect of their proposed method has a main frequency of around six cpy, and hence a reduction of 38 % occurs by applying this model. Within the latest reprocessing campaign, the UT1 libration effect has been considered, which can result in the reduction in the ranges of variations.

To clearly observe the harmonics of the draconitic signal, the 3 harmonics of the annual signal have been considered in the initial functional model. That is, the functional model consists of 8 columns (2 columns for the linear regression and 2 columns for each annual harmonics). To compare the relative oscillations of the annual and draconitic signal, we have analyzed the original data without considering the 3 annual harmonics. The investigation has been done on the time series with the time span of 21 years as in the time series with the time span of 7 years it is not possible to analyze both annual and draconitic signal (due to the shortness of the time series). The results are presented in Table 5.

The mean annual variations of the north, east, and up components are larger than those of the draconitic by factors ranging from 2.5 to 3.4. The maximum annual variations are larger than those of the semiannual by a factor ranging from 2.78 to 3.5. The annual oscillation is due to exchange of ice, snow, water, and atmosphere, mainly between the northern and southern hemispheres (Blewitt et al. 2001).

For further investigation of this phenomenon, two kinds of results are presented in the subsequent subsections.

Fig. 10

Effect of periodic pattern of first reprocessing (red) and second reprocessing (black) campaign estimated for a typical example in which stations are close to each other. CIT1 is the site at California Institute of Technology. OXYC is the site at Occidental College. OXYC and CIT1 are 7 Km apart. The red and black points denote the residual time series after subtracting liner regression terms plus 3 harmonics of the annual signal for first and second reprocessing campaigns, respectively. The dashed red and solid black lines denote the draconitic signal estimated for the first and second reprocessing campaigns, respectively

3.4.1 Visual inspection

We now investigate the possible draconitic peak reduction in the data derived from the 2nd reprocessing campaign. The data sets analyzed consist of 89 GPS stations with the time span of 7 years acquired from the first and second reprocessing campaigns. Using Eq. (8) of Amiri-Simkooei (2013a), the MPS is obtained (Fig. 9). The first, fourth, sixth, and eight draconitic peaks have been reduced by less than 15 %. The third draconitic harmonic experienced a significant reduction; it has been nearly halved. The reduction in the second and fifth draconitic peaks was nearly 25 %. It can thus be concluded that using new models within the second reprocessing campaign resulted in the reduction in the draconitic peaks.

To investigate the behavior of the draconitic signal on different GPS stations, we use visual inspection. Figures 10 and 11 represent typical examples on the nature of the draconitic signal for two nearby and two faraway GPS permanent stations, respectively. As expected (see Amiri-Simkooei 2013a), this signal is of similar pattern for nearby stations (${<}10$ km) (Fig. 10, compare red or black curves for each component of stations CIT1 and OXYC). However, for two faraway stations (${>}10,000\,\hbox {km}$), this statement does not hold true (Fig. 11). The effect is thus location dependent, which originates from the CMEs. But, they are not likely station dependent, and hence multipath cannot be the main source. As expected, this periodic pattern for the 2nd reprocessing campaign (black curve) has been reduced compared to that for the first reprocessing campaign (red curve).

3.4.2 Correlation analysis

The behavior of this periodic pattern can be investigated using the correlation analysis. For this purpose, first we form a zero-mean time series by using all sinusoidal functions of the draconitic signal over one full cycle and collect them in the matrix Y of order $m\times r$. The spatial correlation induced by the matrix Y can be obtained using $\frac{Y^{T}Y}{m}$. Figure 12 presents the results for the data sets with 89 stations. The spatial correlation induced by the draconitic signal is significant over the angular distance ranging from $0{^{\circ }}$ to $20{^{\circ }}$ (2000 km). This is in agreement with the findings of Amiri-Simkooei (2013a). Therefore, this also indicates that this periodic pattern has still common-mode signatures for the adjacent stations.

Fig. 11

Effect of periodic pattern of first reprocessing (red) and second reprocessing (black) campaign estimated for a typical example (CHIL versus ALIC) in which stations are far from each other. CHIL is the site at San Gabriel Mountains, US. ALIC is the site at Alice Springs, Australia. The two sites are 13,000 Km apart. The red and black points denote the residual time series after subtracting liner regression terms plus 3 harmonics of the annual signal for first and second reprocessing campaigns, respectively. The dashed red and solid black lines denote the draconitic signal estimated for the first and second reprocessing campaigns, respectively

3.5 Geodetic and geophysical impact of new time series

This contribution showed improvement on both the functional and stochastic models of GPS position time series of the second reprocessing campaign. Parts of geodetic and geophysical impacts of these improvements are highlighted as follows:

• There is research ongoing in the field of Earth’s elastic deformation response to ocean tidal loading (OTL) using kinematic GPS observations. Martens et al. (2016) estimated GPS positions at 5-min intervals using PPP. They studied the dominant astronomical tidal constituents and computed the OTL-induced surface displacements of each component. Such kinematic GPS processing can have many other geophysical applications. Precise determination of Love numbers, as dimensionless parameters characterizing the elastic deformation of Earth due to body forces and loads, is considered to be another application. Therefore, as a direct effect of the new time series, one would expect further improvements in the realization of such geophysical applications.

• GPS position time series have been widely used to study various geophysical phenomena such as plate tectonics, crustal deformation, post-glacial rebound, surface subsidence, and sea-level change (Thatcher 2003; Argus et al. 2010; Kreemer et al. 2014; Johansson et al. 2002; King et al. 2010; Peltier et al. 2015; Wöppelmann et al. 2007; Lü et al. 2008; Bock et al. 2012). Long-term homogeneous time series reanalysis using the new methods and strategies will directly affect all such phenomena—site velocities along with their uncertainties for instance. Reduction in noise components and the GPS draconitic effect allows other signals to be detected (for example signals with periods of 432.5 and 380 days). More appropriate geophysical interpretation can thus directly be expected, although many of the above references use position time series with CME filtering and hence such signals can be attenuated relative to the “global” solutions discussed in this paper.

• Strain analysis using permanent GPS networks requires proper analysis of time series in which all functional effects are taken into consideration and all stochastic effects are captured using an appropriate noise model. To investigate the effect of the normalized strain parameters on geophysical interpretation, we may recall the statistics theory on the significance of the estimated parameters. To have a statistically significant parameter, one has to compare the parameter with its standard deviation. Flicker noise is the main contributor to make these parameters insignificant (Razeghi et al. 2015). Reduction in flicker noise has thus a direct impact on the significance of the deformation parameters.

• Reduction in colored noise, their spatial correlation, and the GPS draconitic signal have significant benefits on the realization of International Terrestrial Reference Frame (ITRF). These improvements will significantly affect the estimation of the parameters of interest and their uncertainty (Altamimi and Collilieux 2009). They indicated that “IGS is undertaking a great effort of reprocessing the entire time span of the GPS observations with the aim to produce a long-term homogeneous time series. Preliminary analysis of some reprocessed solutions indicates a high performance of these solutions which will play a significant role in the next ITRF release”. This came true based on the results presented in this contribution.

Fig. 12

Spatial correlation originated from draconitic signal of three coordinate components (north, east, and up) for the data set with the time span of 7 years

4 Conclusions

This contribution compared the results of the processing the data derived from the first and second reanalysis campaigns to identify the areas of improvement and/or possible degradation. Daily position time series of 89 (7 years) and 66 (21 years) permanent GPS stations, obtained from the JPL second reprocessing campaign, were analyzed. The former data sets were also derived from the first reprocessing campaign to compare the possible improvements in the most realistic manner. Spatial and temporal correlations and MPS were obtained using the formulas and methodologies presented by Amiri-Simkooei (2013a). The following conclusions are drawn:

• Although the time series of the second reprocessing campaign showed reduction in the spatial correlation among the series by a factor of 1.25, it is nevertheless significant. The spatial cross-correlation also decreases; it is less than 0.1 for the three coordinate components.

• The amplitudes of white noise and flicker noise are reduced by factors ranging from 1.40 to 2.33. The random walk amplitudes are higher than the zero values determined for the first reanalysis campaign. This is likely due to the new time series benefiting from a kind of uniform ‘processing’ noise over time, while the noise of the older series is reduced with time. As a result of the revised analysis techniques, the random walk noise has been detected. Further, white and flicker noise have significantly reduced resulting in better detection of the random walk noise amplitude. For the 89 permanent GPS stations with 7 years of data, white noise, flicker noise, and random walk noise rate errors are 0.01, 0.12, and 0.09 mm/yr, respectively, for the horizontal component. The vertical rate errors are larger than those of the horizontal by the factors ranging from 3.33 to 4.

• Unlike the results derived from the first reprocessing campaign, the noise amplitude of the north component equals that of the east. This is attributed to incorporating the new model for the tropospheric delay and to taking the higher-order ionospheric terms into consideration, which likely improves ambiguity resolution.

• Both MPS applied to the three components and to the individual components clearly show signals with periods of 13.63 and 14.76 days. In addition, the spectra show a cluster of periods around 5.5 days. A cluster of periods around 2.75 days has been identified in the data set with 89 (7 years) and 66 (21 years) GPS stations. Regarding the signals with lower frequencies, a significant signal with period of around 351.4 days (up to its eighth harmonics) is detected. This closely follows the GPS draconitic year. Two other signals with periods of nearly 432.5 and 380 days have been found. While the period of the former signal equals the well-known Chandler period, the latter signal is not known.

• The mean range of variations (max and min) of the draconitic pattern for the series derived from the second reprocessing campaign shows a reduction of 46, 46 and 41% for the north, east, and up components, respectively, compared to those of the first campaign. This significant reduction can be a direct corollary of the improved models in the new campaign. While the first, fourth, sixth, and eight draconitic peaks have been reduced by less than 15 %, the third draconitic harmonic has been nearly halved. The reduction in the second and fifth draconitic peaks was nearly 25 %.

• Two independent measures of visual inspection and correlation analysis were used to investigate the nature of the draconitic pattern. While the effect of the draconitic signal is of similar pattern for nearby stations (Fig. 10), it differs significantly for distant stations (Fig. 11). The periodic pattern was reduced in the second reanalysis campaign.

• A similar behavior for the spatial correlation of the time series (Fig. 2) and the periodic pattern (Fig. 12) is observed. This indicates that although new models and methodologies in the latest reanalysis have reduced the spatial correlation among the series to an extent, the draconitic pattern is still an error source inducing spatial correlation to the time series.

• There are three factors that may prevent random walk to be detected. The first is the dominance of flicker noise, which masks random walk noise (Williams et al. 2004). Flicker noise has been significantly reduced in the second reprocessing. The second factor is the small length of the time series. For some stations, however, there are currently more than two decades of data. A few preliminary tests confirm significant random walk noise on longer time series. 3) The third factor originates from our observation in this contribution, which states that second reprocessing has not only reduced noise but also it shows a kind of uniform processing noise over time (see Fig. 4). These three factors thus indicate that random walk noise can in principle be the subject of the intensive research in future GPS position time series analysis.

Appendices

Appendix 1: models employed within the second IGS reanalysis campaign

1.1 Yaw attitude variations

Inconsistent yaw attitude models affects the precision of the IGS combined clock solutions (Hesselbarth and Wanninger 2008). Therefore, the reliability of the IGS combined clocks is impaired. To diminish the effect of the eclipsing satellites on the IGS clock solutions, consistent modeling of attitude changes is needed (Ray 2009). Distortions in the orientation of the eclipsing satellites follow a simplified yaw attitude model for Block II/IIA and Block IIR satellites (see Kouba 2009a). Attitude behavior of the Block IIF-1 (launched on May 27, 2010) spacecraft during the eclipse has been studied by Dilssner (2010). In addition, with complete modernization of the GLONASS satellites, ACs should include GLONASS observations as well. An appropriate yaw attitude modeling of these satellites may follow the model proposed by Dilssner et al. (2011).

1.2 Modeling of orbit dynamics

Urschl et al. (2007) observed anomalous pattern in the plot of GPS-SLR residuals which they attributed to the GPS orbit mismodeling. This anomalous pattern (particularly, the GPS draconitic year signal) was also identified in the geocenter Z-component (Hugentobler et al. 2006) and GPS position time series (Ray et al. 2008).

One of the potential sources for GNSS orbit mismodeling is the deficiencies in the Earth radiation pressure (ERP) model. Not all IGS ACs are yet modeling ERP. Utilizing a model for Earth radiation, proposed by Rodriguez-Solano et al. (2012), results in the reduction in root mean square (RMS) of orbit’s height component by about 1–2 cm and smaller perturbations of other components related to the orbit. Rodriguez-Solano et al. (2012) showed that the model can compensate the SLR residual bias observed.

The GPS orbit perturbations due to ERP depend on the relative position of Sun, Earth, and satellite. Parts of the observed periodic patterns in GPS time series may stem from failure to correctly model ERP (Rodriguez-Solano et al. 2012). They found that the inclusion of the ERP model results in the reduction in the sixth draconitic signal for the north component at a submillimeter level (equal to reduction of around 38%). Ray (2009) also suggested taking ERP into consideration. Hence, the model proposed by Rodriguez-Solano et al. (2011) has been used within the IGS in the operational reprocessing.

Earth albedo radiation (EAR) is another source for orbit modeling deficiencies. This radiation consists of both visible reflected light and infrared emitted radiation. Most AC contributors have not taken into account the effect of EAR. The albedo acceleration may have a significant effect on the orbit of GPS satellites (a mean reduction in the orbit radial component by 1–2 cm) (Hugentobler et al. 2009). They concluded that for the high-precision GPS orbit determination, EAR and antenna thrust should be taken into consideration. However, regarding the spectra of geocenter and position time series, no significant impact has been observed when the model for EAR was used (Hugentobler et al. 2009). This indicates that there could be still unmodeled effects on the GPS orbit which can be larger than the albedo radiation.

1.3 Geopotential field

In terms of the geopotential model, a new model referred to as EGM2008 has been defined (see Ray 2009). EGM2008 exhibits significant improvements compared to its previous counterpart EGM96, thanks to the availability of CHAMP and most importantly GRACE data in the 2000s. Compared to EGM96, used for the 1st processing campaign, EGM2008 has been modified in the following aspects:

• 1. Its degree and order have been increased by a factor of 6.

• 2. Updated value for secular rate of low-degree coefficients.

• 3. A new model for the mean pole trajectory was proposed.

• 4. Model for geopotential ocean tide has been updated for FES2004.

• 5. A new ocean pole tide model has been introduced.

For more information, the reader is referred to IERS 2010 conventions (Petit and Luzum 2010).

1.4 Tidal effects

Tidal effects are categorized to the following two contributions. (1) Tidal displacement of station positions; (2) Tidal EOP variations. For the former, within the new processing campaign, a new model which is introduced for the mean pole trajectory IERS 2010 (Petit and Luzum 2010) has been used for the pole tide correction. Moreover, model for ocean pole tide loading presented by Desai (2002) should be used. For the latter, the Earth rotation axial component in terms of UT1 contains small diurnal and subdiurnal signals. Thus, the tidal gravitation effect on those features of Earth’s mass distribution results in the astronomical precession-nutation of Earth rotation (Brzeziński 2008). A minor part of the astronomical variations, called libration, is a result of the tidal gravitation effect on the non-zonal terms of geopotential (Brzeziński 2008). In case of UT1, the perturbation is semidiurnal with total amplitude up to $75\,\upmu \hbox {as}$. Brzeziński and Capitaine (2009) studied the subdiurnal libration in UT1. They derived a solution for the structural model of the Earth composing of an elastic mantle and a liquid core not coupling to each other.

A key expectation in tidal EOP variations modeling compared to the 1st reprocessing campaign is the addition of the UT1 libration effect introduced by Brzeziński and Capitaine (2009). It is noted that the maximum effect of UT1 libration is about $105\,\upmu \hbox {as}$, or 13 mm at GPS altitude. It probably severely aliases into the orbit parameters.

1.5 Tropospheric propagation delay

In the second reprocessing, a new slant delay model (GPT2) was suggested. It improves its older models GPT/GMF with refined horizontal resolution, enhanced temporal coverage, and increased vertical resolution (37 isobaric levels compared to 23 ones utilized for GPT/GMF) (Lagler et al. 2013). In addition to mean value, $a_0$, and annual amplitude, A, estimated using the least-squares method in GPT/GMF, semiannual harmonics are incorporated within GPT2. This better accounts for regions with very rainy or dry periods. As for the temperature reduction, in contrast to the GPT/GMF in which a constant $-6.5\,^{\circ }\hbox {C}/\hbox {km}$ was assumed, mean, annual, and semiannual variations of temperature lapse rate are determined each grid point in GPT2. Regarding the pressure reduction, unlike the GPT/GMF which utilizes an exponential formula based on the standard atmosphere, GPT2 deploys an exponential formula based on virtual temperature (Lagler et al. 2013). The improved performance of GPT2 compared to the previous model GPT/GMF has been examined by Lagler et al. (2013). They have recommended to replace GPT/GMF with GPT2 as an empirical model.

Because of the partial compensation of the atmospheric loading by mismodeling the zenith hydrostatic delays (ZHDs) (Kouba 2009b), GPT-derived ZHDs give rise to a better station height repeatability compared to ECMWF ZHDs if atmospheric loading is not corrected for (Steigenberger et al. 2009). On the other hand, if one needs to examine the coordinates time series to reveal atmospheric loading signals, application of ZHDs derived from numerical weather models is a key element.

1.6 Higher-order ionospheric terms

A linear combination of multi-frequency observations allows for taking into consideration the first-order ${\sim }\frac{1}{f^{2}}$ ionospheric term (Hofmann-Wellenhof et al. 2008). The first-order ionospheric delay is in the order of 1 to 50 meters, which depends on the satellite elevation, ionospheric activities, local time, season and solar cycle (Kedar et al. 2003). The higher-order ionospheric terms, which are in the order of submillimeters to several centimeters, are usually neglected. Kedar et al. (2003) stated that the effect of second-order ionospheric term introduced by Bassiri and Hajj (1993) can likely improve the position repeatability and reduce the small biases in geocenter estimates. Fritsche et al. (2005) and Hernández-Pajares et al. (2007) showed that the second-order ionospheric term affects the geocenter Z-component estimates. Fritsche et al. (2005) processed the double difference phase observation of a global network and compared solutions with and without the higher-order ionospheric terms. They concluded that applying these higher terms will became a standard part of precise GPS applications. IERS 2010 conventions (Petit and Luzum 2010) suggested that while the first- and second-order ionospheric terms are to be considered for GNSS applications, the third order is at the limited significance and the fourth order can be neglected.

1.7 Analysis constraints

Ferland (2010) found that high-frequency smoothing may be due to unremovable continuity constraints for some ACs. Ray (2009) suggested that, for the 2nd reprocessing campaign, ACs constraints and procedures should be reconsidered from the following aspects: (1) Reviewing the necessity of applying constraints, (2) Paying particular attention to the constraint on the orbit and UT1/LOD, (3) Elimination and minimization of the constraints as many as possible, and (4) Better understanding of the impacts of constrains retained is necessary. Accordingly, in the IGS2008 recommendations (http://igs.org/overview/pubs/IGSWorkshop2008/), all ACs should report their a-priori constraints. Although removable constraints are acceptable, unconstrained solutions are preferred. Inner constraints (origin, orientation, scale) are acceptable.

Appendix 2: rate errors in multivariate model

Having r time series available, a multivariate linear model is of the form (Koch 1999)

$$\begin{aligned} E\left( {\hbox {vec}\left( Y \right) } \right) =\left( {I_r \otimes A} \right) \hbox {vec}\left( X \right) ,D\left( {\hbox {vec}\left( Y \right) } \right) =Q_{\mathrm {vec}\left( Y \right) }\nonumber \\ \end{aligned}$$

(1)

where vec is the vector operator and $\otimes$ is the Kronecker product. $I_r$ is the identity matrix of size r. X and Y are the matrices of the sizes $n\times r$ and $m\times r$ collecting unknown parameters and observations from r number of series, respectively. A and $Q_{\mathrm {vec}\left( Y \right) }$ are, respectively, the functional and stochastic models describing all deterministic effects and statistical characteristics of the observables. E indicates the expectation operator, and D is the dispersion operator.

The following structure for the stochastic model, referred to as the more practical model, is used (Amiri-Simkooei 2009)

$$\begin{aligned} D\left( {\hbox {vec}\left( Y \right) } \right) ={\Sigma }\otimes Q={\Sigma }\otimes \mathop \sum \nolimits _{k=1}^p s_\mathrm{k} Q_\mathrm{k} \end{aligned}$$

(2)

where $Q_\mathrm{k}$’s are the known cofactor matrices of size $m\times m$. The matrix ${\Sigma }$ and the unknown factors $s_\mathrm{k}$ are to be estimated using LS-VCE.

The least-squares estimate of X reads then (Koch 1999)

$$\begin{aligned} {{\hat{X}}} =\left( {A^{T}Q^{-1}A} \right) ^{-1}A^{T}Q^{-1}Y \end{aligned}$$

(3)

The covariance matrix of the nr-vector$\hbox { vec}\!\left( {{{\hat{X}}}} \right)$ is

$$\begin{aligned} Q_{\mathrm {vec}\left( {{{\hat{X}}} } \right) } ={\Sigma }\otimes \left( {A^{T}Q^{-1}A} \right) ^{-1}={\Sigma }\otimes N^{-1} \end{aligned}$$

(4)

where $N=A^{T}Q^{-1}A$ is the normal matrix. Here, we assume that the functional model contains two columns for the linear regression terms plus two columns for each of the annual, semiannual, and tri-annual signal. A is thus of size $m\times 8$. Its ith row at the time instant $t_i$ is

$$\begin{aligned} \left[ {1 \quad \! {t_i }\quad {\cos 2\pi t_i }\quad \! {\sin 2\pi t_i }\quad \! {\cos 4\pi t_i }\quad \! {\sin 4\pi t_i }\quad \! {\cos 6\pi t_i } \quad \! {\sin 6\pi t_i } } \right] \nonumber \\ \end{aligned}$$

(5)

Therefore, the unknown parameters are the intercept, rate, and amplitudes of the annual, semiannual, and tri-annual signals. The covariance matrix of the slopes (for all series) is given as $Q_r ={\Sigma }\times (N^{-1})_{22}$, where $(N^{-1})_{22}$ is the second diagonal element of $N^{-1}$. It is further assumed that Q matrix has the form

$$\begin{aligned} Q=s_\mathrm{w} I+s_\mathrm{f} Q_\mathrm{f} +s_{\mathrm{rw}} Q_{\mathrm{rw}} \end{aligned}$$

(6)

where $s_\mathrm{w}$, $s_\mathrm{f}$, $s_{\mathrm{rw}}$ are the white, flicker, and random walk noise amplitudes, respectively. $Q_\mathrm{f}$ and $Q_{\mathrm{rw}}$ are the flicker and random walk noise cofactor matrices, respectively. LS-VCE has been employed to estimate $s_\mathrm{w}$, $s_\mathrm{f}$, $s_{\mathrm{rw}}$, and ${\Sigma }$. As the three coordinate components of all stations have been processed simultaneously, ${\Sigma }$ is of the size $r\times r$. Its corresponding, north, east, and up components are referred to as ${\Sigma }_N$, ${\Sigma }_E$, and ${\Sigma }_U$, respectively (block diagonals). To compute the white, flicker, and random walk noise rate errors for the east components, matrix Q in Eq. (4) is substituted with $Q_\mathrm{w} =s_\mathrm{w}I$, $Q_\mathrm{f} =s_\mathrm{f} Q_\mathrm{f}$ or $Q_{\mathrm{rw}} =s_{\mathrm{rw}} Q_{\mathrm{rw}}$, respectively. Matrices $N_\mathrm{w}, N_\mathrm{f}$, $N_{\mathrm{rw}}$ are then obtained. The rate errors of the east component read

$$\begin{aligned}&\sigma _\mathrm{r}^\mathrm{w} =\sqrt{\hbox {diag}\left( {{\Sigma }_\mathrm{E} N_\mathrm{w}^{-1} \left( {2,2} \right) } \right) } \end{aligned}$$

(7)

$$\begin{aligned}&\sigma _\mathrm{r}^\mathrm{f} =\sqrt{\hbox {diag}\left( {{\Sigma }_\mathrm{E} N_\mathrm{f}^{-1} \left( {2,2} \right) } \right) } \end{aligned}$$

(8)

$$\begin{aligned}&\sigma _\mathrm{r}^{\mathrm{rw}} =\sqrt{\hbox {diag}\left( {{\Sigma }_E N_{\mathrm{rw}}^{-1} \left( {2,2} \right) } \right) } \end{aligned}$$

(9)

where $\sigma _\mathrm{r}^\mathrm{w}$, $\sigma _\mathrm{r}^\mathrm{f}$ and $\sigma _\mathrm{r}^{\mathrm{rw}}$ are the vector of rate errors for the east component of all stations. Their mean indicate the average error rates over all stations. The corresponding values for the north and up components can accordingly be obtained.