1 Introduction

Polar motion, or variations in the geocentric location of the pole of the Earth’s instantaneous rotation axis, introduces a differential centrifugal force that causes displacements of the solid Earth and oceans. These displacements are commonly referred to as the pole tide (Munk and Macdonald 1960), because they can be treated in much the same way as the luni-solar tides. The centrifugal potential has similar spatial form to the diurnal luni-solar tidal potential and is temporally dominated by periodic variations in polar motion, primarily at the Chandler wobble and seasonal periods of \(\sim \)14 and 12 months with amplitudes of approximately 0.05–0.25 and 0.12 arcsec, respectively (e.g., Wahr 1985; Desai 2002). The pole tide displacements can be determined by applying tidal Love numbers to the differential centrifugal potential, with that potential derived from polar motion observations. The displacements of the solid Earth, the body pole tide, have amplitudes of up to 10 mm (Wahr 1985), depending on location and the time-varying amplitude of the Chandler wobble. Meanwhile, the displacements of the ocean surface with respect to the ocean bottom, the ocean pole tide, have similar amplitude (Desai 2002). In turn, the loading mass of the ocean pole tide causes displacements of the Earth’s crust, the load pole tide, that are an order of magnitude smaller. Satellite radar altimeters observe geocentric sea surface height (SSH) and therefore contain the sum total of the body, ocean, and load pole tides with amplitudes of up to 20 mm.

In this paper, we evaluate the errors in the pole tide model that is currently adopted by most, if not all, users of satellite altimeter SSH measurements and identify possible improvements to that model. Of the various geophysical models that are typically applied as corrections to these measurements, and made available on the official altimeter geophysical data records (GDRs), those for the pole tide (Wahr 1985) and the luni-solar body tide (Cartwright and Taylor 1971; Cartwright and Edden 1973; Wahr 1981) have not been revised since the launch of the TOPEX/Poseidon (T/P) mission more than two decades ago. Hereinafter, we refer to these versions as the T/P models. A discussion of differences between the T/P luni-solar body tide model versus that recommended by the International Earth Rotation Service (Petit and Luzum 2010) is provided by Ray (2013, appendix). However, errors in the luni-solar tide models are not relevant to the pole tide due to the different spectral content in each. Most users of the satellite altimeter SSH data use these two models exactly as provided on the respective GDRs. They were selected when the pre-launch SSH error budget for T/P was 13.7 cm (RMS) (Fu et al. 1994), and the nominal mission lifetime was 3 years with a possible extension to 6 years. Over two decades of satellite altimeter SSH data are now continuously available from the T/P (Fu et al. 1994), Jason-1 (Ménard et al. 2003), and OSTM/Jason-2 (Lambin et al. 2010) missions, and in-flight performance reflects 1-Hz SSH measurement accuracies of 3–4 cm (RMS). The duration of this unique SSH time series is expected to grow with successor missions already scheduled for launch (e.g., Jason-3) or planned. Perhaps the most demanding applications of this time series are for observations of regional and global mean sea level (GMSL) rise, where 95 % confidence intervals on the latter are reported to be 0.8 mm/year (e.g., Beckley et al. 2010; Leuliette and Willis 2011; Masters et al. 2012). A reevaluation of the pole tide model for satellite radar altimeter SSH measurements and observations thereof is therefore overdue despite its small amplitude and long periods.

Given that accurate polar motion observations are available to define the associated centrifugal potential, then the body pole tide can be modeled quite accurately as a mostly elastic response of the solid Earth to that potential (Wahr 1985). Knowledge of the appropriate body Love number that reflects the response of the Earth is needed (e.g., Petit and Luzum 2010). Similarly, the load pole tide is also easily modeled as an elastic response of the Earth’s crust to the loading mass of the ocean pole tide, using load Love numbers or associated Green’s functions (e.g., Farrell 1972; Guo et al. 2004). Modeling the ocean pole tide may be more complex due to the inherent dynamics of the ocean basins, and as a result directly impacts the ability to model the load pole tide. Ideally, an ocean pole tide model would be determined either empirically from the satellite altimeter SSH data or through the application of hydrodynamic equations of motion perhaps constrained by those data. To the best of our knowledge, there have been no attempts as yet to model the ocean pole tide using hydrodynamic equations of motion constrained by altimeter data. Using an empirical approach with the first 9 years of T/P SSH measurements, Desai (2002) resolved the long wavelength global component of the ocean pole tide but found that observations of the short wavelength ocean pole tide were likely contaminated by oceanographic variability. Furthermore, the long wavelength component was found to be consistent with a so-called self-consistent equilibrium response (Agnew and Farrell 1978). This response defines ocean displacements as following the surface of the forcing potential, and also only requires knowledge of the centrifugal potential, the body and load Love numbers. At the other extreme, Carton and Wahr (1986) solved Laplace’s tidal equations without constraints from altimeter data and concluded that departures from equilibrium are likely to be negligible at the Chandler wobble period.

Here, we use a self-consistent equilibrium model for the ocean pole tide, given that a reliable hydrodynamic model is currently not available and because there is no strong evidence of significant departures from equilibrium. The fundamental argument for self-consistent equilibrium models of ocean tides is based upon the understanding that ocean bottom friction increasingly damps currents at periods longer than a few weeks (Agnew and Farrell 1978). Recent results from Ray and Erofeeva (2014) provide strong supporting evidence through their application of hydrodynamics to the primary long-period luni-solar tidal components. Their observation of decreasing deviations from a self-consistent equilibrium response with increasing period is relevant to the pole tide, even though the spatial forms of the forcing potential for the long-period luni-solar and pole tides are different. The former is represented by a degree 2 zonal spherical harmonic and the latter a degree 2 order 1 spherical harmonic. Of particular relevance is their result that predicts departures from the self-consistent equilibrium response on the order of less than 1 % at the annual period. The pole tide periods are primarily one year and longer, so a self-consistent equilibrium model is justified. In the past, significant departures from equilibrium have been reported for the North and Baltic Seas (e.g., Haubrich and Munk 1959; Wunsch 1974), but have since been attributed to meteorological forcing rather than the pole tide potential (e.g., Ekman and Stigebrandt 1990; Trupin and Wahr 1990; Tsimplis et al. 1994; Xie and Dickman 1996; O’Connor et al. 2000).

Our approach individually accounts for the body, ocean, and load pole tides, with the load pole tide accommodating geocenter variations that arise from the redistribution of mass from the ocean pole tide. The T/P model also accounts for the body pole tide, but ignores the load pole tide and geocenter variations. We recommend the self-consistent equilibrium approach for the ocean pole tide, updated from Desai (2002) as described in this paper, to properly account for the effects of self-gravitation, loading, and conservation of mass, all of which are ignored in the T/P model. Given that an additional 10 years of altimeter SSH data are now available since the study by Desai (2002), we also revisit the global empirical observations of the pole tide and use them to demonstrate that accounting for these various effects provides better agreement with the altimeter observations than when they are ignored. Following similar recommendations by Wahr et al. (2015) for time variable gravity applications, we also recommend that the pole tide model for altimetry products exclude the response due to the long-term drift in polar motion. We similarly do so by computing the altimetry pole tide model using only the deviations from a linear representation of polar motion whose rates have been determined from almost 80 years of observations by Argus and Gross (2004). In practice, this means that we recommend modeling the mean pole location with a bias and rate, whereas the T/P model uses only a bias. The T/P model is effectively misrepresenting the effects of long-term drift in polar motion on observed geocentric sea surface height, and we evaluate the impact of this error on observations of regional and GMSL. While there are multiple sources for the observed long-term drift in polar motion (see Gross 2007), glacial isostatic adjustment (GIA) is considered to be the most important. Users interested in the geocentric sea surface displacements associated with rotational feedback from GIA might then correct for these more complex effects using dedicated GIA models (e.g., A et al. 2012; Tamisiea 2011), which are not addressed in this paper.

2 Pole tide contributions to satellite altimetry observations

In this paper, we only consider the radial component of the body and load pole tides since the satellite altimeter measurements are not sensitive to the transverse components. We represent the body, ocean, and load pole tides by \(\zeta _\mathrm{B}\), \(\zeta _\mathrm{O}\), and \(\zeta _\mathrm{L}\), respectively. In addition, we define the load pole tide to be with respect to the center of mass of the total Earth system (CM), as is appropriate for satellite altimeter SSH measurements (e.g., Desai and Ray 2014). As already mentioned, the satellite altimeter observations, \(\zeta _\mathrm{a}\), yield the sum total of these three contributions. All are functions of colatitude \(\theta \), east longitude \(\lambda \), and time t.

$$\begin{aligned} \zeta _\mathrm{a} \left( {\theta ,\lambda ,t} \right)= & {} \zeta _\mathrm{B} \left( {\theta ,\lambda ,t} \right) +\zeta _\mathrm{O} \left( {\theta ,\lambda ,t} \right) +\zeta _\mathrm{L} \left( {\theta ,\lambda ,t} \right) \end{aligned}$$
(1)
$$\begin{aligned} \zeta _\mathrm{B} \left( {\theta ,\lambda ,t} \right)= & {} H_P {\mathcal {R}}e\left[ {m^{*}\left( t \right) h_2 \overline{P} _{21} \left( {\cos \theta } \right) e^{i\lambda }} \right] \end{aligned}$$
(2)
$$\begin{aligned} \zeta _\mathrm{O} \left( {\theta ,\lambda ,t} \right)= & {} H_P {\mathcal {R}}e\left[ {m^{*}\left( t \right) Z\left( {\theta ,\lambda } \right) } \right] \end{aligned}$$
(3)
$$\begin{aligned} \zeta _\mathrm{L} \left( {\theta ,\lambda ,t} \right)= & {} H_P {\mathcal {R}}e\left[ {m^{*}\left( t \right) Z_\mathrm{L} \left( {\theta ,\lambda } \right) } \right] \nonumber \\= & {} H_P {\mathcal {R}}e\left[ {m^{*}\left( t \right) \mathop \sum \limits _{n=1}^\infty h_n^{\prime } \alpha _n Z_n \left( {\theta ,\lambda } \right) } \right] \end{aligned}$$
(4)

Equations (2)–(4) summarize each contribution using the notation from Desai (2002). The pole tide displacement scaling factor \(H_P\) [Desai 2002, equation (12)] arises from the centrifugal potential and has a value of 138.5 mm/arcsec when the rotation pole location, \(m\left( t \right) \), is given in arcseconds. The angular location of the rotation pole is \(m\left( t \right) =m_1 \left( t \right) +im_2 \left( t \right) \), with \(m_1 \) and \(m_2 \) positive towards the Greenwich and 90 degree east meridians, respectively. We use \({\mathcal {R}}e\left[ f \right] \) and \(f^{*}\) to denote the real part and complex conjugate of the complex function f, respectively, and define the normalized degree 2 and order 1 Legendre polynomial by \(\overline{P} _{21} \left( {\cos \theta } \right) =-\left( {15/32\pi } \right) ^{1/2}\sin 2\theta \). The ocean pole tide admittance, \(Z\left( {\theta ,\lambda } \right) \), has degree n spherical harmonic components \(Z_n \left( {\theta ,\lambda } \right) \), and \(Z_\mathrm{L} \left( {\theta ,\lambda } \right) \) is the associated load pole tide admittance.

If the ocean pole tide is assumed to have a self-consistent equilibrium response, the corresponding admittance function to be used in Eqs. (3) and (4) takes the following form (Desai 2002).

$$\begin{aligned} Z^{s}\left( {\theta ,\lambda } \right)= & {} \gamma _2 {\mathcal {O}}\left( {\theta ,\lambda } \right) \Biggl [ \overline{P} _{21} \left( {\cos \theta } \right) e^{i\lambda }\nonumber \\&+\mathop \sum \limits _{n=0}^\infty \gamma _n^{\prime } \alpha _n Z_n^s \left( {\theta ,\lambda } \right) +K \Biggr ] \end{aligned}$$
(5)

This equation is solved iteratively and convergence to within 0.1 % is achieved after four iterations (e.g., Agnew and Farrell 1978; Desai 2002; Ray and Erofeeva 2014). The degree 2 radial and potential Love numbers are \(h_2 \) and \(k_2\), respectively, and form the combination \(\gamma _2 =\left( {1+k_2 -h_2 } \right) \). The corresponding degree n load Love numbers are \(h_n^{\prime }\), \(k_n^{\prime }\), and \(\gamma _n^{\prime } =\left( {1+k_n^{\prime } -h_n^{\prime } } \right) \). When modeling the pole tide we use Love numbers from the most recent IERS recommendations (Petit and Luzum 2010), \(k_2 =0.3077+i0.0036\) and \(h_2 =0.6207\), where the imaginary component reflects the anelastic response of the solid Earth. The constant, K, is included to force conservation of mass on the self-consistent equilibrium ocean tide. Using \(\rho _E \) and \(\rho _W \) to represent the mean densities of the solid Earth and oceans, 5.518 and \(1.035\hbox { g/cm}^{3}\), respectively, then \(\alpha _n =\left( {3/\left( {2n+1} \right) } \right) \left( {\rho _W /\rho _E } \right) \) (Munk and Macdonald 1960). The ocean function, \({\mathcal {O}}\left( {\theta ,\lambda } \right) \), explicitly accommodates for continental boundaries, and has a value of 1 over the oceans and 0 over land.

When assuming a self-consistent equilibrium ocean response the sum total of the body, ocean, and load pole tides observed by altimeters over the oceans is then as shown in Eq. (6) [which corrects a printing error in equation (22) from Desai (2002)].

$$\begin{aligned} \zeta _\mathrm{a} \left( {\theta ,\lambda ,t} \right)= & {} H_P {\mathcal {R}}e\left[ {m^{*}\left( t \right) \overline{Z}_\mathrm{a} \left( {\theta ,\lambda } \right) } \right] \nonumber \\ \overline{Z}_\mathrm{a} \left( {\theta ,\lambda } \right)= & {} {\mathcal {O}}\left( {\theta ,\lambda } \right) \Biggl [ \left( {1+k_2 } \right) \overline{P} _{21} \left( {\cos \theta } \right) e^{i\lambda } \nonumber \\&+\,\gamma _2 \mathop \sum \limits _{n=0}^\infty \left( {1+k_n^{\prime } } \right) \alpha _n Z_n^s \left( {\theta ,\lambda } \right) +K\Biggr ] \end{aligned}$$
(6)

This representation shows that the total geocentric pole tide admittance under the assumption of a self-consistent equilibrium ocean response is predominantly dependent on \(k_2 \) relative to \(h_2\). The dependence on \(h_2 \) only arises from the second order term of Eq. (6) (through \(\gamma _2\)) that accounts for loading effects. We take advantage of this (in Sect. 4) to use the altimeter data to estimate \(k_2 \) while holding \(h_2 \) fixed to the IERS recommended value. The T/P model effectively also adopts an equilibrium approach for the ocean pole tide, but it ignores the last two terms of Eqs. (5) and (6) that account for self-gravitation, loading, and mass conservation. In effect, it also ignores the load pole tide, \(\zeta _\mathrm{L} \). In doing so, the admittance of the T/P pole tide model is only dependent on the potential Love number for over-ocean measurements, and a value \(k_2 =0.302\) is currently adopted. We note that Eq. (6) is not valid over land and inland water, where the total pole tide consists of only the sum total of the body and load pole tides, with mass conservation effectively eliminating any displacements of inland water relative to the Earth’s crust when the spatial extent of that body of water is small.

We have made a few modifications to the self-consistent equilibrium ocean pole tide model from Desai (2002). Load Love numbers from Guo et al. (2004) are used instead of those from Farrell (1972). Those from the former are derived from the more realistic Preliminary Reference Earth Model, while the latter are from the older Gutenberg–Bullen-A model. Whereas Desai (2002) used the DTM2000.1 terrain map of J. Saleh and N. Pavlis (personal communication) to derive an ocean function, ours is derived from the 2-min resolution TPXO8 ocean tide model (update to Egbert and Erofeeva 2002). We also improve upon the spatial resolution of the self-consistent equilibrium model, from 0.5 to 0.1 degrees in latitude and longitude, making it more suitable for application to the altimeter measurements. The 2-min resolution ocean function is averaged to the 0.1-degree resolution of the ocean pole tide model. Unlike Desai (2002), a Green’s function approach to solving Eq. (5), following Agnew and Farrell (1978), is used instead of a spherical harmonic approach. With the Green’s function approach the second term in Eq. (5) is replaced as follows:

$$\begin{aligned}&\mathop \sum \limits _{n=0}^\infty \gamma _n^{\prime } \alpha _n Z_n^s \left( {\theta ,\lambda } \right) \nonumber \\&\quad =\rho _W a^{2} \mathop \int \nolimits _0^{2\pi } \mathop \int \nolimits _0^\pi Z^{s} \left( {{\theta }',\lambda '} \right) G(\psi )\sin \theta ' \mathrm{d}\theta ' \mathrm{d}\lambda ' \end{aligned}$$
(7a)
$$\begin{aligned}&G\left( \psi \right) = \frac{a}{M}\mathop \sum \limits _{n=0}^\infty \gamma _n^{\prime } P_n \left( {\cos \psi }\right) . \end{aligned}$$
(7b)

The Green’s function, \(G\left( \psi \right) \), is computed using unnormalized Legendre polynomials, \(P_n \left( {\cos \psi } \right) \), that are functions of the angular separation, \(\psi \), between the locations of the loading mass at \(\left( {{\theta }'\lambda '} \right) \) and the response at \(\left( {\theta ,\lambda } \right) \). The mean radius and mass of the Earth are represented by a and M, respectively. Altogether, this means that iteration for a solution of the self-consistent equilibrium ocean pole tide in Eq. (5) is effectively using a spherical harmonic summation to degree 1800, instead of 360. We have verified the expected result that the Green’s function and spherical harmonic approaches to solving Eq. (5) give very similar results when using the maximum spherical harmonic degree associated with the model’s spatial resolution. Of these various changes, the impact on the self-consistent equilibrium ocean tide is typically \(<\)0.1 mm/arcsec at latitudes north of \(-62^{\circ }\)S. The most significant differences are due to the modified ocean function and therefore occur at coastal boundaries, especially near Antarctica where they reach 0.5 mm/arcsec. These modifications amplify the primary degree 2 order 1 spherical harmonic long wavelength component of the self-consistent equilibrium ocean pole tide by 0.4 %, changing the coefficient \(a_{21} \) defined by equation (19) of Desai (2002) from 0.8439 to 0.8469. This change provides some measure of the error due to uncertainties in the load Love numbers and ocean function.

Fig. 1
figure 1

Amplitude of differences between this paper’s and the T/P model for the sum total of the body, ocean, and radial load pole tides in units of mm/arcsecond. Differences are shown over the ocean only and are computed using \(H_P \left| \overline{Z}_\mathrm{a} \left( {\theta ,\lambda } \right) -\left( {1+k_2 } \right) \overline{P}_{21} \left( {\cos \theta } \right) e^{i\lambda } \right| \). Global differences have RMS and maximum of 3.0 and 5.2 mm/arcsec, respectively

Full size image

Here, we determine the load pole tide in a different reference frame compared to Desai (2002), computing it with respect to the CM, instead of the center of mass of the solid Earth (CE). This choice is based upon results from Desai and Ray (2014) who provide evidence to support that satellite altimeter SSH measurements of tidal effects are with respect to the CM. This modification is easily applied by using an effective degree-1 radial load Love number for the CM frame, namely \(h_1^{\prime } -1=-1.286\) in Eq. (4) (e.g., Blewitt 2003), where \(h_1^{\prime } \) is the CE-based value that is typically published (e.g., Farrell 1972; Guo et al. 2004). The self-consistent equilibrium ocean pole tide [Eq. (5)] is independent of the choice of reference frame since it effectively represents ocean displacements with respect to the solid Earth crust. Here, we also use the Green’s function approach for computing the load pole tide, instead of a spherical harmonic approach. Referencing the load pole tide to the CM effectively accounts for the contribution of the ocean pole tide to geocenter motion. We note that the maximum radial load pole tide displacement with respect to the CM (or CE) amounts to 6.4 (4.7) mm/arcsec, and occurs in the south Pacific Ocean. Meanwhile, the maximum of the transverse, namely the east and north, components of the load pole tide are 2.0 (0.6) mm/arcsec. Equation (8) (values have units of mm/arcsec) represents the effect of the self-consistent equilibrium ocean pole tide on variations of the CM relative to the center of figure of the solid Earth surface (CF), using Eqs. (5) and (7) from Desai and Ray (2014).

$$\begin{aligned} \overline{r}_\mathrm{cf}= & {} {\mathcal {R}}e\Bigl [ m^{*}\left( t \right) \Bigl ( \left( {0.69+i0.59} \right) \hat{e} _x \nonumber \\&+\left( {0.52+i1.40} \right) \hat{e} _y +\left( {0.46+i0.74} \right) \hat{e} _z \Bigr ) \Bigr ]. \end{aligned}$$
(8)

The effect of the ocean pole tide on geocenter variations is expected to be no larger than 0.5 mm in any component. It is also worth noting that the pole tide geocenter variations have slightly larger amplitude than the maximum of the CE-referenced transverse load pole tide, effectively resulting in geocenter variations being the primary loading signal in the CM-referenced transverse load pole tide.

The effects neglected in the T/P total pole tide model, as shown in Fig. 1, have long wavelength structure, primarily following a degree 2 order 1 spherical harmonic. In practice, the T/P and our model essentially have identical body pole tide components. Therefore, Fig. 1 effectively represents the difference between the sum total of our self-consistent equilibrium ocean and load pole tides with the T/P ocean pole tide. The over-ocean root-mean-square (RMS) and maximum amplitude of these differences are 3 and 5 mm/arcsec, respectively. For comparison, the body, self-consistent equilibrium ocean, and load pole tide components have maximum amplitudes of approximately 33, 48, and 6 mm/arcsec, respectively. The ocean and load pole tides act in opposite directions, so that the maximum amplitude of the sum total of the self-consistent equilibrium ocean and load pole tides is 42 mm/arcsec. Meanwhile, the effective T/P ocean pole tide has maximum amplitude of 36 mm/arcsec, and therefore has errors of approximately 15 %.

3 Mean pole location

The pole tide [e.g., Eqs. (2)–(4)] is typically computed using a rotation pole, \(m\left( t \right) \), that has a ‘mean pole’ removed from reported pole locations.

$$\begin{aligned} m\left( t \right) =\left( {\textit{PX}\left( t \right) -\overline{\textit{PX}} \left( t \right) } \right) -i\left( {\textit{PY}\left( t \right) -\overline{\textit{PY}} \left( t \right) } \right) \end{aligned}$$
(9)
Fig. 2
figure 2

Power spectral density (PSD) of location of rotation pole, \(m\left( t \right) \), computed from IERS EOPC04 polar motion time series spanning 1980.0–2015.0 shows primary signals at Chandler wobble [\(+0.843\) cycles/year (cpy)], annual (\(\pm \)1 cpy), semi-annual (\(\pm \)2 cpy), and decadal (\(\sim \) \(\pm \)0.0323 cpy) frequencies. PSD after removing linear mean pole [Eq. (10)] from EOPC04 time series is shown in black, and after also removing estimated annual and semi-annual signals is shown in blue

Full size image

The reported pole location, \(\textit{PX}( t)\) and \(\textit{PY}(t)\), is conventionally positive towards the Greenwich and 90 degree west meridians, and the ‘mean pole’ is denoted by \(\overline{\textit{PX}} (t)\) and \(\overline{\textit{PY}} (t)\). Here, we follow the approach of Wahr et al. (2015) for the definition of the mean pole. They recommend that the pole tide should include the Earth’s response (solid Earth and oceans) to all components of polar motion, but that the component due to the long-term drift be treated distinctly from other polar motion variations. They explain that the use of constant Love numbers in Eqs. (2)–(4) is not applicable to the long-term drift in polar motion, and even then should strictly adopt frequency-dependent values. So we follow their recommendation to adopt long-term observations of polar motion drift for the mean pole, implicitly also assuming that GIA is the largest source of that drift. Then, we also leave it to dedicated GIA models that include the effects of rotational feedback to model the associated displacements (e.g., A et al. 2012; Tamisiea 2011), referred to by Wahr et al. (2015) as the ‘GIA pole tide’. The notable distinction is that the GIA pole tide represents displacements associated with polar motion caused by past changes in Earth surface loading, while the remainder represents those due to current changes. As they note, computation of the GIA pole tide is significantly more involved than allowed by Eqs. (2)–(4) and therefore best left to dedicated models. Since prograde Chandler wobble and annual polar motion dominates remaining polar motion, as shown in Fig. 2, we adopt Love numbers that apply to these nearby frequencies, as mentioned earlier from the IERS recommendations (Petit and Luzum 2010). Values of pole tide Love numbers at the other frequencies of observed polar motion are likely to be within 5 % of the Chandler wobble value, based upon consideration of frequency-dependent Love numbers for long-period luni-solar tides (e.g., Petit and Luzum 2010). Furthermore, these other periodic variations have significantly smaller amplitudes.

Fig. 3
figure 3

Models for mean pole location, \(\overline{\textit{PX}} \) (left panel) and \(\overline{\textit{PY}} \) (right panel), spanning 1980 to 2015. The T/P model represents what is currently used to represent the mean pole for the pole tide model on the altimetry products, \(\overline{\textit{PX}} =0.042\hbox { arcsec}\) and \(\overline{\textit{PY}} =0.293\hbox { arcsec}\). The IERS2010 model is from the current IERS recommendation (Petit and Luzum 2010) and represented by a cubic polynomial until 2010 followed by a linear model thereafter. The model used in this paper is as shown in Eq. (10). The moving average is determined from a moving 6-year followed by a moving 433-day average of the EOPC04 reported pole time series, and therefore excludes the first and last 1312 days of the time series

Full size image

The bias for the mean pole only affects the mean sea surface applied to the altimetry observations. We determine this bias from the EOPC04 reported pole location time series from the IERS, spanning 1980–2014. Based upon the spectrum in Fig. 2, we simultaneously fit for this bias, and periodic variations at the Chandler wobble, annual, semi-annual, and 31-year periods. We constrain polar motion drift to be the same values used by Wahr et al. (2015), which are taken from Argus and Gross (2004) for the mean lithosphere frame. The Chandler wobble terms are allowed to vary quadratically and are updated every 7 years. These Chandler wobble terms are also constrained to represent only prograde motion. As a normal mode of the Earth, its amplitude is dependent on the ongoing excitation processes and therefore varies with time (e.g., Gross 2000; Chao and Chung 2012). Our approach facilitates the generation of a residual pole location time series, \(m\left( t \right) \), that retains the original power spectral density of the Chandler and decadal wobble after removing the estimated bias, drift and seasonal variations, as also shown in Fig. 2. This residual time series is used in Sect. 4 for observations of the pole tide from altimeter measurements. Our resulting model for the mean pole, in arcseconds, is as follows, with t measured as years since January 1, 2000 00:00:00.

$$\begin{aligned} \overline{\textit{PX}} \left( t\right)= & {} 0.05097+0.00062 \times t\end{aligned}$$
(10a)
$$\begin{aligned} \overline{\textit{PY}} \left( t \right)= & {} 0.33449+0.00348 \times t. \end{aligned}$$
(10b)

Figure 3 illustrates the decadal polar motion variations using a 6-year moving average of the EOPC04 series followed by a 433-day moving average. We presume that they reflect a combination of the so-called 31-year Markowitz wobble (see Poma 2000 for overview), and the response to recent significant redistribution of mass. The primary Chandler wobble and seasonal variations are mostly eliminated in this moving average since there are approximately five Chandler wobble cycles in 6 years. The estimated 31-year periodic variation has an amplitude of 0.02 arcsec, an order of magnitude smaller than the Chandler wobble. More recent deviations from our mean pole are approaching 0.05 arcsec. By excluding these variations from our representation of the mean pole, we are implicitly allowing for associated total pole tide displacements in altimetry observations of \(<\)4 mm. The use of a constant mean pole in the T/P model does so too, while the IERS mean pole does not. Wahr et al. (2015) estimate the error introduced by applying the Chandler wobble value of \(k_2\) to these recent deviations from the mean pole to be \(<\)20 %. Their estimate can also be applied here, since the total pole tide observed by altimetry is primarily dependent on \(k_2\).

Fig. 4
figure 4

Map of the misrepresentation of regional sea level rise observations from satellite altimetry due to inclusion of long-term polar motion drift in the T/P pole tide model. The map reflects Eq. (11), and represents the drift component of differences in the total pole tide displacement when using the T/P model with and without inclusion of the long-term drift in polar motion in the definition of the mean pole

Full size image
Fig. 5
figure 5

Map of geocentric (\(\hbox {body}+ \hbox {ocean} + \hbox {load}\)) pole tide admittance estimated from 22 years of T/P, Jason-1, and Jason-2/OSTM SSH measurements. Left and right panels are real and imaginary components of admittance

Full size image

Figure 3 also highlights another deficiency in the T/P pole tide model. By using a constant mean pole with a constant Love number it is implicitly mismodeling the displacements due to long-term drifting polar motion, which are primarily induced by GIA. This error can be corrected by subtracting the expression in Eq. (11) from over-ocean altimeter SSHs that have already been corrected with the T/P pole tide model (i.e., the model that uses a constant mean pole), repeating that t is measured as years since January 1, 2000 00:00:00. The difference in the bias component of the mean pole is ignored since it only affects the constant component of mean sea level.

$$\begin{aligned} \Delta \zeta _\mathrm{a} \left( {\theta ,\lambda ,t} \right)= & {} 69.7t\sin 2\theta \nonumber \\&\times ( {0.00062\cos \lambda -0.00348\sin \lambda } )\quad (\hbox {mm}).\nonumber \\ \end{aligned}$$
(11)

This error will manifest, as shown in Fig. 4, into regional sea level rise estimates that are based upon altimeter SSH measurements corrected with the T/P pole tide model. We caution that Eq. (11) and Fig. 4 only represent the error in the T/P model due to the use of a constant mean pole instead of a drifting mean pole (Eq. 10). They do not reflect the error due to ignoring self-gravitation, loading, and conservation of mass, which has the more complex spatial form shown in Fig. 1. In this way, we explicitly distinguish the two error sources in the T/P pole tide model. Dedicated GIA models that include the effects of rotational feedback are best used to model the so-called ‘GIA pole tide’ since they correctly account for the associated viscoelastic response of the Earth (Wahr et al. 2015). While the effects on regional sea level rise are in the range of \(\pm \)0.25 mm/year, the global average of 0.01 mm/year (latitude-weighted average within T/P-Jason sampling latitudes of \(\pm \)66 degrees, and over oceans only) is well below reported uncertainties of GMSL, due to its degree 2 order 1 spherical harmonic distribution.

4 Pole tide observations

Our approach for observing the geocentric pole tide closely follows that from Desai (2002) who used 9 years of T/P SSH measurements. We use more than twice the duration with 22 years of continuous measurements, spanning December 21, 1992 to November 8, 2014, from the T/P, Jason-1, and Jason-2/OSTM missions. For this study, the NASA MEaSURES multi-mission altimeter SSH climate data record is used (Beckley et al. 2013, 2014). While most of the SSH components are taken from the respective mission GDRs, some are from improvements that have been made since the original release of the GDRs. Most importantly, the altimeter measurements are from the T/P version B Merged GDRs, the Jason-1 version C GDRs, and the Jason-2/OSTM version D GDRs, while the satellite orbit positions are from a consistent reanalysis across all three missions in the 2008 International Terrestrial Reference Frame. The altimeter range measurements are corrected for range delays from the wet and dry troposphere, the ionosphere, and the sea state bias. Geophysical corrections for the mean sea surface, luni-solar body, ocean, and load tides are applied, as is the response of the oceans due to atmospheric pressure.

Fig. 6
figure 6

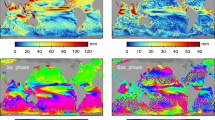
Map of signal-to-noise ratio (SNR) of the geocentric pole tide highlights regions where resolving the short wavelength structure is challenging. The predicted signal is computed using the sum total of the body, ocean, and load pole tide components, using a self-consistent equilibrium model of the ocean pole tide. The background noise is determined from the RMS of the post-fit SSH residuals after removing bias, drift, annual, semi-annual, and pole tide variations in 3 by 3 degree bins

Full size image
Fig. 7
figure 7

Estimate of real part of potential Love number, \(k_2\), from time series of degree 2 order 1 spherical harmonic components of observed SSH with increasing duration of observations. Two different estimates are provided; the first uses our recommended self-consistent equilibrium (SCEQ) response, and the second assumes the T/P response. The left panel a adds observations in the forward sense, sequentially from 1992 to 2014, while the right panel b adds observations in the backward sense from 2014 to 1992. Comparison of a and b indicates that most of the information arises from the earlier observations when the Chandler wobble amplitude was largest

Full size image

The SSH data are partitioned into 3 by 3 degree latitude and longitude bins. In each bin we use the 22 years of SSH data to simultaneously estimate bias, drift, annual, semi-annual variations along with a pole tide admittance response due to residual polar motion (\(m_1 \) and \(m_2\)). The residual polar motion time series is exactly as represented by the blue-lined PSD in Fig. 2 with annual and semi-annual variations removed so that it primarily contains Chandler wobble and decadal variations. Seasonal oceanographic variations in SSH are inseparable from those due to the pole tide, while we assume there are no other signals in the ocean with the Chandler wobble period. Estimates for the geocentric pole tide admittance in Fig. 5 show that resolving the short wavelength component of the pole tide continues to be challenging even with 22 years of observations. Regions with low signal-to-noise ratio (SNR) (\(\sim \) \(<\) \(-\)13 dB), as shown in Fig. 6, continue to contaminate pole tide observations from altimetry. Typically, these are in the equatorial regions where the pole tide signal is especially weak and in areas with strong ocean currents.

Nevertheless, the long wavelength component of the pole tide, and especially regions with high SNR, continue to be distinctly detectible and dominated by the expected degree 2 order 1 spherical harmonic distribution. As in Desai (2002), we form a time series of the degree 2 order 1 spherical harmonic components of SSH but with the 22 years of observations. These spherical harmonic coefficients, \(A_{21} \). and \(B_{21}\), are generated once every exact repeat cycle of the satellite orbit (9.9156 days), using cycle averages of the residual SSH in the 3 by 3 degree latitude and longitude bins after removing the bias, drift, annual, and semi-annual variations estimated as described above. The available spatial sampling from these three missions limits the latitude region to within \(\pm \)66 degrees. Here, the coefficients are derived using a similar procedure to that described in Kang et al. (2014, equation 11a), where \(\zeta \left( {\theta _i ,\lambda _j } \right) \) is the average residual SSH in each bin with colatitude \(\theta _i \) and longitude \(\lambda _j \).

$$\begin{aligned}&A_{21}{=}\frac{\mathop \sum \nolimits _{i=1}^N \mathop \sum \nolimits _{j=1}^N \zeta ( {\theta _i ,\lambda _j } )\overline{P} _{21} ({\cos \theta _i } )\cos \lambda _j \sin \theta _i \mathrm{d}\theta _i \mathrm{d}\lambda _j }{\mathop \sum \nolimits _{i=1}^N \mathop \sum \nolimits _{j=1}^N (\overline{P} _{21} ( {\cos \theta _i } )\cos \lambda _j )^{2}\sin \theta _i \mathrm{d}\theta _i \mathrm{d}\lambda _j} \end{aligned}$$
(12a)
$$\begin{aligned}&B_{21} =\frac{\mathop \sum \nolimits _{i=1}^N \mathop \sum \nolimits _{j=1}^N \zeta ( {\theta _i ,\lambda _j } )\overline{P} _{21} ( {\cos \theta _i } )\sin \lambda _j \sin \theta _i \mathrm{d}\theta _i \mathrm{d}\lambda _j }{\mathop \sum \nolimits _{i=1}^N \mathop \sum \nolimits _{j=1}^N (\overline{P} _{21} ( {\cos \theta _i } )\sin \lambda _j )^{2}\sin \theta _i \mathrm{d}\theta _i \mathrm{d}\lambda _j}\nonumber \\ \end{aligned}$$
(12b)

The time series of these two spherical harmonic coefficients continue to be dominated by Chandler wobble variations through the entire 22 years similar to as shown in Fig. 4 from Desai (2002), and therefore are not explicitly shown here. They once again provide an opportunity to determine the pole tide potential Love number, \(k_2\), by comparing \(A_{21} \) and \(B_{21} \) from the observed and predicted equilibrium pole tide from Eq. (6).

Estimates for \(k_2 \) from the time series of \(A_{21} \) and \(B_{21} \) are shown in Fig. 7, where the predicted response fixes \(h_2 =0.6207\) (Petit and Luzum 2010) and the load Love numbers to those from Guo et al. (2004). Desai (2002) demonstrated that these estimates of \(k_2 \) have small (0.15 %) sensitivity to these fixed Love numbers. Most importantly, the final estimate from the 22-year time series when assuming a self-consistent equilibrium response, \(k_2 =0.298\pm 0.027\) agrees very well with the value from the IERS recommendations (Petit and Luzum 2010) and other authors (see Table 1 from Desai 2002) of 0.308. When assuming the T/P pole tide model the final estimate, \(k_2 =0.347\pm 0.029\), is systematically larger by 16 %, as expected. This provides evidence that the altimetry measurements are capable of resolving the long wavelength effects of self-gravitation, loading, and mass conservation that are ignored in the T/P pole tide model. Figure 7 also suggests that the most recent (last \(\sim \)3–5 years) altimeter SSH observations of the pole tide have not added significant value to observations of the pole tide. Estimates of \(k_2 \) approach the expect value of \(\sim \)0.3, and formal errors approach their final value, more rapidly when adding data sequentially from 1992 onward, rather than when adding data backward from 2014. This is explained by the fact that over the span of our data window of 1992–2014 the Chandler wobble amplitude was in the range of 0.15–0.25 arcsec from 1992–1996, 0.1–0.15 arcsec from 1997–2011, and 0.05 arcsec thereafter.

5 Conclusion

Satellite altimeter SSH data yield observations of the total pole tide displacement relative to the CM, and most users apply a model to remove these effects. However, the model that has been provided on the GDRs for the altimeter missions, and therefore applied by most users, was originally developed over two decades ago prior to the launch of the T/P mission. The actual measurement performance and duration of the altimeter SSH time series has exceeded expectations from that time, providing an opportunity to detect errors in, and consequently develop improvements to, that model. We have identified two categories of errors in the T/P pole tide model, and have recommended approaches to mitigate those errors.

The first category applies to the pole tide displacements that are associated with periodic and decadal variations in polar motion. For these, we recommend upgrading to a self-consistent equilibrium model for the displacement of the ocean surface relative to the Earth’s crust and explicitly modeling the load pole tide with respect to the CM. Doing so amplifies the sum total of these two contributions by 15 % as compared to the T/P model. We show that at least the primary long wavelength component of this effect is detectible from the last two decades of altimetry data, resulting with an observed value of the potential Love number, \(k_2\), that is consistent with independent estimates. In contrast, the observed value is 15 % larger when assuming the T/P model, essentially compensating for the neglected effects of self-gravitation, loading, and mass conservation. Despite being detectible, these errors in the T/P model amount to at most 1.5 mm in SSH in the early years of the altimeter data series (1992–1996) when the Chandler wobble amplitude was near its maximum of 0.25 arcsec. In recent years, the error is up to 0.3 mm when the Chandler wobble amplitude is 0.05 arcsec.

The second category applies to the pole tide displacements that are associated with the long-term drift in polar motion. As described by Wahr et al. (2015), conventional pole tide models cannot be applied to the associated drifting component of the centrifugal potential because the use of constant Love numbers is no longer applicable. There are multiple sources for the long-term drift in polar motion, as described by Gross (2007), but the most important is considered to be GIA. As such, models of GIA that include the effects of rotational feedback provide a potential approach for modeling this component of the pole tide. It then becomes necessary to explicitly exclude this component from conventional (constant Love number) pole tide models, including both the T/P and our recommended models. We follow the recommendation from Wahr et al. (2015) to accomplish this by also recommending that pole tide displacements for altimetry be computed from residual polar motion with respect to a drifting mean pole, with the rate determined from almost 80 years of observations (Argus and Gross 2004). This error in the T/P model manifests as \(\pm \)0.25 mm/year in observed regional sea level rise with a degree 2 order 1 spherical harmonic distribution, and has negligible impact on estimates of GMSL rise. We caution that this approach creates an inherent link, or potential for discrepancies, with GIA models, in that GIA models may not explain the drift in polar motion that is adopted in our recommended model for the mean pole. We note also that GMSL rise observations from altimetry are often reported after applying a correction for the change in volume of the ocean basins resulting from GIA.