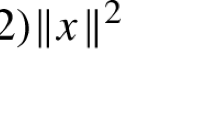Convex optimization under inequality constraints in rank-deficient systems

Abstract

Many geodetic applications require the minimization of a convex objective function subject to some linear equality and/or inequality constraints. If a system is singular (e.g., a geodetic network without a defined datum) this results in a manifold of solutions. Most state-of-the-art algorithms for inequality constrained optimization (e.g., the Active-Set-Method or primal-dual Interior-Point-Methods) are either not able to deal with a rank-deficient objective function or yield only one of an infinite number of particular solutions. In this contribution, we develop a framework for the rigorous computation of a general solution of a rank-deficient problem with inequality constraints. We aim for the computation of a unique particular solution which fulfills predefined optimality criteria as well as for an adequate representation of the homogeneous solution including the constraints. Our theoretical findings are applied in a case study to determine optimal repetition numbers for a geodetic network to demonstrate the potential of the proposed framework.

1 Introduction

Convex optimization problems frequently arise in geodesy. No matter if there is a network to design, the gravity field of the Earth to be estimated or the behavior of a rent index to be calculated, in any case a certain target function—e.g., the sum of squared residuals—has to be minimized or maximized.

1.1 Inequality constrained least-squares problems

For many applications additional knowledge about the parameters is given, which can be formulated as inequality constraints that have to be strictly fulfilled. Two out of many possible examples are sign constraints for non-negative quantities like atmospheric delays in satellite geodesy or a maximal feasible attenuation in filter design.

In the geodetic and mathematical community, a lot of effort has been put into developments in the field of convex optimization under inequality constraints mostly focusing on inequality constrained least-squares (ICLS). Schaffrin et al. (1980) and Koch (1982) formulated ICLS problems to improve the first and second order design (SOD) of geodetic networks by transforming the resulting quadratic programming (QP) problem into a linear complementarity problem (LCP).

In more recent studies, Koch (2006) used object-specific constraints for a semantic integration of data from a geographical information system. Peng et al. (2006) introduced an aggregate constraint method for ICLS problems, combining all inequality constraints to one complex equality constraint. Recently, Roese-Koerner et al. (2012) focused on the problem of determining a stochastic description of ICLS estimates and the determination of changes through the constraints. Also in the method of total least-squares (TLS), introduction of inequality constraints is a topic of current research. Zhang et al. (2013) extended the error-in-variables model by the introduction of inequality constraints. In their approach, they first identify the active constraints by exhaustive search and subsequently solve an equivalent equality constrained problem.

1.2 Unconstrained rank-deficient problems

Solving a rank-deficient normal equation system results in not one unique but a manifold of solutions. In the unconstrained case, a rigorous general solution can easily be computed using the theory of generalized inverses (Koch 1999, p.48–59). This also includes the computation of a unique solution via the Moore–Penrose inverse. However, this is no longer possible in the presence of inequality constraints. Most state-of-the-art optimization algorithms—e.g., the Active-Set-Method (Gill et al. 1981, p.167-173) or primal-dual Interior-Point-Methods (cf. Boyd and Vandenberghe 2004, p. 568–571 and p. 609–613)—are either not able to deal with a rank-deficient objective function or yield only one of an infinite number of particular solutions.

1.3 Rank deficient ICLS problems

Despite the highly sophisticated estimation theory for rank-deficient but unconstrained (Sect. 1.2) and inequality constrained but well-defined systems (Sect. 1.1), only few publications have been devoted to singular optimization problems with inequality constraints. However, in geodesy, these problems occur on many occasions. Examples are the SOD of a geodetic network with more weights to be estimated than entries in the criterion matrix, the adjustment of datum-free networks or a spline approximation with data gaps and additional information on the function behavior.

Barrodale and Roberts (1978) presented a modification of the standard Simplex method for linear programming, which is able to handle rank-deficient problems. However, extending it to a QP is not straightforward.

Schaffrin (1981) treated the special case, that in addition to the linear inequality constraints, all parameters are restricted to be non-negative. He developed a method to compute a particular solution through the introduction of slack variables. However, his approach is only valid for non-negative least-squares problems.

O’Leary and Rust (1986) developed an approach for computing confidence regions for ill-posed weighted non-negative least-squares problems. The inequality $\mathbf {x} \ge \mathbf {0}$ is used to truncate the solution space and eliminate the non-uniqueness of the solution. However, their approach cannot easily be extended to general linear constraints as it aims to resolve the manifold, which is not always possible.

Fletcher and Johnson (1997) proposed a nullspace method for ill-conditioned QPs with solely equality constraints: the aim is to compute the nullspace of the matrix $\bar{\mathbf {B}}^T$ of equality constraints. This allows to reformulate a problem with equality constraints as a problem without constraints. Under certain conditions, it is now possible to compute a solution even if the coefficient matrix or the matrix of constraints is ill-conditioned. This could be applied in an Active-Set-approach to solve a inequality constrained problem as a sequence of equality constrained ones. However, as the focus of their contribution is on ill-conditioned problems and not on rank-deficient ones, the computation of a general solution is not discussed.

Dantzig’s simplex method for quadratic programming ((Dantzig 1998, p. 490–498)) allows for the computation of a particular solution in case of a rank-deficient design matrix. However, no statements about the homogenous solution are given. This method will be used in our framework to compute the solution in case the manifold is eliminated through introduction of inequality constraints.

Xu et al. (1999) analyzed the stability of ill-conditioned linear complementarity problems (LCP) in geodesy, which could be used to solve an ICLS problem. In case of an unstable LCP due to an ill-conditioned LCP matrix (a case often encountered when processing GPS data), they proposed a regularization of the LCP matrix.

Geiger and Kanzow (2002, p. 362–365) described a Tikhonov regularization for ill-conditioned convex optimization problems.

In the projector theoretical approach of Werner (1990) and Werner and Yapar (1996), a rigorous computation of the general solution of ICLS problems with possibly rank-deficient matrices $\mathbf {A}$ and ${\varvec{\Sigma }}$ is performed using generalized inverses. First, an ordinary least-squares solution is computed, then the update to the ICLS solutions is computed in an iterative approach. As the ICLS solution is obtained by testing arbitrary subsets of constraints, this approach is mostly suited for small-scale problems with few constraints.

1.4 Purpose and organization of this article

In this contribution, a line of thought similar to that of Werner and Yapar (1996) will be followed. Accordingly, we propose a two-step approach for a rigorous computation of the general solution. In a first step, the constraints are neglected and a general solution of the unconstrained problem is computed. Subsequently, the constraints are taken into account and a second optimization problem is solved, depending on whether there is an intersection of manifold and feasible region or not.

The proposed approach has four major advantages. First, it allows for a description of the manifold including the constraints as these will be reformulated in terms of a basis for the nullspace of the design matrix. Second, an additional optimization step is performed in this nullspace to provide a particular solution, which fulfills certain optimality criteria. Third, it is not restricted to small-scale problems. Fourth, the proposed method detects if the dimension of the manifold of the unconstrained problem is reduced through the introduction of inequality constraints (up to the case of a unique solution).

This contribution is organized as follows: in Sect. 2 the notation is introduced and basic principles of rank-deficient problems and of inequality constrained optimization are reviewed. Section 3 describes the ideas and computations of our framework for the rigorous computation of general ICLS solutions. The two simple synthetic examples in Sect. 4 illustrate the application of the framework, while the real-data SOD problem reveals its capacities for classic geodetic tasks. Characteristics of our framework as well as future challenges are pointed out in Sect. 5.

2 Background

2.1 Convex optimization

According to Boyd and Vandenberghe (2004, p. 137), convex optimization is defined as the minimization of a convex objective function over a convex set. A commonly used objective function in geodesy is the weighted sum of squared residuals

$$\begin{aligned} {{\varPhi }}(\mathbf {v}) = \mathbf {v}^T {\varvec{\Sigma }}^{-1} \mathbf {v}, \end{aligned}$$

(1)

resulting from the well-known linear Gauss–Markov Model (GMM)

$$\begin{aligned} {\varvec{\ell }} + \mathbf {v} = \mathbf {Ax}. \end{aligned}$$

(2)

${\varvec{\ell }}$ is the $n\times 1$ vector of observations, $\mathbf {v}$ the $n\times 1$ vector of residuals, $\mathbf {A}$ the $n\times m$ design matrix and $\mathbf {x}$ the unknown $m~\times ~1$ vector of parameters. If the variance–covariance (VCV) matrix of the observations ${\varvec{\Sigma }} = {\varvec{\Sigma }} \{ {\varvec{\mathcal {\MakeUppercase {l}}}} \}$ is positive (semi)definite, ${{\varPhi }}(\mathbf {v})$ is a convex function. The observations ${\varvec{\ell }}$ are assumed to be a realization of the normally distributed random vector

$$\begin{aligned} {\varvec{\mathcal {\MakeUppercase {l}}}}&\sim N(\mathbf {A}{\varvec{\xi }}, {\varvec{\Sigma }}). \end{aligned}$$

(3)

${\varvec{\xi }}$ is the vector of true parameters. The weighted least-squares (WLS) problem can now be formulated as follows

(4)

A WLS estimate $\widetilde{\mathbf {x}}$ of the parameters can be computed by assembling and solving the normal equations

$$\begin{aligned} \mathbf {N}&= \mathbf {A}^T\varvec{\Sigma }^{-1} \mathbf {A},\end{aligned}$$

(5a)

$$\begin{aligned} \mathbf {n}&= \mathbf {A}^T\varvec{\Sigma }^{-1} \varvec{\ell },\end{aligned}$$

(5b)

$$\begin{aligned} \widetilde{\mathbf {x}}&= \mathbf {N}^{-1} \mathbf {n}. \end{aligned}$$

(5c)

However, if the column rank of design matrix $\mathbf {A}$ is less than the number of unknown parameters

$$\begin{aligned} Rg(\mathbf {A}) = r < m,&d&= m-r, \end{aligned}$$

(6)

due to the $d$ linear-dependent columns of $\mathbf {A}$, we are facing a rank-deficient problem. This results in a likewise rank-deficient matrix $\mathbf {N}$ and an under-determined system of normal equations

$$\begin{aligned} \mathbf {Nx} = \mathbf {n}, \quad Rg(\mathbf {N}) = r<m. \end{aligned}$$

(7a)

W.l.o.g. we will assume, that $\mathbf {N}$ can be rearranged and partitioned in a way that the $[r \times r]$ matrix $\mathbf {N}_{11}$ is of full rank

$$\begin{aligned} \begin{bmatrix} \mathbf {N}_{11}&\mathbf {N}_{12} \\ \mathbf {N}_{21}&\mathbf {N}_{22} \end{bmatrix} \begin{bmatrix} \mathbf {x}_1 \\ \mathbf {x}_2 \end{bmatrix} =\begin{bmatrix} \mathbf {n}_1 \\ \mathbf {n}_2 \end{bmatrix}. \end{aligned}$$

(7b)

2.1.1 Solving unconstrained rank-deficient problems

It is well known, that for equation systems of type (7b) there exists not one unique solution but a manifold. Therefore, the general solution

$$\begin{aligned} \widetilde{\mathbf {x}}(\varvec{\lambda })&= \mathbf {x}_P + \mathbf {x}_\mathrm{hom}(\varvec{\lambda }) \end{aligned}$$

(8)

consists of a particular solution $\mathbf {x}_P$ and a homogenous solution $\mathbf {x}_\mathrm{hom}(\varvec{\lambda })$ which depends on the free parameters contained in the $d \times 1$ vector $\varvec{\lambda }$, which can be chosen arbitrarily.

The homogeneous solution can be expressed as

$$\begin{aligned} \mathbf {x}_\mathrm{hom}(\varvec{\lambda })&= \mathbf {X}_\mathrm{hom} \ \varvec{\lambda }, \end{aligned}$$

(9)

with the columns of the $m~\times ~d$ matrix $\mathbf {X}_\mathrm{hom}$ being a basis for the nullspace of $\mathbf {A}$, with

$$\begin{aligned} \mathbf {AX}_\mathrm{hom} = \mathbf {0}. \end{aligned}$$

(10)

According to Koch (1999, p. 59), the matrix

$$\begin{aligned} \mathbf {X}_\mathrm{hom} = \left[ \begin{array}{c} - \mathbf {N}_{11}^{-1} \mathbf {N}_{12} \\ \mathbf {I} \end{array}\right] \end{aligned}$$

(11)

fulfills this requirement.

A particular solution of (7b) can for instance be computed by applying the symmetric reflexive generalized inverse

$$\begin{aligned} \mathbf {N}_{RS}^{-} = \left[ \begin{array}{c@{\quad }l} \mathbf {N}_{11}^{-1} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} \end{array}\right] \end{aligned}$$

(12)

(cf. Koch 1999, p.57) resulting in

$$\begin{aligned} \mathbf {x}_P = \mathbf {N}_{RS}^{-} \ \mathbf {n} = \left[ \begin{array}{c} \mathbf {N}_{11}^{-1} \mathbf {n}_{1} \\ \mathbf {0} \end{array}\right] . \end{aligned}$$

(13)

Furthermore, the known basis $\mathbf {X}_\mathrm{hom}$ of the nullspace of $\mathbf {A}$ can be used to compute the Moore–Penrose inverse

$$\begin{aligned} \mathbf {N}^{+}&= \left( \mathbf {N} + \mathbf {X}_\mathrm{hom} \mathbf {X}_\mathrm{hom}^T\right) ^{-1} \nonumber \\&\quad - \mathbf {X}_\mathrm{hom} \left( \mathbf {X}_\mathrm{hom}^T \mathbf {X}_\mathrm{hom} \mathbf {X}_\mathrm{hom}^T \mathbf {X}_\mathrm{hom} \right) ^{-1} \mathbf {X}_\mathrm{hom}^T \end{aligned}$$

(14)

(cf. Koch 1999, p.61).

For some applications, it is possible to directly state a basis $\mathbf {X}_\mathrm{hom}$ for the nullspace of $\mathbf {A}$. This offers the advantage that the free parameters $\varvec{\lambda }$ are interpretable. For example, in the adjustment of a geodetic direction and distance network, the free parameters represent translation, rotation and scaling of the network and an explicit basis for the nullspace is known (cf. Meissl 1969). Despite the fact that all choices of $\varvec{\lambda }$ will result in a mathematically correct solution, Xu (1997) pointed out that not all of them are geodetically meaningful. For example, there may be constraints to the transformation parameters (e.g., a positive scaling parameter) which we will address again later.

In addition, one has to bear in mind, that a rank-deficient design matrix is equivalent to the statement that some quantities are not directly estimable. This does not only influence the parameter estimation, but also possible further processing steps like, e.g., hypothesis testing (Xu 1995).

2.1.2 Solving ICLS problems

We assume that the minimization of (1) should be performed subject to $p$ linear inequality constraints

$$\begin{aligned} \mathbf {B}^T \mathbf {x} \le \mathbf {b}, \end{aligned}$$

(15)

with $\mathbf {B}$ being the $m \times p$ matrix of constraints and $\mathbf {b}$ the $p~\times ~1$ vector containing the corresponding right hand sides. As linear inequality constraints always form a convex set, the linear inequality constrained least-squares (ICLS) problem

(16)

is a convex optimization problem. More specifically, it is a quadratic program (QP) as we minimize a quadratic objective function subject to linear inequality constraints (cf. Gill et al. 1981, p. 76). If the normal equations are well defined (i.e., no rank defect), there exists a big variety of algorithms to solve a QP. As there is no direct analytical relationship between observations and parameters and it is not known beforehand which inequality constraints will influence the estimation of parameters, all methods are iterative algorithms. Most of them can be subdivided into two main classes: Simplex methods and Interior-Point methods.

Simplex algorithms are tailor-made for linear constrained problems. The set of constraints is subdivided into active constraints $\mathbf {B}_a, \mathbf {b}_a$ that hold as equalities and inactive ones $\mathbf {B}_i, \mathbf {b}_i$, which hold as strict inequalities

$$\begin{aligned} \mathbf {B}_{a}^T \mathbf {x} = \mathbf {b}_{a}, \quad \mathbf {B}_{i}^T \mathbf {x} < \mathbf {b}_{i}. \end{aligned}$$

(17)

In an iterative process the active constraints are used to follow the boundary of the feasible set (i.e., the region where all constraints are satisfied) to the optimal solution. Examples for this type of algorithm are the Active-Set method (Gill et al. 1981, p. 167–173) and Dantzig’s simplex method for quadratic programming (Dantzig 1998, p. 490–498).

Interior-Point methods are the second main class of solvers for a QP. They are well suited for but not restricted to the linear constrained case. The basic idea is to start at a point inside the feasible region and solve a sequence of simplified problems converging along a central path towards the optimal solution. Barrier methods and primal-dual methods (cf. Boyd and Vandenberghe 2004, p. 568–571 and p. 609–613, respectively) are the most common among the Interior-Point methods.

Methods to determine the smallest bounding box for the feasible set and finding an initial feasible point are given in Xu (2003) and Boyd and Vandenberghe (2004, p. 579–580), respectively.

3 Rigorous computation of a general solution

Before describing the actual framework, it is instructive to examine how the introduction of inequalities can change the original problem and especially the manifold.

3.1 Changes through inequality constraints

We will distinguish two main cases depending on whether there is an intersection of the feasible region and the manifold of solutions (case 1) or not (case 2). As it is crucial for understanding the theory our proposed framework is built on, the differences to the unconstrained case will be described in some detail.

Figure 1a shows the isolines of the objective function of the unconstrained, bivariate optimization problem stated in Sect. 4.1.1. One particular solution is computed using the Moore–Penrose inverse (14) and depicted as orange cross. The one-dimensional manifold of solutions is shown as dashed black line.

Fig. 1

Isolines of the objective function of the bivariate convex optimization problem, which is stated in Sect. 4.1. The one-dimensional manifold (i.e., a straight line) is plotted as dashed black line. A particular solution of the unconstrained case was computed via the Moore–Penrose inverse and is shown as orange cross. The infeasible region is shaded and inequalities are plotted as red lines. a Isolines of the objective function. b Case 1b: manifold and feasible region intersect and the manifold is restricted by the constraint. c Case 2a: manifold and feasible region are disjunct, unique solution (green croos). d Case 2b: manifold and feasible region are disjunct, but there is still a manifold of solutions due to the active parallel constraint

3.1.1 Case 1: intersection of manifold and feasible region

This case can be subdivided into three sub-cases. Let case 1a be defined as a problem with only one or more inactive inequality constraints that are parallel to the solution manifold. As the unconstrained solution already is in the feasible region, the parallel constraint(s) do not influence the solution at all.

Case 1b, another possible influence of constraints, is shown in Fig. 1b. Here, the constraint is not parallel to the manifold and therefore restricts it. The manifold is still one dimensional. However, due to the constraint, it is no longer a line but a half-line, since it is now bounded in one direction but still unbounded in the other one. Introduction of more constraints can further restrict the manifold to a line segment.

The introduction of constraints can also lead to a decrease of the dimension of the manifold (case 1c). This is always the case for equality constraints which are not parallel to the manifold of solutions. However, same can be true for inequality constraints. An easy to imagine example is the case where one equality constraint is expressed by two inequality constraints.

3.1.2 Case 2: manifold and feasible region are disjunct

In some cases, the introduction of inequality constraints enables us to determine a unique solution (green cross) of a rank-deficient optimization problem (case 2a, Fig. 1c). This is always the case, if the solution of the constrained problem is not contained in the original manifold and there are no active parallel constraints.

In case 2b, the influence of a constraint that is parallel to the manifold of solutions is further examined (cf. Fig. 1d). It is obvious, that the active inequality constraint (red line) shifts the one-dimensional manifold but does not constrain it further. Therefore, there is still a manifold of the same dimension as in the original problem.

3.1.3 General remarks and outline of the framework

It is important to notice that the direction of the manifold cannot be changed through the introduction of inequality constraints. More specifically, a translation (case 2b), a general restriction (case 1b) or a dimension reduction (cases 1c and 2a) of the manifold are possible, but never a rotation. This leaves us in the comfortable situation, that it is possible to determine the homogenous solution of an ICLS problem by determining the homogenous solution of the corresponding unconstrained WLS problem and reformulate the constraints in relation to this manifold. Therefore, our framework consists of the following major parts that will be explained in detail in the next sections.

To compute a general solution of an ICLS problem (16), we compute a general solution of the unconstrained WLS problem and perform a change of variables to reformulate the constraints in terms of the free variables of the homogenous solution. Next, we determine if there is an intersection between the manifold of solutions and the feasible region. In case of an intersection, we determine the shortest solution vector in the nullspace of the design matrix with respect to the inequality constraints and reformulate the homogenous solution and the inequalities accordingly. If there is no intersection, we compute a particular solution using Dantzig’s simplex algorithm for QPs and determine the uniqueness of the solution by checking for active parallel constraints.

3.2 Transformation of parameters

In order to solve the ICLS problem (16), as a first step, we compute a general solution of the unconstrained WLS problem (4) as described in Sect. 2.1.1

$$\begin{aligned} \widetilde{\mathbf {x}}^\mathrm{WLS}(\varvec{\lambda })&= \mathbf {x}^\mathrm{WLS}_P + \mathbf {x}_\mathrm{hom}(\varvec{\lambda }). \end{aligned}$$

(18)

Afterwards, we perform a change of variables and insert (18) and (9) in (15) to reformulate the constraints in terms of the free variables $\varvec{\lambda }$ at the point of the particular solution

$$\begin{aligned}&\mathbf {B}^T \left( \mathbf {x}^\mathrm{WLS}_P + \mathbf {X}_\mathrm{hom} \ \varvec{\lambda } \right) \le \mathbf {b} \end{aligned}$$

(19a)

$$\begin{aligned}&\Longleftrightarrow \mathbf {B}^T \mathbf {x}^\mathrm{WLS}_P + \mathbf {B}^T \mathbf {X}_\mathrm{hom} \ \varvec{\lambda } \le \mathbf {b}. \end{aligned}$$

(19b)

With the substitutions

$$\begin{aligned}&\mathbf {B}^T_{\varvec{\lambda }} {:=} \mathbf {B}^T \mathbf {X}_\mathrm{hom},\end{aligned}$$

(20)

$$\begin{aligned}&\mathbf {b}_{\varvec{\lambda }} {:=} \mathbf {b} - \mathbf {B}^T \mathbf {x}^\mathrm{WLS}_P, \end{aligned}$$

(21)

(19) reads

$$\begin{aligned} \mathbf {B}^{T}_{\varvec{\lambda }} {\varvec{\lambda }} \le \mathbf {b}_{\varvec{\lambda }}, \end{aligned}$$

(22)

being the desired formulation of the inequality constraints. If the extended matrix $[\mathbf {B}^T_{\varvec{\lambda }} |\mathbf {b}_{\varvec{\lambda }} ]$ has rows, that contain only zeros, these rows can be deleted from the equation system, as they belong to inactive inequality constraints which are parallel to the solution manifold but do not shift the optimal solution (cf. case 1a in Sect. 3.1.1).

Next, we examine if the constraints (22) form a feasible set or if they are inconsistent. This can be done by formulating and solving a feasibility problem (cf. Boyd and Vandenberghe 2004, p. 579–580). If the constraints form a feasible set, there is at least one set of free parameters $\lambda _i$ that fulfills all constraints. This is equivalent to the statement, that there is an intersection between the manifold of solutions and the feasible region of the original ICLS problem, which is described in Sect. 3.3. If the constraints are inconsistent, the manifold and the feasible region are disjunct and we will proceed as described in Sect. 3.4.

3.3 Case 1: intersection of manifold and feasible region

If there is an intersection of manifold and feasible region, we aim for the determination of a unique particular solution $\widetilde{\mathbf {x}}_P$, that fulfills certain predefined optimality criteria. This is assured by formulating a second optimization problem using an objective function according to the chosen optimality criteria, the constraints derived in (22) and ${\varvec{\lambda }}$ as optimization variable.

Minimizing the length of the original parameter vector subject to the constraints seems to be a reasonable choice of the objective function. Therefore, we try to estimate $\varvec{\lambda }$ in a way, that

$$\begin{aligned} \mathbf {x}_P^\mathrm{ICLS}({\varvec{\lambda }}) = \mathbf {x}^\mathrm{WLS}_P + \mathbf {x}_\mathrm{hom}(\varvec{\lambda }), \end{aligned}$$

(23)

has shortest length among all possible particular solutions that fulfill the constraints. Therefore, we solve the QP

(24)

e.g., via the Active-Set method. As we minimize over the free parameters ${\varvec{\lambda }}$ only, the whole optimization takes place in the nullspace of the design matrix, ensuring that the manifold of optimal solutions is not left. Inserting (9) in (23) the objective function of problem (24) can be written as

$$\begin{aligned} {\varvec{\varPhi }}_\mathrm{NS}({\varvec{\lambda }})&= \left( \mathbf {x}^\mathrm{WLS}_P + \mathbf {X}_\mathrm{hom} \ \varvec{\lambda } \right) ^T \left( \mathbf {x}^\mathrm{WLS}_P + \mathbf {X}_\mathrm{hom} \ \varvec{\lambda } \right) \nonumber \\&= \varvec{\lambda }^T \mathbf {X}_\mathrm{hom}^T \mathbf {X}_\mathrm{hom} \varvec{\lambda }\nonumber \\&\quad + 2 \left( \mathbf {x}^\mathrm{WLS}_P\right) ^T \mathbf {X}_\mathrm{hom} \varvec{\lambda } + \left( \mathbf {x}^\mathrm{WLS}_P\right) ^T \mathbf {x}^\mathrm{WLS}_P. \end{aligned}$$

(25)

This results in an estimate $\widetilde{\varvec{\lambda }}$, which is used to determine the desired optimal particular solution

$$\begin{aligned} \widetilde{\mathbf {x}}_P^\mathrm{ICLS}&= \mathbf {x}^\mathrm{WLS}_P + \mathbf {x}_\mathrm{hom}(\widetilde{\varvec{\lambda }}). \end{aligned}$$

(26)

In case of solely inactive constraints, the resulting solution will be equivalent to the one obtained via the Moore–Penrose inverse in the unconstrained case. If the constraints prevent that the optimal unconstrained solution is reached, our particular solution will be the one with shortest length of all solutions that minimize the objective function and fulfill the constraints.

As the reformulated constraints depend on the chosen particular solution, we have to adapt them to the new particular solution using (19). Now, we can combine our results to a rigorous general solution of the ICLS problem (16)

$$\begin{aligned}&\widetilde{\mathbf {x}}^\mathrm{ICLS} (\varvec{\lambda }) = \widetilde{\mathbf {x}}_P^\mathrm{ICLS} + \mathbf {x}_\mathrm{hom}(\varvec{\lambda }), \end{aligned}$$

(27a)

$$\begin{aligned}&\mathbf {B}^T_{\varvec{\lambda }} {\varvec{\lambda }} \le \mathbf {b}_{\varvec{\lambda }}. \end{aligned}$$

(27b)

For an horizontal network, where there is a known basis for the nullspace of the design matrix (cf. Sect. 2.1.1), Xu (1997) worked out constraints (like a positive scaling parameter) for the free parameters to obtain a geodetically meaningful solution. These constraints can easily be included in our framework by using the known basis of the nullspace as homogeneous solution $\mathbf {X}_\mathrm{hom}$ and expanding the constraints $\mathbf {B}^{T}_{\varvec{\lambda }}$ and $\mathbf {b}_{\varvec{\lambda }}$ to the free parameters.

3.4 Case 2: manifold and feasible region are disjunct

If there is no intersection between feasible region and the manifold of solutions, there either is a unique solution or at least one active constraint is parallel to the solution manifold, meaning the solution is still non-unique (cf. Sect. 3.1.2). To compute a particular solution of problem (16) a Simplex type QP solver can be used, as discussed in Sect. 2.1.2, resulting in an arbitrary optimal solution $\mathbf {x}_P^\mathrm{ICLS}$. To decide whether the solution is unique, we check for active parallel constraints. If there is at least one, there exists a manifold of solutions, which is a shifted version of the original one. In this case, we proceed as described in Sect. 3.3 using $\mathbf {x}_P^\mathrm{ICLS}$ instead of $\mathbf {x}_P^\mathrm{WLS}$.

If there is a unique solution, it means that the introduction of constraints has resolved the manifold yielding

$$\begin{aligned} \widetilde{\mathbf {x}}^\mathrm{ICLS}&= \mathbf {x}_P^\mathrm{ICLS} \end{aligned}$$

(28)

as final result.

3.5 Framework

Using the tools described, we devised a framework for the computation of a rigorous general solution of rank-deficient ICLS problems, which is shown in Algorithm 1.

The first three lines correspond to the transformation of parameters and the test for intersection of feasible region and solution manifold (described in Sect. 3.2). If there is no intersection (feasible = false), a particular solution is computed as described in Sect. 3.4 and a test for parallel constraints is performed (lines 4–12). If no active constraint is parallel to the manifold, the computed particular solution is unique and the algorithm terminates (line 8).

If there is an intersection of the sets (feasible = true) or an active parallel constraint, we proceed as described in Sect. 3.3 and solve a second optimization problem (lines 13–17).

In lines 2, 10 and 16 a transformation of the constraints is computed. This is necessary, as the constraints with respect to the Lagrange multipliers $k_i$ depend on the chosen particular solution. Fortunately, this transformation is a computationally cheap operation.

One may ask the question: why not directly compute a particular ICLS solution via Dantzig’s algorithm as performed in line 6 of the framework? We intentionally decided to first compute an unconstrained general solution and to check for set intersection in order to achieve optimal runtime behavior. This is because solving the original quadratic program is the most expansive operation performed within this framework. If feasible set and manifold intersect, we can avoid solving the original problem directly. Instead a general unconstrained solution is computed and an optimization problem with respect to the free parameters $\lambda _i$ is solved. Computationally this is a lot cheaper, as the dimension reduces from an $m$-dimensional problem to a $d$-dimensional problem. The number $m$ of parameters is usually a lot bigger than the dimension $d$ of the rank defect. Hence, computations become faster.

4 Applications

The presented framework for the rigorous computation of a general solution of an ICLS problem was applied to two scenarios: a small two-dimensional synthetic example and the second order design (SOD) of a geodetic network.

We chose the small synthetic example, because of its simplicity which allows to concentrate on details of the presented framework and the matter, that it is possible to explicitly draw the objective function of a two-dimensional problem.

The second example—the task of estimating optimal repetition numbers in an underdetermined system—is used to underline the potential of the framework for classical geodetic application using real data.

4.1 2D synthetic example with 1D manifold

The first example is the task of estimating the two summands of a weighted sum

$$\begin{aligned} \ell _i + v_i&= x_1 + 2x_2 \end{aligned}$$

(29)

in a Gauss–Markov model. We assume each observation to follow a normal distribution with a standard deviation of one and state that all observations are independent and identically distributed. Therefore, the VCV matrix $\varvec{\Sigma }$ is an identity matrix. It should be noted that this is done for reasons of simplicity only, as the proposed framework is able to handle the case of correlated observations, too.

The resulting two-dimensional system clearly has a rank defect of one, as it is solely possible to estimate one summand depending on the other one.

$$\begin{aligned} \varvec{\ell } + \mathbf {v} = \left[ \begin{array}{l@{\quad }l} 1 &{} 2\\ 1 &{} 2\\ 1 &{} 2\\ 1 &{} 2 \\ 1 &{} 2 \end{array}\right] \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \mathbf {Ax}. \end{aligned}$$

(30)

Obviously, both columns of the design matrix $\mathbf {A}$ are linear dependent. Given the following synthetic observations

$$\begin{aligned} \varvec{\ell }^T&= \left[ \begin{array}{ccccc}23.2&16.4&12.9&8.2&13.7 \end{array}\right] , \end{aligned}$$

(31)

we will demonstrate the computation of the unconstrained ordinary least-squares (OLS) solution in Sect. 4.1.1, as this is identical to the first steps of our framework. Next, we will introduce two different sets of constraints to cover case 1 where manifold and feasible region intersect (Sect. 4.1.2) as well as case 2, in which there is no such intersection (Sect. 4.1.3). The isolines of the objective function are shown in Fig. 1a.

4.1.1 Unconstrained OLS solution

The elements of the normal equations read

$$\begin{aligned} \mathbf {N} = \mathbf {A}^T \mathbf {A} = \left[ \begin{array}{r@{\quad }l} 5 &{} 10 \\ 10 &{} 20 \end{array}\right] , \quad \mathbf {n} = \mathbf {A}^T \varvec{\ell } = \left[ \begin{array}{r} 74.40 \\ 148.80 \end{array}\right] . \end{aligned}$$

(32)

Inserting (13) and (11) in (8) the general solution reads

$$\begin{aligned} \mathbf {x}(\lambda ) = \left[ \begin{array}{c} 14.88 \\ 0 \end{array}\right] + \left[ \begin{array}{r} -2 \\ 1 \end{array}\right] \lambda = {\mathbf {x}_P} + \mathbf {X}_\mathrm{hom} \lambda . \end{aligned}$$

(33)

As expected, there is no unique optimal solution but a manifold, which is expressed by an arbitrary particular solution ${\widehat{\mathbf {x}}_P}$ and a solution $\mathbf {X}_\mathrm{hom}$ of the homogenous system. The manifold is represented by the dashed black line in Fig. 1a for the arbitrarily chosen interval $2.44 \le \lambda \le 7.44$.

4.1.2 Case 1: restriction of the manifold

Introduction of the constraints

$$\begin{aligned}&x_1 \le 2, \quad x_2 \le 7 \end{aligned}$$

(34a)

$$\begin{aligned}&\Longleftrightarrow \left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} 1 \end{array}\right] \mathbf {x} \le \left[ \begin{array}{l} 2 \\ 7 \end{array}\right] \end{aligned}$$

(34b)

$$\begin{aligned}&\Longleftrightarrow \mathbf {B}^T \mathbf {x} \le \mathbf {b} \end{aligned}$$

(34c)

restricts the manifold as can be seen in Fig. 2. Transforming the constraints in the point ${\widehat{\mathbf {x}}_P}$ of the particular solution with respect to the free parameter $\lambda$ according to (19) yields

$$\begin{aligned}&-2 \lambda \le -12.88, \quad \lambda \> \le 7 \end{aligned}$$

(35a)

$$\begin{aligned}&\Longleftrightarrow \left[ \begin{array}{r} -2 \\ 1 \end{array}\right] \lambda \le \left[ \begin{array}{r} -12.88 \\ 7.00 \end{array}\right] \end{aligned}$$

(35b)

$$\begin{aligned}&\Longleftrightarrow \mathbf {B}^T_{\lambda } \lambda \le \mathbf {b}_{\lambda }. \end{aligned}$$

(35c)

Fig. 2

Isolines of the objective function of the synthetic example, case 1. The manifold is plotted as dashed black line, a particular solution of the unconstrained case (obtained via the Moore–Penrose Inverse) is shown as orange cross. The infeasible region is shaded and inequalities are plotted as red lines. The ICLS solution with shortest length is shown as green cross

Now, a feasibility problem is solved to determine if a feasible solution exists or if the constraints are contradictory. For this trivial example one can easily find a solution that fulfills all constraints, e.g., $\lambda =7$. Therefore, we compute an estimate $\widetilde{\lambda }$ by solving

The resulting value $\widetilde{\lambda } = 6.44$ is used to compute the shortest solution vector that fulfills all constraints

$$\begin{aligned} \widetilde{\mathbf {x}}_P^\mathrm{ICLS} = \mathbf {x}_P + \mathbf {X}_\mathrm{hom} \widetilde{\lambda }= \left[ \begin{array}{c} 2.00 \\ 6.44 \end{array}\right] \end{aligned}$$

(36)

(green cross in Fig. 2). Considering the changed particular solution, we transform the constraints again and achieve as final result

$$\begin{aligned}&\widetilde{\mathbf {x}} = \widetilde{\mathbf {x}}_P^\mathrm{ICLS} + \mathbf {x}_\mathrm{hom}^{OLS} (\lambda ) = \left[ \begin{array}{c} 2.00 \\ 6.44 \end{array}\right] + \lambda \left[ \begin{array}{r} -2 \\ 1 \end{array}\right] \end{aligned}$$

(37a)

$$\begin{aligned}&\text {subject }\text {to} \left[ \begin{array}{r} -2 \\ 1 \end{array}\right] \lambda \le \left[ \begin{array}{c} 0 \\ 0.56 \end{array}\right] . \end{aligned}$$

(37b)

Due to the introduction of inequality constraints the manifold is no longer a line, but a line segment. The constraint $x_1 \le 2$ prevents that the ICLS solution is identical to the solution obtained via the pseudoinverse. This can also be seen in the final solution (37), as there is one value on the right hand side of the transformed constraints, that is zero, meaning that the constraint is active. As the absolute value of the second transformed constraint is small, it can be concluded, that the manifold is only a small line segment, which is also depicted in Fig. 2.

4.1.3 Case 2: unique solution

This section deals with the same synthetic example as described in Sect. 4.1.1, but the second constraint is narrowed to demonstrate the case, in which the introduction of inequality constraints resolves the manifold and yields a unique solution. Let the constraints be

$$\begin{aligned}&x_1 \le 2, \quad x_2 \le 2 \end{aligned}$$

(38a)

$$\begin{aligned}&\Longleftrightarrow \left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array}\right] \mathbf {x} \le \left[ \begin{array}{c} 2 \\ 2 \end{array}\right] \end{aligned}$$

(38b)

$$\begin{aligned}&\Longleftrightarrow \mathbf {B}^T \mathbf {x} \le \mathbf {b}. \end{aligned}$$

(38c)

This setup is depicted in Fig. 1c. The constraint transformation yields

$$\begin{aligned}&-2 \lambda \le -12.88, \,\, \lambda \le 2 \end{aligned}$$

(39a)

$$\begin{aligned} \Longleftrightarrow \mathbf {B}^{T}_{\lambda } \lambda \le \mathbf {b}_{\lambda }. \end{aligned}$$

(39c)

These new constraints (39b) are contradictory as—due to constraint 2—the maximal feasible value of $\lambda$ is 2, which is not enough to satisfy the first inequality. Therefore, one particular solution $\widehat{\mathbf {x}}_P$ of the original problem and the corresponding Lagrange multipliers $\mathbf {k}$ are computed using Dantzig’s simplex algorithm for QPs, resulting in

$$\begin{aligned} \mathbf {x}_P^\mathrm{ICLS} = \left[ \begin{array}{c} 2.00 \\ 2.00 \end{array}\right] , \quad \mathbf {k} = \left[ \begin{array}{r} 88.80 \\ 177.60 \end{array}\right] . \end{aligned}$$

(40)

As there is no active constraint that is parallel to the manifold of solutions, the introduction of inequality constraints resolves the manifold and the computed particular solution is unique

$$\begin{aligned} \widetilde{\mathbf {x}}^\mathrm{ICLS} = \mathbf {x}_P^\mathrm{ICLS} = \left[ \begin{array}{c} 2.00 \\ 2.00 \end{array}\right] . \end{aligned}$$

(41)

This can be geometrically verified, considering Fig. 1c, where $\widetilde{\mathbf {x}}^{ICLS}$ is shown as green cross.

4.2 Second order design (SOD) of a geodetic network

The second application is the design of a geodetic network. This is a classic optimization task in geodesy, which received a lot of attention in the past (cf. Grafarend and Sansò 1985) and still is a topic of ongoing research (cf. Dalmolin and Oliveira 2011).

We focused on the SOD of a direction and distance network as there it is most likely for a rank defect to appear. However, the same methodology can be applied for the SOD of a GNSS network, too. See e.g., Yetkin et al. (2011) for an approach to determine an optimal set of GPS baselines in an horizontal network.

4.2.1 Problem description

Aim of the SOD of an existing geodetic direction and/or distance network is to determine optimal observation weights $p_i$ in order to develop an observation plan, that fulfills some predefined optimality criteria. Usually, one tries to design a network in a way that the estimated coordinates are of a similar accuracy and have only small correlations. Variances and covariances can be described via the cofactor matrix $\mathbf {Q} \{ \varvec{\widetilde{\mathcal {\MakeUppercase {x}}}} \}$ of the estimated parameters. Therefore, a link to the matrix of observation weights $\mathbf {P}$ can be established as

$$\begin{aligned} \mathbf {A}^T \mathbf {PA} = \mathbf {Q} \{ \varvec{\widetilde{\mathcal {\MakeUppercase {x}}}} \}^{-1} . \end{aligned}$$

(42)

$\mathbf {Q} \{ \varvec{\widetilde{\mathcal {\MakeUppercase {x}}}} \}$ can be replaced by a target cofactor matrix. This criterion matrix $\mathbf {Q}_{\mathbf {x}}$ contains the specification of an optimal cofactor matrix (e.g., uncorrelatedness and similar variances) which serves as observations. Classic choices for the criterion matrix are either an identity matrix or a matrix of Taylor–Karman type (cf. Grafarend and Schaffrin 1979). Using the Khatri–Rao product $\odot$ (42) can be rewritten in matrix vector notation

$$\begin{aligned} (\mathbf {A}^T \odot \mathbf {A}^T) \mathbf {p} \overset{!}{=} \mathbf {q_{\mathrm{inv}}}. \end{aligned}$$

(43)

The vectors $\mathbf {p}$ and $\mathbf {q_{\mathrm{inv}}}$ contain the entries of $\mathbf {P}$ and $\mathbf {Q}_{\mathbf {x}}^{-1}$, respectively. Next, our L$_2$-norm objective function can be formulated as

$$\begin{aligned} {{\varPhi }}(\mathbf {p})&= \left( (\mathbf {A}^T \odot \mathbf {A}^T) \mathbf {p} - \mathbf {q_{\mathrm{inv}}}\right) ^T \left( (\mathbf {A}^T \odot \mathbf {A}^T) \mathbf {p} - \mathbf {q_{\mathrm{inv}}}\right) \nonumber \\&= \left( \mathbf {M} \mathbf {p} - \mathbf {q_{\mathrm{inv}}}\right) ^T \left( \mathbf {M} \mathbf {p} - \mathbf {q_{\mathrm{inv}}}\right) , \quad \mathbf {M} {:=} \mathbf {A}^T \odot \mathbf {A}^T.\nonumber \\ \end{aligned}$$

(44)

$\mathbf {Q}_{\mathbf {x}}$ is a symmetric $m \times m$ matrix and all $\frac{m (m+1)}{2}$ elements of its upper right triangle can be used as observations. If the number $n$ of weights $p_i$ that should be determined is less or equal to this length of $\mathbf {q_{\mathrm{inv}}}$, the weights can be estimated using a standard GMM. However, in practice it often occurs, that there are more weights to be estimated than entries of the criterion matrix given. Especially, if we have to deal with small networks or with larger networks with many fixed coordinates. In these cases, the system is underdetermined resulting in a rank-deficient normal equation matrix.

There is a direct relationship between repetition number $n_i$ and the corresponding weight

$$\begin{aligned} p_i = n_i \frac{\sigma _{0}^{2}}{\sigma _{\ell _i}^{2}}. \end{aligned}$$

(45)

$\sigma _{0}^{2}$ is the variance factor and $\sigma _{\ell _i}^{2}$ the variance of observation $\ell _i$. As negative or huge repetition numbers cannot be realized, box constraints are applied to the weights to ensure that they are nonnegative and do not exceed a certain maximal repetition number

$$\begin{aligned}&p_i \ge 0 \Longleftrightarrow -\mathbf {Ip} \le \mathbf {0}\end{aligned}$$

(46)

$$\begin{aligned}&p_i \le n_\mathrm{max} \frac{\sigma _{0}^{2}}{\sigma _{\ell _i}^{2}} \Longleftrightarrow \text {diag}\left( \varvec{\Sigma }\right) \mathbf {p} \le n_\mathrm{max} \sigma _0 \mathbf {e}_n. \end{aligned}$$

(47)

The operator $diag\left( \varvec{\Sigma } \right)$ extracts all diagonal elements of matrix $\varvec{\Sigma }$ and preserves its original dimension. $\mathbf {e}_n$ is a vector of length $n$, that contains only ones. The corresponding optimization problem reads

Naturally, computation of individual weights for each observation does not yield a final result of the network optimization process. This is, because it is not viable in practice to measure some directions from one standpoint more often than others. Therefore, the estimation of individual weights usually presents the first step of a three-step approach. In a second step, measurements with little impact are identified and eliminated. Finally, in the third step, group weights—e.g., for all observations from one standpoint—are estimated (cf. Müller 1985). However, we focused on the first step only, because it is most likely for a rank defect to appear there.

4.2.2 Results

We have applied the framework described in Sect. 3.5 to determine optimal weights for a horizontal network located in the “Messdorfer Feld” in Bonn. The network consists of 3 fixed datum points (black triangles) and 8 new points (black dots), whose coordinates should be estimated (cf. Fig. 3). All points are located within sight distance from each other, so that directions and distances between all pairs of points could be measured theoretically. A criterion matrix of Taylor–Karman type (cf. Grafarend and Schaffrin 1979) is chosen, resulting in the target error ellipses plotted in green. The dimensions of the network yield in $\frac{16 (16+1)}{2} = 136$ entries of the criterion matrix, which serve as observations and 162 weights to be estimated, resulting from the 162 possible direction or distance measurements. A tachymeter with an accuracy of

$$\begin{aligned} \sigma _\mathrm{dir}&= 0.4\,\mathrm{mgon},\end{aligned}$$

(48)

$$\begin{aligned} \sigma _\mathrm{dist}&= 1\,\mathrm{mm}+1\,\mathrm{ppm} \end{aligned}$$

(49)

shall be used. $\sigma _\mathrm{dir}$ is the assumed accuracy of a direction measurement and $\sigma _\mathrm{dist}$ the assumed accuracy of a distance measurement.

The network shown in Fig. 3 has been designed using the quantities stated above, assuming an arbitrary chosen maximum repetition number of 50 and applying the presented framework. Since this approach approximates the inverse of the criterion matrix instead of the criterion matrix itself, a factor was computed and used to rescale $\mathbf {p}$ to prevent over-optimization (proposed in Müller 1985). The red error ellipses indicate values of the resulting cofactor matrix $\mathbf {Q} \{ \varvec{\widetilde{\mathcal {\MakeUppercase {x}}}} \}$.

Fig. 3

SOD of a geodetic network with 3 fixed points (black triangles) and 8 new points (black dots). Distance measurements are shown as dashed lines and direction measurements as solid lines. Green ellipses depict the optimal error ellipses which are approximated by the red ones

As a result of the optimization procedure a total of 146 measurements should be performed (118 direction measurements, dashed lines, and 28 distance measurements, solid lines). No measurement should be repeated more than 5 times. Furthermore, the introduction of inequalities resolves the rank defect resulting in a unique solution. As expected, the resulting error ellipses of points in the center of the network are more circle-like than those of the ones on the borders.

5 Summary and conclusion

A framework for the rigorous computation of a general solution of rank-deficient ICLS problems was developed. Within this framework, it is possible to compute a unique particular solution which has shortest length of all vectors of the solution manifold. If there is an intersection of the feasible region and the manifold of solution, this particular solution is identical to the one computed via the Moore–Penrose inverse.

Besides a description of the manifold of solutions, the inequality constraints are reformulated in terms of the free parameters of the optimization problem to quantify their influence on the manifold. It can be determined, how and if the introduction of inequality constraints reduce the dimension of the manifold culminating in the case of a unique optimal solution.

The order of computations within the framework is chosen in a way to avoid a direct computation of a particular solution of the original ICLS problem if possible, to reduce the computational demand. Instead, if manifold and feasible region intersect, the original inequality constrained problem is split up into an unconstrained problem in the original parameter space and a feasibility and an optimization problem, both in a vector space of lower dimensions. Therefore, the presented framework is not restricted to small-scale problems as the approach by Werner and Yapar (1996).

In this contribution, the minimization of the length of the parameter vector was chosen as second optimality condition for the particular solution. However, this is an arbitrary choice. One could also minimize a different norm which suites a special problem. Potential choices include the $L_1$-norm of the parameter vector to obtain sparse solutions for bigger problems or the $L_{\infty }$-norm to minimize the maximal error.

In addition, the handling of ill-posed problems has not been addressed, yet. In this case, it is more difficult to determine the vector space in which the minimization has to take place. This question was left out intentionally and shall be addressed in the future. Both issues have to be examined and will be in the focus of future work.