1 Introduction

Today, a great variety of global gravity field models (GGFMs) generated from data of European Space Agency’s (ESA) Gravity field and steady-state Ocean Circulation Explorer (GOCE) gravity field observation satellite (ESA 1999) exists. Three different approaches for recovering gravity from the satellite’s measurements, namely the space-wise (SPW) (Migliaccio et al. 2010), the time-wise (TIM) (Pail et al. 2010), and the direct (DIR) (Bruinsma et al. 2010b) method, have been developed, embedded in the ESA High-level Processing Facility (HPF). In March 2013, the fourth generation models of the DIR and TIM approach were published, both effectively relying on more than 26 months of data. From the SPW approach, however, only two early release models exist, which in the following are not considered further.

Looking at the third and fourth generation models of the DIR and TIM approach, not only the amount of data being used differs with respect to their predecessors, but also the processing strategies applied. Due to those changes, improvement may be expected for the new generation models; however, investigations are required. This study evaluates the models’ performance in terms of relative improvement and absolute accuracy and shall assess the models’ formal error estimates.

GOCE gravity models up to the third generation have been evaluated in many publications with different methods and different datasets. A sound description and comparison of the different processing strategies and the performance of the first generation gravity field models can be found in Pail et al. (2011a). In Gruber et al. (2011), the first-generation GOCE GGFMs are assessed globally by means of orbit determination of low-orbiting satellites and regionally by point-wise geoid heights from GPS-levelling data. In Hirt et al. (2011), first generation GOCE GGFMs are evaluated regionally with terrestrial gravity measurements and point-wise astrogeodetic vertical deflections, and globally with quasi-geoid heights derived from EGM2008. To overcome the spectral band limitation of the models the so-called spectral enhancement method (SEM) (see, e.g., Hirt et al. (2011)) was applied, where information of high frequency GGFMs [like EGM2008 (Pavlis et al. 2012)] and residual terrain data (to account for the ultra-high frequencies) is used to make the spectral content of GGFMs and ground truth data largely compatible. In Tscherning and Arabelos (2011), the first- and second-release GOCE models are compared to gravity anomalies and to radial gradients recovered from GOCE gradiometer data using Least-Squares Collocation (LSC), and to ground truth data sets in various regions of the planet. Janák and Pitonák (2011) evaluated the first- and second-release GOCE GGFMs with GNSS/levelling data and gravity observations at 31 stations of the Slovak Terrestrial Reference Frame, and additionally compared the models with EGM2008 and GOCO02 (Pail et al. 2011b) in spatial domain making use of a simple version of the SEM. In Hirt et al. (2012), gravity signals as implied by the Earth’s topography and explained by different isostatic models are used to evaluate the performance of the first- to third-generation GOCE models at various spatial scales. Šprlák et al. (2012) evaluated the first- to third-generation models with an independent data set of SEM-reduced free-air gravity anomalies in Norway and Bouman and Fuchs (2012) assessed the quality and the performance of the GOCE GGFMs and of the underlying processing strategies with band-filtered gradient observations of the GOCE gradiometer, globally. We also acknowledge other existing studies evaluating GOCE GGFMs over different regions with different terrestrial data sets, e.g. over parts of Sudan (Abdalla et al. 2012), Brazil (Guimarães et al. 2012), Hungary (Szücz 2012), Norway (Šprlák et al. 2011; Gerlach et al. 2013) and Germany (Voigt et al. 2010; Voigt and Denker 2011).

The idea and the scope of this study are to evaluate the GOCE gravity field models up to the fourth generation with a new spherical harmonic gravity field model, which is independent of GOCE data and contains terrestrial gravity information in Australia. Using a new and independent model of the disturbing potential parameterized in spherical harmonics offers a number of advantages over using just (regional) point or interpolated (gridded) ground truth data sets for an evaluation. First, there is no restriction to a certain gravity field functional, which would normally be predetermined by the type of available ground truth data. As will be shown in this paper, the combined use of different gravity field functionals facilitates a more complete evaluation of the GOCE gravity fields. Different functionals, e.g. gravity disturbances or gravity gradients, have different sensitivity to different spectral bands of the Earth’s gravity field and provide valuable complementary information on the GOCE model performance. This has been already noticed, e.g., in Szücz (2012), but the sensitivity of different functionals has not been analysed systematically. Second, the evaluation is not restricted to the exact position of the measurement on ground, but can be freely chosen by a triplet of spherical geocentric coordinates (\(\phi , \lambda , r \)) in the spherical harmonic synthesis (SHS). This allows, e.g, straightforward evaluation at ground level and/or at satellite height. Third, comparisons in spherical harmonics avoid the need to overcome a spectral gap, which usually occurs when comparing truncated/band-limited GOCE GGFMs with terrestrial gravity (see SEM approach, e.g. Hirt et al. (2011); Šprlák et al. (2012)). The SEM, however, is not flexible but restricted to the gravity field functional represented by the comparison data on ground level. Alternatively to the SEM, the terrestrial data (or satellite observations) can be lowpass filtered, e.g., with a Butterworth filter in the frequency domain (Šprlák et al. 2011), a Gaussian filter in the spatial domain (Voigt et al. 2010; Voigt and Denker 2011), or by means of wavelet approaches like the second generation wavelets approach (Ihde et al. 2010), to make them comparable to the band-limited GGFMs.

Having the points outlined above in mind, an elegant way to evaluate a GGFM is by comparison with another independent GGFM as a reference. Such a data set in principle is already given, e.g., by EGM2008. However, this model does not include all up-to-date gravity data which is, e.g., available for Australia, today.

In Sect. 2, an overview (of the features) of ESA’s most recent GOCE gravity field models is provided and the changes between the releases are summarized. In Sect. 3, one way of generating a (comparison) GGFM, which we use to evaluate GOCE’s GGFMs above the landmasses of Australia, is presented. A so far little used but effective spherical harmonic analysis (SHA) approach, the so-called coefficient transformation method (Claessens 2006), is used to retrieve spherical harmonic coefficients of the disturbing potential (see Sect. 3.2). This technique is applied to a global grid of free-air gravity anomalies, which includes terrestrial data over Australia (see Sect. 3.1). The resulting GGFM is then combined with GRACE (Gravity Recovery and Climate Experiment) (Tapley and Reigber 2001) data on the basis of normal equations (see Sect. 3.3). The finally created set of spherical harmonic coefficients, named AUS-GGM, and its features are discussed in Sect. 3.4. In a next step, GOCE GGFMs are evaluated over Australia (see Sect. 4) by means of root-mean-square (RMS) errors (see Sect. 3.5) of residual quasi-geoid heights, gravity disturbances and radial gravity gradients (in spherical approximation). The evaluation is based on three gravity functionals of different spectral sensitivity, evaluated on the ellipsoid (Sect. 4.1) and at satellite height (Sect. 4.2), which allows an interpretation of the results in line with the Meissl scheme (Rummel and van Gelderen 1995) in Sect. 4.3. Finally, Sect. 5 summarizes our investigations, and key findings are formulated.

2 GOCE global gravity field models

In this section, a short overview of the second-, third-, and fourth-generation ESA GOCE models of the DIR and TIM approach is given, focusing on the innovation of each release. A general overview on the underlying principles and methods of the two approaches can be found, e.g., in Pail et al. (2010); Pail et al. (2011a); Bruinsma et al. (2010b). Table 1 lists the main characteristics of the models and changes with respect to their previous releases (right column). The information was retrieved from the models’ header information and their respective data sheets, all released via the ICGEM-homepage (http://icgem.gfz-potsdam.de/ICGEM/).

Table 1 Main characteristics of a selection of the most recent gravity field models relying on GOCE data (periods do not reflect the effective amount of data being used) [source: ICGEM (http://icgem.gfz-potsdam.de/ICGEM/ICGEM.html)]
Full size table

DIR models of second and third generation have a maximum spherical harmonic degree \(L_{\mathrm{max}}\) of 240, while the DIR4 model has a higher spatial resolution (\(L_{\mathrm{max}}=260\)). All three DIR releases (in addition to GOCE gravity gradient data) contain GRACE information in the lower to medium range spherical harmonic degrees. In the second DIR release, the ITG-GRACE2010s (Mayer-Gürr et al. 2010) solution is introduced as a priori information until degree and order (d/o) 150. In the DIR3 and DIR4 models GRACE is combined with GOCE and satellite laser-ranging (SLR) data of LAGEOS (Tapley et al. 1993) on the basis of normal equations. In the DIR3 model GRACE normal equations up to d/o 160 are used which entirely rely on the procedures of the second release CNES/GRGS (Centre National d’Etudes Spatiales/Groupe de Recherches de Géodésie Spatiale) models (Bruinsma et al. 2010a). In the DIR4 model, the same GRGS-GRACE normal equations are used only up to d/o 54. From degree 55 up to degree 180, DIR4 is based on GRACE GFZ (GeoForschungsZentrum Potsdam) release 5 gravity field solution (Dahle et al. 2013). The amount of data/observations from all involved satellites is increasing with each DIR release. Effectively, DIR3 and DIR4 are based on 12 and 27.9 months of GOCE data, respectively. In the last three DIR releases consistently a spherical cap regularization (SCR) (Metzler and Pail 2005) was applied using GRACE and LAGEOS information to overcome GOCE’s polar observation gap (Sneeuw and van Gelderen 1997), which is caused by the satellite’s orbit inclination of \(96.7 ^{\circ }\) (ESA 1999). In the third and fourth DIR release, additionally, the predecessor release was used as a priori information (up to d/o 240) and a Kaula regularization (see, e.g., Metzler and Pail (2005)) was applied starting at degree 200. Since the third DIR release the information gathered from each of the three gravity tensor elements measured with GOCE’s on-board SGG is weighted equally in the combination. In the DIR4 release information of the off-diagonal tensor element, \(V_{xz}\) was likewise included. Besides, in DIR4, the spectral band of the bandpass filter used to filter the SGG observations was extended by 1.7 mHz towards the lower frequency domain. Within the DIR approach (in contrary to the TIM approach), the use of GOCE gradient information is restricted to a certain spectral band, which is close to the gradiometer’s designed measurement bandwidth (5–100 mHz, see, e.g. ESA (1999)).

Looking at the TIM models, the models’ maximum spherical harmonic degree is constant at degree 250 for the latest three releases. All TIM models exclusively rely on GOCE SGG and SST-hl (satellite-to-satellite observation in high-low mode) data; however, the amount of data increases with each release. Effectively, TIM3 and TIM4 are based on 12 and 26.5 months of GOCE data, respectively. Each TIM model is constrained according to Kaula’s rule (Kaula 1966) by means of (1) a spherical cap regularization (Metzler and Pail 2005) to deal with the polar observation gap (ESA 1999) and (2) a (full) Kaula regularization starting at degree 180. Since the first TIM release the stochastic models for the gradient observations are estimated from small, coherent data-patches, resulting in improved (tuned) filtering of the gradients in the time domain. Remaining unchanged for the all releases, the filtering procedure within the TIM approach allows to use the information of the gradient observations over the entire spectrum. Since the TIM3 release, the off-diagonal tensor element \(V_{xz}\) finds application in the models. Finally, in the fourth TIM release, the processing strategy for the SST normal equations was changed from the energy integral approach (Badura 2006) to the short-arc integral method (Mayer-Gürr et al. 2006).

Not explicitly included in the table is the introduction of a new Level-1b (L1b) processing procedure (Stummer et al. 2011, 2012) in 2012 due to which a better performance of GOCE’s satellite gravity gradiometer (SGG) is to be expected in the fourth generation models (DIR and TIM). According to Pail et al. (2012), gradiometry-only gravity field estimates show largest improvements in the recovery of lower and medium degree coefficients and the accuracy of combined gravity field models is reported to gain more than 10 %, even in higher degrees, due to the new L1b processing.

3 Data and methods for the creation of a GOCE-independent comparison GGFM

3.1 Data

The aim of the research is to create a set of global spherical harmonic coefficients of the disturbing potential from gridded (terrestrial) gravity data which is (a) completely independent of GOCE, and (b) of sufficient spatial resolution and accuracy (\({\le }\) 1–2 cm geoid height or \(\le \) 1 mGal at a spatial scale of 100 km) (cf. ESA (1999)) to evaluate the performance of GOCE GGFM. Globally, this cannot be achieved, as there is no observation technique with global coverage and similar or higher performance than GOCE. Regionally, however, it is possible to use terrestrial gravity observations to evaluate GOCE. For our research, a comparison GGFM was computed with terrestrial gravity over the land area of Australia.

The Australian terrestrial gravity data set available for this work consists of gridded Faye free-air gravity anomalies on the topography with a resolution of \(1^{\prime } \times 1^{\prime }\) (arc-minutes). In total, about 1.4 million gravity observations over Australia were taken from Australia’s National Gravity Database (hosted at Geoscience Australia) to create the gridded data set (Featherstone et al. 2010). This, e.g., exceeds the amount of observations (905, 483) which have been used to compute EGM2008 (cf. Claessens et al. (2009)). The \(1^{\prime } \times 1^{\prime }\) anomaly grid has been computed from the database in the course of the country’s national (quasi-) geoid AUSGeoid09 (Featherstone et al. 2010) computation. The computation and the gridding of the gravity anomalies refer to the procedure originally described in detail in Featherstone and Kirby (2000). Within the approach, aliasing errors are minimized by interpolating the observed gravity anomalies after a point-wise subtraction of a simple Bouger anomaly (which is then restored after the interpolation to a grid). The finally obtained Faye free-air anomalies are free-air anomalies of Molodensky’s type with the terrain correction applied. The additional terrain correction approximates Molodenski G1 correction term (see, e.g, Torge (2001), p.290; Wang (1989)), which is generally needed for the downward continuation of free-air anomalies to the ellipsoid.

The remainder of the Earth’s gravity field is represented by a global grid of gravity anomalies provided by the Technical University of Denmark’s (DTU) marine gravity model DNSC10GRA, which is the successor of DNSC08GRA described in Andersen et al. (2009). The DTU data set relies on EGM2008 (Pavlis et al. 2012) over land and ArcGP (Forsberg and Kenyon 2004) gravity data and ICEsat’s laser altimetry data (Zwally et al. 2002) over polar regions. Offshore gravity is recovered from the knowledge of the oceans’ mean sea surface height (SSH) derived from satellite altimetry. The mean SSH is determined with a so-called double retracking technique (Andersen et al. 2009), which leads to an augmented spatial coverage (especially in ice-covered regions), using data of the altimetry satellites GEOSAT and ERS-1. Data of the altimeter missions Topex/Poseidon, GFO, ERS-2 and Envisat also found application in the DNSC10GRA development.

3.2 Gridding and spherical harmonic analysis

In this section, the computation steps to obtain coefficients of the disturbing potential from the initial data sets are explained. Figure 1 schematically shows the data flow of the processing (left side of the scheme). In a pre-processing step, the data sets have to be consistently prepared and merged for the subsequent SHA procedure by a coordinate transformation and consecutive down-sampling. The SHA is accomplished based on the coefficient transformation method (CTM) (Claessens 2006). This approach requires (A) a spherical harmonic analysis to compute a set of surface spherical harmonic coefficients and (B) a spectral transformation to transform these into solid spherical harmonic coefficients of the disturbing potential (cf. Fig. 1).

Fig. 1
figure 1

Processing scheme for the generation of a comparison GGFM (left/green) and scheme for the closed loop test relying on EGM2008 (right/orange)

Full size image

For the spherical harmonic analysis (A), a homogeneous global grid of gravity anomalies on the ellipsoid with an equiangular spacing in both 2D directions is needed. As mentioned above, such a grid with an equiangular spacing of 1 arcminute is given with the DNSC10GRA data set, globally. Over the landmass of Australia, the country’s terrestrial gravity anomalies are used while DNSC10GRA is used to describe the Earth’s gravity outside of Australia. Before merging the 2 data sets, however, it is necessary to adapt and harmonize the data sets, taking the following considerations into account:

The analysis procedure (A) relies on a quadrature algorithm based on Fourier transforms and a sampling theorem, both described by Driscoll and Healy (1994). As defined by the sampling theorem, the maximum spherical harmonic degree \(L_{\mathrm{max}}\), that can (exactly) be retrieved from a band-limited function given on a sphere, is defined through

$$\begin{aligned} L_{\mathrm{max}}=\frac{N}{2}-1, \end{aligned}$$
(1)

where \(N\) denotes the even number of point values in latitude direction of an equiangular grid of size \(N \times N\) or \(N \times 2N\) (points in latitude direction \(\times \) points in longitude direction). Here, the latter grid sampling finds application for reasons of convenience, as it is identical to the sampling of the used terrestrial gravity anomaly grid. For the purpose of this study, the maximum degree has to be at least equivalent to the GOCE GGFM with the highest resolution, which is given with the fourth generation model of the DIR approach (\(L_{\mathrm{max}}=260\)). Aimed at a maximum spherical harmonic degree of 539 of the final GGFM—which is more than good enough for the purpose of this study—the gravity anomaly grids are down-sampled accordingly to a 10\(^{\prime }\) (arcminutes) spacing (leading to a global grid of \(1080 \times 2160\) points). The down-sampling is performed by computing block-mean values for all grid-points entirely contained in adjacent, equiangular blocks of \(10^{\prime } \times 10^{\prime }\) size. Prior to the down-sampling, the grids have to be transformed from geodetic to geocentric latitudes. This can, e.g., be done with a 2D-spline interpolation using the simple relation

$$\begin{aligned} {\mathrm{tan}} \Theta =\frac{a^2}{b^2} {\mathrm{tan}}{\phi } \end{aligned}$$
(2)

between the spherical co-latitude \(\Theta \) and the geodetic co-latitude \(\phi \), where \(a\) is the semi-major and b the semi-minor axis of the underlying ellipsoid (see, e.g., Torge (2001), p.95), which is GRS80 (Moritz 2000) in this case.

The set of spherical harmonic coefficients (SHC), which is computed with the Driscoll and Healy’s (DH) algorithm using the SHTOOLS Footnote 1 software, is a set of surface SHCs. It can only be used to retrieve exactly the same gravity functional which was used as input (in this case gravity anomalies). Thus, a subsequent transformation (B) is needed to retrieve solid SHCs of the disturbing potential. This spectral transformation completes the CTM approach, which has been proposed by Claessens (2006). The CTM is used in conjunction with numerical quadrature methods like SHTools’ DH-algorithm, and is based on the possibility to describe function values on the ellipsoidal surface in terms of a set of surface SHCs. Further, the CTM proves to be superior to several existing methods and comparable to the ellipsoidal harmonics method (EHM) (Jekeli 1988) (cf. Claessens (2006)). To be more precise, the CTM shows better accuracy regarding near-zonal coefficients and is slightly worse regarding the near-sectoral coefficients compared to the EHM. It is shown that the CTM’s mean error is 0.3 mm and its maximum error 2.6 mm expressed in geoid height (in the spectral range of degree 20 to degree 340) (cf. Claessens (2006)). For detailed information on the CTM and the transformation, we refer to the cited literature, where the algorithm and its performance is comprehensively described.

The function described by the gravity anomaly grid points on the sphere is not band-limited as it is needed for DH’s algorithm, and thus aliasing is to be expected. However, this effect can be ignored for the purpose of our research. Closed loop tests with a gravity anomaly grid expanded (up to degree 2190) from the EGM2008 gravity field model, passed through the same procedure outlined above (illustrated on the right side of Fig. 1), indicate that the input SHCs can be restored with sufficient accuracy. The gravity residuals reach at maximum \(\pm \) 0.75 mGal at degree 200 and their mean between degree 20 to degree 340 is 0.0025 mGal. Globally, the root-mean-square (RMS) of closed loop discrepancies is 0.068 mGal at a spatial scale of 100 km (degree 200) and 0.07 mGal at a spatial scale of 80 km (degree 250) in terms of gravity anomalies. By comparison, the estimated error of GOCE models is about 0.9 mGal (HPF 2013b) and 0.35 mGal (own computation) at degree 200 for TIM4 and DIR4, respectively.

3.3 Combination with GRACE

As a final step to obtain SHCs eligible to evaluate GOCE GGFMs, we combine the above received solid SHCs from the CTM with data of the GRACE satellite mission. GRACE information can be seen complementary to the high-frequency terrestrial data (present in Australia), as GRACE shows a very high performance in the recovery of the long wavelength part of the spectrum of the Earth’s gravity field. The combination is performed on the basis of full GRACE normal equations (complete up to d/o 180), which have been computed in the course of the ITG-GRACE2010 gravity field model (Mayer-Gürr et al. 2010). The formal error-per-degree estimate of ITG-GRACE2010 at degree 120 is 1.5 mm (and 4.2 mm accumulated error from own computations) in terms of geoid heights (cf. Mayer-Gürr et al. (2010)).

The combination can be expressed as a least-squares problem by introducing a (i) GRACE type system

$$\begin{aligned} l+ v_1 = A \cdot x, \end{aligned}$$
(3)

where \(l\) are the GRACE observations used in the production of ITG-GRACE2010, \(A\) is the design matrix, \(x\) is the unknown parameter vector and \(v_1\) denotes the residuals of the process. Further, we introduce a (ii) system relying entirely on a priori information

$$\begin{aligned} x_0 + v_2 = I \cdot x, \end{aligned}$$
(4)

where \(x_0\) is a priori known parameter vector, \(I\) the identity matrix and \(v_2\) denotes the residuals of the process. Because of the linearized form and the affiliation to the same set of parameters, system i (Eq. 3) and system ii (Eq. 4) can be combined, assuming uncorrelated (pseudo-) observation groups by

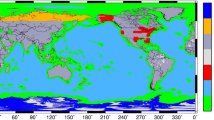
$$\begin{aligned}&\!\!\!(A^{T}\varSigma (l)^{-1}A + I^{T}\varSigma (x_{0})^{-1}I) \cdot x\nonumber \\&\!\!\!\quad = A^{T} \varSigma (l)^{-1} l + I^{T}\varSigma (x_0)^{-1} \cdot x_0, \end{aligned}$$
(5)

where \(A^{T}\varSigma (l)^{-1}A\) is the ITG-GRACE2010 normal equation matrix, \(A^{T} \varSigma (l)^{-1} l\) is the corresponding right-hand side, \(\varSigma (l)\) and \(\varSigma (x_0)\) denote the variance-covariance matrices of system i and system ii, respectively. In our case, the a priori known parameters \(x_0\) are the SHCs related to the terrestrial data grid, and computed by the CTM approach. The variance–covariance matrix \(\varSigma (x_{0})\) only consists of diagonal elements, the variances of the SHCs. The variances were defined empirically and degree-wise (based on the assumption that GRACE provides more accurate information on the long wavelength part of the spectrum), so that their impact in the combination is minor below spherical harmonic degree 120 and dominates beyond degree 120 regarding the given mean GRACE variance (-covariance) information per degree. Expressed numerically in terms of standard deviations (\({\varSigma (x_{0})}\)), we start with \(1 \times 10^{-10}\) at degree 0 and decrease with an increment of \(7.92 \times 10^{-13}\) for each degree, reaching \(4.149 \times 10^{-12}\) at degree 120 (and staying constant up to degree 180). Figure 2 shows the exact ratio of contribution of GRACE information (left side) and terrestrial (and DNSC10GRA) information (right side) per spherical harmonic coefficient. From Fig. 2, it becomes clear that the combination consists of terrestrial data (and DNSC10GRA data outside of Australia), solely, beyond the spherical harmonic degree 140.

Fig. 2
figure 2

Contribution of GRACE (left plot) and terrestrial data (right plot) to the combined solution

Full size image

We have exchanged the zonal spherical harmonic coefficient of degree two (C20) with its equivalent from EGM2008, because GRACE’s J2 coefficient is subject to tidal aliasing (cf., e.g., Chen and Wilson (2010), Lavallée et al. 2010). Within EGM2008, J2 originates from SLR, mainly.

As an aside, discrepancies between the terrestrial Faye free-air gravity anomalies and the DNSC10GRA / EGM2008 free air gravity anomalies over the landmass of Australia could be detected, predominantly of long-wavelength character (up to d/o 50). The highest amplitudes can be found along the Great Dividing Range, the mountain chain in Australia’s South-East, with 15 mGal. In terms of RMS difference, the discrepancy accounts for 1.6 mGal over Australia. These differences have already been reported to the data producers and warrant further investigations which are considered future work. This observation corroborates our strategy to exclusively use GRACE on the long spatial scales. As to be expected the combined solution then shows better agreement with EGM2008 below d/o 50.

3.4 Features and errors of the comparison GGFM

In this section, the features of the created comparison model AUS-GGM are described to judge its ability to evaluate GOCE GGFMs over Australia. The description is based on (approximate) cumulative errors, which formally reflect the models’ performance at a specific spherical harmonic degree on a global scale (and not only over Australia). Figure 3 shows the respective cumulative formal geoid error of AUS-GGM (in yellow) together with the equivalent errors of the other GGFMs which find attention in this research. In Fig. 3, the errors of AUS-GGM’s terrestrial gravity (which is incorporated in the model approximately above degree 120 (see Sect. 3.3) and which is mainly from DNSC10GRA/ EGM2008) are approximated by the standard deviations which are denoted for EGM2008, as we do not obtain a formal error for the terrestrial gravity data from the CTM. As to be expected from the combination of the terrestrial gravity with ITG-GRACE2010 (see Sect. 3.3), we see the cumulative error of AUS-GGM rise around degree 120 where the terrestrial gravity information supersedes GRACE’s information. From degree 2 up to degree 100, the cumulative geoid error of AUS-GGM is smaller or at least comparable to that of DIR4 (blue) and ITG-GRACE2010 (green) and smaller compared to the other illustrated geopotential models. At degree 200, our computations show that AUS-GGM with 35 mm cumulative geoid error seems comparable to the quality of TIM4 (40 mm) and DIR3 (32 mm). It clearly outperforms TIM3 (60 mm) and EGM2008 (72 mm); however, AUS-GGM shows a significantly higher error than DIR4 (12 mm). In the spectral range from degree 120 up to degree 250 DIR4 is the only model which constantly performs significantly better than AUS-GGM from formal perspective. Bear in mind, however, that the cumulative errors reflect the global error and that the formal error of AUS-GGM is approximate. For Australia, where we inserted dense and accurate terrestrial gravity information, the cumulative errors as displayed in Fig. 3 are likely to be too pessimistic. From this perspective, we conclude that AUS-GGM is well designed to serve as a comparison GGFM over Australia to evaluate differences between the GOCE GGFMs and may also be used to give absolute error estimates under consideration of its characteristic cumulative error.

Fig. 3
figure 3

Cumulative formal error of AUS-GGM (approximate) and other geopotential models in meters of geoid height per spherical harmonic degree

Full size image

3.5 Evaluation method

For the evaluation of GOCE GGFMs with the newly created AUS-GGM in spatial domain, we make use of the harmonic_synth software (Holmes and Pavlis 2008) to expand the coefficients to grids. Evaluations are performed in the spatial domain and not in frequency domain, as we only want to focus on the landmass of Australia, where newer terrestrial information has been introduced. A grid-spacing of 10 arcminutes is chosen in the SHS to yield an oversampling compared to the maximum degree of GOCE GGFMs (\(\le \) degree 260). Further, all grid values are computed as point values in geodetic coordinates w.r.t. the GRS80 (Moritz 2000) ellipsoid.

All RMS values are computed from the differences of the AUS-GGM grid and the GOCE GGFM grid under evaluation, w.r.t. the underlying gravity functional. All grid-points outside of Australia’s landmass are not considered in the RMS. The RMS is cumulative in the sense that the spherical harmonic expansion in the synthesis was always done starting at degree 2 up to the denoted maximum spherical harmonic degree.

4 Results and discussion

As outlined in Sect. 1, we focus on the evaluation of the third- and fourth-generation GOCE GGFMs. In Sect. 4.1, the evaluation is done on the ellipsoid, in Sect. 4.2 at an approximate GOCE altitude of \(h=\) 250 km.

The gravity functionals under evaluation are the quasi-geoid height \(\zeta \) in meter [m], the gravity disturbance \(T_r\) (first radial derivative of the disturbing potential) in milli-Gal [mGal] (\(1~\mathrm{mGal}=10^{-5} \frac{m}{s^2}\)), and the radial gravity gradient \(T_{rr}\) (second radial derivative of the disturbing potential) in Eötvös [E] (\(1E=10^{-9}\frac{1}{s^2}\)), all in spherical approximation. With this set-up, we intend to follow the Meissl scheme (Rummel and van Gelderen 1995) and investigate the models’ performances in each of the six domains of the Meissl scheme.

4.1 Evaluation on ground level

With the evaluation on ground level (\(=\)surface of GRS80 ellipsoid), we intend to verify the accuracy of the models at a height which is representative for applications of GOCE data on land (e.g. levelling).

In Fig. 4, the RMS values over Australia of the GOCE GGFMs w.r.t. AUS-GGM are displayed for all three gravity functionals expanded to different maximum degrees. Analyzing all three plots in Fig. 4, one can clearly see that the fourth generation models TIM4 and DIR4 outperform their respective predecessors beyond degree 150. In the spectral range starting at degree 120 up to degree 250, both models show very similar RMS behavior. TIM4 seems to perform marginally better between degree 120 and degree 160 (\(\le \)4 % RMS difference) and DIR4 seems to perform marginally better (\(\le \)6 % RMS difference) in the bands from degree 170 to degree 250. The latter might be explained by the fact that DIR4 holds one additional month of GOCE information compared to TIM4 (see Table 1 in Sect. 2). Table 2 gives the RMS values for each model at the spatial scale of 100 km half wavelength (\(=\)degree 200) for the three functionals. Given those values TIM4 shows an average relative improvement of about 23 % w.r.t. TIM3, and DIR4 shows an average relative improvement of about 39 % w.r.t. DIR3.

Fig. 4
figure 4

RMS values computed from the differences of selected GOCE GGFMs and the newly retrieved AUS-GGM in terms of a quasi-geoid heights \(\zeta \) in meters (left), b gravity disturbances \(T_r\) in mGal (middle) and c radial gravity gradients \(T_{rr}\) (right) on the ellipsoid (\(h=0\)); the bottom row plots zoom into the respective upper plot in the degree range 0–150

Full size image
Table 2 RMS error of GOCE GGFMs w.r.t. AUS-GGM at the spatial scale of 100 km half wavelength (\(=\)degree 200) on the ellipsoid
Full size table

Compared absolutely in terms of geoid heights \(\zeta \), the calculated RMS for DIR4 at degree 200 (4.5 cm) is slightly lower than that of TIM4 (4.7 cm). The absolute (formal) error at degree 200 is officially denoted 1 cm in geoid height for DIR4 (HPF 2013a) and 3.2 cm in geoid height for TIM4 (HPF 2013b) (our own computations show a cumulated geoid error of 1.2 cm and 4 cm for DIR4 and TIM4, respectively). Thus, our calculated RMS values at degree 200 exceed both models’ formal errors by 3.5 cm and 1.5 cm for DIR4 and TIM4, respectively. However, the RMS values from the differences reflect the errors of both involved data sets, the (\(i\)) GOCE models and (\(ii\)) the GRACE / terrestrial data in the AUS-GGM model. Having this in mind and considering that the observed TIM4 RMS is very close to the RMS error of 4.5 cm, which has been estimated for TIM4 independently from comparisons to 675 GPS/levelling observations in Germany at degree 200 (HPF 2013b) our retrieved RMS for TIM4 over Australia seems to be plausible and the TIM4 formal error estimate of 3.2 cm seems to be quite realistic. In the case of DIR4, the true error seems to be larger than the (official) formal error of 1 cm at degree 200, given also that the geoid RMS of the comparison of DIR4 to the 675 GPS/levelling observations in Germany is at the same level as TIM4 (Gruber et al. 2013). However, as indicated by the RMS computed with AUS-GGM, the actual DIR4 error is likely to be lower than that of TIM4 at degree 200. In HPF (2013a), independent comparisons to GPS/levelling observations in several countries show RMS values ranging between 1.7 and 3.3 cm, where DIR4 was taken up to d/o 240 and EGM2008 was filled in starting at degree 241 up to d/o 360.

Compared absolutely in terms of gravity disturbances (\(T_r\)), the calculated RMS for DIR4 at degree 200 (1.2 mGal), again, is slightly lower than that of TIM4 (1.3 mGal). In the case of DIR4, the formal error of 0.35 mGal at degree 200 (own computation) still seems comparatively low to the AUS-GGM RMS. In the case of TIM4, with a formal error of 0.9 mGal at degree 200 (HPF 2013b), the RMS seems to be realistic, given that the RMS reflects the errors in both data sets.

Compared absolutely in terms of the radial gravity gradients (\(T_{rr}\)), similarly to the other two functionals, the RMS for DIR4 at degree 200 (355 mE) is slightly lower than that of TIM4 (374 mE). Only looking at the \(T_{rr}\) formal error estimate for TIM4 at degree 200 (approximately 200 mE), the RMS values from our analyses seem very high. For TIM4, the formal radial gravity gradient error is exceeded by over 150 mE and it cannot be confirmed by our analyses.

Looking at the lower wavelength part of the spectrum (below d/o 120), the quasi-geoid heights seem to be most sensitive for differences among the models (see bottom row plots in Fig. 4). Below d/o 120, the TIM3 solution shows the highest RMS. It is followed by TIM4, DIR3 and then by DIR4 with the lowest RMS in that spectral range. Here, obviously, the DIR models which also contain high accuracy GRACE information in the lower degrees agree better with AUS-GGM. Remarkable is the significant improvement of TIM4 w.r.t. TIM3, which are both independent from GRACE, in the bands below degree 150. This will find further investigation and consideration in Sect. 4.2.

The RMS slope around degree 120 has to be attributed to the comparison model AUS-GGM and not to the GOCE GGFMs, as this is the spectral range where the terrestrial gravity information (with lower accuracy) supersedes GRACE gravity information in AUS-GGM.

In comparison to using EGM2008 for the evaluation of GOCE GGFMs over Australia, we found that AUS-GGM shows significantly lower RMS below d/o 150 (meaning a higher agreement with the GOCE models) and similar RMS above degree 150. To be more precise, EGM2008 shows lower RMS approximately between degree 160 and degree 215 (depending on the functional; maximum discrepancy of 8.8% is found for the radial gravity gradient (\(T_{rr}\)) at degree 160). AUS-GGM shows lower RMS values approximately between degree 215 to degree 260. This is shown in Fig. 5 expressed exemplary in geoid heights (at the ellipsoid). The left plot in Fig. 5 shows the RMS of GGFMS over Australia w.r.t. AUS-GGM (similar to Fig. 4a) in solid lines together with the RMS w.r.t. EGM2008 in dashed lines. The right plot only shows the differences of the RMS obtained by EGM2008 w.r.t. AUS-GGM per spherical-harmonic degree in percent, where positive values indicate a higher discrepancy of EGM2008 to the respective GOCE GGFM over Australia. The agreement of AUS-GGM with GOCE GGFMs is significantly higher below d/o 120. The better performance of AUS-GGM can partly be explained using ITG-GRACE2010s instead of ITG-GRACE03 (the latter was used in the EGM2008 creation (Pavlis et al. 2012)). The weaker performance of EGM2008 may also be affiliated with a loss of ITG-GRACE03 information in the model’s creation, caused by the weighting applied in the combination with terrestrial data, which was detected over poorly surveyed areas by Hashemi Farahani et al. (2013).

Fig. 5
figure 5

RMS values over Australia computed from the differences of selected GOCE GGFMs with the newly retrieved AUS-GGM (solid) and EGM2008 (dashed) in terms of quasi-geoid heights in meters (left plot) and the corresponding RMS deviation of EGM2008 w.r.t. AUS-GGM in percent per GOCE GGFM and spherical harmonic degree (right plot)

Full size image

At degree 120, we observe a slope in the AUS-GGM produced RMS which comes along with the increasing influence of terrestrial gravity information in the comparison model in this degree range. The fact that quite similar results are achieved with EGM2008 in the degrees beyond 150 is seen as a validation of our approach. Keep in mind that the idea of this research to provide methods to produce a GGFM which is regionally completely independent, with up-to date and most accurate terrestrial gravity information. Slightly higher discrepancies to GOCE GGFMs between degree 160 and degree 215 as compared to EGM2008 have to be attributed to errors in the terrestrial gravity data set and the CTM (see Sects. 3.2, 3.3 and 3.4).

4.2 Evaluation at GOCE altitude

In this section, the RMS values over Australia are computed using the same functionals as in the previous section with the only difference that, now, gravity functionals are calculated at 250 km altitude above the ellipsoid. With the evaluation at GOCE satellite height, we demonstrate the attenuation effect and the sensitivity of the functionals at different wavelengths. The results from the evaluation at altitude provide interesting insight into fundamental principles of spectral physical geodesy and allow for some complementary judgment of the models’ performance compared to investigations at ground level.

In Fig. 6, the RMS levels at altitude are generally much lower than those on the ellipsoid (see Fig. 4), which is due to the attenuation of gravity signals and errors with altitude. At satellite height, the three gravity functionals also show very different features. Starting with the RMS expressed in geoid heights (a), the maximum RMS for each model is already reached at about degree 30, where the slope turns into zero. For gravity disturbances (b) the maximum RMS is reached at degree 160 and for the radial gravity gradient (c) the maximum RMS seems to be reached near degree 230 (as the slope changes near this spectral band). Those findings allow the following categorization concerning the spectral sensitivity of the functionals evaluated at a satellite height of 250 km: quasi-geoid heights are most sensitive below degree 30; gravity disturbances are most sensitive below degree 160; gravity gradients are most sensitive below degree 230.

Fig. 6
figure 6

RMS values computed from the differences of selected GOCE GGFMs and the newly retrieved AUS-GGM in terms of a quasi-geoid heights \(\zeta \) in meters (left), b gravity disturbances \(T_r\) in mGal (middle) and c radial gravity gradients \(T_{rr}\) (right) 250 km above the ellipsoid (\(h=250\,\mathrm{km}\))

Full size image

Both fourth generation models show a lower RMS compared to their respective previous release in all three functionals. Looking at the lower wavelength part (below d/o 150), we see again that the DIR models are in better accordance with AUS-GGM because they contain GRACE information in this domain. Further, the interpretation has to be done carefully because the DIR models rely on a different GRACE processing (see Sect. 2) than GRACE data in AUS-GGM (see Sect. 3.3) and the RMS reflects errors in both data sets and/or strategies. However, in all three functionals a clear improvement of the (pure-GOCE) TIM models in the fourth release in the lower wavelength part becomes visible. The three reasons which seem likely to account for this improvement from the third to the fourth TIM release are (1) the change from the energy-integral method (Badura 2006) to the short-arc method (Mayer-Gürr et al. 2006) in the GOCE SST processing strategy, (2) the improved L1b-processing in the gradiometry (Stummer et al. 2011), and (3) more observations (see Table 1). For the other models, we can state that DIR4 followed by DIR3 show the lowest discrepancies to AUS-GGM below d/o 150. Interestingly, in the gravity gradients, there is a sudden RMS increase at degree 55 for the DIR4 solution (solid red line in Fig. 6c), which is the spherical harmonic degree where the GRACE-GFZ (release 5) supersedes the GRACE-GRGS (release 2) solution in the combination (HPF 2013a).

Looking at the higher frequency part of the spectrum (beyond degree 150), where AUS-GGM in Australia solely consists of terrestrial data, we see that the RMS values in the quasi-geoid heights and gravity disturbances are at almost constant level and biased mainly due to the differences in the lower frequency part of the spectrum (as stated above the RMS is cumulative, see Sect. 3.5). Those functionals do hardly (gravity disturbances) or not at all (height anomalies) show sensitivity in the spectral domain above d/o 150. The only functional at GOCE altitude that sufficiently allows for discrimination of the GGFM performance at shorter scales are gravity gradients. This sensitivity shown for \(T_{rr}\) at GOCE altitude is the very reason for applying gravity gradiometry on-board of GOCE satellite. From the slope of the gravity gradients (beyond degree 150), DIR4 and TIM4 are comparable (same RMS increase per degree) and better (lower RMS increase per degree) than their predecessors. Expressed numerically [calculated from gravity disturbance RMS values retrieved at degree 200 (see Table 3)] the relative improvement by the fourth release models at GOCE altitude is 32 and 36.5 % for the DIR- and TIM-approach, respectively. The relative improvement based on the radial gravity gradient RMS at d/o 200 is 36 % by DIR4 and 25 % by TIM4. Interestingly, in terms of the radial gravity gradient at GOCE altitude, TIM4 for the first time shows a lower RMS than DIR4 in the spectral range between degree 130 and degree 250.

Table 3 RMS error of GOCE GGFMs w.r.t. AUS-GGM at the spatial scale of 100 km half wavelength (\(=\) degree 200) at GOCE altitude (\(h=250\) km)
Full size table

The estimated formal error in the radial gravity gradient component \(T_{rr}\) at GOCE altitude at degree 200 is around 0.4 mE and 0.35 mE for TIM3 and TIM4, respectively. Those values are exceeded by the calculated AUS-GGM RMS by 0.36 mE and 0.2 mE (cf. Table 3), respectively.

4.3 Discussion on the linkage between the RMS and the Meissl scheme

The Meissl scheme (Rummel and van Gelderen 1995) establishes the relations between the disturbing potential \(T\), its first radial derivative \(T_r\), and its second radial derivative \(T_{rr}\) at ground level \(R\) and at altitude \((R+h)\) by means of eigenvalues in the spectral domain. It is, e.g., useful to evaluate the design of future gravity missions. Likewise, it can be used to explain the spectral behavior of the RMS of the three functionals on ground level and at satellite height (see Figs. 4, 6), because it is guide for the spectral characteristics of physical geodesy. The main reason for its applicability to RMS values is that it does not only apply to the gravity signal, but also to the associated error of derived gravity quantities.

Our evaluations demonstrate different spectral sensitivity in the RMS relying on different functionals. We can categorize the functionals evaluated at a satellite height of 250 km regarding their sensitivity in the following way: quasi-geoid heights are most sensitive below degree 30; gravity disturbances are most sensitive below degree 160; gravity gradients are most sensitive below degree 230. This is due to the fact that the higher part of the spectrum is amplified from the “smoother” to the “rougher” gravity functionals (from left to right in Figs. 4 and 6). This categorization cannot be observed for the RMS values at ground level in the same way. However, quasi-geoid heights are the most sensitive functional in the spectral bands below d/o 50 on the ellipsoid. Further, we find the RMS values at altitude to be smaller, which is due to the increasing attenuation of the signal (and of the error) with increasing distance from the attracting body.

All those features are explained by the Meissl scheme in terms of the eigenvalues (when the spherical harmonics are regarded as a set of eigenfunctions). Those eigenvalues we find one-by-one embedded in the SHS algorithms used to expand the spherical harmonic coefficients to the grids which form the basis for the RMS calculation.

5 Conclusions

We evaluated the third- and fourth-generation ESA GOCE GGFMs in spherical harmonics and placed focus on a comparison of our evaluation results with the GOCE models’ formal errors. The need for an evaluation stems from differences in the processing strategies and in the amount of GOCE data effectively being used in the latest models (DIR3, TIM3 :12 months; TIM4 : 26.5 months; DIR4 : 27.9 months). We created a spherical harmonic set of coefficients of the disturbing potential which served as an independent reference for the evaluation of GOCE-GGFMs over the landmass of Australia. We made use of the coefficient transformation method, a previously little used but suitable SHA procedure to transform high-frequency terrestrial gravity data into spectral domain. As a result, we obtain the comparison model AUS-GGM which allows the detection of improvements between the GOCE model releases and, under considerations of its inherent features and errors, can be used to make absolute error estimates. AUS-GGM proves to have significantly higher accuracy in the degrees below 120 as compared to EGM2008 and seems to be at least comparable to the accuracy of this model between degree 150 and degree 260. Based on RMS values of three different gravity functionals computed from residual gravity in Australia, we can see a significant improvement of the fourth w.r.t. the third-generation GOCE models. At the ellipsoid, TIM4 and DIR4 are found to show similar RMS values in the high frequency part of the spectrum (beyond degree 120), with the latter performing marginally better between degree 170 to degree 250 which might be linked to one additional month of GOCE gradiometer observations. Relatively, the improvement is about 23 % within the TIM approach and about 39 % within the DIR approach at a spatial scale of 100 km (at degree 200). At this resolution, the models’ official formal error expectations in terms of geoid heights is largely confirmed for TIM4 (3.2 cm), bearing in mind that the comparison data (AUS-GGM) are not free of error. The official DIR4 error estimate of 1 cm (HPF 2013a) cannot be confirmed, but the error seems to be lower than that of TIM4. In terms of gravity disturbances, our RMS of 1.3 mGal for TIM4 (1.2 mGal for DIR4) at degree 200 indicates that also the respective TIM4 error estimate of 0.9 mGal is quite realistic. Our results can hardly affirm the formal cumulative error of 0.35 mGal (own calculation) of DIR4 at degree 200, even when considering that AUS-GGM is not without errors at those spatial scales.

With the Meissl scheme in hand, signal attenuation and spectral sensitivity of the different functionals at different altitude can be explained and the RMS at the six different domains of the Meissl scheme help to get a more complete insight into the composition and features of the models. For example, gravity disturbances at satellite altitude clearly demonstrate the improvements of DIR4 and TIM4 in the spectral domain below 150, as compared to the release 3 models. The improvements generally result from a longer period of GOCE observations and changes in the processing strategy of both models. In the fourth DIR release, now, the second CNES/GRGS GRACE solution only finds application in the very low degrees (up to d/o 54) and is then superseded by the fifth GFZ GRACE solution. Additionally, the GRACE solutions within DIR4 are based on more data equivalent to 2.5 years of observations. In the fourth TIM release, the change from the energy integral approach to the short-arc integral method in the SST processing explains a large part of the improvement in the long wavelength part of the spectrum. Further, both TIM4 and DIR4 benefit from a new L1b-processing procedure for GOCE gradients.

From our evaluations, we conclude that with the fourth-generation GOCE models a better knowledge of the Earth’s gravity field in poorly surveyed areas (e.g. parts of South America, Africa, and Asia) at spatial scales of 80 km up to 120 km is to be expected.