On the skewness of order statistics in multiple-outlier PHR models

Abstract

In this paper, we investigate the skewness of order statistics stemming from multiple-outlier proportional hazard rates samples in the sense of several variability orderings such as the star order, Lorenz order and dispersive order. It is shown that the more heterogeneity among the multiple-outlier components will lead to a more skewed lifetime of a k-out-of-n system consisting of these components. The results established here generalize the corresponding ones in Kochar and Xu (J Appl Probab 48:271–284, 2011, Ann Oper Res 212:127–138, 2014). Some numerical examples are also provided to illustrate the theoretical results.

1 Introduction

Order statistics play an important role in many areas such as reliability, data analysis, goodness-of-fit tests, outliers, robustness and quality control. Let $X_1,\ldots ,X_n$ be independent random variables having possibly different distributions. Denote by $X_{1:n}\le \cdots \le X_{n:n}$ the order statistics arising from $X_i$’s, $i=1,\ldots ,n$. In the reliability context, it is well known that $X_{k:n}$ denotes the lifetime of a $(n-k+1)$-out-of-n system, and $X_{n:n}$ and $X_{1:n}$, respectively, denote the lifetimes of two particular systems called parallel and series systems. For the applications of order statistics in reliability, one may refer to Barlow and Proschan (1981) and Balakrishnan and Balakrishnan and Rao (1998a, b).

Because of the nice mathematical form and the unique memoryless property, the exponential distribution has widely been used in many fields including reliability analysis. One may refer to Balakrishnan and Basu (1995), for an encyclopedic treatment to developments on the exponential distribution. Pledger and Proschan (1971), for the first time, studied the ordering properties of the order statistics arising from two sets of heterogeneous exponential samples. After that, many researchers devoted themselves to conducting the comparisons on the order statistics from different aspects. For more details, the readers are referred to Proschan and Sethuraman (1976), Kochar (1996), Khaledi and Kochar (2000), Lillo et al. (2001), Pǎltǎnea (2008), Zhao et al. (2009), Balakrishnan and Zhao (2013), Torrado and Lillo (2013) and the references therein.

In addition to measuring the length of lifetimes of k-out-of-n system in the sense of magnitude stochastic orders, it would be also great interest of evaluating the degree of variation of lifetimes. For instance, the star and Lorenz orders (formal definitions of various stochastic orders will be given in Sect. 2), which have also been widely used in insurance, reliability theory and economics, serves as very useful tools for comparing variability between two distributions. Let $X_i$’s be independent exponential random variables with hazard rates $\lambda _{1}$ for $i=1,\ldots ,p$, and $\lambda _{2}$ for $i=p+1,\ldots ,n$, respectively, and let $X_i^{*}$’s be independent exponential random variables with hazard rates $\lambda _{1}^{*}$ for $i=1,\ldots ,p$, and $\lambda _{2}^{*}$ for $i=p+1,\ldots ,n$, respectively. Kochar and Xu (2011) showed that

$$\begin{aligned} \frac{\lambda _{(2)}}{\lambda _{(1)}}\ge \frac{\lambda ^{*}_{(2)}}{\lambda ^{*}_{(1)}}\Longrightarrow X_{k:n}\ge _{\star }X_{k:n}^*, \end{aligned}$$

(1)

where ‘$\ge _{\star }$’ denotes the star order, $\lambda _{(1)}=\min \{\lambda _{1},\lambda _{2}\}$ and $\lambda _{(2)}=\max \{\lambda _{1},\lambda _{2}\}$. In this regard, Da et al. (2014) proved that, without any restriction on the parameters, the variability of order statistics from heterogeneous exponential samples is always larger than that from homogeneous exponential samples in the sense of the Lorenz order.

Independent random variables $X_1,\ldots , X_n$ are said to follow proportional hazard rates (PHR) model if, for $i = 1,\ldots ,n$, the survival function of $X_i$ can be written as ${\overline{F}}_i(x)=[ {\overline{F}}(x)]^{\lambda _{i}}$, where ${\overline{F}}(x)$ is the survival function of some underlying random variable X. Let ${r(\cdot )}$ be the hazard rate function of the baseline distribution F. Then, the survival function of $X_i$ can be written as

$$\begin{aligned} {\overline{F}}_i(x) = e^{-\lambda _{i}R(x)} \end{aligned}$$

for $i = 1,\ldots ,n$, where $R(x) =\int _{0}^{x}r(t)\mathrm {d}t$ is the cumulative hazard rate function of X. Many well-known models are special cases of the PHR model such as exponential, Weibull, Pareto, and Lomax et al. In many situations, the results established for exponential case can be generalized to the PHR model. However, the result in (1) cannot be extended to the PHR case directly due to the fact that the scale invariant property of the star order fails to be used for the PHR model. Motivated by this, we would like to find some sufficient conditions for the star order to hold under the PHR framework. It is worth mentioning here that Kochar and Xu (2014) showed that, under some mild conditions, the largest order statistics from heterogeneous PHR samples is larger than that from the homogeneous PHR samples according to the star order. Besides, they also obtained a general result stating that the k-th order statistics from multiple-outlier PHR samples is more skewed than that from the homogeneous PHR samples in the sense of the star order under the assumption that the common hazard rate for the homogeneous sample is greater than the geometric mean of the hazard rates in the multiple-outlier PHR samples.

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$, where $p\ge 1, p+q=n\ge 2$ and the entries of both $\mathbf{1}_p$ and $\mathbf{1}_q$ are all ones. Let $X_1^*,\ldots ,X_n^*$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$. Denote by $X_{k:n}(p,q)$ and $X_{k:n}^*(p,q)$ the corresponding k-th order statistics arising from the two sets of multiple-outlier PHR models, respectively. In this paper, we prove that, under a mild condition on the baseline distribution function,

$$\begin{aligned} (\lambda _1,\lambda _2)\mathop {\succeq }\limits ^\mathrm{w} (\lambda ^*_1,\lambda ^*_2) \Longrightarrow X_{k:n}(p,q)\ge _{\star } X_{k:n}^*(p,q) \end{aligned}$$

and

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)\mathop {\succeq }\limits ^\mathrm{w}(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)\Longrightarrow X_{k:n}(p,q)\ge _{\star } X_{k:n}^*(p,q). \end{aligned}$$

Besides, a weaker condition is also given for comparing the largest order statistics by means of the star order, that is

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{p} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{n:n}(p,q)\ge _{\star } X_{n:n}^*(p,q). \end{aligned}$$

We also present an interesting result for the k-th order statistics in terms of the dispersive order

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{m} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{k:n}(p,q)\ge _\mathrm{disp} X_{k:n}^*(p,q). \end{aligned}$$

The remainder of the paper is organized as follows. Section 2 introduces some pertinent definitions of stochastic orders and majorization orders. The main results are given in Sect. 3. Section 4 presents some discussions concluding this paper.

2 Preliminaries

Throughout this paper, increasing and decreasing mean nondecreasing and nonincreasing, respectively, and let $\mathfrak {R}=(-\infty ,+\infty )$ and $\mathfrak {R}^{+}=[0,+\infty )$. Before proceeding to the main results, we will review some notions used in the sequel.

Definition 2.1

Let X and Y be two absolute continuous random variables with distribution functions F and G; survival functions $\overline{F}$ and $\overline{G}$; and density functions f and g; respectively.

• X is said to be larger than Y in the usual stochastic order (denoted by $X\ge _{st} Y$) if $\overline{F}(x) \ge \overline{G}(x)$ for all x.

• X is said to be larger than Y in the dispersive order (denoted by $X\ge _{disp} Y$) if

  $$\begin{aligned} F^{-1}(v)-F^{-1}(u)\ge G^{-1}(v)-G^{-1}(u), \end{aligned}$$

  for $0\le u\le v\le 1$, where $F^{-1}$ and $G^{-1}$ are the right continuous inverses of the distribution functions F and G of X and Y, respectively.

• X is said to be larger than Y in the star order (denoted by $X\ge _{\star }Y$) if $F^{-1}[G(x)]$ is star-shaped in the sense that $F^{-1}[G(x)]/x$ is increasing in x on the support of X, where $F^{-1}$ is the right continuous inverse of the distribution function F of X.

• X is said to be larger than Y in the Lorenz order (denoted by $X\ge _\mathrm{Lorenz}Y$) if $L_X(p)\le L_Y(p)$ for all $p\in [0,1]$, where the Lorenz curve $L_X$, corresponding to X, is defined as

  $$\begin{aligned} L_X(p)=\frac{\int _0^{p}F^{-1}(u)\mathrm {d}u}{\mu _X}, \end{aligned}$$

  and $\mu _X$ is the mean of X.

The star order is also called the more IFRA (increasing failure rate in average) in reliability theory and is one of the partial orders which are scale invariant. The Lorenz order can be used in economics to measure the inequality of incomes. It is known that

$$\begin{aligned} X\ge _{\star } Y\Longrightarrow X\ge _\mathrm{Lorenz}Y \Longrightarrow CV(X)\ge CV(Y), \end{aligned}$$

where $CV(X)=\sqrt{Var(X)}/E(X)$ denotes the coefficient of variation of X. For more details, one may refer to Shaked and Shanthikumar (2007).

One of the useful tools in deriving various inequalities in statistics and probability is the notion of majorization.

Definition 2.2

Let $x_{(1)}\le \cdots \le x_{(n)}$ be an increasing arrangement of the components of the vector $\mathbf{{x}}=(x_1,\ldots ,x_n)$.

• A vector $\mathbf{{x}}$ in $\mathcal {R}^{n}$ is said to be majorize the vector $\mathbf{{y}}$ also in $\mathcal {R}^{n}$ (written $\mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{m} \mathbf{{y}}$) if $\sum _{i=1}^jx_{(i)}\le \sum _{i=1}^j y_{(i)}$ for $j=1,\ldots ,n-1$ and $\sum _{i=1}^nx_{(i)}= \sum _{i=1}^n y_{(i)}$.

• A vector $\mathbf{{x}}\in \mathcal {R}^n$ is said to be weakly majorize another vector $\mathbf{{y}}$ also in $\mathcal {R}^{n}$ (written $\mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{w} \mathbf{{y}}$) if $\sum _{i=1}^jx_{(i)}\le \sum _{i=1}^j y_{(i)}$ for $j=1,\ldots ,n$.

• A vector $\mathbf{{x}}$ in $\mathcal {R}^{+n}$ is said to be p-larger than another vector $\mathbf{{y}}$ also in $\mathcal {R}^{+n}$ (written $\mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{p} \mathbf{{y}}$) if $\prod _{i=1}^j x_{(i)}\le \prod _{i=1}^j y_{(i)}$, for $j=1,\ldots ,n$.

Khaledi and Kochar (2002) showed that $\mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{m} \mathbf{{y}}$ implies $\mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{p} \mathbf{{y}}$ for $\mathbf{{x}}, \mathbf{{y}} \in \mathcal {R}^{+n}$. The converse is, however, not true. For example, $(0.2, 1, 5)\mathop {\succeq }\limits ^\mathrm{p} (1,2, 3)$, but clearly the majorization order does not hold. Also, $\mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{p} \mathbf{{y}}$ is equivalent to ${\log (\mathbf{{x}})\mathop {\succeq }\limits ^\mathrm{w} \log (\mathbf{{y}})}$ where $\log (\mathbf{{x}})$ is the vector of logarithms of the coordinates of $\mathbf{{x}}$. For any vectors $\mathbf{{x}}$ and $\mathbf{{y}}$ in $\mathcal {R}^{+n}$, the following implications always hold

$$\begin{aligned} \mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{m} \mathbf{{y}}\Longrightarrow \mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{w} \mathbf{{y}}\Longrightarrow \mathbf{{x}}\mathop {\succeq }\limits ^\mathrm{p} \mathbf{{y}}. \end{aligned}$$

Details discussions on majorization, p-larger orders, Schur-convex(concave) functions and their applications may be found in Marshall et al. (2011), Bon and Pǎltǎnea (1999), and Khaledi and Kochar (2002).

3 Main results

In this section, we will present some comparison results on order statistics arising from multiple-outlier PHR models according to the star order, Lorenz order and dispersive order.

We firstly recall the definition of permanents and introduce some useful notation, which are the key tool to proving the main results of this section. It is useful to represent the joint density functions of order statistics by using the theory of permanents when the underlying random variables are not identical. If $\mathbf{{A}}=\{a\}_{i,j}$ is an $n\times n$ matrix, then the permanent of $\mathbf{{A}}$ is defined as

$$\begin{aligned} \mathrm{Perm}\{\mathbf{{A}}\}=\sum _{\pi }\prod _{i=1}^n \{a\}_{i,\pi (i)}, \end{aligned}$$

where the summation is over all permutations $\pi =(\pi (1),\ldots , \pi (n))$ of $\{1,\ldots ,n\}$. We will denote the permanent of the $n\times n$ matrix $\begin{pmatrix} v_1,\ldots , v_n \end{pmatrix}$ by just $[v_1,\ldots , v_n]$. If $\mathbf{{v}}_1,\mathbf{{v}}_2,\ldots$ are column random vectors on $\mathcal {R}^n$, then the permanent

$$\begin{aligned} \left[ \underbrace{\mathbf{{v}}_1}_{r_1},\underbrace{\mathbf{{v}}_1}_{r_1}, \ldots \right] \end{aligned}$$

is obtained by taking $r_1$ copies of $\mathbf{{v}}_1, r_2$ copies of $\mathbf{{v}}_1$ and so on. If $r_i$ equals 1, then we omit it in the notation above. For more details on permanents, we refer the readers to Bapat and Beg (1989), and an excellent monograph by Balakrishnan (2007). Let us define for $\underline{\lambda }=(\lambda , \lambda ^*)$ and for each pair (p, q),

$$\begin{aligned} \left[ \mathbf{{F}}_{\underline{\lambda }}( x) \right] _{p,q}= \begin{pmatrix} F_{\lambda }( x)\mathbf{{1}}_p \\ F_{\lambda ^*}( x)\mathbf{{1}}_q \\ \end{pmatrix},\quad [\mathbf{{\overline{F}}}_{\underline{\lambda }} ( x)]_{p,q}=\begin{pmatrix} \overline{F}_{\lambda }(x)\mathbf{{1}}_p \\ \overline{F}_{\lambda ^*}( x)\mathbf{{1}}_q \\ \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} \left[ \mathbf{{f}}_{\underline{\lambda }}(x) \right] _{p,q}= \begin{pmatrix} f_{\lambda }( x)\mathbf{{1}}_p \\ f_{\lambda ^*}( x)\mathbf{{1}}_q \\ \end{pmatrix}, \end{aligned}$$

where $\overline{F}_{\lambda }(x)=e^{-\lambda R(x)}$ and $\overline{F}_{\lambda ^*}(x)=e^{-\lambda ^* R(x)}$.

The following two lemmas are also needed in the proof of the main results.

Lemma 3.1

(Saunders and Moran 1978, p. 429) Let $\{F_\lambda |\lambda \in R\}$ be a class of distribution functions, such that $F_\lambda$ is supported on some interval $(a, b)\subseteq (0,\infty )$ and has a density $f_\lambda$ which does not vanish on any subinterval of (a, b). Then,

$$\begin{aligned} F_\lambda \le _{\star } F_{\lambda ^*}, \quad \lambda \le \lambda ^*, \end{aligned}$$

if and only if

$$\begin{aligned} \frac{F'_\lambda (x)}{xf_\lambda (x)}\quad \hbox {is decreasing in } x, \end{aligned}$$

where $F'_\lambda$ is the derivative of $F_\lambda$ with respect to $\lambda$.

Lemma 3.2

(Zhao and Zhang 2012) For all $x\ge 0$, the function

• (i) $\frac{x}{1-e^{-x}}$ is increasing in $x\ge 0$;

• (ii) $\frac{xe^{-x}}{1-e^{-x}}$ is decreasing in $x\ge 0$.

We first present a preliminary result that will be helpful for proving the subsequent results.

Theorem 3.3

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda \mathbf{1}_q)$, and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda \mathbf{1}_q)$, where $p\ge 1$ and $p+q=n\ge 2$. If $\lambda _{1}\le \lambda _{1}^{*}\le \lambda$ and

$$\begin{aligned} \frac{R(x)}{xh(x)}~is~increasing~in~x\ge 0, \end{aligned}$$

then

$$\begin{aligned} X_{k:n}(p,q) \ge _\mathrm{\star } X^*_{k:n}(p,q). \end{aligned}$$

Proof

Assume that $b=\lambda -\lambda _{1}$ and $b^{*}=\lambda -\lambda _{1}^{*}$. It can be seen that $b\ge b^{*}$ due to $\lambda _{1}\le \lambda _{1}^{*}$. Let $f_{k,n,b}(x)$ be the density function of $F_{k,n,b}(x)$, and $F_{k,n,b}^{\prime }(x)$ be the partial derivative of $F_{k,n,b}(x)$ with respect to b. Consequently, according to Lemma 3.1, it suffices to prove that

$$\begin{aligned} \frac{F_{k,n,b}^{\prime }(x)}{xf_{k,n,b}(x)}~\hbox {is decreasing in } x \hbox { for }b\in (0,\lambda ). \end{aligned}$$

The distribution of $X_{k:n}(p,q)$ can be written as

$$\begin{aligned} F_{k,n,b}(x)=\sum _{i=k}^{n}\frac{1}{i!(n-i)!} \underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{i}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p,q}}_{n-i}, \end{aligned}$$

with its density function as

$$\begin{aligned} f_{k,n,b}(x)= & {} \frac{1}{(k-1)!(n-k)!} \underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \begin{pmatrix} f_{\lambda -b}(x)\mathbf{{1}}_{p}\\ f_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p,q}}_{n-k}. \end{aligned}$$

Note that, from the proof of Case 1 of Theorem 3.1 in Kochar and Xu (2011), we have

$$\begin{aligned} F_{k,n,b}^{\prime }(x) = -\frac{1}{(k-1)!(n-k)!} \underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \begin{pmatrix} F^{\prime }_{\lambda -b}(x)\mathbf{{1}}_{p}\\ 0 \end{pmatrix}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p,q}}_{n-k}. \end{aligned}$$

Thus, it follows that

$$\begin{aligned}&\frac{F_{k,n,b}^{\prime }(x)}{xf_{k,n,b}(x)}= -\frac{R(x)}{xh(x)}\\&\qquad \times \frac{pe^{-(\lambda -b)R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p-1,q}}_{n-k}}{p(\lambda -b)e^{-(\lambda -b)R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p-1,q}}_{n-k} +q\lambda e^{-\lambda R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p,q-1}}_{n-k}}\\&\quad = -\frac{1}{\lambda -b}\frac{R(x)}{xh(x)} \Bigg [1-\Bigg (1+\frac{p(\lambda -b)e^{-(\lambda -b)R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p-1,q}}_{n-k}}{q\lambda e^{-\lambda R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p,q-1}}_{n-k}}\Bigg )^{-1}\Bigg ], \end{aligned}$$

and it is enough to show that the function

$$\begin{aligned} \Lambda (x)=\frac{e^{-(\lambda -b)R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p-1,q}}_{n-k}}{e^{-\lambda R(x)}\underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right. }_{k-1}, \underbrace{\left. \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p,q-1}}_{n-k}}, \end{aligned}$$

is increasing in $x\in \mathfrak {R}^{+}$ for $b\in [0,\lambda )$.

By Laplace expansion along the first $k-1$ columns of the permanent, then

$$\begin{aligned} \Lambda (x)= & {} \frac{e^{-(\lambda -b)R(x)}\sum _{i\in \mathbb {I}} \begin{pmatrix} q\\ i \end{pmatrix} \begin{pmatrix} p-1\\ k-1-i \end{pmatrix} \underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{k-1-i,i}}_{k-1} \underbrace{\left[ \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p-k+i,q-i}}_{n-k}}{e^{-\lambda R(x)}\sum _{j\in \mathbb {J}} \begin{pmatrix} q-1\\ j \end{pmatrix} \begin{pmatrix} p\\ k-1-j \end{pmatrix} \underbrace{\left[ \begin{pmatrix} F_{\lambda -b}(x)\mathbf{{1}}_{p}\\ F_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{k-1-j,j}}_{k-1} \underbrace{\left[ \begin{pmatrix} \overline{F}_{\lambda -b}(x)\mathbf{{1}}_{p}\\ \overline{F}_{\lambda }(x)\mathbf{{1}}_{q} \end{pmatrix}\right] _{p-k+j+1,q-j-1}}_{n-k}}\\= & {} \frac{\sum _{i\in \mathbb {I}} \begin{pmatrix} q\\ i \end{pmatrix} \begin{pmatrix} p-1\\ k-1-i \end{pmatrix} \big (1-e^{-(\lambda -b)R(x)}\big )^{k-1-i} \big (1-e^{-\lambda R(x)}\big )^{i} e^{-(\lambda -b)R(x)(p-k+i+1)} e^{-\lambda R(x)(q-i)}}{\sum _{j\in \mathbb {J}} \begin{pmatrix} q-1\\ j \end{pmatrix} \begin{pmatrix} p\\ k-1-j \end{pmatrix} \big (1-e^{-(\lambda -b)R(x)}\big )^{k-1-j} \big (1-e^{-\lambda R(x)}\big )^{j} e^{-(\lambda -b)R(x)(p-k+j+1)} e^{-\lambda R(x)(q-j)}}\\= & {} \frac{\sum _{i\in \mathbb {I}} \begin{pmatrix} q\\ i \end{pmatrix} \begin{pmatrix} p-1\\ k-1-i \end{pmatrix}\phi ^{i}(x,b)}{\sum _{j\in \mathbb {J}} \begin{pmatrix} q-1\\ j \end{pmatrix} \begin{pmatrix} p\\ k-1-j \end{pmatrix}\phi ^{j}(x,b)}, \end{aligned}$$

where

$$\begin{aligned} \phi (x,b)=\frac{e^{\lambda R(x)}-1}{e^{(\lambda -b)R(x)}-1} \end{aligned}$$

and

$$\begin{aligned} \mathbb {I}= & {} \{i:\max \{k-p,0\}\le l\le \min \{q,k-1\}\},\\&\mathbb {J}=\{j:\max \{k-p-1,0\}\le j\le \min \{q-1,k-1\}\}. \end{aligned}$$

Then, it suffices to prove that

$$\begin{aligned} \zeta (x,l)=\sum _{i\in \mathbb {I}} \begin{pmatrix} q-l\\ i \end{pmatrix} \begin{pmatrix} p-1+l\\ k-1-i \end{pmatrix}\phi ^{i}(x,b), \end{aligned}$$

is $RR_{2}$ in $(x,l)\in \mathfrak {R}^{+}\times \{0,1\}$. Firstly, we can observe that $\phi (x,b)$ is increasing in $x\in \mathfrak {R}^{+}$ for $b\ge 0$, and hence $\phi ^{i}(x,b)$ is $TP_{2}$ in $(x,i)\in \mathfrak {R}^{+}\times \mathbb {I}$. Secondly, we can obtain that

$$\begin{aligned} \begin{pmatrix} q-l\\ i \end{pmatrix} \begin{pmatrix} p-1+l\\ k-1-i \end{pmatrix}, \end{aligned}$$

is $RR_{2}$ in $i\times l\in \mathbb {I}\times \{0,1\}$. Thus, using the basic composition formula of Karlin (1968), the required result follows. This completes the proof. $\square$

It should be pointed out that, the condition of Theorem 3.1 in Kochar and Xu (2011) is quite general, which includes many special cases. The proof of following result is quite similar to that of Theorem 3.1 in Kochar and Xu (2011) and thus we omit it.

Theorem 3.4

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$ and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$ where $p\ge 1$ and $p+q=n\ge 2$ . If

$$\begin{aligned} \frac{R(x)}{xh(x)}~is~increasing~in~x\ge 0, \end{aligned}$$

then

$$\begin{aligned} (\lambda _1,\lambda _2)\mathop {\succeq }\limits ^\mathrm{m}(\lambda ^*_1,,\lambda _2^*) \Longrightarrow X_{k:n}(p,q) \ge _\mathrm{\star } X^*_{k:n}(p,q). \end{aligned}$$

Upon using Theorems 3.3 and 3.4, we can get the following more general result. It means that for the multiple-outlier PHR model, more heterogeneity among the parameters leads to more skewed order statistics in the sense of the star order.

Theorem 3.5

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$ and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$ where $p\ge 1$ and $p+q=n\ge 2$ . If $\lambda _1\le \lambda _1^*\le \lambda _2^*\le \lambda _2$ and

$$\begin{aligned} \frac{R(x)}{xh(x)}~is~increasing~in~x\ge 0, \end{aligned}$$

then

$$\begin{aligned} (\lambda _{1},\lambda _{2})\mathop {\succeq }\limits ^\mathrm{w}(\lambda ^{*}_{1}, \lambda ^{*}_{2}) \Longrightarrow X_{k:n}(p,q) \ge _\mathrm{\star } X^*_{k:n}(p,q). \end{aligned}$$

Proof

From the definition of the weak majorization order, we have $\lambda _{1}+\lambda _{2}\le \lambda _{1}^{*}+\lambda _{2}^{*}.$ The result for the case $\lambda _{1}+\lambda _{2}=\lambda _{1}^{*}+\lambda _{2}^{*}$ follows from Theorem 3.4. For the case $\lambda _{1}+\lambda _{2}<\lambda _{1}^{*}+\lambda _{2}^{*}$, we set $\lambda _{1}^{\prime }=\lambda _{1}^{*}+\lambda _{2}^{*}-\lambda _{2}$. Therefore,

$$\begin{aligned} \lambda _{1}\le \lambda _{1}^{\prime }\le \lambda _{2}~~\mathrm{and}~~(\lambda '_{1},\lambda _{2}) \mathop {\succeq }\limits ^\mathrm{m}(\lambda _{1}^{*},\lambda _{2}^{*}).\end{aligned}$$

Now, suppose that $Z_{1}$,...,$Z_{p}$ are independent random variables with a common survival function $\overline{F}^{\lambda ^{\prime }_{1}}(x)$, and $Z_{p+1}$,...,$Z_{n}$ are another set of independent random variables with a common survival function $\overline{F}^{\lambda _{2}}(x)$. It follows from Theorem 3.4 that

$$\begin{aligned} Z_{k:n}(p,q)\ge _\mathrm{\star }X^*_{k:n}(p,q). \end{aligned}$$

Also, from Theorem 3.3 it follows that

$$\begin{aligned} X_{k:n}(p,q)\ge _\mathrm{\star }Z_{k:n}(p,q). \end{aligned}$$

Therefore, we obtain the desired result that

$$\begin{aligned}X_{k:n}(p,q)\ge _\mathrm{\star }X^*_{k:n}(p,q). \end{aligned}$$

The proof is completed. $\square$

We now provide a counterexample to illustrate that the condition $\lambda _1\le \lambda _1^*\le \lambda _2^*\le \lambda _2$ cannot be dropped out in Theorem 3.5.

Example 3.6

Set $p=q=1, \lambda _{1}=0.2, \lambda _{2}=0.6, \lambda _{1}^{*}=0.3$ and $\lambda _{2}^{*}=1.1$ in Theorem 3.5. Let $R(x)=x$, which stands for the exponential case. It is easy to check that $(\lambda _{1},\lambda _{2})\mathop {\succeq }\limits ^\mathrm{w}(\lambda ^{*}_{1},\lambda ^{*}_{2})$ but $\lambda _1\le \lambda _1^*\le \lambda _2\le \lambda _2^*$. Through some regular calculations, the coefficient of variation of $X_{2:2}(1,1)$ is 0.88712, and the coefficient of variation of $X_{2:2}^{*}(1,1)$ is 0.914357, which implies that $X_{2:2}(1,1)\ngeq _{\star }X_{2:2}^{*}(1,1)$.

The following result follows from Theorem 3.5 for the Lorenz order.

Corollary 3.7

Under the setup of Theorem 3.5, it holds that

$$\begin{aligned} (\lambda _{1},\lambda _{2})\mathop {\succeq }\limits ^\mathrm{w}(\lambda ^{*}_{1},\lambda ^{*}_{2}) \Longrightarrow X_{k:n}(p,q) \ge _\mathrm{Lorenz} X^*_{k:n}(p,q). \end{aligned}$$

Next, we will give an example to illustrate the result established in Theorem 3.5. Let X be a random variable from Lomax distribution $L(\lambda , b)$ with survival function

$$\begin{aligned} \overline{F}_{b,\lambda }(x)=\left( 1+\frac{x}{b}\right) ^{-\lambda },\quad \mathrm{for ~all}~x>0, \end{aligned}$$

where $b>0$ and $\lambda >0$ are called the scale and shape parameters, respectively. It is known that $\frac{R(x)}{xh(x)}=\frac{b+x}{x}\log (1+\frac{x}{b})$, for any $b>0$, is increasing in x [cf. Kochar and Xu 2014, Sect. 4].

Fig. 1

Density functions of $X_{2:3}(1,2)$ and $X^*_{2:3}(1,2)$

Example 3.8

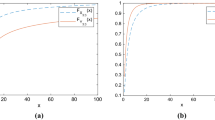
Let $(X_1,X_2,X_3)$ be independent random vector from Lomax distribution with shape parameters $(\lambda _1,\lambda _2,\lambda _2)=(3,6,6)$ and common scale parameter 1. Let $(X_1^*,X_2^*,X_3^*)$ be another set of independent Lomax random vector with shape parameters $(\lambda _1^*,\lambda _2^*,\lambda _2^*)=(4,5,5)$ and common scale parameter 1. It is easy to see that $(3,6)\mathop {\succeq }\limits ^\mathrm{w}(4,5)$ but $(3,6,6)\mathop {\nsucceq }\limits ^\mathrm{w}(4,5,5)$. Figure 1 plots the density functions of $X_{2:3}(1,2)$ and $X_{2:3}^{*}(1,2)$. Clearly, we can observe that $X_{2:3}(1,2)$ is more skewed than $X_{2:3}^{*}(1,2)$. By using Mathematica, the mean of $X_{2:3}(1,2)$ can be computed that

$$\begin{aligned} \mu =\int _0^{\infty }\overline{F}_{X_{2:3}(1,2)}(x)dx=0.1980519. \end{aligned}$$

The variance can be calculated as

$$\begin{aligned} \sigma ^2=\int _0^{\infty }2x\overline{F}_{X_{2:3}(1,2)} (x)dx-\mu ^2=0.02840779. \end{aligned}$$

Therefore the coefficient of variation $X_{2:3}(1,2)$ is

$$\begin{aligned} CV[X_{2:3}(1,2)]=\frac{\sigma }{\mu }=0.8510199. \end{aligned}$$

Similarly, it is easy to check that the coefficient of variation $X^*_{2:3}(1,2)$ is

$$\begin{aligned} CV[X^*_{2:3}(1,2)]=0.8440755, \end{aligned}$$

which means that

$$\begin{aligned} CV[X_{2:3}(1,2)]\ge CV[X^*_{2:3}(1,2)]. \end{aligned}$$

Next, we will present another sufficient condition on the parameter vectors which ensures the star order to hold for the corresponding order statistics stemming from multiple-outlier PHR models.

Lemma 3.9

(Kochar and Xu 2014) Let $\phi$ be a differentiable star-shaped function on $[0,\infty )$ such that $\phi (x)\ge x$ for all $x\ge 0$. Let $\psi$ be an increasing differentiable function such that

$$\begin{aligned} x\frac{\psi '(x)}{\psi (x)}~\hbox {is increasing in }x. \end{aligned}$$

Then, the function

$$\begin{aligned} \psi \phi \psi ^{-1}(x)~\hbox {is also star-shaped in }x. \end{aligned}$$

Theorem 3.10

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$, and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$, where $p\ge 1$ and $p+q=n\ge 2$. If

$$\begin{aligned} \frac{R(x)}{xh(x)}~is~increasing~in~x\ge 0, \end{aligned}$$

then

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{m} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{k:n}(p,q) \ge _\mathrm{\star } X^*_{k:n}(p,q). \end{aligned}$$

Proof

Since R(x) is increasing and $R^{-1}(x)= {\overline{F}}^{-1}(e^{-x})$, we have, for $x\ge 0, i=1,\ldots ,n$,

$$\begin{aligned} \mathbb {P}\left( R(X_{i})>x\right) = \mathbb {P}\left( X_{i}>R^{-1}(x))\right) = {\overline{F}}^{\lambda _{i}} ( {\overline{F}}^{-1}(e^{-x}))=e^{-\lambda _{i}x}. \end{aligned}$$

By making the transformation $X'_{i}=R(X_{i}), i=1,\ldots ,n$, we know that $X'_{i}$ is exponential with hazard rate $\lambda _{1}$ for $i=1,\ldots ,p$, and $\lambda _{2}$ for $i=p+1,\ldots ,n$. Similarly, let $Y'_{i}=R(X_{i}^{*})$ be exponential with hazard rate $\lambda _{1}^{*}$ for $i=1,\ldots ,p$, and $\lambda _{2}^{*}$ for $i=p+1,\ldots ,n$. Observe that

$$\begin{aligned} Y'_{k:n}\mathop {=}\limits ^\mathrm{st}R(X^{*}_{k:n}),~~X'_{k:n}\mathop {=}\limits ^\mathrm{st}R(X_{k:n}), \end{aligned}$$

it holds that

$$\begin{aligned} \mathbb {P}(X^{*}_{k:n}\le x)= & {} \mathbb {P}(R^{-1}(Y'_{k:n})\le x)=\mathbb {P}(Y'_{k:n}\le R(x))=G'_{k:n}(R(x)),\\ \mathbb {P}(X_{k:n}\le x)= & {} \mathbb {P}(R^{-1}(X'_{k:n})\le x)=\mathbb {P}(X'_{k:n}\le R(x))=F'_{k:n}(R(x)), \end{aligned}$$

where $G'_{k:n}(\cdot ), F'_{k:n}(\cdot )$ are distribution functions of $Y'_{k:n}$ and $X'_{k:n}$. By the definition of the star order, it suffices prove that

$$\begin{aligned} R^{-1}F'^{-1}_{k:n}G'_{k:n}R(x)~~\hbox {is star-shaped.} \end{aligned}$$

By Theorem 3.1 of Kochar and Xu (2011), $F'^{-1}_{k:n}G'_{k:n}(x)$ is star-shaped on $[0,\infty )$. According to Pledger and Proschan (1971), it follows that $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{m} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$ implies

$$\begin{aligned} F'^{-1}_{k:n}G'_{k:n}(x)\ge x. \end{aligned}$$

Based on Lemma 3.9, it is enough to show

$$\begin{aligned} x\frac{(R^{-1}(x))'}{R^{-1}(x)}~~\hbox {is increasing in }x, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \frac{R(x)}{xh(x)}~~\hbox {is increasing in }x. \end{aligned}$$

Hence, the desired result follows immediately. $\square$

We also have the following more general result and we omit the proof here because it is quite similar to that of Theorem 3.5.

Theorem 3.11

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$ and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$ where $p\ge 1$ and $p+q=n\ge 2$ . If $\lambda _1\le \lambda _1^*\le \lambda _2^*\le \lambda _2$ and

$$\begin{aligned} \frac{R(x)}{xh(x)}~is~increasing~in~x\ge 0, \end{aligned}$$

then

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{w} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{k:n}(p,q) \ge _\mathrm{{\star }} X^*_{k:n}(p,q). \end{aligned}$$

Corollary 3.12

Under the same setup of Theorem 3.11, it follows that

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{w} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{k:n}(p,q) \ge _\mathrm{Lorenz} X^*_{k:n}(p,q). \end{aligned}$$

Now, we will provide a numerical example to illustrate the result established in Theorem 3.11. Let X be a random variable from Pareto distribution $Pa(\lambda , b)$ with survival function

$$\begin{aligned} \overline{F}_{b,\lambda }(x)=\left( \frac{b}{x}\right) ^\lambda ,~\mathrm{for~all}~x\ge b>0, \end{aligned}$$

where $b>0$ and $\lambda >0$ are called the scale and shape parameters, respectively. It is known that $\frac{R(x)}{xh(x)}=\log (\frac{x}{b}), x\ge b>0$, is increasing in x [cf. Kochar and Xu (2014), Sect. 4].

Fig. 2

Density functions of $X_{4:5}(3,2)$ and $X^*_{4:5}(3,2)$

Example 3.13

Let $(X_1,X_2,X_3,X_4,X_5)$ be independent random vector from Pareto distribution with shape parameters $(\lambda _1,\lambda _1,\lambda _1,\lambda _2,\lambda _2)=(3,3,3,6.2,6.2)$ and common scale parameter 1. Let $(X_1^*,X_2^*,X_3^*,X_4^*,X_5^*)$ be another independent Pareto random vector with shape parameters $(\lambda _1^*,\lambda _1^*,\lambda _1^*,\lambda _2^*,\lambda _2^*) =(4,4,4,5,5)$ and common scale parameter 1. It is easy to see that $(3,3,3,6.2,6.2)\mathop {\succeq }\limits ^\mathrm{w}(4,4,4,5,5)$ but $(3,6.2)\mathop {\nsucceq }\limits ^\mathrm{w}(4,5)$. Figure 2 plots the density functions of $X_{4:5}(3,2)$ and $X_{4:5}^{*}(3,2)$. Clearly, we can observe that $X_{4:5}(3,2)$ is more skewed than $X_{4:5}^{*}(3,2)$. By using Mathematica, the mean of $X_{4:5}(3,2)$ can be computed that

$$\begin{aligned} \mu =\int _1^{\infty }xf_{X_{4:5}(3,2)}(x)dx=1.42503. \end{aligned}$$

The variance can be calculated as

$$\begin{aligned} \sigma ^2=\int _1^{\infty }x^{2}f_{X_{4:5}(3,2)}(x)dx-\mu ^2=0.102654. \end{aligned}$$

Therefore the coefficient of variation $X_{4:5}(3,2)$ is

$$\begin{aligned} CV[X_{4:5}(3,2)]=\frac{\sigma }{\mu }=0.224835. \end{aligned}$$

Similarly, it is easy to check that the coefficient of variation $X^*_{4:5}(3,2)$ is given by

$$\begin{aligned} CV[X^*_{4:5}(3,2)]=0.1757558, \end{aligned}$$

which means that

$$\begin{aligned} CV[X_{4:5}(3,2)]\ge CV[X^*_{4:5}(3,2)]. \end{aligned}$$

Next, a result for the dispersive order is presented when the parameter vectors majorize each other.

Theorem 3.14

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$, and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$, where $p\ge 1$ and $p+q=n\ge 2$. If

$$\begin{aligned} \frac{R(x)}{xh(x)}~is~increasing~in~x\ge 0, \end{aligned}$$

then

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{m} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{k:n}(p,q)\ge _\mathrm{disp} X_{k:n}^*(p,q). \end{aligned}$$

Proof

From Pledger and Proschan (1971), it follows that $X_{k:n}(p,q)\ge _\mathrm{st} X_{k:n}^*(p,q)$. On the other hand, for two continuous random X and Y, if $X \le _{\star }Y$ , then $X \le _\mathrm{st} Y \Rightarrow X \le _\mathrm{disp}Y$ (see Ahmed et al. 1986). We now can conclude that, $X_{k:n}(p,q)\ge _\mathrm{disp} X_{k:n}^*(p,q)$. $\square$

In the next theorem, we partially improve the result in Theorem 3.11 for the case of $k=n$.

Theorem 3.15

Let $X_1,\ldots ,X_n$ be independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)$, and let $X^*_1,\ldots ,X^*_n$ be another set of independent random variables following the multiple-outlier PHR model with parameters $(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q)$, where $p\ge 1$ and $p+q=n\ge 2$. If $\lambda _1\le \lambda _1^*\le \lambda _2^*\le \lambda _2$ and

$$\begin{aligned} \frac{R(x)}{xh(x)}~\hbox {is increasing in }x\ge 0, \end{aligned}$$

then

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{p} (\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{n:n}(p,q)\ge _{\star } X_{n:n}^*(p,q). \end{aligned}$$

Proof

The proof is proceeded by dividing into the following two cases.

Case 1 ${\lambda _1^p\lambda _2^q=(\lambda ^*_1)^p(\lambda ^*_2)^q}$. Denote $t_1=\log \lambda _1, t_2=\log \lambda _2, t_1^*=\log \lambda _1^*$ and $t_2^*=\log \lambda _2^*$. From the assumption, we observe that $t_1\le t_1^*\le t_2^*\le t_2$. Then from these observations, it can be seen that $(t_1\mathbf{1}_p,t_2\mathbf{1}_q) \mathop {\succeq }\limits ^\mathrm{m}(t^*_1\mathbf{1}_p,t_2^*\mathbf{1}_q)$. Therefore, without loss of generality, let $pt_1+qt_2=pt_1^*+qt_2^*=1$. Now, we set $t_2=t$ and $t_2^*=t^*$. Thus, it can be seen that $t\ge t^*$ and $t_1=\frac{1-qt}{p}\le t$. Let $f_{t, n:n}(x)$ be the density function of $F_{t, n:n}(x)$, and $F_{t, n:n}^{\prime }(x)$ be the partial derivative of $F_{t, n:n}(x)$ with respect to t. According to Lemma 3.1, it is enough to show that

$$\begin{aligned} \frac{F'_{t, n:n}(x)}{xf_{t, n:n}(x)}\quad \hbox {is decreasing in } x\; \hbox { for}\; t\in \left[ \frac{1}{p+q},\frac{1}{q}\right) . \end{aligned}$$

The distribution function $X_{n:n}(p,q)$ can be written as

$$\begin{aligned} F_{t,n:n}(x)= & {} [1-e^{-e^{\frac{1-qt}{p}} R(x)}]^p[1-e^{-e^{t} R(x)}]^q\\= & {} [1-e^{-\xi (t) R(x)}]^p[1-e^{-e^t R(x)}]^q, \end{aligned}$$

where $\xi (t)=e^{\frac{1-qt}{p}}$, and the density function $X_{n:n}(p,q)$ also is given by

$$\begin{aligned}&f_{t,n:n}(x)\\&\quad =h(x)[1-e^{-\xi (t) R(x)}]^p[1-e^{-e^t R(x)}]^q \left[ p\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}+q\frac{e^t e^{-e^t R(x)}}{1-e^{-e^t R(x)}}\right] . \end{aligned}$$

Taking the derivative of $F_{t, n:n}(x)$ with respect to t leads to

$$\begin{aligned}&F'_{t,n:n}(x)\\&\quad =R(x)[1-e^{-\xi (t) R(x)}]^p[1-e^{-e^t R(x)}]^q\left[ \frac{-q\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}+\frac{ qe^te^{-e^t R(x)}}{1-e^{-e^t R(x)}}\right] . \end{aligned}$$

By using the above observations, it follows that

$$\begin{aligned} -\frac{F'_{t, n:n}(x)}{xf_{t, n:n}(x)}=\frac{qR(x)}{ xh(x)}.\frac{\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}-\frac{ e^te^{-e^t R(x)}}{1-e^{-e^t R(x)}}}{p\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}+q\frac{e^t e^{-e^t R(x)}}{1-e^{-e^t R(x)}}}. \end{aligned}$$

(2)

Therefore, it is enough to show that the ratio function (2) is increasing in x. Note that, from Lemma 3.2 and the fact that $\xi (t)\le e^t$, it can be seen that the second part of (2) is positive. Since $\frac{R(x)}{xh(x)}$ is increasing in x, it is enough to prove that the positive function

$$\begin{aligned} \phi (x)= & {} \frac{\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}-\frac{ e^te^{-e^t R(x)}}{1-e^{-e^t R(x)}}}{p\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}+q\frac{e^t e^{-e^t R(x)}}{1-e^{-e^t R(x)}}}\\= & {} \frac{\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}} [\frac{ e^te^{-e^t R(x)}}{1-e^{-e^t R(x)}}]^{-1}-1}{p\frac{\xi (t) e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}[\frac{ e^te^{-e^t R(x)}}{1-e^{-e^t R(x)}}]^{-1}+q}\\= & {} \frac{\Lambda _2(x)-1}{p\Lambda _2(x)+q} \end{aligned}$$

is increasing in x, where $\Lambda _2(x)=\frac{\xi (t)e^{-\xi (t) R(x)}}{1-e^{-\xi (t) R(x)}}[\frac{ e^te^{-e^t R(x)}}{1-e^{-e^t R(x)}}]^{-1}$. We observe that last equation is increasing in x if and only if $\Lambda _2(x)$ is increasing in x. Taking derivative of $\Lambda _2(x)$ with respect to x, we have

Now, assume that $\xi (t)R(x)=y_1$ and $e^t R(x)=y_2$. Since $0\le \xi (t)\le e^t$, we have $0\le y_1\le y_2$. So, it follows that

$$\begin{aligned} \frac{\Lambda '_2(x)}{R(x)}\equiv \frac{-y_1}{1-e^{-y_1}}+\frac{y_2 }{1-e^{-y_2}}\ge 0, \end{aligned}$$

where the above inequality follows from Lemma 3.2. This completes the proof of the Case 1.

Case 2 ${\lambda _1^p\lambda _2^q<(\lambda ^*_1)^p(\lambda ^*_2)^q}$. In this case, there exists some $\theta$ such that $\lambda _1\le \theta$ and $\theta ^p\lambda _2^q=(\lambda ^*_1)^p(\lambda ^*_2)^q$. Without loss of generality, assume $\theta \le \lambda _2$ and $\lambda _1^*\le \lambda _2^*$. As a result, we find that it is enough to prove the result under the following condition:

$$\begin{aligned} \theta \le \lambda _2 \quad \hbox {and}\quad \theta ^p\lambda _2^q=(\lambda ^*_1)^p(\lambda ^*_2)^q. \end{aligned}$$

Now, let $Z_1,\ldots ,Z_n$ be independent random variables from PHR model with $Z_i, i=1,\ldots ,p$ having common parameters $(\theta _1\mathbf{1}_p)$ and $Z_i, i=p+1,\ldots ,n$ having common parameters $(\lambda _2\mathbf{1}_q)$ where $p\ge 1$ and $p+q=n\ge 2$. By using the result of Case 1, it follows that

$$\begin{aligned} Z_{n:n}(p,q)\ge _{\star }X_{n:n}^*(p,q). \end{aligned}$$

(3)

Next, from the assumption, we observe that $\lambda _2\ge \theta \ge \lambda _1$, and it is enough to prove that $X_{n:n}(p,q)\ge _{\star }Z_{n:n}(p,q)$. Using Theorem 3.3, we have

$$\begin{aligned} X_{n:n}(p,q)\ge _{\star }Z_{n:n}(p,q). \end{aligned}$$

(4)

Combining (3) and (4) we reach the desired result that $X_{n:n}(p,q)\ge _{\star }X^*_{n:n}(p,q)$. This completes the proof of the Case 2. $\square$

Remark 3.16

One may wonder that whether the result in Theorem 3.15 holds for the minimum order statistics. To answer this, we just imitate the proof of case 1 of Theorem 3.15. Let $t_{1}=t$ and $t_{1}^{*}=t^{*}$ in case 1. Then, we have $t\le t^{*}$. Note that, for $t\in (0,\frac{1}{p+q}]$,

$$\begin{aligned} \frac{F'_{t, 1:n}(x)}{xf_{t, 1:n}(x)}=\frac{R(x)}{xh(x)}\times \frac{p[e^{t} -e^{\frac{1-pt}{q}}]}{qe^{t}+pe^{\frac{1-pt}{q}}} \end{aligned}$$

is decreasing in $x\in \mathfrak {R}^{+}$ for $t\in (0,\frac{1}{p+q}]$. Thus, by Lemma 3.1, it can be concluded that, under the condition $(\log \lambda _1\mathbf{1}_p,\log \lambda _2\mathbf{1}_q)\mathop {\succeq }\limits ^\mathrm{m}(\log \lambda _1^*\mathbf{1}_p,\log \lambda _2^*\mathbf{1}_q)$ and other assumptions in Theorem 3.15, $X_{1:n}(p,q)\le _{\star }X_{1:n}^{*}(p,q)$.

Since the star order implies the Lorenz order, we have the following result.

Corollary 3.17

Under the setup of Theorem 3.15, it holds that

$$\begin{aligned} (\lambda _1\mathbf{1}_p,\lambda _2\mathbf{1}_q)\mathop {\succeq }\limits ^\mathrm{p}(\lambda _1^*\mathbf{1}_p,\lambda _2^*\mathbf{1}_q) \Longrightarrow X_{n:n}(p,q)\ge _\mathrm{Lorenz} X^*_{n:n}(p,q). \end{aligned}$$

Finally, we present an example where the lifetimes of parallel systems arising from two set of independent heterogeneous Weibull random variables are compared in the terms of the star order. Let X be a random variable from Weibull distribution $W(\alpha , b)$ with survival function

$$\begin{aligned} \overline{F}_{\lambda }(x)=\exp \{-(b x)^\alpha \}, \end{aligned}$$

where b and $\alpha$ are called the scale and shape parameters, respectively. It is known that $\frac{R(x)}{xh(x)}=\frac{1}{\alpha }$, is increasing in x (cf. Kochar and Xu 2014, Sect. 4).

Fig. 3

Density functions of $X_{3:3}(2,1)$ it and $X^*_{3:3}(2,1)$

Example 3.18

Let $(X_1,X_2,X_3)$ be independent Weibull random vector with scale parameters $(b_1,b_1,b_2)=(2,2,7)$ and common shape parameter 2. Let $(X_1^*,X_2^*,X_3^*)$ be another independent Weibull random vector with scale parameters $(b_1^*,b_1^*,b_2^*)=(3,3,5)$ and common shape parameter 2. Note that, $\lambda _i=b_i^\alpha$. It is easy to see that, $(2^2,2^2,7^2)\mathop {\succeq }\limits ^\mathrm{p}(3^2,3^2,5^2)$ but $(2^2,7^2)\mathop {\nsucceq }\limits ^\mathrm{w}(3^2,5^2), (2^2,2^2,7^2)\mathop {\nsucceq }\limits ^\mathrm{w}(3^2,3^2,5^2)$. Figure 3 plots the density functions of $X_{3:3}(2,1)$ and $X^*_{3:3}(2,1)$. Therefore, it can be seen that the density function of $X_{3:3}(2,1)$ is more skewed than that of $X^*_{3:3}(2,1)$ which coincides with Theorem 3.15. Using Mathematica, the mean of $X_{3:3}(2,1)$ can be computed that

$$\begin{aligned} \mu =\int _0^{\infty }\overline{F}_{X_{3:3}(2,1)}(x)dx=0.573. \end{aligned}$$

The variance of the largest order statistics can be calculated as

$$\begin{aligned} \sigma ^2=\int _0^{\infty }2x\overline{F}_{X_{3:3}(2,1)} (x)dx-\mu ^2=0.0464. \end{aligned}$$

Therefore the coefficien of variation $X_{3:3}(2,1)$ is

$$\begin{aligned} CV[X_{3:3}(2,1)]=\frac{\sigma }{\mu }=0.376. \end{aligned}$$

Similarly, it is easy to check that the coefficient of variation $X^*_{3:3}(2,1)$ is

$$\begin{aligned} CV[X^*_{3:3}(2,1)]=0.350, \end{aligned}$$

which means that

$$\begin{aligned} CV[X_{3:3}(2,1)]\ge CV[X^*_{3:3}(2,1)]. \end{aligned}$$

4 Discussions

This work presents some new results for comparing the k-out-of-n systems consisting of multiple-outlier PHR components in the sense of the star, Lorenz and dispersive orders. It is demonstrated that the more heterogeneity among the multiple-outlier components will lead to a more skewed lifetime of the k-out-of-n system consisting of these components. Some explicit numerical examples are also provided to illustrate the established results.

Khaledi et al. (2011) have studied some ordering properties of parallel and series systems consisting of heterogeneous scale components. They provided some majorization-type sufficient conditions on the parameter vectors for the hazard rate and reversed hazard rate orders between the lifetimes of the series and parallel systems, respectively. Therefore, a generalization of the present work to the case of parallel and series systems with heterogeneous components under the scale model framework will be of interest. We are currently working on this problem and hope to report these findings in a future paper.