On local divergences between two probability measures

Abstract

A broad class of local divergences between two probability measures or between the respective probability distributions is proposed in this paper. The introduced local divergences are based on the classic Csiszár $\phi$-divergence and they provide with a pseudo-distance between two distributions on a specific area of their common domain. The range of values of the introduced class of local divergences is derived and explicit expressions of the proposed local divergences are also derived when the underlined distributions are members of the exponential family of distributions or they are described by multivariate normal models. An application is presented to illustrate the behavior of local divergences.

1 Introduction

The concept of divergence is of fundamental importance, not only in mathematics but in almost all branches of science and engineering. This concept has also a prominent role in probability theory and mathematical statistics. The Kolmogorov–Smirnov test is based, for instance, on a divergence measure between the empirical distribution function and the respective function which is specified by the null hypothesis. The classical chi-square goodness-of-fit test is based on a divergence measure between the theoretic probabilities and the expected ones. Many other statistical procedures base their origins on a divergence measure between probability distributions.

The most important attempt to define a broad class of divergence measures between two probability measures or between the respective Radon-Nikodym derivatives was made by Csiszár (1963, 1967) and independently by Ali and Silvey (1966). Following these authors, if P and Q are two probability measures on the measurable space $({\mathcal {X}},{\mathcal {A}})$ and $\mu$ is a $\sigma$-finite measure on the same measurable space, such that $P\ll \mu$ and $Q\ll \mu$, then for p and q the respective Radon-Nikodym derivatives, $p=\frac{dP}{d\mu }$ and $q=\frac{dQ}{d\mu }$, a broad class of divergence measures between P and Q, or between p and q , is defined by the following integral,

$$\begin{aligned} D_{\phi }(P,Q)=D_{\phi }(p,q)=\int \limits _{{\mathcal {X}}}\phi \left( \frac{dP}{ dQ}\right) dQ=\int \limits _{{\mathcal {X}}}q(x)\phi \left( \frac{p(x)}{q(x)} \right) d\mu (x), \end{aligned}$$

(1)

where $\phi$ is a real valued convex function, satisfying appropriate conditions (cf. Csiszár 1967). These conditions will be discussed and extended later on.

An important property of $D_{\phi }(P,Q)$ is that if $\phi$ is strictly convex at 1 with $\phi (1)=0$, then (cf. Pardo 2006, p. 9),

$$\begin{aligned} D_{\phi }(p,q)=0\text { if and only if }p(x)=q(x)\text {, a.e. }x\in {\mathcal {X}}. \end{aligned}$$

(2)

This is the reason why $D_{\phi }(P,Q)$ has been established in the literature as a measure of divergence between the probability measures P and Q, or between the respective densities p and q, and it is referred to as Csiszár $\phi$-divergence, or simply, as $\phi$-divergence. As defined, $D_{\phi }(P,Q)$ is not symmetric, but can be expressed as a symmetric measure by taking $D_{\tilde{\phi }}(P,Q)=D_{\tilde{\phi }}(Q,P)= D_{\phi }(P,Q)+D_{\phi }(Q,P),$ for the convex functions $\tilde{\phi } (u)=\phi (u)+u\phi (\frac{1}{u}), u>0$ (cf. Liese and Vajda 1987, p. 14). Moreover, $D_{\phi }(P,Q)$ is not a distance in the usual sense of a metric since it does not satisfy in general the triangular inequality. We can think of divergence measures as distances, in the same way we treat a loss function in a decision theoretic problem; It simply tells us if two probability measures are the same or not and the closer the value of $D_{\phi }$ to 0, the closer P and Q are.

Following Csiszár (1967, p. 301), $\phi$-divergence extends, in essence, the “information for discrimination” or I-divergence, introduced by Kullback and Leibler (1951) and the “information gain” or I-divergence of order $\alpha$, introduced by Rényi (1960). The Kullback–Leibler divergence measure is obtained when the convex function $\phi$ is of the form $\phi (x)=x\log x$ or $\phi (x)=x\log x-x+1$, $x>0$, and Rényi’s divergence is obtained, as a function of Csiszár $\phi$-divergence, for $\phi (x)=sgn(\alpha -1)x^{\alpha }$, $x>0$ and $\alpha >0$. Other choices of the convex function $\phi$ lead to important measures of divergence (cf. Pardo 2006, p. 6, where measures of divergence are tabulated for specific choices of $\phi$). Among these measures of divergence the Cressie and Read or $\lambda$-divergence, introduced independently by Cressie and Read (1984) and Liese and Vajda (1987), plays a prominent role in the development of goodness of fit and $\lambda$-divergence tests. It is obtained from (1), for $\phi (x)=\phi _{\lambda }(x)=\frac{x^{\lambda +1}-x-\lambda (x-1)}{\lambda (\lambda +1)}, \lambda \ne 0,-1$. Kullback–Leibler divergence, $D_{0}(f,g)=\int \limits _{{\mathcal {X}}}p(x)\log \left( \frac{p(x)}{ q(x)}\right) d\mu (x)$, is the limiting case of Cressie and Read $\lambda$ -divergence, as $\lambda \rightarrow 0$, that is, $\underset{\lambda \rightarrow 0}{\lim }D_{\phi _{\lambda }}(p,q)=D_{0}(p,q)$.

After Csiszár (1963, 1967) pioneering work in the subject, a plethora of papers and books have been published. Some of them are concentrated on the characterization and the study of the properties of $\phi$-divergence, while others on generalizations of $\phi$-divergence. A large portion of this literature is concerned with applications of $\phi$-divergence to formulate and solve a great variety of problems in probability and statistics and in almost every branch of science and engineering. The books and monographs by Kullback (1959), Csiszár and Korner (1981), Liese and Vajda (1987), Vajda (1989, 1995), Pardo (2006) and Basu et al. (2011) and the review papers by Papaioannou (1986, 2001), Ullah (1996), Soofi (2000), Ebrahimi et al. (2010) and the references in these works constitute a basis of the existing literature on $\phi$-divergence measures.

The $\phi$-divergence, as it is defined by (1), quantifies the difference between the arguments P and Q, or p and q, in a domain ${\mathcal {X}}$. However, there are situations in practice where the interest is focused on the differences between two probability distributions in a subset of the domain ${\mathcal {X}}$. For example, suppose that a researcher is interested in inferring about the homogeneity or similarity of two populations, regarding a joint characteristic of their members. Consider a population of men and women and suppose that the joint characteristic under study is the level of blood cholesterol of the members of both populations. The joint characteristic of the two populations is described by two probabilistic models, one for each population, and the homogeneity or similarity of the two populations can be quantified by a divergence measure between the two probabilistic models (densities) which describe the populations, with values close to zero indicating equality of the two densities.

However, a divergence measure, resulting from (1) for a specific choice of $\phi$, quantifies the similarity of the populations in the whole domain. Hence, application of (1) provides a misconception about the differences of the two populations if the interest is focused on similarity in a subset of the whole domain, say, if the researcher is focused in the investigation of whether the populations of men and women exhibit the same behavior for high or low levels of blood cholesterol. A first solution to this problem can be achieved if we use a measure, based on (1), by integrating over the desired subset of ${\mathcal {X}}$, instead of the entire space ${\mathcal {X}}$. However, this option leads to intractable measures of divergence and, mainly, based on Lemma 1.1 of Csiszár (1967), they lead to measures of divergence that violate (2), which is essential in the characterization of (1) as a divergence between probability measures. A second solution could be to replace the probability distributions in (1), by the respective truncated distributions, over the desired subset of ${\mathcal {X}}$. However, this second approach is based on the divergence of the truncated models, which are not necessarily the proper models to use to describe the data under consideration. Consequently, a measure of divergence should be defined that helps overcome these problems and in addition provide an indication about the similarity of the two probability distributions in a subset of their common domain.

Based on the above discussion, the main aim of this paper is to introduce a measure of the local divergence between two probability measures or probability distributions and to study its range of values. Ergo, in the next Sect. 2 local $\phi$-divergences are introduced and some numerical examples that illustrate their behavior are given. The range of values of the introduced divergences will be investigated in this section. Section 3 concentrates on explicit forms for a particular case of the local $\phi$ -divergence between members of the exponential family of distributions. The case of multivariate normal distributions will also be considered. An application is presented in Sect. 4, in order to illustrate the usefulness of the methodology introduced. Section 5 presents some concluding remarks.

2 Local $\phi$-divergence and its properties

The aim of this section is to present a measure of local divergence between two probability measures or the respective probability distributions. This measure has its origins on Csiszár $\phi$-divergence, which is defined by (1). The local $\phi$-divergence will be introduced in the next subsection, while the subsequent subsection provides with the range of values of the introduced local divergences. Special cases of local $\phi$-divergence have been studied in the past, see for example McElroy and Holan (2009) for an application of the Kullback–Leibler divergence.

2.1 Local $\phi$-divergence

Following Csiszár (1967, p. 299) and Pardo (2006, p. 5), consider the class $\Phi ^{*}$ of all real convex functions $\phi$ defined on the interval $[0,\infty )$, such that $\phi (1)=0$, $0\phi \left( \frac{0}{0} \right) =0$ and $0\phi \left( \frac{u}{0}\right) =u\underset{v\rightarrow +\infty }{\lim }\frac{\phi (v)}{v}$, where the last two conditions are necessary in order to avoid meaningless expressions in what follows. Moreover, it is assumed that $\phi$ is strictly convex at 1. It should be noted, at this point, that all the convex functions $\phi$ that lead to important particular cases of Csiszár $\phi$-divergences, like Kullback and Leibler (1951) divergence, Kagan (1963) divergence $(\phi (u)=(u-1)^{2}, u>0)$, Vajda (1973) divergence $(\phi (u)=|1-u|^{\alpha },u>0, \alpha \ge 1)$, Cressie and Read (1984) $\lambda$-power divergence, etc. satisfy all the above conditions.

Motivated by Csiszár $\phi$-divergence, given by (1), a measure of local divergence between two probability measures P and Q, or between the respective Radon-Nikodym derivatives p and q, can be defined by means of (1), if an additional function, say $A(\cdot ,\omega )$, would be inserted in Csiszár $\phi$-divergence in order to shift the mass of the integral (1) in the desired subset of ${\mathcal {X}}$. The function $A(\cdot ,\omega )$ plays the role of a kernel and in complete analogy with Csiszár divergence (1), a measure of local divergence can be defined as follows,

$$\begin{aligned} D_{\phi }^{A}(P,Q)=\int \limits _{{\mathcal {X}}}A(x,\omega )\phi \left( \frac{dP }{dQ}\right) dQ=\int \limits _{{\mathcal {X}}}A(x,\omega )q(x)\phi \left( \frac{ p(x)}{q(x)}\right) d\mu (x). \end{aligned}$$

Notice that if $A(x,\omega )=1$, then $D_{\phi }^{1}(P,Q)=D_{\phi }(P,Q)$. The introduction of the kernel $A(x,\omega )$ weighs differently the distance between P and Q providing the ability to focus on specific areas of the domain ${\mathcal {X}}$ that may be of particular interest. In practice, the kernel $A(\cdot ,\cdot )$ can be thought of as a window that can be calibrated to highlight specific features of P and Q and how they differ.

In what follows and in order to avoid problems related to the existence of the above integral, we will restrict on functions $A(x,\omega )$ which are related to a probability measure, say R, in the same measurable space $( {\mathcal {X}},{\mathcal {A}})$ and in particular, the function $A(x,\omega )$ will be considered to be the Radon-Nikodym derivative of R with respect to $\mu$, with $\mu$ a $\sigma$-finite measure on $({\mathcal {X}},{\mathcal {A}})$ . In this setting the definition of the local $\phi$-divergence is formulated as follows.

Definition 1

Let P, Q and R three probability measures on the measurable space $( {\mathcal {X}},{\mathcal {A}})$, dominated by a $\sigma$-finite measure $\mu$ which is defined on the same measurable space. Let p, q and r denote the respective Radon-Nikodym derivatives $p=\frac{dP}{d\mu }$, $q=\frac{dQ}{ d\mu }$ and $r=\frac{dR}{d\mu }$ and $\phi$ a convex function belonging to the class of convex functions $\Phi ^{*}$, defined above. Then, the local $\phi$-divergence between P and Q, driven by R, is defined by

$$\begin{aligned} D_{\phi }^{R}(P,Q)=\int \limits _{{\mathcal {X}}}\frac{dR}{d\mu }\phi \left( \frac{dP}{dQ}\right) dQ=\int \limits _{{\mathcal {X}}}r(x)q(x)\phi \left( \frac{ p(x)}{q(x)}\right) d\mu (x). \end{aligned}$$

(3)

Remark 1

(i) The definition can be modified in such a way as to be valid on a parametric family of probability measures. Consider the measurable space $( {\mathcal {X}},{\mathcal {A}})$ and let $\{P_{\theta }:\theta \in \Theta \subseteq R^{M}\}$ be a parametric family of probability measures on $({\mathcal {X}}, {\mathcal {A}})$. Let $\mu$ be a $\sigma$-finite measure on the same measurable space, such that $P_{\theta }\ll \mu$, for $\theta \in \Theta$. Denote by $f_{\theta }=\frac{dP_{\theta }}{d\mu }$, the Radon-Nikodym derivative, and consider a convex function $\phi$ belonging to the class of convex functions $\Phi ^{*}$. Further consider a probability measure $P_{\omega }\ll \mu$, $\omega \in \Theta$, on $({\mathcal {X}},{\mathcal {A}})$, with Radon-Nikodym derivative $f_{\omega }=\frac{dP_{\omega }}{d\mu }$, for $\omega \in \Theta$. The local $\phi$-divergence between two members of the class $\{P_{\theta }:\theta \in \Theta \subseteq R^{M}\}$, $P_{\theta _{1}}$ and $P_{\theta _{2}}$, or between the respective Radon-Nikodym derivatives $f_{\theta _{1}}$ and $f_{\theta _{2}}$, with kernel the function $f_{\omega }$, is defined as follows,

$$\begin{aligned} D_{\phi }^{\omega }(\theta _{1},\theta _{2})=\int \limits _{{\mathcal {X}}}\frac{ dP_{\omega }}{d\mu }\phi \left( \frac{dP_{\theta _{1}}}{dP_{\theta _{2}}} \right) dP_{\theta _{2}}=\int \limits _{{\mathcal {X}}}f_{\omega }(x)f_{\theta _{2}}(x)\phi \left( \frac{f_{\theta _{1}}(x)}{f_{\theta _{2}}(x)}\right) d\mu (x). \end{aligned}$$

(4)

The local $\phi$-divergence, as defined is a measure of divergence between two members of the above family, and is governed by another measure of the family that determines the weights and the area over which the divergence is calculated. In the latter definition, $f_{\omega }$ depends on a parameter $\omega$ that drives the window over which the integral is computed. Calculation of the measure (4) in a closed form is accomplished easier when the driving measure $P_{\omega }$ or the corresponding density $f_{\omega }$ is in the same parametric family of probability measures $\{P_{\theta }:\theta \in \Theta \subseteq R^{M}\}$, but that need not be the case in practice. Consequently, the distribution $f_{\omega }$ can be chosen in such a way in order to smooth or exemplify certain features of the area over which the integral is calculated.

(ii) If ${\mathcal {X}}$ is finite (or countable), $\mathcal {X=}\{1,2,...,n\}$, and P, Q, R are represented by the discrete probability distributions ${\mathbf {p}}=(p_{1},...,p_{n})$, ${\mathbf {q}}=(q_{1},...,q_{n})$ and $\mathbf {r} =(r_{1},...,r_{n})$, respectively, then the local $\phi$-divergence between $\mathbf {p}$ and $\mathbf {q}$, driven by $\mathbf {r}$, is defined, in view of (3), by

$$\begin{aligned} D_{\phi }^{\mathbf {r}}({\mathbf {p}},{\mathbf {q}})=\sum \limits _{i=1}^{n}r_{i}q_{i}\phi \left( \frac{p_{i}}{q_{i}}\right) . \end{aligned}$$

This last measure is known in the literature as the weighted $\phi$ -divergence and it has been studied in the papers by Landaburu and Pardo (2000, 2003), Landaburu et al. (2005) and the references therein.

(iii) An extension of the local $\phi$-divergence, defined by (3) or (4), can be obtained by a quite similar argument as that of Pardo (2006, p. 8). More precisely, if h is a differentiable increasing real function, then the local $(h,\phi )$-divergence is defined by $D_{h,\phi }^{\omega }(P,Q)=h\left( D_{\phi }^{\omega }(P,Q)\right)$. This last measure allows us to define more general measures of local divergence, for several choices of the functions h and $\phi$. However, the main reason for the above transformation of $D_{\phi }^{\omega }(P,Q)$ is that it allows us to obtain Rényi’s local divergence by means of the local $\phi$ -divergence.

(iv) In general, we cannot obtain $D_{\phi }(P,Q)$ from $D_{\phi }^{R}(P,Q)$ , unless R is, for example, a uniform measure over ${\mathcal {X}}$, in which case $D_{\phi }^{R}(P,Q)$ is a multiple of $D_{\phi }(P,Q)$. Notice that $D_{\phi }^{R}(P,Q)=D_{\phi }(P,Q)$ when $E_{q}\left[ (1-r(X))\phi \left( \frac{p(X)}{q(X)}\right) \right] =0$.

The local $\phi$-divergence, defined by (3) or (4) above, is quite similar to the one defined by (1). The only difference is the distribution function r or $f_{\omega }$ that enters into the expression of the classic Csiszár $\phi$-divergence and in particular the additional parameter $\omega \in \Theta$. The role of the parameter $\omega$ is decisive in the above definition, and exactly this role will be investigated in the following examples. In the first example normal distributions will be used in order to investigate how definition (4) actually quantifies the divergence between two normal models in a subset of their domain. In this example, we clarify the role of the parameter $\omega$ in the definition of $D_{\phi }^{\omega }$.

Example 1

Normal Distributions. Let $P_{\theta }$, $\theta \in \Theta =\left\{ (\mu ,\sigma ^{2}):\mu ,\sigma ^{2}\in R,\;\sigma ^{2}>0\right\}$ be the univariate normal distribution. For three cases of the parameter $\theta$, $\theta _{1}=(\mu _{1},\sigma _{1}^{2})$, $\theta _{2}=(\mu _{2},\sigma _{2}^{2})$ and $\omega =(\mu ,\sigma ^{2})$, denote by $f_{\theta _{1}}$, $f_{\theta _{2}}$ and $f_{\omega }$ the respective univariate normal densities. Consider Cressie and Read (1984) $\lambda$-power divergence and more specifically its local version, as it is obtained from (4), for $\phi (u)=\phi _{\lambda }(u)=\frac{u^{\lambda +1}-u-\lambda (u-1)}{\lambda (\lambda +1)},\lambda \ne 0,-1$. The explicit form of this local divergence $D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})$ between $f_{\theta _{1}}$ and $f_{\theta _{2}}$, driven by $f_{\omega }$, is given by the following expression,

$$\begin{aligned} D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})=\frac{1}{\lambda (\lambda +1)}\left\{ K_{\lambda ,\omega }(\theta _{1},\theta _{2})-(\lambda +1)E_{f_{\theta _{1}}}\left[ f_{\omega }(X)\right] +\lambda E_{f_{\theta _{2}}}\left[ f_{\omega }(X)\right] \right\} , \end{aligned}$$

(5)

where

$$\begin{aligned} K_{\lambda ,\omega }(\theta _{1},\theta _{2})= & {} \int _{{\mathcal {X}}}f_{\omega }(x)f_{\theta _{1}}^{\lambda +1}(x)f_{\theta _{2}}^{-\lambda }(x)d\mu (x) \\= & {} \frac{(2\pi )^{-1/2}\sigma _{1}^{-\lambda }\sigma _{2}^{\lambda +1}}{ \left( \sigma _{1}^{2}\sigma _{2}^{2}+(\lambda +1)\sigma ^{2}\sigma _{2}^{2}-\lambda \sigma ^{2}\sigma _{1}^{2}\right) ^{1/2}}\exp \left\{ - \frac{1}{2}\left( B_{1}+B_{2}\right) \right\} , \end{aligned}$$

with

$$\begin{aligned} B_{1}=-\frac{\lambda (\lambda +1)\left( \mu _{1}-\mu _{2}\right) ^{2}}{ (\lambda +1)\sigma _{2}^{2}-\lambda \sigma _{1}^{2}}\text { , }B_{2}=\left( \mu -\widetilde{\mu }\right) ^{2}\frac{(\lambda +1)\sigma _{2}^{2}-\lambda \sigma _{1}^{2}}{\sigma _{1}^{2}\sigma _{2}^{2}+(\lambda +1)\sigma ^{2}\sigma _{2}^{2}-\lambda \sigma ^{2}\sigma _{1}^{2}}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{\mu }=\frac{(\lambda +1)\mu _{1}\sigma _{2}^{2}-\lambda \mu _{2}\sigma _{1}^{2}}{(\lambda +1)\sigma _{2}^{2}-\lambda \sigma _{1}^{2}}. \end{aligned}$$

Moreover,

$$\begin{aligned} E_{f_{\theta _{i}}}\left[ f_{\omega }(X)\right] =\left( 2\pi (\sigma ^{2}+\sigma _{i}^{2})\right) ^{-1/2}\exp \left\{ -\frac{\left( \mu -\mu _{i}\right) ^{2}}{2(\sigma ^{2}+\sigma _{i}^{2})}\right\} \text {, }i=1,2. \end{aligned}$$

The aforementioned expressions can be obtained as particular cases of the local $\phi$-divergence between members of the exponential family of distributions, which will be obtained in a subsequent section. Using (5), we present $D_{\phi _{2/3}}^{\omega }(\theta _{1},\theta _{2})$, $D_{\phi _{2/3}}^{\omega }(\theta _{2},\theta _{1})$ and the symmetric version $D_{\phi _{2/3}}^{\omega }(\theta _{1},\theta _{2})$ $+D_{\phi _{2/3}}^{\omega }(\theta _{2},\theta _{1}),$ for $\theta _{1}=(0,1)$, $\theta _{2}=(0,2)$ and several values of the parameter $\omega =(\mu ,\sigma ^{2})$, in Table 1. We concentrate on the value $\lambda =2/3$ because this choice for the power $\lambda$ is considered ideal in many statistical applications of the classic Cressie and Read power divergence, which is obtained from (1). Table 1 also includes the classic Cressie and Read power divergence $D_{\phi _{2/3}}(\theta _{1},\theta _{2})=\int _{ {\mathcal {X}}}f_{\theta _{2}}(x)\phi _{2/3}\left( \frac{f_{\theta _{1}}(x)}{ f_{\theta _{2}}(x)}\right) d\mu (x)$ and values of the integral

$$\begin{aligned} I_{i,j}=\int \limits _{{\mathcal {X}}}I_{A}(x)f_{\theta _{j}}(x)\phi _{2/3}\left( \frac{f_{\theta _{i}}(x)}{f_{\theta _{j}}(x)}\right) d\mu (x),\; i,j=1,2,\;i\ne j, \end{aligned}$$

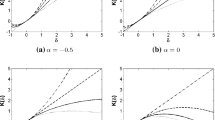
which is, in essence, Csiszár classic $\phi$-divergence, restricted to the set $A\subseteq {\mathcal {X}}$. Based on this table, the Cressie and Read $\lambda$-divergence between two univariate normal models, N(0, 1) and N(0, 2), is equal to $D_{\phi _{2/3}}(\theta _{1},\theta _{2})=0.082$ on the whole domain ${\mathcal {X}}=R.$ Its value is significantly reduced if the interest is focused on specific subsets $A=(\alpha ,\beta )$ of ${\mathcal {X}}$, as it is quantified by the integral $I_{i,j}$. This exemplifies the role of the density $f_{\omega }$, in (3), and more specifically the role of the parameter $\omega$ which adjusts the subset of ${\mathcal {X}}$ over which the divergence between the normal models, N(0, 1) and N(0, 2) is evaluated. Notice that when we focus on the tails (outside the interval $[-5,5])$ of the distributions the more similar the two densities become, as shown in Fig. 1. The choice of $\lambda$ is of great importance, and some measures will not be able to adequately capture the divergence between two distributions.

Table 1 Values of $D_{\phi _{2/3}}(\theta _{1},\theta _{2}), D_{\phi _{2/3}}(\theta _{2},\theta _{1}), \ D_{\phi _{2/3}}^{\omega }(\theta _{1}, \theta _{2}), D_{\phi _{2/3}}^{\omega }(\theta _{2},\theta _{1}), \ D_{\phi _{2/3}}^{\omega }(\theta _{1},\theta _{2})+D_{\phi _{2/3}}^{ \omega }(\theta _{2},\theta _{1}), I_{1,2}, I_{2,1}$ and $\ I_{1,2}+I_{2,1}$ for normal distributions with parameters $\theta _{1}=(\mu _{1},\sigma _{1}^{2})=(0,1)$, $\theta _{2}=(\mu _{2},\sigma _{2}^{2})=(0,2)$ and several values of $\omega =(\mu ,\sigma ^{2})$

Fig. 1

Plot for normal distributions with parameters $\theta _{1}=(0,1)$ and $\theta _{2}=(0,2)$

The next example examines the behavior of the local $\phi$-divergence when the symmetric normal models are replaced by skewed models and more specifically by skew normal models.

Example 2

Skew Normal Distributions. Consider the standard skew-normal model with parameter $\alpha$ and density $2\phi (x)\Phi (\alpha x)$, where $\phi$ and $\Phi$ are used to denote the p.d.f. and the c.d.f. of the standard normal distribution. The next table presents values of the Cressie and Read (1984) $\lambda$-power divergence $D_{\phi _{2/3}}^{\omega }(\alpha _{1},\alpha _{2})$, $\ D_{\phi _{2/3}}^{\omega }(a_{2},a_{1})$ and the symmetric version $D_{\phi _{2/3}}^{\omega }(a_{1},a_{2})$ $+D_{\phi _{2/3}}^{\omega }(a_{2},a_{1}),$ between two skew-normal models with parameters $\alpha _{1}=2$ and $\alpha _{2}=-1$. The density $f_{\omega }$, of the local $\lambda$-power divergence, defined by (3) and (4) for $\phi (u)=\phi _{\lambda }(u)=\frac{u^{\lambda +1}-u-\lambda (u-1) }{\lambda (\lambda +1)},\lambda \ne 0,-1$, is that of the univariate normal distribution with parameters $\omega =(\mu ,\sigma ^{2})$. Table 2 leads to quite similar conclusions as these of the previous example. It illustrates that the divergence between two probability distributions in the whole domain ${\mathcal {X}}$ differs significantly in some subsets of ${\mathcal {X}}$ where the kernel density $f_{\omega }$ centers the main mass of the integral (4). Figure 2 helps us visualize the two skew normal distributions and how the values of Table 2 are exemplifying the different of the two distributions. Notice that globally the measure suggests divergence while locally and in particular near the tails, the distributions are similar.

Table 2 Values of $D_{\phi _{2/3}}(\alpha _{1},\alpha _{2}),D_{\phi _{2/3}}(\alpha _{2},\alpha _{1})$, $D_{\phi _{2/3}}^{\omega }(\alpha _{1}, \alpha _{2})$, $D_{\phi _{2/3}}^{\omega }(\alpha _{2},\alpha _{1})$, $D_{\phi _{2/3}}^{\omega }(\alpha _{1},\alpha _{2})+D_{\phi _{2/3}}^{\omega }(\alpha _{2},\alpha _{1})$, $I_{1,2}$, $I_{2,1},$ and $I_{1,2}+I_{2,1}$ for standard skew-normal distributions with parameters $\alpha _{1}=2$ and $\alpha _{2}=-1$ and several values of $\omega =(\mu ,\sigma ^{2})$

Fig. 2

Plot for standard skew-normal distributions with parameters $\alpha _{1}=2$ and $\alpha _{2}=-1$

In this subsection, the definition of the local $\phi$-divergence was given and its use as a measure of divergence or quasi distance between two probability distributions has been illustrated by two examples. However, the usefulness of a new proposed measure is assessed by the properties which it satisfies. The aim of the next subsection is to investigate the range of values of the local $\phi$-divergence between two distributions.

2.2 Range of values of local $\phi$-divergence

There is a vast list of properties that Csiszár classic $\phi$ -divergence, defined by (1), can satisfy. Some are of a mathematical and statistical nature, while others are motivated by particular problems of the research areas where the classic $\phi$-divergence is applied. Discussions on the properties of Csiszár $\phi$-divergence, are provided in the review papers by Papaioannou (1986, 2001), in the recent paper by Liese and Vajda (2006) and in the books by Liese and Vajda (1987) and Vajda (1989), to name a few.

Typically, measures are non-negative quantities. Hence, in order to avoid negativity of the local $\phi$-divergence, defined by (3) or (4), interest is restricted to real convex functions $\phi$ which are defined on the interval $[0,\infty )$ and belong to the class of convex functions

$$\begin{aligned} \Phi ^{*}=\left\{ \phi :\phi \text { is strictly convex at }1, \phi (1)=0,0\phi \left( \frac{0}{0}\right) =0,0\phi \left( \frac{u}{0} \right) =u\underset{v\rightarrow \infty }{\lim }\frac{\phi (v)}{v}\right\} . \end{aligned}$$

(6)

In addition, following Stummer and Vajda (2010, p. 171), for a function $\phi \in \Phi ^{*}$, the function

$$\begin{aligned} \overline{\phi }(u)=\phi (u)-\phi _{+}^{\prime }(1)(u-1), \end{aligned}$$

(7)

belongs to the class $\Phi ^{*}$ and it moreover satisfies,

$$\begin{aligned} \overline{\phi }(1)=\overline{\phi }^{\prime }(1)=0, \end{aligned}$$

(8)

where $\phi _{+}^{\prime }$ is used to denote the right hand derivative of $\phi$ at the point 1. Based on Stummer and Vajda (2010, p. 171), it holds $\overline{\phi }(u)\ge 0$, for $u\ge 0$. Taking into account that $\overline{\phi }(u)\ge 0$, for $u\ge 0$ and based on (3) and (7),

$$\begin{aligned} 0\le D_{\overline{\phi }}^{R}(P,Q)= & {} \int \limits _{{\mathcal {X}}}r(x)q(x) \overline{\phi }\left( \frac{p(x)}{q(x)}\right) d\mu (x) \nonumber \\= & {} \int \limits _{{\mathcal {X}}}r(x)q(x)\left( \phi \left( \frac{p(x)}{q(x)} \right) -\phi _{+}^{\prime }(1)\left( \frac{p(x)}{q(x)}-1\right) \right) d\mu (x) \nonumber \\= & {} D_{\phi }^{R}(P,Q)-\phi _{+}^{\prime }(1)\int \limits _{{\mathcal {X}} }r(x)\left( p(x)-q(x)\right) d\mu (x). \end{aligned}$$

(9)

It is now clear, from (9), that the local divergence which is defined by means of the convex function $\overline{\phi }$, given in (7), is always non-negative and hence it can be considered as a measure of a local divergence between two probability distributions. Thus, motivated by Stummer and Vajda (2010, p. 171), we refine the definition of the local $\phi$-divergence as follows.

Definition 2

Let P, Q and R three probability measures on the measurable space $( {\mathcal {X}},{\mathcal {A}})$, dominated by a $\sigma$-finite measure $\mu$ which is defined on the same measurable space. If p, q and r denote the respective Radon-Nikodym derivatives and $\phi \in \Phi ^{*}$, then the local $\phi$-divergence between p and q, driven by r, is defined by

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)=D_{\overline{\phi }}^{R}(P,Q)=D_{\phi }^{R}(P,Q)-\phi _{+}^{\prime }(1)\int \limits _{{\mathcal {X}}}r(x)\left( p(x)-q(x)\right) d\mu (x), \end{aligned}$$

(10)

where $D_{\overline{\phi }}^{R}(P,Q)$ is defined by (3).

Based on (9), it is clear that the two divergences $\widetilde{D} _{\phi }^{R}(P,Q)$ and $D_{\phi }^{R}(P,Q)$ coincide if we include the property $\phi ^{\prime }(1)=0$ in the class $\Phi ^{*}$. Thus, if we consider local divergences, defined by (3) and (4), in the set of convex functions

$$\begin{aligned} \Phi =\Phi ^{*}\cap \{\phi :\phi ^{\prime }(1)=0\}, \end{aligned}$$

(11)

then they are always non-negative (see also Pardo 2006, p. 6). It should be noted at this point, that all convex functions $\phi$ that lead to important particular cases of Csiszár $\phi$-divergences, like Kullback and Leibler (1951) divergence $(\phi (u)=u\log u-u+1, u>0)$, Kagan (1963) divergence $(\phi (u)=(u-1)^{2}, u>0)$, Cressie and Read (1984) $\lambda$ -power divergence $\left( \phi _{\lambda }(u)=\frac{u^{\lambda +1}-u-\lambda (u-1)}{\lambda (\lambda +1)},\lambda \ne 0,-1\right)$, and many more, belong to the set $\Phi$, defined by (11).

The theorem that follows investigates the range of values of the local $\phi$-divergence, as defined by (10). The detailed proof is given in “Appendix 1”.

Theorem 1

• (a) For $\phi \in \Phi ^{*}$, the local $\phi$-divergence, as defined by (10), satisfies,

  $$\begin{aligned} 0\le \widetilde{D}_{\phi }^{R}(P,Q)\le \text { }\phi (0)\xi _{0}+\phi ^{*}(0)\xi _{1}+\phi _{+}^{\prime }(1)\left( \xi _{0}-\xi _{1}\right) , \end{aligned}$$

with $\xi _{0}=\int _{{\mathcal {X}}}r(x)q(x)d\mu (x)$, $\xi _{1}=\int _{{\mathcal {X}}}r(x)p(x)d\mu (x)$ and $\phi ^{*}\in \Phi ^{*}$, with $\phi ^{*}$ the adjoint function defined by $\phi ^{*}(u)=u\phi \left( \frac{1}{u}\right)$, $u>0$.

• (b) $\widetilde{D}_{\phi }^{R}(P,Q)=0$ if and only if $P=Q.$

• (c) $\widetilde{D}_{\phi }^{R}(P,Q)=$ $\phi (0)\xi _{0}+\phi ^{*}(0)\xi _{1}+\phi _{+}^{\prime }(1)\left( \xi _{0}-\xi _{1}\right)$ if $P\perp Q,$ where $\perp$ denotes singularity of probability measures. In addition, if $\phi (0)+\phi ^{*}(0)<\infty$ and $\widetilde{D}_{\phi }^{R}(P,Q)=$ $\phi (0)\xi _{0}+\phi ^{*}(0)\xi _{1}+\phi _{+}^{\prime }(1)\left( \xi _{0}-\xi _{1}\right)$, then $P\perp Q$.

3 Local $\phi$-divergence for exponential family of distributions

Measures of entropy or divergence have been widely applied in several disciplines and contexts not only in statistics, classic and contemporary, but in almost every branch of science and engineering. Consequently, it is of great importance to tabulate expressions for entropies or divergences for specific families of distributions. This tabulation is very useful for the development of information theoretic concepts and methods. There is an extensive literature where expressions are derived for Shannon entropy and hence for mutual information, a particular case of Kullback–Leibler divergence. For more details we refer to Soofi and Retzer (2002), Zografos and Nadarajah (2005), Zografos (2008) and the references therein.

Expressions for particular cases of Csiszár $\phi$-divergence between two members of the exponential family of distributions have been obtained in Liese andVajda (1987, p. 43) and they have been utilized in testing statistical hypotheses in Morales et al. (2000, 2004). The exponential family of distributions is a broad family which includes the majority of the well known and used, in practice, statistical distributions.

Consider the exponential family of distributions with probability densities of the form

$$\begin{aligned} f_{C}(x,\theta )=\exp \left\{ \theta ^{t}T(x)-C(\theta )+h(x)\right\} ,\text { }x\in {\mathcal {X}}, \end{aligned}$$

(12)

with natural parameters $\theta \in \Theta \subseteq R^{k}$ and $T(x)=(T_{1}(x),...,T_{k}(x))^{t}, x\in {\mathcal {X}}$, where the superscript $^{t}$ is used to denote the transpose of a vector or a matrix.

For two members of this family, $f_{C}(x,\theta _{i})$, $\theta _{i}\in \Theta \subseteq R^{k}$, $i=1,2$, the Cressie and Read local power divergence is defined, taking into account (4), for $\phi (u)=\phi _{\lambda }(u)=\frac{u^{\lambda +1}-u-\lambda (u-1)}{\lambda (\lambda +1)} ,\lambda \ne 0,-1$, by

$$\begin{aligned} D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})=\frac{1}{\lambda (\lambda +1)}\left[ K_{\lambda ,\omega }(\theta _{1},\theta _{2})-(\lambda +1)E_{\theta _{1}}\left( f_{\omega }(X)\right) +\lambda E_{\theta _{2}}\left( f_{\omega }(X)\right) \right] , \end{aligned}$$

(13)

for $\lambda \ne 0,-1$, with

$$\begin{aligned} K_{\lambda ,\omega }(\theta _{1},\theta _{2})= & {} \int \limits _{{\mathcal {X}} }f_{\omega }(x)\frac{f_{C}^{\lambda +1}(x,\theta _{1})}{f_{C}^{\lambda }(x,\theta _{2})}d\mu (x), \end{aligned}$$

(14)

$$\begin{aligned} E_{\mathbf {\theta }_{i}}\left( f_{\omega }(X)\right)= & {} \int \limits _{\mathcal {X }}f_{\omega }(x)f_{C}(x,\theta _{i})d\mu (x) \end{aligned}$$

(15)

and $\omega , \theta _{i}\in \Theta \subseteq R^{k}$, $i=1,2$.

The next proposition presents the analytic expression for $D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})$ when the kernel density $f_{\omega }$ is defined on ${\mathcal {X}}$ and it does not necessarily belong to the class of densities (12).

Proposition 2

Let the kernel density $f_{\omega }$ be defined on ${\mathcal {X}}$ and consider two members $f_{C}(x,\theta _{1})$ and $f_{C}(x,\theta _{2})$ of (12). If $(\lambda +1)\theta _{1}-\lambda \theta _{2}\in \Theta$, for $\lambda \ne 0,-1$, then the Cressie and Read local power divergence between $f_{C}(x,\theta _{1})$ and $f_{C}(x,\theta _{2})$, driven by the density $f_{\omega }$, is given in view of (13) by

$$\begin{aligned} D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})= & {} \frac{1}{\lambda (\lambda +1)}\left\{ \left( \exp \left[ M_{C,\lambda }^{(1)}(\theta _{1},\theta _{2})\right] \right) E_{(\lambda +1)\theta _{1}-\lambda \theta _{2}}\left( f_{\omega }(X)\right) \right. \nonumber \\&\left. -(\lambda +1)E_{\theta _{1}}\left( f_{\omega }(X)\right) +\lambda E_{\theta _{2}}\left( f_{\omega }(X)\right) \right\} , \end{aligned}$$

(16)

with

$$\begin{aligned} M_{C,\lambda }^{(1)}(\theta _{1},\theta _{2})=\lambda C(\theta _{2})-(\lambda +1)C(\theta _{1})+C((\lambda +1)\theta _{1}-\lambda \theta _{2}) \end{aligned}$$

(17)

and $E_{(\lambda +1)\theta _{1}-\lambda \theta _{2}}\left( f_{\omega }(X)\right)$, $E_{\theta _{i}}\left( f_{\omega }(X)\right)$, $i=1,2$, are defined by (15).

Proof

Based on (14), straightforward calculations give

$$\begin{aligned} K_{\lambda ,\omega }(\theta _{1},\theta _{2})= & {} \int \limits _{{\mathcal {X}} }f_{\omega }(x)\exp \left( [(\lambda +1)\theta _{1}^{t}-\lambda \theta _{2}^{t}]T(x)\right) \exp \left( \lambda C(\theta _{2})-(\lambda +1)C(\theta _{1})\right. \\&\left. +\,h(x)\right) d\mu (x). \end{aligned}$$

Hence,

$$\begin{aligned} K_{\lambda ,\omega }(\theta _{1},\theta _{2})= & {} \int \limits _{{\mathcal {X}} }f_{\omega }(x)\exp \left( [(\lambda +1)\theta _{1}^{t}-\lambda \theta _{2}^{t}]T(x)-C\left( (\lambda +1)\theta _{1}-\lambda \theta _{2}\right) +h(x)\right) \\&\times \exp \left( \lambda C(\theta _{2})-(\lambda +1)C(\theta _{1})\right) \times \exp \left( C\left( (\lambda +1)\theta _{1}-\lambda \theta _{2}\right) \right) d\mu (x), \end{aligned}$$

which leads to the desired result, in view of (13) and (17). $\square$

The proposition that follows states the analytic expression for $D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})$ when the kernel density $f_{\omega }$ belongs to the class of densities (12). The proof is given in “Appendix 2”.

Proposition 3

Consider two members $f_{C}(x,\theta _{1})$ and $f_{C}(x,\theta _{2})$ of (12) and consider the kernel density $f_{\omega }(x)= f_{C}(x,\omega )$ as a member of (12). Then, subject to the assumption $\theta _{i}+\omega \in \Theta$, $i=1,2$ and $(\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega \in \Theta$, for $\lambda \ne 0,-1$, the Cressie and Read local power divergence between $f_{C}(x,\theta _{1})$ and $f_{C}(x,\theta _{2})$, driven by $f_{\omega }$, is given by

$$\begin{aligned} D_{\phi _{\lambda }}^{\omega }(\theta _{1},\theta _{2})= & {} \frac{1}{\lambda (\lambda +1)}\left\{ \left( \exp \left[ M_{C,\lambda }^{(2)}(\theta _{1},\theta _{2},\omega )\right] \right) E_{(\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega }\left( \exp \left( h(X)\right) \right) \right. \nonumber \\&-(\lambda +1)\exp [C(\theta _{1}+\omega )-C(\theta _{1})-C(\omega )]\times E_{\theta _{1}+\omega }\left( \exp \left( h(X)\right) \right) \nonumber \\&\left. +\lambda \exp [C(\theta _{2}+\omega )-C(\theta _{2})-C(\omega )]\times E_{\theta _{2}+\omega }\left( \exp \left( h(X)\right) \right) \right\} , \end{aligned}$$

(18)

with

$$\begin{aligned} M_{C,\lambda }^{(2)}(\theta _{1},\theta _{2},\omega )=\lambda C(\theta _{2})-(\lambda +1)C(\theta _{1})-C(\omega )+C((\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega ) \end{aligned}$$

(19)

and

$$\begin{aligned}&\displaystyle E_{\theta _{i}+\omega }\left( \exp \left( h(X)\right) \right) =\int \limits _{ {\mathcal {X}}}\left\{ \exp \left( h(X)\right) \right\} f_{C}(x,\theta _{i}+\omega )d\mu (x),\quad i=1,2, \end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle E_{(\lambda +1)\theta _{1}-\lambda \theta _{2}\!+\!\omega }\left( \exp \left( h(X)\right) \right) \!=\!\int \limits _{{\mathcal {X}}}\left\{ \exp \left( h(X)\right) \right\} f_{C}(x,(\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega )d\mu (x).\nonumber \\ \end{aligned}$$

(21)

The multivariate normal model is widely used in statistics and related fields and it belongs to the exponential family model (12). The next proposition provides the explicit form of the local Cressie and Read power divergence, defined by (13), between two k-variate normal distributions, as it is driven by another k-variate normal distribution. Let the kernel density $f_{N(\mu ,\Sigma )}$, be the multivariate normal distribution $N(\mu ,\Sigma )$ with mean vector $\mu \in R^{k}$ and covariance matrix $\Sigma$. Consider also two densities $f_{N(\mu _{1},\Sigma _{1})}$ and $f_{N(\mu _{2},\Sigma _{2})}$ on $\mathcal {X=}R^{k}$ , that follow k-variate normal distributions $N_{k}(\mu _{1},\Sigma _{1})$ and $N_{k}(\mu _{2},\Sigma _{2}),$ with parameters $(\mu _{1},\Sigma _{1})$ and $(\mu _{2},\Sigma _{2})$.

The density function of the k-variate normal models with mean vectors $\mu _{i}\in R^{k}$ and covariance matrices $\Sigma _{i}$, $i=1,2$, are given by,

$$\begin{aligned} (2\pi )^{-k/2}|\Sigma _{i}|^{-1/2}\exp \left( -\frac{1}{2}(x-\mu _{i})^{t}\Sigma _{i}^{-1}(x-\mu _{i})\right) ,\text { }i=1,2. \end{aligned}$$

It can be easily seen that the above k-variate normal distributions are included in the exponential family of distributions (12) with

$$\begin{aligned} \theta _{i}= & {} (\theta _{i1},\theta _{i2})=\left( \Sigma _{i}^{-1}\mu _{i},- \frac{1}{2}\Sigma _{i}^{-1}\right) ,T(x)=\left( T_{1}(x),T_{2}(x)\right) =\left( x,xx^{t}\right) , \nonumber \\ C(\theta _{i})= & {} \log \left( (2\pi )^{k/2}|\Sigma _{i}|^{1/2}\right) +\frac{1}{ 2}\mu _{i}^{t}\Sigma _{i}^{-1}\mu _{i}=\log (2\pi )^{k/2}-\frac{1}{2}\log \left( |-2\theta _{i2}|\right) \nonumber \\&-\frac{1}{4}\theta _{i1}^{t}\theta _{i2}^{-1}\theta _{i1}, \\ h(x)= & {} 0,\nonumber \end{aligned}$$

(22)

where $|\; |$ is used to denote the determinant of the respective matrix. It should be noted that the inner product of $\alpha =(u,M)$ and $\beta =(v,N)$ which consist of two parts, a vectorial part u and v and a matrix part M and N, is defined by $\alpha ^{t}\beta =u^{t}v+trace(M^{t}N)$ (cf. Nielsen and Nock 2011, p. 6).

Proposition 4

The Cressie and Read local power divergence, defined by (13), between two k-variate normal distributions $N_{k}(\mu _{1},\Sigma _{1})$ and $N_{k}(\mu _{2},\Sigma _{2})$, driven by a k-variate normal distributions $N_{k}(\mu ,\Sigma )$, is given by

with

$$\begin{aligned} B_{1}= & {} (\lambda +1)\Sigma _{1}^{-1}\mu _{1}-\lambda \Sigma _{2}^{-1}\mu _{2}+\Sigma ^{-1}\mu , \\ B_{2}= & {} \left( (\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}\right) ^{-1}, \end{aligned}$$

provided that $(\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}>0,$ for $\lambda \ne 0,-1$.

The proof of the proposition is given in “Appendix 3”.

Remark 2

Explicit expressions for Cressie and Read local power divergence between univariate normal distributions can be derived by a direct application of the above proposition. The respective formulas are presented in Eq. (5) of the numerical Example 1.

The Kullback–Leibler local divergence is obtained from (3) or (4) for $\phi (u)=u\log u-u+1$. It is defined by

$$\begin{aligned} D_{0}^{R}(P,Q)= & {} \int \limits _{{\mathcal {X}}}\frac{dR}{d\mu }\frac{dP}{dQ}\log \left( \frac{dP}{dQ}\right) dQ-\int \limits _{{\mathcal {X}}}\frac{dR}{d\mu } dP+\int \limits _{{\mathcal {X}}}\frac{dR}{d\mu }dQ \nonumber \\= & {} \int \limits _{{\mathcal {X}}}r(x)p(x)\log \left( \frac{p(x)}{q(x)}\right) d\mu (x)-\int \limits _{{\mathcal {X}}}r(x)p(x)d\mu (x)\nonumber \\&+\int \limits _{{\mathcal {X}} }r(x)q(x)d\mu (x). \end{aligned}$$

(23)

It should be noted that Kullback–Leibler classic divergence is obtained from (1) for $\phi (u)=u\log u$ or $\phi (u)=u\log u-u+1$. Both choices of the convex function $\phi$ lead to the same quantity. This is not the case for Kullback–Leibler local divergence. It is defined by (23), as a particular case of (3) or (4) for $\phi (u)=u\log u-u+1$.

The next Proposition provides the explicit forms of Kullback–Leibler local divergence between two members of the exponential family and between two multivariate normal distributions, as well.

Proposition 5

(a) The Kullback–Leibler local divergence (23) between two members $f_{C}(x,\theta _{1})$ and $f_{C}(x,\theta _{2})$ of the exponential family (12), driven by the kernel density $f_{C}(x,\omega )$ in (12), is given by

$$\begin{aligned} D_{0}^{\omega }(\theta _{1},\theta _{2})= & {} \left( \exp \left( C(\theta _{1}+\omega )-C(\theta _{1})-C(\omega )\right) \right) \left\{ \left( C(\theta _{2})-C(\theta _{1})\right) E_{\theta _{1}+\omega }\left( \exp \left( h(X)\right) \right) \right. \\&+\left. (\theta _{1}-\theta _{2})^{t}E_{\theta _{1}+\omega }\left( T(X)\exp \left( h(X)\right) \right) \right\} \\&-\left( \exp \left( C(\theta _{1}+\omega )-C(\theta _{1})-C(\omega )\right) \right) E_{\theta _{1}+\omega }\left( \exp \left( h(X)\right) \right) \\&+\left( \exp \left( C(\theta _{2}+\omega )-C(\theta _{2})-C(\omega )\right) \right) E_{\theta _{2}+\omega }\left( \exp \left( h(X)\right) \right) , \end{aligned}$$

and $E_{\theta _{i}+\omega }\left( \exp \left( h(X)\right) \right)$, $i=1,2$ , are defined by (20).

(b) The Kullback–Leibler local divergence (23) between two multivariate normal distributions $f_{N(\mu _{1},\Sigma _{1})}$ and $f_{N(\mu _{2},\Sigma _{2})}$, on $\mathcal {X=}R^{k}$, driven by the multivariate normal density $f_{N(\mu ,\Sigma )}$, is given by

where

$$\begin{aligned} E_{(\mu _{i},\Sigma _{i})}\left( f_{N(\mu ,\Sigma )}(X)\right)= & {} (2\pi )^{- \frac{k}{2}}|\Sigma |^{-\frac{1}{2}}|\Sigma _{i}|^{-\frac{1}{2}}\left| \Sigma ^{-1}+\Sigma _{i}^{-1}\right| ^{-\frac{1}{2}} \\&\times \exp \left\{ -\frac{1}{2}(\mu -\mu _{i})^{t}(\Sigma +\Sigma _{i})^{-1}(\mu -\mu _{i})\right\} ,\text { }i=1,2, \end{aligned}$$

and

$$\begin{aligned} \mu ^{*}=(\Sigma ^{-1}+\Sigma _{1}^{-1})^{-1}(\Sigma ^{-1}\mu +\Sigma _{1}^{-1}\mu _{1}). \end{aligned}$$

The proof of the previous proposition is given in “Appendix 4”.

Remark 3

(a) Explicit expressions for Kullback–Leibler local divergence between univariate normal distributions can be derived by a direct application of the part (b) of above proposition. The respective formulas, are given by

$$\begin{aligned} D_{0}^{(\mu ,\sigma ^{2})}((\mu _{1},\sigma _{1}^{2}),(\mu _{2},\sigma _{2}^{2}))= & {} \frac{1}{2}(2\pi (\sigma ^{2}+\sigma _{1}^{2}))^{-\frac{1}{2} }\exp \left( -\frac{(\mu -\mu _{1})^{2}}{2(\sigma ^{2}+\sigma _{1}^{2})} \right) \\&\times \left( \log \frac{\sigma _{2}^{2}}{\sigma _{1}^{2}}-\frac{ \sigma ^{2}(\sigma _{2}^{2}-\sigma _{1}^{2})}{\sigma _{2}^{2}(\sigma ^{2}+\sigma _{1}^{2})}-\frac{(\mu ^{*}-\mu _{1})^{2}}{\sigma _{1}^{2}}+ \frac{(\mu ^* -\mu _{2})^{2}}{\sigma _{2}^{2}}\right) \\&-\,E_{(\mu _{1},\sigma _{1}^{2})}\left( f_{N(\mu ,\sigma ^{2})}(X)\right) +E_{(\mu _{2},\sigma _{2}^{2})}\left( f_{N(\mu ,\sigma ^{2})}(X)\right) , \end{aligned}$$

where

$$\begin{aligned} E_{(\mu _{i},\sigma _{i}^{2})}\left( f_{N(\mu ,\sigma ^{2})}(X)\right) =\left( 2\pi (\sigma ^{2}+\sigma _{i}^{2})\right) ^{-1/2}\exp \left\{ -\frac{ \left( \mu -\mu _{i}\right) ^{2}}{2(\sigma ^{2}+\sigma _{i}^{2})}\right\} ,\ i=1,2, \end{aligned}$$

and

$$\begin{aligned} \mu ^{*}=\frac{\mu \sigma _{1}^{2}+\mu _{1}\sigma ^{2}}{\sigma ^{2}+\sigma _{1}^{2}}. \end{aligned}$$

(b) Proposition 5 (b) can be used in order to obtain the explicit expression for the Kullback–Leibler local divergence between two multivariate normal distributions with common covariance matrix $\Sigma _{1}=\Sigma _{2}=\Sigma _{*}$. It is easily obtained by a straightforward application of Proposition 5 (b) for $\Sigma _{1}=\Sigma _{2}=\Sigma _{*}$.

4 Application

We now illustrate the behaviour of local measures in real life situations. Consider grade point average (GPA) scores for students seeking admission in a business school (Johnson and Wichern 1992, p. 532, Example 11.11). There are three groups of applicants who have been categorized as $\Pi _{1}$: admit, $\Pi _{2}$: don’t admit, and $\Pi _{3}$: borderline, depending on their GPA scores. Note that the support of the three distributions is the same. We are interested in exemplifying any differences between the three populations of students, either globally, i.e., over the whole domain of the distributions describing each population, or locally, by focusing on a specific area of the domain of observation where two populations might differ. The latter is accomplished by considering the center of the kernel distribution to be a convex combination of the means of the two populations under consideration. In this way, the kernel acts as a window that can move across the domain of observation and focus on a small region each time, that depends on the variability or spreadness of the kernel.

In Table 3 we display normality tests along with basic descriptive statistics for the three populations, including sample means and variances. Notice that the normality assumption is reasonable for the three groups of students, and hence we adapt the three univariate normal distributions in order to describe the data. Under normality, knowing the mean and variance completely determines the behavior of the distributions. Figure 3 illustrates the three densities for $\Pi _{1}-\Pi _{3}$ using the estimated means and variances from Table 3.

Fig. 3

Plot for three densities of $\Pi _{1}-\Pi _{3}$ using the estimated means and variances

Table 3 Normality tests and descriptive statistics for the three populations of GPA scores

Using the notation of Example 1, we utilize the Cressie–Read $\lambda$-power divergence in order to compare populations $\Pi _{1}$ with $\Pi _{2},\Pi _{1}$ with $\Pi _{3},$ and $\Pi _{2}$ with $\Pi _{3},$ in Tables 4, 5 and 6, respectively. In all tables, we present the local Cressie–Read divergence $D_{\phi _{\lambda }}^{\omega }(\widehat{\theta }_{1},\widehat{ \theta }_{2})$ for different values of $\lambda ,$ namely, $\lambda =-2,-0.5, \frac{2}{3},1$ or 2. The bottom rows show the values of the global measure $D_{\phi _{\lambda }}(\widehat{\theta }_{1},\widehat{\theta }_{2})$. The kernel and population models are univariate normal distributions, with estimated parameters for $\Pi _{1},$ $\Pi _{2}$ and $\Pi _{3}$ given by $\widehat{\theta }_{1}=(\widehat{\mu }_{1},\widehat{\sigma } _{1}^{2})=(3.40, 0.04){\small ,}$ $\widehat{\theta }_{2}=(\widehat{\mu }_{2}, \widehat{\sigma }_{2}^{2})=(2.48, 0.03){\small ,}$ and $\widehat{\theta } _{3}=(\widehat{\mu }_{3},\widehat{\sigma }_{3}^{2})=(2.99, 0.03){\small ,}$ respectively. Using these estimators, we obtain convex combinations of the means for different values of k, and treat the result as the mean of the kernel. The kernel parameters are displayed in the second column of Tables 4, 5, and 6, i.e., the parameters of the kernel are $\theta =(\mu ,\sigma ^{2})=(k\widehat{\mu }_{1}+ (1-k)\widehat{\mu }_{2},0.1).$ Notice that the variance of the kernel is 0.1 in all cases, a small value that puts more weight on values about $\mu$, thus highlighting the differences of the two populations at a region near the mean of the kernel. The values of k considered are $k=0,0.1,0.3,0.5,0.7,0.9$ and 1,  and lead to a window in the domain of observation that moves from one population mean towards the other. When two populations are close to each other in a certain window, we expect the local measure to take smaller values, unless the two populations are completely different. This assertion is supported by the results in Tables 4, 5 and 6, with all values away from zero, indicating that all populations are different from each other. For example, when comparing $\Pi _{2}$ with $\Pi _{3},$ using $\lambda =\frac{2}{3},$ the global measure is $D_{\phi _{2/3}}(\widehat{\theta }_{2},\widehat{\theta }_{3})=110.3,$ while a value of $k=0,$ yields a local measure with value $D_{\phi _{2/3}}^{\omega }( \widehat{\theta }_{2},\widehat{\theta }_{3})=7.7$. The region we focus in this case is described by the kernel with mean being the same as the mean of $\Pi _{3},$ but the kernel variance ($\sigma ^{2}=0.1$) is much larger than that of $\Pi _{3} (\widehat{\sigma }_{3}^{2}=0.03)$.

Table 4 Displaying the local Cressie–Read divergence $D_{\phi _{ \lambda }}^{\omega }(\widehat{\theta }_{1},\widehat{ \theta }_{2})$ for different values of $\lambda ,$ in order to compare populations $\Pi _{1}$ and $\Pi _{2}$

Table 5 Displaying the local Cressie–Read divergence $D_{\phi _{ \lambda }}^{\omega }(\widehat{\theta }_{1},\widehat{ \theta }_{3})$ for different values of $\lambda ,$ in order to compare populations $\Pi _{1}$ and $\Pi _{3}$

Table 6 Displaying the local Cressie–Read divergence $D_{\phi _{ \lambda }}^{\omega }(\widehat{\theta }_{2},\widehat{ \theta }_{3})$ for different values of $\lambda ,$ in order to compare populations $\Pi _{2}$ and $\Pi _{3}$

We investigate the behavior of the local Kullback–Leibler measure in Table 7, with similar results to the Cressie–Read divergence. All tables suggest that the three populations are clearly different globally, although some values of $\lambda$ indicate that populations $\Pi _{2}$ and $\Pi _{3}$ are not as different locally, when the kernel focuses attention near the mean of $\Pi _{3}.$

Table 7 Displaying the local Kullback–Leibler divergence $D_{0}^{\omega }(.,.),$ in order to compare all populations

5 Conclusions

This paper introduces a broad class of divergence measures between two probability measures or between the respective probability distributions. The proposed measure has its origins on Csiszár classic $\phi$ -divergence, a measure with numerous applications not only in probability and statistics but in many areas of science and engineering. It provides us with a tool to locally quantify the pseudo-distance between two distributions on a specific area of their common domain that might be of particular interest from a theoretical or applied point of view. The range of values of the introduced class of local divergences has been derived and the measures attain their minimum value if and only if the underlined probability measures or the respective probability distributions coincide. Explicit expressions of the proposed local divergences have been derived when the underlined distributions are members of the exponential family of distributions or they are described by multivariate normal models.

Our simulations illustrated the robust behavior of the local against the global measure, in the sense that differences between two populations that cannot be captured or are otherwise obscured globally, are exemplified by using the appropriate kernel locally. Moreover, important aspects of the two models under comparison can be asserted more efficiently at the local level using the right kernel, including tail behavior, central tendency and local variability (see Example 2).

There are several extensions to this work that we will consider. Firstly, the theoretical framework laid down in this paper will be extended to study other important properties of the local divergence including sufficiency and robustness with respect to choice of models and kernel. Secondly, we will explore the use of the local measure in the creation of local tests for the difference in means and variances between the two models. Finally, the local measure will be illustrated as a tool for local goodness-of-fit tests. These are subjects of future research and will be explored elsewhere.

Appendices

Appendix 1

This appendix provides a detailed proof of Theorem 1.

Proof of Theorem 1

(a) It is clear, from (9) and (10), that $0\le \widetilde{D}_{\phi }^{R}(P,Q)$. We proceed with the upper bound of $\widetilde{D}_{\phi }^{R}(P,Q)$. Given that $\overline{ \phi }(1)=0$ and motivated by a similar proof in Stummer and Vajda (2010, p. 174), we can write

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)=\int \limits _{\{p<q\}}r(x)q(x)\overline{\phi } \left( \frac{p(x)}{q(x)}\right) d\mu (x)+\int \limits _{\{q<p\}}r(x)q(x) \overline{\phi }\left( \frac{p(x)}{q(x)}\right) d\mu (x). \end{aligned}$$

(24)

Define the function

$$\begin{aligned} \overline{\phi ^{*}}(u)=\phi ^{*}(u)+\phi _{+}^{\prime }(1)(u-1). \end{aligned}$$

(25)

Then, for $u=\frac{q(x)}{p(x)}=\frac{q}{p}$, $x\in {\mathcal {X}}$,

$$\begin{aligned} {rp}\overline{\phi ^{*}}\left( \frac{q}{p}\right) =rp\phi ^{*}\left( \frac{q}{p}\right) +rp\phi _{+}^{\prime }(1)\left( \frac{q}{p} -1\right) . \end{aligned}$$

(26)

Hence,

$$\begin{aligned} \int \limits _{\{q<p\}}r(x)p(x)\overline{\phi ^{*}}\left( \frac{q(x)}{p(x)} \right) d\mu (x)= & {} \int \limits _{\{q<p\}}r(x)p(x)\phi ^{*}\left( \frac{q(x) }{p(x)}\right) d\mu (x)+\phi _{+}^{\prime }(1)\\&\times \int \limits _{\{q<p\}}r(x)\left( q(x)-p(x)\right) d\mu (x) \end{aligned}$$

and taking into account that $\phi ^{*}(u)=u\phi \left( 1/u\right)$, $u>0$,

$$\begin{aligned} \int \limits _{\{q<p\}}r(x)p(x)\overline{\phi ^{*}}\left( \frac{q(x)}{p(x)} \right) d\mu (x)= & {} \int \limits _{\{q<p\}}r(x)q(x)\phi \left( \frac{p(x)}{q(x) }\right) d\mu (x)-\phi _{+}^{\prime }(1)\nonumber \\&\times \int \limits _{\{q<p\}}r(x)\left( p(x)-q(x)\right) d\mu (x) \nonumber \\= & {} \int \limits _{\{q<p\}}r(x)q(x)\overline{\phi }\left( \frac{p(x)}{q(x)} \right) d\mu (x). \end{aligned}$$

(27)

Therefore, from Eqs. (24) and (27) we conclude

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)=\int \limits _{\{p<q\}}r(x)q(x)\overline{\phi } \left( \frac{p(x)}{q(x)}\right) d\mu (x)+\int \limits _{\{q<p\}}r(x)p(x) \overline{\phi ^{*}}\left( \frac{q(x)}{p(x)}\right) d\mu (x). \end{aligned}$$

(28)

On the other hand, based on Stummer and Vajda (2010, p. 174), for a convex function $\phi \in \Phi ^{*}$ which is strictly convex at 1, with $\phi _{+}^{\prime }(1)=0$, it is true that

$$\begin{aligned} 0=\phi (1)\le \phi (t_{2})\le \phi (t_{1})\le \phi (0),\text { for any } 0\le t_{1}\le t_{2}\le 1. \end{aligned}$$

(29)

Applying inequality (29) to $\phi =\overline{\phi }$, it is clear that on the subset $\left\{ x\in {\mathcal {X}}:p(x)<q(x)\right\}$ of ${\mathcal {X}}$, it holds that $0\le \overline{\phi }\left( \frac{p}{q}\right) \le \overline{\phi }(0)$, and therefore

$$\begin{aligned} 0\le \int \limits _{\{p<q\}}r(x)q(x)\overline{\phi }\left( \frac{p(x)}{q(x)} \right) d\mu (x)\le \overline{\phi }(0)\int \limits _{\{p<q\}}r(x)q(x)d\mu (x). \end{aligned}$$

Moreover, based on the non-negativity of r and q on any subset of ${\mathcal {X}}$, it is true that

$$\begin{aligned} 0\le \int \limits _{\{p<q\}}r(x)q(x)d\mu (x)\le \int \limits _{{\mathcal {X}} }r(x)q(x)d\mu (x)=\xi _{0}. \end{aligned}$$

So, the last two inequalities lead to

$$\begin{aligned} 0\le \int \limits _{\{p<q\}}r(x)q(x)\overline{\phi }\left( \frac{p(x)}{q(x)} \right) d\mu (x)\le \overline{\phi }(0)\xi _{0}. \end{aligned}$$

(30)

In a manner quite similar to the above, applying inequality (29) to $\phi =\overline{\phi ^{*}}$, it is clear that on the subset $\left\{ x\in {\mathcal {X}}:q(x)<p(x)\right\}$ of ${\mathcal {X}}$ it holds that $0\le \overline{\phi ^{*}}\left( \frac{q}{p}\right) \le \overline{\phi ^{*}}(0)$, and therefore

$$\begin{aligned} 0\le \int \limits _{\{q<p\}}r(x)p(x)\overline{\phi ^{*}}\left( \frac{q(x) }{p(x)}\right) d\mu (x)\le \overline{\phi ^{*}}(0)\int \limits _{\{q<p \}}r(x)p(x)d\mu (x). \end{aligned}$$

Hence,

$$\begin{aligned} 0\le \int \limits _{\{q<p\}}r(x)p(x)\overline{\phi ^{*}}\left( \frac{q(x) }{p(x)}\right) d\mu (x)\le \overline{\phi ^{*}}(0)\int \limits _{\{q<p \}}r(x)p(x)d\mu (x)\le \overline{\phi ^{*}}(0)\xi _{1}. \end{aligned}$$

(31)

A combination of (28), (30) and (31) gives

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)\le \overline{\phi }(0)\xi _{0}+\overline{ \phi ^{*}}(0)\xi _{1}. \end{aligned}$$

Based on (7) and (25), $\overline{\phi }(0)=\phi (0)+\phi _{+}^{\prime }(1)$ and $\overline{\phi ^{*}}(0)=\phi ^{*}(0)-\phi _{+}^{\prime }(1)$. These identities along with the previous inequality complete the proof of part (a) of the theorem.

(b) To proceed with the proof of part (b) of the theorem, suppose first that $P=Q$. Then, it is clear from (10) that $\widetilde{D} _{\phi }^{R}(P,P)=D_{\phi }^{R}(P,P)=\phi (1)=0$, because $\phi \in \Phi ^{*}$.

Conversely, let $\widetilde{D}_{\phi }^{R}(P,Q)=0$. Taking into account (9) and the fact that $\phi (1)=0$,

$$\begin{aligned} \phi \left( \frac{p(x)}{q(x)}\right) =\phi (1)+\phi _{+}^{\prime }(1)\left( \frac{p(x)}{q(x)}-1\right) , \end{aligned}$$

(32)

a.e. with respect to measure $\mu$, for Radon-Nikodym derivative r positive on ${\mathcal {X}}$. On the other hand, based on Vajda (1989, p. 58)

$$\begin{aligned} \phi \left( x\right) >\phi (1)+\phi _{+}^{\prime }(1)\left( x-1\right) , \text { for every }x\ne 1, \end{aligned}$$

because $\phi$ is strictly convex at 1. Therefore, the only way equality ( 32) to be valid, taking into account the above inequality, is when $\frac{p(x)}{q(x)}=1$ or $P=Q$, which completes the proof of part (b) of the theorem.

(c) Suppose that $P\perp Q$. Then, following Vajda (1972, p. 227), $u=\frac{dQ}{dP+dQ}=0\;[P]$ and $u=\frac{dQ}{dP+dQ}=1$ [Q]. Taking into account that $u=\frac{q}{p+q}$, we conclude that if $P\perp Q$, then $q(x)=0$, $a.e. \ x\in {\mathcal {X}}\,[P]$ and $p(x)=0$, $a.e. \ x\in {\mathcal {X}}\;[Q]$. Equation (28) is refined as follows,

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)=\int \limits _{\{p<q\}}r(x)\overline{\phi } \left( \frac{p(x)}{q(x)}\right) dQ(x)+\int \limits _{\{q<p\}}r(x)\overline{ \phi ^{*}}\left( \frac{q(x)}{p(x)}\right) dP(x), \end{aligned}$$

and subject to the condition $P\perp Q,$

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)= & {} \int \limits _{\{p<q\}}r(x)\overline{\phi } \left( \frac{p(x)}{q(x)}\right) dQ(x)+\int \limits _{\{q<p\}}r(x)\overline{ \phi ^{*}}\left( \frac{q(x)}{p(x)}\right) dP(x)\nonumber \\= & {} \overline{\phi }\left( 0\right) \int \limits _{\{p<q\}}r(x)dQ(x)+\overline{ \phi ^{*}}\left( 0\right) \int \limits _{\{q<p\}}r(x)dP(x). \end{aligned}$$

(33)

On the other hand, because of $p(x)=0$, $a.e.\ x\in {\mathcal {X}}$ [Q], it is clear that

$$\begin{aligned} Q(\{p\ge q\})=Q(\{p>q\})+Q(\{p=q\})=Q(\{p>q\})=Q(\{q<0\})=Q(\varnothing )=0 \end{aligned}$$

since $Q(\{q=p\})=0$, by taking into account that $P\perp Q$. This last equality leads to $\int _{\{p\ge q\}}r(x)dQ(x)=0,$ and therefore

$$\begin{aligned} \xi _{0}= & {} \int \limits _{{\mathcal {X}}}r(x)q(x)d\mu (x)=\int \limits _{{\mathcal {X}} }r(x)dQ(x)=\int \limits _{\{p<q\}}r(x)dQ(x)+\int \limits _{\{p\ge q\}}r(x)dQ(x)\nonumber \\= & {} \int \limits _{\{p<q\}}r(x)dQ(x). \end{aligned}$$

(34)

Similarly, it can be shown that $P(\{q\ge p\})=0$ and hence

$$\begin{aligned} \xi _{1}=\int \limits _{{\mathcal {X}}}r(x)q(x)d\mu (x)=\int \limits _{\{q<p\}}r(x)dP(x). \end{aligned}$$

(35)

Equations (33), (34) and (35) give that if $P\perp Q$ then $\widetilde{D}_{\phi }^{R}(P,Q)=\overline{\phi }\left( 0\right) \xi _{0}+\overline{\phi ^{*}}\left( 0\right) \xi _{1}$ which completes the proof of this part of the theorem in view of the equations $\overline{\phi } (0)=\phi (0)+\phi _{+}^{\prime }(1)$ and $\overline{\phi ^{*}}(0)=\phi ^{*}(0)-\phi _{+}^{\prime }(1)$.

It remains to prove that if $\phi (0)+\phi ^{*}(0)<\infty$ and $\widetilde{D}_{\phi }^{R}(P,Q)=\overline{\phi }\left( 0\right) \xi _{0}+ \overline{\phi ^{*}}\left( 0\right) \xi _{1}$, then $P\perp Q$. Relationships (24) and (29) immediately lead to

$$\begin{aligned} \widetilde{D}_{\phi }^{R}(P,Q)\le \overline{\phi }\left( 0\right) \int \limits _{\{p<q\}}r(x)dQ(x)+\overline{\phi ^{*}}\left( 0\right) \int \limits _{\{q<p\}}r(x)dP(x). \end{aligned}$$

This last inequality with the assumption $\widetilde{D}_{\phi }^{R}(P,Q)=\overline{\phi }\left( 0\right) \xi _{0}+\overline{\phi ^{*}}\left( 0\right) \xi _{1}$ and $\phi (0)+\phi ^{*}(0)<\infty$ lead to

$$\begin{aligned} \int \limits _{\{p<q\}}r(x)dQ(x)=\xi _{0}\text { and }\int \limits _{\{q<p \}}r(x)dP(x)=\xi _{1}, \end{aligned}$$

and therefore

$$\begin{aligned} \int \limits _{\{p\ge q\}}r(x)dQ(x)=\int \limits _{\{q\ge p\}}r(x)dP(x)=0. \end{aligned}$$

This last equation lead to

$$\begin{aligned} Q(\{p\ge q\})=0\text { and }P(\{q\ge p\})=0, \end{aligned}$$

or

$$\begin{aligned} Q(\{p\ge q\})=0\text { and }P(\{q>p\})=0 \end{aligned}$$

for Radon-Nikodym derivative r positive on ${\mathcal {X}}$. This last conclusion proves that $P\perp Q$ and the proof of the theorem is completed. $\square$

Appendix 2

This appendix provides a detailed proof of Proposition 3.

Proof of Proposition 3

Based on (14), straightforward calculations give

$$\begin{aligned} K_{\lambda ,\omega }(\theta _{1},\theta _{2})= & {} \exp \{\lambda C(\theta _{2})-(\lambda +1)C(\theta _{1})-C(\omega )+C((\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega )\} \\&\times \int \limits _{{\mathcal {X}}}\exp \{h(x)\}\exp \left\{ \left( \sum \limits _{i=1}^{k}[(\lambda +1)\theta _{1i}-\lambda \theta _{2i}+\omega _{i}]T_{i}(x)\right) \right. \\&-C((\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega )+h(x)\}d\mu (x). \end{aligned}$$

Taking into account (19) and (21),

$$\begin{aligned} K_{\lambda ,\omega }(\theta _{1},\theta _{2})=\exp \left\{ M_{C,\lambda }^{(2)}(\theta _{1},\theta _{2},\omega )\right\} E_{(\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega }\{\exp (h(x))\}. \end{aligned}$$

(36)

On the other hand, it can be easily shown that $E_{\theta _{j}}\left( f_{\omega }(X)\right) =\int _{{\mathcal {X}}}f_{\omega }(x)f_{C}(x,\theta _{j})d\mu (x)$, $j=1,2,$ defined by (15), is given by

$$\begin{aligned} E_{\theta _{j}}\left( f_{\omega }(X)\right)= & {} \exp \{-C(\theta _{j})-C(\omega )+C(\theta _{j}+\omega )\} \\&\times \int \limits _{{\mathcal {X}}}\exp (h(x))\exp \left\{ \left( \sum \limits _{i=1}^{k}(\omega _{i}+\theta _{ji})T_{i}(x)-C(\theta _{j}+\omega )+h(x)\right) \right\} \\&\quad d\mu (x),\;j=1,2, \end{aligned}$$

and therefore

$$\begin{aligned} E_{\theta _{j}}\left( f_{\omega }(X)\right) =\exp \{-C(\theta _{j})-C(\omega )+C(\theta _{j}+\omega )\}E_{\theta _{j}+\omega }\left( \exp \left( h(X)\right) \right) ,\text { }j=1,2. \end{aligned}$$

(37)

The result (18) follows as an application of (13), (36) and (37). $\square$

Appendix 3

This appendix provides a detailed proof of Proposition 4.

Proof of Proposition 4

Based on Proposition 3,

(38)

with $\theta _{1}=(\theta _{11},\theta _{12})=(\Sigma _{1}^{-1}\mu _{1},- \frac{1}{2}\Sigma _{1}^{-1})$, $\theta _{2}=(\theta _{21},\theta _{22})=(\Sigma _{2}^{-1}\mu _{2},-\frac{1}{2}\Sigma _{2}^{-1})$, $\omega =(\omega _{1},\omega _{2})=(\Sigma ^{-1}\mu ,-\frac{1}{2}\Sigma ^{-1})$ and

$$\begin{aligned} M_{C,\lambda }^{(2)}(\theta _{1},\theta _{2},\omega )=\lambda C(\theta _{2})-(\lambda +1)C(\theta _{1})-C(\omega )+C((\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega ). \end{aligned}$$

(39)

Based on (22),

$$\begin{aligned} C(\theta _{i})= & {} \log \left( (2\pi )^{k/2}|\Sigma _{i}|^{1/2}\right) +\frac{1}{ 2}\mu _{i}^{t}\Sigma _{i}^{-1}\mu _{i},i=1,2 \nonumber \\ C(\omega )= & {} \log \left( (2\pi )^{k/2}|\Sigma |^{1/2}\right) +\frac{1}{2}\mu ^{t}\Sigma ^{-1}\mu . \end{aligned}$$

(40)

On the other hand,

$$\begin{aligned} \theta _{1}+\omega =\left( \Sigma _{1}^{-1}\mu _{1}+\Sigma ^{-1}\mu ,-\frac{1 }{2}(\Sigma _{1}^{-1}+\Sigma ^{-1})\right) , \end{aligned}$$

and it is immediate to see, by means of (22), that

$$\begin{aligned} C(\theta _{1}+\omega )= & {} \log \left( (2\pi )^{k/2}|\Sigma ^{-1}+\Sigma _{1}^{-1}|^{-1/2}\right) \nonumber \\&+\frac{1}{2}\left( \Sigma ^{-1}\mu +\Sigma _{1}^{-1}\mu _{1}\right) ^{t}\left( \Sigma ^{-1}+\Sigma _{1}^{-1}\right) ^{-1}\left( \Sigma ^{-1}\mu +\Sigma _{1}^{-1}\mu _{1}\right) .\quad \quad \end{aligned}$$

(41)

Taking into account the identity (cf. Pardo 2006, p. 49)

$$\begin{aligned}&\left( \Sigma ^{-1}\mu +\Sigma _{i}^{-1}\mu _{i}\right) ^{t}\left( \Sigma ^{-1}+\Sigma _{i}^{-1}\right) ^{-1}\left( \Sigma ^{-1}\mu +\Sigma _{i}^{-1}\mu _{i}\right) -\mu ^{t}\Sigma ^{-1}\mu -\mu _{i}^{t}\Sigma _{i}^{-1}\mu _{i} \\&\qquad =-(\mu -\mu _{i})^{t}(\Sigma +\Sigma _{i})^{-1}(\mu -\mu _{i}),\quad i=1,2, \end{aligned}$$

straightforward algebra entails that

$$\begin{aligned} C(\theta _{i}+\omega )-C(\theta _{i})-C(\omega )= & {} \log \left( (2\pi )^{-k/2}|\Sigma ^{-1}+\Sigma _{i}^{-1}|^{-1/2}|\Sigma |^{-1/2}|\Sigma _{i}|^{-1/2}\right) \nonumber \\&-\frac{1}{2}(\mu -\mu _{i})^{t}(\Sigma +\Sigma _{i})^{-1}(\mu -\mu _{i}),\quad i=1,2.\nonumber \\ \end{aligned}$$

(42)

It remains to evaluate $M_{C,\lambda }^{(2)}(\theta _{1},\theta _{2},\omega )$, given by (39). It is easy to see that

$$\begin{aligned} (\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega= & {} \left( (\lambda +1)\Sigma _{1}^{-1}\mu _{1}-\lambda \Sigma _{2}^{-1}\mu _{2}+\Sigma ^{-1}\mu ,\right. \\&\left. (-1/2)\left( (\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}\right) \right) , \end{aligned}$$

and therefore

$$\begin{aligned} C((\lambda +1)\theta _{1}-\lambda \theta _{2}+\omega )= & {} \log \left( (2\pi )^{k/2}|(\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}|^{-1/2}\right) \nonumber \\&+\frac{1}{2}\left( (\lambda +1)\Sigma _{1}^{-1}\mu _{1}-\lambda \Sigma _{2}^{-1}\mu _{2}+\Sigma ^{-1}\mu \right) ^{t}\nonumber \\&\times \, \left( (\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}\right) ^{-1} \nonumber \\&\times \left( (\lambda +1)\Sigma _{1}^{-1}\mu _{1}-\lambda \Sigma _{2}^{-1}\mu _{2}+\Sigma ^{-1}\mu \right) , \end{aligned}$$

(43)

with $(\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}>0,$ for $\lambda \ne 0,-1$. Based now on (39), (40) and (43),

$$\begin{aligned} M_{C,\lambda }^{(2)}(\theta _{1},\theta _{2},\omega )= & {} \log \left( (2\pi )^{-k/2}\right) |\Sigma |^{-\frac{1}{2}}|\Sigma _{1}|^{-\frac{ \lambda +1}{2}}|\Sigma _{2}|^{\frac{\lambda }{2}}\nonumber \\&\times \, \left| (\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}\right| ^{- \frac{1}{2}} \nonumber \\&-\frac{1}{2}\left( \mu ^{t}\Sigma ^{-1}\mu +(\lambda +1)\mu _{1}^{t}\Sigma _{1}^{-1}\mu _{1}-\lambda \mu _{2}^{t}\Sigma _{2}^{-1}\mu _{2}-B_{1}^{t}B_{2}B_{1}\right) ,\nonumber \\ \end{aligned}$$

(44)

with

$$\begin{aligned} B_{1}= & {} (\lambda +1)\Sigma _{1}^{-1}\mu _{1}-\lambda \Sigma _{2}^{-1}\mu _{2}+\Sigma ^{-1}\mu , \\ B_{2}= & {} \left( (\lambda +1)\Sigma _{1}^{-1}-\lambda \Sigma _{2}^{-1}+\Sigma ^{-1}\right) ^{-1}. \end{aligned}$$

Taking into account that $h(X)=0$ (cf. Eq. (22)), the result follows as an application of (38), (42) and (44). $\square$

Appendix 4

This appendix provides a detailed proof of Proposition 5.

Proof of Proposition 5

(a) Based on (23) and taking into account (12), straightforward algebra leads to the desired result.

(b) Based on part (a) and on Eq. (22),

$$\begin{aligned} D_{0}^{(\mu ,\Sigma )}((\mu _{1},\Sigma _{1}),(\mu _{2},\Sigma _{2}))= & {} \exp \{C(\theta _{1}+\omega )-C(\theta _{1})-C(\omega )\} \nonumber \\&\times \left( C(\theta _{2})-C(\theta _{1})+(\theta _{1}-\theta _{2})^{t}E_{\theta _{1}+\omega }\left( T(X)\right) \right) \nonumber \\&-\exp \{C(\theta _{1}+\omega )-C(\theta _{1})-C(\omega )\} \nonumber \\&+\exp \{C(\theta _{2}+\omega )-C(\theta _{2})-C(\omega )\}, \end{aligned}$$

(45)

with

$$\begin{aligned} \theta _{i}=\left( \Sigma _{i}^{-1}\mu _{i},- \frac{1}{2}\Sigma _{i}^{-1}\right) ,i=1,2,\;\omega =\left( \Sigma ^{-1}\mu ,- \frac{1}{2}\Sigma ^{-1}\right) \text { and }T(X)=\left( X,XX^{t}\right) . \end{aligned}$$

(46)

Simple algebraic manipulations lead to,

$$\begin{aligned} C(\theta _{2})-C(\theta _{1})=\frac{1}{2}\left( \log \frac{|\Sigma _{2}|}{ |\Sigma _{1}|}+\mu _{2}^{t}\Sigma _{2}^{-1}\mu _{2}-\mu _{1}^{t}\Sigma _{1}^{-1}\mu _{1}\right) . \end{aligned}$$

(47)

On the other hand, taking into account that

$$\begin{aligned} E_{\theta _{1}+\omega }(X)=\int \limits _{{\mathcal {X}}}xf_{C}(x,\theta _{1}+\omega )d\mu (x), \end{aligned}$$

Eq. (46) entails,

$$\begin{aligned} E_{\theta _{1}+\omega }(X)=\left( \Sigma ^{-1}+\Sigma _{1}^{-1}\right) ^{-1}\left( \Sigma ^{-1}\mu +\Sigma _{1}^{-1}\mu _{1}\right) . \end{aligned}$$

(48)

Then,

$$\begin{aligned} E_{\theta _{1}+\omega }\left( XX^{t}\right)= & {} Var_{\theta _{1}+\omega }(X)+\left( E_{\theta _{1}+\omega }(X)\right) \left( E_{\theta _{1}+\omega }(X)\right) ^{t} \nonumber \\= & {} (\Sigma ^{-1}+\Sigma _{1}^{-1})^{-1}+\left\{ (\Sigma ^{-1}+\Sigma _{1}^{-1})^{-1}\left( \Sigma ^{-1}\mu +\Sigma _{1}^{-1}\mu _{1}\right) \right. \nonumber \\&\times \left. \left( \Sigma ^{-1}\mu +\Sigma _{1}^{-1}\mu _{1}\right) ^{t}(\Sigma ^{-1}+\Sigma _{1}^{-1})^{-1}\right\} \end{aligned}$$

(49)

and

$$\begin{aligned} \theta _{1}-\theta _{2}=\left( \Sigma _{1}^{-1}\mu _{1}-\Sigma _{2}^{-1}\mu _{2},-\frac{1}{2}\left( \Sigma _{1}^{-1}-\Sigma _{2}^{-1}\right) \right) . \end{aligned}$$

(50)

Based on (46) and (50), algebraic manipulations entail that,

$$\begin{aligned} (\theta _{1}-\theta _{2})^{t}E_{\theta _{1}+\omega }\left( T(X)\right)= & {} \left( \Sigma _{1}^{-1}\mu _{1}-\Sigma _{2}^{-1}\mu _{2}\right) ^{t}E_{\theta _{1}+\omega }\left( X\right) \nonumber \\&+\,trace\left\{ -\frac{1}{2}\left( \Sigma _{1}^{-1}-\Sigma _{2}^{-1}\right) ^{t}E_{\theta _{1}+\omega }\left( XX^{t}\right) \right\} ,\qquad \end{aligned}$$

(51)

Hence, taking into account (48), (49) and (51)

(52)

with $\mu ^{*}=E_{\theta _{1}+\omega }(X).$ Based on the fact that, for $i=1,2$,

$$\begin{aligned} \exp \left( C(\theta _{i}+\omega )-C(\theta _{i})-C(\omega )\right)= & {} (2\pi )^{-\frac{k}{2}}|\Sigma |^{-\frac{1}{2}}|\Sigma _{i}|^{-\frac{1}{2} }\left| \Sigma ^{-1}+\Sigma _{i}^{-1}\right| ^{-\frac{1}{2}} \\&\times \exp \left\{ -\frac{1}{2}(\mu -\mu _{i})^{t}(\Sigma +\Sigma _{i})^{-1}(\mu -\mu _{i})\right\} \\= & {} E_{(\mu _{i},\Sigma _{i})}\left( f_{N(\mu ,\Sigma )}(X)\right) , \end{aligned}$$

Eqs. (42), (45), (47) and (52) complete the proof of part (b) of the proposition. $\square$