Asymptotic efficiency of new exponentiality tests based on a characterization

Abstract

Two new tests for exponentiality, of integral- and Kolmogorov-type, are proposed. They are based on a recent characterization and formed using appropriate V-statistics. Their asymptotic properties are examined and their local Bahadur efficiencies against some common alternatives are found. A class of locally optimal alternatives for each test is obtained. The powers of these tests, for some small sample sizes, are compared with different exponentiality tests.

1 Introduction

The exponential distribution is probably one of the most applicable distributions in reliability theory, survival analysis, and many other fields. Therefore, ensuring that the data come from the exponential family of distributions is of great importance. Goodness of fit testing for exponentiality has been popular for decades, and in recent times tests based on characterizations have become one of the primary directions. Many interesting characterizations of the exponential distribution can be found in Ahsanullah and Hamedani (2010), Arnold et al. (2008), Balakrishnan and Rao (1998) and Galambos and Kotz (1978). Goodness of fit tests based on characterizations of the exponential distribution are studied in Ahmad and Alwasel (1999), Angus (1982), Koul (1977, (1978), among others. In particular, the Bahadur efficiency of such tests has been considered in, e.g., Nikitin (1996), Nikitin and Volkova (2010), Volkova (2010).

Recently Obradović (2015) proved three new characterizations of the exponential distribution based on order statistics in small samples. In this paper we propose two new goodness of fit tests based on one of those characterizations:

Let $X_0,X_1,X_2,X_3$ be independent and identically distributed (i.i.d.) non-negative random variables from a distribution that has a density f whose Maclaurin’s expansion converges for $x>0$. Let $X_{(2;3)}$ and $X_{(3;3)}$ be the median and maximum of $\{X_1, X_2, X_3\}$, respectively. If

$$\begin{aligned} X_0 + X_{(2;3)}\overset{d}{=} X_{(3;3)} \end{aligned}$$

then $f(x)=\lambda e^{-\lambda x}$ for some $\lambda >0$.

Let $X_1,X_2,\ldots ,X_n$ be i.i.d. observations having a continuous distribution function F. We test the composite hypothesis $H_0$ that F belongs to the family of exponential distributions ${\mathcal {E}}(\lambda )$, where $\lambda >0$ is an unknown parameter.

We shall consider the following integral and Kolmogorov-type test statistics which are invariant with respect to the scale parameter $\lambda$:

$$\begin{aligned} I_n= & {} \int \limits _{0}^{\infty }\int \limits _{0}^{\infty }(H_n(t)-G_n(t))dF_n(t),\\ K_n= & {} \sup \limits _{t\ge 0}\big |H_n(t)-G_n(t)\big |, \end{aligned}$$

where

$$\begin{aligned} G_n(t)&=\frac{1}{n^4}\sum \limits _{i=1}^n\sum \limits _{j=1}^n\sum \limits _{k=1}^n\sum \limits _{l=1}^nI\{X_i+\mathrm{med}(X_j,X_k,X_l)<t\},\\ H_n(t)&=\frac{1}{n^3}\sum \limits _{j=1}^n\sum \limits _{k=1}^n\sum \limits _{l=1}^nI\{\max (X_j,X_k,X_l)<t\}. \end{aligned}$$

In order to determine the quality of our tests that reject $H_0$ for large values of $I_n$ or $K_n$, and to compare them with some other tests we shall use local Bahadur efficiency. We choose this type of asymptotic efficiency since it is applicable to non-normally distributed test statistics such as the Kolmogorov statistic. For asymptotically normally distributed test statistics the local Bahadur efficiency and the classical Pitman efficiency coincide (see Wieand 1976).

The paper is organized as follows. In Sect. 2 we study the integral statistic $I_n$. We find its asymptotic distribution, large deviations and calculate its asymptotic efficiency against some common alternatives. We also present a class of locally optimal alternatives. In Sect. 3 we do the analogous study for Kolmogorov-type statistics. In Sects. 4 and 5 we compare our tests with some existing tests for exponentiality and give a real data example.

2 Integral-type statistic $I_n$

The statistic $I_n$ is asymptotically equivalent to the V-statistic with symmetric kernel (Korolyuk and Borovskikh 1994)

$$\begin{aligned} \varPsi (X_1,X_2,X_3,X_4,X_5)= & {} \frac{1}{5!}\sum \limits _{\pi (1:5)}\big (I\{\max (X_{\pi _2},X_{\pi _3},X_{\pi _4})<X_{\pi _5}\}\\&- I\{X_{\pi _1}+\mathrm{med}(X_{\pi _2},X_{\pi _3},X_{\pi _4})<X_{\pi _5}\}\big ), \end{aligned}$$

where $\pi (1:m)$ is the set of all permutations $\{\pi _1,\pi _2,...,\pi _m\}$.

Its projection on $X_1$ under $H_0$ is

$$\begin{aligned} \psi (s)= & {} E(\varPsi (X_1,X_2,X_3,X_4,X_5)|X_1=s)\\ {}= & {} \frac{1}{5}\Big (P\{\max (X_2,X_3,X_4)<X_5\}-P\{s+\mathrm{med}(X_2,X_3,X_4)<X_5\}\Big )\\&+\frac{3}{5}\Big (P\{\max (s,X_3,X_4)<X_5\}-P\{X_2+\mathrm{med}(s,X_3,X_4)<X_5\}\Big )\\&+ \frac{1}{5}\Big (P\{\max (X_3,X_4,X_5)<s\}-P\{X_2+\mathrm{med}(X_3,X_4,X_5)<s\}\Big ). \end{aligned}$$

After some calculations we get

$$\begin{aligned} \psi (s)=-\frac{1}{20}+\frac{2}{5}e^{-3s}-\frac{9}{10}e^{-2s}+\frac{1}{2}e^{-s}. \end{aligned}$$

The expected value of this projection is equal to zero, while its variance is

$$\begin{aligned} \sigma ^2_{I}=E(\psi ^2(X_1))=\frac{29}{42000}. \end{aligned}$$

Hence this kernel is non-degenerate. and therefore we can consider instead of V-statistic $I_n$ the corresponding U-statistic with the same kernel which has almost identical asymptotic properties. Applying Hoeffding’s theorem (Hoeffding 1948) for non-degenerate U-statistics the asymptotic distribution of $\sqrt{n}I_n$ is normal $\mathcal {N}(0,\frac{29}{1680})$.

2.1 Local Bahadur efficiency

One way of measuring the quality of the tests is calculating their Bahadur asymptotic efficiency. This quantity can be expressed as the ratio of the Bahadur exact slope, a function describing the rate of exponential decrease for the attained level under the alternative, and the double Kullback–Leibler distance between the null and the alternative distribution. More about theory on this topic can be found in Bahadur (1971), Nikitin (1995).

According to Bahadur’s theory the exact slopes are defined in the following way. Suppose that, under an alternative indexed by a parameter $\theta$, the sequence $\{T_n\}$ of test statistics converges in probability to some finite function $b(\theta )$. Suppose also that the large deviations limit

$$\begin{aligned} \lim _{n\rightarrow \infty } n^{-1} \ln P_{H_0} \left( T_n \ge t \right) = - f(t) \end{aligned}$$

(1)

exists for any t in an open interval I,  on which f is continuous and $\{b(\theta ), \, \theta > 0\}\subset I$. Then the Bahadur exact slope is

$$\begin{aligned} c_T(\theta ) = 2f(b(\theta )). \end{aligned}$$

(2)

The exact slopes always satisfy the inequality

$$\begin{aligned} c_T(\theta ) \le 2 K(\theta ),\, \theta > 0, \end{aligned}$$

(3)

where $K(\theta )$ is the Kullback–Leibler distance between the alternative $H_1$ and the null hypothesis $H_0.$

Given (3), the local Bahadur efficiency of the sequence of statistics ${T_n}$ is defined as

$$\begin{aligned} e^B (T) = \lim _{\theta \rightarrow 0} \frac{c_T(\theta )}{2K(\theta )}. \end{aligned}$$

(4)

Let $G(\cdot ,\theta ), \theta \ge 0$, be a family of distribution functions with densities $g(\cdot ,\theta )$, such that $G(\cdot ,0)\in \mathcal {E}(\lambda )$ and the regularity conditions from [Nikitin (1995), Chapter 6], including differentiation along $\theta$ in all appearing integrals, hold. Let $h(x)=g'_{\theta }(x,0)$. It is obvious that $\int _{0}^{\infty }h(x)dx=0$.

We now calculate the Bahadur exact slope for the test statistic $I_n$.

Lemma 1

For the stati stic $I_n$ the function $f_{I}$ from (1) is analytic for sufficiently small $\varepsilon >0$, and we have

$$\begin{aligned} f_{I}(\varepsilon )=\frac{840}{29}\varepsilon ^2+o(\varepsilon ^2),\; \varepsilon \rightarrow 0. \end{aligned}$$

Proof

The kernel $\varPsi$ is bounded, centered and non-degenerate. Therefore we can apply the theorem of large deviations for non-degenerate U-statistics (Nikitin and Ponikarov 2001) and get the statement of the lemma. $\square$

Lemma 2

For a given alternative density $g(x;\theta )$ whose distribution belongs to ${\mathcal {G}}$, we have

$$\begin{aligned} b(\theta )= 5\theta \int \limits _{0}^{\infty }\psi (x)h(x)dx+o(\theta ),\;\;\text {as } \theta \rightarrow 0. \end{aligned}$$

The proof follows from the general result in Nikitin and Peaucelle (2004).

The Kullback–Leibler distance from the alternative density $g(x,\theta )$ from ${\mathcal {G}}$ to the class of exponential densities $\{\lambda e^{-\lambda x}, \quad x\ge 0 \}$, is

$$\begin{aligned} K(\theta ) = \inf _{\lambda >0} \int _0^{\infty } \ln [g(x,\theta ) / \lambda \exp (-\lambda x) ] g(x,\theta ) \ dx. \end{aligned}$$

(5)

It can be shown (Nikitin and Tchirina 1996) that for small $\theta$ Eq. (5) can be expressed as

$$\begin{aligned} 2K(\theta )=\left( \int \limits _{0}^{\infty }h^2(x)e^xdx-\left( \int \limits _{0}^{\infty }xh(x)dx\right) ^2\right) \cdot \theta ^2+o(\theta ^2). \end{aligned}$$

(6)

This quantity can be easily calculated as $\theta \rightarrow 0$ for particular alternatives.

In what follows we shall calculate the local Bahadur efficiency of our test for some alternatives. These alternatives are:

• a Weibull distribution with density

  $$\begin{aligned} g(x,\theta )=e^{-x^{1 + \theta }} (1 + \theta ) x^{\theta },\;\theta > 0,\; x\ge 0; \end{aligned}$$

  (7)

• a Makeham distribution with density

  $$\begin{aligned} g(x,\theta )=(1+\theta (1-e^{-x}))\exp (-x-\theta ( e^{-x}-1+x)),\;\theta > 0, \;x\ge 0; \end{aligned}$$

  (8)

• an exponential mixture with negative weights (EMNW($\beta$)) (Jevremović 1991) with density

  $$\begin{aligned} g(x,\theta )=(1+\theta )e^{-x}-\beta \theta e^{\beta x},\; \theta \in \left( 0,\frac{1}{\beta -1}\right] ,\; x\ge 0; \end{aligned}$$

  (9)

• a generalized exponential distribution (GED) (Nadarajah and Haghighi 2010) with density

  $$\begin{aligned} g(x,\theta )=e^{1 - (1 + x)^{1 + \theta }} (1 + \theta ) (1 + x)^{\theta }\;\theta > 0, x\ge 0; \end{aligned}$$

  (10)

• an extended exponential distribution (EE) (Gomez et al. 2014) with density

  $$\begin{aligned} g(x,\theta )=\frac{1 + \theta x}{1 + \theta }e^{-x},\; \theta > 0,\; x\ge 0. \end{aligned}$$

  (11)

In the following two examples we shall present the calculations of the local Bahadur efficiency.

Example 1

Let the alternative hypothesis be a Weibull distribution with density function (7). The first derivative along $\theta$ of its density at $\theta = 0$ is

$$\begin{aligned} h(x)=e^{-x} + e^{-x} \log x - e^{-x} x \log x. \end{aligned}$$

Using (6) the Kullback–Leibler distance is $K(\theta )=\frac{\pi ^2}{6}\theta ^2+o(\theta ^2),\;\;\theta \rightarrow 0.$ Applying Lemma 2 we have

$$\begin{aligned} b_{I}(\theta )&=5\theta \int \limits _{0}^{\infty }\psi (x)(e^{-x} + e^{-x} \log x - e^{-x} x \log x)dx+o(\theta )\\&=\log \bigg (\frac{3}{2^{11/8}}\bigg )\theta +o(\theta )\approx 0.146\theta + o(\theta ),\;\;\theta \rightarrow 0. \end{aligned}$$

According to Lemma 1 and (4) the local Bahadur efficiency is $e_B(I)=0.746$.

The reasoning for alternatives (8–10) is analogous. Their efficiencies are given in Table 1. The exception is the alternative (11) where Lemma 2 and (6) cannot be applied. We present it in the following example.

Table 1 Local Bahadur efficiency for the statistic $I_n$

Example 2

Consider the alternative (EE) with density function (11). Its first derivative along $\theta$ at $\theta = 0$ is

$$\begin{aligned} h(x)=-e^{-x} + e^{-x} x. \end{aligned}$$

The expressions $\int _{0}^{\infty } h(x)\psi (x)dx$ and $\int _{0}^{\infty }h^2(x)e^xdx-\Big (\int _{0}^{\infty }xh(x)dx\Big )^2$ are equal to zero, hence we need to expand the series for $b_{I}(\theta )$ and $2K(\theta )$ to the first non-zero term. The limit in probability $b_I(\theta )$ is equal to

$$\begin{aligned} b_I(\theta )&=P\{\max (X_2,X_3,X_4)<X_5\}-P\{X_1+\mathrm{med}(X_2,X_3,X_4)<X_5\}\\&=\frac{1}{4}-6\int \limits _{0}^{\infty }g(x,\theta )\int \limits _{0}^{\infty }G(y,\theta )(1-G(y,\theta ))g(y,\theta ) \int \limits _{x+y}^{\infty }g(z,\theta )dz dy dx \\&=\frac{\theta ^2 (168 + 356 \theta + 161 \theta ^2)}{2304 (1 + \theta )^4}=\frac{7}{96}\theta ^2+o(\theta ^2),\;\;\theta \rightarrow 0. \end{aligned}$$

The double Kullback–Leibler distance (5) from (11) to the family of exponential distributions is

$$\begin{aligned} 2K(\theta )=2\frac{(1 + \theta ) \log ( 1 + 2 \theta )-e^{1/\theta } \theta Ei(-(1/\theta ))}{(1 + \theta )^2}=\theta ^4+o(\theta ^4),\;\;\theta \rightarrow 0, \end{aligned}$$

(12)

where $Ei(z)=\int _{-z}^{\infty }u^{-1}e^{-u}du$ is the exponential integral. According to Lemma 1 and (4) the local Bahadur efficiency is $e_B(I)=0.481$.

We can notice from Table 1 that all efficiencies are reasonably high except for case (11), the example which was included to show the exception in calculation.

2.2 Locally optimal alternatives

In this section we determine some of those alternatives for which the statistic $I_n$ is locally asymptotically optimal in the Bahadur sense. More on this topic can be found in Nikitin (1995) and Nikitin (1984). We shall determine some of those alternatives in the following theorem.

Theorem 1

Let $g(x;\theta )$ be a density from ${\mathcal {G}}$ that satisfies the condition

$$\begin{aligned} \int \limits _{0}^{\infty } e^{x}h^2(x)dx<\infty . \end{aligned}$$

Then, for small $\theta$, the alternative densities

$$\begin{aligned} g(x;\theta )=e^{-x}+e^{-x}\theta (C\psi (x)+D(x-1)),\; x\ge 0,\;C>0,\; D\in \mathbb {R}, \end{aligned}$$

are locally asymptotically optimal for the test based on $I_n$.

Proof

Put

$$\begin{aligned} h_0(x)=h(x)-(x-1)e^{-x}\int \limits _{0}^{\infty } h(s)s ds. \end{aligned}$$

(13)

It is easy to show that this function satisfies the following equalities:

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty } h_0^2(x) e^{x}dx=\int \limits _{0}^\infty e^{x}h^{2}(x)dx- \bigg (\int \limits _{0}^{\infty } h(x)x dx\bigg )^2,\\&\int \limits _{0}^{\infty } \psi (x)h_0(x)dx=\int \limits _{0}^{\infty } \psi (x)h(x)dx. \end{aligned} \end{aligned}$$

(14)

The local asymptotic efficiency is

$$\begin{aligned} e^{B}_I&=\lim \limits _{\theta \rightarrow 0}\frac{c_{I}(\theta )}{2K(\theta )}= \lim \limits _{\theta \rightarrow 0}\frac{2f(b_{I}(\theta ))}{2K(\theta )}= \lim \limits _{\theta \rightarrow 0}\frac{2\cdot \frac{840}{29}b^2_{I}(\theta )}{2K(\theta )} =\lim \limits _{\theta \rightarrow 0}\frac{b_{I}^2(\theta )}{25\sigma _{I}^2 2K(\theta )}\\&= \lim \limits _{\theta \rightarrow 0} \frac{25\theta ^2\bigg (\int \limits _{0}^{\infty }\psi (x)h(x)dx\bigg )^2+o(\theta ^2)}{25 \int \limits _{0}^\infty \psi ^2(x) e^{-x}dx \bigg (\theta ^2\left( \int \limits _{0}^\infty e^xh^{2}(x)dx- \Bigg (\int \limits _{0}^{\infty } h(x)x dx\Bigg )^2\right) +o(\theta ^{2})\bigg )}\\ {}&= \frac{\bigg (\int \limits _{0}^{\infty }\psi (x)h(x)dx\bigg )^2}{ \int \limits _{0}^\infty \psi ^2(x) e^{-x}dx \bigg (\int \limits _{0}^\infty e^xh^{2}(x)dx- \Bigg (\int \limits _{0}^{\infty } h(x)x dx\Bigg )^2\bigg )}\\&= \frac{\bigg (\int \limits _{0}^{\infty }\psi (x)h_0(x)dx\bigg )^2}{ \int \limits _{0}^\infty \psi ^2(x) e^{-x }dx \int \limits _{0}^{\infty } h^2_0(x) e^xdx }. \end{aligned}$$

From the Cauchy–Schwarz inequality we have that $e^{B}_I=1$ if and only if $h_0(x)=C\psi (x) e^{-x}$. Inserting this expression in (13) we obtain h(x). The densities from the statement of the theorem have the same h(x), hence the proof is completed. $\square$

3 Kolmogorov-type statistic $K_n$

For a fixed $t>0$ the expression $H_n(t)-G_n(t)$ is a V-statistic with kernel:

$$\begin{aligned} \varXi (X_1,X_2,X_3,X_4,t)&=\frac{1}{4!}\sum \limits _{\pi (1:4)}\Big ( I\{\max (X_{\pi _2},X_{\pi _3},X_{\pi _4})<t\}\\&\,\,\quad -I\{X_{\pi _1}+\mathrm{med}(X_{\pi _2},X_{\pi _3},X_{\pi _4})<t\}\Big ). \end{aligned}$$

The projection of this family of kernels on $X_1$ under $H_0$ is

$$\begin{aligned} \xi (s,t)&=E(\varXi (X_1,X_2,X_3,X_4,t)|X_1=s)\\&=\frac{1}{4}\Big (P\{\max (X_2,X_3,X_4)<t\}-P\{s+\mathrm{med}(X_2,X_3,X_4)<t\}\Big )\\&\quad +\frac{3}{4}\Big (P\{\max (s,X_3,X_4)<t\}-P\{X_2+\mathrm{med}(s,X_3,X_4)<t\}\Big ). \end{aligned}$$

After some calculations we get

$$\begin{aligned} \xi (s,t)&= \frac{1}{4}I\{s<t\}e^{-s-3t}\left( -e^s-2e^{4s}+6e^{2t}+3e^{s+t}+3e^{3s+t}-e^{s+2t}(9-6s)\right) \\&\quad + \frac{1}{4}I\{s\ge t\}e^{-3t}\left( -1+6e^t-2e^{3t}-e^{2t}(3-6t)\right) . \end{aligned}$$

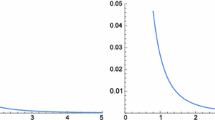
The variances of these projections $\sigma _K^2(t)$ under $H_{0}$ are

$$\begin{aligned} \sigma _K^2(t)&=\frac{9}{80}e^{-6t}-\frac{3}{8}e^{-5t}-\frac{3}{8}e^{-4t}-\frac{9}{8}e^{-3t}+\frac{33}{16}e^{-2t}-\frac{3}{10}e^{-t}. \end{aligned}$$

The plot of this function is shown in Fig. 1.

Fig. 1

Plot of the function $\sigma _K^2(t)$

We find that

$$\begin{aligned} \sigma _K^2=\sup _{ t\ge 0} \sigma _K^2(t)=0.017. \end{aligned}$$

The supremum is attained for $t_0=1.892$. Therefore, our family of kernels $\varXi (X_1,X_2,X_3,X_4,t)$ is non-degenerate as defined in Nikitin (2010). It can be shown (see Silverman 1983) that the U-empirical process

$$\begin{aligned} \sqrt{n} \left( H_n(t) - G_n(t)\right) , \ t\ge 0, \end{aligned}$$

converges weakly in $D(0,\infty )$ as $n \rightarrow \infty$ to a centered Gaussian process $\nu (t)$ with calculable covariance. Thus, the sequence of statistics $\sqrt{n}K_n$ converges in distribution to the random variable $\sup _{t\ge 0} |\nu (t)|$ but its distribution is unknown.

Critical values for the statistic $K_n$ for different sample sizes and levels of significance are shown in the Table 2. They are calculated using Monte Carlo methods based on 10,000 replications.

Table 2 Critical values for the statistic $K_n$

3.1 Local Bahadur efficiency

The family of kernels $\{\varXi _4 (X_1,X_2,X_3,X_4,t),\;t\ge 0\}$ is centered and bounded in the sense described in Nikitin (2010). Applying the large deviation theorem for the supremum of the family of non-degenerate U- and V-statistics from Nikitin (2010), we find the function f from (1).

Lemma 3

For the statistic $K_n$ the function $f_{K}$ from (1) is analytic for sufficiently small $\varepsilon >0$, and

$$\begin{aligned} f_{K}(\varepsilon )=\frac{1}{32\sigma ^{2}_K}\varepsilon ^2+o\left( \varepsilon ^2\right) \approx 1.84\varepsilon ^2+o\left( \varepsilon ^2\right) ,\; \epsilon \rightarrow 0. \end{aligned}$$

Lemma 4

For a given alternative density $g(x;\theta )$ whose distribution belongs to ${\mathcal {G}}$ we have

$$\begin{aligned} b_K(\theta ) = 4\theta \sup \limits _{t\ge 0} \big | \int _{0}^{\infty } \xi (x;t)h(x)dx\big |+o(\theta ), \, \theta \rightarrow 0. \end{aligned}$$

Using the Glivenko–Cantelli theorem for V-statistics (Helmers et al. 1988) we have

$$\begin{aligned} b_K(\theta )&=\sup \limits _{t\ge 0} \big |P\{\max (X_2,X_3,X_4)<t\}-P\{X_1+\mathrm{med}(X_2,X_3,X_4)<t\}\big |\nonumber \\&=\sup \limits _{t\ge 0} \big |G^3(t,\theta )-6\int \limits _{0}^tg(x,\theta )\int \limits _{0}^{t-x}G(y,\theta )(1-G(y,\theta ))g(y,\theta )dydx\big |. \end{aligned}$$

(15)

Put

$$\begin{aligned} a(t,\theta )=G^3(t,\theta )-6\int \limits _{0}^tg(x,\theta )\int \limits _{0}^{t-x}G(y,\theta )(1-G(y,\theta ))g(y,\theta )dydx. \end{aligned}$$

(16)

After differentiating under the integral sign and some more calculations we get

$$\begin{aligned} a_{\theta }'(t,0)&=\int \limits _{0}^{t}h(x)(4\xi (x,t)+e^{-3 t} \left( 1 - 6 e^t + 2 e^{3 t} + e^{2 t} (3 - 6 t)\right) dx\\&=4\int \limits _{0}^{\infty }h(x)\xi (x,t)dx. \end{aligned}$$

Expanding $a(t,\theta )$ in a Maclaurin series and inserting the result into (15) we obtain the statement of the lemma.

Now we calculate the local Bahadur efficiencies in the same manner as we did for the integral-type statistic. For the alternatives (7) and (11) the process of calculations is presented in following two examples, while for the others the values of efficiencies are presented in Table 3.

Table 3 Local Bahadur efficiency for the statistic $K_n$

Example 3

Let the alternative hypothesis be a Weibull distribution with density function (7). Using Lemma 4 we have

$$\begin{aligned} a(t,\theta )=4\theta \int _{0}^{\infty }\xi (x,t)\left( e^{-x} + e^{-x} \log x - e^{-x} x \log x\right) dx+o(\theta ),\;\;\theta \rightarrow 0. \end{aligned}$$

The plot of the function $a_{\theta }'(t,0)$, is shown in Fig. 2. The supremum of $a(t,\theta )$ is attained at $t_1=1.761$, thus $b_K(\theta )=0.34\theta +o(\theta ), \quad \theta \rightarrow 0$.

Using Lemma 3 and Eqs. (2) and (4) we get that the local Bahadur efficiency in case of the statistic $K_n$ is 0.258.

Fig. 2

Plot of the function $a_{\theta }'(t,0)$

Example 4

Let the alternative density function be (11). The function $a(t,\theta )$ from (16) is

$$\begin{aligned} a(t,\theta )&=\frac{3}{4 (1 + \theta )^4} e^{-3 t} \theta ^2 \left( -2 - 8 \theta - 9 \theta ^2 - 2 t^3 \theta ^2 - 4 t^2 \theta (1 + 2 \theta )\right. \\&\quad + 8 e^t (1 + \theta ) \left( 2 + t + 6 \theta + 4 t \theta + t^2 \theta \right) - t \left( 2 + 10 \theta + 13 \theta ^2\right) \\&\quad \left. + e^{2 t} \left( -14 - 56 \theta - 39 \theta ^2 + t \left( 6 + 18 \theta + 11 \theta ^2\right) \right) \right) \\&=\frac{3}{2} \left( -e^{-3t} + 8 e^{-2t} - 7 e^{- t} - te^{-3t} + 4 e^{-2t} t + 3 e^{-t} t\right) \theta ^2+o\left( \theta ^2\right) . \end{aligned}$$

The plot of the function $a_2(t)$, the coefficient next to $\theta ^2$, in the expression above is given in Fig. 3. Thus we have

$$\begin{aligned} \sup _{t\ge 0}|a(t,\theta )|=0.241\theta ^2+o\left( \theta ^2\right) ,\; \theta \rightarrow 0. \end{aligned}$$

The value of the double Kullback–Leibler distance is given in (12). Using Lemma 3 and Eqs. (2) and (4), the local Bahadur efficiency is seen to be 0.213.

Fig. 3

Plot of the function $a_2(t)$

We can see that, as expected, the efficiencies are lower than in case of the integral-type test. However the efficiencies are not that bad compared to some other Kolmogorov-type tests based on characterizations (e. g. Volkova 2010).

3.2 Locally optimal alternatives

In this section we derive one class of alternatives that are locally optimal for the test based on statistic $K_n$.

Theorem 2

Let $g(x;\theta )$ be the density from ${\mathcal {G}}$ that satisfies the condition

$$\begin{aligned} \int \limits _{0}^{\infty } e^{x}h^2(x)dx<\infty . \end{aligned}$$

Then, for small $\theta$, alternative densities

$$\begin{aligned} g(x;\theta )=e^{-x}+e^{-x}\theta (C\xi (x,t_0)+D(x-1)),\; x\ge 0,\;C>0,\; D\in \mathbb {R}, \end{aligned}$$

where $t_0=1.892$, are locally asymptotically optimal for the test based on $K_n$.

Proof

We use the function $h_0$ defined in (13). It can be shown that the function $h_0$ satisfies condition (14), and we have

$$\begin{aligned} \int \limits _{0}^{\infty } \xi (x)h_0(x)dx=\int \limits _{0}^{\infty } \xi (x)h(x)dx. \end{aligned}$$

The local asymptotic efficiency is

$$\begin{aligned} e_{K}&=\lim \limits _{\theta \rightarrow 0}\frac{c_{K}(\theta )}{2K(\theta )}= \lim \limits _{\theta \rightarrow 0}\frac{2f(b_{K}(\theta ))}{2K(\theta )} =\lim \limits _{\theta \rightarrow 0}\frac{b_{K}^2(\theta )}{16\sigma _{K}(t_0)^2 2K(\theta )}\\&= \lim \limits _{\theta \rightarrow 0} \frac{16\theta ^2\sup \limits _{t\ge 0}\bigg (\int \limits _{0}^{\infty }\xi (x,t)h(x)dx\bigg )^2+o(\theta ^2)}{16 \sup \limits _{t \ge 0}\int \limits _{0}^\infty \xi ^2(x,t) e^{-x}dx \bigg (\theta ^2\left( \int \limits _{0}^\infty e^xh^{2}(x)dx- \big (\int \limits _{0}^{\infty } h(x)x dx\big )^2\right) +o(\theta ^{2})\bigg )}\\ {}&= \frac{\sup \limits _{t\ge 0}\bigg (\int \limits _{0}^{\infty }\xi (x,t)h(x)dx\bigg )^2}{ \sup \limits _{t\ge 0}\int \limits _{0}^\infty \xi ^2(x,t) e^{-x}dx \bigg (\int \limits _{0}^\infty e^xh^{2}(x)dx- \big (\int \limits _{0}^{\infty } h(x)x dx\big )^2\bigg )} \\&= \frac{\sup \limits _{t \ge 0}\bigg (\int \limits _{0}^{\infty }\xi (x,t)h_0(x)dx\bigg )^2}{ \int \limits _{0}^\infty \xi ^2(x,t) e^{-x }dx \int \limits _{0}^{\infty } h^2_0(x) e^xdx }. \end{aligned}$$

From the Cauchy–Schwarz inequality we have $e_{K}=1$ if, and only if, $h_0(x)=C\xi (x,t_0) e^{-x}$. Inserting that in (13) we obtain h(x). The densities from the statement of the theorem have the same h(x), hence the proof is completed. $\square$

4 Power comparison

For purpose of comparison we calculated the powers for sample sizes $n=20$ and $n=50$ for some common distributions and compare the results with some other tests for exponentiality which can be found in Henze and Meintanis (2005). The powers are shown in Tables 4 and 5. The labels used are identical to the ones in Henze and Meintanis (2005). Bolded numbers represent cases where our test(s) have the higher or equal power than the competing tests. It can be noticed that in the majority of cases the statistic $I_n$ is the most powerful. Also, the statistic $K_n$ performs better in most cases than the other tests for $n=20$, while it is reasonably competitive for $n=50$. However, there are few cases where the powers of both our tests are unsatisfactory.

Table 4 Percentage of significant samples for different exponentiality tests $n=20, \alpha =0.05$

Table 5 Percentage of significant samples for different exponentiality tests $n=50, \alpha =0.05$

5 Application to real data

This data set represents inter-occurrence times of fatal accidents to British registered passenger aircraft, 1946–1963, measured in number of days and listed in the order of their occurrence in time (see Pyke 1965):

20	106	14	78	94	20	21	136	56	232	89	33	181	424	14
430	155	205	117	253	86	260	213	58	276	263	246	341	1105	50	136.

Applying our tests to these data, we get the following values of the test statistics $I_n$ and $K_n$, as well as the corresponding p values:

Statistic	$I_n$	$K_n$
Value	0.04	0.21
p value	0.32	0.24

so we conclude that the tests do not reject exponentiality.

6 Conclusion

In this paper, we studied two goodness of fit tests for exponentiality based on a characterization. The major advantage of our tests is that they are free of the scale parameter $\lambda$. We calculated the local Bahadur efficiencies for some alternatives and the results are more than satisfactory. We determined a locally optimal class of alternatives for each test. Finally, we compared these tests with some other goodness-of-fit tests and noticed that in most cases our tests were more powerful.