Generalized cumulative residual entropy and record values

Abstract

The Shannon entropy of a random variable has become a very useful tool in Probability Theory. In this paper we extend the concept of cumulative residual entropy introduced by Rao et al. (in IEEE Trans Inf Theory 50:1220–1228, 2004). The new concept called generalized cumulative residual entropy (GCRE) is related with the record values of a sequence of i.i.d. random variables and with the relevation transform. We also consider a dynamic GCRE obtained using the residual lifetime. For these concepts we obtain some characterization results, stochastic ordering and aging classes properties and some relationships with other entropy concepts.

1 Introduction

The classic Shannon entropy of a random variable (r.v.) $X$ is a very useful tool in Probability Theory and Information Theory to measure the uncertainty contained in $X$. If $X$ has an absolutely continuous distribution with probability density function $f$, then the (Shannon) entropy is defined by

$$\begin{aligned} H(X)=-\int f(x) \log f(x)dx, \end{aligned}$$

where, by convention, $0\ln 0=0$. Dynamic versions of the classic Shannon entropy were considered in Ebrahimi and Pellerey (1995), Ebrahimi (1996) and Belzunce et al. (2004). For example, when $X$ is nonnegative, Ebrahimi and Pellerey (1995) considered the entropy of the residual lifetime $X_t=(X-t|X>t)$ given by

$$\begin{aligned} H(X;t)=H(X_t)=-\int \limits _0^\infty \frac{f(x+t)}{\overline{F}(t)} \log \frac{f(x+t)}{\overline{F}(t)}dx \end{aligned}$$

for $t\ge 0$ such that $\overline{F}(t)>0$, where $\overline{F}(t)=\Pr (X>t)$ is the reliability (survival) function of $X$. In particular, $H(X;0)=H(X)$.

Recently, Rao et al. (2004) (see also Rao 2005) defined the cumulative residual entropy (CRE) replacing the probability density function by the reliability function, that is,

$$\begin{aligned} \mathcal E (X)=-\int \overline{F}(t) \log \overline{F}(t) dt. \end{aligned}$$

Several properties of the CRE were obtained in these papers and in Asadi and Zohrevand (2007) and Navarro et al. (2010). Asadi and Zohrevand (2007) also considered a dynamic version of the CRE defined by $\mathcal E (X;t)=\mathcal E (X_t)$. Some characterization results, stochastic ordering and aging classes properties for $\mathcal E (X;t)$ were obtained in Asadi and Zohrevand (2007) and Navarro et al. (2010). Moreover, Kapodistria and Psarrakos (2012), using the relevation transform, gave some new connections of the CRE and the residual lifetime. A cumulative version of Renyi’s entropy was studied in Sunoj and Linu (2012).

In this paper, we extend the concept of cumulative residual entropy relating this concept with the mean time between record values of a sequence of i.i.d. random variables and with the concept of relevation transform. We also consider its dynamic version obtained with the residual lifetime $X_t$. For these concepts we obtain some characterization results, stochastic ordering and aging classes properties and some relationships with other concepts such as the mean residual waiting time defined by Raqab and Asadi (2010) or the Baratpour entropy defined in Baratpour (2010).

The paper is organized as follows. The definitions, motivations and basic properties are given in Sect. 2. In Sect. 3, we include the characterizations of exponential, Pareto and power models and stochastic ordering and aging classes properties. The relationships with other functions are studied in Sect. 4. Some conclusions and open questions are given in Sect. 5.

Throughout the paper when we say that a function $g$ is increasing (decreasing), we mean that it is non-decreasing (non-increasing), that is, $g(x)\le g(y)\,(\ge )$ for all $x\le y$. Whenever we use an expectation or a conditional random variable we are tacitly assuming that they exist.

2 Definitions and basic properties

We use some preliminaries from Sect. 2 of Baxter (1982). It is well known that in a renewal process where the failed units are replaced by new units, the distribution of the process is obtained by using the convolution of the unit distributions. In a similar way, in a relevation process a failed unit is replaced (or repaired) by another unit with the same age. Thus, if the first unit has lifetime $X$ and reliability function $\overline{F}$ and the second has lifetime $Y$ and reliability function $\overline{G}(t+x)/\overline{G}(x)$ given that $X=x$, then the reliability of the relevation process is given by

$$\begin{aligned} \overline{F}\#\overline{G}(t)&=\int \limits _0^\infty \Pr (X+Y>t|X=x) f(x)dx\\&=\int \limits _0^t \Pr (Y>t-x|X=x) f(x)dx+\int \limits _t^\infty f(x)dx\\&=\overline{F}(t)+\int \limits _0^t \frac{\overline{G}(t)}{\overline{G}(x)} f(x)dx, \end{aligned}$$

where $f$ is the probability density function of $X$ and the notation $\#$ stands for the relevation transform of $F$ and $G$.

In particular, if $F=G$ and $\overline{F}_n$ denotes the reliability function of the time to the $n$-th failure $X_n$, then

$$\begin{aligned} \overline{F}_n(t)=\left\{ \begin{array}{ll} \overline{F}(t)&\quad n=1 \\ \overline{F}_{n-1} \# \overline{F}(t)&\quad n \ge 2. \end{array} \right. \end{aligned}$$

An equivalent form (see Krakowski 1973) is

$$\begin{aligned} \overline{F}_n(t) = \overline{F}(t)\sum _{k=0}^{n-1} \frac{[\varLambda (t)]^k}{k!} =q_n(\overline{F}(t)) \end{aligned}$$

(1)

for $n=1,2,\ldots ,$ where $\varLambda (t) = - \log \overline{F}(t)$ is the cumulative hazard function and $q_n(x)=x \sum _{k=0}^{n-1} [-\log x]^k /k!$ is an increasing function such that $q_n(0)=0$ and $q_n(1)=1$. This expression proves that $\overline{F}_n$ is a distorted function from $\overline{F}$ and hence some ordering properties can be obtained from the results for distorted distributions given in Navarro et al. (2012). The density is given by

$$\begin{aligned} f_n(t) = \frac{[\varLambda (t)]^{n-1}}{(n-1)!} f(t) , \;\; n=1,2,\ldots , \end{aligned}$$

(2)

that is, the number of failures in $(0,t]$ forms a nonhomogeneous Poisson process (NHPP) with intensity function $\lambda (t)= f(t)/\overline{F}(t)$, the failure (or hazard) rate of $F$. Through the NHPP Gupta and Kirmani (1988) explained why the study of relevation is equivalent to the study of record values by noting that (2) is the density of the $n$-th upper record value of a sequence of i.i.d. random variables (see also, e.g., David and Nagaraja 2003, p. 32).

Now we consider the mean value of $F_n,\, \mu _n = \int _0^{\infty } \overline{F}_n(x) dx,\,n \ge 1$. Then

$$\begin{aligned} \mu _{n+1} - \mu _n = \int \limits _0^{\infty } \overline{F}(x) \frac{[\varLambda (x)]^n}{n!} dx. \end{aligned}$$

(3)

Let $X$ be a r.v. supported on $[0,\infty )$, with reliability function $\overline{F}(t)$. Rao et al. (2004) (see also Rao 2005), defined the cumulative residual entropy (CRE)

$$\begin{aligned} \mathcal E (X) = \int \limits _0^{\infty } \overline{F}(x) \varLambda (x) dx. \end{aligned}$$

(4)

Notice that $n=1$ in (3) yields (4). Motivating by this fact we define the generalized cumulative residual entropy (GCRE) of $X$ as

$$\begin{aligned} \mathcal E _n(X) = \int \limits _0^{\infty } \overline{F}(x) \frac{[\varLambda (x)]^n}{n!} dx \end{aligned}$$

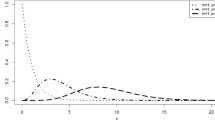
for $n=1,2,\dots$. By convention, $\mathcal E _0(X) =E(X)= \int _0^{\infty } \overline{F}(x) dx$. For more details on the terminology of the integral $\int _0^{\infty } \frac{1}{n!} [\varLambda (x)]^n \overline{F}(x) dx$, see Sect. 4 of Baxter (1982). Note that $\mathcal E _n(X)$ is the area between the functions $\overline{F}_{n+1}$ and $\overline{F}_{n}$. In particular, $\mathcal E _0(X)=E(X)$ is the area under $\overline{F}_1=\overline{F}$. In Fig. 1, we plot these areas for an exponential distribution.

Fig. 1

$\overline{F}_{n}$ for an exponential distribution for $n=1,2,3,4,5$ (from below). The area under $\overline{F}_{1}=\overline{F}$ is $E(X)$ and the areas between these functions correspond to the GCRE $\mathcal E _n(X)$ for $n=1,2,3,4$

Raqab and Asadi (2010) studied the mean residual waiting time (MRWT) between records, using the GCRE (without define it as an entropy measure and just as a mathematical tool) in the following form

$$\begin{aligned} \mathcal E _n(X) = \int \limits _0^{\infty } \tau _n(x) dx, \end{aligned}$$

(5)

where

$$\begin{aligned} \tau _n(x) = \frac{[\varLambda (x)]^n}{n!} \overline{F}(x). \end{aligned}$$

Also notice that from (2), the GCRE can be written as

$$\begin{aligned} \mathcal E _n(X)=\int \limits _0^\infty \frac{[\varLambda (x)]^n}{n!} f(x)\frac{ \overline{F}(x)}{f(x)}dx= E\left(\frac{1}{\lambda (X_{n+1})}\right) \end{aligned}$$

(6)

for $n=0,1,2,\dots ,$ where $\lambda =f/\overline{F}$ is the failure (hazard) rate function of $F$ and $X_{n+1}$ is a random variable with reliability $\overline{F}_{n+1}$. From (2), the ratio

$$\begin{aligned} \frac{f_{n+1}(t)}{f_{n}(t)}=\frac{\varLambda (t)}{n} \end{aligned}$$

is increasing in $t$ and hence $X_n\le _{LR}X_{n+1}$ where $\le _{LR}$ denotes the likelihood ratio order (see Shaked and Shanthikumar 2007, Chap. 1). In particular, this implies that $X_n\le _{ST}X_{n+1}$, where $\le _{ST}$ denotes the usual stochastic order, that is, $\overline{F}_n\le \overline{F}_{n+1}$. Hence, if $\lambda$ is increasing (resp. decreasing), that is, $X$ is IFR (DFR), then, from (6) and the equivalence (1.A.7) in (see Shaked and Shanthikumar 2007, p. 4) we have

$$\begin{aligned} \mathcal E _n(X)\ge \mathcal E _{n+1}(X) \quad (\le ) \end{aligned}$$

(7)

for $n=0,1,2,\dots$. In particular, for the exponential distribution, as the hazard rate is constant, we obtain the following well known property

$$\begin{aligned} \mathcal E _n(X)= \mathcal E _{0}(X)=E(X) \end{aligned}$$

for $n=1,2,\dots$, that is, the areas between the functions in Fig. 1 coincide.

Another interesting property can be obtained by using the hazard rate order $(\le _{HR})$. The definition and the basic properties of this order can be seen (see Shaked and Shanthikumar 2007, Chap. 1). The result can be stated as follows.

Theorem 1

If $X\le _{HR}Y$ and either $X$ or $Y$ are DFR, then

$$\begin{aligned} \mathcal E _n(X)\le \mathcal E _{n}(Y) \end{aligned}$$

for $n=0,1,2,\dots$.

Proof

It is well known that $X\le _{HR}Y$ implies $X\le _{ST}Y$ (see, e.g., Shaked and Shanthikumar 2007, p. 17). Hence the result trivially holds for $n=0$. Moreover, from (1), we have

$$\begin{aligned} \overline{F}_{n+1}(t)=q_{n+1}(\overline{F}(t))\le q_{n+1}(\overline{G}(t))=\overline{G}_{n+1}(t), \end{aligned}$$

where $\overline{G}(t)$ is the reliability function of $Y$ and $\overline{G}_{n+1}(t)$ is the reliability function of $Y_{n+1}$. That is, $X_{n+1}\le _{ST} Y_{n+1}$ holds. This is equivalent (see Shaked and Shanthikumar 2007, p. 4) to have

$$\begin{aligned} E(\phi (X_{n+1}))\le E(\phi (Y_{n+1})) \end{aligned}$$

for all increasing functions $\phi$ such that these expectations exist.

Thus, if we assume that $X$ is DFR and $\lambda _X$ is its hazard rate, then $1/\lambda _X$ is increasing and from (6)

$$\begin{aligned} \mathcal E _n(X)=E\left(\frac{1}{\lambda _X(X_{n+1})}\right) \le E\left(\frac{1}{\lambda _X(Y_{n+1})}\right) \end{aligned}$$

holds.

On the other hand, $X\le _{HR}Y$ implies that the respective hazard rate functions satisfy $\lambda _X\ge \lambda _Y$. Hence, we have

$$\begin{aligned} E\left(\frac{1}{\lambda _X(Y_{n+1})}\right)\le E\left(\frac{1}{\lambda _Y(Y_{n+1})}\right)=\mathcal E _n(Y). \end{aligned}$$

Therefore, using both expressions we obtain $\mathcal E _n(Y)\le \mathcal E _n(Y).$ The proof is similar when we assume that $Y$ is DFR.

Remark 1

As we have already mentioned similar ordering properties can be obtained for $X_n$ (i.e. for record values) by using (1) and the results for distorted distributions given in Navarro et al. (2012). For example, it is easy to see that $q_n(u)$ satisfies that $u q_n^\prime (u)/q_n(u)$ is decreasing in $(0,1)$ for $n=2,3, \dots$ and hence, from Theorem 2.6, $(ii)$, in Navarro et al. (2012), we have that $X\le _{HR}Y$ implies $X_n\le _{HR}Y_n$ for $n=0,1,2,\dots$. Analogously, as $q_n(u)$ is concave, from Theorem 2.6, $(v)$, in Navarro et al. (2012), we have that $X\le _{ICX}Y$ implies $X_n\le _{ICX}Y_n$ for $n=0,1,2,\dots$, where $\le _{ICX}$ represents the increasing convex order (see Shaked and Shanthikumar 2007, Chap. 4).

Analogously, we can also consider the dynamic version of the GCRE, that is, the GCRE of the residual lifetime $X_t=(X-t|X>t)$ given by

$$\begin{aligned} \mathcal E _n(X;t) = \mathcal E _n(X_t) =\frac{1}{n!} \int \limits _t^{\infty } \frac{\overline{F}(x)}{\overline{F}(t)} \bigg [- \log \frac{\overline{F}(x)}{\overline{F}(t)} \bigg ]^n dx \end{aligned}$$

(8)

for $n=0,1,2,\dots$. This function is called dynamic generalized cumulative residual entropy (DGCRE). Notice that $\mathcal E _n(X;0)=\mathcal E _n(X)$ and $\mathcal E _0(X;t)=E(X_t)=m(t)$ is the mean residual lifetime (MRL) function of $X$. It is well known that the hazard rate of the residual lifetime $X_t=(X-t|X>t)$ is $\lambda (x+t)$ for $x\ge 0$. Hence, if $X$ is IFR (DFR), then $X_t$ is IFR (DFR) and from (7), we have

$$\begin{aligned} \mathcal E _n(X;t)\ge \mathcal E _{n+1}(X;t)\quad (\le ) \end{aligned}$$

(9)

for all $t$ and for $n=0,1,\dots$. Moreover, from (6), we get

$$\begin{aligned} \mathcal E _n(X;t)=E\left(\frac{1}{\lambda (t+X_{t,n+1})}\right), \end{aligned}$$

where $X_{t,n}=(X_t)_n$ is a r.v. having the reliability function obtained from (1) and the reliability function of $X_t$. Note that $X_{t,n}$ is not the residual lifetime of $X_n$, that is, $X_{t,n}=(X_t)_n$ is not necessarily equal in law to $(X_n)_t$.

Moreover, by using the binomial expansion, we have

$$\begin{aligned} \mathcal E _n(X;t)&= \frac{1}{n!} \int \limits _t^{\infty } \frac{\overline{F}(x)}{\overline{F}(t)} [\varLambda (x)- \varLambda (t)]^n dx \nonumber \\&= \frac{1}{n! \overline{F}(t)}\int \limits _t^{\infty } \overline{F}(x) \sum _{k=0}^n {n \atopwithdelims ()k} (-1)^{n-k} [\varLambda (x)]^k [\varLambda (t)]^{n-k} dx \nonumber \\&= \frac{1}{n! \overline{F}(t)} \sum _{k=0}^n {n \atopwithdelims ()k} (-1)^{n-k} [\varLambda (t)]^{n-k} \int \limits _t^{\infty } \overline{F}(x) [\varLambda (x)]^k dx \end{aligned}$$

(10)

$$\begin{aligned}&= \frac{1}{\overline{F}(t)} \sum _{k=0}^n \frac{(-1)^{n-k}}{k!(n-k)!} [\varLambda (t)]^{n-k} \int \limits _t^{\infty } \overline{F}(x) [\varLambda (x)]^k dx. \end{aligned}$$

(11)

By (10), solving with respect to $\int _t^{\infty }\overline{F}(x)[\varLambda (x)]^n dx$, we have

$$\begin{aligned} \int \limits _t^{\infty } \overline{F}(x) [\varLambda (x)]^n dx&= n! \overline{F}(t) \mathcal E _n(X;t) \nonumber \\&\quad - \sum _{k=0}^{n-1} {n \atopwithdelims ()k} (-1)^{n-k} [\varLambda (t)]^{n-k} \int \limits _t^{\infty } \overline{F}(x) [\varLambda (x)]^k dx. \end{aligned}$$

(12)

In particular, by (11) for $n=1$, we have

$$\begin{aligned} \mathcal E _1(X;t)&= \frac{1}{\overline{F}(t)} \bigg \{ - \varLambda (t) \int \limits _t^{\infty } \overline{F}(x) dx + \int \limits _t^{\infty } \overline{F}(x) \varLambda (x) dx \bigg \}\\&= - \varLambda (t) m(t) + \frac{1}{\overline{F}(t)} \int \limits _t^{\infty } \overline{F}(x) \varLambda (x) dx. \end{aligned}$$

This is the dynamic cumulative residual entropy considered in formula (14) of Asadi and Zohrevand (2007).

For $n=2$, we have

$$\begin{aligned} \mathcal E _2(X;t)&= \frac{[\varLambda (t)]^2}{2} m(t) - \frac{\varLambda (t)}{\overline{F}(t)} \int \limits _t^{\infty } \overline{F}(x) \varLambda (x) dx + \frac{1}{2\overline{F}(t)}\int \limits _t^{\infty }\overline{F}(x)[\varLambda (x)]^2 dx \end{aligned}$$

and for $n=3$,

$$\begin{aligned} \mathcal E _3(X;t)&= -\frac{[\varLambda (t)]^3}{6} m(t) +\frac{[\varLambda (t)]^2}{2\overline{F}(t)}\int \limits _t^{\infty } \overline{F}(x) \varLambda (x) dx\\&-\frac{[\varLambda (t)]}{2\overline{F}(t)}\int \limits _t^{\infty } \overline{F}(x)[\varLambda (x)]^2 dx+\frac{1}{6\overline{F}(t)} \int \limits _t^{\infty } \overline{F}(x)[\varLambda (x)]^3 dx. \end{aligned}$$

Finally, we can also consider the mean value of $\mathcal E _n(X;X)$ given by

$$\begin{aligned} E[\mathcal E _n(X;X)]=\int \limits _0^{\infty } \mathcal E _n(X;x) f(x)dx. \end{aligned}$$

(13)

3 Monotonicity and characterization results

In this section we study aging classes properties and characterization results. To this purpose we first give an expression for the derivative of $\mathcal E _n(X;t)$.

Theorem 2

If $X$ is absolutely continuous, then

$$\begin{aligned} \mathcal E _n^{^{\prime }}(X;t) = \lambda (t) [\mathcal E _n(X;t)-\mathcal E _{n-1}(X;t)] \end{aligned}$$

(14)

for $n=1,2,\dots$.

Proof

The relation (11) can be written as

$$\begin{aligned} \mathcal E _n(X;t) \overline{F}(t) = \sum _{k=0}^n \frac{(-1)^{n-k}[\Lambda (t)]^{n-k}}{k!(n-k)!} \int \limits _t^{\infty } \overline{F}(x)[\varLambda (x)]^k dx. \end{aligned}$$

Differentiating both sides with respect to $t$ gives

$$\begin{aligned} \mathcal E _n^{^{\prime }}(X;t) \overline{F}(t)-\mathcal E _n(X;t) {f}(t)&= \lambda (t) \sum _{k=0}^{n-1} \frac{(-1)^{n-k}[\varLambda (t)]^{n-k-1}}{k!(n-k-1)!} \int \limits _t^{\infty } \overline{F}(x) [\varLambda (x)]^k dx\\&- [\varLambda (t)]^{n} \overline{F}(t) \sum _{k=0}^n \frac{(-1)^{n-k}}{k!(n-k)!}, \end{aligned}$$

where

$$\begin{aligned} \sum _{k=0}^n \frac{(-1)^{n-k}}{k!(n-k)!} = \frac{1}{n!} \sum _{k=0}^n (-1)^{n-k} {n \atopwithdelims ()k} = (1-1)^n=0. \end{aligned}$$

Hence

$$\begin{aligned} \mathcal E _n^{^{\prime }}(X;t) \overline{F}(t) - \mathcal E _n(X;t) {f}(t) = \lambda (t) \sum _{k=0}^{n-1} \frac{(-1)^{n-k}[\varLambda (t)]^{n-k-1}}{k!(n-k-1)!} \int \limits _t^{\infty } \overline{F}(x) [\varLambda (x)]^k dx , \end{aligned}$$

and using again (11), we have

$$\begin{aligned} \mathcal E _n^{^{\prime }}(X;t) \overline{F}(t) - \mathcal E _n(X;t) {f}(t) =- \lambda (t) \overline{F}(t) \mathcal E _{n-1}(X;t), \end{aligned}$$

that is, (14) holds.

For $n=1$ in (14), we have the relation (3.4) of Navarro et al. (2010),

$$\begin{aligned} \mathcal E _1^{^{\prime }}(X;t) = \lambda (t) [\mathcal E _1(X;t) - m(t)]. \end{aligned}$$

As a consequence of the preceding theorem we have the following result.

Theorem 3

If $X$ is IFR (DFR), then $\mathcal E _n(X;t)$ is decreasing (increasing) for $n=0,1,2,\dots$.

Proof

The result is trivially true for $n=0$ since $\mathcal E _n(X;t)=m(t)$ the MRL function of $X$ and it is well known that IFR (DFR) implies DMRL (IMRL).

For $n\ge 1$, from Theorem 2, we have

$$\begin{aligned} \mathcal E _n^{^{\prime }}(X;t) = \lambda (t) [\mathcal E _n(X;t) - \mathcal E _{n-1}(X;t)] \end{aligned}$$

for $n=1,2,\dots$. Moreover, from (9), we have that if $X$ is IFR (DFR), then

$$\begin{aligned} \mathcal E _n(X;t) \le \mathcal E _{n-1}(X;t) \quad (\ge ). \end{aligned}$$

Therefore, $\mathcal E _n^{^{\prime }}(X;t) \le 0\,(\ge )$ for all $t$.

Using this property we can define the following aging classes.

Definition 1

We say that $X$ has an increasing (decreasing) DGCRE of order $n$, shortly written as $\text{ IDGCRE}_n\,(\text{ DDGCRE}_n)$ if $\mathcal E _n(X;t)$ is increasing (decreasing) in $t$.

Note that Theorem 3 proves that if X is IFR (DFR), then it is $\text{ DDGCRE}_n\,(\text{ IDGCRE}_n)$ for $n=0,1,\dots$. Moreover, $\text{ DDGCRE}_0\,(\text{ IDGCRE}_0)$ is equivalent to DMRL (IMRL).

Using again Theorem 2 we can obtain the following characterization result which extends the result obtained in Theorem 4.8 of Asadi and Zohrevand (2007).

Theorem 4

If for $c>0\,\mathcal E _n(X;t)=c\mathcal E _{n-1}(X;t)$  holds for all $t$ and for a fixed $n\in \{1,2,\dots \}$, then $X$ has an Exponential $(c=1)$, a Pareto type II $(c>1)$ or a power distribution $(c<1)$.

Proof

This result was proved for $n=1$ in Theorem 4.8 of Asadi and Zohrevand (2007). By induction, we assume that the result is true for $n-1$ (for $n>1$) and we are going to prove it for $n$.

We are assuming that for $c>0$,

$$\begin{aligned} \mathcal E _n(X;t)=c\mathcal E _{n-1}(X;t) \end{aligned}$$

holds. Then we have

$$\begin{aligned} \mathcal E _n^\prime (X;t)=c\mathcal E _{n-1}^\prime (X;t). \end{aligned}$$

Moreover, from (14), we have

$$\begin{aligned} \mathcal E _n^\prime (X;t)=c\mathcal E _{n-1}^\prime (X;t)= \lambda (t) [\mathcal E _n(X;t) - \mathcal E _{n-1}(X;t)], \end{aligned}$$

that is,

$$\begin{aligned} c\mathcal E _{n-1}^\prime (X;t)= (c-1) \lambda (t) \mathcal E _{n-1}(X;t). \end{aligned}$$

Analogously, using (14) for $n-1$, we get

$$\begin{aligned} c\mathcal E _{n-1}^\prime (X;t)= c\lambda (t) [\mathcal E _{n-1}(X;t) - \mathcal E _{n-2}(X;t)]. \end{aligned}$$

Therefore,

$$\begin{aligned} \mathcal E _{n-1}(X;t)=c \mathcal E _{n-2}(X;t) \end{aligned}$$

and hence, by the induction hypothesis, we get the stated result.

We have already mentioned that if $X$ is exponential, then $\mathcal E _n(X;t)=\mathcal E _{n-1}(X;t)=\dots =m(t)=\mu$. The preceding theorem proves that $\mathcal E _n(X;t)=\mathcal E _{n-1}(X;t)$ for a fixed $n$ and for all $t \ge 0$ characterizes the exponential model.

Analogously, the Pareto type II (or Lomax) model with reliability $\overline{F}(t)=b^a/(t+b)^a$ for $t \ge 0,\,a,b>0$ is characterized by $\mathcal E _n(X;t)=c\mathcal E _{n-1}(X;t)$ for $c>1$, a fixed $n$ and for $t \ge 0$. Its mean residual lifetime is given by

$$\begin{aligned} m(t)=\frac{t+b}{a-1} \end{aligned}$$

which is an increasing linear function of $t$. Hence the functions $\mathcal E _n(X;t)=c^n m(t),\,n=1,2,\ldots$, are also increasing linear functions of $t$ with

$$\begin{aligned} m(t) \le \mathcal E _1(X;t) \le \mathcal E _2(X;t) \le \cdots \le \mathcal E _n(X;t). \end{aligned}$$

By (9), the above inequalities are expected since Pareto type II is a DFR distribution. From (14) it is easy to see that $c=a/(a-1)$ and hence

$$\begin{aligned} \mathcal E _n(X;t)=a^n (t+b)/(a-1)^{n+1} \end{aligned}$$

for $t \ge 0,\,a>1$ and $b>0$.

In a similar way, the power model with reliability $\overline{F}(t)=(b-t)^a/b^a$ for $0 \le t<b,\,a,b>0$, is characterized by $\mathcal E _n(X;t)=c\mathcal E _{n-1}(X;t)$ for $0<c<1$, a fixed $n$ and for $0\le t<b$. Its mean residual lifetime is given by

$$\begin{aligned} m(t)=\frac{b-t}{a+1} \end{aligned}$$

which is a decreasing linear function of $t$ in $(0,b)$. Hence the functions $\mathcal E _n(X;t)=c^n m(t),\,n=1,2,\ldots$, are also decreasing linear functions of $t$ with

$$\begin{aligned} m(t) \ge \mathcal E _1(X;t) \ge \mathcal E _2(X;t) \ge \cdots \ge \mathcal E _n(X;t). \end{aligned}$$

By (9), the above inequalities are expected since power is an IFR distribution. From (14) it is easy to see that $c=a/(a+1)$ and hence

$$\begin{aligned} \mathcal E _n(X;t)=a^n (b-t)/(a+1)^{n+1} \end{aligned}$$

for $0 \le t<b,\,a>0$ and $b>0$.

4 Relationships with other functions

We first prove the following preliminary result.

Lemma 1

For any $n=1,2,\ldots$, it holds that

$$\begin{aligned} \mathcal E _n(X)=\frac{1}{n!} \int \limits _0^{\infty } \lambda (z) \bigg [ \int \limits _z^{\infty } [\varLambda (x)]^{n-1} \overline{F}(x) dx \bigg ] dz. \end{aligned}$$

(15)

Proof

By (5) and the fact that $\varLambda (x) = \int _0^x \lambda (z) dz$, we have

$$\begin{aligned} \mathcal E _n(X) = \frac{1}{n!} \int \limits _0^{\infty } \int \limits _0^x \lambda (z) [\varLambda (x)]^{n-1} \overline{F}(x) dz dx. \end{aligned}$$

Fubini’s theorem yields

$$\begin{aligned} \mathcal E _n(X) = \frac{1}{n!} \int \limits _0^{\infty } \int \limits _z^{\infty } \lambda (z) [\varLambda (x)]^{n-1} \overline{F}(x) dx dz \end{aligned}$$

and the result follows.

Now we can obtain a recursive formula for $\mathcal E _n(X)$.

Theorem 5

For any $n=1,2,\ldots$, it holds that

$$\begin{aligned} \mathcal E _n(X)&= \frac{1}{n} E[\mathcal E _{n-1}(X;X)]\\&- \frac{1}{n!} \sum _{k=0}^{n-2} {n-1 \atopwithdelims ()k} (-1)^{n-k-1} \int \limits _0^{\infty } \int \limits _z^{\infty } \lambda (z) [\varLambda (z)]^{n-k-1} \overline{F}(x) [\varLambda (x)]^k dx dz. \end{aligned}$$

Proof

Inserting (12) in (15), we have

$$\begin{aligned} \mathcal E _n(X)&= \frac{1}{n!} \int \limits _0^{\infty } \lambda (z) (n-1)! \overline{F}(z) \mathcal E _{n-1}(X;z)dz\\&-\frac{1}{n!} \int \limits _0^{\infty } \lambda (z) \bigg [ \sum _{k=0}^{n-2} {n-1 \atopwithdelims ()k} (-1)^{n-k-1} [\varLambda (z)]^{n-k-1} \int \limits _z^{\infty } \overline{F}(x) [\varLambda (x)]^k dx \bigg ] dz \end{aligned}$$

or, equivalently,

$$\begin{aligned} \mathcal E _n(X)&= \frac{1}{n} \int \limits _0^{\infty } \mathcal E _{n-1}(X,z) f(z) dz\\&- \frac{1}{n!} \sum _{k=0}^{n-2} {n-1 \atopwithdelims ()k} (-1)^{n-k-1} \int \limits _0^{\infty } \int \limits _z^{\infty } \lambda (z) [\varLambda (z)]^{n-k-1} \overline{F}(x) [\varLambda (x)]^k dx dz. \end{aligned}$$

The relation (13) completes the proof.

Raqab and Asadi (2010) defined the mean residual waiting time (MRWT) for the record model as

$$\begin{aligned} \psi _n(t) = \frac{\sum _{j=0}^n \int _t^{\infty } \tau _j(x) dx}{\sum _{j=0}^n \tau _j(t)} = \frac{\sum _{j=0}^n \int _t^{\infty } \frac{[\varLambda (x)]^j}{j!} \overline{F}(x) dx}{\sum _{j=0}^n \frac{[\varLambda (t)]^j}{j!} \overline{F}(t)}. \end{aligned}$$

(16)

The connection between $\mathcal E _n(X)$ and $\psi _n(t)$ is obtained in the following theorem.

Theorem 6

For any $n=1,2,\ldots$, it holds that

$$\begin{aligned} \mathcal E _n(X)=\frac{1}{n} \sum _{k=0}^{n-1} [E(\psi _{n-1}(X_{k+1}))-k \mathcal E _k(X)]. \end{aligned}$$

Proof

By relation (15), we have

$$\begin{aligned} k \mathcal E _k(X)=\frac{1}{(k-1)!} \int \limits _0^{\infty } \lambda (z) \bigg [ \int \limits _z^{\infty } [\varLambda (x)]^{k-1} \overline{F}(x) dx \bigg ] dz. \end{aligned}$$

Summing with respect to $k=1,2,\ldots , n$, we obtain

$$\begin{aligned} \sum _{k=1}^n k \mathcal E _k(X)=\int \limits _0^{\infty } \lambda (z) \sum _{k=1}^n \int \limits _z^{\infty } \frac{1}{(k-1)!} [\varLambda (x)]^{k-1} \overline{F}(x) dx dz, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \sum _{k=1}^n k \mathcal E _k(X)= \int \limits _0^{\infty } \lambda (z) \sum _{k=0}^{n-1} \int \limits _z^{\infty } \frac{1}{k!} [\varLambda (x)]^k \overline{F}(x) dx dz. \end{aligned}$$

Then, using (16), we have

$$\begin{aligned} \sum _{k=1}^n k \mathcal E _k(X)&= \int \limits _0^{\infty } \lambda (z) \psi _{n-1}(z) \sum _{k=0}^{n-1} \frac{1}{k!} [\varLambda (z)]^k \overline{F}(z) dz\\&= \int \limits _0^{\infty } \psi _{n-1}(z) \sum _{k=0}^{n-1} \frac{1}{k!} [\varLambda (z)]^k f(z) dz\\&= \sum _{k=0}^{n-1} \int \limits _0^{\infty } \psi _{n-1}(z) f_{k+1}(z) dz\\&= \sum _{k=0}^{n-1} E(\psi _{n-1}(X_{k+1})). \end{aligned}$$

The fact that

$$\begin{aligned} \sum _{k=1}^n k \mathcal E _k(X) = \sum _{k=1}^{n-1} k \mathcal E _k(X) + n \mathcal E _n(X) = \sum _{k=0}^{n-1} k \mathcal E _k(X) + n \mathcal E _n(X) \end{aligned}$$

completes the proof.

From Remark 1 in Raqab and Asadi (2010), it holds that

$$\begin{aligned} \psi _n(t) = \sum _{j=0}^n M_j(t) p_j(t), \end{aligned}$$

(17)

where

$$\begin{aligned} M_j(t) = \int \limits _t^{\infty } \bigg [ \frac{\varLambda (x)}{\varLambda (t)} \bigg ]^j \frac{\overline{F}(x)}{\overline{F}(t)} dx. \end{aligned}$$

(18)

and

$$\begin{aligned} p_j(t) = \frac{[\varLambda (t)]^j /j!}{\sum _{i=0}^n [\varLambda (t)]^i /i!}. \end{aligned}$$

(19)

To obtain the connection between $\psi _n(t)$ and $\mathcal E _n(X;t)$ we need the following lemma.

Lemma 2

It holds that

$$\begin{aligned} M_j(t) = \sum _{k=0}^j \frac{j!}{(j-k)!} \frac{1}{[\varLambda (t)]^k} \mathcal E _k(X;t). \end{aligned}$$

(20)

Proof

From (18), we have

$$\begin{aligned} M_j(t)&= \int \limits _t^{\infty } \bigg [ \frac{\varLambda (x)}{\varLambda (t)} \bigg ]^j \frac{\overline{F}(x)}{\overline{F}(t)} dx\\&= \int \limits _t^{\infty } \bigg [ \frac{-\log (\overline{F}(x)/\overline{F}(t))}{\varLambda (t)}+1 \bigg ]^j \frac{\overline{F}(x)}{\overline{F}(t)} dx\\&= \int \limits _t^{\infty } \sum _{k=0}^j {j \atopwithdelims ()k} \bigg [ \frac{-\log (\overline{F}(x)/\overline{F}(t))}{\varLambda (t)} \bigg ]^k \frac{\overline{F}(x)}{\overline{F}(t)} dx\\&= \sum _{k=0}^j {j \atopwithdelims ()k} \frac{1}{[\varLambda (t)]^k} \int \limits _t^{\infty } \bigg [ -\log \frac{\overline{F}(x)}{\overline{F}(t)} \bigg ]^k \frac{\overline{F}(x)}{\overline{F}(t)} dx\\&= \sum _{k=0}^j \frac{j!}{(j-k)!} \frac{1}{[\varLambda (t)]^k} \mathcal E _k(X;t). \end{aligned}$$

Now we can obtain the connection between $\psi _n(t)$ and $\mathcal E _n(X;t)$.

Theorem 7

It holds that

$$\begin{aligned} \psi _n(t)= \sum _{k=0}^n \mathcal E _k(X;t) \eta _k(t), \end{aligned}$$

where

$$\begin{aligned} \eta _k(t) = \frac{\sum _{j=0}^{n-k} [\varLambda (t)]^j/j!}{\sum _{i=0}^n [\varLambda (t)]^i/i!}, \;\; k=0,1,2,\ldots , n. \end{aligned}$$

Proof

By (17) and (20), we have

$$\begin{aligned} \psi _n(t) = \sum _{j=0}^n \sum _{k=0}^j \frac{j!}{(j-k)!} \frac{1}{[\varLambda (t)]^k} \mathcal E _k(X;t) p_j(t). \end{aligned}$$

Changing the order of the sums and substituting $p_j$ from (19), we take

$$\begin{aligned} \psi _n(t)&= \sum _{k=0}^n \sum _{j=k}^n \frac{j!}{(j-k)!} \frac{1}{[\varLambda (t)]^k} \mathcal E _k(X;t) p_j(t) \\&= \sum _{k=0}^n \frac{1}{[\varLambda (t)]^k} \mathcal E _k(X;t) \sum _{j=k}^n \frac{j!}{(j-k)!} \frac{[\varLambda (t)]^j/j!}{\sum _{i=0}^n [\varLambda (t)]^i/i!} \\&= \sum _{k=0}^n \mathcal E _k(X;t) \frac{\sum _{j=k}^n [\varLambda (t)]^{j-k}/(j-k)!}{\sum _{i=0}^n [\varLambda (t)]^i/i!} \\&= \sum _{k=0}^n \mathcal E _k(X;t) \frac{\sum _{j=0}^{n-k} [\varLambda (t)]^j/j!}{\sum _{i=0}^n [\varLambda (t)]^i/i!} \end{aligned}$$

which completes the proof.

Remark 2

Theorems 5 and 6 for $n=1$ imply the well known result

$$\begin{aligned} \mathcal E _1(X) = E(m(X)), \end{aligned}$$

(21)

see Asadi and Zohrevand (2007) and Navarro et al. (2010).

Next we present a generalization of (21) using the GCRE, $\mathcal E _n(X)$ instead of the CRE $\mathcal E _1(X)$.

Proposition 1

For any $n=1,2,\ldots$, it holds that

$$\begin{aligned} \mathcal E _n(X) = \frac{1}{n} \bigg \{ \sum _{k=0}^{n-1} \frac{1}{k!} E \bigg ([\varLambda (X)]^k m_n(X) \bigg ) - \sum _{k=0}^{n-2} \frac{1}{k!} E \bigg ( [\varLambda (X)]^k m_{n-1}(X) \bigg ) \bigg \}, \end{aligned}$$

where, by convention, we assume $\sum _{k=0}^j = 0$ when $j<0$ and where

$$\begin{aligned} m_n(t) = \frac{1}{\overline{F}_n(t)} \int \limits _t^{\infty } \overline{F}_n(x) dx, \;\; n=1,2,\ldots . \end{aligned}$$

is the mean residual lifetime of $X_n$.

Proof

By (1), we see that

$$\begin{aligned} \overline{F}_n(t) - \overline{F}_{n-1}(t) = \frac{[\varLambda (t)]^{n-1}}{(n-1)!} \overline{F}(t). \end{aligned}$$

Substituting the last equation in (15), we have

$$\begin{aligned} \mathcal E _n(X)&= \frac{1}{n} \int \limits _0^{\infty } \lambda (z) \bigg \{ \int \limits _z^{\infty } [\overline{F}_n(x) - \overline{F}_{n-1}(x)] dx \bigg \} dz \nonumber \\&= \frac{1}{n} \int _0^{\infty } f(z) \bigg [ \frac{\overline{F}_n(z)}{\overline{F}(z)} m_n(z) - \frac{\overline{F}_{n-1}(z)}{\overline{F}(z)} m_{n-1}(z) \bigg ] dz \nonumber \\&= \frac{1}{n} \int \limits _0^{\infty }f(z)\bigg [\sum _{k=0}^{n-1} \frac{[\varLambda (z)]^k}{k!} m_n(z)-\sum _{k=0}^{n-2} \frac{[\varLambda (z)]^k}{k!} m_{n-1}(z) \bigg ] dz \nonumber \\&= \frac{1}{n} \sum _{k=0}^{n-1} \frac{1}{k!} \int \limits _0^{\infty }f(z) [\varLambda (z)]^k m_n(z) dz\nonumber \\&- \frac{1}{n}\sum _{k=0}^{n-2} \frac{1}{k!} \int \limits _0^{\infty } f(z) [\varLambda (z)]^k m_{n-1}(z) dz \end{aligned}$$

(22)

and the result follows.

Another generalization of (21) can be stated as follows. The proof is immediate from (22).

Proposition 2

For any $n=1,2,\ldots$, it holds that

$$\begin{aligned} \mathcal E _n(X) = \frac{1}{n} \bigg \{ \sum _{k=0}^{n-1} E \bigg (m_n(X_{k+1}) \bigg ) - \sum _{k=0}^{n-2} E \bigg ( m_{n-1}(X_{k+1}) \bigg ) \bigg \}, \end{aligned}$$

where, by convention, we assume $\sum _{k=0}^j = 0$ when $j<0$.

We finish this section with a remark on the Baratpour entropy. Baratpour (2010) defined a generalization of the CRE by using the CRE of $X_{1:n}=\min (X_1,\dots ,X_n)$ given by

$$\begin{aligned} \mathcal E (X_{1:n}) = -n \int \limits _0^{\infty } [\overline{F}(x)]^n \log \overline{F}(x) dx = n \int \limits _0^{\infty } [\overline{F}(x)]^n \varLambda (x) dx \end{aligned}$$

for $n=1,2,\dots$. If $X$ has a Pareto type I distribution with density

$$\begin{aligned} f(x)=\frac{ab^a}{x^{a+1}}, \;\; x \ge b, \end{aligned}$$

where $a,b>0$, then, by Example 2.1 of Baratpour (2010), it holds that

$$\begin{aligned} \mathcal E (X) = \left\{ \begin{array}{l@{\quad }l} \frac{ab}{(a-1)^2}&a > 1, \\ +\infty&a \le 1 \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \mathcal E (X_{1:n})= \left\{ \begin{array}{l@{\quad }l} \frac{nab}{(na-1)^2}&a > \frac{1}{n}, \\ +\infty&a \le \frac{1}{n}. \end{array} \right. \end{aligned}$$

Moreover, he noted that for $a>1$, the uncertainty of $X$ is bigger than that of $X_{1:n}$, namely $\mathcal E (X) - \mathcal E (X_{1:n}) \ge 0$.

For our entropy and keeping in mind that $\mathcal E (X)=\mathcal E _1(X)$, we have

$$\begin{aligned} \mathcal E _n(X) = \frac{a^n b}{(a-1)^{n+1}} \end{aligned}$$

for $n=1,2,\dots$ and $a>1$. Thus,

$$\begin{aligned} \mathcal E _n(X) = \frac{a}{a-1} \mathcal E _{n-1}(X) \end{aligned}$$

and

$$\begin{aligned} \mathcal E _n(X) \ge \mathcal E _{n-1}(X) \ge \cdots \ge \mathcal E _1(X). \end{aligned}$$

These results are expected since Pareto type I is a DFR distribution.

5 Conclusions

The GCRE introduced here and its dynamic version show some interesting connections between some entropy concepts, record values and relevation transforms. The characterizations, stochastic ordering and aging classes properties obtained here prove the interest of these concepts in measuring the uncertainty contained in a nonnegative random variable or in the associated residual lifetime.

The present paper is just a first step in the study of these concepts and new properties are waiting to be discovered. In our opinion, one of the main questions for future research is to study if the dynamic generalized cumulative residual entropy uniquely determines the underlying distribution function.