A new privacy-protecting survey design for multichotomous sensitive variables

Abstract

In this paper, we propose the diagonal model (DM), a survey technique for multicategorical sensitive variables. The DM is a nonrandomized response method; that is, the DM avoids the use of any randomization device. Thus, both survey complexity and study costs are reduced. The DM does not require that at least one outcome of the sensitive variable is nonsensitive. Thus, the model can even be applied to characteristics like income which are sensitive as a whole. We describe the maximum likelihood estimation for the distribution of the sensitive variable and show that the EM algorithm is beneficial to calculate the estimates. Subsequently, we present asymptotic as well as bootstrap confidence intervals. Applying properties of circulant matrices, we show the connection between efficiency loss and the degree of privacy protection (DPP). Here, we prove that the efficiency loss has a lower bound that depends on the DPP. Moreover, for any desired DPP, we derive model parameters that ensure the largest possible efficiency.

1 Introduction

Sensitive variables often appear in surveys. For instance, an interviewer could ask: “How much do you earn?” or “Have you ever evaded taxes?”. However, when such sensitive questions are asked, some interviewees will refuse to respond or will give an untruthful answer. To estimate the distribution of sensitive variables, countless randomized response (RR) models have been developed since the paper by Warner (1965).

What the RR models have in common is that every respondent is supplied with a randomization device (RD). A RD is an instrument (e.g., a coin or a deck of cards) used by the interviewee to conduct a random experiment, where the experiment has—for a fixed respondent—at least two possible results. The outcome of the experiment influences the answer. It follows that RR techniques have a lack of “reproducibility” (the same respondent may give different answers if the survey is conducted again; see Tan et al. (2009), p. 15). A different approach was discussed by Tian et al. (2007), Yu et al. (2008), Tan et al. (2009), and Tang et al. (2009), see Sect. 2. These authors proposed some nonrandomized response (NRR) models. That is, their models do not require any RD, thus reducing both survey complexity and study costs.

The NRR models of the previously mentioned authors are not applicable to multicategorical variables like income when all categories are sensitive. To overcome this drawback, we have developed the nonrandomized diagonal model (DM), which is presented in Sect. 3.1. In Sect. 3.2, we derive the maximum likelihood estimator for the distribution of the sensitive variable. The computation of standard errors and confidence intervals is discussed in Sect. 3.3. Subsequently, in Sect. 3.4, we explain how the design matrices in the diagonal model are related to circulant matrices. In Sect. 3.5, we investigate the degree of privacy protection and the efficiency of the estimator depending on the model parameters. Here, under the assumption of a large sample, we will obtain two key results: first, there are optimal and nonoptimal choices for the model parameters, and second, a decrease in the degree of privacy protection (DPP) is the “price” for increasing efficiency.

In our simulation study (Sect. 4), we examine whether the asymptotic results from Sect. 3.5 hold for fixed, not “too large” sample sizes.

2 Nonrandomized response models

Tian et al. (2007) proposed the hidden sensitivity (HS) model, which does not involve a RD. This model is used to study the association of two sensitive characteristics with binary outcomes. As an example, the authors consider the variables $X_1, X_2 \in \{0,1\}$, where $X_1=1$ if the respondent takes drugs and $X_2=1$ if the respondent has AIDS. The crosswise model, which can be found in Yu et al. (2008) and Tan et al. (2009), is a nonrandomized version of Warner’s model and is suitable for two-valued sensitive variables $X \in \{0,1\}$. The model requires choosing a nonsensitive auxiliary variable $W \in \{0,1\}$ with a known distribution such that $X$ and $W$ are independent. Tan et al. (2009) suggested using the respondent’s birthday to construct $W$. For instance, $W$ may indicate if the respondent is born between January and May. If $X=0$ and $W=0$, the respondent answers $A=1$. The answer $A=1$ is also required if $X=1$ and $W=1$. In any other case, the answer $A=0$ must be given. Another NRR model is the multi-category (MC) model proposed by Tang et al. (2009), which is applicable to sensitive variables $X \in \{1,{\ldots },k\}, k\ge 2$. For this model, an important assumption is made:

$$\begin{aligned} \text{ at} \text{ least} \text{ one} \text{ value} \text{ of} \, X, \text{ say} \, X=1, \text{ is} \text{ nonsensitive.} \end{aligned}$$

(1)

The MC model demands the choice of a nonsensitive auxiliary variable $W \in \{1,{\ldots },k\}$ with a known distribution so that $X$ and $W$ are assumed to be independent. The period of the birthday was suggested as a concrete $W$. If $X=1$, the respondent gives an answer $A$ equal to his or her value of $W$. If $X=j$ ($j=2,{\ldots },k$), the answer $A=j$ is given. The distribution of $X$ can be estimated from the empirical distribution of answers $A$. When $k=2$, the MC model equals the triangular model proposed by Yu et al. (2008). The authors of the MC model argue that truthful answers $A$ can be expected, because the value $X=1$ is nonsensitive. However, we doubt that completely truthful answers will be obtained. To show the reason, consider a respondent with a sensitive attribute $X\ne 1$. This person may be enticed to respond untruthfully $A=1$ with the intention of pretending that he or she possesses the nonsensitive characteristic $X=1$. Furthermore, assumption (1) constrains the applicability of the MC model to a subclass of sensitive variables. For instance, consider $X \in \{1,{\ldots },k\}$ describing income classes. Then, all values of $X$ are usually sensitive and private. For such $X$, we cannot find any outcome $x$ of $X$ with the property: each respondent who possesses the attribute $x$ is willing to reveal it. Hence, the MC model may not perform well with such variables. To avoid these disadvantages of the MC model, we have developed a new nonrandomized response model, which is presented in the following section.

3 Diagonal model

3.1 The answer formula

Let $X \in \{1,{\ldots },k\}$ be a sensitive variable. As in the crosswise model, we choose a nonsensitive auxiliary variable $W$, but now with values $1,{\ldots },k$. We assume that the distribution of $W$ is known and that $X$ and $W$ are independent. The respondent gives the answer

$$\begin{aligned} A:= [(W-X) \text{ mod} \, k] + 1. \end{aligned}$$

(2)

Formula (2) should not be presented to the respondents, because some of them may be not familiar with the modular arithmetic. Instead, every respondent receives a table that gives a simple illustration of (2). For example, for $k=4$, such a table would look as follows:

The number in the table provides the required answer $A$ depending on $X$ and $W$. If we artificially expand this table, we obtain the following form (not presented to the interviewees).

$X / W$	$W=1$	$W=2$	$W=3$	$W=4$
$X=1$	1	2	3	4
$X=2$	4	1	2	3
$X=3$	3	4	1	2
$X=4$	2	3	4	1

$X / W$	1	2	3	4	1	2	3
$1$	1	2	3	4	1	2	3
$2$	4	1	2	3	4	1	2
$3$	3	4	1	2	3	4	1
$4$	2	3	4	1	2	3	4

This table has four (boldfaced) diagonals of length four, where the answer $A$ describes the diagonal the respondent belongs to. This explains the name “diagonal model”. Note that it is not possible to identify the $X$ value with the help of the answer. Unlike the MC model, the answers $A$ do not restrict the possible $X$ values. Thus, there is no temptation to give an untruthful answer. Hence, we assume no nonresponses and truthful answers. Moreover, the diagonal model is applicable even if all the outcomes of $X$ are sensitive (e.g., if $X$ represents income classes).

We complete the section with an example for $W$ where $k=4$: let $W$ depend on the birthday of the respondent’s mother, where $W=1$ if the mother was born between January 1st and August 16th, $W=2$ if the mother was born between August 17th and October 1st, and $W=3$ if the mother was born between October 2nd and November 16th. Otherwise, define $W=4$. Ignoring leap years and assuming a uniform distribution of births over 365 days of the year, we have $(\,\mathbb P (W=1),{\ldots },\mathbb P (W=4))= \begin{pmatrix} \frac{228}{365}&\frac{46}{365}&\frac{46}{365}&\frac{45}{365}\end{pmatrix}$. If census data are available that provide deviating probabilities, one should work with them. In principle, the respondent’s birthday can also be used to construct $W$. However, this variable is dangerous if the respondent thinks that the survey agency knows such data. Another example of an auxiliary characteristic is “last digits of the mother’s phone number”.

3.2 The maximum likelihood estimator (MLE) for $\pi$

Define $\pi _i:=\mathbb P (X=i)$, $\pi :=(\pi _1,{\ldots },\pi _k)^T, c_i:=\mathbb P (W=i)$ and $c:=(c_1,{\ldots },c_k)$ where $\pi$ is unknown and $c$ is known. The answer pattern implies that $\lambda : =(\lambda _1,{\ldots },\lambda _k)^T := (\,\mathbb P (A=1),{\ldots },\mathbb P (A=k))^T = C_0 \cdot \pi$. Here, $C_0$ is a $k\times k$ matrix where every row is a left-cyclic shift of the row above. The first row of $C_0$ equals $c$. We call the probabilities $c_1,{\ldots },c_k$ the model parameters and $C_0$ the design matrix induced by $c$. To estimate $\pi$, assume $n$ persons are interviewed. Let $X_i, W_i$ and $A_i$ denote the $i$-th respondent’s value of the sensitive characteristic, the value of the auxiliary characteristic and the given answer, respectively. We assume:

• (D1) The $n$ vectors $(X_i,W_i)$, $i=1,{\ldots },n$, are i.i.d. with $(X_i,W_i) \sim (X,W)$.

• (D2) $X_i$ and $W_i$ are independent for every $i$.

• (D3) $c_1,{\ldots },c_k \ne 0$. (Otherwise, if a $c_i$ equaled zero, every answer $A$ would restrict the possible $X$ values.)

• (D4) The matrix $C_0$ is invertible.

Assumption (D1) can be fulfilled by selecting the respondents according to simple random sampling with replacement. Further, let $n_i$ be the absolute frequency of answer $A=i$ and define $h_i:=n_i/n$ as well as $h:=(h_1,{\ldots },h_k)^T$. The likelihood function for $\pi$ is

$$\begin{aligned} L(\pi )\!=\!\prod _{i=1}^k \, \mathbb P (A=i)^{n_i}, \quad \pi \!\in \! \{(x_1,{\ldots },x_k)^T: x_i\! \in \![0,1], x_1\!+\!{\cdots }\!+\!x_k=1\}\!=:\!D.\nonumber \\ \end{aligned}$$

(3)

Define $E:=\{C_0 \cdot x:x\in D\}$. It can be shown by standard calculus that $\hat{\pi }=C_0^{-1}\cdot h$ is the unique MLE for $\pi$ if $h \in E$. If $\pi _1,{\ldots },\pi _k>0$, we have $\mathbb P (h\in E) \longrightarrow 1$ as $n\rightarrow \infty$ due to the weak law of large numbers. However, $h \notin E$ (that is $C_0^{-1} h \notin D$) may occur. In this case, the estimation of $\pi$ is most convenient with the expectation maximization (EM) algorithm. The complete data matrix is $Y=(A_i,X_i)_{i=1,{\ldots },n}$. With realizations $(a_i,x_i)$ the complete data log-likelihood for $\pi \in D$ is equal to

$$\begin{aligned} l_{com}(\pi ;a_1,{\ldots },a_n,x_1,{\ldots },x_n)&= \log \left(\prod _{i=1}^n \,\mathbb P (A_i=a_i\,,\, X_i=x_i)\right)\nonumber \\&= C+\sum _{i=1}^k m_i \cdot \log \pi _i, \end{aligned}$$

(4)

where $C$ is a negligible constant and $m_i=\sum _{j=1}^n 1_{\{x_j=i\}}$, that is $m_i$ is the number of persons in the sample whose value of the sensitive variable equals $i$. The observed data log-likelihood for $\pi \in D$ equals $\log L$ where $L$ is from (3). For the E step, suppose we have an estimate $\pi ^{(t)}$ from the preceding iteration $t$ and let $M_i$ be the random variables corresponding to the values $m_i$. Then

$$\begin{aligned} \hat{m}_i:=\mathbb E _{\pi ^{(t)}} \left(M_i\,|\,A_1=a_1,{\ldots },A_n=a_n\right)=\sum _{j=1}^k n_j \cdot \frac{ \pi ^{(t)}_i \cdot C_0(i,j) }{\mathbb P _{\pi ^{(t)}}(A=j)}, \end{aligned}$$

(5)

where $C_0(i,j)$ denotes entry $(i,j)$ of the design matrix $C_0$. Thus, the log-likelihood (4) is estimated by $\widehat{l_{com}}(\pi )= C + \sum _{i=1}^k \hat{m}_i \cdot \log \pi _i.$ At the succeeding M step, the maximum of $\,\widehat{l_{com}}$, which is given by $\pi ^{(t+1)}_i= \hat{m}_i / \sum _{j=1}^k \hat{m}_j$, is calculated. As initial parameter $\pi ^{(0)}_i=1/k$ can be used.

3.3 Standard errors and confidence intervals

To express the dependence of $h$ and the MLE $\hat{\pi }$ on $n$, we will occasionally write $h_n$ and $\hat{\pi }_n$ in the sequel. The multivariate central limit theorem implies $\sqrt{n}(h_n-\lambda ) \stackrel{\mathcal L }{\longrightarrow } N(0,\varSigma )$ with $\varSigma =diag(\lambda )-\lambda \lambda ^T$. Note, $N(0,\varSigma )$ is a singular normal distribution. Consider the estimator $\tilde{\pi }_n:=C_0^{-1}h_n$. If $h_n \in E$, then $\hat{\pi }_n=\tilde{\pi }_n$ holds. The estimator $\tilde{\pi }_{n}$ is unbiased and we have $Var(\tilde{\pi }_n)= \frac{1}{n} \cdot C_0^{-1} \cdot \varSigma \cdot C_0^{-1}= \frac{1}{n} \cdot (\varGamma + \varDelta )$ with

$$\begin{aligned} \varGamma := C_0^{-1} \cdot diag(\lambda ) \cdot C_0^{-1} \,\,-\,\, diag(\pi ) \quad \text{ and}\quad \varDelta :=diag(\pi ) - \pi \cdot \pi ^T \end{aligned}$$

(6)

By the continuous mapping theorem $\sqrt{n}(\tilde{\pi }_n-\pi ) \stackrel{\mathcal L }{\longrightarrow } N(0,\varGamma +\varDelta )$. We claim $\sqrt{n}(\hat{\pi }_n-\pi ) \stackrel{\mathcal L }{\longrightarrow } N(0,\varGamma +\varDelta )$. To prove the claim, it suffices to show the stochastic convergence of $\delta _n:=\sqrt{n}(\hat{\pi }_n-\tilde{\pi }_n)$ to $0$: For $\varepsilon >0$ we have $\mathbb P (|\delta _n| >\varepsilon ) \le \mathbb P (h_n \notin E) \rightarrow 0 (n\rightarrow \infty$), because $h_n$ converges almost surely to $\lambda$.

Now consider a function $\psi =f(\pi ) \in \mathbb R$ of the parameter $\pi$. The MLE for $\psi$ is given by $\hat{\psi } = f(\hat{\pi })$. Let $\hat{\varGamma }$ and $\hat{\varDelta }$ arise by using the MLE $\hat{\pi }$ instead of $\pi$ as well as $C_0\hat{\pi }$ instead of $\lambda$ in (6) and define $S_{\hat{\psi }}^2 = \frac{1}{n} \cdot \nabla ^T f(\hat{\pi }) \cdot (\hat{\varGamma }+ \hat{\varDelta }) \cdot \nabla f(\hat{\pi })$ where $\nabla$ denotes the gradient. Applying the delta method (cf. Van der Vaart 2007, p. 25) and Slutzky’s theorem $(\hat{\psi }- \psi )/S_{\hat{\psi }}$ converges in distribution to the standard normal distribution. Thus, $AS:=[\hat{\psi } - z_{1-\alpha /2} \cdot S_{\hat{\psi }}, \hat{\psi } + z_{1-\alpha /2} \cdot S_{\hat{\psi }} ]$ is an asymptotic $(1-\alpha )$ confidence interval (CI) for $\psi$. Here, $z_{1-\alpha /2}$ is the $(1-\alpha /2)$ quantile of the standard normal distribution.

Bootstrap standard errors and bootstrap confidence intervals can be derived according to Efron and Tibshirani (1993), chapters 6 and 12–13. Assume $\hat{\pi }$ and $\hat{\psi }$ are calculated. A bootstrap replication $\hat{\psi }^{(i)}, i=1,{\ldots },B$, can be generated by drawing new answer frequencies $n^{(i)}:=(n^{(i)}_1,{\ldots },n^{(i)}_k) \sim Multinomial(n, C_0\hat{\pi }),$ computing the MLE $\hat{\pi }^{(i)}$ based on $n^{(i)}$ and defining $\hat{\psi }^{(i)}:=f(\hat{\pi }^{(i)})$. Then, the bootstrap estimate $\hat{SE}(\hat{\psi })$ for the standard error of $\hat{\psi }$ is given by the empirical standard deviation of the replications $\hat{\psi }^{(1)},{\ldots },\hat{\psi }^{(B)}$. Further, if $(\hat{\psi } - \psi )/\hat{SE}(\hat{\psi })$ is approximately standard normal, $BT1:=[\hat{\psi } - z_{1-\alpha /2} \cdot \hat{SE}(\hat{\psi }), \hat{\psi } + z_{1-\alpha /2} \cdot \hat{SE}(\hat{\psi }) ]$ is a $(1-\alpha )$ bootstrap CI for $\psi$. Alternatively, a $(1-\alpha )$ bootstrap CI for $\psi$ without the normality assumption is given by $BT2:=\left[\psi _{\alpha /2}, \psi _{1-\alpha /2} \right]$ where the bounds are the $\alpha /2$ and $(1-\alpha /2)$ quantiles of the replications $\hat{\psi }^{(1)},{\ldots },\hat{\psi }^{(B)}$.

In simulations, which are not included in the paper, we have considered $k=3$, $n \in \{100,200\}$, several values of $\pi$ and $c$, as well as linear functions $f$ (e.g., the projection $f(x_1,x_2,x_3)= x_2$). We have seen that $AS$ and $BT2$ usually provide empirical coverage probabilities (CP) between 93 and 96 % ($\alpha =5\,\%$). The CP of $BT1$ turned out to be lower than the CP of $AS$ and $BT2$. Furthermore, the average width of $AS$ was mostly larger than the average width of $BT2$. For these reasons, we recommend the use of the BT2 confidence intervals.

(A MATLAB program that computes the MLE for $\pi$ and confidence intervals for $\psi$ is provided as online supplemental material.)

3.4 The special shape of the design matrix

In this section, we show the connection between $C_0$ and circulant matrices. Further, we mention some properties of circulant matrices that can be found in Gray (2006), chapter 3, and will be applied in the next section.

If we permute the rows of $C_0$, we obtain a matrix $C$ where every row of $C$ is a right-cyclic shift of the row above. In particular, define $C=S\cdot C_0$ where the entries of $S$ are given by $S(i,j)=1_{\{C_0(i,j)=c_1\}}. C$ is a circulant matrix (circulant matrices are a subset of Toeplitz matrices). Occasionally, we will write $C=circulant(c_1,{\ldots },c_k)$. Define $\psi _1,{\ldots },\psi _{k}$ by

$$\begin{aligned} \psi _l =\sum _{m =1}^{k} \exp {\left(-2\pi i \cdot \frac{(l-1)\cdot (m-1)}{k}\right)} \cdot c_m. \end{aligned}$$

(7)

Then, $\psi :=(\psi _1,{\ldots },\psi _{k})$ is a vector of eigenvalues of $C$ and $\psi$ can be computed by multiplying the $k \times k$ Fourier matrix $F=\left[\exp {\left(-2\pi i \cdot {(l-1)\cdot (m-1)} / {k}\right)}\right]_{l,m}$ with the vector $c^T=(c_1,{\ldots },c_{k})^T$, i.e., $\psi$ is the discrete Fourier transform of $c^T$. Moreover, $C^{-1}$ is circulant if $C$ is circulant and invertible.

3.5 Efficiency loss and degree of privacy protection

To study the efficiency of the MLE $\hat{\pi }=\hat{\pi }_n$, the mean squared error $MSE(\hat{\pi }_n) = \mathbb E \left((\hat{\pi }_n - \pi )(\hat{\pi }_n - \pi )^T\right)$ is suitable. The whole matrix $MSE(\hat{\pi }_n)$ is cumbersome, so we use $trace(MSE(\hat{\pi }_n)) = MSE(\hat{\pi }_{n,1})+{\cdots }+MSE(\hat{\pi }_{n,k}),$ i.e., the sum of the mean squared errors of the components $\hat{\pi }_{n,j}$, as a measure of the estimation inaccuracy. Define $\tilde{\pi }_n$ as in Sect. 3.3. We claim

$$\begin{aligned} \hat{T}\,/\,\tilde{T}:= trace(MSE(\hat{\pi }_n)) \,/\, trace(MSE(\tilde{\pi }_n)) \stackrel{n}{\longrightarrow } 1. \end{aligned}$$

(8)

To see (8), note that $n\cdot MSE(\tilde{\pi }_n) = \varGamma + \varDelta$, as described in Sect. 3.3. Because $\hat{\pi }_n = \tilde{\pi }_n$ for large $n$, we have $\hat{T}/\tilde{T}= (n\cdot \hat{T})/(n \cdot \tilde{T}) \stackrel{n}{\longrightarrow } trace(\varGamma + \varDelta ) \,/\, trace(\varGamma + \varDelta ) =1$. That is, $\hat{\pi }_n$ and $\tilde{\pi }_n$ are equally efficient as $n\rightarrow \infty$. Hence, for large $n$,

$$\begin{aligned} trace(MSE(\hat{\pi }_n))&\approx trace(MSE(\tilde{\pi }_n)) = trace\left(Var(\tilde{\pi }_n)\right)\nonumber \\&= trace\left({\varGamma }/{n}\right)+ trace\left({\varDelta }/{n}\right)\!. \end{aligned}$$

(9)

Imagine the respondents are interviewed directly, i.e., they are requested to tell their values of $X$, and assume that truthful answers are given. If $n$ people are asked, the MLE for $\pi$ is given by $\hat{\pi }^{dir}= (\hat{\pi }_1^{dir},{\ldots },\hat{\pi }_k^{dir})^T$ with $\hat{\pi }_i^{dir}= \frac{1}{n} \sum _{j=1}^n 1_{\{X_j=i\}}$.

The variance matrix of $\hat{\pi }^{dir}$ is then given by $\varDelta /n$. Since $\frac{1}{n} \cdot trace(\varGamma ) \approx trace(MSE(\hat{\pi }_n)) - trace(MSE(\hat{\pi }^{dir}))$, the quantity $\frac{1}{n} \cdot trace(\varGamma )$ describes the efficiency loss caused by questioning according to the diagonal model, instead of direct questioning.

The efficiency loss $trace(\varGamma )/n$ converges to zero as $n$ increases and we have:

Theorem 1

Let $\pi$ and $c=(c_1,{\ldots },c_k)$ describe the distribution of the sensitive variable $X$ and the auxiliary variable $W$, respectively. Further let $\varGamma$ be defined by (6). Then:

• (a) $trace(\varGamma )$ depends on $c$, but not on $\pi$.

• (b) $trace(\varGamma )\ge 0.$

• (c) $trace(\varGamma )$ attains its minimum value zero iff $W$ has a degenerate distribution (i.e., $W$ is a constant variable).

Proof

Define $C_0$ as design matrix induced by $c$ and $C=circulant(c_1,{\ldots },c_k)$. Let $S$ be given by $S(i,j)=1_{\{C_0(i,j)=c_1\}}$. Then, $S$ is a self-inverse permutation matrix.

The equation $C_0=S\cdot C$ implies $D_0:=C_0^{-1}=C^{-1} S$, i.e. $D_0$ arises by column permutation of a circulant matrix. Thus, every row of $D_0$ is a left-cyclic shift of the row above. Let $(d_1,d_2,{\ldots },d_k)$ denote the first row of $D_0$. The vector of the diagonal elements of $\varGamma$ fulfills

$$\begin{aligned} \tilde{\varGamma }:=( \varGamma (1,1),{\ldots }, \varGamma (k,k))^T= \left(D_0^{(2)}\cdot C_0 - I\right) \cdot \pi \end{aligned}$$

(10)

where $D_0^{(2)}$ is the componentwise square of $D_0$. For (10), the definitions of $\varGamma$ and $D_0$ as well as the identity $\pi =D_0\cdot \lambda$ yield $\tilde{\varGamma }=(D_0^{(2)}-D_0)\cdot \lambda =(D_0^{(2)}-D_0)\cdot C_0 \cdot \pi$. This verifies (10).

Using the shape of $C_0$ and $D_0^{(2)}$ it is easy to verify that $E:=\left(D_0^{(2)}\cdot C_0 - I\right)$ is circulant. Since $trace(\varGamma )$ equals the sum of the first column of $E$, we have

$$\begin{aligned} trace(\varGamma )=d_1^2+{\cdots }+d_k^2 -1, \end{aligned}$$

(11)

which shows (a). Consider an arbitrary eigenvalue $\psi$ of $C_0$ with eigenvector $v=(v_1,{\ldots },v_k)^T$ where the 1-norm of $v$ equals 1. Then, by the triangle inequality:

$$\begin{aligned} |\psi |=\Vert C_0v \Vert _1 \le \left( |v_1|+{\cdots }+|v_k| \right)(c_1+{\cdots }+c_k)=1. \end{aligned}$$

(12)

Further, for $i=1,{\ldots },k$ let $\psi _i$ and $\psi _i\left( M\right)$ denote the (not necessarily distinct) eigenvalues of $C_0$ and an arbitrary $k \times k$-matrix $M$, respectively. By a well-known property of the Frobenius norm $\Vert \cdot \Vert _F$ (see Gentle 2007, p. 132) and (12) we have

$$\begin{aligned} d_1^2+{\cdots }+d_k^2=\frac{1}{k} \Vert D_0 \Vert _F^2 = \frac{1}{k} \sum _{i=1}^k \psi _i\left( D_0 \cdot D_0\right) = \frac{1}{k} \left( \frac{1}{\psi _1^2}+{\cdots }+\frac{1}{\psi _k^2} \right) \ge 1,\nonumber \\ \end{aligned}$$

(13)

that is, $trace(\varGamma )\ge 0$ as claimed in (b). Further, we have

$$\begin{aligned} trace(\varGamma )= 0 \Longleftrightarrow \psi _1^2=\psi _2^2={\cdots }=\psi _k^2=1 \Longleftrightarrow C_0\cdot C_0 = I. \end{aligned}$$

Consider $c:=(c_1,{\ldots },c_k)$ and assume $c_j=1$ and $c_i=0$ for $i\ne j$. Then, clearly $C_0^2=I$ holds. Conversely, consider a $c$ with $C_0^2=I$. It follows that $c_1^2+{\cdots }+c_k^2=1$. Thus $c_1(1-c_1)+{\cdots }+c_k(1-c_k)=0$, which is only satisfied if $c_j=1$ for some $j\in \{1,{\ldots },k\}$ and $c_i=0$ for any $i\ne j$. Altogether we have $trace(\varGamma )=0$ iff $c$ corresponds to a degenerate distribution. $\square$

Theorem 1 (a) says that the efficiency loss $trace(\varGamma )$ is independent of the unknown $\pi$. Occasionally, we will write $trace(\varGamma (c))$ to symbolize the dependence of $trace(\varGamma )$ on $c$. Furthermore, Theorem 1(c) states that the diagonal model would be most efficient for a constant auxiliary variable $W$. However, such a $W$ is not appropriate, because the interviewer can conclude the $X$ value from answer (2). This would be contradictory to the idea of the diagonal model and would result in nonresponses and untruthful answers.

In the remainder of this section, we will have a closer look at the connection between the DPP and efficiency loss.

As explained above, the privacy is not protected if $W$ has a degenerate distribution. In contrast, the privacy is protected as much as possible in the case of an exactly uniformly distributed $W$; in this case, any answer $A$ according to the diagonal model does not change the probability that the variable $X$ attains a value $x$, i.e., $A$ and $X$ are independent (notice the constant likelihood function in this case). To measure the DPP, it seems reasonable to consider the closeness of the distribution of $W$ to a degenerate and a uniform distribution. This motivates us to quantify the DPP by the empirical standard deviation of the vector $c$

$$\begin{aligned} \sigma (c):=std(c)= \sqrt{(c_1^2+{\cdots }+c_k^2)/(k-1) - [(k-1)k]^{-1}} \in [0,\sqrt{{1}/{k}}].\qquad \end{aligned}$$

(14)

A large $std(c)$ means an approach to a degenerate distribution and consequently a small DPP, while a small $std(c)$ indicates that the distribution of $W$ is close to a uniform distribution and a high DPP is available.

The efficiency loss $trace(\varGamma )$ has a lower bound depending on $\sigma$:

Theorem 2

 

• (a) Consider a vector $c=(c_1,{\ldots },c_k)$ describing the distribution of the auxiliary variable $W$. Let $\sigma >0$ and $trace(\varGamma )$ denote the corresponding DPP and efficiency loss due to indirect questioning, respectively. Then

  $$\begin{aligned} trace(\varGamma ) \ge \frac{(k-1)\left(\frac{1}{k} - \sigma ^2\right)}{k\sigma ^2}. \end{aligned}$$

  (15)

• (b) Let $\sigma \in \left(0,\sqrt{\frac{1}{k}}\,\right]$ be given. Define $c=(c_1,{\ldots },c_k)$ with

  $$\begin{aligned} c_1=\frac{1}{k}+\frac{k-1}{k}\sqrt{k\sigma ^2} \quad \text{ and} \quad c_2={\cdots }=c_k=\frac{1}{k}-\frac{1}{k}\sqrt{k\sigma ^2}. \end{aligned}$$

  (16)

  Then, we have $std(c)=\sigma$ and $trace(\varGamma (c)) = \frac{(k-1)(\frac{1}{k} - \sigma ^2)}{k\sigma ^2}$.

 

Proof

(a) We first minimize the function

$$\begin{aligned} f(x)=f(x_1,{\ldots },x_{k-1}):= \frac{1}{k} \left( \frac{1}{x_1^2}+{\cdots }+\frac{1}{x_{k-1}^2} \right) -1 + \frac{1}{k}, \quad x_i\ne 0 \end{aligned}$$

under the restriction $g(x)=x_1^2+{\cdots }+x_{k-1}^2-k(k-1)\sigma ^2=0$. Since $f\rightarrow \infty$ if $x_i\rightarrow 0$, $f$ possesses a global minimum $m^*=(m_1^*,{\ldots },m_{k-1}^*)$. By Lagrange multipliers, one can show $\left(m_1^*\right)^2={\cdots }=\left(m_{k-1}^*\right)^2 = k\sigma ^2$. Then

$$\begin{aligned} f(m^*)= \frac{(k-1)\left(\frac{1}{k} - \sigma ^2\right)}{k\sigma ^2} \le f(x), \text{ for} \text{ all} \, x \text{ with} \, x_i\ne 0, g(x)=0. \end{aligned}$$

(17)

Now define $C_0$ as the design matrix formed with the vector $c$. For $i=1,{\ldots },k$ let $\psi _i$ and $\psi _i\left( C_0^2\right)$ denote the eigenvalues of $C_0$ and $C_0^2$, respectively. By a property of the Frobenius norm $\Vert \cdot \Vert _F$ (Gentle 2007, p. 132)

$$\begin{aligned} c_1^2+{\cdots }+c_k^2= \frac{1}{k} \Vert C_0 \Vert _F^2 = \frac{1}{k} \sum _{i=1}^k \psi _i\left( C_0^2\right) = \frac{1}{k} \left( \psi _1^2+{\cdots }+\psi _k^2 \right). \end{aligned}$$

holds. Thus, with (14) we obtain

$$\begin{aligned} \sigma ^2=\frac{1}{(k-1)k}\left( \psi _1^2+{\cdots }+\psi _k^2 -1\right) =\frac{1}{(k-1)k}\left( \psi _2^2+{\cdots }+\psi _{k}^2 \right) \end{aligned}$$

(18)

where the latter equality is true since $C_0$ has an eigenvalue equal to 1 (with eigenvector $(1,{\ldots },1)^T$). According to (11) and (13) we have

$$\begin{aligned} trace(\varGamma )= \frac{1}{k} \left( \frac{1}{\psi _1^2}+{\cdots }+\frac{1}{\psi _k^2} \right) -1= \frac{1}{k} \left( \frac{1}{\psi _2^2}+{\cdots }+\frac{1}{\psi _k^2} \right) -1 + \frac{1}{k}.\qquad \end{aligned}$$

(19)

Then, the claim follows by application of (17).

(b) Consider $c$ as in the claim. Let $C_0$ be the corresponding design matrix with eigenvalues $\psi _1,{\ldots },\psi _k$ and $x=(x_1,{\ldots },x_k)$ the first row of $C_0^2$. It follows straightforwardly that

$$\begin{aligned} x_1=\frac{1}{k}(1+(k-1)k\sigma ^2) \quad \text{ and}\quad x_2={\cdots }=x_k=\frac{1}{k}(1-k\sigma ^2). \end{aligned}$$

(20)

Since $C_0^2$ is a circulant matrix, the eigenvalues can be obtained by a discrete Fourier transform of $x$, cf. (7). Then, $\psi _1^2=\sum _{i=1}^k x_i= 1$ and with the formula for the sum of a geometric sequence we have for $l=2,{\ldots },k$

$$\begin{aligned} \psi _l^2&= \sum _{m =1}^{k} \exp {\left(-2\pi i \cdot \frac{(l-1)\cdot (m-1)}{k}\right)} \cdot x_m \\&= x_1+x_2\cdot \sum _{m =1}^{k-1} \exp {\left(-2\pi i \cdot \frac{(l-1)\cdot m}{k}\right)} = x_1-x_2=k\sigma ^2 . \end{aligned}$$

Hence, by (18) and (19) we can compute that $std(c)$ equals the given $\sigma$ and that $trace(\varGamma (c))$ attains the lower bound $\frac{(k-1)(\frac{1}{k} - \sigma ^2)}{k\sigma ^2}$. $\square$

We immediately attach two remarks concerning this theorem:

• (1) If  $k=2$ or $k=3$,  then for every  $c=(c_1,{\ldots },c_k)$,  the point  $\big (\,std(c),trace(\varGamma (c))\,\big )$  is located on the curve  $\left\{ \,\left(\sigma \,,\, \frac{(k-1)(\frac{1}{k} - \sigma ^2)}{k\sigma ^2}\right) \,:\, 0\le \sigma \le \sqrt{\frac{1}{k}}\, \right\}$. For $k=2$: One eigenvalue of $C_0$, say $\psi _1$, is always equal to 1 and $\psi _2^2$ equals $2\sigma ^2$ due to (18). Then, (19) implies $trace(\varGamma (c))=(\frac{1}{2} - \sigma ^2) \cdot (2\sigma ^2)^{-1}$. Similar in case $k=3$: We obtain $\psi _1=1$ and $\psi _2^2+\psi _3^2=6\sigma ^2$. Additionally, $1=c_1+c_2+c_3=trace(C_0)= \psi _1+\psi _2+\psi _3$ implies $\psi _2=-\psi _3$. Thus, $\psi _2^2=\psi _3^2=3\sigma ^2$ and the claim follows with (19).

• (2) Fix a  $\sigma >0$   and consider  $c$  given in Theorem 2 (b). This c is not the only vector with a provided DPP equal to   $\sigma$  and a caused efficiency loss  $trace(\varGamma )$  that attains the lower bound  $\frac{(k-1)(\frac{1}{k}-\sigma ^2)}{k\sigma ^2}$. Assume $c^{\prime }\ne c$ has design matrix $C_0^{\prime }$ and $(C_0^{\prime })^2 = circulant(x_1,{\ldots },x_k)$ with the $x_i$ from (20). Then, according to the proof of theorem $2(b)$, $std(c^{\prime })=\sigma$ and $trace(\varGamma (c^{\prime }))={(k-1)(\frac{1}{k} - \sigma ^2)}\cdot ({k\sigma ^2})^{-1}$ hold, that is, $c^{\prime }$ would be an alternative to $c$. Now, such a vector $c^{\prime }$ can be found by permuting $c$. However, other choices are also possible: For instance, for $k=4$ and $\sigma =0.4$ we can use $\begin{pmatrix} 0.45+\sqrt{0.1591},&0.02,&0.45-\sqrt{0.1591},&0.08\end{pmatrix}$, too. $\square$

Theorem 2 contains two core statements: first, there are optimal and nonoptimal distributions of $W$. A distribution of $W$ is not optimal if the corresponding vector $c$ has a standard deviation $\sigma$, but $trace(\varGamma (c))\ne \frac{(k-1)(\frac{1}{k} - \sigma ^2)}{k\sigma ^2}$. In this case, $c$ would lead to an efficiency loss larger than necessary for a DPP in the amount of $\sigma$. A vector $c$ is optimal if and only if $(\sigma (c), trace(\varGamma (c)))$ is an element of the “optimality curve” $\mathcal O :=\{ (\sigma , \gamma ^*(\sigma )) : \sigma \in (0,\sqrt{{1}/{k}}], \gamma ^*(\sigma )={(k-1)(k^{-1} - \sigma ^2)}/{(k\sigma ^2)} \}.$ Of course, it is reasonable to use only optimal vectors $c$. For these vectors, the efficiency loss is a function of the DPP. Since $\gamma ^*$ is a decreasing function, the efficiency loss decreases if the standard deviation increases. This implies the second key result: Increasing efficiency of the diagonal model corresponds to decreasing protection of the respondents’ privacy.

4 Simulation study

Remember that the results in 3.5 were obtained under the assumption of a large sample size $n$. In the subsequent simulation study, we are going to examine the validity of the results for a concrete example with different sample sizes. We run all simulations using MATLAB, Version 7.11.

4.1 Simulated MSE sum

For our simulations, we consider a concrete variable $X$ with a known distribution. Let $\hat{\pi }= (\hat{\pi }_1,{\ldots },\hat{\pi }_k)^T$ denote the DM estimator for a known $\pi$. For a fixed and possibly “small” sample size $n$, we cannot calculate $trace(MSE(\hat{\pi }))$ with the help of Sect. 3.5, because (9) holds only for “large” $n$. Therefore, assume $l$ independent realizations of $\hat{\pi }$—denoted with $\hat{\pi }^{(i)}=(\hat{\pi }^{(i)}_1,{\ldots },\hat{\pi }^{(i)}_k)^T$, $i=1,{\ldots },l$—are available. Define $\widehat{MSE(\hat{\pi }_j)}:= \frac{1}{l} \sum _{i=1}^l (\hat{\pi }^{(i)}_j - \pi _j )^2$ for $j=1,{\ldots },k.$ The simulated MSE sum $\widehat{trace(MSE(\hat{\pi }))} : = \sum _{j=1}^k \widehat{MSE(\hat{\pi }_j)}$ is then a suitable approximation for the efficiency measure $trace(MSE(\hat{\pi }))$.

4.2 DPP and efficiency in a simulated example

We assume that the attribute “income” is the subject of a survey. For instance, a company could be interested in the income of customers, because products and prices must be attuned to it. We use Germany’s income distribution published by the Federal Statistical Office, Germany (2009). Suppose we focus on four income classes (in Euro per year): below 10,000 ($X=1$), 10,000–24,999 ($X=2$), 25,000–49,999 ($X=3$), and more than 50,000 ($X=4$). According to the data of the Federal Statistical Office, the distribution $\mathbb P _X$ is given by

$$\begin{aligned} \mathbb P _X \sim \pi = \begin{pmatrix} \pi _1&\pi _2&\pi _3&\pi _4 \end{pmatrix} ^T = \begin{pmatrix} 0.2371&0.3203&0.3343&0.1083 \end{pmatrix} ^T\!. \end{aligned}$$

(21)

To express the dependence of the DM estimator on the sample size $n$ and on the distribution of $W$, i.e., on the vector $c=(c_1,{\ldots },c_4)$, we write $\hat{\pi }_n(c)$. First, we investigate the efficiency of $\hat{\pi }_n(c)$ for randomly drawn vectors $c$. In particular, 500 vectors are drawn so that they are preferably uniformly scattered over the set of valid points $D_k=\{(x_1,{\ldots },x_{k}) \in [0,1]^{k}: x_1+{\cdots }+x_{k}=1\}$. To obtain one such vector $c$, we firstly generate $\tilde{c}:=(c_1,{\ldots },c_{k-1})$ from a Dirichlet distribution with parameter $(1,{\ldots },1)$, see Gentle (1998), p. 111. Subsequently, we define $c_k=1-(c_1+{\cdots }+c_{k-1}).$

For each drawn vector $c$:

• 1. Calculate $\sigma (c)$.

• 2. Generate $l=1,000$ independent simple random samples with replacement of size $n\in \{50,100,250\}$ from the distribution $\mathbb P _X$ in (21). For each sample, we compute the DM estimator, so we have $l$ independent realizations of $\hat{\pi }_n(c)$.

• 3. Calculate the simulated MSE sum $\widehat{trace(MSE(\hat{\pi }_n(c)))}$.

Subsequently, we choose different vectors $c^*$ according to Theorem 2 (b)—see Table 1—and run steps 2 and 3 for these vectors.

Table 1 The vectors $c^*$ that we used from Theorem 2(b)

Fig. 1

Plots of simulated MSE sum against standard deviation for different sample sizes. Each point ($\cdot$) corresponds to a vector $c$ drawn randomly from $D_4$, and each black cross corresponds to a vector $c^{*(i)}$

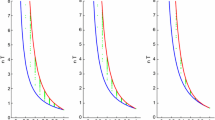
For all considered vectors, we plot the simulated MSE sum against the standard deviation in Fig. 1. Here, we see that the key results described after Theorem 2, which were obtained under the assumption of a “large” $n$, remain valid for $n\in \{50,100,250\}$. In particular, the point clouds for the randomly drawn vectors $c$ have lower bounds. Thus, there are optimal and nonoptimal vectors $c$. For all considered $n$, the points $\left(\sigma (c^{*(i)}), \widehat{trace(MSE(\hat{\pi }_n(c^{*(i)})))}\right)$, which are marked with $\times$ in the figure, are located close to this bound. In other words, $c^{*(i)}$ ($i=1,{\ldots },7$) are good choices for the distribution of $W$ for the corresponding degrees of privacy protection.

Furthermore, if we connect the points marked with $\times$, we obtain a decreasing function. Thus, an increasing standard deviation implies a decreasing estimation inaccuracy. Hence, a decreasing DPP corresponds to increasing efficiency. Finally, for any $c^{*(i)}$, the simulated MSE sum decreases with increasing sample size.

In practice, the investigator should first fix a DPP $\sigma$ around the middle of the range $(0,0.5 ]$. For this $\sigma$, he or she should then choose a vector $c$ using Theorem 2 (b). Subsequently, an auxiliary attribute $W$ such as the “birthday of the respondent’s mother” or the “last digits of the mother’s phone number” should be adapted to the chosen $c$. For example, define $W$ as in the concrete example of Sect. 3.1, where $c=(c_1,{\ldots },c_4)= \begin{pmatrix} \frac{228}{365}&\frac{46}{365}&\frac{46}{365}&\frac{45}{365}\end{pmatrix} \approx \begin{pmatrix} 0.625&0.126&0.126&0.123\end{pmatrix}.$ This $c$ is then a good approximation to $c^{*(4)}$ from Table 1, which was obtained from Theorem  2 (b).

5 Summary

In this paper, we have presented the nonrandomized diagonal model, which is a privacy-protecting survey design for multichotomous sensitive variables. The proposed method can be conducted even if all values of the considered variable are sensitive. We have shown that the formula for the answer can be easily explained to the respondents. After deriving the MLE and confidence intervals, we discussed the DPP and efficiency. Here, a mathematical function for the dependence of the efficiency on the model parameters was derived in Theorem 2. This enables the interviewer to choose optimal model parameters for a desired DPP.