Strong equilibrium in network congestion games: increasing versus decreasing costs

Abstract

A network congestion game is played on a directed, two-terminal network. Every player chooses a route from his origin to his destination. The cost of a route is the sum of the costs of the arcs on it. The arc cost is a function of the number of players who use it. Rosenthal proved that such a game always has a Nash equilibrium in pure strategies. Here we pursue a systematic study of the classes of networks for which a strong equilibrium is guaranteed to exist, under two opposite monotonicity assumptions on the arc cost functions. Our main results are: (a) If costs are increasing, strong equilibrium is guaranteed on extension-parallel networks, regardless of whether the players’ origins and destinations are the same or may differ. (b) If costs are decreasing, and the players have the same origin but possibly different destinations, strong equilibrium is guaranteed on series-parallel networks. (c) If costs are decreasing, and both origins and destinations may differ, strong equilibrium is guaranteed on multiextension-parallel networks. In each case, the network condition is not only sufficient but also necessary in order to guarantee strong equilibrium. These results extend and improve earlier ones by Holzman and Law-Yone in the increasing case, and by Epstein et al. in the decreasing case.

1 Introduction

Networks serve as the infrastructure for various activities, including transportation, communication, computation, etc. Typically, many users share the resources of a network, and are affected by each other’s actions. The study of network congestion games aims at analyzing the strategic aspects of such interactions.

A network congestion game¹ is described by a network and a set of players, each with a designated origin and destination. A player chooses as his strategy any of the routes from his origin to his destination, and incurs a total cost equal to the sum of the costs of the arcs that form his chosen route. For each arc, the per-user cost is determined as a function of the number of users of that arc.

This model was introduced by Rosenthal (1973b).² He proved that a network congestion game always has a Nash equilibrium in pure strategies. This is due to the fact that such a game (and more generally, any congestion game Rosenthal 1973a) has an exact potential in the sense of Monderer and Shapley (1996).

However, a Nash equilibrium does not necessarily entail efficiency or stability with respect to coalitional deviations, as required in the concept of strong equilibrium (Aumann 1959). Without further conditions, a strong equilibrium may fail to exist even in the simple set-up of two players having to choose between two arcs $a$ and $b$ leading from their common origin to their common destination. Indeed, suppose the per-user cost of $a$ is 0 for a single user and 2 when both use it, and the per-user cost of $b$ is 3 for a single user and 1 when both use it. The resulting game is a prisoner’s dilemma: it is a dominant strategy for each player to choose $a$, yielding a unique Nash equilibrium with each player paying 2, whereas a joint deviation to $b$ would reduce each player’s cost to 1.

We may be able to ensure existence of strong equilibrium by imposing various conditions on the structure of the network, the players’ origins and destinations, and the arc cost functions. The above example, in which the cost function of $a$ was increasing and that of $b$ was decreasing, indicates that it is essential to impose one kind of monotonicity on all arc cost functions. If the costs pertain to the usage of the arcs (e.g., they represent the time it takes to traverse an arc), it is natural to assume that they increase with the number of users. This indeed has been the assumption in much of the congestion games literature. But if we are looking at the costs of building and maintaining the arcs, which are shared by the users of each arc, then the per-user cost is likely to decrease with the number of users. Such is the case in the recent network design literature in computer science (see, e.g., Anshelevich et al. 2004).

Here we contrast the two alternative kinds of cost monotonicity, and examine the conditions on network structure and player locations that guarantee the existence of strong equilibrium under each of them. Intuitively, decreasing costs should facilitate strong equilbrium, since the players help each other by sharing the same arcs. This intuition is easily translated to an existence proof of strong equilibrium in the case of decreasing costs, if all players have the same origin and the same destination. But if different players have different origins and destinations, full sharing becomes impossible, and it is not clear how to reach a strong equilibrium.

We consider three regimes regarding the players’ locations: (a) all players have the same origin and the same destination, (b) all players have the same origin but may have any destinations,³ and (c) players may have any origins and any destinations. For each combination of locations regime and monotonicity type (increasing or decreasing costs), we fully characterize the networks for which all the corresponding congestion games possess strong equilibria. The characterizations involve the well-known class of series-parallel networks (introduced originally in the study of electrical networks), and two subclasses: extension-parallel networks (introduced in Holzman and Law-yone 2003) and the somewhat more general multiextension-parallel networks (introduced here). These subclasses are obtained by maintaining the framework of constructing networks via series join and parallel join, but requiring that series join be applied only when one of the two networks being joined is of a simple kind. Table 1 summarizes the results and attributes them to earlier work or to theorems in this paper.

Table 1 The classes of networks guaranteeing existence of strong equilibrium under different combinations of locations regime and cost monotonicity type

We discuss now the relation of our work to the most relevant previous work. The study of strong equilibrium in congestion games with increasing costs was initiated in Holzman and Law-Yone (1997), and specialized to the network set-up in Holzman and Law-yone (2003). The latter considered only the same-origin same-destination regime, and characterized the extension-parallel networks as those guaranteeing strong equilibrium in this case. Here we prove that the same class of networks guarantees strong equilibrium even if origins and destinations may vary across players. This generalization is by no means straightforward. Indeed, a key property of extension-parallel networks in the same-origin same-destination case—the absence of so-called bad configurations in the strategy spaces—is lost when players have different origins and destinations.

Our results for the case of decreasing costs are closely related to the work of Epstein et al. (2009). They considered the class of fair connection games, which amounts to network congestion games in which the per-user cost of an arc is a constant (that may depend on the arc) divided by the number of users of that arc. They gave sufficient conditions for a network to guarantee existence of strong equilibrium in all corresponding fair connection games, under each of the three player locations regimes. In fact their proofs do not exploit the special cost structure of fair connection games, and extend easily to network congestion games with decreasing costs. The main contribution of our work is that our network conditions are also necessary, whereas those of Epstein et al. were not. In the same-origin any-destinations case, this is due to the existence of non-series-parallel networks that guarantee strong equilibrium in all fair connection games, but not in all network congestion games with decreasing costs. In the any-origins any-destinations case, we identify a weaker sufficient condition than theirs—multiextension-parallel instead of extension-parallel—which is moreover a necessary condition. Another point to note is that our definition of a network, unlike that of Epstein et al., allows cycles, which renders it more general and closer to real life. In all nontrivial positive results the networks are acyclic, but this is a consequence of the characterizations rather than a restrictive a-priori assumption.

Strong equilibrium in congestion games with decreasing costs (not necessarily on networks) was first studied by Rozenfeld and Tennenholtz (2006). They showed that, essentially, the only strategy spaces that guarantee existence of strong equilibrium are those with singleton strategies. This negative result is due to the extremely strong sense of ‘guaranteeing’ in their model: for a given strategy space, they considered all ways of deciding which strategies are feasible to each player, and required that all corresponding congestion games possess strong equilibria. In our model, the feasibility of strategies may differ across players, but is not arbitrary—it is fully determined by the players’ origins and destinations. The contrast between Rozenfeld and Tennenholtz’s result and our much more positive ones highlights the importance of this feature of our model.

When comparing our results for the two kinds of cost monotonicity, a few observations stand out. On the one hand, the classes of networks that guarantee strong equilibrium when costs are decreasing are significantly larger, in each of the locations regimes, than the corresponding class for increasing costs. On the other hand, in the increasing case, our result not only yields the existence of strong equilibrium but shows that every Nash equilibrium is strong. The latter is not true in the decreasing case. For example, consider the set-up with two players choosing between two arcs, and suppose the per-user cost of $a$ is 2 for a single user and 0 when both use it, and that of $b$ is 2 for a single user and 1 when both use it. There are two Nash equilibria in which the players choose the same arc, but only one of them—where they choose $a$—is strong. Another observation is that in the decreasing case, the class of networks guaranteeing strong equilibrium is very sensitive to the locations regime, whereas in the increasing case that class is the same regardless of the regime.

We give precise definitions and statements of the main results in the next section. The proof of the result for increasing costs appears in Sect. 3. The treatment of decreasing costs is divided into the sufficiency part (Sect. 4) and the necessity part (Sect. 5). In the latter, we give forbidden substructure characterizations of our network classes, which are of independent graph theoretic interest.

2 Definitions and main results

2.1 Networks

Our networks are directed, may contain cycles, and have two terminals—a source and a sink. These terminals serve as points of reference but not necessarily as the origin and destination of the players. Formally, a network is specified as $D=(V,A,s_0,s_1)$, where:

• $V$ is a finite set of vertices;

• $A$ is a finite set of arcs; each arc $a \in A$ has a tail $t(a) \in V$ and a head $h(a) \in V$;

• $s_0$ (the source) and $s_1$ (the sink) are two distinct vertices in $V$.

A route in $D$ is a sequence of the form $v_0,a_1,v_1,a_2,\ldots ,v_{\ell -1},a_\ell ,v_\ell$ where $v_0,v_1,\ldots ,v_\ell$ are distinct vertices, and $a_1,\ldots ,a_\ell$ are arcs satisfying $t(a_i)=v_{i-1}$ and $h(a_i)=v_i$ for $i=1,\ldots ,\ell$. It is a $u-v$ route if $v_0=u$ and $v_\ell =v$. The following condition, which is part of our definition of a network, expresses the special role of the source and the sink:

• Every vertex in $V$ and every arc in $A$ belongs to at least one $s_0-s_1$ route in $D$.

A subnetwork of $D$ is a network $D^{\prime }$ obtained from $D$ by (possibly) deleting some vertices and arcs, and renaming two of the remaining vertices as the source and the sink of $D^{\prime }$.

The simplest kind of network is a single-arc network, with one arc from the source to the sink. Somewhat more general is the class of multiple-arc networks, with one or more arcs from the source to the sink (which are the only vertices).

Given two networks $D_1$, $D_2$, we define two kinds of join operations. The series join $D=D_1 \rightarrow D_2$ is obtained by identifying the sink of $D_1$ with the source of $D_2$; the source of $D_1$ becomes that of $D$, and the sink of $D_2$ becomes that of $D$. The parallel join $D=D_1 \parallel D_2$ is obtained by identifying their two sources, to become that of $D$, and their two sinks, to become that of $D$. In either operation, the set of vertices of $D$ is the disjoint (except for the identified terminals) union of the vertex sets in $D_1$ and $D_2$, and the set of arcs of $D$ is the disjoint union of the arc sets in $D_1$ and $D_2$.

A network $D$ is series-parallel if there exists a sequence of networks $D_1,D_2,\ldots ,D_m$ with $D_m=D$, so that for every $i=1,\ldots ,m$, either $D_i$ is a single-arc network, or there exist $j,k<i$ such that $D_i=D_j \rightarrow D_k$ or $D_i=D_j \parallel D_k$. Such a sequence is called a series-parallel construction of $D$. The definition of an extension-parallel network is similar, but requires that whenever $D_i$ in the sequence is formed as a series join of $D_j$ and $D_k$, at least one of $D_j$, $D_k$ must be a single-arc network. For a multiextension-parallel network, the requirement is that at least one of $D_j$, $D_k$ involved in a series join must be a multiple-arc network. These classes of networks are nested as extension-parallel $\subseteq$ multiextension-parallel $\subseteq$ series-parallel. See Fig. 1 for examples.

Fig. 1

Examples of networks: a extension-parallel b multiextension-parallel but not extension-parallel c series-parallel but not multiextension-parallel d not series-parallel

2.2 Games

A network $D=(V,A,s_0,s_1)$ is given. To define a game on $D$, we consider a finite set $N$ of players. For each $i \in N$, an origin $o^i \in V$ and a destination $d^i \in V$ are specified, so that $o^i \ne d^i$ and the set $\Sigma ^i$ of all $o^i-d^i$ routes in $D$ is nonempty. This set is player $i$’s strategy space. We look at three nested classes of player locations: SOSD $\subseteq$ SOAD $\subseteq$ AOAD. In SOSD (same-origin same-destination) all $o^i$, $i \in N$, are the same, and all $d^i$, $i \in N$, are the same. In SOAD (same-origin any-destinations) all $o^i$ are the same, but the $d^i$ may be distinct. In AOAD (any-origins any-destinations) both the $o^i$ and the $d^i$ may be distinct.

For each arc $a \in A$, the per-user cost of $a$ is a function of the number $k$ of users of $a$, written as $c_a(k)$. In general, the $c_a(k)$ for $a \in A$ and $1 \le k \le |N|$ are arbitrary nonnegative real numbers, but we focus on two classes of monotone cost assignments. In INC (increasing costs) $k \le \ell$ implies $c_a(k) \le c_a(\ell )$, whereas in DEC (decreasing costs) $k \le \ell$ implies $c_a(k) \ge c_a(\ell )$ for all $a \in A$.⁴

Given the network $D$, the players’ locations, and the cost assignments, the game $G$ is defined as follows. Recall that a strategy $R^i \in \Sigma ^i$ is a $o^i-d^i$ route. We identify each $R^i$ with the set of arcs that belong to this route, so $R^i \subseteq A$. The set of strategy profiles is $\Sigma ^N=\times _{i \in N}\Sigma ^i$. Given $R=(R^i)_{i \in N} \in \Sigma ^N$, the congestion at arc $a \in A$ is

$$\begin{aligned} \sigma _a(R)=|\{i \in N:\, a \in R^i\}|, \end{aligned}$$

and the disutility of player $i \in N$ is

$$\begin{aligned} \pi ^i(R)=\sum _{a \in R^i}c_a(\sigma _a(R)). \end{aligned}$$

Any game $G$ defined in this way from $D$ is called a congestion game on $D$. We shall be interested in subclasses of this class of games, corresponding to conditions imposed on the players’ locations and/or the cost assignments. For example, a SOSD-INC game on $D$ is a game defined as above with SOSD player locations and INC cost assignments, and similarly for the other combinations.

Our games are defined in disutility form, and so the standard game theoretic concepts apply with reverse inequalities. Thus, $R=(R^i)_{i \in N} \in \Sigma ^N$ is a Nash equilibrium if there do not exist a player $i \in N$ and a strategy $P^i \in \Sigma ^i$ such that $\pi ^i(P^i,R^{N \setminus \{i\}})<\pi ^i(R)$. It is a strong equilibrium if there do not exist a nonempty coalition of players $S \subseteq N$ and strategies $P^i \in \Sigma ^i$ for $i \in S$ such that $\pi ^i(P^S,R^{N \setminus S})<\pi ^i(R)$ for every $i \in S$. Here $(P^S,R^{N \setminus S})$ is the strategy profile where each player $i \in S$ chooses $P^i$ and each $j \in N \setminus S$ chooses $R^j$. We refer to such $P^S$ as a profitable deviation of coalition $S$ (from $R$). The sets of Nash equilibria and strong equilibria in the game $G$ are denoted by $\text {NE}(G)$ and $\text {SE}(G)$ respectively, and clearly satisfy $\text {SE}(G) \subseteq \text {NE}(G)$.

We say that a network $D$ is $\Gamma$-strong with respect to a subclass $\Gamma$ of games on $D$, if every game in $\Gamma$ has a strong equilibrium. For example, $D$ is SOSD-INC-strong if $\text {SE}(G) \ne \emptyset$ for every SOSD-INC game $G$ on $D$, and similarly for the other subclasses.

2.3 Results

Theorem 1

Let $D$ be an extension-parallel network, and let $G$ be a AOAD-INC game on $D$. Then $\text {SE}(G)=\text {NE}(G)$.

Since, by Rosenthal’s (1973b) theorem, all congestion games $G$ on any network $D$ have $\text {NE}(G) \ne \emptyset$, it follows from Theorem 1 that extension-parallel networks are AOAD-INC-strong. In the opposite direction, Holzman and Law-yone (2003) showed that non-extension-parallel networks are not SOSD-INC-strong. These facts, together with the containment relations between the player location classes, yield:

Corollary 1

Let $D$ be a network. The following conditions are equivalent:

• 1. $D$ is SOSD-INC-strong.

• 2. $D$ is SOAD-INC-strong.

• 3. $D$ is AOAD-INC-strong.

• 4. $D$ is extension-parallel.

The subclass SOSD-DEC is trivial. Indeed, let $D$ be any network, and let $G$ be a game on $D$ with $o^i=o$, $d^i=d$ for all $i \in N$, and decreasing costs. Then the players have a common strategy space $\Sigma$, consisting of all $o-d$ routes in $D$. Let $\min _{R \in \Sigma }\sum _{a \in R}c_a(|N|)$ be attained at $\hat{R} \in \Sigma$. Then the profile where every player chooses $\hat{R}$ gives the lowest disutility to each player, and is therefore a strong equilibrium in $G$.⁵ Thus, all networks are SOSD-DEC-strong.

For the remaining two subclasses, we have:

Theorem 2

Let $D$ be a network. Then $D$ is SOAD-DEC-strong if and only if $D$ is series-parallel.

Theorem 3

Let $D$ be a network. Then $D$ is AOAD-DEC-strong if and only if $D$ is multiextension-parallel.

3 Increasing costs

In this section we prove Theorem 1. Let $D=(V,A,s_0,s_1)$ be an extension-parallel network, and let $N$ be a set of players with origins $o^i$, $i \in N$, and destinations $d^i$, $i \in N$. For each $i \in N$, we fix a $s_0-o^i$ route and a $d^i-s_1$ route, and denote their union (viewed as a set of arcs) by $F^i$. For each $o^i-d^i$ route $R^i$, the set $R^i \cup F^i$ forms a $s_0-s_1$ route; and conversely, for each $s_0-s_1$ route $R$ that contains $F^i$, the set $R \setminus F^i$ forms a $o^i-d^i$ route. Writing $\overline{R}^i=R^i \cup F^i$ and denoting the set of $s_0-s_1$ routes that contain $F^i$ by $\overline{\Sigma }^i$, we conclude that the mapping $R^i \mapsto \overline{R}^i$ is a bijection from $\Sigma ^i$ to $\overline{\Sigma }^i$. We refer to $\overline{R}^i$ as the extension of strategy $R^i$.⁶

We recall now the main tools developed in Holzman and Law-Yone (1997) and adapt them to our needs here. The set $\Sigma$ of $s_0-s_1$ routes in $D$ admits a tree-representation in the following sense. There exists a tree $T$ with root $r$, and a one-to-one labeling of the non-root nodes of $T$ by the arcs in $A$, so that each branch of $T$ (i.e., a path from $r$ to a terminal node) corresponds to a route in $\Sigma$, and vice versa. Note that the set of labels along the branch has to be equal to the set of arcs along the corresponding route, but they need not appear in the same order. Figure 2 illustrates an extension-parallel network $D$ and a tree-representation $T$ of its $s_0-s_1$ routes.⁷

Fig. 2

An extension-parallel network $D$ and a tree-representation $T$ (the arcs of $D$ are named, and these names appear as labels of the non-root nodes of $T$; for later reference, some of the vertices of $D$ are also named)

Thus, the $s_0-s_1$ routes in $D$ are identified as the branches of the tree-representation $T$. For a player $i \in N$ with origin $o^i$ and destination $d^i$, only those routes containing $F^i$ (defined above) are relevant, and they are identified as the branches of $T$ that contain $F^i$. The strategies in $\Sigma ^i$ are obtained by removing $F^i$ from these branches. To illustrate this, consider the network $D$ in Fig. 2, and suppose player $i$ has $o^i=s_0$, $d^i=v$ and player $j$ has $o^j=u$, $d^j=w$. For $i$, we take $F^i=\{k,\ell \}$ and observe that there are two branches in $T$ containing $\{k,\ell \}$; upon removing $\{k,\ell \}$ from them we get $\{b,f\}$ and $\{b,g\}$ respectively, the two strategies of player $i$. For $j$, we take $F^j=\{b,\ell \}$ and find three branches in $T$ containing $\{b,\ell \}$; upon removing $\{b,\ell \}$ from them we get player $j$’s three strategies: $\{e\}$, $\{k,f\}$, $\{k,g\}$.

Next, we present a technique based on the tree-representation, which allows us to keep track of the changes in congestion experienced by the players when they move from one strategy profile to another. Let $R=(R^i)_{i \in N} \in \Sigma ^N$ be a strategy profile, and let $(P^S,R^{N \setminus S})$ be another profile where each $i \in S$ chooses $P^i \in \Sigma ^i$ instead of $R^i$. For every arc $x$ we define $\delta (x)$ as the change in congestion at $x$, that is,

$$\begin{aligned} \delta (x)=\sigma _x(P^S,R^{N \setminus S})-\sigma _x(R). \end{aligned}$$

Let $T$ be a tree-representation of the network. In order to use $T$, it is convenient to think not of the profiles $R$ and $(P^S,R^{N \setminus S})$ as such, but of the corresponding profiles of $s_0-s_1$ routes $\overline{R}$ and $(\overline{P}^S,\overline{R}^{N \setminus S})$, obtained by extending each $R^i$ to $\overline{R}^i$ and each $P^i$, $i \in S$, to $\overline{P}^i$, as done above. We note that the quantities $\delta (x)$ remain the same when computed with respect to $\overline{R}$ and $(\overline{P}^S,\overline{R}^{N \setminus S})$, because adding the $F^i$’s shifts $\sigma _x(R)$ and $\sigma _x(P^S,R^{N \setminus S})$ by the same amount. Each $\overline{R}^i$ can be written uniquely in the form

$$\begin{aligned} \overline{R}^i=(a_1,\ldots ,a_k,b_1,\ldots ,b_\ell ), \end{aligned}$$

(1)

where the arcs are listed in the order of their appearance on the corresponding branch in $T$, and $b_1$ is the first among them at which the congestion decreases. That is,

$$\begin{aligned} \delta (a_1) \ge 0, \ldots ,\delta (a_k) \ge 0, \quad \delta (b_1)<0. \end{aligned}$$

(Possibly, $k=0$ or $\ell =0$.) If $i \in S$ and $\overline{R}^i$ is as in (1), we say that player $j \in S$ replaces $i$, if

$$\begin{aligned} \overline{P}^j=(a_1,\ldots ,a_k,c_1,\ldots ,c_m), \end{aligned}$$

(2)

where

$$\begin{aligned} \delta (c_1)>0,\ldots ,\delta (c_m)>0. \end{aligned}$$

(Possibly, $m=0$.) Note that a player may replace himself.

A key fact about the replacement relation, proved in Holzman and Law-Yone (1997, p. 93), is the following:

Claim 1

For every player $i \in S$ there exists a player $j \in S$ who replaces $i$.

We prove here an additional fact which is specific to our set-up, and hinges on the way the players’ extended strategy spaces $\overline{\Sigma }^i$ were formed. If $i_1,i_2,\ldots ,i_t$ are distinct players in $S$, we say that they form a replacement cycle if $i_2$ replaces $i_1$, $i_3$ replaces $i_2$, ... , $i_t$ replaces $i_{t-1}$, and $i_1$ replaces $i_t$.

Claim 2

Suppose that players $1,2,\ldots ,t$ form a replacement cycle in $S$. Then $\overline{P}^{i+1} \in \overline{\Sigma }^i$ for $i=1,\ldots ,t$ (with $t+1$ taken as 1).

Proof

Fixing $i$, we have to show that $F^i \subseteq \overline{P}^{i+1}$. Assume, for the sake of contradiction, that $x \in F^i \setminus \overline{P}^{i+1}$. Using the form (1) for $\overline{R}^i$ and (2) for $\overline{P}^{i+1}$, observe that $x$ must appear in (1)—as $F^i \subseteq \overline{R}^i$, but not in (2). Hence $x=b_p$ for some $1 \le p \le \ell$. Now, consider $\overline{P}^i$. This is a branch of $T$ that contains $F^i$, therefore $x$ appears in $\overline{P}^i$, and so does $b_1$ (because it appears on the path from the root to $b_p=x$). As $\delta (b_1)<0$, this prevents $\overline{P}^i$ from being written in the form (2), in contradiction to the fact that player $i$ replaces his predecessor in the cycle. $\square$

Proof of Theorem 1

Let $D$ be an extension-parallel network. Let $G$ be a game on $D$, with player origins $o^i$ and destinations $d^i$ for $i \in N$, and increasing cost functions $c_a(k)$. Let $T$ be a tree-representation of $D$, and let the set of arcs $F^i$, the mapping $R^i\mapsto \overline{R}^i$, and its image $\overline{\Sigma }^i$ be defined as above for all $i \in N$.

We have to show that $\text {NE}(G) \subseteq \text {SE}(G)$. Assume, for the sake of contradiction, that $R=(R^i)_{i \in N} \in \Sigma ^N$ is a Nash equilibrium, but $P^S=(P^i)_{i \in S}$ is a profitable deviation of coalition $S$, for some $\emptyset \ne S \subseteq N$. Consider the profiles of extended strategies before and after the deviation: $\overline{R}$ and $(\overline{P}^S,\overline{R}^{N \setminus S})$. It follows from Claim 1 and the finiteness of $S$ that there is a replacement cycle in $S$. Without loss of generality, assume that this cycle is $1,2,\ldots ,t$ as in Claim 2. Choose a player $i \in \{1,\ldots ,t\}$ for whom $\sum _{x \in \overline{R}^i}c_x(\sigma _x(R))$ is maximal among all players in the cycle.

Consider the set $\overline{P}^{i+1}$, which is a branch in $T$. Its intersection with any branch of $T$ is an initial segment of it. In particular, one of the two sets $\overline{P}^{i+1} \cap \overline{R}^{i+1}$ and $\overline{P}^{i+1} \cap \overline{R}^i$ is contained in the other. The argument breaks into two cases, according to the direction of this containment.

Case 1 $\overline{P}^{i+1} \cap \overline{R}^{i+1} \subseteq \overline{P}^{i+1} \cap \overline{R}^i$

By Claim 2, player $i$ has $Q^i=\overline{P}^{i+1} \setminus F^i$ among his strategies. If he alone deviates from $R$ and chooses $Q^i$, his disutility is given by

$$\begin{aligned} \pi ^i(Q^i,R^{N \setminus \{i\}})&= \sum _{x \in P^{i+1}}c_x(\sigma _x(Q^i,R^{N \setminus \{i\}})) \nonumber \\&+ \sum _{x \in F^{i+1}}c_x(\sigma _x(Q^i,R^{N \setminus \{i\}})) \nonumber \\&- \sum _{x \in F^i}c_x(\sigma _x(Q^i,R^{N \setminus \{i\}})). \end{aligned}$$

(3)

To estimate the first of these three sums, we show that at each arc $x \in P^{i+1}$, the congestion $\sigma _x(Q^i,R^{N \setminus \{i\}})$ is no higher than $\sigma _x(P^S,R^{N \setminus S})$. Indeed, since $i+1$ replaces $i$, the sets $\overline{R}^i$ and $\overline{P}^{i+1}$ can be written in the forms (1) and (2), respectively. By (2), $\delta (x) \ge 0$ and the inequality is strict if $x \notin \overline{R}^i$. Thus, the only way for $\sigma _x(Q^i,R^{N \setminus \{i\}})$ to exceed $\sigma _x(P^S,R^{N \setminus S})$ would be if $x \in Q^i \setminus R^i$ and $x \in \overline{R}^i$, which is impossible: $\overline{R}^i$ is the union of $R^i$ and $F^i$, each of which is disjoint from $Q^i \setminus R^i$. Since the cost functions are increasing, it follows that

$$\begin{aligned}\sum _{x \in P^{i+1}}c_x(\sigma _x(Q^i,R^{N \setminus \{i\}})) \le \sum _{x \in P^{i+1}}c_x(\sigma _x(P^S,R^{N \setminus S})). \end{aligned}$$

Furthermore, as the deviation $P^S$ is profitable for player $i+1$,

$$\begin{aligned} \sum _{x \in P^{i+1}}c_x(\sigma _x(P^S,R^{N \setminus S})) < \sum _{x \in R^{i+1}}c_x(\sigma _x(R)). \end{aligned}$$

Turning now to the second and third sums in (3), we claim that $\sigma _x(Q^i,R^{N \setminus \{i\}})=\sigma _x(R)$ for every arc $x$ that appears in either of them. Indeed, if $x \in F^i$ then neither $R^i$ nor $Q^i$ includes $x$. The remaining case is $x \in F^{i+1} \setminus F^i$. Noting that $F^{i+1} \subseteq \overline{P}^{i+1} \cap \overline{R}^{i+1}$, it follows from the assumption of Case 1 that $F^{i+1} \subseteq \overline{R}^i$, and hence $F^{i+1} \setminus F^i \subseteq R^i$. Also, $F^{i+1} \setminus F^i \subseteq \overline{P}^{i+1} \setminus F^i = Q^i$, so in the remaining case both $R^i$ and $Q^i$ include $x$. Using the claim just proved, and the above estimate for the first sum in (3), player $i$’s disutility at $(Q^i,R^{N \setminus \{i\}})$ can be estimated as follows:

$$\begin{aligned} \pi ^i(Q^i,R^{N \setminus \{i\}})&< \sum _{x \in R^{i+1}}c_x(\sigma _x(R)) + \sum _{x \in F^{i+1}}c_x(\sigma _x(R)) - \sum _{x \in F^i}c_x(\sigma _x(R)) \\&= \sum _{x \in \overline{R}^{i+1}}c_x(\sigma _x(R)) - \sum _{x \in F^i}c_x(\sigma _x(R)) \\&\le \sum _{x \in \overline{R}^i}c_x(\sigma _x(R)) - \sum _{x \in F^i}c_x(\sigma _x(R)) \\&= \pi ^i(R), \end{aligned}$$

where the second inequality follows from the choice of $i$ as a maximizer of $\sum _{x \in \overline{R}^i}c_x(\sigma _x(R))$. This is a contradiction, since $R$ is a Nash equilibrium.

Case 2 $\overline{P}^{i+1} \cap \overline{R}^i \subseteq \overline{P}^{i+1} \cap \overline{R}^{i+1}$

Consider in this case the single deviation of player $i+1$ to $P^{i+1}$. We claim that at each arc $x \in P^{i+1}$, the congestion $\sigma _x(P^{i+1},R^{N \setminus \{i+1\}})$ is no higher than $\sigma _x(P^S,R^{N \setminus S})$. Indeed, as in Case 1 it follows from the replacement relation that $\delta (x) \ge 0$ and the inequality is strict if $x \notin \overline{R}^i$. Thus, the only way for $\sigma _x(P^{i+1},R^{N \setminus \{i+1\}})$ to exceed $\sigma _x(P^S,R^{N \setminus S})$ would be if $x \in P^{i+1} \setminus R^{i+1}$ and $x \in \overline{R}^i$, which is impossible: $P^{i+1} \setminus R^{i+1} = \overline{P}^{i+1} \setminus \overline{R}^{i+1}$ and the latter is disjoint from $\overline{R}^i$ by the assumption of Case 2. Since the cost functions are increasing, it follows that

$$\begin{aligned} \pi ^{i+1}(P^{i+1},R^{N \setminus \{i+1\}})&= \sum _{x \in P^{i+1}}c_x(\sigma _x(P^{i+1},R^{N \setminus \{i+1\}})) \\&\le \sum _{x \in P^{i+1}}c_x(\sigma _x(P^S,R^{N \setminus S})) \\&= \pi ^{i+1}(P^S,R^{N \setminus S}) \\&< \pi ^{i+1}(R) \end{aligned}$$

where the second inequality is due to the profitability of the deviation $P^S$ for player $i+1$. Again, this is a contradiction to $R$ being a Nash equilibrium. $\square$

4 Decreasing costs: sufficiency

In this section we prove the existence of strong equilibrium in a certain class of games on series-parallel networks with decreasing costs. The sufficiency parts of both Theorems 2 and 3 will be deduced from this more general result. In order to formulate the result, we need some additional definitions.

Let $G$ be a game on a series-parallel network $D$, with player set $N$, origin $o^i$ and destination $d^i$ for each $i \in N$. Let $D^{\prime }=(V^{\prime },A^{\prime },s_0^{\prime },s_1^{\prime })$ be a subnetwork formed in one of the steps of a series-parallel construction of $D$. The induced game on $D^{\prime }$, denoted by $G^{\prime }=G[D^{\prime }]$, is a congestion game on $D^{\prime }$ defined as follows. Its set of players $N^{\prime }$ consists of those players $i \in N$ having a $o^i-d^i$ route that meets $A^{\prime }$ (i.e., there exists $R^i \in \Sigma ^i$ such that $R^i \cap A^{\prime } \ne \emptyset$).⁸ For each $i \in N^{\prime }$, his origin $o^{\prime i}$ in the induced game is defined to be $o^i$ if $o^i \in V^{\prime }$, and $s_0^{\prime }$ otherwise; similarly, his destination $d^{\prime i}$ is $d^i$ if $d^i \in V^{\prime }$, and $s_1^{\prime }$ otherwise. The cost functions in the induced game are the restrictions of those in $G$. For illustration, consider the network $D$ in Fig. 3, and the subnetwork $D^{\prime }$ with source $s_0^{\prime }$ and sink $s_1^{\prime }$. In this example, $N=\{1,2,3,4\}$ and $N^{\prime }=\{1,2,3\}$. The origins and destinations in the induced game $G^{\prime }$ are: $o^{\prime 1}=s_0^{\prime }$, $d^{\prime 1}=s_1^{\prime }$, $o^{\prime 2}=s_0^{\prime }$, $d^{\prime 2}=d^2$, $o^{\prime 3}=o^3$, $d^{\prime 3}=d^3$.

Fig. 3

A series-parallel network $D$ with 4 players, and a subnetwork $D^{\prime }$

Given a network $D$ and a player set $N$ with origins $o^i$ and destinations $d^i$ for $i \in N$, we say that player $i$ is complete if for every $j \in N$, there exist a $o^i-o^j$ route and a $d^j-d^i$ route in $D$ (either of these routes may consist of a single vertex, in case $o^i=o^j$ or $d^j=d^i$). For example, in Fig. 3 player 1 is complete, the others are not.

For a player $i$ in a game $G$ we denote by $\text {opt}^i(G)$ the optimal outcome of the game from his point of view, i.e.,

$$\begin{aligned} \text {opt}^i(G)=\min _{R \in \Sigma ^N}\pi ^i(R). \end{aligned}$$

We are now ready to formulate our existence result.

Proposition 1

Let $D$ be a series-parallel network, and let $G$ be a AOAD-DEC game on $D$. Assume that $D$ has a series-parallel construction such that, whenever $D^{\prime }$ and $D^{\prime \prime }$ are joined in series in this construction, the corresponding induced games $G^{\prime }=G[D^{\prime }]$ and $G^{\prime \prime }=G[D^{\prime \prime }]$ with respective player sets $N^{\prime }$ and $N^{\prime \prime }$ satisfy the condition: for at least one of the two induced games, say $G^{\prime }$, all players in $N^{\prime } \cap N^{\prime \prime }$ are complete in $G^{\prime }$. Then $G$ has a strong equilibrium $R$ such that $\pi ^i(R)=\text {opt}^i(G)$ for every complete player $i$ in $G$.

Before proving Proposition 1, we indicate how it implies the sufficiency parts of Theorems 2 and 3. For this, we need to show that under the conditions of those theorems, the assumption of Proposition 1 holds true. Under Theorem 2, all players $i \in N$ have the same $o^i$. So when $D^{\prime } \rightarrow D^{\prime \prime }$ occurs in the construction of $D$, all players $i \in N^{\prime }$ have the same $o^{\prime i}$ in $G^{\prime }$. Moreover, all players $i \in N^{\prime } \cap N^{\prime \prime }$ have $d^{\prime i}=s_1^{\prime }$ (the sink of $D^{\prime }$), and are therefore complete in $G^{\prime }$ as required. Under Theorem 3, $D$ is multiextension-parallel. So when two subnetworks are joined in series in the construction of $D$, one of them is a multiple-arc network. In a game on such a network, all players are complete. We note that Proposition 1 applies also in other cases, not covered by either of the two theorems. For example, one can verify that the assumption of the proposition holds true in Fig. 3, although the network is not multiextension-parallel and the players’ origins and destinations are all distinct.

The proof of Proposition 1 will be inductive. The role of the property added in the conclusion ($\pi ^i(R)=\text {opt}^i(G)$ for complete players) is to strengthen the induction hypothesis so that the induction will go through.⁹

Proof of Proposition 1

Let $D$ be a series-parallel network. Let $G$ be a game on $D$ with player set $N$, and decreasing cost functions. Assuming that $D$ has a series-parallel construction as required in the proposition, we prove by induction on the length of this construction that $G$ has a strong equilibrium $R$ such that $\pi ^i(R)=\text {opt}^i(G)$ for every complete player $i$ in $G$. If $D$ is a single-arc network the statement trivially holds (every player has a single strategy).

For the induction step, we assume that $D=D^{\prime } \rightarrow D^{\prime \prime }$ or $D=D^{\prime } \parallel D^{\prime \prime }$. Let $G^{\prime }=G[D^{\prime }]$ and $G^{\prime \prime }=G[D^{\prime \prime }]$ be the induced games, with respective player sets $N^{\prime }$ and $N^{\prime \prime }$. If one of the player sets, say $N^{\prime }$, is empty, then $G=G^{\prime \prime }$ and we are done by induction. Henceforth we assume that both $N^{\prime }$ and $N^{\prime \prime }$ are nonempty. Note that $N=N^{\prime } \cup N^{\prime \prime }$. By induction, let $R^{\prime }=(R^{\prime i})_{i \in N^{\prime }}$ be a strong equilibrium in $G^{\prime }$ such that $\pi ^i(R^{\prime })=\text {opt}^i(G^{\prime })$ for every complete player $i$ in $G^{\prime }$, and let $R^{\prime \prime }=(R^{\prime \prime i})_{i \in N^{\prime \prime }}$ be a strong equilibrium in $G^{\prime \prime }$ such that $\pi ^i(R^{\prime \prime })=\text {opt}^i(G^{\prime \prime })$ for every complete player $i$ in $G^{\prime \prime }$.

Case 1 $D=D^{\prime } \rightarrow D^{\prime \prime }$

Note that for players in $N^{\prime } \cap N^{\prime \prime }$, the vertex $s_1^{\prime }=s_0^{\prime \prime }$ serves as the destination in $G^{\prime }$ and the origin in $G^{\prime \prime }$. We form a strategy profile $R=(R^i)_{i \in N}$ in $G$ as follows. If $i \in N^{\prime } \setminus N^{\prime \prime }$ then $R^i=R^{\prime i}$, if $i \in N^{\prime \prime } \setminus N^{\prime }$ then $R^i=R^{\prime \prime i}$, and if $i \in N^{\prime } \cap N^{\prime \prime }$ then $R^i$ is the concatenation of $R^{\prime i}$ and $R^{\prime \prime i}$. We show that $R$ has the required properties in $G$.

Assume that coalition $S \subseteq N$ has a profitable deviation $P^S$ from $R$ in $G$. Write $S_{\text {int}}=S \cap N^{\prime } \cap N^{\prime \prime }$, and suppose first that $S_{\text {int}} \ne \emptyset$. By the assumption of the proposition, all players in $S_{\text {int}}$ are complete in $G^{\prime }$, say. If $i \in S_{\text {int}}$, his disutility function in $G$ is the sum of its $G^{\prime }$ and $G^{\prime \prime }$ components. As $i$ is complete in $G^{\prime }$, we have $\pi ^i(R^{\prime })=\text {opt}^i(G^{\prime })$, so the $G^{\prime }$ component of player $i$’s disutility cannot be reduced by the deviation. Therefore all $i \in S_{\text {int}}$ must profit from the deviation in the $G^{\prime \prime }$ component of their disutility function. Thus $P^S$ induces a profitable deviation of $S \cap N^{\prime \prime }$ from $R^{\prime \prime }$, in contradiction to $R^{\prime \prime }$ being a strong equilibrium in $G^{\prime \prime }$. Suppose now that $S_{\text {int}}=\emptyset$. Then $P^S$ induces a profitable deviation of $S \cap N^{\prime }$ from $R^{\prime }$, and a profitable deviation of $S \cap N^{\prime \prime }$ from $R^{\prime \prime }$. At least one of these coalitions is nonempty, yielding again a contradiction. We have shown that $R$ is a strong equilibrium in $G$.

For the second part, note that if player $i$ is complete in $G$, he is complete in both $G^{\prime }$ and $G^{\prime \prime }$. Thus $\pi ^i(R)=\pi ^i(R^{\prime })+\pi ^i(R^{\prime \prime })=\text {opt}^i(G^{\prime })+\text {opt}^i(G^{\prime \prime })=\text {opt}^i(G)$, as required.

Case 2 $D= D^{\prime } \parallel D^{\prime \prime }$

Note that for players in $N^{\prime } \cap N^{\prime \prime }$, the source $s_0^{\prime }=s_0^{\prime \prime }$ is the origin and the sink $s_1^{\prime }=s_1^{\prime \prime }$ is the destination. Playing in $G$, they can choose a route in either $D^{\prime }$ or $D^{\prime \prime }$. The other players are confined to one of the two subnetworks. If $N^{\prime } \cap N^{\prime \prime } = \emptyset$ then $R^{\prime }$ and $R^{\prime \prime }$ together form a strong equilibrium in $G$, and we are done (the second part holds vacuously, as there are no complete players in $G$). Thus, we assume that $N^{\prime } \cap N^{\prime \prime } \ne \emptyset$.

Since the cost functions are decreasing, we have $\text {opt}^i(G)\!=\min \{\text {opt}^i(G^{\prime }),\text {opt}^i(G^{\prime \prime })\}$ for $i \in N^{\prime } \cap N^{\prime \prime }$. Clearly, each of these quantities is independent of the choice of $i \in N^{\prime } \cap N^{\prime \prime }$. Assume, without loss of generality, that $\text {opt}^i(G)=\text {opt}^i(G^{\prime })$ for all $i \in N^{\prime } \cap N^{\prime \prime }$.

Consider the subgame of $G^{\prime \prime }$ with player set $N^{\prime \prime } \setminus N^{\prime }$, which we denote by $G^{\prime \prime \prime }$. Since the assumption of the proposition continues to hold when some players are removed, we may apply the induction hypothesis to $G^{\prime \prime \prime }$. Let $R^{\prime \prime \prime }=(R^{\prime \prime \prime i})_{i \in N^{\prime \prime } \setminus N^{\prime }}$ be a strong equilibrium in $G^{\prime \prime \prime }$. We form a strategy profile $R=(R^i)_{i \in N}$ in $G$ by letting $R^i=R^{\prime i}$ for $i \in N^{\prime }$ and $R^i=R^{\prime \prime \prime i}$ for $i \in N^{\prime \prime } \setminus N^{\prime }$. We show that $R$ has the required properties in $G$.

The complete players in $G$ are all $i \in N^{\prime } \cap N^{\prime \prime }$, and for them we have $\pi ^i(R)=\pi ^i(R^{\prime })=\text {opt}^i(G^{\prime })=\text {opt}^i(G)$. This verifies the second part, and also shows that no member of $N^{\prime } \cap N^{\prime \prime }$ can participate in a profitable deviation from $R$. Therefore, such a deviation can only consist of changes within each subnetwork, which cannot be profitable since $R^{\prime }$ and $R^{\prime \prime \prime }$ are strong equilibria in the respective games. Hence $R$ is a strong equilibrium in $G$. $\square$

5 Decreasing costs: necessity

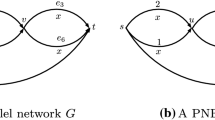
We start with two basic examples of network congestion games with decreasing costs. The network in Fig. 4a is known as the Wheatstone bridge, and is denoted by $W$; the one in Fig. 4b is denoted by $B$. The indicated two-player games have no strong equilibrium, as can be checked from the tables representing their disutility functions.¹⁰ It is straightforward to construct similar examples on the same networks with any higher number of players.

Fig. 4

Two examples of network congestion games with decreasing costs that have no strong equilibrium (for each arc, the first number is the single-user cost, and the second one—where relevant—is the per-user cost for double usage)

These examples are basic in the sense that they can occur on any network that does not fulfill the corresponding requirements for existence of strong equilibrium. This is made precise by the following definition and results. A subdivision of a network $D$ is a network obtained from $D$ upon replacing every arc by a route of one or more arcs. The new vertices introduced in this process have just one incoming arc and one outgoing arc.

Proposition 2

Let $D$ be a network. Then $D$ is series-parallel if and only if $D$ has no subnetwork which is isomorphic to a subdivision of the network $W$ (Fig. 4a).

Proposition 3

Let $D$ be a network. Then $D$ is multiextension-parallel if and only if $D$ has no subnetwork which is isomorphic to a subdivision of one of the following three networks: $W$ (Fig. 4a), $B$ (Fig. 4b), or $B^+$ (obtained from $B$ by splitting the middle vertex into two vertices with an arc between them).

Before proving these propositions, we show how they imply the necessity parts of Theorems 2 and 3. If $D$ is not series-parallel, by Proposition 2 we can find a subdivision $W^{\prime }$ of $W$ contained in $D$. We place the players’ origins and destinations in $W^{\prime }$ as in Fig. 4a. For each arc of $W$, we choose one arc in the corresponding route in $W^{\prime }$, and assign to it the costs associated with the original arc in Fig. 4a. We assign zero costs to all other arcs in $W^{\prime }$, and prohibitively high costs to all arcs of $D$ which are not in $W^{\prime }$. This gives a SOAD-DEC game on $D$ without a strong equilibrium, proving necessity in Theorem 2. If $D$ is not multiextension-parallel, we proceed similarly using Proposition 3. In case we find a subdivision of $B^+$, we mimick the construction on $B$ in Fig. 4b, assigning zero costs to all arcs on the route connecting the two copies of the middle vertex. In any case, we get a AOAD-DEC game on $D$ without a strong equilibrium, proving necessity in Theorem 3.

Propositions 2 and 3 are purely graph theoretic, and give forbidden substructure characterizations of the respective classes of networks. Various results in this format have appeared in the literature, including several analogs of Proposition 2 (Duffin 1965; Valdes 1978; Milchtaich 2006). However, the networks for which these analogs were proved differ from ours in one or more ways, being undirected, or without terminals, or acyclic. Therefore we give our own proofs here.

For the proofs, we introduce some terminology and notation. Let $D=(V,A,s_0,s_1)$ be a network. We denote by $\Sigma$ the set of $s_0-s_1$ routes in $D$. Given a route $R$ in $D$, and two vertices $u,v$ on it such that $u$ weakly precedes $v$, we denote by $R_{uv}$ the $u-v$ subroute of $R$. For a $u-v$ route $R$ and a $v-w$ route $R^{\prime }$, we denote by $RR^{\prime }$ the concatenation of $R$ and $R^{\prime }$. Note that $RR^{\prime }$ may not be a route because vertices may be repeated, but we can obtain a $u-w$ route by short-cutting segments between two occurrences of the same vertex in $RR^{\prime }$. When necessary, we will assume that such short-cuts are made without explicitly saying it. A path in $D$ is defined like a route, except that arcs may be traversed in either direction (for each $i$, $\{t(a_i),h(a_i)\}=\{v_{i-1},v_i\}$). We use the notational conventions above also for paths.

Proof of Proposition 2

One direction is trivial: if $D$ has a series-parallel construction, it follows by induction on the steps of this construction that $D$ cannot contain a subdivision of $W$.

In the other direction, we assume that $D=(V,A,s_0,s_1)$ is not series-parallel and prove that it has a subnetwork isomorphic to a subdivision of $W$. Clearly, $D$ is not a single-arc network. Moreover, we may assume that $D$ is not the series or parallel join of two subnetworks $D_1$ and $D_2$. Indeed, if it is of this form, then at least one of $D_1$, $D_2$ is not series-parallel, and as it is smaller than $D$ we know by induction that it has a subnetwork isomorphic to a subdivision of $W$. That is also a subnetwork of $D$, and we are done. In particular, we may assume that no arc in $A$ has tail $s_0$ and head $s_1$ (or else $D$ would be the parallel join of a single-arc subnetwork and another subnetwork).

Suppose that some vertex $v \in V \setminus \{s_0,s_1\}$ belongs to every route in $\Sigma$. Let

$$\begin{aligned} V_1&= \{u \in V:\, \exists R \in \Sigma \text { such that } u \text { is on } R_{s_0v}\},\\ V_2&= \{u \in V:\, \exists R \in \Sigma \text { such that } u \text { is on } R_{vs_1}\}. \end{aligned}$$

As every vertex in $V$ belongs to some route in $\Sigma$, we have $V=V_1 \cup V_2$. Moreover, $V_1 \cap V_2 =\{v\}$. Indeed, if $u \ne v$ and $u \in V_1 \cap V_2$, let $R, R^{\prime } \in \Sigma$ be such that $u$ belongs to $R_{s_0v}$ and $R^{\prime }_{vs_1}$. Then $R_{s_0u}R^{\prime }_{us_1}$ gives a route in $\Sigma$ that avoids $v$, contrary to our assumption. For a similar reason, there can be no arc in $A$ from a vertex in $V_1 \setminus \{v\}$ to one in $V_2 \setminus \{v\}$. No such arc in the opposite direction is possible, as it would not belong to any route in $\Sigma$. Thus, all arcs in $A$ are either inside $V_1$ or inside $V_2$. It follows that $D$ is the series join of two subnetworks on $V_1$ and $V_2$ respectively, contradicting our assumption.

We conclude that no vertex $v \in V \setminus \{s_0,s_1\}$ belongs to all routes in $\Sigma$. This implies, by Menger’s theorem (see, e.g., Chartrand et al. 2011, Theorem 4.38), the existence of two internally disjoint routes $R,R^{\prime }$ in $\Sigma$. Suppose now that two such routes are given, and there is no path in $V \setminus \{s_0,s_1\}$ joining a vertex of $R$ and a vertex of $R^{\prime }$. Then the undirected graph obtained from $D$ by deleting $s_0,s_1$ and ignoring the directions of arcs has at least two connected components (that of $R$ and that of $R^{\prime }$). Let $V_1$ be the vertex set of one component, and let $V_2$ be the vertex set of the union of the others. Then $D$ is the parallel join of two subnetworks on $V_1 \cup \{s_0,s_1\}$ and $V_2 \cup \{s_0,s_1\}$ respectively, contradicting our assumption.

Thus, we can find two internally disjoint routes $R,R^{\prime }$ in $\Sigma$ and a path $P$ in $V \setminus \{s_0,s_1\}$ joining a vertex $u$ of $R$ and a vertex $v$ of $R^{\prime }$. We may assume that no internal vertex of $P$ is on $R$ or $R^{\prime }$ (otherwise we can replace $P$ by a suitable subpath). Given two consecutive arcs $a$ and $b$ on $P$ with common vertex $w$, we say that a change of direction occurs at $w$ if $w$ is the tail of both $a$ and $b$ or the head of both $a$ and $b$. Note that if no change of direction occurs along $P$, then $R,R^{\prime },P$ form a subnetwork of $D$ which is isomorphic to a subdivision of $W$, as required. If there are changes of direction, we enumerate the vertices at which they occur as $w_1,w_2,\ldots ,w_k$ in order of their appearance when $P$ is traversed from $u$ to $v$. Among all triples $R,R^{\prime },P$ as above, we choose one for which $k$ is the smallest ($k \ge 1$, or else we are done). Among triples with the smallest $k$, we choose one for which the subpath $P_{uw_1}$ is the shortest.

All arcs in $P_{uw_1}$ have the same direction. Suppose first that they all go forward, i.e., $P_{uw_1}$ is a route. As every vertex belongs to some route in $\Sigma$, there exists a $w_1-s_1$ route $Q$. We claim that no internal vertex of $Q$ can belong to either $R_{s_0u}$ or $P_{uw_1}$ or $R^{\prime }$. Indeed, let $z$ be an internal vertex of $Q$. Denote by $Q^*_{zw_1}$ the path obtained by going backwards on $Q$ from $z$ to $w_1$. If $z$ is on $R_{s_0u}$ then $Q^*_{zw_1}P_{w_1v}$ gives a path from a vertex of $R$ to a vertex of $R^{\prime }$ with fewer changes of direction than $P$, a contradiction. If $z$ is on $P_{uw_1}$ (necessarily an internal vertex, as $z \ne w_1$ and by the previous case $z \ne u$), then $P_{uz}Q^*_{zw_1}P_{w_1v}$ gives a $u-v$ path with the same number of direction changes as $P$, but its subpath $P_{uz}$ till the first change is shorter than $P_{uw_1}$, a contradiction. Finally, if $z$ is on $R^{\prime }$ then $P_{uw_1}Q_{w_1z}$ gives a path from a vertex of $R$ to a vertex of $R^{\prime }$ with no changes of direction, so our claim is proved. It follows that $R_{s_0u}P_{uw_1}Q$ is a route in $\Sigma$ which is internally disjoint from $R^{\prime }$. These two routes, together with the path $P_{w_1v}$, yield a triple as above with fewer changes of direction than $R,R^{\prime },P$, contradicting our choice. The remaining case, when all arcs in $P_{uw_1}$ go backward, is treated similarly: $Q$ is taken to be a $s_0-w_1$ route, and the arguments are symmetric to the above. $\square$

Proof of Proposition 3

Here, too, one direction is trivial: if $D$ has a multiextension-parallel construction, it follows by induction on the steps of this construction that $D$ cannot contain a subdivision of $W$, $B$, or $B^+$.

For the other direction, given Proposition 2, it suffices to show that if $D$ is series-parallel but not multiextension-parallel then it has a subnetwork isomorphic to a subdivision of $B$ or $B^+$. We prove this by induction on the number of steps in a series-parallel construction of $D$. Clearly, $D$ is not a single-arc network, so $D$ is the series or parallel join of two subnetworks $D^{\prime }$ and $D^{\prime \prime }$. If either $D^{\prime }$ or $D^{\prime \prime }$ is not multiextension-parallel then, by induction, it has a subnetwork isomorphic to a subdivision of $B$ or $B^+$. That is also a subnetwork of $D$, and we are done. So we may assume that both $D^{\prime }$ and $D^{\prime \prime }$ are multiextension-parallel. As $D$ is not, it must be a series join. Say $D=D^{\prime } \rightarrow D^{\prime \prime }$, with $D^{\prime }=(V^{\prime },A^{\prime },s_0^{\prime },s_1^{\prime })$ and $D^{\prime \prime }=(V^{\prime \prime },A^{\prime \prime },s_0^{\prime \prime },s_1^{\prime \prime })$.

Consider $D^{\prime }$ and the set $\Sigma ^{\prime }$ of all $s_0^{\prime }-s_1^{\prime }$ routes. Suppose that every route in $\Sigma ^{\prime }$ includes all the vertices in $V^{\prime }$. Then the vertices appear in the same order in all routes, because $D^{\prime }$, being series-parallel, is acyclic. Say this order is $s_0^{\prime }=v_0^{\prime },v_1^{\prime },\ldots ,v_\ell ^{\prime }=s_1^{\prime }$. Then every arc in $A^{\prime }$ must go from $v_{i-1}^{\prime }$ to $v_i^{\prime }$ for some $i=1,\ldots ,\ell$. This implies that $D$ is multiextension-parallel: it can be constructed by first joining in series the multiple-arc subnetwork with vertices $v_{\ell -1}^{\prime },v_\ell ^{\prime }$ and $D^{\prime \prime }$, then joining in series the multiple-arc subnetwork with vertices $v_{\ell -2}^{\prime },v_{\ell -1}^{\prime }$ and the subnetwork constructed in the previous step, and so on. This contradicts our assumption on $D$. Hence we can find a route $R^{\prime }$ in $\Sigma ^{\prime }$ and a vertex $v^{\prime } \in V^{\prime }$ that is not on $R^{\prime }$. We can also find a route $Q^{\prime }$ in $\Sigma ^{\prime }$ that includes $v^{\prime }$. Let $u^{\prime }$ be the last vertex on $Q^{\prime }_{s_0^{\prime }v^{\prime }}$ that is also on $R^{\prime }$, and let $w^{\prime }$ be the first vertex on $Q^{\prime }_{v^{\prime }s_1^{\prime }}$ that is also on $R^{\prime }$. Note that $u^{\prime }$, $v^{\prime }$, $w^{\prime }$ are distinct, and $u^{\prime }$ precedes $w^{\prime }$ on $R^{\prime }$ (or else $R^{\prime }_{w^{\prime }u^{\prime }}Q^{\prime }_{u^{\prime }w^{\prime }}$ would give a cycle). This yields a $u^{\prime }-w^{\prime }$ route $R^{\prime }_{u^{\prime }w^{\prime }}$, a $u^{\prime }-v^{\prime }$ route $Q^{\prime }_{u^{\prime }v^{\prime }}$, and a $v^{\prime }-w^{\prime }$ route $Q^{\prime }_{v^{\prime }w^{\prime }}$, such that any internal vertex of one of them does not belong to any of the other two.

Arguing similarly in $D^{\prime \prime }$, we find there three vertices $u^{\prime \prime }$, $v^{\prime \prime }$, $w^{\prime \prime }$ with corresponding $u^{\prime \prime }-w^{\prime \prime }$, $u^{\prime \prime }-v^{\prime \prime }$, and $v^{\prime \prime }-w^{\prime \prime }$ routes as above. If $w^{\prime }=s_1^{\prime }$ and $u^{\prime \prime }=s_0^{\prime \prime }$ then $w^{\prime }=u^{\prime \prime }$ in $D$. The subnetwork of $D$ consisting of $u^{\prime }$, $v^{\prime }$, $w^{\prime }$, $v^{\prime \prime }$, $w^{\prime \prime }$ and the routes between them found above is isomorphic to a subdivision of $B$. Otherwise, if $w^{\prime } \ne s_1^{\prime }$ or $u^{\prime \prime } \ne s_0^{\prime \prime }$, then by concatenating a $w^{\prime }-s_1^{\prime }$ route in $D^{\prime }$ and a $s_0^{\prime \prime }-u^{\prime \prime }$ route in $D^{\prime \prime }$ we get a $w^{\prime }-u^{\prime \prime }$ route in $D$ with at least one arc. The subnetwork of $D$ consisting of $u^{\prime }$, $v^{\prime }$, $w^{\prime }$, $u^{\prime \prime }$, $v^{\prime \prime }$, $w^{\prime \prime }$ and the routes between them found above is isomorphic to a subdivision of $B^+$.

$\square$