The stationary equilibrium of three-person coalitional bargaining games with random proposers: a classification

Abstract

We present a classification of all stationary subgame perfect equilibria of the random proposer model for a three-person cooperative game according to the level of efficiency. The efficiency level is characterized by the number of “central” players who join all equilibrium coalitions. The existence of a central player guarantees asymptotic efficiency. The marginal contributions of players to the grand coalition play a critical role in their expected equilibrium payoffs.

1 Introduction

The three-person cooperative game with side payments in characteristic-function form is a classical problem of game theory in which three players negotiate about coalition formation and payoff allocations. The game serves as a prototype for the economic analysis of efficiency and equity in resource allocation. Since Neumann and Morgenstern (1944), various kinds of solutions have been proposed in the literature on cooperative game theory. There has been no consensus among game theorists about what is an appropriate solution for a three-person game and for an $n$-person cooperative game, in general. This disagreement remains to the present day. It may be argued that the diversity of solutions is a virtue, reflecting the complexity of the real world. However, to apply cooperative game theory to economic analysis, we need a general understanding of when one solution is more suitable than others.

In the last two decades, the non-cooperative game approach to cooperative games has been rapidly growing. Cooperation has been analyzed as a non-cooperative equilibrium under a specified procedure of coalition formation. Ray (2007) has provided an excellent review of this field. Among the bargaining games studied well is the random proposer model (Baron and Ferejohn 1989; Okada 1996). The stationary subgame perfect equilibrium (SSPE) of the model provides a non-cooperative foundation for various cooperative solutions, including the Nash bargaining solution (Okada 2010), the coalitional Nash bargaining solution (Compte and Jehiel 2010), the core (Yan 2002) for a general game, and the kernel (Montero 2002) and the nucleolus (Montero 2006) for a weighted majority game.

The aim of this paper is to characterize all SSPEs of a three-person superadditive game with general parameters played by patient players. The grand coalition of three players is assumed to be a unique efficient coalition. To our knowledge, the full structure of the SSPEs of a three-person random proposer game has not yet been reported in the literature.¹ In particular, when a game has an empty core and the grand coalition is a unique efficient coalition, it is well known that an SSPE outcome must be inefficient,² whereas almost all cooperative solutions presume efficiency even in such a case. A complete analysis of a three-person cooperative game helps us to understand why and how inefficiency and/or inequality may occur in negotiations among rational players under the condition of complete information.

We consider all SSPEs of a three-person game in terms of the support of every player’s mixed strategy, i.e., the set of all coalitions that the player may choose with positive probability. There are 343 possible configurations of supports for players’ strategies. These configurations can be classified into different levels of efficiency, measured by the equilibrium probability of the grand coalition. In the one efficient SSPE, the grand coalition forms with probability one. In an asymptotically efficient SSPE, the grand coalition will form almost surely. In an inefficient SSPE, the probability of the grand coalition is less than one, and may possibly be zero. We show that the existence of a “central” player who joins all equilibrium coalitions guarantees efficiency (in one configuration) and asymptotic efficiency (in 36 configurations). An inefficient SSPE arises when the core of a game is empty. When the grand coalition may form with positive probability (in 162 configurations), the expected payoffs of the players are equal to their marginal contributions to the grand coalition except in three configurations.

This paper is organized as follows. Section 2 gives some definitions. Section 3 provides several lemmas useful for the analysis. Section 4 presents a classification of SSPEs. Section 5 concludes the paper.

2 Preliminaries

An $n$-person game in coalitional form with transferable utility is represented as a pair $(N, v)$, where $N=\{1, 2, \ldots , n\}$ is the set of players. A nonempty subset $S$ of $N$ is called a coalition of players. The number of members of $S$ is denoted by $s$. The characteristic function $v$ is a real-valued function that assigns to each coalition $S$ its value $v(S)$. It is assumed that $v$ satisfies (i) $v(\{i\})=0$ for all $i \in N$ (zero-normalized), (ii) $v(S \cup T) \ge v(S)+v(T)$ for any two disjoint coalitions $S$ and $T$ (superadditive), and (iii) $v(N)>v(S)$ for every $S \subset N, S \ne N$. The last condition is a regularity one that guarantees that only the grand coalition $N$ maximizes the total value. For $S \subset N$, let $R^S$ denote the $s$-dimensional Euclidean space with coordinates indexed by the elements of $S$. Each point in $R^S$ is denoted by $x^S=(x_i^S)_{i \in S}$.

The payoff allocation for a coalition $S$ is a vector $x^S=(x_i^S)_{i \in S}$ of $R^S$, where $x_i^S$ represents the payoff for player $i \in S$. A payoff allocation $x^S$ for $S$ is feasible if $\sum _{i \in S} x_i^S \le v(S)$. Let $X^S$ denote the set of all feasible payoff allocations for $S$, and let $X_+^S$ denote the set of all elements in $X^S$ with nonnegative components. For $S \subset N$ and $x \in R^N$, the excess of $S$ with respect to $x$ is defined by $e(S, x)=v(S) - \sum _{i \in S} x_i$. For $i \in N, m_i=v(N)-v(N-\{ i \})$ is player $i$’s marginal contribution to the grand coalition $N$.

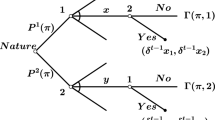
As a non-cooperative bargaining procedure for a game $(N, v)$, we consider the random proposer model with recognition probability $p=(p_1, \ldots , p_n)$, where $p_i>0$ for every $i$. The bargaining rule is simple. Negotiations take place over a possibly infinite number of rounds $t (= 1, 2, \ldots )$ until an agreement is reached. At the start of each round $t$, one player $i\in N$ is randomly selected as a proposer with probability $p_i$. Player $i$ proposes a coalition $S$, with $i\in S$ and a payoff allocation $x^S \in X_+^S$. All other members of $S$ either accept or reject the proposal $(S, x^S)$ sequentially according to a fixed order. The order of responders does not affect the result in any critical way. If all responders accept the proposal, then the game ends with the agreement $(S, x^S)$.³ All members $i$ of $S$ receive payoffs $x_i^S$, and the others receive zero payoffs. Otherwise, negotiations continue in the next round $t+1$ with the same rule as in round $t$. If the game does not stop, all players receive zero payoffs. Let $\delta (0\le \delta <1)$ be the common discount factor for future payoffs. All players have perfect information about the history of play whenever they choose their actions. The bargaining game above is denoted by $\Gamma ^\delta$. The notation $\Gamma$ denotes the limit as the discount factor $\delta$ goes to one in $\Gamma ^\delta$.

A (behavior) strategy $\sigma _i$ for player $i$ in $\Gamma ^\delta$ (and also in $\Gamma$) is a function that assigns a randomized (mixed) action to every possible move of the player, depending on the history of the game. Under the standard assumptions about $v$ above, it is well known that all responders accept a proposal with probability one in every SSPE of $\Gamma ^\delta$ (see Lemma 3.1). A randomized action may occur only in proposing coalitions. For a strategy combination $\sigma =(\sigma _1, \ldots , \sigma _n)$, the expected (discounted) payoff for player $i$ in $\Gamma ^\delta$ is defined in the usual way. A strategy $\sigma _i$ for player $i$ is stationary if the (possibly mixed) action of player $i$ at round $t$ is independent of the history before round $t$.⁴ In what follows, the analysis is restricted to a stationary subgame perfect equilibrium (SSPE), in which the equilibrium strategy of every player is stationary.

For an SSPE $\sigma$ of $\Gamma ^\delta$ and for every $i \in N$, let $v_i$ be player $i$’s expected payoff; let $q_i$ be his random choice of coalitions, a probability distribution over the set of all coalitions $S$ with $i \in S$; let $C_i$ be the support of $q_i$, which is the set of all coalitions that $q_i$ assigns a strictly positive probability to; and let $\theta _i$ be the conditional probability that player $i$ receives an offer from some other player, given that player $i$ becomes a responder. Note that $\theta _i = (1/(1 - p_i)) \sum _{j \in N, j \ne i} p_j \sum _{S: i \in S \in C_j} q_j(S)$. We call the profile $\phi =(v_i, q_i, C_i, \theta _i)_{i \in N}$ the configuration of the SSPE $\sigma$. Whenever we want to emphasize the dependence of elements of $\phi$ on $\delta$, we shall add $\delta$ to them, as in “$v_i^\delta$” and “$q_i^\delta$.” In the following, the collection $(C_i)_{i \in N}$ of supports plays an important role; we call it the support configuration of $\sigma$.

Definition 2.1

Let $\sigma =(\sigma _1,\ldots ,\sigma _n)$ be an SSPE of $\Gamma ^\delta$ with a configuration $\phi =(v_i, q_i, C_i, \theta _i)_{i \in N}$.

• (1) An SSPE $\sigma$ of $\Gamma ^\delta$ is efficient if $\sum _{i \in N} v_i = v(N)$.

• (2) A strategy combination $\sigma ^*=(\sigma _1^*,\ldots ,\sigma _n^*)$ of $\Gamma$ is an asymptotically efficient equilibrium with limit payoff $v^*=(v_1^*, \ldots , v_n^*)$ if there exists a sequence $\{\sigma ^\delta \}$ of SSPEs of $\Gamma ^\delta$ such that $\{\sigma ^\delta \}$ converges to $\sigma ^*$ and the expected payoffs $v^\delta$ of $\sigma ^\delta$ converge to $v^*$ as $\delta$ goes to one, and if $\sum _{i \in N} v_i^*= v(N)$.

• (3) An SSPE $\sigma$ of $\Gamma ^\delta$ is subcoalition-inefficient if the probability of the grand coalition is zero.

• (4) Player $i$ is a central player in $\sigma$ if $\theta _i=1$, that is, $i \in S$ for every $S \in C_j$ and every $j \in N, j \ne i$.

In the case of the random proposer model $\Gamma ^\delta$, it is known that there is no delay in the agreements in any of the SSPEs whenever $\delta <1$ (see Lemma 3.1). Because of this fact, the efficiency of an SSPE is determined solely by coalitions formed in equilibrium. Under the regularity assumption $v(N)>v(S)$ for every $S \subset N, S \ne N$, an SSPE is efficient if and only if the grand coalition $N$ forms with probability one. Thus, an efficient SSPE must be the grand-coalition SSPE. In an inefficient SSPE, the probability of the grand coalition is strictly smaller than one. The notion of asymptotic efficiency describes a situation where the probability of the grand coalition becomes almost equal to one as players become sufficiently patient. Compte and Jehiel (2010) proved that the limit payoff in an asymptotically efficient equilibrium is equal to the coalitional Nash bargaining solution (the core allocation maximizing the Nash product). Whereas an efficient SSPE is given by nonrandomized (pure) strategies, there exists at least one player who uses a mixed strategy in an asymptotically efficient (but not efficient) equilibrium when $\delta <1$. The probability of any subcoalition $S$ with $v(S)<v(N)$ converges to zero as $\delta$ goes to one. In the limit in which $\delta$ becomes close to one, the asymptotically efficient equilibrium provides an efficient allocation of payoffs. The limit of the efficient SSPE as $\delta \rightarrow 1$ is obviously asymptotically efficient.

In the next section, we shall show that the existence of a central player guarantees asymptotic efficiency of an SSPE. A central player is a player who joins a coalition with probability one. In the efficient SSPE, all players are central. The inefficient SSPEs are divided into two types, according to whether or not the probability of the grand coalition is zero. In a subcoalition-inefficient SSPE, the grand coalition never forms.

3 Lemmas

Here, we present several basic properties of an SSPE that are useful for our analysis. First, we review some known results in the literature (Okada 1996, 2011).

Lemma 3.1

• (1) An SSPE of $\Gamma ^\delta$ in behavior strategies exists for every $\delta$ $(0 \le \delta <1)$.

• (2) For every SSPE $\sigma$ of $\Gamma ^\delta$, every proposal is accepted in the initial round. In the proposal, all responders $j$ are offered their discounted expected payoffs $\delta v_j$.

• (3) A strategy combination $\sigma =(\sigma _1,\ldots ,\sigma _n)$ is an SSPE of $\Gamma ^\delta$ if and only if its configuration $\phi =(v_i, q_i, C_i, \theta _i)_{i \in N}$ satisfies the following conditions, for every $i \in N$:

  • (i) Every $S \in C_i$ (i.e., $q_i(S)>0$) is a solution of

    $$\begin{aligned} \max _{i\in T \subset N} \left( v(T)-\sum _{j \in T, j \ne i} \delta v_j \right) . \end{aligned}$$

    (3.1)

  • (ii) $v_i \in R_+$ satisfies

    $$\begin{aligned} v_i = p_i \max _{i \in T \subset N} \left( v(T) - \sum _{j \in T, j \ne i} \delta v_j \right) + (1 - p_i) \theta _i \delta v_i. \end{aligned}$$

    (3.2)

• (4) The grand-coalition SSPE exists if and only if $v(N) \ge v(S) /(1 - \delta \sum _{j \in N-S} p_j)$ for every $S \subset N$. In equilibrium, every player $i \in N$ receives the expected payoff $v_i=p_i v(N)$.

In what follows, we call (3.1) the optimality condition of and (3.2) the payoff equation of an SSPE.

The grand-coalition (efficient) SSPE is fully characterized by Lemma 3.1(4) for an $n$-person cooperative game. The next lemma shows that the existence of a central player guarantees asymptotic efficiency.

Lemma 3.2

Let $\sigma ^*$ be a strategy combination for $\Gamma$. If there exists some sequence $\{ \sigma ^\delta \}$ of SSPEs in $\Gamma ^\delta$ such that every $\sigma ^\delta$ has at least one central player and $\{ \sigma ^\delta \}$ converges to $\sigma ^*$ as $\delta \rightarrow 1$, then the following properties hold.

• (1) $\sigma ^*$ is an asymptotically efficient equilibrium of $\Gamma$.

• (2) The limit payoff $v^*= (v_1^*, \ldots , v_n^*)$ of $\sigma ^*$ belongs to the core of $(N, v)$, and $\sum _{i \in S} v_i^*=v(S)$ holds for every $S$ that may form with positive probability in $\sigma ^\delta$ for any sufficiently large $\delta$.

• (3) For any central player $k$ in $\sigma ^\delta$ where $\delta$ is sufficiently large, $v_k^* \ge p_k v(N)$.

Proof

• (1) Let $\phi ^\delta =(v_i^\delta , q_i^\delta , C_i^\delta , \theta _i^\delta )_{i \in N}$ be the configuration of an SSPE $\sigma ^\delta$. We shall omit $\delta$ in the elements of $\phi ^\delta$ whenever no confusion will arise. For every $i \in N$ and every $S_i \in C_i$, $q_i(S_i)$ denotes the positive probability that player $i$ chooses $S_i$ in $\sigma ^\delta$. Let $x^i(S_i) =(x_j^i(S_i))_{j \in N} \in X_+^N$ be the payoff allocation when player $i$ proposes to $S_i$. Note that $\sum _{j \in N} x_j^i(S_i)=v(S_i)$. It then holds that

  $$\begin{aligned} \sum _{i \in N} v_i&= \sum _{i \in N} \sum _{j \in N} p_j \sum _{S_j \in C_j} q_j(S_j) x_i^j(S_j) = \sum _{j \in N} p_j \sum _{S_j \in C_j} q_j(S_j) \sum _{i \in N} x_i^j(S_j) \nonumber \\&= \sum _{j \in N} p_j \sum _{S_j \in C_j} q_j(S_j) v(S_j). \end{aligned}$$

  (3.3)

  Let $k \in N$ be any central player in $\sigma ^\delta$.⁵ By definition, $\theta _k=1$. Let $S_k \in C_k$. It follows from the payoff Eq. (3.2) that

  $$\begin{aligned} v_k = p_k \left( v(S_k) - \sum _{j \in S_k, j \ne k} \delta v_j \right) + (1-p_k) \delta v_k. \end{aligned}$$

  This can be rewritten as

  $$\begin{aligned} (1-\delta ) v_k = p_k \left( v(S_k)- \sum _{j \in S_k} \delta v_j \right) . \end{aligned}$$

  (3.4)

  It follows from the optimality condition (3.1) that

  $$\begin{aligned} v(S_k)- \sum _{j \in S_k} \delta v_j \ge v(N)- \sum _{j \in N} \delta v_j. \end{aligned}$$

  (3.5)

  Noting (3.3), it follows from (3.4) and (3.5) that

  $$\begin{aligned} (1-\delta ) v_k \ge p_k \left( v(N) - \delta \sum _{j \in N} p_j \sum _{S_j \in C_j} q_j(S_j) v(S_j) \right) . \end{aligned}$$

  This can be rewritten as

  $$\begin{aligned} v_k \ge \frac{p_k}{1-\delta } \sum _{j \in N} p_j \sum _{S_j \in C_j} q_j(S_j) (v(N)- \delta v(S_j)). \end{aligned}$$

  (3.6)

  By way of contradiction, suppose that $\sigma ^*$ is not asymptotically efficient. Then, there exists some $j \in N$ and some $S_j \in C_j, S_j \ne N$, such that

  $$\begin{aligned} \lim _{\delta \rightarrow 1} q_j^\delta (S_j) > 0. \end{aligned}$$

  Since $S_j$ is a proper subset of $N, v(N) > v(S_j)$ by assumption. The right-hand side of (3.6) then becomes infinite as $\delta \rightarrow 1$. This contradicts the assertion that $v_k^*$ is bounded from above. This proves (1).

• (2) Since $\sigma ^*$ is asymptotically efficient by (1), its limit payoff $v^*$ satisfies $\sum _{i \in N} v_i^* = v(N)$. Since $q_i^\delta (N)>0$ for every $i \in N$ and every sufficiently large $\delta$, the optimality condition (3.1) for an SSPE $\sigma ^\delta$ implies

  $$\begin{aligned} v(N)-\sum _{j \in N} \delta v_j^\delta \ge v(S)-\sum _{j \in S} \delta v_j^\delta \end{aligned}$$

  (3.7)

  for every $S \subset N$. As $\delta \rightarrow 1$, (3.7) implies that

  $$\begin{aligned} 0 \ge v(S)-\sum _{j \in S} v_j^*. \end{aligned}$$

  Thus, $v^*=(v_1^*, \ldots , v_n^*)$ belongs to the core of $(N, v)$. If the coalition $S$ is proposed with positive probability in $\sigma ^\delta$ for sufficiently large $\delta$, equality holds in (3.7) by the optimality condition (3.1). Thus, as $\delta \rightarrow 1$ in (3.7), we obtain $\sum _{i \in S} v_i^*=v(S)$.

• (3) Finally, it follows from (3.6) that $v_k^\delta \ge p_k v(N)$ for every $\delta$. This proves that $v_k^* \ge p_k v(N)$. Q.E.D.

The intuition for the first part of the lemma can be explained as follows. By the stationarity of an equilibrium, every player $i$ can receive his discounted expected payoff $\delta v_i$ whenever he is invited to join a coalition. When he is selected as a proposer, player $i$ exploits the excess $e(S^*, \delta v)$ of an equilibrium coalition $S^*$ in addition to his discounted expected payoff $\delta v_i$. Since a central player joins a coalition with probability one, his expected payoff $v_i$ can be represented as

$$\begin{aligned} v_i=\delta v_i + p_i e(S^*, \delta v) \end{aligned}$$

(3.8)

where $p_i$ is the probability that $i$ becomes a proposer (see (3.4)). The first term of (3.8) is the continuation payoff and the second one is interpreted as the proposer’s rent. Since an equilibrium coalition $S^*$ maximizes the excess $e(S, \delta v)$ over $S$ including $i$, it holds that $(1-\delta )v_i \ge p_ie(N, \delta v)$. Thus, as $\delta$ goes to one, $e(N, \delta v)$ converges to zero, equivalently, $\sum _{i \in N} v_i^*$ converges to $v(N)$. This means that an equilibrium is asymptotically efficient.

The second part of Lemma 3.2 can be easily obtained from asymptotic efficiency. The grand coalition is agreed with positive probability in an asymptotically efficient equilibrium, whoever becomes a proposer. Thus, it holds that $e(N, \delta v) \ge e(S, \delta v)$ for every $S$. As $\delta$ goes to one, it must be that $0\ge e(S, v^*)$. This means that the limit payoff vector $v^*$ belongs to the core.

The lemma is closely related to the results of Compte and Jehiel (2010, Proposition 1 and Claim C). These authors introduced a concept of a “key” player who belongs to all binding coalitions in the coalitional Nash bargaining solution, and showed that if there exists at least one key player, then the maximal Nash product subject to the core constraints increases as the values of all coalitions are increased by the same amount (Property P1). They further proved that an asymptotically efficient equilibrium exists if and only if the core is nonempty and Property P1 holds. Two notions of a central player and a key player are closely related. Indeed, suppose (as in Lemma 3.2) that $i^*$ be a central player in every SSPE $\sigma ^\delta$ where $\{ \sigma ^\delta \}$ converges to $\sigma ^*$ as $\delta \rightarrow 1$. Then, Lemma 3.2.(2) shows that every coalition $S$ that forms with positive probability in $\sigma ^\delta$ for any sufficiently large $\delta$ must be a binding coalition in the coalitional Nash bargaining solution and $i^* \in S$. Conversely, for a key player $i^*$ in the coalitional Nash bargaining solution, it can be shown that there exists a sequence $\{\sigma ^\delta \}$ of SSPEs in $\Gamma ^\delta$ such that (i) $i^*$ is a central player in every $\sigma ^\delta$ and (2) the expected payoffs of $\sigma ^\delta$ converge to the coalitional Nash bargaining solution. For the construction of an SSPE $\sigma ^\delta$, see Compte and Jehiel (2010, p.1611-1612). In a wage bargaining game where the values of coalitions without the employer are zero, the employer is both a key player and a central player (Compte and Jehiel 2010 and Okada 2011). Finally, we remark that, in contrast to the notion of a key player, we define a central player in terms of the support configuration of an SSPE. This approach enables us to classify all SSPEs for $n=3$ according to the number of central players.

The final lemma presented here demonstrates some useful properties of the excess of a coalition with respect to the supports of an SSPE. We shall frequently use them to analyze a three-person game in the following section.

Lemma 3.3

Let $\sigma$ be an SSPE of $\Gamma ^\delta$ with expected payoffs $v_i$ and supports $C_i$ for all $i \in N$. For $S \subset N$, let $e(S, \delta v)$ be the excess of $S$ with respect to $\delta v=(\delta v_1, \ldots , \delta v_n)$.

• (1) For all $S$ and $T$ in $C_i$, $e(S, \delta v)=e(T, \delta v)$.

• (2) For $j \in S \in C_i$ and $i \in T \in C_j$, $e(S, \delta v) = e(T, \delta v)$.

• (3) If there exists a way of relabeling the players such that every player $i$’s support $C_i$ includes some $S_i$ satisfying

  $$\begin{aligned} i \in S_{i-1} \cap S_{i} \end{aligned}$$

  (with $S_0=S_n$), then $e(S_{1}, \delta v)= \cdots =e(S_{n}, \delta v)$.

Proof

All of these results follow from the optimality condition (3.1) for an SSPE $\sigma$ given in Lemma 3.1.

• (1) Since $S, T \in C_i$, we have

  $$\begin{aligned} v(S)- \sum _{j \in S, j \ne i} \delta v_j = v(T) - \sum _{j \in T, j \ne i} \delta v_j. \end{aligned}$$

  This yields $e(S, \delta v)=e(T, \delta v)$.

• (2) Since $S \in C_i$ and $i \in T$, we have

  $$\begin{aligned} v(S)-\sum _{j \in S, j \ne i} \delta v_j \ge v(T)-\sum _{j \in T, j \ne i} \delta v_j. \end{aligned}$$

  This yields $e(S, \delta v) \ge e(T, \delta v)$. Similarly, since $T \in C_j$ and $j \in S$, we have $e(T, \delta v) \ge e(S, \delta v)$. Thus, $e(S, \delta v) = e(T, \delta v)$.

• (3) Since $i \in S_{i-1}$ and $S_{i} \in C_{i}$, it holds that $e(S_{i-1}, \delta v) \le e(S_{i}, \delta v)$. By varying $i$ from 1 to $n$, we have

  $$\begin{aligned} e(S_{n}, \delta v) \le e(S_{1}, \delta v) \le \cdots \le e(S_{n}, \delta v). \end{aligned}$$

  This proves (3). Q.E.D.

4 A classification of SSPEs: $n=3$

We can classify all SSPEs in a three-person coalitional bargaining game $\Gamma ^\delta$ according to their support configurations $C = (C_1, C_2, C_3)$. Table 1 gives a list of all seven possible supports for each player’s equilibrium strategy.⁶ There are 343 (= 7 $\times$ 7 $\times$ 7) possible support configurations. We characterize the limit payoff of an SSPE for each configuration of supports as the discount factor $\delta$ converges to one. For the sake of analysis, we assume the uniform distribution $(1/3, 1/3, 1/3)$ for the recognition probabilities $p_i$ for each player $i=1, 2, 3$. A similar analysis can be applied to a general distribution.

Table 1 List of all possible supports of three players’ strategies

We classify all possible support configurations into four cases, according to the number $s^*$ of central players: $s^*=3, 2, 1, 0$.

Case 1. All three players are central ($s^*=3$): one type.

In this case, $C_1= C_2 = C_3 = \{123 \}$. The SSPE is an efficient equilibrium where the grand-coalition is agreed with probability one. From Lemma 3.1(4), the grand-coalition SSPE exists if and only if $v(123) \ge (3/(3 - \delta )) v(S)$ for every two-person coalition $S$. The expected payoff $v_i$ of every player $i=1, 2, 3$ is $v(123)/3$. As the discount factor $\delta$ goes to one, the equilibrium allocation converges to the equity allocation $(v(123)/3, v(123)/3, v(123)/3)$, regardless of the proposer. The equity allocation must belong to the core, i.e., $v(123)/3 \ge v(S)/2$ for every two-person coalition $S$.

Case 2. Only two players are central ($s^*=2$): nine types.

Table 2 shows a list of all three possible configurations of supports when only players 1 and 2 are central. Notice that each player’s support $C_i$ must include the grand coalition $123$, since the SSPE is asymptotically efficient by Lemma 3.2. For example, although only players 1 and 2 are central in a configuration $C_1=C_2=\{ 12 \}, C_3=\{123\}$, we know that there exists no SSPE with such a configuration when $\delta$ is sufficiently high. In total, there are nine types of configurations, considering permutations of players.

Table 2 List of players’ supports when only players 1 and 2 are central

We shall characterize SSPEs for all configurations in Table 2. In each type of SSPE, the payoff Eq. (3.2) for $i=1, 2, 3$ gives

$$\begin{aligned} 3 v_1&= v(123)-\delta v_2 -\delta v_3 + 2 \delta v_1, \end{aligned}$$

(4.1)

$$\begin{aligned} 3 v_2&= v(123)-\delta v_1 -\delta v_3 + 2 \delta v_2, \end{aligned}$$

(4.2)

$$\begin{aligned} 3 v_3&= v(123)-\delta v_1 -\delta v_2 + 2 \delta \theta _3 v_3, \end{aligned}$$

(4.3)

where $\theta _3$ is the conditional probability that player 3 joins a coalition, given that that player becomes a responder. Equations (4.1) and (4.2) solve $v_1 = v_2$ for any $\delta <1$. Since $123, 12 \in C_1$ or $C_2$ in every configuration in Table 2, Lemma 3.3(1) implies $e(123, \delta v)=e(12, \delta v)$. This yields

$$\begin{aligned} v_3=\frac{v(123)-v(12)}{\delta }. \end{aligned}$$

(4.4)

Equations (4.1) and (4.4) with $v_1=v_2$ solve

$$\begin{aligned} v_1=v_2=\frac{v(12)}{3-\delta }. \end{aligned}$$

(4.5)

Thus, the limit payoff $v^*=(v_1^*, v_2^*, v_3^*)$ of an SSPE as $\delta \rightarrow 1$ is given by

$$\begin{aligned} v_1^* = v_2^* = \frac{v(12)}{2}, \quad v_3^* = v(123) -v(12). \end{aligned}$$

(4.6)

The optimality conditions (3.1) for $i=1$ and $2$ imply $e(123, \delta v) \ge e(13, \delta v)$ and $e(123, \delta v) \ge e(23, \delta v)$, respectively. As $\delta \rightarrow 1$, these conditions yield

$$\begin{aligned} \frac{v(12)}{2} \le v(123)-v(13), \quad \frac{v(12)}{2} \le v(123)-v(23). \end{aligned}$$

(4.7)

Substituting (4.4) and (4.5) into (4.3) solves

$$\begin{aligned} \theta _3 = \frac{1}{2(v(123)-v(12))} \left[ \frac{3-\delta }{\delta } v(123) - \frac{9-3\delta -2\delta ^2}{\delta (3-\delta )} v(12) \right] . \end{aligned}$$

From $\theta _3 <1$, this yields $((3 - \delta )/3) v(123) < v(12)$. As $\delta \rightarrow 1$, we obtain

$$\begin{aligned} v(123) - v(12) \le \frac{v(123)}{3}. \end{aligned}$$

(4.8)

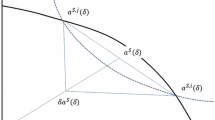
In summary, (4.6), (4.7), and (4.8) show the following bargaining outcome in the limit in which the discount factor $\delta$ is almost equal to one. Two central players, 1 and 2, split their coalitional value $v(12)$ equally. Non-central player 3 receives his marginal contribution $m_3=v(123)-v(12)$ to the grand coalition $\{ 1, 2, 3 \}$. It follows from Lemma 3.2(2) that the limit payoff allocation (4.6) belongs to the core. This fact is also obtained from (4.6) and (4.7). Namely, every player $i$’s payoff $v_i^*$ is less than or equal to his marginal contribution $m_i$ to $\{ 1, 2, 3 \}$. The limit payoff allocation $v^*$ is equal to the coalitional Nash bargaining solution of Compte and Jehiel (2010) which maximizes the Nash product $x_1x_2x_3$ over the core. It follows from (4.8) that the equity allocation $(v(123)/3, v(123)/3, v(123)/3)$ is outside the core, ignoring the degenerate case that the equality holds in (4.8). Figure 1 illustrates the SSPE allocation. Finally, it can be seen that $m_3 \le v(123)/3 \le m_1, m_2$. This inequality naturally shows that central players 1 and 2 are more productive than non-central player 3.

Fig. 1

The SSPE allocation with two central players

Case 3. Only one player is central ($s^*=1$): 27 types.

Table 3 shows a list of all possible configurations of supports when only player 1 is central. Similarly to case 2, the support of each player must include the grand coalition $123$, since the SSPE is asymptotically efficient. There are nine possible configurations in this subcase. Considering permutations of players, there are 27 types in total.

Table 3 All configurations of players’ supports where only player 1 is central

In all nine possible configurations in Table 3, we have $123, 12 \in C_i$ and $123, 13 \in C_j$ for some $i, j \in N$ (including the case $i=j$). It then follows from Lemma 3.3 that $e(123, \delta v)= e(12, \delta v)= e(13, \delta v)$. These equations yield

$$\begin{aligned} \delta v_2&= v(123)-v(13), \end{aligned}$$

(4.9)

$$\begin{aligned} \delta v_3&= v(123)-v(12). \end{aligned}$$

(4.10)

Since player 1 is a central player, the payoff equations for an SSPE yield (4.1), (4.3), and

$$\begin{aligned} 3 v_2 = v(123)-\delta v_1 -\delta v_3 + 2 \delta \theta _2 v_2 \end{aligned}$$

(4.11)

(instead of (4.2)) where $\theta _2$ is the conditional probability that player 2 joins a coalition, given that that player becomes a responder.

From (4.1), (4.9), and (4.10), it follows that

$$\begin{aligned} v_1=\frac{v(12)+v(13)-v(123)}{3-2\delta }. \end{aligned}$$

(4.12)

It can be seen without much difficulty that (4.11) and $\theta _2<1$ imply

$$\begin{aligned} (3-\delta ) v(123) < \delta v(12) + (3-\delta ) v(13). \end{aligned}$$

(4.13)

Similarly, it follows from (4.3) and $\theta _3<1$ that

$$\begin{aligned} (3-\delta ) v(123) < (3-\delta ) v(12) + \delta v(13). \end{aligned}$$

(4.14)

For $\delta <1$, the optimality condition (3.1) implies

$$\begin{aligned} v(123)-\delta v_1-\delta v_3 \ge v(23)-\delta v_3. \end{aligned}$$

Substituting (4.12) into this inequality, we have

$$\begin{aligned} (3-\delta )v(123) \ge \delta v(12) + \delta v(13) + (3-2\delta )v(23). \end{aligned}$$

(4.15)

Finally, as $\delta \rightarrow 1$, we obtain the limit payoff of an SSPE as

$$\begin{aligned} v_1^*=v(12)+v(13)-v(123),\quad v_2^*=v(123)-v(13),\quad v_3^*=v(123)-v(12)\nonumber \\ \end{aligned}$$

(4.16)

from (4.9), (4.10), and (4.12), and obtain

$$\begin{aligned} v(123)-v(13)&\le \frac{v(12)}{2}, \end{aligned}$$

(4.17)

$$\begin{aligned} v(123)-v(12)&\le \frac{v(13)}{2}, \end{aligned}$$

(4.18)

$$\begin{aligned} 2 v(123)&\ge v(12) + v(13) + v(23) \end{aligned}$$

(4.19)

from (4.13), (4.14) and (4.15), respectively. Equation (4.19) is a well-known condition for the core to be nonempty in a three-person game. Notice that (4.7) and (4.17) are disjoint, ignoring the degenerate case that equalities hold.

The bargaining outcome is summarized as follows. Two non-central players 2 and 3 receive their marginal contributions $m_2, m_3$ and the central player 1 exploits the surplus $v(123)-m_2-m_3$. The limit payoff (4.16) is the coalitional Nash bargaining solution in the core. It follows from (4.17)–(4.19) that $m_1 \ge m_2, m_3$. As in case 2, the central player 1 is more productive than non-central players 2 and 3.

The last case has no central players, and it corresponds to a game with an empty core. There are two subcases, cases 4 and 5, depending on whether or not the probability of the grand coalition is positive. Case 4 deals with the case where the grand coalition may form with positive probability. Case 5 examines a subcoalition-inefficient SSPE where the grand coalition never forms.

Case 4. An SSPE without central players where the grand coalition may form with positive probability ($s^*=0$): 162 types.

In this subcase, there are 162 possible types.⁷ We shall show that all support configurations satisfy

$$\begin{aligned} e(123, \delta v)=e(12, \delta v)= e(23, \delta v)=e(13, \delta v), \end{aligned}$$

(4.20)

except for the three configurations

$$\begin{aligned} C_1&= \{123, 12, 13 \}, \quad C_2=\{23 \}, \quad C_3=\{23 \}, \end{aligned}$$

(4.21)

$$\begin{aligned} C_1&= \{13 \}, \quad C_2=\{123, 12, 23 \}, \quad C_3=\{13 \},\end{aligned}$$

(4.22)

$$\begin{aligned} C_1&= \{12 \}, \quad C_2=\{12 \}, \quad C_3=\{123, 13, 23 \}. \end{aligned}$$

(4.23)

Without any loss of generality, we assume $123 \in C_1$, and shall show that (4.20) holds for all possible configurations except (4.21). (4.22) and (4.23) are obtained by similar arguments in other cases, where $123 \in C_2$ and $123 \in C_3$, respectively. Consider four possible cases about $C_1$. In the following arguments, we frequently use Lemma 3.3.

• (i) $C_1=\{123, 12, 13 \}$. In this case, $e(123, \delta v)=e(12, \delta v)=e(13, \delta v)$ by Lemma 3.3(1). Suppose that $23 \in C_2$. Except the case of $C_2= \{ 23 \}$, it can be seen that (4.20) holds. Let $C_2= \{ 23 \}$. If $13 \in C_3$, then $e(12, \delta v) = e(23, \delta v)=e(13, \delta v)$ since $12 \in C_1, 23 \in C_2$ and $13 \in C_3$ (applying Lemma 3.3(3) with the order $(1, 2, 3)$). Thus (4.20) holds. If $123 \in C_3$, then $e(123, \delta v)=e(23, \delta v)$, since $23 \in C_2$, and thus (4.20) holds. Thus, (4.21) remains. Suppose that $23 \notin C_2$. We must then have $23 \in C_3$ so that player 1 is not a central player. If $123 \in C_2$, then $e(123, \delta v)=e(23, \delta v)$ from Lemma 3.1.(2), and thus (4.20) holds. If $12 \in C_2$, then $e(13, \delta v) = e(12, \delta v) = e(23, \delta v)$ from Lemma 3.3(3), and thus (4.20) holds.

• (ii) $C_1=\{123, 12 \}$. In this case, $e(123, \delta v)=e(12, \delta v)$. Suppose that $23 \in C_2$. We must have $13 \in C_3$, so that player 2 is not a central player. Then $e(12, \delta v) = e(23, \delta v)= e(13, \delta v)$ by Lemma 3.3(3). Thus, (4.20) holds. Suppose that $23 \notin C_2$. In this case, we have $C_2=\{123, 12 \}$, $C_2=\{123\}$ or $C_2=\{ 12 \}$. In either case, we must have $13, 23 \in C_3$ so that neither 1 nor 2 is a central player. Thus, $e(13, \delta v)=e(23, \delta v)$. If $C_2=\{123, 12 \}$ or $C_2=\{123\}$, then $e(123, \delta v)=e(23, \delta v)$ by Lemma  3.3(2), and thus (4.20) holds. Finally, consider the case $C_2=\{ 12 \}$. If $C_3=\{123, 13, 23 \}$, then (4.20) holds, since $C_1=\{123, 12 \}$. If $C_3=\{13, 23 \}$, then we have $e(12, \delta v) \ge e(23, \delta v) \ge e(123, \delta v)=e(12, \delta v)$, and thus (4.20) holds.

• (iii) $C_1=\{123, 13 \}$. We must have $12 \in C_2$, so that player 3 is not a central player. This must induce $23 \in C_3$ so that player 1 is not a central player. Then (4.20) holds, from Lemma 3.3(3).

• (iv) $C_1=\{123 \}$. In this case, Neither $C_2=\{ 123 \}$, $C_2=\{ 23 \}$, nor $C_2=\{ 123, 23 \}$ is possible, otherwise 3 would become a central player. Then, there are four possible types of $C_2$: $C_2=\{ 123, 12, 23 \}, \{ 12, 23 \}, \{123, 12 \}, \{ 12 \}$. Suppose that $C_2=\{ 123, 12, 23 \}$. It holds that $e(123, \delta v) = e(12, \delta v)= e(23, \delta v)$. We must have $13 \in C_3$, so that 2 is not a central player. Thus, $e(123, \delta v)=e(13, \delta v)$ from Lemma 3.3(2), since $C_1=\{123 \}$. This yields (4.20). Suppose that $C_2=\{ 12, 23 \}$. We must have $13 \in C_3$, so that 2 is not a central player. Then $e(123, \delta v) = e(12, \delta v)= e(13, \delta v)$ from Lemma 3.3(2). We have $e(12, \delta v)=e(23, \delta v)$, since $C_2=\{ 12, 23 \}$, and thus (4.20) holds. Finally, suppose that $C_2=\{ 123, 12 \}$ or $\{ 12 \}$. We must then have $13, 23 \in C_3$, so that neither 1 nor 2 is a central player. We have $e(123, \delta v)=e(12, \delta v)$ and $e(123, \delta v)=e(13, \delta v)$, since $12 \in C_2$ and $13 \in C_3$, respectively. Since $13, 23 \in C_3$, we have $e(13, \delta v)=e(23, \delta v)$. Thus, (4.20) holds.

Now, by solving (4.20), we obtain

$$\begin{aligned} \delta v_1 =v(123)-v(23),\quad \delta v_2 =v(123)-v(13),\quad \delta v_3 =v(123)-v(12).\nonumber \\ \end{aligned}$$

(4.24)

All players’ discounted expected payoffs are equal to their marginal contributions. In every SSPE where (4.20) applies, the optimality condition is trivially satisfied. As $\delta$ goes to one in (4.24), we have the limit payoff of an SSPE,

$$\begin{aligned} v_1^*=v(123)-v(23),\quad v_2^*=v(123)-v(13),\quad v_3^*=v(123)-v(12).\nonumber \\ \end{aligned}$$

(4.25)

Let $\theta _i (i=1, 2, 3)$ be the conditional probability that player $i$ joins a coalition, given that $i$ becomes a responder. It must hold that $0\le \theta _i < 1$ for each $i=1,2,3$, and

$$\begin{aligned} \frac{3}{2} < \theta _1 + \theta _2 + \theta _3 < 3. \end{aligned}$$

(4.26)

⁸The payoff equation for an SSPE for $i=1$ is given by

$$\begin{aligned} 3 v_1 = v(123)-\delta v_2 -\delta v_3 + 2 \delta \theta _1 v_1. \end{aligned}$$

(4.27)

Equations (4.24) and (4.27) solve

$$\begin{aligned} \theta _1=\frac{(3+\delta )v(123)-\delta v(12) - 3v(23) - \delta v(13)}{2\delta (v(123)-v(23))}. \end{aligned}$$

(4.28)

Letting $\delta \rightarrow 1$, the constraints $\theta _1<1$ and $\theta _1\ge 0$ yield

$$\begin{aligned} 2v(123)&\le v(12) + v(23) + v(13),\end{aligned}$$

(4.29)

$$\begin{aligned} 4v(123)&\ge v(12) + 3 v(23) + v(13), \end{aligned}$$

(4.30)

respectively. Similarly to (4.30), we have

$$\begin{aligned} 4v(123)&\ge v(12) + v(23) + 3 v(13), \end{aligned}$$

(4.31)

$$\begin{aligned} 4v(123)&\ge 3 v(12) + v(23) + v(13). \end{aligned}$$

(4.32)

Notice that (4.19) in case 3 and (4.29) are disjoint except the degenerate case that equalities hold.

The three cases (4.21)–(4.23) remain. Since the analysis is similar, we shall solve the case of (4.21) only. When (4.21) holds, we have $\theta _1=0$ and $e(123, \delta v)=e(12, \delta v)= e(13, \delta v)$. Thus, $\delta v_2 =v(123)-v(13)$ and $\delta v_3 =v(123)-v(12)$. Since $\theta _1=0$, the payoff equation for $i=1$ is $3v_1 = v(12)-\delta v_2$. This solves

$$\begin{aligned} v_1=\frac{v(12)+v(13)-v(123)}{3}. \end{aligned}$$

(4.33)

The payoff equation for $i=2$ is $3v_2=v(23)-\delta v_3 + 2 \delta \theta _2 v_2$. Substituting $v_1, v_2$, and $v_3$, this yields

$$\begin{aligned} \theta _2=\frac{(3+\delta )v(123)-\delta v(12) - \delta v(23) - 3 v(13)}{2\delta (v(123)-v(13))}. \end{aligned}$$

(4.34)

Letting $\delta \rightarrow 1$ in (4.34), the constraints $\theta _2 < 1$ and $\theta _2 \ge 1/2$ (by (4.26)) yield (4.29) and

$$\begin{aligned} 3v(123) \ge v(12) + v(23) +2 v(13), \end{aligned}$$

(4.35)

respectively. Interchanging 2 with 3, we obtain

$$\begin{aligned} 3v(123) \ge 2v(12) + v(23) + v(13). \end{aligned}$$

(4.36)

Finally, as $\delta \rightarrow 1$, the optimality condition $e(23, \delta v) \ge e(123, \delta v)$ yields

$$\begin{aligned} 4v(123) \le v(12) + 3 v(23) + v(13). \end{aligned}$$

(4.37)

We can summarize our analysis of case 4 as follows. In the limit as $\delta$ goes to one, every player $i$’s expected payoff is equal to that player’s marginal contribution $m_i = v(123)-v(jk), i \ne j, k$, in most configurations of supports (159 cases). It holds that $m_i$ is greater than or equal to $(v(123) - m_j - m_k)/3$. In the remaining three cases, two players receive their marginal contributions and the other player receives $(v(123) - m_j - m_k)/3$ more than his or her marginal contribution.

Case 5. An SSPE without central players where the grand coalition never forms ($s^*=0$): 18 types.

Table 4 shows a list of all possible support configurations. The configurations in Table 4 can be divided into four subcases according to the values of $\theta _i$ $(i=1, 2, 3)$.⁹ In this case, note that $\theta _1 + \theta _2 + \theta _3 = 3/2$ (see footnote 8).

In every configuration, all two-person coalitions (i.e., 12, 23, and 13) belong to the support of some players. Because of this fact, the condition for optimality of an SSPE implies $e(12, \delta v), e(23, \delta v), e(13, \delta v) \ge e(123, \delta v)$. Thus, the limit expected payoff $v_i$ of every player $i=1, 2, 3$ as $\delta \rightarrow 1$ is greater than or equal to that player’s marginal contribution $m_i=v(123)-v(jk)$ $(i \ne j, k)$.

Table 4 List of all possible configurations of an SSPE without central players where the grand coalition never forms

Subcase (i). $\theta _1 = \theta _2 = \theta _3 = 1/2$ (Nos. 13 and 18).

From Lemma 3.3(3), $e(12, \delta v)=e(23, \delta v)= e(13, \delta v)$. Together with this, it can be seen without much difficulty that the payoff equations

$$\begin{aligned} 3v_1&= v(12) - \delta v_2 + \delta v_1, \end{aligned}$$

(4.38)

$$\begin{aligned} 3v_2&= v(23) - \delta v_3 + \delta v_2, \end{aligned}$$

(4.39)

$$\begin{aligned} 3v_3&= v(13) - \delta v_1 + \delta v_3 \end{aligned}$$

(4.40)

imply that $v(12)=v(23)=v(13)$ and

$$\begin{aligned} v_1=v_2=v_3= \frac{1}{3} v(12). \end{aligned}$$

(4.41)

The optimality condition $e(12, \delta v) \ge e(123, \delta v)$ implies $v(12) \ge (3/(3 + \delta )) v(123).$ As $\delta \rightarrow 1$, we obtain

$$\begin{aligned} v(12) = v(23) = v(13) \ge \frac{3}{4} v(123). \end{aligned}$$

(4.42)

An SSPE is possible in this case only in a symmetric game where each two-person coalition is productive relative to the grand coalition. All players receive equal expected payoffs $v(12)/3$, and thus the payoff allocation in each two-person coalition is unequal in that a proposer receives a payoff twice as large as a responder.

Subcase (ii). $\theta _i = 1/2$ for only one $i = 1, 2, 3$ (Nos. 5, 7, 10, 12, 16, 17).

We consider only the configuration $C_1= \{12, 13 \}, C_2=\{ 12 \}, C_3=\{ 23 \}$ (No. 5) where $\theta _1 = 1/2$ in Table 4. Other configurations can be solved in the same way. It follows from Lemma 3.3 that $e(12, \delta v)=e(23, \delta v)= e(13, \delta v)$. Together with this, it can be seen without much difficulty that the payoff equations

$$\begin{aligned} 3v_1&= v(12) - \delta v_2 + \delta v_1, \end{aligned}$$

(4.43)

$$\begin{aligned} 3v_2&= v(12) - \delta v_1 + 2 \theta _2 \delta v_2, \end{aligned}$$

(4.44)

$$\begin{aligned} 3v_3&= v(23) - \delta v_2 + 2 \theta _3 \delta v_3 \end{aligned}$$

(4.45)

imply

$$\begin{aligned} v_1&= \frac{v(12)+v(13)-v(23)}{3},\\ \delta v_2&= \frac{\delta v(12)+(3-\delta )v(23)-(3-\delta )v(13)}{3}, \\ \delta v_3&= \frac{-(3-\delta ) v(12)+(3-\delta )v(23)+\delta v(13)}{3}, \\ \theta _2&= \frac{\delta v_1 + 3 v_2 - v(12)}{2 \delta v_2}, \\ \theta _3&= \frac{\delta v_2 + 3 v_3 - v(23)}{2 \delta v_3}. \end{aligned}$$

In the limit as $\delta \rightarrow 1$, we examine the constraints $0 \le \theta _i < 1$ $(i=2, 3)$ ¹⁰ and the optimality condition $e(12, \delta v) \ge e(123, \delta v)$. It can be shown that

$$\begin{aligned}&\displaystyle v(12)+v(13) \ge v(23),&\\&\displaystyle v(12)+5v(23)-5v(13) \ge 0,&\\&\displaystyle -5v(12)+5v(23)+v(13) \ge 0,&\\&\displaystyle v(12) + 2v(23) + v(13) \ge 3v(123).&\end{aligned}$$

The limiting expected payoffs for players are given by

$$\begin{aligned} v_1^*&= \frac{v(12) + v(13) - v(23)}{3}, \quad v_2^* = \frac{v(12)+2v(23)-2v(13)}{3}, \\ v_3^*&= \frac{-2v(12)+2v(23)+ v(13)}{3}. \end{aligned}$$

Subcase (iii). $\theta _i= 0$ for some $i=1, 2, 3$ (Nos. 8, 11, 15).

Consider the configuration $C_1=\{12, 13 \}, C_2=\{ 23 \}, C_3=\{ 23 \}$ (No. 8) in Table 4, where $\theta _1=0$. From the payoff equation $3v_1 = v(12) - \delta v_2$ and the optimality condition $e(12, \delta v) = e(13, \delta v)$, it follows that $\delta v_2=v(12) - 3 v_1$ and $\delta v_3=v(13) - 3 v_1$. We obtain $v_1$ by solving a quadratic equation constructed from $\theta _2 + \theta _3 = 3/2.$ ¹¹

Subcase (iv). Others (Nos. 1, 2, 3, 4, 6, 9, 14).

In all configurations, the optimality conditions $e(12, \delta v)=e(23, \delta v)=e(13, \delta v)$ hold. Thus, $\delta v_2=v(23) - v(13) + \delta v_1$ and $\delta v_3=v(23) - v(12) + \delta v_1$. We obtain $v_1$ by solving a cubic equation constructed from $\theta _1 + \theta _2 + \theta _3= 3/2$.

We summarize the result of a three-person cooperative game in the following proposition and Table 5.

Table 5 Classification of SSPEs $(n=3)$

Proposition

Let $(N, v)$ be a three-person superadditive game, where $N=\{1, 2, 3 \}$ and $m_i=v(N)-v(N-\{ i \})$ is player $i$’s marginal contribution to the grand coalition, and let $\Gamma$ be the random proposer game for $(N, v)$ with a uniform recognition probability. The limit of the expected payoffs for an SSPE in $\Gamma$ when the discount factor goes to one can be classified as follows.

• 1. The equal allocation, where the probability of the grand coalition is one.

• 2. The coalitional Nash bargaining solution, where the probability of the grand coalition converges to one. In equilibrium, there exists at least one player who joins all possible coalitions.

• 3. The marginal contributions $(m_1, m_2, m_3)$, where $m_i \ge n_i \equiv (v(\{1, 2, 3 \}) - m_j - m_k)/3$ for all $i=1, 2, 3$ and $j, k \ne i$.

• 4. The vector $(n_1, m_2, m_3)$ (and two permutations), where $n_1 \ge m_1$, $m_2 \ge n_2$, and $m_3 \ge n_3$.

• 5. Allocations within two-person coalitions.

In the first two cases, the limit of the SSPE payoff belongs to the core of the game. In the remaining cases, the core is empty.

When the players are sufficiently patient, the SSPEs of the random proposer game can be classified according to the level of efficiency, i.e., the equilibrium probability of the grand coalition. The efficiency level is characterized by the number of central players who join all equilibrium coalitions (Table 5). The efficient SSPE (Okada 1996) has the full number of central players, and an asymptotically efficient equilibrium (Compte and Jehiel 2010) has at least one central player. These (asymptotically) efficient equilibria exist only when the core of a game is nonempty. When the core is empty, an SSPE must be inefficient. There are two types of inefficient SSPE, depending on whether or not the probability of the grand coalition is positive.

In a three-person game, the equal allocation $v(123)/3$ and the marginal contributions $m_i$ to the grand coalition for every player $i$ play a critical role in the expected payoffs for players in equilibrium. If the equal allocation $v(123)/3$ is smaller than all players’ marginal contributions $m_i$ (or, equivalently, the equal allocation belongs to the core), then the SSPE expected payoffs are given by the equal allocation. In this case, all players are central. If the equal allocation exceeds the marginal contribution for some player, then that player must be noncentral, and that player receives his or her marginal contribution. The remaining players split the surplus equally. In an inefficient SSPE where the probability of the grand coalition is positive, every player’s expected payoff is equal to their marginal contribution $m_i$ if it exceeds the threshold $(v(\{1, 2, 3 \}) - m_j - m_k)/3$ for $j, k \ne i$. In a subcoalition-inefficient SSPE where the probability of the grand coalition is zero, all players’ expected payoffs are not less than their marginal contributions.

The analysis of three-person games gives us the following insights into $n$-person games. First of all, the existence of a central player plays a critical role in characterizing an SSPE outcome. Lemmas 3.1 and 3.2 hold true for an $n$-person coalitional bargaining game with general recognition probabilities. The existence of a central player guarantees the (asymptotic) efficiency. Moreover. this result does not rely on the stopping rule in this paper that the game stops whenever a coalition forms, and can be generalized to the case that more than one coalition may form sequentially and the game stops when all players join coalitions. In the general case, a central player is defined to be a player who may join a coalition in the initial round with probability one. The assumption that $v(N)>v(S)$ for every $S \ne N$ should be replaced with the property that $v(N) > v(S)+v(N-S)$ for every $S \ne N$.

Second, the results of a three-person game provide us with a heuristics for the analysis of an $n$-person game. Specifically, the classification of SSPEs in a three-person game reveals a variety of the equilibrium outcomes, depending on the number of central players, which covers the unconstrained and the core-constrained Nash bargaining solutions and the marginal contribution payoffs to the grand coalition. This equilibrium variety is carried over to an $n$-person game. The equilibrium probability distribution over coalitions tends to be complicated in an $n$-person game. The analysis of an SSPE without central players (in cases 4 and 5) implies that there may exist many types of an inefficient SSPE in an $n$-person game where only a limited set of coalitions may form with positive probability, and thus that the values of other coalitions never affect the equilibrium payoffs of players. This is in contrast to the case of the Shapley value.

5 Concluding remarks

The classification of the SSPEs of the random proposer model for a three-person game reveals a variety of bargaining outcomes regarding the level of efficiency. When the core is nonempty and the grand coalition is a unique efficient coalition, the grand coalition forms almost surely, and the payoff allocation is characterized by the coalitional Nash bargaining solution (Compte and Jehiel 2010). When the core is empty, the equilibrium is inefficient. Our analysis of a three-person game shows that although no single cooperative solution appropriately describes bargaining behavior, the concepts of the Nash bargaining solution, the core, and the marginal contribution are closely related to an SSPE allocation of the random proposer model.