On the distribution of links in the interbank network: evidence from the e-MID overnight money market

Abstract

Previous literature on statistical properties of interbank networks has reported various power-laws, particularly for the degree distribution (i.e., the distribution of credit links between institutions). In this paper, we revisit data for the Italian interbank network based on overnight loans recorded on the e-MID trading platform during the period 1999–2010 using both daily and quarterly aggregates. In contrast to previous reports, we find no evidence in favor of a power-law characterizing the degree distribution. Rather, the data are best described by negative Binomial distributions. For quarterly data, Weibull, Gamma, and Exponential distributions tend to provide comparable fits. We find similar results when investigating the distribution of the number of transactions, even though in this case, the tails of the quarterly variables are much fatter. The absence of power-law behavior casts doubts on previous claims that these interbank data fall into the category of scale-free networks.

1 Introduction and existing literature

Since the onset of the global financial crisis (GFC) in 2007/2008, the analysis of network structures formed by interbank liabilities has received increasing attention. Considering an ensemble of financial institutions, individual banks are connected to each other through some of their activities (usually credit flows) and the bilateral exposures can be mapped into a credit network. Such a perspective is useful in order to study the knock-on effects on other banks due to disruptions of the system caused by the failure of individual nodes (e.g., insolvency of one bank). A relatively new strand of literature has started to construct financial networks based on empirical data available at supervisory authorities or hypothetical network structures to investigate the contagious effects of failures of single banks.¹

A basic finding of network theory is that the topology of a network is important for its stability, with the interbank network obviously being no exception.² In this regard, the understanding of the structure and functioning of complex networks has advanced significantly in recent years. In particular, uncovering the working of economic networks is extremely useful, as it sheds light on the structure of interactions among economic agents (cf. Schweitzer et al. 2009). Examples include the world trade network (Fagiolo et al. 2010), job information networks (Ioannides and Loury 2004), and bank-firm networks (De Masi and Gallegati 2012).

In this paper, we focus on one of the most prominent network characteristics, namely the degree distribution, where the degree is the number of (incoming/outgoing) connections per node. Even though the degree distribution does not provide sufficient information for all facets of the structure of the network (Alderson and Li 2007), it is often considered as one of the defining characteristics of different network types. For example, networks with random link formation (Erdös and Renyi 1959, or ER random networks) display Poisson degree distributions, i.e., most nodes have degrees within a relatively narrow range. In contrast, many real-world networks have been reported to display fat-tailed degree distributions: most nodes have a very small degree, but the tail contains nodes with substantially larger degrees (cf. Clauset et al. 2009). This feature is shared by the important class known as scale-free (SF) networks, in which the fraction of nodes with degree $k$ is proportional to $k^{-\alpha }$, where $\alpha$ is the so-called scaling parameter. The term scale-free indicates that there is no typical scale of the degrees, i.e., the mean may not be representative. These networks received considerable attention in the literature due to a number of interesting properties (cf. Caldarelli 2007). One reason for the ‘popularity’ of power-laws in the natural sciences is that they are often the signatures of relatively simple and robust generating mechanisms that might apply to a variety of phenomena. An important feature of such scale-free networks is that they can be described as robust-yet-fragile,³ indicating that random disturbances are easily absorbed (robust) whereas targeted attacks on the most central nodes may lead to a breakdown of the entire network (fragile). Quite interestingly, many interbank networks have been reported to resemble scale-free networks with power-law exponents lying in a relatively narrow range around 2.3 (cf. Boss et al. 2004; Soramäki et al. 2007; De Masi et al. 2006; Cont et al. 2013), even though most papers lack a thorough statistical analysis of the issue,⁴ with Bech and Atalay (2010) being a notable exception. If these findings were robust, the known generating mechanisms for scale-free networks would be strong candidates as mechanisms for the formation of interbank links. Furthermore, the well-known reactions of scale-free networks to disturbances would be of immediate concern for macro-prudential regulation. Thus, taking into account the relevance of such topological features, and the documented over-emphasis on power-law behavior, a more rigorous statistical analysis of the distributional properties of interbank network data should be worthwhile. It needs to be emphasized, though, that there is no strict link between the finding of a power-law degree distribution and the fragility of a (banking) network: First, mechanisms like preferential attachment could be also at work for broad degree distributions that are not exactly of a power-law type. Second, for different definitions of ’fragility’ (number of contagious defaults or total loss of bank capital), the complex interaction between network topology, the structure of shocks as well as the balance sheet structure could lead to different rankings of various network classes in terms of their resilience (cf. Roukny et al. 2013).

The distribution of network degrees is just one example among many phenomena in the natural sciences as well as from the socioeconomic sphere that have been claimed to follow a scaling law (power-law or Pareto law). Other well-known examples include: Zipf’s law for the city size distribution (Gabaix 1999), the distribution of firm sizes (Axtell 2001), the size distribution of innovations (Silverberg and Verspagen 2007), the distribution of output growth rates (Castaldi and Dosi 2009; Fagiolo et al. 2008), or the distribution of large asset returns (Mandelbrot 1963; Krämer and Runde 1996; Lux 2000). While these examples appear to be supported by empirical evidence and meanwhile count as stylized facts, a variety of other findings of power-laws seem more questionable. It appears from a number of recent reviews of power-law methodology and power-law findings (cf. Avnir et al. 1998; Stumpf and Porter 2012) that there had been an over-emphasis on scaling laws and often too optimistic interpretation of statistical findings in the natural sciences. For instance, in a meta-study of power-laws reported in publications in the main physics outlet Physical Review between 1990 and 1996, Avnir et al. (1998) found that most claims of power-laws (aka scaling or fractal behavior) had a very modest statistical footing. As they say ‘$\ldots$ the scaling range of experimentally declared fractality is extremely limited, centered around 1.3 orders of magnitude.’ In terms of statistics jargon, this means that the more typical declaration of a power-law in these publications is based on a partially linear slope in a relatively small intermediate range of the empirical cumulative distribution of some observable.

The power-law exponent (like the ones reported for the degree distribution) is typically obtained by a linear regression in a log–log plot of the cumulative distribution. Obviously, this approach suffers from a number of shortcomings: (i) even if the hypothetical data-generating process is a Pareto distribution, this log–log fit would not be an efficient way to extract the parameter of the underlying distribution. It is actually a method that is definitely inferior to maximum likelihood (which is easy to implement), and results are hard to interpret as, due to the dependency of observations in the log–log plot of the cumulative distribution, the statistical properties of this estimator are not straightforward, (ii) the implicit censoring of the data that is exerted by selecting a scaling range makes it easy to deceive oneself. Many distributions might actually have some intermediate range in their ‘shoulders’ where their cdf looks appropriately linear. But their remaining support (small and large realizations) might display a completely different behavior. Since power-laws in the natural sciences are thought to be interesting if they extent over several orders of magnitude, it is unclear what the interpretation of such an intermediate power-law approximation would be.

Statistical extreme value theory (EVT) provides yet another perspective on power-law behavior. The basic result of this branch of statistics is a complete characterization of the limiting distributions of extremes (maximum or minimum) of time series of iid observations (where results for the iid case have been generalized for dependent processes under relatively mild conditions, cf. Leadbetter 1983; Reiss and Thomas 2007, for details). According to EVT, the appropriately scaled minimum or maximum of a series of observations converges in distribution to one of only three functional forms: the Fréchét, Gumbel, or inverted Weibull distribution. Since extremes are by definition very rare, it is often even more relevant that the tail of a distribution converges in distribution in a similar way to one of three adjoint functional forms. For example, the outer part approaches either a power-law decay, an exponential decay, or a decay toward a fixed endpoint for the three types of extremal behavior, respectively. Power-law behavior is, therefore, a very general form of limiting behavior for the large realizations of a stochastic process. EVT has originally been developed for continuous distribution functions. Since degree distributions are discrete (degrees being integer numbers), it is worthwhile to note that corresponding limit laws for discrete variables are available as well, cf. Anderson (1970). In our context, this might imply that very large realizations of the degree distribution could still decay like a power-law even if the bulk of the distribution does not appear to follow such a distribution (and the implications for the fragility of the system might be similar as for ‘true’ scale-free networks). It is important to emphasize that both the limiting behavior of extremes and tails are stable under aggregation. Hence, data at different levels of (time-) aggregation should obey the same extreme value and tail behavior.

In this paper, we consider interbank networks based on the Italian e-MID (electronic market for interbank deposits) data for overnight loans during the period 1999–2010. Our main focus is to fit a set of different candidate distributions to the degrees for different time horizons. Using daily data over the period 1999–2002, De Masi et al. (2006) reported power-laws for the distribution of in- and out-degrees, with tail parameters 2.7 and 2.15, respectively. Finger et al. (2013) have shown recently that the networks’ properties depend on the aggregation period.⁵ We will, therefore, not confine our analysis to daily data (the basic frequency of our dataset), but also look at the distribution of in- and out-degrees for networks constructed on the base of aggregated data over longer horizons. Quite surprisingly in view of the previous literature, we find hardly any support in favor of previously reported power-laws: at the daily level, the degrees are usually fit best by negative Binomial distributions, while the power-law may provide the best fit for the tail data. However, we typically find very large power-law exponents (with values as large as 7), i.e., levels where the power-law is virtually indistinguishable from exponential decay. At the quarterly level, Weibull, Gamma, and Exponential distributions tend to provide comparable fits for the complete degree distribution, while the tails again tend to display exponential decay. We find comparable results when investigating the distribution of the number of transactions, even though in this case, the tails of the quarterly variables are somewhat fatter. However, the Log-normal distribution typically outperforms the power-law. Overall, these findings indicate that the power-law is typically a poor description of the data, implying that scale-free networks are not an appropriate model for the structure of the Italian interbank network. Moreover, the networks contain a substantial level of asymmetry, related to the low correlation between in- and out-degrees. Additionally, we find that the two variables do not follow identical distributions in general.

The remainder of this paper is structured as follows: Sect. 2 gives a short introduction into (interbank) networks, Sect. 3 briefly introduces the Italian e-MID trading system and gives an overview of the dataset we have access to, Sect. 4 describes our findings, and Sect. 5 concludes and discusses the relevance of these findings for future research.

2 Networks

A network consists of a set of $N$ nodes that are connected by $M$ edges (links). Taking each bank as a node and the interbank positions between them as links, the interbank network can be represented as a square matrix of dimension $N\times N$ (data matrix, denoted D). An element $d_{ij}$ of this matrix represents a gross interbank claim, the total value of credit extended by bank $i$ to bank $j$ within a certain period. The size of $d_{ij}$ can thus be seen as a measure of link intensity. Row (column) $i$ shows bank $i$’s interbank claims (liabilities) toward all other banks. The diagonal elements $d_{ii}$ are zero, since a bank will not trade with itself.⁶ Off-diagonal elements are positive in the presence of a link and zero otherwise.

Interbank data usually give rise to directed, sparse, and valued networks.⁷ However, much of the extant network research ignores the last aspect by focusing on binary adjacency matrices only. An adjacency matrix A contains elements $a_{ij}$ equal to 1, if there is a directed link from bank $i$ to $j$ and 0 otherwise. Since the network is directed, both A and D are asymmetric in general. In this paper, we also take into account valued information by using both the raw data matrix as well as a matrix containing the number of trades between banks, denoted as $\mathbf T$. In some cases, it is also useful to work with the undirected version of the adjacency matrices, $\mathbf A ^u$, where $a_{ij}^u=\max (a_{ij},a_{ji})$.

As usual, some data aggregation is necessary to represent the system as a network. In the following, we define interbank networks by aggregating over daily as well as quarterly lending activity.

3 The Italian interbank market (e-MID)

The Italian electronic market for interbank deposits (e-MID) is a screen-based platform for trading of unsecured money-market deposits in Euros, US-Dollars, Pound Sterling, and Zloty operating in Milan through e-MID SpA.⁸ The market is fully centralized and very liquid; in 2006, e-MID accounted for 17 % of total turnover in the unsecured money market in the Euro area, see European Central Bank (2007). Average daily trading volumes were 24.2 bn Euro in 2006, 22.4 bn Euro in 2007 and only 14 bn Euro in 2008. We should mention that researchers from the European Central Bank have repeatedly stated that the e-MID data are representative for the interbank overnight activity, cf. Beaupain and Durré (2012).

Detailed descriptions of the market and the corresponding network properties can be found in Finger et al. (2013).⁹ In this paper, we used all registered trades in Euro in the period from January 1999 to December 2010. For each trade, we know the banks’ ID numbers (not the names), their relative position (aggressor and quoter), and the maturity and the transaction type (buy or sell). The majority of trades is conducted overnight, and due to the global financial crisis (GFC), markets for longer maturities essentially dried up. We will focus on all overnight trades conducted on the platform, leaving a total number of 1,317,679 trades. If not stated otherwise, the reported results are based on trades conducted between Italian banks only, reducing the total number of trades to 1,215,759.

4 Results

In this section, we present empirical results on the dynamics and distribution of the number of links (degrees) and the number of transactions (ntrans) of individual institutions. The degree of a node gives the total number of links that a bank has with all other banks and can thus be seen as a measure for the importance of individual nodes. Undirected networks imply symmetric adjacency matrices. In this case, bank $i$’s total degree $k_i$ is simply the number of relationships bank $i$ has with other banks, i.e.,

$$\begin{aligned} k_i^{\mathrm{total}} = \sum _{j \ne i} a_{ij}^u. \end{aligned}$$

(1)

For directed networks, we differentiate between incoming links (bank $i$ borrows money from other banks) and outgoing links ($i$ lends money to other banks), and define the in- and out-degree of $i$ ($k_i^{\mathrm{in}}$ and $k_i^{\mathrm{out}}$) as

$$\begin{aligned} k_i^{\mathrm{in}}&= \sum _{j \ne i} a_{ji}\nonumber \\ k_i^{\mathrm{out}}&= \sum _{j \ne i} a_{ij}, \end{aligned}$$

(2)

respectively. Note that our networks contain only banks with at least one (directed) link. In this way, the total degree of a sample bank is always at least equal to one, while it may be the case that either the in- or out-degree equals zero for a particular bank. Since we ignore zero values in the distribution fitting approach, this affects the number of observations for the different variables.

For daily data, a link $a_{ij}$ simply equals 1 if there has been a credit extended from bank $i$ to $j$ on that specific day. In the rare case of multiple loans granted between identical counterparties in the same direction, the link count also remains equal to 1. However, when counting the number of transactions (see below), multiple loans are summed up to give the statistics of transactions between counterparties during a certain period of time. Moving from daily to longer horizons, links remain dichotomous quantities, i.e., $a_{ij} = 1$ means that at least once (but may be multiple times) a loan has been granted by bank $i$ to bank $j$. The number of transactions, however, count the overall number of such loans over a month, quarter, etc.

For the number of transactions, we use similar definitions based on the T matrix, with each element $t_{i,j}$ giving the number of trades with credit extended from bank $i$ to bank $j$. To be precise, we calculate the number of in-/out-transactions as the sum over all loans received or granted by bank $i$ over a certain time horizon:

$$\begin{aligned} n_i^{\mathrm{in}}&= \sum _{j \ne i} t_{ji}\nonumber \\ n_i^{\mathrm{out}}&= \sum _{j \ne i} t_{ij}. \end{aligned}$$

(3)

Additionally, we analyze the total number of transactions, for simplicity defined as the sum of in- and out-transactions

$$\begin{aligned} n_i^{\mathrm{total}}=n_i^{\mathrm{in}}+ n_i^{\mathrm{out}}. \end{aligned}$$

(4)

4.1 Dynamics of the degrees and number of transactions

Before investigating the distribution of the variables under study, we provide a brief overview of their dynamics over time, restricting ourselves to quarterly data here. Figure 1 shows the in-/out-degrees (left) from the directed networks and the total degrees from the undirected networks (right). The upper left panel shows the mean and median in-degree and out-degrees over time.¹⁰ Clearly, the mean values are decreasing over time, and so does the median in-degree which is mostly very close to the mean value. For both series, we find a significant structural break after quarter 10. In contrast, the median out-degree fluctuated around an average value of roughly 17 over most of the sample period, but with a significant structural break after quarter 39 due to the GFC. These values are considerably smaller than the values for the in-degree, pointing toward a substantial level of skewness in the out-degree distribution. Thus, the distributions of in- and out-degrees are likely to be not identical. The lower left panel shows the relative mean and median degree over time, i.e., the values in the upper panel standardized by the number of nodes active in each quarter. We see that the negative trend in the upper panel is mostly driven by the negative trend in the number of active banks. Thus, the standardization appears to make the in-degrees of different quarters comparable. This is less so for the median out-degree, which is far more volatile over the sample period.¹¹ For the sake of completeness, the corresponding values for the degrees from the undirected networks are shown on the right-hand side. Both for the absolute and relative values, the mean and median values are very similar, except for the beginning of the sample period. This is driven by the high level of asymmetry in the out-degree distribution for the first half of the sample, which appears to decrease later on.

Fig. 1

Mean and median degree over time. Left In- and out-degree. Right Total degree. Top Absolute levels. Bottom standardized values (divided by the number of active banks per quarter)

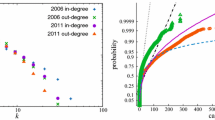
What does the evidence on the differences between the in- and out-degree distributions imply? Given that many studies on interbank markets work with undirected networks, these studies entail the implicit assumption of a high correlation between in- and out-degrees of individual banks. The left panel of Fig. 2 shows a scatter plot of in-degree against out-degree for Italian banks, showing a small correlation of .0899 for all observations. For single quarters, we find that the correlation between these measures may be very small, at times even negative. Thus, banks with a high in-degree do not necessarily have a high out-degree and vice versa. The directed version of the network, thus, contains a considerable amount of information. The right panel of Fig. 2 indeed shows a relatively monotonic decline of the correlation over time. This implies that banks have become more ‘specialized,’ i.e., in any quarter, they appear to enter the market predominantly as lenders or borrowers.

For the number of transactions, Fig. 3 shows the dynamics of the mean and median in-/out-ntrans (left) and the total ntrans (right). The upper left panel shows that the average number of transactions per bank is close to 200 during most quarters, but significantly decreases during and after the GFC. For both variables, the median values are substantially smaller than the mean, which hints toward a high level of skewness. Again, substantial differences in the median values indicate that the in- and out-variables are unlikely to follow identical distributions. The bottom left panel shows the standardized mean and median values. Quite interestingly, the somewhat negative trend of the variables vanishes, except for the GFC period. The same observation applies to the total number of transactions on the right panels. The results concerning the correlation between in- and out-transactions are comparable to those for the degrees (not reported).

Fig. 2

Left Scatter plot of in- versus out-degree. Correlation .0899. Right Correlation between individual banks’ in- and out-degree over time. Italian banks only

Fig. 3

Mean and median number of transactions over time. Left Directed network. Right Undirected network. Top absolute levels. Bottom standardized values (divided by the number of active banks per quarter)

4.2 The degree distributions

Due to the change in the size of the Italian interbank network, and the detection of two candidates for significant structural breaks during our sample period, we split the dataset into three periods: Period 1 covers quarters 1–10, period 2 covers quarters 11–39, and period 3 covers the remaining quarters 40–48.¹² Assuming that the realizations of single days (quarters) are iid draws (or weakly dependent ones) from the same underlying data-generating process, allows us to pool the data of the three subperiods into larger samples for the in-, out-, and total degrees (ntrans) of active banks, respectively. We use both daily and quarterly aggregates, i.e., construct variables that count the number of unique counterparties (degree) and total number of transactions (ntrans) for each bank within each day and quarter, respectively.¹³ For the daily (quarterly) data, this amounts to a total of 96,892 (1780), 188,582 (3,369), and 41,775 (843) pooled observations for the three periods, respectively. For the sake of completeness, we also show the results when pooling all observations for the three time periods (1–3) for each degree measure. We should stress that pooling observations from several periods is crucially necessary in order to obtain reliable parameter estimates, in particular for daily data. We will elaborate on this issue in more detail in the next section.

As a first step, we compare the in- and out-degree distributions and check whether they could be realizations from the same underlying distribution. Figure 4 shows the histograms of the in-, out-, and total degrees for the different time periods using quarterly data. We see that the histograms look very different when comparing in- and out-degrees for each sample period. We should note that a substantial fraction of observations equals zero, both for in- and out-degrees. While the in-degree histograms appear to have a certain hump-shape, the out-degrees look more like a slowly decaying function with monotonic decline of probability from left to right. Furthermore, the L-shaped form of the out-degree distributions appears to be more stable over time, even though the scale on the $x$-axis changes substantially. Individual Kolmogorov–Smirnov (KS) tests provide further evidence against the equality of in- and out-degree distributions for all sample periods. The KS test allows to check whether two variables follow the same probability distribution, and also whether any variable follows a certain specific distribution. In our case, the KS test statistic is calculated as

$$\begin{aligned} {{\mathrm{KS}}}_{n}=\sup _x\,|F_{1,n}(x) - F_{2,n}(x)|, \end{aligned}$$

(5)

where $\sup _x$ denotes the supremum of all possible values, while $F_{1,n}(\cdot )$ and $F_{2,n}(\cdot )$ are the empirical distribution functions of the sample of in-degrees and out-degrees, respectively. At all sensible significance levels, we have to reject the null hypothesis of the equality of both distributions. Similar observations can be made when pooling all observations across the three subperiods, see Fig. 5.

Fig. 4

Quarterly data, degree. Histograms for in-degree (left), out-degree (center), and total degree (right) for Period 1, 2, and 3

Figure 6 shows the complementary cumulative distribution functions (ccdf) for the quarterly degree measures for all sample periods on a log–log scale, the typical way to represent data when suspecting power-law decay. Note that for a power-law, these ccdfs would be straight lines, which upon inspection seems unlikely to provide a good approximation to any of our subsamples, even for the tail regions. Again the distributions of in- and out-degrees look quite different in general, even though the shapes of the tail regions appear to be more homogeneous than what one might have expected after inspection of the raw data in Figs. 4 and 5. Similar arguments hold for the distribution of total degrees, which has a somewhat similar shape as the in-degree distribution. For this reason, we will mostly restrict ourselves to comment on the results for the in- and out-degrees, respectively. We also show the ccdfs for the daily observations in Fig. 7. Again, it is hard to detect a linear decay for most samples, at least not over several orders of magnitude.

Fig. 5

Quarterly data, degree. Histograms for in-degree (left), out-degree (center), and total degree (right) using all observations

Fig. 6

Quarterly data, degree. Complementary cumulative distribution functions (ccdf) for degrees: in-degree (left), out-degree (center), and total degree (right) for all time periods on a log–log scale

Fig. 7

Daily data, degree. Complementary cumulative distribution functions (ccdf) for degrees: in-degree (left), out-degree (center), and total degree (right) for all time periods on a log–log scale

4.2.1 Distribution fitting approach

Our basic approach is to fit a number of candidate distributions in order to investigate which distribution describes the data ‘best’ in a statistical sense. We should note that, similar to the approach in Stumpf and Ingram (2005), we use both discrete and continuous candidate distributions, implying that for the latter, we treat the degrees as continuous variables. The candidate distributions, always fitted using maximum likelihood (ML), are:

• the Exponential distribution, with parameter $\lambda >0$ (rate),

• the Gamma distribution, with parameters $k>0$ (shape) and $\theta >0$ (scale),

• the Geometric distribution, with probability parameter $p \in [0,1]$,

• the Log-normal distribution, with parameters $\mu$ (scale) and $\sigma >0$ (shape),

• the negative Binomial distribution, with parameters $r> 0$ (number of failures) and $p \in [0,1]$ (success probability),

• the Poisson distribution, with parameter $\lambda >0$,

• the discrete power-law or Pareto distribution, with parameters $x_m>0$ (scale) and $\alpha >0$ (shape),

• the Weibull or stretched exponential distribution, with parameters $\lambda >0$ (scale) and $k >0$ (shape).

We should note that a large part of the literature focuses on fitting the power-law only, in particular when the ccdfs have an apparently linear shape. Given that this is not the case here, we test a number of alternative distributions to find the distributions that fit the data best. Nevertheless, even though the power-law might not be a good description of the complete distribution, it could still provide a good fit of the (upper) tail region. Therefore, we conducted two sets of estimations of the above distributions for each sample: first, we fitted the complete distribution using all entries of our samples. Here, we should stress that several of the distributions have strictly positive support, while the others also allow for the occurrence of zero links. For the sake of consistency, we will therefore only use nonzero values for the degree and ntrans variables in the following.¹⁴ This means, for some distribution functions, we are using truncated variables in general (both for the complete and tail observations) and need to adjust the ML estimators for these distributions accordingly, cf. Appendix 1. In a second step, we explicitly fitted three of the eight candidate distributions, namely the Exponential, the Log-normal, and the power-law, to a certain upper tail region for each period and variable (the other candidates would obviously make little sense as tail distributions). There are different possibilities to identify the ‘optimal’ tail region. Here, we employ the approach of Clauset et al. (2009), which has been demonstrated to yield reliable estimates of both power-law parameters for certain distributions converging to Paretian tail behavior. The basic idea of this approach is to find the optimal tail parameter for all possible cutoff points using ML, where the optimal $x_m$ is the one corresponding to the lowest KS statistic. Details can be found in Appendix 2.¹⁵ The tail region is then defined by the scale parameter $x_m$, and the all candidate tail distributions are fitted to all observations where $x \ge x_m$. Note that this approach gives an obvious advantage to the fit of the power-law in the ‘tail’ region. Quite surprisingly, however, in many cases, the power-law is not the best description of the data tailored in this way as we will see below.

In these goodness-of-fits (GOF) experiments, we first estimate the parameters for each candidate distribution, both for the complete dataset and the upper tail region, respectively, using ML. Using these parameters, we calculate the KS test statistic for each candidate distribution and take the one with the lowest value as the ‘best’ fit of the respective data.¹⁶ As a last step, we evaluate the GOF of this candidate distribution based on the KS test statistic. Given that the critical values of the KS distribution are only valid for known distributions (i.e., without estimating parameters), we have to perform individual Monte Carlo exercises.¹⁷ In these exercises, we randomly sample many degree sequences from the best fitting distributions with their estimated parameter values and then calculate the KS test statistic of these synthetic datasets. The reported $p$ values count the relative fraction of observations larger than the observed ones, such that low $p$ values (say 5 %) indicate that the pertinent distribution can be rejected. We should stress that we carry out this analysis only for the best fitting distribution, since the remaining ones have already been found to be inferior under the KS criterion. Details on the Monte Carlo design can be found in Appendix 3.

In the following, we will use this approach to investigate the distribution of degrees and number of transactions for both daily and quarterly aggregates. Already at this point, we should stress that the GOF tests mostly indicate that the distributions have to be rejected at traditional levels of significance for the complete samples, while the fits to the tail tend to perform better. This finding is, however, strongly driven by the significantly smaller number of observations for the tail data, which yields relatively large and more volatile KS statistics compared to the complete distributions.

4.2.2 Daily data

We start our analysis with the daily degree data for which earlier studies have reported power-laws (De Masi et al. 2006). Before turning to the results, we need to stress several complicating issues arising from network data in general, and our data in particular. For example, Stumpf and Porter (2012) note that ‘[a]s a rule of thumb, a candidate power-law should exhibit an approximately linear relationship on a log–log plot over at least two orders of magnitude in both the $x$ and $y$ axes. This criterion rules out many datasets, including just about all biological networks.’ In this sense, finite and possibly very small network sizes make it hard to provide evidence for scale-free networks (Avnir et al. 1998; Clauset et al. 2009).

For our data, Fig. 8 shows the maximum in- and out-degrees for the individual days over time. We see that the criterion of Stumpf and Porter (2012) is typically violated. Thus, it should be hard to find evidence in favor of the power-law hypothesis for the complete distributions. Additionally, the number of observations in the ‘tail’ of the data for a single day becomes very small leading to large fluctuations of estimates across days and large error bands of single estimates. These issues highlight the importance of applying rigorous statistical methods to identify the best fitting distributions, i.e., simply identifying a linear slope of the ccdf on a log–log scale might easily be misleading. Similar remarks also apply for the daily ntrans variables (see below), while quarterly data are typically slightly less problematic.

Fig. 8

Daily data. Maximum in- and out-degrees over time

To highlight our previous comments, Figs. 9 and 10 show the distribution of the estimated daily power-law parameters for the complete and tail observations, respectively, for all sample days. For the complete daily samples, the results are very stable over time and across types of degrees, cf. Fig. 9. In fact, we will see that this stability tends to carry over to the complete distributions of the aggregated data as well. In contrast, there is a substantial level of heterogeneity for the power-law exponent of the tail observations for the individual days, cf. Fig. 10. Thus, we cannot confirm previously reported findings of ‘interesting’ tail parameters between 2 and 3 for any of the degree variables.¹⁸ While numerous observations lie within this range, for many days, we find substantially larger values, at times as large as 7.¹⁹ Apparently, the daily tail data are too noisy to identify a ‘typical’ tail parameter, cf. Fig. 11.²⁰ The mismatch between the narrow range of values obtained for the complete dataset of single days and the broad range of estimates for their tail might also indicate that the former are mainly determined by the more central part of the distribution.

Fig. 9

Daily data, degree. Histograms for the power-law exponents for the complete distributions, in-, out-, and total degree, respectively

Fig. 10

Daily data, degree. Histograms for the power-law exponents for the tail observations, in-, out-, and total degree, respectively

Fig. 11

Daily data, degree. Total number of observations (complete) and number of tail observations for out-degree

Since data for single days are too scarce to allow reliable parameter estimation, pooling observations over longer horizons might be advisable to obtain better estimates. This, of course, requires the assumption of daily data being drawn independently from the same underlying distribution, or only with weak dependence on adjacent observations. While it is not straightforward to check this assumption for complete daily ensembles (as opposed to a time series of univariate daily data), we have made some attempt at checking for statistical breaks for averages of degree statistics and have cut our complete sample into subsamples accordingly. Note also that any analysis of a network structure would be more or less futile, if we could not assume some stationarity of the structural characteristics of the network. Fricke and Lux (2014) demonstrate that the e-MID network is indeed structurally stable along many dimensions.

We report our estimation results for the pooled daily data in Tables 1, 2, and 3. Our main finding is that the negative Binomial distribution provides the best fits (in bold) for all daily degree measures and for all samples (i.e., the complete samples and the three subsamples identified via tests for structural breaks), cf. Table 1. The results from the GOF experiments indicate, however, that the best fitting candidate distributions have to be rejected. Therefore, even the winner among the candidate distributions appears to be an unlikely description of the data. We should also stress that the fit of the power-law is usually rather poor, competing with the Poisson distribution for the worst description of the data. Similar to the findings for the individual days, the estimated tail parameters are between 1.5 and 1.6, cf. Table 2 (top, complete). Figure 7 together with the relatively poor KS statistics for estimated power-laws suggests that estimates in the scaling range 1–2 are obtained as very inaccurate straight lines fitted to a strongly curved distributional shape. Moving to the tail observations, we find that Exponential and power-law distributions tend to provide the best fit for all variables, cf. Table 3. Thus, it appears that the power-law is a better description of the tail observations - a usual finding for many datasets. In contrast to the complete distributions, the GOF experiments suggest that the estimated distributions are mostly not rejected for the tail observations.²¹ Upon closer inspection, however, we see the KS statistics of the Exponential and the power-law are typically close to each other, in particular when the tail exponents are very large, cf. Table 2 (top, complete). Even though the power-law appears to provide the best fit for some of the tail data, the very large parameter values (larger than 4, often close to 7) are in a range where the power-law becomes almost undistinguishable from exponential decay. Often such high values would be obtained spuriously from distributions with an exponential decline as semi-parametric estimators of the tail index would not be able to ‘identify’ the limit of $\alpha \rightarrow \infty$. The huge difference in estimated power-law parameters for the complete sample compared to the tail also indicates that the empirical distribution shows pronounced curvature (actually confirming the visual inspection of absence of a linear slope over the complete support and very fast decline at the end in Fig. 7). On the other hand, it is also interesting to remark that the estimated coefficients are relatively uniform for both the complete sample and the tail, respectively, across periods and for all the measures of degree. This speaks of relatively uniform shapes of the distributions, at least in view of this simple statistic. Summing up, the power-law distribution appears to be a poor description of the data, both for the complete distribution and the tail observations (where it more or less coincides with an Exponential for the high estimates of the tail index). We also need to stress that the identified power-law exponents, both for individual days and pooled observations, are far off from those reported in an earlier study. It is not clear how these estimates were obtained.

Table 1 Daily data, degree. KS statistic for the candidate distributions (complete data)

Table 2 Power-law parameters and standard errors, degree

Table 3 Daily data, degree. KS statistic for the candidate distributions (tail)

4.2.3 Quarterly data

The results for the quarterly data are shown in Tables 4 and 5. Weibull distributions typically provide the best fits for the in- and total degrees, while Exponential and Gamma distributions yield comparable fits as the Weibull for the out-degrees. Similar to the complete distributions for the daily data, the optimal fits are typically rejected at the 5 % significance level, except for three cases. Again, the best fits appear to be unlikely descriptions of the observed data. The power-law exponents for the complete sample are again quite small, typically between 1.25 and 1.3, cf. Table 2 (bottom, complete). Turning to the tail observations, we find that Exponential distributions provide the best fits in all but two cases (in-degree in period 1, out-degree in period 1). Similar to the daily observations, for the best fits of the tail data, the pertinent distributions cannot be rejected as the ‘true’ data-generating process at the 95 % significance level. The poor fit of the power-law again comes along with relatively large tail exponents, cf. Table 2 (bottom, tail). In summary, similar to the daily data, we do not find convincing evidence in favor of a power-law distribution.

Table 4 Quarterly data, degree. KS statistic for the candidate distributions (complete)

Table 5 Quarterly data, degree. KS statistic for the candidate distributions (tail)

4.2.4 Robustness and discussion

A reason for not finding evidence for power-law distributions may be the fact that we focus on the subnetwork formed by Italian banks only. Stumpf et al. (2005) have shown that (randomly chosen) subnetworks of scale-free networks are in fact not scale-free. Therefore, we also checked the distributions including foreign banks as well, similar to the existing papers using the e-MID data. We found that the results (including the tail parameters) remain qualitatively unaffected (not reported). These findings indicate again that the networks including all banks are unlikely to be scale-free, and that our previous findings for Italian banks alone are not biased due to random sampling from a larger scale-free network (indeed, it seems very unlikely that the Italian banks should constitute a random set from the overall sample of all banks). Then, it comes as no surprise that the subnetworks formed by Italian banks only are also not scale-free. In fact, it is remarkable that there appears to be no significant qualitative effect of incorporating foreign banks or not.

In Finger et al. (2013) it has been shown that the quarterly e-MID networks are more complete representations of the underlying ‘latent’ network structure, whereas daily networks might be seen as random activations of parts of the more complex, hidden structure. Under this perspective, the lack of coincidence of the fitted distributions for different levels of time aggregation might not be too surprising.

Summing up, our results indicate that the power-law hypothesis needs to be tested more thoroughly for other networks in general and the interbank network in particular, with the power-law being one of many candidate distributions. The findings are in line with other studies casting doubts on certain claims of power-law and scaling behavior in a broad range of empirical studies (cf. Avnir et al. 1998).

4.3 The distribution of the number of transactions

Note that the quarterly degree of a given bank is not the simple sum of its daily degrees, since a link that has been activated many times over a quarter is counted only as one link on the quarterly level of network activity. If we consider the number of links in the daily data as (possibly power-law distributed) random variables, the number of transactions over a longer time horizon is, in fact, what we obtain from simple aggregation of the daily degrees observed for any bank $i$. Assuming that the degrees of all banks are drawn from the same distribution, we obtain in this way a sample of sums of random variables following the same underlying distribution. Note that we would expect a power-law at the daily level to survive in the aggregation process for an iid random process of link formation as well as for various extensions allowing for ‘weak’ dependency.²² The extremal behavior of the distribution of degrees should, therefore, be preserved in the distribution of the number of transactions over longer horizons. We turn to the analysis of this quantity in this subsection.

Note also that the finite size of the network might pose a problem due to the effective imposition of an upper limit on the observable degrees. It might, therefore, be the case that a scale-free distribution is just hard to verify because of the small number of observations combined with the relatively narrow range of observed values. In contrast, the aggregated ntrans variables have the advantage that they have no obvious upper bound, so testing the power-law hypothesis might be more sensible in this case.

Figures 12 and 13 show the ccdfs of the quarterly and daily ntrans variables. Again, linear decay over several orders of magnitude is hard to detect visually. However, at least for the quarterly data, we see that the variables under study span several orders of magnitude, making the data more useful candidates for our distribution fitting approach.

Fig. 12

Quarterly data, ntrans. Complementary cumulative distribution functions (ccdf) for the number of transactions: in-trans (top), out-trans (center), and total trans (bottom) for all time periods on a log–log scale

Fig. 13

Daily data, ntrans. Complementary cumulative distribution functions (ccdf) for the number of transactions in-trans (top), out-trans (center), and total trans (bottom) for all time periods on a log–log scale

For daily data, the range of the observed variables remains rather limited, even though the maximum value is roughly twice the one for the degrees (not reported). Since for daily realizations of the number of transactions we find virtually identical results to those of the daily degrees, we abstain from presenting these here, and immediately turn to quarterly aggregated observations.

We show the results in Tables 7 and 8, finding that negative Binomial, Gamma, and Weibull distributions appear among the best fits, depending on the concept (in-, out-, or total transactions) and the period considered. However, their KS statistics are typically at a comparable level. The results from the GOF experiments show that the best fitting distributions are nevertheless rejected as data-generating processes (exception: total ntrans in period 3). Again, the fit of the power-law is very poor in general, with tail parameters around 1.20, cf. Table 6, and KS statistics that consistently come in second to last (with the Poisson distribution performing worst). Moving to the quarterly tail data, we find that in most cases, the Log-normal provides the best fit (exceptions: out-degree for the complete sample and total degree in period 3). This is quite surprising, given that the scaling parameters now lie in the ‘typical’ range for power-laws, here between 2.21 and 3.68. Therefore, even though the power-law estimates appear more sensible, the power-law distribution is inferior by some margin in fitting the tail data (with a cut-off determined by the best-fitting Pareto law) to the Log-normal, and sometimes also to the Exponential. As with the previous cases, the results from the GOF experiments indicate that the best fitting tail distributions usually cannot be rejected via KS tests with Monte Carlo distributions. While it is well known that it is hard to distinguish Log-normal from power-law tails, these findings raise doubts on the universality of power-law tails and highlight the need for thorough statistical approaches for testing the power-law hypothesis.

Table 6 Power-law parameters and standard errors, ntrans

Table 7 Quarterly data, ntrans. KS statistic for the candidate distributions (complete data)

Table 8 Quarterly data, ntrans. KS statistic for the candidate distributions (tail)

As another robustness check, we investigated the distribution of transaction volumes (tvol), cf. Appendix 4, again differentiating between in-tvol, out-tvol, and their sum (total tvol), respectively. While the tails of the tvol variables are typically much fatter compared to the degree and ntrans variables, the power-law remains a poor description both for daily and quarterly data.

5 Conclusions

In this paper, we have revisited the distributional properties of interbank loans for the Italian interbank network during the years 1999–2010. Using both the degrees and the number of transactions, we fitted a set of different candidate distributions to these data for daily and quarterly aggregates, respectively. Given that the daily networks have previously been suggested to be scale-free (De Masi et al. 2006), it comes as a surprise that we find no evidence in favor of the power-law hypothesis: at the daily level the degrees are usually fit best by negative Binomial distributions, while the tails tend to decay exponentially, i.e., the fitted power-laws display very large tail parameters. At the quarterly level, Weibull, Gamma, and Exponential distributions tend to provide comparable fits for the complete degree distribution, while the tails again tend to display exponential decay. For the number of transactions, we find comparable results, even though the tails of the quarterly data appear to be fatter. However, in this case, the Log-normal distribution usually outperforms the power-law. Moreover, we found that the networks are characterized by a substantial level of asymmetry, as exemplified by the low correlation between in- and out-degrees. We also find that the two variables do not follow identical distributions in general.

Overall these findings indicate that the power-law is typically a poor description of the data. This implies that preferential attachment and related data-generating processes are not supported by the empirical shape of the degree distribution that appears very far from the implied power-law structure. Note that these findings are also not in line with a large part of the empirical (interbank) network literature for other datasets, raising doubts on the universality of scale-free behavior of interbank networks. Our results indicate that the power-law hypothesis needs to be tested more thoroughly for other networks in general and the interbank network in particular. The findings are related to other studies casting doubts on certain claims of power-law and scaling behavior in a broad range of empirical studies (cf. Avnir et al. 1998; Stumpf and Porter 2012), and it seems possible that claims of scale-free behavior of interbank lending activity may not survive under closer statistical scrutiny.

Appendices

Appendix 1: Truncated distributions and maximum likelihood

The distribution fitting approach described in the main text involves fitting a set of candidate distributions with possibly differing support. For example, some distributions have support at zero, while others do not. Similarly, when focusing on the tail observations, we have to get rid of the probability mass below the cutoff point in order to accurately calculate the statistics. Therefore, we describe the use of truncated distributions and ML fitting in this Appendix in more detail.

1.1 Normalization

When working with truncated variables, we need to make sure to use the correct pdfs and cdfs, since the ML estimation and the evaluation of the fit (KS statistic) depend on them. In order to illustrate this issue, let variable $x$ have the pdf $p(x)$ with support $[0,\infty ]$. As usual, the cdf is defined as

$$\begin{aligned} P(a)=P(X \le a) = \int _0^a p(x) \mathrm{d}x. \end{aligned}$$

(6)

Now, suppose the data are (left-)truncated at some value $x_m$, i.e., the variable $\tilde{x}$ follows the same distribution as $x$, but the pdf has limited support $[x_m,\infty ]$ with minimum value $x_m >0$. For our purposes, it is therefore useful to define the quantity

$$\begin{aligned} P_<(a)=P(X < a) = 1 - \int _a^{\infty } p(x) \mathrm{d}x, \end{aligned}$$

(7)

or more compactly

$$\begin{aligned} P_<(a)= P(a)-p(a). \end{aligned}$$

(8)

We can properly construct the pdf of $\tilde{x}$, say $\tilde{p}$, as

$$\begin{aligned} \tilde{p}(x)={\left\{ \begin{array}{ll} \frac{p(x)}{1-P_<(x_m)}, &{}\quad \text {if }\,\, x \ge x_m\\ 0, &{}\quad \text {else.} \end{array}\right. } \end{aligned}$$

(9)

where the denominator distributes the probability mass of $p(x)$ among the support of $\tilde{x}$.

For the calculation of the KS statistics, we also need the adjusted cdf. For the supported values of $\tilde{x}$ it takes the form

$$\begin{aligned} \tilde{P}(x)=\int _{x_m}^x \frac{p(x)}{1-P_<(x_m)} \mathrm{d}x = \frac{1}{1-P_<(x_m)} \int _{x_m}^x p(x) \mathrm{d}x, \end{aligned}$$

(10)

or

$$\begin{aligned} \tilde{P}(x)=\frac{P(x)-P_<(x_m)}{1-P_<(x_m)}, \end{aligned}$$

(11)

which can be easily evaluated.

1.2 Maximum likelihood for truncated variables

Using the previous definitions, we can show that the ML estimator for left-truncated variables does not coincide with the standard estimator. The standard ML estimator, i.e., using a sample of $n$ observations of $x$ and denoting by $\theta$ the vector of parameters, can be written as

$$\begin{aligned} L(\theta |x_1,\ldots ,x_n)=p(x_1,\ldots ,x_n|\theta )=\prod _i^n p(x_i | \theta ), \end{aligned}$$

(12)

or in logs

$$\begin{aligned} \ln (L)=\sum _i^n \ln [p(x_i | \theta )]. \end{aligned}$$

(13)

Using the definitions from above, we can show that the ML estimator for left-truncated variables differs from the one in Eq. (13). Using Eq. (9), we can write the likelihood as

$$\begin{aligned} L=\prod _i^{\tilde{n}} \tilde{p}(x_i | \theta ) = \prod _i^{\tilde{n}} \frac{p(x|\theta )}{1-P_<(x_m | \theta )}, \end{aligned}$$

(14)

where $x$ ignores those observations smaller than $x_m$ and the total number of observations is $\tilde{n}$ instead of $n$. Taking logarithms we obtain

$$\begin{aligned} \ln (L)=\sum _i^{\tilde{n}} \ln \left[ \frac{p(x_i | \theta )}{1-P_<(x_m | \theta )}\right] = \sum _i^{\tilde{n}} \ln [p(x_i | \theta )] - \sum _i^{\tilde{n}} \ln [1-P_<(x_m | \theta )], \end{aligned}$$

(15)

which can be written as

$$\begin{aligned} \ln (L)= -\tilde{n} \ln [1-P_<(x_m | \theta )] + \sum _i^{\tilde{n}} \ln [p(x_i | \theta )]. \end{aligned}$$

(16)

The second part of this equation looks familiar, as it corresponds to Eq. (13) for the $\tilde{n}$ observations with values $\ge x_m$. However, the normalization term on the left does not vanish (as it depends on the parameter vector) and affects the location of the ML estimator. Therefore, we need to find the $\theta$ that maximizes Eq. (16). The standard ML estimator would not be efficient.

Appendix 2: Discrete power-laws and parameter estimation

This presentation is mostly based on Clauset et al. (2009).

1.1 Discrete power-laws

A power-law distributed variable $x$ obeys the pdf

$$\begin{aligned} p(x) \propto x^{-\alpha }, \end{aligned}$$

(17)

where $\alpha >0$ is the tail exponent with ‘typical’ interesting values in the range between 1 and 3. In many cases, however, the power-law only applies for some (upper) tail region, defined by the minimum value $x_m$. While it is common to approximate discrete power-laws by the (simpler) continuous version, for our (integer-valued) data, we employ the more accurate discrete version in the paper.²³

In the discrete case, the cdf of the power-law can be written as

$$\begin{aligned} P(x)=\frac{\zeta (\alpha ,x)}{\zeta (\alpha ,x_m)}, \end{aligned}$$

(18)

where

$$\begin{aligned} \zeta (\alpha ,x_m)=\sum _{n=0}^\infty (n+x_m)^{-\alpha } \end{aligned}$$

(19)

is the generalized or Hurwitz zeta function.

1.2 Estimation of $\alpha$ and $x_m$

For a given lower bound $x_m$, the ML estimator of $\alpha$ can be found by direct numerical maximization of the log-likelihood function

$$\begin{aligned} \mathcal {L}(\alpha )=-n \ln [\zeta (\alpha ,x_m)] - \alpha \sum _{i=1}^n \ln [x_i], \end{aligned}$$

(20)

where $n$ is the number of observations.²⁴ For simplicity, we approximate the standard error of the estimated $\hat{\alpha }$ (for $\hat{\alpha }>1$) using the closed-form solution based on continuous data.²⁵ Neglecting higher-order terms, this can be calculated as

$$\begin{aligned} \sigma =\frac{\hat{\alpha }-1}{\sqrt{n}}. \end{aligned}$$

(21)

However, the equations assume that $x_m$ is known in order to obtain an accurate estimate of $\alpha$.²⁶ When the data span only a few orders of magnitude, as usual in many social or complex systems, an underpopulated tail would come along with little statistical power. Therefore, we employ the numerical method proposed by Clauset et al. (2007) for selecting the $x_m$ that yields the best power-law model for the data. To be precise, for each $x_m$ over some reasonable range, we first estimate the scaling parameter using Eq. (20) and calculate the corresponding KS statistic between the fitted data and the theoretical distribution with the estimated parameters. The reported $x_m$ and $\alpha$ are those that minimize the KS statistic, i.e., minimize the distance between the observed and fitted probability distribution. According to Clauset et al. (2007, 2009), minimizing the KS statistic is generally superior to other distance measures, e.g., likelihood-based measures such as AIC or BIC.

Appendix 3: Goodness-of-fit test for the estimated distributions

Since the distribution of the KS statistics is unknown for the comparison between an empirical subsample and a hypothetical distribution with estimated parameters, we carry out a Monte Carlo approach. We sample synthetic datasets from the estimated distribution, compute the distribution of KS statistics, and compare the results to the observed value for the original dataset. If the KS statistic of the empirical dataset is beyond the $\alpha$ percent quantile of the Monte Carlo distribution of KS values, we reject the pertinent distribution at the $1-\alpha$ level of significance. In our results, we indicate significant fits at the 5 % confidence level using asterisks. We should stress that we carry out this (very time-consuming) GOF experiment only for the distribution with the minimum KS statistic for each sample and variable, respectively. This can be justified by the fact that, even though other candidate distributions may not be rejected as well, they are clearly inferior to the optimal distribution in terms of the KS statistic.

Fig. 14

Quarterly data, tvol. Complementary cumulative distribution functions (ccdf) in-tvol (top), out-tvol (center), and total tvol (bottom) for all time periods on a log–log scale

Fig. 15

Daily data, tvol. Complementary cumulative distribution functions (ccdf) in-tvol (top), out-tvol (center), and total tvol (bottom) for all time periods on a log–log scale

Appendix 4: Distributional properties of transaction volumes

Here, we report the results using another important measure for interbank networks, namely the transaction volumes (tvol). We use the same distribution fitting approach as before, differentiating between in-tvol, out-tvol, and their sum (total tvol), respectively. Figures 14 and 15 show the ccdfs for the quarterly and daily variables on a log–log scale. We should stress that the minimum trade size on the e-MID market is 50,000 Euros. In order to run our estimation procedure in a reasonable amount of time, we rescale the tvol variables by a factor of $10^{-6}$ such that a transaction size of 50,000 is represented by a value of .05.²⁷ We then round the tvol variable toward the nearest integer (otherwise the discrete candidate distributions could not be accurately evaluated), again ignoring zero values. In this way, we restrict our samples to relatively large transaction volumes with at least 500,000 Euros, represented by positive integer values. Note that, besides the upward bias of the data and the fact that the data now span several orders of magnitude, it is again hard to visually detect linear decay over several orders of magnitude in the ccdfs. We should also stress that we did not perform the GOF exercise for the tvol variables, since it is too time-consuming in this case.

1.1 Daily data

Tables 9, 10, and 11 show the results for the daily data. The complete distributions are now usually fitted best by Log-normal distributions, whereas the fit of the power-law is very poor in general. The power-law parameters are again very small, with typical values around 1.22, cf. Table 10 (top, complete). For the tail observations, the best fit again is always provided by Log-normal distributions, cf. Table 11. Interestingly, the tail exponents of the daily data are within the typical range of meaningful power-laws, cf. Table 10 (top, tail), but the power-law is still not the best description of the data. In the end, for the transaction volumes, we find no evidence in favor of power-laws.

Table 9 Daily data, tvol. KS statistic for the candidate distributions (complete)

Table 10 Power-law parameters and standard errors, tvol. Values obtained via numerical maximization of the log-likelihood for discrete data

Table 11 Daily data, tvol. KS statistic for the candidate distributions (tail)

Table 12 Quarterly data, tvol. KS statistic for the candidate distributions (complete data)

Table 13 Quarterly data, tvol. KS statistic for the candidate distributions (tail)

1.2 Quarterly data

Tables 12 and 13 show the results for the quarterly data. The complete in-, out-, and total degree distributions are now fit best by Weibull, negative Binomial, and Log-normal distributions, respectively. In many cases, these distributions yield comparable KS statistics, but the clear advantage of the Log-normal distribution for the daily data does not carry over to the quarterly level in all cases. Similar to the daily estimates, the power-law parameters are within the usual range of empirical power-laws. As before, however, the tails are best described by Log-normal distributions. Therefore, while the tails of the tvol variables are somewhat fatter compared to the degree and ntrans variables, the power-law remains a poor description of the data.