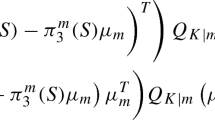Linear discriminant analysis for interval data

Summary

This paper compares different approaches to the multivariate analysis of interval data, focusing on discriminant analysis. Three fundamental approaches are considered. The first approach assumes an uniform distribution in each observed interval, derives the corresponding measures of dispersion and association, and appropriately defines linear combinations of interval variables that maximize the usual discriminant criterion. The second approach expands the original data set into the set of all interval description vertices, and proceeds with a classical analysis of the expanded set. Finally, a third approach replaces each interval by a midpoint and range representation. Resulting representations, using intervals or single points, are discussed and distance based allocation rules are proposed. The three approaches are illustrated on a real data set.

1 Introduction

In the classical model of data analysis, data is represented in a n × p matrix where n individuals (in rows) take exactly one value for each variable (in columns). However, this model is too restrictive to represent complex data, which may, for instance, comprehend variability and/or uncertainty. In this paper we focus on the analysis of interval data, that is, where individuals are described by variables whose values are intervals of ℝ. Interval data may occur in many different situations. We may have ‘native’ interval data, when describing ranges of variable values — for example, daily stock prices. Interval variables also allow to deal with imprecise data, coming from repeated measures or confidence interval estimation. A natural source of interval data is the aggregation of huge data bases, when real values describing the individual observations result in intervals in the description of the aggregated data. Symbolic data — concerning for instance, descriptions of biological species or technical specifications — constitute yet another possible source of interval data.

A multivariate analysis of interval data raises specific problems, which may be addressed in different ways. In this paper linear discriminant analysis will be addressed. Although there are nowadays many alternatives to LDA, it remains an important standard, its results are easily interpretable and it can be used for description as well as for prediction. More sophisticated approaches tend to be less interpretable, and any gains in classification performance they may provide are often small in practical applications (Hand (2004)). Furthermore, it could be argued that before analyzing extensions to other methods, the classical and well-established ones should be investigated. Discriminant analysis of interval data has also been addressed using Support Vector Machines (Do & Poulet (2005)) and Artificial Neural Networks (Sima (1995), Simoff (1996), Beheshti et al (1998), Rossi & Conan Guez (2002)).

A natural way of extending classical discriminant analysis to the case of interval data is to establish appropriate definitions of linear combinations, dispersion and association measures and proceed as in the classical way. However, as it will become clear, there is no single unequivocal manner of defining these concepts and apparently reasonable choices do not necessarily satisfy usual properties.

We will first discuss one approach that follows this line of reasoning, based on the measures proposed by Bertrand and Goupil (Bertrand & Goupil (2000)) and Billard and Diday (Billard & Diday (2003)), assuming an uniform distribution in each interval.

Another approach consists in considering all the vertices of the hypercube representing each of the n individuals in the p-dimensional space, and then perform a classical discriminant analysis of the resulting n × 2^p by p matrix.

This follows previous work by Chouakria et al (Chouakria, Cazes & Diday (2000)) for Principal Component Analysis. This approach avoids some of the limitations of the previous one by not relying on particular definitions of linear combinations, but it has the drawback of enlarging the original data to a potentially unmanageable dimension.

A third approach is to represent each variable by the midpoints and ranges of its interval values, perform two separate classical discriminant analysis on these values and combine the results in some appropriate way, or else analyze midpoints and ranges conjointly. This follows similar work on Regression Analysis by Neto et al (Neto, De Carvalho & Tenório (2004)), and Lauro and Palumbo on Principal Component Analysis (Lauro & Palumbo (2005)).

The three approaches considered are illustrated on a data set describing the main characteristics of four classes of cars.

The structure of the paper is as follows: Section 2 discusses properties of dispersion and association measures, and their implications in the definition of linear combination of interval variables. Section 3 describes in detail the three approaches considered. Section 4 presents the application on real data. Section 5 concludes the paper.

2 Dispersion, association and linear combinations of interval variables

Let I be an n × p matrix representing the values of p interval variables on a set Ω = {ω_i, i = 1,…, n}. Each ω_i ∈ Ω, is represented by a p-uple of intervals, I_i = (I_{i 1},…, I_ip), i = 1,…, n, with I_ij = [l_ij, u_ij], j = 1,…, p (see Table 1).

Table 1: Matrix I of interval data

Let $S_{I}=\left(\begin{array}{cccc}{s_{1}^{2}} & {s_{12}} & {\dots} & {s_{1 p}} \\ {s_{12}} & {s_{2}^{2}} & {\dots} & {s_{2 p}} \\ {\cdots} & {\cdots} & {\cdots} & {\ldots} \\ {s_{1 p}} & {s_{2 p}} & {\cdots} & {s_{p}^{2}}\end{array}\right)$ be a covariance matrix of measures of dispersion $\left(s_{j}^{2}\right)$ and association (s_jj′) for interval data. Furthermore, let $Z=I \otimes \beta$ be r appropriately defined linear combinations of the Y’s based on p × r real coefficients β_jℓ stacked in the matrix

$$\beta=\left(\begin{array}{cccc}{\beta_{11}} & {\beta_{12}} & {\ldots} & {\beta_{1 r}} \\ {\beta_{21}} & {\beta_{22}} & {\ldots} & {\beta_{2 r}} \\ {\cdots} & {\cdots} & {\cdots} & {\ldots} \\ {\beta_{p 1}} & {\beta_{p 2}} & {\cdots} & {\beta_{p r}}\end{array}\right)$$

Arguably, the above mentioned definitions should satisfy the following basic properties, for any p × r real matrix β:

$$I_{i} \otimes \beta_{\ell}=\sum_{j=1}^{p} \beta_{j \ell} \times I_{i j}$$

((P1))

where β_ℓ denotes the ℓ-th column of matrix β.

$$S_{Z}=S_{I \otimes \beta}=\beta^{t} S_{I} \beta$$

((P1))

that is, the covariance between interval variables should be a symmetric bilinear operator.

Unfortunately, the apparently natural definition of linear combination of interval variables

Definition A: $I_{i} \otimes_{A}\beta_{\ell}=z_{i \ell A}=\left[\underline{z}_{i \ell A}, \overline{z}_{i \ell A}\right], i=1, \ldots, n$, with

$$\left\{\begin{array}{l}{\underline{z}_{i \ell A}=\sum\limits_{j=1}^{p} \beta_{j \ell}\ l_{i j}} \\ {\overline{z}_{i \ell A}=\sum\limits_{j=1}^{p} \beta_{j \ell}\ u_{i j}}\end{array}\right.$$

does not satisfy property (P1) if at least one element of β_ℓ is negative. This follows from the fact that when β_jℓ < 0 then the lower bound of the interval βj_ℓ × I_{i j} equals β_jℓ u_ij and its upper bound equals β_jℓ l_ij, i.e. multiplying one interval by a negative coefficient leads to a reversal in the interval limits.

A definition of linear combination of interval variables that respects (P1) is given by:

Definition B: $I_{i} \bigotimes\nolimits_{B} \beta_{\ell}=z_{i \ell B}=\left[\underline{z}_{i \ell B}, \overline{z}_{i \ell B}\right], i=1, \ldots, n$, with

$$\left\{\begin{aligned} \underline{z}_{i \ell B} &=\sum\limits_{\beta_{j \ell}>0} \beta_{j \ell}\ l_{i j}+\sum\limits_{\beta_{j} e<0} \beta_{j \ell}\ u_{i j} \\ \overline{z}_{i \ell B} &=\sum\limits_{\beta_{j} e>0} \beta_{j \ell}\ u_{i j}+\sum\limits_{\beta_{j} \ell<0} \beta_{j \ell}\ l_{i j} \end{aligned}\right.$$

Definition B is the definition obtained by applying the rules of Interval Calculus (Case (1999), Moore (1966)), since the resulting intervals include all possible values that are scalar linear combinations of the values within the intervals I_ij. However, definition B ignores any connection that may exist between corresponding interval bounds in the original data. The existence (or lack of it) of such connection and the relevance of property (P1) depends on how a set of interval data ought to be interpreted.

Interval variables often arise from one of the following situations:

• 1. Each element ω_i ∈ Ω represents a group of individuals of a set Γ, which have been aggregated on the basis of some criteria. Each element of Γ is described by real variables y_j and the interval variables Y_j represent the variability of y_j in each group.

• 2. Each interval variable Y_j represents the possible values of an uncertain real variable y_j (e.g. Y_j may be an uncertain assessment of a decision maker regarding an alternative under evaluation).

The source of variability is different in these two situations. In the first situation, the variability results from the aggregation, the intervals of Y_j usually represent the range of a finite set of observations, while in the second one the variability in inherent to the original individual data. In both cases, correlations between the underlying real variables y_j, y_j′ may lead to a connection between values within the intervals associated to the corresponding interval variables. When such a connection is present, we will say that the variables Y_j, Y_j′ are inner correlated. In the case where the rankings of the values of the two underlying real variables y_j and y_j′ have a perfect match, then the lower bound (resp. upper bound) of Y_j will always be associated with the lower bound (resp. upper bound) of Y_j′; of course, the reverse happens for perfect reverse rankings.

Definition A is particularly appropriate for the case of a positive inner correlation, since in this case corresponding bounds tend to occur together and this connection should be preserved. On the other hand, when no connection exists between values within the intervals associated to interval variables, these variables are said to be inner independent. In this case, definition B is more adequate.

Property (P2) is usually satisfied by a combination of definition A with reasonable measures of interval dispersion and association. However, that is not necessarily the case for definition B. We will show that for an important family of dispersion and association measures, together with a class of linear combination definitions, that includes definitions A and B as two special cases, property (P2) still holds.

A family of dispersion and association measures will be said to be extreme invariant if property (P2) is satisfied for all definitions of interval linear combinations of the form

$$\left(L C_{t(\beta, \ell)}\right) I_{i} \otimes_{t(\beta, \ell)} \beta_{\ell}=z_{i \ell t(\beta, \ell)}=\left[\underline{z}_{i \ell t(\beta, \ell)}, \overline{z}_{i \ell t(\beta, \ell)}\right], i=1, \ldots, n, \ell=1, \ldots, r$$

with

$$\left\{\begin{aligned} \underline{z}_{i \ell t(\beta, \ell)} &=\sum\limits_{j=1}^{p} \beta_{j \ell}\ e_{i j s(t(\beta, \ell), j)} \\ \overline{z}_{i \ell t(\beta, \ell)} &=\sum\limits_{j=1}^{p} \beta_{j \ell}\ e_{i j \overline{s}(t(\beta, \ell), j)} \end{aligned}\right.$$

where

$$s(t(\beta, \ell), j) \in\{0,1\}, \overline{s}(t(\beta, \ell), j)=1-s(t(\beta, \ell), j), e_{i j 0}=l_{i j}, e_{i j 1}=u_{i j}.$$

and

t(β, ℓ) ∈ {1, 2, …,2^p} denotes one particular choice of combination of extreme pairs to be used in the computation of $\underline{z}_{i \ell t}$ and $\overline{z}_{i \ell t}$.

For linear combination definitions of the form $\left(L C_{t(\beta, \ell)}\right), \underline{z}_{i \ell t(\beta, \ell)}$ is a linear combination of extremes of I_i, $\overline{z}_{i \ell t(\beta, \ell)}$ is a combination of the remaining extremes of I_i; the same extremes are used for a single variable across individuals but different extremes may be used for different variables.

We now prove the following result:

Theorem 1

If $s_{j}^{2}$ and s_jj′ are dispersion and association measures satisfying the conditions:

• (i) $s_{j}^{2}$ and s_jj′ depend on the values of the extremes of I₁,…, I_n but do not distinguish between lower and upper bounds.

• (ii) Property (P2) is satisfied for definition A.

  then $s_{j}^{2}$ and s_jj′ are extreme-invariant.

Proof

As $s_{j}^{2}$ and s_jj′ do not depend on which extreme is the lower or the upper bound (and, in particular, do not depend on the fact that l_{i j} ≤ u_ij), from the $s_{j}^{2}$ and s_jj′ perspective these bounds can be viewed as labels that may be freely interchanged.

Let $I_{i} \otimes_{a} \beta_{\ell}$ be a linear combination definition of the form (LC_{t (β,ℓ)}) such that property (P2) is not known to be true. Denote by θ = {j : s(a, j) ≠ s(A, j)} the set of indices for which $\otimes_{A}$ and $\otimes_{a}$ use different extremes. Create a new set of variables $\overline{Y}_{j}$ such that $\overline{Y}_{j}\left(\omega_{i}\right)=\left[u_{i j}, l_{i j}\right], j \in \theta$.

Let J = [J_ij] be a new data matrix such that J_ij = Y_j(ω_i) for $j \notin \theta, J_{i j}=\overline{Y}_{j}\left(\omega_{i}\right)$ for j ∈ θ. Then, $I \otimes_{a} \beta=J \otimes_{A} \beta$ which implies that $S_{I} \otimes_{a} \beta=S_{J} \otimes_{A} \beta=\beta^{t} S_{J} \beta$ since (P2) holds for $\otimes_{A}$. But S_J = S_I because $s_{j}^{2}$ and s_jj′ do not depend on a particular labeling choice, and thus $S_{I} \otimes_{a} \beta=\beta^{t} S_{I} \beta$ for any $\otimes_{a}$ of the form $\bigotimes\nolimits_{t(\beta, \ell)}$.

Thus, when the measures of dispersion and association are such that conditions (i) and (ii) of Theorem 1 hold, for any linear combination of the form (LC_t(βℓ)) the covariance operator is symmetric bilinear and it follows that the maximization of ratios of quadratic forms can be based on a traditional eigenanalysis.

3 Approaches to Linear Discriminant Analysis

3.1 Distributional approach

In this approach we will consider linear combinations of interval variables Y’s of the form (LC_t(βℓ)) together with dispersion and association measures satisfying conditions (i) and (ii) of Theorem 1.

In a problem with k groups there will be r = min{p, k − 1} new variables collected in a n × r matrix $Z=I \otimes \beta$, where β is the p × r matrix of the real coefficients.

Given definitions of dispersion and association, the inertia between classes is measured by a positive-definite matrix B, and similarly, the inertia within classes is measured by a definite positive matrix W. Then, the between and within groups inertia of Z_ℓ are given, respectively, by $\beta_{\ell}^{t} B \beta_{\ell}$ and $\beta_{\ell}^{t} W \beta_{\ell},$ $\ell=1, \ldots, r$.

Known results from traditional discriminant analysis (Gnanadesikan et al (1989)) show that the ratio of between to within class inertia is maximized by the highest eigenvalue of W⁻¹ B, and that the coefficients of the corresponding linear combination are given by the first eigenvector of this matrix. Furthermore, uncorrelated $Z_{\ell}^{\prime} s$ that maximize the ratios of the remaining between and within inertias are defined in a similar manner by the following eigenvectors of the same matrix. These results remain valid for interval data, as long as property (P2) is satisfied.

In this approach it is assumed that each interval variable represents the possible values of an underlying real-valued variable. Bertrand and Goupil (Bertrand & Goupil (2000)) assume an equidistribution hypothesis, which consists in considering each observation as equally likely and that the values of the underlying variable are uniformly distributed. The empirical distribution function of an interval variable is then defined as the uniform mixture of n uniform distributions. More specifically, we have, for every ξ ∈ ℝ

$$F_{j}(\xi)=\frac{1}{n} \sum_{i=1}^{n} Pr\left(X_{i j} \leq \xi\right)$$

((1))

where X_ij is a uniformly distributed random variable in the interval [l_ij, u_ij]. It follows that the empirical density function is given by

$$f_{j}(\xi)=\frac{1}{n} \sum_{i=1}^{n} \frac{\mathbf{1}_{I_{i j}}(\xi)}{u_{i j}-l_{i j}}$$

((2))

where $\mathbf{1}_{I_{i j}}$ denotes the indicator function on I_ij

Let

$$m_{j}=\frac{1}{n} \sum_{i=1}^{n} \frac{l_{i j}+u_{i j}}{2} =\frac{1}{2}\left(\overline{l}_{j}+\overline{u}_{j}\right)$$

((3))

be the mean value of the interval midpoints for variable Y_j, for j = 1,…, p. The empirical variance is given by

$$s_{j}^{2}=\int_{-\infty}^{+\infty}\left(\xi-m_{j}\right)^{2} f_{j}(\xi) d \xi=\frac{1}{3 n} \sum_{i=1}^{n}\left(l_{i j}^{2}+l_{i j} u_{i j}+u_{i j}^{2}\right)-\frac{1}{4 n^{2}}\left[\sum_{i=1}^{n}\left(l_{i j}+u_{i j}\right)\right]^{2}$$

((4))

Following the same reasoning, Billard and Diday (Billard & Diday (2003)) have derived the joint density function of two interval variables as

$$f_{j j^{\prime}}\left(\xi_{1}, \xi_{2}\right)=\frac{1}{n} \sum_{i=1}^{n} \frac{1_{I_{i_{j}} \times I_{i j^{\prime}}}\left(\xi_{1}, \xi_{2}\right)}{\left(u_{i j}-l_{i j}\right)\left(u_{i j^{\prime}}-l_{i j^{\prime}}\right)}$$

((5))

It follows that the empirical covariance between two interval variables Y_j, Y_j′ is given by

$$\begin{array}{c}{s_{j j^{\prime}}=cov\left(Y_{j}, Y_{j^{\prime}}\right)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\left(\xi_{1} - m_{j}\right)\left(\xi_{2}-m_{j^{\prime}}\right) f_{j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}=} \\ {\frac{1}{4 n} \sum\limits_{i=1}^{n}\left[\left(l_{i j}+u_{i j}\right)\left(l_{i j^{\prime}}+u_{i j^{\prime}}\right)\right]-\frac{1}{4 n^{2}}\left[\sum\limits_{i=1}^{n}\left(l_{i j}+u_{i j}\right)\right]\left[\sum\limits_{i=1}^{n}\left( l_{i j^{\prime}}+u_{i j^{\prime}}\right)\right]}\end{array}$$

((6))

These measures of dispersion (4) and association (6) clearly satisfy condition (i) of Theorem 1 since they treat lower and upper bounds symmetrically.

Assume now that the n observations are partitioned into k groups, C₁,…, C_k. We define the empirical density function of variable Y_j in group C_α as

$$f_{\alpha j}(\xi)=\frac{1}{n_{\alpha}} \sum_{\omega_{i} \in C_{\alpha}} \frac{1_{I_{i j}}(\xi)}{u_{i j}-l_{i j}}$$

((7))

and the joint density function of two interval variables Y_j, Y_j′ in group C_α as

$$f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right)=\frac{1}{n_{\alpha}} \sum_{\omega_{i} \in C_{\alpha}} \frac{1_{I_{i j} \times I_{i j^{\prime}}}\left(\xi_{1}, \xi_{2}\right)}{\left(u_{i j}-l_{i j}\right)\left(u_{i j^{\prime}}-l_{i j^{\prime}}\right)}$$

((8))

It follows that the global empirical density functions are mixtures of the corresponding group specific functions:

$$f_{j}(\xi)=\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} f_{\alpha j}(\xi)$$

((9))

$$f_{j j^{\prime}}\left(\xi_{1}, \xi_{2}\right)=\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right)$$

((10))

It can be easily shown that these densities satisfy the usual properties

Property 1

$$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}=1$$

Property 2

• a) $\int\nolimits_{-\infty}^{+\infty} \int\nolimits_{-\infty}^{+\infty} \xi_{1} f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}=m_{\alpha j}$

• b) $\int\nolimits_{-\infty}^{+\infty} \int\nolimits_{-\infty}^{+\infty} \xi_{2} f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}=m_{\alpha j^{\prime}}$

where m_αj,m_αj′ are the mean values of the interval midpoints in group C_α for variables Y_j and Y_j′ respectively.

Using these properties, and after some algebra, the following proposition can be proved.

Proposition 1

The global variance can be decomposed as

$$\begin{array}{l}{s_{j}^{2}=\int_{-\infty}^{+\infty}\left(\xi-m_{j}\right)^{2} f_{j}(\xi) d \xi=} \\ {=\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty}\left(\xi-m_{\alpha j}\right)^{2} f_{\alpha j}(\xi) d \xi+\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty}\left(m_{\alpha j}-m_{j}\right)^{2} f_{\alpha j}(\xi) d \xi}\end{array}$$

where

$$\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty}\left(\xi-m_{\alpha j}\right)^{2} f_{\alpha j}(\xi) d \xi=\frac{1}{3 n} \sum_{i=1}^{n}\left(u_{i j}^{2}+u_{i j} l_{i j}+l_{i j}^{2}\right)-\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} m_{\alpha j}^{2}$$

is the within-group component and

$$\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty}\left(m_{\alpha j}-m_{j}\right)^{2} f_{\alpha j}(\xi) d \xi=\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} m_{\alpha j}^{2}-m_{j}^{2}$$

is the between-group component.

Similarly, the global covariance can be decomposed as

$$\begin{array}{l}s_{j j^{\prime}}=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\left(\xi_{1}-m_{j}\right)\left(\xi_{2}-m_{j^{\prime}}\right) f_{j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}= \\ =\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\left[\left(\xi_{1}-m_{\alpha j}\right)\left(\xi_{2}-m_{\alpha j^{\prime}}\right)\right] f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}+ \\ +\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\left[\left(m_{\alpha j}-m_{j}\right)\left(m_{\alpha j^{\prime}}-m_{j^{\prime}}\right)\right] f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2} \\ {\text { where }} \\ {=\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\left[\left(\xi_{1}-m_{\alpha j}\right)\left(\xi_{2}-m_{\alpha j^{\prime}}\right)\right] f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}=} \\ =\frac{1}{4 n} \sum\limits_{i=1}^{n}\left(u_{i j}+l_{i j}\right)\left(u_{i j^{\prime}}+l_{i j^{\prime}}\right)-\sum_{\alpha=1}^{k} \frac{n_{\alpha}}{n} m_{\alpha j} m_{\alpha j^{\prime}}\end{array}$$

is the within-group component and

$$\begin{array}{l}{\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\left[\left(m_{\alpha j}-m_{j}\right)\left(m_{\alpha j^{\prime}}-m_{j^{\prime}}\right)\right] f_{\alpha j j^{\prime}}\left(\xi_{1}, \xi_{2}\right) d \xi_{1} d \xi_{2}=} \\ {=\sum\limits_{\alpha=1}^{k} \frac{n_{\alpha}}{n} m_{\alpha j} m_{\alpha j^{\prime}}-m_{j} m_{j^{\prime}}}\end{array}$$

is the between-group component.

The terms of the matrices W and B are then given by:

$$w_{j j}=\frac{1}{3} \sum_{i=1}^{n}\left(u_{i j}^{2}+u_{i j} l_{i j}+l_{i j}^{2}\right)-\sum_{\alpha=1}^{k} n_{\alpha} m_{\alpha j}^{2}$$

((11))

$$w_{j j^{\prime}}=\frac{1}{4} \sum_{i=1}^{n}\left(u_{i j}+l_{i j}\right)\left(u_{i j^{\prime}}+l_{i j^{\prime}}\right)-\sum_{\alpha=1}^{k} n_{\alpha} m_{\alpha j} m_{\alpha j^{\prime}}, j \neq j^{\prime}$$

((12))

$$b_{j j^{\prime}}=\sum_{\alpha=1}^{k} n_{\alpha} m_{\alpha j} m_{\alpha j^{\prime}}-n m_{j} m_{j^{\prime}}$$

((13))

for j, j′ = 1,…, p.

As in the classical case, the discriminant functions coefficients are given by the eigenvectors of the product W⁻¹ B. Single point representations on a discriminant space may be obtained using the interval midpoints and interval representations can be determined by applying definitions A or B.

3.2 Vertices approach

This approach consists in considering all the vertices of the hypercube representing each of the n individuals in the p-dimensional space, and then perform a classical discriminant analysis of the resulting n × 2^p by p matrix, in line with previous work by Chouakria et al (Chouakria, Cazes & Diday (2000)) for Principal Component Analysis.

From the values of interval matrix I (see Table 1), a new matrix of single real values M is created, where each row i of I gives rise to 2^p rows of M, corresponding to all possible combinations of the limits of intervals [l_ij, u_ij], j = 1,…, p.

Performing a classical discriminant analysis on matrix M, we obtain a factorial representation of points, one for each of the 2^p vertices. From this, we may recover a representation in the form of intervals, proceeding as Chouakria et al in PCA:

• Let Q_i be the set of row indices q in matrix M which refer to the vertices of the hypercube corresponding to ω_i.

• For q ∈ Q_i let ζ_qℓ be the value of the ℓ-th real-valued discriminant function for the vertex with row index q.

• The value of the ℓ-th interval discriminant variate z for ω_i is then defined by

  $$\begin{aligned} \underline{z}_{i \ell} &=\operatorname{Min}\left\{\zeta_{q \ell}, q \in Q_{i}\right\} \\ \overline{z}_{i \ell} &=\operatorname{Max}\left\{\zeta_{q \ell}, q \in Q_{i}\right\} \end{aligned}$$

These variates may be used for description purposes as well as for classification, as will be presented in Section 3.4.

3.3 Midpoints and ranges approach

The idea here is to represent each interval variable by its midpoints and ranges, perform two separate classical discriminant analysis on these values, and combine the results in some appropriate way. This follows similar work on Regression Analysis by Neto et al (Neto, De Carvalho & Tenório (2004)) and on Principal Component Analysis by Lauro and Palumbo (Lauro & Palumbo (2005)).

Let

$$C=\left(\begin{array}{ccccc}{c_{11}} & {\dots} & {c_{1 j}} & {\dots} & {c_{1 p}} \\ {\cdots} & {\cdots} & {\dots} & {\dots} & {\dots} \\ {c_{i 1}} & {\dots} & {c_{i j}} & {\dots} & {c_{i p}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} & {\ldots} \\ {c_{n 1}} & {\cdots} & {c_{n j}} & {\cdots} & {c_{n p}}\end{array}\right)\quad R=\left(\begin{array}{ccccc}{r_{11}} & {\dots} & {r_{1 j}} & {\dots} & {r_{1 p}} \\ {\cdots} & {\cdots} & {\dots} & {\dots} & {\dots} \\ {r_{i 1}} & {\dots} & {r_{i j}} & {\dots} & {r_{i p}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} & {\ldots} \\ {r_{n 1}} & {\cdots} & {r_{n j}} & {\cdots} & {r_{n p}}\end{array}\right)$$

where $c_{i j}=\frac{l_{i j}+u_{i j}}{2}$ and r_ij = u_ij − l_ij are, respectively, the center and range of the interval value of variable Y_j for ω_i.

A classical discriminant analysis is then performed separately for matrices C and R. Let $z_{i 1}^{C}$ be the score of ω_i in the first discriminant function of the analysis based on the midpoints and $z_{i 1}^{R}$ the corresponding score for the analysis based on the ranges. A graphical representation of $z_{i 1}^{C}$ versus $z_{i 1}^{R}$ gives an image of the group separation simultaneously given by the midpoints and ranges of the original variables’ values.

Alternatively, a combined discriminant analysis may be performed simultaneously for midpoints and ranges. This is particularly relevant when midpoints and ranges are related in such a way that their contribution to group separation cannot be recovered by two independent analysis.

3.4 Allocation rules

Allocation rules may be derived from the representations on the discriminant space. These representations may assume the form of single points or intervals. Allocation rules will hence be based on point distances or distances between intervals, accordingly.

In the distributional approach, a natural rule based on point distances consists in allocating each observation to the group with nearest centroïd in the discriminant space, according to a simple Euclidean distance. Distinct prior probabilities and/or misclassification costs may be taken into account as in the classical case by adding or subtracting their natural logarithms to those distances (Gnanadesikan et al (1989)).

Applying definitions A and B, linear combinations of the interval variables are determined, that produce interval-valued discriminant variates. In this case, allocation rules may be derived by using distances between interval vectors. In this paper we use the following rule, proposed by Lauro, Verde & Palumbo (2000): allocate ω_i to the group C_α for which

$$D\left(\omega_{i}, C_{\alpha}\right)=\frac{1}{n_{\alpha}} \sum_{\omega_{i^{\prime}} \in C_{\alpha}} d\left(\omega_{i}, \omega_{i^{\prime}}\right)$$

((14))

is minimum; where

$$d\left(\omega_{i}, \omega_{i^{\prime}}\right)=\sqrt{\sum_{\ell=1}^{r} \lambda_{\ell} \delta\left(z_{i \ell}, z_{i^{\prime} \ell}\right)^{2}}$$

((15))

and λ_ℓis the ℓ-th eigenvalue of W⁻¹ B. Different interval distances δ may be used, we chose the Haudorff distance between $z_{i \ell}=\left[\underline{z}_{i \ell}, \overline{z}_{i \ell}\right] \text { and } z_{i^{\prime} \ell}=$$\left[\underline{z}_{i^{\prime} \ell}, \overline{z}_{i^{\prime} \ell}\right]$:

$$\delta\left(z_{i \ell}, z_{i^{\prime} \ell}\right)=\operatorname{Max}\left\{\left|\underline{z}_{i \ell}-\underline{z}_{i^{\prime} \ell}\right|,\left|\overline{z}_{i \ell}-\overline{z}_{i^{\prime} \ell}\right|\right\}$$

((16))

In the vertices approach, discriminant variates are interval-valued, so this same allocation rule is applied.

For the midpoints and ranges approach, only point distances are used to define allocation rules. However, two different situations occur: when two separate analysis are performed for midpoints and ranges, generally the discriminant variates are correlated, for this reason, the Mahalanobis distance is used; when a single discriminant analysis is performed taking into account both midpoints and ranges, the simple Euclidean distance is adequate.

4 Application: the ‘car’ data set

The ‘car’ data set is a set of 33 car models described by 8 interval, 2 categorical multi-valued and one nominal variables (see Table 2). In this application, the 8 interval variables — Price, Engine Capacity, Top Speed, Acceleration, Step, Length, Width and Height — have been considered as descriptive variables, the nominal variable Category has been used as a a priori classification.

Table 2: ‘Car’ data set with 8 interval and one nominal variables

The a priori classification, indicated by the suffix attached to the car model denomination, is as follows:

Figures 1 to 3 show single point representations, on a two dimensional discriminant space, resulting from the analysis performed using the distributional approach (Fig. 1), performing two separate analysis on the midpoints and ranges (Fig. 2) and analyzing midpoints and ranges jointly (Fig. 3).

Figure 1:

Point representations — distributional approach

Figure 2:

Point representations — midpoints and ranges separate analysis

Figure 3:

Point representations — midpoints and ranges combined analysis

From Figure 1, it can be seen that the first discriminant function of the analysis following the distributional approach clearly separates the Sportive cars from the remaining ones, while the second function helps to distinguish (although imperfectly), the Utilitarian, Berlina and Luxury classes. Figure 2, shows that the first discriminant function of an analysis on the ranges performs a similar role to that of the second function of the former analysis. However, in this example, a combined analysis of both ranges and midpoints (see Figure 3) better separates the groups, isolating also the Utilitarian class and decreasing the degree of intersection between the Berlina and Luxury classes.

The following classification methods were also applied to this data set:

• Distributional approach, with allocation based on Euclidean point distances (Table 3).

• Midpoints and ranges separate analysis, with allocation based on Mahalanobis point distances (Table 4).

• Midpoints and ranges combined analysis, with allocation based on Euclidean point distances (Table 5).

• Distributional approach, with allocation based on HaudorfF distances between intervals obtained according to delinition A (Table 6).

• Distributional approach, with allocation based on Haudorff distances between intervals obtained according to definition B (Table 7).

• Vertices approach, with allocation based on Haudorff interval distances (Table 8).

Table 3: Classification results for the distributional approach, using point distances. Hit rates: 85% (Res.), 73% (L.O.O.).

Table 4: Classification results for the midpoints and ranges separate analysis, using point distances. Hit rates: 94% (Res.), 64% (L.O.O.).

Table 5: Classification results for the midpoints and ranges combined analysis, using point distances. Hit rates: 94% (Res.), 55% (L.O.O.).

Table 6: Classification results for the distributional approach using Haudorff interval distances with linear combinations given by definition A. Hit rates: 91% (Res.), 67% (L.O.O.).

Table 7: Classification results for the distributional approach using Haudorff interval distances with linear combinations given by definition B. Hit rates: 88% (Res.), 67% (L.O.O.).

Table 8: Classification results for the vertices approach, using Haudorff interval distances. Hit rates: 88% (Res.), 70% (L.O.O.).

Tables 3–8 present the classification results obtained by resubstitution (Res.), i.e. on the learning set, and by cross-validation (Leave-One-Out — L.O.O.).

All methods show tendency to ovcrfit the data, this was to be expected given that the size of the training set is relatively small for a problem with eight variables and four groups. However, in this example, the distributional approach with point distances was the one where this effect was less pronounced. The distributional approaches with linear combination definitions A and B have similar performances. The degree of separation between classes is not uniform, with the Sportive cars being easily recognized by all methods, while it is considerably more difficult to distinguish the Berlina from both the Luxury and the Utilitarian cars.

5 Conclusion

Extensions of classical methodologies to interval data are not trivial and may depend on the intrinsic nature of the data. In particular, the notion of linear combination is not straightforward in the case of interval data, and the proper definition to use requires careful attention.

Different discriminant representations of interval data may highlight different aspects and may be useful for different purposes: interval representations have the advantage to put in evidence the inherent variability within the original intervals; point representations can reveal the different contributions of interval locations and ranges to group separation.

The approaches considered in this paper differ in the way they use the information contained in the interval data. When the interval ranges vary across groups, approaches that take these ranges into account have the potential to reduce misclassification rates. Furthermore, when the ranges are correlated with the interval midpoints, a simultaneous analysis of both midpoints and ranges may improve the results by taking this dependence into account. However, the inclusion of ranges into the analysis should be done with care, since it may lead to overfitting. Distances applied to interval representations can be a good compromise, when no information about the true nature of group separation is available. These expected tendencies have been confirmed by preliminary simulation results, available from the authors upon request.

Many of the aspects discussed in this paper are not restricted to discriminant analysis, but are also relevant for other multivariate methodologies. In particular, the properties of dispersion and association measures, the proper way of defining linear combinations of interval variables, the relative advantages between point and interval representations in low dimensional spaces and the risk of overfitting are recurrent issues for several types of multivariate data analysis.