1 Introduction

With the development of technology, the demand for the ultra-precision machining of parts with complex shapes is increasing, and the increase in the number of machine tool axes has become a development trend for ultra-precision machine tools. As the number of machine tool axes increases, the geometric error terms of machine tools also increase. A three-axis ultra-precision machine tool contains 24 geometric error terms, while a five-axis ultra-precision machine tool contains 43 geometric error terms [1, 2]. During the machining process, the error terms of the axis are coupled with other error terms, causing the tool to deviate from the perfect functional point and finally forming the machining error of the machine tool. If researchers want to improve the machining accuracy of machine tools, it is necessary to compensate for errors [3], but the premise of error compensation is to measure errors accurately, so it is very important to study the error measurement of ultra-precision machine tools.

In ultra-precision machine tools, the geometric error is an important factor affecting the machining accuracy of parts [4]. However, due to the characteristics of small batches and the strong customization of ultra-precision machine tools, there is currently no mature testing standard. The methods in the standards ISO-230–1 to ISO-230–7 are mainly used to detect the geometric errors of ultra-precision machine tools [5]. In previous studies, scholars have performed a large amount of work on the detection and identification of machine tool geometric errors, and many results have been achieved.

For the linear axis, a laser interferometer was generally used to measure the positioning error and straightness error [6]. In addition, some scholars proposed various identification methods for the geometric errors of linear axes based on laser trackers [7], photoelectric autocollimators [8], and other instruments. The geometric error of the rotary axis includes the radial error and the axial error, which can be measured using the R-test [1, 9]. Ibaraki [10], Jiang [11], and Chen [12] installed a trigger probe or stylus on machine tools and used the on-machine measurement method to measure the geometry error of the rotary axis on a five-axis ultra-precision machine tool. Other scholars used instruments such as double ballbar (DBB) [13], laser displacement sensor, and interference sensor of angular micro deflection [14] to measure the geometric error of the rotary axis. There is also a squareness error between the axes in machine tools. The squareness error can be measured with displacement sensors and a standard square ruler [15], and it can be quickly measured using a DBB [6].

Except for the above errors, in some cases, the diagonal error of machine tools will also be a matter of concern. By measuring the diagonal error, the squareness error and geometric error terms can be indirectly evaluated [16]. The body diagonal error can be measured using a laser interferometer [5]. Wang firstly presented the step-diagonal test [5], and then, Chapman[17] and Ibaraki [18] studied the issues in the step-diagonal test. Sun et al. [19] developed a method for measuring the body diagonal error with a multi-beam laser interferometer and measured the body diagonal error of a five-axis machining center. Yang et al. [20] measured the face diagonal error and body diagonal error with a DBB.

In addition, some scholars developed different measuring instruments and methods to measure the geometric errors of machine tools. Kim et al. [21] proposed that if quantum entangled states were preset in photons, the measurement accuracy of an interferometer could be improved by 100 times under the same conditions. Hong et al. [22] used a non-contact laser displacement sensor to replace the contact displacement sensor in a traditional R-test instrument and measured the rotary axis error of a machine tool. Wang et al. [23] developed a new measuring instrument J-DBB that added a ball joint structure to a traditional DBB and effectively improved the measurement space.

The methods described above all directly measured the machine tool’s geometric error, and they could also indirectly evaluate the geometric error of the machine tool by measuring the error of the test part. Currently, the commonly used test parts include the NAS 979 test part [24], the M1 to M4 test parts proposed in ISO 10791–7:2020 [25], and the S-shaped test part [26]. Ibaraki [27,28,29] analyzed the geometric error of a five-axis machining center, designed and processed a variety of different forms of test parts, and verified the machine tool error in reverse. Liu [4] and Gao [6] et al. obtained the geometric error for a three-axis ultra-precision machine tool according to the test part error.

Although scholars have proposed many measurement methods for geometric errors, most of them are aimed at the geometric errors of a single axis or some error terms. When all five axes of the machine tool are required to participate in the machining, due to the couple relationship of all the errors, it is difficult to identify and measure the geometric errors. It requires repetitive and tedious work to measure all the error terms of a five-axis ultra-precision machine tool with many specialized instruments, and the measurement results need to be simulated based on the error model to obtain the geometric error curves in interpolated five-axis motion. Many scholars [6, 13, 20, 23] used DBB to measure different geometric errors. Ni [13], Chu [30], Wang [31], Chen [32], and other scholars obtained the rotary axis geometric errors by designing the motion trajectory of machine tools to ensure that the length of the DBB keeps constant during the measurement process. A measurement method of five-axis machine tool geometric errors is mentioned in ISO 230–1 [2]; in order to exercise all axes of motion, the workpiece rotary axis needs to rotate to a certain angle. However, this method can only be used on machine tools with two serial rotary axes, and thus, the method is limited by the machine tool layout.

As a five-axes motion trajectory is designed, the length of the DBB is kept constant to measure the geometric error of the machine tool in the interpolated five-axis motion. The geometric error measurement results can provide guidance for the design and error compensation of machine tools, reduce the error of machine tools, and improve machining accuracy.

In this research, a measurement method is proposed for the geometric error measurement problem of five-axis ultra-precision machine tools in interpolated five-axis motion. The principle of the measurement method and the method of instrument installation and adjustment are described in Sect. 2. The error measurement experiment is carried out on a five-axis ultra-precision machine tool in Sect. 3. Finally, the measurement results and the theoretical calculation results are compared and discussed in Sect. 4.

2 Methodology

2.1 Motion trajectory design

The DBB is a high-precision linear telescopic sensor, the two ends of which are connected with a precision sphere. The measurement of the distance change between the two spheres can reflect the errors of machine tools, such as the squareness error and backlash, which have been included in ISO 230–1:2012 [2].

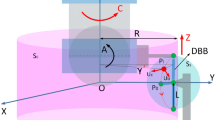
The five-axis ultra-precision machine tool studied in this research is illustrated in Fig. 1. The machine tool contains five axes, including the three linear axes of X, Y, and Z, and the two rotary axes of B and C, adopting the w–C-Y–Z-b-X-B-t layout, where w means workpiece, b means machine bed, and t means tool. The X-axis and the Z-axis are vertically set on the base. The Y-axis is set on the Z-axis, which can drive the C-axis to move in the Y direction. The B-axis is set on the X-axis.

Fig. 1
figure 1

Five-axis ultra-precision machine tool structure

Full size image

When the two spheres of the DBB are installed on the B-axis and C-axis of the machine tool, respectively, the motion trajectory of the five axes can be designed accordingly. The positions of the two spheres change steadily according to the designed test trajectory. The designed test trajectory must ensure that the distance between the two spheres of the DBB remains constant, and the direction of the DBB is parallel to the tested axis. However, because of the manufacturing, assembly, and control errors of the machine tool, the relative position of the two spheres will change inevitably, and thus, the geometric error of the machine tool in interpolated five-axis motion can be measured by the DBB. Therefore, the principle of the motion trajectory design is that the relative position of the two spheres of the DBB remains constant.

It is assumed that the sphere attached on the C-axis is sphere 1, and the sphere attached on the B-axis is sphere 2. When sphere 1 rotates with the C-axis, its X and Y coordinates also change accordingly. Assuming that the rotation angular velocity of the C-axis is ω1, the distance between sphere 1 and the C-axis rotation axis is R1, and the initial angle is the positive direction of the Y-axis, and the position of sphere 1 at time t can be described as

$$\left\{\begin{array}{c}{x}_{1}\left(t\right)=-{R}_{1}sin\left({\omega }_{1}t\right)\\ {y}_{1}\left(t\right)=-{R}_{1}\left[1-\mathrm{cos}\left({\omega }_{1}t\right)\right]\end{array}\right.$$
(1)

where x1 (t) and y1 (t) are the X and Y coordinates of the center of sphere 1, respectively.

In the same way, assuming that the rotational angular velocity of the B-axis is ω2, the distance between sphere 2 and the B-axis rotation axis is R2, and the initial angle is the positive direction of the Z-axis, and the position of sphere 2 at time t can be described as

$$\left\{\begin{array}{c}{x}_{2}\left(t\right)={R}_{2}sin\left({\omega }_{2}t\right)\\ {z}_{2}\left(t\right)=-{R}_{2}\left[1-\mathrm{cos}\left({\omega }_{2}t\right)\right]\end{array}\right.$$
(2)

where x2 (t) and z2 (t) are the X and Z coordinates of the center of sphere 2, respectively.

First, it is assumed that ω1 = ω2 to synchronize the motion of the two spheres. When the C-axis rotates, the X-axis moves as x1 (t) to compensate for the displacement of sphere 1 in the X direction, and the Y-axis moves as – y1 (t) to compensate for the displacement of sphere 1 in the Y direction. When the B-axis rotates, the X-axis moves as –x2 (t), and the Z-axis moves as z2 (t) to compensate for the displacement of sphere 2 in the X direction and the Z direction. It is evident that when the B-axis and the C-axis rotate at the same angular velocity ω, the X-axis moves as x1 (t) – x2 (t), the Y-axis moves as – y1 (t), and the Z-axis moves as z2 (t), the relative position of the two spheres remains synchronized. The final designed motion trajectory can be described as

$$\left\{\begin{array}{c}{\theta }_{B}\left(t\right)=\omega t\\ {\theta }_{C}\left(t\right)=\omega t\\ x\left(t\right)=-\left({R}_{1}+{R}_{2}\right)sin\left(\omega t\right)\\ y\left(t\right)={R}_{1}\left[1-\mathrm{cos}\left(\omega t\right)\right]\\ z\left(t\right)=-{R}_{2}\left[1-\mathrm{cos}\left(\omega t\right)\right]\end{array}\right.$$
(3)

where θB (t) and θC (t) are the B-axis and C-axis motion trajectories, respectively, and x (t), y (t), and z (t) are the X-axis, Y-axis, and Z-axis motion trajectories, respectively.

Assuming that R1 = R2 = 10 mm, the length of the DBB is 50 mm. According to Eq. (3), the motion trajectory of the two spheres when the DBB is installed toward the Z direction can be drawn as demonstrated in Fig. 2.

Fig. 2
figure 2

DBB sphere movement tracks

Full size image

The positions of the two spheres are solved separately, and the change of the coordinates of sphere 1 with time is deduced as

$$\left\{\begin{array}{c}{x}_{1}^{^{\prime}}\left(t\right)={x}_{1}\left(t\right)=-{R}_{1}\cdot sin\left(\omega t\right)\\ {y}_{1}^{^{\prime}}\left(t\right)={y}_{1}\left(t\right)+y\left(t\right)=-{R}_{1}\left[1-\mathrm{cos}\left(\omega t\right)\right]+{R}_{1}\left[1-\mathrm{cos}\left(\omega t\right)\right]=0\\ {z}_{1}^{^{\prime}}\left(t\right)=z\left(t\right)=-{R}_{2}\cdot \left(1-\mathrm{cos}\omega t\right)\end{array}\right.$$
(4)

The change of the coordinates of sphere 2 with time is deduced as

$$\left\{\begin{array}{c}{x}_{2}^{^{\prime}}\left(t\right)={x}_{2}\left(t\right)+x\left(t\right)={R}_{2}sin\left(\omega t\right)-\left({R}_{1}+{R}_{2}\right)sin\left(\omega t\right)=-{R}_{1}sin\left(\omega t\right)\\ {y}_{2}^{^{\prime}}\left(t\right)=0\\ {z}_{2}^{^{\prime}}\left(t\right)={z}_{2}\left(t\right)=-{R}_{2}\left[1-\mathrm{cos}\left(\omega t\right)\right]\end{array}\right.$$
(5)

Subtracting Eq. (4) from Eq. (5) can produce the relative position relationship of the two spheres under ideal conditions, as shown below:

$$\left\{\begin{array}{c}\Delta x\left(t\right)={x}_{1}^{^{\prime}}\left(t\right)-{x}_{2}^{^{\prime}}\left(t\right)=0\\ \Delta y\left(t\right)={y}_{1}^{^{\prime}}\left(t\right)-{y}_{2}^{^{\prime}}\left(t\right)=0\\ \Delta z\left(t\right)={z}_{1}^{^{\prime}}\left(t\right)-{z}_{2}^{^{\prime}}\left(t\right)=0\end{array}\right.$$
(6)

According to Eq. (6), when the machine tool moves with the motion trajectory set by Eq. (3), the two spheres of the DBB remain relatively static for the case of no error.

The DBB is installed toward the X, Y, and Z directions, as illustrated in Fig. 3, the error curves δx (t), δy (t), and δz (t) are measured, respectively. Since the starting positions of the X-, Y-, and Z-axes are different during the measurement process, the peak-valley (PV) values δx, δy, and δz of the error curves are taken as the error values in each direction. The total geometric error δ of the machine tool in interpolated five-axis motion can be described as

Fig. 3
figure 3

Diagram of the DBB installation: a X direction, b Y direction, and c Z direction

Full size image
$${\delta }\text{=}\sqrt{{\delta }_{x}^{2}+{\delta }_{y}^{2}+{\delta }_{z}^{2}}$$
(7)

When the DBB is installed toward the X direction, the errors in the Y and Z directions of the machine tool affect the measurement results. Similarly, when the DBB is installed toward the Y and Z directions, it is also affected by the errors in the other directions. With the assumption that the DBB is installed toward the X direction, the error in the Y direction can be taken as an example to calculate its influence on the measurement result. In the Y direction, there are mainly EYX (straightness error of X-axis), EYY (positioning error of Y-axis), EYZ (straightness error of Z-axis), and other error terms. The Y direction error is usually in the order of 5–10 μm, and the length of the DBB is 50 mm. Assume that the error in Y direction is 10 μm, the influence Δ of the Y direction error on the length of the DBB can be calculated as

$$\Delta =\sqrt{{50}^{2}+{0.01}^{2}}-50=1.6\mathrm{E}-6\mathrm{mm}$$
(8)

Based on the above calculation results, the deformation of the length of the DBB caused by the error in the non-sensitive direction does not have an impact on the measurement results, so this method can accurately measure the error.

2.2 Installation errors analysis

According to Eq. (3), the motion trajectory of the five axes of the machine tool can be fully defined by ω, R1, and R2, while the ω is controlled by the numerical control (NC) program, and only the length of the R1 and R2 is needed to be measured accurately. At the same time, the B-axis and C-axis should rotate from the start angle 0°, so the orientations of R1 and R2 are also need to be measured accurately. Limited by the resolution of the measurement instrument, the lengths and orientations of R1 and R2 are not absolutely accurate. Therefore, it is necessary to measure and compensate the installation errors of the DBB. All the four installation errors are illustrated in Fig. 4.

Fig. 4
figure 4

Diagram of the DBB installation errors

Full size image

If the installation errors of the DBB are measured with the five-axis NC program, three equations including the installation errors can be obtained, but the installation errors value is 4, which cannot be solved. Therefore, it is necessary to control the number of installation errors included in the equations so that the number of error equations is greater than or equal to the number of installation errors.

When the B-axis remains stationary and the C-axis rotates, there are only two installation errors (ΔR1 and Δθ1) involved in the error curves. Likewise, when the C-axis remains stationary and the B-axis rotates, there are only two installation errors (ΔR2 and Δθ2) involved in the error curves. Therefore, by designing the motion trajectories of XYC and XZB and measuring the respective errors, four equations including the installation errors can be obtained.

The XYC motion trajectory can be expressed as

$$\left\{\begin{array}{c}{\theta }_{C}\left(t\right)=\omega t\\ {\theta }_{B}\left(t\right)=0\\ x\left(t\right)=-{R}_{1}sin\left(\omega t\right)\\ y\left(t\right)={R}_{1}\left[1-\mathrm{cos}\left(\omega t\right)\right]\\ z\left(t\right)=0\end{array}\right.$$
(9)

The XZB motion trajectory can be expressed as

$$\left\{\begin{array}{c}{\theta }_{B}\left(t\right)=\omega t\\ {\theta }_{C}\left(t\right)=0\\ x\left(t\right)=-{R}_{2}sin\left(\omega t\right)\\ y\left(t\right)=0\\ z\left(t\right)=-{R}_{2}\left[1-\mathrm{cos}\left(\omega t\right)\right]\end{array}\right.$$
(10)

If there is no error, then when the machine tool moves as shown in Eq. (9), the two sphere motion trajectories are the same, and the position remains relatively static. If there are installation errors ΔR1 and Δθ1, the coordinates of sphere 1 change with time, as follows:

$$\left\{\begin{array}{c}{x}_{1}\left(t\right)\text{=}-\left({R}_{1}+\Delta {R}_{1}\right)\cdot sin\left(\omega t+\Delta {\theta }_{1}\right)\\ {y}_{1}\left(t\right)=y\left(t\right)-\left({R}_{1}+\Delta {R}_{1}\right)\cdot \left[1-\mathrm{cos}\left(\omega t+\Delta {\theta }_{1}\right)\right]\\ {z}_{1}\left(t\right)=z\left(t\right)=0\end{array}\right.$$
(11)

The coordinates of sphere 1 that change with time are

$$\left\{\begin{array}{c}{x}_{2}\left(t\right)=x\left(t\right)=-{R}_{1}\cdot sin\omega t\\ {y}_{2}\left(t\right)=0\\ {z}_{2}\left(t\right)=0\end{array}\right.$$
(12)

Because both ΔR1 and Δθ1 are extremely small quantities, therefore, by letting cosΔθ1 ≈ 1, sinΔθ1 ≈ Δθ1, subtracting Eq. (12) from Eq. (11), and ignoring the higher-order error terms in the equation, when there are installation errors, the relative position between the two spheres is

$$\left\{\begin{array}{c}\Delta x\left(t\right)\approx -{R}_{1}\Delta {\theta }_{1}cos\omega t-\Delta {R}_{1}sin\omega t\\ \Delta y\left(t\right)\approx -{R}_{1}\Delta {\theta }_{1}sin\omega t+\Delta {R}_{1}cos\omega t-\Delta {R}_{1}\\ \Delta z\left(t\right)=0\end{array}\right.$$
(13)

Based on trigonometry, Eq. (13) can be simplified to

$$\left\{\begin{array}{c}\Delta x\left(t\right)=-{A}_{1}cos(\omega t-{\varphi }_{1})\\ \Delta y\left(t\right)={A}_{1}sin(\omega t-{\varphi }_{1})-\Delta {R}_{1}\\ \Delta z\left(t\right)=0\end{array}\right.$$
(14)

where \({A}_{1}=\sqrt{{({R}_{1}\Delta {\theta }_{1})}^{2}+\Delta {R}_{1}^{2}}\) and \({\varphi }_{1}=\mathrm{arctan}\left(\frac{\Delta {R}_{1}}{{R}_{1}\Delta {\theta }_{1}}\right)\).

It is easy to determine that the influence of ΔR1 and Δθ1 on the measurement results in the X and Y directions is a sinusoid with the frequency f = ω/2π. Therefore, with the sinusoidal fitting of original error data for the X and Y directions, two sinusoids with the frequency f = ω/2π can be obtained. First, the offset between the Y direction sinusoid and the straight line y = 0 is ΔR1, and then, Δθ1 can be calculated with A1. Then, the ratio between ΔR1 and Δθ1 for the X direction sinusoid is calculated according to φ1, and the ratio is brought into A1 to calculate ΔR1 and Δθ1 sequentially. A total of six solutions of ΔR1 and Δθ1 can be obtained. Then, the average values are used as the installation error to compensate.

Similarly, when the machine tool moves in accordance with the XZB motion trajectory, the relative position between the two spheres can be expressed as

$$\left\{\begin{array}{c}\Delta x\left(t\right)=-{A}_{2}cos(\omega t-{\varphi }_{2})\\ \Delta y\left(t\right)=0\\ \Delta z\left(t\right)={A}_{2}sin(\omega t-{\varphi }_{2})-\Delta {R}_{2}\end{array}\right.$$
(15)

where \({A}_{2}=\sqrt{{({R}_{2}\Delta {\theta }_{2})}^{2}+\Delta {R}_{2}^{2}}\) and \({\varphi }_{2}=\mathrm{arctan}\left(\frac{\Delta {R}_{2}}{{R}_{2}\Delta {\theta }_{2}}\right)\).

ΔR2 and Δθ2 can be calculated by referring to the processing of the XYC motion data. After completing the calculation for the installation errors, the errors are compensated for before measurement.

2.3 Measurement uncertainty

To evaluate the accuracy of the geometric error measured with the DBB, the uncertainty of the geometric error in the X direction is calculated as an example. The geometric error EGeo in the X direction is obtained indirectly by measuring the difference ε between the actual offset distance of the machine tool and the calibration length of the DBB, and it can be expressed as shown in the following equation:

$$\varepsilon \text{=}{L}_{M}-{L}_{DBB}$$
(16)

where LM is the machine tool offset distance and LDBB is the calibration length of DBB, ideally LM _ideal = LDBB _ideal = 50 mm.

The difference ε includes the ideal difference εideal of the DBB, the display error EDis, and the time drift error Et, which can be expressed as

$$\varepsilon \text{=}{\varepsilon }_{ideal}+{E}_{Dis}+{E}_{t}$$
(17)

The machine tool offset distance LM includes the geometric error EGeo of the machine tool in the X direction and the installation error EIn of the DBB, which can be expressed as

$${L}_{M}={L}_{M\_ideal}+{E}_{Geo}+{E}_{In}$$
(18)

The calibration length LDBB of the DBB includes the sphericity error ESp of the DBB sphere and the calibration ruler error ECali, which can be expressed as

$${L}_{DBB}={L}_{DBB\_ideal}+{E}_{Sp}+{E}_{Cali}$$
(19)

Combining the equations, the expression of the geometric error EGeo in the X direction of the machine tool can be obtained as

$${E}_{Geo}\text{=}f\text{(}{\varepsilon }_{ideal},{E}_{Dis},{E}_{t},{E}_{In},{E}_{Sp},{E}_{Cali}\text{)}={\varepsilon }_{ideal}+{E}_{Dis}+{E}_{t}-{E}_{In}-{E}_{Sp}-{E}_{Cali}$$
(20)

The geometric error EGeo includes the display error, time drift error, installation error, and other error terms, so it is necessary to calculate the combined standard uncertainty. The ideal difference εideal of the DBB has no error, and its uncertainty is not calculated. The combined standard uncertainty u(EGeo) of the geometric error EGeo can be expressed as

$${u}^{2}\left({E}_{Geo}\right)\text{=}{\mathrm{c}}_{{E}_{Dis}}^{2}{u}^{2}\left({E}_{Dis}\right)+{\text{c}}_{{E}_{t}}^{2}{u}^{2}\left({E}_{t}\right)+{\text{c}}_{{E}_{In}}^{2}{u}^{2}\left({E}_{In}\right)+{\text{c}}_{{E}_{Sp}}^{2}{u}^{2}\left({E}_{Sp}\right)+{\text{c}}_{{E}_{Cali}}^{2}{u}^{2}\left({E}_{Cali}\right)$$
(21)

where u(EDis), u(Et), u(EIn), u(ESp), and u(ECali) are uncertainty of each error term, and \({c}_{{E}_{Dis}}\), \({c}_{{E}_{t}}\), \({c}_{{E}_{In}}\), \({c}_{{E}_{Sp}}\), and \({c}_{{E}_{Cali}}\) are the uncertainty coefficients of each error term, which can be obtained by taking the partial derivative with respect to f, \({c}_{{E}_{Dis}}={c}_{{E}_{t}}=1\),\({c}_{{E}_{In}}={c}_{{E}_{Sp}}={c}_{{E}_{Cali}}=-1\).

In the X direction, the installation error EIn includes the four installation errors ΔR1, Δθ1, ΔR2, and Δθ2, and the installation error EIn in the X direction can be expressed as

$${E}_{In}=-{R}_{1}\Delta {\theta }_{1}\mathrm{cos}\omega t-\Delta {R}_{1}\mathrm{sin}\omega t-{R}_{2}\Delta {\theta }_{2}\mathrm{cos}\omega t-\Delta {R}_{2}\mathrm{sin}\omega t$$
(22)

The uncertainty u(EIn) can be expressed as

$${u}^{2}\left({E}_{In}\right)\text{=}{\mathrm{c}}_{\Delta {R}_{1}}^{2}{u}^{2}\left(\Delta {R}_{1}\right)+{\text{c}}_{\Delta {\theta }_{1}}^{2}{u}^{2}\left(\Delta {\theta }_{1}\right)+{\mathrm{c}}_{\Delta {R}_{2}}^{2}{u}^{2}\left(\Delta {R}_{2}\right)+{\text{c}}_{\Delta {\theta }_{2}}^{2}{u}^{2}\left(\Delta {\theta }_{2}\right)$$
(23)

where \({c}_{\Delta {R}_{1}}={c}_{\Delta {R}_{2}}=-\mathrm{cos}\omega t\), \({c}_{\Delta {\theta }_{1}}={R}_{1}\mathrm{sin}\omega t\), and \({c}_{\Delta {\theta }_{2}}={R}_{2}\mathrm{sin}\omega t\).

The uncertainty calculation is divided into a type A standard uncertainty and a type B standard uncertainty. The type A standard uncertainty is obtained with a limited number of measurements or observations. It is a statistic, and the standard deviation can be calculated as the standard uncertainty. The type B standard uncertainty is obtained from the verification data of reliable testing institutions or manufacturers. The specific calculation method can be determined by referring to reference [33] according to the probability distribution of each term.

3 Geometric error measurement

3.1 Equipment and instrument

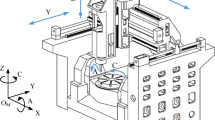
The machine tool used in the geometric error measurement experiment is a five-axis ultra-precision machine tool designed and manufactured by the center of precision engineering of Harbin Institute of Technology as illustrated in Fig. 5, with a stroke of 200 mm*100 mm*200 mm. The machine tool adopts the layout shown in Fig. 1.To ensure the machining accuracy, the error motion of the five-axis ultra-precision machine tool within the range of 50 mm*50 mm*50 mm needs to be less than ± 3 μm. To improve the accuracy of the machine tool, the X-, Y-, Z-, and B-axes are all hydrostatic guide rails, and the C-axis is an aerostatic spindle. The bed, X-axis, and Z-axis of the machine tool are made of granite with a small thermal expansion coefficient to avoid thermal errors that have a great impact on the machining accuracy of the machine tool. The measuring instrument is a Renishaw’s QC-20W DBB with a resolution of 0.1 μm and a range of ± 1 mm, which can fulfill the measurement requirements.

Fig. 5
figure 5

Five-axis ultra-precision machine tool

Full size image

To avoid the interference of the thermal error with the measurement results, a constant temperature room is built around the machine tool to isolate the influence of the external environmental temperature on the machine tool, as illustrated in Fig. 6a. The interior of the constant temperature room is air-bathed by the precision air conditioner, and four temperature sensors are up to monitor the temperature in the constant temperature room, as shown in Fig. 6c. The temperature change rate is less than ± 0.05 °C/24 h, as demonstrated in Fig. 6d.

Fig. 6
figure 6

Constant temperature room: a constant temperature room, b temperature sensor, c schematic diagram of temperature monitoring, and d temperature curves

Full size image

Before measurement, it is necessary to turn on the precision air conditioner to air bathe the equipment for more than 7 days to stabilize the internal temperature of the machine tool and the DBB. Since the temperature change rate is less than ± 0.05 °C/24 h, the thermal error in the measurement process is ignored. Additionally, the load error is ignored because the mass of the DBB is much smaller than that of the moving parts of the machine tool.

3.2 Measurement process

3.2.1 DBB installation

First, the two magnetic sockets of the DBB are installed, and their positions are measured. A standard sphere is installed on the C-axis, and the C-axis rotation axis is measured with the Renishaw touch probe OMP400 with a resolution of ± 0.13 μm, as illustrated in Fig. 7a. Magnetic socket 1 is installed at the end of the fixture, and the distance is offset from the C-axis rotation axis. A precision sphere of the same size as the DBB sphere is placed on magnetic socket 1, as illustrated in Fig. 7b. The Renishaw touch probe is used to measure the sphere coordinates, and the offset distance R1 and the offset angle θ1 are calculated.

Fig. 7
figure 7

Magnetic socket 1 installation: a C-axis rotation axis measurement. b Precision sphere coordinate measurement

Full size image

Next, a sharp needle is placed on the B-axis, as illustrated in Fig. 8a. The B-axis is rotated, CCD camera with a resolution of ± 0.01 μm is used to obtain the trajectory of the needle tip, the center of the trajectory is fitted, and the coordinates of the B-axis rotation axis are obtained. Magnetic socket 2 is installed on the B-axis, and the precision sphere is placed on magnetic socket 2, as illustrated in Fig. 8b. The CCD camera is used to measure the sphere coordinates, and the offset distance R2 and the offset angle θ2 are calculated.

Fig. 8
figure 8

Magnetic socket 2 installation: a B-axis rotation axis measurement. b Precision sphere coordinate measurement

Full size image

At this point, the installation of the magnetic sockets and the measurement of the coordinates are completed. R1 = 24.4985 mm, θ1 = 24.3681º, R2 = 23.5697 mm, and θ2 = 1.6073º. The C-axis and the B-axis are rotated through θ1 and θ2, respectively, and then, the angle at this time is defined as 0º in the program coordinate system.

The linear axes are moved so that the coordinates of sphere 1 and sphere 2 coincide in the machine tool coordinate, and then, the X-axis is moved in the positive direction by 50 mm. This point is set as the program zero point, and the DBB is installed as illustrated in Fig. 9a. The Y-axis and Z-axis are reciprocated to observe whether the DBB indication is the smallest at the zero point. If the DBB indication is the smallest at the zero point, the DBB installation toward X direction is completed, and the error measurement work has begun. If the minimum indication appears outside the zero point, then the coordinates of the B-axis, the C-axis rotation axes, and the magnetic sockets are re-measured. The installation method for the Y direction and the Z direction is similar to that for the X direction.

Fig. 9
figure 9

DBB installation: a X direction, b Y direction, and c Z direction

Full size image

3.2.2 Measurement of installation errors

After completing the installation work, the installation errors of the DBB are measured. First, the DBB toward the X direction is installed, and R1 is brought into the Eq. (9) to generate the NC program. The NC program is executed, and the error values are measured during the progress. The measurement is repeated three times to obtain the error curves as illustrated in Fig. 10a, and then, the DBB toward the Y direction is installed. The error curves shown in Fig. 10b are obtained. In the experiment for the measurement of the installation errors, the C-axis speed is 2.76º per second, the program running time is 130 s, and the DBB sampling frequency is 13.889 Hz.

Fig. 10
figure 10

Error curves in XYC-axis motion: a X direction error curves. b Y direction error curves

Full size image

It can be observed from the curves in Fig. 10 that the measurement results have a good repeatability, so the first measured data are taken for sinusoidal fitting, and the sinusoid of the X direction error curves is obtained:

$$\Delta x\left(t\right)=-0.0121\cdot \mathrm{cos}(\omega t+21.9199^\circ )$$

The sinusoid of the Y direction error curves is

$$\Delta y\left(t\right)=0.0120\cdot \mathrm{cos}(\omega t-69.2323^\circ )-0.00460$$

Then, the sinusoid of the Y direction error curves is deformed based on the trigonometric function:

$$\Delta y\left(t\right)=0.0120\cdot \mathrm{sin}(\omega t+20.7677^\circ )-0.00460$$

The sinusoids of the X direction and the Y direction are compared. It can be found that the amplitudes and phase angles of the two are approximately equal, so the installation errors are the main component in the fundamental frequency signal of the error curves. The calculation is performed according to the original data. The calculation results of ΔR1 and Δθ1 are shown in Table 1. Taking the average values, the installation errors are ΔR1 = 0.0046 mm and Δθ1 = 0.00046º.

Table 1 The ΔR1 and the Δθ1 values
Full size table

Similarly, by running the XZB three-axis NC program, the error curves illustrated in Fig. 11 can be obtained.

Fig. 11
figure 11

Error curves in XZB-axis motion: a X direction error curves. b Z direction error curves

Full size image

In accordance with the curves in Fig. 11, the calculation results of ΔR2 and Δθ2 are listed in Table 2; taking the average values, the installation errors are ΔR2 = 0.0063 mm and Δθ2 = 0.00013º.

Table 2 The ΔR2 and the Δθ2 values
Full size table

At this point, the measurement and the calculation of all installation errors are completed. The compensated rotational radii are R1 = 24.5031 mm and R2 = 23.5760 mm. The compensated R1 and R2 are brought into Eq. (3), and the NC program can be generated. The NC program is executed, and the DBB is used to measure the geometric errors of the machine tool. The measurement is repeated three times. In the experiment, the rotational speeds of the C-axis and the B-axis are both 2.83º per second, the program running time is 127 s, and the DBB sampling frequency is 13.889 Hz.

4 Result and discussion

4.1 Measurement result and theoretical result

The five-axis NC program is executed, and the DBB is used to measure the errors of motion along the test trajectory to obtain the error curves, as illustrated in Fig. 12.

Fig. 12
figure 12

Error curves in five-axis motion: a X direction error curves, b Y direction error curves, and c Z direction error curves

Full size image

As shown in Fig. 12, the three measurement results have a good repeatability, the δx are 2.5 μm, 2.4 μm, and 2.4 μm; the δy are 3.7 μm, 3.6 μm, and 3.6 μm; and the δz are 2.9 μm, 3.1 μm, and 3.1 μm. The average value of total error δ is 5.26 μm, which equals to ± 2.63 μm.

The geometric error model of the machine tool is established by using the multi-body system theory, and the accuracy of the error measurement results is analyzed. In accordance with ISO 230–1 [2] and ISO 230–7[34], the 43 geometric error terms of the five-axis ultra-precision machine tool are listed in Table 3.

Table 3 Error terms of five-axis ultra-precision machine tool
Full size table

The five-axis machine tool has three linear axes, which can realize the translation of the B-axis and the C-axis; thus, the position errors can be compensated by calibration in advance. Therefore, the position errors EXOB, EZOB, EXOC, and EYOC can be ignored, and the initial angles of the B-axis and the C-axis are redefined in the NC program, so the zero angle position errors EBOB and ECOB are ignored. Therefore, this research mainly studies the remaining 37 error terms.

In multi-body system theory, a 4 × 4 homogeneous transformation matrix is generally used to describe coordinate transformation in space. The error matrix in the static or moving state between adjacent axes can be obtained by multiplying the basic error matrix. Because only the geometric error of the machine tool is considered in this study and attention is not paid to the installation error of the tool and workpiece, the homogeneous transformation matrixes between the C-axis and workpiece as well as the B-axis and tool are unit matrixes. The ideal static state transformation matrix and the real static state transformation matrix between adjacent axes are listed in Table 4. The ideal motion state transformation matrix and the real motion state transformation matrix between adjacent axes are listed in Table 5.

Table 4 Static state transformation matrix between adjacent axes
Full size table
Table 5 Motion state transformation matrix between adjacent axes
Full size table

When the five-axis ultra-precision machine tool has no error, the measuring point trajectory is consistent with the ideal trajectory, and the real measuring point is consistent with the ideal measuring point. Assume that the coordinate of the measuring point along the tool path is Pt = [Ptx, Pty, Ptz, 1]T, the coordinate of the measuring point along the workpiece is Pw = [Pwx, Pwy, Pwz, 1]T, and the ideal measuring point along the workpiece Pw_ideal can be calculated with the following equation:

$$\left[\prod_{i=1}^{4}{T}_{ip}{T}_{is}\right]{P}_{w\_ideal}=\left[\prod_{j=5}^{7}{T}_{jp}{T}_{js}\right]{P}_{t}$$
(24)

For the tool coordinate, the ideal measuring point along the workpiece Pw_ideal can be expressed as

$${P}_{w\_ideal}={\left[\prod_{i=1}^{4}{T}_{ip}{T}_{is}\right]}^{-1}\left[\prod_{j=5}^{7}{T}_{jp}{T}_{js}\right]{P}_{t}$$
(25)

In the real machining process, due to the 37 geometric error terms in the five-axis ultra-precision machine tool, for the tool coordinate, the real measuring point along the workpiece Pw_real can be expressed as

$${P}_{w\_real}={\left[\prod_{i=1}^{4}{T}_{ip}\Delta {T}_{ip}{T}_{is}\Delta {T}_{is}\right]}^{-1}\cdot \left[\prod_{j=5}^{7}{T}_{jp}\Delta {T}_{jp}{T}_{js}\Delta {T}_{js}\right]{P}_{t}$$
(26)

The resultant error E at the measuring point can be considered as the difference between the Pw_real and the Pw_ideal, which can be calculated with the following equation:

$$E ={[{E}_{x},{E}_{y},{E}_{z},1]}^{\text{T}}={P}_{w\_real}-{P}_{w\_ideal}$$
(27)

where Ex, Ey, and Ez are the error components of the resultant error E in the X, Y, and Z directions.

Thirty-seven geometric error terms of the five-axis ultra-precision machine tool are measured. Part of the measurement process is demonstrated in Fig. 13. The values of each error term are listed in Table 6.

Fig. 13
figure 13

Measurement of geometric error terms: a X-axis positioning error, b X-axis straightness error, c B-axis positioning error, d C-axis rotation error, e squareness error between X-axis and Z-axis, and f squareness error between C-axis and X-axis, g C-axis orientation errors, and h B-axis orientation errors

Full size image
Table 6 Measured values of 37 error terms
Full size table

The 37 geometric error terms and the test trajectory are brought into the machine tool error model, and the theoretical curves of the resultant errors in the X, Y, and Z directions by the interpolated five-axis motion are obtained. These curves are compared with the measurement curves in Fig. 14.

Fig. 14
figure 14

Error curves comparison between theory and measurement: a X direction, b Y direction, and c Z direction

Full size image

From Fig. 14, it can be found that the tendencies of the theoretical curves and measurement curves are generally consistent. The PV values of the theoretical errors in the X, Y, and Z directions are 2.2 μm, 3.4 μm, and 2.8 μm, and the total error δ is 4.92 μm, which is equal to ± 2.46 μm. The differences between the PV values and the total error of theoretical results and measurement results are less than 0.4 μm, which shows good agreement, but there is a large deviation in some areas.

In this research, the error model based on the multi-body system theory is used to calculate the resultant errors of the test trajectory. The tendency, the PV values, and the total error δ of the theoretical results and the measurement results are basically consistent, indicating that the DBB can be used to accurately measure the geometric error of the machine tool. This also proves that the geometric error model of the machine tool established with the multi-body system theory has high reliability and can be used to evaluate the geometry error of the five-axis ultra-precision machine tool.

The reasons for the theoretical curves are not as regular as the measurement curve in the beginning and end areas are as follows:

  1. (1)

    The dynamic error of the machine tool. In the multi-body system theory, only the geometric error of the machine tool is considered, and the dynamic error is not involved. In the measurement process, the geometric error and the dynamic error of the machine tool are both included in the result.

The dynamic errors include the response delays and servo mismatches. The motion speed can be obtained with the derivation of the motion trajectory. When t = 0, the speed in the X direction suddenly accelerates from 0 to – (R1 + R2), while the speeds in the Y and Z directions are still 0. The X-axis motor cannot complete the response in such a short time, so there is a large deviation between the theoretical results and the measurement results in the X direction near the time t = 0, and the deviation between the Y direction and the Z direction is small.

  1. (2)

    Instrument time drift error. In the measurement experiment, at the end of the NC program, the indication of the DBB sometimes changes from 50.0000 to 50.0002 mm or 50.0004 mm, which is an increase of 0.2 − 0.3 μm. The increased length may be the time drift error of the DBB. The existence of the time drift error of the DBB causes the deviation between the theoretical results and the measurement results to gradually increase with time, so the deviation in the end area of the curve is significantly larger than that in the initial area.

  2. (3)

    Machine tool structure. In ultra-precision machine tools, an unloading cylinder is generally used to balance the mass of the Y-axis slider and the C-axis. The connection between the Y-axis slide and the unloading cylinder of the five-axis ultra-precision machine tool used in this experiment is a ball joint. Due to the manufacturing error of the ball joint, there is backlash when the Y-axis reciprocates. In addition, when the Y-axis moves downward, the unloading cylinder is in the exhaust state, and when the Y-axis moves upward, the unloading cylinder is in the suction state. When the movement direction of the Y-axis changes, due to the existence of air damping, the unloading cylinder cannot switch the operating state quickly. These two factors lead to the backlash error when the Y-axis reciprocates.

As shown in Fig. 14b, after the 1000th measurement point, the deviation between the theoretical results and measurements result begins to increase, corresponding to the change of the movement direction of the Y-axis. Therefore, this part of the deviation may be caused by the backlash when the Y-axis reciprocates. When the unloading cylinder structure is used in the Y-axis, the position and the movement direction of the Y-axis should be kept unchanged during the machining process. If the Y-axis reciprocating motion is genuinely required, the Y-axis movement speed should be reduced to avoid large geometric tolerances for the workpiece.

In addition, in the measurement process, the machine tool is affected by external vibration, the fluctuations of air pressure and oil pressure, so the measurement curves are not as regular as the theoretical curves.

4.2 Measurement uncertainty calculation

The resolution of the DBB is 0.1 μm, the display error EDis has a rectangular distribution, and equal probability lies within (− 0.05, 0.05), with associated variance

$$u{\left({E}_{Dis}\right)}^{2}=0.{1}^{2}/12=0.00083{\mu m}^{2}$$

The standard uncertainty of the display error EDis is

$$u\left({E}_{Dis}\right)=0.029{\mu m}$$

Et is the time drift error of the DBB, which increases with the measurement time and presents a rectangular distribution. In 21 measurement experiments, the maximum value is 0.3 μm, and the degrees of freedom is 20. By checking the Appendix Table E.1 in reference [33], it is determined that the inclusion probability is 84%. The standard uncertainty of the time drift error Et is

$$u\left({E}_{t}\right)=0.3/\sqrt{3}=0.173{\mu m}$$

The installation errors ΔR1, Δθ1, ΔR2, and Δθ2 are obtained with a limited number of measurements categorized as type A standard uncertainty, so the standard deviation is calculated as the standard uncertainty. According to the discussion in Sect. 3.2.2, the standard deviation of ΔR1 is 0.051 μm, the standard deviation of Δθ1 is 0.0000043º, the standard deviation of ΔR2 is 0.040 μm, and the standard deviation of Δθ2 is 0.0000023º. Taking sin ωt = cos ωt = 1, the standard uncertainty of the installation error EIn is

$${u}^{2}\left({E}_{In}\right)\text{=}{0.051}^{2}+{24503.1}^{2}\cdot {0.0000043}^{2}+{0.04}^{2}+{23576}^{2}\cdot {0.0000023}^{2}=0.0182{\mu m}^{2}$$

or \(u\left({E}_{In}\right)=0.134{\mu m}\)

The diameter of the DBB sphere is 12.7 mm, and the diameter of the contact area between the magnetic socket and sphere is 8 mm. According to the geometric relationship, the error coefficient caused by the sphericity error ESp in the length direction is 8/12.7 = 0.63. The precision level of the DBB sphere is AFBMA10. The sphericity error is less than 0.15 μm, and it is normally distributed. The inclusion probability is 99%. By checking the Appendix Table G.2 in reference [33], using the t factor t99(∞) = 2.576, it is determined that the standard uncertainty of the sphericity error ESp is

$$u\left({E}_{Sp}\right)=0.63\cdot 0.15/2.576=0.037{\mu m}$$

The calibration ruler error ECali is less than 0.1 μm, with a normal distribution, and the inclusion probability is 99%. Using the t factor t99(∞) = 2.576, the standard uncertainty of the calibration ruler error ECali is

$$u\left({E}_{Cali}\right)=0.1/2.576=0.039{\mu m}$$

In summary, the combined standard uncertainty of the geometric error in the X direction is

$${u}^{2}\left(\varepsilon \right)\text{=}{0.029}^{2}+{0.173}^{2}+{0.134}^{2}+{0.037}^{2}+{0.039}^{2}=0.052{\mu m}^{2}$$

or \(u\left(\varepsilon \right)=0.227{\mu m}\)

After calculation, the standard uncertainty of the X direction geometric error is determined to be 0.227 μm, and the relative uncertainty is determined to be 0.077. Similarly, the standard uncertainty of the Y direction geometric error is 0.175 μm, and the relative uncertainty is 0.048, the standard uncertainty of the Z direction geometric error is 0.022 μm, and the relative uncertainty is 0.007.

According to the measurement uncertainty calculation, the uncertainty of the geometric error is less than 0.2 μm, and the relative uncertainty is less than 0.1, which proves that the measurement results are credible. At the same time, according to the calculation process, the time drift error Et and the installation error EIn account for a large proportion of the uncertainty. Therefore, a faster running speed should be chosen, and the measurement time should be decreased to reduce the influence of the time drift error Et. Additionally, when measuring the installation error, measurement equipment with higher accuracy should be selected as often as possible or the number of measurements should be increased to reduce the uncertainty of the installation error EIn.

In this research, a new measurement method is proposed that uses a DBB to measure the geometric error of a five-axis ultra-precision machine tool in the interpolated five-axis motion. Although the deviation is large in some areas, the tendency, the PV values, and the total error of the theoretical results and the measurement results are basically consistent. The difference between the PV values and the total error is less than 0.4 μm.

It is proven that the DBB can accurately measure the geometric error of the five-axis ultra-precision machine tool, and this method can be used as a more stringent measurement method to measure the geometric error of the machine tool. When the geometric error measured with this method meets the design index, the accuracy of the machine tool can be considered qualified.

At the same time, the method in this research can be used to complete the geometric error measurement of the five-axis machine tool effectively using only a DBB, and it is simpler than the traditional method. In addition, the large deviation in some areas also reflects the limitation of the multi-body system theory. In follow-up research, the theory needs to be further optimized, and the dynamic error part needs to be added to the multi-body system theory to make it closer to the error situation of machine tools.

5 Conclusions

In this paper, a measurement method based on the DBB is proposed that can measure the geometric error of a five-axis ultra-precision machine tool, and the measurement experiments are carried out using a five-axis ultra-precision machine tool with a w–C-Y–Z-b-X-B-t layout. The method can be used to measure the resultant errors in the X, Y, and Z directions of a five-axis ultra-precision machine tool by only one measurement equipment and one-time installation. Compared with the measurement methods mentioned in the ISO 230–1, the method proposed in this research is less limited by the layout of machine tools and can be used to perform the error measurement for five-axis ultra-precision machine tools.