1 Introduction

The improvement of machine tools’ accuracy is of great importance for modern precision manufacturing process [1, 2]. The error modeling and compensation is widely used to improve the machine tool accuracy due to its economy and convenience. Multi-body theory system, screw theory, and vector chain expression are the main error modeling methods which have been widely used [3,4,5]. But the measurement accuracy of kinematic errors will directly affect the effects of error compensation. Therefore, rapid and accurate measurement of kinematic errors is significant for machine tool error compensation. Various approaches have been presented to improve the error modeling methods to increase the machine tool error compensation accuracy.

Machine tool error compensation is to establish the error transfer model and offset the error that causes the deviation between the tool tip and the workpiece. The determination of appropriate error parameters can directly affect the accuracy of the error model, which will deal with the certain hierarchy of geometric errors, kinematic errors, and volumetric errors. Ekinci et al. [6] proposed the methodology based on the derivation of tool position error and experimentally verified the relationships between straightness and angular kinematic errors. Ekinci et al. [7] further established an improved analytical model in which the internal mechanisms causing motion errors are considered, and the relationship between the motion errors of the axis’ carriage and the guideways’ geometric errors are investigated. Majda [8] presented an analytical method to investigate the effects of geometric errors on joint kinematic errors. Zhang et al. [9] presented a novel model of the hydrostatic guideways motion errors, and the effects of geometric errors of guide rails on motion errors are studied. Generally, it is clear that using the kinematic error is easier and more accurate than using geometric errors to establish the volumetric error model.

The optic methods are extensively used to measure the kinematic errors of machine tools and the error compensation strategies are established based on the measured errors [10,11,12,13]. Aguado et al. [14] discussed different error identification methods and presented an error identification strategy in volumetric error compensation of machine tools based on laser tracker measurements. Ezedine et al. [15] proposed a novel method for error calibration and compensation of a compact extra-small CNC bridge machine tool. Linares et al. [16] proposed a novel error measurement and compensation strategy based on a tracking interferometer and the multilateration method. Xiang et al. [17] measured the kinematic errors of a multi-axis spiral bevel gears milling machine, and volumetric error prediction and compensation models are gained by the forward and inverse kinematics modeling via the screw theory. Givi et al. [18] discussed the relevance of the volumetric error and the machined feature, and the corresponding optimized error compensation are subsequently proposed. Zhou et al. [19] investigated the geometric modeling and compensation of machine tools, and homogenous transformation and differential motion matrix using multi-body theory were used to enhance the machine tool accuracy. Fu et al. [20] presented one novel model of squareness errors using the D-H matrix to improve the accuracy of integrated geometric errors of the machine tools. Khan et al. [21] measured the kinematic errors, and an efficient recursive compensation methodology was used to remove the machine tool errors. Vahebi et al. [22] categorized the linear axis in two different extruding type, and sliding type with different error models and corresponding error compensation strategies are proposed. Wu et al. [23] proposed an iterative compensation method to improve the machining accuracy of a non-orthogonal five-axis machine tool, and nine-line method was used to obtain the geometric errors. Zha et al. [24] presented an approach to model and compensate the vertical straightness error of gantry type open hydrostatic guideways. Zhong et al. [25] presented an improved volumetric compensation method based on a squareness error identification method. Mostafa et al. [26, 27] considered the Abbe effects in homogeneous transformation matrix–based models and proposed an improved kinematic error model.

The volumetric error models and error compensation methods abovementioned have been investigated by some scholars in order to improve the machine tool volumetric accuracy. However, due to the distortion of the slide table, there exists some ambiguity in the identification of positioning and straightness errors, which may lead to some inaccuracy of volumetric error compensation. Furthermore, the measurement of the squareness error is usually performed only within the local stroke range of two measuring axes, which results in some differences between the global squareness values and the measurement results. The forward error modeling needs accurate kinematic errors as input; however, the measurement errors of linear and squareness errors caused by aforementioned reasons have not been considered in the previous error models. Therefore, different error measuring tests may obtain different linear and squareness error results, especially for the machine tool with large size worktable and long stroke guideways.

In order to solve these problems, a novel solution for decreasing the measurement errors of linear and squareness error measurement is proposed in this paper. The aim is to obtain the contribution of linear and squareness errors in machine tool volumetric error transfer and enhance the accuracy of volumetric error compensation. For linear errors, the decreasing of the measurement errors is based on a multi-laser calibrator (MLC) and corresponding error correction calculation. The peculiarity of the MLC is that it can obtain six kinematic errors of a translational axis at the same time. In this way, the effects of the distortion of the slide table on measured kinematic errors are equivalent, thereby the correction of linear errors can be implemented. For squareness errors, the correlation between the measured local squareness errors and global squareness errors is theoretically analyzed and the corresponding error correction method is presented. The squareness errors are corrected through modifying local squareness errors measured with double ball bar to global squareness errors, with the aid of straightness errors measured with MLC. Finally, some experiments are completed to verify the error correction methods in JIG630 precision machine tool.

The remains of this paper are organized as follows. The methodology of the improved error compensation method, including volumetric error modeling, mechanism of measurement error, and the corresponding error correction method, is proposed in Section 2. In Section 3, the 18 errors of three axes are experimentally measured, corrected, and validated. Furthermore, the squareness errors are measured with a double ball bar with different bar lengths. And the correction from local squareness errors to global squareness errors is investigated. In Section 4, the effects of linear and squareness error correction method (LSECM) is validated in a machine tool volumetric error compensation. Four compensated volumetric diagonal errors with LSECM and direct measurement method (DMM) are measured and compared. Finally, conclusions are presented in Section 5.

2 The methodology of the improved error compensation

In order to decrease the measurement errors of kinematic errors of machine tools, an improved error compensation method is proposed in this paper. Not only the mechanism of the measurement errors is theoretically analyzed but also the validating experiments are carried out. For clarity, the flow-process diagram of improved error compensation method is given in Fig. 1. Detailed process of the improved error compensation based on LSECM is described as follows:

  1. 1.

    Volumetric error modeling. The machine tool structure and the corresponding spatial error expressions are given.

  2. 2.

    Mechanism analysis of measurement errors. The mechanism of measurement errors of linear and squareness errors is analyzed in detail and the error correction method is proposed then.

  3. 3.

    21 error measurement. The 18 kinematic errors of three axes and the squareness errors are measured with Renishaw MLC and double ball bar respectively.

  4. 4.

    Volumetric diagonal error measurement. The volumetric diagonal errors without error compensation are measured with Renishaw XL-80 laser interferometer to validate the volumetric error modeling method.

  5. 5.

    The error correction of linear and squareness errors. The linear and squareness errors are corrected based on the proposed error correction method and the corresponding verification experiments are taken then.

  6. 6.

    Uncertainty analysis. The uncertainty of the kinematic errors is analyzed with Monte Carlo method and the influence of random measurement error on the standard deviation of each identified error motion is analyzed.

  7. 7.

    Volumetric diagonal errors with different compensation methods. The volumetric error compensation data is calculated with LSECM and DMM and the volumetric diagonal errors are measured subsequently to evaluate the effects of measurement errors on volumetric accuracy.

  8. 8.

    Data comparison and analysis. The comparison between calculated and experimental results is carried out and systematic analysis is taken then.

Fig. 1
figure 1

Flow-process diagram of error compensation based on LSECM

Full size image

2.1 Volumetric error modeling

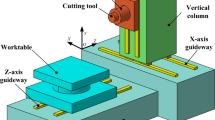
For the machine tool with the topology as shown in Fig. 2, the error transfer chain can be divided into two chains, from bed to workpiece and from bed to tooltip. The relative displacement between tooltip and workpiece in the machine tool can be regarded as the vector stacking of its linear and angular displacement in the reference coordinate system. The multi-body system theory is used to model the mapping relationship between 21 errors and volumetric errors. According to the previous researches [28,29,30], the spatial errors Δe in X, Y, and Z directions can be formulated as follows:

$$ {\displaystyle \begin{array}{c}\varDelta {e}_x={\delta}_x(X)+{\delta}_x(Y)-{\delta}_x(Z)-Y\left({\alpha}_{xy}+{\varepsilon}_z(X)\right)+{z}_{34}\left({\varepsilon}_y(X)+{\varepsilon}_y(Y)\right)+Z{\varepsilon}_y(Z)\\ {}+{\gamma}_{xz}{z}_{01}-{\varepsilon}_z(X){y}_{23}+{\varepsilon}_y(Z){z}_{01}-\left({\gamma}_{xz}+{\varepsilon}_y(Z)\right)\left({z}_{02}+{z}_{23}+{z}_{34}\right)+{\varepsilon}_z(Z)\left(Y+{y}_{02}+{y}_{23}+{y}_{34}\right)\\ {}+{z}_{tool}\left({\varepsilon}_y(X)-{\beta}_{xz}+{\varepsilon}_y(Y)-{\varepsilon}_y(Z)\right)\end{array}} $$
(1)
$$ {\displaystyle \begin{array}{c}\varDelta {e}_y={\delta}_y(X)+{\delta}_y(Y)-{\delta}_y(Z)+{\varepsilon}_z(Z){x}_{01}+\left({\beta}_{yz}+{\varepsilon}_x(Z)\right)\left({z}_{02}+{z}_{23}+{z}_{34}\right)-{\varepsilon}_z(Z)\left(X+{x}_{02}\right)\\ {}-{z}_{34}\left({\varepsilon}_x(X)+{\varepsilon}_x(Y)\right)-Z{\varepsilon}_x(Z)-{\beta}_{yz}{z}_{01}-{z}_{01}{\varepsilon}_x(Z)+{z}_{tool}\left[{\beta}_{yz}+{\varepsilon}_x(Z)-{\varepsilon}_x(Y)-{\varepsilon}_x(X)\right]\end{array}} $$
(2)
$$ {\displaystyle \begin{array}{c}\varDelta {e}_z={\delta}_z(X)+{\delta}_z(Y)-{\delta}_z(Z)-\left({\gamma}_{xz}+{\varepsilon}_y(Z)\right){x}_{01}-\left({\beta}_{yz}+{\varepsilon}_x(Z)\right)\left(Y+{y}_{02}+{y}_{23}\right)\\ {}+{\varepsilon}_x(X)\left(Y+{y}_{23}\right)-{y}_{tool}\left({\beta}_{yz}+{\varepsilon}_x(Z)-{\varepsilon}_x(X)-{\varepsilon}_x(Y)\right)+\left(X+{x}_{02}\right)\left({\gamma}_{xz}+{\varepsilon}_y(Z)\right)\end{array}} $$
(3)
Fig. 2
figure 2

Machine tool structure and coordinates

Full size image

2.2 Mechanism and correction of the measurement errors of linear errors

2.2.1 The mechanism of the measurement errors of linear errors

The laser interferometer is one of the widely used instruments to measure the kinematic errors of translational axis. The accuracy of the measured machine tool kinematic errors has direct and significant effects on machine tool volumetric error compensation. Therefore, accurate measurement of each error component and the data extraction analysis are critical for error compensation. Taking Z axis as an example, due to the existing of the machining error and assembling error, the slide table will distort while moving along the guideways. For a general interferometer, it is time-consuming work to obtain all six kinematic errors of a translational axis since six times optic collimations are necessary. And more importantly, the installation places of the interference mirror inevitably variate in each measurement setting and may lead to some unexpected errors. The illustration of the measurement error mechanism of linear errors is shown in Fig. 3. The measured errors by the interferometer include two parts: (1) kinematic errors in the slide table, (2) interferential measurement error caused by the distortion of the worktable. The measured positioning and straightness errors can be formulated as following equations:

Fig. 3
figure 3

Schematic diagram of measurement error generating of linear errors

Full size image
$$ {\delta}_z{(Z)}_{mea}={\delta}_z{(Z)}_{wt}+\varDelta {\delta}_z(Z)={\delta}_z{(Z)}_{wt}+{L}_{w-o}^{p_1}\sin \left({\varepsilon}_x{(Z)}_{p_1}\right) $$
(4)
$$ {\delta}_x{(Z)}_{mea}={\delta}_x{(Z)}_{wt}+\varDelta {\delta}_x(Z)={\delta}_x{(Z)}_{wt}+{L}_{w-o}^{p_2}\sin \left({\varepsilon}_z{(Z)}_{p_2}\right) $$
(5)
$$ {\displaystyle \begin{array}{c}{\delta}_y{(Z)}_{mea}={\delta}_y{(Z)}_{wt}+\varDelta {\delta}_y{(Z)}_1+\varDelta {\delta}_y{(Z)}_2\\ {}={\delta}_y{(Z)}_{wt}-{L}_{w-o}^{p_3}\left[2-\cos \left({\varepsilon}_x{(Z)}_{p3}\right)-\mathit{\cos}\left({\varepsilon}_z{(Z)}_{p3}\right)\right]\end{array}} $$
(6)

where δz(Z)mea, δx(Z)mea, and δy(Z)mea are the measured positioning and straightness errors, and δz(Z)wt, δx(Z)wt, and δy(Z)wt are the pragmatic kinematic errors in worktable surface plane.

Due to the slide table distortion and the variation of the installation positions of the interference mirror in 6 kinematic error measurement, the angular errors of the mounting rod of the interference mirror are different in each kinematic error measurement. Therefore, the ambiguity of the workbench kinematic errors is hard to be eliminated through mathematical calculation.

2.2.2 The linear error correction method

The linear measurement error through the implementation of the error correction method is addressed in this paper. The linear error correction method is constructed by a novel MLC and the corresponding mathematical calculation. For a 95% confidence level, the accuracy of the MLC in positioning, straightness, and angular error measurement are ± 0.5 ppm, ± 0.01A ± 2 μm, and ± 0.006B ± (0.5 μrad + 0.1M μrad), where A is the display straightness error, B is the display angular error, and M is the measurement length.

For the purpose of minimizing the effects of random error on kinematic error measurement, the six errors of an axis should be measured at least five times. The MLC is shown in Fig. 4, four laser beams are generated by a laser launcher and received by the receiver. Three laser beams are used to detect the yaw and pitch errors. The yaw error can be calculated from the deviations between lasers 1 and 2 and the pitch error can be obtained from the differences between lasers 2 and 3. The positioning, vertical and horizontal straightness errors at the position of beam 4 are obtained by the combination of beams 1, 2, and 3. In addition, the roll error are measured by the deviation of laser beam 4 on the position sensitive detector. Part of the straightness beam is split onto a separate roll detector and the roll error is measured optically.

Fig. 4
figure 4

Measuring principle of multi-laser calibrator

Full size image

The MLC can detect six errors of a translational axis simultaneously in a single setup. In this way, compared with the general interferometer, the time of a translational axis kinematic error measurement can reduce at least five sixths. Since the six errors of a translational axis are measured simultaneously, the ambiguity of the measurement kinematic errors can be eliminated by mathematical calculation and the kinematic errors of the slide table can be formulated as follows:

$$ {\delta}_z{(Z)}_{wt}={\delta}_z{(Z)}_{mea}-\varDelta {\delta}_z(Z)={\delta}_z{(Z)}_{mea}-{L}_{w-o}\sin \left({\varepsilon}_x{(Z)}_{mea}\right) $$
(7)
$$ {\delta}_x{(Z)}_{wt}={\delta}_x{(Z)}_{mea}-\varDelta {\delta}_x(Z)={\delta}_x{(Z)}_{mea}-{L}_{w-o}\sin \left({\varepsilon}_z{(Z)}_{mea}\right) $$
(8)
$$ {\displaystyle \begin{array}{c}{\delta}_y{(Z)}_{wt}={\delta}_y{(Z)}_{mea}-\varDelta {\delta}_y{(Z)}_1-\varDelta {\delta}_y{(Z)}_2\\ {}={\delta}_y{(Z)}_{mea}+{L}_{w-o}\left[2-\cos \left({\varepsilon}_x{(Z)}_{mea}\right)-\mathit{\cos}\left({\varepsilon}_z{(Z)}_{mea}\right)\right]\end{array}} $$
(9)

2.3 Mechanism and the correction of the measurement errors of squareness errors

2.3.1 The mechanism of the measurement errors of squareness errors

Squareness error is an important part of a machine tool kinematic errors which can significantly affect the machine tool volumetric accuracy. Double ball bar is one of the most widely used instruments to measure squareness as shown in Fig. 5. The double ball bar can detect the squareness errors of XY, YZ, and XZ planes through the machine movements along path 1, path 2, and path 3. It is recommended to use measuring rod as long as possible to avoid the effect of local squareness. Unfortunately, it is barely possible for the double ball bar to accurately measure the global squareness unless the length of measuring rod rm is equal as half of the measured guideway stroke.

Fig. 5
figure 5

Measuring paths of squareness error with double ball bar

Full size image

Generally, the double ball bar can only measure the local squareness error of two axes. The mechanism of the measurement error between local and global squareness error is depicted in Fig. 6. For the case 1, when the worktable moves along measuring stroke 1, the slide table moves along measuring stroke 3, the measured local squareness error is recorded as\( {{}^l\beta}_{yz}^{1,3} \). However, for the case 2, that worktable moves along measuring stroke 2 and the slide table moves along measuring stroke 4, the measured local squareness error is \( {{}^l\beta}_{yz}^{2,4} \). According to Fig. 5, the measured local squareness error \( {{}^l\beta}_{yz}^{1,3} \) exceeds 90° but \( {{}^l\beta}_{yz}^{1,3} \) is less than 90°, which leads to some ambiguity of the angel between Y and Z axes. Furthermore, both squareness errors obtained in two measurements cannot present the actual global squareness.

Fig. 6
figure 6

The mechanism of the measurement error of squareness error

Full size image

2.3.2 The local squareness error correction method

In order to correct the local squareness error to global squareness error, the global squareness error correction method is presented in this subsection.

For the case 1, that the worktable moves within measurement stroke 1 and slide table moves within measurement stroke 3, the measured local squareness error is \( {{}^l\beta}_{yz}^{1,3} \). Observing the geometric correlations in Fig. 5, for the triangles ΔBJK and ΔEKL, the angles in two triangles satisfy the following equations:

$$ \left\{\begin{array}{c}{{}^l\beta}_{yz}^{1,3}+\theta \hbox{'}+{\theta}_1=\pi \\ {}{{}^g\beta}_{yz}+\theta \hbox{'}+{\theta}_2=\pi \end{array}\right. $$
(10)

Eliminating θ' from Eq. (10) and the global squareness gβyz can be expressed as:

$$ {{}^g\beta}_{yz}={{}^l\beta}_{yz}^{1,3}+{\theta}_1-{\theta}_2 $$
(11)

Similarly, in the case 2 of shorter measurement strokes, when the worktable moves within measurement stroke 2 and slide table moves within measurement stroke 4, the measured local squareness error is\( {{}^l\beta}_{yz}^{2,4} \). Obviously, the measured local squareness error \( {{}^l\beta}_{yz}^{2,4} \). is larger than\( {{}^l\beta}_{yz}^{1,3} \)., but the pragmatic global squareness errors of two axes in two measurements are consistent. According to the angular correlations in triangles ΔDMN and ΔNRG, the following equations can be obtained:

$$ \left\{\begin{array}{c}{{}^l\beta}_{yz}^{2,4}+\theta \hbox{'}\hbox{'}+{\theta}_3=\pi \\ {}{{}^g\beta}_{yz}+\theta \hbox{'}\hbox{'}+{\theta}_4=\pi \end{array}\right. $$
(12)

Eliminating θ ' ' from Eq. (12) and the global squareness gβyz can be expressed as:

$$ {{}^g\beta}_{yz}={{}^l\beta}_{yz}^{2,4}+{\theta}_3-{\theta}_4 $$
(13)

Finally, the angles θ1, θ2, θ3, and θ4 can be calculated by the straightness errors of Z and Y axes as follows:

$$ \left\{\begin{array}{c}{\theta}_1=\left({\delta}_y{\left(\mathrm{Z}\right)}_A-{\delta}_y{\left(\mathrm{Z}\right)}_B\right)/2{r}_m\\ {}{\theta}_2=\left({\delta}_z{\left(\mathrm{Y}\right)}_F-{\delta}_z{\left(\mathrm{Y}\right)}_E\right)/2{r}_m\\ {}{\theta}_3=\left({\delta}_y{\left(\mathrm{Z}\right)}_C-{\delta}_y{\left(\mathrm{Z}\right)}_D\right)/2{r}_m\\ {}{\theta}_4=\left({\delta}_z{\left(\mathrm{Y}\right)}_H-{\delta}_z{(Y)}_G\right)/2{r}_m\end{array}\right. $$
(14)

Thus, though the measured local squareness errors are different in two cases, theoretically, the calculated global squareness errors are consistent. But, considering the effects of the random errors, the longer radius of the double ball bar is recommended to detect the squareness.

3 The validation of the linear and squareness error correction methods

To eliminate the effects of the ambient temperature fluctuating, all experiments were carried out in a thermostatic laboratory with a constant temperature of 20 ± 0.5 °C. The stroke of X axis is 1000 mm and the other two axes are 900 mm, positive directions of the angular error and the squareness error are based on the right-hand rule.

3.1 The corrected linear errors

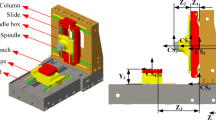
The kinematic errors of the Z axis are measured with the Renishaw XL80 interferometer and MLC simultaneously as seen in Fig. 7. The interferometer and the laser launcher of the XM60 are placed on the worktable while the laser reflector and the receiver are installed on the spindle. The measured positioning error and straightness error by MLC is corrected through Eqs. (7)–(9). In the ideal situation, the measured linear errors by interferometer and MLC should be equal with each other. However, due to the existing of measurement errors discussed in Subsection 2.2 and uncertainty of the instruments, there are some little difference among the measured linear errors. Take Z axis as an example, the deviations of the detected linear errors by two instruments are depicted in Fig. 8. The deviations of the positioning error δz(Z) and straightness error δx(Z) δy(Z) measured by the laser interferometer are approximately 2.1 μm, 1.2 μm, and 1.5 μm, respectively, compared to the corrected results by MLC.

Fig. 7
figure 7

The kinematic error measurement experiment with XM60 MLC and XL80 Interferometer

Full size image
Fig. 8
figure 8

The measurement results of linear errors with different instruments. a Positioning error of Z axis. b Straightness error of Z axis

Full size image

In order to eliminate the effects of measurement errors on linear errors, the measured results are corrected according to the Eqs. (7)–(9) in Section 2. The length of Lw-o is 75 mm and the corrected errors of three translational axes errors are presented in Fig. 9. The solid line in Fig. 9 presents the measured linear errors and the dash dot line presents the corrected final kinematic errors. Comparing three axes kinematic errors, the basic kinematic accuracy of the X axis and the Z axis is higher than that of the Y axis. The maximum positioning errors of the X, Y, and Z axes are about 4 μm, 16 μm, and − 12 μm respectively. The three angular errors of the Z axis are all less than 8 μm/m in its full stroke, and the maximum angular error of the X axis and the Y axis can reach 25 μm/m and 60 μm/m, respectively. The measured and corrected linear errors of X and Z axes are basically the same, whereas the measured and corrected positioning error δy(Y) and straightness error δx(Y) have some deviations. Since the angular errors of Y axis are bigger than that of X and Z axes, thereby the variation of the measured and corrected Y axial linear errors are more obviously than other two axes.

Fig. 9
figure 9

18 kinematic errors of three axes with error bars including corrected linear errors. a X axis. b Y axis. c Z axis

Full size image

The uncertainty analysis based on Monte Carlo method is carried out for the purpose of evaluating the effect of MLC random error on each measured kinematic error. The simulated results are marked by error bar as shown in Fig. 9. For the purpose of minimizing the effects of random measurement error, the six errors of each axis are measured five times and the measured results are of good repeatability. Therefore, the corrected linear errors have high confidence.

3.2 The corrected squareness errors

The squareness errors of a precision machine tool are measured with the Renishaw RC-20 double ball bar and the radius of the circular test is selected as 100 mm/300 mm. Figure 10 showns the straightness errors at the position of different squareness error measurements. The difference of the straightness errors in different squareness error measurement range can be calculated as shown in Table 1. Therefore, the local squareness errors can be corrected to global squareness errors by the LSECM presented in Subsection 2.3. Furthermore, the measured, calculated and corrected squareness errors are given in Table 2 and the experimental photos are presented in Fig. 11. The negative symbol of the squareness error means that the angle between the two positive axes is less than 90°.

Fig. 10
figure 10

The straightness errors used for correction of squareness errors. a X axis. b Y axis. c Z axis

Full size image
Table 1 The straightness errors in different squareness measurement ranges
Full size table
Table 2 The measured and corrected squareness errors
Full size table
Fig. 11
figure 11

Squareness error measurement using double ball bar. a Bar length of 300 mm. b Bar length of 100 mm

Full size image

The measured squareness errors with diverse radiuses are different and have about 2.8~11.3 μm/m deviations. Note that the sign of the measured XZ squareness error in two cases are different. The measured squareness in case 1 indicates that the angle between X axis and Z axis is an acute angle. However, the measured squareness in case 2 indicates that the angle between X axis and Z axis is an obtuse angle. And this difference lies that only local squareness errors are measured in both cases. Thus, in order to eliminate this difference, the squareness error correction should be carried out to obtain the global squareness. According to the squareness correction method mentioned in Section 2.3, the deviations of the measured local squareness errors can be calculated. By substituting the calculated squareness deviations into measured local squareness errors, the corrected global squareness errors are obtained.

The uncertainty of the identified squareness error is evaluated by Monte Carlo method and depicted in Table 2. The standard deviations of the calculated squareness errors in case 1 are about 3 μm/m. However, the standard deviations of the calculated squareness errors in case 2 are about 9 μm/m and they are about 3 times bigger than case 1. According to Eq. (14), the denominators in both cases are smaller than 1, which means that the measurement errors are amplified. Furthermore, the denominator in case 2 is three times smaller than case 1. Thus, the measurement error in case 2 is about three times larger than case 1. This error amplification phenomenon will be improved in the case of a longer measurement stroke. Therefore, for the precision machine tool, the measuring radius of the double ball bar should be as long as possible. In this paper, the obtained kinematic errors are measured with multiple times for the purpose of minimizing the effects of random measurement error.

The comparison of the measured, calculated, and corrected squareness errors is shown in Fig. 12. It can be seen that the corrected global squareness errors in XY and ZX planes are absolutely inconformity with the measured results. Taking squareness of XY plane as example, the measured results show that the angle between the positive X and Y axes is less than 90°, but the corrected results are opposed. Note that the straightness error δx(Y) shown in Figs. 9 and 10 is positive and the measuring stroke of the slide table is between 38 mm and 638 mm. Furthermore, the straightness error δx(Y) in position 638 mm is larger than which in 38 mm; thereby, the measured squareness in this stroke is negative.

Fig. 12
figure 12

Comparison of the measured, calculated, and corrected squareness errors

Full size image

4 The error compensation experiments and analysis

4.1 The setup of the experiments

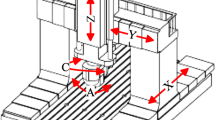
Experiments are carried out in this section for the purpose of comparing the accuracy of the models based on LSECM and DMM respectively. The errors of four volumetric diagonals without error compensation and with different error compensation methods are measured and analyzed. According to the ISO 230-6 [31], four volumetric diagonals are named as PPP, NPP, PPN, and NPN, where P and N means the positive and negative moving orientation of the axis (see Fig. 13). The Renishaw interferometer XL80 has been adopted to complete the diagonal error measurement as shown in Fig. 14.

Fig. 13
figure 13

Sketch of volumetric diagonal measuring paths

Full size image
Fig. 14
figure 14

The measurement of volumetric diagonal errors. a PPP. b NPP. c PPN. d NPN

Full size image

4.2 The comparison of the volumetric diagonal errors of measurement and modeling

According to the volumetric modeling and error corrected methods proposed in Section 2, the volumetric diagonal errors based on LSECM and DMM are obtaind. The comparision of the predicted volumetric diagonals based on LSECM and DMM are presented in Fig. 15. The results indicate that the calculated diagonal curves with LSECM have better fitting ability than DMM. In other words, the deviations of the diagonal curves with DMM and LSECM are caused by the measurement errors. The mean squared error (MSE) and the R-square of the calculated diagonal curves based on LSECM and DMM are calculated in Table 3 to evaluate the fitting performance. Theoretically, the smaller MSE is and the closer R-square is to 1, the better fitting performance the predicted models have [32]. The calculated MSEs based on LSECM are much smaller than DMM and the R-square values of the diagonal curves calculated by LSECM are closer to 1. The maximum improvement of the MSE of four diagonals is 67.1286 and the R-square value is improved from 0.8204 to 0.9958.

Fig. 15
figure 15

The comparison of the measured and calculated volumetric diagonal errors. a PPP. b NPP. c PPN. d NPN

Full size image
Table 3 The MSE and R-square of the calculated diagonal curves
Full size table

4.3 The comparison of the compensation effects with LSECM and DMM

The NC coordinates adjustment method is used to compensate the volumetric diagonal errors for the purpose of evaluating the error compensation performance of LSECM and DMM. Figure 16 indicates the compensated volumetric diagonal errors with LSECM and DMM. Both error compensation methods significantly improved volumetric diagonal accuracy. However, LSECM has better compensation performance than DMM. In contrast with DMM, the bidirectional systematic deviation of the positioning of PPP, NPP, PPN, and NPN with LSECM are reduced from 19.8 μm, 12.2 μm, 9.6 μm, 6.7 μm to 3.7 μm, 7.9 μm, 6.8 μm, and 6.4 μm respectively.

Fig. 16
figure 16

The comparison of the volumetric diagonal errors compensated with LSECM and DMM. a PPP. b NPP. c PPN. d NPN

Full size image

The LSECM can significantly improve the volumetric accuracy of the machine tool. On the one hand, the deviations of the linear errors are corrected and the volumetric diagonal accuracy is improved. On the other hand, the measured local squareness errors are corrected to global squareness errors; thereby, the effects of the squareness errors on volumetric errors are corrected. Furthermore, in some conditions, the directions of the measured local squareness and the global squareness are opposite, and may lead to the poor volumetric compensation effects. Thus, the squareness error correction is essential for volumetric accuracy improvement. According to the experimental results, the bidirectional systematic deviation of positioning of four volumetric diagonals with improved error compensation method reduced about 81.3%, 35.2%, 29.2%, and 4.5% respectively.

5 Conclusion

An improved error compensation method for machine tools is proposed and described in this paper. The mechanism of the measurement errors of linear and squareness errors is investigated in detail. The linear errors, including position errors and straightness errors, are corrected by considering the distance effect between optical mirror groups and the surface of worktable. The squareness errors are corrected through modifying local squareness errors measured with double ball bar to global squareness errors, with the aid of straightness errors measured with multi-laser calibrator.

The experiments illustrated that the squareness errors measured in different measuring strokes have marked difference. Furthermore, the calculated volumetric diagonal errors based on improved error compensation method have better fitting performance than which using direct measurement method. The values of the mean squared error and R-square of calculated and measured diagonal errors can be improved with the improved error compensation method. The maximum improvement of the mean squared error of four diagonals is 67.1286 and the R-square value is increased from 0.8204 to 0.9958. Contrast with the direct measurement method, the bidirectional systematic deviation of positioning of PPP, NPP, PPN, and NPN with improved error compensation method reduced about 81.3%, 35.2%, 29.2%, and 4.5% respectively.

The improved error compensation method with measurement error correction proposed in this paper has universal applicability, which can be used for error prediction and analysis of other topological machine tools and robots.