1 Introduction

To date, product assembly technology is going through a critical period of transition from manual and experienced assembly to automated and intelligent assembly. Digital twin assembly technology provides a new development idea and manufacturing paradigm for the realization of scientific assembly, which is triggering a major and profound technological change in the complex product assembly industry [1, 2]. As one of key enabling technologies in digital twin-based assembly precision analysis, assembly tolerance analysis technology is of great significance for effectively guiding the actual assembly operation process, improving assembly efficiency, accuracy, and quality, and improving product assembly performance [3, 4].

With the continuous development of electromechanical products in the direction of complexity, high precision, and stable performance, the product AFRs are getting higher and higher, and the assembly performance assurance is becoming more and more difficult. Assembly accuracy, as one of the most key parameters, is an important evaluation indicator to measure the product assembly quality and assembly performance, which refers to the maximum allowable error value of the specified geometric elements in a specified direction after assembling. The assembly tolerance analysis technology is mainly used to verify whether the geometric dimensioning and tolerancing (GD&T) design scheme in the product design stage can meet the AFRs of mechanical assemblies, which is generally determined by part manufacturing error modeling, assembly deviation propagation, and accumulation. With the continuous pursuit of higher accuracy for high precision mechanical assemblies, the accuracy requirements of assembly tolerance analysis are also continuously improved. Therefore, as one of important means to ensure product performance, assembly tolerance analysis is an effective method of predicting the final assembly accuracy by using relevant technical approaches and calculation models before implementing assembling so as to obtain assembly accuracy in advance and provide a guidance to optimize parameters in tolerance specification and allocation in mechanical assemblies [5,6,7].

Compared with traditional one or two dimensional (1/2D) assembly tolerance analysis methods which only consider dimensional and positional tolerances, 3D assembly tolerance analysis methods are many natural advantages on tolerance representation and tolerance propagation in 3D Euclidean space, which can take all of tolerances (such as dimensional tolerance, geometric tolerance, and their interaction) into account [8, 9]. Hence, 3D assembly tolerance analysis methods are mainly used for assembly precision analysis to predict the effects of parts and components deviations on assembly accuracy and verify whether the specified GD&T design scheme can satisfy the AFRs of mechanical assemblies. However, current most of tolerance models in 3D assembly tolerance analysis methods are analyzed based on the size, position, and orientation errors and rarely consider form errors on the influence of final assembly accuracy. Due to the inevitability of the manufacturing errors and measurement uncertainties for actual parts, the inevitable differences between the actual surfaces and the ideal surfaces have always existed. With the continuous improvement of product accuracy requirements, some simplification operations, such as ignoring form defects and substituting variation of the manufactured surface as translation and rotation of the ideal surface, may obtain a less convincible assembly tolerance analysis result, which can no longer accurately reflect the influence of actual surface features on the assembly accuracy.

In addition to the influence of actual surface features on the analysis results of product assembly accuracy, the assembly connection style, such as serial and parallel connections, will also affect the final assembly accuracy of mechanical assemblies. Two reasons may account for this problem. On one hand, due to the manufacturing errors, the AFRs will deviate from the nominal position through positioning and connecting between assembly features. On the other hand, during the assembly process, the assembly constraint of every assembly feature pairs exists assembly positioning priority when assembly fitting or matching in parallel connections, which will cause different assembly contact status based on different positioning priority in the assembly connection topological structure. However, most mechanical assemblies with parallel connections or partial parallel connections are always simplified into a serial connection, which will cause a greater gap of the final assembly accuracy compared with the actual assembly. Therefore, in order to improve the accuracy of assembly precision analysis and provide more accurate guidance for product tolerance design, a novel solution of assembly tolerance analysis considering form errors and partial parallel connections in mechanical assemblies is proposed in this paper.

The remainder of this paper is structured as follows. Literature review of the related works is given in Sect. 2. Section 3 proposes an integrated Jacobian-skin model shapes model for assembly tolerance analysis based on the two advantages of unified Jacobian-Torsor model and skin model shapes. Section 4 elaborates a novel solution of assembly tolerance analysis with consideration of form errors and partial parallel connections based on the proposed integrated model. Section 5 presents a case study to implement the proposed solution and discusses these assembly tolerance analysis results. Conclusions are drawn in Sect. 6.

2 Literature review

Driven by continuous competition to improve the assembly accuracy and quality, tolerance representation modeling and assembly deviation propagation and accumulation are progressively receiving tremendous attentions in the 3D assembly tolerance analysis from the research academia.

To date, a large number of tolerance representation models have been presented and studied deeply over recent three decades, mainly including offset solid model [10], matrix model [11], vector loop [12], Jacobian matrix [13], small displacement torsor (SDT) model [14], unified Jacobian-Torsor model [15], GapSpace [16], tolerance map (T-Map) model [17], polytope [18], and so on. But these above mentioned models cannot deal with form tolerances for geometric variation modeling of part surface features. Moreover, most of them have severe assumptions on geometric deviations and can therefore hardly handle all kinds of 3D dimensional and geometrical tolerances [19]. To this end, more and more studies have tried to introduce the concept of skin model conforming to dimensional and geometric product specification and verification (GPS) standard, and proposed the skin model shape paradigm to simulate non-ideal geometry surface and reconstruct geometric variation modeling for the manufactured parts [20,21,22]. Currently, the geometry representation based on skin model shapes has successfully incorporated into dimension, position, orientation, form, and profile tolerance in the published literatures. Andrea and Wilma [23, 24] proposed a skin model representation under point cloud-based discrete geometry framework for 2D tolerance analysis considering the manufacturing signature in Jacobian, torsor, variational, and vector-loop models, respectively. Furthermore, Corrado et al. [25] also presented a variational model for 3D tolerance analysis with manufacturing signature and assembly operating conditions in order to predict geometric interferences of assembly and reproduce the actual assembly process. Zhang et al. [26] utilized Markov Chain Monte Carlo simulation technique and statistical shape analysis method to construct the skin model shape with random and systematic deviations for geometric variation modeling. Schleich and Wartzack [27] provided approaches for the generation and evaluation of geometric variational representatives based on skin model shapes. On this basis, a general framework and the combination approaches of different registration and relative positioning methods are presented for assembly simulation considering geometric deviations [28]. Schleich et al. [29, 30] further studied a novel approach of assembly contact and mobility simulation based on skin model shapes and proposed a comprehensive reference model for the management of geometrical deviations so as to serve as digital twin in product lifecycle management (PLM). Yi et al. [31] introduced a generic integrated approach of assembly tolerance analysis based on skin model shapes and state space model. Liu et al. [32] presented a novel assembly accuracy analysis method based on skin model shapes by integrating form errors and local surface deformations into tolerance analysis. Similarly, Zhang et al. [33] further introduced a polytope-based tolerance analysis model considering form errors and surface deformations to obtain a more realistic and accurate analysis result.

The above researches on the geometric variation modeling based on skin model shape lay a solid foundation for the high-fidelity accurate geometric representation of the actual surfaces in manufactured parts. However, current assembly tolerance analysis methods based on skin model shapes generally provide relative positioning approach by non-linear optimization solutions (such as iHLRF [34] and sequential quadratic programming [35]) to determine assembly contact status and estimate calculation results, which have quite complicated and inefficient analysis procedures. There may exist two reasons to restrict the application of skin model shape in assembly tolerance analysis. On one hand, the computation of modeling skin model shapes of all surfaces for each part is complex for mechanical assembly containing a large number of parts. On the other hand, the previous studies of skin model shape-based assembly relative positioning calculation and deviation propagation methods have not been sufficiently studied for mechanical product with complex connection topological structures containing partial parallel connections.

Meanwhile, the propagation and accumulation of assembly deviations have always been one of hotspot researches in the assembly tolerance analysis, which is crucial to determine the cumulative variation results among two or more assembly features during the assembly process. A reasonable assembly deviation propagation modeling method will benefit to calculate the cumulative variation results and analyze the impact of part geometric deviation on the AFRs. Zuo et al. [36] presented a modeling method for calculating mating variation and specifying mating coordinate with consideration of form errors to improve the accuracy of assembly deviation propagation model. Cao et al. [37] addressed the dynamic prediction and compensation problem of aeroplane assembly and studied the assembly variation propagation based on state space model and SDT theory. Chen et al. [38] applied the unified Jacobian-Torsor model to solve the assembly deviation propagation and accumulation containing partial parallel connections in mechanical assemblies. Mao et al. [39] proposed a method of constructing the assembly variation propagation model based on state space model for predicting the assembly accuracy of mechanical assembly system. Guo et al. [40] developed the coordination dimension chain along the assembly error propagation process to control the consistency of accumulated assembly errors at different assembly stations. Sun et al. [41] proposed an assembly deviation estimation method considering the real mating status to achieve assembly accuracy prediction. In the references mentioned above, these researches on assembly deviation propagation and accumulation have made some progress, but did not fully considered the integration of form errors and parallel connections caused by manufacturing defects and assembly topological structures.

Overall, most of the existing literatures prone to separately investigate geometric variation modeling with form errors based on skin model shape and assembly deviation propagation/accumulation containing complex connection topological structures (serial and parallel connections). Few studies have explored assembly tolerance analysis considering form errors and parallel connections together, which brings inconvenience to the solution of practical assembly problems. Hence, a novel assembly tolerance analysis method considering form errors and partial parallel connections in mechanical assemblies is introduced in the following. Compared with the conventional methods, this solution may explore a new improved method to further enhance the efficiency and accuracy of assembly tolerance analysis by means of the improvement of the existing models and approaches.

3 Unified Jacobian-Torsor model and skin model shapes

3.1 Unified Jacobian-Torsor model

As one of innovative modeling methods for 3D tolerance analysis, the unified Jacobian-Torsor model proposed by Laperrière et al. [42] is the combination of the Jacobian matrix and the Torsor model, which is suitable for tolerance propagation and tolerance representation, respectively. Therefore, small displacements of geometric functional element (GFE) within its tolerance zone can be represented by the Torsor model, and through the assembly deviation propagation and analysis by 3D dimension chain, the Jacobian matrix can be used to obtain the mathematical relationship between AFR and GFEs, so as to calculate variation errors of position and orientation for the AFR.

Assuming that two matrix vectors, i.e., [AFR] and [GFE], respectively represent tolerance domain of AFR and GFEs in mechanical assemblies, expression of which can be used screw parameters to represent small displacements of each features in tolerance zones, and the matrix [J] represents the Jacobian matrix, the expression of the unified Jacobian-Torsor model can be written as follows:

$$[{AFR}] = [{J}] \cdot [{GFE}]$$
(1)
$$\left[ {\begin{array}{*{20}c} {d{\varepsilon }_{AFR} } \\ {d{\rho }_{AFR} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{J}_{1} } & \cdots & {{J}_{n} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {d{q}_{{GFE_{1} }} } \\ \vdots \\ {d{q}_{{GFE_{n} }} } \\ \end{array} } \right]$$
(2)

where dεAFR and dρAFR represent translational matrix ([u v w]T) and rotational matrix ([α β γ]T) in the global reference system for AFR respectively, in which u, v, and w are three translational vectors and α, β, and γ are three rotational vectors around the axes x, y, and z in the local reference system respectively; dqGFEi represents translational and rotational matrix of the i-th GFE in the local reference system; Ji represents the 6 × 6 Jacobian matrix for the i-th assembly feature pair, with i is equal 1 to n, expression of which can be written as follows:

$$\left[ {{J}_{i} } \right] = \left[ {\begin{array}{*{20}c} {[R_{0}^{i} ]_{3 \times 3} \cdot [R_{{{\varvec{PT}}}}^{i} ]_{3 \times 3} } &\vline & {[W_{i}^{n} ]_{3 \times 3} \cdot \left( {[R_{0}^{i} ]_{3 \times 3} \cdot [R_{{{\varvec{PT}}}}^{i} ]_{3 \times 3} } \right)} \\ \hline {[0]_{3 \times 3} } &\vline & {[R_{0}^{i} ]_{3 \times 3} \cdot [R_{{{\varvec{PT}}}}^{i} ]_{3 \times 3} } \\ \end{array} } \right]_{6 \times 6}$$
(3)

where \([R_{0}^{i} ]_{3 \times 3}\) represents the orientation transformation matrix of the i-th GFE in the local reference system with respect to the global reference system (the 0-th frame), defined in Eq. (4); \([R_{{{\varvec{PT}}}}^{i} ]_{3 \times 3}\) is a projection matrix, which represents projection coefficient of three axes in the i-th local reference system according to the variation direction of tolerance zone; \([R_{0}^{i} ]_{3 \times 3} \cdot [R_{{{\varvec{PT}}}}^{i} ]_{3 \times 3}\) ensures that the Jacobian matrix can account for the tilted reference system of a projected tolerance zone; \([W_{i}^{n} ]_{3 \times 3}\) represents the position transformation matrix among the i-th and n-th local reference system, which is a skew-symmetric matrix and defined in Eq. (5). More detailed information and discussion about these matrices can be found in reference [43].

$$[R_{0}^{i} ]_{3 \times 3} = \left[ {\begin{array}{*{20}c} {[C_{1i} ]_{3 \times 1} } & {[C_{2i} ]_{3 \times 1} } & {[C_{3i} ]_{3 \times 1} } \\ \end{array} } \right]$$
(4)

where [C1i]3×1, [C2i]3×1, and [C3i]3×1 respectively represent unit direction transformation vectors around the axes xi, yi, and zi in the local reference system with respect to the global reference system.

$$[W_{i}^{n} ]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & { - dz_{i}^{n} } & {dy_{i}^{n} } \\ {dz_{i}^{n} } & 0 & { - dx_{i}^{n} } \\ { - dy_{i}^{n} } & {dx_{i}^{n} } & 0 \\ \end{array} } \right]$$
(5)

where \(dx_{i}^{n} = dx_{n} - dx_{i}\), \(dy_{i}^{n} = dy_{n} - dy_{i}\), and \(dz_{i}^{n} = dz_{n} - dz_{i}\); dxi and dxn, dyi and dyn, and dzi and dzn represent the coordinate value around the axes x, y, and z in the i-th and n-th local reference system with respect to the global reference system, respectively.

The surface type and tolerance value of GFEs will determine the tolerance variation domain interval and constraint relationship between surface features. Each screw parameters of GFE will be constrained within the allowable limit of variation domain in the tolerance zone where dqGFEi must lie in. As we known, there are only seven elementary surface types (i.e., invariance classes) proven by Clément et al. [44] based on the displacement set theory, as illustrated in Table 1. Meanwhile, we have also listed the tolerance domain and their corresponding variations and constraints of the first four elementary surface features as shown in Table 2, where T and t are the position and parallelism (or coaxiality) tolerance of the corresponding surface features, respectively.

Table 1 Seven elementary surface types and screw parameters
Full size table
Table 2 The tolerance domain and their corresponding variations and constraints of the first four elementary surface features
Full size table

Therefore, on the premise of satisfying variations and constraints of surface features in mechanical assemblies, the typical unified Jacobian-Torsor model can be further written as follows:

$$\left[ {\begin{array}{*{20}c} {(\underline{u} ,\overline{u} )} \\ {(\underline{v} ,\overline{v} )} \\ {(\underline{w} ,\overline{w} )} \\ {(\underline{\alpha } ,\overline{\alpha } )} \\ {(\underline{\beta } ,\overline{\beta } )} \\ {(\underline{\gamma } ,\overline{\gamma } )} \\ \end{array} } \right]_{AFR} = \left[ {\begin{array}{*{20}c} {[{J}]_{{GFE_{1} }} } & \cdots & {[{J}]_{{GFE_{n} }} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {(\underline{{u_{1} }} ,\overline{{u_{1} }} )} \\ {(\underline{{v_{1} }} ,\overline{{v_{1} }} )} \\ {(\underline{{w_{1} }} ,\overline{{w_{1} }} )} \\ {(\underline{{\alpha_{1} }} ,\overline{{\alpha_{1} }} )} \\ {(\underline{{\beta_{1} }} ,\overline{{\beta_{1} }} )} \\ {(\underline{{\gamma_{1} }} ,\overline{{\gamma_{1} }} )} \\ \end{array} } \right]_{{GFE_{1} }} } & \cdots & {\left[ {\begin{array}{*{20}c} {(\underline{{u_{n} }} ,\overline{{u_{n} }} )} \\ {(\underline{{v_{n} }} ,\overline{{v_{n} }} )} \\ {(\underline{{w_{n} }} ,\overline{{w_{n} }} )} \\ {(\underline{{\alpha_{n} }} ,\overline{{\alpha_{n} }} )} \\ {(\underline{{\beta_{n} }} ,\overline{{\beta_{n} }} )} \\ {(\underline{{\gamma_{n} }} ,\overline{{\gamma_{n} }} )} \\ \end{array} } \right]_{{GFE_{n} }} } \\ \end{array} } \right]^{T}$$
(6)
$$s.t. \, \left\{ {\begin{array}{*{20}l} {C_{1} \left( {u_{1} ,v_{1} ,w_{1} ,\alpha_{1} ,\beta_{1} ,\gamma_{1} } \right) \in \{ {{Constraint}}_{1} \} } \hfill \\ { \, \vdots } \hfill \\ {C_{n} \left( {u_{n} ,v_{n} ,w_{n} ,\alpha_{n} ,\beta_{n} ,\gamma_{n} } \right) \in \{ {{Constraint}}_{n} \} } \hfill \\ \end{array} } \right.$$
(7)

where \(\underline{u}\) and \(\overline{u}\) are the lower and upper deviation limit of the screw parameter of AFR around the axes x, respectively; \(\left( {\underline{u} ,\overline{u} } \right)\) is the tolerance interval where u must lie in; other vectors follow the same way; \(C_{i} ( \cdot )\) need to satisfy the constraint condition of the screw parameter of the i-th GFE.

In summary, the unified Jacobian-Torsor model is a concise efficient and reliable computation method in the 3D tolerance analysis, no matter with worst case or statistical analysis. However, this unified model can not consider the influence of form errors in the tolerance zone, and previous studies about the model mostly ignored the consideration of parallel connections in mechanical assemblies. These above deficiencies will cause the inaccuracy of assembly precision analysis and the inconformity with actual assembly. Therefore, it is necessary to further improve the unified Jacobian-Torsor model to realize a more generic solution considering form errors and partial parallel connections in mechanical assemblies.

3.2 Skin model shape-based non-ideal surface model

Due to manufacturing defects in the actual part, geometrical errors are inevitable and the ideal surface model in the part design phase will turn into the non-ideal surface model through manufacturing. Thus, these geometrical errors of surface features cannot be negligible in assembly tolerance analysis.

According to the new-generation GPS standard, it can be seen that skin model is used as a geometrical surface model of the physical interface of a workpiece with its environment, also called non-ideal surface model that meets the design requirements of tolerance specifications. The non-ideal surface model is a continuous surface composed of infinite points and can be used as a bridge between the nominal surface model and the real surface model of actual workpiece. In order to use finite discrete points and reasonable parameters to define the position, orientation, and form of surface model through computer simulation, Schleich et al. [22] have further proposed a paradigm of skin model shapes derived by skin model, as shown in Fig. 1. The practice indicates that skin model shapes have shown a great potential in part tolerance analysis and synthesis, assembly deviation prediction, and accuracy analysis. Established researches have shown that the skin model shape can realize high-fidelity geometric representation of actual manufactured part or physical workpiece by the summation of the position, orientation, and form errors in manufacturing defects [31].

Fig. 1
figure 1

Different representation schematic of the nominal model, skin model, physical workpiece, and skin model shapes [22]

Full size image

Figure 2 gives a cuboid part with geometric tolerance, and the top rectangular surface is taken as the key GFE, including tolerances of position tp, parallelism to, and flatness tf. In order to explain the modeling procedure of skin model shape-based non-ideal surface model conforms to the tolerance specification, this section introduces a general generation method of modeling a valid skin model shape taking the top rectangular surface with position, orientation, and form errors as an example.

  • Representation of position and orientation errors

Fig. 2
figure 2

Tolerance zone of the top rectangular surface in a cuboid part

Full size image

As shown in Fig. 2, the tolerance of position tp and parallelism to constrain the position and orientation of the rectangular surface. Based on the SDT theory, the deviation of the rectangular surface can be expressed by three parameters [dz θx θy], where dz represents small translation (i.e., position error) along z-axis direction; θx and θy represent small rotations (i.e., orientation errors) along x- and y-axis direction, respectively. Under the restriction of the variation and constraint of the rectangular surface tolerance illustrated in Table 2, the position and orientation errors of the planar surface with a specific tolerance relative to the nominal surface can be represented by the combination of variation parametric model and Monte Carlo sampling method. Taking the variation of z-coordinate value as an example, the variation parametric model of the rectangular surface can be expressed by function operator f on the sampling points (xi, yj) as follows:

$${D}_{p}=f\left({x}_{i},{y}_{j}\right)$$
(8)

where Dp represents the position and orientation errors of sampling points (xi, yj) around z-axis direction; f indicates the basic function restricted by the variation and constraint of the planar surface tolerance in the variation parametric model; i and j represent the sample point number of the biased surface in the x- and y-axis direction, respectively, 1 ≤ i ≤ m, 1 ≤ j ≤ n, and the total number of sampling points is m × n.

  • Representation of form errors

Compared with the position and orientation errors, the representation of form errors has more high-order characteristics. In order to obtain form errors for non-ideal surface model, various different methods have been proposed to represent form errors according to surface feature types and analysis process stage. In this paper, at the specification process stage, the modal-based method (such as trigonometric functions or spectral method) is utilized to realize the mathematical representation of form errors for different surface features, while at the verification process stage, the wavelet transform analysis method can be used to realize multi-scale filter processing and decomposition reconstruction so as to obtain form errors from the measured surface of physical workpiece. It should be pointed out that these mentioned methods above are not the only alternatives, the other feasible methods for form errors have already categorized and compared by Yan and Ballu, and these details can be seen in the reference [45].

Similarly, for the form tolerance zone of the rectangular surface shown in Fig. 2, the surface with a specific form error can be represented at the different analysis process stage, expression of which can be written as follows:

$${D}_{f}=\left\{\begin{array}{ll}{D}_{f}^{(SP)}={F}_{f}\left({x}_{i},{y}_{j}\right)=\sum\limits_{k-1}^{m\times n}{\lambda }_{k}{g}_{k}& \left(SP\right):\mathrm{specification\;process\;stage}\\ {D}_{f}^{(VE)}={H}_{f}\left({x}_{i},{y}_{j}\right)& \left(VE\right):\mathrm{verification\;process\;stage}\end{array}\right.$$
(9)

where Df represents the form errors of sampling points (xi, yj) at the specification or verification process stage; Ff indicates the basic function corresponding to a set of basis shapes at the specification process stage; gk indicates the operator of kernel basic function; λk represents the weight coefficient of a specified kernel basic function, which means that the value of λk is a random number between −1 and 1 which conforms to statistical regularity; Hf indicates the extraction function corresponding to frequency domain of form errors at the verification process stage. It should be pointed out that these different basis shapes at the specification process stage can be generated by using different methods, as listed in Table 3. Theoretically, the discrete cosine transform (DCT) method, the Zernike polynomials method, and the Legendre-Fourier polynomials method can be used for rectangular surfaces, circular or annular surfaces, and cylindrical surfaces, respectively. More detailed computation about these above methods can be referred to references [45,46,47].

Table 3 Basic function of different basis shapes for the representation of form errors [47]
Full size table

Here, the form errors of the rectangular surface can be modeled based on the DCT method at the specification process stage, while based on the wavelet transform analysis method at the verification process stage. In summary, after obtaining the results (i.e., Dp and Df) of the position, orientation, and form errors of the rectangular surface, the skin model shape for non-ideal surface model can be generated by summing Dp and Df, which is represented as follows:

$$D_{t} = D_{p} + D_{f} = \left\{ {\begin{array}{*{20}l} {D_{p} + D_{f}^{(SP)} = f\left( {x_{i} ,y_{j} } \right) + F_{f} \left( {x_{i} ,y_{j} } \right)} \hfill \\ {D_{p} + D_{f}^{(VE)} = f\left( {x_{i} ,y_{j} } \right) + H_{f} \left( {x_{i} ,y_{j} } \right)} \hfill \\ \end{array} } \right.$$
(10)

where Dt represents the deviations of sampling points (xi, yj) in the skin model shape.

It should be noted that Dt is still constrained by the tolerance of position, i.e., Dt ≤ tp. Nevertheless, the value of Dt calculated by Eq. (10) is not always satisfied with the constraint of tp. The valid skin model shape needs to be regenerated by resampling or scaling operation [27] of manufacturing errors so as to avoid violating the constraint of tp. Figure 3 shows the modeling procedure of generating a valid skin model shape for a non-ideal surface model.

Fig. 3
figure 3

Modeling procedure of generating a valid skin model shape for a non-ideal surface model

Full size image

3.3 Jacobian-Torsor model and skin model shapes integration

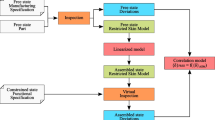
As mentioned above, the unified Jacobian-Torsor model is effective in tolerance representation and propagation for mechanical assemblies, whereas geometrical tolerances are reduced to position and orientation deviations without consideration of form errors in the Torsor model. Meanwhile, the representation of part dimensional and geometrical tolerance for non-ideal surface model based on skin model shapes have successfully been well-defined and available for tolerance analysis. Hence, combining with two advantages of the Jacobian-Torsor model and skin model shapes, thus integrating skin model shapes into the Jacobian-Torsor model and resulting an integrated Jacobian-skin model shapes model, can properly alleviate the shortcomings of skin model shapes, and we can directly realize the more accurate computation of accumulated deviations for AFR. On one hand, it can introduce form errors into the Jacobian-Torsor model for further improving assembly precision analysis results; on the other hand, it can only reconstruct these key GFEs of assembly feature pairs based on skin model shapes, which will avoid the necessity of generating every surface features of each part in mechanical assemblies. Figure 4 illustrates the difference between the conventional unified Jacobian-Torsor model and integrated Jacobian-skin model shapes model.

Fig. 4
figure 4

Difference between the conventional unified Jacobian-Torsor model and integrated Jacobian-skin model shapes model

Full size image

It should be noted that the definition and classification of assembly feature pairs between key GFEs in the integrated Jacobian-skin model shapes model are still retained and alike with the traditional unified Jacobian-Torsor model, as enumerated in reference [44]. For further detailed illustration purpose, taking the assembly connection graph illustrated in the left of Fig. 5 as an example, it includes eight internal functional element pairs (IFEPs) and four contact functional element pairs (CFEPs). A brief introduction to the assembly connection graph and the relationship of relative positioning is given in this section for the sake of completeness.

Fig. 5
figure 5

Assembly connection graph (left) and assembly feature pairs (right)

Full size image

Each CFEP is consist of assembly datum feature and assembly matched feature, where the label i.j represents the j-th GFE of the i-th part. Surfaces 1.1 and 2.1, surfaces 1.2 and 2.2, and surfaces 2.3 and 3.2 make up planar pairs, and the cylindrical pair is composed of two cylindrical GFEs, i.e., surfaces 2.4 and 3.1. Meanwhile, the planar pair between surfaces 1.1 and 2.1 is illustrated in the right of Fig. 5. The actual surface feature of GFE1.1 and GFE2.1 in the planar pair can be represented by skin model shapes. The SDT of CFEP (GFE1.1, GFE2.1) is determined by the relative positioning between the actual assembly matched feature (GFE2.1) and the actual assembly datum feature (GFE1.1), while the variation torsors of IFEPs, including (GFE1.0, GFE1.1) and (GFE2.0, GFE2.1), are related to the deviation between the actual assembly datum feature and its nominal assembly datum feature. On this basis, a novel assembly tolerance analysis method is proposed in the next section where the integrated Jacobian-skin model shapes model is used to analyze the assembly deviation results with consideration of partial parallel connection.

4 Assembly tolerance analysis based on skin model shapes considering partial parallel connection

Theoretically, it is necessary to analyze the assembly deviation propagation on serial and parallel connections for mechanical assemblies due to the complicated interactions of the mixed joints among multiple assembly error transfer routes than solely serial connections. For the sake of completeness, we first discuss a simple serial assembly for the assembly deviation propagation based on skin model shapes.

4.1 Assembly deviation propagation in serial assembly

Due to the consideration of skin model shapes, it is necessary to study the actual assembly deviation propagation for non-ideal surface model in serial assembly. As can be known, product assembly process has the characteristics of dynamic evolution and iterative updating in the assembly deviation propagation. The assembly accumulative error can be obtained from the low-order part to the high-order part based on the assembly sequence, where these main assembly error sources that affect the accumulative error of AFR include position, orientation, and form errors of part surface and relative positioning errors of assembly feature pairs, as shown in Fig. 6. Therefore, after generating skin model shape-based non-ideal surface model, how to calculate the relative positioning errors for serial assembly is a critical issue in order to realize the assembly deviation propagation.

Fig. 6
figure 6

Illustration of assembly deviation propagation

Full size image

Here, a simple example of two cuboid parts for serial assembly is used to provide such an explanation of the relative positioning error calculation with consideration of skin model shape-based non-ideal surface model, as shown in Fig. 7. As for two cuboid parts with the defined tolerances, these valid skin model shapes (i.e., Sa and Sb) of the top surface (\(S_{a}^{0}\)) in part A and the bottom surface (\(S_{b}^{0}\)) in part B can be obtained through using the method of subsection 3.2. To further obtain the assembly contact status of relative positioning between Sa and Sb, it is necessary to determine the three non-collinear contact points and calculate the position and orientation deviations of the skin model shape-based non-ideal planar pair by using the difference surface method and progressive contact method [48, 49].

Fig. 7
figure 7

An example of assembly contact in a planar pair for serial assembly: a tolerance zone of two planar surfaces and b procedure of relative positioning of a planar pair with consideration of skin model shape-based non-ideal surface model

Full size image

As shown in Fig. 8, the procedure of calculating the relative positioning error of a planar pair for serial assembly can be summarized as follows:

Fig. 8
figure 8

Illustration and procedure for relative positioning of a non-ideal planar pair for serial assembly [31]

Full size image

  • Step 1: The assembly mating problem between the actual top surface of part A and the actual bottom of part B, denoted as Sa and Sb respectively, will be converted into the assembly mating problem between the nominal surface of bottom surface and the difference surface of top surface, denoted as \(S_{a}^{0}\) and \(S_{b}^{df}\) respectively, through the difference surface method.

  • Step 2: The first contact point (pc1) can be obtained between \(S_{a}^{0}\) and \(S_{b}^{df}\) through moving the nominal surface (\(S_{a}^{0}\)) along the ZL-axis direction of local coordinate system by the minimum translational distance, denoted as \(d_{z}^{{{\varvec{min}}}}\), expression of which can be written as follows:

    $$d_{z}^{\min } = \mathop {\arg \min }\limits_{1 \le i \le m,1 \le j \le n} \left( {p_{Z}^{{(S_{b}^{df} )}} - p_{Z}^{{(S_{a}^{0} )}} } \right)$$
    (11)

    where \(p_{Z}^{{(S_{a}^{0} )}}\) and \(p_{Z}^{{(S_{b}^{df} )}}\) are the z-axis coordinate value in the nominal surface (\(S_{a}^{0}\)) and the difference surface (\(S_{b}^{df}\)), respectively.

  • Step 3: Finding and calculating the minimum rotational angle (\(\varphi_{1}^{{{\varvec{min}}}}\)) around the first contact point (pc1) for the nominal surface (\(S_{a}^{0}\)) can be implemented, and the second contact point (pc2) can be acquired between \(S_{a}^{0}\) and \(S_{b}^{df}\). It should be pointed out that although the position variation of the first contact point will be happened caused by rotating of the nominal surface, it is not considered in this paper due to a very small displacement of the posture adjustment relative to the geometrical dimension of mating surface. Therefore, by building two direction vectors (i.e., \({v}_{1}^{{(S_{a}^{0} )}}\) and \({v}_{1}^{{(S_{b}^{df} )}}\)) to obtain the corresponding vector sets, the minimum rotational angle (\(\varphi_{1}^{{{\varvec{min}}}}\)) can be computed as follows:

    $$\varphi_{1}^{\min } = \mathop {\mathop {\arg \min }\limits^{{(i,j) \notin p^{c1} }} }\limits_{1 \le i \le m,1 \le j \le n} \left[ {\arccos \left( {\frac{{{v}_{1}^{{(S_{a}^{0} )}} \cdot {v}_{1}^{{(S_{b}^{df} )}} }}{{\left| {{v}_{1}^{{(S_{a}^{0} )}} } \right| \times \left| {{v}_{1}^{{(S_{b}^{df} )}} } \right|}}} \right)} \right]$$
    (12)
    $$\left\{ {\begin{array}{*{20}l} {{v}_{1}^{{(S_{a}^{0} )}} = \left( {p_{X}^{{(S_{a}^{0} )}} - p_{X}^{c1} ,p_{Y}^{{(S_{a}^{0} )}} - p_{Y}^{c1} ,p_{Z}^{{(S_{a}^{0} )}} - p_{Z}^{c1} } \right)} \hfill \\ {{v}_{1}^{{(S_{b}^{df} )}} = \left( {p_{X}^{{(S_{b}^{df} )}} - p_{X}^{c1} ,p_{Y}^{{(S_{b}^{df} )}} - p_{Y}^{c1} ,p_{Z}^{{(S_{b}^{df} )}} - p_{Z}^{c1} } \right)} \hfill \\ \end{array} } \right.$$
    (13)

    where \(p_{X}^{c1} ,p_{Y}^{c1} ,p_{Z}^{c1}\) are the x-, y-, and z-axis coordinate value of point pc1, respectively; \(p_{X}^{{(S_{a}^{0} )}} ,p_{Y}^{{(S_{a}^{0} )}} ,p_{Z}^{{(S_{a}^{0} )}}\) and \(p_{X}^{{(S_{b}^{df} )}} ,p_{Y}^{{(S_{b}^{df} )}} ,p_{Z}^{{(S_{b}^{df} )}}\) are the x-, y-, and z-axis coordinate value of the corresponding point pc2 in the nominal surface (\(S_{a}^{0}\)) and the difference surface (\(S_{b}^{df}\)), respectively.

  • Step 4: On the basis of step 3, rotating the nominal surface (\(S_{a}^{0}\)) around line \(\overline{{p^{c1} p^{c2} }}\) of points pc1 and pc2 can find different contact points between the nominal surface (\(S_{a}^{0}\)) and the difference surface (\(S_{b}^{df}\)). In order to obtain the minimum rotational angle (\(\varphi_{2}^{{{\varvec{min}}}}\)) and find the third contact point pc3, two normal vectors of nominal surface before and after rotating need to be constructed, denoted as \({v}_{N}^{{(S_{a}^{0} )}}\) and \({v}_{N}^{{(S_{b}^{df} )}}\), expression of which can be written as follows:

    $$\left\{ {\begin{array}{*{20}l} {{v}_{N}^{{(S_{a}^{0} )}} = {v}_{1}^{{(S_{a}^{0} )}} \times {v}_{2}^{{(S_{a}^{0} )}} } \hfill \\ {{v}_{N}^{{(S_{b}^{df} )}} = {v}_{1}^{{(S_{b}^{df} )}} \times {v}_{2}^{{(S_{b}^{df} )}} } \hfill \\ \end{array} } \right.$$
    (14)
    $$\left\{ {\begin{array}{*{20}l} {{v}_{2}^{{(S_{a}^{0} )}} = \left( {p_{X}^{{(S_{a}^{0} )}} - p_{X}^{c2} ,p_{Y}^{{(S_{a}^{0} )}} - p_{Y}^{c2} ,p_{Z}^{{(S_{a}^{0} )}} - p_{Z}^{c2} } \right)} \hfill \\ {{v}_{2}^{{(S_{b}^{df} )}} = \left( {p_{X}^{{(S_{b}^{df} )}} - p_{X}^{c2} ,p_{Y}^{{(S_{b}^{df} )}} - p_{Y}^{c2} ,p_{Z}^{{(S_{b}^{df} )}} - p_{Z}^{c2} } \right)} \hfill \\ \end{array} } \right.$$
    (15)

    where \({v}_{2}^{{(S_{a}^{0} )}}\) and \({v}_{2}^{{(S_{b}^{df} )}}\) represent direction vectors with relevant to point pc2 and other points on the difference surface (\(S_{b}^{df}\)).

Through obtaining the corresponding vector sets of \({v}_{N}^{{(S_{a}^{0} )}}\) and \({v}_{N}^{{(S_{b}^{df} )}}\), the minimum rotational angle (\(\varphi_{2}^{{{\varvec{min}}}}\)) of finding the third contact point pc3 can be computed as follows:

$$\varphi_{2}^{\min } = \mathop {\mathop {\arg \min }\limits^{{(i,j) \notin p^{c1} \& p^{c2} }} }\limits_{1 \le i \le m,1 \le j \le n} \left[ {\arccos \left( {\frac{{{v}_{N}^{{(S_{a}^{0} )}} \cdot {v}_{N}^{{(S_{b}^{df} )}} }}{{\left| {{v}_{N}^{{(S_{a}^{0} )}} } \right| \times \left| {{v}_{N}^{{(S_{b}^{df} )}} } \right|}}} \right)} \right]$$
(16)

According to the analysis and calculation of above steps, the assembly variation error between part A and part B for serial assembly can be obtained, expression of which can be achieved by the SDT parameter [dz θx θy] of relative positioning error in the non-ideal planar pair. As the position and orientation offsets of relative positioning satisfies the differential assumption, the SDT parameter [dz θx θy] can be computed as follows:

$$\left\{ {\begin{array}{*{20}l} {d_{z} = - d_{z}^{\min } } \hfill \\ {\theta_{x} = \sin \left( { - \varphi_{1}^{\min } } \right)} \hfill \\ {\theta_{y} = \sin \left( { - \varphi_{2}^{\min } } \right)} \hfill \\ \end{array} } \right.$$
(17)

Therefore, by searching for the deterministic contact points and obtaining the relative positioning error between two skin model shape-based non-ideal surfaces, the assembly deviation error for serial assembly can be calculated by tolerance propagation. However, once existing parallel assembly or partial parallel connection in the assembly error transfer route, the above method still needs to be improved in order to implement a more generic solution of assembly tolerance analysis with consideration of partial parallel connection.

4.2 A novel assembly tolerance analysis method considering partial parallel connection

As we know, the assembly accumulative error of all potential joint surfaces which form a serial and/or parallel CFEP will ultimately produce the final assembly error of mechanical assemblies along the assembly process. Therefore, on the basis of the exploration of serial assembly, it is necessary to study partial parallel connection involving more than two non-ideal CFEPs in order to provide a novel assembly tolerance analysis method based on skin model shapes with consideration of partial parallel connection.

Taking the typical parallel joints composed of planar surfaces and cylindrical surfaces as example, as illustrated in Table 4, these two joints form a parallel connection and produce an alternative error transfer route for tolerance propagation, which will resulted in the ambiguity of assembly deviation propagation at multiple deviation component directions due to different constraints. Therefore, it is necessary to consider the mutual interaction of two parallel joints in the assembly process, especially with consideration of connection type, mating attribute, and assembly positioning priority.

Table 4 The typical parallel joints
Full size table

In fact, the solution of parallel joints based on skin model shapes for assembly tolerance analysis can be still used by algebraic operations of Torsor model [38]. Compared with the previous methods, the only difference is considering the assembly positioning priority into the situations where parallel joints exist, because the assembly positioning priority of parallel assembly will determine the relative positioning error in the assembly tolerance analysis. As we know, once the free surface feature containing six degrees of freedoms (DOFs) is specified by a tolerance, its DOFs will be reduced and the variation of partial remaining DOFs will be restricted by constraints. Thus, the assembly deviation propagation in mechanical assemblies depends on these remaining DOFs of assembly features restricted by tolerances or constraints. Under the restriction of assembly positioning priority of parallel joints, a parallel connection will further reduce the number of DOFs and assembly tolerance propagation should be further modified so as to be more suitable for the situations of parallel assembly.

Taking the parallel assembly of cylindrical joint and planar joint as example, as illustrated in the no. 3 of Table 4, the Torsor model of planar joint and cylindrical joint is T1 = [u 0 0 0 β γ]T and T2 = [0 v w 0 β γ]T, respectively, and we assume that the assembly positioning priority of cylindrical joint is higher than that of planar joint. Due to the existence of assembly positioning priority, the mating attribute of planar joint may be changed from the original [u 0 0 0 β γ]T to the actual [u 0 0 0 0 0]T. It means that the rotational displacements (i.e., β and γ) in planar joint around its local coordinate axis have no effect on the assembly deviation propagation. Theoretically, based on the algebraic operations of SDT belonging to Lie subgroup [50], an additive operation of two screw parameters for planar joint and cylindrical joint can be implemented, which can be expressed by a new torsor T for tolerance propagation of the parallel joint. And then, through combining two screw parameters, the new torsor T can be written as follows:

$$T{ = }T_{1} \cup T_{2} { = }\left[ {\begin{array}{*{20}l} u \hfill & v \hfill & w \hfill & 0 \hfill & \beta \hfill & \gamma \hfill \\ \end{array} } \right]^{T}$$
(18)

Furthermore, it should be noted that there may be interference between β1 of T1 and β2 of T2 because of the interaction of T1 and T2 in the x–z plane. To avoid interference and obtain the screw parameter β of the new torsor T, an intersection operation for two variations needs to be implemented properly, which means that β in T depends on the minimal value between β1 and β2. So does γ. For the three translational displacements of T, there is no overlap between u of T1 and v and w of T2, thus a composition operation is still applicable for these translational variations. Hence, the expression of Eq. (18) can be further rewritten by variations of T (denoted as V) as follows:

$$V = V_{1} \prod V_{2} = \left[ {\begin{array}{*{20}c} {V_{u} = V_{u1} \cup V_{u2} } \\ {V_{v} = V_{v1} \cup V_{v2} } \\ {V_{w} = V_{w1} \cup V_{w2} } \\ 0 \\ {V_{\beta } = V_{\beta 1} \cap V_{\beta 2} } \\ {V_{\gamma } = V_{\gamma 1} \cap V_{\gamma 2} } \\ \end{array} } \right]$$
(19)

where the symbol \(\prod\) is a composition or intersection operator which depends on an overlap relationship between two participated vectors [38].

Similarly, the analysis methods of other typical parallel joints listed in Table 4 can be described with the above method. They are not further discussed here. More specifically, it should be mentioned that the advantage of this solution is that parallel joints can be turned into serial joints through composition and intersection operations, which will be conveniently applied for assembly tolerance analysis based on the integrated Jacobian-skin model shapes model. Therefore, a novel assembly tolerance analysis method with consideration of partial parallel connections using the integrated Jacobian-skin model shapes model can be summarized and is shown in Fig. 9. The detailed procedure is as follows:

  • Step 1: Establish the expression of the Jacobian model and obtain the Jacobian matrices. According to the detailed 2D or 3D drawing of assembly, we can firstly identify all GD&T, key GFEs, assembly feature pairs, and AFR and establish assembly connection graph. We can further set each local coordinate systems of key GFEs in assembly feature pairs, then creating the assembly chain based on assembly deviation propagation. On this basis, the Jacobian matrices can be computed for all these assembly feature pairs by Eq. (3).

  • Step 2: Generate the skin model shapes and distinguish the type of assembly contact. Generation of skin model shapes-based surface features of all key GFEs can be realized according to subsection 3.2. As for the IFEP and CFEP, it should be pointed out that the IFEP is serial joint, while the CFEP can be serial joint that consist of two GFEs, i.e., serial functional element pairs (SFEP), or parallel joint that are formed by three or more GFEs, i.e., parallel functional element pairs (PFEP).

  • Step 3: Perform the calculation of relative positioning error and obtain small displacement torsors for the serial and parallel joints. The calculation process of relative positioning error is carried out by difference surface method and progressive contact method for serial joints, while by transformed into serial joints by algebraic operations (composition or intersection) for parallel joints, to obtain the SDT of relative positioning error.

  • Step 4: Calculate the assembly deviations and evaluate the accuracy results of AFR. According to the integrated Jacobian-skin model shapes model, the obtained Jacobian matrices and the SDT of all key GFEs can be used to calculate the variations of the AFR by using the statistical analysis (such as Monte Carlo simulation method). Finally, the accuracy result analysis and evaluation of the AFR can be implemented so as to determine whether the AFR is satisfied for mechanical assembly.

Fig. 9
figure 9

Flow diagram of assembly tolerance analysis method with consideration of partial parallel connections using the integrated Jacobian-skin model shapes model

Full size image

5 Case study

This section discusses the validity and feasibility of the proposed method for assembly tolerance analysis considering form errors and partial parallel connections. Here, a 3D typical mechanical assembly involving three parts, as shown in Fig. 10, will be used as an example to demonstrate the analysis procedure and application of this solution. Figure 10 gives the exploded diagram and each local coordinate systems of this assembly that consists of three parts (i.e., the base, support, and inserter) and their detailed drawing including GD&T, respectively. The distance between left center point G of the inserter and the upper surface of the base is recognized as the AFR, which is the key to reflect assembly accuracy by the fluctuation of point G in the inserter. Meanwhile, it should be mentioned that these local coordinate systems of each part are set at the theoretical center point of assembly feature, and the assembly positioning priority of assembly feature pairs is assigned as follows: (GFE1.1, GFE2.1) is prior to (GFE1.2, GFE2.2), and (GFE2.3, GFE3.2) is prior to (GFE2.4, GFE3.1).

Fig. 10
figure 10

An example of typical mechanical assembly: a exploded diagram and local coordinate systems and b detailed drawing

Full size image

At first, based on the detailed drawing of this assembly, the assembly constraint relationship and geometric constraints of this assembly can be extracted, which can establish an assembly connection graph in order to obtain assembly chains based on assembly deviation propagation around the AFR, as shown in Fig. 11. Each GFEs designated i.j represents the j-th surface feature of the i-th part with corresponding to the local coordinate system. The studied assembly includes the most common CFEP (i.e., the planar pair and cylindrical pair), where (GFE1.1, GFE2.1), (GFE1.2, GFE2.2), and (GFE2.3, GFE3.2) make up planar pairs, (GFE2.4, GFE3.1) makes up cylindrical pair, respectively; parallel joint of planar-planar connection is composed of (GFE1.1, GFE2.1) and (GFE1.2, GFE2.2), and parallel joint of cylindrical-planar connection is composed of (GFE2.3, GFE3.2) and (GFE2.4, GFE3.1), respectively. Therefore, the current case study can be used as a typical example to illustrate the proposed assembly tolerance analysis method with consideration of partial parallel connections based on integrated Jacobian-skin model shapes model.

Fig. 11
figure 11

Assembly connection graph of the studied assembly

Full size image

In order to compare with the different results by using different methods, i.e., the conventional unified Jacobian-Torsor model and integrated Jacobian-skin model shapes model with consideration of serial and parallel joints, the same studied assembly is used in this section. For detailed comparison, the different methods of case study are shown in Table 5.

Table 5 A brief summary of different methods in case study
Full size table

Here, according to the specified local coordinate systems in Fig. 10a and the topological structure of assembly connection graph (see Fig. 11), we can obtain an assembly error transfer route under the restriction of assembly positioning priority, i.e., IFEP1-SFEP2-IFEP3-SFEP4-IFEP5-AFR, which can determine to the construction of the Jacobian matrices. Based on the Eq. (3), the corresponding Jacobian matrices for each assembly feature pairs can be calculated and the obtained results are shown in Table 6.

  • Case 1

Table 6 The Jacobian matrices of the studied assembly
Full size table

The conventional unified Jacobian-Torsor model-based assembly tolerance analysis can be conducted in this subsection. As we can see, the difference between method 1# and method 2# is whether to consider parallel joints in the studied assembly.

For method 1#, the unified Jacobian-Torsor model can be directly implemented based on the Eq. (6), where the cylindrical joint (SFEP4) between GFE2.3 and GFE3.2 is shaft and hole loose fit, the maximum clearance is equal to the difference between the maximum material size of the hole and the minimum material size of the shaft, and the relative position of two axes between shaft and hole can be equivalent to a position tolerance. For method 2#, there are two partial parallel joints mixed in this serial route, i.e., (GFE1.1, GFE2.1) and (GFE1.2, GFE2.2), which is formed by a planar joint (GFE1.2, GFE2.2) combined with a planar joint (GFE1.1, GFE2.1); (GFE2.3, GFE3.2) and (GFE2.4, GFE3.1), which is formed by a cylindrical joint (GFE2.3, GFE3.2) combined with a planar joint (GFE2.4, GFE3.1). There is a key step to change partial parallel joints into serial joints in the conventional unified Jacobian-Torsor model. Based on the Eq. (19), the variations of partial parallel joints can be calculated by algebraic operations of screw parameters between two torsors of CFEPs.

More specifically, through the above analysis and the GD&T information of each GFEs in the studied assembly, variations and constraints of each torsors with corresponding to assembly feature pairs can be obtained based on Table 2. Final result of the AFR in Case 1 can be calculated by these SDTs based on the Eq. (20).

$$\left\{ {\begin{array}{*{20}l} {\left[ {{AFR}} \right]_{1\# } = \left[ {\begin{array}{*{20}c} {J_{1} } & {J_{2} } & {J_{3} } & {J_{4} } & {J_{5} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {dq_{IFEP1} } & {dq_{SFEP2} } & {dq_{IFEP3} } & {dq_{SFEP4} } & {dq_{IFEP5} } \\ \end{array} } \right]^{T} } \hfill \\ {\left[ {{AFR}} \right]_{2\# } = \left[ {\begin{array}{*{20}c} {J_{1} } & {J_{2} } & {J_{3} } & {J_{4} } & {J_{5} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {dq_{IFEP1} } & {dq_{{SFEP2^{\prime}}} } & {dq_{IFEP3} } & {dq_{{SFEP4^{\prime}}} } & {dq_{IFEP5} } \\ \end{array} } \right]^{T} } \hfill \\ \end{array} } \right.$$
(20)

On more reasonably accurate analysis purpose, a statistical analysis using Monte Carlo simulation method is necessary under the constraints of surface features. Assumption that these variations of screw parameters conform to normal distribution, after calculating the assembly accumulated deviations of the AFR by running 2000 times simulations, the variation domain and distribution of specified screw parameters at point G can be obtained and is displayed in Fig. 12. A more detailed comparison of assembly tolerance analysis results is further discussed in next subsection.

  • Case 2

Fig. 12
figure 12

Spatial position distribution of final assembly accumulated deviation of point G: a with consideration of serial joints, b with consideration of serial and parallel joints

Full size image

The integrated Jacobian-skin model shapes model-based assembly tolerance analysis can be conducted in this subsection. At first, a series of skin model shapes for key surface features of studied assembly can be generated, that is, planar surfaces GFE1.1 and GFE2.1 of SFEP2, GFE1.2 and GFE2.2 of PFEP2, cylindrical surfaces GFE2.3 and GFE3.2 of SFEP4, and annular surfaces GFE2.4 and GFE3.1 of PFEP4. It should be noted that the assembly contact area of PFEP4 is annular surface and the computing area of GFE2.4 is consistent with that of GFE3.1. Following the modeling method illustrated in Fig. 3, these skin model shapes are generated based on the specification process method in subsection 3.2. Specifically, the number of discrete points in the corresponding surface features and the generated skin model shapes is given in Table 7, in which Dir_a and Dir_b represent the two directions of the corresponding surface, i.e., the length and width directions for rectangular surface, the axial and circumferential directions for cylindrical surface, and the radial (external and internal) and circumferential directions for annular surface.

Table 7 Number of discrete points and the generated skin model shapes in the corresponding surface features
Full size table

Furthermore, according to Sect. 4, the relative positioning error of assembly deviation propagation with consideration of form defects can be obtained in serial and parallel assembly. Based on the integrated Jacobian-skin model shapes model, the SDTs of three IFEPs (i.e., IFEP1, IFEP3 and IFEP5) can be obtained by calculating the relative variations of the corresponding GFEs compared with their nominal positions, while the SDTs of four CFEPs (i.e., SFEP2, PFEP2, SFEP4, and PFEP4) can be obtained by the application of difference surface, progressive contact method, and algebraic operations of screw parameters to skin model shapes with consideration of serial and parallel joints in subsection 4.2.

It should be mentioned that the SDTs of all assembly feature pairs can be obtained by one time simulation for the corresponding generated skin model shapes, as expressed in Table 8. Final result of the AFR in Case 2 can be calculated with similar to the form of Eq. (20). Similarly, it is worth mentioning that a Monte Carlo simulation method in the statistical analysis can be performed in Case 2 for accurate analysis and comparison. In the same way, 2000 runs of assembly simulations are embedded to calculate the assembly accumulated deviations of the AFR for obtaining the variation domain and distribution of specified screw parameters at point G, as shown in Fig. 12. A more detailed comparison of assembly tolerance analysis results is also discussed in next subsection.

  • Results and discussion

Table 8 SDTs of all assembly feature pairs based on skin model shapes in Case 2
Full size table

In order to quantitatively analyze the accuracy results of assembly tolerance analysis in Case 1 and Case 2, the spatial position distribution of the final assembly accumulated deviations of point G can be obtained by Monte Carlo simulation, as shown in Fig. 12. The difference between Fig. 12a and b indicates that the calculation results of Case 1 and Case 2 exist an offset. Especially when considering the non-ideal surface model and parallel joints into assembly tolerance analysis, the offset at the final spatial position distribution has a more extent effects. Additionally, it can be found that the spatial position distribution of Fig. 12b is sparser and more scattered than that of Fig. 12a due to the consideration of parallel joints. Although the calculation result is relatively larger in Case 2, the assembly accuracy is higher, which can reflect the actual assembly more reasonably and be more conducive to the evaluation of the assembly feasibility.

Furthermore, it can be obtained that the z-direction or vertical positional displacement of the AFR between the inserter and the base is illustrated in Fig. 13 when 2000 runs of assembly simulations are carried out. As shown in Fig. 13a, the vertical positional variation varies from −0.1402 to + 0.2003 with a mean deviation + 3.7776e-4 in method 1#, while the vertical positional displacement lies in an interval of [39.7311, 40.2717] with a mean value 39.9970 in method 2#. Similarly, as shown in Fig. 13b, the vertical positional variation varies from −0.3544 to + 0.2990 with a mean deviation −0.01459 in method 3#, while the vertical positional displacement lies in an interval of [39.6656, 40.2959] with a mean value 39.9957 in method 4#. Therefore, these above results are different from the ideal vertical displacement of the AFR. Meanwhile, there also exists a significant difference between Case 1 and Case 2.

Fig. 13
figure 13

The vertical position variation results of point G in statistical analysis: a for serial assembly in Case 1, b for serial and parallel assembly in Case 2

Full size image

The vertical positional variation domain obtained from the integrated Jacobian-skin model shapes model is wider than these domain obtained from the conventional unified Jacobian-Torsor model. It can be seen that the probability of variation will increase for the spatial position of point G due to the consideration of skin model shapes, because the deviations of surface features are ignored form defects and simplified to translational and rotational imperfections in the conventional unified Jacobian-Torsor model. Furthermore, considering the parallel joints of mechanical assembly will make the final spatial position of point G more reasonable and accurate in the assembly deviation propagation. At last, we choose the CPU calculation time of the two cases of simulations to reflect the computation efficiency of these different methods on the author’s ordinary desktop computer. The CPU calculation time is the total time for 2000 Monte Carlo simulation runs, and these results of the CPU calculation time are 18.157 s in method 1# and 39.286 s in method 2# at Case 1, 25.395 s in method 3# and 51.012 s in method 4# at Case 2, respectively, which can meet the computation efficiency requirement of assembly tolerance analysis. Because the average calculation time is less than 0.1 s for one simulation; even for Case 2, in which form errors and partial parallel connections are considered. Therefore, the proposed novel assembly tolerance analysis method (i.e., method 4#) can be efficiently completed, and the proposed integrated Jacobian-skin model shapes model can provide a more generic solution and viable methodology in the assembly tolerance analysis considering form errors and partial parallel connections in mechanical assemblies.

6 Conclusions

The unified Jacobian-Torsor model is one typical assembly tolerance analysis model, whereas it ignores the combined effects of form errors and partial parallel connections in mechanical assembly, which may cause inaccuracy and unreliability in assembly tolerance analysis results. To overcome these shortcomings, this paper proposes a novel assembly tolerance analysis method considering form errors and partial parallel connection based on the integration of the unified Jacobian-Torsor model and skin model shapes. The integrated Jacobian-skin model shapes model combines the benefits of both initial models with assembly accuracy and reliability guarantees. Specifically, form errors are considered based on skin model shapes for parts with geometrical deviations, and parallel connections in mechanical assemblies are considered by transforming into serial connections based on algebraic operations between participated torsors in the unified Jacobian-Torsor model. On this basis, an improved approach combined with difference surface and progressive contact method is proposed to determine the actual assembly contact status and calculate assembly relative positioning errors for serial and parallel connections in mechanical assemblies. The calculation scheme of assembly accuracy with a statistical way is also elaborated for assembly tolerance analysis based on the integrated Jacobian-skin model shapes model. Through the comparison and analysis with the conventional Jacobian-Torsor model and the integrated Jacobian-skin model shapes model, the proposed solution can obtain a more accurate and reliable assembly precision analysis result when considering form errors and partial parallel connections. However, this research still belongs to the category of rigid body assembly, and further research should be considered on the aspects of assembly deformation by reasons of realistic contact force, external load, and environment conditions to cover a wider range of solving more complex assembly problems.