1 Introduction

Thermal errors account for 40–70% of the total errors in precision machine tools and coordinate measurement machines (CMMs) [1, 2]. The prediction, identification, and compensation of thermal errors is crucial for improving the volumetric accuracy of machine tools and CMMs. Therefore, it is critical to establish an efficient and robust thermal error compensation model.

Thermal error prevention and compensation are two effective means to deal with the thermal error problem [3]. Thermal errors can be reduced in various ways, such as optimizing the mechanical structure of a machine, reducing the influence of possible heat sources, using high-performance materials, controlling the workshop environment temperature, etc. [4]. With the increase in accuracy requirements, the cost and difficulty of implementing this strategy are also increasing. Error compensation eliminates thermal error by modifying the tool position and orientation. Therefore, error compensation has become a cost-efficient and convenient method for reducing the impact of thermal errors in machines [5].

The thermal error compensation strategy can be divided into two categories: theoretical and empirical thermal error modelling [6]. Theoretical thermal error modelling involves the collection of related theoretical knowledge and uses finite element simulation software, such as ANSYS and ABAQUS. Ma et al. [7] proposed closed-loop iterative thermal behaviour modelling based on error mechanism analysis. Zhang et al. [8] studied the thermal error characteristics of a machining tool by establishing a heat transfer function. However, theoretical thermal error modelling requires the consideration of many factors, and the model is extremely simplified, resulting in distorted models and inaccurate prediction results [9].

In recent years, empirical models based on statistical learning have attracted considerable attention owing to their simplicity and efficiency. The empirical thermal error model has two key points: the selection of the thermal error model algorithm and processing of temperature variables. Owing to their strong ability to deal with multi-input problems, machine learning models such as multiple regression [10, 11], support vector machine [12], and neural network models [13] are frequently employed to build thermal error models. Temperature variable processing is employed to decrease the number of input variables and reduce the collinearity of input variables. Vyroubal [14] chose relevant temperature variables according to the statistical assessment using sample correlation coefficient, where deformation of selected machine part and temperature changes are compared to find the best fit value. Liu et al. [15] proposed a grey relation split unbiased estimation thermal error robust modeling method to improve the multiple linear regression algorithm and inhibited the influence of collinearity of temperature sensitive points. Yang et al. [16] selected temperature-sensitive variables based on a fuzzy clustering method and established a neural-network-based thermal error model. Abdulshahed et al. [17] selected temperature sensitive points using the fuzzy clustering and grey correlation method and established the adaptive neuro-fuzzy inference system thermal error model.

Although the conventional grouping and selecting method can reduce the collinearity between temperature variables, it also reduces the correlation between the selected input temperature variables and thermal error, thus reducing the robustness of the model [11]. Many methods have been developed to simultaneously reduce the collinearity of the temperature variables and improve the correlation between temperature variables and thermal errors. Li et al. [18] used a reconstructed variable regression algorithm to strengthen the correlation between the selected temperature variables and thermal error. Miao et al. [19] proposed a principal component regression (PCR) method that could eliminate the influence of multi-collinearity among temperature variables. Liu et al. [20] used a correlation coefficient to select temperature-sensitive points and the PCR algorithm to establish the thermal error model. Although it used only two temperature sensors, the results showed that the model was highly robust. Tan et al. [21] proposed a wrapper-approach-based method to select temperature-sensitive points and established a thermal error model using a least squares support vector machine.

To improve the robustness of the thermal error model and strengthen the intrinsic relation between input and output variables, this study presents an integrated temperature regression method, which uses synchronization and collinearity as the temperature measurement point variables. Owing to the special structure and low-speed movement of the CMM in this study, the change in the temperature of its moving shaft is affected only by the ambient temperature. The ambient temperature, which affects the thermal error of the machine, is influenced by daily variations and seasonal transitions [8]. Therefore, as the ambient temperature changes, the temperature measurement points change synchronously. However, owing to uneven heat transfer, the changes in the values of the temperature variables may not be completely consistent. With regard to the thermal error characteristics of a transmission system, Wang et al. [22] determined that the slope of the positioning error curves changes linearly with temperature, thus causing slight variations in the shape of the error curve. In this study, we examine the relationship between temperature and the overall slope of the error curve. However, the accuracy of the thermal positioning error predicted by different temperature variables under the influence of a single ambient temperature is not high enough. Therefore, the use of multiple temperature variables (under the influence of ambient temperature) to optimize the temperature, which results in higher correlation with the thermal error, can improve the model accuracy compared with single temperature modelling. Furthermore, under the influence of a single temperature factor, calculating an equivalent temperature is visually comprehended.

This study aimed at accurately determining the mapping relation between environmental temperature and thermal error. The remainder of this paper is organized as follows. The experimental condition for thermal error, including the structure of the CMM, measurement methods of temperature points, and thermal error are described in Sect. 2. The necessity of temperature integration and the integrated temperature regression method for thermal error modelling are deduced in Sect. 3. In Sect. 4, the proposed model is verified by comparing it with the single temperature modelling and ridge regression methods. Finally, the conclusions of this study are drawn in Sect. 5.

2 Analysis and measurement of thermal error

2.1 Structure of the CMM

A CMM at the workshop level can avoid repeated circulation of the workpiece in machining and measuring shops. However, its positioning accuracy is sensitive to temperature variation. Therefore, a thermal error model for the CMM must be established.

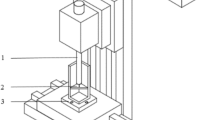
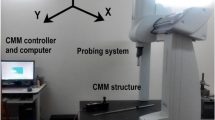
In this study, a θFXZ-type of CMM was considered, as shown in Fig. 1, where θ indicates that the workpiece rotates with the turntable, and XZ indicates that the probe moves linearly in the X- and Z-directions. The turntable rotates the workpiece, and the column can move in the horizontal and vertical directions. The column slide is equipped with a counterweight to counteract the effects of gravity along the Z-axis. The components of the column sliding seat, which moves linearly on the Z-axis, are connected by rolling linear guides and driven by a ball screw, and a grating ruler is used to ensure positioning accuracy. To obtain a linear expansion grating ruler, an installation method in which one end is fixed and the other is free is adopted.

Fig. 1
figure 1

Structure of the moving shaft of the CMM

Full size image

The main function of the CMM is to use the laser probe to scan the workpiece by moving the z-axis up and down while keeping the x-axis stopped. As a result, the main factor affecting the accuracy of this special CMM is the positioning accuracy of the z-axis. Therefore, this paper only studied the z-axis thermal error of the special CMM.

To eliminate the negative thermal influence of the heat generated by the ball screw system, the grating ruler is fixed far away from the ball screw. Thus, the heat generated by the ball screw, which moves along the Z-axis at a low speed, can be further reduced. In the measurement experiment, which was conducted every 30 min, it was found that the value of each temperature measurement point did not change significantly as shown in Table 1. In Table 1, “Ambient temperature” represents the set of temperatures in the constant temperature room, “Number” represents the number of measurements, and “T0,” “T1,” and “T2” represent the temperature measurement points. T0, T1, and T2 are the measured ambient temperature, temperature at the upper end of the grating, and temperature at the lower end of the grating, respectively.

Table 1 Various temperature changes in the experiment
Full size table

In the experiment, it was found that the temperature of each temperature measurement point did not change for approximately 30 min during the measurement of thermal error on the Z-axis. This confirmed one of the advantages of the structure of the CMM. Therefore, the influence of the internal heat source on the scale can be neglected, and we can consider that only the ambient temperature influences the thermal error in this study.

2.2 Temperature measurement

In the previous section, it was shown that the most obvious difference compared to the machine tool is that the moving shaft of the θFXZ coordinate measuring machine used in the study has no internal heat source. For measurements along the Z-axis of the measuring machine positioned with the grating ruler, which is affected by a single heat source, we placed temperature sensors near the two ends of the grating ruler. The temperature sensor used was pt100 of HangZhou Meacon Automation Technology Co., LTD. The locations of the temperature sensors are shown in Fig. 2, indicated by T0, T1, and T2.

Fig. 2
figure 2

Placement locations of temperature sensors

Full size image

For workshop-level measurements, temperature changes caused by seasonal variations have a greater impact on the measuring machine. To simulate a wide range of temperature changes with respect to changing seasons, thermal error experiments were performed in a temperature-controllable constant temperature room. In the experiment, the temperature of the constant temperature room was set to 10, 15, 20, 30, and 35 °C. The thermal error was measured when the temperature in the room remained constant for more than 10 h after setting the temperature values.

2.3 Thermal-error measurement

A laser interferometer is generally used to measure the thermally induced positioning error of transmission systems [23, 24]. In this study, the Renishaw XL-80 laser interferometer was used. It provides an accuracy of ± 0.5 ppm with a resolution of 1 nm. The thermal error data under the experimental temperature conditions can be accurately obtained using the laser interferometer with a precise environmental compensation module. The positioning error is calculated by comparing the ideal and measured positions along the Z-axis. The linear positioning accuracy along the Z-axis is obtained by comparing the movement data displayed on the machine’s controller with the data measured by the laser interferometer. The optics are arranged as shown in Fig. 3, with a measurement interval of 20 mm.

Fig. 3
figure 3

Linear setup measurement of positional accuracy along the Z-axis

Full size image

3 Thermal error modelling

The positioning errors at different Z-axis positions and ambient temperatures were measured and collected, and the results are as shown in Fig. 4. The thermally induced positioning error of the shaft moving along the Z-axis is related to both the temperature and position. Therefore, the thermally induced positioning error can be divided into a geometric component and thermal component [22, 25]. In summary, the thermal error modelling includes two parts: error separation and integrated temperature regression.

Fig. 4
figure 4

Characteristics of the positioning error curves

Full size image

3.1 Error separation

The profile of the thermal-variant slope is shown in Fig. 5. Because the positioning error profiles show a linear trend relationship with the position, the profiles are fitted by straight lines that pass through the origin using the least square method. This will simplify the final model.

Fig. 5
figure 5

Variation characteristic of the thermal-variant slopes

Full size image

From Fig. 5, it can be seen that the shape of the thermal positioning error curve remains unchanged when the temperature changes. The positioning and thermal errors in the thermally induced positioning error can be separated by.

$${E}_{z}=E{(P)}_{z}+E{(T)}_{z},$$
(1)

where \(E_{z}\) is the comprehensive positioning error along the z-axis; \(E(P)_{z}\) is the geometric component of the positioning error at the reference temperature, 20 ℃; and \(E(T)_{z}\) is the thermally induced error related to temperature change.

Each term is defined as follows:

$$E{(P)}_{z}={\sum }_{i=0}^{n}{a}_{i}{z}^{i}={a}_{0}+{a}_{1}z+{a}_{2}{z}^{2}+\cdot \cdot \cdot +{a}_{n}{z}^{n}$$
(2)
$$E{(T)}_{z}=({K}_{T}-{K}_{20})z$$
(3)
$${K}_{T}={b}_{0}+{b}_{1}{T}_{{integrated}},$$
(4)

where ɑi is a coefficient of the polynomials; z is the position of the shaft moving along the Z-direction of the CMM; \(K_{T}\) is the slope of the thermal error at temperature T; and \(K_{{{20}}}\) is the slope of the thermal error when the preset temperature is 20 °C (it is used as the reference slope in this study). Further, b0 and b1 are the coefficients, and Tintegrated is the integrated temperature, which is explained in detail in Sect. 3.2.

Combining Eqs. (1), (2), (3), and (4), a prediction model for the Z-axis thermal positioning error can be obtained, and it is expressed as follows:

$${E}_{z}={a}_{0}+{a}_{1}z+{a}_{2}{z}^{2}+\cdot \cdot \cdot +{a}_{n}{z}^{n}+\left({T}_{{integreted}}-{T}_{{integreted}}^{20}\right){b}_{1}z.$$
(5)

In Eq. (5), \(T_{{{{integrated}}}}^{20}\) is the integrated temperature when the preset temperature is 20 °C.

The positioning error at the reference temperature is used to fit the polynomial curve at 20 °C using the least square method.

3.2 Integrated temperature regression

3.2.1 Necessity for the integrated temperature

In this study, because the shaft of the CMM moving in the Z-direction is only affected by a single external heat source (ambient temperature), it is appropriate to integrate all the temperature measurement points. Compared to that of the machine tool, which is significantly affected by the internal heat source, the temperature measurement point changes in this experiment show stronger similarity and consistency. The values of the temperature measurement points are listed in Table 2.

Table 2 Values of the temperature measuring points (unit: °C)
Full size table

Cosine similarity is used to measure the degree of similarity between the temperature measurement points and is expressed as

$$CS(X,Y)=\frac{{\sum }_{i=1}^{n}({x}_{i}{y}_{i})}{\sqrt{{\sum }_{i=1}^{n}{({x}_{i})}^{2}}\sqrt{{\sum }_{i=1}^{n}{({y}_{i})}^{2}}}$$
(6)

where \(CS(X,Y)\) is the cosine similarity between X and Y, and X = {x1, x2, …, xn} or Y = {y1, y2, …, yn} is the collection of observation from a temperature measuring point (T0 – T2). The closer the value of cosine similarity is to one, the higher the similarity. The cosine similarities between the temperature measuring points are shown in Table 3.

Table 3 Cosine similarities between the temperature measuring points
Full size table

There is a strong similarity between the temperature measurement points and the input variables, which results in high collinearity. Collinearity indicates that the explanatory variables in the linear regression model are distorted or complex to be estimated accurately owing to precise or high correlation. Highly relevant features do not provide much information. This indicates that the information provided by each data is highly correlated, and it does not increase the upper limit of the data. Therefore, integrating the input variables with high similarity can compress the information and eliminate collinearity. It is necessary and statistically significant to integrate various temperature variables into one.

3.2.2 Method of the integrated temperature regression

Unlike reconstructed variable regression [18], integrated temperature regression uses the correlation distance algorithm to optimize multiple temperature values into one to obtain a stronger linear correlation between this temperature value and the thermal-variant slope KT. The relationship between the temperature and thermal-variant slopes is shown in Fig. 6. The temperature measurement points affected by a single external heat source are integrated into a temperature value, and a regression model is established between the integrated temperature and slope. Figure 6 shows that there is a strong linear relationship between the temperature and slope.

Fig. 6
figure 6

Relationship between temperature and thermal-variant slopes

Full size image

The integrated temperature expression is as follows:

$${T}_{{{in}}{{tegrated}}}={\sum }_{i=0}^{m}{l}_{i}{T}_{i}={l}_{0}{T}_{0}+{l}_{1}{T}_{1}+\cdot \cdot \cdot +{l}_{m}{T}_{m}$$
(7)

where Tintegrated is the integrated environment temperature, referred to as the integrated temperature in this study; T0, T1, …, Tm are the temperatures at different locations of the machine affected by the environment; and l0, l1, …, lm are the weights of the ith temperature variable.

To provide physical meaning to the integrated environment temperature, or to make the integrated environment temperature equivalent to the actual temperature of the CMM to a certain extent, the weights in this study are limited as follows:

$$\left\{\begin{array}{c}{\sum }_{i=0}^{m}{l}_{i}=1\\ {l}_{i}\ge 0\end{array}\right.,i=0,1,\cdot \cdot \cdot ,m.$$
(8)

Correlation distance D(Tintegrated, KT) is used to reflect the linearity between the integrated temperature Tintegrated and thermal-variant slope KT, which is defined as follows:

$$D\left({T}_{{integrated}},{K}_{T}\right)=1-P\left({T}_{{integrated}},{K}_{T}\right).$$
(9)

P(Tintegrated, KT) represents the Pearson correlation coefficient, which is expressed as.

$$\begin{array}{c}P({T}_{{integrated}},{K}_{T})=\frac{Cov({T}_{{integrated}},{K}_{T})}{\sqrt{D({T}_{{integrated}})}\sqrt{D({K}_{T})}}\\ =\frac{{\sum }_{j}^{n}({T}_{{}_{{integrated}}}^{k}-{\overline{T} }_{{integrated}})({K}_{T}^{j}-{\overline{K} }_{T})}{\sqrt{[{{\sum }_{j}^{n}({T}_{{}_{{integrated}}}^{k}-{\overline{T} }_{{integrated}})}^{2}]\times [{{\sum }_{j}^{n}({K}_{T}^{j}-{\overline{K} }_{T})}^{2}]}}\end{array},$$
(10)

in which

$${\overline{T} }_{{integrated}}=\frac{1}{card(n)}{\sum }_{j}^{n}{T}_{{}_{{integrated}}}^{j},{\overline{K} }_{T}=\frac{1}{card(n)}{\sum }_{j}^{n}{K}_{T}^{j},$$
(11)

where \(T_{{{{integrated}}}}^{j}\) is the integrated temperature when the constant temperature is set to j degrees Celsius. \(K_{{{T}}}^{j}\) is the slope of the thermal error when the constant temperature is set to j degrees Celsius, and card(n) is the number of set temperatures.

The correlation distance can be obtained from Eq. (13), (15), (16), and (17):

$$\begin{aligned}&D\left({T}_{{integrated}},{K}_{T}\right)\\&=1-\frac{{\sum }_{j}^{n}\left({\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}-\frac{{\sum }_{j}^{n}{\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}}{card\left(n\right)}\right)\left({K}_{T}^{j}-\frac{{\sum }_{j}^{n}{K}_{T}^{j}}{card\left(n\right)}\right)}{\sqrt{\left[{{\sum }_{j}^{n}\left({\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}-\frac{{\sum }_{j}^{n}{\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}}{card\left(n\right)}\right)}^{2}\right]\times \left[{{\sum }_{j}^{n}\left({K}_{T}^{j}-\frac{{\sum }_{j}^{n}{K}_{T}^{j}}{card\left(n\right)}\right)}^{2}\right]}}.\end{aligned}$$
(12)

The smaller the value of D(Tintegrated, KT), the higher the linear positive correlation between the integrated temperature and thermal-variant slope is and the higher the fitting accuracy of the thermal model will be. When D(Tintegrated, KT) is between 0 and 0.2, it can be considered that there is a strong linear positive correlation between the features. Because \(T_{i}^{j}\) and \(K_{{{T}}}^{j}\) are known, D(Tintegrated, KT) is only related to li. Therefore, the objective function is obtained as follows:

$$\begin{array}{l}min\ Object({l}_{0},{l}_{1},\cdot \cdot \cdot ,{l}_{m})=1-\frac{{\sum }_{j}^{n}({\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}-\frac{{\sum }_{j}^{n}{\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}}{card(n)})({K}_{T}^{j}-\frac{{\sum }_{j}^{n}{K}_{T}^{j}}{card(n)})}{\sqrt{[{{\sum }_{j}^{n}({\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}-\frac{{\sum }_{j}^{n}{\sum }_{i=0}^{m}{l}_{i}{T}_{i}^{j}}{card(n)})}^{2}]\times [{{\sum }_{j}^{n}({K}_{T}^{j}-\frac{{\sum }_{j}^{n}{K}_{T}^{j}}{card(n)})}^{2}]}}\\ s.t. \, \left\{\begin{array}{c}{\sum }_{i=0}^{m}{l}_{i}=1\\ {l}_{i}\ge 0\end{array}\right.i=0,1,\cdot \cdot \cdot ,m\end{array}.$$
(13)

This is a nonlinear optimization problem that can be solved using Python or MATLAB. Thus, the optimal solution is obtained, which implies that l0, l1, …, lm are known, and the integrated temperature can be obtained. Therefore, the thermal error model can be obtained using Eq. (5). The modelling process is simplified by the integrated temperature regression method. More importantly, the integrated temperature has an apparent physical meaning in this study.

4 Experimental validation

4.1 Positioning error modelling

In this study, the positioning error curve obtained when the constant temperature is set to 20 °C is used as the geometric component of thermally induced positioning error. The least square method is used to fit the positioning error curve. And, the highest order term of the polynomial fitting is selected as 17 times. The expression is.

$$E{(P)}_{z}={a}_{0}+{a}_{1}z+{a}_{2}{z}^{2}+\cdot \cdot \cdot +{a}_{17}{z}^{17}=\left[{a}_{17},{a}_{16},\cdot \cdot \cdot ,{a}_{0}\right]{\left[{z}^{17},{z}^{16},\cdot \cdot \cdot ,1\right]}^{T}=A\cdot {Z}^{T},$$
(14)

in which.

A = 

[-9.86402064e-4 51.25539203e-40 -7.26303338e-372.52699965e-33.

-5.89404690e-30 9.72430065e-27 -1.16681849e-23 1.03076751e-20.

-6.70915993e-183.18720424e-15 -1.08272441e-12 2.54237949e-10.

-3.91153291e-083.59829515e-06 -1.54886835e-04 -1.63970781e-03.

2.25572864e-01 9.62676061e-01].

The collected data points are relatively dense, and the fitting effect is shown in Fig. 7.

Fig. 7
figure 7

Positioning error curve

Full size image

4.2 Integrated temperature

Table 4 lists the values of each temperature measurement point and thermal gradient when the set temperature in the constant temperature room is 10, 15, 20, 30, and 35 °C.

Table 4 Temperature measurement points and thermal-variant slopes (unit: ℃)
Full size table

The objective function of the integrated temperature method is obtained using Eq. (15), where l0, l1, and l3 are the unknown weights. The objective function and the boundary conditions are expressed as follows:

$$\begin{array}{l}min\;Object({l}_{0},{l}_{1},{l}_{2})=1-\frac{{\sum }_{j=10}^{35}({l}_{0}{T}_{0}^{j}+{l}_{1}{T}_{1}^{j}+{l}_{2}{T}_{2}^{j}-\frac{1}{{5}}{\sum }_{set=10}^{35}({l}_{0}{T}_{0}^{j}+{l}_{1}{T}_{1}^{j}+{l}_{2}{T}_{2}^{j}))({K}_{T}^{j}-\frac{1}{{5}}{\sum }_{set=10}^{35}{K}_{T}^{j})}{\sqrt{[{{\sum }_{j=10}^{35}({l}_{0}{T}_{0}^{j}+{l}_{1}{T}_{1}^{j}+{l}_{2}{T}_{2}^{j}-\frac{1}{{5}}{\sum }_{j=10}^{35}({l}_{0}{T}_{0}^{j}+{l}_{1}{T}_{1}^{j}+{l}_{2}{T}_{2}^{j}))}^{2}]\times [{{\sum }_{set=10}^{35}({K}_{T}^{j}-\frac{1}{{5}}{\sum }_{set=10}^{35}{K}_{T}^{j})}^{2}]}}\\ s.t.\left\{\begin{array}{c}{l}_{0}+{l}_{1}+{l}_{2}=1\\ {l}_{0}\ge 0\\ {l}_{1}\ge 0\\ {l}_{2}\ge 0\end{array}\right.\end{array}.$$
(15)

The optimal solution of the nonlinear multivariate function can be obtained using the gradient method. The results are l0 = 0, l1 = 0.4393, and l2 = 0.5607. Therefore, the integrated temperature can be expressed as follows:

$${T}_{{integrated}}=0.4393{T}_{1}+0.5607{T}_{2}.$$
(16)

The integrated ambient temperature at each preset temperature is shown in Table 5.

Table 5 Integrated ambient temperature values(Unit: ℃)
Full size table

The relationship between the available slope and the integrated temperature is obtained using Eq. (4). The regression equation is as follows:

$${K}_{T}={0.0108T}_{integrated}-0.2057$$
(17)

4.3 Comparison and analysis of thermal error models

On the one hand, to prove the necessity of the method proposed in this study, we compared the thermal error modelling of a single temperature with the integrated environmental temperature modelling. On the other hand, to verify the effectiveness of the method, the newer ridge regression modelling [11] was used as a comparative model. Finally, another group of experimental data was collected to compare the practicality of each model.

4.4 Integrated temperature thermal error modelling (IR)

According to Eqs. (5), (14) and (17), the final thermal error model can be expressed as.

$$E{(P)}_{z}=A\cdot {Z}^{T}+0.0108\times \left({T}_{{integrated}}-{20}.6607\right)z.$$
(18)

4.5 Single temperature for thermal error modelling

R0: Only ambient temperature T0 is used for modelling. The modelling results are as follows:

$$\left\{\begin{array}{l}{K}_{T}=0.0111{T}_{0}-0.2157\\ E\left(P)_{z}=A\cdot {Z}^{T}+0.0111\times \left({T}_{0}-21.0\right.\right)z\end{array}\right.$$
(19)

R1: Only ambient temperature T1 is used for modelling. The modelling results are as follows:

$$\left\{\begin{array}{l}{K}_{T}=0.0105{T}_{0}-0.{1971}\\ E(P)_{z}=\varvec{A} \cdot \varvec{Z}^{T}+0.0105\times ({T}_{1}-{20.1})z\end{array}\right.$$
(20)

R2: Only ambient temperature T2 is used for modelling. The modelling results are as follows:

$$\left\{\begin{array}{l}{K}_{t}=0.0110{T}_{0}-0.2124\\ E\left(P)_{z}=A\cdot {Z}^{T}+0.0109\times \left({T}_{2}-21.1\right.\right)z\end{array}\right.$$
(21)

Ridge regression modelling (RR for short) can effectively reduce the collinearity of the input variables, and the relevant hyperparameters are selected by the grid parameter method of Python. The modelling results are as follows:

$$\left\{\begin{array}{l}{K}_{T}={0.0021788T}_{0}+t{0.00433348T_{1}}+0.00432128{T}_{2}-0.20678767\\ E(P)_{z}=A\cdot {Z}^{T}+0.0021788\times ({T}_{0}-{21}.{0})z\\ +0.00433348\times ({T}_{1}-{20}.{1})z+0.00432128\times ({T}_{2}-{21}.{1})z\end{array}\right..$$
(22)

The performance of the above five thermal error models can be evaluated in terms of the root mean square error (RMSE), mean sum of the absolute residual (MSAR), adjusted coefficient of determination (R2_adjusted), and whether the model has a physical meaning (PM).

$$RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^{n}{({x}_{i}-{\widehat{x}}_{i})}^{2}}$$
(23)
$$MSAR=\frac{1}{n}{\sum }_{i=1}^{n}\left|{x}_{i}-{\widehat{x}}_{i}\right|$$
(24)
$${R}_{adjusted}^{2}=1-\frac{\left(1-{R}^{2}\right)\left(n-1\right)}{n-p-1},$$
(25)

where \(x_{i}\) is the measured value; \(\hat{x}_{i}\) is the fitted or predicted value of the models; R2 is the coefficient of determination; n is the number of samples; and p is the number of features. The performance of the different models is compared in Table 6.

Table 6 Performance of the different models
Full size table

The smaller the values of the RMSE and MSAR and the larger the value of R2_adjusted, the better the prediction accuracy of the thermal positioning error model. Table 7 shows that the various indicators of the IR model are optimal. This indicates that the integrated temperature regression method for thermal error modelling has an excellent predictive effect. Overall, the prediction effect of the integrated temperature model is no less than that of the ridge regression model, and it is significantly better than the single temperature model. Compared with the ridge regression model, the integrated temperature algorithm made the overall thermal error model simpler and calculated a temperature value with PM. A single temperature variable with PM that helps many mature CNC systems realize thermal error compensation in engineering applications.

Table 7 Validation effects of different models
Full size table

To test the model's validity, the temperature of the constant temperature room was set to 25 ℃ as a verification experiment, and the values of the temperature measuring points were obtained as follows: T0 = 24.7, T1 = 24.5, and T2 = 25.3.

Therefore, the integrated temperature can be calculated using Eq. (16):

$${T}_{{integreted}}^{25}=0.4393\times {24.5}+0.5607\times {25.3}={24.9486}{.}$$
(26)

According to Eq. (18), the thermal positioning error can be expressed as.

$$IR:E{(P)}_{z}=A\cdot {Z}^{T}+0.0108\times \left(24.9486-{20}.6607\right)z=A\cdot {Z}^{T}+0.0463z.$$
(27)

The thermal error models for a single temperature, namely R0, R1, and R2, are expressed as follows:

$$\left\{\begin{array}{c}R0:E(P)_{z}=A\cdot {Z}^{T}+0.0111\times (24.7-{2}1.{0})z=A\cdot {Z}^{T}+0.0411z\\ R1:E(P)_{z}=A\cdot {Z}^{T}+0.0105\times (24.5-{20}.1)z=A\cdot {Z}^{T}+0.0462z\\ R2:E(P)_{z}=A\cdot {Z}^{T}+0.01{09}\times (25.3-{2}1.{1})z=A\cdot {Z}^{T}+0.04{58}z\end{array}\right..$$
(28)

The ridge regression thermal error model is expressed as follows:

$$\begin{array}{l}RR:E(P)_{z}=A\cdot {Z}^{T}+0.0021788\times (24.7-{21}.{0})z+0.00433348\times (24.5-{20}.{1})z\\ +0.00432128\times (25.3-{21}.{1})z=A\cdot {Z}^{T}+0.0453z\end{array}$$
(29)

The prediction results of three categories (five in total) are shown in Fig. 8 and Table 7.

Fig. 8
figure 8

Fitting results and residual of different models. a IR (our model). b R0. c R1. d R2. e RR

Full size image
$${\eta }_{q}=\frac{card({Z}_{Rq})}{card({Z}_{R})}\times 100\%,{Z}_{Rq}=\{-q<x<q|x\in {Z}_{R},q>0\}$$
(30)

In Eq. (30), ZR is the set of residuals of thermal error compensation, ZRq is the set with residual values less than q, card() is used to calculate the total number of elements in the set, and ƞq is the percentage of the absolute value of residuals less than q (it is referred to as the error accuracy guarantee in this study).

In the experiment, we found that the prediction accuracy of the single temperature model and the integrated temperature model would decrease depending on its deviation from the reference temperature. However, the prediction accuracy of the single temperature model dropped more sharply. The results of the modelling experiment showed that the integrated temperature has no relationship with the ambient temperature T0. On comparing models R1 and R2 to the IR model, it can be observed that integrated temperature modelling is better than single temperature modelling. Compared to the ridge regression model, which reduces collinearity, the IR model has an easy-to-understand PM and a higher prediction accuracy. The maximum error in the verification experiment is 95 μm, and after the IR model error compensation, the error accuracy guarantee is ƞ5 = 92.11% and ƞ10 = 100.00%. Therefore, for a moving shaft that is only affected by ambient temperature owing to the unevenness of heat transfer, the integrated temperature is essential, and the integrated temperature regression thermal error modelling is a good choice.

5 Conclusion

This paper proposed an integrated temperature thermal error modelling for the high-precision moving shaft that is mainly affected by the ambient temperature. The experimental results showed that the proposed method reduces the collinearity of the input variables and simplifies the thermal error model by calculating the integrated temperature. The following conclusions can be drawn.

  1. 1.

    The thermally induced positioning error of the moving shaft of the special CMM includes a heat-affected part and a reference part. The reference part was the linear positioning error of the moving shaft when the constant temperature room was set to 20 °C, and by integrating the ambient temperature, a concise thermal error model was established. The proposed model significantly reduces the influence of ambient temperature on the positioning error and enables the realization of workshop-level measurement.

  2. 2.

    We split the ambient temperature into several temperature variables and then built the corresponding single-temperature thermal error model. By using the integrated temperature algorithm, the multiple-input problem becomes a single-input problem. Compared to the single temperature and ridge regression models, the proposed model is more accurate, more concise and easier to compensate.

  3. 3.

    The integrated temperature thermal error modelling is suitable for a wide range of temperature changes, such as seasonal variations. However, depending on its deviation from the reference temperature, the prediction accuracy of the model will decrease slightly. The causes and solutions of this problem can be considered in future studies.