1 Introduction

With an increasing need for machined components with geometric complexity in a high efficiency, five-axis machine tools (FAMT) are extensively used in various manufacturing applications requiring higher machining accuracy. [1] However, compared with a three-axis machine tool, the structure of FAMT is relatively complex, which leads to an increase in geometric error sources. It has significantly restricted the improvement of its machining accuracy. In order to improve the machining accuracy of FAMT, geometric error identification and compensation techniques have been widely studied. At present, the geometric error parameter identification of translational axis has been well developed. For example, 9-line method [2], 14-line method [3] and 22-line method [4] have been proposed and standardized by international standards [5]. Compared with the horizontal axis, the structure and motion form of the rotation axis are more complex. Thus, the identification of the geometric error parameters of the rotation axis is still a difficult problem in the field of error identification.

In the past decades, the identification and measurement of geometric error of rotation axis for multi-axis machine tool has become a hot topic. Lee and Yang [6] optimized two measurement trajectories to identify two position-dependent geometric errors (PDGEs) and two position-independent geometric errors (PIGEs) of the rotation axis. Tsutumi et al. [7] calibrated geometric errors of rotary axis by measuring the actual trajectories with two settings of ball bar. Measurements with different coordinate frames were compared and analyzed for identification precision. Lei et al. [8] presented a particular circular test path for motion errors of two rotary axes, in which the circular path is caused by two rotary axes moving simultaneously without three linear axes. Chen and Lin [9] proposed a geometric error identification method for the rotation table of a four-axis machine tool by using the double bar-ball system and got some verified results according to the comparison between the measured and predicted results. To reduce the influence of installation error, Xia et al. [10] proposed a sensitivity analysis method to guide the correction of error parameters. However, the installation error correction of these identification instruments is relatively tedious and time-consuming. Due to the existence of installation bias, the identification results of the model may be distorted from actual error values.

With the continuous development of measurement technology, some new measuring instruments have been applied to the error measurement and identification of the rotation axis. Weikert and Knapp [11] proposed a novel calibrated method for the FAMT based on a newly developed 4D probe and ball artifact. Based on R-test measurement, the displacement error and rotation error of the rotating shaft are measured and the installation error is analyzed. Zargarbashi and Mayer [12] developed a non-contact measuring instrument where the Cartesian volumetric error has been measured by using a programmed end point constraint procedure. Huang et al. [13] developed two different schemes to calibrate the error map of rotation axes by on-the-machine measuring of test pieces. The geometric errors of each rotation axis are identified by indirectly measuring the coordinates of the reference point on the specimen at different rotation axis positions. Compared with traditional instruments, its advantages are high identification efficiency and simple installation. However, because of its high cost, it is difficult to promote in practical measurement. Moreover, the identification method adopts multi-axis linkage, which results in high coupling of error terms. It will increase the error separation work imperceptibly.

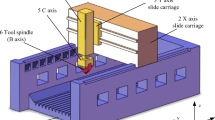
As can be observed in the abovementioned researches, the measuring approaches and identification methods introduced are all for five-axis machine tools with rotation tables. There are few studies on geometric error identification of five-axis machine tools with double swing heads. In addition, the identification model is relatively complex and the identification results are highly nonlinear, which will affect the subsequent error compensation effect. Thus, an accurate, simple and low-cost identification method of rotation axis is urgently developed. To overcome the drawbacks of above problems, this paper developed a novel approach for geometric error identification of rotation axis. The rest of the paper is arranged as follows: Based on Homogeneous Transformation Matrix and DBB measurement principle, an uniaxial identification model is established, which maps the relationship between rod length increment and C-axis error parameters in Sect. 2. In Sect. 3, the five measure paths about C-axis are present and the five geometric error parameters of C-axis are identified by fourth-order truncated Fourier series. In Sect. 4, a compensation experiment on proposed identification method is implemented to verify the feasibility and effectiveness of the proposed identification method. In Sect. 5, this paper is summarized.

2 Geometric error model

2.1 Description of geometric error

The C-axis is the key axis of multi-axis machine tool, which is the premise of realizing flexible machining of tool in space. Therefore, it is of great significance to improve the operation accuracy of C axis to improve the machining accuracy of multi-axis machine tools. Because of structural design defects and assembly of multi-axis machine tools, it will generate 3 angle errors and 3 straightness errors for each axis [14]. In order to describe it more clearly, this paper selects a double-swing head five-axis machine tool as the research object. The six PDGEs of C-axis are illustrated in Table 1, where \(\varepsilon_{z} (c)\) represents the positioning error, \(\delta_{{\text{x}}} (c)\) \(\delta_{{\text{y}}} (c),\delta_{z} (c)\) are on behalf of straightness errors along in the X, Y and Z direction, \(\varepsilon_{x} (c),\varepsilon_{y} (c)\) represent the angle errors around the X and Y direction. To further describe the characteristics of geometric error, the geometric definition of C-axis geometric error is depicted in Fig. 1. When C-axis rotates, each geometric error will change irregularly. As the existence of geometric error, the actual coordinate system will deviate from the ideal coordinate system. In order to further study the variation rule of C-axis geometric error, this paper will measure the C-axis of the pendulum head with the experimental tool of the double-ball bar.

Table 1 The PDGEs of C-axis
Full size table
Fig. 1
figure 1

The geometric errors of C-axis

Full size image

2.2 Identification principle of C-axis geometric error

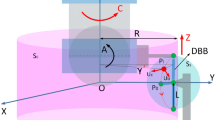
This section is mainly focuses on the identification and derivation of PDGEs of C-axis based on the measurement principle of double ball bar. To map the relationship between tool location in workpiece coordinate system and the NC code in machine coordinate system, the kinematic transformation model is established by using HTM based on rigid body assumption. As can be seen from Fig. 2, the measuring schematic diagram of the double ball bar is depicted, which consists of two precision balls and a sensor. For the measurement, tool ball is designed to be located at a predetermined position in tool coordinate system and the workpiece ball to be located at a predetermined position in workbench coordinate system. A displacement sensor is used to measure the elongation of the rod.

Fig. 2
figure 2

The measuring schematic diagram of double ball bar

Full size image

Assume that the position of the workpiece ball \(M = (x_{m} ,y_{m} ,z_{m} ,0)\) and the initial position of the tool ball \(Q_{0} = (x_{0} ,y_{0} ,z_{0} ,0)\). According to HTM, the ideal position of the tool ball Qi can be represented by

$$Q_{i} = \left[ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \left( c \right)} & { - \sin \left( c \right)} & 0 & 0 \\ {\sin \left( c \right)} & {\cos \left( c \right)} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\;Q_{0} = \left[ {\begin{array}{*{20}c} {\cos (c)x_{0} - \sin (c)y_{0} } \\ {\cos (c)y_{0} + \sin (c)x_{0} } \\ {z_{0} } \\ 1 \\ \end{array} } \right]$$
(1)

The actual position of the tool ball Qa can be expressed as

$$Q_{a} = \left[ {\begin{array}{*{20}c} {x_{a} } \\ {y_{a} } \\ {z_{a} } \\ 1 \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\cos \left( c \right)} & { - \sin \left( c \right)} & 0 & 0 \\ {\sin \left( c \right)} & {\cos \left( c \right)} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{{\text{z}}} \left( c \right)} & {\varepsilon_{{\text{y}}} \left( c \right)} & {\delta_{{\text{x}}} \left( c \right)} \\ {\varepsilon_{{\text{z}}} \left( c \right)} & 1 & { - \varepsilon_{{\text{x}}} \left( c \right)} & {\delta_{{\text{y}}} \left( c \right)} \\ { - \varepsilon_{{\text{y}}} \left( c \right)} & {\varepsilon_{{\text{x}}} \left( c \right)} & 1 & {\delta_{{\text{z}}} \left( c \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]Q_{0}$$
(2)

Thus, according to Eqs. (1) and (2), the volume deviation of tool ball △E can be obtained

$$\Delta E = \left[ {\begin{array}{*{20}c} {\Delta x} & {\Delta y} & {\Delta z} & 1 \\ \end{array} } \right] = Q_{a} - Q_{i}$$
(3)
$$\left\{ {\begin{array}{*{20}c} {\Delta x = \delta_{x} (c) + z_{0} \varepsilon_{y} (c) - y_{0} \cos (c)\varepsilon_{z} (c) - x_{0} \sin (c)\varepsilon_{z} (c)} \\ {\Delta y = \delta_{y} (c) - z_{0} \varepsilon_{x} (c) - y_{0} \sin (c)\varepsilon_{z} (c) + x_{0} {\text{cos}}(c)\varepsilon_{z} (c)} \\ \begin{gathered} \Delta z = \delta_{z} (c) - y_{0} (\cos (c)\varepsilon_{x} (c) + \sin (c)\varepsilon_{y} (c)) \hfill \\ - x_{0} (\cos (c)\varepsilon_{y} (c)\sin (c)\varepsilon_{x} (c)) \hfill \\ \end{gathered} \\ \end{array} } \right.$$
(4)

In addition, the actual and ideal rod length can be calculated as follows, respectively

$$\left\{ {\begin{array}{*{20}c} {\left| {Q_{{\text{a}}} M} \right| = L_{a} = \sqrt {(x_{a} - x_{m} )^{2} + (y_{a} - y_{m} )^{2} + (z_{a} - z_{m} )^{2} } } \\ {\left| {Q_{i} M} \right| = L = \sqrt {(x_{0} - x_{m} )^{2} + (y_{0} - y_{m} )^{2} + (z_{0} - z_{m} )^{2} } } \\ \end{array} } \right.$$
(5)

The club length increment of the double ball bar can be expressed as

$$\begin{aligned} \Delta L & = \left| {Q_{{\text{a}}} M} \right| - \left| {QM} \right| = \sqrt {(x_{a} - x_{m} )^{2} + (y_{a} - y_{m} )^{2} + (z_{a} - z_{m} )^{2} } - L \\ & = \sqrt {(x_{i} + \Delta x - x_{m} )^{2} + (y_{i} + \Delta y - y_{m} )^{2} + (z_{i} + \Delta z - z_{m} )^{2} } - L \end{aligned}$$
(6)

By ignoring higher-order terms, Eq. (5) can be deserved as

$$\Delta L = \frac{1}{L}[(x_{i} - x_{a} )\Delta x + (y_{i} - y_{a} )\Delta y + (z_{i} - z_{a} )\Delta z]$$
(7)

In order to quantitatively analyze the contribution of geometric error to rod length increment, rod length increment is assumed here

$$\Delta L = {\varvec{k}}*{\varvec{Ge}}$$
(8)

where \({\varvec{k}}{\text{ = [k}}_{{1}} ,{\text{k}}_{2} ,{\text{k}}_{{3}} ,{\text{k}}_{4} ,{\text{k}}_{5} ,{\text{k}}_{6} ]\), \({\varvec{Ge}} = [\delta_{{\text{x}}} (c),\delta_{{\text{y}}} (c),\delta_{z} (c),\varepsilon_{x} (c),\varepsilon_{y} (c),\varepsilon_{z} (c)]\).

According to Eqs. (3)–(7), the coefficients k can be calculated

$$\left\{ {\begin{array}{*{20}c} {k_{1} = \frac{1}{L}[x_{0} \cos (c) - y_{0} \sin (c) - x_{m} ]} \\ {k_{2} = \frac{1}{L}[x_{0} \sin (c) + y_{w} \cos (c) - y_{m} ]} \\ {k_{3} = \frac{1}{L}(z_{0} - z_{m} )} \\ {k_{4} = \frac{1}{L}[y_{m} z_{0} - x_{m} z_{0} - y_{0} z_{m} ]} \\ {k_{5} = \frac{1}{L}[x_{0} z_{m} \cos (c) - x_{m} z_{0} - y_{o} z_{m} \sin (c)]} \\ {k_{6} = \frac{1}{L}[x_{m} y_{0} \cos (c) - x_{0} y_{m} \cos (c) + x_{0} x_{m} \sin (c) + y_{0} y_{m} \sin (c)]} \\ \end{array} } \right.$$
(9)

The positioning error identification principle of C-axis is independent of the model proposed in this paper. The positioning error identification principle of C-axis is shown in Eq. (10). The actual positioning error parameters are calculated by comparing each actual measuring point with the ideal measuring point using XR20-W.

$$\varepsilon_{c} (c) = \frac{1}{n}\sum\limits_{j = 1}^{n} {(c_{a} - c_{i} )}$$
(10)

where \(c_{i}\) and \(c_{a}\) are represent the ideal angle and actual angle of C axis.

In order to further prove this, the following deduction is developed based on measuring principle of double ball bar. During testing with double ball bar, the ideal length of the rod should be equal to the initial length of the rod. Thus, according to Eq. (5), this identity can be derived as

$$\begin{aligned} L^{2} & = x_{0}^{2} - 2z_{0} z_{m} + y_{0}^{2} + z_{0}^{2} + x_{m}^{2} + y_{m}^{2} + z_{m}^{2} - 2x_{0} x_{m} \cos (c) \\ & - 2y_{0} y_{m} \cos (c) - 2x_{0} y_{m} \sin (c) + 2y_{0} x_{m} \sin (c) \end{aligned}$$
(11)

It can be observed from Eq. (11) that the polynomial with respect to parameter c is identity. Thus, it can be written as follows

$$- 2x_{0} x_{m} \cos (c) - 2y_{0} y_{m} \cos (c) - 2x_{0} y_{m} \sin (c) + 2y_{0} x_{m} \sin (c) = const$$
(12)

Suppose that the constants of a and b are expressed as, respectively.

$$\left\{ {\begin{array}{*{20}c} {a = x_{0} x_{m} + y_{0} y_{m} } \\ {b = y_{0} x_{m} - x_{0} y_{m} } \\ \end{array} } \right.$$
(13)

According to Eqs. (12) and (13), it can be calculated as

$$\left\{ {\begin{array}{*{20}c} {\sqrt {a^{2} + b^{2} } = 0,\sqrt {a^{2} + b^{2} } \sin (c + ar\tan \frac{a}{b}) = const} \\ {k_{6} = x_{m} y_{0} \cos (c) - x_{0} y_{m} \cos (c) + x_{0} x_{m} \sin (c) + y_{0} y_{m} \sin (c) = 0} \\ \end{array} } \right.$$
(14)

In summary, it can be reasonably concluded that the c-axis positioning error has no contribution to the rod length increment. Thus, only five PDGEs of C-axis need to be measured and identified, respectively.

3 Identification method

3.1 Measurement path

As described in the previous section, the club length increment relates only to the five PDGEs of the C-axis in the double ball bar test. According to the PDGEs linear relationship between rod length increment and C-axis determined in Eq. (8), five sets of equations are required to determine the PDGEs of C-axis. As can be seen from Fig. 3, the five measurement paths of the double ball-bar are developed to measure the geometric errors of the C-axis. Figure 3a, b measured error increment of rod length in X direction, when axis C rotates at different heights. Similarly, Fig. 3c, d are applied to the increment of rod length measured in the Y direction. The measurement track in Fig. 3e is used to determine the error increment in the Z direction. Thus, the increment of rod length △L measured at different trajectories can be expressed as

$$\Delta L{ = }\left[ {\begin{array}{*{20}c} {\Delta L_{{1}} } & {\Delta L_{{2}} } & {\Delta L_{{3}} } & {\Delta L_{{4}} } & {\Delta L_{{5}} } \\ \end{array} } \right]^{T}$$
(15)
Fig. 3
figure 3

Measurement model for C-axis geometric error (a)(b) Error measurement in X direction at different heights (c)(d) Error measurement in Y direction at different heights (e) Error measurement in Z direction

Full size image

Therefore, according to the linear relationship between rod length increment and C-axis geometric error parameter given in Eq. (8), the five PDGEs of C-axis can be identified. As shown in Fig. 4, the geometric error of the C-axis of the FAMT with swing head is being identified. Before the measurement experiment, the machine should be preheated for 20 min to reduce the interference of thermal error on the identification results. In addition, the experimental site temperature was maintained at 20 + 0.1 °C. In the experiment, the length of the double ball bar is L = 150 mm. The measure results of rod length increment under five trajectories are illustrated in Fig. 5. Among them, the rod instrument trajectories 1–5 represent the height of the tool end in the five corresponding measurement modes, respectively.

Fig. 4
figure 4

The measurement scene of five PDGEs of C-axis

Full size image
Fig. 5
figure 5

The measure results of rod length increment a The increments of rod in X direction b The increments of rod in Y direction c The increments of rod in Z direction

Full size image

3.2 Characterization of error parameters

Geometric errors can be described by functions related to the position of the coordinate axis because they are position related. Taking the C-axis as an example, it is necessary to reasonably establish the mapping relationship between its rotation angle and geometric error parameters. This approach is convenient for the description of geometric error and simplifies the identification process of geometric error parameters. Different functions are used to describe geometric errors, which affects the approximation accuracy of geometric errors. In previous studies, polynomial method [16], Fourier method [17] and Chebyshev polynomial [18, 19] method were used to fit error parameters. They focus on the randomness and aperiodicity of geometric error parameters. In this paper, the truncated Fourier series is applied to describe the geometric error characteristics quantitatively, considering the boundary and discontinuity of geometric error parameters.

Therefore, the geometric error parameter of C-axis can be expressed as

$$Ge = \sum\limits_{i}^{n} {A_{i} } \sin (i*c_{i} )$$
(16)

where Ai (i = 1,2…n) represents the coefficient of the polynomials describing the PDGEs. The n represents the order of the polynomial, determined by checking the SSE of the residual error. It is worth noting that the fitting model starts from zero order. It means that when the C axis is 0 degrees, the geometric error is not considered 0, which is different from other models. In other mathematical models, the geometric error is considered to be absolutely 0 points when the C-axis rotation is 0 degrees. However, in practical measurement, the geometric error exists at any angle. Thus, the identification result deviates from the actual error value.

Reasonable selection of polynomial fitting order is the basis of effective error fitting. When the order is small, it cannot truly reflect the change trend of error parameters, which will affect the compensation effect. On the contrary, when the order is large, the relative amount of calculation will increase, which leads to overfitting. Therefore, according to literature [15], polynomials of order 4 ~ 6 are generally sufficient to describe the variation law of PDGEs. Therefore, this paper selects fourth-order polynomial to fit the geometric error of C-axis. When the increment of measuring point rod length is obtained, it is put into Eq. (8) to obtain the error parameter value of C-axis of each measuring point. MATLAB 2016 software is used to fit these discrete parameter values. The fitting results of C-axis geometric error parameters are shown in Fig. 6. The fitting method is based on the least square method as shown below.

Fig. 6
figure 6

C-axis geometric error identification results a The identification result of \(\delta_{x} (c)\) b The identification result of \(\delta_{y} (c)\) c The identification result of \(\delta_{z} (c)\) d The identification result of \(\varepsilon_{x} (c)\) e The identification result of \(\varepsilon_{y} (c)\)

Full size image

The following equation can be obtained according to the relationship between geometric error parameters and measured points.

$${\varvec{A}}^{T} {\mathbf{C}} = {\varvec{B}}$$
(17)

The matrix of coefficients A can be obtained

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} {A_{10} } & {A_{20} } & {A_{30} } & {A_{40} } \\ {A_{11} } & {A_{20} } & {A_{30} } & {A_{40} } \\ {...} & {...} & {...} & {...} \\ {A_{1i} } & {A_{2i} } & {A_{3i} } & {A_{4i} } \\ {A_{1n} } & {A_{2n} } & {A_{3n} } & {A_{4n} } \\ \end{array} \begin{array}{*{20}c} {A_{50} } \\ {A_{50} } \\ {...} \\ {A_{5i} } \\ {A_{5n} } \\ \end{array} } \right]_{n \times 5}$$
(18)

Similarly, the independent variable matrix C can be written as

$${\varvec{C}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ {\sin c_{1} } \\ {\sin 2c_{1} } \\ {...} \\ {\sin nc_{1} } \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ {\sin c_{2} } \\ {\sin 2c_{2} } \\ {...} \\ {\sin nc_{2} } \\ \end{array} } & {\begin{array}{*{20}c} {...} \\ {...} \\ {...} \\ {...} \\ {...} \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ {\sin c_{j} } \\ {\sin 2c_{j} } \\ {...} \\ {\sin nc_{j} } \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ {\sin c_{k} } \\ {\sin 2c_{k} } \\ {...} \\ {\sin nc_{k} } \\ \end{array} } \\ \end{array} } \right]_{n \times k}$$
(19)

where

$${\varvec{B}} = \left[ {\begin{array}{*{20}c} {\delta_{{\text{x}}} (c_{0} )} & {\delta_{{\text{x}}} (c_{1} )} & {...} & {\delta_{{\text{x}}} (c_{j} )} & {\delta_{{\text{x}}} (c_{k} )} \\ {\delta_{y} (c_{0} )} & {\delta_{y} (c_{1} )} & {...} & {\delta_{y} (c_{j} )} & {\delta_{y} (c_{k} )} \\ {\delta_{z} (c_{0} )} & {\delta_{z} (c_{1} )} & {...} & {\delta_{z} (c_{j} )} & {\delta_{z} (c_{k} )} \\ {\varepsilon_{x} (c_{0} )} & {\varepsilon_{x} (c_{1} )} & {...} & {\varepsilon_{x} (c_{j} )} & {\varepsilon_{x} (c_{k} )} \\ {\varepsilon_{y} (c_{0} )} & {\varepsilon_{y} (c_{1} )} & {...} & {\varepsilon_{y} (c_{j} )} & {\varepsilon_{y} (c_{k} )} \\ \end{array} } \right]_{5 \times k}$$
(20)

where dependent variable matrix B can be obtain from Eq. (8).

According to the principle of least square method, the coefficient matrix can be calculated

$${\varvec{A}} = ({\varvec{C}}^{T} {*}{\mathbf{C}})^{ - 1} {\varvec{C}}^{T} {\varvec{B}^{T}}$$
(21)

The identification matrix contains the rotation axis angle variable c. The specific parameters of the measured species are shown in Table 2. Therefore, firstly, the identification calculation needs to discretize the angle variable and substitute it into each group of "angle measured value" parameters, which is used to calculate the five geometric errors under the current angle. Finally, the discrete measurement results of each geometric error parameter are fitted, respectively. The C-axis angle range of the CNC machine tool studied in this study is limited to 0°–360°, and the measured C-axis angle is discretized for 20 segments. Record the measurement data every 18°.

Table 2 Measure the parameters of the experiment
Full size table

The fitting results of C-axis geometric error parameters are shown in Eq. (22)

$$\left\{ {\begin{array}{*{20}c} {\delta_{{\text{x}}} \left( c \right) = 7.91*10^{ - 3} + 5.754*10^{ - 3} *\sin c - 2.97*10^{ - 3} *\sin 2c + 3.98*10^{ - 3} *\sin 3c - 1.13*10^{ - 4} *\sin 4c} \\ {\delta_{{\text{y}}} \left( c \right) = 8.59*10^{ - 3} + 8.773*10^{ - 2} *\sin c - 5.72*10^{ - 2} *\sin 2c + 1.1*10^{ - 2} *\sin 3c - 6.34*10^{ - 4} *\sin 4c} \\ {\delta_{{\text{z}}} \left( c \right) = - 1.47*10^{ - 3} + 8.22*10^{ - 3} *\sin c - 5.11*10^{ - 3} *\sin 2c + 9.26*10^{ - 4} *\sin 3c - 4.89*10^{ - 5} *\sin 4c} \\ {\varepsilon_{x} \left( c \right) = 2.74*10^{ - 4} + 1.82*10^{ - 4} *\sin c - 1.1*10^{ - 4} *\sin 2c - 1.95*10^{ - 5} *\sin 3c + 9.84*10^{ - 7} *\sin 4c} \\ {\varepsilon_{y} \left( c \right) = 1.89*10^{ - 5} + 1.27*10^{ - 4} *\sin c - 6.13*10^{ - 5} *\sin 2c + 6.57*10^{ - 6} *\sin 3c - 1.92*10^{ - 9} *\sin 4c} \\ \end{array} } \right.$$
(22)

3.3 Identification result analysis

Since the installation error of double ball bar is inevitable, it will cause the distortion of identification results. At present, there are two methods to eliminate the installation error. One is to add the installation error parameter term to the identification model, which is usually considered as a fixed value. The other is to calibrate the club instrument with high-precision instrument in the experiment, which requires high cost and precision. Because of its limitations, it is difficult to extend and apply to practical measurement. However, the error parameter model established in this paper is solved by the least square method. It means that when there is enough data, the identification result will eliminate the influence of installation error. In addition, the R-square model is used to judge the fitting effect to observe whether it meets the accuracy requirements.

It can be seen from Fig. 6 that even if there are very few out-of-tolerance discrete points, the discrete points are near the fitted curve. Taking the geometric error \(\delta_{{\text{x}}} \left( c \right)\) for example, it can be seen that the minimum and maximum fitted straightness error value of C-axis are 0.018 mm and 0.041 mm, respectively, which means the range of the fitted straightness error \(\delta_{{\text{x}}} \left( c \right)_{f}\) is 0.059 mm. And the minimum and maximum measured position error value of X axis guideway is -0.020 mm and 0.038 mm, respectively, which means the range of the measured position error \(\delta_{{\text{x}}} \left( c \right)_{m}\) is 0.058 mm. That is to say, the range of fitting curve includes the range of discrete points. Moreover, it can be seen from Table 3 that the values of R-square are more than 0.9. Among them, the R-square value of geometric error parameter \(\varepsilon_{x} \left( c \right)\) has reached 0.9677. It means that the fitting equation has strong ability to explain the error value of discrete points, and the fitting degree of the model is excellent and accurate.

Table 3 Results of model fitting
Full size table

At last, by comparing with the measured results, the feasibility and effectiveness of the proposed identification model of C-axis has been further validated. The results of the comparison between the fitting and measured results are presented in Table 4. In the fitting result of straightness errors and angle errors, the maximum residuals are 8.2*10–3 mm and 4.3*10–5 rad, respectively. It means that compared with measurement points, the vast majority of residual errors are considerably small. The average residual errors of straightness errors and angle errors are even less than 2.3*10–3 mm and 3.8*10–6 rad. The residual errors can be caused by many factors such as thermal error, servo error and so on. Thus, there is no doubt that the identification of the geometric error parameters of the c-axis is feasible and effective.

Table 4 The results of maximum and average residual errors
Full size table

4 Experiment

To prove the validity and feasibility of the proposed method, a geometric error compensation experiment based on the proposed error identification method is implemented. Due to the complex surface characteristics of S-shaped specimen [20], it has been widely used in the machining accuracy detection of multi axis NC machine tools. Thus, in this paper, S-shaped specimen is selected as the workpiece to be processed, and the five-axis machine tool with swing head is taken as the research object. The processing scene is shown in Fig. 7. Similarly, the machine should be preheated before the error compensation experiment to reduce the influence of thermal errors.

Fig. 7
figure 7

The machining scene of S-shaped specimen

Full size image

The validity of compensation was judged by comparing the processing quality of S-shaped specimen before and after compensation. The geometric error compensation process of axis C is illustrated in Fig. 8. The main processes of experiment are as follows. There are two samples of S-shaped piece after rough machining. Firstly, the S-shaped specimen is characterized by mathematical model, which usually uses B spline curve before geometric error compensation experiment. Secondly, the post-processing processor will postprocess to generate the desired NC code. Moreover, the RTCP is enabled to compensate for the C-axis position error, which is used to process the first S-shaped specimen. RTCP [21] only compensates the tool center point, regardless of the machine structure parameters. Meanwhile, the ideal NC code is modified based on the identification of C-axis geometric error method to generate the modified NC code by the post-processor. The modified NC code is applied to process the second S-shaped specimen. Finally, the ideal NC code and the modified NC code are used to process the S-shaped specimen. It is important to note that the frequency of correction should usually be lower than the machine displacement resolution. When the two S-shaped specimens are machined, the three coordinate measuring machine (CMM) is used to detect their machining accuracy. The error value of processing point on the curve Z = 30 mm of S-shaped specimen is measured and shown in Fig. 9.

Fig. 8
figure 8

C-axis error compensation flow chart

Full size image
Fig. 9
figure 9

The testing scene of S-shaped specimen

Full size image

The machining error results of S-shaped specimens are illustrated in Fig. 10. In order to better illustrate the effectiveness of compensation, the error average values of S-shaped specimen compensated by RTCP compensation method and the proposed compensation method are calculated, respectively, and the maximum machining error is calculated, respectively. The calculation results are shown in Table 5. It is evident that compared with RTCP method, the average value of machining error reduces by 0.004 mm, which machining accuracy has improved by 28.6%. Moreover, the max value of machining error has decreased by which of value has reduced by 4.25%. The result indicates that machining accuracy of S-shaped specimen compensated by the proposed method is better than that compensated by RTCP. It can be reasonably concluded that machining accuracy have been significantly improved by the proposed error compensation. However, the measured values at points 6 and 18 are out of tolerance; it may be influenced by two main reasons. On one hand, the environment during machining process has some influences on the accuracy, such as the noise and vibration. On the other hand, the errors caused by thermal error and cutting force error also affect the machining accuracy. Therefore, the machining accuracy of FAMT can be improved with the presented geometric error compensation which strongly proves the validity and feasibility of the identification model.

Fig. 10
figure 10

The machining error of S-shaped specimen

Full size image
Table 5 Machining error of S-shaped specimen
Full size table

5 Conclusion

This paper presented an approach for improving machining accuracy of five-axis machine tools. Firstly, based on HTM theory, a C-axis identification model of rod length increment of double ball bar was established, which maps the relationship between rod length increment and geometric error parameters of C-axis. Then, the five measurement trajectories are developed to identify the geometric error of C-axis. Moreover, the geometric error of the C-axis is characterized by the fourth-order truncated Fourier series, which transforms the qualitative description of geometric error parameters into quantitative analysis. At last, a geometric error experiment on S-shaped specimen is conducted to validate the developed methodology. Compared with RTCP, the machining accuracy of FAMT has been significantly improved. Therefore, it can be reasonably concluded that the proposed method is simple, reliable, and efficient, which is beneficial to enhance the machining accuracy of FAMT.

In this paper, the modeling, identification and compensation of geometric errors are focused. However, some other errors also have great influences on the precision of machine tools, such as thermal error and cutting force error.