1 Introduction

Due to the high productivity and flexibility, high-speed milling (HSM) has been widely adopted in aerospace and automobiles industry [1]. However, owing to the detrimental effect on tool life, material removal efficiency, and workpiece surface equality, chatter has become a major obstacle to high performance milling [2]. In order to remove this obstacle, more and more scholars are attracted in chatter avoidance or suppression. In general, the methods for chatter avoidance or mitigation are mainly divided into three categories, including stability prediction, passive control, and active control [2,3,4].

Stability analysis can provide the guidance for selection of milling parameters (spindle speed and axial cutting depth). The present study aims to obtain the stability lobe diagram (SLD) more quickly and accurately. On the one hand, lots of methods and their improved methods are proposed to acquire the SLD. For instance, Altintas et al. put forward the zero-order approximation method [5] and the multi-frequency method [6] in frequency domain. The former is the most efficient method, but cannot be applicable for small radial cutting depth. The latter is suitable to low-immersion milling, but time-consuming due to the higher-order items’ approximation. As to the time domain, many discretization methods are developed. For example, the semi discretization method [7] and its higher-order methods [8] have been a popular method for a long time. Unfortunately, the matrix exponential function in SDM depends on both spindle speed and axial cutting depth, which would increase the calculation and lead to low efficiency. The full discretization method [9] constructs the Floquet matrix through direct integration and linear interpolation, where the matrix exponential function is just related with spindle speed. Besides the discretization strategies, the temporal finite element analysis is also developed for milling stability analysis with high accuracy and efficiency [10]. On the other hand, lots of researchers try to obtain the SLD as accurately as possible, through considering practical factors, such as helix angle [11, 12], runout [13], process damping [14], tool deflection [12, 15], thin-walled workpiece [16], and material removal [17, 18]. However, this method cannot expand the stability zone of SLD. However, the accurate prediction of SLD can just guide for cutting parameter selection; however, it cannot guarantee that the cutting parameters remain constant and the original stable system may lose stabilization owning to the time-varying property of cutting process [19].

The passive control technique attempted to suppress chatter by changing the system behavior, which is based on improving the design of the machine tool to change its performance against vibration (variable pitch [20] or variable helix [21]) or on the use of extra devices (tuned mass damper [22]) that can absorb extra energy or disrupt the regenerative effect. However, due to the time-varying property and uncertainty of cutting process, the passive control cannot show good performance without extra energy input [23, 24].

As the third strategy, active control is an effective method for chatter suppression, which can satisfy the real-time requirements of the online control system and realize high-performance and high-efficiency cutting. Different actuators can be integrated into spindle, such as electrostrictive actuator [18], active magnetic bearing [19], and piezoelectric stack [20, 21]. With extra energy input, the active control system is able to change the dynamics property of machine tool and afford additional forces for chatter suppression, so that the stable cutting region can be expanded. For example, Niels and Verschuren [25] adopted the robust active control method for chatter suppression, which can guarantee the robust stability. Monnin et al. [26, 27] adopted the optimal control algorithm for chatter suppression using active spindle equipped with piezoelectric stacks. Using piezoelectric patch as the actuator, Zhang et al. [24] applied LMS active control method to milling process and suppress chatter vibration energy almost by 50%.

The traditional active chatter control algorithm takes the vibration signals in time domain as the feedback signals, which will suppress all the vibration frequencies, including both chatter frequencies and normal frequencies. Therefore, actuators in traditional control strategies have to waste much energy for rotation frequency and its frequency multiplications, which cannot obtain the optimal performance and cause the saturation effect of actuators. In order to solve this problem, Wang et al. [23] adopted the adaptive vibration reshaping algorithm for line spectrum control, which can suppress chatter frequencies effectively without changing rotation frequency and its frequency multiplications. However, this algorithm is just suitable to the condition where chatter frequencies keep unchanged. On the basis of researches [28,29,30], chatter frequencies vary in thin-walled workpiece milling.

In order to suppress time-varying chatter frequencies, this research introduced the real-time FFT identification into ANE [23] and modified NFXLMS [31]. ANE can suppress chatter frequencies effectively without changing rotation frequency and its frequency multiplications; however, it is sensitive to the chatter frequencies’ identification errors. With the chatter frequencies’ identification errors increasing, the controller performance decreases until fail. Therefore, the real-time FFT identification can modify the identified reference frequencies for better controller performance. However, if the real-time FFT identification is implemented at every step, it will increase the calculation burden of controller and the control delay, which will decrease the controller performance a lot [23]. Thus, in this research, the real-time FFT identification is implemented at every N steps, where N depends on the convergence factors [12]. In that case, a new problem arises; that is, chatter frequencies vary during the N steps. Hence, the modified NFXLMS is adopted to replace ANE, where the reference frequencies can be updated iteratively by a new adaptive algorithm during two chatter frequencies identifications by FFT. Simulation results show that the modified NFXLMS has better control effect than ANE.

The remainder of this paper is arranged as follows. In Sect. 2, the time-varying chatter frequencies phenomenon is introduced and verified by milling tests. Section 3 presents the chatter suppression algorithm based on ANE and modified NFXLMS with FFT. Besides, the numerical simulation is provided. In Sect. 4, the measured vibration data in thin-wall workpiece milling is applied for algorithm verification. Finally, some conclusions and future works are drawn in Sect. 5.

2 The time-varying chatter frequencies phenomenon in thin-walled workpiece milling

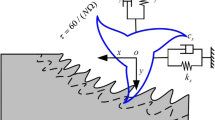
As seen in Fig. 1, the milling tool is usually assumed to be rigid in thin-walled part milling [32, 33]. Then, the governing equation can be expressed by:

$$\left[\begin{array}{cc}{m}_{x}& 0\\ 0& {m}_{y}\end{array}\right]\left[\begin{array}{c}\ddot{x}(t)\\ \ddot{y}(t)\end{array}\right]+\left[\begin{array}{cc}{c}_{x}& 0\\ 0& {c}_{y}\end{array}\right]\left[\begin{array}{c}\dot{x}(t)\\ \dot{y}(t)\end{array}\right]+\left[\begin{array}{cc}{k}_{x}& 0\\ 0& {k}_{y}\end{array}\right]\left[\begin{array}{c}x(t)\\ y(t)\end{array}\right]=\left[\begin{array}{c}{F}_{x}(t)\\ {F}_{y}(t)\end{array}\right]$$
(1)

where \(\left[\begin{array}{cc}{m}_{x}& 0\\ 0& {m}_{y}\end{array}\right]\), \(\left[\begin{array}{cc}{c}_{x}& 0\\ 0& {c}_{y}\end{array}\right]\), and \(\left[\begin{array}{cc}{k}_{x}& 0\\ 0& {k}_{y}\end{array}\right]\) are the modal mass, modal damping, and modal stiffness matrixes of the thin-walled components, respectively; \({[{F}_{x}\left(t\right) {F}_{y}\left(t\right)]}^{\mathrm{T}}\) and \({[x\left(t\right) y\left(t\right)]}^{\mathrm{T}}\) are the milling forces and vibration displacement vectors in the x and y directions.

Fig. 1
figure 1

The schematic representation of the milling process

Full size image

To calculate the instantaneous milling forces, the tool is discretized into \({N}_{a}\) axial disk layers with \(dz={a}_{p}/{N}_{a}\), where \({a}_{p}\) is the axial milling depth and \(dz\) is the height of each axial discretization disk. Hence, the milling forces can be written as follows:

$$\begin{aligned}\left[\begin{array}{c}{F}_{x}\left(t\right)\\ {F}_{y}\left(t\right)\end{array}\right]=&\sum_{z=1}^{Na}\sum_{j=1}^{N}\left[\begin{array}{cc}-\mathrm{cos}\left({\phi }_{j}\left(z,t\right)\right)& -\mathrm{sin}\left({\phi }_{j}\left(z,t\right)\right)\\ -\mathrm{sin}\left({\phi }_{j}\left(z,t\right)\right)& -\mathrm{cos}\left({\phi }_{j}\left(z,t\right)\right)\end{array}\right]\\&\left\{\left[\frac{{K}_{t}}{{K}_{n}}\right]{h}_{j}\left(z,t\right)+\left[\begin{array}{c}{K}_{te}\\ {K}_{ne}\end{array}\right]\right\}\mathrm{g}\left({\phi }_{j}\left(z,t\right)\right)dz\end{aligned}$$
(2)

where \(N\) is the number of teeth; \({K}_{t}\) and \({K}_{n}\) are the tangential and radial shearing force coefficients; \({K}_{te}\) and \({K}_{ne}\) are the tangential and radial ploughing force coefficients; and \(g({\phi }_{j}(z,t))\) is a switch function for determining whether the tooth is in or out of cut, which can be expressed as \(\left\{\begin{array}{l}g\left(\phi_j\left(z,t\right)\right)=1\phi_{st}<\phi_j\left(z,t\right)<\phi_{ex}\\g(\phi_j\left(z,t\right))=0otherwise\;\;\;\;\;\;\;\;\;\;\end{array}\right.\), where \({\phi }_{st}\) and \({\phi }_{ex}\) are the start and exit angles of the cutter tooth.

\({\phi }_{j}\left(z,t\right)\) is the angular position of the jth tooth at the zth axial disk, which can be given by:

$${\phi }_{j}\left(z,t\right)=(2\pi\Omega /60)t+(\kern 0.1500em j-1)\cdot 2\pi /N-2z\mathrm{tan}\gamma /\mathrm{D}$$
(3)

where \(\Omega\), \(\gamma\), and \(D\) are the spindle speed (in rpm), helix angle, and diameter of milling tool, respectively.

The instantaneous uncut chip thickness \({h}_{j}\left(z,t\right)\) can be obtained as follows:

$${h}_{j}\left(z,t\right)={f}_{t}\mathrm{sin}\left({\phi }_{j}\left(z,t\right)\right)+{\Delta x}_{jz}\mathrm{sin}\left({\phi }_{j}\left(z,t\right)\right)+{\Delta y}_{jz}\mathrm{cos}\left({\phi }_{j}\left(z,t\right)\right)$$
(4)

where \({f}_{t}\) is the feed per tooth (in mm/tooth); \({\Delta x}_{jz}\) and \({\Delta y}_{jz}\) are the instantaneous uncut chip thickness of the jth tooth at the zth axial disk in the x and y directions, respectively.

The modal parameters are usually obtained by finite element analysis or experiment modal analysis. In thin-walled workpiece milling, the corresponding modal parameters are time-varying with the workpiece material removal and the change of tool position, which will cause the variation of chatter frequencies [30]. The detailed description about milling forces can refer to the literature [33]. The dominant chatter frequencies can be calculated with the developed theory in [34]. Similar as Fig. 2, the experimental results in [18, 28,29,30] have verified the existence of the time-varying chatter frequencies phenomenon. For the small-sized thin-walled part in milling tests, the chatter frequency varies from 225 to 220 Hz.

Fig. 2
figure 2

The time-varying plane of acceleration signals in thin-walled workpiece milling

Full size image

For the implementation of the successive control algorithm in time domain, the Euler approximation method [35] is adopted to solve the milling dynamic equation numerically to investigate the dynamic behavior under a specific cutting condition:

$$\ddot{x}\left({t}_{i}\right)=\frac{{F}_{x}\left({t}_{i}\right)-{c}_{x}\dot{x}\left({t}_{i}\right)-{k}_{x}x\left({t}_{i}\right)}{{m}_{x}}, \ddot{y}\left({t}_{i}\right)=\frac{{F}_{y}\left({t}_{i}\right)-{c}_{y}\dot{y}\left({t}_{i}\right)-{k}_{y}y\left({t}_{i}\right)}{{m}_{y}}$$
(5)
$$\dot{x}\left({t}_{i}\right)=\dot{x}\left({t}_{i-1}\right)+\ddot{x}\left({t}_{i}\right)\mathrm{d}t, \dot{y}\left({t}_{i-1}\right)+\ddot{y}\left({t}_{i}\right)\mathrm{d}t$$
(6)
$$x\left({t}_{i}\right)=x\left({t}_{i-1}\right)+\dot{x}\left({t}_{i}\right)\mathrm{d}t, y\left({t}_{i}\right)=y\left({t}_{i-1}\right)+\dot{y}\left({t}_{i}\right)\mathrm{d}t$$
(7)

where \(i\) is an integer number starting from one and \(\mathrm{d}t\) is the time step. The time domain simulation results have been verified by the stability lobe diagram [23] and milling tests [36], which can be used for control algorithm simulation verification in the following sections.

3 Real-time FFT identification-based time-varying chatter frequency mitigation

3.1 Real-time FFT identification-based ANE

In order to elaborate the control block diagram conveniently, some explanations for Figs. 3 and 4 are listed as follows: The transfer function P(n) is the tooltip impulse response function. The transfer function S(n) is the impulse response function between actuators and tooltip. The red lines and blocks are in physical domain, which are realized by hardware in control process. The black lines and blocks are in electrical domain, which are realized by programs. is the adder in physical domain; is the logical adder in electrical domain.

Fig. 3
figure 3

The block diagram with ANE based on real-time FFT identification

Full size image
Fig. 4
figure 4

The block diagram with modified NFXLMS based on real-time FFT identification

Full size image

The ANE based on real-time FFT identification is presented in Fig. 3. Compared with the classical ANE control (Fig. 2 in [23]), this research adds the FFT identification every N steps in the diagram. As for the detailed description, please refer to the literature [23]. Here, just summarize the ANE algorithm as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{{\varvec{x}}}_{a}\left(n\right)=\mathrm{cos}\left({\varvec{\Omega}}n\right),{{\varvec{x}}}_{b}\left(n\right)=\mathrm{sin}\left({\varvec{\Omega}}n\right)\\ y\left(n\right)={{\varvec{w}}}_{a}^{\mathbf{T}}\left(n\right){{\varvec{x}}}_{a}\left(n\right)+{{\varvec{w}}}_{b}^{\mathrm{T}}\left(n\right){{\varvec{x}}}_{b}\left(n\right)\end{array}\\ \begin{array}{c}{y}_{c}\left(n\right)=\left(1-\beta \right)y\left(n\right),{y}_{b}\left(n\right)=\beta y\left(n\right)\\ e\left(n\right)=d\left(n\right)-{y}_{c}\left(n\right)*s\left(n\right)\end{array}\\ \begin{array}{c}{e}_{s}\left(n\right)=d\left(n\right)-{y}_{b}\left(n\right)*s\left(n\right)\\ {{\varvec{w}}}_{l}\left(n+1\right)={{\varvec{w}}}_{l}\left(n\right)+{\mu }_{l}{e}_{s}\left(n\right)\left[{{\varvec{x}}}_{l}\left(n\right)*s\left(n\right)\right], \left(l=a,b\right)\end{array}\end{array}\right.$$
(8)

3.2 Real-time FFT identification-based modified NFXLMS

The modified NFXLMS based on real-time FFT identification is presented in Fig. 4. Compared with Fig. 3, it adds another adaptive algorithm to update the reference frequencies during two chatter frequency identifications by FFT. The detailed derivation is as follows [31].

The output of controller can be expressed by:

$$y\left(n\right)={{\varvec{w}}}_{a}^{\mathrm{T}}\left(n\right){{\varvec{x}}}_{a}\left(n\right)+{{\varvec{w}}}_{b}^{\mathrm{T}}\left(n\right){{\varvec{x}}}_{b}\left(n\right)$$
(9)

where \({{\varvec{w}}}_{l}\left(n\right),l=a,b\) is the coefficient vector of controller; \({{\varvec{x}}}_{a}\left(n\right)\) and \({{\varvec{x}}}_{b}\left(n\right)\) are the reference signals defined by reference chatter frequencies. The error signal can be written as follows:

$$e\left(n\right)=d\left(n\right)-y\left(n\right)*s\left(n\right)$$
(10)

where \(d\left(n\right)\) is the primary vibration signal through primary path; \(s\left(n\right)\) is the impulse response function between actuators and tooltip.

The reference signals from sinusoids generator can be written as follows:

$${{\varvec{x}}}_{l}\left(n\right)=2\mathrm\;{cos}\;{{\varvec{\Omega}}}_{r}\cdot{{\varvec{x}}}_{l}\left(n-1\right)-{{\varvec{x}}}_{l}\left(n-2\right),\left(l=a,b\right)$$
(11)

where:

$$\mathrm{cos}{{\varvec{\Omega}}}_{r}\equiv \mathrm{diag}\left[\mathrm{cos}{{\varvec{\omega}}}_{r}\right]$$
(12)

where \({{\varvec{\omega}}}_{r}\) is the identified reference signal frequency.

Substituting Eq. (11) into Eqs. (9) and (10) leads to:

$$\begin{aligned}e\left(n\right)=&d\left(n\right)-\big[2{{\varvec{w}}}_{a}^{T}\left(n\right)\mathrm{cos}\;{{\varvec{\Omega}}}_{r} \cdot{{\varvec{x}}}_{a}\left(n-1\right)+2{{\varvec{w}}}_{b}^{T}\left(n\right)\\&\mathrm{cos}\;{{\varvec{\Omega}}}_{r}\cdot{{\varvec{x}}}_{b}\left(n-1\right)-{{\varvec{w}}}_{a}^{T}\left(n\right){{\varvec{x}}}_{a}\left(n-2\right)-{{\varvec{w}}}_{b}^{T}\\&\left(n\right){{\varvec{x}}}_{b}\left(n-2\right)\big]*s\left(n\right)\end{aligned}$$
(13)

It can be seen that the residual error is a non-linear function of the reference frequencies due to the nonlinear function \(\mathrm{cos}{{\varvec{\Omega}}}_{r}\) . Through the steepest descent method, the updating equation of the reference frequencies can be expressed by:

$${{\varvec{\Omega}}}_{r}\left(n+1\right)={{\varvec{\Omega}}}_{r}\left(n\right)+\frac{{\mu }_{\omega }}{2}\frac{\partial {e}^{2}\left(n\right)}{\partial {{\varvec{\Omega}}}_{r}}$$
(14)

where \({\mu }_{\omega }\) is the convergence factor of adaptive algorithm 2 and the gradient is as follows:

$$\frac{\partial {e}^{2}\left(n\right)}{\partial {{\varvec{\Omega}}}_{r}}=\mathrm{sin}\;{{\varvec{\Omega}}}_{r}\left[{\varvec{Y}}\left(n\right)\mathbf{*}\widehat{s}\left(n\right)\right]e\left(n\right)$$
(15)

where:

$${\varvec{Y}}\left(n\right)=\left[{{\varvec{w}}}_{a}\left(n\right){{\varvec{x}}}_{a}^{T}\left(n-1\right)+{{\varvec{w}}}_{b}\left(n\right){{\varvec{x}}}_{b}^{T}\left(n-1\right)\right]$$
(16)

where \(\widehat{s}\left(n\right)\) is the identified model of \(s\left(n\right)\).

Then, summarize the NFXLMS algorithm as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{{\varvec{x}}}_{a}\left(n\right)=2\mathrm{cos}\;{{\varvec{\Omega}}}_{r}\left(n\right){{\varvec{x}}}_{a}\left(n-1\right)-{{\varvec{x}}}_{a}\left(n-2\right)\\ {{\varvec{x}}}_{b}\left(n\right)=2\mathrm{cos}\;{{\varvec{\Omega}}}_{r}\left(n\right){{\varvec{x}}}_{b}\left(n-1\right)-{{\varvec{x}}}_{b}\left(n-2\right)\end{array}\\ \begin{array}{c}y\left(n\right)={{\varvec{w}}}_{a}^{T}\left(n\right){{\varvec{x}}}_{a}\left(n\right)+{{\varvec{w}}}_{b}^{T}\left(n\right){{\varvec{x}}}_{b}\left(n\right)\\ e\left(n\right)=d\left(n\right)-y\left(n\right)*s\left(n\right)\end{array}\\ \begin{array}{c}{{\varvec{w}}}_{l}\left(n+1\right)={{\varvec{w}}}_{l}\left(n\right)+{\mu }_{l}e\left(n\right)\left[{{\varvec{x}}}_{l}\left(n\right)*\widehat{s}\left(n\right)\right], \left(l=a,b\right)\\ {{\varvec{\Omega}}}_{r}\left(n+1\right)={{\varvec{\Omega}}}_{r}\left(n\right)+{\mu }_{\omega }\mathrm{sin}\;{{\varvec{\Omega}}}_{r}\left[{\varvec{Y}}\left(n\right)*\widehat{s}\left(n\right)\right]e\left(n\right)\end{array}\end{array}\right.$$
(17)

3.3 Numerical simulation for time-varying chatter frequency suppression

In order to verify the proposed algorithm, numerical simulation is implemented in this section. The milling parameters are presented in Table 1 with spindle speed 7500 rpm and axial cutting depth 1 mm. In milling process, the stiffness of thin-wall workpiece change by 4%, which will cause time-varying chatter frequencies [30]. The controller parameters in control process are as follows. The convergence factors of ANE are 0.0015 and 0.001 in the x and y directions, respectively. The convergence factors of two adaptive algorithms in modified NFXLMS are 0.014 and 0.05.

Table 1 The time domain simulation parameters
Full size table

Figure 5 gives the vibration displacement in time domain with ANE control based on FFT. For comparison, the simulation result without FFT is also presented. Results show that ANE with FFT keeps normal working condition, while the controller performance without FFT decreases until fails. The vibration displacement in frequency domain for the whole cutting process and the stable control time are presented in Figs. 6 and 7, respectively, which display that time-varying chatter frequencies are suppressed while normal chatter frequencies are not influenced.

Fig. 5
figure 5

The vibration displacement in time domain with ANE control based on FFT

Full size image
Fig. 6
figure 6

The vibration displacement in frequency domain with ANE control based on FFT for the whole cutting process

Full size image
Fig. 7
figure 7

The vibration displacement in frequency domain with ANE control based on FFT for the stable control time

Full size image

Figure 8 gives the vibration displacement in time domain with modified NFXLMS based on FFT. For comparison, the simulation result with ANE based on FFT is also presented. Results show that the modified NFXLMS has better control effect than ANE. The vibration displacement in frequency domain for the whole cutting process and the stable control time are presented in Fig. 9 and Fig. 10, respectively, which display that time-varying chatter frequencies are suppressed while normal chatter frequencies are hardly influenced and the modified NFXLMS based on FFT has better control results. In addition, the iteratively updated reference frequencies in modified NFXLMS are also provided Fig. 11, which shows that the reference frequencies vary during two chatter frequency identifications by FFT.

Fig. 8
figure 8

The vibration displacement comparison under ANE and NFXLMS control in time domain

Full size image
Fig. 9
figure 9

The vibration displacement comparison under ANE and NFXLMS control in frequency domain for the whole cutting process

Full size image
Fig. 10
figure 10

The vibration displacement comparison under ANE and NFXLMS control in frequency domain for the stable control time

Full size image
Fig. 11
figure 11

The iteratively updated reference frequencies in modified NFXLMS

Full size image

4 Case study using experimental data

In order to verify the proposed algorithm, the measured data in Sect. 2 is used to off-line simulation. The detailed description about set-up and experimental parameters can refer the literature [30]. The calculation results are given in Fig. 12, 13, 14, 15, 16, 17. These figures indicate that, with two developed algorithms, the time-varying chatter frequencies (marked with numbers) are suppressed while normal frequencies keep unchanged. The off-line simulation using experimental data displays that the proposed algorithm can suppress the time-varying chatter frequencies with no influence on normal frequencies.

Fig. 12
figure 12

The vibration signals with ANE control based on FFT

Full size image
Fig. 13
figure 13

The vibration signal in frequency domain with ANE control based on FFT for the whole cutting process

Full size image
Fig. 14
figure 14

The vibration signal in frequency domain with ANE control based on FFT for the stable control time

Full size image
Fig. 15
figure 15

The vibration signals with NFXLMS control based on FFT

Full size image
Fig. 16
figure 16

The vibration signal in frequency domain with NFXLMS control based on FFT for the whole cutting process

Full size image
Fig. 17
figure 17

The vibration signal in frequency domain with NFXLMS control based on FFT for the stable control time

Full size image

5 Conclusions

In this research, the real-time FFT identification is introduced into ANE and modified NFXLMS for time-varying chatter frequencies suppression in thin-walled workpiece milling. Simulation results show that the proposed two control algorithms can both suppress the time-varying chatter frequencies effectively. The modified NFXLMS has better control effect than ANE, but it has larger impacts every time the chatter frequencies are identified by FFT, which is harmful to part surface quality. Finally, the off-line simulation based on practical experimental data is implemented that indicates that the developed algorithms work well in practice. In this research, the chatter frequency identification based on FFT is not continuous; therefore, the continuous chatter frequencies tracking algorithm need to be developed for time-varying chatter detection and mitigation in the future.