A machine learning–based methodology for identification of the plastic flow in aluminum sheets during incremental sheet forming processes

Abstract

This study presents a calibration method based on machine learning techniques to identify parameters of hardening law of aluminum alloy sheets in complex manufacturing processes. A V-shape test is designed to characterize material behavior during an incremental sheet forming (ISF) process. A series of virtual materials is first generated using three physical features observed in a standard uniaxial tensile test: initial yield stress, maximum uniform plastic strain, and yield-to-strength ratio. These virtual materials are then employed in simulating the designed V-shape tests to numerically collect the material responses, such as forming forces, displacements, or their combinations. Several feed-forward neural networks (FFNNs) are developed and trained to relate the collected material responses to the relevant virtual materials. Then, the trained FFNNs were used to estimate the flow curve of AA5052-H32 sheets up to a plastic strain value of 1.0 using the experimentally measured response from the V-shape test during ISF. The FFNN-based flow curves appear to capture well the stress–strain data obtained from the uniaxial tensile test with the coefficients of determination up to 0.98. The identified flow curves are also employed to simulate the uniaxial tensile and ISF truncated cone tests. The simulated uniaxial tensile forces are in good agreement with the experimentally measured results. A maximum difference of 5% is observed in the comparison between the simulated and measured ISF loading forces in the steady-state deformations. The comparisons demonstrate the efficiency of the proposed method to characterize the plastic flow of metal.

1 Introduction

For decades, incremental sheet forming (ISF) processes have received considerable attention due to their high flexibility in shaping a blank sheet into parts with complex geometries. In these manufacturing processes, small rigid tools move along a prescribed path to deform a blank sheet incrementally to form the desired shapes. These methods are suitable in making parts for rapid prototyping, small batch productions, and customized and personalized products. Understanding the deformation mechanics in the ISF processes and determining the optimal process parameters are keys to improving the quality of the formed parts. To achieve the goals, the finite element (FE) method is an essential tool as an alternative to expensive trial and error experiments. However, accurate material models for sheet metals during ISF processes are mandatory to secure accurate FE simulations.

Phenomenological constitutive models are often used in ISF simulations owing to their efficiency [1,2,3]. In these models, a hardening law describing the relationship between the flow stress and the equivalent plastic strain is coupled with a yield surface that governs the plastic deformation under multi-axial stress states. Previous studies have pointed out that the material planar anisotropy exhibits a minor effect on the deformations of several aluminum alloy sheets subjected to ISF processes [2, 4,5,6]. Therefore, an isotropic yield function is often assumed, and an isotropic hardening law needs to be calibrated before conducting an ISF simulation.

Many calibration methods for identifying the hardening laws of sheet metals in ISF processes have been proposed in the literature. Ai et al. [7] employed a curve fitting method to identify the parameters of Hollomon’s power laws from the stress–strain data obtained from uniaxial tensile tests of AA1100 and AA5052 sheets up to fracture strains of 8% and 18%, respectively. To characterize the hardening behavior of sheet metal in a more extensive strain range, Liu et al. [8] applied the digital image correlation (DIC) technique to measure the strain evolution of a local area located on the surface of an AA7075-O uniaxial tension coupon. The measured stress–strain curve was reported up to a strain of 50%, from which a Hollomon’s hardening law could be identified. A similar approach was applied in [9] for AA7075-O sheets with different thicknesses, in which Swift’s hardening laws were identified. Haque and Yoon [10] compared the applications of Swift’s and Voce’s models in capturing the hardening behavior of AA6022-T4E32 sheets, showing that the Swift model provides a better result. Alternatively, Dejardin et al. [11] conducted a bugle test to determine Swift’s law parameters for AA1050 sheets, which was subsequently applied to analyze the springback effects and shape distortions during the ISF process. In another study, a finite element update method (FEMU) was applied to calibrate the parameters of a Voce’s hardening law for a copper foil [12]. This calibrated hardening law was then employed to simulate a micro-ISF deformation process for a pyramidal shape. Moreover, this study demonstrated that the deformation observed in the ISF process is very large (> 200%) and significantly exceeds the values observed in the uniaxial tensile test (< 30%). This high strain level was also observed in the benchmark results reported for AA7075-O sheets in Elford et al. [13]. Moser et al. [14] utilized a Voce’s hardening law to describe the hardening behavior of AA5754-O sheets. The calibrated hardening law was then considered in simulating a double-side ISF process. Although the principal strains predicted by the simulations are in good agreement with the experimental measurements, the resulting loading force is significantly higher than the measured data. Otherwise, the hybrid numerical-experimental method, which is widely used to calibrate hardening law parameters for ductile metals [15, 16], was adopted in the work of Chang and Chen [17]. The calibrated hardening laws were coupled with a modified Gurson-Tvergaard-Needleman damage model to evaluate the void evolution during the forming of conical and pyramidal samples of AA6024 and AA6061 sheets.

The above publications reveal the importance of calibrating the plastic flow of sheet metals up to large strains for the FE simulation of ISF processes. The before-mentioned methods can still be used but they require high experimental costs in preparing the specimen and setting up the equipment [18, 19]. Furthermore, the appearance of damage suppression in the ISF processes leads to extreme deformations compared to traditional forming processes such as stamping, rolling, and deep drawing [20,21,22,23,24]. Even though these methods are successful in the determination of the hardening laws in a traditional forming process, their applications in ISF simulations have not been extensively studied. Thus, calibration of a hardening law up to large strain ranges for ISF simulations remains a challenge.

Recently, machine learning (ML) techniques have been used to calibrate the plastic flow curves of sheet metals. In an early work of Rao and Prasad [25], several artificial neural networks (ANNs) have been trained to reproduce the strain-rate and temperature-dependent flow curves of medium-carbon steels. Later, Phaniraj and Lahiri [26] extended this approach to take the percentage of carbon in the steels into account. Similar approaches have been applied to identify the flow stresses of different materials, such as stainless steels [27], casted titanium alloys [28], aluminum alloys [29], pressure-cast polypropylene [30], and advanced high strength steels [31]. Although these approaches provide promising results, a huge number of experimental tests should be conducted to obtain a sufficient number of experimental stress–strain curves used to train the networks. However, performing many experiments to generate data for ML models is costly and exhausting. Therefore, replacing the experimentally measured data with numerically simulated data would be a solution for this drawback.

Haj-Ali et al. [32] developed a system of two-dimensional (2D) and three-dimensional (3D) FE models to simulate nano-indentation. Several ANNs have been trained to approximate the relationship between the inputs consisting of the material properties (i.e., Young’s modulus, Poisson’s ratio, and the Ramberg–Osgood’s stress–strain relationship) and the indentation depth, and the indentation force as an output. The trained ANNs showed good predictions for the indentation force–displacement curves of different materials. However, the application of these ANNs to determine the material properties from the experimental force–displacement curves exhibits a large discrepancy from the measured stress–strain data obtained from the uniaxial tensile test. Similarly, Li et al. [33] used the ANN technique to build a surrogate model that estimates the indentation force from the inputs of Young’s modulus, Swift’s hardening law parameters, and the indentation depth. Lu et al. [34] proposed combinations of several ANNs to identify material parameters from single and dual/multiple indentations. In such a case, different datasets with different fidelity levels arising from different sources (experiment or computation) can be combined to train a multi-fidelity neural network, improving the accuracy as well as the training efficiency. Compared to the experimental data, the trained networks give accurate predictions for the flow curves of several aluminum alloys and printed titanium alloys.

The previous studies demonstrate the potential of neural networks in regenerating the link between the material response characterized by an indentation test and the related material properties such as the plastic flow stresses. In a more general case, it is suggested that the relation between the material response and the material properties can be reproduced by using an arbitrary test or even a combination of different tests. Accordingly, different kinds of material property can be identified, for example, kinematic hardening behavior and yield surface. To provide evidence supporting this suggestion, this study develops an ML-based calibration method to identify the flow curve of aluminum alloy sheets during ISF processes. The proposed method aims to simultaneously meet three requirements for industrial applications:

• The calibrated flow curve should be comparable to the stress–strain data obtained from a standard uniaxial tensile test to ensure its accuracy.

• The derived results should be reliable up to a large strain range (i.e., $\overline{\upvarepsilon }$ = 1.0) for their usefulness in ISF simulations.

• The proposed method can be used to estimate the flow curve of different materials.

The paper is organized as follows. “Sect. 2” presents in detail the experimental tests conducted for AA5052-H32 sheets to obtain the necessary data to calibrate the flow curves and to validate the obtained results. In “Sect. 3,” a general ML-based calibration method is proposed for a generic material model using the data obtained from FE simulations of a generic test. “Sect. 4” presents an application of the proposed framework in calibrating the plastic flow curve for aluminum alloy sheets using an ISF V-shape test. The trained neural networks are then used to predict the flow curve of AA5052-H32 sheets as an application of the proposed methodology. “Sect. 4.2.3” provides thorough validations of the calibrated flow curve of AA5052-H32 sheets. “Sect. 4.3” summarizes the work and discusses the perspectives and limitations of the proposed framework.

2 Experiments

In this study, standard uniaxial tensile tests are first carried out to investigate the hardening behavior and planar anisotropy of AA5052-H32 sheets. Then, an ISF experiment to form a V-shape specimen is performed to determine the flow curve of the tested material using the proposed calibration method. Finally, a truncated cone is made by ISF to derive necessary data for validating the calibrated flow curves.

2.1 Uniaxial tensile test

Uniaxial tensile tests are conducted for AA5052-H32 sheets with a thickness of 1.0 mm. Specimens were prepared in three orientations, including the rolling direction (RD), diagonal direction (DD), and transversal direction (TD) following the Korean standard KS B0810 13B [35]. Figure 1 reports the engineering stress–strain curves obtained with these three orientations. According to this figure, the maximum uniform strains are approximated to 0.1, which is significantly smaller than the deformation observed in a typical ISF process [36]. In addition, a minor anisotropy effect is observed in the stress–strain curves prior to the softening. Table 1 presents the mechanical properties of the investigated material directly obtained from these tests. The true stress–strain data of the RD specimen will be compared with the feed-forward neural network (FFNN) predictions in “Sect. 4.2.3”.

Fig. 1

Stress–strain curves obtained from uniaxial tensile tests

Table 1 Mechanical properties of AA5052-H32 sheets obtained from uniaxial tensile tests

2.2 Incremental sheet forming of V-shape specimen

An ISF experiment, in which the blank sheet was formed into a V-shape, is performed to characterize the material’s behavior. In this test, a blank sheet with a 150 mm × 100 mm dimension is clamped between a rigid die and a rigid blank holder. A semi-spherical tool with a diameter of 12 mm is programmed to follow a V-shape tool path to deform the sheet, as shown in Fig. 2. At the beginning of the process, the initial position of the tool is at point A, which is higher than the upper surface of the blank by an amount of c = 0.3 mm (see Fig. 2b). The clearance between the tool and the blank sheet is determined to ensure a zero loading force at the beginning of every loading cycle. The slide-way oil with an ISO viscosity grade of 68 was used to reduce the friction between the tool and sheet. When the process starts, the tool moves with a constant speed of 100 mm/min along linear paths from point A to point O₁ and then point B to complete the first loading cycle. Point B is located at the same vertical coordinate and at a distance of 60 mm away from point A. In the second loading cycle, the tool moves in a sequence of B—> O₂—> A to continuously deform the sheet. The process is repeated to deform the sheet until a crack is visualized on the outer surface of the V-shape specimen. It is worth noting that points A, B, and O_n are located in the vertical surface, and the increment of the forming depth (Δz) is set to be equal in each cycle, i.e., Δz = 0.5 mm.

Fig. 2

The designed incremental sheet forming process of a V-shape specimen (a) Concept of incremental sheet forming; (b) Tool path; (c) Experiment setup; (d) Deformed specimen

Since the deformation is observed at a narrow area in the center of the blank sheet, a groove with a size of 100 mm × 50 mm has been made on the die to reduce unnecessary elastic vibration (Fig. 2c). According to Fig. 2d, the fracture is visualized at a pole accommodated with the tool position at point O_n shown in Fig. 2b. During the test, reaction forces acting on the tool are measured by a load cell.

Figure 3 presents a comparison between the recorded forces obtained from two testing times. It is seen that the measured forces show good repeatability where the two curves are almost identical. The peak of the loading force is always observed at the middle of the cycle within every loading cycle. In other words, the loading force always reaches the maximum when the tool position is at the point O_n. Therefore, the peak force of each cycle is recorded according to the number of loading cycles. In addition, the relative error of these peak forces is calculated as follows:

$$RE= \left|1-\frac{{F}_{1}}{{F}_{2}}\right|$$

(1)

where F₁ and F₂ are the maximum forces of the considering cycle obtained from tests 1 and 2, respectively.

Fig. 3

Measured loading force during the ISF of two V-shape specimens

Figure 4 shows the evolution of the peak forces and their RE with respect to the number of loading cycles. It is seen that the RE tends to stay below 0.05, except for its value observed in the first cycle. The averages of the peak forces with respect to the number of loading cycles obtained from the two tests are used to identify the hardening behavior of the investigated material, which is discussed in “Sect. 4.2.3”.

Fig. 4

Maximum loading force according to the loading cycles during the ISF V-shape tests

2.3 Incremental sheet forming of a truncated cone

An ISF experiment is performed to deform the blank sheet into a truncated cone. The dimension of the initial blank sheet is 150 mm × 150 mm. Similar to the ISF V-shape specimen, the sheet is clamped around its contour by a die and a holder. Process parameters used to deform the sheet, including tool diameter, tool speed, and lubrication, are identical to those used in the ISF V-shape specimen reported in “Sect. 2.2”. Fig. 5 shows the tool paths used to deform the blank sheet, consisting of a series of circular movements combined with in-plane downward straight movements. After every circumferential path, the tool moved horizontally, followed by a vertical step to penetrate the sheet and then proceeded to the next circular path. Figure 5b shows a deformed specimen obtained from the ISF of the truncated cone.

Fig. 5

ISF truncated cone test (a) Tool path; (b) Deformed specimen

Two specimens were formed with the prescribed tool paths. During the tests, loading forces are recorded and plotted in Fig. 6 to show their repeatability. In addition, the average value of the measured loading forces within each cycle is calculated and plotted in this figure. As shown in the figure, there exist fluctuations during the test. A detailed explanation of the force fluctuation during the ISF truncated cone test can be found in [37, 38]. In the early loading cycles, the force is significantly increased when the tool dented to the upper surface of the testing specimen. Then, within a circular tool path, the force was increased gradually, followed by a decrease. After several cycles, the average loading force approaches a saturated value (F^s), indicating a steady-state situation in which the average forces are mostly unchanged. Within a given testing condition, the value of F^s characterizes the hardening behavior of the tested material, particularly at large strains [5, 39, 40]. The difference between the saturated forces of the two tests is approximately 20 N, which is smaller than 2% of the saturated values. The average forces will be compared with the FE predictions in “Sect. 4.2.3” aiming to validate the accuracy of the identified hardening laws.

Fig. 6

Measured loading force obtained from ISF of truncated cone

3 Machine learning–based calibration method

This section introduces an ML-based calibration method based on the FFNN to identify the plastic flow of the material subjected to large strain. In the following, the theory of the FFNN is first summarized. Then, the different steps involving the proposed framework are detailed.

3.1 Feed-forward neural network

An ANN contains numerous artificial neurons. As shown in Fig. 7a, each artificial neuron is a simple mathematical model consisting of three parts: (i) a set of weights ${w}_{1}$, … ${w}_{n}$ corresponding to $n$ inputs ${x}_{1}$, …, ${x}_{n}$, (ii) a summation operator $\Sigma$ which sums the inputs weighted by their corresponding weights and its bias $b$, and (iii) an activation function $f$ yielding the output $y$ from the weighted sum. Mathematically, an artificial neuron is described by the following equation:

Fig. 7

The architecture of the developed FFNNs (a) A single artificial neuron (b) A feed-forward neural network

$$y=f\left(b+\sum{_{i=1}^{n}}{w}_{i}{x}_{i}\right).$$

(2)

FFNN is the fundamental architecture composing several connected layers of artificial neurons, as shown in Fig. 7b. The FFNN can be viewed as a universal model of an n-input m-output function

$${\varvec{Y}}={\varvec{F}}\left({\varvec{X}};{\varvec{W}}\right),$$

(3)

where ${\varvec{X}}={\left[{x}_{1} {x}_{2}\dots {x}_{n}\right]}^{T}$ and ${\varvec{Y}}={\left[{y}_{1} {y}_{2}\dots {y}_{m}\right]}^{T}$ are respectively the input and output vectors and ${\varvec{W}}$ is the matrix of the fitting parameters consisting of all weights and biases in the network. The FFNN is used in this study thanks to its simple implementation.

An important feature of the FFNN is its ability to learn the relationship between the provided inputs and outputs through a training process, in which the fitting parameters ${\varvec{W}}$ can be found. Based on the training dataset consisting of ${N}_{T}$ pairs of observations $({{\varvec{X}}}^{i}, {\widehat{{\varvec{Y}}}}^{i})$, a loss function can be defined to measure the discrepancy between the observations and the corresponding outputs of the FFNN for each input as

$$MSE\left({\varvec{W}}\right)= \frac{1}{{N}_{T}}\sum{_{k=1}^{{N}_{T}}}||{{\varvec{Y}}}^{k}-{\widehat{{\varvec{Y}}}}^{k} ||,$$

(4)

where $||.||$ denotes the squared norm of a vector. The training process is carried out by back propagation in which the value of ${\varvec{W}}$ is iteratively updated in order to minimize the value of $MSE$. In this work, this training process is performed in the TensorFlow library.

3.2 Proposed framework

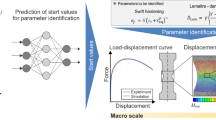
In general, a mechanical testing method is specified by its geometry, material, and prescribed boundary conditions. Such a test can be modeled using the FE framework, of which the geometry and boundary conditions are known a priori. However, a computational material model must be identified to minimize the discrepancy between the numerical and experimental observations. This study proposes a data-driven framework to infer the material model from experimental observations. As shown in Fig. 8, the proposed method consists of three steps:

Fig. 8

Proposed framework for identification of material properties using feed-forward neural networks

Step 1: Data acquisition

An FE model of a selected testing method is first built to simulate the test. Then a series of virtual material models is generated by varying randomly the material model parameters. With each individual virtual material in this generated dataset, the corresponding FE simulation is performed, and the corresponding structure response is obtained. As a result, a dataset is constructed, of which each datum includes a pair of the virtual structure response and the corresponding virtual material models.

Step 2: Development of FFNN

Once the dataset is collected, an FFNN-based mapping is built through a training process to match the recorded virtual structure responses as inputs with the corresponding virtual material models as outputs.

Step3: Identification

For any given investigated material, the trained FFNN can estimate the material model as soon as the experimental structure response of the given test is provided.

The proposed framework is general and can be used to determine the parameters of new material models using an appropriate experimental test. To illustrate the proposed methodology, the following section presents in detail the determination of the plastic flow curve of aluminum alloy 5052-H32 sheets using the ISF V-shape test.

4 Calibration of plastic flow of aluminum alloy 5052-H32 sheets

In this section, the ISF of the V-shape specimen reported in “Sect. 2.2” is considered to identify the flow curve of AA5052-H32 sheets using the framework proposed in “Sect. 3”. As reported in “Sect. 2.1”, the AA5052-H32 sheets exhibit a minor anisotropy effect in the stress–strain response. Therefore, an isotropic von Mises elastoplastic constitutive law governing the evolution of the yield surface is used in this study. Since the elastic properties consisting of Young’s modulus and Poisson’s ratio can be easily identified (see Table 1), only the flow curve needs to be identified.

For this purpose, a hardening law is used to generate virtual material models by varying its parameters. In this work, we employ the hardening law model proposed by Pham and Kim [41], in which a good capacity in extending the stress–strain relationship into the large strain ranges for aluminum alloy was demonstrated [42, 43]. This hardening model is expressed as follows:

$${\sigma }^{y}\left(\overline{\varepsilon }\right)=Y+K\left[1-\mathrm{exp}(-t\overline{\varepsilon })\right]{\left(\overline{\varepsilon }+0.002\right)}^{h},$$

(5)

where Y is the initial yield stress, K denotes a scaling parameter, t is a parameter relating to the pre-necking region in the uniaxial tension, and h is a parameter regarding the extrapolation beyond the maximum uniform deformation.

4.1 Data acquisition

The FE simulation of the ISF of the V-shape specimen is performed in Abaqus/Explicit, version 2021. The maximum force obtained at each loading cycle is used as the structural response considered in the calibration framework reported in “Sect. 3”.

Figure 9 shows the full mesh of the V-shape ISF used in the FE simulation. The die is meshed by discrete rigid elements (R3D4) while the tool is modeled as a rigid analytical body. An initial study was carried out to decrease the blank sheet dimension, aiming to reduce the simulation time. Furthermore, since the deformation is concentrated at the center area of the blank sheet, the clamping area of the blank sheet can be removed from the FEM model. Therefore, a central region of the blank sheet with a dimension of 120 mm × 70 mm is modeled. A review of recently published papers relating to ISF simulations indicates that more than two-thirds of the publications adopted shell elements in their studies [2]. Therefore, the reducing 4-node finite-strain shell elements (S4R) with nine integration points through the thickness are applied to model the sheet. The S4R element is used because it was developed based on the finite-strain theory, which is suitable for capturing the plastic deformation in ISF. For a small-strain simulation, small-strain (S4RS) elements can be used to reduce computational time. In both finite-strain (S4R) or small-strain (S4RS) shell elements in Abaqus/Explicit, the through-thickness strain is calculated from Poisson’s ratio and the membrane section strains under the plane stress condition [44]. The central region of the blank sheet, where the deformation is concentrated, is meshed by square elements with an edge size of 0.5 mm. The element size is enlarged gradually from the central region to the boundary region, of which the element edge size is 4 mm.

Fig. 9

FEM model for V-shape ISF simulation (a) Assembly (b) Mesh on the sheet

During the FE simulation, the die is fixed while the displacement of the blank outer bounds is enclosed. A Mohr–Coulomb’s contact law with a constant coefficient of 0.05 is employed to model all contact pairs. The process contains various tool moves in the XZ plane following the tool paths shown in Fig. 2. The physical time cannot be used in the dynamic explicit simulations because using such small time step leads to an enormous simulation time. In practical, determining a virtual simulation time is essential to guarantee good agreement between the simulation and experiment results. Simultaneously, the virtual simulation time could not be too small so as to avoid introducing the non-physical dynamic effects into the derived simulation results. After several tries, the virtual simulation time is set to 0.4 s for the entire process. The imposed simulation time is equivalent to a tool moving speed of 1800 mm/s.

Regarding the sampling of the hardening law parameters, three physical parameters, the initial yield stress (σ₀), the maximum uniform strain (ε^*), and the yield-to-strength ratio (σ^*/σ₀), are used in this task. Consequently, parameters of the hardening law can be determined explicitly from these physical parameters as follows [43]:

$$Y={\sigma }_{0}$$

(6)

$$h=\frac{{\sigma }^{*}/{\sigma }_{0}}{{\sigma }^{*}/{\sigma }_{0}-1}{\varepsilon }^{*}$$

(7)

$$t=\frac{5}{{\varepsilon }^{*}}$$

(8)

$$K=\frac{{\sigma }^{*}-{\sigma }_{0}}{{{\varepsilon }^{*}}^{h}}$$

(9)

The variation ranges for each parameter are carefully considered following previous studies [45, 46] to cover different types of aluminum alloys. These ranges are reported in Table 2.

Table 2 The variation range of physical parameters observed during a uniaxial tensile test for aluminum alloy sheets

According to Table 2, the design space is defined as $\mathcal{D}=\left[100, 250\right](MPa)\times \left[0.1, 0.25\right]\times \left[1.1, 2.5\right]$. Theoretically, there exists an unlimited number of virtual materials that can be generated within the space. However, only a limited number of simulations can be conducted due to the restriction of computational time and resources. Thus, considering a successful simulation of the ISF V-shape test takes almost 2 hours in this study, only a set of 100 individually virtual materials are generated. Subsequently, the corresponding simulations are conducted to collect the inputs and outputs. Several sampling methods could be used for the task, for example, full factorial sampling, Latin hypercube sampling (LHS), distributed hypercube sampling, and Latin centroidal Voronoi tessellation [47]. Previous studies compared applications of the methods in different engineering problems and suggested using the LHS for the case study of size 100 each [48, 49]. Consequently, this study utilizes the LHS method for generating virtual materials.

Figure 10 shows a typical result obtained from the simulation of the ISF V-shape specimen with a pre-defined virtual material. According to Fig. 10a, the deformation is concentrated on the central region where the fine mesh is designed. Moreover, a maximum equivalent plastic strain of 1.58 was observed in this figure, which is significantly larger than the maximum uniform strain observed in the uniaxial test shown in Fig. 1. In addition, Fig. 10b shows the numerical prediction of loading forces, which exhibits a similar trend to that shown in the experiment. This good agreement confirms the reason for the use of the maximum loading force according to the number of loading cycles as the inputs for neural network training, as discussed in the next section.

Fig. 10

A typical simulation result of an ISF V-shape test with an imposed pertinent parameter set: σ₀ = 200 MPa, ε^* = 0.15, σ^*/σ₀ = 1.5 (a) PEEQ; (b) Predicted loading force

Figure 11 presents the recorded maximum loading forces according to the loading cycles for several virtual materials. In addition, the measured maximum forces obtained from the ISF of the V-shape specimen of the AA5052-H32 sheet are also illustrated in this figure for comparison purposes. It can be seen from the figure that all the experimental data are ranged intermediate to the upper and lower limits of the numerical data, which ensures avoiding extrapolation in the identification of a tested materials’ flow curve.

Fig. 11

Maximum loading forces evaluations obtained from the experiment of AA5052-H32 sheets and the simulations of three virtual materials

4.2 FFNN training

This work develops two strategies to calibrate the hardening behavior of sheet metals. The first strategy identifies the hardening law parameters to reproduce sheet metal flow curves. The second approach calibrates a list of discrete stress–strain data to illustrate the flow curve. Both strategies show advantages and disadvantages that will be discussed in detail.

The entire achieved dataset is randomly divided into training, validation, and test datasets whose ratios are 70%, 15%, and 15%, respectively. After training, the coefficient of determination (R²) is calculated on the test dataset to evaluate the performance of FFNN on the unseen data. The formulation of R² is expressed as follows:

$${R}^{2}=1-\frac{\sum_{i=1}^{{N}_{e}}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}{\sum_{i=1}^{{N}_{e}}{\left({y}_{i}-\overline{y }\right)}^{2}}$$

(10)

where N_e denotes the number of observations; and $\overline{y }$ denotes the average value of the output data of these observations.

4.2.1 FFNN1: identification of hardening law parameters

The output layer of FFNN1 includes four hardening law parameters: Y, K, t, and h (see Eq. 5), while the input layer includes the maximum loading force observed in several loading cycles during the ISF V-shape test. However, only the last seventeen loading cycles were used as the input for FFNN1 because their deformations are dominated by plastic deformation. Meanwhile, the elastic deformation involves significantly the material responses observed in the first three cycles, which were not used for training. In addition, to reduce the number of possible network architectures, all hidden layers of the FFNN consist of the same number of hidden nodes, denoted by p.

Since the material responses observed from the first three loading cycles were not involved in the FFNN1 input, the information of the first three loading cycles was removed from the dataset. Therefore, the accuracy of the model prediction may be insufficient, especially in the early stages of plastic deformation. Thus, an alternative to FFNN1, named FFNN1*, is also developed, taking the initial yield stress as one of the inputs. As a result, the output layer of FFNN1* contains three hardening parameters: K, t, and h. It is worth noting that the initial yield stress can be determined experimentally by standard testing methods, such as uniaxial tensile test, small punch test, indentation test, and hardness test. However, discussion on the means used to determine the initial yield stress is beyond the scope of this study; the interested reader can find the detail in the references [50, 51].

Architecture selection

Previous studies clarified the importance of model selection through determining hyperparameters: the number of hidden layers q and the number of nodes in each layer p [52, 53]. In parametric studies, several values of q were considered, i.e., q = 2, 3, 4, 5, 6, 7 layers. For a given value of q, several values of p were examined, i.e., p = 30, 40, 50, 60, 70 nodes. The weights and biases are randomly initiated before training, which causes poor repeatability of the trained models [54]. For each given construction (q, p), the FFNNs are trained ten times with random initialization of weights and biases, and the average of their losses is used to evaluate their performance and reported in Fig. 12.

Fig. 12

Hyperparameter selection for (a) FFNN1 and (b) FFNN1*

The results shown in Fig. 12a indicate an advantage in using multiple hidden layers. Considering the training errors of FFNN1, deeper networks generally show better performance. However, the performances of the networks with q = 6, 7 appear to be more or less equivalent. Therefore, a network structured with six hidden layers q = 6 is selected for the FFNN1. Furthermore, comparing the validation losses of the networks with q = 6 suggests the use of 40 nodes per hidden layer to balance the training accuracy with the computational time.

A similar observation is noted for FFNN1* in Fig. 12b where the deeper networks (q = 5, 6, 7) perform better than the others (q = 3, 4) in terms of training and validation losses. The obtained results suggest the same architecture of q = 6 and p = 40 for FFNN1*.

Training and validation losses of the selected architecture

The selected model structure (q = 6 and p = 40) has been trained with 100 individual runs; and weights and biases are recorded accordingly. To avoid overfitting, an early stopping criterion is used to terminate the training process when the MSE of the validation dataset starts increasing. Furthermore, a stochastic gradient descent training is adopted in this application to increase the training stability and generalization performance [55]. In addition, a model checkpoint function is imposed to save weights and biases at the instance of the best validation loss.

Figure 13 presents the distribution of the MSE evaluated on the test dataset for all pre-trained models of FFNN1 and FFNN1*. It is seen that the performance of the FFNN1* on the testing dataset seems to be better than the FFNN1, statistically. In detail, the mean and standard deviation of the errors of FFNN1* are 1.63 × 10⁻³ and 6.45 × 10⁻⁴, whereas those of FFNN1 are 3.13 × 10⁻³ and 6.81 × 10⁻⁴, respectively. Among these models, the best performance models are focused, and their predictions for each output are compared with the corresponding target values, as illustrated in Fig. 14.

Fig. 13

MSE distribution of 100 training runs of FFNN1 and FFNN1* calculated on the test dataset ($\overline{m }$, mean value; S.D., standard deviation)

Fig. 14

Evaluation of the pre-trained FFNN1 and FFNN1* (a) Training progressive of FFNN1; (b) Correlation of FFNN1 predictions and the targe values (test dataset); (c) Training progressive of FFNN1*; (d) Correlation of FFNN1* predictions and the target values (test dataset)

The training process for the selected FFNN1 achieves an MSE of 4.92 × 10⁻⁴ on the training dataset and an MSE of 3.26 × 10⁻³ on the validation dataset, which indicates that the model was well generalized. As a result, a significant relationship between the predicted and target values is exhibited in Fig. 14b. In detail, the R² coefficients are more significant than 0.98, except those of parameter t, which is approximately 0.95. A similar result is observed in FFNN1*, which confirms the reliability of the training approach.

4.2.2 FFNN2: identification of discrete data of the flow curve

The input of FFNN2 contains a node of the effective plastic strain besides the seventeen nodes of maximum loading forces. As a result, the output layer involves only a single node of the corresponding effective stress. Similar to the before-mentioned FFNN1*, the initial yield stress is introduced in the input layer of FFNN2*, which is an alternative to the FFNN2. Consequently, the target of FFNN2* contains the subsequent strain-induced flow stress, which is defined as follows:

$$\widehat{Y}={\sigma }^{y}-{\sigma }_{0}$$

(11)

In the FFNN1 models, the training data size is embedded regarding the number of generated virtual materials. In contrast, the size of the FFNN2 training data is arbitrary according to the number of the additional effective plastic strains. Since this study aims to estimate the plastic flow stresses up to a large strain range, i.e., $\overline{\varepsilon }=1.0$, a fixed 101 values of strain in the interval [0, 1] with an increment of 0.01 belonging with 50 other random values are imposed in the input layer. Thus, the size of the training and validation datasets is 12,835 samples.

The same algorithm described in the previous subsection is applied to determine the hyperparameters of FFNN2 and FFNN2* and to train the selected architecture. Overall, an architecture of five hidden layers (q = 5) with 50 nodes per each layer (p = 50) is selected for both two networks. The training processes for the selected architectures were converged well with the training and validation errors of around 10⁻⁶. Additionally, the performance of the trained networks on the test dataset exhibits a good evaluation (R² > 0.99996). The details of the training process and the validation of the FFNN models are described in Appendix 9..

4.2.3 Discussions

For easy tracking of network configurations and their performances on the unseen dataset, Table 3 summarizes the training and validation losses and the R² score of the four selected FFNNs. Overall, four suggested FFNNs associated with the training algorithms demonstrate excellent approximation ability on the entire dataset generated by FE simulations of the ISF V-shape test.

Table 3 Training results of the developed FFNNs

Both of the two modeling strategies for the flow curve of aluminum alloy sheets, associated with FFNN1 and FFNN2, were trained and validated successfully. The first approach identifies parameters of a hardening law. That allows the use of the law in special-purpose FE simulations requiring the implementation of a user-defined subroutine to describe the constitutive equations. However, the strong sensitivity of the calibrated hardening law to its parameters, which are the targets of the network’s outputs, raises difficulties in the training processes. In other words, the difference between the best and the worst networks reported in Fig. 13a, b is approximately 4 × 10⁻³, although the same network architecture was applied. Therefore, the network showing the best performance on the test dataset is recommended for practical applications.

In the second approach, the calibrated flow curve is less sensitive to the model outputs than the first one, demonstrating the difference between the best and the worst networks, as shown in Fig. 19a, b in Appendix 9.. Consequently, the average of the FFNN2 outputs of 100 training runs could be used in the application to provide more stable predictions. In addition, the FFNN2 outputs as a list of stress–strain data can be used in general-purpose FE simulations following the Plasticity option in Abaqus format. Unlike the first approach, the training and validation dataset size in the second approach is unlimited, which strongly influences the computational time. With the reported data samples, the training time of the FFNN2 is approximately triple as those of the FFNN1.

4.3 Identification for plastic flow curve of AA5052-H32 sheets

This section presents an application of the trained FFNNs to predict the hardening behavior of AA5052-H32 sheets with a thickness of 1.0 mm. The measured maximum loading forces reported in “Sect. 2.2” and the initial yield stress determined from the uniaxial tensile test for the RD specimen (see Table 1) are fed into the input layer of these FFNNs to estimate the outputs.

Figure 15 presents the FFNN predictions for the plastic flow curves of the tested material in a wide strain range, i.e., $\overline{\varepsilon }=1.0$. A previous study used the average of the outputs of multiple training runs to reproduce the predicted flow curve [52]. As discussed before, the network showing the best performance on the test dataset is recommended in the cases of FFNN1 and FFNN1*. Therefore, the results of two extracting methods are reported in Fig. 15a, b as “Model A” and “Model B,” respectively. It is seen that the FFNN predictions are close to each other, except in the case of the Model A of FFNN1 which is higher than the others. The validations of these models are presented in the next section.

Fig. 15

Identification of plastic flow curve of AA5052-H32 sheets based on different FFNNs (a) Model A: the network showing the best performance on the test dataset; (b) Model B: the average of all networks' outputs

5 Validation

In this section, the FFNN-based flow curves are first compared to the experimental data obtained from the uniaxial tensile test, which is widely used to determine experimentally the flow curve of sheet metals. Then, the identified flow curves are employed to simulate the uniaxial tensile and ISF truncated cone tests.

5.1 Comparison between the FFNN-calibrated flow curves and the uniaxial tension data

Figure 16 compares FFNN predictions of the plastic flow stresses with the experimental data obtained from the uniaxial tensile test of the RD specimen. According to Fig. 16a, both predictions of FFNN1 deviate significantly from the experimental data. In contrast, FFNN1* provides more accurate predictions owing to the introduction of the initial yield stress in the model’s input, as shown in Fig. 16b. With an R² coefficient of nearly 0.98, it is concluded that the FFNN1* predictions are in good agreement with the experimental data. In comparing the results shown in Fig. 16c, d, a similar conclusion can be explored where the FFNN2* provides significantly better predictions than those of FFNN2. The observation is due to the lack of material responses regarding early plastic deformation contained in the input layer of the FFNN1 and FFNN2. It is therefore recommended to include the initial yield stress as an additional input for network training to improve the accuracy of the FFNN model.

Fig. 16

Comparison between the flow stresses predicted by four FFNNs and the experimental data obtained from the uniaxial tension test. Model A: the network showing the best performance on the test dataset, and Model B: the average of all networks’ outputs (a) FFNN1; (b) FFNN1*; (c) FFNN2; (d) FFNN2*

According to Fig. 16c, d, the Model A of FFNN2 and FFNN2* yield unsmooth predictions of the flow curves. The observation is a pure numerical issue, which is surmounted by using the average results of 100 runs. In addition, the standard deviation of these outputs is of approximately 3 MPa, which assures the robustness of the predictions. The comparison demonstrates the accuracy of FFNN1* and FFNN2* predictions, which agree well with the experimental data. Therefore, further evaluation is needed to clarify their accuracy in larger strain ranges. The flow curves based on the Model A of FFNN1* and Model B of FFNN2* are considered in the subsequent simulations.

5.2 Comparison between the FFNN-calibrated flow curves and the result of an inverse finite element method

Several methods can be used to identify the hardening sheet metals’ behavior in large strain ranges. Here, the FEMU method is adopted to identify the parameters of the hardening law expressed in Eq. 5 for AA5052-H32 sheets. Details regarding the implementation of the FEMU method are described in the references [18, 56, 57].

Values of the hardening law parameters determined from different methods are reported in Table 4. Moreover, Fig. 17 compares the FFNNs’ predictions for plastic flow curves with those determined by the FEMU method. In addition, Fig. 17b presents the applications of these curves in FE simulation of the uniaxial tensile test. It is seen that the flow curve predicted by FFNN1* is agreed well with the FEMU result in the small-strain range, e.g., $\overline{\varepsilon }<0.1$. However, its extension to a more extensive strain range (e.g., $\overline{\varepsilon }<0.3$) is higher than the reference curve. As a result, the tensile force prediction of the FFNN1* is in agreement with the experimental data, except for a slight misalignment is observed at the tails of the measured curve. Besides, the FFNN2* seems to overestimate the tensile forces since its prediction for the plastic flow curves is slightly higher than the others. Remarkably, the differences between these examined flow curves estimated at $\overline{\varepsilon }=0.3$ are less than 5%, which demonstrates the accuracy of FFNNs’ predictions. However, the validation is useful in this particular strain range, i.e., $\overline{\varepsilon }<0.3$, because the maximum effective plastic strain observed during the uniaxial tensile simulation is less than 0.22, as shown in Fig. 17b.

Table 4 Calibrated hardening law parameters of AA5052-H32 sheets based on different methods

Fig. 17

Comparison between the FFNNs’ predictions and the hardening laws determined by the FEMU method (a) Calibrated flow curves; (b) Their applications in simulation of the uniaxial tensile test

5.3 Application of the FFNN-calibrated flow curves in the ISF simulation of a truncated cone

An FE model is developed to simulate the ISF truncated cone test for AA5052-H32 sheets to verify the capabilities of FFNN-based flow curves in practice. For the sake of simplicity, the detail of the developed FE model is described in Appendix 10..

Figure 18a compares the force predictions of the FE simulations based on the identified flow curves with the experimental measurements. According to this figure, significant vibrations are observed in both the experimental and numerical results. It is noted that the vibrations are unavoidable due to the nature of the experimental processes and computational scheme. Therefore, the averages of the measured and predicted loading forces are calculated for every loading cycle and plotted in Fig. 18b to simplify the visualization. The measured forces are significantly higher than those obtained from FEM simulations within the first five loading cycles. However, the deviations are observed at the middle of each loading cycle, although the force increments after every cycle being in good agreement. This deviation relates to the effect of the unexpected elastic vibration in the flattened regions in several early loading cycles. After that, the forces approach their saturations in steady-state deformations in the ISF process [9, 39]. Thus, the good agreement between the measured and predicted saturated forces demonstrates the accuracy of the identified flow curves at large strains.

Fig. 18

Comparison between experimental measurement and numerical prediction for loading forces observed during the ISF truncated cone test (a) Loading forces according to the forming depth; (b) Average forces according to the loading cycles

According to Fig. 18b, the identified FFNN-based flow curves yield similar predictions of the loading forces during the ISF truncated cone test simulations. Furthermore, these predictions are higher than the measured forces by about 5%. This amount of error is agreed well with those errors reported in a previous ISF benchmark test conducted for AA7075-O sheets [13]. In addition, the maximum effective plastic strain observed at the end of the FE simulation, which was imposed the FFNN1*-based hardening law, is approximated to one, i.e., $\overline{\varepsilon }\approx 1.0$. This remark shows that the calibrated flow curves can be used at extensive strain ranges. The comparison clarifies the potential of the trained FFNNs in predicting the plastic flow curve of sheet metals subjected to an ISF process.

6 Discussion and conclusion

6.1 Discussion

This work aims to calibrate the plastic flow curve of aluminum alloy sheets using an ISF process. The trained FFNNs can predict the hardening behavior even up to $\overline{\varepsilon }=1.0$ for different aluminum alloy sheets with the same thickness of 1.0 mm. In future works, sheet thickness would be considered as an input for training the FFNNs for different practical applications.

In this study, the measured maximum loading forces are used to characterize the material response during an ISF V-shape specimen test. Due to the limitations of the current experimental facilities, information regarding the displacement fields does not include in the training processes. In addition to these forces, further studies would consider the maximum strains observed in each loading cycle as the material response to enrich the training inputs. Such strain fields could be obtained using advanced optical measurement methods.

The number of FE simulations of the ISF V-shape test and the accuracy of each individual are essential to derive a training dataset with high quality. In this work, only 100 simulations are performed due to the limitation of computational resources. In this regard, applying the parallel computing technique should be used to obtain a larger training dataset. Moreover, instead of using shell elements, solid elements can be used to increase the accuracy [2, 6, 7, 58]. However, a balance between the time-consumption and the accuracy is always an issue of ISF simulations. Several methods reported in the literature could be considered in coping with this task [5, 59].

The proposed framework presented in Fig. 8 can be straightforwardly applied to calibrate other material models. For instance, a bending/reverse-bending test can be used to characterize the parameters of a kinematic hardening model [60]. However, the application of the calibrated material model in another test should be provided to validate the FFNN predictions.

6.2 Conclusion

This study developed an ML-based calibration method for hardening law parameters of aluminum alloy sheets using the material response experimentally characterized by an ISF V-shape test. The developed method was then applied to determine the flow curve of AA5052-H32 sheets up to large strains, i.e., $\overline{\varepsilon }=1.0$. The calibrated flow curves were compared with experimental data obtained from a uniaxial tensile test and a reference hardening law determined by the FEMU method. Finally, these curves were validated through an ISF simulation of a truncated cone.

The following conclusions can be made from this study:

• 1. Four FFNNs were developed to estimate the flow curve of aluminum alloy sheets, which could be represented by hardening laws or a series of discrete points. The FFNNs are trained and used to estimate the flow curves of AA5052-H32 sheets up to a strain value of 1.0 using the experimental data obtained from the ISF V-shape test.

• 2. Compared to the experimental data obtained from a uniaxial tensile test of AA5052-H32 sheets, the FFNN-based flow curves seem to overestimate the flow stresses at small strains. The introduction of the initial yield stress in the training inputs allows improving the FFNNs’ predictions in the entire strain range observed in the uniaxial tensile test with an R² coefficient of 0.98. The observation suggests that the material response used to train the FFNNs could be characterized not only by a single test but also by combination of different tests.

• 3. The calibrated flow curves based on FFNN1* and FFNN2* for AA5052-H32 sheets are compared to a hardening law calibrated by the FEMU method. In addition, these curves are employed to simulate the uniaxial tensile and ISF truncated cone tests, which deform the investigated material in extensive strain ranges [36, 61]. The simulated tensile forces are in good agreement with the experimentally measured results, while a maximum difference of 5% is observed in the comparison between the simulated and measured loading forces in the steady-state deformations of the ISF truncated cone test.

Appendices

Appendix 1

This section provides the details of the architecture selection and training processes of FFNN2 and FFNN2*. Various architectures have been trained using the algorithm described in “Sect. 4.2.1” in the main text. Figure 19 shows the results used for the evaluation. In both models, introducing deeper hidden layers does not significantly improve the training losses, which are mainly ranged from 2 × 10⁻⁵ to 4 × 10⁻⁵. Therefore, according to this figure, an architecture of five hidden layers (q = 5) coupling with 50 nodes per each (p = 5) is selected for both two models.

Fig. 19

Hyperparameters selection for (a) FFNN2 and (b) FFNN2*

The selected architecture has been trained for 100 runs with individual random seeds. The same training algorithm used to train the FFNN1 and FFNN1* is adopted here, except a change of the batch size to M = 64 due to the change of the training data size [55]. Figure 20 presents the MSE distribution of 100 training runs evaluated on the test dataset. It is seen that the mean value and standard deviation of both two models are closed to 1.1 × 10⁻⁵ and 2.0 × 10⁻⁵, respectively.

Fig. 20

MSE distribution of 100 training runs of FFNN2 and FFNN2* calculated on the test dataset ($\overline{m }$, mean value; S.D., standard deviation)

Figure 21 shows the training progress of the selected FFNN2 and FFNN2*, which show the lowest error estimated on the test dataset. Specifically, after 910 training epochs, the selected FFNN2 obtains the lowest MSE of 9.91 × 10⁻⁷ and 1.15 × 10⁻⁶ on the training and validation dataset, respectively. Figure 21b depicts the link between the target values and their corresponding approximations made by the FFNN2 on the test set. According to this figure, with an R² of 0.99996, the approximations are well aligned with their goals. A similar result is observed in the case of FFNN2* after 697 epochs with errors of 2.54 × 10⁻⁶ and 1.76 × 10⁻⁶ measured on the training and validation datasets.

Fig. 21

Evaluation of the pre-trained FFNN2 and FFNN2* (a) Training progressive of FFNN2; (b) Correlation of FFNN2 predictions and the targe values (test dataset); (c) Training progressive of FFNN2*; (d) Correlation of FFNN2* predictions and the target values (test dataset)

Appendix 2

This appendix describes more detail in FE simulation of the ISF truncated cone test. Similar to the ISF V-shape test simulation, the blank sheet is modeled by S4R elements with nine integration points. The die and tool are modeled by analytical rigid bodies, whereas the holder is described by discrete rigid elements (R3D4). Figure 22 shows the developed FE model used for ISF truncated cone test simulation. Fine mesh is designed in the wall region, where the deformation is focused. In detail, a mesh with 384 elements in the circumferential direction is generated with an increment of 0.5 mm in the radial direction. The forming process is modeled within two steps. In the first step, the blank holder is moved downward an amount of 0.02 mm and then kept its position to clamp the sheet. The tool moves following the tool path shown in Fig. 5 in the main text to form the sheet to the designated shape in the second step. Similar to the ISF V-shape test simulation, a virtual tool speed of 1800 mm/s is employed in this simulation to speed up the calculation.

Fig. 22

FEM model for ISF truncated cone test (a) FEM model; (b) Mesh on the sheet