Optimization design method of machine tool static geometric accuracy using tolerance modeling

Abstract

Existing precision design methods cannot directly guide the tolerance design. Therefore, in this study, an optimization design method of machine tool static geometric accuracy based on tolerance modeling is proposed. In this methodology, the mapping relationship between the geometric error of machine tools and tolerance design is established using the small displacement torsor to represent the tolerance information and the Monte Carlo simulation method is used to establish the response model of the torsor parameters and the tolerance variation bandwidths. An assembly accuracy model is then established by combining a machine tool topology analysis and the forming mechanism of the joint surface error. To calculate the tolerances of the component joint surface, a tolerance response model related to the component joint surface tolerance and torsor parameters is developed. Finally, according to the state function of assembly accuracy reliability, a function response model of the assembly accuracy, reliability, and tolerance is developed. Combining the assembly’s processing cost model with the accuracy, reliability, and tolerance principles, a tolerance optimization model of the static geometric accuracy of a CNC machine tool, a linear axis motion guide, is constructed as a case study. Using a simulated annealing genetic algorithm to solve the tolerance optimization model, the tolerance optimization value is obtained, thereby verifying the effectiveness of the proposed method.

1 Introduction

Static geometric accuracy is the basis of machine tool design, where the static geometric accuracy of a machine tool refers to its overall geometric and position accuracy under no external load and includes the flatness error of each part of the machine tool, circumferential runout error of the rotating parts, straightness error of the moving parts, positioning error, etc. [1]. With the increasing complexity of machine tool structures and their accuracy now entering the submicron level, especially for high-end CNC equipment, errors previously assumed insignificant have evolved into factors that must be considered. Efforts must be made to further research into static geometric accuracy design theory and practice. The static geometric accuracy of a machine tool is mainly determined by the geometric accuracy of the translational and rotational axes and can be evaluated by six geometric error elements (also called the six degrees of freedom error) produced by each moving part during the movement process [2]. Due to the mapping relationship between them, the static geometric accuracy of a machine tool can be guaranteed by the tolerance of the machine parts. The geometric accuracy robust design method, also known as the robust design method for machining accuracy, is the most commonly used static accuracy design method for machine tools. In this method, the geometric error elements of machine tools are optimized based on the volumetric error modeling, geometric error element identification, and key geometric error element traceability, and by comparing the accuracy reliability at different positions in the machine tool workspace to improve the error parameters according to identified sensitivity coefficients.

Researchers have aimed to improve the optimization process of geometric accuracy in machine tools in various ways. Dorndorf et al. [3] established a precision prediction model for a two-axis machine tool and, based on the predicted machine tool accuracy, proposed an optimized quasi-static error estimation method to determine the best level of geometric error. However, this method does not consider reliability sensitivity; further, the reliability probability based on this narrow-bound method under multiple failure modes should be an interval value rather than a specific value. Krishna [4] and Jain [5] used optimization methods to simultaneously allocate machine tool manufacturing and assembly tolerances based on their minimum manufacturing cost but did not consider the importance of reliability sensitivity for optimizing the error distribution parameters. Huang [6] established a sequential linear optimization model based on process capability design. Jin [7] proposed a tolerance design method in the early design stage of auto parts. In their investigation of a large-scale CNC gantry rail grinder, Yu et al. [8] established a volumetric error model by employing the multibody system theory to predict the machine tool geometric accuracy. However, their design method based on reliability theory does not consider the cost of the machine tools; further, the machine tool’s performance can only be improved by optimizing the sensitivity under single-failure mode. Cheng et al. [9] proposed an accuracy allocation method for multi-axis machine tools. Based on the prediction of the five-axis CNC machine tool’s accuracy and the traceability of key geometric errors, their method established a machine tool geometric accuracy optimization model in which the machine cost was minimized using the key geometric error source as the control variable and the machining performances as constraint conditions. Cai et al. [10] proposed an optimization method based on a robust design to ensure machining accuracy using a high-order moment normalization technology to derive the machining accuracy reliability under single and multiple failure modes. Unfortunately, this high-order moment normalization technique is greatly affected by the skewness of the performance function, i.e., a large skewness induces large errors. Based on the traditional cost and reliability analysis models [3,4,5,6], Zhang et al. [11, 12] introduced a weighting function to propose a geometric error optimal allocation method for machine tool cost and reliability; however, the reliability of machining accuracy was determined using the ideal and actual working time of adjacent parts, thereby requiring a lot of statistical data. Cheng et al. [13] proposed an error estimation method to improve the reliability of the machining accuracy of multiaxis machine tools by constructing an sensitivity analysis model of accuracy reliability based on the combination of a comprehensive volumetric error prediction model of the machine tool, Rackwite Fiessler theory, and improved first-order second-moment method using the minimum cost of the machine tool as the objective function and the reliability of the machining accuracy as the constraint condition. Wu [14] proposed a geometric accuracy optimization method of three-axis vertical machining design based on reliability theory, in which the volumetric error model of a machine tool is used to predict the machining accuracy, reliability theory is used to derive the machine tool machining accuracy reliability calculation model, and the working position with the worst reliability is found. Then, according to the reliability sensitivity analysis of the worst reliability position, the geometric error variables that have a significant impact on the reliability of the machining accuracy of the machine tool are found and the geometric parameters of the machine tool are optimized under the condition of ensuring the reliability of machining accuracy.

In each of these machine tool design methods, the geometric error elements are used as decision variables during optimization [2, 11, 15, 16]. In some cases, the flatness and perpendicularity tolerances of the assembly joint surface can be estimated using the optimized geometric error element values based on the control relationship between the geometric error elements and tolerances of the moving parts. However, other tolerance types (such as dimensional tolerances, straightness, and cylindricity) cannot be improved. A relationship model reflective of both the geometric error elements of machine tool parts and the tolerance of the joint surface of the parts is thus required to better realize a machine tool’s early-stage accuracy design and later-stage accuracy evaluation.

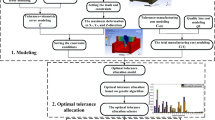
Therefore, an optimization design method of a machine tool’s static geometric accuracy based on tolerance modeling is proposed in this study, and the work flow chart is shown as in Fig. 1. The specific steps of the method are as follows. An in-depth study of the tolerance analysis methods based on mathematical definitions employing the small displacement torsor (SDT) to express tolerance information is performed. Considering the tolerance principle and constraint conditions, the constraint relationship between the torsor parameters of the SDT and the tolerance is found. Then, a Monte Carlo simulation is used to establish the response model of the SDT parameters and actual tolerance change bandwidth. Next, an experimental analysis is performed using the size tolerance to verify this tolerance modeling method. Subsequently, an accuracy model of the assembly is established according to the formation mechanism of the joint surface error and the topology of the machine tool, thus allowing the tolerance information of the joint surface of the parts to be integrated into the accuracy model. Then, a tolerance optimization model is developed in which the tolerance manufacturing cost is minimized, the tolerances of the component joint surface are the design variables, and the assembly accuracy reliability and tolerance design principles are the design constraints. Thus, the lowest tolerance manufacturing cost under the given set of joint surface tolerances meeting the accuracy reliability and tolerance design principle constraints is obtained and can be used to guide the actual tolerance of the joint surface when designing machine parts. Finally, this methodology is verified using a case study of a machine tool linear axis motion guide assembly, in which a simulated annealing genetic algorithm is used to solve the tolerance optimization model.

Fig. 1

The work flow chart of the optimization design method of machine tool static geometric accuracy using tolerance modeling

2 Tolerance modeling based on Monte Carlo simulation

2.1 Tolerance representation based on small displacement torsor

In the new geometrical product specifications standards, the surface of an object can be abstracted into basic elements such as points, lines, and surfaces. The variation of these basic elements with respect to the nominal position can be expressed by SDTs [17, 18], in which a rotational vector, θ = (α,β,γ), represents the small displacement vector of the rotational degree of freedom; a translational vector, d = (u,v,w), represents the small displacement vector of the translational degree of freedom; and the composite vector, or SDT, D = (θ,d) = (α,β,γ,u,v,w), where α, β, γ, u, v, and w are the torsor parameters, represents the deviation of the surface of the geometric feature’s tolerance relative to the nominal position. Bourdet [18] used the variation of these parameters to describe the change of the surface of the tolerance within the tolerance domain. The SDT can quantitatively describe the dimensional, shape, directional, position, and runout errors of the feature deviation [19], allowing complex modeling of 3D tolerance zones. Tolerance domains and the SDT representation corresponding to common tolerances are summarized in Table 1.

Table 1 Tolerance type and small displacement torsor (SDT) representation

2.2 Mathematical model of size tolerance based on Monte Carlo simulation

Size tolerance comprises fixed and positioning size tolerances [20]. According to the constant characteristics of geometric shapes in the new GPS standard system, the shape of the surface was assumed to remain unchanged after the size tolerance changes, i.e., a straight line remains straight and a plane remains unchanged [21]. Commonly used positioning size tolerances include Type I and Type II plane positioning dimensions [22]. In a Type I dimension composition ring, the workpiece dimension chain constitutes a ring in which both end elements are restricted, one of which has a tolerance value. In a Type II dimension composition ring, the elements at both ends are bound by tolerances. Here, a Type I plane positioning size tolerance was used to establish a tolerance mathematical model comprising three steps: expressing the size tolerance via the SDT, determining the tolerance boundary and deriving constraint equations, and Monte Carlo simulation.

2.2.1 Expression of size tolerance based on the SDT and constraint inequalities

The Type I plane positioning tolerance zone is shown in Fig. 2, where D is the nominal size; T_U and T_L represent the upper and lower tolerances of the tolerance zone, respectively; and tolerance, T = T_U + T_L. The z-axis of the local coordinate system is parallel to the plane normal, and the origin of the coordinate system is at the center of the plane, where z = 0 represents the nominal tolerance plane and z(x,y) represents the changing plane.

Fig. 2

Type I plane positioning tolerance zone

From Table 1, the SDT representation corresponding to the variation plane z(x,y) of the Type I plane positioning tolerance is (α,β,0,0,0,w). According to the control conditions of the tolerance domain boundary, the constraints of the dimensions of the changing plane and the position of change can be expressed respectively as

$$ {\displaystyle \begin{array}{c}-{T}_L\le z\left(x,y\right)\le {T}_U\\ {}-\left({T}_L+{T}_U\right)\le \varDelta z\left(x,y\right)\le {T}_L+{T}_U\end{array}} $$

(1)

where z(x,y) = d_Z + x∙β + y∙α is the equation of the changing plane and Δz(x,y) is the difference between the z value of any two points on the changing plane z(x,y).

At its extremum, the z value lies at one of the four vertices of the matrix plane; thus, compliance with the tolerance range can be studied by checking the four vertices—A, B, C, and D—of the changing plane, i.e., in x and y coordinates, (a,b), (−a,b), (a,−b), and (−a,−b), respectively. According to the equation of the changing plane, the coordinates of the four vertices can be expressed as

$$ \left\{\begin{array}{c}{S}_A=\left(a,b,{d}_z+a\cdot \beta +b\cdot \alpha \right)\\ {}{S}_B=\left(-a,b,{d}_z-a\cdot \beta +b\cdot \alpha \right)\\ {}\begin{array}{c}{S}_C=\left(a,-b,{d}_z+a\cdot \beta -b\cdot \alpha \right)\\ {}{S}_D=\left(-a,-b,{d}_z-a\cdot \beta -b\cdot \alpha \right)\end{array}\end{array}\right. $$

(2)

By introducing Eq. (2) into Eq. (1), we can get

$$ \left\{\begin{array}{c}-{T}_L\le {d}_z+a\cdot \beta +b\cdot \alpha \le {T}_U\\ {}-{T}_L\le {d}_z-a\cdot \beta +b\ \alpha \le {T}_U\\ {}\begin{array}{c}-{T}_L\le {d}_z+a\cdot \beta -b\cdot \alpha \le {T}_U\\ {}-{T}_L\le {d}_z-a\cdot \beta -b\cdot \alpha \le {T}_U\end{array}\end{array}\right. $$

(3)

From Eqs. (1) and (3), the variation and constraint inequalities of the SDT parameters of the Type I plane position tolerance can be expressed as

$$ \left\{\begin{array}{c}-\frac{T}{2b}\le \alpha \le \frac{T}{2b}\\ {}-\frac{T}{2a}\le \beta \le \frac{T}{2a}\\ {}-{T}_L\le w\le {T}_U\end{array}\right. $$

(4)

$$ {\displaystyle \begin{array}{l}-T\le x\cdot \beta +y\cdot \alpha \le T\\ {}-{T}_L\le w+x\cdot \beta +y\cdot \alpha \le {T}_U\end{array}} $$

(5)

where x and y represent the coordinate values of the four vertices in the x- and y-directions, respectively.

These constraint inequalities cause the relative ideal variation interval of the torsor parameters to be smaller, making it difficult to clarify the relationship between the tolerance zone and actual variation area of the torsor parameters.

2.2.2 Using Monte Carlo simulation to solve the SDT size tolerance parameters

According to the variation and constraint inequalities presented in Eqs. (4) and (5), Monte Carlo simulation can be used to simulate the parameter variation order and the type of torsor parameter distribution. In this process, a random number is used to simulate the changing surface of the actual tolerance. When the random number meets the constraint conditions, it is retained; otherwise, it is eliminated. When the random number samples were large enough and met the conditions, the samples were analyzed and the bandwidth of the fluctuation interval of each torsor parameter was computed. The mean bandwidth was then used to obtain the actual fluctuation interval of the torsor parameter in the following three-step process.

• (1). Assuming normal distribution functions of each size tolerance torsor parameter, the probability density function φ(x) was expressed as

$$ \varphi (x)=\frac{1}{\sqrt{2\pi}\sigma }{e}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma}^2}}\kern1.5em \left(x=\alpha, \beta, w\right) $$

(6)

where the effective distribution range of the normal distribution curve is 6σ and the distribution center coincides with the center of the variation interval. The nonzero torsor parameters of the size tolerance are α, β, w. According to the variation inequality (Eq. (4)), the mean and standard deviation of the ideal distribution parameters—α, β, and w—are (0, T/6b), (0, T/6a), and ((T_U–T_L)/2, T/6), respectively.

• (2). Simulated sampling of torsor parameters was then performed for the six variation sequences of the three torsor parameters. To accurately simulate the formation mechanism of dimensional errors, sampling tests were performed for all variation sequences. The sampling process is shown in Fig. 3.

Fig. 3

Sampling sequence: α→β→ w

The sequence of changes is α→β→w, k = 1, K is the number of qualified samples, and K1 and K2 are constants and determined using the research object. The discriminants, k1 ≤ K1 and k2 ≤ K2, prevent oversampling of parameters from the previous stage to avoid falling into an infinite loop due to the inability of the parameters of the latter stage to meet the constraints. After six types of variation sequence sampling tests, the variation interval bandwidth sample number of α, β, w is 6K.

• (3). Finally, the χ² fitting test method was used to test the distribution type of the torsor parameters; as an example, the workflow of this test for x (x = α, β, w) is shown in Fig. 4.

Fig. 4

Workflow of the χ² fit test method

2.2.3 Establishing the response surface function of the bandwidth of the change interval and SDT size tolerance parameters

Although the Monte Carlo simulation method allows performing sampling tests of arbitrary plane size tolerances and obtaining the response value of the change in bandwidth of the torsor parameters, it is difficult to clarify the mapping relationship between the size tolerance and change in bandwidth response of the torsor parameter using this method. Here, a response surface model of the variation intervals of the torsor parameter and tolerance bandwidth was constructed using the response surface method [14], as detailed below.

• (1). Given the maximum range of variation of the size tolerance (T_min,T_max), n values of T_i (i = 1, 2,...,n) at equal intervals within (T_min,T_max) were selected, where T_i is used as the research object. Monte Carlo simulation was used to obtain the actual variation interval bandwidths F_i^a, F_i^β, F_i^w (i = 1, 2,...,n) of the torsor parameters (α, β, w) of the size tolerance. Finally, the n interval bandwidth response values of the torsor parameters were obtained.

• (2). Suppose that the design variables are the set of tolerances T, Fy (y = α, β, w) is the performance function sought, and (T_i, F_i^y)(i = 1,2,..., n; y = α, β, w) is a modeling sample. Then, selecting the quadratic polynomial without cross terms as the response function [14], the constructed response surface function between Fy and T was constructed as

$$ Fy={c}_0^y+{c}_1^yT+{c}_2^y{T}^2\kern1em \left(y=\alpha, \beta, w\right) $$

(7)

where c^y_i (i = 0,1,2) is the coefficient to be calculated.

The method of least squares was used to solve the unbiased estimate of C = [c₀^y c₁^y c₂^y]^T.

$$ {\hat{C}}^y={\left({X}^TX\right)}^{-1}{X}^TY $$

(8)

where $X=\left[\begin{array}{c}1\\ {}1\\ {}\begin{array}{c}\vdots \\ {}1\end{array}\end{array}\begin{array}{c}{T}_1\\ {}{T}_2\\ {}\begin{array}{c}\vdots \\ {}{T}_n\end{array}\end{array}\begin{array}{c}{T}_1^2\\ {}{T}_2^2\\ {}\begin{array}{c}\vdots \\ {}{T}_n^2\end{array}\end{array}\right]$,$Y=\left[\begin{array}{c}{F}_1^y\\ {}{F}_2^y\\ {}\begin{array}{c}\vdots \\ {}{F}_n^y\end{array}\end{array}\right]$, and $\hat{C}=\left[{\hat{c}}_0^y\kern0.5em {\hat{c}}_1^y\kern0.5em {\hat{c}}_2^y\right]$ is the set of unbiased estimators of C.

• (3). The multiple correlation coefficient R², expressed in Eq. (9), was then used to verify the prediction accuracy of the response surface model.

$$ {R}^2=1-\frac{\sum \limits_{i=1}^n\left({\hat{F}}_i^y-{\overline{F}}^y\right)}{\sum \limits_{i=1}^n\left({F}_i^y-{\overline{F}}^y\right)}\kern0.75em \left(y=\alpha, \beta, w\right) $$

(9)

where ${\hat{F}}_{\mathrm{i}}^y$ represents the response surface prediction value of i^th test point, ‾F^y is the mean value of experimental calculation, F_yⁱ represents the calculated test value of the i^th test point, and the multiple correlation coefficient R² describes the degree of dispersion between the predicted and true values, where 0 < R² < 1. The larger the R² value, the smaller the degree of dispersion.

2.2.4 Case analysis

Assuming that a = 30 mm and b = 50 mm in Fig. 2, the torsor parameters (α, β, w) of the size tolerance obey normal distribution and the maximum variation ranges of T_S and T_F are 0.3~0.8 and 0.05~0.3 mm, respectively. Fifteen values were selected at equal intervals within the maximum tolerance range to obtain 150 test points, (T_i,S,T_i,F)(i = 1,2,...,150). The program was coded in MATLAB and was used to calculate the actual variation interval F_i^x (i = 1, 2,...,150; x = α, β, w) of the torsor parameters at each point. The 150 points, representing response surface modeling samples, were then used to establish the response surface model of the torsor parameters (α, β, w) between the actual variation interval bandwidth and size tolerance as

$$ \left\{\begin{array}{l}{F}^w=0.0657+0.57{T}_S+0.84{T}_F+0.076{T}_S^2+0.359{T}_F^2\\ {}{F}^{\alpha }=0.0026+0.024{T}_S+0.0124{T}_F+0.003{T}_S^2+0.0059{T}_F^2\\ {}{F}^{\beta }=0.0014+0.188{T}_S+0.086{T}_F+0.002{T}_S^2+0.0085{T}_F^2\end{array}\right. $$

(10)

The resulting variation interval bandwidths were compared with their ideal counterparts, as determined using Eq. (2); the results are shown in Figs. 5, 6, and 7 (representing α, β, and w, respectively).

Fig. 5

Bandwidth of α variation interval

Fig. 6

Bandwidth of β variation interval

Fig. 7

Bandwidth of w variation interval

From the calculated residual bandwidth or the difference between the ideal and actual change in interval bandwidth, it can be seen that the actual change interval bandwidth is smaller than the ideal change interval bandwidth; the trend of change remains the same, and the residual bandwidth fluctuates less. To evaluate this decrease with respect to the bandwidth of the ideal variation interval, the average reduction ratio (i.e., the residual bandwidth divided by the ideal variation interval bandwidth × 100) was calculated and is summarized in Table 2.

Table 2 Reduction ratio in the variation interval bandwidth and accuracy of the response surface model

After comprehensively considering the constraint conditions and the sequence of torsor parameters, the actual variation interval bandwidths of the three torsor parameters (α, β, w) of the size tolerance obtained via Monte Carlo simulation were reduced by 20.11%, 17.24%, and 16.87%, indicating the improved design capability of the proposed method. Further, the R² values of the response surface models of all three spinner parameters of the size tolerance were >0.985, indicating their high prediction accuracy.

3 Static precision design method of machine tools

3.1 Error modeling of the joint surface of the assembly

Part assembly can be regarded as the cooperation and constraints between the geometric features of the parts. The joint surface formed by assembling the part surfaces through the assembly connection is the assembly node that realizes the product performance [23]. In an ideal joint surface, the assembly surfaces of the two assembly parts are considered coincident. However, due to the size and shape errors of the assembly surface, the coupling surface gathers coupling errors of multiple tolerances, which results in the nonoverlapping of the ideal assembly planes of the parts and assembly errors. Here, the plane of the joint surface was used to illustrate the formation mechanism of the joint surface error in the assembly process, where the joint surface error was modeled by combining the actual positional and orientational deviations from the ideal assembly plane. As shown in Fig. 8, the position and posture of the two ideal assembly planes deviate due to the dimensional, shape, position, and assembly errors in the assembly plane of the parts. This deviation can be described as a change in the position and orientational of the ideal assembly plane, PB, relative to the ideal reference assembly plane, PA. Among them, the error transfer relationship from PA to PB is PA→PA′→PB′→PB, which is used to describe the formation mechanism of the joint surface error, as shown in Fig. 9.

Fig. 8

Position and posture change of the assembly joint surface

Fig. 9

Formation mechanism of joint surface error

Let M_AA′, M_A′B′, and M_B′B represent the positional and orientational error transformation matrix from plane PA to plane PA′, from plane PA′ to plane PB′, and from plane PB to plane PB′, respectively. Assuming that flatness is the main tolerance item of the assembly plane, the tolerance zone is the area between two parallel planes, as shown in Table 1. The SDT of the flatness tolerance is expressed as [α, β, 0, 0, 0, w], and M_AA′ and M_B′B can be written as

$$ \left\{\begin{array}{l}{M}_{A{A}^{\prime }}=\left[\begin{array}{c}1\\ {}0\\ {}\begin{array}{c}-{\beta}_{A{A}^{\prime }}\\ {}0\end{array}\end{array}\begin{array}{c}0\\ {}1\\ {}\begin{array}{c}{\alpha}_{A{A}^{\prime }}\\ {}0\end{array}\end{array}\begin{array}{c}{\beta}_{A{A}^{\prime }}\\ {}-{\alpha}_{A{A}^{\prime }}\\ {}\begin{array}{c}1\\ {}0\end{array}\end{array}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}{w}_{A{A}^{\prime }}\\ {}1\end{array}\end{array}\right]\\ {}{M}_{B^{\prime }B}=\left[\begin{array}{c}1\\ {}0\\ {}\begin{array}{c}-{\beta}_{B{B}^{\prime }}\\ {}0\end{array}\end{array}\begin{array}{c}0\\ {}1\\ {}\begin{array}{c}{\alpha}_{B{B}^{\prime }}\\ {}0\end{array}\end{array}\begin{array}{c}{\beta}_{B{B}^{\prime }}\\ {}{\alpha}_{B{B}^{\prime }}\\ {}\begin{array}{c}1\\ {}0\end{array}\end{array}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}{w}_{B{B}^{\prime }}\\ {}1\end{array}\end{array}\right]\end{array}\right. $$

(11)

Plane PA and plane PB are a pair of assembly planes. We express the assembly error of plane PA as the change of the positional and orientational error of the ideal assembly plane relative to the actual assembly plane, which is represented by M_AA′. The assembly error of the plane PB is expressed as the change of the positional and orientational error of the actual assembly plane relative to the ideal assembly plane, which is expressed by M_B′B. Because the assembly errors of plane PA and plane PB have been defined separately, it is assumed that plane PA and plane PB are ideal assembly, that is, the positional and orientational error transformation matrix of the two planes is the identity matrix [24], thus, M_A′B′ can be written as

$$ {M}_{A^{\prime }{B}^{\prime }}=E=\left[\begin{array}{c}1\\ {}0\\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}1\\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}1\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}0\\ {}1\end{array}\end{array}\right] $$

(12)

According to the homogeneous transformation principle of rigid body motion, the transformation matrix of the positional and orientational errors of the ideal assembly plane PB relative to the ideal reference assembly plane PA is equal to the joint surface error model of the assembly plane and can be expressed as

$$ {\displaystyle \begin{array}{l}{M}_{AB}={M}_{A{A}^{\prime }}\ast {M}_{A^{\prime }{B}^{\prime }}\ast {M}_{B^{\prime }B}\\ {}\kern2.25em =\left[\begin{array}{c}1\\ {}0\\ {}\begin{array}{c}-{\beta}_{A{A}^{\prime }}\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}1\\ {}\begin{array}{c}{\alpha}_{A{A}^{\prime }}\\ {}0\end{array}\end{array}\ \begin{array}{c}{\beta}_{A{A}^{\prime }}\\ {}-{\alpha}_{A{A}^{\prime }}\\ {}\begin{array}{c}1\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}{w}_{A{A}^{\prime }}\\ {}1\end{array}\end{array}\right]\left[\begin{array}{c}1\\ {}0\\ {}\begin{array}{c}-{\beta}_{B{B}^{\prime }}\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}1\\ {}\begin{array}{c}{\alpha}_{B{B}^{\prime }}\\ {}0\end{array}\end{array}\ \begin{array}{c}{\beta}_{B{B}^{\prime }}\\ {}-{\alpha}_{B{B}^{\prime }}\\ {}\begin{array}{c}1\\ {}0\end{array}\end{array}\ \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}{w}_{B{B}^{\prime }}\\ {}1\end{array}\end{array}\right]\end{array}} $$

(13)

3.2 Assembly accuracy model

The accuracy of a machine tool can be described by a chain of assembly error transmissions comprising multiple components’ joint surfaces as the joint surface is an important node for assembly error transmission [25]. The size tolerance between different bonding surfaces directly affects the error range of the bonding surface. If the cumulative law of error transmission of each bonding surface is mastered, the impact of part accuracy on machine tool accuracy can be described quantitatively. The associated size error of the joint surface on both sides of a part is summarized in Fig. 10, where T_SP1 and T_SP2 represent the variation range of the shape and positional error of the two sides of the part, respectively, T_D represents the dimensional error, and T_D limits the variation range of T_SP1 and T_SP2. As the error transmission process of machine tool parts is similar to the homogeneous transformation of rigid body motion and because the assembly accuracy of each part of a machine tool can be understood as the allowable range of motion of the movement of the pair in the system, the assembly error of a machine tool can be calculated according to the principle of homogeneous transformation.

Fig. 10

Size error of the joint surface of the part

Using the machine tool geometric error transfer model detailed by Fu [26] and Ding [27], an error model of each joint surface was established. Then, the parts participating in the assembly were numbered according to the transfer order based on the machine tool topology. Finally, a geometric error transfer model from the base assembly to the final assembly was established. The resulting assembly error transfer relationship of n parts assembled in the form of joint surfaces is shown in Fig. 11.

Fig. 11

Geometric error transmission of the assembly

Here, the right plane of part P_n is the precision output plane and the left side of part P₁ is the reference assembly plane. The transformation matrix M_all of the positional and orientational errors of the precision output plane relative to the reference assembly plane was derived as

$$ {\displaystyle \begin{array}{l}{M}_{all}={E}_1\ast M{1}_{12}\ast {E}_{12}\ast M{2}_{12}\ast {E}_{23}\ast M{3}_{12}\ast {E}_{34}\ast \dots \ast {Mi}_{12}\ast \dots \\ {}\kern3em \ast {E}_{n-2n-1}\ast Mn-{1}_{12}\ast {E}_{n-1n}\ast M{n}_{12}\ast {E}_n\end{array}} $$

(14)

where E₁, E₁₂, E₂₃, E₃₄, and E_n represent the transformation matrix of the positional and orientational errors of the junction plane of the reference assembly plane and part P₁, joint surface of parts P₁ and P₂, joint surface of parts P₂ and P₃, joint surface of parts P₃ and P₄, and precision output plane, respectively. Further, M1₁₂, M2₁₂, M3₁₂, Mi₁₂, and Mn₁₂ respectively represent the positional and orientational transformation matrices of the actual assembly plane relative to the ideal assembly plane in the assembly direction of parts P₁ to P_n.

In an ideal state, the positional and orientational error matrix M₀ of the precision output plane relative to the reference assembly plane can be expressed as

$$ {M}_0=M{1}_{12}\ast M{2}_{12}\ast M{3}_{12}\ast M{4}_{12}\ast \dots \ast {Mi}_{12}\ast \dots \ast Mn-{1}_{12}\ast {Mn}_{12} $$

(15)

The geometric error transfer matrix of the assembly, also known as the assembly accuracy model, which expresses the deviation of output accuracy from the ideal state owing to the existence of the joint surface error of the various parts of machine tools, can be expressed as

$$ {E}_{all}={M}_{all}-{M}_0 $$

(16)

3.3 Tolerance-cost model

The tolerance optimization allocation method aims to provide reasonable optimization criteria and appropriate constraints to ensure product assembly accuracy and optimize tolerance allocation [1, 28]. Reasonable tolerance allocation requires a variety of factors to be considered, such as product quality, manufacturing cost, and process stability. Manufacturing cost is often used as the objective function for tolerance optimization. As many factors affect product processing costs, the production costs of products also vary greatly. Existing tolerance-cost models [7, 10, 15] each provide different processing cost relationships. Although the coefficients used in different tolerance-cost models vary, processing costs are generally proportional to the processing size. Thirteen commonly used tolerance-cost models [24], including exponential, reciprocal, reciprocal square, reciprocal power, and modified exponential models, as well as their manufacturing costs corresponding to different types of tolerances, are summarized in Table 3.

Table 3 Tolerance-cost model of different features

In the commonly used reciprocal square model, the dimension chain of machine tool parts comprises n tolerances to be determined; the total part-processing cost function C of the tolerance manufacturing of the machine tool can be expressed as

$$ \mathrm{C}=\sum \limits_{i=1}^n\left({A}_i+\frac{B_i}{T_i^2}\right) $$

(17)

where T_i is the i^th tolerance, i = 1,2,…,n, A is the fixed cost constant not related to the tolerance, and B is the characteristic parameter of the cost curve related to the tolerance. The parameters A and B are calculated using empirical data from production curves.

3.4 Reliability constraint inequality of assembly accuracy

In mechanical reliability theory, there can be m assembly accuracy reliability state functions representing machine tool accuracy. The i^th reliability state function H_i can be expressed as

$$ {H}_i-{f}_i(U)={I}_i-{S}_i $$

(18)

where I_i is the assembly error required by the precision design of the machine tool and S_i is the assembly error obtained using the geometric error transfer model; S_i is a function of the error parameters included in the error transfer model.

After the assembly accuracy reliability status function of the assembly is determined, if the mean value and distribution law of each error parameter are known, the bandwidth of the variation interval of each error component can be used to determine the assembly accuracy reliability. According to the tolerance modeling method based on Monte Carlo simulation detailed in Section 2.2, the response surface function between the SDT parameters of different tolerance types and the actual variation bandwidth of the tolerance can be converted into a tolerance function. This tolerance function is a function of an independent variable, represented as R_i(T)(T = T₁,T₂,...,T_n), where n is the number of tolerance items related to the assembly accuracy and T_i is the i^th tolerance related to the output accuracy of the assembly end. As R_i(T) has no explicit function expression, it is an implicit function. Assuming that the reliability value of the output accuracy of the assembly end that must be satisfied is r_i, the reliability constraint of the output accuracy of the assembly end can be expressed as

$$ {r}_i-{R}_i(T)\le 0\kern0.75em i=1,2,\dots, m $$

(19)

3.5 Tolerance optimal allocation model of machine tool geometric accuracy

Tolerance optimization allocation allows the optimal allocation of tolerances by selecting the appropriate optimization criteria and constraints while ensuring product accuracy requirements [21, 29]. In practice, processing cost is the primary factor considered in tolerance design and machine tool accuracy design requirements are the preconditions that must be met. Here, a machine tool static geometric accuracy tolerance optimization model was constructed by minimizing the processing cost [30] using the tolerance contained in the joint surface of the parts as decision variables and the reliability of the output accuracy of the assembly end and the tolerance selection principle as the constraints. The latter of these constraints indicates that for the same functional element, the size tolerance T_D is greater than the position tolerance T_P, which is greater than the shape tolerance T_S, i.e., T_D > T_P > T_S, which can be expressed as

$$ \left\{\begin{array}{c}{T}_{jS}-{T}_{jP}\le 0\\ {}{T}_{jP}-{T}_{jD}\le 0\end{array}\ j=1,2,\cdots, t\ \right. $$

(20)

Suppose that the total processing cost C_F of the machine tool is

$$ {C}_F(T)=\sum \limits_{i=1}^n{C}_i\left({T}_i\right)T=\left({t}_1,{t}_2,\cdots, {t}_n\right) $$

(21)

From Eqs. (19), (20), and (21), the tolerance optimization model of machine tool static geometric accuracy can be written as

$$ \left\{\begin{array}{l}\begin{array}{c}\min {C}_F(T)\\ {}s.t.{r}_i-{R}_i(T)\le 0\kern0.5em i=1,2,\dots, m;\kern0.5em T=\left({t}_1,{t}_2,\cdots, {t}_n\right)\kern1.25em \end{array}\\ {}{T}_{jS}-{T}_{jP}\le 0\\ {}{T}_{jP}-{T}_{jD}\le 0\end{array}\kern0.5em \right. $$

(22)

where r_i is the reliability value that must be met by the i^th assembly accuracy, i = 1,2,...,m, and n is the number of tolerance items related to the output accuracy of the assembly.

A simulated annealing genetic algorithm was used to solve the tolerance optimization model, thereby minimizing the tolerance manufacturing cost while maintaining the reliability of the assembly accuracy and tolerance design principles.

4 Example analysis of machine tool linear axis motion guide based on tolerance modeling

A simplified structure of the linear axis motion guide used for this case study comprised three parts, as shown in Fig. 12: the slider, screw, and guide rail and support. The slider and screw nut were simplified into a spiral surface, whereas the slider and guide rail were simplified as a flat surface.

Fig. 12

Simplified structure of linear axis motion guide of the machine tool

The linear axis motion guide moves in the x-direction; accuracy in this direction is mainly affected by the accuracy of the motion of the screw–nut pair. The tolerances were selected according to the tolerance design principle (see Section 3.5). From the simplified drawings of the parts shown in Fig. 13, it can be seen that the size tolerances were mainly concentrated in the y-direction and that the influence on the z-direction was relatively small. The y-direction accuracy was mainly affected by the precision of the guide rail manufacturing. The guide rail errors caused by machining include the straightness error in the horizontal plane, straightness error in the vertical plane, and parallelism (torsion) errors of the front and rear guide rails in the vertical plane. If the displacement error of the origin P of the slider coordinate system in the x-, y-, and z-directions are represented as u, v, and w, respectively, then the design requirement of the linear axis motion guide is S ($S=\sqrt{u^2+{v}^2+{w}^2}$) < 0.03 mm with a reliability of ≥97%. Finally, the relative tolerances of the joint surface of the screw–nut motion pair and the joint surface of the guide rail are analyzed.

Fig. 13

Simplified drawing of the parts. (a) Guide rail and support. (b) Screw. (c) Slider

The reference coordinate systems O1, O2, O3, and O4 used in Fig. 12 are set on plane D, plane C, axis b, and axis a, respectively. In the tolerance design process, the minimum assembly failure boundary must not be exceeded under any working conditions, i.e., the minimum limit size is constant; thus, the coordinate origins of O1, O2, and O3 were set to the minimum limit size position. Planes C and D are the ideal assembly planes of the slide rail groove and support rail, respectively, and together form the plane-connecting surface S1. The spiral surfaces A and B are the ideal assembly cylindrical surfaces of the screw nut and screw, respectively, and constitute the joint spiral surface S2. Axis a is the ideal axis of the helix surface A and axis b is the ideal axis of the helix surface B. The shape error of the spiral joint S2’s surface is not considered; the position and orientational errors of the axis of the joint surface determine the position and orientational errors of the shaft. The joint surface of the linear axis motion guide assembly and the tolerance items are shown in Table 4; the tolerance design follows the principle of tolerance independence.

Table 4 Joint surface of the linear axis motion guide assembly and tolerance items

4.1 Assembly accuracy model and accuracy reliability status function

To develop the model, several assumptions were made, including that the plane D of the linear axis motion guide assembly is the reference assembly plane, D′ is the actual assembly plane, and E_D′D is the transformation matrix of the positional and orientational errors between the ideal and actual assembly planes D and D′, respectively. Similarly, if plane C is the reference assembly plane and C′ is the actual assembly plane, then E_CC′ is the transformation matrix of the positional and orientational errors between the ideal and actual assembly planes C and C′, respectively. If a and a′ represent the actual and ideal axes, respectively, then E_aa′ is the transformation matrix of the positional and orientational errors between the ideal and actual axes a and a′. If b and b′ represent the ideal and actual axes, respectively, then E_b′b is the transformation matrix of the positional and orientational errors between the ideal and actual axes b and b′, respectively. Finally, M_Cb is the position transformation matrix between the ideal axis b and the ideal plane C, and M_aP is the position transformation matrix between point P and the ideal axis a. According to the tolerance representation method based on the SDT [5, 17], the transformation matrix of the positional and orientational errors between the ideal and actual assembly planes can be expressed as

$$ {\displaystyle \begin{array}{c}{E}_{D{D}^{\prime }}=\left[\begin{array}{cccc}1& 0& {\beta}_{D{D}^{\prime }}& 0\\ {}0& 1& -{\alpha}_{D{D}^{\prime }}& 0\\ {}-{\beta}_{D{D}^{\prime }}& {\alpha}_{D{D}^{\prime }}& 1& {w}_{D{D}^{\prime }}\\ {}0& 0& 0& 1\end{array}\right]\\ {}{E}_{C{C}^{\prime }}=\left[\begin{array}{cccc}1& 0& {\beta}_{C{C}^{\prime }}& 0\\ {}0& 1& -{\alpha}_{C{C}^{\prime }}& 0\\ {}-{\beta}_{C{C}^{\prime }}& {\alpha}_{C{C}^{\prime }}& 1& {w}_{C{C}^{\prime }}\\ {}0& 0& 0& 1\end{array}\right]\end{array}}{\displaystyle \begin{array}{c}{E}_{b{b}^{\prime }}=\left[\begin{array}{cccc}1& 0& {\beta}_{b{b}^{\prime }}& 0\\ {}0& 1& 0& {v}_{b{b}^{\prime }}\\ {}-{\beta}_{b{b}^{\prime }}& 0& 1& {w}_{b{b}^{\prime }}\\ {}0& 0& 0& 1\end{array}\right]\\ {}{E}_{a{a}^{\prime }}=\left[\begin{array}{cccc}1& -{\delta}_{a{a}^{\prime }}& {\beta}_{a{a}^{\prime }}& {u}_{a{a}^{\prime }}\\ {}{\delta}_{a{a}^{\prime }}& 1& 0& {v}_{a{a}^{\prime }}\\ {}-{\beta}_{a{a}^{\prime }}& 0& 1& {w}_{a{a}^{\prime }}\\ {}0& 0& 0& 1\end{array}\right]\end{array}} $$

(23)

$$ {M}_{Cb}=\left[\begin{array}{cccc}1& 0& 0& 41\\ {}0& 1& 0& 0\\ {}0& 0& 1& 35\\ {}0& 0& 0& 1\end{array}\right]{M}_{aP}=\left[\begin{array}{cccc}1& 0& 0& 150\\ {}0& 1& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right] $$

(24)

The accuracy model of the linear motion axis guide rail assembly can then obtained from Eq. (16) as

$$ {M}_{DP}=\left[\begin{array}{cccc}1& -\delta & \beta & u\\ {}\delta & 1& \alpha & v\\ {}\beta & -\alpha & 1& w\\ {}0& 0& 0& 1\end{array}\right]=\left(\begin{array}{c}{E}_{D{D}^{\prime }}\ast {E}_{D^{\prime }{C}^{\prime }}\ast {E}_{C^{\prime }C}\ast {M}_{Cb}\\ {}\ast {E}_{b{b}^{\prime }}\ast {E}_{b^{\prime }{a}^{\prime }}\ast {E}_{a^{\prime }a}\ast {M}_{aP}\\ {}-{M}_{Db}\ast {M}_{aP}\end{array}\right) $$

(25)

Here, plane C, plane D, spiral surface A, and spiral surface B are positioned during the assembly process. Therefore, the changing planes C′ and D′ and the actual axes a′ and b′ are assumed entirely coincident. The positional and orientational error transformation matrix of C′, D′, a′, and b′ can be expressed as an identity matrix, namely E_D′C′ = E_b′a′ = I₄×₄。

As the comprehensive error S ($S=\sqrt{u^2+{v}^2+{w}^2}$) of the linear axis motion guide assembly is used as a technical index to evaluate the reliability of assembly accuracy, the main factor affecting the performance of the motion guide is the displacement error of the screw working point in the x-, y-, and z-directions. Therefore, according to the design requirements of the linear axis motion guide assembly accuracy, E_DD′, E_C′C, E_bb′, E_a′a, M_Cb, and M_aP were substituted into Eq. (25), ignoring the high-order small items. The assembly accuracy model of the linear axis motion guide can then be expressed as

$$ \left\{\begin{array}{l}\begin{array}{l}u=35\cdotp \left[{\beta}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}\right]+{\beta}_{b{b}^{\prime }}\cdotp \left({\beta}_{a{a}^{\prime }}-{\beta}_{D{D}^{\prime }}-{\beta}_{C^{\prime }C}\right)+{w}_{C^{\prime }C}\cdotp {\beta}_{D{D}^{\prime }}\\ {}\kern1.75em +{w}_{a^{\prime }a}\cdotp \left({\beta}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}+{\beta}_{b{b}^{\prime }}\right)+{w}_{bb^{\prime }}\cdotp \left({\beta}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}\right)-191\cdotp {\beta}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}+{u}_{a^{\prime }a}\cdotp {\beta}_{b{b}^{\prime }}\\ {}\begin{array}{l}v=-150\cdotp {\delta}_{a^{\prime }a}\cdotp \left({\alpha}_{D{D}^{\prime \cdotp }}+{\alpha}_{C^{\prime }C}-1\right)-{v}_{a^{\prime \cdotp }a}\cdotp \left({\alpha}_{D{D}^{\prime }}+{\alpha}_{C^{\prime }C}-1\right)\cdotp \left({\alpha}_{D{D}^{\prime }}+{\alpha}_{C^{\prime }C}\right)\\ {}\kern1.72em +\left({\alpha}_{D{D}^{\prime }}+{\alpha}_{c^{\prime }c}\right)\cdotp \left(150\cdotp {\beta}_{b{b}^{\prime }}+150\cdotp {\beta}_{a^{\prime }a}-{w}_{b{b}^{\prime }}-{w}_{a^{\prime }a}\right)+191{\alpha}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}\\ {}\kern2.25em -35\cdotp \left({\alpha}_{D{D}^{\prime }}+{\alpha}_{C^{\prime }C}\right)-{\alpha}_{D{D}^{\prime}\cdotp }{w}_{C^{\prime }C}\end{array}\end{array}\\ {}w={w}_{C^{\prime }C}+{w}_{D{D}^{\prime +}}{w}_{a^{\prime }a}+{w}_{b{b}^{\prime }}-150\cdotp \left[{\beta}_{a^{\prime }a}+{\beta}_{b{b}^{\prime }}\right]-{u}_{a^{\prime }a}\cdotp \left[{\beta}_{b{b}^{\prime }}+{\beta}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}\right]+150\cdotp {\delta}_{a^{\prime }a}\left({\alpha}_{D{D}^{\prime }}+{\alpha}_{C^{\prime }C}\right)\\ {}\kern1.75em +\left({v}_{a^{\prime }a}+{v}_{b{b}^{\prime }}\right)\cdotp \left({\alpha}_{D{D}^{\prime }}\cdotp {\alpha}_{C^{\prime }C}\right)-35\cdotp \left[{\alpha}_{D{D}^{\prime }}\cdotp {\alpha}_{C^{\prime }C}+{\beta}_{D{D}^{\prime }}\cdotp {\beta}_{C^{\prime }C}\right]-191\cdotp \left[{\beta}_{D{D}^{\prime }}+{\beta}_{C^{\prime }C}\right]\end{array}\right. $$

(26)

4.2 Solution of response surface function of the torsor parameter and the actual change interval bandwidth based on Monte Carlo simulation

When using the response surface method, the correlation of the tolerance screw parameters influences the optimized design value of the tolerance. Here, as the principle of tolerance independence, i.e., the dimensional and shape tolerances are independent, was employed during optimization, the torsor parameters of the tolerance were also independent. Therefore, the correlation between parameters was not considered when performing response surface fitting. Monte Carlo simulation was used to establish the response surface function between the corresponding tolerance and actual variation interval bandwidth of each error parameter in the position and attitude error transformation matrices E_DD′, E_C′C, E_bb′, and E_a′a, which can be expressed as Eqs. (27) and (28).

$$ \left\{\begin{array}{l}{F}^{\alpha_{D{D}^{\prime }}}=3.306\mathrm{x}{10}^{-5}+0.0056{t}_1+0.0087{t}_i^2+0.0069{t}_2+0.0042{t}_2^2+0.0012{t}_3+0.0043{t}_3^2+0.0096{t}_4+0.0075{t}_4^2\\ {}{F}^{\beta_{D{D}^{\prime }}}=2.653\mathrm{x}{10}^{-5}+0.0082{t}_1+0.0030{t}_i^2+0.0077{t}_2+0.0031{t}_2^2+0.0031{t}_3+0.0056{t}_3^2+0.0075{t}_4+0.0083{t}_4^2\\ {}\begin{array}{l}{F}^{w_{D{D}^{\prime }}}=0.0014+0.64{t}_1+0.067{t}_i^2+0.48{t}_2+0.099{t}_2^2+0.93{t}_3+0.055{t}_3^2+0.41{t}_4+0.068{t}_4^2\\ {}{F}^{\alpha_{C^{\prime}\mathrm{C}}}=6.35\mathrm{x}{10}^{-5}+0.115{t}_5+0.045{t}_5^2+0.0124{t}_6+0.013{t}_6^2+0.0356{t}_7+0.069{t}_7^2+0.0893{t}_8+0.078{t}_8^2\\ {}\begin{array}{c}{F}^{\beta_{C^{\prime}\mathrm{C}}}=2.28\mathrm{x}{10}^{-5}+0.115{t}_5+0.045{t}_5^2+0.308{t}_6+0.016{t}_6^2+0.308{t}_7+0.016{t}_7^2+0.17{t}_8+0.032{t}_8^2\\ {}{F}^{w_{C^{\prime}\mathrm{C}}}=0.0015+0.115{t}_5+0.045{t}_5^2+0.133{t}_6+0.058{t}_6^2+0.496{t}_7+0.065{t}_7^2+0.25{t}_8+0.0562{t}_8^2\end{array}\end{array}\end{array}\right. $$

(27)

$$ \left\{\begin{array}{l}{F}^{\beta_{b{b}^{\prime }}}=4.66\mathrm{x}{10}^{-5}+0.0124{t}_9+0.013{t}_9^2+0.0082{t}_{10}+0.034{t}_{10}^2+0.0063{t}_{11}+0.014{t}_{11}^2\\ {}{F}^{v_{b{b}^{\prime }}}=0.0014+0.115{t}_9+0.045{t}_9^2+0.0079{t}_{10}+0.064{t}_{10}^2+0.0081{t}_{11}+0.062{t}_{11}^2\\ {}\begin{array}{l}{F}^{w_{b{b}^{\prime }}}=0.0017+0.133{t}_9+0.058{t}_9^2+0.089{t}_{10}+0.0036{t}_{10}^2+0.011{t}_{11}+0.0035{t}_{11}^2\\ {}{F}^{\beta_{\alpha^{\prime}\upalpha}}=1.023\mathrm{x}{10}^{-5}+0.0082{t}_{12}+0.034{t}_{12}^2+0.0063{t}_{13}+0.014{t}_{13}^2+\\ {}\begin{array}{l}{F}^{\delta_{\alpha^{\prime}\upalpha}}=0.997\mathrm{x}{10}^{-4}+0.0079{t}_{12}+0.064{t}_{12}^2+0.0081{t}_{11}+0.62{t}_{11}^2\\ {}\begin{array}{c}{F}^{u_{\alpha^{\prime}\upalpha}}=0.0020+0.089{t}_{12}+0.0036{t}_{12}^2+0.011{t}_{13}+0.0035{t}_{13}^2\\ {}\begin{array}{c}{F}^{v_{\alpha^{\prime}\upalpha}}=0.0014+0.016{t}_{12}+0.0017{t}_{12}^2+0.013{t}_{13}+0.0033{t}_{13}^2\\ {}{F}^{w_{\alpha^{\prime}\upalpha}}=0.0015+0.029{t}_{12}+0.0038{t}_{12}^2+0.036{t}_{13}+0.0087{t}_{13}^2\end{array}\end{array}\end{array}\end{array}\end{array}\right. $$

(28)

By setting the coordinate system of each component of the linear axis motion guide assembly, the resulting relationships between the mean value, standard deviation, and actual variation interval of the geometric error parameters of each joint surface were obtained and are shown in Table 5. The torsor parameters of each tolerance were assumed to follow a normal distribution and the random numbers were generated using the rands function in MATLAB. Monte Carlo simulation was then performed to obtain the true tolerance distribution. Finally, the response surface method was used to fit the tolerances and torsor parameters; the mapping relationship between them was then obtained for the next step of tolerance optimization.

Table 5 Variation interval, mean value, and standard deviation of torsor parameters

4.3 Determination of the tolerance optimization model

As summarized in Table 4, the linear axis motion guide assembly contained 13 tolerances, including six plane feature tolerances (t₁, t₂, t₃, t₄, t₅, t₆, t₇, t₈), three inner hole feature tolerances (t₉, t₁₀, t₁₁), and two-axis feature tolerances (t₁₂, t₁₃). From the tolerance-cost model described in Table 3 and the total cost model of component tolerance manufacturing (see Eq. (17)), the objective function c(T) of the processing cost of the linear axis motion guide assembly can be expressed as

$$ \min =\left(c(T)\right)=\min\ {A}^{\ast}\left[\begin{array}{l}\sum \limits_{i=1}^8\left(5.026{e}^{-15.8903{t}_i}+\frac{t_i}{0.3927{t}_i+0.1176}\right)\\ {}+\sum \limits_{i=9}^{11}\left(12.6691{e}^{-37.5279{t}_i}+2.486{e}^{\frac{0.000978}{t_i}}\right)\\ {}+\sum \limits_{i=12}^{13}\left(15.1138{e}^{-42.2874{t}_i}+\frac{t_i}{0.8611{t}_i+0.01508}\right)\end{array}\right] $$

(29)

where T = t₁, t₂,..., t₁₃. As the current cost model, developed in the 1990s, varied from current cost data, a cost coefficient A = 15 was added to the processing cost objective function.

From Eq. (19), the reliability state function H of the assembly accuracy of the linear axis motion guide can be written as

$$ H=\mathrm{g}(U)=0.03-S=0.03-\sqrt{u^2+{v}^2+{w}^2} $$

(30)

From Eq. (26), the reliability state function H of the assembly accuracy of the linear axis motion guide is a function of 14 SDT parameters, as

$$ {\displaystyle \begin{array}{c}U=\left({u}_1,{u}_2,{u}_3,{u}_4,{u}_5,{u}_6,{u}_7,{u}_8,{u}_9,{u}_{10},{u}_{11},{u}_{12},{u}_{13},{u}_{14}\right)\\ {}=\left({\alpha}_{D{D}^{\prime }},{\beta}_{D{D}^{\prime }},{w}_{D{D}^{\prime }},{\alpha}_{C^{\prime }C},{\beta}_{C^{\prime }C},{w}_{C^{\prime }C},{\beta}_{b{b}^{\prime }},{v}_{b{b}^{\prime }},{w}_{b{b}^{\prime }},{\beta}_{a^{\prime }a},{\delta}_{a^{\prime }a},{u}_{a^{\prime }a},{v}_{a^{\prime }a},{w}_{a^{\prime }a}\right)\end{array}} $$

(31)

If the mean value and distribution law of each error parameter (14 SDT parameters) are known, then the accuracy reliability status function of the linear axis motion guide (Eq. (30)) can be determined from the change interval bandwidth of the 14 SDT parameters. When the SDT parameters obey normal distribution, according to the tolerance modeling method detailed in Section 2.2, the response surface function between the 14 SDT parameters and the actual variation bandwidth of the tolerance can be constructed.

The accuracy reliability R(T) of the linear axis motion guide rail assembly can be expressed as a function of tolerance T(T = t₁, t₂,..., t₁₃). According to the design requirements of the linear axis motion guide, the inequality of the assembly accuracy and reliability of the linear axis motion guide can be written as

$$ 0.97-R(T)\le 0 $$

(32)

According to the tolerance selection principle, the size tolerance is greater than the position tolerance and the position tolerance is greater than the shape tolerance. The tolerance constraint condition of the linear axis motion guide assembly can then be expressed as

$$ \left\{\begin{array}{c}{T}_{jS}-{T}_{jP}\le 0\\ {}{T}_{jP}-{T}_{jD}\le 0\end{array}\right. $$

(33)

From the cost function (Eq. (29)) and constraint inequality (Eqs. (32) and (33)) of the linear axis motion guide assembly, the tolerance optimization model of the linear axis motion guide assembly was obtained as

$$ \left\{\begin{array}{l}\min \kern0.75em C(T)\\ {}\mathrm{s}.\mathrm{t}.\kern0.75em 0.97-R(T)\le 0T=\left({t}_1,{t}_2,\cdots {t}_{13}\right)\\ {}\begin{array}{c}{T}_{jS}-{T}_{jP}\le 0\\ {}{T}_{jP}-{T}_{jD}\le 0\end{array}\end{array}\right. $$

(34)

4.4 Results analysis

The experiment was performed on a PC using a 2.80GHz CPU and 32G of memory and required a calculation time of 319.72 s. Using a simulated annealing genetic algorithm to solve the tolerance optimization model (i.e., Eq. (34)), the resulting tolerance optimization values corresponding to the lowest cost are detailed in Table 6.

Table 6 Tolerance optimization results of the linear axis motion guide rail assembly (mm)

Because the tolerance design of the hole and shaft needs to refer to the tolerance design standard, the optimized values were compared with those in the Chinese standards JB/T 1800.3–1998 as the best tolerance design values for the linear axis motion guide assembly. To verify the effect of tolerance optimization, the assembly accuracy reliability and processing cost corresponding to the initial tolerance value and the optimized values are summarized in Table 5. The optimized assembly processing cost and accuracy reliability were 762.61 RMB and 97.57%, representing a cost reduction by 11.34% and an increase in the reliability of 2.19%. Therefore, the proposed optimization method can achieve tolerance optimization and processing cost control while ensuring the reliability of assembly accuracy.

5 Conclusion

In this study, an optimization-based design method of machine tool static geometric accuracy based on tolerance modeling is proposed to address the lack of tolerance design capabilities in state-of-the-art robust machine tool accuracy designs based on reliability theory. The proposed method employs the SDT, Monte Carlo simulation method, response surface method, and reliability theory. Using the proposed method, a case study involving the tolerance optimization of a linear axis motion guide was described and solved. Optimization allowed for a reduction in assembly processing cost of 11.34% and an increase in the reliability of assembly accuracy from 95.38% to 97.57%, thereby meeting the assembly accuracy requirements and verifying the effectiveness of the proposed method.

Due to the wide variety of tolerances, the tolerance principles used in different applications vary, as do the constraint inequalities and variation inequalities of the established tolerance volume parameters and the final tolerance response models. Future efforts should aim to establish a tolerance model library, as this would allow a more convenient realization of the static precision and high-efficiency design of CNC machine tools. In addition, due to the complexity of the static precision design method and the structure of machine tools, realizing precision CNC machine tools requires a targeted software system. Further, experimental verification is required to effectively perform the static precision design of machine tools.