1 Introduction

Chatter is a type of unexpected self-excited vibration occurring in almost all machining processes, which limits the productivity, damages the machined surface, and shortens the tool life [1]. With the development of automation, the flexibility of the machine tool leads to diverse working conditions in milling processes. Therefore, it is impossible to completely avoid chatter. Over the past decades, researchers devote their efforts to chatter prediction before milling. They focus on the stability lobe chart based on the identified dynamic model of the milling system [2]. Nonetheless, chatter may still occur when machining under stable conditions indicated by theoretical prediction, because the lobe chart is sensitive to the system parameters that are uncertain in engineering.

Real-time chatter detection is an online approach necessitating the least a priori information on the milling system. Combined with the subsequent controlling operation, this strategy helps to eliminate chatter in time. In real-time chatter detection, various signals are collected to provide substantial information, including the cutting force [3], spindle acceleration [4], spindle torque [5], workpiece displacement [6], and machining noise [7]. Signal processing methods are applied then to extract the crucial feature, and the corresponding cutting state indicator can be established. The effectiveness of such an indicator is the key to achieve the chatter prognosis at an early stage.

Characterizing the variation in the vibration energy distribution from stable cutting to chatter, entropy-based indicators are widely used, such as the approximate entropy [8] and multiscale entropy [9] in the time domain, and the normalized spectral entropy [10] and spectral Rényi entropy [11] in the frequency domain. However, these indices fail to reflect the cutting state timely when raw data are analyzed, because the complexity of milling responses reduces their sensitivity. Under such a circumstance, signal decomposition techniques are utilized as a pre-processor to decompose the original signal into a series of simple intrinsic components. Although the well-known empirical mode decomposition (EMD) [12] has been applied [13], the lack of a rigorous mathematical foundation makes this classic method extremely sensitive to noise and thus difficult to put into practice. The later developed variational mode decomposition (VMD) [14] outperforms the EMD in robustness but requires the number of signal components as a priori parameter [15], which is difficult to obtain in engineering. Moreover, nonlinearity and time-delay in milling systems result in the wideband property of milling responses [16, 17]. Therefore, when the narrowband filter bank–based approaches like the VMD and empirical wavelet transform (EWT) [18] are applied, the obtained signal components tend to be physically meaningless [19,20,21].

In real-time condition monitoring of rotating equipment, the Vold-Kalman filter (VKF) [22] is of great importance. Strong robustness and low computational cost are achieved thanks to the framework of the widely used Kalman filter [23]. As a tachometer measurement-based order tracker [22], the VKF simultaneously extracts all the order-based harmonic components from measured vibration responses, which characterize tooth-passing dynamics in milling processes. However, when chatter occurs, non-harmonic modes become the main concern, and thus, the order-tracking is no longer helpful [24]. This is because the chatter signal can only be effectively decomposed with the information about the instantaneous chatter frequency. In the meanwhile, as machining dynamics become more complex and the number of signal components increases, the joint optimization (i.e., the simultaneous extraction of all the components) in the VKF tends to be computationally unstable [25]. That being the case, the framework of the VKF needs to be improved and the accurate instantaneous frequency (IF) of each chatter mode is required to adaptively determine the filter parameter.

In this work, based on the spectrum concentration index (SCI) [26], a measure to evaluate the degree of signal demodulation, a novel technique is developed to parametrically estimate the signal IF. This technique transforms the estimation of a continuous IF into the optimization of a few polynomial coefficients, and thus works effectively even in the presence of strong noises. With this approach, only the IF of the dominant mode with the highest energy in the signal can be obtained. Therefore, under the framework of the greedy algorithm, the original VKF is modified to recursively extract each component based on the latest available IF information, just like the EMD does [12]. As a result, the number of components is automatically determined and the filter becomes more stable and more adaptive compared to the original VKF. The procedures above lead to a new multicomponent signal decomposition tool named the iterative Vold-Kalman filter (I-VKF). A numerical example is given to demonstrate the superiority of the I-VKF over the EMD, VMD, and original VKF. Then, the energy entropy [27], a generalization of Shannon’s entropy [28] in the energy domain, is computed based on extracted signal components to capture the decreasing randomness [29] of vibration responses when chatter occurs. Based on collected stable milling responses, the chatter alarm threshold of the entropy is set by the maximum likelihood estimation [30] and the three-sigma criterion [31]. Using the developed strategy, chatter can be detected accurately and timely, which has been demonstrated by dynamic simulation and experimental verification.

The remainder of this paper is organized as follows. The proposed iterative Vold-Kalman filter is detailed in Section 2. Section 3 introduces the energy entropy as the cutting state indicator. Section 4 presents dynamic simulation to demonstrate the effectiveness of the proposed method. In Section 5, the procedure for determining the threshold is given. Section 6 describes the detailed implementation of the online strategy and several milling experiments conducted. Section 7 concludes this paper.

2 Iterative Vold-Kalman filter

2.1 Chatter frequency estimation based on spectrum concentration index (SCI)

The complex dynamic response s(t) measured during milling processes can be regarded as a superposition of multiple single modes as

$$ s(t)=\sum \limits_{j=1}^N{s}_j(t), $$
(1)

where the jth mode sj(t) is parametrically modeled here as a polynomial phase signal as

$$ {s}_j(t)={a}_j(t)\exp \left(\sqrt{-1}\left(2\pi \left({c}_0t+\sum \limits_{i=1}^k\frac{c_i}{i+1}{t}^{i+1}\right)+{\varphi}_0\right)\right), $$
(2)

where aj(t) is the amplitude, \( c(t)={\sum}_{i=0}^k{c}_i{t}^i \) stands for the IF of the mode, k is the order of the polynomial phase, c0 represents the initial frequency,ci(i = 1, ⋯, k) denotes IF parameters, and φ0 is the initial phase. In this manner, the estimation of the continuous IF is equivalent to the estimation of polynomial parameters, which greatly simplifies the problem. If the term \( {\sum}_{i=1}^k{c}_i{t}^{i+1}/\left(i+1\right) \) is removed from the polynomial, the energy of sj(t) will concentrate on c0 in the frequency domain; that is, the signal mode sj(t) will be fully demodulated. As a result, a demodulation operator can be defined as

$$ \Phi \left(t;\tilde{\mathbf{C}}\right)=\exp \left(-\left(\sqrt{-1}\right)2\pi \sum \limits_{i=1}^k\frac{{\tilde{c}}_i}{i+1}{t}^{i+1}\right), $$
(3)

where \( \tilde{\mathbf{C}}=\left\{{\tilde{c}}_1,{\tilde{c}}_2,\cdots, {\tilde{c}}_k\right\} \) are the estimated IF parameters. Then, the demodulated mode can be obtained as

$$ {s}_{j,d}\left(t;\tilde{\mathbf{C}}\right)={s}_j(t)\Phi \left(t;\tilde{\mathbf{C}}\right). $$
(4)

When the estimated IF is exactly the true one (i.e., \( \tilde{\mathbf{C}}=\mathbf{C} \)), the signal is fully demodulated as

$$ {s}_{j,d}\left(t;\mathbf{C}\right)={a}_j(t)\exp \left(\sqrt{-1}\left(2\pi {c}_0t+{\varphi}_0\right)\right), $$
(5)

where the spectrum has a single peak at the constant frequency c0. Following this idea, the SCI is adopted to evaluate the spectrum concentration degree of the demodulated signal as [26]

$$ \mathrm{SCI}\left(\tilde{\mathbf{C}}\right)=E\left({\left|\mathrm{\mathcal{F}}\left({s}_{j,d}\left(t;\tilde{\mathbf{C}}\right)\right)\right|}^4\right), $$
(6)

where E(·) stands for the expectation and ℱ(·) denotes the Fourier transform. The optimized \( \tilde{\mathbf{C}} \) can be expressed as

$$ {\tilde{\mathbf{C}}}_{\mathrm{opt}}={\left\{{\tilde{c}}_1,{\tilde{c}}_2,\cdots, {\tilde{c}}_k\right\}}_{\mathrm{opt}}=\underset{\tilde{\mathbf{C}}}{\arg \max}\mathrm{SCI}\left(\tilde{\mathbf{C}}\right), $$
(7)

and then \( {\tilde{c}}_0 \) can be naturally worked out as

$$ {\tilde{c}}_0=\underset{f}{\arg \max}\left|\mathrm{\mathcal{F}}\left({s}_{j,d}\left(t;{\tilde{\mathbf{C}}}_{\mathrm{opt}}\right)\right)\right|, $$
(8)

i.e., the peak frequency in the Fourier spectrum of the demodulated modesj, d, and this frequency can be easily detected. A modified particle swarm optimization with dynamic adaptation (DAPSO), of which the ability to jump out of the local extrema is greatly improved and the convergence is accelerated compared with the original PSO [32], is adopted to solve the nonlinear optimization problem in Eq. (7) [33]. The size of the population is set to 30 and the initial values are set as zero in this work. Obtaining the \( \tilde{\mathbf{C}} \) and \( {\tilde{c}}_0 \) through Eqs. (7) and (8), the IF of the target mode sj(t) can be accurately estimated. Since the SCI is to be maximized, the IF of the strongest mode with the highest energy in the synthetic signal will be estimated first.

2.2 Signal decomposition via iterative Vold-Kalman filter (I-VKF)

With the estimated IF, the VKF can be employed to extract the target component sj(t). The center frequency for the VKF can be adjusted adaptively according to the estimated IF, which makes it possible to separate closely distributed or even crossed signal modes in the time-frequency plane. However, in the original VKF, the tachometer information has to be collected and a joint optimization is adopted (i.e., all the components are simultaneously extracted) [22], while by using the approach in Section 2.1, only the IF of the dominant mode with the highest energy can be obtained. Therefore, the VKF is modified in this work under the framework of the greedy algorithm to recursively extract each component.

The mode sj(t) in model (1) can be given in another form as

$$ {s}_j(t)={a}_j(t){\Theta}_j(t), $$
(9)

where aj(t) represents the amplitude envelope and Θj(t) denotes the carrier signal as

$$ {\Theta}_j(t)=\exp \left(\sqrt{-1}{\int}_0^t{\omega}_j\left(\tau \right) d\tau \right), $$
(10)

where \( {\int}_0^t{\omega}_j\left(\tau \right) d\tau \) denotes the instantaneous phase with ωj(τ) being the instantaneous circular frequency. In the original VKF [22], it is assumed that ωj(τ) is an integer or fractional multiple of the fundamental frequency (i.e., the spindle rotational frequency), but this assumption is not made here. Target components are no longer limited to the order-based harmonics.

For discrete signals, the smooth degree of the slowly varying amplitude function aj(t) can be evaluated by

$$ {\nabla}^s{\mathbf{a}}_j(m)={\boldsymbol{\upvarepsilon}}_j(m),\kern0.5em m=1,2,\cdots, M, $$
(11)

where s is the difference order, ∇ denotes the difference operator, M is the signal length, and εj stands for the higher order term. Setting s = 2 (i.e., the second-order VKF is employed), Eq. (11) can be formulated as

$$ {\mathbf{a}}_j\left(m-1\right)-2{\mathbf{a}}_j(m)+{\mathbf{a}}_j\left(m+1\right)={\boldsymbol{\upvarepsilon}}_j(m), $$
(12)

where aj(0) = 0 and aj(M + 1) = 0 for a practical causal signal. The matrix form of Eq. (12) is given as

$$ \left[\begin{array}{ccccc}-2& 1& 0& \cdots & 0\\ {}1& -2& 1& \cdots & 0\\ {}0& 1& -2& \cdots & \vdots \\ {}\vdots & \vdots & \vdots & \ddots & 1\\ {}0& 0& \cdots & 1& -2\end{array}\right]\left[\begin{array}{c}{\mathbf{a}}_j(1)\\ {}{\mathbf{a}}_j(2)\\ {}{\mathbf{a}}_j(3)\\ {}\cdots \\ {}{\mathbf{a}}_j(M)\end{array}\right]=\left[\begin{array}{c}{\boldsymbol{\upvarepsilon}}_j(1)\\ {}{\boldsymbol{\upvarepsilon}}_j(2)\\ {}{\boldsymbol{\upvarepsilon}}_j(3)\\ {}\vdots \\ {}{\boldsymbol{\upvarepsilon}}_j(M)\end{array}\right]. $$
(13)

Equation (13) can be written as

$$ {\mathbf{Ra}}_j={\boldsymbol{\upvarepsilon}}_j, $$
(14)

which is the structural equation corresponding to the state equation in the Kalman filter [23]. In the meanwhile, the measured signal s(t) in Eq. (1) can be re-formulated in a discrete form as

$$ \mathbf{s}(m)={\mathbf{a}}_j(m){\boldsymbol{\Theta}}_j(m)+{\boldsymbol{\upxi}}_j(m),\kern0.5em m=1,2,\cdots, M. $$
(15)

Note that in the original VKF [22], all the components are jointly estimated and ξj(m) in Eq. (15) only includes the estimation error and noise, while in this work ξj(m) also includes the non-target components (i.e., sp(m), p = 1, 2, ⋯, N, p ≠ j). Such an idea coincides with the greedy algorithm; that is, the non-target components are regarded as the unwanted noise, and the target component is extracted greedily in each round of optimization. In other words, the obtained mode in each extraction takes away as much energy as possible from the current signal. This strategy is effective because it is consistent with the technique of the chatter frequency estimation developed in Section 2.1, where only the IF of the dominant mode is estimated. Finally, all the extractions together formulate the signal decomposition. Equation (15) can be expressed in the form of a matrix equation as

$$ \left[\begin{array}{c}\mathbf{s}(1)\\ {}\mathbf{s}(2)\\ {}\vdots \\ {}\mathbf{s}(M)\end{array}\right]-\left[\begin{array}{cccc}{\boldsymbol{\Theta}}_j(1)& 0& \cdots & 0\\ {}0& {\boldsymbol{\Theta}}_j(2)& \cdots & 0\\ {}\vdots & \vdots & \ddots & \vdots \\ {}0& 0& \cdots & {\boldsymbol{\Theta}}_j(M)\end{array}\right]\left[\begin{array}{c}{\mathbf{a}}_j(1)\\ {}{\mathbf{a}}_j(2)\\ {}\vdots \\ {}{\mathbf{a}}_j(M)\end{array}\right]=\left[\begin{array}{c}{\boldsymbol{\upxi}}_j(1)\\ {}{\boldsymbol{\upxi}}_j(2)\\ {}\vdots \\ {}{\boldsymbol{\upxi}}_j(M)\end{array}\right], $$
(16)

which can also be written as

$$ \mathbf{s}-{\mathbf{B}}_j{\mathbf{a}}_j={\boldsymbol{\upxi}}_j. $$
(17)

Similarly, Eq. (17) is a variant of the data equation corresponding to the measurement equation in the Kalman filter [23].

Combining the structural equation (14) and the data equation (17), a weighted loss function ℒ in the sense of ℓ2 norm is given as

$$ \mathcal{L}={\lambda}^2{\left\Vert {\boldsymbol{\upvarepsilon}}_j\right\Vert}_2^2+{\left\Vert {\boldsymbol{\upxi}}_j\right\Vert}_2^2={\lambda}^2{\boldsymbol{\upvarepsilon}}_j^{\mathrm{H}}{\boldsymbol{\upvarepsilon}}_j+{\boldsymbol{\upxi}}_j^{\mathrm{H}}{\boldsymbol{\upxi}}_j, $$
(18)

where λ is a weighting factor and the superscript H denotes the conjugate transpose. To minimize the function ℒ, the normal equation is introduced as

$$ \frac{\partial \mathcal{L}}{\partial {\mathbf{a}}_j}=\left({\lambda}^2{\mathbf{R}}^{\mathrm{T}}\mathbf{R}+\mathbf{I}\right){\mathbf{a}}_j-{\mathbf{B}}_j^{\mathrm{H}}\mathbf{s}=\mathbf{0}, $$
(19)

where I denotes the identity matrix. Equation (19) leads to the optimal solution for aj as

$$ {\tilde{\mathbf{a}}}_j={\left({\lambda}^2{\mathbf{R}}^{\mathrm{T}}\mathbf{R}+\mathbf{I}\right)}^{-1}{\tilde{\mathbf{B}}}_j^{\mathrm{H}}\mathbf{s}\triangleq {\mathbf{G}}^{-1}{\tilde{\mathbf{B}}}_j^{\mathrm{H}}\mathbf{s}. $$
(20)

The target mode sj can be finally reconstructed as

$$ {\tilde{\mathbf{s}}}_j={\tilde{\mathbf{B}}}_j{\tilde{\mathbf{a}}}_j, $$
(21)

where the square matrix \( {\tilde{\mathbf{B}}}_j \) can be easily formulated because the ωj(τ) in Eq. (10) has been worked out with the estimated IF. Thanks to the sparsity of matrix G in Eq. (20), the Cholesky factorization of matrix G [34] can be employed as the fastest algorithm to solve Eq. (19). Besides, the weighting factor λ is set to 1 ×  106 in this work to achieve a trade-off between the accuracy and computational cost [25].

Thus far, the entire I-VKF method can be summarized in Fig. 1. The extraction of signal modes is implemented recursively until the residual energy ratio is less than a pre-set value (5% is used here); that is, the mode number N is determined automatically. Considering that the mode number (i.e., the highest order) is empirically specified in the original VKF, the improved framework makes the filter more adaptive. Besides, the recursive decomposition rather than simultaneous extraction makes the filter more stable, which will be verified by the following example.

Fig. 1
figure 1

Flow chart of the developed iterative Vold-Kalman filter (I-VKF)

Full size image

2.3 An example

To validate the proposed method, an example of a four-component signal is given as

$$ {\displaystyle \begin{array}{l}s(t)={s}_1(t)+{s}_2(t)+{s}_3(t)+{s}_4(t),\kern1em 0\le t\le 15\ \mathrm{s},\\ {}\left\{\begin{array}{l}{s}_1(t)=\exp \left(-0.1t\right)\cos \left(2\pi (5t)\right),\\ {}{s}_2(t)=\exp \left(-0.1t\right)\cos \left(2\pi \left(10t+1.5{t}^2-\frac{1}{30}{t}^3\right)\right),\\ {}{s}_3(t)=\exp \left(-0.1t\right)\cos \left(2\pi \left(20t+1.8{t}^2-\frac{1}{20}{t}^3\right)\right),\\ {}{s}_4(t)=\exp \left(-0.1t\right)\cos \left(2\pi \left(40t+0.5{t}^2-\frac{1}{15}{t}^3\right)\right),\end{array}\right.\end{array}} $$
(22)

where IFs of four modes are f1(t) = 5, f2(t) = 10 + 3t − 0.1t2, f3(t) = 20 + 3.6t − 0.15t2, and f3(t) = 40 + t − 0.2t2 respectively.

The signal in Eq. (22) is contaminated by white Gaussian noise with the signal-to-noise ratio (SNR) as 2 dB. The sampling frequency is set to 100 Hz. The waveform of the noisy signal is shown in Fig. 2a. Figure 2c gives the time-frequency representation (TFR) generated by the short-time Fourier transform (STFT), while Fig. 2b is the noise-free version. In the parametric estimation of IFs, the order of the polynomial model is set to three (although true IFs here are of the second-order type).

Fig. 2
figure 2

Example of a four-component signal. a Waveform of the noisy signal. b TFR of the noise-free signal. c TFR of the noisy signal. All the TFRs are generated by the STFT

Full size image

Table 1 lists the estimated IF parameters by the SCI optimization with corresponding estimation error. Using the I-VKF, extracted four components and their TFRs are shown in Fig. 3. With accurately estimated IFs, four single components are successfully separated and embedded noises are removed. The SNRs of four reconstructed modes are 17.5516 dB, 17.0363 dB, 18.5479 dB, and 16.7213 dB, respectively.

Table 1 Estimated IF parameters based on the SCI optimization (values in parentheses denote the relative estimation errors)
Full size table
Fig. 3
figure 3

Extracted components by the I-VKF. a–d give s1 ~ s4 respectively. Top panels are waveforms (blue lines denote the estimated ones while red lines denote the true ones). Bottom panels are corresponding TFRs generated by the STFT

Full size image

For comparison, decomposition results by the EMD, VMD, and original VKF are also given (note that when the original VKF is used, the number of modes and IF of each mode are taken as known information to initiate the filtering). When the EMD is applied, the strong noise leads to severe mode aliasing [35], as Fig. 4 shows. The filter bank property of the VMD [36] makes obtained single modes physically meaningless as Fig. 5 shows, because four real components, which overlap in the time-frequency domain, cannot be separated by a filter in the frequency domain. When the original VKF is used, four chirp modes are indeed tracked but are distorted by noise (see Fig. 6), which is due to the instability of the joint optimization [25]. Moreover, the computational time consumed by the I-VKF does not exceed that consumed by the VKF (all the tests are carried out with MATLAB® R2018b on a personal computer with a 3.60-GHz Intel® Core™ i7-7700 CPU).

Fig. 4
figure 4

Extracted components by the EMD. a–d give TFRs of s1 ~ s4 generated by the STFT respectively

Full size image
Fig. 5
figure 5

Extracted components by the VMD. a–d give TFRs of s1 ~ s4 generated by the STFT respectively

Full size image
Fig. 6
figure 6

Extracted components by the original VKF. a–d give TFRs of s1 ~ s4 generated by the STFT respectively

Full size image

The above example demonstrates that the developed I-VKF method, which acts as an adaptive time-frequency filter, works effectively in the decomposition of multi-chirp signals with a low SNR, and thus will be of great help in chatter detection.

3 Energy entropy–based feature extraction

It is vital to extract the fault feature from measured signals accurately and timely for chatter detection. The selected feature quantity should not only make it simple and feasible for the signal acquisition and data processing but also reflect the essence of milling processes; that is, this quantity should be closely related to the change in cutting states. As an indicator of the internal confusion degree of a system, entropy, such as the permutation entropy [37] and approximate entropy [38], can be expressed as a function of the probability distribution of a signal and has been widely applied in fault diagnosis. The energy entropy [27] is utilized in this work to characterize the energy distribution of signal modes {s1(t), s2(t), ⋯, sN(t)} of a milling response s(t), which are extracted based on the I-VKF approach in Section 2. The energy of each mode is given by

$$ {E}_j=\int {\left|{s}_j(t)\right|}^2 dt,\kern1em j=1,2,\cdots, N. $$
(23)

Neglecting the residual, the aggregate energy of all modes should be equal to that of the original signal. Then, the energy entropy is defined based on Shannon’s entropy [28] as

$$ {H}_{\mathrm{energy}}=-\sum \limits_{j=1}^N{p}_j{\log}_2{p}_j, $$
(24)

where pj = Ej/E and \( E={\sum}_{j=1}^N{E}_j \).

Energy entropy in Eq. (24) is a dimensionless index larger than zero. The larger the index, the more dispersed the energy distribution in the frequency domain [27]. Since each mode is located within a specific frequency band, the energy entropy characterizes the degree of randomness of milling dynamics that underlie a vibration response.

In stable milling, the vibration obeys a Gaussian-like distribution in the time domain and shows a wideband property in the frequency domain. At an early stage of chatter, the amplitudes at certain frequencies (i.e., chatter frequency and its harmonics) gradually increase, and the vibration energy tends to gather within several narrow bands. As chatter becomes more severe, the vibration resembles a sinusoidal oscillation, which results in a rapid decrease in signal randomness in the time domain.

According to the above mechanism, a strategy is proposed for chatter detection, which combines the I-VKF-based decomposition in Section 2 and the energy entropy–based feature extraction in Section 3. In this way, the progressive change in cutting states can be accurately captured by the energy entropy that is computed based on signal modes extracted from milling responses. The effectiveness of this strategy will be demonstrated by dynamic simulation and experiments in Section 4 and Section 6, respectively.

4 Dynamic simulation

In this section, milling vibration responses are simulated using the Runge-Kutta algorithm. The classic Balachandran two-degree-of-freedom milling model [39] is considered and the simulation parameters follow those in the original investigation [39]. We give two cases where the spindle speed and the axial cutting depth linearly increase, respectively. As Fig. 7 shows, the process from stable cutting to chatter can be observed in both cases, and the corresponding transition points A, B, and C coincide with those predicted by the stability lobe [39].

Fig. 7
figure 7

Two simulation cases. a Case #1 with linearly increasing spindle speed. b Case #2 with linearly increasing axial cutting depth. Top panels denote the variations of the processing parameters and bottom panels denote the milling force responses in the feed direction

Full size image

A preliminary time-frequency analysis of the response in case #1 is given in Fig. 8a. The force signal consists of three types of components: the tooth-passing modes resulting from spindle rotations, random modes due to system noises, and chatter modes caused by regenerative effects [40], which together lead to an intricate spectrum.

Fig. 8
figure 8

TFR for case #1. a Original simulated force signal. b Tooth-passing components filtered out by the VKF

Full size image

Since the spindle speed is known, the VKF is applied as a pre-processor to remove the tooth-passing components before the decomposition, with the aim to eliminate the interference of spindle rotations and intermittent cutting. The TFR of the components filtered out is shown in Fig. 8b. The remaining signal is then decomposed by the I-VKF into eight modes as Fig. 9 shows (note that in all the following simulated and experimental cases, only the third-order polynomial model is considered in the SCI optimization to minimize the computational cost). The energy of the extracted mode reduces as the order increases, which is consistent with the idea of the greedy algorithm. Eight modes exhibit chatter-related dynamics, showing the chatter frequencies that are spindle speed–independent [40]. Similar characteristics can be observed when the same processing is applied to the response in case #2.

Fig. 9
figure 9

TFRs of extracted components from the simulated milling force in case #1 by the proposed I-VKF

Full size image

The VMD and EMD are also applied to decompose the milling force signal and the results are given in Fig. 10 and Fig. 11, respectively. Mode aliasing can be observed in eight components extracted by the VMD and this problem is even exacerbated when the EMD is used, which makes the introduction of the I-VKF technique necessary.

Fig. 10
figure 10

TFRs of extracted components from the simulated milling force in case #1 by the VMD

Full size image
Fig. 11
figure 11

TFRs of extracted components from the simulated milling force in case #1 by the EMD

Full size image

As Fig. 9 shows, TFRs of extracted modes during chatter (the intermediate interval surrounded by two white borders) are much more condensed than those during stable cutting, which suggests a more concentrated energy distribution. This decrease in signal randomness can be captured by the energy entropy that is computed using a sliding window with a length of 0.1 s, as Fig. 12 shows. The energy entropy is sensitive to changes in the cutting state, and the variations of the entropy always precede such changes, which demonstrates the effectiveness of the proposed strategy in timely chatter detection.

Fig. 12
figure 12

Simulated milling force signals with computed energy entropies. a Case #1. b Case #2

Full size image

5 Threshold determination

Since chatter is expected to be detected automatically, an alarm threshold is needed. In many existing studies, the threshold is determined by manually observing the deviation between index values under chatter and stable cutting [4, 38, 41]. This empirical strategy suffers from the sensitivity to working conditions. In this work, a robust threshold is determined statistically. In many fault diagnosis problems, the fault feature is assumed to obey the Gaussian distribution, which simplifies the model construction for fault classification [42,43,44]. The same null hypothesis is made here in the analysis of the statistical distribution of milling signals.

At the incipient stage of a machining task, vibration signals under stable cutting can be collected and corresponding energy entropies can be calculated as a sample. Then, the normality test can be carried out on the sample, where the Lilliefors test [45] is adopted in this work because the population mean μ and variance σ2 are not known. The statistic is given by

$$ {D}_N=\underset{x\in R}{\max}\left|{\hat{F}}_N(x)-{G}_0(x)\right|, $$
(25)

where x is the sample, N is the sample size, \( {\hat{F}}_N(x) \) is the empirical cumulative distribution function (CDF) of the sample, and G0(x) is the CDF of the hypothesized distribution with the estimated parameters equal to the sample parameters, that is,

$$ \left\{\begin{array}{l}\hat{\mu}=\overline{X}=\frac{1}{N}\sum \limits_{k=1}^N{X}_k,\\ {}{\hat{\sigma}}^2={S}^2=\frac{1}{N-1}\sum \limits_{k=1}^N{\left({X}_k-\overline{X}\right)}^2.\end{array}\right. $$
(26)

Equation (26) exactly gives the maximum likelihood estimate under a Gaussian distribution [30]. The null hypothesis will be rejected when the observation of DN is larger than the critical value at a specified significance level (5% is set here), and this critical value can be obtained by the Monte Carlo method [46].

Once the normality test is approved, the three-sigma criterion [31] will be adopted to calculate the allowable range of the fluctuating energy entropy under stable cutting, which is given by \( \left[\hat{\mu}-3\hat{\sigma},\hat{\mu}+3\hat{\sigma}\right] \). Considering the decrease in randomness when chatter occurs, the alarm threshold is set as the lower limit, i.e., \( \hat{\mu}-3\hat{\sigma} \).

6 Implementation and experimental verification

The detailed implementation of chatter detection in the industry is introduced in this section, and a series of milling experiments are conducted to show the performance of the proposed approach.

6.1 Implementation of chatter detection

Dynamic simulations in Section 4 show promising results of chatter detection based on the I-VKF technique and subsequent energy entropy monitoring. Herein, the practical implementation is given in Fig. 13, which consists of the following steps:

  1. 1.

    Processing parameters’ definition: Define the spindle speed, feed rate, and cutting depth. All these parameters can be variable in a milling task.

  2. 2.

    Vibration signal acquisition: Collect milling system-related vibration signals. The milling force is collected in this work since it suffers from the least influence of the displacement of transducers [47], but the developed approach can also be utilized to analyze displacement and acceleration signals because the cutting force and vibration are strongly coupled in milling dynamics; i.e., other types of vibration signals would exhibit the same chatter features [40].

  3. 3.

    Online energy entropy computation: Calculate the real-time energy entropy of the collected signal based on the procedure given in Fig. 13a. A sliding window with a specified window length is used for online monitoring.

  4. 4.

    Threshold determination: Obtain the alarm threshold of the entropy using the incipient stable milling response, according to the strategy in Section 5.

  5. 5.

    Cutting state monitoring: The moment when discrete data points of the computed entropy cross the given threshold three consecutive times triggers the chatter alarm. The situation where only one or two data points cross the threshold and the following point falls back will be regarded as not chatter but an accident.

    Fig. 13
    figure 13

    Implementation of chatter detection. a Flowchart of the energy entropy computation. b Flowchart of the online chatter detection

    Full size image

6.2 Experimental setup

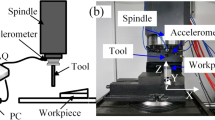
The experimental setup is shown in Fig. 14. All the tests were conducted on a DMG five-axis CNC milling machine. The carbon-steel end-milling tool has four teeth and a diameter of 4 mm, and the spindle has an overhang of 40 mm. The workpiece is an aluminum alloy block. The full-immersion cutting was adopted. Chatter vibrations were monitored with a Kistler 9123C dynamometer that was attached to the workpiece. Signals were recorded by a data acquisition card and were analyzed using a PC. The sampling frequency was set to 20 kHz.

Fig. 14
figure 14

Experimental setup. a Picture. b Schematic

Full size image
Fig. 15
figure 15

Measured milling force signals in the offline experiment I. a Temporal waveforms. b Fourier spectra (where f denotes the tooth-passing frequency)

Full size image
Fig. 16
figure 16

Energy distribution of single modes extracted from milling force signals in the offline experiment I. a Normalized energy ratio of each mode. b Energy entropy of each test signal

Full size image
Fig. 17
figure 17

The empirical CDF of the sample versus the CDF of the hypothesized Gaussian distribution in the Lilliefors test

Full size image
Fig. 18
figure 18

The collected milling force signal in test #5 with the corresponding energy entropy computed online: (a) Overall view; (b) Local close-up view

Full size image
Fig. 19
figure 19

Three signal segments corresponding to S1 (stable), S2 (transition), and S3 (chatter) in Fig. 18 respectively. a Temporal waveforms. b Original Fourier spectra. c Fourier spectra after the VKF filtering (where f denotes the tooth-passing frequency)

Full size image
Fig. 20
figure 20

Signal decompositions of sample 3 in Fig. 19. a By the EMD. b By the I-VKF (both after the pre-filtering by the VKF)

Full size image
Fig. 21
figure 21

Energy distribution of single modes from test #5 signal in online experiment II. a Based on the EMD. b Based on the I-VKF

Full size image
Fig. 22
figure 22

Energy entropy of each sample in experiment II. a Based on the EMD. b Based on the I-VKF

Full size image

The stability of milling is closely related to the spindle speed and depth of cut. Herein, the axial cutting depth varies from 2.6 to 6.7 mm and the spindle speed varies from 3600 to 4200 rpm. Five sets of processing parameters are listed in Table 2. Tests #1–#4 in experiment I give four different cutting states. Test #5 in experiment II gives a dynamic process from stable cutting to chatter.

Table 2 Milling tests with parameters
Full size table

6.3 Results

6.3.1 Offline experiment I

Four test signals are shown in Fig. 15. In tests #1 and #2, the amplitudes of milling forces are relatively small and the spectra are dominated by the evenly distributed tooth-passing frequencies, which indicates a stable cutting. With an increase in the spindle speed and cutting depth, the slight and the severe chatter occur in tests #3 and #4, respectively, leading to the large amplitudes and conspicuous chatter frequencies that are modulated by the spindle rotational frequency. The uncertainty of the distribution is reduced in these cases. With the I-VKF applied, the single modes of four test signals are obtained and the normalized energy ratios of each mode are calculated and given in Fig. 16a. The results verify the aforementioned Gaussian randomness in stable cutting and the harmonic concentration in chatter. The gathering of energy is also revealed in the computed energy entropies of four test signals, as shown in Fig. 16b.

The above offline results demonstrate the effectiveness of the proposed method, and the industrial application of this strategy will be further shown in the following online results.

6.3.2 Online experiment II

In the second experiment, the cutting state is monitored online. The length of the sliding window is set as 100 points with no overlap. The incipient milling force signals under stable cutting were collected and the corresponding energy entropy was computed. With the Lilliefors test performed, the empirical CDF of the sample versus the theoretical CDF of the hypothesized Gaussian distribution is obtained and given in Fig. 17. The linear regression shows an excellent fit between the two functions. Therefore, the strategy in Section 5 can be used to determine the alarm threshold. The allowable range of the fluctuation is obtained as [2.081, 2.145], and thus, the threshold is set as 2.081.

The collected milling force signal with the corresponding energy entropy computed online is shown in Fig. 18. The indicator detects the premature chatter at t = 0.58 s, around 0.12 s ahead of the moment when the amplitude suddenly increases (which means the destruction of the workpiece). For further verification, the machine was not shut down after the chatter alarm. Three signal samples with an equal duration of 0.3 s marked with S1, S2, and S3 in Fig. 18, respectively, are extracted and given in Fig. 19. The VKF is applied as a pre-filter to remove the tooth-passing components, and the Fourier spectra after are shown in Fig. 19c.

During the stable cutting (0~0.3 s), the vibration energy disperses within a wide band (see the first panel in Fig. 19c). With a drastic increase in the vibration amplitude at around 0.6 s, the chatter emerges, which is accompanied by the noticeable chatter frequencies as shown in the second panel in Fig. 19c. At about 1.8 s, chatter has been fully developed. A modulated waveform appears (see the third panel in Fig. 19a) and the chatter frequencies become dominant, which absorb most of the energy as the third panel in Fig. 19c shows.

The proposed I-VKF and the classic EMD are both applied to decompose the chatter response. As Fig. 20a shows, severe mode aliasing can be observed when the EMD is used, because the collected signal contains noise that is inevitable in engineering. Based on the I-VKF, the harmonic-like components have been recovered from the noisy signal, which makes the characteristic peaks of chatter in the spectra conspicuous (see Fig. 20b). The superiority of the I-VKF over EMD is further shown in analyses of the energy distribution and energy entropy based on extracted single modes. As Fig. 21 and Fig. 22 show, three different cutting states cannot be distinguished by means of the EMD. This came as no surprise because an ineffective signal decomposition will render the subsequent computation of the chatter index ineffective too.

7 Conclusions

To protect the machine tool and workpiece from the damage caused by chatter, it is necessary to detect chatter timely and accurately in machining processes. Since the chatter can be characterized by the progressive variation in the energy distribution, when chatter occurs, the decreasing randomness of vibration responses can be captured by energy entropy, a generalization of Shannon’s entropy in the energy domain. To make such an index more sensitive to transitions of the cutting state, the energy entropy should be computed based on single signal modes that are obtained by means of signal decompositions. Considering that the applications of the well-known EMD and VMD are limited due to the sensitivity to noise and the need for a priori information, respectively, the I-VKF is proposed in this work as an efficient multicomponent signal decomposition tool.

Based on the idea of the greedy algorithm, the original VKF, which adopts a joint optimization framework, is modified to recursively extract each chatter mode (i.e., signal modes are no longer simultaneously extracted). This modification improves the stability and adaptability of the filter, and does not increase the computational cost. In the meanwhile, a novel technique based on the SCI is developed to parametrically estimate the instantaneous chatter frequency of the dominant mode in the current signal, and thus to initiate each round of extraction. This technique transforms the estimation of a continuous IF into the optimization of a few polynomial parameters, which simplifies the problem and improves the robustness of the filter. As a result, the proposed I-VKF acts as an adaptive time-frequency filter and achieves much better performance than the EMD, VMD, and original VKF do, especially in the presence of strong noises, which has been verified by numerical examples.

By modeling the distribution of the energy entropy sample under stable cutting as a Gaussian type, we determine the alarm threshold of chatter through the maximum likelihood estimation and three-sigma criterion. With this threshold, an online chatter detection strategy is detailed. Through dynamic simulation and experimental verification, it has been demonstrated that chatter can be detected timely when the proposed strategy is used. The variation in entropy can be clearly observed during the transition from stable cutting to chatter. When other similar schemes such as the EMD-based entropy monitoring are employed, the decrease in the randomness of the collected signal cannot be revealed because the fundamental signal decomposition is ineffective in this case. Despite the fact that the focus of this work is milling chatter, the developed approach can be applied to other common machining operations such as turning and boring, because chatter in these processes can also be explained by the regenerative effect and be characterized by non-harmonic frequency components and decreasing entropy.