Theoretical investigation of machining-induced residual stresses in longitudinal torsional ultrasonic–assisted milling

Abstract

In order to realize the compressive stress and antifatigue manufacturing of titanium alloy TI-6Al-4V, a compound processing of longitudinal-torsional ultrasonic vibration and milling (LTUM) is proposed, a theoretical prediction model of machining-induced residual stress (RS) is established, and it is validated by experiments. The trajectory model of cutting edge in LTUM is constructed; furthermore, the undeformed chip thickness (UCT) model of LTUM is structured; The mechanical stress model of LTUM is established from the shear stress and plow stress; the thermal stress model of LTUM is established from shear thermal stress and plow thermal stress; Considering mechanical and thermal stress, the residual stress of longitudinal-torsional ultrasonic milling is established by loading and releasing stress. From numerical simulation of mechanical stress and thermal stress model, it shows that in LTUM, stress fluctuates with ultrasonic vibration, and mechanical stress absolute value is larger than that of traditional machining (TM); thermal stress absolute value is less than that of TM. A series of experiments are carried out to verify the RS model of LTUM. From present work, through theoretical prediction and experimental verification of machining-induced residual stress, it is concluded that established theoretical model predicts properties, and distribution of residual stress with high accuracy and the LTUM significantly increases surface compressive stress and compressive stress layer depth. It lays a foundation for the compressive stress and fatigue resistance of titanium alloys.

1 Introduction

Titanium alloy has become an indispensable material in modern aerospace industry [1, 2]. However, as a typical difficult-to-cut material, it has a poor cutting-performance, and it is easy to distribute residual tensile stress on the machined surface after machining, shortened service life [3, 4].

Since MARTENS was proposed in 1912, machining-induced residual stress (RS) has been paid enough attention and taken as an important evaluation criterion of machined surface quality [5, 6]. A multitude of results has shown that appropriate RS is obtained through process method, to improve fatigue strength, wear resistance and corrosion resistance [7]. To get the mechanism of RS generation, and improve the fatigue resistance of parts, fruitful conclusions and results were obtained by researchers.

Zeng [8] and Peng [9] presented analytical models to predict machining induced RS, by considering tool geometrical, material property, and processing parameters. Zhou [10] based on mechanical loading and thermal loading in cutting process, proposed an analytical model of RS. Wan [11] presented a theoretical model to predict the machining-induced RS in milling process by taking the 3D instantaneous contact status. Ji [12] developed a model of machining-induced residual. Aliakbari [13] and Huang [14] have also been made achievements about machining induced RS model.

Obtaining residual compressive stress on machined surface is an effective method to realize anti-fatigue manufacturing of components [15, 16]. Compared with traditional machining (TM), one-dimensional ultrasonic vibration machining, reduces cutting force and cutting temperature, and improve the quality of machining [17], but with the high-frequency vibration of the tool, tool flank is extruded with the machined surface, it seriously affects the life of the tool and the surface quality of the machined surface. Contrastively, in the longitudinal-torsional ultrasonic vibration-assisted machining (LTUM), cutting edge moves in a 3D space, the extrusion-friction between the flank and machined surface is effectively avoided, while the shear angle is increased, the average cutting force and cutting temperature are further reduced, and the compressive stress manufacturing of parts is realized, it plays an important role in the antifatigue manufacturing technology [18, 19].

TRAVIESO [20] found that it was highly improved in ultrasonic machining comparison with TM. Sharma [21] presented effect of cutting and ultrasonic parameters on RS generation, found feed rate significantly affected RS. Hu [22] proposed the method of ultrasonic-assisted turning and made a comparison with conventional turning; the effect of ultrasonic vibration on RS has been investigated by the finite-element model. Zhou [23], Maurotto [24], and Ye [25] proved that the ultrasonic-assisted machining greatly improved RS as well.

Up to the literatures, fruitful researching achievements about RS have been open in traditional cutting; however, for ultrasonic vibrations assisted cutting (especially LTUM), researches of RS were mainly based on experiment and simulation; litter literatures explore a theoretical model. Meanwhile, it proved that the ultrasonic-assisted machining improved residual compressive stress, but most of studies were focused on one-dimensional ultrasonic method, and considered workpiece as vibration carrier. Contrastively, it has more advantages for LTUM than one-dimensional ultrasonic vibration; moreover, tool as vibration carrier, machinability of different sizes, and complex shapes are improved, energy output is uniform and stable, and it has a wider application prospect.

In the present work, a model of cutting edge trajectory and undeformed chip thickness (UCT) in longitudinal-torsion ultrasonic–assisted milling (LTUM) of titanium alloy Ti-6Al-4V has been explored, and a theoretical prediction model of LTUM induced residual stress has been proposed at first place. From presented work, through theoretical prediction and experimental verification of machining-induced residual stress, it is concluded that established theoretical model predicts properties and distribution of residual stress with high accuracy. It lays a foundation for the compressive stress and fatigue resistance of titanium alloys.

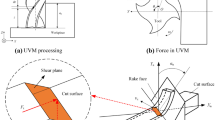
2 Characteristic analysis of LTUM

In LTUM, principle of LTUM was shown in Fig. 1. Compared with TM, the trajectory of LTUM has a great difference; it has a directly impact on the cutting force, cutting temperature, RS, and other processing processes and results.

Fig. 1

Principle of LTUM

2.1 Kinematics analysis of LTUM

2.1.1 Trajectory model of cutting edge in LTUM

For TM, the cutting edge trajectory equation is the following:

$$ \left\{\begin{array}{c}x(t)={v}_ft+{R}_t\mathit{\sin}\left(2\pi nt/60\right)\\ {}y(t)={R}_t\mathit{\cos}\left(2\pi nt/60\right)\\ {}z(t)=0\end{array}\right. $$

(1)

Furthermore, according to the characteristics of ultrasonic vibration, cutting edge trajectory equation of LTUM is established.

$$ \left\{\begin{array}{c}x(t)={v}_f\cdot t+{R}_t\cdot \mathit{\sin}\left({\omega}_{n-t}\right)\\ {}y(t)={R}_t\cdot \mathit{\cos}\left({\omega}_{n-t}\right)\\ {}z(t)={A}_l\mathit{\sin}\left(2\pi ft\right)\end{array}\right. $$

(2)

where, ƒ is ultrasonic frequency, A_l is longitudinal amplitude in LTUM, ω_n-t is actual turning angle of tool, calculated by Eq. (3).

$$ {\omega}_{n-t}=2\pi \left( nt/60\right)+{\omega}_{l-t} $$

(3)

where, ω_l-t is torsional vibration angle in LTUM, calculated by Eq. (4).

$$ {\omega}_{l-t}={A}_t\cdot \mathit{\cos}\left(2\pi ft+{\varphi}_{l-t}\right) $$

(4)

where, A_t is torsional amplitude in LUTM, φ_l-t is longitudinal-torsional phase difference.

From Eqs. (1) and (2), trajectories of the cutting edges in LTUM and TM were illustrated as shown in Fig. 2.

Fig. 2

Cutting edge trajectory model of LUM and CM

In Fig. 2, suppose A1, A2...An point is the starting separation position of tool-workpiece, B1, B2...Bn point is the starting contact point, named feature point, it can be seen that the cutting edge moves along the blue line in LTUM, and the tool-workpiece undergoes periodic changes of separation-contact-separation with ultrasonic vibration, caused quite different from TM.

2.1.2 Solving model of feature point in LTUM

Compared with TM, with periodic separation-contact of tool-workpiece, actual cutting time (ACT), and its duty cycle have changed dramatically in LTUM. Such as in Fig. 2, ACT is the time when the cutting edge moves from B1 to A2, and its duty cycle is the ratio of the time from B1 to A2 to the time from A1 to A2. Therefore, solving these feature points is meaningful for evaluating ACT and its duty cycle.

From Fig. 2, feature point is related not only to the cutting edge trajectory, but also to the tool geometry, the relationship is the following:

$$ {\psi}_l=\frac{Z\tan \beta }{R_t} $$

(5)

$$ {\alpha}_l= arc\ \tan \frac{a_p}{R_t{\psi}_l} $$

(6)

$$ \beta = arc\ \tan \frac{R_t{\psi}_l}{a_p} $$

(7)

where, β is the helix angle, α_l is the lead angle, R_t is the tool radius, α_p is the depth of cut, ψ_l is the axial hysteresis angle, calculated by Eqs. (5)–(7).

Then, discrete the cutting edge trajectory, as shown in Fig. 3, the separation point is calculated by judging the relationship between space angle α_l-n and tool lead angle α_l of two adjacent points A_n-1 and A_n-1. When α_l-n > α_l, tool-workpiece separated, the separation point is obtained.

Fig. 3

Solving principle of the separation point

Discrete the cutting edge trajectory, as shown in Fig. 4, the contact point solution is similar to that of separation point. Separation and contact points solving process was shown in Fig. 5.

Fig. 4

Solving principle of combination point

Fig. 5

Solving flow of feature point

2.1.3 Trajectory characteristic of cutting edge in LTUM

According to the solution model of feature point, the separation and contact points of LTUM were calculated, as shown in Fig. 6, A1, A2, and A3 are the separation points of tool-workpiece, B1, B2, and B3 are the contact points. The cutting edge is separated from the workpiece in the process from A1 point to B1 point, contacting from B1 point to A2 point.

Fig. 6

Cutting edge trajectory characteristics in LTUM

Further, it is concluded that for LTUM, the tool-workpiece produces periodic separation; at the same time, it realizes the movement of cutting edge in three-dimensional, effectively avoids the extrusion-friction between the flank and machined surface, reduces the cutting force and temperature, and improves the quality of the machined surface.

Figure 7 is the cutting edge trajectory and feature points under different parameters in LTUM; it found that ultrasonic and machining parameters have a great influence on cutting edge trajectory and feature points; further, it affects the processing and results in LTUM. Getting the calculation results of cutting edge trajectory and feature points laid the foundation for establishing the milling induced RS theoretical model.

Fig. 7

Cutting edge trajectory and feature points under different parameters in LTUM. (a. ƒ = 35 kHz,A_l = 8 μm,A_t = 4 μm,φ_l-t = 90°,n = 400 r/min; b. ƒ = 35 kHz,A_l = 8 μm,A_t = 4 μm,φ_l-t = 90°,n = 1200 r/min; c. ƒ = 49 kHz,A_l = 8 μm,A_t = 4 μm,φ_l-t = 90°; d. ƒ = 35 kHz,A_l = 5 μm,A_t = 4 μm,φ_l-t = 90°)

2.2 Undeformed chip thickness of LTUM

Undeformed chip thickness (UCT) has a great influence on the mechanical, thermal, and RS in milling process; however, from analysis of cutting edge trajectory and feature points, UCT is more complicated in LTUM than TM, and it is necessary to establish UCT model, to reveal the mechanism of RS.

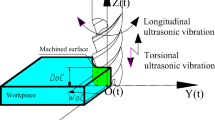
According to Fig. 1, the tool coordinate system is established by taking the feed direction as X axis, the vertical feed direction as Y axis, and the spindle axis direction as Z axis, tool rotation center as the origin, then UCT model was constructed, as shown in Fig. 8.

Fig. 8

Model of undeformed chip thickness

At time t, the position of the jth tool teeth was shown by the solid line in the Fig. 8; angular displacement of the tool teeth and the Y_t axis was expressed as:

$$ {\phi}_j(t)=\frac{2\pi n}{60}t-\left(j-1\right)\frac{2\pi }{N} $$

(8)

Then, UCT h_j(t) at time t, equal to the distance between the position Q of the jth teeth and the position P of the j–1th teeth at the time (t-ṷ_j(t)), where, ṷ_j(t) is the time delay of Jth teeth and j–1th teeth.

At time t, Q point coordinate value could be expressed:

$$ \left[\begin{array}{c}{Q}_x\\ {}{Q}_y\end{array}\right]=\left[\begin{array}{c}{O}_{tx}(t)\\ {}{O}_{ty}(t)\end{array}\right]+\left[\begin{array}{c}x(t)\\ {}y(t)\end{array}\right]+\left[\begin{array}{c}{R}_t\cdot \sin \left({\phi}_j(t)\right)\\ {}{R}_t\cdot \cos \left({\phi}_j(t)\right)\end{array}\right] $$

(9)

where, [O_txO_ty]^T is the coordinates of moving coordinate system origin in the fixed coordinate system XOY, [x(t) y(t) ]^T is the coordinates of tool center in the moving coordinate system O(t)X(t)Y(t).at time(t-ṷ_j(t)), point P coordinate value can be expressed:

$$ \left[\begin{array}{c}{P}_x\\ {}{P}_y\end{array}\right]=\left[\begin{array}{c}{O}_{tx}\left(t-{\underset{\wedge }{u}}_j(t)\right)\\ {}{O}_{ty}\left(t-{\underset{\wedge }{u}}_j(t)\right)\end{array}\right]+\left[\begin{array}{c}x\left(t-{\underset{\wedge }{u}}_j(t)\right)\\ {}y\left(t-{\underset{\wedge }{u}}_j(t)\right)\end{array}\right]+\left[\begin{array}{c}{R}_t\cdot \sin \left({\phi}_{j-1}\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\\ {}{R}_t\cdot \cos \left({\phi}_{j-1}\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\end{array}\right] $$

(10)

Meanwhile, P point coordinate value is expressed in moving coordinate system as well:

$$ \left[\begin{array}{c}{P}_x\\ {}{P}_y\end{array}\right]=\left[\begin{array}{c}{O}_{tx}(t)\\ {}{O}_{ty}(t)\end{array}\right]+\left[\begin{array}{c}x(t)\\ {}y(t)\end{array}\right]+\left[\begin{array}{c}\left({R}_t-{h}_j(t)\right)\cdot \sin \left({\phi}_j(t)\right)\\ {}\left({R}_t-{h}_j(t)\right)\cdot \cos \left({\phi}_j(t)\right)\end{array}\right] $$

(11)

Obviously, Eqs. (10) and (11) are equal, considering the tool coordinate system moves along with feed direction, then:

$$ {O}_{tx}(t)={O}_{tx}\left(t-{\underset{\wedge }{u}}_j(t)\right)+{\int}_{t-{\tau}_j}^t{v}_f(t) dt $$

(12)

$$ {O}_{ty}\left(t-{\underset{\wedge }{u}}_j(t)\right)={O}_{ty}(t) $$

(13)

Substituted Eqs. (12) and (13) into Eq. (10) and subtract from Eq. (11):

$$ \left[\begin{array}{c}x\left(t-{\underset{\wedge }{u}}_j(t)\right)\\ {}y\left(t-{\underset{\wedge }{u}}_j(t)\right)\end{array}\right]+\left[\begin{array}{c}{R}_t\cdot \sin \left({\phi}_{j-1}\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\\ {}{R}_t\cdot \cos \left({\phi}_{j-1}\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\end{array}\right]=\left[\begin{array}{c}{\int}_{t-{\tau}_j}^t{v}_f(t) dt\\ {}0\end{array}\right]+\left[\begin{array}{c}x(t)\\ {}y(t)\end{array}\right]\kern0.33em +\left[\begin{array}{c}\left({R}_t-{h}_j(t)\right)\cdot \sin \left({\phi}_j(t)\right)\\ {}\left({R}_t-{h}_j(t)\right)\cdot \cos \left({\phi}_j(t)\right)\end{array}\right] $$

(14)

Left multiplication transform matrix at both ends of Eq. (14)$\left[\begin{array}{cc}\sin {\phi}_j(t)& \cos {\phi}_j(t)\\ {}\cos {\phi}_j(t)& -\sin {\phi}_j(t)\end{array}\right]$, by substituting Eqs. (15) into (14), the expression of UCT was shown in Eqs. (16).

$$ {\phi}_{j-1}\left(t-{\underset{\wedge }{u}}_j(t)\right)={\phi}_j(t)-\frac{2\pi n}{60}{\underset{\wedge }{u}}_j(t)+\frac{2\pi }{N} $$

(15)

$$ {\displaystyle \begin{array}{c}{h}_j(t)=\sin \left({\phi}_j(t)\right)\cdot {\int}_{t-{\underset{\wedge }{u}}_j}^t{v}_f(t) dt+{R}_t\cdot \left[1-\cos \left(\frac{2\pi }{N}-\frac{2\pi n}{60}{\underset{\wedge }{u}}_{\mathrm{j}}(t)\right)\right]\\ {}+\left[x(t)-x\left(t-{\underset{\wedge }{u}}_j(t)\right)\right]\cdot \sin \left({\phi}_j(t)\right)+\left[y(t)-y\left(t-{\underset{\wedge }{u}}_j(t)\right)\right]\cdot \cos \left({\phi}_j(t)\right)\end{array}} $$

(16)

where,

$$ {\displaystyle \begin{array}{c}{R}_t\cdot \sin \left(\frac{2\pi }{N}-\frac{2\pi n}{60}{\underset{\wedge }{u}}_j(t)\right)=\cos \left({\phi}_j(t)\right)\cdot {\int}_{t-{\tau}_j}^t{v}_f(t) dt\kern0.33em +\left(x(t)-x\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\cdot \cos \left({\phi}_j(t)\right)\\ {}\kern.3em -\left(y(t)-y\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\cdot \sin \left({\phi}_j(t)\right)\end{array}} $$

(17)

$$ \underset{\wedge }{u}\approx T=\frac{60}{Nn} $$

(18)

Assuming that the tool moved uniformly with feed speed, the UCT h_j(t) was expressed as the static cutting thickness h_js and dynamic cutting thickness h_jd caused by the regeneration effect, as following:

$$ {h}_j(t)={h}_{js}(t)+{h}_{jd}(t) $$

(19)

$$ {h}_{js}(t)={f}_z\sin \left({\phi}_j(t)\right) $$

(20)

$$ {h}_{jd}(t)=\left(x(t)-x\left(t-{\underset{\wedge }{u}}_j(t)\right)\right)\sin \left({\phi}_j(t)\right)+\left(y(t)-y\left(t-{\underset{\wedge }{u}}_j(t)\right)\cos \left({\phi}_j\right.(t)\right) $$

(21)

For LTUM, cutting edge trajectory was shown in Eq. (2), considering both linear feed and rotary motion of the tool, actually, the cutting edge trajectory is still similar to the subcycloid motion, the cutting edge generates the subcycloid motion with a longer period as the spindle rotates, meanwhile, the with a shorter period is as ultrasonic vibration. Then, at time t, UCT of LTUM h_jlt(t) is calculated by Eq. (22).

$$ {\displaystyle \begin{array}{c}{h}_{jlt}(t)={f}_z\cdot \sin \left[{A}_t\cdot \mathit{\cos}\left(2\pi ft+{\varphi}_{l-t}\right)-\left(j-1\right)\cdot \frac{2\pi }{N}\right]\kern0.33em +\sin \left[\left({A}_t\cdot \mathit{\cos}\left(2\pi ft+{\varphi}_{l-t}\right.\right)-\left(j-1\right)\cdot \frac{2\pi }{N}\right]\\ {}\cdot \left[\begin{array}{c}{v}_f\cdot t+{R}_t\cdot \mathit{\sin}\left({\omega}_{n-t}\right)-{v}_f\cdot \left(t-T\right)\\ {}+{R}_t\cdot \mathit{\sin}\left({\omega}_{n-t}\left(t-T\right)\right)\end{array}\right]\kern0.33em +\cos \left[\left({A}_t\cdot \mathit{\cos}\left(2\pi ft+{\varphi}_{l-t}\right.\right)-\left(j-1\right)\cdot \frac{2\pi }{N}\right]\\ {}\cdot \left[{v}_f\cdot t+{R}_t\cdot \mathit{\sin}\left({\omega}_{n-t}\right)-{v}_f\cdot \left(t-T\right)+{R}_t\cdot \mathit{\sin}\left({\omega}_{n-t}\left(t-T\right)\right)\right]\end{array}} $$

(22)

3 Stress distribution in LTUM

3.1 Mechanical stress in LTUM

In LTUM, the mechanical stress mainly comes from two aspects: chip-forming force and plow-cutting force, the relationship was shown in Eq. (23). Chip-forming force, mainly comes from shear action, occurs in the shear zone. Plow-cutting force is mainly caused by extrusion friction between cutting edge radius and workpiece. The stress properties and directions were shown in Fig. 9.

$$ \left[\begin{array}{c}{\sigma}_{xx}^{me}\\ {}{\sigma}_{yy}^{me}\\ {}{\sigma}_{xy}^{me}\end{array}\right]=\left[\begin{array}{c}{\sigma}_{xx}^s\\ {}{\sigma}_{yy}^s\\ {}{\sigma}_{xy}^s\end{array}\right]+\left[\begin{array}{c}{\sigma}_{xx}^p\\ {}{\sigma}_{yy}^p\\ {}{\sigma}_{xy}^p\end{array}\right] $$

(23)

Fig. 9

Stress and its direction under the action of mechanical load

3.1.1 Shear stress in LTUM

Based on the cutting force model MERCHANT, it was modified to solve the shear stress in LTUM. Firstly, the LTUM was transformed into oblique cutting model, as shown in Fig. 10, and geometric relationship was given in Fig. 11.

Fig. 10

Model of oblique cutting

Fig. 11

Geometric relationship of shear force model in oblique cutting

From Figs. 10 and 11:

$$ \sin {\theta}_{si}=\sin {\beta}_{sf}\sin {\eta}_f $$

(24)

$$ \tan \left({\theta}_{sn}+{\alpha}_{sn}\right)=\mathit{\tan}{\beta}_{sf}\cos {\eta}_f $$

(25)

According to Stabler’s criterion, there is a relationship between chip flow direction angle and inclination angle (helix angle):

$$ {\eta}_f=\beta $$

(26)

where, β_sf is friction angle, the direction of cutting speed and force is determined by ϕ_sn, ϕ_si, θ_sn, and θ_si.

Then, the normal force F_n in the shear zone was obtained:

$$ {F}_n={F}_x\cos \beta \sin {\phi}_{sn}+{F}_y\cos {\phi}_{sn} $$

(27)

where, Fx and Fy respectively represent the cutting forces in the feed direction (X direction) and the vertical feed direction (Y direction).

From the previous analysis, LTUM alters UCT and cutting force, a nonlinear cutting force model [26] is adopted. For any teeth j, the instantaneous cutting forces are related to the UCT. The expressions are the following:

$$ \left\{\begin{array}{c}{F}_{tj}={K}_t{a}_p{h}_{jlt}{(t)}^q\\ {}{F}_{rj}={K}_r{a}_p{h}_{jlt}{(t)}^q\end{array}\right. $$

(28)

then, Fx and Fy were solved by:

$$ \left[\begin{array}{c}{F}_x\\ {}{F}_y\end{array}\right]=\sum \limits_{j=1}^Ng\left({\phi}_j(t)\right)\left[\begin{array}{cc}-\cos \left({\phi}_j(t)\right)& -\sin \left({\phi}_j(t)\right)\\ {}\sin \left({\phi}_j(t)\right)& -\cos \left({\phi}_j(t)\right)\end{array}\right]\left[\begin{array}{c}{F}_{tj}\\ {}{F}_{rj}\end{array}\right] $$

(29)

where, g(ϕ_j(t)) is window function, to judge whether the teeth are in cutting or not, calculated by Eq. (30).

$$ g\left({\phi}_j(t)\right)=\left\{\begin{array}{c}1,{\phi}_{st}\le {\phi}_j(t)\le {\phi}_{ex}\\ {}0,\mathrm{otherwise}\end{array}\right. $$

(30)

where, ϕ_st, ϕ_ex is cutting-in and cutting-out angle.

From Eqs. (28)–(30), cutting force at any time can be obtained:

$$ {\displaystyle \begin{array}{c}{F}_x(t)\\ {}{F}_y(t)\end{array}}={a}_p\sum \limits_{j=1}^Ng\left({\phi}_j(t)\right)\left(\left[\begin{array}{c}-{K}_t\cos {\phi}_j(t)-{K}_r\sin {\phi}_j(t)\\ {}{K}_t\sin {\phi}_j(t)-{K}_r\cos {\phi}_j(t)\end{array}\right]\cdotp {\left({h}_{jlt}(t)\right)}^q\right) $$

(31)

where, Kt, Kr is cutting force coefficient, solved by Eq. (32).

$$ {\displaystyle \begin{array}{c}{K}_t=\frac{\tau_{sf}\left(\mathit{\cos}{\theta}_{sn}+\mathit{\tan}{\theta}_{si} tan\beta \right)}{\left[\cos \left({\theta}_{sn}+{\phi}_{sn}\right)\mathit{\cos}{\phi}_{si}+\tan {\theta}_{si}\sin {\phi}_{si}\right]\sin {\phi}_{sn}}\\ {}{K}_r=\frac{\tau_{sf}\sin {\theta}_{sn}}{\left[\cos \left({\theta}_{sn}+{\phi}_{sn}\right)\mathit{\cos}{\phi}_{si}+\tan {\theta}_{si}\sin {\phi}_{si}\right] cos\beta \sin {\phi}_{sn}}\end{array}} $$

(32)

In the shear plane, the shear stress q_s and the normal stress p_s:

$$ {q}_s={\tau}_{sf} $$

(33)

$$ {p}_s=\frac{F_n\cos \beta \sin {\phi}_{sn}}{a_p{h}_{jlt}} $$

(34)

Then, the shear stress in the workpiece is calculated by the contact theory [27].

$$ \left\{\begin{array}{c}{\sigma}_{xx}^s=-\frac{2z}{\pi }{\int}_{-a}^a\frac{p_s{\left(x-s\right)}^2}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds-\frac{2}{\pi }{\int}_{-a}^a\frac{q_s{\left(x-s\right)}^3}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds\\ {}{\sigma}_{zz}^s=-\frac{2{z}^3}{\pi }{\int}_{-a}^a\frac{p_s}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds-\frac{2{z}^2}{\pi }{\int}_{-a}^a\frac{q_s\left(x-s\right)}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds\\ {}{\sigma}_{xz}^s=-\frac{2{z}^2}{\pi }{\int}_{-a}^a\frac{p_s\left(x-s\right)}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds-\frac{2z}{\pi }{\int}_{-a}^a\frac{q_s(s){\left(x-s\right)}^2}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds\end{array}\right. $$

(35)

where, ɑ is about one-half of the shear plane length:

$$ a\approx \frac{l_{sp}}{2}=\frac{h_{jlt}}{\sin {\phi}_{sn}{\cos}_{si}} $$

(36)

3.1.2 Plow stress in LTUM

In the shear force calculation model, it was assumed that the tool was absolutely sharp, and the influence of cutting edge radius was neglected, but actually, it does not meet the cutting edge radius of 0. For LTUM, it is often used in finishing, and the cutting force is smaller. Therefore, plow stress caused by cutting edge radius cannot be neglected in the analysis of machining induced RS. At the same time, with the increase of the radius, the contact area between the cutting surface and cutting edge is smaller; the region is in a higher stress state. Therefore, the influence of plow stress is not ignored to the RS in LTUM.

The plow stress of LTUM is calculated on the basis of Waldorf plow slip line model [28], as shown in Fig. 12, r_e is cutting edge radius, ϕ_s is shear angle, h_jlt is UCT of LTUM, solved by Eq. (22).

Fig. 12

Slip-line field for plow

According to the theory of slip line field by Dewhurst [29], friction stress in CA τ_sfrregion is:

$$ {\tau}_{sfr}={m}_f\cdot {k}_f $$

(37)

where, m_f is friction coefficient, k_f is function of unidirectional yield stress Y_u

The angle η_sp between the slip line and the bottom of the extrusion zone is obtained:

$$ {\eta}_{sp}=0.5\cdot \operatorname{arccos}\left({m}_f\right) $$

(38)

The radius of the circular fan field centered R_sp is solved by Eq. (39),

$$ {R}_{sp}=\sin \left({\eta}_{sp}\right)\cdot \sqrt{\begin{array}{c}{\left({r}_e\cdot \tan \left(\frac{\pi }{4}+\frac{\alpha_{tr}}{2}\right)+\frac{\sqrt{2}\cdotp {R}_{sp}\cdotp \sin \left({\rho}_{sp}\right)}{\tan \left(\frac{\pi }{2}+{\alpha}_{tr}\right)}\right)}^2\\ {}+2\cdotp {\left[{R}_{sp}\cdotp \sin \left({\rho}_{sp}\right)\right]}^2\end{array}} $$

(39)

where,

$$ {\theta}_{sp}=\frac{\pi }{4}-{\rho}_{sp}-{\phi}_{sp} $$

(40)

$$ {\gamma}_{sp}={\eta}_{sp}+{\phi}_{sp}-\arcsin \left(\sqrt{2}\cdot \sin \left({\rho}_{sp}\right)\cdot \sin \left({\eta}_{sp}\right)\right) $$

(41)

Shear angel ϕ_s is solved by Eq. (42).

$$ \tan \left({\phi}_s\right)=\frac{\frac{h_{jlt}}{h}\cdot \cos \left({\alpha}_{tr}\right)}{1-\frac{h_{jlt}}{h}\cdot \sin \left({\alpha}_{tr}\right)} $$

(42)

where, α_tr is rake angle.

Then, plow force is obtained from Eqs. (43) and (44).

$$ {P}_{cut}={q}_s\left[\begin{array}{c}\cos \left(2{\eta}_{sp}\right)\mathit{\cos}\left({\phi}_s-{\gamma}_{sp}+{\eta}_{sp}\right)+\\ {}\left(1+2{\theta}_{sp}+2{\gamma}_{sp}+\sin \left(2{\eta}_{sp}\right)\right.\sin \left({\phi}_s-{\gamma}_{sp}+{\eta}_{sp}\right)\end{array}\right]\overline{CA} $$

(43)

$$ {P}_{thrust}={q}_s\left[\begin{array}{c}\left(1+2{\theta}_{sp}+2{\gamma}_{sp}+\sin \left(2{\eta}_{sp}\right)\right.\\ {}\sin \left({\phi}_s-{\gamma}_{sp}+{\eta}_{sp}\right)-\\ {}\cos \left(2{\eta}_{sp}\right)\sin \left({\phi}_s-{\gamma}_{sp}+{\eta}_{sp}\right)\end{array}\right]\overline{CA} $$

(44)

where, q_s is solved by Eq. (33), $\overline{CA}$ is solved by Eq. (45).

$$ \overline{CA}=\frac{R_{sp}}{\sin \left({\eta}_{sp}\right)} $$

(45)

Plow stress can be calculated by Eq. (46):

$$ \left\{\begin{array}{c}{p}_e=\frac{4{P}_{thrust}\cos \beta }{\pi {a}_p\cdotp \overline{CA}}\\ {}{q}_e=\frac{m_f{P}_{cut}\cos \beta }{a_p\cdotp \overline{CA}}\end{array}\right. $$

(46)

Then, the plow stress in the workpiece can be calculated:

$$ \left\{\begin{array}{c}{\sigma}_{xx}^p=-\frac{2z}{\pi }{\int}_{-a}^a\frac{p_e{\left(x-s\right)}^2}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds-\frac{2}{\pi }{\int}_{-a}^a\frac{q_e{\left(x-s\right)}^3}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds\\ {}{\sigma}_{zz}^p=-\frac{2{z}^3}{\pi }{\int}_{-a}^a\frac{p_e}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds-\frac{2{z}^2}{\pi }{\int}_{-a}^a\frac{q_e\left(x-s\right)}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds\\ {}{\sigma}_{xz}^p=-\frac{2{z}^2}{\pi }{\int}_{-a}^a\frac{p_e\left(x-s\right)}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds-\frac{2z}{\pi }{\int}_{-a}^a\frac{q_e(s){\left(x-s\right)}^2}{{\left[{\left(x-s\right)}^2+{z}^2\right]}^2} ds\end{array}\right. $$

(47)

3.2 Thermal stress in LTUM

In LTUM, thermal load will also have a greater impact on the RS. In presented work, it is considered that the temperature in the workpiece mainly comes from two aspects: the shear heat θ_s-Pt in the shear zone and the plow heat θ_p-Pt in the plow zone, in which the shear heat plays a major role. The temperature at any point P_t in the workpiece was expressed as:

$$ {\theta}_{total-{P}_t}={\theta}_{s-{P}_t}+{\theta}_{p-{P}_t} $$

(48)

when the time increment of ultrasonic vibration is dt, the temperature change at any point can be obtained by Eq. (49).

$$ d{\theta}_{P_t}={\theta}_{total- Pt}\left(t+ dt\right)-{\theta}_{total- Pt}(t) $$

(49)

3.2.1 Shear thermal in LTUM

For dry milling, air can be assumed to be an insulator, due to the thermal conductivity of air is much smaller than that of workpiece material. Therefore, the shear surface heat source actually propagates in semiinfinite medium. It is assumed that the adiabatic boundary is taken as the mirror surface, and a heat source is mirrored above the shear heat source band; heat source and shear zone heat source have the same thermal intensity. In LTUM, infinite medium heat model consists of workpiece-chip-air; the heat flux from air medium returns to the workpiece-chip; that is, the air is an adiabatic boundary, and the workpiece-chip and air form a semiinfinite medium, as shown in Fig. 13.

Fig. 13

Model of an oblique moving band heat source in a semi-infinite medium

In the Fig. 13, OX axis is parallel to feed speed direction, while OY axis is vertical to machined surface. Suppose the coordinate system XOY moves with the feed speed, the temperature at any point P_t (x, y) affected by two aspects: the shear heat source band and its mirror heat source band. Each heat source can be composed of countless microelements dli, and each microelement can be solved as an infinite heat source line. So that, point P_t (x, y) temperature is mainly determined by the moving heat source line. For any moving heat source line dli:

$$ {q}_{w-l}={q}_{w- pl} dli $$

(50)

where, q_w-l is the heat source density of moving heat source line, calculated by Eq. (51):

$$ {q}_{w-l}=\frac{\sin {\varphi}_t\left({F}_X\cos {\varphi}_t-{F}_Y\sin {\varphi}_t\right)\frac{v_f\cos {a}_{sn}}{\cos \left({\varphi}_t-{a}_{sn}\right)}}{a_p\cdotp {h}_{jlt}} $$

(51)

Distance from point P_t to heat source line is:

$$ {R}_{ts1}=\left[{\left(X(t)- li\sin {\varphi}_t\right)}^2+{\left(Y(t)- li\cos {\varphi}_t\right)}^2\right] $$

(52)

Distance from point P_t to mirror heat source line is:

$$ {R}_{ts2}=\left[{\left(X(t)- li\sin {\varphi}_t\right)}^2+{\left(Y(t)+ li\cos {\varphi}_t\right)}^2\right] $$

(53)

Thus, point P_t temperature caused by moving heat source line was obtained from Eq. (54).

$$ {\theta}_{s-{P}_t}=\frac{q_{w- pl} dli}{2\pi {\lambda}_t}\cdotp {e}^{\frac{-{v}_f\left[\left(X(t)- li\cdotp \sin \right.\left({\varphi}_t\right)\right]}{2{a}_t}}\kern0.33em \cdotp {K}_{to}\frac{v_f}{2{a}_t}\left[\sqrt{\begin{array}{c}{\left(X(t)- li\sin {\varphi}_t\right)}^2\\ {}+{\left(Y(t)- li\cos {\varphi}_t\right)}^2\end{array}}\right] $$

(54)

Point P_t temperature caused by mirror heat source line was obtained from Eq. (55).

$$ {\theta}_{s-{P}_t}=\frac{q_{w- pl} dli}{2\pi {\lambda}_t}\cdotp {e}^{\frac{-{v}_f\left[\left(X(t)- li\cdotp \sin \left({\varphi}_t\right)\right.\right]}{2{a}_t}}\cdotp {K}_{to}\frac{v_f}{2{a}_t}\left[\sqrt{\begin{array}{c}{\left(X(t)- li\sin {\varphi}_t\right)}^2\\ {}+{\left(Y(t)+ li\cos {\varphi}_t\right)}^2\end{array}}\right] $$

(55)

Point P_t temperature caused by two heat source line can be obtained from Eq. (56).

$$ {\theta}_{s-{P}_t}=\frac{q_{w- pl} dli}{2\pi {\lambda}_t}\cdotp {e}^{\frac{-{v}_f\left[\Big(X(t)- li\cdotp \sin \left({\varphi}_t\right)\right]}{2{a}_t}}{K}_{to}\kern0.33em \cdotp \frac{v_f}{2{a}_t}\left[\begin{array}{c}\sqrt{{\left(X(t)- li\sin {\varphi}_t\right)}^2+{\left(Y(t)- li\cos {\varphi}_t\right)}^2}\\ {}+\sqrt{{\left(X(t)- li\sin {\varphi}_t\right)}^2+{\left(Y(t)+ li\cos {\varphi}_t\right)}^2}\end{array}\right] $$

(56)

By integrating Eq. (56), point P_t temperature subjected to moving heat source band and its mirror heat source band can be obtained from Eq. (57).

$$ {\theta}_{s-{P}_t}=\frac{q_{w- pl}}{2\pi {\lambda}_t}{\int}_{li=0}^L{e}^{\frac{-{v}_f\left[\left(X(t)- li\cdotp \sin \left({\varphi}_t\right)\right.\right]}{2{a}_t}}{K}_{to}\cdotp \frac{v_f}{2{a}_t}\left[\begin{array}{c}\sqrt{{\left(X(t)- li\sin {\varphi}_t\right)}^2+{\left(Y(t)- li\cos {\varphi}_t\right)}^2}\\ {}+\sqrt{{\left(X(t)- li\sin {\varphi}_t\right)}^2+{\left(Y(t)+ li\cos {\varphi}_t\right)}^2}\end{array}\right] dli $$

(57)

3.2.2 Plow thermal in LTUM

According to the literatures of contact angle between cutting tool and workpiece [30], the contact angle is usually small. Therefore, the plow thermal source of LTUM is approximated to a horizontal thermal source. Similar to shear thermal model, air is regarded as an adiabatic body. Workpiece-tool and air form an adiabatic boundary, Mirror a plow thermal source on the horizontal surface of plow thermal source, as shown in the Fig. 14.

Fig. 14

Heat transfer model of plow heat source

Then, point Pt temperature caused by plow thermal and its mirror thermal source can be solved by Eq. (58).

$$ {\theta}_{p-{P}_t}=\frac{q_{p- pl}}{2\pi {\lambda}_t}{\int}_0^{\overline{CA}}{\gamma}_p{e}^{\frac{-{v}_f\left( li-X(t)\right)}{2{a}_t}}\cdotp {K}_{to}\frac{v_f}{2{a}_t}\left[\sqrt{{\left( li-X(t)\right)}^2+{\left(Y(t)\right)}^2}\right] dli $$

(58)

where, γ_p is proportion of cutting thermal transferred to workpiece in machining process, solved by Eq. (59); q_p − pl is plow thermal source density, solved by Eq. (60).

$$ {\gamma}_p=\frac{\sqrt{k_w{\rho}_w{C}_w}}{\sqrt{k_w{\rho}_w{C}_w}+\sqrt{k_t{\rho}_t{C}_t}} $$

(59)

$$ {q}_{p- pl}=\frac{P_{cut}{v}_f}{a_p\cdotp \overline{CA}} $$

(60)

3.2.3 Thermal stress in LTUM

From the Eqs. (48), (49), (57), and (58), point Pt temperature caused by shear and plow thermal can be solved; then, the thermal stress at any point in the workpiece can be calculated by Eq. (61).

$$ \left\{\begin{array}{c}{\sigma}_{xx}^{th}=-\frac{a_e{E}_Y}{1-2{\nu}_p}{\int}_0^{\infty }{\int}_{-\infty}^{\infty}\left[{G}_{xh}\frac{\partial {\theta}_{total- Pt}\left(x,y\right)}{\partial x}+{G}_{xv}\frac{\partial {\theta}_{total- Pt}\left(x,y\right)}{\partial y}\right]\cdotp dxdy\\ {}\kern2.31em +\frac{2y}{\pi }{\int}_{-\infty}^{\infty}\frac{p_w(t){\left(t-x\right)}^2}{\left[{\left(t-x\right)}^2+{y}^2\right]} dt-\frac{a_e{E}_YT\left(x,y\right)}{1-2{\nu}_p}\\ {}{\sigma}_{yy}^{th}=-\frac{a_e{E}_Y}{1-2{\nu}_p}{\int}_0^{\infty }{\int}_{-\infty}^{\infty}\left[{G}_{yh}\frac{\partial {\theta}_{total- Pt}\left(x,y\right)}{\partial x}+{G}_{yv}\frac{\partial {\theta}_{total- Pt}\left(x,y\right)}{\partial y}\right]\cdotp dxdy\\ {}\kern2.31em +\frac{2{y}^3}{\pi }{\int}_{-\infty}^{\infty}\frac{p_w(t)}{{\left[{\left(t-x\right)}^2+{y}^2\right]}^2} dt-\frac{a_e{E}_YT\left(x,y\right)}{1-2{\nu}_p}\\ {}{\tau}_{xy}^{th}=-\frac{a_e{E}_Y}{1-2{\nu}_p}{\int}_0^{\infty }{\int}_{-\infty}^{\infty}\left[{G}_{xy h}\frac{\partial {\theta}_{total- Pt}\left(x,y\right)}{\partial x}+{G}_{xy v}\frac{\partial {\theta}_{total- Pt}\left(x,y\right)}{\partial y}\right]\cdotp dxdy\\ {}\kern2.31em +\frac{2{y}^2}{\pi }{\int}_{-\infty}^{\infty}\frac{p_w(t)}{{\left[{\left(t-x\right)}^2+{y}^2\right]}^2} dt\end{array}\right. $$

(61)

where, ɑ_e, E_Y, ν_p is thermal expansion coefficient, Young’s modulus and Poisson’s ratio of workpiece materials, respectively; Gxh, Gxv, Gyh, Gyv, Gxyh, and Gxyv are Green’s function of plane strain, calculated from literatures [31], p_w(t) can be solved by Eq. (62).

$$ {p}_w(t)=\frac{a_e{E}_YT\left(x,y=0\right)}{1-2{\nu}_p} $$

(62)

3.3 Milling-induced residual stress in LTUM

For LTUM, the stress at any point Pt in the workpiece is mainly composed of mechanical stress and thermal stress, while the mechanical stress includes shear stress and plow shear stress, as Eq. (63), the RS properties and directions were shown in Fig. 15.

$$ \left[\begin{array}{c}{\sigma}_{xx}^{el}\\ {}{\sigma}_{yy}^{el}\\ {}{\sigma}_{xy}^{el}\end{array}\right]=\left[\begin{array}{c}{\sigma}_{xx}^s\\ {}{\sigma}_{yy}^s\\ {}{\sigma}_{xy}^s\end{array}\right]+\left[\begin{array}{c}{\sigma}_{xx}^p\\ {}{\sigma}_{yy}^p\\ {}{\sigma}_{xy}^p\end{array}\right]+\left[\begin{array}{c}{\sigma}_{xx}^{th}\\ {}{\sigma}_{yy}^{th}\\ {}{\sigma}_{xy}^{th}\end{array}\right] $$

(63)

Fig. 15

Stresses and its direction from mechanical and thermal loading

3.3.1 Stress loading process

As shown in Fig. 16, assuming any point P_t in the workpiece, the tool coordinate system XOY moves along the feed direction, and the origin O is located at the cutting edge. When the tool is far away from point P_t (such as point A), it is mainly affected by elastic stress. As the tool moves, the stress at the point P_t gradually accumulates. When the tool moves to point B, plastic deformation occurs. When the tool moves to point C, the elastic-plastic deformation disappears. The cutting process can be equivalent to elastic-plastic rolling contact model.

Fig. 16

Model of stress loading process in workpiece

It is assumed that the stress is an invariant, i.e.,

$$ {\sigma}_{xx}={\sigma}_{xx}^{el},{\sigma}_{yy}={\sigma}_{yy}^{el},{\sigma}_{xy}={\sigma}_{xy}^{el} $$

(64)

Assuming that the workpiece is isotropic and follows Von Mises yield criterion, the yield surface is defined as follows:

$$ {F}_y=\frac{1}{2}\left({S}_{ij}-{a}_{ij}\right)\left({S}_{ij}-{a}_{ij}\right)-{k_{ys}}^2=0 $$

(65)

where, k_ys is the shear yield strength of the workpiece material, S_ij is the deviation stress, ɑ_ij is the back stress. And it has the following relationship:

$$ {a}_{ij}=\left\langle {S}_{kl}{n}_{kl}\right\rangle {n}_{ij} $$

(66)

$$ {S}_{ij}={\sigma}_{ij}-\frac{1}{3}{\sigma}_{kk}{\delta}_{ij} $$

(67)

where, δ_ij is a Kronecker symbol, n_ij is unit normal vector in the direction of plastic strain rate, 〈〉 is MacCauley symbol.

From the previous analysis, Z direction strain can be regarded as plane strain. At the same time, with the tool moving, the point Pt temperature also changes dθ_pt, it satisfies the following relationship:

$$ d{\varepsilon}_{zz}=d{\varepsilon}_{zz}^{el}+d{\varepsilon}_{zz}^{th}+d{\varepsilon}_{zz}^{pl} $$

(68)

That:

$$ \left\{\begin{array}{c}d{\varepsilon}_{xx}=\frac{1}{E_e}\left[d{\sigma}_{xx}^{plastic}-{\upsilon}_p\left(d{\sigma}_{zz}^{plastic}+d{\sigma}_{yy}^{el}\right)\right]+{a}_ed{\theta}_{P_t}\kern0.33em +\frac{1}{h_p}\left(\begin{array}{c}{n}_{xx}{n}_{xx}d{\sigma}_{xx}^{plastic}+{n}_{yy}{n}_{xx}d{\sigma}_{zz}^{plastic}+{n}_{yy}{n}_{xx}d{\sigma}_{yy}^{el}\\ {}+2{n}_{xy}{n}_{xx}d{\sigma}_{xy}^{el}+2{n}_{yz}{n}_{xx}d{\sigma}_{yz}^{el}+2{n}_{xz}{n}_{xx}d{\sigma}_{xz}^{el}\end{array}\right)\\ {}d{\varepsilon}_{zz}=\frac{1}{E_e}\left[d{\sigma}_{zz}^{plastic}-{\upsilon}_p\left(d{\sigma}_{xx}^{plastic}+d{\sigma}_{yy}^{el}\right)\right]+{a}_ed{\theta}_{P_t}\kern0.33em +\frac{1}{h_p}\left(\begin{array}{c}{n}_{zz}{n}_{xx}d{\sigma}_{xx}^{plastic}+{n}_{zz}{n}_{zz}d{\sigma}_{zz}^{plastic}+{n}_{yy}{n}_{zz}d{\sigma}_{yy}^{el}\\ {}+2{n}_{xy}{n}_{zz}d{\sigma}_{xy}^{el}+2{n}_{yz}{n}_{zz}d{\sigma}_{yz}^{el}+2{n}_{xz}{n}_{zz}d{\sigma}_{xz}^{el}\end{array}\right)=0\end{array}\right. $$

(69)

Equation (69) can be converted to:

$$ \left\{\begin{array}{c}d{\varepsilon}_{xx}={\psi}_m\left[\frac{1}{E_e}\left(d{\sigma}_{xx}^{el}-{\upsilon}_p\left(d{\sigma}_{zz}^{plastic}+d{\sigma}_{yy}^{el}\right)\right)+\frac{1}{h_p}\kern0.33em \left(\begin{array}{c}{n}_{xx}{n}_{xx}d{\sigma}_{xx}^{el}+{n}_{zz}{n}_{xx}d{\sigma}_{zz}^{plastic}+{n}_{yy}{n}_{xx}d{\sigma}_{yy}^{el}\\ {}+2{n}_{xy}{n}_{xx}d{\sigma}_{xy}^{el}+2{n}_{yz}{n}_{xx}d{\sigma}_{yz}^{el}+2{n}_{xz}{n}_{xx}d{\sigma}_{xz}^{el}\end{array}\right)\right]\\ {}\kern2.97em \\ {}\\ {}d{\varepsilon}_{zz}=0\end{array}\right. $$

(70)

where

$$ {\psi}_m=1-\exp \left(-\frac{3{\kappa}_m{h}_p}{2{G}_s}\right) $$

(71)

κ_m is the coefficient of the algorithm; h_p is the plastic modulus function; G_s is the shear modulus, solved by Eq. (72).

$$ {G}_s=\frac{E_e}{2+\left(1+{\upsilon}_p\right)} $$

(72)

3.3.2 Stress-releasing process

From the previous analysis, the stress after loading in the material is obtained, but it does not accord with the RS. Therefore, it is necessary to consider stress distribution after the release process.

In unloading process, a boundary conditions conversion model proposed by Merwin, that:

$$ \left\{\begin{array}{c}{\varepsilon}_{r- xx}=0,\kern0.99em {\varepsilon}_{r- zz}=0,\kern0.99em {\varepsilon}_{r- yz}=0;\\ {}{\varepsilon}_{r- yy}={f}_1(y),\kern0.99em {\sigma}_{r- zz}={f}_2(y),\kern0.99em {\sigma}_{r- yz}={f}_3(y);\\ {}{\sigma}_{r- yy}=0,\kern0.99em {\sigma}_{r- xy}=0,\kern0.99em {\varepsilon}_{r- xz}=0;\\ {}{\varepsilon}_{r- xy}={f}_4(y),\kern0.99em {\sigma}_{r- xx}={f}_5(y),\kern0.99em {\sigma}_{r- xz}={f}_6(y)\kern0.66em \end{array}\right. $$

(73)

where, ƒ_i(y) is the projection of a point P_t on the Y axis.

In unloading process, each stress component is gradually released to zero stress state. Assuming that there are n times stress releases, when reach zero stress, then:

$$ \varDelta {\varepsilon}_{xx}=\frac{\varepsilon_{f- xx}}{N_r},\varDelta {\sigma}_{yy}=\frac{\sigma_{f- yy}}{N_r},\varDelta {\sigma}_{xy}=\frac{\sigma_{f- xy}}{N_r},\varDelta {\theta}_r=\frac{\theta_r}{N_r} $$

(74)

where, θr is temperature before stress release.

When there is only elastic deformation in the release process, the change rate of stress follows Hooke’s law.

$$ \left\{\begin{array}{c}\varDelta {\sigma}_{xx}=\frac{E_e\left(\varDelta {\varepsilon}_{xx}+{a}_t\varDelta {\theta}_r\right)+{\upsilon}_p\left(1+{\upsilon}_p\right)\varDelta {\sigma}_{zz}}{1-{\upsilon_p}^2}\\ {}\varDelta {\sigma}_{zz}=\frac{\upsilon_p{E}_e\left(\varDelta {\varepsilon}_{xx}+{a}_t\varDelta {\theta}_r\right)+{\upsilon}_p\left(1+{\upsilon}_p\right)\varDelta {\sigma}_{yy}}{1-{\upsilon_p}^2}\\ {}\varDelta {\sigma}_{xz}=2{G}_s\varDelta {\sigma}_{xz}\end{array}\right. $$

(75)

In the process of elastic-plastic release, from Eqs. (69), (70), and (74):

$$ \left\{\begin{array}{c}\varDelta {\sigma}_{zz}=\frac{\left(-\frac{v_p}{E_e}+\frac{n_{xx}{n}_{yy}}{h_p}\right)\left({C}_s-{a}_t\varDelta \theta \right)-\left(\frac{1}{E_e}+\frac{{n_{xx}}^2}{h_p}\right)\left({D}_s-{a}_t\varDelta \theta \right)}{{\left(-\frac{v_p}{E_e}+\frac{n_{xx}{n}_{yy}}{h_p}\right)}^2-\left(\frac{1}{E_e}+\frac{{n_{xx}}^2}{h_p}\right)\left(\frac{1}{E_e}+\frac{{n_{yy}}^2}{h_p}\right)}\\ {}\varDelta {\sigma}_{xx}=\frac{D_s-\left(\frac{1}{E_e}+\frac{{n_{yy}}^2}{h_p}\right)\varDelta {\sigma}_{yy}-{a}_t\varDelta \theta}{-\frac{v_p}{E_e}+\frac{n_{xx}{n}_{yy}}{h_p}}\end{array}\right. $$

(76)

where:

$$ \left\{\begin{array}{c}{C}_s=\varDelta {\varepsilon}_{xx}+\left(\frac{v_p}{E_e}-\frac{n_{xx}{n}_{yy}}{h_p}\right){\sigma}_{zz}-\frac{2}{h_p}{\sigma}_{xy}{n}_{xy}{n}_{xx}\\ {}{D}_s=\left(\frac{v_p}{E_e}-\frac{n_{yy}{n}_{zz}}{h_p}\right){\sigma}_{yy}-\frac{2}{h_p}{\sigma}_{xy}{n}_{xy}{n}_{zz}\end{array}\right. $$

(77)

After the release process is completed, the RS is regarded as the initial condition of the next cycle stage. According to such a cycle process, when the stress and strain are in steady state, the stress in the workpiece is the RS in LTUM.

4 Numerical simulation and verification of theoretical model

4.1 Numerical simulation and analysis of mechanical stress

According to the established stress model and direction in Fig. 10, the stress distribution in the workpiece was calculated. The workpiece material was Ti-6Al-4V, material properties and tool parameters were shown in Table 1. Cutting and ultrasonic parameters were shown in Tables 2 and 3. The shear and plow stress were combined by Eq. (23) to obtain the stress of the workpiece under mechanical load. The mechanical stress calculation results were shown in Fig. 17.

Table 1 Workpiece material and tool geometry parameters [32]

Table 2 Numerical simulation processing parameters

Table 3 Numerical simulation ultrasonic parameters

Fig. 17

Numerical simulation results of mechanical stress model a: comparison results of LTUM and TM in less than single tooth cycle, parameters group (a); stress δyy simulation results in LTUM (b)

Figure 17a shows the comparison result of LTUM and TM in less than single tooth cycle with parameters group (a), where, for TM, ultrasonic parameters (in Table 3) are equal to 0. It can be seen that δxx stress fluctuated greatly with ultrasonic vibration in LTUM, but it is closer to a smooth curve in TM; meanwhile, the stress absolute value is larger than that of TM. Figure 17b is stress δyy simulation results in LTUM; as seen, the stress values have an imparity distribution under different parameters.

4.2 Numerical simulation and analysis of thermal stress

According to the established thermal stress model, through parameters in Tables 1–3, workpiece temperature and thermal stress were calculated, as shown in Fig. 18.

Fig. 18

Numerical simulation results of thermal stress model. a Thermal stress comparison results of LTUM and TM; b distribution of the cutting temperature stress in LTUM

Figure 18a is thermal stress comparison result of LTUM and TM with parameters group (c), where, for TM, ultrasonic parameters (Table 3) are equal to 0. It can be seen that thermal stress fluctuates greatly with ultrasonic vibration in LTUM, but it is closer to a smooth curve in TM, meanwhile, the stress absolute value is less than that of TM.

Figure 18b is distribution of the cutting temperature stress in LTUM with parameters group (a); it can be seen that highest temperature is located near the cutting edge and radiated in LTUM, but the temperature distribution is relatively concentrated. Therefore, the influence of thermal stress should be taken into account when analyzing the machining induced RS on the workpiece surface. In the subsurface layer, the effect of thermal stress on the RS is weak. For simplified calculation, the influence of thermal stress can be neglected.

4.3 Numerical simulation and experimental verification of residual stress

4.3.1 Experimental setup

The side-down milling of Ti-6Al-4V experiments were carried out on vertical machining center VMC-850E with dry cutting condition. Self-developed wireless transmission ultrasonic vibration system (as shown in Fig. 19) and cemented carbide UNION four-flute end mill (C-CES 10*25) were adopted, the parameters were listed in Table 4, and Ti-6Al-4V mechanical property parameters were given in Table 5, experimental devices were shown in Fig. 20.

Fig. 19

Longitudinal-torsional ultrasonic vibration system

Table 4 Tool parameters

Table 5 Ti-6Al-4V mechanical property parameters

Fig. 20

Experimental devices

RS was measured with helping of the PROTO X-ray by using XRD method, and Cu target was been chosen; the RS in feed direction is used to evaluate the physical property of machined quality; the average of two measurements results was taken as the results; main measuring parameters of RS were listed in Table 6. Meanwhile, the subsurface RS was measured by stripping the layer through electrolytic polishing method.

Table 6 Measuring parameters of RS.

4.3.2 Results and analysis

According to the established RS model, the parameters of (a) group were selected, and the distribution of RS in the workpiece was calculated by numerical simulation. Firstly, it was compared with the experimental results in TM, as shown in Fig. 21a; secondly, comparison in LTUM was shown in Fig. 21b.

Fig. 21

Simulation results and verification of RS in workpiece: a with TM; b with LTUM

From Fig. 21, the surface RS of workpiece is compressive stress in LTUM and TM, it increases first and then decreases along with depth of workpiece, similar to the “√” shape distribution. Comparing the simulation results of the theoretical model with the experimental results, there are some errors between them; it is mainly due to model cannot cover all the physical parameters in the experiment; on the other hand, the material properties, processing conditions, and tool parameters in model are all in ideal state. However, the properties and distribution trend of RS obtained from the analytical model are well matched with the experimental results in both TM and LTUM; it proves that theoretical model of RS for LTUM is reasonable and reliable for judging and analyzing the properties and distribution of RS.

Moreover, compared with TM, it could be seen that it effectively improved the RCS on surface of workpiece and maximum RCS in the workpiece by LTUM. Meanwhile, it also increased the depth of the maximum RCS layer to a certain extent.

5 Conclusions

In presented work, a machining method of longitudinal-torsion ultrasonic assisted milling (LTUM) is put forward to realize the antifatigue manufacturing of Ti-6Al-4V; for machining-induced residual stress, it is still difficult to predict by theoretical models, especially in ultrasonic-assisted milling. Therefore, a theoretical prediction model of LTUM-induced residual stress is established for the first time, through establishment model of cutting edge trajectory, undeformed chip thickness, mechanical stress, and thermal stress in LTUM. From validation experiments, it is concluded that predicted results are high agreement with experimental results.

• (1) Through cutting edge trajectory model, compared with TM, in LTUM, besides the intermittent cutting caused by tool multiteeth, the workpiece-tool undergoes periodic separation-contact, caused quite different from TM.

• (2) Through undeformed chip thickness model, in LTUM, it is quite different from TM, and it has a great influence on the mechanical, thermal, and residual stresses.

• (3) In LTUM, mechanical stress comes from shear and plow stress; meanwhile, thermal stress comes from shear and plow stress; the biggest difference of mechanical and thermal stress between LTUM and TM is due to the difference from cutting edge trajectory and UCT.

• (4) Based on the elastic-plastic rolling contact model and considering the interaction of mechanical stress and thermal stress, a theoretical model of residual stress in LTUM is established by loading and releasing stress, and the formation mechanism of residual stress in LTUM is revealed.

• (5) From numerical simulation of mechanical stress and thermal stress model, it shows that in LTUM, stress fluctuates with ultrasonic vibration and mechanical stress absolute value is larger than that of TM; thermal stress absolute value is less than that of TM.

• (6) Through experimental verification, it shows that established theoretical model of residual stress predicts properties and distribution of residual stress with high accuracy.