Residual stress prediction in axial ultrasonic vibration–assisted milling in situ TiB₂/7050Al MMCs

Abstract

As a new method developed for machining difficult-to-cut materials, ultrasonic vibration–assisted machining technology not only could be effective in reducing cutting force and temperature but also could be significant in obtaining residual compressive stress. Especially, residual compressive stress is essential to realize anti-fatigue manufacturing for components. However, in recent years, research on residual stresses of ultrasonic vibration–assisted machining mainly focuses on experimental and finite element analysis methods. In this paper, an analytical model was established by considering the effect of ultrasonic vibration to predict residual stresses and reveal the mechanism for UVM of in situ TiB₂/Al-MMCs. And a series of experiments were conducted to verify the residual stress model proposed and analyze the effect of ultrasonic vibration and cutting parameters on the surface residual stress. The results show that the predicted residual stresses are in good agreement with measured residual stress. Cutting parameters have a significant effect on the surface residual stress by influencing cutting force and cutting temperature. Residual compressive stresses could be achieved in both UVM and conventional milling, and residual compressive stresses in the former are larger than that in the latter. With cutting speed and cutting depth increasing, the relative increase ratio between UVM, and CM decreased gradually, while with feed rate increasing, it increased first and then decreased slightly.

1 Introduction

As is well-known, machining residual stress mainly comes from uneven plastic deformation during tool-workpiece contacting, which has a significant influence on the fatigue life, corrosion resistance, and static strength [1,2,3]. With the application of ultrasonic vibration, ultrasonic vibration–assisted machining technology has been regarded as an advanced method to improve surface residual compressive stresses.

Sharma and Pandey [4, 5] pointed out that residual compressive stresses were generated during ultrasonic-assisted turning (UAT) the difficult-to-cut materials, which was important to enhance the fatigue life of aerospace components. Nestler and Schubert [6] found that ultrasonic vibrations in the radial direction and higher ultrasonic amplitude were beneficial for obtaining greater compressive residual stresses in ultrasonic vibration–assisted turning particle reinforced aluminum matrix composites. And the same experimental results were given in the research on surface quality and residual stress study of high-speed ultrasonic vibration turning Ti-6Al-4 V alloys [7]. Iwabe et al. [8] found that residual stresses were generated on the machined surface in both feed and axial direction during ultrasonic vibration side milling, and ultrasonic vibration could improve residual compressive stresses. Chen et al. [9] observed that residual compressive stresses of ultrasonic vibration helical milling (UVHM) were larger than those of helical milling (HM). Especially, surface compressive stresses were increased by 85% and 99% at the hole surface for axial and circumferential directions, respectively. And Zhang et al. [10] found that the compressive residual stress gradually decreased with increasing vibration amplitudes at low cutting speeds during rotary ultrasonic elliptical end milling of Ti-6Al-4 V. However, as the cutting speed increased to 160 m/min, the compressive residual stress increased with increasing amplitude, resulting from comprehensive mechanical deformation and thermal effects. Varun and Pandey [11] conducted an experimental investigation on the effect of cutting and vibration parameters on residual stresses and optimized machining parameters to achieve compressive residual stresses.

Hu et al. [12] adopted the 2D finite element method to analyze the influence of processing parameters and workpiece materials on machining residual stresses. The results showed that the surface residual stresses decreased with ultrasonic vibration frequency increasing, but they increased with spindle speed increasing. Furthermore, a bigger elastic modulus of workpiece material would result in more residual compressive stresses. Maroju and Pasam [13] gave out that residual compressive stresses were more dominant in ultrasonic vibration assisted turning compared to conventional turning Ti6Al4V. Furthermore, a 3D finite element model was proposed to analyze the reason for compressive residual stress generation and distribution.

Analytical mathematical modeling effort has been made to fully address the cutting residual stress generation during the ultrasonic vibration–assisted machining process. Feng et al. [14] analyzed three types of tool-workpiece separation criteria and developed an analytical predictive model to predict residual stresses for ultrasonic vibration–assisted milling. The model was validated by ultrasonic vibration–assisted milling AISI 316L alloy, and it was found that higher ultrasonic vibration amplitude and spindle rotation frequency were significant in obtaining residual compressive stresses. Niu et al. [15] proposed a theoretical prediction model to predict residual stresses in longitudinal-torsional ultrasonic–assisted milling (LTUM) by considering mechanical and thermal stress, and then, the model was validated by experiments on titanium alloy Ti-6Al-4 V. Moreover, it was noted that LTUM could significantly increase surface residual compressive stresses and its layer depth. These models were built based on analyzing the change of cutting tool motion due to ultrasonic vibration. However, the action of the cutting tool on the workpiece was changed during ultrasonic vibration–assisted machining, which has not been taken into consideration. Especially, the impact effect of the cutting tool on the workpiece due to ultrasonic vibration plays an important role in generating residual compressive stresses.

From above, a lot of research on residual stresses in ultrasonic vibration–assisted machining has been investigated through experiments, simulation, and modeling. However, the mechanism of residual stress is complex, and there are still a few attempts to establish an analytical model to predict residual stress in ultrasonic vibration–assisted machining. UVM has shown advantages in reducing tool wear and cutting force, improving machining quality in cutting in-situ TiB₂/7050Al composites, which is a typical difficult-to-cut material [16,17,18]. Due to the application of ultrasonic vibration, intermittent cutting and impact effect has a significant influence on mechanical and thermal stress, which determines residual stress generation. Hence, it is reasonably necessary and important to perform an analytical modeling investigation for ultrasonic vibration–assisted milling in situ TiB₂/7050Al composites for fully and comprehensively understanding the influence of ultrasonic vibration on residual stress generation and distribution.

Therefore, in this paper, an analytical model of residual stress was proposed in UVM in situ TiB₂/7050Al composites. Firstly, cutting force and temperature models were developed by considering the influence of ultrasonic vibration, which would affect mechanical and thermal stress. Then, the impact effect caused by ultrasonic vibration was taken into consideration to establish the residual stress model based on Hertz elastic contact theorem. Finally, the proposed model was validated by UVM experiments on in situ TiB₂/7050Al composites, and the effect of force-temperature coupled-effect on residual stress was analyzed.

2 Modeling of residual stress in UVM

2.1 Mechanical loads considering ultrasonic vibration

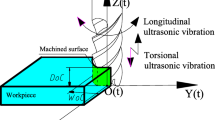
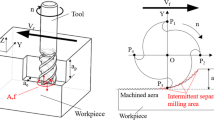
UVM is an advanced machining method that an ultrasonic signal of a sinusoidal wave is added to the milling tool, which is shown in Fig. 1a. The motion of the tool impacts the workpiece during the cutting process. It is quite different from that in conventional milling (CM). Due to the application of ultrasonic vibration, the cutting force in UVM is different from that in CM. As described in Fig. 1b, the forces of the tool in UVM are composed of tangential force F_t, radial force F_r and axial force F_a, which are affected by tool geometry, material properties, cutting parameters and vibration parameters. For exploring the mechanical of cutting force generation in UVM, the cutting edge is discrete into a number of elements, and each element is equivalent to oblique cutting. The cutting force was composed of forces of parallel and vertical cutting speed direction, which is described in Fig. 1c. In this paper, it is mainly considered that cutting force is significantly determined by cutting parameters and vibration parameters, which are expressed as follows:

Fig. 1

Mechanical loads in UVM. a UVM processing. b Force in UVM. c Composition of cutting force

$$\left\{\begin{array}{c}{F}_{t}=f({v}_{c},{f}_{z},{a}_{p},A,f)\\ {F}_{a}=f({v}_{c},{f}_{z},{a}_{p},A,f)\end{array}\right.$$

(1)

where F_t and F_a were the forces of parallel and vertical cutting speed, v_c is the cutting speed, f_z is the feed rate, and a_p is the cutting depth.

Due to the application of ultrasonic vibration, the chip between the rake face and the shear plane is accelerated during the material removal in UVM. Therefore, the inertia force is necessary to be considered in force analysis. Based on Newton’s third law of motion, the forces acted on the chip are shown in Fig. 2.

Fig. 2

Forces acted on the chip in UVM

Then, a new force balance relationship considering the inertia force caused by ultrasonic vibration is established; force components in the Cartesian coordinate system X_nY_nZ_n are expressed as follows:

$${{\varvec{F}}}_{\mathrm{r}}^{\mathrm{^{\prime}}}+{{\varvec{F}}}_{\mathrm{c}}^{\mathrm{^{\prime}}}=M{{\varvec{a}}}_{c}$$

(2)

where F_r^′ is the vector of the reaction of the resultant force applied on the shear plane F_r, F_c^′ is the vector of the reaction of the resultant cutting force F_c, M is the mass of the chip, and a_c is the chip acceleration, which was calculated in Ref. [18].

Furthermore, the instantaneous cutting force in UVM was given out as follows [18]:

$$\left\{\begin{array}{l}{F}_{x}\left(t\right)=\sum\limits_{j=1}^{r}\sum\limits_{k=1}^{N}\left(-{F}_{\mathrm{t}\left(j,k\right)}\mathrm{cos}{\theta }_{j,k}(t)-{F}_{\mathrm{r}\left(j,k\right)}\mathrm{sin}{\theta }_{j,k}(t)\right) \\ {F}_{y}\left(t\right)=\sum\limits_{j=1}^{r}\sum\limits_{k=1}^{N}\left({F}_{\mathrm{t}\left(j,k\right)}\mathrm{sin}{\theta }_{j,k}(t)-{F}_{\mathrm{r}\left(j,k\right)}\mathrm{cos}{\theta }_{j,k}(t)\right) \\ {F}_{z}\left(t\right)={\frac{1}{2}R}_{\mathrm{c}}\sum\limits_{j=1}^{r}\sum\limits_{k=1}^{N}{F}_{a\left(j,k\right)}\end{array}\right.$$

(3)

where θ_j,k(t) is the angular position of the cutting point of the jth slice in the kth flute, which was determined by cutting parameters and tool geometry. The index of the slices j = 1, 2, 3, …, r, where r is the number of the slices. The index of the flutes k = 1, 2, 3, …, N, where N is the number of the teeth of the milling tool, R_c refers to the tool-workpiece contact rate [16], and its coefficient 1/2 means that the tool-workpiece contact time was half vibration period. The cutting force model is essential to provide force data for cutting residual stress calculating.

2.2 Thermal loads in UVM

It is well known that cutting temperature is directly determined by cutting force in mechanical machining. As analyzed in Sect. 2.1, cutting force was obviously influenced by ultrasonic vibration in UVM, which had a further effect on the shear heat intensity q_shear, and it was expressed as follows:

$${q}_{\mathrm{shear}}=\frac{({F}_{\mathrm{t}}\mathrm{cos}\phi -{F}_{a}\mathrm{sin}\phi ){v}_{e}\mathrm{cos}\alpha }{1000\mathrm{d}l\mathrm{csc}\phi \mathrm{cos}(\phi -\alpha )}$$

(4)

where α is the rake angle of the cutting tool, ϕ is the shear angle, and v_e is the instantaneous velocity of the cutting edge element. In this paper, workpiece temperature was induced mainly by considering the effect of the shear heat source and its imaginary heat source, which is shown in Fig. 3. Then, the temperature of an arbitrary point M_(x,y,z) in the workpiece in UVM could be expressed as follow:

Fig. 3

Heat source and image for the workpiece

$${T}_{M(x,y,z)}={T}_{M(x,y,z)}^{\mathrm{shear}}+{T}_{M(x, y,z)}^{\mathrm{image}-s}$$

(5)

where ${T}_{M(x,y,z)}^{\mathrm{shear}}$ is the temperature caused by the shear plane heat source and ${T}_{M(x, y,z)}^{\mathrm{image}-\mathrm{s}}$ is the temperature effected by the imaginary shear heat source.

Furthermore, according to Komanduri and Hou [19], the temperature rise T_{workpiece-shear} caused by the shear heat source and the imaginary heat source for point M_t(x_t, z_t) could be calculated as follow:

$$\left\{\begin{array}{l}{T}_{\mathrm{workpiece}-\mathrm{shear}}=\frac{{B}_{s}{q}_{\mathrm{shear}}}{2\pi {\lambda }_{w}}{\int }_{0}^{L}{e}^{-({x}_{\mathrm{t}}-{l}_{i}\mathrm{cos}\phi ){{v}_{\mathrm{e}}}^{2}/2{a}_{\mathrm{w}}}{\times K}_{0}^{\mathrm{shear}}\frac{{{v}_{\mathrm{e}}}^{2}}{2{a}_{\mathrm{w}}}({R}_{t1}+{R}_{t2})d{l}_{i}\\ {R}_{t1}=\sqrt{{({x}_{\mathrm{t}}-{l}_{i}\mathrm{cos}\phi )}^{2}+{({z}_{\mathrm{t}}+{l}_{i}\mathrm{sin}\phi )}^{2}}\\ {R}_{t2}=\sqrt{{({x}_{\mathrm{t}}-{l}_{i}\mathrm{cos}\phi )}^{2}+{(2{t}_{\mathrm{c}}+{z}_{\mathrm{t}}-{l}_{i}\mathrm{sin}\phi )}^{2}}\end{array}\right.$$

(6)

where B_s stands for heat partition ratio, λ_w is the thermal conductivity of the workpiece, a_w is the thermal diffusion coefficient of the workpiece, and ${\text{K}}_{0}^{\text{shear}}$ denotes the modified Bessel function of the second kind of order zero.

In the same way, the temperature rise on the chip side could be gotten. According to Venuvinod and Lau [20], the heat partition ratio in equivalent oblique cutting could be calculated as follows:

$$\left\{\begin{array}{l}{B}_{s}=\frac{{H}_{\mathrm{c}}}{{H}_{\mathrm{w}}+{H}_{\mathrm{c}}}\\ {H}_{c}={\int }_{0}^{L}{e}^{-\left({x}_{\mathrm{c}}-{L}_{\mathrm{c}}+{l}_{i}\mathrm{sin}\left(\phi -\alpha \right)\right){v}_{\mathrm{ch}}^{{M}_{\mathrm{c}}}/{2a}_{\mathrm{ch}}}\times {K}_{0}^{\mathrm{shear}}\frac{{v}_{\mathrm{ch}}^{{M}_{\mathrm{c}}}}{{2a}_{\mathrm{ch}}}\left({R}_{\mathrm{c}1}+{R}_{\mathrm{c}2}\right){\mathrm{d}l}_{i}\\ {H}_{\mathrm{w}}={\int }_{0}^{L}{e}^{-\left({x}_{\mathrm{t}}-{l}_{i}\mathrm{cos}\phi \right){v}_{\mathrm{e}}/{2a}_{\mathrm{w}}}\times {K}_{0}^{\mathrm{shear}}\frac{{v}_{\mathrm{e}}}{{2a}_{\mathrm{w}}}\left({R}_{\mathrm{t}1}+{R}_{\mathrm{t}2}\right){\mathrm{d}l}_{i}\end{array}\right.$$

(7)

where ${v}_{\mathrm{ch}}^{{M}_{\mathrm{c}}}$ stands for the flow velocity of the chip and a_ch is the thermal diffusion coefficient of the chip.

2.3 Contact modeling

During the cutting process, contact of tool-workpiece could be regarded as a cylinder rolling on a semi-infinite plane, which is described in Fig. 4a. Furthermore, the contact zone of the tool-workpiece is much smaller than the workpiece dimension, and the machined surface could be taken as a semi-infinite elastic solid of a boundary. According to Hertz’s contact theory, instantaneous stress in workpiece could be calculated as follow:

Fig. 4

Contact model. a Tool-workpiece contact. b Model of half-space distributed load

$$\left\{\begin{array}{l}{\sigma }_{xx}=-\frac{2z}{\uppi }{\int }_{-a}^{a}\frac{p(s){(x-s)}^{2}}{{[{\left(x-s\right)}^{2}+{z}^{2}]}^{2}}\mathrm{d}s-\frac{2}{\pi }{\int }_{-a}^{a}\frac{q(x){(x-s)}^{3}}{{[{\left(x-s\right)}^{2}+{z}^{2}]}^{2}}\mathrm{d}s\\ {\sigma }_{zz}=-\frac{2{z}^{3}}{\uppi }{\int }_{-a}^{a}\frac{p\left(s\right)}{{\left[{\left(x-s\right)}^{2}+{z}^{2}\right]}^{2}}\mathrm{d}s-\frac{2{z}^{2}}{\uppi }{\int }_{-a}^{a}\frac{q(x)(x-s)}{{\left[{\left(x-s\right)}^{2}+{z}^{2}\right]}^{2}}\mathrm{d}s\\ {\tau }_{xz}=-\frac{2{z}^{2}}{\uppi }{\int }_{-a}^{a}\frac{p\left(s\right)\left(x-s\right)}{{\left[{\left(x-s\right)}^{2}+{z}^{2}\right]}^{2}}\mathrm{d}s-\frac{2z}{\pi }{\int }_{-a}^{a}\frac{q(s){(x-s)}^{2}}{{\left[{\left(x-s\right)}^{2}+{z}^{2}\right]}^{2}}\mathrm{d}s\end{array}\right.$$

(8)

where p(s) is the normal distribution loading, q(s) is the tangential distribution loading, a is approximated as one half the length of tool-workpiece contact, and x and z is the coordinate of an arbitrary point M in the workpiece, which is shown in Fig. 4b.

2.4 Mechanical stress in UVM

Cutting residual stress is generated because of non-uniform plastic deformation, which is dramatically determined by the couple effect of force-temperature between the cutting tool and workpiece during machining. Due to radial force being parallel to the cutting edge, normal and shear stress is caused by tangential force and axial force in the shear zone, which is presented in Fig. 5. Furthermore, in the third deformation zone, stress results from the axial impact effect generated by ultrasonic vibration. Moreover, it is assumed that normal and shear stresses are uniformly distributed on the shear plane and tool-edge impacting zone. Hence, the internal stress of an arbitrary point in the workpiece resulting from mechanical stress could be described as follows:

Fig. 5

Mechanical stress in UVM

$${{\varvec{\sigma}}}^{\mathrm{mech}}={{\varvec{\sigma}}}^{\mathrm{shear}}+{{\varvec{\sigma}}}^{\mathrm{impact}}$$

(9)

2.4.1 Shear stress in UVM

Normal stress is perpendicular to the shear plane in the shear zone, and shear stress is parallel to the shear plane. These would directly influence the internal stress of the workpiece, which is shown in Fig. 6.

Fig. 6

Internal stress induced by shear stress source

Therefore, normal stress p_shear and shear stress q_shear in the shear plane could be calculated as follows:

$$\left\{\begin{array}{l}{p}_{\mathrm{shear}}=\frac{{F}_{\mathrm{t}}\mathrm{sin}\phi {+F}_{\mathrm{a}}\mathrm{cos}\phi }{Lw}\\ {q}_{\mathrm{shear}}={\tau }_{\mathrm{s}}=\frac{\sigma }{\sqrt{3}}\end{array}\right.$$

(10)

where L and w are the length and width of the shear plane, τ_s is the shear yield strength of workpiece material, and σ is the flow stress of the material which is applied modified Johnson–Cook (JC) model by Lin [21]:

$$\upsigma =\left({A}_{c}+B{\varepsilon }^{n}\right)\left(1+Cln\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\right)\left[1-{\left(\frac{T-{T}_{\mathrm{r}}}{{T}_{\mathrm{m}}-{T}_{\mathrm{r}}}\right)}^{m}\right]$$

(11)

where A_c, B, C, m, and n are constants of the workpiece materials; ε is the strain of the material; $\dot{\varepsilon }$ is the strain rate; and $\dot{{\varepsilon }_{0}}$ is the reference strain rate. Then, the internal stress of the workpiece induced by shear stress is simplified as in Fig. 3, which could be calculated by substituting Eq. (3) into Eq. (1). And the internal stress of arbitrary point in the workpiece coordinate system XOZ could be obtained by transformation, which is described as follow:

$${{\varvec{\sigma}}}^{\mathrm{shear}}=\left[\begin{array}{cc}{\sigma }_{xx}^{\mathrm{shear}}& {\tau }_{xz}^{\mathrm{shear}}\\ {\tau }_{zx}^{\mathrm{shear}}& {\sigma }_{zz}^{\mathrm{shear}}\end{array}\right]={{\varvec{Q}}}^{\mathrm{T}}\left[\begin{array}{cc}{\sigma }_{{x}_{1}{x}_{1}}^{\mathrm{shear}}& {\tau }_{{x}_{1}{z}_{1}}^{\mathrm{shear}}\\ {\tau }_{{z}_{1}{x}_{1}}^{\mathrm{shear}}& {\sigma }_{{z}_{1}{z}_{1}}^{\mathrm{shear}}\end{array}\right]{\varvec{Q}}$$

(12)

where ${\sigma }_{{x}_{1}{x}_{1}}^{\mathrm{shear}}$, ${\sigma }_{{z}_{1}{z}_{1}}^{\mathrm{shear}}$, ${\tau }_{{x}_{1}{z}_{1}}^{\mathrm{shear}}$, and ${\tau }_{{z}_{1}{x}_{1}}^{\mathrm{shear}}$ are the stress induced by shear stress source in the coordinate system X₁O₁Z₁ and Q is the transformation matrix which is expressed as follows:

$${\varvec{Q}}=\left[\begin{array}{cc}\mathrm{cos}\phi & -\mathrm{sin}\phi \\ \mathrm{sin}\phi & \mathrm{cos}\phi \end{array}\right]$$

(13)

2.4.2 Impact stress in UVM

In the tertiary deformation zone, due to the application of ultrasonic vibration, the cutting tool would impact the machined surface periodically, which could be seen from Fig. 7a. Due to the cutting edge radius, the contact between the cutting tool and workpiece could be approximate to contact type in ultrasonic-assisted burnishing, which is shown in Fig. 7b. Deformation of the contact zone is small; stresses could be simplified normal stress p_impact perpendicular to contact surface and tangential stress q_impact parallel to contact surface, which is shown in Fig. 7c.

Fig. 7

Impact stress simplified process. a Impact effect of ultrasonic vibration. b Contact model approximation. c Impact stress simplification

Based on the research [22], normal stress p_impact and tangential stress q_impact could be calculated as follow:

$$\left\{\begin{array}{l}{p}_{\mathrm{impact}}=\frac{4}{\uppi }{(5{\uppi }^{3}{\rho }_{\mathrm{t}}{E}_{\mathrm{eq}}{A}^{2}{f}^{2})}^\frac{1}{5}\\ {q}_{\mathrm{impact}}=\mu {p}_{\mathrm{impact}}\end{array}\right.$$

(14)

where ρ_t is density of the tool, μ is the sliding friction coefficient, E_eq is equivalent elasticity modulus which is given out as follows:

$${E}_{\mathrm{eq}}=\frac{1-{\nu }_{w}^{2}}{{E}_{w}}+\frac{1-{\nu }_{t}^{2}}{{E}_{t}}$$

(15)

where E_w and E_t are the elasticity modulus of the workpiece material and cutting tool and ν_w and ν_t are the Poisson ratio of the workpiece material and cutting tool. Furthermore, the internal stress of the arbitrary point induced by the impact effect in the tertiary deformation zone could be calculated by substituting Eq. (4) into Eq. (1), whose component could be expressed as follow:

$${{\varvec{\sigma}}}^{\mathrm{impact}}=\left[\begin{array}{cc}{\sigma }_{xx}^{\mathrm{impact}}& {\tau }_{xz}^{\mathrm{impact}}\\ {\tau }_{zx}^{\mathrm{impact}}& {\sigma }_{zz}^{\mathrm{impact}}\end{array}\right]$$

(16)

2.5 Thermal stress in UVM

On the other hand, thermal stress mainly comes from temperature gradient, which also would have an influence on internal stress distribution. The temperature of an arbitrary point in the workpiece is known; then, the thermal stress could be obtained. In UVM, thermal stress consists of three parts: thermal stress induced by body-force, surface tension, and hydrostatic pressure. Thermal stress induced by body-force could be expressed as follow [14]:

$$\left\{\begin{array}{c}{\sigma }_{xx}^{\mathrm{v}}=-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}}{1-2{\nu }_{\mathrm{w}}}\cdot \frac{\partial T}{\partial x}\\ {\sigma }_{zz}^{\mathrm{v}}=-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}}{1-2{\nu }_{\mathrm{w}}}\cdot \frac{\partial T}{\partial z}\end{array}\right.$$

(17)

Surface tension could be calculated as following:

$${\sigma }^{\mathrm{s}}=\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}T}{1-2{\nu }_{\mathrm{w}}}$$

(18)

Hydrostatic pressure could be given out as follow:

$${\sigma }^{\mathrm{h}}=\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}T}{1-2{\nu }_{\mathrm{w}}}$$

(19)

Therefore, the total thermal stress would be performed as follows:

$$\left\{\begin{array}{c}{\sigma }_{xx}^{\mathrm{therm}}\left(x,z\right)=-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}}{1-2{\nu }_{\mathrm{w}}}{\int }_{0}^{\infty }{\int }_{-\infty }^{\infty }\begin{array}{c}\left({G}_{\mathrm{xh}}\frac{\partial T}{\partial x}\left(x,z\right)+{G}_{\mathrm{xv}}\frac{\partial T}{\partial x}\left(x,z\right)\right)dxdz\end{array}\\ +\frac{2z}{\uppi }{\int }_{-\infty }^{\infty }\frac{p(t){(t-x)}^{2}}{{\left({\left(t-x\right)}^{2}+{z}^{2}\right)}^{2}}\mathrm{d}t-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}T}{1-2{\nu }_{\mathrm{w}}}\\ {\sigma }_{zz}^{\mathrm{therm}}\left(x,z\right)=-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}}{1-2{\nu }_{\mathrm{w}}}{\int }_{0}^{\infty }{\int }_{-\infty }^{\infty }\begin{array}{c}\left({G}_{\mathrm{zh}}\frac{\partial T}{\partial x}\left(x,z\right)+{G}_{\mathrm{zv}}\frac{\partial T}{\partial x}\left(x,z\right)\right)dxdz\end{array}\\ +\frac{2{z}^{3}}{\uppi }{\int }_{-\infty }^{\infty }\frac{p(t)}{{\left({\left(t-x\right)}^{2}+{z}^{2}\right)}^{2}}\mathrm{d}t-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}T}{1-2{\nu }_{\mathrm{w}}}\\ {\sigma }_{xz}^{\mathrm{therm}}\left(x,z\right)=-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}}{1-2{\nu }_{\mathrm{w}}}{\int }_{0}^{\infty }{\int }_{-\infty }^{\infty }\begin{array}{c}\left({G}_{\mathrm{xzh}}\frac{\partial T}{\partial x}\left(x,z\right)+{G}_{\mathrm{xzv}}\frac{\partial T}{\partial x}\left(x,z\right)\right)dxdz\end{array}\\ +\frac{2{z}^{2}}{\uppi }{\int }_{-\infty }^{\infty }\frac{p(t)(x-t)}{{\left({\left(t-x\right)}^{2}+{z}^{2}\right)}^{2}}\mathrm{d}t-\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}T}{1-2{\nu }_{\mathrm{w}}}\end{array}\right.$$

(20)

where a_w is the thermal diffusivity; G_xh, G_xv, G_zh, G_zv, G_xzh, and G_xzv are Green’s function of plane strain; and p(t) is the stress resulting from the surface temperature, which could be expressed as follow:

$$p\left(t\right)=\frac{{a}_{\mathrm{w}}{E}_{\mathrm{w}}T(x,z=0)}{1-2{\nu }_{\mathrm{w}}}$$

(21)

Hence, the total thermal stress would be described as follow:

$${{\varvec{\sigma}}}^{\mathrm{therm}}=\left[\begin{array}{cc}{\sigma }_{xx}^{\mathrm{therm}}& {\sigma }_{xz}^{\mathrm{therm}}\\ {\sigma }_{zx}^{\mathrm{therm}}& {\sigma }_{zz}^{\mathrm{therm}}\end{array}\right]$$

(22)

2.6 Residual stress in UVM

2.6.1 Stress loading

During the ultrasonic vibration cutting process, as shown in Fig. 8, an arbitrary point M of the workpiece would experience elastic deformation, plastic deformation, and elastic–plastic deformation during the cutting tool travels from B to E. And the total stress resulting from the deformation could be expressed as follows:

Fig. 8

Loading–unloading processes during machining

$${{{\varvec{\sigma}}}^{\mathrm{total}}={\varvec{\sigma}}}^{\mathrm{mech}}+{{\varvec{\sigma}}}^{\mathrm{therm}}={{\varvec{\sigma}}}^{\mathrm{shear}}+{{\varvec{\sigma}}}^{\mathrm{impact}}+{{\varvec{\sigma}}}^{\mathrm{therm}}$$

(23)

Then, it is needed to judge deformation type according to stress state at the end of each loading step. It is assumed that the workpiece is isotropic; the von Mises criterion could be used to estimate the stress state, which is described as follows [3]:

$$F\left({\sigma }_{ij}\right)=\frac{1}{2}\left({S}_{ij}-{\alpha }_{ij}\right)\left({S}_{ij}-{\alpha }_{ij}\right)-{\tau }_{s}^{2}$$

(24)

where S_ij and α_ij are deviatoric and back stresses respectively, which are given out as follows:

$$\left\{\begin{array}{l}{S}_{ij}={\sigma }_{ij}-\frac{1}{3}{\sigma }_{kk}{\delta }_{ij}\\ {\alpha }_{ij}=\langle {S}_{kl}{n}_{kl}\rangle {n}_{ij}\end{array}\right.$$

(25)

where δ_ij is the Kronecker symbol and $\langle \rangle$ is the MacCauley symbol whose mathematical definition is $\langle x\rangle =0.5\left(x+\left|x\right|\right)$. And n_ij is the component of unit normal in plastic strain rate direction, which is expressed as follows:

$${n}_{ij}=\frac{{S}_{ij}-{\alpha }_{ij}}{\sqrt{2}{\tau }_{s}}$$

(26)

During the elastic deformation process, when F(σ_ij) < 0, the stress of point M is less than yield strength, stress tensor could be expressed as follow:

$$\left\{\begin{array}{l}{\sigma }_{xx}^{\mathrm{elastic}}={\sigma }_{xx}^{\mathrm{shear}}+{\sigma }_{xx}^{\mathrm{impact}}+{\sigma }_{xx}^{\mathrm{therm}}\\ {\sigma }_{zz}^{\mathrm{elastic}}={\sigma }_{zz}^{\mathrm{shear}}+{\sigma }_{zz}^{\mathrm{impact}}+{\sigma }_{zz}^{\mathrm{therm}}\\ {\tau }_{xz}^{\mathrm{elastic}}={\tau }_{xz}^{\mathrm{shear}}+{\tau }_{xz}^{\mathrm{impact}}+{\tau }_{xz}^{\mathrm{therm}}\\ {\sigma }_{yy}^{\mathrm{elastic}}={\nu }_{\mathrm{w}}\left({\sigma }_{xx}^{\mathrm{elastic}}+{\sigma }_{zz}^{\mathrm{elastic}}\right)-{a}_{\mathrm{w}}{E}_{\mathrm{w}}T(x,z)\end{array}\right.$$

(27)

where ${\sigma }_{xx}^{\mathrm{elastic}}$, ${\sigma }_{yy}^{\mathrm{elastic}}$, ${\sigma }_{zz}^{\mathrm{elastic}}$, and ${\tau }_{xz}^{\mathrm{elastic}}$ are the elastic stress in the X-direction, Y-direction, Z-direction, and XZ-direction. Moreover, based on Hooke’s law, strain tensors are given out as follows:

$$\left\{\begin{array}{l}{\varepsilon }_{xx}^{\mathrm{elastic}}=\frac{1}{{E}_{\mathrm{w}}}\left({\sigma }_{xx}^{\mathrm{elastic}}-{\nu }_{\mathrm{w}}\left({\sigma }_{yy}^{\mathrm{elastic}}+{\sigma }_{zz}^{\mathrm{elastic}}\right)\right)\\ {\varepsilon }_{yy}^{\mathrm{elastic}}=\frac{1}{{E}_{\mathrm{w}}}\left({\sigma }_{yy}^{\mathrm{elastic}}-{\nu }_{\mathrm{w}}\left({\sigma }_{xx}^{\mathrm{elastic}}+{\sigma }_{zz}^{\mathrm{elastic}}\right)\right)\\ {\varepsilon }_{zz}^{\mathrm{elastic}}=\frac{1}{{E}_{\mathrm{w}}}\left({\sigma }_{zz}^{\mathrm{elastic}}-{\nu }_{\mathrm{w}}\left({\sigma }_{xx}^{\mathrm{elastic}}+{\sigma }_{yy}^{\mathrm{elastic}}\right)\right)\\ {\gamma }_{yz}^{\mathrm{elastic}}=G{\tau }_{yz}^{\mathrm{elastic}}\\ {\gamma }_{xz}^{\mathrm{elastic}}=G{\tau }_{xz}^{\mathrm{elastic}}\\ {\gamma }_{xy}^{\mathrm{elastic}}=G{\tau }_{xy}^{\mathrm{elastic}}\end{array}\right.$$

(28)

where ${\varepsilon }_{xx}^{\mathrm{elastic}}$, ${\varepsilon }_{yy}^{\mathrm{elastic}}$, ${\varepsilon }_{zz}^{\mathrm{elastic}}$, ${\gamma }_{yz}^{\mathrm{elastic}}$, ${\gamma }_{xz}^{\mathrm{elastic}}$ and ${\gamma }_{xy}^{\mathrm{elastic}}$ are the strain in the X-direction, Y-direction, Z-direction, YZ-direction, XZ-direction and XY-direction. And G is the elastic shear modulus, which is given as follows:

$$G=\frac{{E}_{\mathrm{w}}}{2(1+{\nu }_{\mathrm{w}})}$$

(29)

During the plastic deformation process, when F(σ_ij) = 0, the stress of point M is more than yield strength, plastic deformation of workpiece occurs. In general, the McDowell hybrid algorithm was applied to calculate plastic stress components [23]. Meanwhile, the strain rate in the Y-direction is 0 based on the plane-strain condition. The strain rates in UVM could be obtained as follow:

$$\left\{\begin{array}{c}\mathrm{d}{\varepsilon }_{xx}=\frac{1}{{E}_{\mathrm{w}}}\left(\mathrm{d}{\sigma }_{xx}^{\mathrm{plastic}}-{\nu }_{w}\left(\mathrm{d}{\sigma }_{yy}^{\mathrm{plastic}}+\mathrm{d}{\sigma }_{zz}^{\mathrm{elastic}}\right)\right)+{a}_{\mathrm{w}}\mathrm{d}T \\ +\frac{1}{{h}_{\mathrm{s}}}\left({n}_{xx}\mathrm{d}{\sigma }_{xx}^{\mathrm{plastic}}+{n}_{yy}\mathrm{d}{\sigma }_{yy}^{\mathrm{plastic}}+{n}_{zz}\mathrm{d}{\sigma }_{zz}^{\mathrm{elastic}}\right.\left.+2{n}_{xz}\mathrm{d}{\tau }_{xz}^{\mathrm{elastic}}\right){n}_{xx}\\ =\psi \left[\frac{1}{{E}_{\mathrm{w}}}\right.\left(\mathrm{d}{\sigma }_{xx}^{\mathrm{elastic}}-{\nu }_{\mathrm{w}}\left(\mathrm{d}{\sigma }_{yy}^{\mathrm{plastic}}+\mathrm{d}{\sigma }_{zz}^{\mathrm{elastic}}\right)\right) \\ +\frac{1}{{h}_{\mathrm{s}}}\left({n}_{xx}d{\sigma }_{xx}^{\mathrm{elastic}}\right.+{n}_{yy}d{\sigma }_{yy}^{\mathrm{plastic}}+{n}_{zz}d{\sigma }_{zz}^{\mathrm{elastic}} \left.\left.+2{n}_{xz}d{\tau }_{xz}^{\mathrm{elastic}}\right){n}_{xx}\right]\\ d{\varepsilon }_{yy}=\frac{1}{{E}_{\mathrm{w}}}\left(d{\sigma }_{yy}^{\mathrm{plastic}}-{\nu }_{w}\left(d{\sigma }_{xx}^{\mathrm{plastic}}+d{\sigma }_{zz}^{\mathrm{elastic}}\right)\right)+{a}_{\mathrm{w}}dT \\ +\frac{1}{{h}_{\mathrm{s}}}\left({n}_{xx}d{\sigma }_{xx}^{\mathrm{plastic}}+{n}_{yy}d{\sigma }_{yy}^{\mathrm{plastic}}+{n}_{zz}d{\sigma }_{zz}^{\mathrm{elastic}}\right.\left.+2{n}_{xz}d{\tau }_{xz}^{\mathrm{elastic}}\right){n}_{yy}=0\end{array}\right.$$

(30)

where h_s is the plastic modulus of workpiece material, $d{\sigma }_{xx}^{plastic}$ $d{\sigma }_{yy}^{plastic}$ are the plastic stress in X-direction and Y-direction which could be derived by solving the system of linear Eq. (19), and ψ is a blending function which is expressed as follows:

$$\psi =1-\mathrm{exp}\left(-\kappa \frac{3}{2}\frac{{h}_{\mathrm{s}}}{G}\right)$$

(31)

where κ is the algorithm constant.

2.6.2 Stress releasing

After the stress loading process, the stress equilibrium condition is not satisfied; the residual stress could be obtained by stress releasing. The residual stress and strain would meet the followed boundary conditions [24]:

$$\left\{\begin{array}{l}{\sigma }_{xx}^{\mathrm{r}}={f}_{1}\left(z\right), {\sigma }_{yy}^{\mathrm{r}}={f}_{2}\left(z\right), {\varepsilon }_{zz}^{\mathrm{r}}={f}_{3}\left(z\right), {\gamma }_{xz}^{\mathrm{r}}={f}_{4}(z)\\ {\sigma }_{zz}^{\mathrm{r}}={\tau }_{xz}^{\mathrm{r}}={\tau }_{xy}^{\mathrm{r}}={\tau }_{yz}^{\mathrm{r}}=0, {\varepsilon }_{xx}^{\mathrm{r}}={\varepsilon }_{yy}^{\mathrm{r}}={\gamma }_{xy}^{\mathrm{r}}={\gamma }_{yz}^{\mathrm{r}}=0, {T}^{r}=0\end{array}\right.$$

(32)

where f(z) stands for a nonzero parameter which is associated with z and T^r is the temperature at the beginning of the relaxation procedure. To meet the boundary condition, nonzero stress components would be required to release being 0 gradually. It is assumed that the relaxation procedure is done in Q steps; the stress and strain increments could be calculated by:

$$\begin{array}{l}\Delta {\sigma }_{zz}^{\mathrm{r}}=-\frac{{\sigma }_{xx}^{\mathrm{r}}}{Q},\Delta {\tau }_{xz}^{\mathrm{r}}=-\frac{{\tau }_{xz}^{\mathrm{r}}}{Q},\Delta {\varepsilon }_{xx}^{\mathrm{r}}=-\frac{{\varepsilon }_{xx}^{\mathrm{r}}}{Q},\Delta {T}^{\mathrm{r}}=-\frac{{T}^{\mathrm{r}}}{Q}\\ \end{array}$$

(33)

During stress releasing process, it is necessary to confirm the stress relaxation type. When F(σ_ij) < 0, elastic stress relaxation occurs; stress increments of relaxation could be given out based on Hooke’s law, which is given out as following:

$$\left\{\begin{array}{l}\Delta {\sigma }_{xx}=\frac{{E}_{\mathrm{w}}\Delta {\varepsilon }_{xx}^{\mathrm{r}}+\left(1+{\nu }_{\mathrm{w}}\right)\left({\nu }_{\mathrm{w}}\Delta {\sigma }_{zz}^{\mathrm{r}}-{E}_{\mathrm{w}}{\alpha }_{\mathrm{w}}\Delta {T}^{\mathrm{r}}\right)}{1-{\nu }_{\mathrm{w}}^{2}}\\\Delta {\sigma }_{yy}=\frac{{{\nu }_{\mathrm{w}}E}_{\mathrm{w}}\Delta {\varepsilon }_{xx}^{\mathrm{r}}+\left(1+{\nu }_{\mathrm{w}}\right)\left({\nu }_{\mathrm{w}}\Delta {\sigma }_{zz}^{\mathrm{r}}-{E}_{\mathrm{w}}{\alpha }_{\mathrm{w}}\Delta {T}^{\mathrm{r}}\right)}{1-{\nu }_{\mathrm{w}}^{2}}\end{array}\right.$$

(34)

When F(σ_ij) = 0 and dS_ijn_ij < 0, elastic–plastic stress relaxation occurs; stress increments could be calculated as follows:

$$\left\{\begin{array}{l}\Delta {\sigma }_{xx}=\frac{D-\left(\frac{1}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{yy}{n}_{yy}\right)\Delta {\sigma }_{yy}-{\alpha }_{\mathrm{w}}\Delta {T}^{\mathrm{r}}}{-\frac{{\nu }_{\mathrm{w}}}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{xx}{n}_{yy}}\\\Delta {\sigma }_{yy}=\frac{\left(-\frac{{\nu }_{\mathrm{w}}}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{xx}{n}_{yy}\right)\left(C-{\alpha }_{\mathrm{w}}\Delta {T}^{\mathrm{r}}\right)-\left(\frac{1}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{xx}{n}_{xx}\right)\left(D-{\alpha }_{\mathrm{w}}\Delta {T}^{\mathrm{r}}\right)}{{\left(-\frac{{\nu }_{\mathrm{w}}}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{xx}{n}_{yy}\right)}^{2}-\left(\frac{1}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{xx}{n}_{xx}\right)\left(\frac{1}{{E}_{\mathrm{w}}}+\frac{1}{{h}_{\mathrm{s}}}{n}_{yy}{n}_{yy}\right)}\end{array}\right.$$

(35)

where

$$\left\{\begin{array}{l}C=\Delta {\varepsilon }_{xx}^{\mathrm{r}}+\left(\frac{{\nu }_{\mathrm{w}}}{{E}_{\mathrm{w}}}-\frac{1}{{h}_{\mathrm{s}}}{n}_{xx}{n}_{zz}\right)\Delta {\sigma }_{zz}^{\mathrm{elastic}}-\frac{2}{{h}_{\mathrm{s}}}\Delta {\tau }_{xz}^{\mathrm{elastic}}{n}_{xz}{n}_{xx}\\ D=\left(\frac{{\nu }_{\mathrm{w}}}{{E}_{\mathrm{w}}}-\frac{1}{{h}_{\mathrm{s}}}{n}_{yy}{n}_{zz}\right)\Delta {\sigma }_{zz}^{\mathrm{elastic}}-\frac{2}{{h}_{\mathrm{s}}}\Delta {\tau }_{xz}^{\mathrm{elastic}}{n}_{xz}{n}_{yy}\end{array}\right.$$

(36)

The final residual stress in ultrasonic vibration–assisted milling would be obtained when all loading cycles are completed. Calculation of the residual stress is shown in the flow chart in Fig. 9.

Fig. 9

The flow chart of residual stress calculation

3 Experiments

3.1 Materials and tool

In order to validate the residual stress model, a set of down milling experiments were performed on the material of 6 wt% in situ TiB₂/7050Al MMCs, the mechanical and physical properties of the material are shown in Table 1, and material’s constitutive parameters are presented in Table 2. Cutting tools used were TiAlN coated carbide end milling tools with a diameter of 7 mm and 4 flutes, whose specifications and mechanical properties are shown in Table 3.

Table 1 Mechanical and physical properties of TiB₂/7050Al MMCs

Table 2 Material’s constitutive parameters of TiB₂/7050Al MMCs [21]

Table 3 Specifications and mechanical properties of coated carbide milling tool

3.2 Testing and measuring

All experiments were done on a CY-VMC850 machine under dry machining condition, as shown in Fig. 6 (Fig. 10). The ultrasonic vibration system is mainly composed of ultrasonic generator, non-contact electromagnetic unit, ultrasonic tool holder and fixing ring. UVM and CM were carried out by controlling the ultrasonic generator. During the milling process, the cutting force was measured using a 9255B Kistler dynamometer, and the cutting temperature was obtained with a semi-artificial thermocouple. After all experiments, the machined surface residual stresses were measured using a Proto LXRD MG2000, which is shown in Fig. 11. And the residual stress distribution under the machined surface was measured after electrolytic polishing with a solution of HCl:HF:H₂O = 2:3:95 by the Proto 8818-V3 (60 s for peeling 5 μm), which is shown in Fig. 12.

Fig. 10

Schematic diagram of experimental setup

Fig. 11

Residual stress testing

Fig. 12

Electrolytic polishing

3.3 Experimental design

The cutting force and temperature are validated in Tables 4 and 5. The detailed residual stress model validating is listed in Table 6; the effect of cutting parameters on machined surface residual stress with and without ultrasonic vibration is designed in Table 7.

Table 4 Experimental parameters for cutting force prediction validating [18]

Table 5 Experimental parameters for cutting temperature prediction validating [25]

Table 6 Experimental parameters for residual stress model validating

Table 7 Cutting parameters for effect on machined surface residual stress in UVM

4 Results and discussions

The predicted cutting force validation is shown in Fig. 13. It could be seen that the predicted cutting forces were in good agreement with the measured cutting forces in tendency and peak value of forces. It indicated that the cutting force model could be used to provide force data for residual stress calculating in UVM. In addition, it could be found that cutting forces in UVM were smaller than that in CM. Previous research [18] showed that ultrasonic vibration could reduce the cutting force in the machining process. Furthermore, it indicates that ultrasonic vibration has a significant influence on the residual stress in UVM.

Fig. 13

Cutting force prediction. a Test #1 (UVM). b Test #2 (CM)

During residual stress modeling, cutting temperature is one of the important factors to be considered. In this work, the cutting temperature model was used to provide temperature data. And the cutting temperature validation is shown in Fig. 14. It has shown a good concordance of the predicted values with the experimental ones, and the relative error is less than 16%. This indicates that the temperature model has better accuracy for temperature prediction and could be used for residual stress calculating.

Fig. 14

Cutting temperature prediction

Furthermore, the ultrasonic vibration–assisted cutting residual stress model was validated by experiments for UVM in situ TiB₂/7050Al MMCs, and the results are shown in Fig. 15 and Table 8. In Fig. 15a, the measured and predicted maximum ultrasonic vibration–assisted cutting residual stresses were − 144.54 MPa and − 155.38 MPa, respectively, and the relative error was 7.5%. And the depth of compressive residual stress layer corresponding measurement and prediction was 60 μm and 75 μm. In Fig. 15b, the measured and predicted maximum ultrasonic vibration–assisted cutting residual stresses were − 197.64 MPa and − 232.88 MPa, respectively, and the relative error was 17.8%. And the depth of compressive residual stress layer corresponding measurement and prediction was 60 μm and 90 μm. In Fig. 15c, the measured and predicted maximum ultrasonic vibration–assisted cutting residual stresses were − 205.88 MPa and − 246.57 MPa, respectively, and the relative error was 19.8%. And the depth of compressive residual stress layer corresponding measurement and prediction was 90 μm and 105 μm. In Fig. 15d, the measured and predicted maximum ultrasonic vibration–assisted cutting residual stresses were − 198.06 MPa and − 230.96 MPa, respectively, and the relative error was 16.6%. And the depth of compressive residual stress layer corresponding measurement and prediction was 90 μm and 90 μm. It can be seen that maximum compressive stress measured and predicted was on the machined surface, and it decreased with exponential type along the cutting depth direction.

Fig. 15

Validation of cutting residual stress distribution in UVM. a v_c = 45 m/min, f_z = 0.07 mm/z, a_p = 0.8 mm, f = 30 kHz, A = 3 μm. b v_c = 30 m/min, f_z = 0.03 mm/z, a_p = 0.5 mm, f = 30 kHz, A = 4 μm. c v_c = 30 m/min, f_z = 0.07 mm/z, a_p = 0.5 mm, f = 30 kHz, A = 3 μm. (d) v_c = 15 m/min, f_z = 0.05 mm/z, a_p = 0.8 mm, f = 30 kHz, A = 4 μm

Table 8 Surface residual stress of model prediction and experiments

The results presented in Table 8 indicated that some relative error below 20% existed between the theoretical calculation and experimental measurement. However, the distribution and variation of predicted results were in good agreement with measured results. In this paper, there are two primary sources of error: model error and measuring error. During modeling, the analytical method was used, and there were some simplifications and assumptions, which is the reason for the model error. In addition, the accuracy of equipment and process of measurement has a significant influence on the measured residual stress, which would result in measuring error.

The residual stress is produced mainly because of materials' plastic deformation, which is significantly influenced by mechanical-thermal coupling. The cutting parameters affect the residual stress during the metal cutting process by influencing the cutting force and temperature. Figure 16 shows the influence of cutting parameters on the residual stress for UVM in situ TiB₂/7050Al MMCs with an ultrasonic frequency of 30 kHz and amplitude of 4 μm.

Fig. 16

Influence of force-temperature on the machined surface residual stress in UVM. a Effect of cutting speed. b Effect of feed rate. c Effect of cutting depth

From Fig. 16a, the residual compressive stress is decreased significantly with the cutting speed increasing. Because the cutting force is reduced and the cutting temperature is increased with an increase of cutting speed, which would result in the burning effect reducing and the thermal effect increasing. The coupling effect of mechanical-thermal leads to a reduction of residual compressive stress. From Fig. 16 b and c, it can be seen that the residual compressive stress is first increased slightly and then decreased slowly with the feed rate and cutting depth increasing. It might be that the cutting force and temperature are increased gradually with the feed rate and cutting depth increasing. When the feed rate and cutting depth are small, the increase of cutting force is more significant than that of cutting temperature, and the mechanical effect plays a major role; when the feed rate and cutting depth increase to a certain value, an increase of cutting temperature is more obvious than that of cutting force, the thermal effect plays a leading role. In brief, the residual stress is significantly influenced by the coupled effect of mechanical-thermal.

In this paper, the cutting residual stresses between UVM and CM were comparatively analyzed by conducting experiments on in situ TiB₂/7050Al MMCs, and the results are shown in Fig. 17. It can be seen that residual compressive stresses are produced in the UVM and CM, and the value of residual compressive stresses in the former are larger than that in the latter. It indicates that ultrasonic vibration is conducive to increasing residual compressive stress during machining. In this paper, the residual compressive stress in UVM could be improved by 9.9 ~ 37.3%. The reason for this might be that tool wear and cutting temperature are reduced because of ultrasonic vibration [26]. Under the same cutting condition, tool wear is worn slower, and the cutting edge is sharper. The burnishing effect on the machined surface is stronger in UVM, and cutting residual compressive stress in UVM is bigger than that in CM. On the other hand, cutting force and temperature in UVM are smaller than those in CM. Furthermore, the reduction of cutting force and temperature gradient would result in smaller cutting residual tensile stress in UVM.

Fig. 17

Comparison of residual stress between UVM and CM. a f_z = 0.05 mm/z, a_p = 0.5 mm, f = 30 kHz, A = 4 μm. b v_c = 30 m/min, a_p = 0.5 mm, f = 30 kHz, A = 4 μm. c v_c = 30 m/min, f_z = 0.05 mm/z, f = 30 kHz, A = 4 μm

Moreover, it can be seen that cutting parameters have a significant effect on the relative increase ratio of residual compressive stress between UVM and CM. From Fig. 17a, the relative increase ratio of residual compressive stress is decreased with the cutting speed increasing. It is mainly because that increased cutting speed would result in ultrasonic impacting effect reducing to influence the cutting residual compressive stress. From Fig. 17b, the relative increase ratio is increased first and then decreased with the feed rate increasing. It is well known that feed rate has an important influence on the residual height of the machined surface both in UVM and CM. However, micro-dimples caused by ultrasonic vibration are distributed regularly, peaks and troughs are produced on the machined surface in UVM, and extrusion of materials near peaks is strengthened because of ultrasonic vibration. Chen et al. [27] pointed out that greater residual compressive stress could be achieved because the periodic friction effect generates extrusion on the materials near peaks in UVM process. In this paper, when the feed rate is more than 0.05 mm/z, tool wear, cutting force, and temperature are increased; the burning effect is weakened, which would lead to residual compressive stress decreased; plastic bulging effect and thermal effect is strengthened which would result in residual tensile stress increased. From Fig. 17c, the relative increase ratio of residual compressive stress is reduced with cutting depth increasing. It might be that the ultrasonic impacting effect is decreased with the cutting depth increasing. Comprehensively, both ultrasonic vibration and cutting parameters are important factors to influence residual compressive stress in UVM.

5 Conclusions

In this paper, an analytical model of cutting residual stress prediction was developed with considering the effect of ultrasonic vibration for axial UVM. And the model proposed was validated by conducting UVM in situ TiB₂/7050Al composites. Based on the results and analysis, the following conclusions could be made:

• 1. The predicted cutting residual stress by the proposed model shows a good agreement with measured cutting residual stress in the distribution and variation trend along the cutting depth direction. Errors below 20% exist between the predicted and measured surface residual stress in UVM. It indicates that the model has a certain accuracy in predicting residual stress in UVM. And the impacting effect caused by ultrasonic vibration has an important effect on the residual stress.

• 2. Cutting parameters play an important role in residual stress by influencing the cutting force and temperature. With cutting speed increasing, cutting force is decreased, cutting temperature is increased, and mechanical-thermal coupling effect results in the cutting residual compressive stress reducing. With feed rate and cutting depth increasing, cutting residual compressive stress increases slightly and then decreases slowly.

• 3. Surface residual stresses in both UVM and CM are compressive. It is found that residual compressive stress in UVM is larger than that in CM, which could be increased by 9.9 ~ 37.3%. With cutting speed and cutting depth increases, the relative increase ratio of residual compressive stress is reduced gradually between UVM and CM. With increase in feed rate, the relative increase ratio is increased first and then decreased slightly.