Analytical modeling of residual stress in direct metal deposition considering scan strategy

Abstract

Existence of high tensile residual stress in the additively manufactured parts result in part failure due to crack initiation and propagation. Herein, a physics-based analytical model is proposed to predict the stress distribution much faster than experimentation and numerical methods. A moving point heat source approach is used to predict the in-process temperature field within the build part. Thermal stresses induced by steep temperature gradient is determined using the Green’s functions of stresses due to the point body load in a homogeneous semi-infinite medium. Then, both the in-plane and out of plane residual stress distributions are found from incremental plasticity and kinematic hardening behavior of the metal, in coupling with the equilibrium and compatibility conditions. Due to the steep temperature gradient in this process, material properties vary significantly. Hence, material properties are considered temperature dependent. Moreover, the specific heat is modified to include the latent heat of fusion required for the phase change. Furthermore, the multi-layer and multi-scan aspects of the direct metal deposition process are considered by incorporating the temperature history from the layers and scans. Results from the analytical residual stress model showed good agreement with X-ray diffraction measurements, which is used to determine the residual stresses in the IN718 specimens.

1 Introduction

Direct metal deposition (DMD) is an additive manufacturing (AM) process that creates three-dimensional complex parts through layer by layer addition of metallic powders [1]. DMD can be the pillar of the next industrial revolution since the high working volume make it ideal for repair, rework, and modification of large industrial components. Metal parts and assemblies produced via DMD provide substantial advantages over traditional manufacturing. Reduction in density, flexibility in design, reduction of lead time due to the elimination of multi-step manufacturing, and production of single step net shape 3D complex parts are among these advantages [2]. However, due to the steep thermal gradients induced by high intensity laser power, additively manufactured parts experience undesirable residual stress and part distortion. Existence of high-level residual stress may induce crack initiation and propagation and consequently reduces the fatigue life of the part and impact the microstructure of the additively manufactured part [3, 4]. Parts produced via DMD process can be used in medical, aerospace, and automobile industries [5, 6]. For DMD parts to be used in these industries, high quality and defect free components are required. Knowledge on stress state within the build part could enable manufacturers to more effectively control and optimize the process to reach a high-quality component.

Different types of research have been done to predict the residual stress build up in an additively manufactured part [7]. The researches in this domain can be classified into three main categories including experimentation, numerical modeling, and analytical modeling. The experimental measurement can be classified into destructive and non-destructive methods [8]. X-ray and neutron diffraction are the most commonly used non-destructive methods which are capable of providing near-surface and volumetric residual stress measurements, respectively. Hole drilling, sectioning, and crack compliance are the sub-categories of destructive methods. Strantza et al. measured the residual strains within the Ti-6Al-4V parts built via laser powder bed fusion (L-PBF) process. They have used X-ray diffraction to determine the strain pattern within the built part [9].

Numerical modeling is used by many researchers to predict the residual stress build-up during the AM process. Zhao et al. developed a numerical model to simulated heat transfer and residual stress distribution in direct metal laser sintering. They indicated that based on the simulations, the melting and solidification happens at about 1 ms. Moreover, the obtained horizontal normal residual stresses are the dominant stress component compared with vertical normal stress and shear stress [10]. Hajializade et al. proposed a thermomechanical numerical model to predict the residual stress in the additively manufactured part using coarsening approach [11]. Zekovic et al. developed a thermo-mechanical finite element model to predict the residual stress in the straight wall as well as a cylindrical wall. The results postulate that the residual stress in the cylindrical wall is more uniformly distributed and has a lower magnitude compared with the straight wall [2].

Although experimental measurements of stresses within the part play a crucial role in understanding of this phenomenon, but experimental measurement of the entire part is challenging and expensive. Finite element modeling (FEM) is also used by many researchers; however, the simulation of the entire process could not be achieved in a traceable amount of time. Consequently, many simplifications in modeling should be undertaken [12]. Moreover, the inverse analysis to optimize the process parameters to achieve the desired part performance cannot be achieved via FEM in a reasonable amount of time [13,14,15]. In contrast, analytical models validated by physical experiments provide a means to effectively understand, control, and optimize the process parameters by allowing for in situ analysis. In the past few years, analytical modeling is getting attention for the modeling of AM process since it provides rapid and reliable prediction of AM process mechanics [16, 17]. Knowledge on temperature field and thermal stress history are the crucial part of the modeling of residual stress. Although many types of analytical temperature models are introduced by other researchers to predict the temperature field [18,19,20], to the best of our knowledge, no research is conducted to predict the thermal stress and residual stress in metal additive manufacturing analytically by considering temperature-sensitive material properties, phase change, hatch spacing, scan pattern, and layer thickness.

In the present work, a novel physics-based analytical model is proposed to determine the residual stress distribution within the build part during the DMD process. The work presented herein solves the full thermomechanical system through pure analytical solutions. First, a moving point heat source approach is used to predict the temperature field during the DMD process. Following from the temperature profile, thermal stress induced by non-uniform heating is calculated based on plane strain Green’s function of stresses due to a point body load. The stress is a combination of three different sources named as body forces, normal tension, and hydrostatic stress. Last, both the in-plane and out of plane residual stress distributions are predicted from incremental plasticity and kinematic hardening behaviors of the metal, in coupling with the equilibrium and compatibility conditions. In this work, IN718 is used as a material system example to illustrate the modeling methodology and to pursue experimental validation. The proposed model can be used for all the material systems. Herein, the material properties of IN718 are considered temperature-dependent since the high thermal gradient in this process could vary the material properties significantly. Moreover, due to the repeated heating and cooling, material experiences several melting and solidification cycles [21]. The energy needed for solid-state phase change is considered by modifying the heat capacity using latent heat of fusion. Furthermore, the multi layers and multi scans aspects of DMD process are also considered since the interaction of successive layers and scans have a crucial impact on heat transfer mechanisms [22,23,24]. Also, the proposed model is based upon the premises of plane strain condition in the build of isotropic and homogeneous properties. Specimens built via DMD process are used for experimental measurements of residual stress via X-ray diffraction and compared with the modeling results. Good qualitative and quantitative agreements are achieved between the proposed analytical model and experimentation of residual stress.

2 Process modeling

A fully coupled thermomechanical analytical model is proposed herein to predict the residual stress distribution within the additively manufactured part in less than 30 s with a. The analytical models are implemented in MATLAB. The high computational efficiency of the proposed model affects a wide range of applications becoming a powerful tool for design and also fatigue assessment when component undergoes cyclic loading. It also enables efficient control and optimization of process parameters to achieve a high-quality part. Consequently, the proposed analytical model could enable manufacturers to achieve a desired residual stress by the optimization of process parameters.

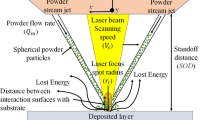
Figure 1 represents a volumetric heat source in which the laser thermal energy deposited into a control volume absorbed by material thermodynamic latent heat, conducted through the contacting solid and liquid boundaries, and convected and radiated through the open surfaces. The volumetric heat source moves along the layer according to the set scan strategy. In this work, the laser scan strategy is bi-directional as shown in Fig. 2. This section goes into more detail regarding the specific thermal and mechanical model used.

Fig. 1

Heat transfer mechanisms in DMD

Fig. 2

Scan strategy for build of IN718 samples

2.1 Thermal analysis

The thermal energy conservation associated with dynamic heat deposition in a homogeneous solid is governed by linear partial differential equation [25]

$$ \frac{\partial u\rho}{\partial t}+\frac{\partial \rho hV(x)}{\partial x}+\frac{\partial \rho hV(y)}{\partial y}+\frac{\partial \rho hV(z)}{\partial z}=\nabla .\left(k\nabla T\right)+\dot{q} $$

(1)

where u represents the internal energy, h is the enthalpy, ρ is the density, k is the conductivity, $\dot{q}$ is a volumetric heat source, T is the temperature, V is the speed of either the heat source or the medium, and ∇. referring to gradient operator.

The x direction corresponds to the constant speed of a moving heat source, y is directed inside the processed material, and z, the direction perpendicular to x in the plane of the processed material surface. The first term in Eq. (1) on the left-hand side represents the change of internal energy, and the rest is a convective term in 3D medium. On the right-hand side, there is the conductive term and a heat source or sink. For =0, this equation becomes the heat conduction equation (Eq. (2)), given that du = C dT, with C being the heat capacity

$$ C\frac{\partial \rho T}{\partial t}+\frac{\partial \rho hV(x)}{\partial x}+\frac{\partial \rho hV(y)}{\partial y}+\frac{\partial \rho hV(z)}{\partial z}=\nabla .\left(k\nabla T\right)+\dot{q} $$

(2)

The convection-diffusion equation becomes the differential equation (Eq. (3)) of heat conduction which can be expressed as

$$ \frac{\partial^2T}{\partial {x}^2}+\frac{\partial^2T}{\partial {y}^2}+\frac{\partial^2T}{\partial {z}^2}+\frac{1}{k}q\left(x,y,z,t\right)=\frac{1}{D}\frac{\partial T}{\partial t} $$

(3)

where T≡T(x, y, z, t). k is thermal conductivity, and D is the thermal diffusivity. The heat source q is related to the equivalent volumetric source q(x, y, z, t) (W/m³) by the delta function notation as (Eq. (4))

$$ q\left(x,y,z,t\right)=q\ \delta \left(x- Vt\right)\delta \left(y-{y}_0\right)\delta \left(z-{z}_0\right) $$

(4)

where δ denotes the Dirac delta function.

To consider the moving heat source, it is assumed that the coordinate system transfers from the x, y, z fixed coordinate system to ζ, y, z moving coordinate system by using the transformation equation (Eq. (5))as

$$ \zeta =x- Vt $$

(5)

Using the abovementioned transformation, the heat conduction equation for the moving coordinate system (Eq. (6)) can be written as

$$ \frac{\partial^2T}{\partial {\zeta}^2}+\frac{\partial^2T}{\partial {y}^2}+\frac{\partial^2T}{\partial {z}^2}+\frac{1}{k} Q\delta \left(\zeta \right)\delta (y)\delta (z)=\frac{1}{D}\left(\frac{\partial T}{\partial t}-V\frac{\partial T}{\partial \zeta}\right) $$

(6)

The transient moving point heat source solution (Eq. (7)) is developed by Carslaw and Jeager [19] as

$$ T=\frac{P\eta}{8\rho (T){C}_p^m\left(\mathrm{T}\right){\left(\pi D(T)t\right)}^{3/2}}{\int}_0^t\frac{\exp \left(-\frac{{\left(\left(x-{x}^{\prime}\right)-V\left(t-{t}^{\prime}\right)\right)}^2+{\left(y-{y}^{\prime}\right)}^2+{\left(z-{z}^{\prime}\right)}^2}{4D(T)\left(t-{t}^{\prime}\right)}\right)}{{\left(t-{t}^{\prime}\right)}^{3/2}}d{t}^{\prime }+{T}_0 $$

(7)

Equation (8) can be solved by the assumption of the quasi-stationary condition by setting $\frac{\partial T}{\partial t}=0$ [20]. Using the separation of variables, the closed form solution of the temperature field can be obtained as

$$ T=\frac{P\eta}{4\pi k(T)R}\exp \frac{-V\left(R-x\right)}{2D(T)}+{T}_0 $$

(8)

where P is the laser power, η represents the absorption coefficient, k is thermal conductivity and assumed to be temperature dependent, V is scan speed, T₀ is the initial temperature, $R=\sqrt{x^2+{y}^2+{z}^2}$ is the radial distance from the heat source.

D is thermal diffusivity and can be obtained from (Eq. (9))

$$ D(T)=\frac{k(T)}{\rho (T){C}_p^m(T)} $$

(9)

where ρ is material density and ${C}_p^m(T)$ is the modified heat capacity. The energy required for phase change from solid to liquid and vice versa is taken into account by modifying the heat capacity using latent heat of fusion (Eq. (10)).

$$ {C}_p^m\left(\mathrm{T}\right)={C}_p(T)+{L}_f\frac{\partial f}{\partial T} $$

(10)

In which C_p(T) is temperature dependent specific heat, L_f is latent heat of fusion, and f is liquid fraction which can be calculated from (Eq. (11))

$$ f=\left\{\begin{array}{c}0,\kern0.5em T<{T}_s\\ {}\frac{T-{T}_s}{T_L-{T}_s},\kern0.5em {T}_s<T<{T}_L\\ {}1,\kern2.75em T>{T}_L\end{array}\right. $$

(11)

where T_s is solidus temperature and T_L is liquidus temperature.

2.2 Mechanical analysis

2.2.1 Thermal stress analysis

Quite fast irradiation of the laser to melt the metallic powders and also rather slow conduction through the solid induced steep temperature gradient. Consequently, non-uniform heating may lead the thermal stress to appear in the structure. Moreover, most of the previously melted powders may experience several re-melting and re-solidification in DMD process. This would cause repeated expansion and contraction in the material which is another source of the existence of thermal stress. Furthermore, different thermal expansion coefficients at different temperatures for the same material is another source of stress in the AM part.

The average normal strain in the build part along the scan direction can be obtained from (Eq. 12) [26]:

$$ {\varepsilon}_{xx}=\frac{1}{E(T)}\left(1-\nu {(T)}^2\right){\sigma}_{xx}+\alpha (T)T\left(1+\nu (T)\right) $$

(12)

where the plane strain condition has been used, and the E(T), ν(T), and α(T) are the temperature dependent elastic modulus, Poisson’s ratio, and coefficient of thermal expansion, respectively. σ_xx is the normal stress in the build part along the scan direction. The in-process thermal stresses can be obtained from the temperature distribution and temperature gradient knowledge. The thermal stresses are obtained by combining the stress components including; (1) stresses due to body forces ${F}_x=-\frac{\alpha (T)E(T)}{1-2\nu (T)}\frac{\partial T}{\partial x}$, ${F}_z=-\frac{\alpha (T)E(T)}{1-2\nu (T)}\frac{\partial T}{\partial z}$ along the x and z directions. Corresponding stresses (Eqs. (13)–(16)) can be obtained from:

$$ \left\{\sigma \right\}={\int}_0^{\infty }{\int}_{-\infty}^{\infty}\Big(G\left(x,z,{x}^{\prime },{z}^{\prime}\right)\ B\ d{x}^{\prime }d{z}^{\prime } $$

(13)

$$ \mathrm{where}\ \left\{\sigma \right\}={\left\{{\sigma}_{xx}{\sigma}_{zz}{\sigma}_{xz}\right\}}^T $$

(14)

$$ G=\left(\begin{array}{cc}{G}_{xh}& {G}_{xv}\\ {}{G}_{zh}& {G}_{zv}\\ {}{G}_{xzh}& {G}_{xzv}\end{array}\right) $$

(15)

$$ B=\left\{\begin{array}{c}-\frac{\alpha (T)E(T)}{1-2\nu (T)}\frac{\partial T}{\partial x}\\ {}-\frac{\alpha (T)E(T)}{1-2\nu (T)}\frac{\partial T}{\partial z}\end{array}\right\} $$

(16)

The element of G represents the stresses in half plane due to an applied unit body force at (x^′, z^′).For instance, G_xh(x, z, x^′, z^′) is equal to the σ_xx(x, z) due to the unit load action along the scan direction applied at (x^′, z^′), whereas G_xv(x, z, x^′, z^′) is equal to the σ_xx(x, z) due to the unit load action in the transverse direction applied at (x^′, z^′).

(2) stress due to normal stress tension $N=\frac{\alpha (T)E(T)T}{1-2\nu (T)}$ on the boundary (z = 0). The normal stress σ_xx due to the tension (Eq. (17)) can be obtained from

$$ {\sigma}_{xx}=\frac{2}{\pi }{\int}_{-\infty}^{\infty}\frac{\left[\left(s-x\right)T- zN\right]{\left(s-x\right)}^2}{{\left({\left(s-x\right)}^2+{z}^2\right)}^2} ds $$

(17)

By putting temperature (T = 0) and normal tension $N=\frac{\alpha (T)E(T)T}{1-2\nu (T)}$, the integral reduces (Eq. (18)) to

$$ {\sigma}_{xx}\left(x,z=0\right)=\frac{\alpha (T)E(T)T}{1-2\nu (T)} $$

(18)

and (3) hydrostatic stress can be obtained as -$\frac{\alpha (T)E(T)T}{1-2\nu (T)}$ [27].

Accordingly, the stress due to the non-uniform temperature in the build part could be obtained by the combination of the Green’s functions due to the body forces, normal stress tension, and hydrostatic stress (Eqs. (19) and (20)) as [28]:

$$ {\sigma}_{xx}\left(x,z\right)=-\frac{\alpha (T)E(T)}{1-2\nu (T)}{\int}_0^{\infty }{\int}_{-\infty}^{\infty}\left({G}_{xh}\frac{\partial T}{\partial x}\left({x}^{\prime },{z}^{\prime}\right)+{G}_{xv}\frac{\partial T}{\partial z}\left({x}^{\prime },{z}^{\prime}\right)\right)d{x}^{\prime }d{z}^{\prime }+\frac{2z}{\pi }{\int}_{-\infty}^{\infty}\frac{p(s){\left(s-x\right)}^2}{{\left({\left(s-x\right)}^2+{z}^2\right)}^2} ds-\frac{\alpha (T)E(T)T\left(x,z\right)}{1-2\nu (T)} $$

(19)

$$ {\sigma}_{zz}\left(x,z\right)=-\frac{\alpha (T)E(T)}{1-2\nu (T)}{\int}_0^{\infty }{\int}_{-\infty}^{\infty}\left({G}_{zh}\frac{\partial T}{\partial x}\left({x}^{\prime },{z}^{\prime}\right)+{G}_{zv}\frac{\partial T}{\partial z}\left({x}^{\prime },{z}^{\prime}\right)\right)d{x}^{\prime }d{z}^{\prime }+\frac{2{z}^3}{\pi }{\int}_{-\infty}^{\infty}\frac{p(s)}{{\left({\left(s-x\right)}^2+{z}^2\right)}^2} ds-\frac{\alpha (T)E(T)T\left(x,z\right)}{1-2\nu (T)} $$

(20)

$$ {\sigma}_{xz}\left(x,z\right)=-\frac{\alpha (T)E(T)}{1-2\nu (T)}{\int}_0^{\infty }{\int}_{-\infty}^{\infty}\left({G}_{xz h}\frac{\partial T}{\partial x}\left({x}^{\prime },{z}^{\prime}\right)+{G}_{xz v}\frac{\partial T}{\partial z}\left({x}^{\prime },{z}^{\prime}\right)\right)d{x}^{\prime }d{z}^{\prime }+\frac{2{z}^2}{\pi }{\int}_{-\infty}^{\infty}\frac{p(s)\left(s-x\right)}{{\left({\left(s-x\right)}^2+{z}^2\right)}^2} ds $$

(21)

$$ {\sigma}_{zz}\left(x,z\right)=\nu (T)\left({\sigma}_{xx}+{\sigma}_{zz}\right)-\alpha (T)E(T)T\left(x,z\right) $$

(22)

where α represents the coefficient of the thermal expansion, E is the elastic modulus. G_xh, G_xV, G_zh, G_zv, G_xzh,G_xzv are the plane strain Green’s function which explained in appendix A, $\frac{\partial T}{\partial x}$ is the temperature gradient, and p(s) is expressped by:

$$ p(s)=\frac{\alpha (T)E(T)T\left(x,z=0\right)}{1-2\nu (T)} $$

(23)

2.2.2 Residual stress analysis

Non-uniform heating and steep temperature gradient in the DMD process lead to residual stress. The magnitude and nature of residual stresses highly depend on the thermal stresses experienced by the medium.

Both the in-plane and out of plane residual stress distributions are obtained from incremental plasticity and kinematic hardening behavior of metal in coupling with equilibrium and compatibility conditions. The thermal stresses obtained from the previous section is used as an input for solving the residual stress, Eqs. (21)–(24) as

$$ {\sigma}_{xx}^{\ast }={\sigma}_{xx},{\sigma}_{zz}^{\ast }={\sigma}_{zz},{\sigma}_{xz}^{\ast }={\sigma}_{xz} $$

(24)

Due to the nature of DMD process, high strain, strain rate, and temperature are generated in the metallic part. A consecutive model that captures these effects is required. In this effort, the Johnson-Cook flow stress model is used to model the material flow stress as a function of strain, strain rate, and temperature to determine the yield threshold (Eq. (25)) as;

$$ k=\frac{1}{\sqrt{3}}\left(A+B{\varepsilon_{eff}^p}^n\right)\left(1+ Cln\left(\frac{{\dot{\varepsilon}}_{eff}^p}{{\dot{\varepsilon}}_0}\right)\right)\left(1-{\left[\frac{T-{T}_0}{T_m-{T}_0}\right]}^m\right) $$

(25)

where k represents effective stress, ${\varepsilon}_{eff}^p$ is the effective plastic strain, ${\dot{\varepsilon}}_{eff}^p$ is the effective plastic strain rate, T is the temperature of material, T_m is the melting point of material, and T₀ is the initial temperature. The terms A, $B,C,n,m,\mathrm{and}\ {\dot{\varepsilon}}_0$ are the material constant which is listed in Table 1 for IN718.

Table 1 Johnson-Cook parameters for IN718 [31]

The effective plastic strain and strain rate are defined (Eqs. (26) and (27)) as

$$ {\varepsilon}_{eff}^p=\frac{\sqrt{2}}{3}\sqrt{{\left({\varepsilon}_{xx}^p-{\varepsilon}_{yy}^p\right)}^2+{\left({\varepsilon}_{yy}^p-{\varepsilon}_{zz}^p\right)}^2+{\left({\varepsilon}_{zz}^p-{\varepsilon}_{xx}^p\right)}^2+6{\left({\varepsilon}_{xz}^p\right)}^2} $$

(26)

$$ {\dot{\varepsilon}}_{eff}^p=\sqrt{\frac{2}{3}}\ \sqrt{{\left({\dot{\varepsilon}}_{xx}^p\right)}^2+{\left({\dot{\varepsilon}}_{yy}^p\right)}^2+{\left({\dot{\varepsilon}}_{zz}^p\right)}^2+{\left({\dot{\varepsilon}}_{xz}^p\right)}^2} $$

(27)

The yielding criterion is obtained for an isotropic material. Kinematic hardening is considered by employing backstress tensor (α_ij) (Eq. (28))

$$ {\displaystyle \begin{array}{c}{F}_{\_ yeild}=\frac{3}{2}\left({S}_{ij}-{\alpha}_{ij}\right)\left({S}_{ij}-{\alpha}_{ij}\right)-{k}^2=0\ \\ {}\left\{\begin{array}{c}{F}_{\_ yeild}<0\ elastic\ deformation\\ {}{F}_{\_ yeild}>0\ plastic\ deformation\end{array}\right.\end{array}} $$

(28)

where ${S}_{ij}={\sigma}_{ij}-\left(\raisebox{1ex}{${\sigma}_{kk}$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right){\delta}_{ij}$ is the deviatoric stress, k is the material yield threshold which is determined using material flow stress model.

$\dot{\alpha_{ij}}=\left\langle \dot{S_{kl}}{n}_{kl}\right\rangle {n}_{ij}$ shows the evolution of back stress tensor in linear kinematic hardening, where <> is MacCauley bracket and is defined as 〈x〉 = 0.5(x+| x| ), and ${n}_{ij}=\frac{S_{ij}-{\alpha}_{ij}}{\sqrt{2}\ k}$ which is the components of unit normal in plastic strain rate direction (on yield surface), and k is the material flow stress threshold.

Elasticity module and yield stress are considered temperature dependent, which force the model to be updated incrementally. If F_yield < 0, material is in elastic region and the stresses can be obtained from the Hook’s law.

If F_yield > 0,incremental plastic strains are calculated and accumulated during the stress history to determine the total plastic strain. Plastic strain is irreversible and path dependent, and consequently, the governing equations should be written in the form of differential equations. The plastic strain rate is determined (Eq. (29)) as [29].

$$ {\dot{\varepsilon}}_{ij}^P=\frac{1}{h}\left\langle \dot{S_{kl}}{n}_{kl}\right\rangle {n}_{ij} $$

(29)

where h is the plastic modulus. In the elastic-plastic case where the F_yield ≥ 0, the strain rate along the scan direction and transverse direction can be calculated using McDowell algorithm (Eq. (30)) [30] as

$$ {\dot{\varepsilon}}_{xx}=\frac{1}{E}\left[{\dot{\sigma}}_{xx}-\upsilon \left({\dot{\sigma}}_{yy}-{\dot{\sigma}}_{zz}^{\ast}\right)\right]+\alpha \Delta T+\frac{1}{h}\left({\dot{\sigma}}_{xx}{n}_{xx}+{\dot{\sigma}}_{yy}{n}_{yy}+{\dot{\sigma}}_{zz}^{\ast }{n}_{zz}+2{\dot{\sigma}}_{xz}^{\ast }{n}_{xz}\right){n}_{xx}=\psi \left(\frac{1}{E}\left[{\dot{\sigma}}_{xx}^{\ast }-\upsilon \left({\dot{\sigma}}_{yy}-{\dot{\sigma}}_{zz}^{\ast}\right)\right]+\alpha \Delta T+\frac{1}{h}\left({\dot{\sigma}}_{xx}^{\ast }{n}_{xx}+{\dot{\sigma}}_{yy}{n}_{yy}+{\dot{\sigma}}_{zz}^{\ast }{n}_{zz}+2{\dot{\sigma}}_{xz}^{\ast }{n}_{xz}\right){n}_{xx}\right) $$

(30)

Additionally, the plane strain condition (Eq. (31)) is imposed as

$$ {\dot{\varepsilon}}_{yy}=\frac{1}{E}\left[{\dot{\sigma}}_{yy}-\upsilon \left({\dot{\sigma}}_{xx}-{\dot{\sigma}}_{zz}^{\ast}\right)\right]+\alpha \Delta T+\frac{1}{h}\left({\dot{\sigma}}_{xx}{n}_{xx}+{\dot{\sigma}}_{yy}{n}_{yy}+{\dot{\sigma}}_{zz}^{\ast }{n}_{zz}+2{\dot{\sigma}}_{xz}^{\ast }{n}_{xz}\right){n}_{yy}=0 $$

(31)

where ${\dot{\sigma}}_{xx}^{\ast },{\dot{\sigma}}_{zz}^{\ast },{\dot{\sigma}}_{xz}^{\ast }$ are the elastic thermal stresses calculated from Eqs. (21)–(24). In McDowell model, a hybrid function (ψ) is proposed, which depends on the instantaneous value of the modulus ratio h/G as;

$$ \psi =1-\exp \left(-\xi \frac{3h}{2G}\right) $$

(32)

where ξ = 0.2 is the algorithm constant, h is the plastic modulus, and G = E/(2(1 + υ)) is the elastic shear modulus. ψ approaches zero as h approaches zero (perfect plasticity), and ψ approaches unity as h approaches infinity (initial yielding). ψ is always between unity and zero.

Equations (32) and (33) are solved simultaneously for ${\dot{\sigma}}_{xx}$ and ${\dot{\sigma}}_{yy}$ for each elastic-plastic increment of strain.

2.2.3 Stress relaxation

After passing the laser, elastic stresses are relaxed to satisfy the boundary condition prescribed by Merwin and Johnson [32] as

$$ {\displaystyle \begin{array}{c}{\varepsilon}_{xx}^r=0,{\sigma}_{xx}^r={f}_1(z),{\varepsilon}_{yy}^r=0,{\sigma}_{yy}^r={f}_2(z),{\varepsilon}_{zz}^r={f}_3(z),{\sigma}_{zz}^r=0,\\ {}{\gamma}_{xz}^r={f}_4(z),\kern0.5em {\sigma}_{xz}^r=0\ \end{array}} $$

(33)

Finally, only stresses and strains parallel to the surface (${\sigma}_{xx}^r,\kern1em {\sigma}_{yy}^r,{\begin{array}{c}\kern0.5em \\ {}\gamma \end{array}}_{xz}^r\Big)$ remain non-zero. The only non-zero strain is${\varepsilon}_{zz}^r$, resulting from surface compression. Accordingly, the non-zero components ${\varepsilon}_{xx}^r,{\sigma}_{zz}^r,{\sigma}_{xz}^r$, and T^r at the end of each pass should incrementally relaxed to zero (Eq. (34)) as;

$$ \Delta {\sigma}_{zz}=-\frac{\sigma_{zz}^r}{M},\Delta {\sigma}_{xz}=-\frac{\sigma_{xz}^r}{M},\Delta {\varepsilon}_{xx}=-\frac{\varepsilon_{xx}^r}{M} $$

(34)

where M is the number of increments (e.g., 100–1000) taken into the relaxation process.

Using Eq. (35), for the case of purely elastic relaxation increment (F_yield  ≤ 0 ),the relaxation process is described by general Hook’s law as

$$ \left\{\begin{array}{c}\Delta {\sigma}_{xx}=\frac{E\Delta {\varepsilon}_{xx}+\left(1+\upsilon \right)\left(\Delta {\sigma}_{zz}\upsilon - E\alpha \Delta T\right)}{\left(1-{\upsilon}^2\right)}\\ {}\Delta {\sigma}_{yy}=\frac{\upsilon E\Delta {\varepsilon}_{xx}+\left(1+\upsilon \right)\left(\Delta {\sigma}_{zz}\upsilon - E\alpha \Delta T\right)}{\left(1-{\upsilon}^2\right)}\end{array}\right. $$

(35)

∆^′s replace the time derivative.

For the elastic-plastic case (F_yield > 0), the released stresses calculated (Eq. (36 a and b)) as.

$$ \left\{\begin{array}{c}\Delta {\sigma}_{xx}=\frac{D-\left(\frac{1}{E}+\frac{1}{h}{n}_{xx}{n}_{yy}\right)\Delta {\sigma}_{yy}-\alpha \Delta \mathrm{T}}{-\frac{\upsilon }{E}+\frac{1}{h}{n}_{xx}{n}_{yy}}\\ {}\Delta {\sigma}_{yy}=\frac{\left(-\frac{\upsilon }{E}+\frac{1}{h}{n}_{xx}{n}_{yy}\right)\left(C-\alpha \Delta \mathrm{T}\right)-\left(\frac{1}{E}+\frac{1}{h}{n}_{xx}{n}_{xx}\right)\left(D-\alpha \Delta \mathrm{T}\right)}{\left[{\left(-\frac{\upsilon }{E}+\frac{1}{h}{n}_{xx}{n}_{yy}\right)}^2-\left(\frac{1}{E}+\frac{1}{h}{n}_{xx}{n}_{xx}\right)\left(\frac{1}{E}+\frac{1}{h}{n}_{yy}{n}_{yy}\right)\right]}\end{array}\right. $$

(36 a, b)

$$ \mathrm{where}\left\{\begin{array}{c}C=\Delta {\varepsilon}_{xx}+\left(\frac{\upsilon }{E}-\frac{1}{h}{n}_{xx}{n}_{zz}\right)\Delta {\sigma_{zz}}^{\ast }-\frac{2}{h}\ \Delta {\sigma_{xz}}^{\ast }{n}_{xz}{n}_{xx}\\ {}D=\left(\frac{\upsilon }{E}-\frac{1}{h}{n}_{yy}{n}_{zz}\right)\Delta {\sigma_{zz}}^{\ast }-\frac{2}{h}\ \Delta {\sigma_{xz}}^{\ast }{n}_{xz}{n}_{yy}\end{array}\right. $$

(37)

The residual stresses in the scan direction and transverse direction is then calculated (Eq. (37)) as the remaining stresses after relaxation. Residual stress and stress relaxation algorithm are shown in Fig. 3.

Fig. 3

Residual stress and relaxation algorithm

3 Temperature dependent material properties

In the analytical modeling of residual stress, thermal and mechanical material properties of IN718 are temperature sensitive. The reason is that during the DMD process, the material is heated up from room temperature to thousands of degrees in a very short time, and it undergoes several melting and solidification cycles through the entire process. Consequently, the material properties in this process could change drastically, and it is not a fair assumption to consider them as constant. The temperature-dependent material properties used in the present work are density, conductivity, specific heat, yield strength, Young’s modulus, Poisson’s ratio, and thermal expansion coefficient, as shown in Fig. 4. Linear interpolation is used to calculate the properties between the data points. The melting temperature range of IN718 is from 1210 to 1344°C . In this modeling, the melting temperate is considered to be 1260°C.

Fig. 4

Thermal and mechanical material properties of IN718 as a function of temperature. a Density. b Conductivity. c Specific heat. d Elastic modulus. e Yield strength. f Coefficient of thermal expansion. g Poisson’s ratio

For the material thermal properties, the density of IN718 decreases with increase in temperature and a sudden decrease appear at the melting temperature; thermal conductivity increases with increase in temperature and a sudden decrease appear at around the melting temperature; specific heat increases gradually with increase in temperature and reaches a constant value at melting temperature. For the mechanical properties, elastic modulus decreases more gradually at lower temperature and more rapidly at higher temperatures and reaches almost zero value at around melting temperature which shows the material at liquid phase has negligible elasticity; coefficient of thermal expansion increases as the temperature increases and reaches a constant value at around melting temperature; yield strength decreases rapidly from room temperature up to 1000°C to a very low value and changes only slightly when over 1000°C. This implies that the IN718 is very soft, and it is very easy to undergo plastic deformation in the temperature domain near the melting temperature which causes the residual stress to have a high value; Poisson’s ratio decrease by increasing temperature up to 580°C, and after that it increases by increasing the temperature, which shows the material is in tension and contraction, respectively.

The formula for temperature dependent material properties can be obtained using the curve fitting. The temperature dependent material properties for IN718 are listed in Table 2.

Table 2 Temperature dependent material properties of IN718 (Temperature is in °C)

4 Experimental residual stress measurements

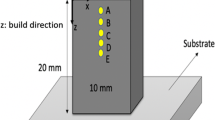
Three blocks of IN718 specimens with the size of 20 × 10 × 3 mm are produced via DMD process using LENS CS 1500 SYSTEMS under different process conditions as shown in Table 3. The building process is housed in a chamber which is purged with argon such that the oxygen level stays below 10 ppm to ensure there is no impurity pick-up during deposition. The approach to identify processing parameters for producing high-density parts was employed to select the processing conditions as described in previous studies [33,34,35,36].The selected laser powers are 920 W, 743 W, and 485 W, and the scan speeds are 25 mm/s, 40 mm/s, 40 mm/s, respectively. The laser power has three levels, and the scan speed has two levels. The main reason for the selection of these process parameters is to investigate the effect of process parameters such as scan speed and laser power on residual stress while other parameters such as layer height, hatching space, and scan strategy are kept the same. The deposited layer thickness for all the samples is 250 μm,and hatch spacing is 105 μm. A bi-directional continuous scan strategy is used as shown in Fig. 2.

Table 3 Process parameters for DMD of IN718 specimens

PANalytical Empyrean multipurpose X-ray diffractometer is used to measure the residual stress of the specimens. The effective spectrum of the X-ray beam is from 50 to 150 eV. The incident X-ray beam is masked to a 0.2 mm × 0.2 mm cross-section by incident beam slits. The samples are positioned in a goniometer with built-in translation stages that enabled the automated rotation and positioning of the sample to collect diffraction data over the XZ cross-section. Each sample is oriented so that the incident rays are perpendicular to the growth direction. An absolute scan is then taken of the material to establish peak values generated by the crystalline structure as a function of 2θ, where θ is the incident angle. At lower angles of theta (θ), the background noise can be very high, so it is preferable to use high angle peaks where possible. This is due to the material surface roughness diffracting the incident radiation in non-uniform diffraction patterns and reducing layer penetration. Once a peak was selected, a stress program was created. The program takes twenty measurements over a range of chi values at four different phi values of 0°, 45°, 90°, and 135° as shown in Fig. 5. This allows stress analysis in four planes including scan direction and transverse direction. Once the data is gathered, the data is fed into the PANalytical stress program which calculates the stress values by looking for peaks in the intensity vs 2θ plot at each point. To generate through thickness measurement of residual stress, samples are polished using liquid abrasive of 1 μm and 0.05 μm at a very slow speed to eliminate macroscopic residual stresses. Measurements are collected every 0.5 mm along the build direction (Z-axis) of the samples.

Fig. 5

Illustration of the rotation of the build parts for X-ray

The residual strains are determined (Eq. (38)) as

$$ \varepsilon =\frac{d-{d}_0}{d_0} $$

(38)

where d and d₀ are the stressed and unstressed lattice parameter, respectively.

The generalized Hook’s law for isotropic material is used to calculate stress (Eq. (39)) as

$$ {\sigma}_i=\frac{E}{\left(1+\upsilon \right)\left(1-2\upsilon \right)}\left(\left(1-\upsilon \right){\varepsilon}_i+\upsilon \left({\varepsilon}_j+{\varepsilon}_k\right)\right) $$

(39)

where i, j, k ∈ x, y, z.

In Eq. 39, an elastic modulus (E) and Poisson’s ratio of 206 GPa and 0.28 are used, respectively.

5 Results and discussion

Residual stress could be classified into three main categories based on the length scale; type Ι residual stress is on macroscale; type ΙΙ residual stress is on microscale which always exists due to the anisotropic material properties on grain-scale; type ΙΙΙ residual stress which is on nanoscale and it is due to the coherency and dislocation. Type ΙΙ and ΙΙΙ residual stress has very limited effect on mechanical properties of the material and are beyond the scope of this work. Herein, our main focus is on type Ι residual stress. The residual stress can be beneficial by the proper selection of process parameters such as laser power, scan speed, layer thickness, and hatching space. For instance, changing the stress state from tensile to compressive could be more beneficial for the fatigue life of the component. Consequently, having a validated model to predict the residual stress state of the component within a few seconds rather than hours or days using FEM and/or experimentation is extremely valuable.

Rapid heating and cooling thermal cycles of AM leads to residual stress formation in an additively manufactured part. During the heating cycle, the laser deposited its energy to heat up the metallic powders rapidly over the melting temperature. This would create a melt pool area and a heat affected zone (HAZ) as shown in Fig. 6. The heated material tends to expand but the thermal expansion is restrained by surrounding powders at a lower temperature. Therefore, a compressive stress state is formed in the heated zone. During the cooling cycle, when the heat source is gone, the heated zone begins to cool down and the shrinkage of material in this zone tend to occur, but the shrinkage is restrained by the plastic strain formed during the heating stage. Finally, tensile residual stress builds up in the heated zone. Moreover, during the DMD process, the previously melted powders experience re-melting and re-solidification cycles. This repeated melting and solidification could result in shrinkage of the material which is restrained by the previously deposited material. Consequently, a tensile stress state is formed in the newly deposited material.

Fig. 6

An illustration of melt pool area and heat affected zone

The proposed analytical model enables the prediction of the residual stress throughout the part rapidly and accurately. The moving point heat source approach is used to predict the temperature field and temperature gradient during the DMD process. In the present work, the medium is semi-infinite, and the heat loss due to convection and radiation is ignored. Powders are considered to be stable, and the effect of powder feed velocity is not considered. As shown in our previous works, the moving point heat source model can be used for both powder bed fusion systems and direct metal deposition systems [23, 37]. High-temperature gradient induced thermal stresses exceed the yield stress. Therefore, material experience plastic deformation. By employing incremental plasticity and kinematic hardening behavior of metal, residual stress is obtained. The model presented in this work is based upon the premises of plane strain condition in the build of isotropic and homogeneous properties.

For the validation of the proposed analytical model, X-ray diffraction is used to measure the in-depth residual stress at the middle of the samples (X = 10 mm, Y = 1.5 mm) at every 0.5 mm along the build direction. The scan strategy in both experimentation and analytical modeling is bi-directional. Moreover, the hatching space and layer thickness are 105 μm and 250 μm. Good qualitative and quantitative agreements are observed between predicted residual stress from the analytical model and those obtained via X-ray diffraction.

Figure 7 illustrates predicted temperature field for three specimens in Table 3. Since the evaporation of the metallic powders is not considered in the modeling, the maximum temperature does not go beyond the evaporation temperature point which is 2800°C [38]. As the laser deposited its energy into the medium, a melt pool geometry and a heat affected zone will be created. Figure 7a shows the temperature field for the laser power of 485 W and scan speed of 40 mm/s. Melt pool area is the region where the temperature is above the melting temperature. In this figure, the melt pool depth is around 0.75 mm based on the melting point of 1260°C. Also, the heat affected zone is the region where the temperature is above the initial temperature and below the melting temperature. In this figure, the heat affected zone is up to 1.1 mm in depth and below this depth, the rapid change in temperature is observed which shows the material below the depth of 1.1 mm is not affected by the laser as marked with a red mark. This rapid change in temperature at the border of heat affected zone would cause a change in stress state which will be explained further in the following parts of this manuscript.

Fig. 7

Predicted temperature field for DMD of IN718. aP = 485 W, V = 40 mm/s. bP = 743 W, V = 40 mm/s. cP = 920, V = 25 mm/s

Figure 7b illustrates the temperature field developed within the medium with the laser power of 743 W and scan speed of 40 mm/s. The melt pool depth is 0.9 mm and the heat affected zone continued up to 1.3 mm in depth. Figure 7c depicts the temperature field within the additively manufactured part with the scan speed of 920 W and scan speed of 25 mm/s. The obtained melt pool depth is 1.25 mm and the depth of heat affected zone is 1.7 mm. The border of maximum heat affected zone is shown with a red mark in all three plots. This border is of great importance since the temperature drop in this region would change the stress state from tensile to compressive which will be explained later on in this manuscript.

Figure 8 a, b, and c illustrate evolution of temperature as a function of time in different depth. Figure 8 a and b illustrate that for the same scan speed (40 mm/s), the increase in laser power leads the material to spend more time at a higher temperature, consequently bigger melt pool geometry and heat affected zone will build up. Figure 8 a, b, and c also show the evolution of temperature as a function of time in three different depth of 1.1 mm, 1.3 mm, and 1.7 mm where the residual stress state alters from tensile to compressive state in three samples with the laser power of 485 W, 743 W, and 920 W, respectively. In these plots, the rapid drop in temperature is more obvious. As explained before, since the evaporation of material is not considered in this modeling, the temperature does not go beyond evaporation temperature of IN718 which is around 2800°C [38].

Fig. 8

Predicted temperature evolution at different depth along the build direction. a P = 485 W, V = 40 mm/s. b P = 743 W, V = 40 mm/s. c P = 920, V = 25 mm/s

Figures 9, 10, and 11 illustrate the predicted residual stress for three different samples as listed in Table 3. Residual stress along the scan direction and transverse direction are obtained using the proposed model. Figure 9 and b show the residual stress along the scan direction and transverse direction for the first sample in Table 3 which has the laser power of 485 W, the scan speed of 40 mm/s, the layer thickness of 250 μm, and the hatch spacing of 105 μm. It should be noted that the absorption coefficient for IN718 is 0.3 [39,40,41]. Residual stresses in both scan and transverse directions are highly tensile in coherence with most of the reported results in literature as explained in introduction section. The change of residual stress from tensile to compressive in both directions are observed around the depth of 1.1 mm. This is due to the rapid change of temperature at the border of HAZ. As discussed previously, the laser heats up the metallic powders and creates a melt pool and a HAZ. The melt pool area and HAZ are under tension upon cooling. Since the material below the HAZ is at a lower temperature, this leads to the compressive stress state in the build part. Figure 7a illustrates the predicted temperature field for the first sample with a laser power of 485 W and scan speed of 40 mm/s. As it is shown in this figure, the melt pool geometry and heat affected zone are extended up to 1.1 mm in depth. Below this area, the temperature of the material rapidly decreases and causes the compressive state of stress to occur at this border. The experimental measurement of residual stress shows good agreement with predicted results.

Fig. 9

Predicted residual stress along a scan direction and b transverse direction for the laser power of 485 W and scan speed of 40 mm/s in the DMD build of IN718 specimens

Fig. 10

Predicted residual stress along a scan direction and b transverse direction for the laser power of 743 W and scan speed of 40 mm/s in the DMD build of IN718 specimens

Fig. 11

Predicted residual stress along a scan direction and b transverse direction for the laser power of 920 W and scan speed of 25 mm/s in the DMD build of IN718 specimens

Figure 10 a and b illustrate predicted residual stress along the scan direction and transverse direction for the laser power of 743 W and scan speed of 40 mm/s, respectively. Good agreement is achieved between predicted and measure residual stresses. As shown in these figures, the tensile state of stress changes to compressive at the depth around 1.3 mm. This change corresponds to the rapid change of temperature below the HAZ as shown with a red mark in Fig. 7b.

Figure 11 a and b demonstrate predicted and measured residual stress for the laser power of 920 mm/s and a scan speed of 25 mm/s. Good agreement is achieved between predicted and measured residual stress. Predicted and measured residual stress show that the residual stress for the additively manufactured IN718 parts is highly tensile. However, the change in stress state is observed at the depth of 1.7 mm which corresponds to the dramatic change of temperature below the HAZ as explained before. Good agreement is achieved between predicted and measured residual stress in all three cases. The residual stress experimental measurements are measured at every 0.5 mm in-depth as explained in previous section. While, the change in stress state in experimental measurements are captured in most of the cases, this change of stress state is not captured in some cases since the measurements’ intervals were not around the HAZ (since the authors want the intervals to be the same for all the measurements).

In summary, the predicted and measured residual stress for IN718 parts built via DMD process depict that the residual stress is highly tensile and the change in stress state is related to the melt pool geometry and heat affected zone. Consequently, proper control and optimization of process are needed to reduce or eliminate the tensile residual stress which has a substantial impact on fatigue life, corrosion resistance, crack initiation and propagation, dimensional accuracy, and microstructure evolution of the AM part.

6 Sensitivity analysis

The proposed analytical model is used to conduct parametric study to investigate effects of laser power and scan speed on residual stress. This study looked at changing the laser power and scan speed while the layer thickness and hatching space are kept constant at 250 μm and 105 μm, respectively. The average residual stress up to 1 mm below the surface is calculated (the residual stress is predicted at every 250 μm through thickness, and the average of four predicted residual stress is calculated). Three different laser powers of 100 W, 300 W, and 500 W are selected with the scan speed of 20 mm/s, 40 mm/s, and 60 mm/s (melting of metallic powders are obtained based on these parameters). As shown in Fig. 12 a and b, for given laser power, the increase in scan speed would reduce the residual stress both along the scan direction and transverse direction. This is due to the fact that the increase in scan speed would result in a lower temperature gradient since the material has less time to absorb the energy. Consequently, reduction in temperature gradient leads to lower residual stress. Furthermore, an increase in laser power for a given scan speed leads to higher residual stress in both scan direction and transverse direction since the material absorbs more energy which would result in a higher temperature gradient. Moreover, the residual stress along the scan direction has a higher magnitude compared with the residual stress in the transverse direction. The main reason is that the thermal gradient is higher in scan direction compared with transverse direction.

Fig. 12

Predicted residual stress. a Scan direction. b Transverse direction

7 Conclusion

A physics-based thermomechanical analytical model is proposed to predict the residual stress buildup in IN718 parts produced via direct metal deposition process. A moving point heat source approach is used to predict the temperature field within the build part. Due to the high temperature gradient, the material properties could change drastically from point to point. Consequently, it is not fair to consider the material properties as constants. Herein, the thermal and mechanical material properties such as thermal conductivity, specific heat, density, elastic modulus, yield strength, Poisson’s ratio, and coefficient of thermal expansion are considered temperature dependent. Moreover, due to the repeated heating and cooling material experience phase change. This physical aspect of DMD process is considered by modifying the heat capacity using the latent heat of fusion. Furthermore, the multi-layer and multi-scan aspect of this process are considered by incorporating temperature histories from previous layers and scans.

The steep temperature gradient leads to the formation of thermal stresses due to the expansion and contraction of material induced by cyclic heating and cooling. Thermal stress within the material is obtained using the Green’s functions of stresses due to the point body load. The predicted thermal stress is the combination of three main sources known as stresses due to body forces, normal tension, and hydrostatic stress. High amount of thermal stress induced by temperature gradient leads the material yielded and experience the plastic deformation.

Due to the repeated loading (heating) and unloading (cooling) of the part during the production of the part, residual stresses appear in the structure. Both the in-plane and out of plane residual stress distributions is found from incremental plasticity and kinematic hardening behavior of the metal, in coupling with the equilibrium and compatibility conditions. The model presented in this work is based upon the premises of plane strain condition in the build of isotropic and homogeneous properties.

X-ray diffraction measurements are performed on block-shaped specimens produced with different laser powers and scan speeds via DMD process to determine the residual stress presents in those parts. Comparisons between the measured and predicted residual stresses showed good agreement. The agreement between predicted and measured residual stresses results allows for confidence in using the proposed model to obtain the residual stress state throughout the part within a few seconds.

The results show that the residual stress along the scan direction and transverse direction is mostly tensile. Also, magnitude of the residual stress along the scan direction is higher than transverse direction. It is shown that the stress state in heat affected zone is tensile while the rapid decrease in temperature below the heat affected zone would result in the stress state to change to compressive. This is due to the fact that upon cooling material at heat affected zone tends to shrink; however, they restrained by plastic strain formed during heating stage. Consequently, tensile residual stress is formed in the heat affected zone which is in balance with compressive zone below the heat affected zone.

Additionally, a sensitivity analysis is performed to investigate the effect of process parameters on residual stress. The results show that the increase in scan speed would decrease the residual stress in both scan and transverse direction due to the decrease in temperature gradient. Besides, the increase in laser power would increase the residual stress in the DMD of IN718 parts.

Appendix. Elements of G matrix

Let the X_m = x − x^′, Z_P = z + z^′, Z_m = z − z^′,

The Green functions G_xh(x, z, x^′, z^′) and G_xv(x, z, x^′, z^′) are the normal stress due to a unit point body load acting at (x^′, z^′) along the x and z directions, respectively.

$$ {G}_{xh}=\frac{1}{4\pi}\frac{1-2{\nu}^{\prime }}{1-{\nu}^{\prime }}\left[\frac{3-2{\nu}^{\prime }}{1-2{\nu}^{\prime }}\left(\frac{X_m}{X_m^2+{Z}_p^2}-\frac{X_m}{X_m^2+{Z}_m^2}\right)+\frac{2}{1-2{\nu}^{\prime }}\left(\frac{X_m{Z}_m^2}{{\left({X}_m^2+{Z}_m^2\right)}^2}-\frac{X_m{Z}_p^2}{{\left({X}_m^2+{Z}_p^2\right)}^2}\right)\right]-\frac{1}{\pi}\frac{1}{1-{\nu}^{\prime }}\times \left(\left(3-2{\nu}^{\prime}\right)\frac{X_m\left({z}^{\prime }{Z}_p+{X}_m^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^2}-\frac{3{z^{\prime}}^2{X}_m{Z}_p^2+{X_m}^3\left(4{z^{\prime}}^2+6z{z}^{\prime }+{z}^2+{X}_m^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^3}\right) $$

$$ {G}_{zh}=-\frac{1}{4\pi}\frac{1-2{\nu}^{\prime }}{1-{\nu}^{\prime }}\left[\left(\frac{X_m}{X_m^2+{Z}_p^2}-\frac{X_m}{X_m^2+{Z}_m^2}\right)+\frac{2}{1-2{\nu}^{\prime }}\left(\frac{X_m{Z}_m^2}{{\left({X}_m^2+{Z}_m^2\right)}^2}-\frac{X_m{Z}_p^2}{{\left({X}_m^2+{Z}_p^2\right)}^2}\right)\right]-\frac{1}{\pi}\frac{y}{1-{\nu}^{\prime }}\times \left(\left(3-2{\nu}^{\prime}\right)\frac{X_m{Z}_p}{{\left({X}_m^2+{Z}_p^2\right)}^2}-\frac{X_m\Big(4{z^{\prime}}^3+9z{z}^{\prime 2}+6{z}^2{z}^{\prime }+{z}^3+z{X}_m^2}{{\left({X}_m^2+{Z}_p^2\right)}^3}\right) $$

$$ {G}_{xzh}=\frac{1}{4\pi}\frac{1-2{\nu}^{\prime }}{1-{\nu}^{\prime }}\left[\left(\frac{Z_P}{X_m^2+{Z}_p^2}-\frac{Z_m}{X_m^2+{Z}_m^2}\right)+\frac{2}{1-2{\nu}^{\prime }}\left(\frac{Z_p{X}_m^2}{{\left({X}_m^2+{Z}_p^2\right)}^2}-\frac{Z_m{X}_m^2}{{\left({X}_m^2+{Z}_m^2\right)}^2}\right)\right]-\frac{1}{\pi}\frac{1}{1-{\nu}^{\prime }}\times \left(\left(3-2{\nu}^{\prime}\right)\frac{z^{\prime }{Z}_p^2+{X}_m^2\left(2z+{z}^{\prime}\right)}{2{\left({X}_m^2+{Z}_p^2\right)}^2}-\frac{{z^{\prime}}^3\left({z^{\prime}}^2+3z{z}^{\prime }+3{z}^2\right)+{z}^3{z^{\prime}}^2+{X}_m^2\left({z^{\prime}}^3+6z{z^{\prime}}^2+6{z}^2{z}^{\prime }+{z}^3\right)+z{X}_m^4}{{\left({X}_m^2+{Z}_p^2\right)}^3}\right) $$

$$ {G}_{xv}=-\frac{1}{4\pi}\frac{1-2{\nu}^{\prime }}{1-{\nu}^{\prime }}\left[\left(\frac{Z_P}{X_m^2+{Z}_p^2}-\frac{Z_m}{X_m^2+{Z}_m^2}\right)+\frac{2}{1-2{\nu}^{\prime }}\left(\frac{Z_m{X}_m^2}{{\left({X}_m^2+{Z}_m^2\right)}^2}-\frac{Z_p{X}_m^2}{{\left({X}_m^2+{Z}_p^2\right)}^2}\right)\right]-\frac{1}{2\pi}\frac{1}{1-{\nu}^{\prime }}\times \left(2\left(1-{\nu}^{\prime}\right)\frac{Z_p}{\left({X}_m^2+{Z}_p^2\right)}-\frac{\left[2\left(1-{\nu}^{\prime}\right)z-{z}^{\prime}\right]\left({Z}_p^2-{X}_m^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^2}+\frac{2z{z}^{\prime }{Z}_p\left(3{X}_m^2-{Z}_p^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^3}\right) $$

$$ {G}_{zv}=\frac{1}{4\pi}\frac{1}{1-{\nu}^{\prime }}\left[\left(3-2{\nu}^{\prime}\right)\left(\frac{Z_P}{X_m^2+{Z}_p^2}-\frac{Z_m}{X_m^2+{Z}_m^2}\right)+2\left(\frac{Z_m{X}_m^2}{{\left({X}_m^2+{Z}_m^2\right)}^2}-\frac{Z_p{X}_m^2}{{\left({X}_m^2+{Z}_p^2\right)}^2}\right)\right]-\frac{1}{2\pi}\frac{1}{1-{\nu}^{\prime }}\times \left(2\left(1-{\nu}^{\prime}\right)\frac{Z_p}{\left({X}_m^2+{Z}_p^2\right)}+\frac{\left[2\left(1-{\nu}^{\prime}\right)z+{z}^{\prime}\right]\left({Z}_p^2-{X}_m^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^2}-\frac{2z{z}^{\prime }{Z}_p\left(3{X}_m^2-{Z}_p^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^3}\right) $$

$$ {G}_{xzv}=\frac{X_m}{4\pi}\frac{1-2{\nu}^{\prime }}{1-{\nu}^{\prime }}\left[\left(\frac{1}{X_m^2+{Z}_p^2}-\frac{1}{X_m^2+{Z}_m^2}\right)+\frac{2}{1-2{\nu}^{\prime }}\left(\frac{Z_p^2}{{\left({X}_m^2+{Z}_P^2\right)}^2}-\frac{Z_m^2}{{\left({X}_m^2+{Z}_m^2\right)}^2}\right)\right]-\frac{X_m}{2\pi}\frac{1}{1-{\nu}^{\prime }}\times \left(4\left(1-{\nu}^{\prime}\right)\frac{z{Z}_p}{{\left({X}_m^2+{Z}_p^2\right)}^2}+\frac{2z{z}^{\prime }{Z}_p\left(3{Z}_p^2-{X}_m^2\right)}{{\left({X}_m^2+{Z}_p^2\right)}^3}\right) $$