Robust machine tool thermal error compensation modelling based on temperature-sensitive interval segmentation modelling technology

Abstract

Establishing a mathematical model that can reflect the relationship between temperature increase and thermal error during machining is the core of thermal error compensation technology for CNC machine tools. The collinearity between temperature-sensitive points and the correlation between temperature-sensitive points and thermal errors are important factors affecting the prediction accuracy and robustness of the thermal error compensation model. Based on the thermal error measurement experiments of the Leaderway-V450 CNC machine tool in different periods of the year, the principal component regression (PCR) modelling algorithm, which can eliminate the collinearity effect, is proposed to establish the thermal error compensation model of the machine tool on the basis of selecting the temperature-sensitive points by using the correlation coefficient. It is compared with the newly proposed ridge regression thermal error compensation modelling algorithm. The results show that the thermal error compensation modelling method proposed in this paper can basically control the Z-direction thermal error of the CNC machine tool spindle within 10 μm with only two temperature sensors and has higher engineering practicability. It is found that the thermal error compensation model of machine tools has a jump interval affected by the ambient temperature. This interval is called the temperature-sensitive interval, and a temperature-sensitive interval subsection point selection algorithm is proposed to build a subsection model on both sides of the segment point. The results show that the Z-direction thermal error of the spindle of CNC machine tools can be basically controlled within 5 μm with only two temperature sensors and that the model is highly robust and has great engineering application value.

1 Introduction

In precision machining, the thermal error accounts for 40–70% of the total machine error [1, 2]. The core of thermal error compensation technology of the CNC machine tool is to establish a mathematical model that can reflect the relationship between the temperature increase in the process of machine tool processing and the thermal error. The collinearity between temperature-sensitive points and the correlation between temperature-sensitive points and thermal errors are important factors affecting the prediction accuracy and robustness of the thermal error compensation model. In particular, the robustness of prediction reflects the predictive accuracy of the thermal error model under various external conditions. It is an important index to measure the thermal error compensation efficiency of machine tools [3]. Generally, in the thermal error compensation model, the stronger the correlation between the input temperature and thermal deformation is, the higher the prediction accuracy of the model [4,5,6]. However, if there is a strong collinearity between the input temperatures of the model, the sensitivity of the model to external interference will be increased [6, 7], which makes it difficult to maintain good fitting accuracy under the influence of environmental temperature, rotational speed, and other factors and reduces the predictive robustness of the model, resulting in the low engineering applicability of the compensation model. In short, to ensure the accuracy and robustness of the multi-input model, the correlation between the input temperature and thermal deformation must be guaranteed, and the interference of collinearity between the input temperatures on the robustness of the model prediction must be reduced. Therefore, the establishment of a thermal error compensation model must solve two key technologies:

• 1. Temperature-sensitive point selection technology

• 2. Thermal error modelling algorithms

In view of the above two key technologies, many scholars at home and abroad have conducted in-depth research to varying degrees.

• 1: Research status of temperature-sensitive point selection technology:

In recent research on temperature-sensitive point selection technology [3, 5, 6, 8,9,10,11,12,13,14,15,16], the Gauss integral, grey system theory, fuzzy clustering method, and finite element simulation technology are widely used in temperature-sensitive point selection. Most of these methods are based on the idea of classification and optimization to select temperature-sensitive points. The purpose of these methods is to reduce the collinearity between temperature-sensitive points and improve the robustness of the modelling algorithm.

• 2: Research status of thermal error modelling algorithms:

The recent research on thermal error modelling algorithms [3, 5, 6, 17,18,19,20,21,22,23,24,25,26,27] has mainly focused on modelling the thermal error by finite element simulation and statistical analysis. The thermal error model based on statistical analysis is beneficial to real-time compensation of the thermal error. Minimizing residuals is the core idea of modelling algorithms, which aim to minimize fitting errors when modelling data are brought into the model. Around this idea, multiple regression and neural networks are commonly used thermal error modelling algorithms.

At present, the commonly used thermal error compensation model has some shortcomings. Taking the robust thermal error compensation model proposed by Miao Enming’s team [5] as an example, the construction process of the model is as follows: First, the temperature measurement points are classified by fuzzy clustering, and the temperature sensors with larger collinearity are classified into one class. Then, the grey relational analysis method is used to select the temperature measurement points that have the greatest similarity with the trend of thermal errors in each category as the temperature-sensitive points. Finally, the selected temperature-sensitive points are brought into the multivariate regression algorithm for modelling. However, in a recent study [6], Miao’s team found that this method of selecting temperature-sensitive points leads to a strong collinearity between the selected temperature-sensitive points. For this reason, they proposed using a ridge regression algorithm to build a thermal error model to suppress the influence of collinearity between temperature-sensitive points on the prediction accuracy and robustness of the thermal error model. However, the ridge regression thermal error modelling algorithm involves the determination of ridge parameters, which requires a large amount of data and is time-consuming.

In this paper, based on the newly proposed correlation coefficient method for temperature-sensitive point selection, the principal component regression modelling algorithm is used for thermal error modelling. The purpose of the ridge regression algorithm is to solve the problem of collinearity between temperature-sensitive points involved in the establishment of a thermal error compensation model, and the same problem can be solved by using a principal component regression algorithm. More importantly, the principal component regression (PCR) algorithm theory eliminates the effect of collinearity among independent variables on the robustness of the model by using PCT to make the principal component variables orthogonal (uncorrelated), such that the collinearity between independent variables obtained by backdating has no effect on the robustness of the model. There is no need to determine additional parameters according to a large number of experimental data to participate in the modelling. Therefore, compared with the ridge regression modelling algorithm, the proposed algorithm can greatly enhance the practical value of engineering.

At the same time, this paper also finds that the thermal error compensation model of the machine tool has a jump interval affected by the ambient temperature, which is named the temperature-sensitive interval, and further proposes a temperature-sensitive interval subsection point selection algorithm to model both sides of it. The results show that the thermal error compensation modelling method proposed in this paper can basically control the Z-direction thermal error of the CNC machine tool spindle within 5 μm with only two temperature sensors and that the model has high robustness, giving it great engineering application value.

2 Introduction to the experiment

This paper carries out a year-round tracking experiment focused on the Z-direction thermal error of the machine tool spindle, which has the greatest variation. The experimental environment is as follows: indoors, no air conditioning, and every batch of experiments having different rotational speeds. A total of 18 batches of experiments were conducted. The measurement of the thermal error involves the “five-point method” from the international standard “Test code for machine tools - Part 3: Determination of thermal effects” (ISO 230-3: 2001 IDT) [28]. At the same time, 10 temperature sensors are arranged in the key parts of the machine to collect temperature values synchronously.

2.1 Measuring device for thermal error

The thermal error measuring device is shown in Fig. 1:

Fig. 1

Thermal error measuring device

The (1) in the figure is called the “test bar”. It is a metal bar, and it is fixed to the spindle. The (3) in the figure is the fixture tool, and it is fixed to the workbench. The (2) in the figure is a displacement sensor, and it is fixed to the fixture tool. The displacement sensor (2) is used to measure the displacement of the “test bar” (1) in the Z-direction to measure the thermal error.

2.2 Position of temperature sensor

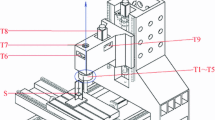
A total of 10 temperature sensors are arranged in each part of the machine tool, which are recorded as T1~T10. These 10 temperature sensors are located near the main heat source of the machine tool, which affects the Z-direction thermal deformation of the machine tool spindle; for specific details, refer to references [3, 5, 6, 11, 29]. The positions of these 10 temperature sensors can reflect the main temperature field of the spindle system, which has a strong correlation with the thermal error. The purpose of these sensors is to measure the temperature near the main heat source of the machine tool, which affects the Z-direction thermal deformation of the machine tool. The temperature sensor is a DS18B20 digital temperature sensor. The range of the sensor is − 55~125 °C. The resolution of the sensor is 0.0625 °C. The accuracy of the sensor can reach ± 0.5 °C (− 10~85 °C). It is mounted onto the machine tool by magnetic adsorption. The position of the temperature sensor on the machine is shown in Figs. 2 and 3 and Table 1.

Fig. 2

Temperature sensor placement diagram

Fig. 3

Detailed positions of T1~T5

Table 1 Position table of temperature sensors

2.3 Thermal error measurement process

The thermal error measurement process is shown in Fig. 4:

Fig. 4

Diagram of the thermal error measurement process

2.4 Test data

The Z-axis thermal error of the Leaderway-V450 CNC machining centre is studied. The experimental data were measured every 3 min with a fixed worktable and idle spindle assumed. Each experiment lasted more than 4 h. A total of 18 batches of experimental data for the whole year were obtained, and the specific parameters are shown in Table 2. The Z-direction thermal error of the machine tool spindle in these 18 batches of experimental data is shown in Fig. 5.

Table 2 18 Batches of experimental data for the whole year

Fig. 5

18 Batch machine tool spindle Z-directional thermal error

3 Analysis of the mechanism of eliminating collinearity by two algorithms

3.1 Collinearity effect mechanism on the accuracy of the multivariate linear regression model

For multivariate linear regression algorithms:

$$ y={k}_0+{k}_1{x}_1+\cdots +{k}_m{x}_m $$

(1)

In formula (1), y denotes the thermal error, and x₁, …, x_m represent the temperature-sensitive points brought into the thermal error compensation model. The model coefficients k = {k₀, k₁, …, k_m} can be estimated by a multiple linear regression algorithm, as shown in Eq. (2):

$$ {\hat{\boldsymbol{k}}}^{\boldsymbol{T}}={\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}{\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}\boldsymbol{Y} $$

(2)

$\hat{\boldsymbol{k}}$ is the estimated value of the model coefficient k,${\boldsymbol{X}}_{\boldsymbol{c}}=\left(\mathbf{1},{\boldsymbol{X}}_{\mathbf{0}}\right)=\left(\begin{array}{ccccc}1& {x}_{11}& {x}_{21}& \dots & {x}_{m1}\\ {}1& {x}_{12}& {x}_{22}& \dots & {x}_{m2}\\ {}\vdots & \vdots & \vdots & \dots & \vdots \\ {}1& {x}_{1n}& {x}_{2n}& \dots & {x}_{mn}\end{array}\right)$

Y=y, y is the thermal error observation value synchronized with the data at the temperature-sensitive point.

Expectation E(k₀, k₁, k₂…) and variance Var(k₀, k₁, k₂…) of the estimated independent coefficient are as follows:

$$ \mathrm{E}\left(\hat{\boldsymbol{k}}\right)=\boldsymbol{k}=\mathrm{E}\left({k}_0,{k}_1,{k}_2\dots \right)={k}_0,{k}_1,{k}_2 $$

(3)

$$ \mathrm{Var}\left(\hat{\boldsymbol{k}}\right)=\mathrm{Var}\left({k}_0,{k}_1,{k}_2\dots \right)=\operatorname{diag}\left[{\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}\right]\upsigma $$

(4)

Among them, σ is the sum of squares of the model residuals and $\upsigma =\sum \limits_{i=1}^n{\left({y}_i-{\hat{y}}_i\right)}^2$;$\operatorname{diag}\left[{\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}\right]$ are column vectors composed of principal diagonal elements of matrix ${\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}$. From formula (4), it can be seen that the variance of coefficients estimated in the multivariate linear regression model is proportional to ${\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}$ principal diagonal elements. However, the value of ${\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}$ principal diagonal elements is related to the degree of collinearity between temperature observations at temperature-sensitive points. If the collinearity is large, ${\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}$ will approach the singular matrix, that is, it will become very small, which will increase the value of ${\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}$ principal diagonal elements, resulting in the estimation of model coefficients easily deviating from the true value, and the probability of model coefficients being too large will increase significantly.

3.2 The mechanism of ridge regression to eliminate collinearity

For the coefficient estimation formula of the multivariate linear regression model shown in formula (1), the ridge regression algorithm proposed by Hoerl [30] estimates the coefficients of the model as follows:

$$ {\hat{\boldsymbol{k}}}^{\ast \boldsymbol{T}}={\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}+\beta \boldsymbol{I}\right)}^{-1}{\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}\boldsymbol{Y} $$

(5)

β is the ridge parameter, and β ≥ 0,I is the unit matrix. From formula (5), we can see that the ridge regression algorithm adds a normal number matrix βI to${\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}$, which means that the ridge regression algorithm abandons the unbiased estimation of model coefficients and reduces the degree of ${\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}$ approaching the singular matrix caused by collinearity. This has been proved by Hoerl [30]. A. E. Hoerl proved that by reasonably increasing the ridge parameter β, one can greatly reduce the variance of the estimated coefficient of the model coefficient under the condition that the estimated value of the model coefficient deviates slightly from the true value, as shown in Fig. 6.

Fig. 6

Probability distribution of estimated coefficients in multivariate linear regression and ridge regression models with collinear problems

MLR refers to the multivariate linear regression model, and RR refers to the ridge regression algorithm model. Figure 6 shows a comparison of the probability distribution of the estimation coefficients between the multivariate linear regression and ridge regression models when the input variables of the model are collinear. It can be seen from the graph that although the ridge regression deviates slightly from the expected and true values of the model coefficients estimated by multiple linear regression, the probability of the model coefficients approaching the true values increases greatly due to the small variance, which restrains the influence of collinearity on the model coefficients estimated and improves the prediction accuracy and robustness of the model.

3.3 The mechanism of principal component regression to eliminate collinearity

The core idea of the principal component regression algorithm is dimensionality reduction, which combines multiple features in high-dimensional space into a few unrelated principal components and contains most variation information in the original data, thus reducing the multiple collinearity between features. That is, on the premise of minimizing data loss as much as possible, after linear transformation and discarding part of the information, a few new comprehensive variables (principal component variables) are used to replace the original multi-dimensional variables.

Variation information in the above concepts is measured by variance. The first principal component is a vector in high-dimensional space, and the sum of squares of distances from all points to straight lines is the smallest. As shown in Fig. 7, the sum of squares of distances from all points to the blue line is the smallest, which represents the first principal component vector. With the first principal component, the principal component can be selected backwards, and the principal components are orthogonal vectors. The yellow line shown in Fig. 7 represents the second principal component vector. For high-dimensional space, there can be countless orthogonal vectors of a vector. After determining the first principal component, the vector searched by the sum of distance squares in the orthogonal vector is regarded as the second principal component, and then the principal component is analogized in turn.

Fig. 7

Principal component regression algorithms

Suppose that for two strongly collinear independent variables x₁ and x₂, the measured values of the two variables are drawn. Taking x₁ and x₂ as two coordinate axes of the coordinate system, respectively, and then making scatter plots of x₂ changing with x₁ according to the measured data, we find that there is a strong linear relationship between them. However, if by transformation, x₁ and x₂ are transformed into new variables z₁ and z₂, then the following holds:

$$ \left\{\begin{array}{c}{z}_1={p}_{11}{x}_1+{p}_{12}{x}_2\\ {}{z}_2={p}_{21}{x}_1+{p}_{22}{x}_2\end{array}\right. $$

(6)

In the process of transformation, if the correlation between z₁ and z₂ is removed, two completely non-collinear independent variables, i.e., principal component variables, will be obtained. The effect of collinearity on model accuracy can be eliminated by using principal component variables and regression. In the process of transformation, if the correlation between z₁ and z₂ is removed, two completely non-collinear independent variables, i.e., principal component variables, will be obtained. The effect of collinearity on model accuracy can be eliminated by using principal component variables and regression. It can also be seen from Fig. 6 that the information contained in the two principal component variables is completely different. When z₁ increases gradually, z₂ fluctuates only in a small range near zero. Therefore, z₂ is removed from the model, and only the main information z₁ is retained. This will help to further eliminate the interference of noise information in the data to the accuracy of the model. That is, the principal component regression algorithm is used to obtain the function expression:

$$ \mathrm{y}={k}_0+{k}_1{z}_1 $$

(7)

By introducing formula (6) into formula (7), the following results are obtained:

$$ \mathrm{y}={k}_0+{k}_1\left({p}_{11}{x}_1+{p}_{12}{x}_2\right) $$

(8)

Formula (8) still contains independent variables x₁ and x₂ with collinearity, but it eliminates the influence of collinearity on the robustness of the model. This is because the so-called elimination of collinearity does not mean eliminating the collinearity between independent variables, such that the independent variables in the model do not have collinearity, but means making the collinearity between independent variables in the model have no effect or no obvious influence on the robustness of the model.

The effect of collinearity on the robustness of the model occurs in the least squares step:

$$ \left(\begin{array}{c}{k}_0\\ {}\begin{array}{c}{k}_1\\ {}\vdots \end{array}\\ {}{k}_l\end{array}\right)={\left({\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}{\boldsymbol{X}}_{\boldsymbol{c}}\right)}^{-\mathbf{1}}{\boldsymbol{X}}_{\boldsymbol{c}}^{\boldsymbol{T}}\boldsymbol{Y} $$

(9)

For the PCR algorithm, the only step that involves least squares is that involving finding the pre-principal component coefficients:

$$ \left(\begin{array}{c}{b}_1\\ {}\vdots \\ {}{b}_k\end{array}\right)={\left({\boldsymbol{Z}}^T\boldsymbol{Z}\right)}^{-1}{\boldsymbol{Z}}^T{\boldsymbol{y}}^{\ast } $$

(10)

y^∗is a column vector consisting of all measurements of variable y^∗.

$$ {y}^{\ast }=y/{STD}_y $$

(11)

STD_y is the standard deviation of y.

$$ \boldsymbol{Z}=\left({\boldsymbol{Z}}_{\mathbf{1}}{\boldsymbol{Z}}_{\mathbf{2}}\cdots {\boldsymbol{Z}}_{\boldsymbol{k}}\right)\kern1em k=1,2,\dots $$

(12)

Z_k is a column vector consisting of all measurements of variable Z_k.

The principal component variables have become orthogonal (irrelevant) through the COV matrix. Therefore, although the final modelling results obtained by principal component transformation contain independent variables x₁and x₂ with coefficients not equal to 0, the collinearity between x₁and x₂ has no effect on the robustness of the model.

4 Comparing and analysing the accuracy of the two algorithms in establishing models

4.1 Selection of temperature-sensitive points by correlation coefficient method

Liu Hui’s article [6] has proved that when using an algorithm that can effectively eliminate the collinearity effect, the temperature-sensitive points can be selected with the correlation coefficient method, which can reduce the change in temperature-sensitive points and make the model more robust and more accurate in prediction. In this paper, the correlation coefficient method is used to select temperature-sensitive points. The results of selecting temperature-sensitive points for the 18 batches of experimental data covering the whole year are shown in Table 3.

Table 3 Screening results of temperature-sensitive points for 18 batches of data

The temperature-sensitive points selected by the correlation coefficient have little variation, which indicates that the temperature-sensitive points and thermal errors do have a long-term and stable strong correlation.

4.2 Machine tool thermal error compensation model based on ridge regression

In this paper, the method of selecting ridge parameters mentioned in Liu Hui’s article [6] is used, and the β value of ridge parameters is gradually increased from β=0 to β=25 for the experimental data covering the whole year. The prediction accuracy and robustness of the model with different β values are analysed to find the best ridge parameters for modelling. Finally, the optimum ridge parameter is determined to be β = 20, and the model R-M1~R-M18 is established based on the 18 batches of experimental data. Due to limited space, only some models are listed:

$$ {\displaystyle \begin{array}{c}R-M1:y=2.04+2.10x1+1.78x2\\ {}\vdots \\ {}R-M18:y=2.44+3.97x1+1.41x2\end{array}} $$

The standard deviation of the prediction residual of the 18 batch models based on the ridge regression algorithm is shown in Fig. 8 (in which fitting is regarded as the prediction of the model itself).

Fig. 8

Standard deviation of prediction residuals for 18 batch models based on ridge regression algorithm

4.3 Establishment of thermal error compensation model of machine tool based on principal component regression

The temperature-sensitive points selected by correlation coefficients are brought into the principal component regression (PCR) algorithm for modelling, and the model P-M1~P-M18 is established based on the 18 batches of data. Due to limited space, only some models are listed:

$$ {\displaystyle \begin{array}{c}P-M1:y=0.61+2.10x1+2.07x2\\ {}\vdots \\ {}P-M18:y=0.66+3.16x1+2.91x2\end{array}} $$

The standard deviation of the prediction residual of the 18 batch models based on the principal component regression algorithm is shown in Fig. 9 (in which fitting is regarded as the prediction of the model itself

Fig. 9

Standard deviation of prediction residuals for 18 batch models based on principal component regression algorithm

4.4 Comparison and analysis of the accuracy of the two models

The correlation coefficient method is used to select the temperature-sensitive points for the 18 batches of experimental data. The ridge regression algorithm and principal component regression algorithm are used to build two models. The accuracy analysis of these two models is shown in Figs. 10 and 11.

Fig. 10

Precision accuracy analysis of ridge regression model

Fig. 11

Prediction accuracy analysis of principal component model

Among them, S is the fitting standard deviation of the model, which is used to characterize the fitting accuracy of the model. The smaller the value is, the higher the fitting accuracy of the model. S_m is the mean of the prediction standard deviation of the model for other batch data, which is used to characterize the prediction accuracy of the model. The smaller the value is, the higher the prediction accuracy of the model. S_d is the standard deviation of the standard deviation for the prediction of other batches of data. It is used to characterize the dispersion degree of the prediction accuracy of the model. The smaller the value is, the higher the robustness of the model.

The formulas for S_m and S_d are as follows:

$$ {S}_m=\left(\sum \limits_{i=1}^{17}{S}_{ri}\right)/17 $$

(13)

$$ {S}_d=\sqrt{\left[\sum \limits_{i=1`}^{17}{\left({S}_{ri}-{S}_m\right)}^2\right]/16} $$

(14)

From Figs. 10 and 11, it can be seen that under the premise of selecting temperature-sensitive points by the correlation coefficient method, the thermal error compensation model established by the principal component regression algorithm has lower fitting accuracy, prediction accuracy, and model robustness than the those of the model established by the ridge regression algorithm. However, it still ensures that the Z-direction thermal error of the CNC machine tool spindle can be basically controlled within 10 μm with two temperature sensors [6]. More importantly, the completeness of the principal component regression modelling algorithm theory makes it unnecessary to determine additional parameters based on the experimental data covering the whole year. Therefore, compared with the ridge regression modelling algorithm, the proposed algorithm can greatly enhance the practical value to engineering.

5 Study on temperature-sensitive intervals of the two models

Further analysis of the two models reveals that the thermal error compensation model established by the two algorithms combined with the 18 batches of data has a jump interval affected by the ambient temperature. In this paper, the interval is called a temperature-sensitive interval, and a temperature-sensitive interval subsection point selection algorithm is proposed to select subsection points for subsection modelling.

5.1 Temperature-sensitive intervals of the two models

Draw the data in Fig. 8 as a three-dimensional model, as shown in Fig. 12, and draw the effect of the ambient temperature on the data in Fig. 8, as shown in Fig. 13. An analysis of Figs. 12 and 13 shows that for the 18 batch models based on the ridge regression algorithm, the low-temperature section (R-M1~R-M10) predicts the low-temperature section and the high-temperature section (R-M11~R-M18) predicts the high-temperature section, i.e., the mutual prediction effect between the same temperature sections is better, the average prediction accuracy of the low-temperature section is 4.72 μm, and the average prediction accuracy of the high-temperature section is 4.53 μm. The average prediction accuracy of the high-temperature section and the low-temperature section reached 9.22 μm (low-temperature section predicted high-temperature section) and 13.09 μm (high-temperature section predicted low-temperature section), respectively, and the prediction accuracy decreased sharply.

Fig. 12

Three-dimensional model of each batch model based on the ridge regression algorithm

Fig. 13

Prediction accuracy trend of 18 batch models based on ridge regression algorithm

Similarly, the data in Fig. 9 are drawn as a three-dimensional model, as shown in Fig. 14, and the effect of the ambient temperature on the data in Fig. 9 is shown in Fig. 15. An analysis of Figs. 14 and 15 shows that for the 18 batch models based on the principal component regression algorithm, the low-temperature section (P-M1~P-M10) predicts the low-temperature section and the high-temperature section (P-M11~P-M18) predicts the high-temperature section, i.e., the mutual prediction effect between the same temperature sections is better. The average prediction accuracy of the low-temperature section is 5.22 μm and that of the high-temperature section is 4.99 μm. The average prediction accuracy of the high-temperature section and the low-temperature section reached 10.18 μm (low-temperature section predicts high-temperature section) and 15.73 μm (high-temperature section predicts low-temperature section), respectively, and the prediction accuracy decreased sharply.

Fig. 14

Three-dimensional model of each batch model based on the principal component regression algorithm

Fig. 15

Prediction accuracy trend of 18 batch models based on principal component regression algorithm

The above shows that there is a sudden change in the thermal error characteristics of machine tools due to the change in ambient temperature, which will seriously affect the accuracy of the thermal error compensation. The temperature range from low-temperature to high-temperature (R(P)-M10~R(P)-M11) is named the temperature-sensitive interval.

5.2 Segmented point selection algorithms for temperature-sensitive interval

The focus here is on the abrupt change in the thermal error characteristics caused by the change in ambient temperature of the machine tools. To improve the accuracy of the thermal error compensation, a piecewise point selection algorithm in a temperature-sensitive interval is proposed to select piecewise points for piecewise modelling. The flow chart of the temperature-sensitive section point selection algorithm is shown in Fig. 16.

Fig. 16

Flow chart of the temperature-sensitive interval subsection point selection algorithm

The specific steps of the algorithm are as follows:

• 1. First, the prediction accuracy tables of the thermal error compensation model for other batch data are obtained, and the Kolmogorov-Smirnov test of a single sample is used to verify whether the sequence of prediction accuracy of each model for other batch data obeys the normal distribution or another distribution.

The K-S test of a single sample mainly examines the maximum absolute value

$$ {\mathrm{D}}_{max}=\max \left|{\mathrm{S}}_n\left(\mathrm{x}\right)-{F}_0\left(\mathrm{x}\right)\right| $$

(15)

of the empirical distribution function and theoretical distribution function. In formula (11), S_n(x) is the cumulative probability distribution function of random sample observations, i.e., the empirical distribution function with a sample size n; F₀(x) is a specific cumulative probability distribution function, i.e., the theoretical distribution function. If S_n(x) and F₀(x) are very close to each x value, the fitting degree between the empirical distribution function and the theoretical distribution function is very high. It is reasonable to think that the sample data come from the population subject to the theoretical distribution. The steps of the single-sample K-S test are as follows:

• (1) Hypothesis:

$$ {H}_0:{S}_n(x)={F}_0(x),{H}_1:{S}_n(x)\ne {F}_0(x). $$

(16)

• (2) Calculate the statistic D_max.

• (3) According to the given significance level α and the amount of sample data n, the critical value D_α of the single-sample K-S test is determined.

• (4) If D_max < D_α, H₀ cannot be rejected at the level of significance of α; otherwise, H₀ can be rejected.

Because the data in this paper obey a normal distribution through the K-S test of a single sample, the following are illustrated with a normal distribution as an example.

• 2. The confidence interval of σ² is derived from the parameter estimation of a single normal population when μ is unknown.

  The parameters of the normal distribution are obtained from the unbiased estimation $\overline{\boldsymbol{x}}$ of μ. When μ is unknown, the random variable

$$ {\chi}^2=\left(n-1\right){S}^2/{\sigma}^2\sim {\chi}^2\left(n-1\right) $$

(17)

Then, the confidence interval of σ with a confidence coefficient of 1 − α is obtained as $\left(\sqrt{\frac{\left(n-1\right)}{\chi_{\alpha /2}^2\left(n-1\right)}}\mathrm{S},\sqrt{\frac{\left(n-1\right)}{\chi_{1-\alpha /2}^2\left(n-1\right)}}\mathrm{S}\right)$, and then the normal distribution x~N(μ, σ²) is obtained by unbiased estimation of $\overline{x}$ of μ.

• 3. According to the obtained normal distribution, the prediction accuracy of the thermal error compensation model for the remaining batches of data falls outside the 3σ range of the normal distribution. If it is outside the scope, this point is marked; otherwise, it is not marked. When all the thermal error compensation models have completed the above steps, the judgement table of the modelling points in the temperature-sensitive interval can be obtained.

• 4. According to the judgement table, the jump threshold is selected according to the actual engineering needs, and the modelling points of the temperature-sensitive interval are obtained.

According to the actual engineering needs, the jump threshold is 90%, and the confidence is 99%. The judgement result of temperature-sensitive interval segmentation modelling points based on the ridge regression algorithm for the 18 batch models is shown in Fig. 17. The judgement result of the temperature-sensitive interval segmentation modelling points based on the 18 batch models established by the principal component regression algorithm is shown in Fig. 18:

Fig. 17

Temperature-sensitive interval segmentation modelling point judgement result based on ridge regression algorithm for 18 batch models

Fig. 18

Temperature-sensitive interval segmentation modelling point judgement result based on 18 batch models established by principal component regression algorithm

In Figs. 17 and 18, the black blocks represent the emergence of the segmentation points for the prediction accuracy of the data of this line using the thermal error compensation model of this row. In contrast, the white blocks indicate that there are no segmentation points in the prediction accuracy.

From Figs. 17 and 18, it can be seen that the prediction accuracy of the high-temperature segment (R(P)-M11~ R(P)-M18) model for batches of data above 24 °C is improved from 24 °C (Batch 11). Most of the low-temperature segment (R(P)-M1~ R(P)-M10) that models the prediction accuracy of batch data above 24 °C (11th data batch) deteriorates, that is, 94.4% of the data at 24 °C have jumped, which is larger than the selected threshold. Therefore, 24 °C is selected as the modelling point of the temperature-sensitive interval. The mean predictive accuracy of the two models in the high-temperature section is 3.75 μm (ridge regression) and 4.18 μm (principal component), respectively, at 24 °C (11th batch). The mean prediction accuracy of the two models in the low-temperature section is 4.97 μm (ridge regression) and 5.75 μm (principal component). It can be concluded that the prediction accuracy of the high-temperature section model is better than that of the low-temperature section model at 24 C (11th batch); thus, the high-temperature section model is adopted at 24 C (11th batch).

5.3 Piecewise modelling of temperature-sensitive interval

According to the temperature-sensitive interval subsection point selection algorithm, the subsection point is 24 C (11th batch of data). Based on the ridge regression algorithm and the temperature-sensitive interval subsection modelling, the Z-direction thermal error compensation model of the machine tool spindle is established as follows:

$$ y=\left\{\begin{array}{c}3.13+2.75x1+1.39x2\kern0.5em T<24{}^{\circ}C\\ {}2.44+3.97x1+1.41x2\kern0.5em T\ge 24{}^{\circ}C\end{array}\right. $$

(18)

The model is recorded as R-M0.

The Z-direction thermal error compensation model of the machine tool spindle is based on principal component regression and piecewise modelling of the temperature-sensitive interval, which is established with 24 C (11th batch of data) as the demarcation point as follows:

$$ y=\left\{\begin{array}{c}0.87+2.24x1+2.22x2\kern0.5em T<24{}^{\circ}C\\ {}\begin{array}{cc}0.55+3.02x1+2.78x2& T\ge 24{}^{\circ}C\end{array}\end{array}\right. $$

(19)

The model is recorded as P-M0.

The prediction accuracy of the R-M0 and P-M0 models for the 18 batches of data covering the whole year is shown in Table 4. The prediction accuracy analysis of the R-M0 and P-M0 models is shown in Table 5.

Table 4 Prediction accuracy of R-M0 and P-M0 for 18 batches of data covering the whole year (μm)

Table 5 Precision analysis of R-M0 and P-M0 models

It can be seen that for the phenomenon of the temperature-sensitive interval existing in CNC machine tools, the temperature-sensitive interval modelling method can be used to achieve the thermal error of the CNC machine tool spindle Z to 5 μm with two temperature sensors. The piecewise modelling technology of the temperature-sensitive interval can improve the prediction accuracy of the correlation coefficient selection temperature-sensitive point, the machine tool thermal error compensation model based on the ridge regression algorithm, and the machine tool thermal error compensation model based on principal component regression by a factor of approximately two. Moreover, it can reduce the dispersion degree of the prediction accuracy of the model, improve the prediction robustness of the model throughout the year, and make the prediction accuracy of the model change within ± 2 μm. The piecewise modelling technology of temperature-sensitive intervals has great engineering application value.

6 Conclusions

• 1. This paper is based on a Z-direction thermal error experiment of the idle spindle of the Leaderway-V450 NC machining centre under different conditions (different rotational speeds and different ambient temperatures). On this basis, the PCR algorithm is used to establish the Z-direction thermal error compensation model of machine tools on the premise of using the correlation coefficient method to select temperature-sensitive points, and the model is compared with the newly proposed ridge regression algorithm. In this paper, the mechanism of ridge regression and principal component regression to eliminate collinearity is analysed. It is proved that the PCR modelling theory does not need to determine additional parameters based on experimental data covering the whole year. Mathematical analysis of the two models is carried out based on experimental data covering the whole year. The results show that the Z-direction thermal error of the CNC machine tool spindle can be basically controlled within 10 μm by using a PCR modelling algorithm with only two temperature sensors. Therefore, the PCR modelling algorithm has stronger engineering practical value.

• 2. In this paper, the ridge regression model and the principal component regression model are further analysed based on experimental data covering the whole year. It is found that the Z-direction thermal error compensation model of machine tools established by the two algorithms has a jump range affected by the ambient temperature. The interval is called the temperature-sensitive interval, and a piecewise point selection algorithm for the temperature-sensitive interval is proposed to select piecewise points for piecewise modelling.

• 3. It is found that the Z-direction thermal error of the CNC machine tool spindle can be basically controlled within 5 μm with only two temperature sensors by using the piecewise modelling technology of the temperature-sensitive interval. The piecewise modelling technology of the temperature-sensitive interval can improve the prediction accuracy of the machine tool thermal error compensation model based on the ridge regression algorithm and the machine tool thermal error compensation model based on principal component regression by approximately two times. Moreover, it can reduce the dispersion degree of the prediction accuracy of the model, improve the prediction robustness of the model over the course of a year, and keep the prediction change of the model over the whole year to within ± 2 μm. This method has great engineering application value.

• 4. “Robust Machine Tool Thermal Error Compensation Modelling Based on Temperature-Sensitive Interval Segmentation Modelling Technology” can basically control the Z-direction thermal error of the CNC machine tool spindle within 5 μm with only two temperature sensors, and it does not require determining additional parameters according to the annual experimental data to participate in the modelling; thus, it has great engineering application value.

• 5. The predictive effect of “Robust Machine Tool Thermal Error Compensation Modelling Based on Temperature-Sensitive Interval Segmentation Modelling Technology” on the thermal error is validated only when the machine tool is idle, and the compensation effect of the thermal error in the tangent state requires further validation.