The use of support vector machine, neural network, and regression analysis to predict and optimize surface roughness and cutting forces in milling

Abstract

In the present study, prediction and optimization of the surface roughness and cutting forces in slot milling of aluminum alloy 7075-T6 were pursued by taking advantage of regression analysis, support vector regression (SVR), artificial neural network (ANN), and multi-objective genetic algorithm. The effects of process parameters, including cutting speed, feed per tooth, depth of cut, and tool type, on the responses were investigated by the analysis of variance (ANOVA). Grid search and cross-validation methods were used for hyperparameter tuning and to find the best ANN and SVR models. The training algorithm of developed NNs was one of the hyperparameters which was chosen from Levenberg-Marquardt and RMSprop algorithms. The performance of regression, SVR, and ANN models were compared with each other corresponding to each machining response studied. The ANN models were integrated with the non-dominated sorting genetic algorithm (NSGA-II) to find the optimum solutions by means of minimizing the surface roughness and cutting forces. In addition, the desirability function approach was utilized to select proper solutions from the statistical tools.

1 Introduction

Machining is considered as a complex mode of manufacturing process, involving several input variables. Although careful selection of input variables is a critical step to achieve desired machining products, this is not a simple decision due to complexity of the process and lack of suitable formulas to establish relationships between input and output variables. In addition, proper selection of input variables, such as cutting parameters, is crucial because of its strong influence on machining economy, work part quality as well as production time. Therefore, prediction of the outcome of a metal removal process is a crucial stage of process planning.

There are three major categories for modeling the machining processes, including numerical, analytical, and empirical models. Empirical models can take into account almost all machining parameters and, hence, are more practical. However, numerous experiments are needed in order to employ empirical models, such as machine learning methods [1].

End milling process has a wide range of applications in numerous industrial sectors. In addition, modeling of milling process is more complicated than the other traditional machining operations, such as turning. Periodic interactions between the milling cutting tool and the work part tend to appear as cyclic cutting forces, complicating the process modeling [28]. Moreover, end milling operation is one of the final steps in manufacturing in most cases. Controlling this operation, therefore, is significant in terms of the surface integrity [24]. With regard to these facts, prediction and optimization of surface roughness and cutting forces in end milling through empirical modeling and metaheuristic optimization are the focus of attention in this work.

Several research have been conducted to model and optimize the surface roughness in milling operations in the past few years [12, 13, 15, 20]. Karkalos et al. [15] used response surface methodology (RSM) and artificial neural network (ANN) models to investigate surface roughness in milling of titanium alloy by using depth of cut, cutting speed, and feed rate. Cutting parameters were also optimized through RSM and it became clear that higher depth of cut and cutting speed and lower feed rate reduce surface roughness. Authors concluded that ANN model is more precise. Mahesh et al. [20] examined the effect of radial rake angle, feed rate, radial and axial depth of cut, and spindle speed on surface roughness in end milling of AA 6063 by combining RSM for prediction and GA for optimization. It was observed that radial rake angle has significant effect on the output variables and the combination of techniques performs rather well. Using potential support vector machine (PSVM) and RSM, Kadirgama et al. [12] studied the impact of radial and axial depth of cut, cutting speed and feed rate on surface roughness in end milling of AA 6061-T6. It was concluded that better modeling results were observed when PSVM was used. Furthermore, radial depth of cut has the least effect on surface roughness variation. Kant and Sangwang [13] took advantage of the combination of ANN and GA to predict and optimize the surface roughness in face milling by controlling the variation of cutting speed, feed rate, depth of cut, and flank wear. It was exhibited that under similar experimental conditions, ANN is superior to regression and fuzzy logic models.

The majority of the reported works in the literature have considered cutting forces besides the other output parameters, such as surface roughness [8, 19, 21]. Cutting force, surface roughness, and power consumption in milling of aluminum metal matrix composite were predicted by using RSM and optimized through multi-objective optimization approaches by Malghan et al. [21]. It became apparent that spindle speed has the most prominent impact on all the responses, followed by feed rate and depth of cut. Karabulut [14] studied the effect of workpiece material, cutting speed, depth of cut and feed rate on surface roughness, and the resultant cutting force in milling of AA 7039 and Al2O3 reinforced composite. Moreover, the Taguchi method was used for optimization purposes, and it was shown that ANN was superior to the regression model in response prediction. The results of ANOVA also denoted that the most effective input variables for surface roughness and cutting force are the work material and feed rate respectively. Farahnakian et al. [7] developed a PSO based neural network (PSONN) to model surface roughness and the resultant cutting force separately in milling a polymer nanocomposites. Feed rate had the most dominating influence on the output parameters, followed by spindle speed. It was demonstrated that PSONN had better performance and faster convergence than conventional neural networks.

Cutting tool geometry and coating properties play important roles in the machining performance and final quality of the machined part. For instance, several studies reported that insert nose radius and coating material have a substantial influence on surface roughness and cutting forces in milling operations [17, 18, 23]. However, few studies have employed cutting tool properties as process parameters to optimize machining conditions, particularly in milling. For instance, Pinar et al. [25] optimized the surface roughness in pocket milling in two different cooling conditions by using the Taguchi method and considering the effect of cutting speed, feed rate, radial/axial depth of cut, and nose radius of an uncoated cemented carbide cutting tool. Using the Taguchi and regression models, Kivak [16] conducted a research to study the effects of PVD TiAlN- and CVD TiCN/Al2O3-coated carbide inserts, along with cutting speed and feed rate, on surface roughness and tool wear under dry milling conditions. In another work, Niknam et al. [22] utilized desirability function technique to optimize surface roughness and exit burr size by including depth of cut, cutting speed, feed per tooth, and different kinds of end milling inserts and workpiece materials. With regard to these studies, various tools with different insert coating and nose radius were employed to predict and optimize the output parameters in this work.

Less attention has been paid to the use of support vector machine (SVM) in prediction of machining outputs. Çaydas and Ekici [2] showed that support vector regression (SVR) outperformed ANN in predicting surface roughness in turning operation. Moreover, Gupta et al. [9] compared the performance of regression model and AI techniques, such as SVM and ANN, in separate optimization of the surface roughness, tool wear, and the required power by GA algorithm. They exhibited the merit of SVM in prediction of turning parameters. In another case [29], SVM was coupled with multi-objective GA to optimize processing time and electrode wear in micro-electrical discharge machining (EDM), which produced satisfying results.

In the present work, the cutting speed, depth of cut, feed rate, and type of cutting tool are chosen as the input variables to predict and optimize the surface roughness and cutting forces in slot milling of AA 7075-T6. According to the literature review, some authors [2, 9] have reported that SVM outperformed the ANN model in prediction of turning responses, but a study comparing ANN and SVM performance in predicting the surface roughness and/or cutting forces in milling operations has not been conducted, to the authors’ knowledge. In addition, the application of a dummy variable to represent nominal machining parameters, such as type of cutting tool or workpiece material, has not been appropriately investigated in prediction and optimization of responses. Thus, the main aims of the present paper can be categorized to three major tasks (1) The performance of ANN, SVM, and regression models in predicting the surface roughness and cutting forces in milling are compared. (2) Non-dominated sorting genetic algorithm-II (NSGA-II), coupled with desirability function approach, is selected to minimize the responses simultaneously with regard to its great performance as well as its limited use in the milling optimization. (3) Utilization of dummy variables is presented to incorporate tool type, as a non-numeric machining parameter, into prediction and optimization of the responses. The rest of the paper is organized as follows. The experimental setup and design of the experiment is presented in Section 2. A brief overview of ANN, SVM, NSGA-II, and desirability function are stated in Section 3. Section 4 highlights the development of prediction models, comparison of predictive models, and optimization of responses. Conclusions are presented in Section 5.

2 Experimental procedure

A multi-level full factorial experimental design with 54 trials was used to examine the effect of cutting speed (V_c), depth of cut (a_p), feed per tooth (f_z), and cutting tool type (Tool) on surface roughness and cutting forces in milling of AA 7075-T6. The experimental factors and their levels are shown in Table 1. An end milling cutting tool with three teeth (Z = 3), tool diameter (D) 19.05 mm and Helix angle 30^° with various carbide inserts, having different nose radius and coatings (Table 1), was used to perform slot milling operation under dry conditions. Coatings were selected based on their suitability for the cutting conditions and work-piece material. The rectangular blocks of AA 7075-T6 were used in milling. This material finds its applications mostly in aviation, aerospace, automotive, and arms industries.

Table 1 Experimental parameters and their levels

Single-pass slot milling tests were performed on a three-axis CNC machine tool (HURON - K2X10, power 50 kW, speed 28,000 rpm, torque 50 Nm). A three-axis table dynamometer (Kistler 9255-B) with a sampling frequency of 1000 Hz was employed to obtain three orthogonal force components in Cartesian coordinates. After finishing the operation, the most widely used roughness parameter, Ra, was measured by using surface profilometer Mitutoyo SJ 400.

To avoid possible deviations in the test results because of tool wear, new insert was utilized after each milling operation. In addition, the average values of two experiments’ records were considered as milling responses for modeling and optimization of the operation. A brief summary of observed responses data is exhibited in Table 2. Moreover, the following simplifying assumptions and checks are made to develop the experimental setup and to reduce the effect of work material adhesion to the cutting tool which is a major concern in AA machining.

• The vibrations in the machine and cutting tools were evaluated through preliminary tests. The stability of the cutting process, as a result, was verified and the milling operation was assumed chatter free.

• By using rigid tools and work-piece fixtures, the deflections of cutting tool and work-piece were neglected.

Table 2 A brief summary of responses value

3 Modeling approach

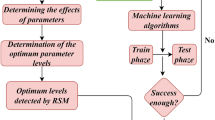
Figure 1 exhibits the research procedure followed in this study. Having conducted the milling of AA, regression analysis, support vector regression, and neural network are employed to predict each response separately. The results of analysis of variance are used to choose input variables for SVR modeling. Moreover, varied modeling techniques, such as hyperparameter tuning, are applied to make the best possible predictive models out of the limited data. In the next step, various created models for each response are compared with each other in order to find the most suitable model among regression analysis, SVR, and ANN. The selected models for each response are then coupled with NSGA-II so that the optimum cutting conditions for simultaneous minimization of surface roughness and cutting forces are acquired. Since many optimum solutions are obtained by NSGA-II, desirability function approach is used to find suitable solutions out of the Pareto Front.

Fig. 1

The research procedure

3.1 Artificial neural network

The structure of ANN is inspired by the biological neural network to mimic the brain performance to solve complex problems. The artificial neurons are connected to each other to construct the ANN. The input vector of each neuron is multiplied by the weight vector, added to a bias term to comprise the input of an activation function. The output of the activation function is the output of a neuron. The equation of the process, shown in Fig. 2, is as follows:

$$ {y}_k=\varphi \left(\sum \limits_{j=1}^m{w}_{kj}{x}_j+{b}_k\right) $$

(1)

where y_k and b_k are respectively the output and bias term of the k-th neuron and φ is the activation function. In addition, x_j and w_kj , j = 1,2, … ,m are the j-th input of the neuron and its synaptic weight respectively.

Fig. 2

An artificial neuron

Feedforward neural network is one of the most popular networks for function approximation, which entails one or more hidden layers besides input and output layers, as it can be seen in Fig. 5. The function of hidden layers is to discover the salient features of the input data, but the input layer does not process information. Input signal is propagated through neurons in the network on a layer-by-layer basis while the synaptic weights are fixed. The output layer presents the amounts of response variables.

Backpropagation (BP) algorithms are usually used to train feedforward neural networks. In BP algorithms, an error signal is propagated backward to successively adjust connection weights and biases through minimizing a cost function. The cost function is defined as:

$$ C=\frac{1}{2}\ \sum \limits_{j\in K}{e}_j^2=\frac{1}{2}\ \sum \limits_{j\in K}{\left({d}_j-{y}_j\right)}^2 $$

(2)

where C is the cost function and the set K includes all neurons in the output layer. e_j, d_j , and y_j are respectively error term, desired response, and output of the j-th neuron in the output layer.

There are various criteria to stop a BP algorithm. If the algorithm iterates for a predefined epoch number, training can be halted. Early stopping method, which takes validation set error into account, is another rule to stop the training algorithm.

The Levenberg-Marquardt and RMSProp algorithms were chosen for neural network training in this study. The Levenberg-Marquardt algorithm (LMA) is a good choice to train small- and medium-sized networks. The LMA is based on the gradient descent and Gauss-Newton algorithms so that the convergence and the speed of the algorithm are assured. This is because the gradient descent algorithm converges so slowly to the optimum solution; however, the Gauss-Newton algorithm performs fast near a local or global minimum. In LMA, the Jacobian matrix (J) is used to approximate the Hessian matrix of the cost function and to rewrite the gradient vector (g) of the cost function w.r.t. the network parameters. Thus, weights are updated through the equation:

$$ {w}_{n+1}={w}_n-{\left({J}_n^T{J}_n+\mu I\right)}^{-1}{J}_n^T{e}_n $$

(3)

where e is the error vector, w is weight vector, and n is the number of iterations. Term μ is a positive scalar parameter, and I is the identity matrix. The parameter μ plays a key role in LMA. When the cost function increases, μ is multiplied by an update factor so that LMA acts like the gradient descent algorithm. On the other hand, whenever there is a decrement in the cost function, μ is divided by the update factor to simulate the Gauss-Newton method [10].

In the gradient descent, the learning rate has a significant effect on the speed and performance of the algorithm. However, it is difficult to properly select the learning rate. Moreover, it is not possible to use diverse learning rates for different network parameters in the gradient descent. To deal with these difficulties, algorithms with adaptive learning rates were introduced, in which the learning rate is adapted to the training data’s properties and the network parameters. RMSprop is one of the most effective training algorithms with adaptive learning rate. The learning rate in RMSprop algorithm is modified by taking advantage of all the gradients of the cost function w.r.t the network parameters in the entire learning process. Thus, the running average of gradients is presented as:

$$ E{\left[{g}^2\right]}_n=\rho E{\left[{g}^2\right]}_{n-1}+\left(1-\rho \right){g}_n^2 $$

(4)

where g_n is the gradient of cost function w.r.t. the network parameters in the n-th iteration of the algorithm and ρ is decay rate. Likewise, the update rule of RMSprop is expressed as:

$$ {w}_{n+1}={w}_n-\frac{\alpha }{\sqrt{E{\left[{g}^2\right]}_n+\epsilon }}{g}_n $$

(5)

In this update rule, α is a global learning rate, and ϵ is a smoothing term to avoid zero value in the denominator [26].

3.2 Support vector machine

SVM, which was first invented for classification purposes [3], was soon extended for regression problems. In support vector regression (SVR), the estimated model is only sensitive to a subset of the training data that produces an error beyond a predetermined threshold ε. Given a statistically independent and identically distributed (iid) data set (x_i, d_i), x ∈ R^z, d ∈ R, i = 1, 2, …, N ,which x and d indicate the z-dimensional input and the desired output data respectively, a linear model is considered as:

$$ y={w}^Tx+b $$

(6)

where weight vector w and bias b are unknown. To solve the model and estimate unknown parameters, a loss function called ε-insensitive loss function is introduced as:

$$ {L}_{\varepsilon}\left({d}_i,{y}_i\right)=\left\{\begin{array}{c}\left|{d}_i-{y}_i\right|-\varepsilon \kern1em for\kern0.75em \left|{d}_i-{y}_i\right|\ge \varepsilon\ \\ {}0\kern9.25em O.W.\kern3.25em \end{array}\right. $$

(7)

In this function, d and y denote the desired response and the estimated response respectively. Deviation more than ε , however, cannot be avoided in many cases. Thus, nonnegative slack variables ξ_i and ${\xi}_i^{{}^{\circ}}$ are proposed to tackle this issue, described as below:

$$ {\xi}_i={d}_i-{y}_i-\varepsilon \kern1.5em if\kern1.25em {d}_i>{y}_i+\varepsilon $$

(8)

$$ {\xi}_i^{{}^{\circ}}={y}_i-{d}_i-\varepsilon \kern1.5em if\kern1.25em {d}_i<{y}_i-\varepsilon $$

(9)

It is obvious that the value of slack variables is zero if |d_i − y_i| ≤ ε. Figure 3 depicts all the notations used in SVR.

Fig. 3

a Linear SVM regression model. bε-insensitive loss function

The problem in SVR is to find the minimum amount of error while all the data points fall in the desired space. Hence, the objective function is to minimize the function:

$$ \frac{1}{2}\ {\left\Vert w\right\Vert}^2+C\sum \limits_{i=1}^N\left({\xi}_i+{\xi}_i^{{}^{\circ}}\right) $$

(10)

Smaller w contributes to the flatness of the estimated regression equation and prevents overfitting and model complexity. Regularization parameter C determines the trade-off between the flatness of the regression function and the allowable absolute deviation greater than ε. Proper selection of this parameter is critical because the high value of C makes the model overfitted, but small values aggravate the model error. The constraints of the optimization problem are:

$$ \left\{\begin{array}{c}{d}_i-{y}_i\le \varepsilon +{\xi}_i\\ {}{y}_i-{d}_i\le \varepsilon +{\xi}_i^{{}^{\circ}}\\ {}{\xi}_i,{\xi}_i^{{}^{\circ}}\ge 0\end{array}\right. $$

(11)

If the input data do not have a linear relationship to the response, the input space is transformed into a higher dimensional m feature space by utilizing a set of nonlinear functions $\left\{{\varphi}_j\right\}\genfrac{}{}{0pt}{}{m}{j=1}$ so that the linear regression model can be applied. The feature vector that describes mapping from the z-dimensional input vector x_i into a m-dimensional feature space is expressed as:

$$ {\phi}_{\left({x}_{\mathrm{i}}\right)}={\left[{\varphi}_1\left({x}_i\right),{\varphi}_2\left({x}_i\right),\dots, {\varphi}_m\left({x}_i\right)\right]}^T\kern1.5em m\gg z $$

(12)

To make computations less expensive in this manner, some kernels$k\left({x}_i,x\right)={\phi}_{\left({x}_i\right)}^T{\phi}_{(x)}$ are employed to replace dot product of feature vectors in solving the optimization problem. According to Mercer’s theorem, the admissible kernels must be symmetric and positive definite functions. Further, Karush–Kuhn–Tucker (KKT) conditions are applied to solve the nonlinear problem and find the estimates of w and b. Finally, the solution of the regression problem is:

$$ y=\sum \limits_{i=1}^N\left({\alpha}_i-{\alpha}_i^{{}^{\circ}}\right)k\left({x}_i,x\right)+\hat{b} $$

(13)

where α and α^° are Lagrange multipliers and K(x, x_i) is an admissible kernel [10, 27]. Radial basis function (RBF) and sigmoidal kernels are among the most common kernels used with SVM. Besides kernel type and its parameters, C and ε must be selected prior to SVR modeling.

3.3 Non-dominated sorting genetic algorithm-II

Genetic algorithm is one of the most popular evolutionary algorithms, which is developed on the basis of natural selection to search the feasible region. It is expected that GA converges to near to global solution since it is a population-based algorithm that randomly explores the search space. In the algorithm, a population of feasible solutions, called individuals, is initially created. The individuals contain the problem decision variables, called genes. By means of random search in the decision space, the individuals are evolved to become more optimized.

Prior to initializing a population, the algorithm’s operators, population size, stopping criterion, crossover, and mutation probabilities should be chosen. During iterations, each individual’s fitness value is evaluated and if the termination criterion, e.g., a predefined number of iterations, is met, the algorithm is stopped. Otherwise, selection, crossover, and mutation operators are successively performed to create a new generation. In the selection operator, appropriate individuals with better fitness value, called parents, are selected to create offspring. The parents exchange information in the crossover operator to produce new offspring. Altering some characteristics in the new individuals, the mutation operator maintains diversity in the population [5] .

In multi-objective optimization problems, a number of equally optimal solutions exist. These optimal solutions, known as Pareto-optimal solutions, can be achieved in one single simulation by multi-objective evolutionary algorithms (MOEAs). NSGA-II is a computationally fast, elitist, non-dominated sorting-based MOEA, proposed by Deb et al. [4]. They have shown the superiority of the proposed algorithm in terms of the spread of solutions and convergence to the true Pareto-optimal front. A fast non-dominated sorting procedure is employed in NSGA-II. By using the domination concept, the Pareto-optimal front and the other fronts can successively be found in the objective space, and a rank is assigned to each front’s solutions. Furthermore, the crowded-comparison operator is used wherever selecting an individual is necessary in NSGA-II. According to this operator, the solution with a lower rank is always preferred. When both individuals belong to the same front, the individual with the higher crowding distance, located in a less crowded region in the objective space, is chosen. Crowding distance presents an estimation of the density of solutions in a specific front. In each front, the crowding distance of the i-th solution pertains to the m-th objective is computed as:

$$ {d}_i=\frac{\left|{f}_m\left(i+1\right)-{f}_m\left(i-1\right)\right|}{f_m^{max}-{f}_m^{min}} $$

(14)

For each solution, the absolute difference between two adjacent solutions’ objective values is divided by the difference between the minimum and maximum value of the objective function. The sum of distance values for all the objectives determines the crowding distance for each solution in a front. Although the main loop in NSGA-II is similar to that in the single-objective GA, there are some differences. Selection operator in NSGA-II, for example, is based on crowded-comparison operator. To ensure elitism in the algorithm, the parent population P_t and the offspring population Q_t are combined in each iteration to form R_t. Crowded-comparison operator is then utilized to select appropriate individuals according to the population size. This procedure is illustrated in Fig. 4. It is notable that initializing the first population, crossover, and mutation operators are the same as it is in the single-objective GA.

Fig. 4

NSGA-II procedure [4]

3.4 Desirability function

Derringer and Suich [6] developed an easy, practical method for simultaneous optimization of several responses by converting the estimated responses ($\hat{\mathbf{y}}$) into an overall desirability (D). In this method, desirability function (d) is calculated for each response in a way that desirable instances have higher desirability function value, i.e., their d is closer to 1. In Smaller-The-Best response type, desirability function for each response is calculated as:

$$ {d}_i={\left(\frac{\hat{y_i}-{U}_i}{L_i-{U}_i}\right)}^r,{L}_i\le \hat{y_i}\le {U}_i $$

(15)

L_i and U_i are respectively the lower and upper bound of the i-th response. r determines the shape of the desirability function; for example, the shape of d is linear if r is equal to 1. After calculation of the desirability functions, the overall desirability is defined as:

$$ D={\left({d_1}^{w_1}\times {d_2}^{w_2}\times \dots \times {d_n}^{w_n}\right)}^{\frac{1}{\sum {w}_i}} $$

(16)

where n is the number of responses, and w_i is the weight assigned to the i-th response. The higher the weight of a response is, the more important it is for the decision-maker. Thus, simultaneous optimization of several responses changes to finding the maximum value of the overall desirability (D).

4 Results and discussion

4.1 Analysis of variance

Analysis of variance (ANOVA) approach was used to determine statistically significant factors and their effects on the response variables. The ANOVA table for R_a, F_x, F_y, and F_z are respectively presented in Tables 3, 4, 5, and 6, and all the analyses were conducted at the level of confidence 95%. Contribution percent is calculated based on sequential sum of squares, but adjusted sum of squares is used for P value calculation. Minitab 18 statistical software was used to carry out ANOVA.

Table 3 ANOVA for surface roughness (R_a)

Table 4 ANOVA for infeed force (F_x)

Table 5 ANOVA for cross feed force (F_y)

Table 6 ANOVA for thrust force (F_z)

Based on Table 3, it is obvious that various levels of cutting speed, feed per tooth, and tool type have significantly different mean values for surface roughness. The interactions between tool type and feed rate as well as cutting speed is also significant. Feed rate has the highest portion in explaining surface roughness variation with 45.81% contribution, followed by its interaction with tool type (20.54%), tool type (14.66%), and the interaction between tool type and cutting speed (4.96%).

From Table 4, feed per tooth, depth of cut, the interactions between feed rate and cutting speed, depth of cut and cutting speed, and feed rate and depth of cut are statistically significant predictors for F_x. The most important independent variables to explain infeed force deviation are feed per tooth with 70.06% contribution, depth of cut (19.60%), and the interaction between these two factors (5.74%).

By Investigating Table 5 to study the influence of independent variables on cross feed force, it is found that all the main effects and their interactions are statistically significant at the 0.05 significance level except for cutting speed and its interaction with tool type. Feed rate, depth of cut, and tool type are the most important variables to explain Fy with 49.08, 34.49, and 8.03 contribution percent.

According to Table 6, all the main effects and the interactions between feed per tooth and other factors are statically significant for thrust force. In addition, tool type is the most influential variable to explain the variation of dependent variable with 49.35% contribution, followed by feed rate (23.13%), depth of cut (15.38%), and their interaction (4.95%).

Based on the ANOVA results, all the factors included in the experiments have significant effect on the responses; moreover, factors besides interactions should be considered in further modeling because of interactions’ high contribution percent.

4.2 Predicting responses using regression analysis

To get a thorough understanding and achieve better results, it is essential to include categorical variables, such as tool type, in regression analysis, and other kinds of models. Accordingly, dummy variables were used to take tool type into account for modeling and optimization in this study. Hence, tool type 3 was considered as the baseline, and two new variables were defined as below to encode the other tool types.

$$ \mathrm{Tool}.1=\left\{\begin{array}{c}1\kern3.5em \mathrm{If}\ \mathrm{tool}\ \mathrm{No}.1\ \mathrm{is}\ \mathrm{used}\ \mathrm{for}\ \mathrm{the}\ \mathrm{experiment}\\ {}0\kern1.5em \mathrm{If}\ \mathrm{tool}\ \mathrm{No}.1\ \mathrm{is}\ \mathrm{not}\ \mathrm{used}\ \mathrm{for}\ \mathrm{the}\ \mathrm{experiment}\end{array}\right. $$

(17)

$$ \mathrm{Tool}.2=\left\{\begin{array}{c}1\kern3.5em \mathrm{If}\ \mathrm{tool}\ \mathrm{No}.2\ \mathrm{is}\ \mathrm{used}\ \mathrm{for}\ \mathrm{the}\ \mathrm{experiment}\\ {}0\kern1.5em \mathrm{If}\ \mathrm{tool}\ \mathrm{No}.2\ \mathrm{is}\ \mathrm{not}\ \mathrm{used}\ \mathrm{for}\ \mathrm{the}\ \mathrm{experiment}\end{array}\right. $$

(18)

Moreover, the best subset selection approach was utilized to create the best possible regression model for each response. In this method, least-square regression models with different combinations of predictors are compared with each other. Specifically, all the possible models with k predictors, out of the overall P independent variables, are fitted, and their R-squared are then weighed to select the best model with exactly k independent variables. The procedure is done for k = 0,1,2,..,P predictors; therefore, the selected P + 1 regression models should be compared with each other to discover the most suitable one [11]. Since the selected models have diverse number of predictors, the adjusted R-squared was used to determine the best model.

It needs to be mentioned that linear terms of the main effects were fixed in the modeling, while the best combination of interaction and quadratic terms were chosen by the best subset selection method. Further, numeric variables were centered to avoid multi-collinearity. R software environment was employed to find the most appropriate regression models for R_a, F_x, F_y, and F_z, which are respectively as follows:

$$ {\displaystyle \begin{array}{l} Ra=0.329-0.000160\times Vc+3.00\times fz+0.0471\times ap+0.0302\times Tool.1\\ {}\kern5em -0.152\times Tool.2+46.0\times f{z}^2+3.71\times fz\times Tool.1+0.000270\\ {}\kern5em \times Vc\times Tool.2+0.000200\times Vc\times Tool.1-0.00211\times Vc\times fz\\ {}\kern5em -1.74\times fz\times Tool.2+1.09\times fz\times ap\\ {}{R}^2=84.61\%\kern6.24em {R}^2(adj)=80.10\%\end{array}} $$

(19)

$$ {\displaystyle \begin{array}{l} Fx=70.6-0.0138\times Vc+1176\times fz+45.8\times ap-5.89\times Tool.1-0.417\\ {}\kern5em \times Tool.2+0.0000575\times V{c}^2+2208\times f{z}^2+674\times fz\times ap\\ {}{R}^2=97.76\%\kern7em {R}^2(adj)=97.36\%\end{array}} $$

(20)

$$ {\displaystyle \begin{array}{l} Fy=117-0.0113\times Vc+1130\times fz+70.4\times ap-24.9\times Tool.1-37.6\\ {}\kern5em \times Tool.2+0.0000384\times V{c}^2+612\times fz\times ap-238\times fz\times Tool.2\\ {}\kern5em -17.1\times ap\times Tool.2\\ {}{R}^2=97.87\%\kern6.24em {R}^2(adj)=97.44\%\end{array}} $$

(21)

$$ {\displaystyle \begin{array}{l} Fz=22.5-0.00361\times Vc+130\times fz-10.2\times ap-5.89\times Tool.1+15.5\\ {}\kern2.4em \times Tool.2+0.00000720\times V{c}^2-154\times fz\\ {}\kern2.4em \times ap-113\times fz\times Tool.2+0.0411\times Vc\times fz\\ {}{R}^2=96.9\%\kern5.519997em {R}^2(adj)=96.27\%\end{array}} $$

(22)

The results of the regression models support the findings of ANOVA, for variables with higher contribution percent are present in the selected models.

4.3 Predicting responses using SVR

Four different SVR models were developed to separately predict R_a, F_x, F_y, and F_z. The input variables for each SVR model were selected based on the results of ANOVA, shown in Tables 3, 4, 5, and 6. Indeed, the main effects and interactions with more than 1 percent contribution percent were chosen to participate in SVR modeling.

As mentioned earlier, regularization parameter C, epsilon ε, and kernel type and its parameters should be defined previous to modeling since the result of SVR is strongly affected by these parameters. Two different kernels, including sigmoid and radial basis function (RBF), were examined in this study, which are respectively defined as follows:

$$ k\left(x,{x}_i\right)=\tanh \left(\gamma {x}^T{x}_i+r\ \right) $$

(23)

$$ k\left(x,{x}_i\right)=\exp \left(-\gamma {\left\Vert x-{x}_i\right\Vert}^2\right) $$

(24)

γ and r in sigmoid kernel and γ in RBF kernel are hyperparameters, which their values must be determined besides C and ε before the learning process. In fact, kernel type and its parameters as well as C and ε are hyperparameters of SVR that their best values are selected by grid search in this work. In grid search, having assigned several reasonable values to each hyperparameter, the performance of models with different hyperparameters’ values is compared with each other. To perform the grid search for each response, the powers of 2 and integer numbers were used to determine C, ε, and γ in both kernels and r in the sigmoid kernel respectively, shown in Table 7. Cross-validation method is usually utilized with grid search; thus, the specific combination of hyperparameters values that optimizes the cross-validation performance metric is regarded as the suitable values for model’s hyperparameters. Thus, hyperparameters values that simultaneously minimized 10-fold cross-validation mean squared error (MSE) and mean absolute percentage error (MAPE) were selected for SVR modeling. Desirability function was used to minimize cross-validation MSE and MAPE simultaneously. In addition, the available input variables were normalized to 0–1 range prior to hyperparameter tuning. The scikit-learn library in Python programming language was used for SVR modeling.

Table 7 Hyperparameters’ values used in grid search

According to Table 3, feed per tooth, depth of cut, tool type dummy variables, cutting speed interaction with feed rate, and the interactions of tool type with feed rate and cutting speed were selected for surface roughness prediction. The sigmoid kernel with γ=0.25 and r = − 3 as well as C = 64, and ε = 2⁻¹⁰ were picked to predict Ra. Moreover, the reported cross-validation MSE and MAPE were 0.0080 and 23.92% respectively. Based on Table 4, cutting speed, feed rate, depth of cut, and the interactions of feed rate with cutting speed and depth of cut were utilized to model infeed force. The RBF kernel with γ = 0.25, C = 2¹⁸ and ε = 2⁻¹⁰ resulted in the best model. Cross-validation MSE and MAPE were 24.28 and 5.82% respectively. From Table 5, cutting speed, feed per tooth, depth of cut, tool type dummy variables, the interaction of feed rate with cutting speed and depth of cut were employed to model cross feed force. The best result was obtained by the sigmoid kernel with γ = 0.125, C = 2048, r = − 1, and ε = 2 , producing cross-validation MSE = 89.48 and MAPE = 7.46%. All the main variables as well as all the interactions of feed rate were picked for thrust force modeling according to Table 6. The sigmoid kernel with γ = 0.125 and r = − 2 besides C = 8192 and ε = 2⁻⁷ led to the best model. The cross-validation MSE and MAPE were respectively 5.64 and 7.35%.

In addition to the ANOVA results to choose the SVR input variables, the same procedure was followed by using only the main effects of each response. By comparing these two approaches, it was approved that selecting variables based on contribution percent led to better results for all the responses.

4.4 Predicting responses using ANN

In this section, a procedure to find suitable feedforward neural networks was followed individually for each response, leading to four different ANN models. The hyperparameters of the network structure as well as training algorithm affect the performance of ANN models; as a result, there are two different sets of hyperparameters for ANN model selection. To tune hyperparameters, grid search was used separately for each response, and a model with a hyperparameter combination resulting in lower 5-fold cross-validation MSE was regarded as the best model.

The network structure hyperparameters include activation function in each layer and number of layers and neurons. In this study, ANN input layer consists of five neurons for cutting speed, feed per tooth, depth of cut, and tool type dummy variables. The output layer has one neuron pertaining to a specific response. To find the best number of layers and neurons, one and two hidden layers networks were tested since using more layers led to a high prediction error. Specifically, one hidden layer networks with 4, 8, and 12 neurons as well as two hidden layers networks with combinations of 3, 6, and 9 neurons were investigated by grid search. A schematic of an ANN structure used in this work is illustrated in Fig. 5. In addition, linear activation function was employed for the output layers in all the structures. The hidden layers’ activation functions were selected by grid search among some non-linear activation functions, including Sigmoid, Tanh, Elu, LeakyRelu, and Softplus.

Fig. 5

Schematic of a neural network structure used in this study

Levenberg-Marquardt and RMSprop algorithms were used to train networks. LMA is a famous optimization algorithm, which is used in several machining research [2, 7, 14, 15]. RMSprop, on the other hand, is an effective, newer algorithm, which has not been used for response prediction in the machining field, to the authors’ knowledge. As it was mentioned in Section 3.1, μ besides its update factor is LMA hyperparameters. The learning rate α is RMSprop hyperparameter to be tuned, while the smoothing term ϵ was set to be 1e-5, and the decay rate ρ had a fixed value of 0.9. Moreover, it is possible to determine mini-batch size with RMSprop. In this circumstance, a network’s weights and biases are updated for every mini-batch size of the training dataset, instead of the whole training dataset. The values of the training algorithms’ hyperparameters used in the grid search for all the responses are shown in Table 8.

Table 8 Values of the training algorithms’ hyperparameters used in grid search

Furthermore, the training algorithm will stop if one of the criteria listed below is satisfied.

• Algorithm iterations reach to a constant epoch number of 1500.

• There is a considerable increase in training or validation error.

It is noteworthy that the test fold in cross-validation method was used to calculate validation error. After termination of the network training, weights and biases leading to the lowest validation error during the learning process were considered as parameters of the trained network. To provide a comparison between various values of hyperparameters, folds of cross-validation method as well as the initial weights and biases for all the network trainings were set the same. Additionally, process and response data were normalized to 0-1 range prior to hyperparameter tuning. The NeuPy library version 0.6.5 was deployed for ANN modeling in Python programming language. The hyperparameter values of the best ANN models and their cross-validation error resulted from the grid search, are gathered in Table 9. Deeper networks with two hidden layers showed better performance. Moreover, Levenberg-Marquardt could predict F_x and F_y more precisely, while RMSprop outperformed LMA in the prediction of R_a and F_z.

Table 9 Hyperparameter values and CV errors of the selected ANN models

4.5 Comparison between prediction models

To find the best model for each response from selected ANN, SVR, and regression models, four performance metrics, including mean absolute error (MAE), MSE, MAPE, and correlation coefficient (r) between the predicted and experimental values, were deployed. Specifically, 5-fold cross-validation was implemented for each selected model, and their performance was compared with each other, shown in Table 10. Same folds were used for cross-validation to make the comparison valid. It is obvious that SVR surpassed regression models, while ANN far outperformed both SVR and regression models for all the responses.

Table 10 5-fold cross-validation to compare prediction models

After that final models were selected, models trained by the entire experimental data were prepared to participate in GA. The corresponding MAPE of these ANN models were respectively 13.65, 1.04, 0.27, and 7.60 percent for R_a, F_x, F_y, and F_z.

4.6 Optimization using NSGA-II

Optimization problem, presented as below, aims to find the best process parameters so that surface roughness and cutting forces are simultaneously minimized.

$$ {\displaystyle \begin{array}{c}\operatorname{Min}\left(R{a}_{\left({V}_c,{f}_z,{a}_p,\boldsymbol{Tool}\right)},F{x}_{\left({V}_c,{f}_z,{a}_p,\boldsymbol{Tool}\right)},F{y}_{\left({V}_c,{f}_z,{a}_p,\boldsymbol{Tool}\right)},F{z}_{\left({V}_c,{f}_z,{a}_p,\boldsymbol{Tool}\right)}\right)\\ {}\mathrm{Subject}\ \mathrm{to}\\ {}300\le {V}_c\le 1200\\ {}0.01\le {f}_z\le 0.1\\ {}1\le {a}_p\le 2\\ {}1\le \mathrm{Tool}\le 3,\mathrm{integer}\end{array}} $$

(25)

Each individual in GA was set to have five real coded variables, including V_c, f_z, a_p and two tool-type dummy variables. The parameters of GA were determined by trial and error in a way that lower responses were obtained. Thus, algorithm parameters were set as 125 for population size, 0.6 for crossover probability, and 0.4 for mutation probability. Further, the algorithm was stopped when 300 generations had been created. NSGA-II was executed in Python programming language by taking advantage of pygmo library.

Tournament selection was preferred for selection operator, in which a predefined number of individuals are randomly chosen from the original generation. Then the crowded-comparison operator is employed to select parents. Arithmetic crossover, in which two offspring are created based on convex combinations of two random selected parents, was used as crossover operator. Gaussian mutation operator was chosen for mutation. In Gaussian mutation, a vector containing numbers that are randomly drawn from the standard normal distribution is added to an offspring vector to create a mutated one. Several optimum solutions were obtained by implementing NSGA-II. Results that led to the minimum value for each response in the Pareto Front are presented in Table 11. When Table 11 and Table 2 are compared, it can be concluded that the procedure followed in this work led to lower values for each individual response. The amount of the improvement is 1.0% for R_a, 24.6% for F_x, 22.7% for F_y, and 7.1% for F_z.

Table 11 The best results pertaining to each response in the Pareto Front

Since no solution in Pareto Front is better than the other solutions, the desirability function approach was deployed to select and present some of the optimal solutions. Various weights were assigned to responses to determine their relative importance for decision-making, while the shape of desirability function was linear. The optimum solutions acquired by desirability function approach are demonstrated in Table 12. To conclude, medium values of cutting speed, lower feed per tooth, and depth of cut besides using the cutting tool with TiCN coating and nose radius of 0.5 mm led to the optimum results.

Table 12 The Pareto Front solutions obtained by desirability function approach

5 Conclusion

A comprehensive procedure, exhibited in Fig. 1, was followed in this study to predict and optimize the surface roughness and cutting forces in slot milling of AA 7075-T6. The findings are summarized as follows:

• 1. Cutting speed, feed per tooth, depth of cut, and tool type strongly affected responses. However, the effect of feed rate was more profound, followed by tool type and depth of cut.

• 2. Using dummy variables to include different tool types in prediction models and optimization algorithm was successful. Thus, it is recommended to deploy this technique to incorporate the other categorical variables, such as material type, into machining modeling.

• 3. Hyperparameter tuning is absolutely crucial to select proper ANN and SVR models. Since ANN models own many hyperparameters, tuning is time-consuming, but the importance of this task cannot be overemphasized.

• 4. RMSprop could predict Ra and Fz more precisely in contrast with LMA. Therefore, training algorithms with adaptive learning rate may lead to better response prediction, especially for complicated responses such as surface roughness.

• 5. ANN outperformed both SVR and regression models in predicting responses. Nonetheless, neural network hyperparameter tuning is demanding, so SVR models can be utilized when prediction accuracy is less important.

• 6. The integration of ANN and NSGA-II resulted in several optimum solutions. The Pareto-optimal solutions were combined with desirability function approach to help with decision-making.