Spatial competition with quadratic transport costs and one online firm

Abstract

d’Aspremont (Econometrica 47:1145–1150 , 1979) showed that a Hotelling (Econ J 39:41–57 , 1929) duopoly model with quadratic transport costs yields maximal differentiation. However, the introducing of an online firm ensures that the duopolist will never be located at the end points of the market. In other words, an online firm can raise a market effect that induces two firms to be finitely differentiated. The implication of the socially optimal solution is derived. The results herein can be extended to allow multiple firms. Finally, a free-entry equilibrium and the Stackelberg equilibrium are also discussed.

1 Introduction

Online business has developed rapidly in the past decade. Now, traditional firms must not only compete with other traditional firms but also face competition from online firms. The latter can open 24-h daily, whereas doing so is very costly for the traditional firms (brick-and-mortar stores). However, the making of an online purchase has the obvious disadvantage that the customer must typically wait 3–7 days for delivery.

An increasing number of studies are investigating competition by online firms with physical firms. For instance, Balasubramanian (1998) establishes a circular spatial model to analyze price competition between directed marketers and conventional retailers, in which the locations of all firms are exogenously given. Bouckaert (2000) proposes a similar structure in which one mail order business competes with many retail stores. Under the condition of free entry, he shows that the number of firms in equilibrium is fewer than that determined by Salop (1979) and that competition from the mail order firm reduces the profits of retailers. Chevalier and Goolsbee (2003) suggest that significant competition exists between online and conventional retailers of computer equipment. Prince (2007) provides both demand-side and supply-side explanations of increasing cross-price elasticity for personal computers that are sold online or in traditional stores.¹ So far, limited theoretical studies have discussed a traditional spatial duopoly framework with online business. The purpose of this study is to establish a theory to analyze competition among two physical firms and one online firm. This work constructs a bridge between online businesses and traditional spatial duopoly models, with a focus on endogenous locations.

This study takes into account the findings of a rich literature of price–location models of the role of physical firms.² d’Aspremont et al. (1979) revise the Hotelling (1929) model and show that competition between two firms with quadratic transport costs yields maximal differentiation. However, introducing an online firm prevents the duopolists from being located at the end points of the market. Intuitively, consumers who are far away from the physical firm tend to purchase from the online firm. Accordingly, if the physical firms remain located at the end points of the market, then they will lose a considerable number of remote consumers who reside close to the market center. Restated, this online firm can have the market effect of causing two physical firms to be finitely differentiated whenever the waiting cost of an online purchase is low enough.

In the proposed model, the waiting cost of purchasing goods from an online firm represents all of the disadvantages of an online firm.³ This study will show that a decrease in the waiting cost leads to an increase in the equilibrium price charged by the online firm and a decrease in the equilibrium price charged by the physical firms. We also solve the socially optimal problem. When the transport rate and the waiting cost of an online purchase satisfy some relationships, the socially optimal solution is reached. The implication of taxation is also provided. Finally, a free-entry equilibrium and the Stackelberg equilibrium are also discussed.

The rest of this paper is organized as follows. Section 2 describes the presented model, and Sect. 3 solves the location–price equilibrium. It also presents comparative statics and discusses the implication of social welfare. Section 4 extends duopolistic physical firms to multiple firms. An extension with the free entry of physical firms is included in Sect. 5. The robustness for a Stackelberg competition is established in Sect. 6. Conclusions are provided in Sect. 7.

2 The model

Consider two physical firms (1, 2) that are located on a linear market of unit length at $x_1, x_2$, respectively. The market also includes an online firm (3), which has no specific location. Consider a two-stage game, and only pure strategies on location–price are discussed. In the first stage of the game, both physical firms determine their locations simultaneously, and in the second stage, these two firms and the online firm set their prices ($p_1, p_2$ and $p_3$) simultaneously at zero marginal costs. Marginal costs are assumed to be zero to simplify the analysis. Consumers are uniformly distributed along this linear market. Each consumer buys a product from either one of the two physical firms or from the online firm. The utility for a consumer at $x\in [0,1]$ who purchases from firm 1 is

$$\begin{aligned} u_1 =v-p_1 -k(x_1 -x)^{2}, \end{aligned}$$

(1)

where $v$ is a reservation price and $k$ is the unit transportation cost. Similarly, if the consumer at $x\in [0,1]$ purchases the product from firm 2, its utility is

$$\begin{aligned} u_2 =v-p_2 -k(x_2 -x)^{2}. \end{aligned}$$

(2)

The online firm has no specific location, and thus, the utility ($u_3$) of its consumers includes no physical transportation cost:

$$\begin{aligned} u_3 =v-p_3 -z, \end{aligned}$$

(3)

where $z$ is the waiting cost of purchasing online.

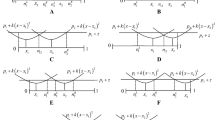
Now consider a set of pure strategy equilibria in which both physical firms occupy disjoint regions of the market and the online firm takes out all remaining markets. This is the case of interior locations. Those cases of boundary locations, when at least one of the physical firms is located at the boundaries ($x_1 =0$ or $x_2 =1$), will be shown never to be equilibria with the assumption that the online firm is not redundant just before Proposition 1. Let $n_1^R, n_1^L$ and $n_2^L, n_2^R$ be the market boundaries of firm 1 and firm 2, respectively (Fig. 1), where “$R$” represents “right”, and “$L$” represents “left”. The equilibrium conditions should be $n_1^L >0, n_1^R <n_2^L$, and $n_2^R <1$.

Fig. 1

The market regions of three firms

Solving $u_1 =u_3$ yields

$$\begin{aligned} n_1^R =x_1 +\frac{\sqrt{kp_3 +kz-kp_1 }}{k},\quad \quad n_1^L =x_1 -\frac{\sqrt{kp_3 +kz-kp_1 }}{k}. \end{aligned}$$

Solving $u_2 =u_3$ yields

$$\begin{aligned} n_2^R =x_2 +\frac{\sqrt{kp_3 +kz-kp_2 }}{k},\quad \quad n_2^L =x_2 -\frac{\sqrt{kp_3 +kz-kp_2 }}{k}. \end{aligned}$$

Let $N_1, N_2$ and $N_3$ be the market shares for firms 1, 2 and 3, respectively, then

$$\begin{aligned} N_1&= n_1^R -n_1^L =\frac{2\sqrt{k(p_3 +z-p_1 )}}{k},\end{aligned}$$

(4)

$$\begin{aligned} N_2&= n_2^R -n_2^L =\frac{2\sqrt{k(p_3 +z-p_2 )}}{k},\end{aligned}$$

(5)

$$\begin{aligned} N_3&= 1-N_1 -N_2. \end{aligned}$$

(6)

The profit functions are

$$\begin{aligned} \pi _1&= p_1 \cdot N_1 =\frac{2p_1 \sqrt{k(p_3 +z-p_1 )}}{k},\end{aligned}$$

(7)

$$\begin{aligned} \pi _2&= p_2 \cdot N_2 =\frac{2p_2 \sqrt{k(p_3 +z-p_2 )}}{k}, \end{aligned}$$

(8)

$$\begin{aligned} \pi _3&= p_3 \cdot N_3 =\frac{p_3 \left( {k-2\sqrt{k(p_3 +z-p_1 )}-2\sqrt{k(p_3 +z-p_2 )}} \right) }{k}. \end{aligned}$$

(9)

3 Location–price equilibrium with an online firm

Using backward induction, the price competition in the second stage of the game is solved for the location–price game. Solving $\partial \pi _1 /\partial p_1 =0, \partial \pi _2 /\partial p_2 =0$, and $\partial \pi _3 /\partial p_3 =0$ simultaneously yields⁴

$$\begin{aligned} p_1^*&= p_2^*=\frac{2z}{5}+\frac{k}{100}+\frac{\sqrt{k(k+80z)}}{100},\end{aligned}$$

(10)

$$\begin{aligned} p_3^*&= -\frac{2z}{5}+\frac{3k}{200}+\frac{3\sqrt{k(k+80z)}}{200}. \end{aligned}$$

(11)

The solution satisfies the second-order conditions, because $\partial ^{2}\pi _1 /\partial p_1^2 =\partial ^{2}\pi _2 /\partial p_2^2 =-30\sqrt{2}/B<0$, and $\partial ^{2}\pi _3 /\partial p_3^2 =(-10k\sqrt{2}(240+z+k+\sqrt{k(k+80z)})/B^{3}<0$, where $B=\sqrt{k(40z+k+\sqrt{k(k+80z})}$. Substituting the equilibrium prices into the market shares yields

$$\begin{aligned} N_1^*&= N_2^*=\frac{\sqrt{2}\sqrt{40z+k+\sqrt{k}\sqrt{80z+k}}}{10\sqrt{k}},\end{aligned}$$

(12)

$$\begin{aligned} N_3^*&= \frac{5k-\sqrt{2k}\sqrt{40z+k+\sqrt{k}\sqrt{80z+k}}}{5k}. \end{aligned}$$

(13)

The necessary conditions for the existence of equilibrium are $n_1^L >0, n_2^R <1$ and $n_1^R <n_2^L$. Solving $n_1^L >0$ yields

$$\begin{aligned} x_1 >x_1^{\min } \equiv \frac{\sqrt{2k\left( {k+40z+\sqrt{k(k+80z)}} \right) }}{20k} >0. \end{aligned}$$

(14)

Solving $1-n_2^R >0$ yields

$$\begin{aligned} x_2 <x_2^{\max } \equiv 1-\frac{\sqrt{2k\left( {k+40z+\sqrt{k(k+80z)}} \right) }}{20k} <1. \end{aligned}$$

(15)

Solving $n_2^L -n_1^R >0$ yields

$$\begin{aligned} x_2 -x_1 >(x_2 -x_1 )^{\min }=\frac{\sqrt{2k\left( {k+40z+\sqrt{k(k+80z)}} \right) }}{10k}\equiv x_d^{\min } . \end{aligned}$$

(16)

Therefore, the necessary condition to guarantee the existence of pure strategy equilibria is

$$\begin{aligned}&x_2^{\max } -x_1^{\min } -x_d^{\min }\nonumber \\&\quad =1-\frac{\sqrt{2}\sqrt{40z/k+1+\sqrt{80z/k+1}}}{5k}>0,\quad \hbox {if and only if}\quad z<\frac{3}{16}k.\qquad \end{aligned}$$

(17)

In other words, if $z<3k/16$, then $x_2^{\max } -x_1^{\min } >x_d^{\min }$ is satisfied. Hence, when the waiting cost of online purchase is low enough such that $z<3k/16$, there exist a set of equilibria locations ($x_1^*,x_2^*$) in some interior ranges. Accordingly, the proposed model ensures that a set of equilibria exist whenever no firm locates at the end points of the market.

In the cases when at least one of the firms is located at boundaries, either $(x_1 =0,x_2 =1)$ or $(x_1 =0,x_2 =x_2^*)$,⁵ and the profit of firm 1 will be shown to become lower than its profit in previous interior solutions. For $(x_1 =0,x_2 =1)$, the solution to the second stage of the game yields $p_1 =p_2 =\frac{2}{5}z+\frac{k}{25}+\frac{1}{25}\sqrt{k(k+20z)}$ and $p_3 =-\frac{2}{5}z+\frac{3}{50}k+\frac{3}{50}\sqrt{k(k+20z)}$ and thus $\pi _1 (x_1 =0,x_2 =1)=\frac{\sqrt{2}\left( {10z+k+\sqrt{k(k+20z)}} \right) ^{\frac{3}{2}}}{250\sqrt{k}}$. Comparing $\pi _1 (x_1 =0,x_2 =1)$ with $\pi _1^*$ yields

$$\begin{aligned}&\pi _1 (x_1 =0,x_2 =1)-\pi _1^*\\&\quad =\frac{-\sqrt{2}k}{250}\left( {250\left( {40\frac{z}{k}+1+\sqrt{1+80\frac{z}{k}}} \right) ^{\frac{3}{2}}-\left( {10\frac{z}{k}\!+\!1\!+\!\sqrt{1+20\frac{z}{k}}} \right) ^{\frac{3}{2}}}\right) <0. \end{aligned}$$

Therefore, the corner solutions are worse than the interior solutions.

In the case of $(x_1 =0,x_2 =x_2^*)$, the equilibrium prices are

$$\begin{aligned} p_1&= p_2 =\frac{2}{5}z+\frac{4}{225}k+\frac{4}{225}\sqrt{k(k+45z)},\\ p_3&= -\frac{2}{5}z+\frac{2}{75}k+\frac{2}{75}\sqrt{k(k+45z)}, \end{aligned}$$

and the profit of firm 1 is

$$\begin{aligned} \pi _1 =\frac{2\left( {45z+2k+2\sqrt{k(k+45z)}} \right) ^{3/2}}{3375\sqrt{k}}. \end{aligned}$$

Similarly,

$$\begin{aligned} \pi _1 (x_1 =0,x_2 =x_2^*)-\pi _1^*&= -\frac{\sqrt{2}k}{3375}\left[ {3375\left( {40\frac{z}{k}+1+\sqrt{1+80\frac{z}{k}}}\right) ^{3/2}}\right. \\&\left. {-\sqrt{2}\left( {45\frac{z}{k}+2+2\sqrt{1+45\frac{z}{k}}} \right) ^{3/2}} \right] <0. \end{aligned}$$

Therefore, the brick-and-mortar stores will not deviate from their interior locations to the boundary locations.⁶

Proposition 1

When two physical firms compete with an online firm, the only possible equilibrium is that both physical firms occupy unconnected regions of the market, and the online firm takes all other markets when $z<3k/16$. The equilibrium prices ($p_1^*, p_2^*, p_3^*$) must satisfy (10), the equilibrium locations $(x_1^*, x_2^*)$ must satisfy $x_1^*>x_1^{\min }, x_2^*<x_2^{\max }$ and $x_2^*-x_1^*>x_d^{\min }$ and the equilibrium market shares must satisfy (12) and (13).

The above proposition suggests that, when one online firm competes with two physical firms, there exists a set of pure strategy equilibria such that both physical firms occupy unconnected market areas, and the online firm takes all remaining markets. Accordingly, the spatial duopolists will never be located at the end points of the market. Instead, both physical firms will remain a distance from the end points ($x_1^*<x_1^{\min }$ and $x_2^*<x_2^{\max })$. Additionally, they will not be located so close to each other, such that $x_2^*-x_1^*>x_d^{\min }$, that each of them enjoys a local monopolistic market. Restated, the online firm can raise a market effect of causing the spatial duopolistic firms to be finitely differentiated.

When $z\ge \frac{3k}{16}$, the online firm will exit the market. As predicted by d’Aspremont et al. (1979), the two brick-and-mortar firms have an incentive to move far away. However, they may not be far apart when there is an online firm as a potential entrant. By symmetry, if $p_1 +k(\frac{1}{2}-x_1 )^{2}>z$, then the online firm will reenter again. Solving $p_1 +k(\frac{1}{2}-x_1 )-z=0$ yields $x_1 =\frac{6k-4\sqrt{k^{2}+kz}}{4k}$, when $z<\frac{5}{4}k$. When $z\ge \frac{5}{4}k$, the equilibrium locations of these two brick-and-mortar firms will reduce to those obtained by d’Aspremont et al. ($x_1 =0$).⁷ $^{,}$ ⁸ This result can be summarized as the following corollary.

Corollary 1

When $\frac{3k}{16}\le z<\frac{5}{4}k$, the online firm will exit from the market and the equilibrium (symmetric) locations of the brick-and-mortar stores will be $(x_1^*,x_2^*)=\left( \frac{6k-4\sqrt{k^{2}+kz}}{4k},1-x_1^*\right)$, with a potential (online) entrant. When $z\ge \frac{5}{4}k$, the equilibrium locations reduce to those of d’Aspremont et al. (1979) as boundary locations $(x_1 =0,x_2 =1)$.

Example 1

Consider the following simple example. Let $k=1$, and $z=1/64$. From Proposition 1, $x_1^{\min } =0.025, x_2^{\max } =0.875, x_d^m =0.25$ and $p_1^*=p_2^*=p_3^*=0.03125$. In other words, a set of locations such that $x_1^*>0.125, x_2^*<0.875$ and $x_2^*-x_1^*>0.25$ can sustain location–price equilibria. This result shows the existence of finite differentiation equilibria and demonstrates that the equilibrium range of locations can be very large.

In order to emphasize the role of the online firm in spatial models, $z<3k/16$ is assumed hereafter. Differentiating (14), (15) and (16) yields

$$\begin{aligned} \frac{\hbox {d}x_1^{{\min }} }{\hbox {d}(z/k)}&= \frac{2\left( {\sqrt{1+80z/k}-1} \right) }{\sqrt{2+80z/k-2\sqrt{1+80z/k}} \sqrt{1+80z/k}}>0, \end{aligned}$$

(18)

$$\begin{aligned} \frac{\hbox {d}x_2^{{\max }} }{\hbox {d}(z/k)}&= -\frac{2\left( {\sqrt{1+80z/k}-1} \right) }{\sqrt{2+80z/k-2\sqrt{1+80z/k}} \sqrt{1+80z/k}}<0, \end{aligned}$$

(19)

$$\begin{aligned} \frac{\hbox {d}x_d^{{\min }} }{\hbox {d}(z/k)}&= \frac{4\left( {\sqrt{1+80z/k}-1} \right) }{\sqrt{2+80z/k-2\sqrt{1+80z/k}} \sqrt{1+80z/k}}>0. \end{aligned}$$

(20)

Accordingly, the properties of the location limits are summarized as the following proposition.

Proposition 2

Define $\lambda =z/k$, then $\hbox {d}x_1^{\min } /\hbox {d}\lambda >0, \hbox {d}x_2^{\max }/\hbox {d}\lambda <0$ and $d(x_d^{\min })/\hbox {d}\lambda >0$. In other words, the range of equilibrium locations becomes wider as the waiting cost decreases (unit transportation cost increases).

Proposition 2 implies that an online firm will enjoy a greater competitive advantage as the waiting cost declines, perhaps because of technological progress, much of which has occurred in the last decade. As the advantage of the online firm increases, such as when oil prices rise, increasing transportation costs, or when online business becomes more convenient, reducing the waiting cost, the two physical firms move closer to the end points and the minimal distance between them increases. Therefore, the equilibrium range of locations becomes narrower.

The property of equilibrium prices described by (8) is now discussed. Further calculations yield

$$\begin{aligned} p_1^*-p_3^*=k\left( \frac{4}{5}\frac{z}{k}-\frac{1}{200} \left( 1+\sqrt{1+80\frac{z}{k}}\right) \right) <0,\quad \hbox {if and only if}\quad z<\frac{k}{64}, \end{aligned}$$

(21)

$$\begin{aligned} \frac{\hbox {d}p_1^*}{\hbox {d}z}&= \frac{\hbox {d}p_2^*}{\hbox {d}z}=\frac{2\left( {\sqrt{k(k+80z)}+k} \right) }{5\sqrt{k(k+80z)}}>0,\\ \frac{\hbox {d}p_3^*}{\hbox {d}z}&= -\frac{2\sqrt{k(k+80z)}-3k}{5\sqrt{k(k+80z)}}<0, \;\;\;\hbox {if}\;z>\frac{k}{64},\\ \frac{\hbox {d}p_1^*}{\hbox {d}k}&= \frac{\hbox {d}p_2^*}{\hbox {d}k}=\frac{k+40z+\sqrt{k(k+80z)}}{100\sqrt{k(k+80z)}}>0,\\ \frac{\hbox {d}p_3^*}{\hbox {d}k}&= \frac{3\left( {k+40z+\sqrt{k(k+80z)}} \right) }{200\sqrt{k(k+80z)}}>0. \end{aligned}$$

The above results can be summarized as the following proposition.

Proposition 3

In equilibrium, the online firm charges a higher price than the physical firms ($p_1^*<p_3^*$) if and only if $z<k/64$. As the waiting cost decreases, the equilibrium prices that are charged by the online firm increase if and only if $z>k/64$, while the equilibrium prices that are charged by the physical firm decreases. As the unit transportation cost increases, all of the equilibrium prices increase.

Intuitively, the waiting cost is a relative disadvantage (advantage) for the online (physical) firms. If the waiting cost of online purchases is lower than a proportion of the physical transportation rate, then the equilibrium prices charged by the online firm will exceed the prices that are charged by the physical firms to reflect the convenience it provides. The online firm generally does not charge the same price as the physical firms, except when $z=k/64$.⁹ As the waiting cost declines, the online firm can charge a higher price that reflects the greater convenience that it offers. However, the unit transportation cost is a disadvantage for all firms, so as $k$ increases, all equilibrium prices increase.

In the following, the first-best solution is investigated. Since each consumer buys one unit of product from one of these three firms, the socially optimal solution is equal to the result of minimizing the total transportation costs (denoted by TTC):

$$\begin{aligned} \mathop {\min \hbox {TTC}}\limits _{\{N_1 ,N_2 ,N_3 \}}&= 2\left( {\mathop \int \limits _{y=0}^{\frac{1}{2}N_1 } ky^{2} \hbox {d}y+\mathop \int \limits _{y=0}^{\frac{1}{2}N_2 } ky^{2} \hbox {d}y} \right) +N_3 \cdot z\nonumber \\&= \frac{k}{12}N_1^3 +\frac{k}{12}N_2^3 +z(1-N_1 -N_2 ). \end{aligned}$$

(22)

The first-order condition for the above minimization is

$$\begin{aligned} \frac{\partial \hbox {TTC}}{\partial N_1 }=\frac{kN_1^2 }{4}-z=0. \end{aligned}$$

(23)

The optimal market sizes are therefore

$$\begin{aligned} N_1^w =N_2^w =\frac{2\sqrt{kz}}{k}, \end{aligned}$$

(24)

and

$$\begin{aligned} N_3^w =1-N_1^w -N_2^w =\frac{k-4\sqrt{kz}}{k}. \end{aligned}$$

(25)

Solving $N_1^*=N_1^w, N_2^*=N_2^w$ and $N_3^*=N_3^w$ for $z$ yields $z^{*}=k/64$. Restated, when $z=k/64$, the market equilibrium is socially optimal. This result can be summarized as the following proposition.

Proposition 4

When $z=k/64$, the equilibrium solution is identical to the socially optimal solution.

Intuitively, when $z=k/64, p_1^*=p_2^*=p_3^*$, representing a minimal TTC. The implication of the above proposition suggests an implication for taxation policy. When $k>64z$ ($k<64z$), an optimal unit subsidy (taxation) $t$ on the transportation costs of the consumer such that $k+t=64z$ reaches the socially optimum.

4 Multiple physical firms and one online firm

This section extends the previous results to cases that involve multiple physical firms. Suppose each consumer buys a product from one of the $m$ physical firms ($1,2,\ldots ,m$) that are located at $x_i \in [0,1], i=1,\ldots ,m$, and $x_1 \le x_2 \le \cdots \le x_m$, or an online firm ($m+1$) that has no specific location. Suppose that their prices for one unit of good are $p_i, i=1,\ldots ,m+1$, respectively. The utility functions of a consumer who is located at $x$ and purchases from the physical firms $i=1,\ldots ,m$ and online firm $m+1$ are, respectively,

$$\begin{aligned} u_i&= v-p_i -k(x-x_i )^{2},\quad i=1,\ldots , m,\\ u_{m+1}&= v-p_{m+1} -z. \end{aligned}$$

Each consumer purchases one unit of product from the firm that maximizes his/her utility. Similar to Proposition 1, consider the case of interior locations, summarized as Fig. 2.

Fig. 2

Equilibrium market configuration in multifirms case

Suppose $n_i^L (n_i^R )$ is the left (right) indifferent consumer between firm $i$ and firm $m+1$.

Solving $u_i =u_{m+1}$ yields

$$\begin{aligned} n_i^R =x_i \!+\!\frac{\sqrt{kp_{m+1} \!+\!kz-kp_i }}{k},\quad n_i^L =x_i -\frac{\sqrt{kp_{m+1} +kz-kp_i }}{k},\quad i=1,\ldots ,m. \end{aligned}$$

The market share of firm $i$ is

$$\begin{aligned} N_i =(n_i^R -n_i^L )=\frac{2\sqrt{k(p_{m+1} +z-p_i )}}{k},\quad i=1,\ldots ,m, \end{aligned}$$

and the market share of firm $m+1$ is $N_{m+1} =1-\mathop \sum \nolimits _{i=1}^m N_i$.

The profit functions are

$$\begin{aligned} \pi _i&= p_i \cdot N_i =\frac{2p_i \sqrt{k(p_{m+1} +z-p_i )}}{k},\quad i=1,\ldots ,m, \end{aligned}$$

(26)

$$\begin{aligned} \pi _{m+1}&= p_{m+1} \cdot N_{m+1} =p_{m+1} \left( {1-\mathop \sum \limits _{i=1}^m \frac{2\sqrt{k(p_{m+1} +z-p_i )}}{k}} \right) . \end{aligned}$$

(27)

Solving $\partial \pi _i/\partial p_i =0, i=1,\ldots , m+1$ yields

$$\begin{aligned} p_i^*&= \frac{10m^{2}z+k+\sqrt{k(20m^{2}z+k)}}{25m^{2}},\quad i=1,\ldots ,m, \end{aligned}$$

(28)

$$\begin{aligned} p_{m+1}^*&= \frac{3k+3\sqrt{20m^{2}zk+k^{2}}-20m^{2}z}{50m^{2}}. \end{aligned}$$

(29)

The necessary conditions for the existence of equilibrium are $n_1^L >0, n_2^R <1$ and $n_i^R <n_{i+1}^L, i=1,\ldots ,m-1$, which yield:

$$\begin{aligned} n_{i+1}^L -n_i^R >0&\Rightarrow x_{i+1} -x_i >\frac{\sqrt{2}\sqrt{10m^{2}z+k+\sqrt{k} \sqrt{20m^{2}z+k}}}{5\sqrt{k}m} \nonumber \\&\equiv x_d^{\min }, \quad i=1,\ldots , m-1, \end{aligned}$$

(30)

$$\begin{aligned} n_1^L >0\quad&\Rightarrow x_1 >\frac{\sqrt{2}\sqrt{10m^{2}z+k+\sqrt{k}\sqrt{20m^{2}z+k}}}{10\sqrt{k}m}\equiv x_1^{\min }, \end{aligned}$$

(31)

$$\begin{aligned} n_m^R <1\quad&\Rightarrow x_m <1-\frac{\sqrt{2}\sqrt{10m^{2}z+k+\sqrt{k}\sqrt{20m^{2}z+k}}}{10\sqrt{k}m}\equiv x_m^{\max }.\quad \end{aligned}$$

(32)

Since $x_{i+1} >x_i$ by assumption, applying the lower bound of $x_1$ and the upper bound of $x_m$ yields:

$$\begin{aligned}&x_m^{\max } -x_1^{\min } -\mathop {\sum \limits _{i=1}^{m-1}} x_d^{\min } >0 \Rightarrow \\&\quad 1-\frac{\sqrt{2}\sqrt{10m^{2}z/k+1+\sqrt{20m^{2}z/k+1}}}{5}>0,\quad \hbox {if and only if}\; z<\frac{3}{4m^{2}}. \end{aligned}$$

Therefore, to ensure the existence of equilibrium, $z<3/(4m^{2})$ is required. Intuitively, the waiting cost of online purchases must be lower than a proportion of the transportation rate so that the online firm can capture some of the market between the physical firms. The online firm cannot compete with the physical firms if waiting cost is relatively high such that $z\ge 3/(4m^{2})$.

Substituting the equilibrium prices into the market shares yields:

$$\begin{aligned} N_i^*&= \frac{\sqrt{2}\sqrt{10m^{2}z+k+\sqrt{k}\sqrt{20m^{2}z+k}}}{5\sqrt{k}m},\quad i=1,\ldots ,m, \end{aligned}$$

(33)

$$\begin{aligned} N_{m+1}^*&= \frac{5k-\sqrt{2k}\sqrt{10m^{2}z+k+\sqrt{k}\sqrt{20m^{2}z+k}}}{5k}. \end{aligned}$$

(34)

This result can be summarized as the following proposition.

Proposition 5

When $m$ physical firms compete with an online firm, there exist a set of pure strategy equilibria such that each physical firm occupies a region of the market that is unconnected with other physical firms, and the online firm takes the rest of the market when $z<3/(4m^{2})$. The equilibrium locations $(x_i^*,i=1,\ldots ,m)$ must satisfy (30), (31) and (32), the equilibrium prices must satisfy (28) and (29), and the market shares satisfy (33) and (34).

Proposition 6

The equilibrium prices $p_i^*i=1,\ldots , m$ are increasing in $k$ and $z$, while $p_{m+1}^*$ is increasing in $k$ and decreasing in $z$. Moreover, $p_i^*<p_{m+1}^*$ if and only if $z<k/(16m^{2})$.

The detailed calculations to show the above proposition can be derived easily from (30) and (31). The intuition of Proposition 6 is similar to Proposition 3. Moreover, if $m$ increases, then $p_i^*<p_{m+1}^*$ is more difficult to satisfy.

From (33) and (34), the market shares can be compared:

$$\begin{aligned} N_{m+1}^*-N_i^*=\frac{5m-\sqrt{2}\sqrt{10m^{2}\frac{z}{k}+1+\sqrt{20m^{2}\frac{z}{k}+1}}\cdot (m+1)}{5m}. \end{aligned}$$

(35)

This function is strictly decreasing in $z/k$ and positive at $z/k=0$. Thus, (35) is positive when $z/k < (3m-2)/(4(m^{2}+2m+1)\cdot m)$. However, $(3m-2)/(4(m^{2}+2m+1)\cdot m)>1/(4m^{2})$, when $m\ge 1+\sqrt{6}/2\approx 2.225$. Therefore, the condition $z/k<1/(4m^{2})$ in Proposition 5 guarantees that $N_{m+1}^*-N_i^*>0$. Since $z<k/m$ is assumed, $N_{m+1}^*$ definitely exceeds $N_i^*, i=1,\ldots ,m$. Moreover,

$$\begin{aligned}&N_{m+1}^*-\mathop \sum \limits _{i=1}^m N_i^*\nonumber \\&\quad \quad =\frac{5-2\sqrt{2}\sqrt{10m^{2}\frac{z}{k}+1+\sqrt{20m^{2}\frac{z}{k}+1}}}{5}>0\quad \hbox {if and only if}\quad z<\frac{k}{16m^{2}}.\nonumber \\ \end{aligned}$$

(36)

These results can be summarized as the following proposition.

Proposition 7

In equilibrium, the market share of the online firm is larger than that of a physical firm. When $z<k/(16m^{2})$, the market share of the online firm is larger than the total market share of all of the physical firms.

The next step is to consider social welfare. Since the product demand is inelastic, the socially optimal solution is identical to the result of minimizing the sum of transportation costs and waiting costs (denoted by TTC):

$$\begin{aligned} \mathop {\min }\limits _{x_i ,i=1,\ldots , m} \;\hbox {TTC}&= N_{m+1} \cdot z+\mathop \sum \limits _{i=1}^m \mathop \int \limits _{n_i^L}^{n_i^R } k(x-x_i )^{2}\hbox {d}x\nonumber \\&= \frac{k}{12}\mathop \sum \limits _{i=1}^m N_i^3 +z\left( {1-\mathop \sum \limits _{i=1}^m N_i} \right) . \end{aligned}$$

(37)

Then, the optimal solutions become:

$$\begin{aligned} N_i^o =\frac{2\sqrt{kz}}{k}\quad i=1,\ldots ,m,\quad \quad N_{m+1}^o =\frac{k-2m\sqrt{kz}}{k}. \end{aligned}$$

(38)

Comparing $N_i^*$ with $N_i^o$ yields the following proposition.

Proposition 8

When $z=k/(16m^{2})$, the equilibrium solution is identical to the socially optimal solution.

This fact suggests that when $z=k/(16m^{2}), p_i^*=p_{m+1}^*, i=1,\ldots ,m,$ which represents a minimal TTC. Proposition 8 provides a rationale for the taxation of online businesses. Intuitively, when $z$ is very low ($z<k/(16m^{2})$), the online firm will set a higher price than the physical firms. Hence, the optimal taxation must be lower for the online firm to equalize these prices and reach to the social optimum.

5 Endogenous number of firms with free entry

This section extends to a framework in which an endogenous number of physical firms is assumed. From (24) and (29), the equilibrium profits of physical firms become

$$\begin{aligned} \pi _i (k,z,m)&= p_i^*N_i^*\\&= \frac{10m^{2}z+k+\sqrt{k(20m^{2}z+k)}}{25m^{2}}\cdot \frac{\sqrt{2}\sqrt{10m^{2}z+k+\sqrt{k}\sqrt{20m^{2}z+k}}}{5\sqrt{k}m},\\&i=1,\ldots , m. \end{aligned}$$

It can be shown that $\partial \pi _i (k,z,m)/\partial m<0, \forall i=1,\ldots ,m+1$ consider that each physical firm involves a fixed cost $F$, while the online firm has no fixed cost. The profit function of the physical firm $i$ is

$$\begin{aligned} \pi _i^F =\pi _i (k,z,m)-F\quad i=1,\ldots , m. \end{aligned}$$

The equilibrium number ($m^{*}$) of physical firms is specified by the following proposition:

Proposition 9

Allowing free entry for physical firms, the equilibrium number of physical firms $m^{*}$. satisfies

$$\begin{aligned} \pi _i (k,z,m)-F\ge 0>\pi _i (k,z,m+1)-F. \end{aligned}$$

(39)

Additionally, $m^{*}$ is non-increasing in $F$, non-decreasing in $z$ and non-decreasing in $k$ if k is relatively large (or $z$ is close to zero).

Proof

By detailed calculations for comparative statics, $\partial \pi _i (k,z,m)/\partial z>0$ and $\partial \pi _i (k,z,m)/\partial m<0$, and

$$\begin{aligned} \frac{\partial \pi _i (k,z,m)}{\partial k} = A (z,k,m)\cdot \end{aligned}$$

$$\begin{aligned} (k^{2}+\sqrt{20m^{2}z+k}k^{3/2}+15km^{2}z+ 5m^{2}z\sqrt{k}\sqrt{20m^{2}z+k}-100m^{4}z^{2}), \end{aligned}$$

(40)

where $A(z,k,m)$ is a positive function. Since the second term on the right-hand side of (40) is strictly increasing in $k$, implying $\partial \pi _i (k,z,m)/\partial k>0$ if $k$ is large or $z$ is close to zero. From $\partial \pi _i^F /\partial F<0$, the comparative statics in the proposition are proved by performing detailed calculations. $\square$

Example 2

Given $k=10, z=1$, and $F=0.15, \pi _i^F (m=7)=0.031$ and $\pi _i^F (m=8)=-0.026$. Therefore, $m^{*}=7$. If $F=0.02$, then $\pi _i^F (m=3)=0.028$ and $\pi _i^F (m=4)=-0.082$, and $m^{*}=3$.

6 Stackelberg competition

After the complete analysis on Nash equilibria, in this section, our model is extended to a von Stackelberg structure for comprehensiveness.¹⁰ Consider a different game in which an online firm sets its price ($p_{m+1}$) prior to the $M$ brick-and-mortar firms setting their prices. From (26), solving $\partial \pi _i /\partial p_i =0$ yields $p_i =\frac{2}{3}(p_{m+1} +z)$, $i = 1, \ldots , m$. Plugging $p_i$ into (27) yields

$$\begin{aligned} p_{m+1}^{s*} =\frac{k+\sqrt{4m^{2}zk+k^{2}}-4m^{2}z}{6m^{2}}. \end{aligned}$$

(41)

Plugging (41) into $p_i$ yields

$$\begin{aligned} p_i^{s*} =\frac{k+\sqrt{4m^{2}zk+k^{2}}-4m^{2}z}{9m^{2}},\quad i=1,\ldots ,M. \end{aligned}$$

(42)

Therefore, the necessary conditions for the existence of equilibrium are $n_1^L >0, n_2^R <1$ and $n_i^R <n_{i+1}^L, i=1,\ldots ,m-1$, yielding:

$$\begin{aligned} n_{i+1}^L -n_i^R >0&\Rightarrow x_{i+1} -x_i >\frac{\sqrt{2}\sqrt{2m^{2}z+k+\sqrt{k}\sqrt{4m^{2}z+k}}}{3\sqrt{k}m}\nonumber \\&\equiv x_d^{\min } ,\quad i=1,\ldots ,m-1, \end{aligned}$$

(43)

$$\begin{aligned} n_1^L >0&\Rightarrow x_1 >\frac{\sqrt{2}\sqrt{2m^{2}z+k+\sqrt{k}\sqrt{4m^{2}z+k}}}{6\sqrt{k}m}\equiv x_1^{\min } , \end{aligned}$$

(44)

$$\begin{aligned} n_m^R <1&\Rightarrow x_m <1-\frac{\sqrt{2}\sqrt{2m^{2}z+k+\sqrt{k}\sqrt{4m^{2}z+k}}}{6\sqrt{k}m}\equiv x_m^{\max } . \end{aligned}$$

(45)

Since $x_{i+1} >x_i$, using the lower bound of $x_1$ and the upper bound of $x_m$ yields:

$$\begin{aligned}&x_m^{\max } -x_1^{\min } -\mathop \sum \limits _{i=1}^{m-1} x_d^{\min } >0 \nonumber \\&\qquad \Rightarrow 1-\frac{\sqrt{2}\sqrt{2m^{2}z/k+1+\sqrt{4m^{2}z/k+1}}}{3}>0,\quad \hbox {if and only if}\; z<\frac{3}{4m^{2}}. \end{aligned}$$

Comparing (41) and (42) yields

$$\begin{aligned} p_i^{s*} -p_{m+1}^{s*} =\frac{-k-\sqrt{k(4m^{2}z+k)}+16m^{2}z}{18m^{2}}<0\quad \hbox {iff}\quad z<\frac{9k}{64m^{2}}. \end{aligned}$$

(46)

Comparing (28) and (29) with (41) and (42) yields $p_{m+1}^{s*} -p_{m+1}^*>0$, since $z<\frac{3k}{4m^{2}}$ is assumed in Proposition 5. Similarly, $p_i^{s*} -p_i^*>0$ since we have assumed $z<\frac{3k}{4m^{2}}$. The above results can be summarized as the following proposition.

Proposition 10

Under a Stackelberg competition in the price game such that the online firm sets its price $p_{m+1}$ before the $M$ brick-and-mortar firms, the equilibrium prices $(p_{m+1}^{s*}, p_i^{s*})$ satisfy (41) and (42), respectively. The equilibrium locations $(x_i^{s*}, i = 1, \ldots , m)$ must satisfy (43), (44) and (45). Moreover, $p_i^{s*} <p_{m+1}^{s*}, i=1,\ldots ,M,$ if and only if $z<\frac{9k}{64m^{2}}$. Finally, the equilibrium Stackelberg prices are higher than those in the Cournot competition ($p_{m+1}^{s*} >p_{m+1}^*$ and $p_i^{s*} >p_i^*$).

These results imply that the degree of competition in a Stackelberg game is less than that in a Nash game, while the equilibrium locations are similar to those in Cournot competition. Therefore, the equilibrium prices are higher under Stackelberg competition.

7 Conclusions

Introducing an online firm into a spatial duopoly model yields a type of non-maximal differentiation equilibrium that has seldom been discussed in the literature. The model presented in this paper demonstrates that the online firm plays an important role in affecting the traditional location–price equilibrium. The online firm may charge either a higher or lower price than the physical firms, depending on its relative advantages. Our model is extended to the situations of multiple firms and the Stackelberg framework.

Our analysis relies on the assumption that the online firm has no specific location. This assumption could be true in a metropolitan area, but for a large market scale, such as a national market, an online firm may consider the optimal locations of its distribution facilities. For example, Amazon has recently increased the number of its distribution centers in order to get close to customers and so reduce consumers’ waiting costs. In this situation, the transportation costs are endogenously determined by the online firm. This spatial scale issue is left for future research.