Unsteady ballistic heat transport in harmonic crystals with polyatomic unit cell

Abstract

We study thermal processes in infinite harmonic crystals having a unit cell with an arbitrary number of particles. Initially, particles have zero displacements and random velocities, corresponding to some initial temperature profile. Our main goal is to calculate spatial distribution of kinetic temperatures, corresponding to degrees of freedom of the unit cell, at any moment in time. An expression for the temperatures is derived from solution of lattice dynamics equations. It is shown that the temperatures are represented as a sum of two terms. The first term describes high-frequency oscillations of the temperatures caused by local transition to thermal equilibrium at short times. The second term describes slow changes in the temperature profile caused by ballistic heat transport. It is shown that during heat transport, local values of temperatures, corresponding to degrees of freedom of the unit cell, are generally different. Analytical findings are supported by results of numerical solution of lattice dynamics equations for diatomic chain and graphene lattice. Strong anisotropy of ballistic heat transport in graphene is demonstrated. Presented theory may serve for description of unsteady ballistic heat transport in real crystals with low concentration of defects. In particular, solution of the problem with sinusoidal initial temperature profile can be used for proper interpretation of experimental data obtained by the transient thermal grating technique.

1 Introduction

At macroscale, heat transport in solids is usually diffusive and well-described by the Fourier law. The law states that heat flux is proportional to temperature gradient with proportionality coefficient referred to as the thermal conductivity. Recent experiments for materials with low defect concentration have shown that at micro- and nanoscale heat propagates ballistically [12, 15, 31, 65]. In particular, it is demonstrated for many materials including nanowires [3, 31], nanotubes [14], graphene [6, 60, 76], silicon membranes [36], etc., that thermal conductivity strongly depends on sample size and the Fourier law is violated. Therefore development of theoretical models describing ballistic heat transport is required.

In continuum mechanics, heat transfer equations are usually derived using phenomenological approach. Development of phenomenological models for ballistic heat transport is limited by small amount of available experimental data. In this case, various microscopic models can be used for derivation of constitutive laws describing ballistic heat transport. One of microscopic approaches is based on Boltzmann transport equation (BTE), formulated for distribution function of phonons [47, 61]. Given known the distribution function, the temperature field can be calculated. The BTE is usually simplified using the relaxation time approximation [9, 39, 47] for the collision term. It allows to solve the BTE numerically [32, 56, 68] and to derive heat conduction equations [13, 44, 59, 75]. In both cases, additional approximations are introduced [70]. In particular, contribution of optical vibrations to heat transport is often neglected. Comprehensive review on application of the BTE to simulation of thermal transport can be found, e.g. in review papers [12, 52, 70]. In the present paper, we use another approach for description of ballistic heat transport. Expressions describing evolution of temperature profile are derived directly from equations of motion of a crystal in harmonic approximation. This approach allows to investigate heat transport in ballistic limit taking into account all important features of lattice dynamics.

Analysis of heat transport in lattices is usually carried out in the so-called nonequilibrium steady-state. In this case, a material is kept between two thermostats with different temperatures. Given known the difference of temperatures, distance between thermostats, and the heat flux, one can calculate the effective heat conductivity of a material. This statement of the problem is widely used in both analytical studies [7, 53, 66, 71] and computer simulations [18, 37, 52, 74] of heat transport. Comprehensive reviews of results obtained in steady-state formulation are given e.g. in papers [11, 17, 52]. Calculating heat conductivity as a function of a sample length, allows to distinguish between ballistic and diffusive heat transport regimes. However, the steady-state formulation does not address the issue of temperature field evolution. Additionally, results of steady-state simulations significantly depend on the type of thermostat being used [29, 37]. Therefore in the present paper we consider unsteady heat transport.

One of the goals of unsteady heat transport simulations is to describe time evolution of initial temperature profile. The initial profile can be prescribed by assigning random initial velocities to particles [5, 21, 25, 27, 41, 50, 55, 63, 69]. Then no thermostat is needed. Heat transport simulations are usually carried out numerically using, for example, molecular dynamics method [24, 45, 54, 62, 72]. The method allows to use realistic interatomic potentials and to consider effect of nonlinearity (anharmonicity), defects, interfaces, and other features of real systems, which are hard to describe analytically. Though numerical modeling is a powerful tool for investigation of heat transport, many issues can not be addressed numerically. In particular, for crystals with several branches of dispersion relation, in numerical simulations it is hard to distinguish between contributions of acoustic and optical vibrations to the heat transport. Therefore analytical studies of unsteady heat transport are of great importance.

A promising model for investigation of ballistic heat transport is a harmonic crystal, i.e. a set of material points forming a perfect crystal lattice and interacting via linearized forces. In this model, harmonic waves do not interact with each other and therefore the heat transport is purely ballistic. Unsteady ballistic heat transport in harmonic crystals is investigated e.g. in papers [5, 21, 25, 27, 41, 43, 50, 55, 63, 69]. In paper [41], an equation, referred to as the ballistic heat equation, describing evolution of temperature field in a one-dimensional chain with interactions of the nearest neighbors is derived. The equation is also valid [5] for one-dimensional chain with harmonic on-site potential (elastic foundation). An expression for temperature field in scalar lattices with one degree of freedom per unit cell is derived in paper [50]. Similar results are obtained by entirely different means in papers [27, 55]. In realistic crystals, each unit cell usually has several degrees of freedom. To our knowledge, no closed-form expressions describing evolution of temperature field in crystals with several degrees of freedom per unit cell are available in literature.

The main goal of the present paper is to calculate spatial distribution of kinetic temperatures, corresponding to degrees of freedom of the unit cell, at any moment in time. The paper is organized as follows. In Sect. 3, equations of motion for harmonic crystals are represented in a general form valid for one-, two-, and three-dimensional lattices with arbitrary number of particles per unit cell. In Sect. 4, random initial conditions corresponding to an initial temperature profile are formulated. In Sect. 5, an exact solution of equations of motion is derived. The solution is used for calculation of temperatures, corresponding to different degrees of freedom, defined in Sect. 6. In Sect. 7, an exact expression describing temporal and spatial evolution of the temperatures is obtained. In Sect. 8, simple approximate formula for the temperatures is derived. In Sect. 9, analysis of specific initial temperature profiles is presented. In particular, decay of a spatially sinusoidal profile of initial temperature is considered in Sect. 9.5. This problem is important, because it is closely related to experimental technique referred to as the transient thermal grating (TTG) [33, 36, 67]. In the framework of the TTG, a sinusoidal initial temperature profile is generated using the interference of two laser pulses. Decay of temperature profile yields information about thermal properties of a material. Results obtained in Sects. 5–9 are applicable to crystals with an arbitrary lattice. In Sects. 10, 11 the general theory is employed for analysis of two particular cases, namely one-dimensional diatomic chain and graphene lattice. Analytical results are compared with numerical solution of lattice dynamics equations.

2 Nomenclature

Here and below matrices are denoted by bold italic symbols, while invariant vectors, e.g. position vector, are denoted by bold symbols. The following notation is used:

• N is a number of degrees of freedom per unit cell;

• ${\mathbf{x}}{}, {\mathbf{y}}{}$ are position vectors of unit cells;

• ${\mathbf{a}}{}_{\alpha }$ is vector connecting unit cell with neighboring cell number $\alpha$;

• d is space dimensionality;

• ${\mathbf{b}}{}_j, j=1,\ldots ,d$ are primitive vectors of the lattice;

• $\tilde{{\mathbf{b}}{}}_j, j=1,\ldots ,d$ are vectors of the reciprocal basis;

• $\varvec{{u}}{}({\mathbf{x}}{}), \varvec{{v}}{}({\mathbf{x}}{})$ are columns of length N, consisting of components of displacements and velocities of particles from unit cell ${\mathbf{x}}{}$;

• $u_j, j=1,\ldots ,N$ are components of column $\varvec{{u}}{}$;

• $\varvec{{v}}{}_0({\mathbf{x}}{})$ is column of initial velocities of particles from unit cell ${\mathbf{x}}{}$;

• $\varvec{{C}}{}_{\alpha }$ is a matrix describing interactions between a unit cell and neighboring cell number $\alpha$;

• $\varvec{{M}}{}{}$ is diagonal matrix composed of masses of particles from a unit cell;

• ${\mathbf{k}}{}$ is wave vector;

• $\omega _j({\mathbf{k}}{})$, ${\mathbf{v}}{}_g^j({\mathbf{k}}{})$ are jth branch of dispersion relation and corresponding group velocity;

• $\varvec{\varOmega }({\mathbf{k}}{})$ is dynamical matrix of the lattice;

• $\varvec{{P}}{}{}({\mathbf{k}}{})$ is polarization matrix, composed of normalized eigenvectors of dynamic matrix $\varvec{\varOmega }({\mathbf{k}}{})$;

• $T({\mathbf{x}}{})$ is kinetic temperature, proportional to mathematical expectation of kinetic energy of the unit cell;

• $\varvec{{T}}{}({\mathbf{x}}{})$ is $N \times N$ temperature matrix of unit cell ${\mathbf{x}}{}$;

• $\varvec{{T}}{}_0({\mathbf{x}}{})$ is initial temperature matrix of unit cell ${\mathbf{x}}{}$;

• $T_{ij}$ is element i, j of the temperature matrix;

• $\varvec{{T}}{}_\mathrm{F}$, $\varvec{{T}}{}_\mathrm{S}$ are “fast” and “slow” parts of the temperature matrix;

• $\Bigl \langle {...}\Bigr \rangle$ stands for mathematical expectation;

• $\top$ is transpose sign;

• $\varvec{{E}}{}$ is $N \times N$ identity matrix;

• $\delta _D({\mathbf{x}}{}-{\mathbf{y}}{})$ is equal to 1 for ${\mathbf{x}}{}={\mathbf{y}}{}$ and equal to zero otherwise;

• $\delta _{ij}$ is the Kronecker delta;

• $\delta ({\mathbf{x}}{})$ is Dirac delta function in d-dimensional space;

• H is Heaviside step function.

3 Equations of motion of a crystal

We consider infinite crystals in d-dimensional space, $d=1,2,3$. Unit cell of a crystal contains an arbitrary number of particles. In this section, we represent equations of motion of the unit cell in a matrix form [51], convenient for analytical derivations.

Unit cells of the lattice are identified by their position vectors, ${\mathbf{x}}{}$, in the undeformed state.¹ Each unit cell has N degrees of freedom $u_i({\mathbf{x}}{}), i=1,\ldots ,N$, corresponding to components of particle displacements.² The displacements form a column:

$$\begin{aligned} \varvec{{u}}{}({\mathbf{x}}{}) = \begin{bmatrix} u_1&u_2&...&u_N\end{bmatrix}^{\top }, \end{aligned}$$

(1)

where $\top$ stands for the transpose sign.

Particles from the cell ${\mathbf{x}}{}$ interact with each other and with particles from neighboring unit cells, numbered by index $\alpha$. Vector connecting the cell ${\mathbf{x}}{}$ with neighboring cell number $\alpha$ is denoted ${\mathbf{a}}{}_{\alpha }$. Vectors ${\mathbf{a}}{}_{\alpha }$ are numbered such that the following identity is satisfied:

$$\begin{aligned} {\mathbf{a}}{}_{\alpha }= -{\mathbf{a}}{}_{-\alpha }. \end{aligned}$$

(2)

Here ${\mathbf{a}}{}_{0} = 0$. Vectors ${\mathbf{a}}{}_{\alpha }$ for a sample lattice are shown in Fig. 1.

Fig. 1

Example of a two-dimensional lattice with three particles per unit cell (three sublattices). Particles forming sublattices have different color and size (color figure online)

In the present paper, an infinite crystal is considered as a limiting case of a crystal under periodic boundary conditions. A periodic cell contains $n^d$ unit cells (n cells in each direction). Displacements of particles satisfy periodic boundary conditions:

$$\begin{aligned} \varvec{{u}}{}({\mathbf{x}}{}) = \varvec{{u}}{}\left( {\mathbf{x}}{}+ \sum _{j=1}^d \gamma _j n {\mathbf{b}}{}_j\right) , \end{aligned}$$

(3)

where ${\mathbf{b}}{}_j$ are primitive vectors of the lattice; $\gamma _j$ are integers. Further analytical derivations are carried out for $n \rightarrow \infty$, while in computer simulations n is finite.

We represent equations of motion in a quite general form, applicable to one-, two-, and three-dimensional lattices with an arbitrary number of degrees of freedom per unit cell. In harmonic crystals, the total force acting on each particle is represented as a linear combination of displacements of all other particles. Using this fact, we write equations of motion of the unit cell in the form [51, 55]:

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{M}}{}{}{\dot{\varvec{{v}}{}}}({\mathbf{x}}{}) = \sum _{\alpha } \varvec{{C}}{}_{\alpha } \varvec{{u}}{}({\mathbf{x}}{}+ {\mathbf{a}}{}_{\alpha }), \qquad \varvec{{C}}{}_{\alpha } = \varvec{{C}}{}_{-\alpha }^{\top }, \end{array} \end{aligned}$$

(4)

where $\varvec{{v}}{}={\dot{\varvec{{u}}{}}}$; $\varvec{{u}}{}({\mathbf{x}}{}+ {\mathbf{a}}{}_{\alpha })$ is a column of displacements of particles from unit cell $\alpha$; $\varvec{{M}}{}{}$ is diagonal $N \times N$ matrix composed of particles’ masses; coefficients of matrix $\varvec{{C}}{}_{\alpha }$ determine stiffnesses of springs connecting particles from unit cell ${\mathbf{x}}{}$ with particles from neighboring cell $\alpha$; matrix $\varvec{{C}}{}_{0}$ describes interactions of particles inside the unit cell ${\mathbf{x}}{}$.³ In formula (4) summation is carried out with respect to all unit cells $\alpha$, interacting with unit cell ${\mathbf{x}}{}$ (including $\alpha =0$).

Remark 1

Relation $\varvec{{C}}{}_{\alpha } = \varvec{{C}}{}_{-\alpha }^{\top }$ guarantees that dynamical matrix (10) of the lattice is Hermitian (see Sect. 5 for more details).

Formula (4) describes motion of monoatomic and polyatomic crystals in one-, two- , and three-dimensional cases. For $N=1$ (one degree of freedom per unit cell), Eq. (4) governs dynamics of the so-called scalar lattices,⁴ considered, for example, in papers [27, 50, 52, 55, 57, 58]. Monoatomic two- and three-dimensional lattices are covered if we put $N=d$ and $\varvec{{C}}{}_{\alpha }=\varvec{{C}}{}_{\alpha }^{\top }$ in formula (4). In the present paper, for illustration we consider crystals with two particles per unit cell, namely one-dimensional diatomic chain (Sect. 10) and out-of-plane motions of graphene lattice (Sect. 11).

4 Initial conditions

In this section, we specify initial conditions for particles, corresponding to an initial temperature profile.

The following initial conditions, typical for molecular dynamics modeling of thermal processes [2, 5, 21, 25, 41, 50, 63, 69], are used:

$$\begin{aligned} \varvec{{u}}{}({\mathbf{x}}{}) = 0, \quad \varvec{{v}}{}({\mathbf{x}}{}) = \varvec{{v}}{}_0({\mathbf{x}}{}), \end{aligned}$$

(5)

Here $\varvec{{v}}{}_0({\mathbf{x}}{})$ is a column of random initial velocities of particles from unit cell ${\mathbf{x}}{}$ such that

$$\begin{aligned} \Bigl \langle {\varvec{{v}}{}_0({\mathbf {x}}{})}\Bigr \rangle = 0, \qquad \Bigl \langle {\varvec{{v}}{}_0({\mathbf {x}}{})\varvec{{v}}{}_0({\mathbf {y}}{})^{\top }}\Bigr \rangle = \varvec{{B}}{}({\mathbf {x}}{})\delta _D({\mathbf {x}}{}-{\mathbf {y}}{}), \end{aligned}$$

(6)

where $\Bigl \langle {...}\Bigr \rangle$ stands for mathematical expectation;⁵$\delta _D(0) = 1$; $\delta _D({\mathbf{x}}{}-{\mathbf{y}}{})=0$ for ${\mathbf{x}}{}\ne {\mathbf{y}}{}$. In other words, components of $\varvec{{v}}{}_0({\mathbf{x}}{})$ are random numbers with zero mean⁶ and generally different variances given by diagonal elements of matrix $varvec{{B}}{}({\mathbf {x}}{})=\langle {\varvec{{v}}{}_0({\mathbf {x}}{})\varvec{{v}}{}_0({\mathbf {x}}{})^{\top }}\rangle$. Off-diagonal elements of matrix $\varvec{{B}}{}({\mathbf{x}}{})$ are equal to covariances of initial velocities, corresponding to different degrees of freedom of unit cell, ${\mathbf{x}}{}$. Initial velocities of particles from different unit cells are statistically independent.

From macroscopic point of view, initial conditions (5), (6) specify some initial temperature profile [see formulas (17), (18)] and zero initial heat fluxes.⁷ Examples of initial conditions (5), (6) are given by formulas (48), (62). Initial conditions (5), (6) can be considered as a result of heating of a crystal by an ultrashort laser pulse [33, 34, 36, 64, 67].

In the following section, an exact solution of equations of motion (4) with initial conditions (5) is obtained. The solution is employed for description of thermal processes, such as the ballistic heat transport.

5 Exact solution of equations of motion

In this section, we derive an exact solution of Eq. (4) with initial conditions (5), (6) using the discrete Fourier transform with respect to components of position vector ${\mathbf{x}}{}$.⁸

Position vector, ${\mathbf{x}}{}$, of a unit cell is represented as

$$\begin{aligned} {\mathbf{x}}{}= \sum _{j=1}^d z_j {\mathbf{b}}{}_j, \end{aligned}$$

(7)

where ${\mathbf{b}}{}_j, j=1,\ldots ,d$ are primitive vectors of the lattice; $z_1,\ldots ,z_d$ are integer indices of the unit cell; d is space dimensionality. Direct and inverse discrete Fourier transforms with respect to variables $z_1, .., z_d$ for an infinite lattice are defined as

$$\begin{aligned} \begin{array}{l} \displaystyle {\hat{\varvec{{u}}{}}}({\mathbf{k}}{}) = \sum _{{\mathbf{x}}{}} \varvec{{u}}{}({\mathbf{x}}{}) e^{-\mathrm{i}{\mathbf{k}}{}\cdot {\mathbf{x}}{}}, \qquad {\mathbf{k}}{}= \sum _{j=1}^d p_j \tilde{{\mathbf{b}}{}}_j, \\ \displaystyle \varvec{{u}}{}({\mathbf{x}}{}) = \int _{{\mathbf{k}}{}} {\hat{\varvec{{u}}{}}}({\mathbf{k}}{}) e^{\mathrm{i}{\mathbf{k}}{}\cdot {\mathbf{x}}{}} \mathrm{d} {\mathbf{k}}{}. \end{array} \end{aligned}$$

(8)

Here ${\hat{\varvec{{u}}{}}}({\mathbf{k}}{})$ is Fourier image of $\varvec{{u}}{}$; $\mathrm{i}^2=-1$; ${\mathbf{k}}{}$ is wave vector; $p_j \in [0; 2\pi ]$; $\tilde{{\mathbf{b}}{}}_j$ are vectors of the reciprocal basis, i.e. ${\mathbf{b}}{}_i\cdot \tilde{{\mathbf{b}}{}}_j = \delta _{ij}$, where $\delta _{ij}$ is the Kronecker delta. For brevity, the following notation is used:

$$\begin{aligned} \int _{{\mathbf{k}}{}} ... \mathrm{d}{\mathbf{k}}{}\,{\mathop {=}\limits ^{\text{ def }}}\,\frac{1}{(2\pi )^d}\int _{0}^{2\pi }..\int _{0}^{2\pi } ... \mathrm{d} p_1.. \mathrm{d} p_d, \qquad \sum _{{\mathbf{x}}{}}... \,{\mathop {=}\limits ^{\text{ def }}}\,\sum _{z_1=-\infty }^{+\infty }...\sum _{z_d=-\infty }^{+\infty }... \end{aligned}$$

(9)

Applying the discrete Fourier transform (8) to formulas (4), (5), (6), yields equation

$$\begin{aligned} \varvec{{M}}{}{}^{\frac{1}{2}} \ddot{{\hat{\varvec{{u}}{}}}} = -\varvec{\varOmega }\varvec{{M}}{}{}^{\frac{1}{2}}{\hat{\varvec{{u}}{}}}, \qquad \varvec{\varOmega }({\mathbf{k}}{}) =- \sum _{\alpha } \varvec{{M}}{}{}^{-\frac{1}{2}}\varvec{{C}}{}_{\alpha }\varvec{{M}}{}{}^{-\frac{1}{2}} e^{\mathrm{i}{\mathbf{k}}{}\cdot {\mathbf{a}}{}_{\alpha }}, \end{aligned}$$

(10)

with initial conditions

$$\begin{aligned} {\hat{\varvec{{u}}{}}} = 0, \qquad \dot{{\hat{\varvec{{u}}{}}}} = {\hat{\varvec{{v}}{}}}_0 = \sum _{{\mathbf{x}}{}}\varvec{{v}}{}_0({\mathbf{x}}{}) e^{-\mathrm{i}{\mathbf{k}}{}\cdot {\mathbf{x}}{}}. \end{aligned}$$

(11)

Matrix $\varvec{\varOmega }$ in formula (10) is the dynamical matrix of the lattice [19]. Here $\varvec{{M}}{}{}^{\frac{1}{2}}\varvec{{M}}{}{}^{\frac{1}{2}} = \varvec{{M}}{}{}$.

To simplify Eq. (10), we use the fact that dynamical matrix $\varvec{\varOmega }$ is Hermitian, i.e. it is equal to its own conjugate transpose.⁹ Then it can be represented as

$$\begin{aligned} \varvec{\varOmega }= \varvec{{P}}{}{}\varvec{\varLambda }\varvec{{P}}{}{}^{*{\top }}, \qquad \Lambda _{ij} = \omega _j^2 \delta _{ij}, \end{aligned}$$

(12)

where $\omega _j^2, j=1,\ldots ,N$ are eigenvalues of matrix $\varvec{\varOmega }$ and $\omega _j({\mathbf{k}}{})$ are branches of dispersion relation for the lattice (below we consider only nonnegative frequencies, i.e. $\omega _j({\mathbf{k}}{}) \ge 0$); $*$ stands for complex conjugate; matrix $\varvec{{P}}{}{}$ is composed of normalized eigenvectors of matrix $\varvec{\varOmega }$.¹⁰ The eigenvectors are referred to as the polarization vectors [19].

Remark 2

We assume that branches of dispersion relation do not intersect with each other, i.e. all eigenvalues of the dynamic matrix $\varvec{\varOmega }$ are distinct. The case of intersecting branches should be considered separately.

We substitute formula (12) into Eq. (10), multiply both parts by $\varvec{{P}}{}{}^{*{\top }}$ and introduce new variable $\varvec{{w}}{} = \varvec{{P}}{}{}^{*{\top }} \varvec{{M}}{}{}^{\frac{1}{2}}{\hat{\varvec{{u}}{}}}$. Then we obtain a system of decoupled equations for elements $w_j$ of vector $\varvec{{w}}{}$:

$$\begin{aligned} \ddot{\varvec{{w}}{}} = -\varvec{\varLambda }\varvec{{w}}{} \quad \Leftrightarrow \quad \ddot{w}_j = -\omega _j^2 w_j. \end{aligned}$$

(13)

Solving these equations with initial conditions (11) we obtain the following expression for $\dot{\varvec{{w}}{}}$:

$$\begin{aligned} {\dot{w}}_j = \{\varvec{{P}}{}{}^{*\top } \varvec{{M}}{}{}^{\frac{1}{2}} {\hat{\varvec{{v}}{}}}_0\}_j \cos \left( \omega _j t\right) \quad \Leftrightarrow \quad \dot{\varvec{{w}}{}} = \varvec{{D}}{}\varvec{{P}}{}{}^{*\top } \varvec{{M}}{}{}^{\frac{1}{2}} {\hat{\varvec{{v}}{}}}_0, \qquad D_{ij}({\mathbf{k}}{}, t) = \cos \left( \omega _j({\mathbf{k}}{}) t\right) \delta _{ij}. \end{aligned}$$

(14)

Here $\{...\}_j$ stands for jth element of a column. Then using definition of $\varvec{{w}}{}$, we represent Fourier-images of velocities in the form

$$\begin{aligned} {\hat{\varvec{{v}}{}}} = \varvec{{M}}{}{}^{-\frac{1}{2}} \varvec{{P}}{}{}\varvec{{D}}{}\varvec{{P}}{}{}^{*\top } \varvec{{M}}{}{}^{\frac{1}{2}} {\hat{\varvec{{v}}{}}}_0. \end{aligned}$$

(15)

Applying the inverse discrete Fourier transform to formula (15), yields the following expression for particle velocities:

$$\begin{aligned} \varvec{{v}}{}({\mathbf{x}}{}) = \varvec{{M}}{}{}^{-\frac{1}{2}}\int _{{\mathbf{k}}{}} \varvec{{P}}{}{}({\mathbf{k}}{}) \varvec{{D}}{}({\mathbf{k}}{},t) \varvec{{P}}{}{}({\mathbf{k}}{})^{*{\top }} \varvec{{M}}{}{}^{\frac{1}{2}} {\hat{\varvec{{v}}{}}}_0 e^{\mathrm{i}{\mathbf{k}}{}\cdot {\mathbf{x}}{}} \mathrm{d} {\mathbf{k}}{}, \end{aligned}$$

(16)

where ${\hat{\varvec{{v}}{}}}_0$ is Fourier image of initial velocities [see formula (11)]; diagonal matrix $\varvec{{D}}{}$ is defined by formula (14).

Thus formula (16) is an exact solution of Eq. (4) with initial conditions (5). In the following sections, temperature profile is calculated using solution (16).

6 Kinetic temperature and temperature matrix

Since initial conditions (5), (6) are random then particle velocities given by formula (16) are also random. Following [40,41,42] we consider an infinite number of realizations of initial conditions (5), (6). It allows to introduce statistical characteristics such as kinetic temperature.

In harmonic crystals, kinetic temperatures, corresponding to degrees of freedom of the unit cell, are generally different (see, e.g., Figs. 4, 5, 6). Therefore in order to characterize thermal state of the unit cell, ${\mathbf{x}}{}$, we use $N\times N$ matrix, $\varvec{{T}}{}({\mathbf{x}}{})$, further referred to as the temperature matrix [51]:

$$\begin{aligned} k_B\varvec{{T}}{}({\mathbf{x}}{}) = \varvec{{M}}{}{}^{\frac{1}{2}}\Bigl \langle {\varvec{{v}}{}({\mathbf{x}}{}) \varvec{{v}}{}({\mathbf{x}}{})^{\top }}\Bigr \rangle \varvec{{M}}{}{}^{\frac{1}{2}} \quad \Leftrightarrow \quad k_B T_{ij} = \sqrt{M_iM_j} \Bigl \langle {v_i v_j}\Bigr \rangle , \end{aligned}$$

(17)

where $M_i$ is i-th element of matrix $\varvec{{M}}{}{}$, equal to a mass corresponding to i-th degree of freedom of the unit cell; $k_B$ is the Boltzmann constant; brackets $\Bigl \langle {..}\Bigr \rangle$ stand for mathematical expectation. Diagonal element, $T_{ii}$, of the temperature matrix is referred to as kinetic temperature, corresponding to i-th degrees of freedom of the unit cell. Off-diagonal elements, $T_{ij}$, characterize correlation between components, i, j, of velocity column, $\varvec{{v}}{}({\mathbf{x}}{})$.

We also use conventional kinetic temperature, T, proportional to the total kinetic energy of the unit cell:

$$\begin{aligned} T({\mathbf{x}}{}) = \frac{1}{N}\,\mathrm{tr}\varvec{{T}}{}({\mathbf{x}}{}) = \frac{1}{N}\sum _{i=1}^N T_{ii}({\mathbf{x}}{}), \end{aligned}$$

(18)

where N is a number of degrees of freedom per unit cell, $\mathrm{tr}(..)$ stands for trace (sum of diagonal elements). If kinetic energy is uniformly distributed among degrees of freedom of the unit cell then kinetic temperatures, corresponding to all degrees of freedom of the unit cell, are equal to T.

7 Exact formula for the temperature matrix

7.1 The general case

In this section, we derive an exact expression for the temperature matrix using the solution (16) of lattice dynamics equation.

To calculate temperature matrix, we substitute solution (16) into definition (17):¹¹

$$\begin{aligned} k_B\varvec{{T}}{}({\mathbf{x}}{}) = \int _{{\mathbf{k}}{}_1}\int _{{\mathbf{k}}{}_2} \varvec{{P}}{}{}_1 \varvec{{D}}{}_1 \varvec{{P}}{}{}_1^{*{\top }} \varvec{{M}}{}{}^{\frac{1}{2}} \Bigl \langle {{\hat{\varvec{{v}}{}}}_0({\mathbf{k}}{}_1) {\hat{\varvec{{v}}{}}}_0({\mathbf{k}}{}_2)^{*{\top }}}\Bigr \rangle \varvec{{M}}{}{}^{\frac{1}{2}} \varvec{{P}}{}{}_2\varvec{{D}}{}_2\varvec{{P}}{}{}_2^{*\top } e^{\mathrm{i}\left( {\mathbf{k}}{}_1-{\mathbf{k}}{}_2\right) \cdot {\mathbf{x}}{}} \mathrm{d} {\mathbf{k}}{}_1\mathrm{d} {\mathbf{k}}{}_2. \end{aligned}$$

(19)

Here and below $\varvec{{P}}{}{}_j = \varvec{{P}}{}{}({\mathbf{k}}{}_j)$, $\varvec{{D}}{}_j = \varvec{{D}}{}({\mathbf{k}}{}_j)$, $j=1,2$.

Initial conditions (5), (6) are such that initial velocities of any pair of unit cells ${\mathbf{y}}{}_1, {\mathbf{y}}{}_2$ are uncorrelated. Therefore the following identity is satisfied 

$$\begin{aligned} \Bigl \langle {\varvec{{v}}{}_0({\mathbf{y}}{}_1) \varvec{{v}}{}_0({\mathbf{y}}{}_2)^{*{\top }}}\Bigr \rangle = \varvec{{M}}{}{}^{-\frac{1}{2}} k_B \varvec{{T}}{}_0({\mathbf{y}}{}_1) \delta _D({\mathbf{y}}{}_1-{\mathbf{y}}{}_2)\varvec{{M}}{}{}^{-\frac{1}{2}}. \end{aligned}$$

(20)

Here $\varvec{{T}}{}_0$ is the initial temperature matrix, which is calculated by substituting initial velocities, $\varvec{{v}}{}_0({\mathbf{x}}{})$, into formula (17); $\delta _D$ is defined after formula (6). Using formula (20), we make the following transformations:

$$\begin{aligned} \begin{array}{l} \displaystyle \Bigl \langle {{\hat{\varvec{{v}}{}}}_0({\mathbf{k}}{}_1) {\hat{\varvec{{v}}{}}}_0({\mathbf{k}}{}_2)^{*{\top }}}\Bigr \rangle = \sum _{{\mathbf{y}}{}_1, {\mathbf{y}}{}_2} \Bigl \langle {\varvec{{v}}{}_0({\mathbf{y}}{}_1) \varvec{{v}}{}_0({\mathbf{y}}{}_2)^{*{\top }}}\Bigr \rangle e^{-\mathrm{i}\left( {\mathbf{k}}{}_1\cdot {\mathbf{y}}{}_1 - {\mathbf{k}}{}_2\cdot {\mathbf{y}}{}_2\right) } \\ \qquad \displaystyle = k_B \sum _{{\mathbf{y}}{}} \varvec{{M}}{}{}^{-\frac{1}{2}} \varvec{{T}}{}_0({\mathbf{y}}{}) \varvec{{M}}{}{}^{-\frac{1}{2}} e^{-\mathrm{i}\left( {\mathbf{k}}{}_1-{\mathbf{k}}{}_2\right) \cdot {\mathbf{y}}{}}. \end{array} \end{aligned}$$

(21)

Then substitution of formula (21) into (19), yields

$$\begin{aligned} \varvec{{T}}{}({\mathbf{x}}{}, t) = \int _{{\mathbf{k}}{}_1}\int _{{\mathbf{k}}{}_2}\sum _{{\mathbf{y}}{}} \varvec{{P}}{}{}_1 \varvec{{D}}{}_1 \varvec{{P}}{}{}_1^{*{\top }} \varvec{{T}}{}_0({\mathbf{y}}{}) \varvec{{P}}{}{}_2\varvec{{D}}{}_2\varvec{{P}}{}{}_2^{*\top } e^{\mathrm{i}\left( {\mathbf{k}}{}_1-{\mathbf{k}}{}_2\right) \cdot ({\mathbf{x}}{}-{\mathbf{y}}{})} \mathrm{d} {\mathbf{k}}{}_1\mathrm{d} {\mathbf{k}}{}_2. \end{aligned}$$

(22)

Formula (22) is an exact expression for the temperature matrix.

Remark 3

Formula (22) for the temperature matrix is symmetric with respect to time, i.e. invariant with respect to substitution t by $-t$. This fact follows from the same property of equations of motion (4).

The temperature matrix can be exactly represented as a sum of “fast” and “slow” terms:

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}= \varvec{{T}}{}_\mathrm {F} + \varvec{{T}}{}_\mathrm {S}, \qquad \varvec{{T}}{}_\mathrm {F}({\mathbf {x}}{}) = \int _{{\mathbf {k}}{}_1}\int _{{\mathbf {k}}{}_2}\sum _{{\mathbf {y}}{}} \varvec{{P}}{}{}_1 \varvec{{T}}{}'_\mathrm {F}\varvec{{P}}{}{}_2^{*\top } e^{\mathrm {i}\left( {\mathbf {k}}{}_1-{\mathbf {k}}{}_2\right) \cdot ({\mathbf {x}}{}-{\mathbf {y}}{})} \mathrm {d} {\mathbf {k}}{}_1\mathrm {d} {\mathbf {k}}{}_2,\\ \displaystyle \varvec{{T}}{}_\mathrm {S}({\mathbf {x}}{}) = \int _{{\mathbf {k}}{}_1}\int _{{\mathbf {k}}{}_2}\sum _{{\mathbf {y}}{}} \varvec{{P}}{}{}_1 \varvec{{T}}{}'_\mathrm {S}\varvec{{P}}{}{}_2^{*\top } e^{\mathrm {i}\left( {\mathbf {k}}{}_1-{\mathbf {k}}{}_2\right) \cdot ({\mathbf {x}}{}-{\mathbf {y}}{})} \mathrm {d} {\mathbf {k}}{}_1\mathrm {d} {\mathbf {k}}{}_2,\\ \displaystyle \{\varvec{{T}}{}'_\mathrm {F}\}_{ij} = \frac{1}{2}\{\varvec{{P}}{}{}_1^{*\top } \varvec{{T}}{}_0({\mathbf {y}}{}) \varvec{{P}}{}{}_2\}_{ij} \left[ \cos \bigl ((\omega _i({\mathbf {k}}{}_1) + \omega _j({\mathbf {k}}{}_2))t\bigr ) + (1-\delta _{ij})\cos \bigl ((\omega _i({\mathbf {k}}{}_1) - \omega _j({\mathbf {k}}{}_2))t\bigr )\right] ,\\ \displaystyle \{\varvec{{T}}{}'_\mathrm {S}\}_{ij} = \frac{1}{2}\{\varvec{{P}}{}{}_1^{*\top } \varvec{{T}}{}_0({\mathbf {y}}{}) \varvec{{P}}{}{}_2\}_{ij} \delta _{ij}\cos \bigl ( (\omega _j({\mathbf {k}}{}_1) - \omega _j({\mathbf {k}}{}_2))t\bigr ). \end{array} \end{aligned}$$

(23)

Here $\{...\}_{ij}$ is element i, j of the matrix. The representation (23) is based on the observation that $\varvec{{T}}{}_\mathrm{F}$ and $\varvec{{T}}{}_\mathrm{S}$ have different characteristic time scales. The difference of time scales is most clearly demonstrated by example, considered in Sect. 9.5. Physical meaning of $\varvec{{T}}{}_\mathrm{F}$ and $\varvec{{T}}{}_\mathrm{S}$ is discussed in Sect. 8.

Exact formulas (22), (23) for the temperature matrix require intensive calculations (double integration with respect to wave vectors ${\mathbf{k}}{}_1, {\mathbf{k}}{}_2$ and summation with respect to all unit cells). Therefore in Sect. 8 we present a simple approximate formula for the temperature matrix.

7.2 Example: monoatomic one-dimensional chain

For illustration, consider a simple particular case, namely a one-dimensional chain consisting of identical particles. Then unit cell of the lattice contains one particle with one degree of freedom ($N=1$). In this case, temperature matrix has only one element, equal to conventional kinetic temperature, T(x, t). Exact formula (22) for the temperature takes form:

$$\begin{aligned} T(x, t) = \sum _{y}T_0(y)\int _{k_1}\int _{k_2}\cos \bigl ( \omega (k_1)t\bigr ) \cos \bigl ( \omega (k_2)t\bigr ) \cos \bigl ( \left( k_1- k_2\right) (x-y)\bigr ) \mathrm {d} k_1\mathrm {d} k_2. \end{aligned}$$

(24)

According to formula (23), “fast” and “slow” parts of the temperature are defined as

$$\begin{aligned} \begin{array}{l} \displaystyle T_\mathrm{F}(x, t) = \sum _{y}\frac{T_0(y)}{2}\int _{k_1}\int _{k_2}\cos \left( \left( \omega (k_1) +\omega (k_2)\right) t\right) \cos \left( \left( k_1- k_2\right) (x-y)\right) \mathrm{d} k_1\mathrm{d} k_2, \\ \displaystyle T_\mathrm{S}(x, t) = \sum _{y}\frac{T_0(y)}{2}\int _{k_1}\int _{k_2}\cos \left( \left( \omega (k_1) -\omega (k_2)\right) t\right) \cos \left( \left( k_1- k_2\right) (x-y)\right) \mathrm{d} k_1\mathrm{d} k_2. \end{array} \end{aligned}$$

(25)

Double integral in the right side is a contribution of particle y to temperature of particle x. It is represented as a superposition of harmonic waves with wave vectors $k_1-k_2$ and frequencies $\omega (k_1) + \omega (k_2)$ (in the fast term), $\omega (k_1) - \omega (k_2)$ (in the slow term).

8 Approximate formula for the temperature matrix: fast and slow thermal processes

The main result of the present paper is the following approximate formula for the temperature matrix (derivation is presented in “Appendix”):

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}= \varvec{{T}}{}_\mathrm {F} + \varvec{{T}}{}_\mathrm {S}, \qquad \varvec{{T}}{}_\mathrm {F} \approx \int _{{\mathbf {k}}{}}\varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm {F}\varvec{{P}}{}{}^{*\top } \mathrm {d} {\mathbf {k}}{}, \qquad \displaystyle \varvec{{T}}{}_\mathrm {S} \approx \int _{{\mathbf {k}}{}} \varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm {S} \varvec{{P}}{}{}^{*\top } \mathrm {d} {\mathbf {k}}{}, \\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {F}\}_{ij} = \frac{1}{2}\{\varvec{{P}}{}{}^{*\top } \varvec{{T}}{}_0({\mathbf {x}}{}) \varvec{{P}}{}{}\}_{ij} \Bigl [ \cos \bigl ((\omega _i + \omega _j)t\bigr ) + (1-\delta _{ij})\cos \bigl ((\omega _i - \omega _j)t\bigr )\Bigr ] , \\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {S}\}_{ij} = \frac{1}{4}\Bigl \{\varvec{{P}}{}{}^{*\top } \left( \varvec{{T}}{}_0({\mathbf {x}}{}+ {\mathbf {v}}{}_g^j t) + \varvec{{T}}{}_0({\mathbf {x}}{}- {\mathbf {v}}{}_g^j t)\right) \varvec{{P}}{}{}\Bigr \}_{jj}\delta _{ij}. \end{array} \end{aligned}$$

(26)

Here $\varvec{{P}}{}{}=\varvec{{P}}{}{}({\mathbf{k}}{})$; ${\mathbf{v}}{}_g^j$ is the group velocity corresponding to j-th branch of dispersion relation, $\omega _j$:¹²

$$\begin{aligned} {\mathbf{v}}{}_{g}^{j} = \frac{\mathrm{d} \omega _{j}}{\mathrm{d} {\mathbf{k}}{}} = \sum _{i=1}^d \frac{\partial \omega _{j}}{\partial p_i} {\mathbf{b}}{}_i, \qquad {\mathbf{k}}{}= \sum _{i=1}^d p_i \tilde{{\mathbf{b}}{}}_i. \end{aligned}$$

(27)

Since formula (26) contains only a single integral with respect to ${\mathbf{k}}{}$, it is significantly more convenient for analysis and calculations than exact expression (23).

Remark 4

Function $\varvec{{T}}{}_0$ is originally defined on a discrete set of position vectors, ${\mathbf{x}}{}$, of unit cells [see formula (17)], while argument of this function ${\mathbf{x}}{}\pm {\mathbf{v}}{}_g^j t$ in formula (26) changes in space continuously. Therefore further we assume that $\varvec{{T}}{}_0$ can be defined for the whole space in such a way that at points ${\mathbf{x}}{}$ it coincides with values given by formula (17) and slowly changes at distances of order of lattice constant.

The first term, $\varvec{{T}}{}_\mathrm{F}$, in formula (26) describes short time behavior of the temperature matrix (fast process [40, 50, 51]). At short times, the temperature matrix oscillates. The oscillations are caused by redistribution of energy among kinetic and potential forms and redistribution of energy among degrees of freedom of the unit cell. These oscillations at different spatial points are independent. At large time scale $\varvec{{T}}{}_\mathrm{F}$ tends to zero.

The second term, $\varvec{{T}}{}_\mathrm{S}$, in formula (26) describes large time behavior of the temperature matrix (slow process [41, 42, 50]). At large time scale, changes in the temperature profile are caused by ballistic heat transport. The temperature matrix is represented as a superposition of waves traveling with group velocities ${\mathbf{v}}{}_g^j({\mathbf{k}}{})$. Shapes of the waves are determined by initial temperature profile $\varvec{{T}}{}_0$. Note that according to formula (26), accurate description of ballistic heat transport requires knowledge of the dispersion relation and corresponding group velocities.

Remark 5

Approximate formula (26) for the temperature matrix have the same property as the exact formula (22). It is symmetric with respect to time, i.e. substitution t by $-t$. At the same time, analysis of formula (26) and results of numerical simulations suggest that thermal processes in infinite harmonic crystals are irreversible.

Remark 6

According to formula (23), the temperature matrix of the unit cell ${\mathbf{x}}{}$ at any moment in time depends on initial temperatures of all other unit cells. This fact is a consequence of infinite propagation speed of disturbances in discrete systems described by equations of motion (4). In contrast, approximate formula (26) does not contain this artifact. According to formula (26), temperature matrix of the unit cell ${\mathbf{x}}{}$ at time t depends on initial temperature matrices of unit cells which are not farther from cell ${\mathbf{x}}{}$ than ${\max \nolimits _{{\mathbf{k}}{}, j}}\left( |{\mathbf{v}}{}_g^j|\right) t$.

Remark 7

Comparison of formula (26) with results of paper [51] shows that $\varvec{{T}}{}_\mathrm{S}({\mathbf{x}}{})$ at $t=0$ is equal to the equilibrium value of the temperature matrix in the uniformly heated crystal with initial temperature matrix $\varvec{{T}}{}_0({\mathbf{x}}{})$. Therefore, at short times, each point of a crystal tends to local thermal equilibrium. However, at large times, ballistic heat transport leads to substantial deviation from thermal equilibrium (see examples in Sects. 10.3, 10.4).

The majority of further results follows from the general formula (26).

9 Specific profiles of initial temperature

In this section, we apply general solution (26) to several particular initial temperature profiles. The results are valid for a wide class of one-, two-, and three-dimensional crystals described by equations of motion (4).

9.1 Uniform initial temperature profile

In this subsection, we consider spatially uniform distribution of initial temperature ($\varvec{{T}}{}_0$ is independent of ${\mathbf{x}}{}$). In this case changes in the temperature matrix are caused by two physical processes accompanying transition of the system to thermal equilibrium: redistribution of energy between kinetic and potential forms and redistribution of energy between degrees of freedom. These processes are usually observed in the beginning of molecular dynamics simulations [2]. Analytical description of these processes for several specific one- and two-dimensional monoatomic lattices is presented in papers [4, 40, 48,49,50]. Generalization for the case of polyatomic crystals is carried out in paper [51]. In these works, the approach, originally proposed in paper [40] and based on analysis of velocity covariances, is used. Here we show that identical results follow from formula (26) derived from solution of lattice dynamics equations.

In the case of spatially uniform distribution of temperature matrix ($\varvec{{T}}{}_0 = \mathrm{const}$), formula (26) reads

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}_\mathrm {F} = \int _{{\mathbf {k}}{}}\varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm {F}\varvec{{P}}{}{}^{*\top } \mathrm {d} {\mathbf {k}}{}, \qquad \varvec{{T}}{}_\mathrm {S} = \int _{{\mathbf {k}}{}}\varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm {S} \varvec{{P}}{}{}^{*\top } \mathrm {d} {\mathbf {k}}{},\\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {F}\}_{ij} = \frac{1}{2}\{\varvec{{P}}{}{}^{*\top } \varvec{{T}}{}_0 \varvec{{P}}{}{}\}_{ij} \Bigl [ \cos \bigl ((\omega _i + \omega _j)t\bigr ) + (1-\delta _{ij})\cos \bigl ((\omega _i - \omega _j\bigr )t)\Bigr ] .\\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {S}\}_{ij} = \frac{1}{2}\{\varvec{{P}}{}{}^{*\top }\varvec{{T}}{}_0\varvec{{P}}{}{}\}_{jj}\delta _{ij}. \end{array} \end{aligned}$$

(28)

Expressions (28) coincide with exact formulas for the temperature matrix, obtained in paper [51] by entirely different means. In particular, the expression for $\varvec{{T}}{}_\mathrm{S}$ coincides with equilibrium value of the temperature matrix [51].

Therefore in the case of spatially uniform distribution of temperature, formula (26) is exact.

9.2 Initial equipartition

In this section, we consider the case, when initial kinetic temperatures, corresponding to all degrees of freedom of the unit cell, are equal. Then initial temperature matrix is isotropic,¹³ i.e. $\varvec{{T}}{}_0 = T_0({\mathbf{x}}{}) \varvec{{E}}{}$, where $\varvec{{E}}{}$ is the identity matrix. Substitution of this expression into formula (26) yields:

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}_\mathrm{F} = \int _{{\mathbf{k}}{}} \varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm{F} \varvec{{P}}{}{}^{*\top } \mathrm{d} {\mathbf{k}}{}, \qquad \varvec{{T}}{}_\mathrm{S} = \int _{{\mathbf{k}}{}} \varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm{S} \varvec{{P}}{}{}^{*\top } \mathrm{d} {\mathbf{k}}{}, \\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm{F}\}_{ij} = \frac{1}{2}T_0({\mathbf{x}}{})\delta _{ij} \cos (2\omega _j t), \qquad \{{\tilde{\varvec{{T}}{}}}_\mathrm{S}\}_{ij} = \frac{1}{4}\left( T_0({\mathbf{x}}{}+ {\mathbf{v}}{}_g^j t) + T_0({\mathbf{x}}{}- {\mathbf{v}}{}_g^j t)\right) \delta _{ij}. \end{array} \end{aligned}$$

(29)

The kinetic temperature, proportional to trace of the temperature matrix (29), has form

$$\begin{aligned} \begin{array}{l} \displaystyle T = T_\mathrm {F} + T_\mathrm {S}, \qquad T_\mathrm {F} = \frac{T_0({\mathbf {x}}{})}{2N} \sum _{j=1}^N\int _{{\mathbf {k}}{}} \cos (2\omega _j t) \mathrm {d}{\mathbf {k}}{}, \\ \displaystyle T_\mathrm {S} = \frac{1}{4N}\sum _{j=1}^N\int _{{\mathbf {k}}{}}\left( T_0\bigl ({\mathbf {x}}{}+ {\mathbf {v}}{}_g^j t\bigr ) + T_0\bigl ({\mathbf {x}}{}- {\mathbf {v}}{}_g^j t\bigr )\right) \mathrm {d} {\mathbf {k}}{}. \end{array} \end{aligned}$$

(30)

Remark 8

For scalar lattices ($N=1$), formula (30) coincides with the result obtained in paper [50]. In paper [50] the expression for temperature is derived by approximate solution of equation for covariances of velocities, while in the present paper it is derived from solution of lattice dynamics equations.

Remark 9

Expression for $T_\mathrm{S}$ in formula (30) is also consistent with results obtained in paper [55] by entirely different means. In paper [55], the expression for the total energy of the unit cell at large times is derived. At large times, kinetic and potential energies equilibrate [40, 51] and therefore behavior of the total energy and kinetic temperature are similar.

Formula (29) shows that the temperature matrix for $t>0$ is generally not isotropic, i.e. local values of temperatures, corresponding to degrees of freedom of the unit cell, are different even though initially they are equal. Further, this important fact is illustrated by Figs. 4, 5, 6.

9.3 Fundamental solution, heat front, and the Huygens principle

In this subsection, we derive fundamental solution of ballistic heat transport problem and show how it can be used for reconstruction of the heat front in the case of an arbitrary initial temperature profile.

The following spatial distribution of initial temperature matrix is considered

$$\begin{aligned} \varvec{{T}}{}_0({\mathbf{x}}{}) = A\delta ({\mathbf{x}}{})\varvec{{E}}{}, \end{aligned}$$

(31)

where $\delta ({\mathbf{x}}{})$ is Dirac delta function; A is a constant. Distribution of kinetic temperature at large times is given by formula (30):

$$\begin{aligned} T \approx T_\mathrm{S} = \frac{A}{4N}\sum _{i=1}^N\int _{{\mathbf{k}}{}}\left( \delta ({\mathbf{x}}{}+ {\mathbf{v}}{}_g^i t) + \delta ({\mathbf{x}}{}- {\mathbf{v}}{}_g^i t)\right) \mathrm{d} {\mathbf{k}}{}. \end{aligned}$$

(32)

Nonzero contribution to integral (32) comes from values, ${\mathbf{k}}{}_{ij}^*$, of wave vector such that argument of the delta function vanishes:

$$\begin{aligned} {\mathbf{v}}{}_g^i({\mathbf{k}}{}_{ij}^*) = \frac{{\mathbf{x}}{}}{t} \qquad \mathrm {or} \qquad {\mathbf{v}}{}_g^i({\mathbf{k}}{}_{ij}^*) = -\frac{{\mathbf{x}}{}}{t}. \end{aligned}$$

(33)

Here $j=1,\ldots ,n_i$, where $n_i$ is the number of real roots of Eq. (33) for ith branch of dispersion relation. Then calculation of integrals in formula (32) yields

$$\begin{aligned} \begin{array}{l} \displaystyle T = \frac{A}{4N(2\pi )^d t^d}\sum _{i=1}^N \sum _{j=1}^{n_i}\frac{1}{|\det \varvec{{G}}{}_i^d({\mathbf{k}}{}_{ij}^*)|}, \end{array} \end{aligned}$$

(34)

where summation is carried out with respect to all real roots ${\mathbf{k}}{}_{ij}^*, i=1,\ldots ,N, j=1,\ldots ,n_i$ of Eq. (33);¹⁴$\det (...)$ stands for determinant of a matrix; $\varvec{{G}}{}_i^d$ is the Jacobian matrix in d-dimensional case:

$$\begin{aligned} \varvec{{G}}{}_i^{1} = \frac{\partial v_{g}^i}{\partial p}, \qquad \varvec{{G}}{}_i^{2} = \begin{bmatrix} \frac{\partial v_{gx}^i}{\partial p_1}&\frac{\partial v_{gx}^i}{\partial p_2} \\ \frac{\partial v_{gy}^i}{\partial p_1}&\frac{\partial v_{gy}^i}{\partial p_2} \end{bmatrix}, \qquad \varvec{{G}}{}_i^{3} = \begin{bmatrix} \frac{\partial v_{gx}^i}{\partial p_1}&\frac{\partial v_{gx}^i}{\partial p_2}&\frac{\partial v_{gx}^i}{\partial p_3}\\ \frac{\partial v_{gy}^i}{\partial p_1}&\frac{\partial v_{gy}^i}{\partial p_2}&\frac{\partial v_{gy}^i}{\partial p_3}\\ \frac{\partial v_{gz}^i}{\partial p_1}&\frac{\partial v_{gz}^i}{\partial p_2}&\frac{\partial v_{gz}^i}{\partial p_3} \end{bmatrix}, \end{aligned}$$

(35)

where $v_{gx}^i, v_{gy}^i, v_{gz}^i$ are components of vector of group velocity ${\mathbf{v}}{}_g^i({\mathbf{k}}{})$.

Note that ${\mathbf{k}}{}_{ij}^*$ in formula (34) is a function of ${\mathbf{x}}{}/t$, implicitly given by Eq. (33). Therefore the fundamental solution multiplied by $t^d$ is a self-similar function of ${\mathbf{x}}{}/t$. This fact clearly shows the difference between ballistic and diffusive heat transport regimes. In the latter case, fundamental solution depends on ${\mathbf{x}}{}/\sqrt{t}$.

Remark 10

For one-dimensional and two-dimensional scalar lattices ($N=1$) fundamental solutions are obtained in papers [41, 50]. These solutions coincide with particular cases of formula (34).

Remark 11

Fundamental solution (34) can be used for calculation of temperature field in a crystal subjected to point heat supply of constant intensity. In papers [21, 22] it is demonstrated that the temperature field is equal to integral of the fundamental solution with respect to time.

Consider motion of the heat front, corresponding to the fundamental solution, i.e. a boundary of a region with nonzero temperature. Since the group velocity is usually bounded then from formulas (33), (34), it follows that the heat front, corresponding to fundamental solution, is a d-dimensional sphere given by

$$\begin{aligned} \begin{array}{l} |{\mathbf{x}}{}| = t\,\underset{{\mathbf{k}}{}, j}{\max }|{\mathbf{v}}{}_{g}^j({\mathbf{k}}{})|. \end{array} \end{aligned}$$

(36)

In other words, in all lattices the heat front, corresponding to fundamental solution, propagates equally in all directions with finite speed equal to the maximum group velocity (see, e.g., Fig. 9).

Formula (36) allows to use the Huygens principle for reconstruction of the heat front in the case of an arbitrary initial temperature profile. Heat front at time t is a surface tangent to set of spheres with centers at all points of initial front and radii being equal to $t\,{\max \nolimits _{{\mathbf{k}}{}, j}}|{\mathbf{v}}{}_{g}^j({\mathbf{k}}{})|$.

9.4 Thermal contact of cold and hot half-spaces

Consider thermal contact of two half-spaces with initial temperatures $T_b$ and $T_b + \Delta T$. This problem is important, because it is closely related to classical definition of temperature [30]. By the definition, temperatures of two bodies in thermodynamic equilibrium are equal. The problem considered below demonstrates the transition to thermodynamic equilibrium.

The initial temperature distribution in direction, given by unit vector ${\mathbf{e}}{}$, has form:

$$\begin{aligned} \varvec{{T}}{}_0 = \bigl (T_b + \Delta T H(x)\bigr )\varvec{{E}}{}, \qquad x = {\mathbf{{\mathbf{x}}{}}}{} \cdot {\mathbf{e}}{}, \end{aligned}$$

(37)

where H is the Heaviside function. Substituting formula (37) into (29), yields

$$\begin{aligned} \begin{array}{l} \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {F}\}_{ij} = \frac{1}{2}\Bigl (T_b + \Delta T H(x)\Bigr )\delta _{ij} \cos (2\omega _j t),\\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {S}\}_{ij} = \frac{T_b}{2}\delta _{ij} + \frac{\Delta T}{4}\Bigl (H\left( x + {\mathbf {v}}{}_g^j \cdot {\mathbf {e}}{} t\right) + H\left( x - {\mathbf {v}}{}_g^j \cdot {\mathbf {e}}{} t\right) \Bigr )\delta _{ij}. \end{array} \end{aligned}$$

(38)

Computing kinetic temperature by formulas (29), (38) and using the property of Heaviside function $H(ax)=H(x), a>0$, yields

$$\begin{aligned} \begin{array}{l} \displaystyle T = T_\mathrm{F} + T_\mathrm{S}, \qquad T_\mathrm{F} = \frac{1}{2N}\Bigl (T_b + \Delta T H(x)\Bigr )\sum _{j=1}^N\int _{{\mathbf{k}}{}} \cos (2\omega _j t)\mathrm{d}{\mathbf{k}}{},\\ \displaystyle T_\mathrm{S}\left( \frac{x}{t}\right) = \frac{T_b}{2} + \frac{\Delta T}{4N}\sum _{j=1}^N\int _{{\mathbf{k}}{}}\Bigl (H\left( \frac{x}{t} + {\mathbf{v}}{}_g^j \cdot {\mathbf{e}}{}\right) + H\left( \frac{x}{t} - {\mathbf{v}}{}_g^j \cdot {\mathbf{e}}{}\right) \Bigr )\mathrm{d}{\mathbf{k}}{}. \end{array} \end{aligned}$$

(39)

Formula (39) shows that slow part of the temperature matrix, $T_\mathrm{S}$, is a self-similar function of x / t. This fact is used for comparison with results of numerical solution of equations of motion in Sects. 10.3, 11.4.

9.5 Sinusoidal initial temperature profile: application to the transient thermal grating

In this subsection, we consider spatially sinusoidal profile of initial temperature. This problem is closely related to transient thermal grating technique [36, 67]. In the framework of this experimental technique, the sinusoidal profile is generated in a thin film or on a surface of a bulk material using the interference of two laser pulses. Amplitude of the temperature profile decays in time due to heat transport. Measurement of the amplitude yields information on thermal properties of a material. Here, we present an analytical solution of this problem, corresponding to purely ballistic regime of heat transport.

The initial temperature profile in direction given by unit vector ${\mathbf{e}}{}$ has form:

$$\begin{aligned} \varvec{{T}}{}_0({\mathbf{x}}{}) = \left( T_b + \Delta T \sin \frac{2\pi x}{L}\right) \varvec{{E}}{}, \qquad x = {\mathbf{x}}{}\cdot {\mathbf{e}}{}, \end{aligned}$$

(40)

where $T_b$, $\Delta T$ are constants; $\Delta T < T_b$; L is length of the periodic cell. Note that initial temperatures, corresponding to all degrees of freedom of the unit cell, are equal.

Remark 12

Heat transport in several scalar lattices with initial temperature distribution (40) is considered in papers [41, 42, 50]. In the present paper, we derive a general solution valid for any lattice described by equations of motion (4).

The temperature matrix at time t is calculated by formula (29). Substitution of initial temperature profile (40) into (29) after some transformations yields

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}_\mathrm{F} = \frac{1}{2}\left( T_b + \Delta T\sin \frac{2\pi x}{L}\right) \varvec{{F}}{}(t), \qquad \varvec{{T}}{}_\mathrm{S} = \frac{T_b}{2} \varvec{{E}}{}+ \frac{\Delta T}{2}\varvec{{S}}{}(t) \sin \frac{2\pi x}{L},\\ \displaystyle \varvec{{F}}{} = \int _{{\mathbf{k}}{}} \varvec{{P}}{}{}\tilde{\varvec{{F}}{}} \varvec{{P}}{}{}^{*\top } \mathrm{d} {\mathbf{k}}{}, \quad \varvec{{S}}{} = \int _{{\mathbf{k}}{}} \varvec{{P}}{}{}\tilde{\varvec{{S}}{}} \varvec{{P}}{}{}^{*\top } \mathrm{d} {\mathbf{k}}{}, \qquad \displaystyle {\tilde{F}}_{ij} = \cos (2\omega _j t) \delta _{ij} , \quad {\tilde{S}}_{ij} = \cos \frac{2\pi {v}_g^j t}{L} \delta _{ij}. \end{array} \end{aligned}$$

(41)

Here $v_g^j = {\mathbf{v}}{}_g^j \cdot {\mathbf{e}}{}$. Calculating trace in formula (41) we obtain simple expression for kinetic temperature:

$$\begin{aligned} \begin{array}{l} \displaystyle T = T_\mathrm{F} + T_\mathrm{S}, \qquad \displaystyle T_\mathrm{F} = \frac{1}{2N}\left( T_b+ \Delta T\sin \frac{2\pi x}{L}\right) \sum _{j=1}^N \int _{{\mathbf{k}}{}} \cos (2\omega _j t) \mathrm{d} {\mathbf{k}}{},\\ \displaystyle T_\mathrm{S} = \frac{T_b}{N} + \frac{\Delta T}{2N} \sin \left( \frac{2\pi x}{L}\right) \sum _{j=1}^N\int _{{\mathbf{k}}{}} \cos \frac{2\pi {v}_g^j t}{L} \mathrm{d} {\mathbf{k}}{}. \end{array} \end{aligned}$$

(42)

Formula (42) shows that temperature profile remains sinusoidal at any moment in time. Therefore we compute amplitude of a sin as a function of time. In real experiment, the amplitude can be measured using the transient thermal grating technique [36, 67]. In one-dimensional case the amplitude is calculated as

$$\begin{aligned} \varvec{{A}}{} = \frac{2}{L} \int _{0}^{L} \varvec{{T}}{}(x,t) \sin \frac{2\pi x}{L} \mathrm{d}x, \qquad A = \frac{1}{N} \mathrm{tr}\varvec{{A}}{} =\frac{2}{L} \int _{0}^{L} T(x,t) \sin \frac{2\pi x}{L} \mathrm{d}x, \end{aligned}$$

(43)

To increase the accuracy, in two-, and three-dimensional cases, results are additionally integrated in directions, orthogonal to ${\mathbf{e}}{}$. Substituting expression for temperature (41) into formula (43), yields

$$\begin{aligned} \varvec{{A}}{} = \Delta T \bigl (\varvec{{F}}{}(t) + \varvec{{S}}{}(t) \bigr ), \qquad A = \frac{\Delta T}{2N} \sum _{j=1}^N \int _{{\mathbf{k}}{}} \left( \cos (2\omega _j t) + \cos \frac{2\pi {v}_g^j t}{L}\right) \mathrm{d} {\mathbf{k}}{}. \end{aligned}$$

(44)

Formula (44) shows that time evolution of amplitude A depends on direction, ${\mathbf{e}}{}$, of initial thermal perturbation. Therefore heat transport in two- and three-dimensional lattices is generally anisotropic (see, for example, Fig. 12).

According to formula (41), $\varvec{{T}}{}_\mathrm{F}$ and $\varvec{{T}}{}_\mathrm{S}$ have different time scales, proportional to $1/\omega _j$ and $L/v_g^j$, respectively. The first time scale is determined by frequencies of vibrations of individual atoms. The second time scale is determined by a time required for a wave, traveling with group velocity, to pass distance L. The ratio of these time scales is a large parameter. Therefore time scales of fast and slow thermal processes are well separated.

From formula (44) and the stationary phase method [20] it follows that amplitude, A, of temperature profile in ballistic regime decays according to power law $1/t^\frac{d}{2}$. Note that solution of analogous problem using Fourier and hyperbolic (Maxwell–Cattaneo–Vernotte [16, 73]) heat transfer equations yields exponential decay of the amplitude.

Thus decay of amplitude of sinusoidal temperature profile in a purely ballistic regime is described by formulas (44). Presented results may serve for interpretation of experimental data obtained by transient thermal grating technique [36, 67]. In particular, in a recent paper [33] it is shown experimentally that decay of a sinusoidal profile in polycrystalline graphite at temperatures about 100K is nonmonotonic. Similar effect is predicted by our formula (44) (see, e.g., Fig. 12). Formula (44) also shows that at time scale of real experiment, amplitude, A, depends on time, t, and grating period, L, as $A(t,L) = f(t/L)$. Therefore results for different grating periods, $L_1$, $L_2$, at large times are related as $A(t, L_1) = A({\tilde{t}}, L_2),~~{\tilde{t}} =t L_2/L_1$. In particular, characteristic frequency of temperature oscillations is inversely proportional to grating period L. This fact is consistent with experimental observations [33].

10 Example: diatomic chain

In this section, ballistic heat transport in the simplest one-dimensional polyatomic lattice is analyzed. We demonstrate that formulas (26) describe time evolution of a temperature profile with high accuracy. Also, we show that during heat transport local values of temperatures, corresponding to two degrees of freedom of the unit cell, are generally different even if their initial values are equal.¹⁵

10.1 Equations of motion and initial conditions

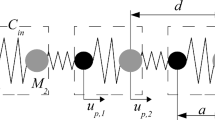
We consider a diatomic chain with alternating masses $m_1$, $m_2$ and stiffnesses $c_1$, $c_2$ (see Fig. 2). The chain consists of two sublattices, one formed by particles with mass $m_1$ and another formed by particles with mass $m_2$.

Fig. 2

Two unit cells of a diatomic chain with alternating masses and stiffnesses. Particles of different size and color form two sublattices (color figure online)

We write equations of motion of the chain in matrix form (4). Unit cells, containing two particles each, are numbered by index j. Position vector of the unit cell j has form

$$\begin{aligned} {\mathbf{x}}{}_j= x_j{\mathbf{e}}{}, \qquad x_j= a \left( j- \frac{n_\mathrm{c}}{2}\right) , \end{aligned}$$

(45)

where a is a distance between unit cells; ${\mathbf{e}}{}$ is a unit vector directed along the chain; $n_\mathrm{c}$ is the total number of unit cells in the periodic cell. Each particle has one degree of freedom. Displacements of particles, belonging to the unit cell j, form a column

$$\begin{aligned} \varvec{{u}}{}_j = \varvec{{u}}{}({\mathbf{x}}{}_j) = \begin{bmatrix} u_{1j}&u_{2j}\end{bmatrix}^{\top }, \end{aligned}$$

(46)

where $u_{1j}, u_{2j}$ are displacements of particles with masses $m_1$ and $m_2$, respectively. Then equations of motion have form

$$\begin{aligned} \begin{array}{l} \varvec{{M}}{}{}\ddot{\varvec{{u}}{}}_j = \varvec{{C}}{}_1 \varvec{{u}}{}_{j+1} + \varvec{{C}}{}_0 \varvec{{u}}{}_{j} + \varvec{{C}}{}_{-1} \varvec{{u}}{}_{j-1}, \\ \displaystyle \varvec{{M}}{}{}= \begin{bmatrix} m_{1} &{} 0 \\ 0 &{} m_{2} \end{bmatrix}, \quad \varvec{{C}}{}_0 = \begin{bmatrix} -c_1-c_2 &{} c_1 \\ c_1 &{} -c_1-c_2 \end{bmatrix}, \quad \varvec{{C}}{}_1 = \varvec{{C}}{}_{-1}^{\top }= \begin{bmatrix} 0 &{} 0 \\ c_2 &{} 0 \end{bmatrix}. \end{array} \end{aligned}$$

(47)

Initially, particles have random velocities and zero displacements. In this section we consider isotropic initial temperature matrices, i.e. $\varvec{{T}}{}_0(x_j)=T_0(x_j)\varvec{{E}}{}$. Then initial temperatures of the sublattices are equal ($T_{11}^0 = T_{22}^0 = T_0$). Corresponding initial conditions for the particles have form:

$$\begin{aligned} u_{1j} = u_{2j} = 0, \quad {\dot{u}}_{1j} = \beta _{j}\sqrt{\frac{k_B}{m_1} T_0(x_j)}, \quad {\dot{u}}_{2j} = \gamma _{j}\sqrt{\frac{k_B}{m_2} T_0(x_j)}, \end{aligned}$$

(48)

where $\beta _{j}$, $\gamma _{j}$ are uncorrelated random values with zero mean and unit variance, i.e. $\Bigl \langle {\beta _j}\Bigr \rangle =\Bigl \langle {\gamma _j}\Bigr \rangle = 0$, $\Bigl \langle {\beta _j^2}\Bigr \rangle =\Bigl \langle {\gamma _j^2}\Bigr \rangle = 1$, $\Bigl \langle {\beta _i\gamma _j}\Bigr \rangle =0$ for all i, j.

10.2 Dispersion relation and group velocities

In this subsection, we calculate the dispersion relation, polarization matrix $\varvec{{P}}{}{}$, and group velocities. These values are included in formulas (26) for the temperature matrix.

We calculate dynamical matrix, $\varvec{\varOmega }$, by formula (10). Substituting expressions (47) for matrixes $\varvec{{M}}{}{}, \varvec{{C}}{}_{\alpha }$, $\alpha =0, \pm 1$ into formula (10), we obtain:

$$\begin{aligned} \varvec{\varOmega }= \begin{bmatrix} \frac{c_1+c_2}{m_1}&-\frac{c_1 +c_2 e^{-\mathrm{i}p}}{\sqrt{m_1m_2}} \\ -\frac{c_1 +c_2 e^{\mathrm{i}p}}{\sqrt{m_1m_2}}&\frac{c_1+c_2}{m_2} \end{bmatrix}, \qquad {\mathbf{k}}{}= p \tilde{{\mathbf{b}}{}}, \qquad \tilde{{\mathbf{b}}{}} = \frac{{\mathbf{e}}{}}{a}, \end{aligned}$$

(49)

where ${\mathbf{k}}{}$ is the wave vector; $p \in [0; 2\pi ]$. Calculation of eigenvalues of matrix $\varvec{\varOmega }$, yields the dispersion relation:

$$\begin{aligned} \begin{array}{l} \displaystyle \omega ^2_{1,2}(p) = \frac{\omega _\mathrm{max}^2}{2} \left( 1 \pm \sqrt{1 - \frac{16 c_1c_2 \sin ^2\frac{p}{2}}{ m_1m_2\omega _\mathrm{max}^4}}\right) , \quad \omega _\mathrm{max}^2 = \frac{(c_1+c_2)(m_1+ m_2)}{m_1m_2}, \end{array} \end{aligned}$$

(50)

where index 1 corresponds to plus sign in the brackets. Functions $\omega _{1}(p), \omega _{2}(p)$ are referred to as optical and acoustic branches of the dispersion relation, respectively. Dispersion relations for different ratios of masses and equal stiffnesses are shown in Fig. 3.

Fig. 3

Dispersion relation for a chain with alternating masses and equal stiffnesses ($c_1=c_2$). Curves correspond to different stiffness ratios: $\frac{m_1}{m_2}= 1$ (solid line); $\frac{1}{2}$ (dots); $\frac{1}{4}$ (dashed line); $\frac{1}{8}$ (dash-dotted line)

Group velocities are calculated by definition (27). Projections of group velocities on direction of the chain for $p \in (0; 2\pi )$ have form

$$\begin{aligned} v_g^{j} = a\frac{\mathrm{d} \omega _{j}}{\mathrm{d}p}, \qquad v_g^{1} = \frac{c_1 c_2a \sin p}{m_1m_2\omega _1(\omega _1^2-\omega _2^2)}, \qquad v_g^{2} = \frac{c_1 c_2a \sin p}{m_1m_2\omega _2(\omega _1^2-\omega _2^2)}. \end{aligned}$$

(51)

Here $\omega _{j}$ is a nonnegative frequency in formula (50). The maximum group velocity is as follows

$$\begin{aligned} v_* = \underset{p, j}{\max }|v_g^{j}(p)| = a\sqrt{\frac{c_1 c_2}{(c_1+c_2)(m_1 + m_2)}}. \end{aligned}$$

(52)

Matrix $\varvec{{P}}{}{}$ is calculated as follows. By the definition, columns of matrix $\varvec{{P}}{}{}$ are equal to normalized eigenvectors of dynamical matrix $\varvec{\varOmega }$. Eigenvectors $\varvec{{d}}{}_{1,2}$, corresponding to eigenvalues $\omega _{1}^2, \omega _{2}^2$, have form:

$$\begin{aligned} \varvec{{d}}{}_{1,2} = \begin{bmatrix} 1-\frac{m_1}{m_2} \pm \sqrt{\left( 1-\frac{m_1}{m_2}\right) ^2 + 4|g|^2\frac{m_1}{m_2}}&\,\,-2g\sqrt{\frac{m_1}{m_2}}\end{bmatrix}^{\top }, \qquad g = \frac{c_1 + c_2e^{\mathrm {i}p}}{c_1 + c_2}. \end{aligned}$$

(53)

Normalization of vectors $\varvec{{d}}{}_{1,2}$ yields columns of matrix $\varvec{{P}}{}{}$.

In the following sections, formulas (29), (50), (51), (53) are employed for calculation of temperatures of sublattices $T_{11}, T_{22}$.

10.3 Thermal contact of cold and hot parts of the chain

In this section, we consider thermal contact of cold and hot parts of the chain and show that temperatures of sublattices in this problem are different even though their initial values are equal.

Initial spatial distribution of temperature matrix has form

$$\begin{aligned} \varvec{{T}}{}_0(x) = T_0(x)\varvec{{E}}{}, \qquad T_0(x) = T_b + \Delta T H(x). \end{aligned}$$

(54)

According to formula (54) initial temperatures of sublattices at each unit cell are equal. In our calculations $\Delta T=T_b$. Since the chain is harmonic, the value $\Delta T/T_b$ does not change results qualitatively.¹⁶

Analytical solution of this problem is given by formulas (29), (38). Integrals in formulas (29), (38) are evaluated numerically using Riemann sum approximation. Interval of integration is divided into $2 \cdot 10^4$ equal segments.

To check formulas (29), (38), we compare them with results of numerical solution of equations of motion (47) with initial conditions (48), (54). Numerical integration is carried out using symplectic leap-frog integrator with time-step $5 \cdot 10^{-3} \tau _\mathrm{min}$. According to formulas (29), (38) temperature matrix at large times is self-similar, i.e. it depends on x / t only. Therefore it is sufficient to compare numerical and analytical results at a single moment in time. We compare results at $t = 500 \tau _\mathrm{min}$, where $\tau _\mathrm{min} = 2\pi /\omega _\mathrm{max}$, $\omega _\mathrm{max}$ is defined by formula (50). The chain consists of $10^{4}$ unit cells under periodic boundary conditions. During the simulation, kinetic temperatures of sublattices $T_{11}, T_{22}$, at each unit cell, j, are calculated as

$$\begin{aligned} k_B T_{11}(x_j) = m \Bigl \langle {{\dot{u}}_{1j}^2}\Bigr \rangle _r, \qquad k_B T_{22}(x_j) = m \Bigl \langle {{\dot{u}}_{2j}^2}\Bigr \rangle _r, \end{aligned}$$

(55)

where $\Bigl \langle {...}\Bigr \rangle _r$ stands for averaging over realizations of random initial conditions. In the present example, number of realizations is equal to $7 \cdot 10^4$. Resulting temperatures of sublattices $T_{11}, T_{22}$ at $t=500 \tau _\mathrm{min}$ for $m_2=2m_1, c_1=c_2$ are shown in Fig. 4. The figure shows that numerical results are accurately described by our approximate analytical formulas (29), (38).

Fig. 4

Thermal contact of hot and cold parts of the diatomic chain ($m_2=2m_1, c_1=c_2$). Temperatures of sublattices $T_{11}$ (solid red line and squares) and $T_{22}$ (dashed blue line and circles) at $t=500\tau _\mathrm{min}$ are shown. Lines correspond to analytical solution (38). Squares and triangles are results of numerical solution of equations of motion (color figure online)

It is seen that temperatures of sublattices in the central part of the plot are different even though initially they are equal everywhere. This fact is predicted by formulas (29), (38).

Remark 13

Difference of temperatures of light and heavy particles of a diatomic chain has also been observed in steady problems considered in papers [37, 38]. Our results suggest that in unsteady problems light and heavy particles also have generally different temperatures even if their initial values are equal.

10.4 Sinusoidal initial temperature profile

In the present section, we consider decay of sinusoidal temperature profile (40) in a diatomic chain and show that, as in the previous example, temperatures of sublattices, $T_{11}, T_{22}$, at each unit cell are generally different. Decay of amplitude of sin is nonmonotonic.

Initial spatial distribution of temperature matrix has form

$$\begin{aligned} \varvec{{T}}{}_0(x) = T_0(x)\varvec{{E}}{}, \qquad T_0(x)= T_b + \Delta T \sin \frac{2\pi x}{L}, \end{aligned}$$

(56)

where L is length of a periodic cell; in further calculations $\Delta T=T_b/2$. Note that according to formula (56) initial temperatures of sublattices at each unit cell are equal. Analytical solution of this problem is given by formula (41). The solution shows that temperature profile remains sinusoidal at any moment in time. Therefore it is sufficient to compute matrix $\varvec{{A}}{}$, defined by formula (43). Elements $A_{11}, A_{22}$ of this matrix correspond to amplitudes of temperatures $T_{11}, T_{22}$. Decay of these amplitudes is investigated.

Analytical expression for $\varvec{{A}}{}$ is given by formula (44). Integrals in formula (44) are evaluated numerically using Riemann sum approximation. Interval of integration is divided into $10^3$ equal segments. Below we compare predictions of this formula with results of numerical solution of equations of motion.

In computer simulations, the chain consists of $10^{4}$ unit cells under periodic boundary conditions. Equations of motion (47) are solved numerically with initial conditions (48), (56). During the simulation matrix $\varvec{{A}}{}$ is calculated by formula (43), where integral is replaced by summation with respect to all unit cells. Temperatures of unit cells are calculated by formula (55). Resulting value of $\varvec{{A}}{}$ is averaged over $10^2$ realizations with random initial conditions. Note that number of realizations is less than in the previous example, because formula (43) involves additional spatial averaging, increasing the accuracy. Amplitudes $A_{11}, A_{22}$ of temperatures $T_{11}, T_{22}$ for $m_2=2m_1, c_1=c_2$ are shown in Figs. 5, 6. Figures show that numerical results are accurately described by our approximate analytical formula (44).

Fig. 5

Amplitude, $A_{11}$, of sinusoidal temperature profile in a diatomic chain ($m_2=2m_1, c_1=c_2$) at short times (left) and large times (right). Analytical solution (44) (line) and numerical solution of equations of motion (squares). Here $v_*$ is the maximum group velocity (52)

Fig. 6

Amplitude, $A_{22}$, of sinusoidal temperature profile in a diatomic chain ($m_2=2m_1, c_1=c_2$) at short times (left) and large times (right). Analytical solution (44) (line) and numerical solution of equations of motion (triangles). Here $v_*$ is the maximum group velocity (52)

Thus, similarly to the previous example, temperatures of sublattices for $t>0$ are different ($T_{11}({\mathbf{x}}{}) \ne T_{22}({\mathbf{x}}{})$), while their initial values are equal. We also note that decay of amplitude of sinusoidal temperature profile is nonmonotonic.

11 Example: graphene (out-of-plane motions)

In this section, we consider ballistic heat transport in a stretched graphene sheet [6, 10, 28] (see Fig. 7). Only out-of-plane vibrations are considered. In-plane vibrations can be taken into account separately, since in harmonic approximation in-plane and out-of-plane vibrations are decoupled. The main goal of this section is to show that approximate formulas (26) describe behavior of temperature with high accuracy. Using these formulas we demonstrate that ballistic heat transport in graphene is anisotropic. Additionally, we analyze individual contributions of acoustic and optical vibrations to thermal transport.

11.1 Equations of motion and initial conditions

In this subsection, we represent equations of motion for the graphene lattice in matrix form (4).

Fig. 7

Numbering of unit cells in graphene lattice. Here ${\mathbf{b}}{}_1$, ${\mathbf{b}}{}_2$ are primitive vectors of the lattice. Particles move along the normal to lattice plane. x, y axes correspond to zigzag and armchair directions, respectively

The lattice is shown in Fig. 7. Unit cells, containing two particles each, are numbered by pair of indices i, j. Primitive vectors ${\mathbf{b}}{}_1, {\mathbf{b}}{}_2$ for the lattice have form

$$\begin{aligned} {\mathbf{b}}{}_1 = \frac{\sqrt{3}a}{2} \left( {\mathbf{i}}{} + \sqrt{3}{\mathbf{j}}{} \right) , \qquad {\mathbf{b}}{}_2 = \frac{\sqrt{3}a}{2} \left( \sqrt{3}{\mathbf{j}}{} - {\mathbf{i}}{}\right) , \end{aligned}$$

(57)

where ${\mathbf{i}}{}, {\mathbf{j}}{}$ are Cartesian unit vectors directed along x and y axes, respectively; a is equilibrium distance between the nearest particles. Vector ${\mathbf{b}}{}_1$ connects centers of cells i, j and $i+1,j$. Vector ${\mathbf{b}}{}_2$ connects centers of cells i, j and $i,j+1$. Position vector of cell i, j is represented in terms of the primitive vectors as

$$\begin{aligned} {\mathbf{x}}{}_{i,j} = i {\mathbf{b}}{}_1 + j {\mathbf{b}}{}_2. \end{aligned}$$

(58)

Each particle has one degree of freedom (displacement normal to lattice plane). Displacements of a unit cell i, j form a column:

$$\begin{aligned} \varvec{{u}}{}_{i,j} = \varvec{{u}}{}({\mathbf{x}}{}_{i,j}) = \begin{bmatrix} u^1_{i,j}&u^2_{i,j}\end{bmatrix}^{\top }, \end{aligned}$$

(59)

where $u^1_{i,j}, u^2_{i,j}$ are displacements of two sublattices.

Consider equations of motion of unit cell i, j. Each particle is connected with three nearest neighbors by linear springs (solid lines in Fig. 7). Equilibrium length of the spring is less than initial distance between particles, i.e. the graphene sheet is uniformly stretched.¹⁷ Stiffness of the spring, determined by stretching force, is denoted by c. Then equations of motion have form

$$\begin{aligned} \begin{array}{l} \varvec{{M}}{}{}\ddot{\varvec{{u}}{}}_{i,j} = \varvec{{C}}{}_{2} \varvec{{u}}{}_{i,j+1} + \varvec{{C}}{}_{1} \varvec{{u}}{}_{i+1,j} + \varvec{{C}}{}_{0} \varvec{{u}}{}_{i,j} + \varvec{{C}}{}_{-1} \varvec{{u}}{}_{i-1,j} + \varvec{{C}}{}_{-2} \varvec{{u}}{}_{i,j-1},\\ \displaystyle \varvec{{M}}{}{}= m\varvec{{E}}{}, \quad \varvec{{C}}{}_0 = \begin{bmatrix} -3c &{} c \\ c &{} -3c \end{bmatrix}, \quad \varvec{{C}}{}_1 = \varvec{{C}}{}_2 = \begin{bmatrix} 0 &{} 0 \\ c &{} 0 \end{bmatrix}. \end{array} \end{aligned}$$

(60)

Here $\varvec{{C}}{}_{-1} = \varvec{{C}}{}_{1}^{\top }$, $\varvec{{C}}{}_{-2} = \varvec{{C}}{}_{2}^{\top }$; m is mass of a particle.

Initially, particles have random velocities and zero displacements. In this section we consider isotropic initial temperature matrices:

$$\begin{aligned} \varvec{{T}}{}_0(x_{i,j}, y_{i,j}) = T_0(x_{i,j}, y_{i,j})\varvec{{E}}{}, \end{aligned}$$

(61)

where $x_{i,j}, y_{i,j}$ are Cartesian coordinates of position vector ${\mathbf{x}}{}_{i,j}$. In this case initial temperatures of the sublattices are equal ($T_{11}^0 = T_{22}^0 = T_0$). Corresponding initial conditions for the particles have form:

$$\begin{aligned} u_{i,j}^1 = u_{i,j}^2 = 0, \quad {\dot{u}}_{i,j}^1 = \beta _{i,j}\sqrt{\frac{k_B }{m}T_0(x_{i,j}, y_{i,j})}, \quad {\dot{u}}_{i,j}^2 = \gamma _{i,j}\sqrt{\frac{k_B}{m} T_0(x_{i,j}, y_{i,j})}, \end{aligned}$$

(62)

where $\beta _{i,j}$, $\gamma _{i,j}$ are uncorrelated random values with zero mean and unit variance, i.e. $\Bigl \langle {\beta _{i,j}}\Bigr \rangle =\Bigl \langle {\gamma _{i,j}}\Bigr \rangle = 0$, $\Bigl \langle {\beta _{i,j}^2}\Bigr \rangle =\Bigl \langle {\gamma _{i,j}^2}\Bigr \rangle = 1$, $\Bigl \langle {\beta _{i,j}\gamma _{s,p}}\Bigr \rangle =0$ for all i, j, s, p.

Further we consider time evolution of kinetic temperature $T = \frac{1}{2}\left( T_{11} + T_{22}\right)$.

11.2 Dispersion relation and group velocities

In this subsection, we calculate the dispersion relation, matrix matrix $\varvec{{P}}{}{}$ [see formula (12)], and group velocities.

We calculate dynamical matrix $\varvec{\varOmega }$ using formula (10). Substituting expressions (60) for matrixes $\varvec{{M}}{}{}, \varvec{{C}}{}_{\alpha }$, $\alpha =0;\pm 1; \pm 2$ into formula (10), yields

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{\varOmega }= \omega _*^2 \begin{bmatrix} 3 &{} -1 -e^{-\mathrm{i}p_1}-e^{-\mathrm{i}p_2} \\ -1 -e^{\mathrm{i}p_1}-e^{\mathrm{i}p_2} &{} 3 \end{bmatrix}, \qquad p_1 = {\mathbf{k}}{}\cdot {\mathbf{b}}{}_1, \quad p_2 = {\mathbf{k}}{}\cdot {\mathbf{b}}{}_2, \end{array} \end{aligned}$$

(63)

where ${\mathbf{k}}{}$ is wave vector; $\omega _*^2 = \frac{c}{m}$; $p_1, p_2 \in [0; 2\pi ]$ are dimensionless components of the wave vector.

Eigenvalues $\omega _{1}^2, \omega _{2}^2$ of matrix $\varvec{\varOmega }$ determine dispersion relation for the lattice. Solution of the eigenvalue problem yields:

$$\begin{aligned} \omega _{1,2}^2 = \omega _*^2 \bigl ( 3 \pm R(p_1,p_2)\bigr ) , \qquad R(p_1,p_2) = \sqrt{3 + 2 \left( \cos p_1 + \cos p_2 + \cos \left( p_1-p_2\right) \right) }, \end{aligned}$$

(64)

where index 1 corresponds to plus sign. Functions $\omega _{1}(p_1,p_2)$, $\omega _{2}(p_1,p_2)$ are referred to as optical and acoustic dispersion surfaces, respectively (see Fig. 8). Eigenvectors of matrix $\varvec{\varOmega }$ are columns of matrix $\varvec{{P}}{}{}$:

$$\begin{aligned} \varvec{{P}}{}{}= \frac{1}{\sqrt{|b|^2 + b^2}} \begin{bmatrix} |b|&|b| \\ -b&b \end{bmatrix}, \qquad b = 1 + e^{\mathrm{i}p_1} + e^{\mathrm{i}p_2}. \end{aligned}$$

(65)

Fig. 8

Acoustic ($\omega _{2}(p_1,p_2)/\omega _*$, left) and optical ($\omega _{1}(p_1,p_2)/\omega _*$, right) dispersion surfaces (64) for out-of-plane vibrations of graphene

Group velocities ${\mathbf{v}}{}_{g}^{1}, {\mathbf{v}}{}_{g}^{2}$ for $p_1, p_2 \in (0; 2\pi )$ are calculated by definition (27) as

$$\begin{aligned} \begin{array}{l} \displaystyle {\mathbf{v}}{}_{g}^{j} = \frac{\partial \omega _{j}}{\partial {\mathbf{k}}{}} = \frac{\partial \omega _{j}}{\partial p_1} {\mathbf{b}}{}_1 + \frac{\partial \omega _{j}}{\partial p_2} {\mathbf{b}}{}_2,\\ \displaystyle \frac{\partial \omega _{1}}{\partial p_1} = \frac{-\omega _*^2 \left( \sin p_1 + \sin (p_1-p_2)\right) }{2\omega _{1}R(p_1,p_2)}, \qquad \frac{\partial \omega _{2}}{\partial p_1} = \frac{\omega _*^2 \left( \sin p_1 + \sin (p_1-p_2)\right) }{2\omega _{2}R(p_1,p_2)}, \\ \displaystyle \frac{\partial \omega _{1}}{\partial p_2} = \frac{-\omega _*^2 \left( \sin p_2 - \sin (p_1-p_2)\right) }{2\omega _{1}R(p_1,p_2)}, \qquad \frac{\partial \omega _{2}}{\partial p_2} = \frac{\omega _*^2 \left( \sin p_2 - \sin (p_1-p_2)\right) }{2\omega _{2}R(p_1,p_2)}. \end{array} \end{aligned}$$

(66)

Here $\omega _{1} \ge 0, \omega _{2} \ge 0$; function $R(p_1,p_2)$ is defined by formula (64); primitive vectors ${\mathbf{b}}{}_1, {\mathbf{b}}{}_2$ are given by formula (57).

According to formulas (66), the maximum absolute values of group velocities corresponding to acoustic and optical branches are as follows

$$\begin{aligned} \max _{p_1,p_2} |{\mathbf{v}}{}_{g}^{1}| \approx 0.448v_*, \qquad \max _{p_1,p_2} |{\mathbf{v}}{}_{g}^{2}| \approx 0.897v_*, \qquad v_*=\omega _*a. \end{aligned}$$

(67)

In the following sections, formulas (63), (64), (65), (66) are employed for description of ballistic heat transport.

11.3 Circular initial temperature profile: anisotropy of heat transport

In this subsection, we show that ballistic heat transport in graphene is anisotropic. Also, we analyze contributions of acoustic and optical vibrations to heat transport.

Initially the temperature has constant value, $T_1$, inside a circle of radius R and vanishes outside:

$$\begin{aligned} \varvec{{T}}{}_0 = T_0(x,y)\varvec{{E}}{}, \qquad T_0(x,y) = {\left\{ \begin{array}{ll} T_1, &{} x^2 + y^2 \le R^2, \\ 0, &{} x^2 + y^2 > R^2, \end{array}\right. } \end{aligned}$$

(68)

In our calculations $R=10a$. Analytical solution of this problem is calculated using formula (30). Integrals in formula (30) are evaluated numerically using Riemann sum approximation. Integration area is divided into $300\times 300$ equal square elements.

In computer simulations a square graphene sheet of length $L=300a$ is considered. Equations of lattice dynamics (60) with initial conditions (62), (68) are solved numerically using leap-frog integrator with time-step $5 \cdot 10^{-3}\tau _*$, $\tau _*=2\pi /\omega _*$. Kinetic temperatures of all unit cells $T(x_{i,j}, y_{i,j})$ at $t=20 \tau _*$ are calculated as

$$\begin{aligned} k_B T(x_{i,j}, y_{i,j}) = \frac{1}{2} m \Bigl \langle {\left( {\dot{u}}^1_{i,j}\right) ^2 + \left( {\dot{u}}^2_{i,j}\right) ^2}\Bigr \rangle _r, \end{aligned}$$

(69)

where averaging is carried out with respect to realizations of random initial conditions. The moment in time is chosen such that fast relaxation process can be neglected. Resulting temperature fields averaged over $10, 10^2, 10^3, 10^4$ realizations are shown in Fig. 9. With increasing number of realizations, results of numerical solution of equations of motion converges to analytical solution given by formula (30). For $10^4$ realizations plots of analytical and numerical solutions are visually indistinguishable.

Fig. 9

Temperature profile in graphene at $t=20\tau _*$. Results of numerical solution of lattice dynamics equations averaged over $10, 10^2, 10^3, 10^4$ realizations are shown. Initial temperature is equal to $T_1$ inside a circle with radius $R=10a$ and equal to zero outside [see formula (68)]. Color bars show $T/T_1$ (color figure online)

Figure 9 shows, in particular, that the heat front is a circle as predicted by formula (36) and the Huygens principle. At the same time, the temperature field has a symmetry of the lattice, i.e. the heat transport is strongly anisotropic.

Fig. 10

Contributions of acoustic (left) and optical (right) vibrations to temperature profile in graphene at $t=20\tau _*$. Initial temperature is equal to $T_1$ inside a circle with radius $R=10a$ and equal to zero outside [see formula (68)]. Plus signs mean that the resulting temperature profile is equal to a sum of acoustic and optical contributions. Color bars show $T/T_1$ (color figure online)

According to formula (30), temperature field has contributions from acoustic and optical branches of dispersion relation. The contributions are shown in Fig. 10. Acoustic waves have larger group velocities than optical waves [see e.g. formula (67)]. Therefore temperature front on the left plot from Fig. 10 propagates faster.

Thus formula (30) describes anisotropic ballistic heat transport in graphene with high accuracy. In contrast to numerical results, formula (30) allows to analyze individual contributions of acoustic and optical vibrations to the temperature profile.

11.4 Thermal contact of cold and hot half-planes

In this subsection, we consider thermal contact of two half-planes with initial temperatures $T_b$ and $2T_b$ [see formula (37)]. Temperatures of sublattices are equal. Since thermal transport in graphene is anisotropic, we consider two problems with temperature distributions in zigzag (x) and armchair (y) directions:

$$\begin{aligned} \varvec{{T}}{}_0 = T_0(x,y)\varvec{{E}}{}, \qquad T_0(x,y) = T_b\bigl ( 1 + H(x)\bigr ) \quad \mathrm {or} \quad T_0(x,y) = T_b\bigl ( 1 + H(y)\bigr ) . \end{aligned}$$

(70)

Analytical solution of these problems is given by formula (39).

To check formula (39), we compare it with results of numerical solution of equations of motion. Formula (39) shows that at large times the solution is self-similar. Therefore it is sufficient to consider temperature field at a single moment in time. In our calculations it is equal to $t= 20 \tau _{*}$. Nearly square graphene sheet containing $301 \times 348$ unit cells is considered. Particles have random initial velocities corresponding to initial temperature distributions (70). Initial particle displacements are equal to zero. Periodic boundary conditions in both directions are used. During the simulation, kinetic energy of each unit cell is calculated. In order to calculate temperatures, results are averaged over $1.5\cdot 10^3$ realizations with random initial conditions. Temperature distributions in x and y directions are shown in Fig. 11.

Fig. 11

Thermal contact of hot and cold parts of graphene. Solutions of two problems with temperature distributions in x (solid red line) and y (dashed blue line) directions at $t=19.5\tau _{*}$ are shown. Analytical solution (39) (lines) and results of numerical solution of equations of motion (squares and crosses). Here $v_* = \omega _*a$ (color figure online)

Figure 11 shows that numerical results are accurately described by our approximate formulas (26).

11.5 Sinusoidal initial temperature profile

In the present section, we consider decay of spatially sinusoidal temperature profile (40) in graphene. We investigate the influence of lattice anisotropy on heat transfer by comparing solutions of two problems with temperature changing in zigzag (x) and armchair (y) directions:

$$\begin{aligned} \varvec{{T}}{}_0 = T_0(x,y)\varvec{{E}}{}, \qquad T_0(x,y) = T_b + \Delta T \sin \frac{2\pi x}{L} \quad \mathrm {or} \quad T_0(x,y) = T_b + \Delta T \sin \frac{2\pi y}{L}, \end{aligned}$$

(71)

where L is length of a periodic cell. In our calculations $\Delta T=T_b/2$.

Analytical solution of this problem is given by formula (41). The solution shows that spatial distribution remains sinusoidal at any moment in time. Therefore, we compute amplitude, A, of temperature profile [see formula (43)]. Analytical expression for A is given by the second formula from (44). Integrals in formula (44) are evaluated numerically using Riemann sum approximation. Interval of integration is divided into $200 \times 200$ equal segments. Below we compare predictions of this formula with results of numerical solution of equations of motion.

We check the accuracy of formula (44) using numerical solution of equations of motion. Particles have random initial velocities corresponding to initial temperature distributions (71). Initial particle displacements are equal to zero. Periodic boundary conditions in both directions are used. The periodic cell contains $200 \times 232$ unit cells. During simulation amplitude, A, is calculated using two-dimensional version of formula (43):

$$\begin{aligned} A = \frac{2}{L^2} \int _{0}^{L}\int _{0}^{L} T(x,y) \sin \frac{2\pi x}{L} \mathrm{d}x \mathrm{d}y \quad \mathrm {or} \quad A = \frac{2}{L^2} \int _{0}^{L}\int _{0}^{L} T(x,y) \sin \frac{2\pi y}{L} \mathrm{d}x. \end{aligned}$$

(72)

Integral in formula (72) is replaced by sum with respect to unit cells.

Dependence of dimensionless amplitude, $A/\Delta T$, on dimensionless time, $c_* t/L$, is shown in Fig. 12. Every circle on the plot corresponds to average over 100 realizations. Figure 12 shows that analytical solution (44) practically coincides with results of numerical solution of lattice dynamics equations. Results for x and y directions practically coincide for $t \le L/v_*$, while for $t > L/v_*$ they are significantly different.

Fig. 12

Amplitude, A, of sinusoidal temperature profile in graphene at short times (left) and large times (right). Solutions of two problems with temperature distributions in zigzag (red line) and armchair (blue line) directions are shown. Analytical solution (44) (lines) and numerical solution of equations of motion (squares and triangles). Here $v_* = \omega _*a$ (color figure online)

Thus, our analytical solution (44) shows that decay of amplitude of the sinusoidal profiles in zigzag and armchair directions is nonmonotonic. Similar nonmonotonic behavior has been recently observed experimentally in polycrystalline graphite [33] at temperatures about $T_b \sim 100 K$ and length scales $L \sim 1 \mu m$.

12 Conclusions

We have shown that time evolution of initial temperature profile in infinite harmonic crystals is described by our formulas (26), (30) with high accuracy.

At short times, behavior of temperatures at different spatial points is approximately independent. At each point, temperatures, corresponding to degrees of freedom of the unit cell, oscillate in time and tend to generally different equilibrium values. The oscillations are caused by redistribution of energy between kinetic and potential forms and redistribution of energy between degrees of freedom of the unit cell. In infinite crystals,¹⁸ the oscillations usually practically vanish at times of order of 100 periods of atomic vibrations.

Evolution of temperature profile at large times is caused by ballistic heat transport. At large times, the temperature profile is represented as a superposition of waves having a shape of initial temperature distribution and traveling with group velocities depending on the wave vector. Therefore formulas (26), (30) clearly demonstrate wave nature of heat transfer in ballistic regime. Additionally, formulas (26), (30) show that accurate description of ballistic heat transport requires knowledge of the complete dispersion relation and corresponding group velocities.

It is noteworthy that local values of temperatures, corresponding to degrees of freedom of the unit cell, at large times are generally neither equal to each other nor equal to their equilibrium values. Therefore, thermal state of unit cells reached by thermal waves is strongly nonequilibrium (see, e.g., Figs. 4, 5, 6).

Formula (26) for temperature has the same property as equations of lattice dynamics, it is invariant with respect to change t by $-t$. At the same time, thermal processes in infinite harmonic crystals are irreversible.

Though formula (26) allows to calculate the temperature profile, it does not yield an equation describing ballistic heat transport. So far the closed equation has been derived only for several particular lattices [5, 41, 42]. Derivation of the general equation valid for all harmonic crystals would be an interesting extension of the present work.

Presented theory may serve for proper statement and interpretation of experiments on unsteady ballistic heat transport in crystals. Analytical solution of the problem with sinusoidal profile of initial temperature can be used for interpretation of results obtained by the transient thermal grating technique [33, 36, 67]. In particular, the solution predicts nonmonotonic decay of the temperature profile, which was recently observed experimentally in graphite [33].

The present paper is focused on ballistic heat transport in crystals at nanoscale. However, presented approach can be extended for description of energy transport in macroscopic phononic crystals and acoustic metamaterials [23, 26, 46].

Approximate formula for the temperature matrix

In this “Appendix,” approximate formula (26) for the temperature matrix is derived. The derivation is based on the assumption that the main contribution to integrals $\varvec{{T}}{}_\mathrm{F}$, $\varvec{{T}}{}_\mathrm{S}$ comes from the points such that ${\mathbf{k}}{}_1 \approx {\mathbf{k}}{}_2$. This assumption is satisfied if function $\varvec{{T}}{}_0({\mathbf{x}}{})$ slowly changes at distances of order of lattice constant.

The expression for $\varvec{{T}}{}_\mathrm{F}$ in formula (26) is derived as follows. We introduce new variables in formula (23) for $\varvec{{T}}{}_\mathrm{F}$:

$$\begin{aligned} {\mathbf{p}}{}_1={\mathbf{k}}{}_1, \qquad {\mathbf{p}}{}_2={\mathbf{k}}{}_1-{\mathbf{k}}{}_2. \end{aligned}$$

(73)

Jacobian of this transformation is equal to unity. Using periodicity of the integrand in formula (23), it can be shown that integration is carried out in the same domain as in formula (9). We assume that the main contribution to the integral (26) comes form the points ${\mathbf{p}}{}_2 \approx 0$ (${\mathbf{k}}{}_1\approx {\mathbf{k}}{}_2$). Then integrand is expanded into series with respect to ${\mathbf{p}}{}_2$. In particular, the following approximate formulas are used:

$$\begin{aligned} \varvec{{P}}{}{}({\mathbf{p}}{}_1-{\mathbf{p}}{}_2) \approx \varvec{{P}}{}{}({\mathbf{p}}{}_1), \qquad \omega _j({\mathbf{p}}{}_1-{\mathbf{p}}{}_2) \approx \omega _j({\mathbf{p}}{}_1). \end{aligned}$$

(74)

Then formula (23) for $\varvec{{T}}{}_\mathrm{F}$ reads

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}_\mathrm {F} \approx \int _{{\mathbf {p}}{}_1}\varvec{{P}}{}{}\int _{{\mathbf {p}}{}_2}\sum _{{\mathbf {y}}{}} {\tilde{\varvec{{T}}{}}}_\mathrm {F}({\mathbf {y}}{}, {\mathbf {p}}{}_1)e^{\mathrm {i}{\mathbf {p}}{}_2 \cdot ({\mathbf {x}}{}-{\mathbf {y}}{})} \mathrm {d} {\mathbf {p}}{}_2 \varvec{{P}}{}{}^{*\top }\mathrm {d} {\mathbf {p}}{}_1, \qquad \varvec{{P}}{}{}= \varvec{{P}}{}{}({\mathbf {p}}{}_1),\\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {F}\}_{ij} = \frac{1}{2}\{\varvec{{P}}{}{}^{*\top } \varvec{{T}}{}_0({\mathbf {y}}{}) \varvec{{P}}{}{}\}_{ij} \Bigl [ \cos \bigl ((\omega _i({\mathbf {p}}{}_1) + \omega _j({\mathbf {p}}{}_1))t\bigr ) + (1-\delta _{ij})\cos \bigl ((\omega _i({\mathbf {p}}{}_1) - \omega _j({\mathbf {p}}{}_1))t\bigr )\Bigr ] . \end{array} \end{aligned}$$

(75)

According to the definition of the discrete Fourier transform the following identity is satisfied:

$$\begin{aligned} \int _{{\mathbf{p}}{}_2}\sum _{{\mathbf{y}}{}} {\tilde{\varvec{{T}}{}}}_\mathrm{F}({\mathbf{y}}{}, {\mathbf{p}}{}_1)e^{\mathrm{i}{\mathbf{p}}{}_2 \cdot ({\mathbf{x}}{}-{\mathbf{y}}{})} \mathrm{d} {\mathbf{p}}{}_2 = {\tilde{\varvec{{T}}{}}}_\mathrm{F}({\mathbf{x}}{}, {\mathbf{p}}{}_1). \end{aligned}$$

(76)

Substituting this identity into formula (75) yields the expression for $\varvec{{T}}{}_\mathrm{F}$ in formula (26).

To derive approximate expression for $\varvec{{T}}{}_\mathrm{S}$ in formula (26), we introduce new variables (73) in formula (23). The integrand in formula (23) is expanded into series with respect to ${\mathbf{p}}{}_2$. In particular, the following approximate formulas are used:

$$\begin{aligned} \varvec{{P}}{}{}({\mathbf{p}}{}_1-{\mathbf{p}}{}_2) \approx \varvec{{P}}{}{}({\mathbf{p}}{}_1), \qquad \omega _j({\mathbf{p}}{}_1) - \omega _j({\mathbf{p}}{}_1-{\mathbf{p}}{}_2) \approx {\mathbf{p}}{}_2 \cdot {\mathbf{v}}{}_g^j({\mathbf{p}}{}_1), \end{aligned}$$

(77)

where ${\mathbf{v}}{}_g^j$ is the group velocity, defined by formula (26). Then formula (23) for $\varvec{{T}}{}_\mathrm{S}$ reads

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{{T}}{}_\mathrm {S} \approx \int _{{\mathbf {p}}{}_1}\int _{{\mathbf {p}}{}_2}\sum _{{\mathbf {y}}{}} \varvec{{P}}{}{}{\tilde{\varvec{{T}}{}}}_\mathrm {S}({\mathbf {y}}{})\varvec{{P}}{}{}^{*\top } e^{\mathrm {i}{\mathbf {p}}{}_2 \cdot ({\mathbf {x}}{}-{\mathbf {y}}{})} \mathrm {d} {\mathbf {p}}{}_2\mathrm {d} {\mathbf {p}}{}_1, \qquad \varvec{{P}}{}{}=\varvec{{P}}{}{}({\mathbf {p}}{}_1),\\ \displaystyle \{{\tilde{\varvec{{T}}{}}}_\mathrm {S}\}_{ij} \approx \frac{1}{2}\{\varvec{{P}}{}{}^{*\top } \varvec{{T}}{}_0({\mathbf {y}}{}) \varvec{{P}}{}{}\}_{ij} \delta _{ij}\cos \bigl ({\mathbf {p}}{}_2 \cdot {\mathbf {v}}{}_g^j({\mathbf {p}}{}_1) t\bigr ). \end{array} \end{aligned}$$

(78)

Using identity $2\cos ({\mathbf{p}}{}_2 \cdot {\mathbf{v}}{}_g^j t) = e^{\mathrm{i}{\mathbf{p}}{}_2 \cdot {\mathbf{v}}{}_g^j t} + e^{-\mathrm{i}{\mathbf{p}}{}_2 \cdot {\mathbf{v}}{}_g^j t}$ and properties of the discrete Fourier transform, we show that

$$\begin{aligned} \begin{array}{l} \displaystyle \int _{{\mathbf {p}}{}_2}\sum _{{\mathbf {y}}{}}\{\varvec{{P}}{}{}^{*\top } \varvec{{T}}{}_0({\mathbf {y}}{}) \varvec{{P}}{}{}\}_{jj} \cos \bigl ({\mathbf {p}}{}_2 \cdot {\mathbf {v}}{}_g^j t\bigr ) e^{\mathrm {i}{\mathbf {p}}{}_2 \cdot ({\mathbf {x}}{}-{\mathbf {y}}{})} \mathrm {d} {\mathbf {p}}{}_2\\ \qquad \displaystyle = \frac{1}{2}\Bigl \{\varvec{{P}}{}{}^{*\top } \left( \varvec{{T}}{}_0({\mathbf {x}}{}+ {\mathbf {v}}{}_g^j t) + \varvec{{T}}{}_0({\mathbf {x}}{}- {\mathbf {v}}{}_g^j t)\right) \varvec{{P}}{}{}\Bigr \}_{jj}. \end{array} \end{aligned}$$

(79)

Substituting formula (79) into formula (78), yields the expression (26) for $\varvec{{T}}{}_\mathrm{S}$.

More rigorous derivation of formula (26) is beyond the scope of the present paper. In the present paper, we show that formula (26) has high accuracy by comparison of analytical solutions of several problems with corresponding results of numerical simulations (see Sects. 10, 11).