1 Introduction

Topology optimization provides an effective design tool to search for the optimal material distributions of structures and achieve novel conceptual designs, which can meet the increasing requirements of the modern equipment to a large extent. Topology optimization has experienced great popularity and a series of achievements has been developed over the past decades (Sigmund and Maute 2013; Dbouk 2017). Most topology optimization methods are developed for structures under the mechanical field or the thermal field. However, the structures in advanced equipment generally work under complex multi-physics service conditions. Since the high temperature and the mechanical loading would both have great influence of the performance of the structure, it is important to consider the thermo-mechanical coupled effect in the topology optimization.

In order to improve the mechanical performance and ensure the service reliability of structures, Rodrigues and Fernandes (1995) early explored the structural topology optimization considering thermal and mechanical coupling loadings. Since then, a series of thermo-mechanical topology optimization methods have been developed. Based on the level set method, Xia and Wang (2008) investigated topology optimization of thermoelastic structures under volume constraint. In recent years, level set methods have also been introduced in thermoelastic topology optimization for problems with multi-material, non-linearity, and thermal buckling (Vermaak et al. 2014; Deng and Suresh 2017; Chung et al. 2020). Based on the solid isotropic material with penalization (SIMP) method, Gao and Zhang (2010) developed a topology optimization method for structures involving thermoelastic stress loads based on the definition of thermal stress coefficient and also applied the method to multi-material topology optimization problems. Later, Yang and Li (2013) proposed a topology optimization method to minimize the dynamic compliance in a thermal environment. Yan et al. (2016) developed the multi-scale concurrent topology optimization method under mechanical and thermal loads based on the porous anisotropic material with penalization model. In order to meet the manufacturing requirements of mechanical equipment, Hostos et al. (2021) proposed a topology optimization method for thermo-mechanical metadevices.

In thermo-mechanical topology optimization problems, the heat conduction property is also an important concern of the structural design. For heat storage devices, the mechanical stiffness should be maintained under high temperature conditions, while the heat retaining capacity should also be ensured. Focus on this problem, Yang et al. (2019) proposed a topological optimization method for integrated thermal protection systems to achieve both low thermal conductivity and high mechanical performance. In some industrial fields i.e., electron components design, the heat conduction property should be improved to reduce the temperature of the structure. For example, Matsumori et al. (2019) developed a topology optimization method based on the density method for a power semiconductor module to provide efficient cooling and reduce the thermal stress. Zhu et al. (2019) studied a temperature-constrained topology optimization method for thermo-mechanical coupled problem. Kambampati et al. (2020) built the topology optimization model to minimize stress and compliance under volume and temperature constraints and solved this problem based on a level set method. These developments and achievements contribute much for the structural design optimization of advanced equipment.

At present, the topology optimizations considering thermo-mechanical loadings are generally based on deterministic assumption. However, the material properties and loadings parameters related to the physical fields inevitably have multi-source uncertainties (Fragiadakis et al. 2008), and these uncertainties may have great influence on the design optimizations or even result in failure designs. Nevertheless, the importance of uncertainties has already been noticed in the topological design problems and a number of research works have been proposed for topology optimization considering uncertainties which can be divided into two categories, namely, reliability-based topology optimization (RBTO) and robust topology optimization (RTO) (Guo and Cheng 2010). In RBTO, reliability constraints are introduced into the topology optimization model, in order to achieve a reliable design under the uncertain parameters (Kharmanda et al. 2004; Jung and Cho 2004; Meng et al. 2020; Luo et al. 2021). RTO problems is the main concern of this work, in which the lower statistical moments of the structural response are optimized to receive a robust design. Guest and Igusa (2008) presented an RTO method under loading and structural nodes location uncertainties. Chen et al. (2010) developed a Karhunen–Loeve (KL) and univariate dimension-reduction-based RTO method for structures with material and loading uncertainties. Tootkaboni et al. (2012) proposed an RTO method considering random field material uncertainties based on polynomial chaos expansion and stochastic Galerkin formulation. Recently, the RTO framework is introduced in the design of optical cloaks to deal with the topology optimization designs considering the uncertainties in the wave number and angle in the incident wave (Sato et al. 2020). Due to some physical characteristics, it could be more appropriate to model the uncertainties with certain bounded ranges by bounded probability models. Schevenels et al. (2011) presented a robust approach based on a Monte Carlo method considering uniform and non-uniform spatially varying manufacturing errors modeled by bounded random variables and random fields. Zhang et al. (2017) developed a new level set-based framework for robust topology optimization (RTO) problems with geometric uncertainties modeled by uniformly distributed random fields, in which the Karhunen–loeve (KL) decomposition and the polynomial chaos expansion are utilized to evaluate the stochastic response. Considering uncertainties arising from different sources, Bai et al. (2021) also proposed an RTO method for structures with bounded loads and spatially correlated material uncertainties by using the ellipsoid convex model.

Among the topology optimizations considering uncertainties, the uncertain parameters are often assumed to follow the probability distributions based on enough experimental samples. However, due to the difficulty and high cost of testing, it is often difficult to get the accurate distributions of uncertain parameters. Therefore, the interval model provides an effective way to describe the uncertain parameters by the variation bounds. Early in 1993, Ben-Haim and Elishakoff (2013) introduced interval methods into structural analysis problems, and then a number of achievements for interval analysis have been developed afterward (Ben-Haim and Elishakoff 2013; Jiang et al. 2008; Wei et al. 2016; Wang et al. 2020; Xu et al. 2020). Thus, the bounded interval uncertainties have also been paid attention in the topology optimization to obtain robust designs. Guo et al. (2013) studied an RTO problem based on a level set framework considering the unknown-but-bounded boundary variations. Wu et al. (2016) employed the Chebyshev polynomial for the interval analysis in the RTO problems. Considering the interval uncertainties in magnitude and direction of loadings, da Silva et al. (2019) proposed a non-probabilistic RTO approach for topology optimization problems with stress constrains. Wang and Gao (2020) proposed an RTO method based on Taylor expansions for structures with loading position uncertainties.

With the increasing complexity of engineering structures and requirements for structural safety design, it is not appropriate to model the multi-source uncertainties only by one type of uncertainties. Random and interval hybrid uncertainties are considered as a more general uncertain model (Jiang et al. 2018) and a series of RTO problems with hybrid uncertainties have been developed based on Taylor expansions (Chen et al. 2016; He et al. 2020), orthogonal polynomial expansions (Wu et al. 2017; Chen et al. 2019), dimension reduction methods (Zheng et al. 2018, 2019a) and so on. Among those, the orthogonal polynomial expansion-based method has become one of the most popular type due to the powerful function approximation ability of the expansion represented by a suitably polynomial basis. Wu et al. (2015) proposed a Polynomial-Chaos-Chebyshev-Interval method (PCCI) method for hybrid uncertainties analysis and investigated an RTO method for mechanical metamaterials with negative Poisson’s ratio based on the PCCI method (Wu et al. 2017). Later, the PCCI method has also been introduced in topology optimization problems (Zheng et al. 2019b; Li et al. 2020) for structures and composite materials under hybrid uncertainties. A robust microstructural topology optimization method has been proposed based on Gegenbauer polynomial expansion to minimize the sound pressure of structural–acoustic system with bounded hybrid uncertainties (Chen et al. 2019). By the projection method, the polynomial coefficients are calculated multiple integrations, in which the dimensionality is equal to the number of the uncertain variables. Hence, the computational cost in calculating the expansion coefficients would increase exponentially with the increase of the uncertain variables, which is a main difficulty for the hybrid uncertainty analysis.

In the thermo-mechanical coupled analysis problem, there may exist uncertain parameters related to the Young’s module, Poison’s ratio, thermal expansion coefficient, temperature field, and applied loadings. Thus, the computational burden becomes heavier for problem with a relatively large number of uncertain parameters. Dimension reduction (DR) integration methods (Rahman and Xu 2004; Xu and Rahman 2004) are proved to be efficient to deal with multiple integrations. The univariate DR method has been proposed to calculate statistical moments of the structural response, in which the multi-dimensional integral can be approximated by a series of one-dimensional integrals. For structures involving small-to-moderate uncertainties, the univariate DR method has been verified to show very good efficiency and accuracy in reference (Rahman and Xu 2004). For problems with large uncertainties and/or high non-linearity, the univariate DR may not be adequate since the contributions from two- and higher-dimensional integrations could not be neglected, and the errors can be further reduced by applying bivariate or multivariate DR methods (Xu and Rahman 2004). Taking advantage of the DR methods, the integration formulations for calculating the mean and variance have previously been efficiently solved in (Zheng et al. 2018, 2019a). However, this type of scheme could improve the efficiency, but sometimes may have a relatively large sacrifice on accuracy. In order to efficiently analyze the structural compliance of thermo-mechanical coupled structures with hybrid uncertainties, a DR-based orthogonal polynomial expansion method is developed for hybrid uncertainty analysis in this work. In this case, the advantage of the orthogonal polynomial expansion is maintained, while the efficiency of calculating the expansion coefficients has been greatly improved. Based on the proposed hybrid uncertainty analysis method, a new robust topology optimization method has been developed. Firstly, the robust topology optimization model is built in which the robust objective function is defined as the combination of the mean and standard variance of the structural compliance under the worst case. After the evaluation of the robust objective function, the sensitivities with respect to the design variables are obtained. Finally, the effectiveness of the proposed method is verified by several numerical examples.

2 Thermo-mechanical topology optimization

Under a thermo-mechanical coupled field, the global finite element equation is expressed as follows:

$${\mathbf{KU}} = {\mathbf{F}} + {\mathbf{F}}_{{\Delta {\mathbf{T}}}},$$
(1)

in which K is the global stiffness matrix of the structure, and U denotes the global displacement field. F and \({\mathbf{F}}_{{\Delta {\mathbf{T}}}}\) are the mechanical and thermal loading vectors of the structure, respectively. The thermal loading \({\mathbf{F}}_{{\Delta {\mathbf{T}}}}\) related to thermal stress can be calculated by assembling the elemental thermal loading \({\mathbf{F}}_{{\Delta {\mathbf{T}}}}^{{(e)}}\) which can be obtained as follows:

$${\mathbf{F}}_{{\Delta {\mathbf{T}}}}^{{(e)}} = \int_{{V_{e} }} {\left( {{\mathbf{B}}_{e} } \right)^{{\text{T}}} {\mathbf{D}}_{e} {\mathbf{\varepsilon }}_{e}^{{\Delta {\mathbf{T}}}} {\text{d}}V_{e} } ,$$
(2)

in which \({\mathbf{B}}_{e}\) and \({\mathbf{D}}_{e}\) are strain–displacement matrix and elastic matrix of the eth element. \({\mathbf{\varepsilon }}_{e}^{{\Delta {\mathbf{T}}}}\) is the thermal strain caused by the temperature variation:

$${\mathbf{\varepsilon }}_{e}^{{\Delta {\mathbf{T}}}} = \alpha \left( {{\mathbf{t}}_{e} - {\mathbf{t}}_{{ref}} } \right)\phi ^{{\text{T}}} ,$$
(3)

where \(\alpha\) is the thermal expansion coefficient. \({\mathbf{t}}_{e}\) and \({\mathbf{t}}_{e}\) denote the temperature and reference temperature of the element, respectively. \(\phi = [1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0]\) for 2D problems. When the temperature field of the structure is achieved, the relevant thermal loading \({\mathbf{F}}_{{\Delta {\mathbf{T}}}}\) can be obtained. Considering both mechanical and thermal loadings, the topology optimization aiming at minimizing structural compliance can be formulated as follows:

$$\begin{aligned} & \min {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C = {\mathbf{U}}^{{\text{T}}} {\mathbf{KU}}{\text{ = }}\sum\limits_{{e = 1}}^{N} {\left( {{\mathbf{U}}_{e} } \right)^{{\text{T}}} {\mathbf{K}}_{e} {\mathbf{U}}_{e} } \\ & {\text{s.t.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{e = 1}}^{N} {\rho _{e} V_{e} } \le fV_{0} \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{KU}} = {\mathbf{F}} + {\mathbf{F}}_{{\Delta {\mathbf{T}}}} \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{0}} < \rho _{{{\text{min}}}} \le \rho _{e} \le {\text{1,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} e = 1,2, \cdots ,N \\ \end{aligned}$$
(4)

in which \(C\) represents the compliance of the structure. \(V_{e}\) and \(V_{0}\) represent the volume of the element and the structure, respectively, and \(f\) is the volume fraction. \(\rho_{e}^{{}} (e = 1,2, \cdots ,N)\) denotes the design variable of the eth element, while \({\kern 1pt} \rho_{\min }^{{}}\) is the minimum element relative density to avoid singularity.

The density-based SIMP method is applied to solve the topology optimization in Eq. (3), in which the elastic matrix and the thermal stress coefficient (Gao and Zhang 2010) need to be determined by material interpolations:

$${\mathbf{D}}_{e} \left( {\rho _{e} } \right){\text{ = }}E\left( {\rho _{e} } \right){\mathbf{D}}_{0} {\text{ = }}\left( {\rho _{e} } \right)^{p} E_{0} {\mathbf{D}}_{0} ,$$
(5)
$$\beta \left( {\rho_{e} } \right){ = }E\left( {\rho_{e} } \right)\alpha \left( {\rho_{e} } \right){ = }\left( {\rho_{e} } \right)^{p} E_{0} \alpha_{0} ,$$
(6)

in which \({\mathbf{D}}_{0}\) is a constant matrix, while \(E_{0}\) and \(\alpha_{0}\) are the Young’s modulus and the thermal expansion coefficient of the solid material. \(p\) is the penalization factor. The gradient-based optimization algorithm is implemented for updating the design variables, so the sensitivities of the objective function with respect to the design variables are required for the iteration. The sensitivities can be calculated as follows:

$$\frac{{\partial C}}{{\partial \rho _{e} }}{\kern 1pt} = 2{\mathbf{U}}^{{\text{T}}} \frac{{\partial {\mathbf{F}}_{{\Delta {\mathbf{T}}}} }}{{\partial \rho _{e} }} - {\mathbf{U}}^{{\text{T}}} \frac{{\partial {\mathbf{K}}}}{{\partial \rho _{e} }}{\mathbf{U}} .$$
(7)

Substituting Eq. (2)-(3) and Eq. (5)-(6) into Eq. (7), it can be obtained that:

$$\frac{{\partial C}}{{\partial \rho _{e} }}{\kern 1pt} = 2{\mathbf{U}}_{e}^{{\text{T}}} p(\rho _{e} )^{{p - 1}} \alpha _{0} E_{0} \left( {{\mathbf{t}}_{e} - {\mathbf{t}}_{{ref}} } \right)\int_{{V_{e} }} {{\mathbf{B}}_{e}^{{\text{T}}} {\mathbf{D}}_{0} \phi ^{{\text{T}}} dV_{e} } - p\left( {\rho _{e} } \right)^{{p - 1}} E_{0} {\mathbf{U}}_{e}^{{\text{T}}} \left( {\int_{{V_{e} }} {{\mathbf{B}}_{e} {\mathbf{D}}_{0} {\mathbf{B}}_{e} dV_{e} } } \right){\mathbf{U}}_{e} .$$
(8)

3 Robust topology optimization under thermo-mechanical loadings

3.1 Robust topology optimization formulation

Considering random and interval hybrid uncertainties related to material properties and loadings, the structural compliance C is no longer a constant value but a function \(C\left( {{\mathbf{X}},{\mathbf{Y}}} \right)\) with random and interval parameters, in which \({\mathbf{X}} = \left( {X_{1} ,X_{2} ,...,X_{n} } \right)\) represents the random vector and \({\mathbf{Y}} = \left( {Y_{1} ,Y_{2} ,...,Y_{m} } \right)\) represents the interval vector. The robust objective function can then be defined as a linear combination of the mean and standard variance of the structural compliance under the worst case as:

$$g = \max {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu \left( {C\left( {{\mathbf{X}},{\mathbf{Y}}} \right)} \right) + h\sigma \left( {C\left( {{\mathbf{X}},{\mathbf{Y}}} \right)} \right) ,$$
(9)

in which h is the weight factor. The robust topology optimization is formulated as:

$$\begin{aligned} & \min {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g = \max {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu \left( {C\left( {{\mathbf{X}},{\mathbf{Y}}} \right)} \right) + h\sigma \left( {C\left( {{\mathbf{X}},{\mathbf{Y}}} \right)} \right) \\ & {\text{s.t.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{e = 1}}^{N} {\rho _{e} V_{e} } \le fV_{0} \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{K}}\left( {{\mathbf{X}},{\mathbf{Y}}} \right){\mathbf{U}}\left( {{\mathbf{X}},{\mathbf{Y}}} \right) = {\mathbf{F}}\left( {{\mathbf{X}},{\mathbf{Y}}} \right) + {\mathbf{F}}_{{\Delta {\mathbf{T}}}} \left( {{\mathbf{X}},{\mathbf{Y}}} \right) \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{0}} < \rho _{{{\text{min}}}} \le \rho _{e} \le {\text{1,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} e = 1,2, \cdots ,N \\ \end{aligned}$$
(10)

where the weight factor value is set as 1 in this work. Similarly, as the topology optimization in Eq. (4), the above robust topology optimization can also be conveniently solved after obtaining the robust objective function value and the sensitivities of the robust objective function and constraints. However, the hybrid uncertainties cause difficulties in calculating the robust objective function value and the sensitivities with respect to the design variables. In order to efficiently solve the topology optimization problem, an efficient DR-based hybrid uncertainty analysis method is developed, and the explicit sensitivity expressions are achieved based on the uncertainty analysis.

3.2 DR-based hybrid uncertainty analysis method

3.2.1 Hybrid uncertainty analysis based on orthogonal polynomials

In this part, we will introduce the hybrid uncertainty analysis based on orthogonal polynomials, in which the performance function will be approximated using the PC expansion by firstly considering the random uncertainties, and then be expanded by the CI method taking the interval uncertainties into account (Wu et al. 2015). The expansion coefficients for the PC and CI expansions are calculated by integration formations. At first, the random variables \(X_{i} ,i = 1,2, \cdots ,n\) are transformed into standard random variables \(\xi_{i} ,i = 1,2, \cdots ,n\) and interval variables \(Y_{i} ,i = 1,2, \cdots ,m\) are turned into standard interval variables \(\eta_{i} ,i = 1,2, \cdots ,m\) through linear transformations. For an uncertain performance function \(\psi \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right)\) with n random variables \({{\varvec{\upxi}}}{ = }\left[ {\xi_{1} ,\xi_{2} , \cdots ,\xi_{n} } \right]\) and m interval variables \({{\varvec{\upeta}}}{ = }\left[ {\eta_{1} ,\eta_{2} , \cdots ,\eta_{m} } \right]\), the p1th order PC expansion with fixed interval variables can be expressed as:

$$\psi \left( {{\mathbf{\xi }},{\mathbf{\eta }}} \right) = \sum\limits_{{{\mathbf{\chi }}_{{\text{1}}} \in \mathbb{N}^{n} }} {h_{{{\mathbf{\chi }}_{{\text{1}}} }} \left( {\mathbf{\eta }} \right)H_{{{\mathbf{\chi }}_{{\text{1}}} }} \left( {\mathbf{\xi }} \right)} ,$$
(11)

in which \({\mathbf{\chi }}_{1} = \left\{ {{\mathbf{\chi }}_{1} \in \mathbb{N}^{n} :\sum\limits_{{i = 1}}^{n} {\chi _{1}^{i} \le p_{1} } } \right\}\) represents the index set to identify the components of the multivariate polynomials. \(H_{{{\mathbf{\chi }}_{1} }} \left( {\mathbf{\xi }} \right) = \prod\limits_{{i = 1}}^{n} {H_{{\chi _{1}^{i} }} \left( {\xi _{i} } \right)} {\text{, }}\chi _{1}^{i} = 0,1, \cdot \cdot \cdot ,p_{{\text{1}}}\) is the multivariate polynomial built from a set of univariate orthonormal polynomials \(H_{{\chi_{1}^{i} }} \left( {\xi_{i} } \right)\) that satisfies the following orthogonality condition:

$$\left\langle {H_{i} \left( \xi \right),H_{j} \left( \xi \right)} \right\rangle = \int {\omega (\xi )H_{{\chi_{1}^{i} }} (\xi )H_{{\chi_{1}^{j} }} (\xi )} {\text{d}}\xi = \left\langle {H_{i} \left( \xi \right),H_{j} \left( \xi \right)} \right\rangle \delta_{ij} ,$$
(12)

where \(\omega (\xi )\) is the weighting function corresponding to the type of the orthogonal polynomial, \(\delta_{ij}\) is the Kronecker delta. For standard random variable \(\xi\), the base function is Hermite polynomial, and the corresponding weighting function \(\omega_{H} (\xi ) = \frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}\xi^{2} }}\). \(h_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} \left( {{\varvec{\upeta}}} \right)\) is the expansion coefficient which can be calculated by the projection method:

$$h_{{{\mathbf{\chi }}_{{\mathbf{1}}} }} \left( {\mathbf{\eta }} \right) = \left( {\prod\limits_{{i = 1}}^{n} {\frac{1}{{\left\langle {H_{{\chi _{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\int_{{ - \infty }}^{{ + \infty }} { \cdot \cdot \cdot } \int_{{ - \infty }}^{{ + \infty }} {\left( {\prod\limits_{{i = 1}}^{n} {\omega _{H} \left( {\xi _{i} } \right)} } \right)\psi \left( {{\mathbf{\xi }},{\mathbf{\eta }}} \right)} H_{{{\mathbf{\chi }}_{{\mathbf{1}}} }} \left( {\mathbf{\xi }} \right){\text{d}}\xi _{1} \cdot \cdot \cdot {\text{d}}\xi _{n} .$$
(13)

The above Eq. (13) is a multi-dimensional integration function and it can be calculated by the Gaussian quadrature. The multivariate Gaussian quadrature points are achieved by a tensor product of univariate integration points, so the number of integration points increases exponentially with the number of uncertain variables.

From the PC expansion in Eq. (11), it can be seen that the performance function with hybrid uncertainties can be approximated by polynomial terms and the corresponding expansion coefficients. Considering the interval uncertain variables, the coefficients in Eq. (13) can be approximated using the p2th order Chebyshev polynomials:

$$h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right) = \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} }} {c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} .$$
(14)

Thus, the uncertain function \(\psi \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right)\) can be rewritten as:

$$\psi \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right) = \sum\limits_{{{{\varvec{\upchi}}}_{{1}} \in {\mathbb{N}}^{n} }} {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} }} {c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} H_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upxi}}} \right)} ,$$
(15)

where \({{\varvec{\upchi}}}_{2}\) is the index set and \(C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right) = \prod\limits_{i = 1}^{m} {C_{{\chi_{2}^{i} }} \left( {\eta_{i} } \right)} ,\chi_{2}^{i} = 0,1, \cdot \cdot \cdot ,p_{{2}}\) denote the multivariate Chebyshev polynomials built from univariate Chebyshev polynomial:

$$C_{{\chi_{2}^{i} }} \left( {\eta_{i} } \right){ = }\cos \left( {\chi_{2}^{i} \left[ {\theta_{i} } \right]} \right),$$
(16)

where \(\theta_{i} = \arccos \left( {\eta_{i} } \right) = \left[ {0,\pi } \right]\). The inner product of the univariate Chebyshev polynomial is as follows:

$$\left\langle {C_{i} \left( \eta \right)^{2} } \right\rangle = \left\{ {\begin{array}{*{20}c} {\pi ,i = 0} \\ {\frac{\pi }{2},i \ne 0} \\ \end{array} } \right..$$
(17)

Similarly, the Chebyshev expansion coefficient \(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\) can be calculated by the projection method in a multi-dimensional integration formation:

$$c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} = \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} ,$$
(18)

where \(\omega_{C} \left( \eta \right) = \frac{1}{{\sqrt {1 - \eta^{2} } }}\) is the weighting function corresponding to the Chebyshev polynomial. The Eq. (18) is also a multi-dimensional integration in which \(h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right)\) is calculated by Eq. (13). It can be seen that a nested multi-dimensional integration is required to evaluate the coefficient \(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\). Hence, the computational burden becomes extremely heavy for the hybrid uncertainty analysis especially for problems with a large number of uncertain variables.

Taken advantage of the orthogonality of the polynomials, the mean and variance of the performance function can be acquired after the evaluation of the expansion coefficients:

$$\mu \left( {\psi \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right)} \right) = h_{0} \left( {{\varvec{\upeta}}} \right) = \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} }} {c_{{0,{{\varvec{\upchi}}}_{2} }} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} ,$$
(19)
$$\sigma^{2} \left( {\psi \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right)} \right) = \sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}} {\left( {h_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} \right)}^{2} \left\langle {H_{{{{\varvec{\upchi}}}_{{1}} }} \left( \xi \right)^{2} } \right\rangle = \sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}} {\left( {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} }} {c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} } \right)}^{2} \left\langle {H_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} (\xi )^{2} } \right\rangle .$$
(20)

Based on the bounded characteristic of the univariate Chebyshev polynomials, it can be seen that \(C_{0} \left( \eta \right) = 1\) and \(C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right) = [ - 1,1]\). Hence, the bounds of the mean and standard variance can be easily approximated as follows:

$$\underline{\mu } \left( {\psi \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right)} \right) = c_{0,0} - \left( {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\left| {c_{{0,{{\varvec{\upchi}}}_{2} }} } \right|} } \right),\overline{\mu }(\psi ({{\varvec{\upxi}}},{{\varvec{\upeta}}})) = c_{0,0} + \left( {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}}^{{}} {\left| {c_{{0,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} } \right|} } \right),$$
(21)
$$\begin{aligned} & \underline {\sigma } (\psi ({{\varvec{\upxi}}},{{\varvec{\upeta}}})) = \sqrt {\sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}}^{{}} {\left( {c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,0}} - \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}}^{{}} {\left| {c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} } \right|} } \right)}^{2} \left\langle {H_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} (\xi )^{2} } \right\rangle } \\ & \overline{\sigma }(\psi ({{\varvec{\upxi}}},{{\varvec{\upeta}}})) = \sqrt {\sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}}^{{}} {\left( {c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,0}} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}}^{{}} {\left| {c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} } \right|} } \right)}^{2} \left\langle {H_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} (\xi )^{2} } \right\rangle } . \\ \end{aligned}$$
(22)

In Eqs. (21) and (22), each interval term of the expansion is assumed to reach their bounds simultaneously. In this case, the worst-case mean and standard variance values calculated from the proposed method is not with respect to a certain interval realization, but a bound estimation for an interval function with given interval variations. However, this approximation scheme provides a same trend of a direct evaluations of the interval functions in Eqs. (19) and (20), so it can be used to formulate the robust objective function value in Eq. (9).

3.2.2 Coefficient evaluation by DR integration

The coefficients are obtained through multi-dimensional integrations in the uncertainty analysis based on orthogonal polynomials using the projection method. Considering the random and interval hybrid uncertainties, the coefficients in the expansion are evaluated by nested multi-dimensional integrations. During the process of the uncertainty analysis, coefficient evaluation is the main time-consuming part in which a large number of function calls are required corresponding to the integration points or samples. In this work, the uncertain parameters in structures are considered to have a small level of variations, and the univariate DR method is introduced to calculate the expansion coefficients. Follow the main idea of the univariate DR method, the multi-dimensional performance function can be approximated by a series of one-dimensional functions. Hence, the multi-dimensional integration can be expressed by a series of one-dimensional integrations, and the exponentially increasing computational cost can be greatly relieved.

Typically, by the univariate DR method, the multi-dimensional problem will be transformed into a series of one-dimensional problems. The uncertain function can be approximated as (Rahman and Xu 2004):

$$C\left( {\mathbf{Z}} \right) \cong \sum\limits_{j = 1}^{n} {\hat{C}_{j} \left( {\mathbf{Z}} \right) - \left( {n - 1} \right)C\left( {u_{1} , \cdot \cdot \cdot ,u_{n} } \right)} ,$$
(23)

in which \({\mathbf{Z}} = \left[ {Z_{1} ,Z_{2} , \cdots ,Z_{n} } \right]\) denotes the random or interval vector, \(u_{j}\) represents the mean value or the midpoint value of the variable \(Z_{j}\), \(\hat{C}_{j} \left( {\mathbf{Z}} \right) = C\left( {u_{1} , \cdot \cdot \cdot ,u_{j - 1} ,Z_{j} ,u_{j + 1} , \cdot \cdot \cdot ,u_{n} } \right)\). After this approximation, the multi-dimensional Gauss integral can be changed to a one-dimensional Gauss integral. By applying Eq. (23) for \(h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right)\), the Eq. (18) can be rewritten as:

$$\begin{gathered} c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} = \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)\left( {\sum\limits_{j = 1}^{m} {\hat{h}_{{{{\varvec{\upchi}}}_{{1}} ,j}} \left( {{\varvec{\upeta}}} \right) - \left( {m - 1} \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)} } \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} \\ = \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)\left( {\sum\limits_{j = 1}^{m} {\hat{h}_{{{{\varvec{\upchi}}}_{{1}} ,j}} \left( {{\varvec{\upeta}}} \right)} } \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} \\ - \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\left( {m - 1} \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right) \cdot \int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} . \\ \end{gathered}$$
(24)

The coefficient \(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\) can be calculated from two terms. For the second term, it can be figured out that the later part of this term can be expressed as follows when and only when \(\chi_{2}^{1} = \chi_{2}^{2} = \cdot \cdot \cdot = \chi_{2}^{n} = 0\) due to the orthogonality of the Chebyshev polynomial:

$$\int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} = \left\langle {C_{0} \left( \eta \right)^{2} } \right\rangle^{m} = \pi^{m} .$$
(25)

For the first term of \(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\):

$$\begin{gathered} \int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)\left( {\sum\limits_{j = 1}^{m} {\hat{h}_{{{{\varvec{\upchi}}}_{{1}} ,j}} \left( {{\varvec{\upeta}}} \right)} } \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} \\ = \int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)\left( {\sum\limits_{j = 1}^{m} {h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{j - 1}^{c} ,\eta_{j} ,\eta_{j + 1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)} } \right)} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} , \\ \end{gathered}$$
(26)

in which \(\eta_{j}^{c}\) is the midpoint of the interval variable \(\eta_{j}\). It can be seen that Eq. (26) composed of m integrations, and the jth integration can be rewritten as:

$$\begin{gathered} \underbrace {{\int_{ - 1}^{ + 1} { \cdot \cdot \cdot \int_{ - 1}^{ + 1} {} } }}_{m}\left( {\prod\limits_{i = 1}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{j - 1}^{c} ,\eta_{j} ,\eta_{j + 1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{m} \\ = \underbrace {{\int_{ - 1}^{ + 1} { \cdot \cdot \cdot \int_{ - 1}^{ + 1} {} } }}_{m - 1}\left( {\prod\limits_{i = 1,i \ne j}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)\left( {\prod\limits_{i = 1,i \ne j}^{m} {C_{{\chi_{{_{2} }}^{i} }} \left( {\eta_{i} } \right)} } \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{j - 1} {\text{d}}\eta_{j + 1} \cdot \cdot \cdot {\text{d}}\eta_{m} \\ \cdot \int_{ - 1}^{ + 1} {\omega_{C} \left( {\eta_{j} } \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{j - 1}^{c} ,\eta_{j} ,\eta_{j + 1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)} C_{{\chi_{{_{2} }}^{j} }} \left( {\eta_{j} } \right){\text{d}}\eta_{j} . \\ \end{gathered}$$
(27)

To make the description clear, we also consider Eq. (27) as two parts. The first part of Eq. (27) can be expressed as follows when and only when \(\chi_{2}^{1} = \cdot \cdot \cdot = \chi_{2}^{j - 1} = \chi_{2}^{j + 1} = \cdot \cdot \cdot = \chi_{2}^{m} = 0\):

$$\int_{ - 1}^{ + 1} { \cdot \cdot \cdot } \int_{ - 1}^{ + 1} {\left( {\prod\limits_{i = 1,i \ne j}^{m} {\omega_{C} \left( {\eta_{i} } \right)} } \right)} \left( {\prod\limits_{i = 1,i \ne j}^{m} {C_{{\chi_{{_{2} }}^{i} }} \left( {\eta_{i} } \right)} } \right){\text{d}}\eta_{1} \cdot \cdot \cdot {\text{d}}\eta_{j - 1} {\text{d}}\eta_{j + 1} \cdot \cdot \cdot {\text{d}}\eta_{m} = \left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle^{m - 1} = \pi^{m - 1} .$$
(28)

The second part of the term \(\int_{ - 1}^{ + 1} {\omega_{C} \left( {\eta_{j} } \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{j - 1}^{c} ,\eta_{j} ,\eta_{j + 1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)} C_{{\chi_{{_{2} }}^{j} }} \left( {\eta_{j} } \right){\text{d}}\eta_{j}\) can be evaluated easily by the Gaussian quadrature. Hence, Eq. (24) can be rewritten as follows when \(\chi_{2}^{1} = \chi_{2}^{2} = \cdot \cdot \cdot = \chi_{2}^{m} = 0\):

$$\begin{gathered} c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} = \pi^{m - 1} \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\left( {\sum\limits_{j = 1}^{m} {\int_{ - 1}^{ + 1} {\omega_{C} \left( {\eta_{j} } \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{j - 1}^{c} ,\eta_{j} ,\eta_{j + 1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)} C_{{\chi_{{_{2} }}^{j} }} \left( {\eta_{j} } \right){\text{d}}\eta_{j} } } \right) \\ + \pi^{m} \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\left( {m - 1} \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right), \\ \end{gathered}$$
(29)

When \(\chi_{2}^{1} = \cdot \cdot \cdot = \chi_{2}^{j - 1} = \chi_{2}^{j + 1} = \cdot \cdot \cdot = \chi_{2}^{m} = 0\) but \(\chi_{{_{2} }}^{j} \ne {0}\), Eq. (24) is:

$$c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} = \pi^{m - 1} \left( {\prod\limits_{i = 1}^{m} {\frac{1}{{\left\langle {C_{{\chi_{2}^{i} }} \left( \eta \right)^{2} } \right\rangle }}} } \right)\int_{ - 1}^{ + 1} {\omega_{C} \left( {\eta_{j} } \right)h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {\eta_{1}^{c} , \cdot \cdot \cdot ,\eta_{j - 1}^{c} ,\eta_{j} ,\eta_{j + 1}^{c} , \cdot \cdot \cdot ,\eta_{m}^{c} } \right)} C_{{\chi_{{_{2} }}^{j} }} \left( {\eta_{j} } \right){\text{d}}\eta_{j} ,$$
(30)

When \(\sum\limits_{i = 1,i \ne j}^{m} {\chi_{{_{2} }}^{i} } \ne 0\), \(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} = 0\).

It can be seen that the coefficient \(h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right)\) is required when calculate the \(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\). \(h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right)\) is also a multi-dimensional integration by Eq. (13), which can similarly be achieved by introduction the DR method:

$$\begin{gathered} h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right) = \left( {\prod\limits_{i = 1}^{n} {\frac{1}{{\left\langle {H_{{\chi_{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\int_{ - \infty }^{ + \infty } { \cdot \cdot \cdot } \int_{ - \infty }^{ + \infty } {\left( {\prod\limits_{i = 1}^{n} {\omega_{H} \left( {\xi_{i} } \right)} } \right)\left( {\sum\limits_{j = 1}^{n} {\hat{\psi }_{j} \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right) - \left( {n - 1} \right)\psi \left( {\xi_{{_{1} }}^{\mu } , \cdot \cdot \cdot ,\xi_{{_{n} }}^{\mu } ,{{\varvec{\upeta}}}} \right)} } \right)} H_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} \left( {{\varvec{\upxi}}} \right){\text{d}}\xi_{1} \cdot \cdot \cdot {\text{d}}\xi_{n} \\ = \left( {\prod\limits_{i = 1}^{n} {\frac{1}{{\left\langle {H_{{\chi_{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\int_{ - \infty }^{ + \infty } { \cdot \cdot \cdot } \int_{ - \infty }^{ + \infty } {\left( {\prod\limits_{i = 1}^{n} {\omega_{H} \left( {\xi_{i} } \right)} } \right)\left( {\sum\limits_{j = 1}^{n} {\hat{\psi }_{j} \left( {{{\varvec{\upxi}}},{{\varvec{\upeta}}}} \right)} } \right)} H_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} \left( {{\varvec{\upxi}}} \right){\text{d}}\xi_{1} \cdot \cdot \cdot {\text{d}}\xi_{n} \\ - \left( {\prod\limits_{i = 1}^{n} {\frac{1}{{\left\langle {H_{{\chi_{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\left( {n - 1} \right)\psi \left( {\xi_{{_{1} }}^{\mu } , \cdot \cdot \cdot ,\xi_{{_{n} }}^{\mu } ,{{\varvec{\upeta}}}} \right) \cdot \int_{ - \infty }^{ + \infty } { \cdot \cdot \cdot } \int_{ - \infty }^{ + \infty } {\left( {\prod\limits_{i = 1}^{n} {\omega_{H} \left( {\xi_{i} } \right)} } \right)H_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} }} \left( {{\varvec{\upxi}}} \right){\text{d}}\xi_{1} \cdot \cdot \cdot {\text{d}}\xi_{n} } . \\ \end{gathered}$$
(31)

Similarly, repeating the process in Eqs. (25)-(28), it can be concluded that when \(\chi_{1}^{1} = \chi_{1}^{2} = \cdot \cdot \cdot = \chi_{1}^{n} = 0\):

$$\begin{gathered} h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right) = \left( {\prod\limits_{i = 1}^{n} {\frac{1}{{\left\langle {H_{{\chi_{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\sum\limits_{j = 1}^{n} {\left( {\int_{ - \infty }^{ + \infty } {\omega_{H} \left( {\xi_{j} } \right)\psi \left( {\xi_{1}^{\mu } , \cdot \cdot \cdot ,\xi_{j - 1}^{\mu } ,\xi_{j} ,\xi_{j + 1}^{\mu } , \cdot \cdot \cdot ,\xi_{n}^{\mu } } \right)H_{{\chi_{1}^{j} }} \left( {\xi_{j} } \right){\text{d}}\xi_{j} } } \right)} \\ + \left( {\prod\limits_{i = 1}^{n} {\frac{1}{{\left\langle {H_{{\chi_{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\left( {n - 1} \right)\psi \left( {\xi_{1}^{\mu } , \cdot \cdot \cdot ,\xi_{n}^{\mu } } \right), \\ \end{gathered}$$
(32)

When \(\chi_{1}^{1} = \cdot \cdot \cdot = \chi_{1}^{j - 1} = \chi_{1}^{j + 1} = \cdot \cdot \cdot = \chi_{1}^{n} = 0\) while \(\chi_{1}^{j} \ne {0}\):

$$h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right) = \left( {\prod\limits_{i = 1}^{n} {\frac{1}{{\left\langle {H_{{\chi_{1}^{i} }} \left( \xi \right)^{2} } \right\rangle }}} } \right)\int_{ - \infty }^{ + \infty } {\omega_{H} \left( {\xi_{j} } \right)\psi \left( {\xi_{1}^{\mu } , \cdot \cdot \cdot ,\xi_{j - 1}^{\mu } ,\xi_{j} ,\xi_{j + 1}^{\mu } , \cdot \cdot \cdot ,\xi_{n}^{\mu } } \right)H_{{\chi_{1}^{j} }} \left( {\xi_{j} } \right){\text{d}}\xi_{j} } ,$$
(33)

When \(\sum\limits_{i = 1,i \ne j}^{n} {\chi_{{_{1} }}^{i} } \ne 0\), \(h_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upeta}}} \right) = 0\).

Therefore, by the proposed DR-based hybrid uncertainty analysis method, the coefficients of the hybrid expansion can be efficiently obtained, and then the mean and standard variance of the uncertain function (i.e., the structural compliance) can be easily approximated by Eqs. (21) and (22). For a problem with n random variables and m interval variables, 3n+m integration points are required for the full tensor product multi-dimensional integration if the univariate integration points are chosen as three, while by the proposed method, only (3n + 1) × (3 m + 1) function calls are needed during the hybrid uncertainty analysis process. Thus, the exponentially increasing computational cost can be greatly relieved to improve the computational efficiency. At the same time, very good computational accuracy can also be kept for the analysis which will be illustrated in the numerical examples.

3.3 The solving of the robust topology optimization

By applying the hybrid uncertainty analysis method, the interval mean and variance of the structural compliance can be calculated by Eq. (21) and (22), and then the robust objective function can be obtained:

$$g = c_{0,0} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\left| {c_{{0,{{\varvec{\upchi}}}_{2} }} } \right|} + \sqrt {\sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}} {\left( {c_{{{{\varvec{\upchi}}}_{{1}} ,0}} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\left| {c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{{2}} }} } \right|} } \right)^{2} } \left\langle {H_{{{{\varvec{\upchi}}}_{{1}} }} (\xi )^{2} } \right\rangle } .$$
(34)

In order to solve the robust topology optimization, the method of moving asymptotes (Svanberg 1987) method is used to update the design variables, and the sensitivities with respect to the design variables are:

$$\frac{\partial g}{{\partial \rho_{e} }} = \frac{{\partial c_{0,0} }}{{\partial \rho_{e} }} + \left( {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\frac{{\partial \left| {c_{{0,{{\varvec{\upchi}}}_{2} }} } \right|}}{{\partial \rho_{e} }}} } \right) + \frac{\gamma }{{\overline{\sigma }}}\sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}} {\left( {\frac{{\partial c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,0}} }}{{\partial \rho_{e} }} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\frac{{\partial \left| {c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} } \right|}}{{\partial \rho_{e} }}} } \right)} ,$$
(35)

in which:

$$\gamma = \sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}} {\left( {c_{{{{\varvec{\upchi}}}_{{1}} ,0}} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\left| {c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{{2}} }} } \right|} } \right)} \left\langle {H_{{{{\varvec{\upchi}}}_{{1}} }} (\xi )^{2} } \right\rangle .$$
(36)

The sensitivities can be rewritten as:

$$\begin{gathered} \frac{\partial g}{{\partial \rho_{e} }} = \frac{{\partial c_{0,0} }}{{\partial \rho_{e} }} + \left( {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}} {\left( {\frac{{\partial c_{{0,{{\varvec{\upchi}}}_{2} }} }}{{\partial \rho_{e} }}\left( {{\text{sign}}(c_{{0,{{\varvec{\upchi}}}_{2} }} ) + \frac{{\partial {\text{sign}}(c_{{0,{{\varvec{\upchi}}}_{2} }} )}}{{\partial \rho_{e} }}c_{{0,{{\varvec{\upchi}}}_{2} }} } \right)} \right)} } \right) \\ + \frac{\gamma }{{\overline{\sigma }}}\sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}} {\left( {\frac{{\partial c_{{{{\varvec{\upchi}}}_{{1}} ,0}} }}{{\partial \rho_{e} }} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}}^{{}} {\frac{{\partial c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{{2}} }} }}{{\partial \rho_{e} }}\left( {{\text{sign}}(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} ) + \frac{{\partial {\text{sign}}(c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} )}}{{\partial \rho_{e} }}c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} } \right)} } \right)} . \\ \end{gathered}$$
(37)

Since sign function is not differentiable at x = 0, hyperbolic tangent function is used to approximate the sign function. The sensitivities are then be expressed as:

$$\begin{array}{*{20}l} {\frac{{\partial g}}{{\partial \rho _{e} }} = \frac{{\partial c_{{0,0}} }}{{\partial \rho _{e} }} + \left( {\sum\limits_{{{\mathbf{\chi }}_{2} \in \mathbb{N}^{m} ,{\mathbf{\chi }}_{2} \ne 0}} {\left( {\frac{{\partial c_{{0,{\mathbf{\chi }}_{2} }} }}{{\partial \rho _{e} }}\left( {\tanh (\ell c_{{0,{\mathbf{\chi }}_{2} }} ) + \frac{{\partial \tanh (\ell c_{{0,{\mathbf{\chi }}_{2} }} )}}{{\partial \rho _{e} }}c_{{0,{\mathbf{\chi }}_{2} }} } \right)} \right)} } \right)} \hfill \\ {\quad \;\; + \frac{\gamma }{\bar{\sigma }}\sum\limits_{{{\mathbf{\chi }}_{1} \in \mathbb{N}^{n} ,{\mathbf{\chi }}_{1} \ne 0}} {\left( {\frac{{\partial c_{{{\mathbf{\chi }}_{{\text{1}}} ,0}} }}{{\partial \rho _{e} }} + \sum\limits_{{{\mathbf{\chi }}_{2} \in \mathbb{N}^{m} ,{\mathbf{\chi }}_{2} \ne 0}} {\frac{{\partial c_{{{\mathbf{\chi }}_{{\text{1}}} ,{\mathbf{\chi }}_{{\text{2}}} }} }}{{\partial \rho _{e} }}\left( {\tanh (\ell c_{{{\mathbf{\chi }}_{{\text{1}}} ,{\mathbf{\chi }}_{2} }} ) + \frac{{\partial \tanh (\ell c_{{{\mathbf{\chi }}_{{\text{1}}} ,{\mathbf{\chi }}_{2} }} )}}{{\partial \rho _{e} }}c_{{{\mathbf{\chi }}_{{\text{1}}} ,{\mathbf{\chi }}_{2} }} } \right)} } \right)} } \hfill \\ {\quad \;\; = \frac{{\partial c_{{0,0}} }}{{\partial \rho _{e} }} + \left( {\sum\limits_{{{\mathbf{\chi }}_{2} \in \mathbb{N}^{m} ,{\mathbf{\chi }}_{2} \ne 0}} {\left( {\frac{{\partial c_{{0,{\mathbf{\chi }}_{2} }} }}{{\partial \rho _{e} }}\left( {\tanh (\ell c_{{0,{\mathbf{\chi }}_{2} }} ) + \ell c_{{0,{\mathbf{\chi }}_{{\mathbf{2}}} }} {\text{sech}}^{{\text{2}}} \left( {\ell c_{{0,{\mathbf{\chi }}_{{\mathbf{2}}} }} } \right)} \right)} \right)} } \right)} \hfill \\ {\quad \;\; + \frac{\gamma }{{\bar{\sigma }}}\sum\limits_{{{\mathbf{\chi }}_{1} \in \mathbb{N}^{n} ,{\mathbf{\chi }}_{1} \ne 0}} {\left( {\frac{{\partial c_{{{\mathbf{\chi }}_{{\text{1}}} ,0}} }}{{\partial \rho _{e} }} + \sum\limits_{{{\mathbf{\chi }}_{2} \in \mathbb{N}^{m} ,{\mathbf{\chi }}_{2} \ne 0}} {\frac{{\partial c_{{{\mathbf{\chi }}_{{\text{1}}} ,{\mathbf{\chi }}_{{\text{2}}} }} }}{{\partial \rho _{e} }}\left( {\tanh (\ell c_{{{\mathbf{\chi }}_{{\text{1}}} ,{\mathbf{\chi }}_{2} }} ) + \ell c_{{{\mathbf{\chi }}_{{\mathbf{1}}} ,{\mathbf{\chi }}_{{\mathbf{2}}} }} {\text{sech}}^{{\text{2}}} \left( {\ell c_{{{\mathbf{\chi }}_{{\mathbf{1}}} ,{\mathbf{\chi }}_{{\mathbf{2}}} }} } \right)} \right)} } \right)} } \hfill \\ \end{array} .$$
(38)

in which the constant \(\ell\) is set as 100 here.

On the other hand, considering the uncertainties for the sensitivities in Eq. (8), the deterministic sensitivity function can also be expanded as follows:

$$\frac{\partial C}{{\partial \rho_{e} }} = \sum\limits_{{{{\varvec{\upchi}}}_{{1}} \in {\mathbb{N}}^{n} }} {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} }} {\gamma_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} H_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upxi}}} \right)} ,$$
(39)

where \(\gamma_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\) represent the expansion coefficients. At the same time, by differentiating Eq. (15) in regard to the structural compliance with respect to the design variables:

$$\frac{\partial C}{{\partial \rho_{e} }} = \sum\limits_{{{{\varvec{\upchi}}}_{{1}} \in {\mathbb{N}}^{n} }} {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} }} {\frac{{\partial c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{{2}} }} }}{{\partial \rho_{e} }}C_{{{{\varvec{\upchi}}}_{2} }} \left( {{\varvec{\upeta}}} \right)} H_{{{{\varvec{\upchi}}}_{{1}} }} \left( {{\varvec{\upxi}}} \right)} .$$
(40)

It can be figured out that:

$$\frac{{\partial c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{{2}} }} }}{{\partial \rho_{e} }} = \gamma_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}$$
(41)

Hence, the values of \(\gamma_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }}\) are obtained after the uncertainty analysis of the deterministic sensitivity functions in Eq. (8). Finally, the sensitivities of the robust objective function can be calculated by:

$$\begin{gathered} \frac{\partial g}{{\partial \rho_{e} }} = \gamma_{0,0} + \left( {\sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}}^{{}} {\left( {\gamma_{{0,{{\varvec{\upchi}}}_{2} }} \left( {\tanh (\ell c_{{0,{{\varvec{\upchi}}}_{2} }} ) + \ell c_{{0,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} {\text{sech}}^{{2}} \left( {\ell c_{{0,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} } \right)} \right)} \right)} } \right) \\ + \frac{\gamma }{{\overline{\sigma }}}\sum\limits_{{{{\varvec{\upchi}}}_{1} \in {\mathbb{N}}^{n} ,{{\varvec{\upchi}}}_{1} \ne 0}}^{{}} {\left( {\gamma_{{{{\varvec{\upchi}}}_{{1}} ,0}} + \sum\limits_{{{{\varvec{\upchi}}}_{2} \in {\mathbb{N}}^{m} ,{{\varvec{\upchi}}}_{2} \ne 0}}^{{}} {\gamma_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} \left( {\tanh (\ell c_{{{{\varvec{\upchi}}}_{{1}} ,{{\varvec{\upchi}}}_{2} }} ) + \ell c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} {\text{sech}}^{{2}} \left( {\ell c_{{{{\varvec{\upchi}}}_{{\mathbf{1}}} ,{{\varvec{\upchi}}}_{{\mathbf{2}}} }} } \right)} \right)} } \right)} . \\ \end{gathered}$$
(42)

4 Numerical examples

In this part, three numerical examples are provided in this part to verify the proposed robust topology optimization method in this work. The material properties and loadings related to thermo-mechanical coupled field are considered as hybrid uncertain variables. For comparison, the deterministic topology optimization results are also provided, in which the random variables are set as the mean values and the interval variables are set as the midpoint values. A double loop sampling method termed as Monte-Carlo-Scanning (MCS) test has been applied to verify the hybrid uncertainty analysis results of the DR-based method, in which the Monte Carlo (MC) simulation is applied in the inner loop for the random variables and the scanning method is used in the outer loop for the interval variables (Wu et al. 2015). In the MC simulation, the sampling points of the random variables are obtained randomly from the corresponding probability functions. By the scanning method, equidistant points are generated for each interval variable to formulate different combinations of the interval variables. For an uncertain performance function with n random variables and m interval variables, if the number of Monte Carlo sampling points of the random variables is \(N_{0}\), and the scanning points in each dimension of interval variables is \(q\), then the total number of sampling points is \(N_{0} \times q^{m}\). In this work, 10,000 random sample points are selected for random variables and 10 equidistant points for the interval variables are chosen in each dimension.

4.1 Example 1

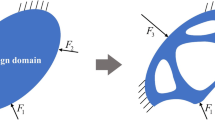
A cantilever beam with 1 m length and 0.45 m height is investigated in this example. The left side of the beam is fixed, \(F_{1}\) and \(F_{2}\) are applied on the upper right and the lower right corners, as shown in Fig. 1. The magnitudes of the two loads are random normal variables with mean values \(\left[ {{7}00{\text{KN,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {7}00{\text{KN}}} \right]\) and standard variances \(\left[ {{7}0{\text{KN,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {7}0{\text{KN}}} \right]\). The directions of the two loads \(\theta_{1}\) and \(\theta_{2}\) are interval variables. \(\theta_{1} { = }\left[ { - \pi /{2}0, \, \pi /{2}0} \right]\) is the angle of the direction of \(F_{1}\) and the horizontal direction, and \(\theta_{2} { = }\left[ { - \pi /{2}0, \, \pi /{2}0} \right]\) is the angle of the direction of \(F_{2}\) and the vertival direction. A temperature rise \(\Delta T\sim N\left( {1,\,0.1} \right)\) °C is considered over the design domain. The elastic tensor \(E{ = 70}\,{\text{GPa}}\), the Poisson’s ratio \(\nu { = }0.3\), and thermal expansion coefficient \(\alpha = {2}.{3} \times {1}0^{{ - {5}}} /\)°C. The structure is discretized by 45 × 100 four-node quadrilateral elements, and the volume fraction is set as 0.5.

Fig. 1
figure 1

Design domain and boundary condition

Full size image

There are three random variables and two interval variables in this example. The temperature rise related to the thermal field and the applied loadings related to the mechanical field are regarded as hybrid uncertain parameters. The deterministic and robust optimization design results are given in Fig. 2, in which a(1) and b(1) are the structural topological designs of deterministic topology optimization and robust topology optimization, respectively, and a(2) and b(2) are the iteration histories of the optimization process of deterministic topology optimization and robust topology optimization, respectively. It is obvious to see that the design considering uncertainties is different from the design under deterministic assumption, for example, the local topologies from the central lower boundary to the right top of the robust result in Fig. 2 b(1) is more straight than the determinist result in Fig. 2 a(1). It is noticed that the uncertainty parameters would influence the result of the topology optimization. In Fig. 2 a(2), the structural compliance C corresponding to each iteration of robust optimization process is provided. In order to better illustrate the robustness of the intermediate design, the value changes of the mean μ, the standard deviation σ and the robust objective function g are presented in Fig. 2 b(2) in red, pink and blue colors, respectively. The three curves in Fig. 2 b(2) have the similar trend during the robust topology optimization process. After some iterations, the values of the mean, the standard deviation and the robust objective function maintain stable and the optimization process become convergent gradually. Hence, it can be seen that the proposed robust topology optimization method has good stability and convergence.

Fig. 2
figure 2

Optimized results for deterministic and robust designs

Full size image

In order to show the importance and necessity of the optimization considering uncertainties, the uncertain parameters related to material properties and loadings are also considered for the deterministic design. We can then obtain the worst-case mean and standard variance of the structural compliance under the hybrid uncertainties for the deterministic design. For verification purpose, the robust objective values for both deterministic and robust designs obtained by MCS method are also provided. In this case, there are in total \(10^{4} \times 10^{2} { = }10^{6}\) samples in the MCS reference test. There are 100 combinations of the interval variables in the outer loop, and the mean and standard variance of each interval combination can be obtained from the Monte Carlo simulations in the inner loop. The “worst-case” mean and standard variance of the structural compliance are chosen to formulate the robust objective function. In order to clearly show the Monte Carlo simulation results under different combinations of the interval variables, we also list the values corresponding to selected interval combinations. In Tables 1 and 2, the means and standard variances under different realizations of the interval variables are presented, respectively. The worst-case mean and standard variance values in each example are marked in bold type, and these results are used to verify the accuracy of the results achieved from the proposed DR-based hybrid uncertainty analysis method.

Table 1 Means and standard variances of deterministic design
Full size table
Table 2 Means and standard variances of robust design
Full size table

To quantificationally compare the optimized designs of both deterministic and robust cases, we present the robust objective values as well as the corresponding mean and standard variance values obtained from the proposed DR-based method and the MCS reference method under the same hybrid uncertainties for both deterministic and robust designs in the Table 3. Smaller mean and standard variance values indicate better robustness for structural stiffness under uncertainties. The robust objective value of the deterministic design is 908.61, while the value of the robust design is 841.11. That is to say, the robustness of the robust design is 7.4% better than that of the deterministic design. For robust design, the robust objective value is 841.11 calculated by the proposed DR-based method and 837.45 calculated by the MCS method, so the errors of the robust objective function values for both designs are less than 0.5%. The accuracies of the mean value and standard variance values can also be clearly seen in Table 1. During the robust topology optimization process, the hybrid uncertainty analysis is required in each iteration of the robust topology optimization. In this example, if a traditional multi-dimensional integration is applied for the polynomial expansion coefficients, the function calls would be 243 times. By the proposed DR-based method, the number of the FEA calls is only 70 in each evaluation, while still maintain a very good accuracy.

Table 3 Hybrid uncertainty analysis results of optimized designs
Full size table

4.2 Example 2

As shown in Fig. 3, a simply supported beam is considered in this example. The length of the beam is 0.8 m, and the width of the beam is 0.4 m. A temperature rise \(\Delta T\sim N\left( {1,\,0.1} \right)\) °C is considered over the design domain.

Fig. 3
figure 3

Design domain and boundary condition

Full size image

The Poisson’s ratio \(\nu\) is set as 0.3. The elastic tensor and the thermal expansion coefficient are given as random normal variables with mean values \(E{ = 7}0{\text{GPa}}\) and \(\alpha = {2}.{3} \times {1}0^{{ - {5}}} /\)°C, and the variation coefficients are both 0.1. The lower left and lower right corners of the beam are fixed and three mechanical loads \(F_{1} = 300{\text{KN}}\), \(F_{2} = 1000{\text{KN}}\) and \(F_{3} { = }300{\text{KN}}\) are vertically applied on the lower side of the beam at one-fourth, half, and three-fourth points, respectively. The angles of directions of the three external loads and the vertival directions are regarded as interval variables \(\theta_{1} { = }\left[ { - \pi /{2}0, \, \pi /{2}0} \right]\), \(\theta_{2} { = }\left[ { - \pi /{2}0, \, \pi /{2}0} \right]\) and \(\theta_{3} { = }\left[ { - \pi /{2}0, \, \pi /{2}0} \right]\). The structure is discretized by 80 × 40 elements, and the volume fraction is set as 0.4.

The optimized results for deterministic and robust designs are shown in Fig. 4. The topological designs of the deterministic and robust topology optimizations are provided in Fig. 4 a(1) and b(1), and the iteration histories of the deterministic and robust topology optimizations are provided in Fig. 4 a(2) and b(2). In the robust design results, the structure topology in Fig. 4 b(1) is obviously different from the structure topology in Fig. 4 a(1). From Fig. 4 a(1) and b(1), we can intuitively feel that the robust topological design is more stable. Several additional transverse supports appear in the robust design in some local places in the robust design comparing with the deterministic design. These changes may expect to have some positive effects for the structure with uncertainties. To quantificationally compare the deterministic and robust optimized designs, the robust objective function values including the mean and standard variance of the structural compliance for the robust and deterministic design under the same uncertain conditions are given in Table 4. Both the results achieved from the proposed DR-based hybrid uncertainty analysis method and the reference MCS method are provided for comparison. Under the same uncertain conditions, the robust objective function value for the deterministic design is 423.89, which is 6.5% larger than the value for the robust design. By comparison, it can also be seen that the results of the proposed method are quite close to the reference results of MCS. However, the number of the FEA calls are only 100 in the proposed method, while the function calls would be 729 times by traditional multi-dimensional integration. In conclusion, the hybrid uncertainties have important influence on the thermo-mechanical topology optimization. By the proposed RTO method, the robust designs are proved to have better robustness compared with the deterministic ones. It is also verified that the proposed method has very good accuracy and stability (Fig. 5).

Fig. 4
figure 4

Optimized results for deterministic and robust designs

Full size image
Table 4 Hybrid uncertainty analysis results of optimized designs
Full size table
Fig. 5
figure 5

Design domain and boundary condition

Full size image

4.3 Example 3

A two-side clamped beam is investigated in this work. The length of the beam is 0.8 m, and the width of the beam is 0.4 m. A temperature rise \(\Delta T = 1\) °C is considered over the design domain. The elastic tensor \(E{ = 7}0{\text{GPa}}\), the Poisson’s ratio \(\nu { = }0.3\), and thermal expansion coefficient \(\alpha = {2}.{3} \times {1}0^{{ - {5}}} /\)°C. Three mechanical loads are vertically applied on the lower side of the beam at one-fourth, half, and three-fourth points, respectively. The magnitudes of the loads are considered to obey normal distributions with mean values \(F_{1} = 300{\text{KN}}\), \(F_{2} = 800{\text{KN}}\) and \(F_{3} { = }300{\text{KN}}\), and the variation coefficients are 0.1. The directions of the three external loads are regarded to have interval uncertainties. The interval variables \(\theta_{1} ,\theta_{2}\) and \(\theta_{3}\) represent the angles of the direction of the loadings and the vertical directions. The lower bounds and the upper bounds of the interval variables are \(\left[ { - \pi /{2}0, - \pi /{2}0, - \pi /{2}0} \right]\) and \(\left[ {\pi /{2}0,\pi /{2}0,\pi /{2}0} \right]\). The structure is discretized by 80 × 40 elements, and the volume fraction is set as 0.3.

In this example, the loading magnitudes and directions are considered as hybrid uncertain parameters. The robust design is obtained based on the proposed RTO method, and the deterministic design is obtained when the random variables are set as the mean values and the interval variables are set as the midpoint values. The structural topologies and the iteration histories are presented in Fig. 6. It is obvious that the robust design taken the hybrid uncertainties into consideration is different from the deterministic design, so it is important to incorporate uncertainties during the optimization process. In Table 5, we evaluate the robust objective function values for both deterministic and robust design results. The robust objective function value of the deterministic design is 317.15, which is much higher than the robust design. The mean and standard deviation of the deterministic design (284.16 and 32.99, respectively) are both larger than those of the robust design (234.61 and 30.22, respectively). This shows that the robust design performs better than the deterministic design when uncertainty involves. Reference results are also provided by the MCS method in Table 5 to verify the accuracy. For this problem with six uncertain variables, the number of the required FEA calls of the DR-based method is far below that of the traditional multi-integration, but the numerical accuracy is kept well. In summary, the proposed method can get a robust topological design considering hybrid uncertainties, and the method is proved to have good accuracy and calculation efficiency.

Fig. 6
figure 6

Optimized results for deterministic and robust designs

Full size image
Table 5 Hybrid uncertainty analysis results of optimized designs
Full size table

5 Conclusion

In engineering, the structures of advanced equipment generally work under thermo-mechanical coupling field, while the thermal field as well as the mechanical field may both have unneglectable influence on the structural performances. Hybrid uncertainties related to material properties and loadings unavoidably exist in the thermo-mechanical coupled structures, so it is important to study RTO problems for topology optimization incorporating the uncertainties. Considering random and interval hybrid uncertainties, a new robust topology optimization method for structures under thermo-mechanical coupled loadings is proposed in this work. In order to efficiently calculate the statistical moments of the structural compliance, an efficient DR-based orthogonal polynomial expansion method is developed for hybrid uncertainty analysis, in which the multi-dimensional integrations to calculate the expansion coefficients is approximated by a series of univariate integrations. Several numerical examples are provided to verify the effectiveness of the proposed method. It is proved that the robust designs have better robustness than the deterministic designs considering uncertainties. The proposed DR-based hybrid uncertainty analysis method is a general approach that can be applied for structural response analysis in many robust topology optimization problems with hybrid uncertainties. However, for problems with large uncertainties or high non-linearity, the proposed method can be further extended by introducing bivariate or multivariate DR methods to maintain good accuracy as well as good efficiency.