1 Introduction

Structural topology optimization is a mathematical method that determines material layout within a given design space with the purpose of maximizing some structural performances for a given set of constraints (Rozvany et al. 1995). Compared with shape optimization and sizing optimization which deal with predefined configurations, topology optimization can attain any shape within the design space. This leads topology optimization to be one of the most promising development directions in the field of structural optimization (Rozvany 2009; Bendsœ and Sigmund 2003; Deaton and Grandhi 2014). Moreover, topology optimization has been adopted to a wide range of design problems in aerospace, mechanical, bio-chemical, and civil engineering (Liu and Ma 2016; Zhu et al. 2020a; Dehghani et al. 2020; Zhu et al. 2016).

For a continuum topology design problem, the conventional topology optimization formulation uses finite element analysis (FEA) to evaluate the structural performance. In the FEA, the design space is discretized into sub-regions of known shapes (e.g., triangle, square, or hexagonal cells) (Nguyen et al. 2020; Zhu et al. 2020b; Andreassen et al. 2011; Kumar et al. 2020). The material state of each sub-region is modelled as a function of the design variables, which is often known as the mathematical parameterization of the design space (Aulig and Olhofer 2016; Zhu et al. 2020a). The difference between various continuum topology optimization methods lies in their mathematical representations. Up to now, the representations that are used in the field of topology optimization can be roughly categorized into two classes: grid and geometric representation (Wein et al. 2020).

In the grid representation-based topology optimization methods, the allowable design space is firstly discretized into finite elements. The optimization procedure will determine which elements should contain solid material to form the structure and which elements should be void. The first topology optimization method based on this strategy is the so-called homogenization method (Bendsœ and Kikuchi 1988). This approach introduces a void hole into each element with solid material to represent composite material. Each element’s state (void or solid) is determined by three design variables (the size and orientation of the void hole). The presently most popular topology optimization method in grid representation is the SIMP (Solid Isotropic Material Penalization) method (Andreassen et al. 2011; Ferrari and Sigmund 2020). When a topology optimization is performed, it deals with a pure [0,1] problem. However, the algorithm can not deal with Boolean variables. The SIMP method helps to overcome this problem by relaxing the design variables, so intermediate values can be used in the optimization algorithm. To suppress the intermediate material problem, one must penalize the elements with intermediate Young’s moduli (Rozvany 2009). The ESO (Evolutionary Structural Optimization) method has been developed based on the simple idea of gradually removing inefficient material from a structure to obtain the optimal structure. In an ideal structure, the stress at every point is near the same safe level, which leads to a rejection criterion based on the local stress level. Any material under low stress is assumed to be inefficient and therefore, can be removed (Xia et al. 2018; Wang et al. 2020). Although, for the most part, the topology optimization methods use gradient information for searching optima, one can also find papers that use global search, which is called genetic algorithm-based topology optimization (Yoshimura et al. 2017; Boichot and Fan 2016). However, non-gradient topology optimization methods are generally inefficient for solving grid representation-based topology optimization problems where often millions of variables are involved (Sigmund 2011).

The grid representation-based topology optimization methods have reached a great level of maturity over the past decades and have been applied in industrial software (Schramm and Zhou 2006; Qu et al. 2016). However, from the very start, there have existed several numerical instabilities, e.g., checkerboards and mesh-dependence, in the grid representation based topology optimization methods (Sigmund and Petersson 1998). Precautions must be taken to deal with such instabilities (Bendsœ and Sigmund 2003). Since early 2000, researchers started to do topology optimization using the propagation of structural boundaries (Osher and Santosa 2001; Wang et al. 2003a; Allaire et al. 2004). In this case, intermediate densities can be completely avoided. This kind of topology optimization method can be regarded as the geometric representation based method. In such a method, the structural geometry is defined by properties of a set of movable shape primitives. It uses geometry mapping to connect the design variable and the phenotypic finite element mesh. Instead of the number of finite elements, the potential structural complexity only depends on the number of shape primitives. This can inherently avoid mesh dependency and checkerboard patterns that are inevitable in the grid representation based methods (van Dijk et al. 2013; Zhu et al. 2013; Yamasaki et al. 2010). A typical method that uses this idea is the level set method (LSM) (Wang et al. 2003a; Allaire et al. 2004; Yamada et al. 2010). The LSM was originally introduced by Osher and Sethian (Osher and Sethian 1988; Osher and Fedkiw 2006). The seminal works incorporating LSMs into structural optimization can be found in Osher and Santosa (2001). Then the method is further developed in Allaire et al. (2004) and Wang et al. (2003a) in which the optimized structural configuration is obtained by solving a Hamilton-Jacobi partial differential equation. Recently developed LSMs are quite different from the conventional one. Examples can be found in Jiang and Chen (2017) where the level set function is defined by using a series of radial basis functions, or in Kim et al. (2020) where a reaction-diffusion equation is used to update the level set function. The LSM utilizes a level set function to represent the structural boundaries implicitly. Although a smooth structural boundary can be obtained, it is difficult to establish a direct relationship between the optimized results and the computer-aided design (CAD) system (Guo et al. 2016). In order to overcome this issue, the moving morphable component (MMC)-based methods which allow one to conduct topology optimization in an explicit and geometrical way have been developed (Xu et al. 2014; Guo et al. 2016).

These methods use explicit geometrical representation in which the design problem is formulated using a set of morphable components, and the optimized structural topologies are obtained by optimizing shapes, sizes, and locations of these components (Zhu et al. 2018; Yang and Huang 2020). Over the years, the effectiveness of the MMC-based topology optimization method has been demonstrated through the use of different component geometries, e.g., moving morphable bars (Hoang and Jang 2017), moving morphable voids (Zhang et al. 2019), extruded geometric components (Hoang and Nguyen-Xuan 2020), adaptive geometric component (Hoang et al. 2020a; Hoang et al. 2020b), and curved skeletons (Guo et al. 2016). In addition, the MMC-based topology optimization methods have also been applied for the solving of various problems, such as minimum length scale control (Wang et al. 2019), nonlinear structures (Zhu et al. 2018), stress constraints (Zhang et al. 2018b), multi-material (Zhang et al. 2018c), thermal-fluid problem (Yu et al. 2019), and isogeometric topology optimization (Xie et al. 2020).

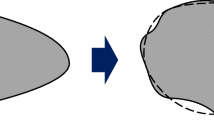
However, in the conventional MMC-based methods, invalid topologies often occur (input and fixed boundaries are not connected by solid material, as shown in Fig. 1) during the optimization process (Zhu et al. 2018; Zhang et al. 2016a). This phenomenon has a strong influence on the stabilization of the optimization process and will be even worse when a non-convex design problem, e.g., compliant mechanisms, is considered (Zhang et al. 2016a). In this paper, to overcome this issue, we adopt the basic idea of MMC and present a new structural topology optimization method that uses moving wide Bezier components with constrained ends. In the proposed method, components which are determined by using wide Bezier curves are regarded as design units. These design units are represented as the zero level sets of one higher-dimensional level set function. The complexity of the structural topology is controlled by the control points of such Bezier curves. The ends of the utilized wide Bezier curves are constrained based on the boundary conditions of the design problem so that it can essentially avoid any structurally invalid designs and thereby smooth the optimization process.

Fig. 1
figure 1

Input and fixed boundaries are not connected by solid material within the design domain. This case can occur even the curved skeleton components are used (Guo et al. 2016)

Full size image

The remainder of the paper is organized as follows. In Section 2, the underlying idea of the proposed method is presented. In Section 3, optimization problems to be considered are introduced. In Section 4, sensitivity analysis is presented. In Section 5, the optimization algorithm to implement the proposed method is presented. In Section 6, several numerical examples are presented to demonstrate the effectiveness of the proposed method. Conclusions are documented in Section 7.

2 Structural topology optimization using moving wide Bezier components with constrained ends

2.1 Geometric representation scheme

For structural topology optimization, the goal is to seek a sufficiently regular elastic body Ω ⊂ Rd(d = 2,3) within a given design domain D. In the following, we only consider d = 2 for simplicity since the extension to d = 3 is straightforward. Similar to the conventional MMC-based methods, we use a set of movable wide Bezier components to represent the structural boundaries/topologies. As demonstrated in Guo et al. (2016), the optimized structural topology can be achieved by properly arranging the positions and sizes/geometries of these components.

As shown in Fig. 2, to form the component, we use a Bezier curve as the skeleton. The shape of this curve can be controlled by its control points Pi(xi,yi)(i = 0,1,...,p) where p + 1 is the total number of control points. In order to form a valid design, the width of each component is set to 2r (Fig. 2) in which r is also taken as a design variable. Therefore, the used component is called the moving wide Bezier component. In this case, suppose we use M components, then the topology of the structural shape can be entirely determined by a vector \(\textbf {d} = {\left [ {\begin {array}{*{20}{c}} {{\textbf {d}_{1}}} \hfill & {{\textbf {d}_{2}}} \hfill & {\cdots } \hfill & {{\textbf {d}_{m}}} \hfill & {\cdots } \hfill & {{\textbf {d}_{M}}} \hfill \end {array}} \right ]^{\mathrm {T}}}\), where dm consists of geometry parameters of the m th component:

$$ {\textbf{d}_{m}} = {\left[ {{x_{0}},{y_{0}},{x_{1}},{y_{1}},...,{x_{i}},{y_{i}},...,{x_{p}},{y_{p}},r_{m}} \right]} $$
(1)

where (xi,yi) are the coordinates of the control point i and r is the half width of the wide Bezier curve (Fig. 2).

Fig. 2
figure 2

A cantilever example to show the underlying idea of the presented method

Full size image

As mentioned in Tai and Chee (2000), Wang and Zhang (2012), and Zhou and Ting (2005), while it is still unknown how the design space is occupied by the optimized structure, the loading, supporting and/or some other functional interactions must be connected in order to form a valid structural design.

Following this idea, in this paper, we use the moving wide Bezier components as the bridges to connect all Dirichlet and Neumann boundaries in the design domain. Specifically, the control points at both ends of the component can be constrained on the design condition in which the support, loading, and other functional interactions are predefined. Taking the cantilever design as an example, we briefly introduce the connection ways. In addition to the free boundaries, the design domain of the cantilever normally contains two specific areas, i.e., the loaded area and the fixed part. To form a valid design, these two areas must be connected to each other with solid material. Suppose we use four moving wide Bezier components to connect these two areas, a valid design can be shown in Fig. 2 (left). Figure 2 (right) shows one example where the fixed and loaded areas are connected by one wide Bezier component. According to the fixed boundary condition, during the optimization process, it only needs to restrict the horizontal coordinates of the control point at the left end of the component so that it can move along the displacement boundary. Whereas, since the input force is applied at one point, the right end of the component needs to be completely fixed. This means the values of x0, xp, and yp in \(\textbf {d}_{m}^{E}\) can be predefined. This strategy will not render any structurally invalid designs and thereby significantly smooth the optimization process.

Therefore, the moving wide Bezier components with constrained ends (MWB-CE) is defined in this paper. The design variable vector dm can be separated into two parts:

$$ {\textbf{d}_{m}} = \left[ \begin{array}{l} \mathbf{d}_{m}^{E} \\ \mathbf{d}_{m}^{F} \end{array} \right] $$
(2)

where \(\textbf {d}_{m}^{E} = \left [ {{x_{0}},{y_{0}},{x_{p}},{y_{p}}} \right ]^{\top }\) and \(\textbf {d}_{m}^{F} = \left [ {{x_{1}},{y_{1}},{x_{2}},{y_{2}},..., {x_{p - 1}},{y_{p - 1}},{r_{m}}} \right ]^{\top }\) represent the coordinates of the end and intermediate control points, respectively.

2.2 Construction of the level set function ϕ m of the component m

In the proposed method, the material domain Ω is determined by M moving wide Bezier components with constrained ends, i.e.:

$$ {\Omega}=C_{1}\cup C_{2} ...\cup C_{m}...\cup C_{M} $$
(3)

where Cm denotes the m th component that is defined using a level set function ϕm as:

$$ \left\{ {\begin{array}{*{20}{l}} {\phi_{m} ({\textbf{x}}) > 0} & {\text{if}} & {{\textbf{x}} \in C_{m} } \\ {\phi_{m} ({\textbf{x}}) = 0} & {\text{if}} & {{\textbf{x}} \in \partial C_{m} } \\ {\phi_{m} ({\textbf{x}}) < 0} & {\text{if}} & {{\textbf{x}} \in D\backslash C_{m} } \end{array}} \right. $$
(4)

where x is a point in the design domain. In this case, the structure Ω can be determined by a level set function ϕs as:

$$ \phi^{s}(\textbf{x})=\max(\phi_{1}(\textbf{x}),\phi_{2}(\textbf{x}),...,\phi_{m}(\textbf{x}),...,\phi_{M}(\textbf{x})). $$
(5)

The position vector C of any point on a Bezier polynomial curve can be determined by using the following general equation:

$$ \textbf{C} = \textbf{C}\left( t \right) = \sum\limits_{i = 0}^{p} b_{i,p}(t) \mathbf{P}_{i} $$
(6)

where t varying from 0 to 1 is the intrinsic parameter along the curve, bi,p(t) denotes the Bezier coefficient of degree p, and Pi is the coordinates vector of the i th control point:

$$ b_{i,p}(t)=\frac{p!}{i!(p-i)!}(1-t)^{p-i}t^{i}. $$
(7)

The 1st derivative of the Bezier curve can be expressed as:

$$ \mathbf{C}^{(1)}(t)=p \sum\limits_{i=0}^{p-1}b_{i,p-1}(t)(\mathbf{P}_{i+1}-\mathbf{P}_{i}). $$
(8)

We use a signed distance function ϕm to represent the moving wide Bezier component Cm. A signed distance field is constructed in the discrete domain and offset by r unit lengths along the z-axis:

$$ \phi_{m}(\mathbf{x})=r-s^{\min}=r-|\mathbf{C}(t)-\mathbf{x}| $$
(9)

where \(s^{\min \limits }\) is the signed distance function reflecting the shortest distance from point x to the curve. These points can be taken as element nodes in the discrete domain. The shortest distance from any point xk to the parameterized curve can be obtained by solving the following extreme value problem:

$$ s^{\min}_{k}=\underset{t_{k}\in[0,1], k\in I}{\min}|\mathbf{C}(t_{k})-\mathbf{x}_{k}| $$
(10)

where I is the set of nodes in the discrete domain. Since the closed-form solution of the derivative of the Bezier curve has been deduced in (8), the problem can be solved directly by Newton’s iterative method. Obviously, the more control points there are in a Bezier curve, the higher the order and thus the more complex the shape of the curve. This can lead to a larger search space, which allows the Bezier component to construct a structure closer to the optimal solution. But this introduces more design variables and requires higher costs to estimate the boundary of the component, which introduces an increased computational burden (Tai and Chee 2000). It is up to the designer to weigh it against personal choice.

2.3 Mathematical formulas for solving structural topology optimization under the MWB-CE framework

By using the proposed MWB-CE, a topology optimization problem with the goal of minimizing an objective functional J for a specific physical type described by j(u) under a constraint on material usage V can be formulated as:

$$ \begin{array}{ll} \underset{\textbf{d}}{\min} :~~~~&J = J(u,{\phi^{s}}(\textbf{d})) = {\int}_{D} {j(u)H({\phi^{s}}\left( \textbf{d} \right))d{\Omega} } \\ \textrm{s.~t.}:~~~~&{V / {{V^{*}}}} = {{{\int}_{D} {H\left( {{\phi^{s}}\left( \textbf{d} \right)} \right)d{\Omega} } } / {{V^{*}}}} \le \chi \end{array} $$
(11)

where V∗ denotes the total volume when D is fully occupied by solid material, χ is the requested volume fraction, and u is the state variable. H(ϕs) is the Heaviside function and is defined as:

$$ H(\phi^{s}) = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} 1 &~~~~ {\text{if}} ~~~~& {\phi^{s} \geq 0} \end{array}} \\ {\begin{array}{*{20}{c}} 0 &~~~~ {\text{if}} ~~~~& {\phi^{s} < 0} \end{array}} \end{array}} . \right. $$
(12)

In this paper, the discrete domain is filled by bilinear elements. In order to address the finite element problem with an irregular interface, the Ersatz material model is employed (Zhang et al. 2016a), in which the level set function or topological description function is transformed into a 0–1 distribution using the Heaviside function as given in (12). To make the Heaviside function differentiable, this paper uses a smoothed version of the Heaviside function \(\tilde {H}(\phi )\):

$$ \tilde{H}(\phi)=\left \{ {\begin{array}{llll} &1,&&~~~~\text{if}~~~~\phi>{\Delta},\\ &\frac{3(1-\alpha)}{4}(\frac{\phi}{\Delta}-\frac{\phi^{3}}{3{\Delta}^{3}})+\frac{1+\alpha}{2},&&~~~~\text{if}~~~~-{\Delta} \leq \phi \leq {\Delta}, \\ &\alpha,&&~~~~\text{otherwise}. \end{array}} \right. $$
(13)

where Δ is the parameter to control the magnitude of the smoothing interval. α is taken as a very small positive number to avoid the singularity of the stiffness matrix.

3 Considered design problems

3.1 Stiffness design

A stiffness design problem can be illustrated as in Fig. 3 (left) where Γd represents the Dirichlet boundary condition and only surface load F is considered. The most commonly used objective function is to minimize the sum compliance which can be expressed as Bendsœ and Sigmund (2003) and Sigmund (2007):

$$ \min:~~~~J = \textbf{F}^{\top}\textbf{u} $$
(14)

where u is the displacement field due to external force vector F and is obtained by solving the following bilinear equilibrium:

$$ {\int}_{D} {{\textbf{E}_{ijkl}}{\varepsilon_{ij}}\left( \textbf{u} \right){\varepsilon_{kl}}\left( \textbf{v} \right)H\left( {{\phi^{s}}} \right)d{\Omega} } = {\int}_{{D}} {\textbf{F}\textbf{u}\delta \left( {{\phi^{s}}} \right)\left| {\nabla {\phi^{s}}} \right|d{\Omega}} $$
(15)

where v denotes the arbitrary virtual displacement. Eijkl and εij denote the elasticity tensor and the strain tensor, respectively. \(\delta \left (\phi ^{s}\right )\) is the Dirac delta function defined as:

$$ \delta \left( {{\phi^{s}}} \right) = \frac{{\partial H\left( {{\phi^{s}}} \right)}}{{\partial {\phi^{s}}}} $$
(16)
Fig. 3
figure 3

The design problems considered in this study

Full size image

The smoothed version of Dirac delta function \(\tilde {\delta }(\phi )\) can be expressed as:

$$ \tilde{\delta}(\phi)=\left \{ \begin{array}{llll} &0,&&~~~~\text{if}~~~~\phi>{\Delta},\\ &\frac{3(1-\alpha)}{4}(\frac{1}{\Delta}-\frac{\phi^{2}}{{\Delta}^{2}}),&&~~~~\text{if}~~~~-{\Delta} \leq \phi \leq {\Delta}, \\ &0,&&~~~~\text{otherwise}. \end{array} \right. $$
(17)

3.2 Compliant mechanisms

The compliant mechanism design problem with single input-output behavior can be illustrated in Fig. 3 (right). An input force F is applied at the input port i and the displacement uo at output port o due to F is expected to be maximized. Two artificial springs ki and ko are attached to the input and output port, respectively. Then the objective function J can be expressed as Bendsœ and Sigmund (2003) and Sigmund (2007):

$$ \min:~~~~J = -\textbf{l}^{\top}\textbf{u} $$
(18)

where u is the displacement field due to external force vector F and l is a vector which consists of all zero except for the output port o which is 1. The displacement u can be obtained by solving the bilinear equilibrium with the same form in (15).

4 Sensitivity analysis

The aforementioned problems are solved using the gradient-based optimization algorithm. The objective functions as described in (14) and (18) can be unified into the following matrix form:

$$ J=\mathbf{Q}^{\top} \mathbf{U} $$
(19)

where Q = F in the stiffness design problem and Q = l in the compliant mechanisms problem, and U is the displacement vector.

According to the adjoint method, the sensitivity of the objective function J with respect to any design variable a can be calculated as:

$$ \begin{array}{ll} \frac{\partial J}{\partial a}&=\frac{\partial}{\partial a} \left( \mathbf{Q}^{\top} \mathbf{U} \right)+{\lambda}^{\top} \frac{\partial}{\partial a} \left( \mathbf{F}-\mathbf{K}\mathbf{U} \right) \\ &=\left( \mathbf{Q}^{\top} - {\lambda}^{\top} \mathbf{K} \right)\frac{\partial \mathbf{U}}{\partial a}-{\lambda}^{\top} \frac{\partial \mathbf{K}}{\partial a} \mathbf{U} \end{array} $$
(20)

Since λ⊤ is a Lagrange multiplier, the derivative term of the displacement can be further eliminated by solving the adjoint equation Q⊤− λ⊤K = 0. K is the global stiffness matrix. The sensitivity of the element stiffness with respected to the design variable a can be expressed as:

$$ \begin{array}{ll} \frac{\partial \mathbf{K}_{e}}{\partial a}&={\int}_{D_{e}}\mathbf{B}^{\top} \mathbf{D} \mathbf{B} \frac{\partial H(\phi^{s})}{\partial a} d{\Omega} \end{array} $$
(21)

where D is the elasticity matrix under the state of plane stress and B denotes a matrix for displacement gradients interpolation. Suppose a is a design variable relate to the m th component, the region that can be affected by perturbations of the design variable can be expressed by \((1-H({\phi _{m}^{s}}))H(\phi _{m})\) where \({\phi _{m}^{s}}=\max \limits (\phi _{1}(\textbf {x}),\phi _{2}(\textbf {x}),...,\phi _{m-1}(\textbf {x}),\phi _{m+1}(\textbf {x}),...,\phi _{M}(\textbf {x}))\) (Zhang et al. 2018a). The sensitivity of the element stiffness matrix can be rewritten as:

$$ \begin{array}{ll} \frac{\partial \mathbf{K}_{e}}{\partial a}&={\int}_{D_{e}}\mathbf{B}^{\top} \mathbf{D} \mathbf{B} \frac{\partial}{\partial a}\left( (1-H({\phi_{m}^{s}}))H(\phi_{m}) \right) d{\Omega} \\ &={\int}_{D_{e}}\mathbf{B}^{\top} \mathbf{D} \mathbf{B} (1-H({\phi_{m}^{s}})) \delta(\phi_{m}) \frac{\partial \phi_{m}}{\partial a} d{\Omega} \end{array}. $$
(22)

For component m, when the variable a represents the half-width rm, the term ∂ϕm/∂a can be written as:

$$ \frac{\partial \phi_{m}}{\partial r_{m}}=\frac{\partial}{\partial r_{m}}(r_{m}-|\mathbf{C}_{m}(t)-\mathbf{x}|)=1 $$
(23)

and when a is the coordinate of the ith control point Pi(xi,yi), the term ∂ϕm/∂a yields:

$$ \frac{\partial \phi_{m}}{\partial {x_{i}}}=\frac{\partial}{\partial {x_{i}}}(r_{m}-|\mathbf{C}_{m}(t)-\mathbf{x}|)=\frac{-(C_{x,m}(t)-x)}{\sqrt{((C_{x,m}(t)-x)^{2}+(C_{y,m}(t)-y)^{2})}}b_{i,p}(t) $$
(24)
$$ \frac{\partial \phi_{m}}{\partial {y_{i}}}=\frac{\partial}{\partial {y_{i}}}(r_{m}-|\mathbf{C}_{m}(t)-\mathbf{x}|)=\frac{-(C_{y,m}(t)-y)}{\sqrt{((C_{x,m}(t)-x)^{2}+(C_{y,m}(t)-y)^{2})}}b_{i,p}(t) $$
(25)

where x and y are the coordinates of the point x.

The sensitivity of the volume constraint function can be written as:

$$ \frac{\partial}{\partial a}\left( \frac{V}{V^{*}}\right) =\frac{1}{V^{*}}{\int}_{D} \delta_{m}(\phi_{m}) \frac{\partial \phi_{m}}{\partial a}d{\Omega} $$
(26)

5 Optimization algorithm

The optimization algorithm can be described as an iterative process in Algorithm 1. The optimization process begins with the initialization of all parameters related to the design problem, including material properties, boundary conditions, the number of control points p + 1 for each Bezier curve, and the total number of components M to represent the structural topology. Then, the design variable \(\textbf {d}_{m}^{E}\) will be preset according to the boundary conditions. The initial structural configuration is made up of a randomly generated \(\textbf {d}_{m}^{F}\). The level set functions of all components are calculated and the configuration of the structure is obtained using (5). After that, the finite element analysis is performed to obtain the structural response and the sensitivity analysis is performed. The design variables are updated by using the Method of Moving Asymptotes (MMA) (Svanberg 1987). Finally, the optimized results are visualized. The optimization process will be repeated if the convergence check fails. The convergence is achieved if the volume fraction is within 0.0005 of the required value χ and the values of the objective in the previous 5 steps are also within 0.05% tolerance of the values in the current step, or a predefined maximum iteration number is achieved.

figure a

6 Numerical examples

In this section, we present several examples to demonstrate the validity of the proposed method. The artificial material properties are described as follows. Young’s modulus for solid material is E = 1 and Poisson’s ratio is υ = 0.3. The design domain is discretized by square finite elements.

6.1 Cantilever

The first considered optimization problem is the cantilever design problem, which is a well-known example in the literature of topology optimization. The design domain is shown in Fig. 4. The ratio of the length and height of the design domain is 2 : 1. The left side of the design domain is fixed. A single vertical load F = 1 is applied at the center of its right side. A volume ratio 0.3 is considered. The fixed design domain is discretized using 80 × 40 elements for finite element analysis.

Fig. 4
figure 4

The design domain of the cantilever

Full size image

For this example, we use 12 Bezier curves to represent the structural topology and each Bezier curve has 8 control points. According to the boundary conditions, all the right end control points of the utilized curves have the same coordinates with the input load port i. The x-coordinates of all left control points are zero while the y-coordinates are able to vary along the y direction.

The optimized topology is shown in Fig. 5 in which both components and structural configuration plots are presented. The obtained topology is nearly identical to the results that have been well accepted (Bendsœ and Sigmund 2003). The obtained cantilever has the mean compliance of 103.6 which is slightly higher than that obtained by using a standard MMC method (99.5) (Zhang et al. 2016a). This is because we set the thickness r of the components to be uniform. One may use parametric wide Bezier curves (Zhou and Ting 2005) to obtain a better result. In this study, the thickness r can reach 0 which means the corresponding Bezier curve becomes dead and has no contribution to the structural configuration, as shown in Fig. 5a.

Fig. 5
figure 5

The final dsign of the cantilever which is shown in both its components plot (a) and structural configuration plot (b)

Full size image

The optimization process runs for 346 steps. The randomly generated initial design and several intermediate designs are shown in Fig. 6. The convergence history of the mean compliance is shown in Fig. 7. During the whole optimization process, topology, shape, and size of the structure can be conveniently described and fully controlled by the parameters of the utilized wide Bezier components with constrained ends. Moreover, the optimization process is relatively smooth since structurally invalid designs, e.g., the loading and supporting areas that are not connected with solid material (Zhu et al. 2018), can be naturally avoided.

Fig. 6
figure 6

Intermediate designs shown in their component and topology plots of the cantilever obtained using the proposed method.a initial. b step 5. c step 20. d step 80. e step 320

Full size image
Fig. 7
figure 7

Convergence history of the mean compliance when designing the cantilever using the proposed method

Full size image

6.1.1 Design with different initial topologies

In this section, we examine the effect of different initial configurations upon the resulting optimized structural topology. For all the four studied cases, the initial value r that determines the width of the components is set to 0.01\(\max \limits (L,W)\) where L and W are the length and width of the design domain, respectively. Since in the proposed method, the structural configuration is completely determined by the parameters of the Bezier curves which are randomly predefined, we simply run our program four times in which the initial configurations are shown in Fig. 8. The corresponding optimized topologies are shown in Fig. 9. The mean compliances of all studied cases are shown in Table 1. For all studied cases, the obtained optimized topologies are clear and almost the same, although the resulting compliances are slightly different. Thus, the dependency of the obtained optimized configurations upon the initial configurations is extremely low. Although in this study the initial values of the design variables are randomly given, one can also set these values artificially as has been done in Zhang et al. (2016a). The principle is to let curves cross each other enough times, i.e., create many holes in the initial configuration so as to form a complex topology. This strategy has been proved to be effective in the standard level set methods (Allaire et al. 2004; Wang et al. 2003b).

Fig. 8
figure 8

The four different initial configurations of the cantilever design problem generated by randomly generating the initial value of design variables. a Case 1. b Case 2. c Case 3. d Case 4

Full size image
Fig. 9
figure 9

The corresponding optimized topologies of the cantilever with different initial configurations. a Case 1. b Case 2. c case 3. d Case 4

Full size image
Table 1 Resulted values of mean compliance of the cantilevers
Full size table

6.2 Bridge

In this section, we consider a Michell type bridge structure with fixed-fixed supports, as shown in Fig. 10. The ratio of the length and height of the design domain is 2 : 1. Both the left and right bottom corners are fixed. A vertical unit load F is applied at the center point of the bottom. For this example, the volume ratio χ is set to 0.2. The design domain is discretized by using 100 × 50 finite elements for the elastic analysis.

Fig. 10
figure 10

The design domain of the bridge problem

Full size image

6.2.1 Design with different number of components

We first examine the effect of a different number of wide Bezier curves upon the resulting optimized structural topology. Four cases are studied in which the number of used curves is set to 3, 6, 9, and 12. The number of control points of each curve is set to 10.

Due to the boundary conditions, we use the same number of curves to connect points A and B, points A and i, and points i and B (Fig. 11). For all the studied cases, the initial configurations are shown in Fig. 11 in which only component plots are given. The corresponding optimized topologies are shown in Fig. 12. For all four studied cases, the obtained optimized topologies are the same and identical to the results that have been published such as in Zhu et al. (2015). The mean compliances of all studied cases are shown in Table 2.

Fig. 11
figure 11

The initial configuration of the bridge problem with different number of components: a 3 (Case 1), b 6 (Case 2), c 9 (Case 3), and d 12 (Case 4)

Full size image
Fig. 12
figure 12

The optimized configurations of the bridge problem with different number of components: a 3 (Case 1), b 6 (Case 2), c 9 (Case 3), and d 12 (Case 4)

Full size image
Table 2 Resulted values of mean compliance of the bridges
Full size table

Although an optimized topology can still be obtained when the number of curves used is relatively small, e.g., 3, it is still recommended to use a large number of curves to stabilize the optimization process and obtain a better design (Table 2). However, when the used number of curves is too large, the number of design variables will increase dramatically. This can affect the optimization speed as demonstrated in Zhu et al. (2018). For the studied bridge problem, it is shown that 9 curves are an appropriate choice since it can result in a smooth configuration with the lowest mean compliance.

6.2.2 Design with different number of control points

Following Section 6.2.1, we further examine the effect of the number of control points upon the optimized structural configuration. The bridge problem is resolved with a fixed number of wide Bezier curves, which is 9. In addition to the result shown in Fig. 12c in which the number of control points is 10, we examine two extra cases where the number of control points is set to 4 and 20.

The optimized topologies of the two studied cases are shown in Fig. 13 both in their component and topology plots. Compared with Fig. 12c, although the same topology can be obtained, the shapes are quite different to each other. The obtained structures have mean compliances of 22.8 (Fig. 13a) and 20.9 (Fig. 13b).

Fig. 13
figure 13

The optimized configurations of the bridge problem with different number of control points: a 4 and b 20

Full size image

One can see that, with a small number of control points, the Bezier curve can not form complex shapes, which will slightly affect the outcome mean compliance of the optimized structure. With a large number of control points, the Bezier curves can be quite twisted during the optimization process, which lead to unsmooth boundaries of the optimized structure. Moreover, a large number of control points lead to a large number of design variables which also will slow down the optimization speed. Based on the authors’ numerical experiences, around ten control points would be a good choice to obtain a clear and smooth optimization result.

6.2.3 Another design condition

In this section, the bridge problem is resolved by using the boundary conditions as shown in Fig. 14. The ratio of the length and height of the design domain is 4 : 1. The boundaries at points A and B are fixed. Point A and Point B are respectively at 1/4 and 3/4 of the bottom of the design domain. A unit surface load f is applied at the top of the design domain. For this example, the volume ratio χ is set to 0.35. The design domain is discretized by using 160 × 40 finite elements for the elastic analysis. The number of used curves is set to 12. The number of control points of each curve is set to 8. The initial configuration (Fig. 15a) is also randomly generated. The optimized topology and its corresponding component plot are shown in Fig. 15b. One can see that, with a different design boundary condition, an optimized design with higher structural complexity can be obtained.

Fig. 14
figure 14

The design domain of another bridge problem

Full size image
Fig. 15
figure 15

The initial configuration a and final design b of the bridge problem. Both of the component and topology plots are given

Full size image

6.3 Displacement inverter

From this section on, we use compliant mechanism design problems to further demonstrate the validity of our method. A displacement inverter is firstly considered. The design domain can be seen in Fig. 16 in which only the bottom half part is shown due to the symmetry. The ratio of the length and width of the design domain is also set to 2 : 1. The left bottom corner is fixed and a unit load F is applied at the input port i. The output displacement uo at o is expected to be maximized. Two springs, ki = 0.5 and ko = 0.1, are attached to the input port i and output port o, respectively. The maximum allowable material usage χ is set to 0.25. We use 9 wide Bezier curves to form the structural configuration as was done in Section 6.2. Each Bezier curve has 10 control points.

Fig. 16
figure 16

The design domain of the displacement inverter

Full size image

6.3.1 Comparison study with the standard MMC method

Compared with the standard MMC method, such as proposed in Zhang et al. (2016a), the proposed method has the advantage of naturally avoiding generating structurally invalid designs during the optimization process, which is helpful to smooth and stabilize the optimization process. To illustrate this, the displacement inverter design problem is firstly solved by using the MMC program provided in Zhang et al. (2016a) under the design conditions and convergence criteria used in this study. The optimization process converges at step 161. However, since the generated topology at step 161 has some broken areas, we let the optimization process keep running for 500 steps. The generated topology is shown in Fig. 17a. The design problem is solved by using the proposed method and the optimization process converges at step 176. The optimized configuration is shown in Fig. 17b.

Fig. 17
figure 17

The optimized configuration of the displacement inverter with: a the standard MMC method and b the proposed method

Full size image

For the standard MMC method, the initial configuration and some intermediate designs, as well as the convergence history of the output displacement uo, are shown in Fig. 18. It is shown that, during the first 50 iteration steps, invalid designs in which the input port, output port, and fixed boundary are not connected to each other are generated. This makes the output displacement uo remaining 0 for around 40 iteration steps before it goes down. For the proposed method, the initial configuration and some intermediate designs, as well as the convergence history of the output displacement uo, are shown in Fig. 19. It is shown that, since no invalid designs occur during the optimization process, the convergence history of uo is smoothed.

Fig. 18
figure 18

The convergence history of the objective function uo when using the standard MMC method. The initial configuration and some intermediate designs at step 10, step 40, and step 80 are shown. The optimized configuration under the convergence criteria in Section 5 is also shown. The maximized output displacement is 0.18

Full size image
Fig. 19
figure 19

The convergence history of the objective function uo when using the proposed method. The initial configuration and some intermediate designs at step 10, step 40, and step 80 are shown. The optimized configuration under the convergence criteria in Section 5 is also shown. The maximized output displacement is 0.21

Full size image

It has to be pointed out that the use of standard MMC method (components with straight skeletons) can lead to non-smooth structural boundaries (Fig. 17a). In order to overcome this issue, Guo et al. (2016) suggested to use moving morphable components with curved skeletons, which is helpful to smooth the obtained structural boundaries. However, as demonstrated in the provided numerical examples in Guo et al. (2016), the disconnection issue as demonstrated in Fig. 1 still exits, especially in the first few iterations of the optimization process. Therefore, in the authors’ opinion, the idea proposed in this study should be more helpful to stabilize the optimization process meanwhile smoothing the structural boundaries.

6.3.2 Minimum length control

The minimum length scale or thickness control is a very important issue in topology optimization. Many methods have been proposed to deal with this problem (Wang et al. 2019; Lazarov et al. 2016; Zhang et al. 2016b). By using the proposed method, the minimum length scale control can be easily done without adding extra constraint. One can directly set the lower bound of the design variable r that is used to control the thickness of the wide Bezier curve.

To illustrate this, we resolve the displacement inverter design problem by setting the lower bound of r to 0.01W instead of 0, where W is the width of the design domain. The optimized topology is shown in Fig. 20 both in its component and topology plots. One can see that, since r is not allowed to decrease to be 0, there are no longer any dead components. The components will sit together to form a reasonable design while the minimum length scale control can be naturally done. As a result, the de facto hinges (Zhu et al. 2020a; Zhan and Luo 2019; Chen and Wang 2007), which are quite common when designing compliant mechanisms using topology optimization, have been avoided.

Fig. 20
figure 20

a, b The optimized displacement inverter when setting the lower bound of r to 0.01W

Full size image

6.3.3 Design with different mesh refinements

In this section, we examine the effect of the finite element mesh size upon the optimized configurations obtained. Four cases are studied in which the mesh size is restricted to 60 × 30, 100 × 50, 160 × 80, and 200 × 100. All the other design parameters remain the same as those used in Section 6.3.1.

The optimized displacement inverters for each case are shown in Fig. 21 both in their component and topology plots. All obtained optimized configurations are smooth, clear, and have the same topology. This indicates that a reasonable optimized configuration can be obtained by using the proposed method regardless of which mesh size is used.

Fig. 21
figure 21

The optimized displacement inverters obtained with different mesh refinement: a60 × 30 = 1800, b 100 × 50 = 5000, c 160 × 80 = 12800, and d 200 × 100 = 20000

Full size image

6.4 Push gripper

For using the proposed method, it is also possible and easy to obtain the optimized results by incorporating them with the free movable components. In this case, the number of moving wide Bezier components with constrained ends can be decreased. To illustrate this, we consider a push gripper design problem. The design domain can be seen in Fig. 22 in which only half of the part is considered due to the symmetry. The ratio of the length and width of the design domain is set to 2 : 1. The left bottom corner is fixed. A horizontal unit load F is applied at the left top corner of the design domain. A vertical displacement of the outer jaw is expected to be maximized. The design domain is discretized with 80 × 40 finite elements. Maximal material usage χ is restricted to 0.25. Two springs, ki = 0.1 and ko = 0.1, are attached to the input port i and output port o, respectively.

Fig. 22
figure 22

The design domain of the push gripper

Full size image

According to the boundary conditions, we use 6 wide Bezier curves with constrained ends and 4 wide Bezier curves with free ends to represent the structural topology. The configurations of the constrained end components are randomly generated, while the free end components are given following the methods in Zhang et al. (2016a). The initial configuration is shown in Fig. 23a. The optimized configuration is shown in Fig. 23b. The convergence history of the output displacement uo is shown in Fig. 24. It shows that the proposed method can provide meaningful results by incorporating the free movable components without generating invalid designs that affect the stabilization of the optimization process.

Fig. 23
figure 23

The initial a and final b topologies of the gripper

Full size image
Fig. 24
figure 24

The convergence history of the displacement uo of the gripper problem

Full size image

7 Conclusions

A structural topology optimization method that uses moving wide Bezier components with constrained ends (MWB-CE) is presented in this paper. The design units are set to a number of wide Bezier curves which are represented by the level set functions. The design variables are set to the control points and width of such wide Bezier curves. The optimized topology is obtained by updating the coordinates and the width of the Bezier curves by using the MMA. The two ends of each wide Bezier curve are constrained based on the principle that, in order to form one single connected load-bearing structure, the loading, supporting, and/or some other functional interactions must be connected. The validity of the proposed method is demonstrated by designing several benchmark examples in the literature of structural topology optimization. The results show that the proposed MWB-CE method can avoid generating invalid designs thereby smoothing the optimization process. In addition to that, the proposed method can achieve minimum length scale control easily without adding extra constraints. Future works will extend the proposed method by solving three-dimensional and geometrically nonlinear structural topology optimization problems.