Design sensitivity analysis with polynomial chaos for robust optimization

Abstract

Polynomial chaos (PC) methods with Gauss-type quadrature formulae have been widely applied for robust design optimization. During the robust optimization, gradient-based optimization algorithms are commonly employed, where the sensitivities of the mean and variance of the output response with respect to design variables are calculated. For robust optimization with computationally expensive response functions, although the PC method can significantly reduce the computational cost, the direct application of the classical finite difference method for the analysis of the design sensitivity is impractical with a limited computational budget. Therefore, in this paper, a semi-analytical design sensitivity analysis method based on the PC method is proposed, in which the sensitivity is directly derived based on the Gauss-type quadrature formula without additional function evaluations. Comparative studies conducted on several mathematical examples and an aerodynamic robust optimization problem revealed that the proposed method can reduce the computational cost of robust optimization to a certain extent with comparable accuracy compared with the finite difference-based PC method.

1 Introduction

The objective of robust design optimization is the optimization of the product performance while minimizing the sensitivity of the performance to uncertainties, which has been widely applied to aerospace engineering (Xiong et al. 2015a; Li et al. 2013; Wu et al. 2018), automobile engineering (Zhang et al. 2007), and civil engineering (Cheng et al. 2016) fields. As is common knowledge, a key component of robust design optimization is the estimation of the mean and variance of the output response, which can be achieved by the use of a metamodel to replace the original output response (Rehman et al. 2014; Janusevskis and Rodolphe 2013). An alternative method involves the development of efficient uncertainty propagation approaches, among which the polynomial chaos (PC) method has been widely studied and applied, as it provides a solid mathematical foundation and fast convergence rate (Xiu and Karniadakis 2002). With the PC method, a random variable can be represented as a stochastic metamodel, and the mean and variance of the random variable can then be analytically obtained. Wu et al. (Wu et al. 2017) and Dodson and Parks (Dodson and Parks 2015) respectively applied the PC method to aerodynamic robust optimization design. Suryawanshi and Ghosh employed the PC method to analyze the aeroelastic stability problems on a rectangular unswept cantilever wing model (Suryawanshi and Ghosh 2016). Xia et al. applied an adaptive PC method to quantify the performance impact of flow and geometric uncertainties for a turbine blade (Xia et al. 2019). Fisher et al., Xiong et al., and Wang et al. respectively applied the PC method to robust trajectory optimization (Fisher and Bhattacharya 2011; Xiong et al. 2015b; Wang et al. 2019a), to increase the robustness of the planned trajectory in response to various disturbances that is beneficial to closed-loop control. In addition to the aleatory uncertainty, the PC method was proposed for the realization of robust design optimization under mixed (aleatory and epistemic) uncertainties, in which the evaluation method for the robustness index under mixed uncertainties was presented (Zhang and Serhat 2013; Zhang 2013). The focus of this study was on PC-based robust optimization under the consideration of aleatory uncertainties.

It is common knowledge that during the gradient-based robust optimization process, the calculation of the design sensitivity is required, i.e., the sensitivities of the first two statistical moments (mean and standard deviation) of the output response with respect to the design variables. The commonly used method for sensitivity analysis is the finite difference method (FDM). For robust optimization, although the PC method can significantly reduce the computational cost when compared with the traditional Monte Carlo simulation (MCS) method for statistical moment calculations, a certain number of additional function evaluations are required for the design sensitivity analysis when employing the traditional FDM. In addition, there is a significant increase in the number of function evaluations required for high-dimensional problems. However, for practical engineering design problems, nonlinear, high-dimensional, and time-consuming high-fidelity simulation is typically required, such as the finite element analysis (FEA) and the computational fluid dynamics (CFD). Furthermore, the direct application of FDM to the analysis of the design sensitivity during robust optimization is impractical with a limited computational budget.

Design sensitivity analysis has been previously investigated in relation to robust design optimization (Keshavarzzadeh et al. 2016; Keshavarzzadeh et al. 2017; Kumar et al. 2018; Miranda et al. 2016; Du and Leifsson 2019; Rumpfkeil 2013) and reliability-based design optimization (Keshavarzzadeh et al. 2016; Keshavarzzadeh et al. 2017; Cho et al. 2016; Lee et al. 2011a; Lee et al. 2011b), for the improvement of the efficiency and accuracy of design. The studies conducted by Cho et al., Lee et al., and Choi et al. in refs. (Cho et al. 2016; Lee et al. 2011a; Lee et al. 2011b) were focused on reliability-based design optimization, in which the MCS method was employed for reliability analysis, and the design sensitivity of the probability of failure was derived using a first-order score function. Rumpfkeil developed a gradient-based robust optimization algorithm based on kriging, in which the design sensitivity was derived analytically based on the kriging metamodel (Rumpfkeil 2013). For PC-based design optimization under uncertainties, several studies have been conducted to develop design sensitivity approaches to save computational cost (Keshavarzzadeh et al. 2016; Keshavarzzadeh et al. 2017; Kumar et al. 2018; Miranda et al. 2016; Du and Leifsson 2019). In these works, the PC method was applied for uncertainty quantification and the design sensitivity was derived based on the PC model by using the adjoint method. However, it is limited to systems with known governing equations, and user familiarity with the physical system mechanism is required, given that the sensitivity information from adjoint method is utilized. In practical engineering, oftentimes the response models in optimization design are computationally expensive black-box-type response functions, such as the CFD/FEA simulation model that has been calibrated by specialists, and the complex coupled multidisciplinary car or flight vehicle system involving various simulation models from different disciplines, and it is difficult or even impossible to derive the governing equation of the entire system. Therefore, the abovementioned design sensitivity method for PC-based design optimization under uncertainties in refs. (Keshavarzzadeh et al. 2016; Keshavarzzadeh et al. 2017; Kumar et al. 2018; Miranda et al. 2016; Du and Leifsson 2019) may be difficult to apply in this case.

For the construction of the PC model for the statistical moment estimation, a commonly used method for the calculation of the PC coefficients is the least square estimation method (Ghisu and Shahpar 2017; Ghisu and Shahpar 2018). An alternative method is the Galerkin projection method (Xiu and Karniadakis 2003), in which the PC coefficients are calculated using a series of Gaussian-type quadrature formulae, such as the full factorial numerical integration (Lee et al. 2009; Lee et al. 2008) and sparse grid numerical integration (Xiong et al. 2010). The Gaussian quadrature is formulated as a weighted summation of the function response values on several Gaussian quadrature nodes, which provides a potential method for the calculation of the design sensitivity of statistical moments. Therefore, in this study, a semi-analytic design sensitivity analysis method was developed for the PC-based robust optimization, for the reduction of the computational cost. The design sensitivities of the first two statistical moments with respect to the design variables are directly derived based on the Gaussian quadrature formula employed for the statistical moment estimation within the PC method by using the chain rule in conjunction with the FDM strategy, instead of referring to several additional function evaluations, as is the case with the direct FDM. Moreover, when compared with the existing approach by Keshavarzzadeh et al., the proposed method can be more conveniently applied to systems with black-box-type response functions (Keshavarzzadeh et al. 2016; Keshavarzzadeh et al. 2017).

The remainder of this paper is organized as follows. In Section 2, the Gaussian quadrature-based PC method is briefly reviewed. In Section 3, the proposed semi-analytic design sensitivity analysis method is described in detail. Section 4 presents comparative studies on the robust optimization of several mathematical examples, in addition to an airfoil aerodynamic optimization problem, for the verification of the effectiveness of the proposed method. The conclusion is then presented in Section 5.

2 Review of Gaussian quadrature-based PC method in robust optimization

In this study, given that the probability-based robust optimization with random uncertainty was considered, a typical and widely applied robust design optimization problem that can be classified as “sensitivity robustness approach” (Beyer and Sendhoff 2007) was addressed, which can be expressed as follows:

$$ {\displaystyle \begin{array}{l} Find\ {\mu}_{x_1},\cdots, {\mu}_{x_d}\\ {}\operatorname{Min}\kern0.5em F\left(\boldsymbol{x}\right)={w}_1\frac{\mu_f\left(\boldsymbol{x},\boldsymbol{q}\right)}{\mu_f^{\ast }}+{w}_2\frac{\sigma_f\left(\boldsymbol{x},\boldsymbol{q}\right)}{\sigma_f^{\ast }}\\ {}\mathrm{s}.\mathrm{t}.\kern1em {G}_i\left(\boldsymbol{x}\right)={\mu}_{g_i}\left(\boldsymbol{x},\boldsymbol{q}\right)-{k}^{\ast }{\sigma}_{g_i}\left(\boldsymbol{x},\boldsymbol{q}\right)\ge 0\kern0.24em \left(i=1,\cdots, nc\right)\\ {}{\mu}_{x_j}^L<{\mu}_{x_j}<{\mu}_{x_j}^U\left(j=1,\cdots, d\right)\end{array}} $$

(1)

where x = [x₁, ⋯, x_d] is the random design vector with mean values of ${\mu}_{x_1},\cdots, {\mu}_{x_d}$; q = [q₁, ⋯, q_m] is the random parameter vector; μ and σrepresent the mean and standard deviation of the variable, respectively; the subscripts f and g denote the objective and constraint functions corresponding to the original deterministic optimization problem, respectively; k* is a constant employed in robust optimization to ensure the robustness of optimal solution that is typically set as k* = 3; ${\mu}_f^{\ast }$ and ${\sigma}_f^{\ast }$are the constant scaling factors specified by users to scale μ_f and σ_f to the same magnitude that is beneficial to find the optimum; and w₁ w₂ are weight coefficients defined by the users with some preferences or a priori assumptions.

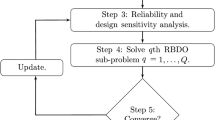
Figure 1 presents the flowchart of the PC-based robust design optimization using the gradient-based optimization algorithm. During each optimization iteration, the mean and standard deviation values of the original objective f(x) and constraint functions g_i(x) (μ_f,σ_f, ${\mu}_{g_i}$, and ${\sigma}_{g_i}$) are calculated using the PC method at the current design point. Moreover, the procedure can be briefly expressed as follows, by using the response function y = g(x) for illustration.

Fig. 1

Flowchart of the PC-based robust optimization with gradient-based optimization algorithm

Step 1: represent the output response y as a pth-order PC model with respect to the random design variables x and random parameters q using the generalized PC method (Xiu and Karniadakis 2003). Here, p represents the maximum order of the polynomial terms (Φ_i(ξ), i = 0, ⋯, P) in the PC model.

$$ y\approx \sum \limits_{i=0}^P{b}_i{\Phi}_i\left(\boldsymbol{\upxi} \right) $$

(2)

where ξ = [ξ₁, ⋯, ξ_d, ξ_d + 1, ⋯, ξ_d + m] represents the standard random vector transformed from the original random vector X = [x₁, ⋯, x_d, q₁, ⋯, q_m] based on their distribution information (Xiu and Karniadakis 2002); the number of polynomial terms is P + 1 = (p + d + m)!/(d + m)!/p! = (p + D)!/D!/p! with D as the sum of the dimensions of x and q; and ${\Phi}_i\left(\boldsymbol{\upxi} \right)=\prod \limits_{k=1}^D{\varphi}_i^k\left({\xi}_k\right)$ is the product of the one-dimensional orthogonal polynomial basis function (${\varphi}_i^k\left({\xi}_k\right)$) that corresponds to the standard random variable in each dimension.

Step 2: calculate the PC coefficient b_i(i = 0, ⋯, P).

Using the Galerkin projection method, the two sides of Eq. (2) are projected onto each orthogonal polynomial Φ_i(ξ). Then, each PC coefficient is calculated as follows using the orthogonality of the orthogonal polynomials.

$$ {b}_i=\mathrm{E}\left[y{\Phi}_i\left(\boldsymbol{\upxi} \right)\right]/\mathrm{E}\left[{\Phi}_i\left(\boldsymbol{\upxi} \right){\Phi}_i\left(\boldsymbol{\upxi} \right)\right],\left(i=0,1,\cdots, P\right) $$

(3)

where E[·] indicates the expectation.

The computational cost of Eq. (3) is mainly due to the calculation of the numerator, which can be carried out using a Gaussian quadrature-type numerical integration method such as the commonly used full factorial numerical integration (FFNI) (Lee et al. 2009; Lee et al. 2008) for lower-dimensional problems, or sparse grid numerical integration (SGNI) for higher-dimensional problems (Ghisu and Shahpar 2017). With FFNI, the numerator can be calculated using a direct full tensor product Gaussian quadrature formula, as expressed below.

$$ \mathrm{E}\left[y{\Phi}_i\left(\boldsymbol{\upxi} \right)\right]=\sum \limits_{j_1=1}^{m_1}{\omega}_{1.{j}_1}\cdots \sum \limits_{j_D=1}^{m_D}{\omega}_{D.{j}_D}y\left({x}_{1.{j}_1},\cdots, {x}_{D.{j}_D}\right){\Phi}_i\left(\boldsymbol{\upxi} \right) $$

(4)

where ω_{j. k} and x_{j. k} are the kth weight and one-dimensional node for the jth input random variable of X = [x₁, ⋯, x_d, q₁, ⋯, q_m], respectively; m_j represents the corresponding number of nodes; and the value of ξ employed in Φ_i(ξ) is calculated by transforming from the d-dimensional node $\left({x}_{1.{j}_1},\cdots, {x}_{D.{j}_D}\right)$ based on the distribution information of X.

With SGNI, the D-dimensional sparse grid nodes with an accuracy level K are first obtained using a special tensor product operation, as follows:

$$ {U}_D^K=\underset{K+1\le \left|i\right|\le Q}{\cup }{U}_1^{i_1}\otimes {U}_1^{i_2}\otimes \cdots \otimes {U}_1^{i_D} $$

(5)

where i₁, i₂, ⋯, i_D determines the number of nodes in each dimension m_j(j = 1, ⋯, D), |i| = i₁ + i₂ + ⋯ + i_D, Q = K + D; and ${U}_D^K$ represents the collection of sparse grids, i.e., the combination of all the multi-dimensional nodes produced by a certain number of direct smaller-size tensor products.

For each combination {i₁, ⋯, i_D} that satisfies K + 1 ≤ |i| ≤ Q, the direct full tensor product is used to generate D-dimensional nodes. Based on Eq. (5), a total of N D-dimensional nodes {x₁, ⋯x_k, ⋯, x_N} can be obtained, and the weight coefficient for ${\boldsymbol{x}}_k=\left[{x}_{1.{j}_1}^k,\cdots, {x}_{D.{j}_D}^k\right]$ is calculated as follows:

$$ {\omega}_k={\left(-1\right)}^{Q-\left|i\right|}\left(\begin{array}{c}D-1\\ {}Q-\left|i\right|\end{array}\right)\left({\omega}_{1.{j}_1}\kern0.5em \cdots \kern0.5em {\omega}_{D.{j}_D}\right) $$

(6)

where ${\omega}_{1.{j}_1}\kern0.5em \cdots \kern0.5em {\omega}_{D.{j}_D}$ denotes the product of the one-dimensional weights.

Thus, E[yΦ_i(ξ)] can be calculated as follows:

$$ \mathrm{E}\left[y{\Phi}_i\left(\boldsymbol{\upxi} \right)\right]=\sum \limits_{k=1}^N{\omega}_k\left(y\left({\boldsymbol{x}}_k\right){\Phi}_i\left(\boldsymbol{\upxi} \right)\right) $$

(7)

Step 3: when the PC coefficients are obtained, estimate the first two statistical moments of the random output response y.

$$ {\mu}_y=\mathrm{E}\left[y\right]=\sum \limits_{i=0}^P{b}_i\mathrm{E}\left[{\Phi}_i\left(\boldsymbol{\upxi} \right)\right]={b}_0 $$

(8)

$$ {\sigma_y}^2=\mathrm{E}\left[{y}^2\right]-\mathrm{E}{\left[y\right]}^2=\mathrm{E}\left[{\left(\sum \limits_{i=0}^P{b}_i{\Phi}_i\left(\boldsymbol{\upxi} \right)\right)}^2\right]=\sum \limits_{i=1}^P{b_i}^2\mathrm{E}\left[{\Phi_i}^2\left(\boldsymbol{\upxi} \right)\right] $$

(9)

3 Proposed semi-analytical design sensitivity analysis method based on PC

As shown in Fig. 1, in addition to the statistical moment calculation, the design sensitivity ($\frac{\mathrm{d}F}{\mathrm{d}{\mu}_{x_j}}$, $\frac{\mathrm{d}{G}_i}{\mathrm{d}{\mu}_{x_j}}$, j = 1, ⋯, d) should also be obtained. To reduce the computational cost, a semi-analytical design sensitivity analysis method based on PC was developed. Based on Eqs. (8), (9), and (3), the design sensitivity of the mean (μ_y) and standard deviation (σ_y) of the output response with respect to the design variable ${\mu}_{x_j}$ can be calculated as follows.

$$ \frac{\mathrm{d}{\mu}_y}{\mathrm{d}{\mu}_{x_j}}=\frac{\mathrm{d}{b}_0}{\mathrm{d}{\mu}_{x_j}}=\frac{\mathrm{d}\left(\mathrm{E}\left[y{\Phi}_0\left(\boldsymbol{\upxi} \right)\right]/\mathrm{E}\left[{\Phi_0}^2\left(\boldsymbol{\upxi} \right)\right]\right)}{\mathrm{d}{\mu}_{x_j}} $$

(10)

$$ {\displaystyle \begin{array}{c}\frac{d{\sigma}_y}{d{\mu}_{x_j}}=\frac{d{\left(\sum \limits_{i=1}^P{b_i}^2E\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{d{\mu}_{x_j}}\\ {}\kern2.25em ={\left(\sum \limits_{i=1}^P{b_i}^2E\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\sum \limits_{i=1}^P{b}_iE\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]\frac{d{b}_i}{d{\mu}_{x_j}}\right)\\ {}={\left(\sum \limits_{i=1}^P\frac{E{\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}^2}{E\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]}\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\sum \limits_{i=1}^P\frac{E\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}{E\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]}\frac{dE\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}{d{\mu}_{x_j}}\right)\end{array}} $$

(11)

Equations (10) and (11) can be further expressed as the following equations:

$$ \frac{d{\mu}_y}{d{\mu}_{x_j}}=\frac{1}{E\left[{\varPhi_0}^2\left(\boldsymbol{\upxi} \right)\right]}\left(\sum \limits_{i_j=1}^{m_j}\frac{\partial E\left[y{\varPhi}_0\left(\boldsymbol{\upxi} \right)\right]}{\partial {x}_{j.{i}_j}}\frac{d{x}_{j.{i}_j}}{d{\mu}_{x_j}}+\sum \limits_{i_j=1}^{m_j}\frac{\partial E\left[y{\varPhi}_0\left(\boldsymbol{\upxi} \right)\right]}{\partial {\omega}_{j.{i}_j}}\frac{d{\omega}_{j.{i}_j}}{d{\mu}_{x_j}}\right) $$

(12)

$$ \frac{d{\sigma}_y}{d{\mu}_{x_j}}={\left(\sum \limits_{i=1}^P\frac{E{\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}^2}{E\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]}\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\sum \limits_{i=1}^P\frac{E\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}{E\left[{\varPhi_i}^2\left(\boldsymbol{\upxi} \right)\right]}\left(\sum \limits_{i_j=1}^{m_j}\frac{\partial E\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}{\partial {x}_{j.{i}_j}}\frac{d{x}_{j.{i}_j}}{d{\mu}_{x_j}}+\sum \limits_{i_j=1}^{m_j}\frac{\partial E\left[y{\varPhi}_0\left(\boldsymbol{\upxi} \right)\right]}{\partial {\omega}_{j.{i}_j}}\frac{d{\omega}_{j.{i}_j}}{d{\mu}_{x_j}}\right)\right) $$

(13)

where ${x}_{j.{i}_j}$and ${\omega}_{j.{i}_j}$ are the node and weight coefficients in the jth dimension, respectively, which correspond to the random variable x_j.

In Eqs. (12) and (13), given that the value of the weight ${\omega}_{j.{i}_j}$ is only determined by the number of nodes m_j and distribution of x_j, $\frac{\mathrm{d}{\omega}_{j.{i}_j}}{\mathrm{d}{\mu}_{x_j}}=0$. Moreover, given that the nodes ${x}_{j.{i}_j}\left({i}_j=1,\cdots, {m}_j\right)$ in each dimension are centered around the mean ${\mu}_{x_j}$ with fixed spacing, $\frac{\mathrm{d}{x}_{j.{i}_j}}{\mathrm{d}{\mu}_{x_j}}$ = 1. Therefore, the critical task is the calculation of the partial derivative $\frac{\mathrm{\partial E}\left[y{\Phi}_i\left(\boldsymbol{\upxi} \right)\right]}{\partial {x}_{j.{i}_j}}$.

3.1 Design sensitivity analysis method based on PC-FFNI

When FFNI is used for the PC coefficient calculation based on Eq. (4), the partial derivatives $\frac{\mathrm{\partial E}\left[y{\Phi}_i\left(\boldsymbol{\upxi} \right)\right]}{\partial {x}_{j.{i}_j}}$ in Eqs. (12) and (13) can be expressed as follows.

$$ \frac{\partial E\left[y{\varPhi}_i\left(\boldsymbol{\upxi} \right)\right]}{\partial {x}_{j.{i}_j}}=\sum \limits_{i_1=1}^{m_1}{\omega}_{1.{i}_1}\cdots \sum \limits_{i_{j-1}=1}^{m_{j-1}}{\omega}_{j-1.{i}_{j-1}}\sum \limits_{i_{j+1}=1}^{m_{j+1}}{\omega}_{j+1.{i}_{j+1}}\cdots \times \cdots \sum \limits_{i_D=1}^{m_D}{\omega}_{D.{i}_D}\frac{\partial y\left({x}_{1.{i}_1},\cdots, {x}_{D.{i}_D}\right)}{\partial {x}_{j.{i}_j}}\cdot {\omega}_{j.{i}_j}\times {\varPhi}_i\left(\boldsymbol{\upxi} \right) $$

(14)

The partial derivative with respect to the node in Eq. (14) can be approximately calculated based on the data (nodes) employed for the previous statistical moment estimation using the finite difference strategy, without the requirement of additional function evaluations. Using the two-dimensional node as an example for illustration, it is assumed that the one-dimensional nodes are located from left to right in each dimension by their sequence numbers (i.e., the subscripts). Based on the three-point Lagrange interpolation polynomial, the partial derivative at any location can be calculated using the forward, center, and backward difference methods as follows.

Three adjacent nodes l₁, l₂, and l₃ with their corresponding function response values g₁, g₂, and g₃ are selected, based on which two approximate partial derivatives ${r}_1=\frac{g_2-{g}_1}{l_2-{l}_1}$ and ${r}_2=\frac{g_3-{g}_2}{l_3-{l}_2}$ that correspond to nodes ${l}_1^{\hbox{'}}=\frac{l_1+{l}_2}{2}$ and ${l}_2^{\hbox{'}}=\frac{l_2+{l}_3}{2}$, respectively, can be obtained. The partial derivatives r_a at any location l_a can then be approximately calculated using the Lagrange linear interpolation polynomial (Abramowitz et al. 1966), as follows:

$$ {r}_a=\frac{l_a-{l}_2^{\prime }}{l_1^{\prime }-{l}_2^{\prime }}{r}_1+\frac{l_a-{l}_1^{\prime }}{l_2^{\prime }-{l}_1^{\prime }}{r}_2 $$

(15)

According to the locations of nodes l₁, l₂, and l₃, there are three possible cases with respect to the calculation of Eq. (15).

Case 1: when i_j = 1(j = 1, ⋯, d), as shown in Fig. 2a, let l₁ = x_j.1,l₂ = x_j.2,l₃ = x_j.3, and l_a = l₁. The partial derivative can be approximated by the forward difference method based on Eq. (15), as follows.

$$ {\displaystyle \begin{array}{c}\frac{\partial y\left({x}_{1.{i}_1},\cdots, {x}_{D.{i}_D}\right)}{\partial {x}_{j.{i}_j}}=\frac{l_1-\frac{l_2+{l}_3}{2}}{\frac{l_1+{l}_2}{2}-\frac{l_2+{l}_3}{2}}\cdot \frac{g_2-{g}_1}{l_2-{l}_1}+\frac{l_1-\frac{l_1+{l}_2}{2}}{\frac{l_2+{l}_3}{2}-\frac{l_1+{l}_2}{2}}\cdot \frac{g_3-{g}_2}{l_3-{l}_2}\\ {}=\frac{l_1-{l}_2+{l}_1-{l}_3}{l_1-{l}_3}\cdot \frac{g_2-{g}_1}{l_2-{l}_1}+\frac{l_1-{l}_2}{l_3-{l}_1}\cdot \frac{g_3-{g}_2}{l_3-{l}_2}\\ {}=\frac{2{h}_1+{h}_2}{h_1+{h}_2}\cdot \frac{g_2-{g}_1}{h_1}+\frac{l_1-{l}_2}{h_1+{h}_2}\cdot \frac{g_3-{g}_2}{h_2}\\ {}\kern6.75em =\frac{g_3-{g}_1}{h_1+{h}_2}-\frac{g_3-{g}_2}{h_2}+\frac{g_2-{g}_1}{h_1}\end{array}} $$

(16)

Fig. 2

Calculation of partial derivatives with FFNI nodes

Case 2: when i_j = m_j, as shown in Fig. 2b, let ${l}_1={x}_{j.{i}_j-2}$,${l}_2={x}_{j.{i}_j-1}$, ${l}_3={x}_{j.{i}_j}$, and l_a = l₃. Similar to the derivation of Eq. (16), the partial derivative can be approximated using the backward difference method as follows.

$$ \frac{\partial y\left({x}_{1.{i}_1},\cdots, {x}_{D.{i}_D}\right)}{\partial {x}_{j.{i}_j}}=\frac{g_3-{g}_1}{h_1+{h}_2}+\frac{g_3-{g}_2}{h_2}-\frac{g_2-{g}_1}{h_1} $$

(17)

Case 3: when i_j ≠ 1 and i_j ≠ m_j, as shown in Fig. 2c, let ${l}_1={x}_{j.{i}_j-1}$,${l}_2={x}_{j.{i}_j}$, ${l}_3={x}_{j.{i}_j+1}$, and l_a = l₂. The partial derivative can be approximated using the central difference method as follows.

$$ \frac{\partial y\left({x}_{1.{i}_1},\cdots, {x}_{D.{i}_D}\right)}{\partial {x}_{j.{i}_j}}=-\frac{g_3-{g}_1}{h_1+{h}_2}+\frac{g_3-{g}_2}{h_2}+\frac{g_2-{g}_1}{h_1} $$

(18)

In Eqs. (16)–(18), h₁ = l₂ − l₁, h₂ = l₃ − l₂, and

$$ {\displaystyle \begin{array}{c}{g}_1=y\left({x}_{1.{i}_1},\cdots, {x}_{j.1},\cdots, {x}_{D.{i}_D}\right)\\ {}{g}_2=y\left({x}_{1.{i}_1},\cdots, {x}_{j.2},\cdots, {x}_{D.{i}_D}\right)\\ {}{g}_3=y\left({x}_{1.{i}_1},\cdots, {x}_{j.3},\cdots, {x}_{D.{i}_D}\right)\end{array}} $$

(19)

For higher-dimensional cases (D ≥ 3), the partial derivative can be easily derived for each dimension using the abovementioned methods. To apply the proposed design sensitivity analysis method, the number of one-dimensional nodes for each dimension is required to be m_j ≥ 3. This requirement is satisfied for practical problems using the PC method with FFNI. It should be noted that the design sensitivity obtained by the proposed method is theoretically inaccurate when the performance function g(x) is highly nonlinear. However, the local sensitivity requires calculation within a very small design region; thus, the error induced by the Lagrange linear interpolation is not excessively large, as verified in the comparative studies on robust optimization, which are presented further in this paper.

3.2 Design sensitivity analysis method for PC-SGNI

When SGNI is employed for the PC coefficient calculation, the partial derivatives in Eqs. (12) and (13) can be calculated as follows, based on Eq. (7).

$$ \frac{\partial E\left[y{\varPhi}_0\left(\boldsymbol{\upxi} \right)\right]}{\partial {x}_{j.{i}_j}}=\sum \limits_{i_1,{i}_2,\cdots, {i}_D\in \varOmega }{\left(-1\right)}^{Q-\left|i\right|}\left(\begin{array}{c}D-1\\ {}Q-\left|i\right|\end{array}\right)\left(\sum \limits_{i_1=1}^{m_1}{\omega}_{1.{j}_1}\cdots \sum \limits_{i_D=1}^{m_D}{\omega}_{D.{j}_D}\frac{\partial y\left({x}_{1.{i}_1},\cdots, {x}_{D.{i}_D}\right)}{\partial {x}_{j.{i}_j}}\cdot {\varPhi}_i\left(\boldsymbol{\upxi} \right)\right) $$

(20)

where Ω represents the collection of all the multi-index combinations {i₁, ⋯, i_D} that satisfy K + 1 ≤ |i| ≤ Q; and ${x}_{j.{i}_j}$ and ${\omega}_{j.{i}_j}$ are the node and weight coefficients in the jth dimension, respectively, which correspond to one small-size direct full tensor product.

The partial derivative with respect to the node in Eq. (20) can be calculated in the same manner as the FFNI. However, given that SGNI employs the special tensor product, which is a combination of certain small-size direct full tensor products, for the removal of several unimportant integration nodes, the number of one-dimensional nodes for each dimension in the small-size full tensor product may be m_j = 1, 2, ⋯, which cannot satisfy m_j ≥ 3. Therefore, minor modifications should be made. Using the two-dimensional node with K = 2 as an example for illustration, five groups of small-size full tensor products were generated using SGNI (see Fig. 3). The partial derivative with respect to x_j can be calculated with respect to the following two cases.

Fig. 3

Calculation of partial derivatives with SGNI nodes

Case 1: when there are one or two nodes present in the jth dimension x_j for a given group, as illustrated in Fig. 3 (Case 1). The partial derivative cannot be calculated in this case. Several additional nodes based on the original response function are employed for the calculation of the partial derivative, and the induced number of function evaluations is large, especially for higher-dimensional problems. Therefore, the response values of the added nodes are approximately calculated by the PC model, to reduce the computational cost. The partial derivative is then calculated in the same manner as that of FFNI presented above. Given that the PC method is a metamodel in the stochastic domain, such an approximation of the original function response on a few nodes during the design sensitivity analysis calculation would definitely induce some error especially when nonlinear terms with higher polynomial order are involved in the response function. However, such error can be reduced to some extent by increasing the order of PC model. Here, the added nodes are selected as the Gaussian quadrature nodes to ensure a high accuracy.

Case 2: when there is a minimum of three nodes in the jth dimension, as shown in Fig. 3 (Case 2). The calculation procedure of the partial derivative is the same as that of the FFNI.

Compared with FFNI, the application of SGNI to design sensitivity analysis by the proposed method would clearly save the number of functional calls and relieve the curse of dimensionality, which however would reduce the accuracy. As fewer sample points are employed, the accuracy of PC model by SGNI is reduced, which would further reduce the accuracy of statistical moment calculation of output response as well as output response prediction, and finally decrease the accuracy of design sensitivity analysis.

For certain larger-scale problems with very high-dimensional random inputs, adaptive methods have been developed by removing several unimportant orthogonal polynomials from the full PC model, or by the adaptive collocation of the integration nodes during the calculation of the PC coefficients for the reduction of the computational cost (Blatman and Sudret 2011; Perkó et al. 2014; Lucor and Karniadakis 2004). In this case, the design sensitivity is calculated using the developed PC model in the same manner without any modifications. In this paper, the Gaussian-type quadrature formula was employed for constructing PC model. However, due to its high flexibility and low computational cost, the least square estimation method is increasingly applied to the PC method for uncertainty propagation and robust optimization. Therefore, it is necessary to implement a design sensitivity analysis for the least square estimation-based PC method for robust optimization in future work.

4 Comparative studies

To demonstrate the effectiveness of the proposed semi-analytical design sensitivity analysis method, the evaluation of the design sensitivity of two mathematical examples is presented in Section 4.1, followed by the robust optimization of three mathematical examples using the proposed design sensitivity method in Section 4.2. The order of the PC models was set as p = 2, the number of one-dimensional Gaussian quadrature nodes for the FFNI was set as m = 3, and the accuracy level for the SGNI was set as K = 2. Based on the data employed for the statistical moment estimation using the PC method, the design sensitivity was derived for the PC model using the proposed semi-analytical DSA method (denoted by DSA-PC). The traditional finite difference method (FDM) in conjunction with the PC method was also employed for comparison (denoted by FDM-PC), in which the PC method was used for the statistical moment calculation, and the FDM for the sensitivity analysis, by carrying out uncertainty propagation (UP) with the PC method at two points adjacent to the current design point. For the FDM, to ensure the accuracy as much as possible, the central difference method was used to calculate the design sensitivity at x_j in Section 4.1.

$$ \frac{\partial y(x)}{\partial {x}_j}=\frac{y\left({x}_1,\cdots, {x}_j+\varDelta, \cdots, {x}_d\right)-y\left({x}_1,\cdots, {x}_j-\varDelta, \cdots, {x}_d\right)}{2\varDelta } $$

(21)

The step size clearly has a substantial impact on the calculated partial derivative. Therefore, before calculating design sensitivity, a step convergence test that calculates design sensitivities with different step sizes was conducted, based on which a suitable step size was selected for each example in Section 4.1; while for robust optimization in Sections 4.2 and 4.3, as the optimization toolbox in MATLAB was employed, Δ and the finite difference method (central/back/forward-difference) were automatically assigned by the optimization algorithm in MATLAB. The design sensitivity was simultaneously calculated by the FDM based on the estimated statistical moments with the MCS (denoted by FDM-MCS), for which the MCS was employed for the statistical moment estimation, and the FDM for the sensitivity analysis, by carrying out UP with MCS at two points adjacent to the current design point. The results generated by FDM-MCS were employed as the reference values. The total number of function calls (N) required by the moment estimation and design sensitivity analysis was compared. The sequential quadratic programming (SQP) provided in MATLAB was employed as the optimization algorithm considering its high efficiency and good performance. As SQP is a gradient-based optimization algorithm, a local optimal solution may be obtained if a poor initial point is provided. Therefore, as is commonly done in practice, optimization with different starting points is tested to obtain the optimal solutions, among which the best feasible one is selected as the final optimal solution.

4.1 Design sensitivity analysis of mathematical examples

A two-dimensional problem with normal distributed random inputs was first tested:

$$ {\displaystyle \begin{array}{c}g\left({x}_1,{x}_2\right)={\left({x}_1-3\right)}^2+{\left({x}_2+1\right)}^2+5\\ {}{x}_1\sim N\left(4,1\right),{x}_2\sim N\left(\mathrm{5,0.25}\right)\end{array}} $$

(22)

The FFNI was employed to calculate the PC coefficients. The convergence test for MCS with different number of sample points (n) was firstly done for this example to determine a suitable number of sample points (n), and the 95% confidence interval that was estimated by running 20 times the MCS was calculated. The results of the convergence test were shown in Fig. 4. It was found that when n = 10⁷, the confidence interval was very small and the mean and standard deviation tended to be constants, indicating that the results are accurate enough and very close to the real values. Therefore, to ensure the effectiveness of comparison, MCS with n = 10⁷ were conducted to estimate statistical moments for FDM-MCS. For all the rest mathematical examples (Sections 4.1 and 4.2), the same convergence test was also done for FDM-MCS to determine a suitable n for MCS firstly. For space limit, the results of the convergence test for the rest examples were not shown. The step size was set as Δ = 10⁻⁴ considering accuracy after the step convergence test.

Fig. 4

Convergence test for FDM-MCS with different number of sample points

The results obtained by the three approaches (DSA-PC, FDM-PC, FDM-MCS) were shown in Table 1. The proposed DSA-PC method was found to generally produce the same results as the FDM-PC, which were similar to those generated by the FDM-MCS. However, the DSA-PC required significantly fewer function calls than FDM-PC (9 vs. 36), as it carried out no additional function calls to calculate the design sensitivity.

Table 1 Results of sensitivity analysis for Example 1

A higher-dimensional problem (d = 10) with normal distributed random inputs was then tested to verify the effectiveness of the proposed method in a higher-dimensional design sensitivity analysis. The step size was set as Δ = 10⁻⁴.

$$ {\displaystyle \begin{array}{c}f\left({x}_1,\cdots, {x}_{10}\right)=\frac{{\left({x}_1+{x}_2+{x}_3\right)}^2+3{x_4}^3+4\left({x}_5\times {x}_6\right)}{5\left({x}_7+{x}_8\right)\left({x}_9+{x}_{10}\right)}\\ {}{x}_1\sim N\left(3,4\right),{x}_2\sim N\left(4,1\right),{x}_3\sim N\left(5,4\right),{x}_4\sim N\left(4,4\right),{x}_5\sim N\left(3,1\right)\\ {}{x}_6\sim N\left(6,1\right),{x}_7\sim N\left(8,4\right),{x}_8\sim N\left(6,4\right),{x}_9\sim N\left(9,1\right),{x}_{10}\sim N\left(10,4\right)\end{array}} $$

(23)

For the DSA-PC and FDM-PC, the PC coefficients were calculated by SGNI, given that the dimension was relatively high. Similarly, for FDM-MCS, the number of sample points of MCS was set as n = 10⁷ by the convergence test. The results obtained by DSA-PC, FDM-PC, and FDM-MCS were shown in Table 2. The proposed DSA-PC method was found to basically produce very similar results to the FDM-PC, and the results of both methods were similar to those of the FDM-MCS. However, the FDM-PC generally exhibited a slightly higher accuracy than the DSA-PC. This can be attributed to the use of SGNI for the calculation of the PC coefficients for the DSA-PC, in which several response values were approximated by the PC method instead of referring to the original response function, to reduce the computational cost. Thus, a degree of error was presented into the design sensitivity analysis, which only had a slight influence, given that the approximation by the PC was relatively accurate. However, the design sensitivity with respect to x₄ produced by the DSA-PC was clearly less accurate than that of the FDM-MCS; the difference of DSA-PC relative to FDM-PC is up to 15.43%. This is because the response function was more nonlinear with respect to x₄, and the PC model with order p = 2 would produce relatively large error on response prediction, which would induce large error on sensitivity calculation for x₄ when SGNI is employed. The FDM-PC exhibited a higher accuracy than the DSA-PC, but the DSA-PC required a significant lower number of function calls (231 vs. 4620) due to the employment of the proposed design sensitivity method. To reduce such error, the order of PC model is increased from p = 2 to p = 3 and the design sensitivities were calculated again. As the errors of sensitivities with respect to x₄ were relatively large with p = 2, here only results with respect to x₄ are shown: $\mathrm{d}{\mu}_g/\mathrm{d}{\mu}_{x_4}$ = 0.1419, $\mathrm{d}{\sigma}_g/\mathrm{d}{\mu}_{x_4}$ = 0.1197. Cleary, with the increase of PC order, the accuracy of design sensitivity by the proposed DSA-PC method is improved. The results from the two examples demonstrate the accuracy and effectiveness of the proposed semi-analytical design sensitivity method.

Table 2 Results of sensitivity analysis for Example 2

4.2 Robust optimization of mathematical examples

4.2.1 Example 1

$$ {\displaystyle \begin{array}{c}\underset{\mu_{x_1},{\mu}_{x_2}}{\mathit{\operatorname{Min}}}F=\frac{\sigma_f}{15}\\ {}\mathrm{s}.\mathrm{t}.\kern1.75em G={\mu}_g-3{\sigma}_g\ge 0\\ {}1\le {\mu}_{x_1}\le 10,1\le {\mu}_{x_2}\le 10\\ {}\mathrm{where}\kern0.5em f\left({x}_1,{x}_2\right)={\left({x}_1-4\right)}^3+{\left({x}_1-3\right)}^4+{\left({x}_2-5\right)}^2+10\\ {}g={x}_1+{x}_2-6.45\end{array}} $$

(24)

The two random design variables x₁ and x₂ were assumed to be normally distributed with the standard deviation as σ = 0.4. The robust optimization was carried out using the DSA-PC, FDM-PC, and FDM-MCS (with n = 10⁷ for MCS); and FFNI was employed to calculate the PC coefficients. In optimization, the starting point was set as x₀ = [3.0, 5.0]. Once optimization is completed, the confirmed results (F^c and G^c) were obtained by substituting the obtained optimal design variables into the original functions (f and g), respectively, using the MCS method (n = 10⁷) with the consideration of the same uncertainties. The optimal design variables, the confirmed results, and the total number of function calls of the three methods were presented in Table 3.

Table 3 Optimization results of Example 1

As can be seen from Table 3, the three methods obtained feasible optimal solutions with the satisfied constraint G. Moreover, the optimal design variables (${\mu}_{x1}^{\ast },{\mu}_{x2}^{\ast }$), in addition to the confirmed objectives of the FDM-PC and DSA-PC, were slightly different. However, they were very similar to those generated by the FDM-MCS. As the value of constraint G = μ_g − 3σ_g ≥ 0 depends on μ_g, and the magnitude order of the constraint function G is small (10⁻¹), a small difference in ${\mu}_{x1}^{\ast }$ or ${\mu}_{x2}^{\ast }$ would induce relatively large difference in G^c (FDM-MCS: 0.2149; DSA-PC: 0.2968; FDM-PC = 0.2580). Therefore, the error of G^c seems substantially high. To reduce such error, a higher PC order for constraint function g can be employed. However, for practical optimization problems, it is required to find an effective design solution that is feasible (i.e. satisfies the constraints), and it is the optimal design solution that is cared about by users, not the exact values of constraints (only need to be feasible). Moreover, the total number of function calls (N) during optimization was reduced by 27.8% using the proposed DSA-PC method when compared with the FDM-PC.

4.2.2 Example 2

$$ {\displaystyle \begin{array}{c}\underset{\mu_{x_1},{\mu}_{x_2}}{\mathit{\operatorname{Min}}}F=0.5\frac{\mu_f}{10}+0.5\frac{\sigma_f}{2}\\ {}\mathrm{s}.\mathrm{t}.\kern1.25em {G}_1={\mu}_{g_1}-3{\sigma}_{g_1}\ge 0\\ {}{G}_2={\mu}_{g_2}-3{\sigma}_{g_2}\ge 0\\ {}0.2\le {\mu}_{x_1}\le \mathrm{20,0.1}\le {\mu}_{x_2}\le 1.6\\ {}\mathrm{where}\ f\left({x}_1,{x}_2\right)=\rho {x}_1\sqrt{1+{x_2}^2}\\ {}{g}_1={x}_1{x}_2-\frac{0.06Q{x}_1{x}_2}{\sqrt{65}S}\sqrt{1+{x_2}^2}\times \left(8{x}_1+1\right)\ge 0\\ {}{g}_2={x}_1{x}_2-\frac{0.06Q{x}_1{x}_2}{\sqrt{65}S}\sqrt{1+{x_2}^2}\times \left(8{x}_1-1\right)\ge 0\end{array}} $$

(25)

The distribution parameters of the random variables and random parameters are shown in Table 4. The robust design optimization was carried out using the DSA-PC, FDM-PC, and FDM-MCS (n = 10⁷ for MCS). The FFNI was employed to calculate the PC coefficients for the moment estimation. In optimization, the starting point was set as x₀ = [3.0, 0.1].

Table 4 Distribution parameters for input random variable and parameters

Table 5 presents the optimization results, in which F^c, ${G}_1^c$, and ${G}_2^c$ represent the results confirmed using the MCS method (n = 10⁷). As can be seen from Table 5, the results obtained by the FDM-PC and DSA-PC were approximately equal, which were in good agreement with those obtained by the FDM-MCS. Moreover, when compared with the FDM-PC, the function evaluations of the original objective f and constraints g for the DSA-PC were both reduced by 38.9%. The proposed DSA-PC method can significantly reduce the computational cost while maintaining an adequate accuracy of design sensitivity.

Table 5 Optimization results of Example 2

4.2.3 Example 3

$$ {\displaystyle \begin{array}{c}\underset{\mu_{x_1},,\dots, {\mu}_{x_8}}{\mathit{\operatorname{Min}}}F=1.5{\mu}_f+0.4{\sigma}_f\\ {}\kern0.75em \mathrm{s}.\mathrm{t}.\kern1.25em {G}_1={\mu}_{g_1}-3{\sigma}_{g_1}\ge 0\\ {}\mathrm{where}\;f\left({x}_1,\dots, {x}_8\right)={\left(\frac{\left({x}_1-5\right)}{2}+\frac{\left({x}_2-4\right)}{3}-3\right)}^2+{\left({x}_3-3\right)}^4+{\left({x}_3+{x}_4-4\right)}^2\\ {}+{\left({x}_5-4\right)}^2+{\left(4{x}_6-6\right)}^4+{\left({x}_7-7\right)}^2+{\left({x}_8-8\right)}^2\\ {}g=2+\left({x}_3+{x}_4-4\right)\left({x}_1+{x}_2-14\right)\end{array}} $$

(26)

The distribution parameters of the random variables are shown in Table 6, in which “Range” represents the design region of the design variable during optimization; “Std” denotes the standard deviation of the distribution; and A and B represent the upper and lower limits of the uniform distributed random design variable, respectively. The robust design optimization was carried out using the DSA-PC, FDM-PC, and FDM-MCS (n = 10⁷ for MCS). Considering that it was a relatively high-dimensional problem, SGNI was employed to calculate the PC coefficients for the moment estimation. In optimization, the starting point was set as x₀ = [8.0, 4.0, 2.0, 1.0, 3.0, 1.0, 5.0, 6.0].

Table 6 Distribution parameters of input random variable

As can be seen from the optimization results shown in Table 7, the optimal solutions obtained by the FDM-PC and DSA-PC were very similar, but the FDM-PC exhibited a slightly higher accuracy than the DSA-PC. This can be attributed to the use of additional nodes based on the approximation of PC model, for the calculation of a sensitivity term, which introduces a degree of error into the final design sensitivity. Such error does not have large impact on the optimal solution of this example when p = 2, even if the highest order of the response functions is 4, demonstrating the effectiveness of approximation with PC for high-dimensional problems in the DSA-PC. However, when compared with the FDM-PC, the DSA-PC reduced the required number of function evaluations of the original objective f and constraint g by 43.0%. The proposed DSA-PC method can significantly reduce the computational cost while maintaining an adequate accuracy of design sensitivity.

Table 7 Optimization results of Example 3

Further, to investigate the impact of sensitivity estimation error induced by Lagrange linear interpolation on the optimization convergence speed, the evolutions of the objective function (F) for the proposed DSA-PC and the FDM-MCS during the optimization process for the three examples above were shown in Figs. 5, 6, and 7, respectively. Three noteworthy observations were made.

Fig. 5

Evolution of F during optimization (Example 1)

Fig. 6

Evolution of F during optimization (Example 2)

Fig. 7

Evolution of F during optimization (Example 3)

Firstly, it was found that with the increase of iteration number, the values of F for both methods (DSA-PC and FDM-MCS) for the three examples were generally decreased rapidly, and remained almost unchanged at the end of optimization, indicating that the optimal solutions were convergent. Meanwhile, the values of F produced by both approaches were close to each other, especially for Example 2. Generally, only slightly more (1 or 3) iteration numbers were required by DSA-PC.

Secondly, compared with Example 1 and Example 2, more iterations were required for Example 3. The interpretation is as follows. Example 3 was relatively a high-dimensional (d = 8) problem; and meanwhile, the SGNI technique was employed for calculating the PC coefficients, and the response values of some added nodes were approximately calculated by the PC model, inducing another source of error in sensitivity calculation. However, from Fig. 7, it was noticed that F of the proposed DSA-PC method rapidly approached to the optimal solution.

Thirdly, it was also noticed that the difference in F during the whole iteration process produced by both methods for Example 1 was the largest, which was relatively large even at the initial starting design point. The interpretation is that for Example 1, the response function f(x₁, x₂) is relatively more nonlinear and the standard deviation of design variable is relatively large (σ=0.4, 8% ~ 12% of the mean value), and thus relatively large errors would be induced in the statistical moment calculation using 2-order PC and further in sensitivity analysis. However, from the optimal results shown in Table 3, it was found that the results produced by DSA-PC were close to that of FDM-MCS, which further demonstrated the high accuracy of sensitivity estimation.

All these observations indicated that the sensitivity estimation error induced by Lagrange linear interpolation of the proposed DSA-PC method had a very small impact on the optimization convergence, which was attributed to the high accuracy of sensitivity estimation.

4.3 Airfoil robust optimization design

The proposed DSA-PC method was applied to an airfoil robust optimization problem, and the NACA0012 airfoil was considered the baseline (Wang et al. 2019b). The objective was the determination of the optimal geometric parameters of the airfoil, to maximize the lift-drag ratio of the airfoil subject to the thickness constraint of the airfoil. The nominal flow condition considered corresponds to the angle of attack α = 1.55°, Mach number M_a = 0.70 and Reynolds number Re = 9e6. It is a typical flight Reynolds number of a commercial aircraft. The B-spline curve (Wang and Liu 2016) with eight control points was employed for the shape parameterization of the airfoil, where the horizontal locations of the eight control points were fixed as l = [0.2, 0.4, 0.6, 0.8, 0.8, 0.6, 0.4, and 0.2] and the vertical locations were free to move, as shown in Fig. 8. The original airfoil was considered the baseline with the vertical locations of the eight control points as z_baseline = [0.0574, 0.0580, 0.0456, 0.0262, − 0.0262, − 0.0456, − 0.0580, and − 0.0574]. The vertical locations of the eight control points were considered design variables x = [x₁, ⋯, x₈].

Fig. 8

Airfoil parametric modeling

Clearly, from the physical mechanism, Re and α have large impacts on the result of CFD simulation. Generally, only one category of fluid viscosity is investigated in a study, and it is impossible to study the impacts of all the different kinematic viscosities. Therefore, as for the impact of Re, we mainly considered the influence of Ma. For robust optimization, all the design variables x_i(i = 1, …, 8) were assumed to be uncertain considering the manufacturing error and in accordance with the normal distribution, with the standard deviation as ${\sigma}_{x_i}=0.0015$. Meanwhile, M_a and α were assumed to follow uniform distribution with variations ±0.1 and ±0.5° around their nominal values (α = 1.55, M_a = 0.70), respectively. The airfoil robust optimization was formulated as follows.

$$ {\displaystyle \begin{array}{c}\underset{\mu_{x_1},\dots, {\mu}_{x_8}}{\mathit{\operatorname{Min}}}F=-{\mu}_f+3{\sigma}_f\\ {}\mathrm{s}.\mathrm{t}.\kern1em G={\mu}_{T_w}\ge 0.1\\ {}{\mu}_{x_i}+3{\sigma}_{x_i}\le 0.005\\ {}{\mu}_{x_i}-3{\sigma}_{x_i}\ge -0.005\\ {}-0.005\le {\mu}_{x_i}\le 0.005\end{array}} $$

(27)

where ${\mu}_{T_w}$ is the mean value of the maximum relative thickness T_w.

Computational fluid dynamics (CFD) was employed for the aerodynamic analysis, to obtain the lift and drag. In addition, the mesh was generated using the CFD pre-processor Gambit software. During the aerodynamic analysis, the k-omega two-equation turbulent model was employed, and Fluent 17.0 was used as the CFD solver. In order to verify the accuracy of the result of CFD simulation, the grid convergence test was firstly performed on the baseline airfoil at the nominal flow condition (α = 1.55°, = 0.70, and Re = 9e6) and the results were shown in Table 8. From Table 8, it was observed that when the grid density was increased to some value (far field: 150; airfoil boundary: 300), the lift-drag ratio remained almost unchanged. Thus, the number of nodes in the grid far field was set as 150, whereas the number of airfoil boundary nodes was set as 300 in CFD simulation of this study.

Table 8 Grid convergence test on the baseline airfoil

Then, the lift (C_l) and drag (C_d) coefficients of the baseline NACA 0012 for the nominal flow condition (α = 1.55°, = 0.70 and Re = 9e6) calculated by CFD were compared with the experimental data from Harris’s test in the Langley 8-Foot Transonic Pressure Tunnel (Harris 1981), which were shown in Table 9. It was noticed that the CFD results were very close to the experimental data, validating the effectiveness of CFD analysis in this work.

Table 9 Comparison of CFD results and experimental data

Robust optimization was carried out using the DSA-PC and FDM-PC, and the deterministic optimization (DO) was carried out without considering any uncertainties for comparison. Moreover, SGNI with an accuracy level of K = 2 was employed for the PC coefficient calculation. For${\mu}_{T_w}$, given that it did not require a computationally complex CFD analysis, it was directly obtained using the MCS method.

The optimal airfoil geometries generated using the DSA-PC, FDM-PC, and DO were shown in Fig. 9. It was observed that when compared with the original airfoil, the airfoils optimized using the deterministic optimization (DO) and robust optimization (RO) methods were both more bent, and the curvatures of the upper wings were increased, especially for the one produced by DO, which increased the airflow speed. Therefore, the air pressure of the upper wing decreased after optimization, resulting in an increase in the lift coefficient. In addition, the thickness of the leading edge of the optimized airfoils was obviously reduced compared with the original baseline one, which would weaken the shock wave area, and thus reduce the drag coefficient. Finally, an increase in lift-drag ratio was obtained through optimization. Furthermore, the airfoil generated from the robust optimization using the DSA-PC was almost overlapped to that of the FDM-PC. These results demonstrate the effectiveness of the proposed DSA-PC method.

Fig. 9

Optimized and baseline airfoils

The static pressure contours were shown in Fig. 10. As can be seen from the figure, when compared with the baseline airfoil, the static pressures of the upper surfaces of the airfoils generated by the RO and DO methods were smaller (the area in blue increased after optimization); whereas the static pressures of the lower surface were larger (the area in green increased after optimization). This indicates an increase in the differential pressure between the upper and lower surfaces; thus, there would be an increase in the lift of the airfoil after optimization. Moreover, the static pressure cloud produced by the DSA-PC was very similar to that of the FDM-PC. These results further demonstrate the effectiveness of the proposed DSA-PC method.

Fig. 10

Static pressure clouds for: (a) baseline of NACA0012, (b) optimized result of deterministic optimization, (c) optimized result of robust optimization with FDM-PC, (d) optimal result of robust optimization with DSA-PC

The pressure coefficients of the upper and lower surfaces of the airfoil were illustrated in Fig. 11. It could be noticed that compared with the baseline airfoil, the upper surface pressure coefficients of all the optimized airfoils were decreased, while the lower surface pressure coefficients were increased. Meanwhile, the gap between the lower and upper surfaces was increased after optimization, which was the largest for DO. These results indicate that the pressure difference between the upper and lower surfaces is increased, resulting in an increase in lift after optimization.

Fig. 11

Pressure coefficient along the upper and lower airfoil surfaces for: (a) baseline of NACA0012, (b) optimal result of deterministic optimization, c) optimized result of robust optimization with FDM-PC, (d) optimized result of robust optimization with DSA-PC

The evolution of the objective function (F) during the optimization process was shown in Fig. 12. As the computational cost using MCS-PC (MCS was directly employed for statistical moment calculation) was relatively large, it was not tested for this example and only FDM-PC was compared. It was found that with the increase of iteration number, the values of objective function F of both methods (DSA-PC and FDM-PC) were generally decreased, and remained almost unchanged at the end of the optimization, indicating that the optimal results were convergent. Meanwhile, the values of F produced by DSA-PC and FDM-PC were similar to each other, and slightly more iterations were required by DSA-PC. These observations showed great agreements with those of the mathematical examples in Section 4.2. For DSA-PC, SGNI was used as it was relatively a high-dimensional problem, in which PC was employed to approximate the response values of some added nodes, and thus more or less errors would be induced. Therefore, a larger iteration number of DSA-PC was required. However, such approximation basically did not have any impact on the obtained performance of the airfoil.

Fig. 12

Evolution of objective function during optimization

The optimal results of the different methods are shown in Table 10, in which N represents the function evaluations of the CFD for the calculation of the lift-drag ratio during optimization. From Table 10, several noteworthy observations can be made. First, both RO and DO increased the lift-drag ratio of the airfoil (μ_f) by optimization and satisfied the thickness constraint. This was consistent to the results shown in Figs. 6, 7, and 8, that the lift was increased and the drag was decreased after optimization. Second, the obtained lift-drag ratio (μ_f) of the DO was larger than those of the two ROs; whereas the standard deviation (σ_f) of the two ROs were significantly smaller, thus exhibiting better robustness with respect to uncertainties. This was consistent with the scenario of robust optimization. Third, the airfoil thickness of the leading edge of the two ROs and DO was obviously reduced compared with that of the original baseline airfoil, and it was decreased more for ROs, which could result in a decrease in the drag coefficient. This perfectly corresponded to the drag valueμ_Cdthat it was decreased after optimization. In conclusion, the results provided in Figs. 9, 10, 11, and 12 and Table 10 suggested that the increase in the lift-drag ratio for DO was mainly ascribed to the increase in lift, while it was mainly ascribed to the decrease in drag for ROs. Fourth, the results of the proposed DSA-PC were similar to those of the FDM-PC, whereas the DSA-PC significantly reduced the computational cost (N) by approximately 41.6% due to the employment of the semi-analytical design sensitivity analysis method. All these results presented above demonstrate the effectiveness of the proposed DSA-PC method.

Table 10 Optimal results of the airfoil

In addition, optimization was also done considering only uncertainties from design variables, of which the optimized airfoils were shown in Fig. 13. It was found that the airfoils generated by DO and ROs did not exhibit clear difference, indicating that the uncertainty in airfoil geometry has small impact on the lift-to-drag ratio. According to all the optimal results provided, we can conclude that Ma and α have large impact on the airfoil performance, which should be taken into account during the airfoil design.

Fig. 13

Optimal airfoils considering manufacturing uncertainty

5 Conclusion

In this paper, to reduce the computational cost of the calculation of the local design sensitivity during robust design optimization with computationally expensive response functions and difficulty in applying the adjoint method, a semi-analytical sensitivity method is proposed based on the PC method in conjunction with the Gaussian quadrature formulae. With the proposed method, the local design sensitivity during the optimization iteration is directly derived in the PC model using the nodes for the statistical moment calculation, instead of employing many additional function evaluations. Several mathematical examples and an aerodynamic robust optimization problem were used to demonstrate the effectiveness of the proposed design sensitivity analysis method. The results proved that the proposed method can lead to satisfactory design sensitivities and optimal solutions that are close to those produced by the traditional finite difference method, while clearly reduce the computational cost of robust optimization. For input random dimension within 10, the proposed method can save up to 43.0% functional calls. The higher of the random input dimension, the more obvious of the computational saving. For problems with highly nonlinear response functions, the proposed method with a low PC order may yield evident errors, which however can be reduced by increasing the PC order. Future work will be focused on developing a design sensitivity analysis approach for the least square estimation-based PC method for robust optimization.