A B-spline multi-parameterization method for multi-material topology optimization of thermoelastic structures

Abstract

A B-spline multi-parameterization method (MPM) is presented in this paper for topology optimization of thermoelastic structures. As thermoelastic topology optimization belongs to a kind of design-dependent problems that are complicated to deal with, this method is aimed to solve thermoelastic problems with multiple materials by means of B-spline parameterization that integrates together the recursive multiphase material interpolation (RMMI) and the uniform multiphase material interpolation (UMMI) schemes. The commonly used discrete pseudo-density variables related to the finite element model are thus replaced with continuous pseudo-density fields dominated by control parameters in the B-spline space. In this sense, B-spline multi-parameterization is used for the first time to represent multiple pseudo-density fields and multi-material properties including elasticity matrix and thermal stress coefficient. Compared with traditional pseudo-density method, the current method has the advantage of not only attaining a reduction of design variables in number but also achieving a regularized distribution of pseudo-density fields with a clear material layout over the whole structure domain. Numerical results show that the stable convergences are achieved with the avoidance of gray elements, checkerboards, and multi-material overlapping owing to the high continuity of B-spline preserved for multi-material distributions. Besides, it is found that the RMMI scheme distributes less stiff materials around stiff materials, while the UMMI scheme tends to gather less stiff materials together.

1 Introduction

Structural topology optimization has been recognized as an effective and versatile design method in engineering community. Among others, density-based method has been extensively studied and applied to deal with different kinds of problems such as multi-component layout design (Bendsøe and Sigmund 2003; Zhang et al. 2011), thermoelastic structures (Gao et al. 2016), and lattice structure design (Gu et al. 2012). This method is characterized by the fact that the optimal material layout of a structure is thought for based on the discrete finite element (FE) model. In other words, design variables, i.e., the so-called pseudo-density variables, are associated with elements or nodes and vary continuously between 0 and 1 to represent the void or solid materials at concerned elements. Solid isotropic material with penalization (SIMP) scheme (Bendsøe and Sigmund 1999), rational approximation of material properties (RAMP) (Stolpe and Svanberg 2001), and (bidirectional) evolutionary structural optimization (ESO/BESO) schemes (Xie and Steven 1993; Xia et al. 2016) are usually applied to drive each design variable toward a 0/1 solution. Level set method is an alternative method that employs high-dimensional level set functions as boundary representations to drive topology optimization of a structure (Wang et al. 2003; Luo et al. 2008). In the earlier time, this method realized the structural evolution according to the velocity field of the boundary by resolving the Hamilton-Jacobi equation.

The extension of density-based method was initiated by Thomsen (Thomsen 1992) to deal with multi-material problems and later applied to multiphysics actuators (Sigmund 2001), lattice structures (Wu et al. 2017), and acoustic-structure interaction problems (Yoon et al. 2007). Its ESO version was also developed (Huang and Xie 2009). Especially, laminate composite structures were optimized as a discrete material optimization (DMO) problem (Stegmann and Lund 2005). In this sense, multi-material interpolation schemes such as shape functions with penalization (SFP) (Bruyneel 2011), bi-value coding parameterization (BCP) (Gao et al. 2012), recursive multiphase material interpolation (RMMI), and uniform multiphase material interpolation (UMMI) (Gao and Zhang 2011) were systematically developed for the layout and fiber orientation design. It is shown that the UMMI has advantages in convergence rate and reduction of the gray elements. Detailed works about solving multi-material problems with the level set method can be found in (Mei and Wang 2004; Wang and Wang 2004; Wang et al. 2015).

Concerning multi-material topology optimization of thermoelastic structures, the challenge is that the involving thermal stress is a kind of design-dependent load (Rodrigues and Fernandes 1995; Li et al. 1999; Xia and Wang 2008). Within the scope of density-based method, materials with extreme thermal expansion were designed through a three-phase topology method (Sigmund and Torquato 1997). Strength-based topology optimization of thermoelastic structures was performed to achieve a uniform distribution of energy density (Pedersen and Pedersen 2010). The concept of thermal stress coefficient (TSC) was introduced to favor the consistent penalty between stiffness and load (Gao and Zhang 2010). Meanwhile, dynamic compliance minimization of a thermally stressed bi-material plate and thermoelastic buckling problems were studied in (Yang and Li 2012; Wu et al. 2019).

However, numerical artifacts such as checkerboard and mesh-dependence are troublesome for the resulting distribution of pseudo-density field due to the FE discretization (Sigmund and Petersson 1998). Various treatments such as sensitivity filter (Sigmund and Maute 2012), density filter (Bourdin 2001), and Heaviside projection (Guest et al. 2004; Wang et al. 2011) were thus proposed to overcome the aforementioned drawbacks.

In recent years, attempts are made to parameterize globally the pseudo-density field independently of the discrete FE model of a structure. B-spline parameterization was adopted to construct continuous pseudo-density field owing to its design flexibility in CAD community (Qian 2013; Taheri and Suresh 2017). In this way, design variables dominating the pseudo-density field are defined by a grid of control parameters. A non-local Shepard interpolation strategy was also developed to construct the pseudo-density field independently of the FE mesh of analysis model in (Kang and Wang 2011).

In this paper, multi-material topology optimization of thermoelastic structures with thermal load strongly dependent of structural topology is dealt with by means of the B-spline multi-parameterization method. Available multi-material properties such as elasticity matrix and thermal stress coefficient (TSC) are firstly interpolated to obtain a global material field using the UMMI or RMMI scheme. Then, each involving pseudo-density field is independently parameterized in its own B-spline space. It is shown that the high-order continuity of the multi-parameterization method (MPM) produces effective solutions with stable convergence.

The remainder of this paper is organized as follows: In Section 2, basic ideas of multi-parameterization method of multiple fields are briefly presented. In Section 3, the formulation of finite element analysis of thermoelastic structures using fixed mesh is developed. In Section 4, topology optimization and sensitivity analysis are discussed. Several numerical examples are illustrated in Section 5; conclusions are given in Section 6.

2 B-spline multi-parameterization method of multiple fields

In general case, consider a multi-material structure occupying physical domain Ω_p with inner and outer boundaries defined by a level set function ϕ(x). The structural boundary can be represented by the zero contour of the level set function, and any point x inside the domain can be classified according to the sign of the level set function.

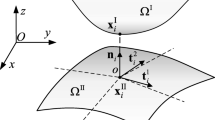
Assume the structure has its Dirichlet and Neumann boundary conditions and is embedded in a regular enlarged domain Ω. The level set function ϕ(x) is employed only for boundary description but not designable; thus, both Dirichlet and Neumann boundary conditions are not movable. ΔT represents the temperature rise, as illustrated in Fig. 1. The structure is then governed by the following equilibrium equation:

$$ {\int}_{\varOmega}\upvarepsilon \left(\mathbf{w}\right):\mathbf{D}:\upvarepsilon \left(\mathbf{u}\right)\cdot H\left(\phi \right) d\varOmega ={\int}_{\varOmega}\mathbf{w}\cdot \mathbf{f}\left(\varDelta T\right)\cdot \kern0.33em H\left(\phi \right) d\varOmega +{\int}_{\varGamma_N}\kern0.33em \mathbf{w}\cdot \mathbf{t} d\varGamma . $$

(1)

Fig. 1

A thermoelastic structure

Here, ε, D, f(∆T), and t denote the strain tensor, elasticity tensor, body force related to ΔT, and boundary traction force on Γ_N. u and w refer to the real and virtual displacement fields, respectively. H(ϕ) is the Heaviside function with H(ϕ(x)) = 1, x ∈ Ω_p   and  H(ϕ(x)) = 0, x ∈ Ω_p. To be specific, the body force related to ∆T can be expressed as:

$$ \mathbf{f}\left(\varDelta T\right)={\mathbf{B}}^{\mathrm{T}}\cdot \mathbf{D}\cdot \varPhi \cdot \alpha \cdot \varDelta T\cdot H\left(\phi \right) $$

(2)

where B and α denote the strain-displacement matrix and coefficient of thermal expansion. Φ refers to the prescribed vector with Φ = [1 1 0]^T in 2D and Φ = [1 1 1 0 0 0]^T in 3D.

As discussed below, the proposed multi-parameterization method is to model multi-material distributions by pseudo-density fields, and each of them is independently parameterized in B-spline space.

2.1 Multi-material interpolation of thermoelastic structures

Assume there exist m solid materials for topology optimization of the above thermoelastic structure. Let ρ^(k) (0 ≤ ρ^(k) ≤ 1, k = 1,...,m) represents the pointwise pseudo-density variables related to the solid material phases. D_k, β_k, and γ_k denote the elasticity matrix, vector of coefficient of thermal stress, and mass density of material k. According to our previous work (Wang et al. 2015), multi-material interpolations can be carried out by the UMMI or RMMI schemes. For example, interpolations of elasticity matrix produce

$$ \mathrm{UMMI}:\kern1.65em \mathbf{D}=\sum \limits_{k=1}^m\chi \left({\rho}^{(k)}\right)\underset{\begin{array}{l}j=1\\ {}j\ne k\end{array}}{\overset{m}{\varPi }}\left(1-\chi \left({\rho}^{(j)}\right)\right){\mathbf{D}}_k $$

(3)

$$ {\displaystyle \begin{array}{l}\mathrm{RMMI}:\kern1.98em \mathbf{D}=\chi \left({\rho}^{(m)}\right){\mathbf{D}}_{\left(1,m\right)}\\ {}\mathrm{with}\kern3.63em \left\{\begin{array}{l}{\mathbf{D}}_{\left(m,m\right)}={\mathbf{D}}_m\\ {}{\mathbf{D}}_{\left(m-j,m\right)}=\chi \left({\rho}^{(j)}\right){\mathbf{D}}_{\left(m-j+1,m\right)}+\left(1-\chi \left({\rho}^{(j)}\right)\right){\mathbf{D}}_{m-j}\kern1.32em \left(j=1,\dots, m-1\right)\end{array}\right.\end{array}} $$

(4)

Here, χ represents the penalty function in the form of SIMP or RAMP:

$$ \chi \left({\rho}^{(k)}\right)=\left\{\begin{array}{l}{\left({\rho}^{(k)}\right)}^q,\kern4.2em \mathrm{SIMP}\\ {}\frac{\rho^{(k)}}{1+s\left(1-{\rho}^{(k)}\right)},\kern1.65em \mathrm{RAMP}\end{array}\right. $$

(5)

q and s denote the penalty coefficients in SIMP and RAMP, respectively. Both the UMMI and RMMI schemes are nonlinear in terms of ρ^(k).

To have a clear idea, consider the case of two solid materials (m = 2) with SIMP penalty coefficient q = 3. We have then:

$$ {\displaystyle \begin{array}{l}\mathrm{UMMI}:\\ {}\mathbf{D}={\left({\rho}^{(1)}\right)}^3\left(1-{\left({\rho}^{(2)}\right)}^3\right){\mathbf{D}}_1+{\left({\rho}^{(2)}\right)}^3\left(1-{\left({\rho}^{(1)}\right)}^3\right){\mathbf{D}}_2=\left\{\begin{array}{l}{\mathbf{D}}_1,\kern0.99em \mathrm{if}{\rho}^{(1)}=1,\kern0.66em {\rho}^{(2)}=0\\ {}{\mathbf{D}}_2,\kern0.99em \mathrm{if}{\rho}^{(1)}=0,\kern0.66em {\rho}^{(2)}=1\\ {}\mathbf{0},\kern1.65em \mathrm{if}{\rho}^{(1)}={\rho}^{(2)}=0\kern0.66em \mathrm{or}\kern0.66em {\rho}^{(1)}={\rho}^{(2)}=1\end{array}\right.\end{array}} $$

(6)

$$ {\displaystyle \begin{array}{l}\mathrm{RMMI}:\\ {}\mathbf{D}={\left({\rho}^{(1)}\right)}^3\left[{\left({\rho}^{(2)}\right)}^3{\mathbf{D}}_1+\left(1-{\left({\rho}^{(2)}\right)}^3\right){\mathbf{D}}_2\right]=\left\{\begin{array}{l}{\mathbf{D}}_1,\kern0.99em \mathrm{if}{\rho}^{(1)}=1,\kern0.66em {\rho}^{(2)}=1\\ {}{\mathbf{D}}_2,\kern0.99em \mathrm{if}{\rho}^{(1)}=1,\kern0.66em {\rho}^{(2)}=0\\ {}\mathbf{0},\kern1.65em \mathrm{if}{\rho}^{(1)}=0\end{array}\right.\end{array}} $$

(7)

The same interpolation can also be made for thermal stress coefficient β_k defined by:

$$ {\upbeta}_k={\alpha}_k\cdot {\mathbf{D}}_k\cdot \varPhi $$

(8)

where α_k represents the coefficient of thermal expansion of material k.

For example, take m = 2 with RAMP(s = 0) or SIMP(q = 1). It follows that:

$$ {\displaystyle \begin{array}{l}\mathrm{UMMI}:\\ {}\boldsymbol{\upbeta} ={\rho}^{(1)}\left(1-{\rho}^{(2)}\right){\boldsymbol{\upbeta}}_1+{\rho}^{(2)}\left(1-{\rho}^{(1)}\right){\boldsymbol{\upbeta}}_2\end{array}} $$

(9)

$$ {\displaystyle \begin{array}{l}\mathrm{RMMI}:\\ {}\boldsymbol{\upbeta} ={\rho}^{(1)}\left({\rho}^{(2)}{\boldsymbol{\upbeta}}_1+\left(1-{\rho}^{(2)}\right){\boldsymbol{\upbeta}}_2\right)\end{array}} $$

(10)

Notice that in the conventional density-based method, pseudo-density variable ρ^(k) is discretized as a set of design variables attached to the discrete elements of the FE model.

2.2 B-spline space

As shown in Fig. 2, a B-spline surface is constructed over the parametric space (ξ,η) and dominated by a set of control parameters {P_ij}. In fact, the similar parameterization can also be made using non-uniform rational B-spline (NURBS) or other forms. By modifying the corresponding control parameters, the B-spline surface can be changed locally and smoothly. Mathematically, the B-spline parametric surface is expressed as:

$$ \rho \left(\xi, \eta \right)=\sum \limits_{i=0}^{n_x-1}\sum \limits_{j=0}^{n_y-1}{N}_{i,p}\left(\xi \right){N}_{j,p}\left(\eta \right){P}_{ij},\kern0.66em 0\le \xi, \eta \le 1 $$

(11)

Fig. 2

Illustration of B-spline parametric surface and its control points

Here, n_x and n_y denote the numbers of control parameters distributed along ξ and η direction, respectively. N_i,p and N_j,p denote the p-order B-spline basis functions in ξ and η directions (see Fig. 3 for illustration of N_i,p(ξ)). The strong convex hull property of B-splines ensures that interpolated densities respect the same upper and lower bounds of the control parameters. For example, the knot vector $\varXi =\left\{{\xi}_0,\dots, {\xi}_{n_x+p}\right\}$ contains n_x + p + 1 knots that are uniformly distributed along ξ direction. B-spline basis functions N_i,p(ξ) can be calculated below.

$$ \left\{\begin{array}{l}{N}_{i,0}\left(\xi \right)=\left\{\begin{array}{l}1,\kern0.99em {\xi}_i\le \xi <{\xi}_{i+1}\\ {}0,\kern0.99em \mathrm{otherwise}\end{array}\right.,\kern0.66em i=0,1,\kern0.33em \dots, {n}_x-1\\ {}{N}_{i,p}\left(\xi \right)=\frac{\xi -{\xi}_i}{\xi_{i+p}-{\xi}_i}{N}_{i,p-1}\left(\xi \right)+\frac{\xi_{i+p+1}-\xi }{\xi_{i+p+1}-{\xi}_{i+1}}{N}_{i+1,p=1}\left(\xi \right),i=0,1,\kern0.66em \dots, \kern0.33em {n}_x-1\\ {}\mathrm{provide}\kern0.9100001em \frac{0}{0}=0\end{array}\right. $$

(12)

Fig. 3

B-spline basis functions of order p = 2

2.3 B-spline parameterization of multiple pseudo-density fields

As mentioned in Section 2.1, there exist m pseudo-density fields ρ^(k),(k = 1,...,m) when m solid materials are available. Each pseudo-density field can change independently of others. As shown in Fig. 4, a uniform parametric mesh of m_x × m_y is firstly established within the domain of (ξ, η) ∈ [0,1] × [0,1]. Thus, the regular embedded domain (x,y) ∈ [0,l_x] × [0,l_y] can be projected to the parametric domain (ξ,η) through the following formulation and vice versa:

$$ \xi =\frac{x}{l_x},\kern0.66em \eta =\frac{y}{l_y} $$

(13)

Fig. 4

Illustration of mesh of parametric domain, grid of control parameters, and distribution of pseudo-density

Two uniform knot vectors can be obtained from the parametric mesh in each direction: {ξ} = {0, ξ₁, …, 1} and η = {0, η₁, …, 1}. Then, the mesh of n_x × n_y control parameters {P_ij} is generated while the location of each P_ij is obtained by the following equation with knot vector {ξ}, {η}, and order p:

$$ \left\{\begin{array}{l}{\xi}_{Pij}=\frac{1}{p}\left({\xi}_{i+1}+\dots +{\xi}_{i+p}\right)\\ {}{\eta}_{Pij}=\frac{1}{p}\left({\eta}_{j+1}+\dots +{\eta}_{j+p}\right)\end{array}\right. $$

(14)

Afterwards, the B-spline space is generated according to the values and locations of control parameters {P_ij}. In order to ensure the tangency property of B-splines with control polygons, duplicate knots of number p + 1 are defined at two ends of the knot vector {ξ} and {η}. Relations between nx/ny and m_x/m_y are n_x = m_x + p − 1, n_y = m_y + p − 1. As a result, non-uniform control parameters exist near the domain boundaries due to the duplicate knots. Finally, the pseudo-density distribution of the structure is projected and calculated by the B-spline space. And pseudo-densities outside the boundary are tailored. For a better understanding, the shape of B-spline space is illustrated in Fig. 2.

According to (11), the B-spline parameterization of pseudo-density field ρ^(k) (k = 1,...,m) involved in (3) and (4) corresponds to:

$$ {\rho}^{(k)}\left(x,y\right)={\rho}^{(k)}\left(\xi, \eta \right)=\sum \limits_{i=0}^{n_x^{(k)}-1}\sum \limits_{i=0}^{n_y^{(k)}-1}{N}_{i,p}\left(\xi \right){N}_{j,p}\left(\eta \right){P}_{ij}^{(k)},k=1,\dots, m $$

(15)

As an example, Fig. 5 illustrates the multi-parameterization of three pseudo-density fields. Three grids of control parameters and the corresponding pseudo-density fields, ρ⁽¹⁾, ρ⁽²⁾, and ρ⁽³⁾, are projected to the whole physical domain while each grid can have its proper number of control points.

Fig. 5

Multi-parameterization of three pseudo-density fields

3 Structural analysis of thermoelastic structures with fixed mesh

Figure 6 shows the fixed mesh applied to the embedding domain illustrated in Fig. 1. Compared with the standard isogeometric analysis, the fixed mesh with level set function makes it possible to avoid not only the exhausting patch-cutting and jointing process but also the mesh updating process in the optimization, while still keeping a good computing accuracy (Cai et al. 2014). The FE equation then corresponds to:

$$ \mathbf{K}\left(\boldsymbol{\uprho} \right)\mathbf{U}={\mathbf{F}}_{\mathrm{Me}}\left(\boldsymbol{\uprho} \right)+{\mathbf{F}}_{\mathrm{Th}}\left(\boldsymbol{\uprho} \right) $$

(16)

where ρ = {ρ⁽¹⁾, ρ⁽²⁾,... ρ^(m)} denotes the vector of pseudo-density fields. K, U, F_Me, and F_Th denote the global stiffness matrix, displacement vector, mechanical load vector, and thermal load vector, respectively. They are given as:

$$ \mathbf{K}=\sum {\mathbf{k}}_{\mathrm{e}} $$

(17)

$$ {\mathbf{F}}_{\mathrm{Me}}={\int}_{\varGamma_N}{\mathbf{N}}^{\mathrm{T}}\mathbf{t}\kern0.33em d\varGamma $$

(18)

$$ {\mathbf{F}}_{\mathrm{T}\mathrm{h}}={\int}_{\varOmega}\mathbf{f}\left(\varDelta T\right) d\varOmega =\varDelta T{\int}_{\varOmega }{\mathbf{B}}^{\mathrm{T}}\cdot \boldsymbol{\upbeta} \cdot H\left(\phi \right) d\varOmega $$

(19)

where D(ρ) denotes the elasticity matrix interpolated by (3) or (4).

Fig. 6

Structural analysis with fixed mesh

As shown in Fig. 6, finite elements can be classified into three categories: inner element, boundary element, and void element according to their relative positions with respect to the structural boundary. The level set function ϕ describing the boundary can be defined by R-function, K-S function, or P-norm function (Zhou et al. 2016) through Boolean operation of basic shape primitives.

In our B-spline MPM, each element is supposed to possess homogenous material property. Boundary elements are thus approximated by numerical schemes. Assume the centroid of the boundary element is (x_c,y_c) and the stiffness matrix of corresponding solid element is given as k_s(ρ). The stiffness matrix of the boundary element can be expressed as:

$$ {\mathbf{k}}_{\mathrm{b}}\left(\boldsymbol{\uprho} \right)=H\left(\phi \left({x}_c,{y}_c\right)\right)\cdot {\mathbf{k}}_{\mathrm{s}}\left(\boldsymbol{\uprho} \right)=H\left(\phi \left({x}_c,{y}_c\right)\right){\int}_{\varOmega_{\mathrm{e}}}{\mathbf{B}}^{\mathrm{T}}\mathbf{D}\left(\boldsymbol{\uprho} \right)\mathbf{B} d\varOmega $$

(20)

H(ϕ) takes the form of approximated and smoothed Heaviside function expressed as:

$$ H\left(\phi \right)=\left\{\begin{array}{ll}0& \phi <-\varDelta \\ {}\frac{1}{2}+\frac{3}{4}\left(\frac{\phi }{\varDelta }-\frac{\phi^3}{3\varDelta}\right)& -\varDelta <\phi \\ {}1& \phi >\varDelta \end{array}\right.<\varDelta $$

(21)

The curves of smoothed Heaviside function with different values of parameter Δ are depicted in Fig. 7. L denotes element length. It is indicated that the smaller Δ is, the steeper H(ϕ) becomes. The parameter Δ also represents the width of a narrow band around the structural boundary defined by the level set function ϕ. In the calculation of element stiffness, the narrow band should cover the centroid of the element to well reflect its stiffness contribution to the whole structure. In the rest of this paper, Δ is set to be half of the element length, i.e., Δ = 0.5 L. By using this approximation scheme, the boundary element is considered a weakened solid element with homogenous property. In this way, fixed mesh is allowed to implement easily in the multi-parameterization method.

Fig. 7

Approximated and smoothed Heaviside function with different values of parameter Δ

Practically, pseudo-density fields ρ = {ρ⁽¹⁾, ρ⁽²⁾,... ρ^(m)} can be approximated in different ways for the calculation of elemental stiffness matrix k_s(ρ).

• Average of nodal pseudo-density values

$$ {\rho}^{(k)}=\frac{1}{N_e}\sum \limits_{i=1}^{N_e}{\rho}^{(k)}\left({x}_i/{l}_x,{y}_i/{l}_y\right) $$

(22)

where N_e represents the number of nodes of one single element. (x_i,y_i) is the coordinate of node i.

• Density value at element center (x_c,y_c)

$$ {\rho}^{(k)}={\rho}^{(k)}\left({x}_c/{l}_x,{y}_c/{l}_y\right) $$

(23)

• Gauss quadrature

$$ {\rho}^{(k)}=\frac{1}{V_e}{\int}_{\varOmega_e}{\rho}^{(k)}\left(\xi, \eta \right) d\varOmega =\frac{1}{V_e}\sum \limits_{i=1}^{n_{gp}}{c}_i{\rho}^{(k)}\left({x}_{\mathrm{gp}}/{l}_x,{y}_{\mathrm{gp}}/{l}_y\right) $$

(24)

where n_gp and c_i denote the number and weights at Gauss point (x_gp,y_gp). V_e represents the elemental volume. For simplicity, (23) is used for the approximation in this paper.

4 Topology optimization problem

4.1 Formulation of optimization problem

In the optimization process, the control parameters of pseudo-density fields $\left\{{P}_{ij}^{(k)}\right\}$ are taken as design variables to minimize the structural compliance:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\ \left\{{P}_{ij}^{(k)}\right\}\kern0.91em ,\kern0.66em k=1,...,\mathrm{m}\\ {}\operatorname{minimize}\kern1em J=\frac{1}{2}{\mathbf{U}}^{\mathrm{T}}\mathbf{K}\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)\mathbf{U}\\ {}s.t.\left\{\begin{array}{l}\mathbf{K}\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)\mathbf{U}={\mathbf{F}}_{\mathrm{Me}}+{\mathbf{F}}_{\mathrm{T}\mathrm{h}}\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)\\ {}g\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)\le 0\\ {}0<{P}_{\mathrm{min}}\le {P}_{ij}^{(k)}\le 1\end{array}\right.\end{array}} $$

(25)

To avoid numerical singularity, a small number P_min = 1 × 10⁻⁵ is used as the lower bound of control parameters. Here, $g\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)$ denotes either the volume constraint or mass constraint. It is expressed as:

Volume constraint to material k:

$$ {g}_k\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)=\frac{1}{V_{\varOmega_p}}{\int}_{\varOmega }{\rho}^{(k)}H\left(\phi \right) d\varOmega -{\overline{V}}_k\le 0,\kern0.66em \left(k=1,...,m\right) $$

(26)

Mass constraint:

$$ g\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)={\int}_{\varOmega}\left(\sum \limits_{k=1}^m{\rho}^{(k)}{\gamma}_k\right)H\left(\phi \right) d\varOmega -\overline{V}\le 0,\kern0.66em \left(k=1,...,m\right) $$

(27)

where ${\overline{V}}_k\kern0.33em \mathrm{and}\kern0.33em \overline{M}$ denote the upper bounds of structural volume fraction occupied by material k and the total mass, respectively. ${V}_{\varOmega_p}$ denotes the total volume of physical domain. γ_k is the mass density of material k for which linear interpolation scheme is adopted in (27).

4.2 Sensitivity analysis

In this paper, the mechanical force F_Meis assumed to be irrelevant to design variables. The sensitivity of structural compliance can thus be derived as:

$$ \frac{\partial J}{\partial {P}_{ij}^{(k)}}=\frac{\partial {\mathbf{F}}_{\mathrm{T}\mathrm{h}}}{\partial {P}_{ij}^{(k)}}-\frac{1}{2}{\mathbf{U}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial {P}_{ij}^{(k)}}\mathbf{U} $$

(28)

Clearly, the sign of ∂J/∂P_ij^(k) is always negative if no thermal load and body force exist. In thermoelastic condition, the sign depends on the sensitivity magnitude of thermal load. Here, terms ∂F_Th/∂P_ij^(k) and ∂K/∂P_ij^(k) can be calculated by assembling the contribution of each element. We have then:

$$ \frac{\partial {\left({\mathbf{f}}_{\mathrm{T}\mathrm{h}}\right)}_e}{\partial {P}_{ij}^{(k)}}=\varDelta T{\int}_{\varOmega_e}\kern0.33em {\mathbf{B}}^{\mathrm{T}}\frac{\partial \boldsymbol{\upbeta}}{\partial {P}_{ij}^{(k)}}H\left(\phi \right)d{\varOmega}_e $$

(29)

$$ \frac{\partial {\mathbf{k}}_e}{\partial {P}_{ij}^{(k)}}={\int}_{\varOmega_e}\kern0.33em {\mathbf{B}}^{\mathrm{T}}\frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial {P}_{ij}^{(k)}}\mathbf{B}\cdot H\left(\phi \right)d{\varOmega}_e $$

(30)

By using the chain rule, the term ∂D(ρ)/∂P_ij^(k) reads:

$$ \frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial {P}_{ij}^{(k)}}=\frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial \chi \left({\rho}^{(k)}\right)}\frac{\partial \chi \left({\rho}^{(k)}\right)}{\partial {\rho}^{(k)}}\frac{\partial {\rho}^{(k)}}{\partial {P}_{ij}^{(k)}} $$

(31)

For a bi-material case, the derivatives of ∂D(ρ)/∂χ(ρ^(k)) are written as:

UMMI with SIMP (q = 1):

$$ \left\{\begin{array}{l}\frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial \chi \left({\rho}^{(1)}\right)}=\left(1-\chi \left({\rho}^{(2)}\right)\right)\mathbf{D}-\chi \left({\rho}^{(2)}\right){\mathbf{D}}_2\\ {}\frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial \chi \left({\rho}^{(2)}\right)}=-\chi \left({\rho}^{(1)}\right){\mathbf{D}}_1+\left(1-\chi \left({\rho}^{(1)}\right)\right){\mathbf{D}}_2\end{array}\right. $$

(32)

RMMI with SIMP (q = 1):

$$ \left\{\begin{array}{l}\frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial \chi \left({\rho}^{(1)}\right)}=\chi \left({\rho}^{(2)}\right){\mathbf{D}}_1+\left(1-\chi \left({\rho}^{(1)}\right)\right){\mathbf{D}}_2\\ {}\frac{\partial \mathbf{D}\left(\boldsymbol{\uprho} \right)}{\partial \chi \left({\rho}^{(2)}\right)}=\chi \left({\rho}^{(1)}\right)\left({\mathbf{D}}_1-{\mathbf{D}}_2\right)\end{array}\right. $$

(33)

Afterwards, the derivatives of χ(ρ^(k)) and ρ^(k) are expressed as:

$$ \frac{\partial \chi \left({\rho}^{(k)}\right)}{\partial {\rho}^{(k)}}=\left\{\begin{array}{l}q{\left({\rho}^{(k)}\right)}^{q-1}\kern3.9em \mathrm{SIMP}\\ {}\frac{1+s}{{\left(1+s\left(1-{\rho}^{(k)}\right)\right)}^2}\kern1.32em \mathrm{RAMP}\end{array}\right. $$

(34)

$$ \frac{\partial {\rho}^{(k)}}{\partial {P}_{ij}^{(k)}}={N}_{i,p}\left(\xi \right)\cdot {N}_{j,p}\left(\eta \right) $$

(35)

The sensitivities of vector β(ρ) can be calculated in the same manner as ∂D(ρ)/∂P_ij^(k). Finally, the sensitivities of volume constraint and mass constraint are expressed as:

$$ {\displaystyle \begin{array}{l}\mathrm{Volume}\kern0.33em \mathrm{constraint}\\ {}\frac{\partial {g}_k\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)}{\partial {P}_{ij}^{(k)}}=\frac{1}{V_{\varOmega_p}}{\int}_{\varOmega }H\left(\phi \right) d\varOmega =\frac{1}{V_{\varOmega_p}}{\int}_{\varOmega }{N}_{i,p}\left(\xi \right){N}_{j,p}\left(\eta \right)H\left(\phi \right) d\varOmega \end{array}} $$

(36)

Mass constraint:

$$ \frac{\partial {g}_k\left(\boldsymbol{\uprho} \left({P}_{ij}^{(k)}\right)\right)}{\partial {P}_{ij}^{(k)}}=\frac{1}{V_{\varOmega_p}}{\int}_{\varOmega}\frac{\partial {P}^{(k)}}{\partial {P}_{ij}^{(k)}}H\left(\phi \right) d\varOmega =\frac{1}{V_{\varOmega_p}}{\int}_{\varOmega }{N}_{i,p}\left(\xi \right){N}_{j,p}\left(\eta \right)H\left(\phi \right) d\varOmega $$

(37)

4.3 Optimization procedure

A flowchart of the optimization procedure is depicted in Fig. 8. The optimization starts with the input of control parameters P_ij⁽¹⁾,..., P_ij^(m) for different pseudo-density fields. Then, global pseudo-density fields are established with respect to each grid of control parameters. Afterwards, finite element analysis with thermoelastic load is carried out on fixed mesh and the sensitivity analysis is implemented. The problem is solved by the optimization solver Globally Convergent Method of Moving Asymptotes (GCMMA), and the convergence criterion is checked to update the design. In this paper, the convergence criterion is attained when the successive variation of the objective function is smaller than 0.01%.

Fig. 8

Flowchart of optimization procedure

5 Numerical examples

In this section, several numerical examples are presented to illustrate the effectiveness of the B-spline MPM. The first test concerns the bi-material cantilever beam loaded uniquely under mechanical force. Then, thermoelastic cases are considered for structures with curved boundaries and multiple materials.

5.1 Bi-material cantilever beam

Figure 9 shows a cantilever beam of size 100 × 50 loaded by a concentrated force of F = 1. Two candidate materials are used: E₁ = 20, E₂ = 1, ν₁ = ν₂ = 0.3. Volume constraints are imposed with the volume fraction being 40% for the first material and 10% for the second material. In other words, the total volume fraction is no more than 50%. The material interpolation is realized by means of the UMMI with SIMP (q = 3). The penalty coefficient q is 3 in all cases. But it starts with q = 1 and is increased at the increment of 0.04 per iteration until it reaches 3 to obtain a smooth result.

Fig. 9

Cantilever beam

5.1.1 Influence of B-spline space size

A study of different B-spline space sizes is illustrated. The FE mesh is generated with 80 × 40 linear Q4 elements a priori. Firstly, assume the B-spline space size of {P_ij⁽¹⁾} is fixed to be nx⁽¹⁾ × ny⁽¹⁾ = 50 × 25. Different B-spline space sizes of {P_ij⁽²⁾} are then employed in a series of optimization tests.

Figure 10 shows the optimized results with different B-spline space sizes of {P_ij⁽²⁾}. The red and yellow zones represent the areas of the two materials, respectively, and the transition areas are marked by transition colors. With a refined mesh of {P_ij⁽²⁾}, more details for the second material layout are revealed and a reduction of structural compliance is obtained.

Fig. 10

Optimized cantilever beam with different B-spline space sizes of {P_ij⁽²⁾}. a B-spline space size 16 × 8, compliance C = 2.581. b B-spline space size 20 × 10, compliance C = 2.575. c B-spline space size 40 × 20, compliance C = 2.058. d B-spline space size 50 × 25, compliance C = 2.056. e B-spline space size 60 × 30, compliance C = 2.054. f B-spline space size 80 × 40, compliance C = 2.050

5.1.2 Influence of the fixed FE mesh size

Here, suppose that both B-spline space sizes are set to 60 × 30 for {P_ij⁽¹⁾}and {P_ij⁽²⁾}. Figure 11 shows the optimized results with different FE mesh sizes.

Fig. 11

Cantilever beam with different fixed mesh sizes. a FE mesh size 20 × 10, C = 2.197. b FE mesh size 60 × 30, C = 2.058. c FE mesh 80 × 40, C = 2.075. d FE mesh size 100 × 50, C = 2.088

When the FE mesh is coarse, the optimized result is not clear due to the inaccurate calculation and the presence of gray elements. When the FE mesh is finer than the parametric mesh, the layouts of the optimized results become quite similar with nearly identical value of the compliance. Therefore, the FE mesh should have at least the same mesh size of B-spline space. From another aspect, a number reduction of design variables can be attained by using less refined mesh for B-spline spaces than the FE mesh.

5.1.3 Discussions about RMMI and UMMI schemes

Here, the optimized result with the mesh of n_x⁽¹⁾ × n_y⁽¹⁾ = n_x⁽²⁾ × n_y⁽²⁾ = 70 × 35 for ρ⁽¹⁾ and ρ⁽²⁾ is further analyzed. The model is refined with finer mesh and larger B-spline order p to obtain a better result. The UMMI- and RMMI-based results, the convergence histories of the objective function, and volume fraction are shown in Figs. 12, 13, 14, and 15. In the UMMI, each pseudo-density field defined in the B-spline space represents one material, and the less stiff material is gathered together. In the RMMI, the first B-spline space ρ⁽¹⁾ represents the overall solid material zone MAT1 + MAT2, while ρ⁽²⁾ represents the MAT 1. And the less stiff material is distributed around the stiff material.

Fig. 12

Optimized result of bi-material cantilever beam with the UMMI and convergence history, compliance C = 2.03

Fig. 13

Optimized material distribution related to MAT1 (left) and MAT2 (right) using the UMMI

Fig. 14

Optimized result of bi-material cantilever beam (left) and convergence history (right) using RMMI, compliance C = 2.04

Fig. 15

Optimized material distribution related to MAT1 (left) and MAT2 (right) using RMMI

Figure 16 indicates the optimized result using level set method (Wang et al. 2015). Here, the compliance value is scaled by a factor of 1/2. Although similar values of the compliance are obtained, material layouts are different. The UMMI tends to gather less stiff materials together, while the level set method and the RMMI distribute the less stiff materials around the stiff materials. This implies that the UMMI has the aggregation effect that might be beneficial for the fabrication of multi-material structures (Meng et al. 2019). With this in mind, the UMMI scheme is used in the following examples.

Fig. 16

Optimized result with level set method (Wang et al. 2015)(left) and convergence history (right), compliance C = 2.04

In order to measure the gray level of multi-material distribution, the index function I_ρ is defined below based on the idea of “measure of discreteness” proposed in (Sigmund 2007):

$$ {I}_{\rho}^{(k)}\left({\rho}^{(k)}\right)=4{\rho}^{(k)}\left(1-{\rho}^{(k)}\right)\times 100\% $$

(38)

In this example, I_ρ⁽¹⁾ = 1.82% and I_ρ⁽²⁾ = 0.56% for results shown in Fig. 13.

Figure 17 shows I_ρ⁽¹⁾ over the whole domain. It is found that the gray zones only appear along the structural boundaries due to the inevitable smooth transition between P_ij⁽¹⁾ = 0 and P_ij⁽¹⁾ = 1. Clearly, the low value of the index I_ρ^(k) indicates that the control parameters are well converged and the whole structure contains few gray zones. The index I_ρ^(k) = 0% if all the B-spline control parameters are P_ij^(k) = 0 or 1, and I_ρ^(k) = 100% if it is a complete gray design with all control parameters being P_ij^(k) = 0.5.

Fig. 17

The gray level measurement index for ρ⁽¹⁾ in B-spline space

5.1.4 Three-material case under thermoelastic load

A third candidate material is added to better illustrate the results. The third material has the largest Young’s modulus and coefficient of thermal expansion: E₃ = 70, ν₃ = 0.3, α₃ = 13.4 × 10⁻⁶. A thermal load related to a temperature rise of ∆T = 50 is employed. The volume fractions of three materials are all constrained under 16.67%. The optimized result with UMMI scheme is depicted in Fig. 18. The gray level indexes for three pseudo-density fields are I_ρ⁽¹⁾ = 1.46%, I_ρ⁽²⁾ = 2.35%, and I_ρ⁽³⁾ = 1.67%. It can be seen that the distributions of the three materials verify the gathering effect of UMMI scheme under thermal loads.

Fig. 18

Three-material cantilever with thermoelastic load

5.2 Bi-clamped structure under mechanical and thermal loads

This is the typical bi-material thermoelastic structure studied in (Gao et al. 2016) (Fig. 19). The structure has a dimension of 72 cm × 47.7 cm and clamped on two sides. It has a thickness of 1 cm and is loaded by a concentrated force F = 300 kN on the middle point of the bottom side. The structure suffers a temperature rise of ∆T = 80 °C. Two candidate materials are involved: E₁ = 105GPa, ν₁ = 0.34, α₁ = 9.1 × 10⁻⁶/°C, γ₁ = 4440 kg/m³ and E₂ = 190GPa, ν₂ = 0.28, α₂ = 12.4 × 10⁻⁶/°C, γ₂ = 7850 kg/m³, respectively.

Fig. 19

Bi-clamped structure under mechanical and thermal loads

Suppose the structure is parameterized by 36 × 24 control parameters for both {P_ij⁽¹⁾} and {P_ij⁽²⁾}. The RAMP penalty function is employed instead of SIMP. The RAMP penalty factors are set to be s = 16 for D and s = 10 for β, respectively.

5.2.1 Optimization with volume constraints for each material

The volume fractions for two candidate materials are all constrained below 20%. In order to better illustrate the influence of different load cases, optimization results with pure mechanical load F = 300 kN, pure thermal load with ∆T = 80 °C, and the combined load are illustrated in Table 1.

Table 1 Optimized results of bi-material case in different loading conditions

It can be seen that the result with pure thermal load turns out to be free of materials in the sense of minimization of structural compliance. This is a typical result with design-dependent load. For the last two configurations shown above, it is found that the connection area (in red) with two sides has different orientations. One is downward while the other is upward.

In the case of combined load, the final shape forms a “spring-like” structure that can absorb thermal deformation. While in the case of the pure mechanical load, the “V-shape” structure is obtained to produce a minimum elastic deformation. Here, in both cases, two volume constraints imposed to materials no. 1 and no. 2 attain their upper bound (20%).

Then, the three-material case is further tested with separate volume constraints. A third material is added with the largest Young’s modulus and coefficient of thermal expansion: E₃ = 210GPa, ν₃ = 0.3, α₃ = 13.4 × 10⁻⁶/°C, γ₃ = 8900 kg/m³. The volume fraction for each material is constrained below 13.33%, leading to a total volume fraction constraint of 40%. The load cases of pure mechanical load and combined load are applied separately. The results demonstrate similar conclusions as in the bi-material case and verify the effectiveness of the proposed method in multi-material case (Table 2).

Table 2 Optimized results of three-material case in different loading conditions

5.2.2 Optimization with total mass constraint

To fully investigate the potential of candidate materials, the volume constraints for each material are replaced by a total mass constraint. Thus, a best ratio of materials can be attained with a balance of thermal response and elastic response.

The total mass constraint is set to be $\overline{M}$=10. The optimized result and convergence history are depicted in Fig. 20. Three-dimensional plots of ρ⁽¹⁾ and ρ⁽²⁾ fields are shown in Fig. 21. Here, I_ρ⁽¹⁾ = 0.022% and I_ρ⁽²⁾ = 2.15%. The optimized result is found to have only one material, i.e., the stiffer one, with clear material boundaries and no gray zones. This implies that the mechanical load is dominant so that only the stiffer material is used.

Fig. 20

Optimized result (left) and convergence history (right) of thermoelastic structure

Fig. 21

Pseudo-density fields related to ρ⁽¹⁾ (left) and ρ⁽²⁾ (right)

The comparison with previous work (Gao et al. 2016) is illustrated in Fig. 22. With the MPM, the optimized configuration only consists of the stiff material, resulting in a small value of objective function. With the discrete density method, the optimized configuration consists of two materials with a relatively large value of the objective function, attained by introducing additional penalties to push design variables toward 0 or 1.

Fig. 22

Comparison of optimized configurations obtained by multi-parameterization method and discrete density method using RAMP scheme. a Result using multi-parameterization method C = 317.5 J. b Result using discrete density method in (Gao et al. 2016), C = 331.2 J

Last, the three-material case is studied. The loading condition and constraints are kept unchanged. The optimized result with mass constraint is illustrated below. One can see that the same result is obtained as in the bi-material case. This implies that under a total mass constraint, the second material produces the lowest compliance for thermal and elastic loads per mass unit (Fig. 23).

Fig. 23

Optimized result of three-material bi-clamped structure (left) and convergence history (right)

5.3 Bracket structure under thermal and mechanical loads

This example aims at highlighting the capacity of the proposed method in optimizing structures with freeform boundaries and inner holes. As shown in Fig. 24, a bracket structure is fixed at the bottom and loaded by a horizontal force F = 1 at the top. Suppose two candidate materials can be used: E₁ = 10, E₂ = 30, ν₁ = ν₂ = 0.3. The outer boundary is modeled by a level set function constructed by K-S function, shown in Fig. 25. Assume three circular rings with E₀ = 1 × 10³, ν₀ = 0.3 and the central hole are non-designable. The whole structure is embedded into a finite element mesh of 60 × 80. The same number of control points for two density spaces are used in the definition of design variables.

Fig. 24

Bracket structure

Fig. 25

Level set function of bracket structure

5.3.1 Optimization with pure mechanical load in case of bi-materials

The volume constraints for each material usage are set to be 25%; thus, the total volume fraction is under 50%. The optimized structure and evolution histories are illustrated in Fig. 26. The 3D plots of density fields ρ⁽¹⁾ and ρ⁽²⁾ are shown in Fig. 27 with I_ρ⁽¹⁾ = 0.39% and I_ρ⁽²⁾ = 0.73%. This shows that the structure contains few gray zone even with the presence of curved boundaries. The optimized result confirms the effectiveness of the proposed method for structures with curved outer boundaries and non-designable holes. The soft material is placed inside the bracket and enveloped by strong material to make the structure less deformed.

Fig. 26

Optimized bi-material bracket structure (left) and convergence history (right)

Fig. 27

Plot of pseudo-density fields ρ⁽¹⁾ (left) and ρ⁽²⁾ (right)

5.3.2 Influence of thermal load in case of bi-materials

Apart from the mechanical load, consider the case that the structure is also loaded by a uniform temperature rise ΔT = 15. The coefficients of thermal expansion of two materials are α₁ = 9.1 × 10⁻⁶ and α₂ = 12.4 × 10⁻⁶. The objective function and volume constraints are kept unchanged. Figure 28 shows the optimized result and the convergence histories of compliance and total volume fraction. In this case, I_ρ⁽¹⁾ = 0.30% and I_ρ⁽²⁾ = 0.86%. Clearly, the compliance and total material volume show a stable convergence. Compared with the case of purely mechanical load, inner voids and gaps are generated to release the thermal effect. The main frame of the structure is made of stiffer materials to bear the mechanical load. Figure 29 shows the effect of temperature rise on structural layout and the compliance. It can be concluded that more voids are generated and the compliance value increases as the thermal load rises.

Fig. 28

Optimized bi-material bracket structure with temperature rise ΔT = 15 (left) and convergence history (right)

Fig. 29

Influence of temperature rise on structural layout and compliance

5.3.3 Influence of thermal load in case of four materials

Suppose four materials are now available. The third and fourth materials have larger Young’s modulus and coefficient of thermal expansion: E₃ = 40, ν₃ = 0.3, α₃ = 13.4 × 10⁻⁶, E₄ = 40, ν₄ = 0.3, α₄ = 15.0 × 10⁻⁶. The temperature rise holds ΔT = 25. The volume constraints for each material are 12.5%. The optimization problem is then solved with four materials and a refined model with finer mesh and larger B-spline order. As shown in Fig. 30, in this case, a high alternation of materials is obtained due to the limited volume fraction of each material phase. Correspondingly, the indexes are I_ρ⁽¹⁾ = 1.06%, I_ρ⁽²⁾ = 0.81%, and I_ρ⁽³⁾ = 0.63%, I_ρ⁽⁴⁾ = 0.64%, respectively. It can be deduced that the thermal load acts as the dominant role. Inner voids are generated near material interfaces. The more material phases are involved, the larger index values are probably generated.

Fig. 30

Optimized four-material bracket structure with temperature rise ΔT = 25 (left) and convergence history (right)

6 Conclusions

This paper presents a multi-parameterization method (MPM) to optimize thermoelastic structures with multiple materials. Independent B-spline spaces are employed to provide high-order continuities for each material layout over the whole design domain. The structure is optimized through modifying the control parameters related to different materials of these B-spline spaces. Optimized results present smooth boundaries and material distributions. Specially, level set functions are integrated with the fixed FE mesh to deal with freeform structures. The RMMI and UMMI schemes are tested in combination with the B-spline MPM. The UMMI scheme demonstrates an aggregation effect with different materials gathering together, while the RMMI tends to disperse materials. This paper also shows the gathering effect of UMMI scheme with few material alternations in distribution when compared with the RMMI scheme. Numerical results show that a number reduction of design variable can be attained using less refined mesh for B-spline spaces. Under thermal elastic condition and mass constraint, the B-spline MPM with the UMMI produces a lower compliance than the discrete density-based method and that no additional treatment is needed for convergence. Its advantages also include the great reduction of gray elements, checkerboards, and overlapping materials.