Stress-based shape and topology optimization with cellular level set in B-splines

Abstract

A parametric level set approach based on B-splines is developed for the stress-based shape and topology optimization of cellular structures. In this method, the whole design domain is divided into a set of non-overlapping sub-domains, within each of which the structure is represented by an implicit B-spline level set function. This parameterization scheme ensures that the adjacent cells can be smoothly connected. The stress value of the structure is computed by using a p-norm function-based aggregation. The extended finite element method is implemented to calculate the structural stress. Moreover, a new optimization strategy based on a two-field formulation is proposed to eliminate numerical instability in the optimization process. A continuity scheme based on the least square method is proposed to guarantee the high-order connectivity at the adjacent cell boundary. In addition, optimized cellular structures with different cell partitions are obtained and discussed. Several numerical examples are presented to illustrate the applicability of the approach.

1 Introduction

The structural strength is a critical factor in structural design since a large local stress will lead to structural failures such as fracture, fatigue and creep (Andkjær & Sigmund, 2011). Topology optimization is an effective structural design approach that satisfies design requirements by rationally distributing materials. In recent years, many scholars have attempted to apply the topology optimization to stress-related structural designs.

Duysinx and Bendsøe (Duysinx & Bendsøe, 1998) introduced stress constraints into structural topology optimization. Similar to SIMP (solid isotropic material with penalization) method, they proposed a stress interpolation with ε-relaxation approach to solve the so-called singularity issue (Cheng & Guo, 1997) of the stress constraints in structural topology optimization. The stress is a local feature of structures, which implies that the stress in every material point of the structure needs to be constrained. This will result in a large number of local stress constraints. Generally, an integrated stress constraint function is used to aggregate the local stress constraints, such as the p-norm function (Duysinx & Sigmund, 1998) and the Kresselmeier-Steinhauser (KS) function (Yang & Chen, 1996). However, these aggregation functions cannot perfectly capture the maximum stress in the structure. Le et al. (Le et al., 2010) proposed an effective measure to solve the stress-based topology optimization in the SIMP framework. Together with an adaptive normalization scheme, the approach can accurately constrain the actual maximum stress in the structure.

Within the level set framework, the pioneer works for stress-based topology optimization are carried out by van Miegroet and Duysinx (Van Miegroet & Duysinx, 2007) and Allaire and Jouve (Allaire & Jouve, 2008). Miegroet et al. applied the level set-based topology optimization to solve the problem of structural stress concentration. Allaire et al. obtained the structural design of a minimized stress through the shape derivative and the topological derivative. Guo et al. (Guo et al., 2011) used the extended finite element method (XFEM) to ensure the analysis accuracy of the structural stress. This approach was also extended to multi-material stress-based topology optimization (Guo et al., 2014). Picellide et al. (Picelli et al., 2018) used the p-norm stress aggregation and an adaptive scaling scheme to the stress-constrained topology optimization. Numerical results show that this method can efficiently yield solutions with smooth boundaries for single and multiple load cases.

For cellular structural design (Liu et al., 2019), many design methods have been proposed such as the multi-scale methods (Rodrigues et al., 2002; Coelho et al., 2008; Xia & Breitkopf, 2014; Xia & Breitkopf, 2015; Xia & Breitkopf, 2017; Liu et al., 2008; Gao & Ma, 2015), the projection or mapping methods (Groen & Sigmund, 2018; Zhu et al., 2019), and partition or sub-domain methods (Liu et al., 2019; Zhang & Sun, 2006; Lazarov, 2013; Alexandersen & Lazarov, 2015a; Alexandersen & Lazarov, 2015b; Wang et al., 2019).

In the multi-scale methods, Rodrigues et al. proposed a hierarchical optimization method to optimize the material distribution in two scales (Rodrigues et al., 2002). It underlines the design of microstructures to optimize the local material properties of elements. This work was extended to three dimensions by Coelho et al. (Coelho et al., 2008). Xia and Breitkopf (Xia & Breitkopf, 2014; Xia & Breitkopf, 2015; Xia & Breitkopf, 2017) introduced a nonlinear multi-scale framework for the concurrent optimization. In this work, a cellular model is defined at microscopic scale and it is optimized to adapt to the macroscopic structural response. However, the connectivity between the adjacent cellular structures cannot be guaranteed. Liu et al. (Liu et al., 2008) proposed a concurrent optimization method, which adopts a single microstructure to represent the macrostructure to satisfy the connection requirements. Based on this idea, Gao et al. (Gao & Ma, 2015) proposed a modified model by introducing the microstructure orientation as a new design variable. Li et al. designed some unchangeable connectors at cell boundaries to ensure the connectivity between adjacent cells. Connectivity is an important issue in the multi-scale optimization. Failure to connect adjacent cells will result in a non-manufacturable structural design. Moreover, the stress concentration occurs where the parts are not smoothly connected, which severely affects the physical properties of the structure. In the abovementioned method by Gao et al. (Gao & Ma, 2015), geometric connectors are designed to ensure connectivity. However, the connector is a strong geometric constraint and it compromises the mechanical performance of an optimized structure.

Recently, a few approaches have been developed to design cellular structures based on the projection or the mapping methods. Groen et al. (Groen & Sigmund, 2018) proposed a projection method to obtain high-resolution topology optimization results. The projection method bridges up the coarse and the fine scales, so that a complex periodic microstructure can be represented by smooth and continuous lattices on the fine mesh. Based on the asymptotic analysis, Zhu et al. (Zhu et al., 2019) proposed a homogenisation framework to design the structure that filled with quasi-periodic microstructures. By introducing a mapping function, the infill graded microstructures are transformed to spatially-periodic configurations.

For the partition or sub-domain based methods, Zhang et al. (Zhang & Sun, 2006) developed a two-level cellular design method combining the macroscale layout design with the refined topology optimization of the microstructure. Based on the multiscale finite element method, Lazarov (Lazarov, 2013) and Alexandersen et al. (Alexandersen & Lazarov, 2015a; Alexandersen & Lazarov, 2015b) designed the cellular structures with refined structural details. Wang et al. (Wang et al., 2019) proposed a parametric level set approach based on B-splines for modelling and topology optimization of cellular structures, which is called CLIBS (cellular set in B-Splines). In this method, the design domain is divided into a set of sub-domains, which can naturally guarantee the geometric connectivity with a desirable smoothness at the structural boundaries between adjacent cells. Liu et al. (Liu et al., 2019) used the same partition scheme to design graded cellular structures with the radial basis functions.

In this paper, the CLIBS approach is further developed for the stress-based shape and topology optimization. By using this approach, arbitrary two adjacent cells can be perfectly connected. In addition, the sub-domains can be updated freely without geometric restrictions. Besides, a p-norm function based aggregation is used to obtain the stress value of the structure. The XFEM is implemented to compute the structural stress. Moreover, a new optimization strategy is proposed to eliminate numerical instability caused by the XFEM scheme. A continuity scheme based on the least square method is proposed to guarantee the high-order connectivity at the boundary of adjacent cells.

The reminder of this paper is organized as follows. In Section 2, the concept of CLIBS and the approach to ensure the cell connectivity are introduced. In Section 3, the stress-based topology optimization by CLIBS is introduced in details, including the optimization problem formulation, sensitivity derivation, computational implementation, optimization strategy, and procedure. In Section 4, different cellular structural design examples and the discussion on the applicability of the approach are provided. Conclusions are given in Section 5.

2 Cellular level set in B-splines

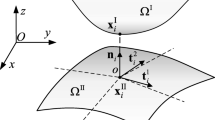
In the level set method, the boundary of the structure is defined as the zero level set of a higher-dimensional level set function ϕ, which is shown in Fig. 1. The structure can be implicitly expressed as follows:

$$ \left\{{\displaystyle \begin{array}{cc}\phi \left(\boldsymbol{x}\right)>0& \forall \boldsymbol{x}\in \varOmega \backslash \partial \varOmega \\ {}\phi \left(\boldsymbol{x}\right)=0& \forall \boldsymbol{x}\in \partial \varOmega \\ {}\phi \left(\boldsymbol{x}\right)<0& \forall \boldsymbol{x}\in D\backslash \varOmega \end{array}}\right. $$

(1)

where x is the coordinate of a point in the design domain D, which can be expressed as x = (x, y, z) in three-dimensional space. Ω and ∂Ω are the material domain and the boundary, respectively. The conventional level set method-based structural topology optimization usually requires a solution of the Hamilton-Jacobi equation, which poses a few numerical issues, such as the selection of appropriate upwind difference scheme, velocity field extension, and re-initialisation (Wang et al., 2003). One pertinent way to avoid the issues is to transform the partial differential equation into an ordinary differential equation using the CLIBS model (Wang et al., 2019).

Fig. 1

Level set model with the signed distance function

Table 1 Parameter values of numerical examples

As illustrated in Fig. 2, the design domain is divided into n sub-domains, and the B-spline basis functions are used to parameterize the level set function of each sub-region. The global level set function ϕ is defined as follows:

$$ \phi =\underset{s=1}{\overset{n}{\cup }}{\phi}_s $$

(2)

Fig. 2

Cellular level set representation on sub-domain cells. a The design domain of a L-bracket with 16 cells. b The structure of the s-th cell. c The level set function of the s-th cell

For two-dimensional problems, the design domain can be divided into several non-overlapping rectangular sub-domains. The level set function of each sub-domain is expressed by m×n piecewise B-spline polynomials:

$$ {\phi}_s\left(x,y\right)=\sum \limits_{i=0}^m\sum \limits_{j=0}^n{P}_{ij}{\phi}_{ij}\left(x,y\right) $$

(3)

where P_ij is the B-spline coefficient. ϕ_ij(x, y) is the basis function which can be expressed as follows:

$$ {\phi}_{ij}\left(x,y\right)={N}_{i,p}(x){N}_{j,q}(y) $$

(4)

where N_{i, p}(x) and N_{j, q}(y) are the B-spline basis functions defined by knot vectors in x and y directions, respectively. The basis functions can be recursively derived from the following Cox-de-Boor recursion formula:

$$ {N}_{i,1}(u)=\left\{\begin{array}{cc}1& {t}_i\le u<{t}_{i+1}\\ {}0& u<{t}_i oru\ge {t}_{i+1}\end{array}\right. $$

(5)

$$ {N}_{i,k}(u)=\frac{u-{t}_i}{t_{i+k-1}-{t}_i}{N}_{i,k-1}(u)+\frac{t_{i+k}-u}{t_{i+k}-{t}_{i+1}}{N}_{i+1,k-1}(u) $$

(6)

where t_i is the i^th value of the knot vector t = {t₀, t₁, t₂, …, t_np}, and k is the order. In order to satisfy the partition of unity (POU) property (Ho et al., 2011; Ho et al., 2013) for the basis functions in each cell, the values of the first and last k numbers of the knot vector are set equal; i.e., t₀ = t₁ = … = t_{k − 1} and t_{np − k + 1} = t_{np − k + 2} = …t_np, meaning that the first and last knots are multiple knots with a multiplicity of k.

In order to ensure the continuity between adjacent cells, the outmost B-spline coefficients of each cell should satisfy the so-called continuity equations (Wang et al., 2019). Figure 3 illustrates the idea with two one-dimensional cells. The blue and red lines represent the basis functions in cell 1 and cell 2, respectively. P⁻ andP⁺represent the B-spline coefficients in cell 1 and cell 2, respectively. The continuity equations for C⁰,C¹, and C² continuities are given as follows:

$$ \left({C}^0\right){P}_0^{+}={P}_n^{-} $$

(7)

$$ \left({C}^1\right)\left\{\begin{array}{c}{P}_0^{+}={P}_n^{-}\\ {}{P}_1^{+}-{P}_0^{+}=-{P}_{n-1}^{-}+{P}_n^{-}\end{array}\right. $$

(8)

and

$$ \left({C}^2\right)\left\{\begin{array}{c}{P}_0^{+}={P}_n^{-}\\ {}{P}_1^{+}-{P}_0^{+}+-{P}_{n-1}^{-}={P}_n^{-}\\ {}{P}_2^{+}-3{P}_1^{+}+2{P}_0^{+}={P}_{n-2}^{-}-3{P}_{n-1}^{-}+2{P}_n^{-}\end{array}\right. $$

(9)

Fig. 3

The basis functions and the notations of the corresponding coefficients of two one-dimensional cells

3 Stress-based topology optimization by CLIBS

3.1 Optimization problem

In this paper, a p-norm function-based stress aggregation scheme is used as the design response of the structural stress:

$$ G\left(\boldsymbol{u},\phi \right)={\sigma}_{pn}={\left({\int}_D{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^PH\left(\phi \right)d\boldsymbol{x}\right)}^{\frac{1}{P}} $$

(10)

where p is the von Mises Stress. H is the Heaviside function, which is defined as follows:

$$ H\left(\phi \right)=\left\{\begin{array}{cc}0& \phi <0\\ {}1& \phi \ge 0\end{array}\right. $$

(11)

Note that, as p increases, the p-norm-based value is closer to the actual maximum stress value of the structure. However, the increase of p may lead to the increase of nonlinearity and a poorer convergence.

By considering the volume fraction of the structure, which is expressed as follows:

$$ V\left(\phi \right)=\frac{\int_DH\left(\phi \right)d\boldsymbol{x}}{\int_Dd\boldsymbol{x}} $$

(12)

The stress-based shape and topology optimization problem can be expressed as follows:

$$ {\displaystyle \begin{array}{cc}\underset{P}{\mathit{\min}}& G\left(\boldsymbol{u},\phi \right)={\left({\int}_D{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^PH\left(\phi \right)d\boldsymbol{x}\right)}^{\frac{1}{p}}\\ {}s.t.& a\left(\boldsymbol{u},\boldsymbol{w},\phi \right)=l\left(\boldsymbol{w},\phi \right)\forall \boldsymbol{w}\in \boldsymbol{U}\\ {}& \boldsymbol{V}\left(\phi \right)=\frac{\int_DH\left(\phi \right)d\boldsymbol{x}}{\int_Dd\boldsymbol{x}}\le {\boldsymbol{V}}^{\ast}\end{array}} $$

(13)

where P is the set of B-spline coefficients. Alternatively, the p-norm stress can also be used as the constraint for the minimization of the structural volume. Correspondingly, the optimization problem is given as follows:

$$ {\displaystyle \begin{array}{cc}\underset{P}{\mathit{\min}}& V\left(\phi \right)=\frac{\int_DH\left(\phi \right)d\boldsymbol{x}}{\int_Dd\boldsymbol{x}}\\ {}s.t.& a\left(\boldsymbol{u},\boldsymbol{w},\phi \right)=l\left(\boldsymbol{w},\phi \right)\forall \boldsymbol{w}\in \boldsymbol{U}\\ {}& G\left(\boldsymbol{u},\phi \right)={\left({\int}_D{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^pH\left(\phi \right)d\boldsymbol{x}\right)}^{\frac{1}{p}}\le {\sigma}^{\ast}\end{array}} $$

(14)

In the above optimization problems, V^* and σ^* are the upper bound of the volume fraction and stress, respectively. u represents the displacement and w denotes an arbitrary displacement in the set of kinematically admissible displacement field U. a(u, w, ϕ) and l(w, ϕ) are the energy bilinear form and the force linear form, which are defined as follows:

$$ a\left(\boldsymbol{u},\boldsymbol{w},\phi \right)={\int}_D{\boldsymbol{\varepsilon}}^T\left(\boldsymbol{u}\right)\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)H\left(\phi \right)d\boldsymbol{x} $$

(15)

$$ l\left(\boldsymbol{w},\phi \right)={\int}_D{\boldsymbol{f}}^T\boldsymbol{w}H\left(\phi \right)d\boldsymbol{x}+{\int}_{\Gamma_t}{\boldsymbol{\tau}}^T\boldsymbol{w}d\boldsymbol{x} $$

(16)

where ε denotes the strain, E denotes the stiffness tensor, f and τ are the body force and traction, respectively.

3.2 Sensitivity analysis

By introducing an augmented functional as follows:

$$ \Lambda =J+a-l $$

(17)

where

$$ J\left(\boldsymbol{u},\phi \right)={\int}_DF\left(\boldsymbol{u}\right)H\left(\phi \right)d\boldsymbol{x} $$

(18)

the derivative with respect to the variables can be expressed as follows:

$$ \frac{\mathrm{\partial \Lambda }}{\partial {P}_{ij}}=\frac{\partial J}{\partial {P}_{ij}}+\frac{\partial a}{\partial {P}_{ij}}-\frac{\partial l}{\partial {P}_{ij}} $$

(19)

where

$$ \frac{\partial J}{\partial {P}_{ij}}={\int}_{\Omega}\frac{\partial \boldsymbol{F}\left(\boldsymbol{u}\right)}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\mathrm{\partial \Omega }}\boldsymbol{F}\left(\boldsymbol{u}\right)\frac{\partial \phi }{\partial {P}_{ij}}\frac{1}{\left\Vert \nabla \phi \left(\boldsymbol{x}\right)\left\Vert \right.\right.}d\boldsymbol{x} $$

(20)

$$ \frac{\partial a}{\partial {P}_{ij}}={\int}_{\Omega}\frac{\partial {\boldsymbol{\varepsilon}}^{\boldsymbol{T}}\left(\boldsymbol{u}\right)}{\partial \phi}\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\Omega}{\boldsymbol{\varepsilon}}^{\boldsymbol{T}}\left(\boldsymbol{u}\right)\boldsymbol{E}\frac{\partial \boldsymbol{\varepsilon} \left(\boldsymbol{w}\right)}{\partial {P}_{\phi }}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\mathrm{\partial \Omega }}{\boldsymbol{\varepsilon}}^{\boldsymbol{T}}\left(\boldsymbol{u}\right)\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\frac{\partial \phi }{\partial {P}_{ij}}\frac{1}{\left\Vert \nabla \phi \left(\boldsymbol{x}\right)\right\Vert }d\boldsymbol{x} $$

(21)

$$ \frac{\partial l}{\partial {P}_{ij}}={\int}_{\Omega}{\boldsymbol{f}}^T\frac{\partial \boldsymbol{w}}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\Gamma_r}{\boldsymbol{\tau}}^{\boldsymbol{T}}\frac{\partial \boldsymbol{w}}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x} $$

(22)

Since a(u, w, ϕ) = l(w, ϕ), ∀ w ∈ U and the derivative of w with respect to the level set function ϕ also satisfies that $\frac{\partial \boldsymbol{w}}{\partial \phi}\in \boldsymbol{U}$, the following terms can be cancelled by:

$$ {\int}_{\Omega}{\boldsymbol{\varepsilon}}^{\boldsymbol{T}}\left(\boldsymbol{u}\right)\boldsymbol{E}\frac{\partial \boldsymbol{\varepsilon} \left(\boldsymbol{w}\right)}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}={\int}_{\Omega}{\boldsymbol{f}}^{\boldsymbol{T}}\frac{\partial \boldsymbol{w}}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\mathrm{\partial \Omega }}{\boldsymbol{\tau}}^{\boldsymbol{T}}\frac{\partial \boldsymbol{w}}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x} $$

(23)

Considering the following adjoint equation:

$$ {\int}_{\Omega}\frac{\partial F\left(\boldsymbol{u}\right)}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\Omega}\frac{\partial {\boldsymbol{\varepsilon}}^T\left(\boldsymbol{u}\right)}{\partial \phi}\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}=0 $$

(24)

the derivative of the augmented function now becomes

$$ \frac{\mathrm{\partial \Lambda }}{\partial {P}_{ij}}={\int}_{\mathrm{\partial \Omega }}\left[F\left(\phi \right)+{\boldsymbol{\varepsilon}}^T\left(\boldsymbol{u}\right)\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\right]\frac{\partial \phi }{\partial {P}_{ij}}\frac{1}{\left\Vert \nabla \phi \left(\boldsymbol{x}\right)\right\Vert }d\boldsymbol{x} $$

(25)

For the p-norm-based functional, the objective function in Eq. (10) can be transformed as follows:

$$ J\left(\boldsymbol{u},\phi \right)=G{\left(\boldsymbol{u},\phi \right)}^P={\int}_D{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^PH\left(\phi \right)d\boldsymbol{x} $$

(26)

Thus, the corresponding adjoint equation is

$$ p{\int}_{\Omega}{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^{p-1}\frac{\partial {\sigma}_{vm}\left(\boldsymbol{u}\right)}{\partial \phi}\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}+{\int}_{\Omega}\frac{\partial {\boldsymbol{\varepsilon}}^T\left(\boldsymbol{u}\right)}{\partial \phi}\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\frac{\partial \phi }{\partial {P}_{ij}}d\boldsymbol{x}=0 $$

(27)

Based on the implicit B-spline level set function, the derivative of the augmented function can be rewritten as follows:

$$ \frac{\mathrm{\partial \Lambda }}{\partial {P}_{ij}}={\int}_{\mathrm{\partial \Omega }}\left[{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^p+{\varepsilon}^T\left(\boldsymbol{u}\right)\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\right]{N}_{i,p}\left(\boldsymbol{x}\right){N}_{j,q}(y)\frac{1}{\left\Vert \nabla \phi \left(\boldsymbol{x},y\right)\right\Vert }d\boldsymbol{x} $$

(28)

As a result, the sensitivity of the p-norm functional G(u, ϕ) is given as follows:

$$ \frac{\partial G\left(\boldsymbol{u},\phi \right)}{\partial {P}_{ij}}=\frac{G{\left(\boldsymbol{u},\phi \right)}^{1-p}}{p}{\int}_{\mathrm{\partial \Omega }}\left[{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^p+{\boldsymbol{\varepsilon}}^T\left(\boldsymbol{u}\right)\boldsymbol{E}\boldsymbol{\varepsilon } \left(\boldsymbol{w}\right)\right]{N}_{i,p}\left(\boldsymbol{x}\right){N}_{j,q}(y)\frac{1}{\left\Vert \nabla \phi \left(\boldsymbol{x},y\right)\right\Vert }d\boldsymbol{x} $$

(29)

The sensitivity of the volume fraction V(ϕ) can be obtained by the chain rule as follows:

$$ \frac{\partial V\left(\phi \right)}{\partial {P}_{ij}}=\frac{\int_{\mathrm{\partial \Omega }}{N}_{i,p}(x){N}_{j,q}(y)\frac{1}{\left\Vert \nabla \phi \left(x,y\right)\right\Vert }d\boldsymbol{x}}{\int_Dd\boldsymbol{x}} $$

(30)

3.3 Computational details

3.3.1 XFEM scheme

The XFEM method is implemented herein for structural analysis. Similar to the previous works (Wei et al., 2010; Daux et al., 2000; Sukumar et al., 2001), the displacement field is represented as follows:

$$ \boldsymbol{u}\left(\boldsymbol{x}\right)=\sum \limits_{i\in I}{N}_i\left(\boldsymbol{x}\right){\boldsymbol{u}}_iH\left(\phi \left(\boldsymbol{x}\right)\right) $$

(31)

where x is a point located inside the i^th element of the element set I and, N_i(x) is the shape function. The global stiffness matrix K is obtained by matrix assembly:

$$ \boldsymbol{K}=\sum \limits_{i\in I}{\boldsymbol{K}}_e=\sum \limits_{i\in I}{\int}_{\Omega_i}{\boldsymbol{B}}^T\boldsymbol{DB}d\boldsymbol{x} $$

(32)

where B denotes the strain-displacement matrix, D is the elasticity matrix of the solid material, and Ω_i is the solid domain inside the i^th element. For rectangular elements, the element stiffness matrix of the solid element K₀ are constants, which can be obtained by direct integration. For non-rectangular elements, the element stiffness matrix of the solid element is usually obtained by the numerical integration. The element stiffness matrix of a cutting element is evaluated by Gaussian Quadrature, for which the structural boundary is reconstructed explicitly first and then divided into several sub-triangles by a partition process. Then, the element stiffness matrix can be obtained by adding together the stiffness matrices calculated in sub-triangular regions. Figure 4 illustrates such a partition and the Gaussian points sampling scheme. Besides, Fig. 5 shows all possible cases of the solid partition in the cutting elements .

Fig. 4

Gaussian points sampling scheme for finite element analysis

Fig. 5

Cases of the solid partition in cutting elements

It should be noticed that in order to avoid numerical singularity, the stiffness matrix of the void element should be set as the multiplication of a small number to the constant matrix K₀, which is known as the ersatz material approach (Wang et al., 2003; Allaire & Jouve, 2004). In this paper, the small number is set as 10⁻⁹.

In this paper, the following two techniques are used to ensure the accuracy of XFEM stress calculation. Firstly, the boundary of the structure is described by using the dense grids. For all examples herein, the B-spline orders of x and y direction are both taken as 3, which means that the level set function is composed of piecewise bivariate quadratic polynomial functions. The interval between B-spline nodes is 3 times of the edge length of the finite elements, and thus, there are 4 × 4 points for each bivariate quadratic polynomial function to describe the structure boundary. Secondly, the cutting elements are divided into several triangular regions. Each triangular region contains three Gaussian points, which is shown in Fig. 5. The stress of each Gaussian points in cutting elements is calculated to describe the stress distribution at the structure boundary.

3.3.2 Discrete forms

With the discretized finite element model, the p-norm functional Eq. (10) is rewritten as follows:

$$ G\left(\boldsymbol{u},\phi \right)={\left(\sum \limits_{i\in I}{\int}_{D_i}{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^PH\left(\phi \right)d\boldsymbol{x}\right)}^{\frac{1}{p}} $$

(33)

where D_i is the domain of the i^th element. The von Mises stress can be calculated as follows:

$$ {\sigma}_{vm}^2={\sigma}^T V\sigma ={\boldsymbol{u}}^T{\boldsymbol{B}}^T{\boldsymbol{D}}^T\boldsymbol{VDBu}\equiv {\boldsymbol{u}}^T\boldsymbol{Mu} $$

(34)

where σ is the stress vector, M=B^T D^TVDB and V are given as follows:

$$ V=\left[{\displaystyle \begin{array}{ccc}1& -0.5& 0\\ {}-0.5& 1& 0\\ {}0& 0& 3\end{array}}\right] $$

(35)

As a result, Eq. (33) can be rewritten as follows:

$$ G\left(\boldsymbol{u},\phi \right)={\left(\sum \limits_{i\in O}\sum \limits_{j\in {P}_i}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_j{\boldsymbol{u}}_i\right)}^{\frac{p}{2}}\left|{\boldsymbol{J}}_j\right|\right)}^{\frac{1}{p}} $$

(36)

where O is the set of the solid elements and cutting elements. P_i is the set of Gaussian points inside the i^th element. M_j and J_j are obtained by evaluating M and the Jacobian matrix J at the j^th Gaussian point. s_j is the corresponding weight factor for the Gaussian quadrature.

The adjoint Eq. (27) is rewritten as follows:

$$ \boldsymbol{K}w=-p\left(\sum \limits_{i\in O}\sum \limits_{j\in {P}_i}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_J{\boldsymbol{u}}_i\right)}^{\frac{P}{2}}{\boldsymbol{M}}_j{\boldsymbol{u}}_i{s}_j{\left|{\boldsymbol{J}}_j\right|}^{\frac{1}{P}}\right) $$

(37)

For the structure with rectangular elements, the integral of M in solid elements M₀ and the Jacobian matrix J₀ are constants. Equations (36) and (37) can be rewritten as follows:

$$ G\left(\boldsymbol{u},\phi \right)={\left[\sum \limits_{i\in {I}_{\boldsymbol{solid}}}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_0{\boldsymbol{u}}_i\right)}^{\frac{p}{2}}\left|\boldsymbol{J}{`}_0\right|+\sum \limits_{i\in {I}_{cut}}\sum \limits_{j\in {P}_i}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_j{\boldsymbol{u}}_i\right)}^{\frac{p}{2}}{s}_j\left|{\boldsymbol{J}}_0\right|\right]}^{\frac{1}{p}} $$

(38)

$$ \boldsymbol{K}w=-p{\left[\sum \limits_{i\in {I}_{\boldsymbol{solid}}}{\left({\boldsymbol{u}}_u^T{\boldsymbol{M}}_0{\boldsymbol{u}}_i\right)}^{\frac{p}{2}-1}{\boldsymbol{M}}_0{\boldsymbol{u}}_i\left|{\boldsymbol{J}}_0\right|+\sum \limits_{i\in {I}_{cut}}\sum \limits_{j\in {P}_i}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_j{\boldsymbol{u}}_i\right)}^{\frac{p}{2}}{\boldsymbol{M}}_j{\boldsymbol{u}}_i{s}_J\left|{\boldsymbol{J}}_0\right|\right]}^{\frac{1}{p}} $$

(39)

where I_solid and I_cut are the sets of the solid elements and cutting elements, respectively.

Besides, the sensitivity of the p-norm functional in Eq. (29) is calculated as follows:

$$ \frac{\partial G\left(\boldsymbol{u},\phi \right)}{\partial {P}_{ij}}=\frac{G{\left(\boldsymbol{u},\phi \right)}^{1-p}}{p}\sum \limits_{r\in {I}_{cut}}\sum \limits_{s\in {B}_r}{l}_s\left[{\left({\boldsymbol{u}}_r^T{\boldsymbol{M}}_s{\boldsymbol{u}}_r\right)}^{\frac{p}{2}}+{\boldsymbol{u}}_r^T{\boldsymbol{B}}_s^T{\boldsymbol{DB}}_s{\boldsymbol{w}}_r\right]\frac{\phi_{ij}\left({x}_s,{y}_s\right)}{\left\Vert \nabla \phi \left({x}_s,{y}_s\right)\right\Vert } $$

(40)

where B_r is the set of Gaussian points at the boundary of the r^th cutting element. l_s denotes the weight factor of the s^th Gaussian point in B_r. (x_s,y_s) and B_s are the coordinates and the strain matrix of that Gaussian point, respectively.

The volume fraction of the structure in Eq. (12) and the corresponding sensitivity in Eq. (30) are rewritten as follows:

$$ V\left(\phi \right)=\frac{1}{A}\left({A}_{solid}+\sum \limits_{i\in {I}_{cut}}\sum \limits_{j\in {P}_i}{s}_j\left|{\boldsymbol{J}}_i\right|\right) $$

(41)

$$ \frac{\partial V\left(\phi \right)}{\partial {P}_{ij}}=\frac{1}{A}\sum \limits_{r\in {I}_{cut}}\sum \limits_{s\in {B}_r}{l}_s\frac{\phi_{ij}\left({x}_s,{y}_s\right)}{\left\Vert \nabla \phi \left({x}_s,{y}_s\right)\right\Vert } $$

(42)

where A_solid and A are the areas of the solid and the design domain, respectively.

Three Gaussian points in each direction are used in this work, for sensitivity evaluation. According to Gauss-Legendre quadrature, for a line segment whose endpoint coordinates are (x₁,y₁) and (x₂,y₂), the three Gaussian point coordinates can be expressed as (0.89x₁ + 0.11x₂ ,0.89y₁ +0.11y₂) ,(0.50x₁ + 0.50x₂ ,0.50y₁ + 0.50y₂ ) and (0.11x₁ + 0.89x₂ ,0.11y₁ +0.89y₂ ). The corresponding integral weights are 0.28, 0.44, and 0.28, respectively.

3.3.3 Numerical instability and two-field optimization scheme

Numerical instabilities in the level set-based topology optimization with the XFEM were firstly studied by Makhija et al. (Makhija & Maute, 2014). It is observed that small holes or floating materials appear in the optimized design, which affect the physical properties of the structure. In their work, a generalized formulation of the XFEM combined with a perimeter constraint was proposed to eliminate the artefacts. Similarly, Sharma et al. (Sharma & Maute, 2018) added a term related to the perimeter of the structure boundary to the objective function. Since small geometry feature will increase the perimeter of the structure, which will increase the objective function, this method can also eliminate the numerical instability. Jansen (Jansen, 2019) proposed to construct the density field based on an explicit level set model. The density field is then used to control the structural minimum length (Zhou et al., 2015) and hence to eliminate the numerical instability. Based on Jansen’s work, Andreasen et al. (Andreasen & Aage, 2019) proposed a robust shape and topology optimization scheme using CutFEM, which can also avoid the numerical artefacts.

Similar to the checkerboard patterns in density methods (Diaz & Sigmund, 1995), the level set topology optimization with the XFEM formulation may encounter small geometric features near the boundary of the optimized structures, such as holes and hollows. This is essentially due to the discretization of the design domain in the finite element method, which causes the physical properties of the structure to be incorrectly estimated. In the finite element method, the cutting elements are similarly treated as the grey elements in density methods (Makhija & Maute, 2014). The small geometric features caused by the XFEM are assembled by several connected cutting elements. These ‘grey-element’ regions cannot be easily removed, because the stress of these regions is often underestimated by the finite element method.

With the density-based topology optimization method, Sigmund (Sigmund, 2009) proposed a worst-case formulation based on dilated, intermediate, and eroded designs to realize a minimum length scale control in structural topology optimization. Wang et al. (Wang et al., 2011) suggested a two-field formulation, where the calculation is further simplified by constraining the volume of the blueprint design and minimizing the compliance of the eroded design. These methods can control the minimum membrane width of the optimized structure, such that the small features that below the length scale can be effectively eliminated in the optimized designs.

Inspired by the above approaches, a two-field level set scheme is proposed in this work to avoid the numerical instability and guarantee a smooth convergence for the structural stress-based design optimization. The parametrized level set function is firstly regularized with an approximate re-initialisation scheme for each iteration by (Wei et al., 2018):

$$ \overset{\sim }{\phi =\frac{\phi }{\frac{1}{n_{gp}}\sum \limits_{i=1}^{n_{gp}}\left\Vert \nabla \phi \left({x}_i\right)\right\Vert }} $$

(43)

where n_gp is the number of Gaussian points at the boundary. Because the relationship between the level set function ϕ and the design variables P_ij is linear, Eq. (43) can be rewritten as an update scheme as follows:

$$ \overset{\sim }{P_{ij}}=\frac{P_{ij}}{\frac{1}{n_{gp}}\sum \limits_{i=1}^{n_{gp}}\left\Vert \nabla \phi \left({x}_i\right)\right\Vert } $$

(44)

This regularization scheme can control the gradient norm of the level set function at the boundary of the structure near 1 ($\nabla \overset{\sim }{\phi}\approx 1$), and it does not change the shape of the structure boundary. Owing to the approximate signed distance function property, a specific offset of level set function can result in a nearly constant physical offset of the design during the whole optimization process.

By introducing the parameter h, an eroded design ϕ^e to the blueprint (the zero level set) is defined as follows:

$$ {\phi}^e=\overset{\sim }{\phi }-h=\underset{s=1}{\overset{t}{\cup }}\left(\overset{\sim }{\phi_s}-h\right)=\underset{s=1}{\overset{t}{\cup }}\left(\sum \limits_{i=0}^m\sum \limits_{j=0}^n\left(\overset{\sim }{P_{ij}}-h\right){\phi}_{ij}\left(x,y\right)\right) $$

(45)

In this work, the stress design response is evaluated based on the eroded design, while the structural volume is calculated from the blueprint.

Accordingly, the design response of the structural stress is defined as follows:

$$ G\left(\boldsymbol{u},{\phi}^e\right)={\left({\int}_D{\sigma}_{vm}{\left(\boldsymbol{u}\right)}^pH\left({\phi}^e\right)d\boldsymbol{x}\right)}^{\frac{1}{p}} $$

(46)

and the volume fraction of the structure is defined as follows:

$$ V\left(\overset{\sim }{\phi}\right)=\frac{1}{A}\left({A}_{solid}+\sum \limits_{i\in {I}_{cut}}\sum \limits_{j\in {P}_i}{s}_j\left|{\boldsymbol{J}}_j\right|\right) $$

(47)

Similarly, for the sensitivity calculation of the stress p-norm function and the volume fraction, the level set function ϕ in Eqs. (40) and (42) should be replaced by ϕ^e and $\overset{\sim }{\phi }$, respectively. This optimization strategy can efficiently eliminate numerical instability in the optimization process. For detailed explanations, please refer to the numerical example in Section 4.1.1.3.

With the proposed two-field scheme, the discrete optimization problem for the volume-constrained stress minimization problem is given as follows:

$$ {\displaystyle \begin{array}{cc}\underset{P}{\mathit{\min}}& G\left(\boldsymbol{u},{\phi}^e\right)={\left(\sum \limits_{i\in O}\sum \limits_{j\in {P}_i}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_j{\boldsymbol{u}}_i\right)}^{\frac{p}{2}}{s}_j\left|{\boldsymbol{J}}_j\right|\right)}^{\frac{1}{p}}\\ {}s.t.& V\left(\overset{\sim }{\phi}\right)=\frac{1}{A}\left({A}_{solid}+\sum \limits_{i\in {I}_{cut}}\sum \limits_{j\in {P}_i}{s}_j\left|{\boldsymbol{J}}_j\right|\right)\le {V}^{\ast}\\ {}& \boldsymbol{K}\left({\phi}^e\right)\boldsymbol{U}=\boldsymbol{F}\end{array}} $$

(48)

and the stress-constrained volume minimization problem as follows

$$ {\displaystyle \begin{array}{cc}\underset{P}{\mathit{\min}}& V\left(\overset{\sim }{\phi}\right)=\frac{1}{A}\left({A}_{solid}+\sum \limits_{i\in I}\sum \limits_{j\in {P}_i}{s}_j\left|{J}_j\right|\right)\\ {}s.t.& G\left(\boldsymbol{u},{\phi}^e\right)={\left(\sum \limits_{i\in O}\sum \limits_{j\in {P}_i}{\left({\boldsymbol{u}}_i^T{\boldsymbol{M}}_j{\boldsymbol{u}}_i\right)}^{\frac{p}{2}}{s}_j\left|{\boldsymbol{J}}_j\right|\right)}^{\frac{1}{p}}\le {\sigma}^{\ast}\\ {}& \boldsymbol{K}\left({\phi}^e\right)\ \boldsymbol{U}=\boldsymbol{F}\end{array}} $$

(49)

where K(ϕ^e) is the global stiffness matrix of the eroded structure. U and F are the displacement matrix and the force matrix, respectively.

3.3.4 Continuity equations

In order to ensure smooth connections between adjacent cells, the continuity equations in Section 2.3 must be satisfied. In an earlier work (Wang et al., 2019), it was suggested to update the coefficients independently and then imposing the equal constraints afterwards in each design iteration. However, such a solution may alter the structural geometry during the optimization process and results in a discontinuous optimization. In order to mitigate the impact, a least square-based solution is proposed here by minimizing the difference of the structure before and after imposing the continuity constraints.

For the C⁰ continuity, the design variables should satisfy Eq. (7) in both x and y directions. For the C¹ continuity, suppose that the coefficients ${P}_{n-1}^{-}$,${P}_n^{-}$, ${P}_0^{+}$, and ${P}_1^{+}$become ${Q}_{n-1}^{-}$, ${Q}_n^{-}$, ${Q}_0^{+}$, and ${Q}_1^{+}$, respectively, ${Q}_0^{+}$ and ${Q}_1^{+}$expressed as ${Q}_n^{-}$ and $2{Q}_n^{-}-{Q}_{n-1}^{-}$, respectively, the sum residual of squares function $f\left({Q}_n^{-},{Q}_{n-1}^{-}\right)$ can be defined as follows:

$$ f\left({Q}_n^{-},{Q}_{n-1}^{-}\right)={\left({Q}_{n-1}^{-}-{P}_{n-1}^{-}\right)}^2+{\left({Q}_n^{-}-{P}_n^{-}\right)}^2+{\left({Q}_n^{-}-{P}_0^{+}\right)}^2+{\left(2{Q}_n^{-}-{Q}_{n-1}^{-}-{P}_1^{+}\right)}^2 $$

(50)

By letting $\frac{\partial f}{\partial {Q}_n^{-}}$ and $\frac{\partial f}{\partial {Q}_{n-1}^{-}}=0$, the coefficients after imposing the equal constraints can be determined by as follows:

$$ \left\{\begin{array}{c}{Q}_{n-1}^{-}=\frac{3{P}_{n-1}^{-}+{P}_n^{-}+{P}_0^{+}-{P}_1^{+}}{4}\\ {}{Q}_n^{-}=\frac{P_{n-1}^{-}+{P}_n^{-}+{P}_0^{+}+{P}_1^{+}}{4}\\ {}{Q}_0^{+}={Q}_n^{-}\\ {}{Q}_1^{+}=2{Q}_n^{-}-{Q}_{n-1}^{-}\end{array}\right. $$

(51)

Similarly, for the C² continuity, the relationship between the coefficients before and after imposing the equal constraints can be expressed as follows:

$$ \left\{\begin{array}{c}{Q}_{n-2}^{-}=\frac{19{P}_{n-2}^{-}+3{P}_{n-1}^{-}-3{P}_1^{+}+{P}_2^{+}}{20}\\ {}{Q}_{n-1}^{-}=\frac{3{P}_{n-2}^{-}+6{P}_{n-1}^{-}+5{P}_1^{-}+5{P}_0^{+}+4{P}_1^{+}-3{P}_2^{+}}{20}\\ {}\begin{array}{c}{Q}_{n-1}^{-}=\frac{P_{n-1}^{-}+{P}_n^{-}+{P}_0^{+}+{P}_1^{+}}{4}\\ {}{Q}_0^{+}={Q}_n^{-}\\ {}\begin{array}{c}{Q}_1^{+}=-{Q}_{n-1}^{-}+2{Q}_n^{-}\\ {}{Q}_2^{+}=-{Q}_{n-2}^{-}-6{Q}_{n-1}^{-}+6{Q}_n^{-}\end{array}\end{array}\end{array}\right. $$

(52)

3.4 Optimization procedure

The optimization steps are given as follows:

• 1. Model initialisation: including the initial structural guess, the CLIBS model, the XFEM model, and the optimization parameters. Re-initialize the level set function based on Eq. (43).

• 2. Perform the XFEM based structural analysis.

• 3. Evaluate the structural stress on the eroded design Eq. (46) and the structural volume fraction of the blueprint Eq. (47).

• 4. Perform sensitivity analysis based on Eq. (39, 40, 42).

• 5. Update the design variables by the method of moving asymptotes (MMA) (Svanberg, 1987).

• 6. Apply the approximate re-initialisation scheme to the design variables from Eq. (43).

• 7. Impose the continuity to the design variables.

• 8. Check if the convergence condition is satisfied, otherwise go back to step 2.

4 Numerical examples

4.1 L-bracket

The first example is to optimize an L-bracket with the proposed approach. Figure 6a shows the design domain and boundary conditions. The design domain of a length L=150 is divided into 16 cells, each of which has 30 × 30 four-node square finite elements. For the B-spline basis functions, the knot spans in both x and y directions are 3, and the order is 3. The structure of each cell is determined by 12 ×12 coefficients. An external force of a magnitude F=1.0 is exerted downwards to a small region of the right tip, while the top of the structure is fixed. The Young’s modulus of the material is 1.0, and the Poisson ratio is 0.3. The offset parameter h for the eroded design is set as 0.02.

Figure 6b shows an initial design, which is intentionally designed to have the outer boundary offset from the boundary of the design domain. For comparison, another initial design with the structural boundary starting on the domain boundary is also given in Fig. 6c, in which a few small holes are predefined on the structural boundary.

4.1.1 Volume-constrained stress minimization

Optimization with cells

The first study is to minimize the structural stress of the L-bracket subjected to a volume constraint. The optimization problem is formulated as Eq. (48), in which V* is set to 0.4. Figures 7 and 8 demonstrate the optimized structures from different initial guesses and with different p values 4, 6, and 8, respectively. For each set of designs, the p-norm stress values and the actual stress values σ_max are compared.

It is observed that when p increases, the maximum stress of the structure decreases. Besides, the re-entrant corner of the initial design is successfully removed and replaced by a hollow-like-curved shape. However, considering that a higher p value may increase the nonlinearity of the optimization problem and jeopardize a smooth convergence, p is set as 6 in the subsequent examples, which can give reasonable design results according to the author’s experiences. Comparing the optimization results with two different initial designs, the same structural topology and similar stress values are obtained. Note that, the designable structural boundary corresponds to the zero level set. However, in practice, for an initial design whose boundary coincides with or cut by the boundary of a design domain, it requires an additional parameter fitting for the proposed method to ensure that the level set value at the outermost boundary is exactly equal to zero. Such a calculation may be cumbersome for an irregular domain boundary.

Without the cells

In order to verify the correctness and effectiveness of the proposed cellular parameterization scheme, the L-bracket minimum stress problem is also implemented without the cell partition scheme on the design domain. The finite element model, the number of the B-spline coefficients, the B-spline order and the optimization parameters keep the same as the CLIBS model in the Section 4.1.1.1. The only difference between the two methods is that the level set function herein is parameterized by considering the design domain as one cell. Figure 9 shows the optimization results of the L-bracket without the cell partition scheme. By comparing with the results in Fig. 7, it can be found that the geometries of the optimized results with two different cell partition schemes are nearly the same, and the corresponding stress values are similar. This comparison proves that the proposed cellular parameterization scheme will not affect the accuracy and effectiveness of the stress-based topology optimization results. Furthermore, it provides flexibility for the design and optimization of cellular structures.

Numerical artefacts

The above results are obtained with the proposed two-field-based approach. For comparison, the stress minimization problem of the L-bracket is solved in this section by considering only one field that both the stress and the structural volume are evaluated on the blueprint design, the zero level set. Figure 10 shows the optimized structure and its corresponding stress field. The value of the p-norm function and maximum stress of the optimized structure are 0.86 and 0.45, respectively. In Fig. 10a, a few small features are observed and illustrated in enlarged views. The small features appear at the structural boundary and each consists of several cutting elements. However, for finite element analysis, these regions are treated approximately as grey elements. It is difficult to obtain an accurate stress evaluation at these small features, which can be verified from Fig. 10b, since no stress concentration occurs at these small features. This phenomenon is known as the numerical artefacts in the XFEM-based level set solution for the structural shape and topology optimization (Makhija & Maute, 2014).

For the proposed two-field-based formulation in this work, the blueprint structure is used to represent the geometry of the structure, while an eroded structure is used to calculate the stress-based design response. Under the situation when the blueprint is about to generate small hollow or holes, the corresponding areas in the eroded structure are already exhibiting hollows and holes, which leads to a substantial increase of the stress. By minimizing the structural stress, these small features will be removed from the eroded structures and hence from the blueprint. Besides, the proposed approach has a filtering effect due to the B-spline parameterization to eliminate floating materials in the design domain. Hence, the numerical artefacts of the XFEM-based level set solution can be avoided by the proposed approach.

Moreover, in order to illustrate the influence of the parameter h on the optimization results, different h values are studied in the two-field-based optimization scheme. The optimized structure and corresponding stress distribution are given in Fig. 11, where h values are 0.001, 0.01, 0.02, 0.1, and 0.2, respectively. It is observed that when h is set to a small value, e.g., h < 0.01, the eroded structure and the blueprint structure are almost the same. As a result, the numerical artefacts cannot be eliminated. However, when h is too large, e.g., h > 0.2, since the approximate re-initialisation strategy can only guarantee that the slope of the level set model near the structure boundary is approximately equal to 1, it cannot ensure a constant physical offset when it is far from the zero level set. As a result, the optimization process may not be stable and it may be difficult to guarantee a meaningful design result. To the authors’ experiences, setting the h value at the range of 0.01 to 0.2 can produce reasonable optimization results with the proposed solution.

4.1.2 Stress-constrained volume minimization

In this example, the problem of minimizing the structural volume subject to the stress constraint in Eq. (49) is studied. All the optimization parameters remain the same as the previous example. Starting from the initial design as shown in Fig. 6b and with different allowable stress values σ^* = 0.9, 1.0, 1.1, and 1.2, the optimized structures and the corresponding stress distributions are obtained as shown in Fig. 12.

Fig. 6.

L-bracket optimization problem. The blue-dotted lines are the cell boundaries. a Design domain and boundary condition. b Initial design A. c Initial design B

Fig. 7

Different designs and the corresponding stress fields. a initial design A and b–d optimized structures with different p values. σ_max is the actual maximum von Mises stress

Fig. 8

Different designs and the corresponding stress fields. a initial design B and b–d optimized structures with different p values

Fig. 9

Different designs and the corresponding stress fields. a Initial design A and b–d optimized structures without the cell partition scheme

Fig. 10

Examples of numerical instability in the level set method with XFEM for the stress minimization problem. a Numerical artefacts. b Stress field

Fig. 11

Optimized designs and the corresponding stress fields of an L-bracket with different h

Fig. 12

Optimized designs and the corresponding stress fields of an L-bracket with different allowable p-norm stresses

Fig. 13

Definition of the curved cantilever beam optimization problem and the mapping of a rectangular cantilever beam to a curved cantilever beam

Fig. 14

Initial designs of curved cantilever beams with different cell partition schemes. a 4 × 2 cells. b 4 × 3 cells. c 3 × 4 cells. d 6 × 3 cells

Fig. 15

Optimized designs and the corresponding stress fields of a curved cantilever beam with different types of periodicity.

Fig. 16

Optimized structures and the correspondent stress fields of a curved cantilever beam with different cell partition schemes

Fig. 17.

Optimized radial periodic cellular designs and the corresponding stress fields of a curved cantilever beam with different continuity orders

As the allowable stress value increases, the structural volume decreases and the structure tends to a nearly full-stress state. Besides, smooth boundaries are generated at the re-entrant corner to avoid the stress concentration. It can also be pointed out that due to the stress concentration, there is no linear correlation between the volume and allowable stress value of the optimized structure. The volume does not linearly decrease as the allowable stress value increases. Another issue is that by using the p-norm formulation, it cannot control the actual maximum stress if a low p value is used (Zhou & Sigmund, 2017). However, in practice, if the actual maximum stress is concerned, an adaptive constraint strategy proposed by Le et al. (Le et al., 2010) can be easily implemented with the proposed approach by adjusting the relationship between the p-norm stress and the actual maximum stress in the iteration process.

4.2 Curved cantilever beam

The second example is to design a curved cantilever beam structure as shown in Fig. 13. The volume-constrained stress minimization problem is considered as expressed in Eq. (48). The boundary conditions and design domain are shown in Fig. 13, where R=5 and r=3. A force F=1.0 is applied to the left lower corner of the structure. The design domain is divided into several cells, and the isoparametric elements are used for the finite element analysis. As shown in Fig. 13b, a rectangular domain with a=144 and b=288 is first constructed. Then, the mapping relationship between the coordinate (x,y) of the curved beam and the coordinate (ξ,η) of the rectangle is established as follows:

$$ \left(x,y\right)=\left(\left(R-r+\frac{r\eta}{b}\right)\mathit{\sin}\frac{\pi \xi}{2a},\left(R-r+\frac{r\eta}{b}\right)\mathit{\cos}\frac{\pi \xi}{2a}\right) $$

(53)

According to the above equation, the Jacobian matrix J can be calculated by the following:

$$ \boldsymbol{J}=\left[\begin{array}{cc}\frac{\partial x}{\partial \xi }& \frac{\partial y}{\partial \xi}\\ {}\frac{\partial x}{\partial \eta }& \frac{\partial y}{\partial \eta}\end{array}\right] $$

(54)

As a result, the element stiffness matrix in Eq. (32) is rewritten as follows:

$$ \boldsymbol{K}=\sum \limits_{i\in I}{\boldsymbol{K}}_e=\sum \limits_{i\in I}{\int}_{\Omega_e}{\boldsymbol{B}}^T\boldsymbol{DB}\left|\boldsymbol{J}\right|d\boldsymbol{x} $$

(55)

where |J| denotes the determinant of J. The knots of the B-splines are located in the rectangle domain, which is discretized with 288 × 144 four-node bilinear elements. In both x and y directions, the order of the B-spline basis functions is 3, and the knot spans are 3. The level set offset parameter h is taken as 0.02. The p-norm value is set as 6. The initial designs with different cell partitions are given in Fig. 14.

4.2.1 Cell periodicity

By using the design shown in Fig. 14d as the initial guess, the optimized structures with non-periodicity, radial periodicity, circumferential periodicity, and cell-wise periodicity are shown in Fig. 15. The radial and circumferential periodic cellular structures correspond to the replication of unit cells along the radial and the circumferential layers, respectively. By imposing a C⁰ continuity at the junctions of adjacent cells, the proposed approach can effectively avoid the stress concentration caused by the non-smooth transition between the neighbouring cells. Moreover, since the shape and topology of the cell are required to be the same, which can be viewed as a strong geometric constraint, it is difficult to obtain a fully-stress design for the periodic cellular structure.

4.2.2 Cell partition

To illustrate the impact of the cell partition scheme, the curved beam is re-designed with 4 × 2, 4 × 3, 3 × 4, and 6 × 3 cells, respectively, with C⁰ continuity between adjacent cells. By using the initial guesses as shown in Fig. 14, the corresponding optimized designs are obtained as shown in Fig. 16.

From this example, it can be found that the stress values of the optimized structures vary for different cell partitions. Particularly, the stress value becomes higher as cell number increases. However, the cell partition is a very important issue for the cellular structure design. It is in principle a very difficult task to propose a general strategy for cellular partition, especially for a structure with complex stress distribution. Nonetheless, the CLIBS method shows great flexibility in the modelling and the design optimization of cellular structures for a design domain of an arbitrary shape. It is targeted as a separate future work to investigate the cell partition strategy for cellular structure design.

4.2.3 Continuity order

Furthermore, the effect of the continuity order between adjacent cells is also studied. The design domain is divided by 4 × 2 cells. The C⁰, C¹, and C² continuities are selected to design the radial periodic cellular structures. Figure 17 shows the optimized radial periodic cellular designs with different continuity orders. The corresponding stress fields are also provided. It is observed that all the three designs share a similar topology. Besides, it leads to a higher p-norm stress value with a higher order of continuity condition, although the result exhibits a smoother geometric connection between neighbouring cells. It is because that the additional geometric requirement of continuities restricts the design freedom at the cell connection regions.

5 Conclusion

In this paper, a shape and topology optimization approach to design cellular structures considering the structural stress-based problems is proposed. It leverages the CLIBS model which consists of several independent and well-connected sub-domains parameterized by B-splines, thus ensuring the cell connectivity and manufacturability of the optimized structure. Each individual cell has its own independent configuration without any geometric constraints or predetermined connectors. The structural stress value and the sensitivity of the optimization problem are obtained by using an XFEM scheme. Besides, to cope with the numerical instability caused by the XFEM scheme, a two-field-based formulation and a corresponding optimization strategy are proposed to suppress the generation of small geometric features. A least square approach is also proposed to impose the high-order continuity between cells and ensures a smooth optimization. The results of numerical examples show that the proposed approach exhibit flexibility and effectiveness for modelling the cellular structures. The CLIBS parameterization scheme can ensure geometrical continuities of adjacent cells, which can avoid the stress concentration caused by discontinuities between cells. However, a high-resolution of cells may lead to a high definition of large-scale data and computation, for which parallel computing can be leveraged for a more efficient solution. Another important issue for the cellular structure design is the cell partition, which is generally a difficult task to be predetermined, especially for a structure with complex stress distribution. Nonetheless, with the flexibility in modelling cellular structures for an arbitrary shape of design domain by the proposed approach, it is targeted as a separate future work to investigate this issue.