Single and multi-objective shape optimization of streamlined bridge decks

Abstract

Civil engineers focus on developing an optimum design that is cost-effective without compromising the performance. Experiences from optimizing airplane wings in aerospace engineering have been extensively made for the last decades where the aim is to maximize the lift-to-drag ratios. In civil engineering, shape optimization of tall buildings and bridge cross-sections is still an open research field where the aim is to enhance the aerodynamic behavior of these structures. The main challenge, however, is to develop bridge decks that avoid excessive deformations and ensure a sufficient structural reliability. Within this framework, the paper outlines the single and multi-objective shape optimization for static aerodynamic forces of a streamlined box section. Computational fluid dynamic simulation based on vortex particle method provides the quantities of interest which are approximately treated by a Kriging surrogate for the optimization. Later, the performance of the optimized structure is checked against flutter instability.

1 Introduction

For long-span bridges, the deck may be exposed to wind from both sides. Thus, a box design, symmetrical about the vertical center plane and featuring rounded edges, is preferable. The main challenge for designers is to save material while simultaneously ensuring the efficiency and the reliability of the structure, so that buffeting and vortex shedding responses are kept within acceptable limits. Main effects like reducing the vortex shedding excitation, achieving the functionality of the structure against buffeting, and reducing the aeroelastic instability are considered during the design process. As compared to other cross-sections, the streamlined box girder is the most common in long-span bridges since it can minimize the wind forces (Larsen 2008; Wang et al. 2011). The construction of the Severn Bridge UK in 1966 marked a revolutionary progress in bridge design. In general, the key structural parameters that affect the aerodynamic performance of bridges are mass, stiffness properties, and the structural damping. Structural configurations are mainly related to the climatic characteristics of the area and the budget allocated for each project.

Aerodynamic shape optimization of airfoils was extensively studied in the recent years (Huyse and Lewis 2001; Diwakar et al. 2010; Sadrehaghighi et al. 1995), where the aim is to minimize the drag when airfoils are subjected to a minimum lift requirement. After the collapse of the old Tacoma Narrows bridge, more attention has been given to develop the performance in structural designs. However, despite the great improvement, wind storms may still cause damage to buildings resulting in financial losses and threats to human lives. Several examples of losses are documented every year even in developed countries. Methods are implemented from early stages of construction to ensure sufficient structural safety and avoid large deformations under wind flow. To determine the aerodynamic optimum design, experience-based design approaches were used, matching the environmental threat. Intensive studies have been performed to detect the effects of various cross-sections of bridge decks on the wind coefficients (Wardlaw 2012; Tolstrup 1992; Larsen 2017). However, it is still challenging to predict the aerodynamic behavior while changing the geometric layout of the structure since small changes can lead to different results of wind forces (Wang et al. 2009; Amin and Ahuja 2010; Bruno and Mancini 2002). Within this framework, computational fluid dynamics (CFD) simulations have been implemented.

The width to depth ratio of bridge decks is an important factor in bridge aerodynamics and experience has shown that increasing this ratio improves the behavior of the bridge against large aerodynamic forces (Poon 2009; Larose and Livesey 1997). Shimada and Ishihara (2002) investigated the behavior of the wake in rectangular cylinders while varying the width over depth ratio in the range of 0.6 to 8.0. Lin et al. (2005) studied the influence the shape of the deck has on bridge aerodynamics while considering flutter and buffeting characteristics. They tested two basic deck sections: closed box girder and a plate girder in smooth and turbulent flow fields. The results show that bridges with closed box girder deck have higher critical wind speeds than those with a plate girder. Optimization techniques in structural design of bridges have gained a lot of attention in the last decades. Reliability based design optimization of long-span bridges considering flutter was intensively studied by Kusano et al. (2014, 2015, 2018). The aim is to minimize the bridge girder weight, and to find the minimum volumes of the main cables and bridge girder while satisfying the required safety level under flutter. Montoya et al. (2018) proposed a novel approach for the optimization of deck shape and cables size of long-span cable-stayed bridge, while combining aeroelastic and structural constraints.

Studies related to the effect of shape modifications of the building on the aerodynamic behaviors were intensely presented (Amin and Ahuja 2010; Kulkarni and Muthumani 2016; Lohade and Kulkarni 2016). CFD calculations suffer, however, of higher computational time. Approximation using surrogate models becomes, therefore, a good alternative to avoid iterative processes in CFD evaluations. Kareem et al. (2013, 2014) investigated the shape optimization of tall buildings by developing a surrogate-based optimization strategy. Montoya et al. (2016, 2018) used, also, the surrogate model evaluated for the aerodynamic coefficients and slopes of a bridge deck cross-section, while varying its depth and width up to a percentage of 10%. Then, an optimization process is carried out on these surrogate models in order to obtain the optimal designs that reduce the total amount of material, while considering structural and aeroelastic constraints.

Enhancing the aerodynamic behavior of the structure requires reducing its aerodynamic responses which is related to the aerodynamic forces. This can be done by minimizing the static wind coefficients: drag, lift, and moment. This paper proposes a new optimization framework regarding the aerodynamic responses in bridge design. In order to find the optimal layout of streamlined bridge decks, shape optimization is carried out based on the response surface method derived from Kriging approximation. The static wind coefficient models represent the objective functions to be optimized. A penalty function method is used to transfer the constrained optimization problems into unconstrained problems and the optimization process is carried out for single objectives in the first stage. Then, a multi-objective function is formulated by adding the single objective functions using weighting parameters. The particle swarm optimization method is applied to both cases and the optimal shapes are obtained. The performance of the latter is checked against flutter instability.

Two approaches are introduced based on meta-model strategies. The first approach is direct and considers the optimization of the bridge deck cross-section using static wind coefficients at zero angle of attack. The second approach is advanced and considers the static wind coefficients at multiple angles of attack.

2 Theory and implemented methods

2.1 Aerodynamic phenomenon

A bluff body embedded in the fluid flow causes separation of the flow near the surface. The boundary layer separation occurs because the fluid particles are decelerated by inertial forces. The separated layers generate vortices, which are shed into the wake flow behind the body. Such vortices can cause extremely high suctions near separation points such as corners or eaves, and they create alternating forces in a direction normal to the wind flow. This motion is called vortex shedding excitation as a result of such forces.

An important factor affecting this phenomenon is the Reynolds number (R_e), which is a measure of the ratio of inertial to viscous forces. Depending upon the magnitude of R_e, the flow can be laminar or turbulent. The difference between a laminar and a turbulent boundary layer is that the transfer of momentum occurs on a molecular rather than a macroscopic scale. The vortex shedding phenomenon is also observed in different shapes, such as triangles, rectangles and other regular and irregular prisms. This process is described in terms of a non-dimensional number, which is the Strouhal number. For more details, the reader can refer to Simiu and Scanlan (1996) and Holmes (2015).

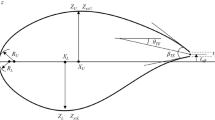
The immersion of a section in a flow of velocity $U_{\infty }$, as shown in Fig. 1, is conducive to development of local pressures over the body. The integration of these pressures over the surface results in a mean wind load, which can be split into three parts (measured per unit of span): The drag force F_D in the mean wind direction causes lateral displacements in the structure, the lift force F_L, is perpendicular to the mean wind direction and the moment F_M with respect to the centroid of the section that constitutes the torsion.

Fig. 1

Schematic of deck section with aerodynamic forces, lift F_L, drag F_D, and moment F_M and the corresponding vertical displacement h, lateral displacement p, and rotation α

The static wind coefficients for bridge deck sections, which represent the functions to be optimized, can be rendered dimensionless and seen as functions of net wind force coefficients, the wind velocity $U_{\infty }$, the angle of attack α, and the deck width B. These mean wind coefficients can be expressed as follows:

$$ C_{L}(\alpha) = \frac{F_{L}(\alpha)}{\frac{1}{2}\rho U_{\infty}^{2} B}, $$

(1)

$$ C_{D}(\alpha) = \frac{F_{D}(\alpha)}{\frac{1}{2}\rho U_{\infty}^{2} B}, $$

(2)

$$ C_{M}(\alpha) = \frac{F_{M}(\alpha)}{\frac{1}{2}\rho U_{\infty}^{2} B^{2}}, $$

(3)

where ρ is the mass density of air. The mean static wind coefficients are non-dimensional aerodynamic forces which are functions of wind angle of attack. These coefficients are not only used to calculate the static aerodynamic forces but also their derivatives with respect to the angle of attack, and commonly used to determine the buffeting forces and the aerodynamic stability (Xu 2013).

It is important to note that in two-dimensional flow, the terms F_L, F_D, and F_M represent the corresponding values per unit of dimension, normal to the plane of observation. In a three-dimensional case, the dimensionality is preserved by including an additional factor B in the denominator of each expression. The wind force coefficients depend on the shape of the body, the roughness of the surface, and the value of R_e. Simiu and Scanlan (1996) presented examples on the circulation of the flow with different body shapes and R_e. Optimized shapes are obtained by the minimization of the previous static wind coefficients presented in the equations (1), (2), and (3).

Bridge designs must fulfill structural and aerodynamic requirements for service life and user proficiency. The wind induced stresses have to be below the allowable stress limit, and the aeroelastic stability of the bridge deck section has to be ensured. Analysis of the stability of the bridge cross-sections can be performed in two ways: dynamic tests in wind tunnels or by CFD simulations. Usually, checking the performance of bridge structures is done by evaluating the dynamic wind induced responses which refer to the vortex induced oscillations and the self-excited oscillations, i.e., flutter. The static behaviors are rarely considered for the design of bridges.

Flutter instability occurs usually at very high wind speeds, as a result of self-excited aerodynamic forces. It is due to the coupling of structural motion and aerodynamic forces, involving both vertical and torsional movements and can lead to the collapse of the bridge. Therefore, it is important to evaluate the flutter limit of the bridge U_cr below which section models must be stable. A comprehensive review on flutter instability is presented by the co-authors (Abbas et al. 2017). When the wind speed exceeds U_cr, the structure no longer fulfills the design criteria and the situation corresponds to the ultimate limit state. For flat plate sections, the critical flutter limit U_cr,FP can be evaluated according to Theodorsen’s theory (Theodorsen 1949). Generally, it is considered that wide streamlined decks have critical velocities close to the theoretical flat plate flutter limit (Gimsing and Christos 1983). This difference can easily be presented by the ratio of the computed flutter limit to flat plate prediction, which is defined as follows:

$$ {\upbeta}_{f}=U_{\text{cr}}/U_{\text{cr,FP}}. $$

(4)

Higher values of this ratio indicate that the sections are similar to a flat plate. Vortex shedding excitation is a result of the interaction between the bridge and the vortex flow leading to the lock-in phenomenon. Formation of vortices alternately on the upper and lower surfaces of the deck creates alternating forces parallel to the flow direction. Usually, it occurs at relatively low wind speeds when the frequency of the vortices shed in the wake of the solid bluff body, coinciding with one of the natural frequencies of the structure. Buffeting excitation is caused by fluctuating forces induced by turbulent flow. It occurs over a wide range of wind speeds, and it can affect the functionality of the bridge. Therefore, it is considered in the design stage as well as the service stage of the bridge.

Tests are often performed using wind tunnel experiments on dynamically mounted section models to study the aerodynamic instability characteristics. Due to the computational advances, CFD simulations have become a useful tool for such analyses. Generally, streamlining the girder cross-section can reduce the effects of the vortex shedding. In our case, due to small depth to width ratios resulting in the optimized structures, the vortex shedding oscillations are assumed to be insignificant, and confirmation with regards to this phenomenon is not considered. However, our study focuses on the static mean wind response and no additional aerodynamic forces such as in the case of uniform inflow behavior are considered. Therefore, the buffeting response is not evaluated. The performance of the optimized structure is assessed by solely considering the flutter instability.

Checks for flutter instability are made by evaluating the vertical and torsional instability. Commonly, torsional motion develops divergent amplitudes in a short period of time leading to critical wind speed. A usual method for checking the flutter instability is identification of the aerodynamic derivatives (Wang and Dragomirescu 2016; Abbas and Morgenthal 2012), as it is adopted in this paper. Scanlan introduced expressions for the motion-induced aerodynamic forces on a cross-section (Scanlan and Tomo 1971; Scanlan 1978). He assumed that the self-excited lift F_L and moment F_M of a bluff body can be expressed as a function of the linear displacement h, the rotation α, and their first derivatives in a linearized form as follows:

$$ \begin{array}{@{}rcl@{}} F_{L} &=& \frac{1}{2} \rho U_{\infty}^{2} B \left[ K H_{1}^{*} \frac{\dot{h}}{U_{\infty}}+ K H_{2}^{*} \frac{B \dot{\alpha}}{U_{\infty}}\right.\\ &&\qquad\qquad \left. + K^{2} H_{3}^{*} \alpha + K^{2} H_{4}^{*} \frac{h}{B} \right], \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} F_{M} &=& \frac{1}{2} \rho U_{\infty}^{2} B^{2} \left[ K A_{1}^{*} \frac{\dot{h}}{U_{\infty} }+ K A_{2}^{*} \frac{B \dot{\alpha}}{U_{\infty}} \right.\\ &&\qquad\qquad \left.+ K^{2} A_{3}^{*} \alpha + K^{2} A_{4}^{*} \frac{h}{B} \right], \end{array} $$

(6)

$$ K = \frac{B \omega}{U_{\infty}}. $$

(7)

$A_{i}^{*}$ and $H_{i}^{*} \quad (i=1,...,4)$ are non-dimensional functions of K known as aerodynamic flutter derivatives, associated with self-excited lift and moment, respectively. K is the reduced frequency and ω is the frequency of bridge oscillation under aerodynamic forces. The aerodynamic derivatives are usually measured in special wind tunnel tests and can also be computed from the CFD simulations. The motion-induced aerodynamics can be evaluated from forced vibration simulations. The resulting lift and moment forces are used to compute the aerodynamic derivatives as explained in the following formula:

$$ \begin{array}{@{}rcl@{}} F_{L} &=& \overbrace{...H_{1}^{*} \dot{h} + ...H_{2}^{*} \dot{\alpha}}^{\text{damping terms}} + \overbrace{ ...H_{3}^{*} \alpha + ...H_{4}^{*} h }^{\text{stiffness terms}}, \end{array} $$

(8a)

$$ \begin{array}{@{}rcl@{}} F_{M} &=& \underbrace{...A_{1}^{*} \dot{h}}_{\text{heave}} + \underbrace{...A_{2}^{*} \dot{\alpha} + ...A_{3}^{*} \alpha}_{\text{pitch}} + \underbrace{...A_{4}^{*} h }_{\text{heave}}. \end{array} $$

(8b)

The terms of the self-excited lift F_L and moment F_M in (8a) and (8b) can be considered as the summation of damping terms (associated with the velocity of motion) and stiffness terms (associated with the displacement of motion). Also, these terms can be classified into two parts as the result of the heave and pitch velocities. The aerodynamic derivative $H_{1}^{*}$, which corresponds to the aeroelastic lift force induced as a result of heave velocity, controls the vertical flutter. However, the term $A_{2}^{*}$, which is the aeroelastic moment induced due to the pitch velocity, governs the torsional flutter instability. These flutter instabilities are related to the negative aerodynamic damping.

The aerodynamic derivatives describe the aerodynamic behavior of the oscillating deck section. Usually, they are evaluated via experimental wind tunnel tests by the implementation of different methods, and they can be used for the examination of aerodynamic coupled instability. The assessment is fulfilled by considering all of the aerodynamic derivatives of the deck cross-section. Some current aerodynamic derivative identification studies and methods have been reported in Poulsen et al. (1992), Imai et al. (1989), and Yamada et al. (1992). In this work, in order to evaluate the aerodynamic derivatives, a flow solver is used to perform forced vibration simulations on the optimized cross-sections in the sinusoidal heave and pitch motion over a range of reduced speed v_r defined as follows:

$$ v_{r} = \frac{U_{\infty}}{B f_{o}}=\frac{U_{\infty}}{B}T_{o}, $$

(9)

where f_o and T_o are the frequency and period of the forcing motion, respectively. The aerodynamic derivatives are computed from the resulting force and moment time histories of the sections by applying least squares fit.

The coupled flutter limit of the cross-section is computed using the aerodynamic derivatives in the frequency domain. For this purpose, eigenvalue analysis is utilized to describe the nature of the system stability at different wind speeds. For further explanation about the method, the reader is referred to the work accomplished by the author (Abbas 2016). This method has been amply used. However, advanced method for the evaluation of the critical flutter velocity is introduced by Kavrakov and Morgenthal (2018a) where a coupling between the 2D velocity-based turbulence generation (VTG) method for free-stream turbulence and the laminar Pseudo-3D vortex particle method (VPM) is accomplished and lead to the introduction of a turbulent Pseudo-3D VPM. In his work, the first method was utilized.

2.2 Numerical simulations for aerodynamic parameters

To analyze the effect of the wind on bridges, three main methods are utilized: analytical, numerical, and experimental methods. The last is considered to be the most common approach but has uncertainties related to scale effects, while the other two are still in the development stage.

The numerical analysis has been performed by using a CFD flow solver, VXflow, based on vortex particle method. This code is developed by Morgenthal (2002) and shows reliable results in comparison to wind tunnel test (WTT) (Morgenthal and Asia 2006; Morgenthal 2005; Morgenthal and Walther 2007; Morgenthal et al. 2014; Abbas and Morgenthal 2016). Recent studies (Kavrakov and Morgenthal 2018b; 2017) validated the results provided by this solver with regards to flutter and buffeting analysis. This solver is based on VPM which is a virtual wind tunnel analogue to the laboratory wind tunnel. In this framework, the aerostatic simulations are performed on a streamlined bridge section in uniform flow to determine the static wind coefficients.

2.3 Kriging approximation

Despite the development of the computational field of computers, calculations with CFD are still expensive. The procedures employed in optimization require, frequently, several analyses within an iterative process. Approximations using surrogate models are, therefore, a good alternative to avoid these problems.

In literature, several methods are used to build response surfaces. Polynomial regression and Kriging have shown adequate approximation for complex problems in engineering, in particular for the optimization of aerodynamic problems (Montoya et al. 2016; Bernardini et al. 2015; Díaz et al. 2016). Therefore, both approaches were implemented, and the models obtained from Kriging are used to build the response surface and adopted later for further analysis and optimization.

Kriging is one of the response surface methods, that gives a mathematical approximation of the model, linking the output to the design variables (input) through stochastic processes (Forrester et al. 2008; Martin and Simpson 2005; Gano et al. 2006; Joseph et al. 2008; Kanevski and Maignan 2004). Generally, Kriging is able to produce a model that represents a nonlinear and vector-valued function efficiently. Considering the point $X^{*}=[x_{1}^{*},...,x_{k}^{*}]^{T}$ in the sample space, the scalar value $\widehat {Y}$ in X^∗ can be evaluated using the Kriging approximation as follows:

$$ \widehat{Y}(X^{*})=\mu+\epsilon(X^{*}), $$

(10)

where μ is an unknown constant trend that needs to be estimated based on the observed response values and 𝜖(X^∗) is a random function with zero mean and variance σ². A special weighted distance is used:

$$ d(X_{i}, X_{j})=\sum\limits_{h=1}^{k} \theta_{h} \left| x_{ih}- x_{jh} \right|^{2}. $$

(11)

The Kriging basis has a vector $\theta =\{\theta _{1},\theta _{2},..., \theta _{k} \}^{T}$ which allows the width of the basis function to vary from sample point to another. The covariance matrix of 𝜖(X^∗) is expressed as follows:

$$ \text{cov}[\epsilon(X_{i}), \epsilon(X_{j})]=\sigma^{2} \text{cor}[\phi(X_{i}), \phi(X_{j})], $$

(12)

where ϕ is the correlation function selected by the user, which is symmetric with unit values on the diagonal. Various correlation functions can be used; however, in literature, ϕ is often chosen to be an exponential correlation function, and it is defined as follows:

$$ \phi_{\text{ij}}= {\Psi} (X_{i}, X_{j})= \exp[-d(X_{i}, X_{j})]. $$

(13)

The estimation of the Kriging parameters {μ,σ²,𝜃} given a set of observations $\overline {Y}$ is generally obtained by the maximum likelihood approach (Badawy et al. 2017) or by minimizing the coefficient of prognosis CoP (Most and Will 2008; 2010) which is defined as follows:

$$ \text{CoP}=1-\frac{\text{SS}_{E}^{\text{Prediction}}}{\text{SS}_{T}}, $$

(14)

where SS_T is the total sum of squares and $\text {SS}_{E}^{\text {Prediction}}$ is the sum of squared prediction errors (Most and Will 2011; Chatterjee and Hadi 2015). In this work, the approximation of Kriging models is made while minimizing the CoP coefficient. CoP is calculated based on p-fold cross-validation (Viana et al. 2009; Wang and Shan 2007; Lin 2004), where the data are divided into 10 subsets.

2.4 Sensitivity analysis

Sensitivity analysis is implemented in this paper in order to evaluate how much each input is contributing to the output of the model and to quantify their relative importance. In this current work, the input parameters are the five geometric design variables (see Fig. 2), and the outputs are the static wind coefficients taken separately: lift, drag, and moment.

Fig. 2

Variation of the design variables for deck geometry

There are two main approaches in sensitivity analysis: local and global approaches. The local sensitivity analysis is a deterministic approach, where the model may be run many times by varying one parameter each time to evaluate its impact on the model output. Variance-based sensitivity analysis is a form of global sensitivity method and it has been used to calculate the first and total effects sensitivity indices. Considering a model with a scalar output Y as a function of a given set of k random input parameters X_i: Y = f(X₁,X₂,...,X_k), the first-order sensitivity index S_i is a direct measure and it evaluates the decoupled influence of each input variable solely. It is defined as follows (Sobol 1993):

$$ \begin{array}{@{}rcl@{}} S_{i} &=& \frac{V_{X_{i}}(E_{X_{\sim i}}(Y \mid X_{i}))}{V(Y)}\\ &=& 1- \frac{E_{X_{i}}(V_{X_{\sim i}}(Y \mid X_{i}))}{V(Y)},\quad \sum\limits_{i=1}^{n} S_{i} \leq 1, \end{array} $$

(15)

where X_i is the i th factor and $X_{\sim i}$ is the matrix of all factors except X_i. $V_{X_{i}}(E_{X_{\sim i}}(Y \mid X_{i}))$ measures the first-order effect of X_i on the model output, V (Y ) is the unconditional variance of the model output and $E_{X_{i}}(V_{X_{\sim i}}(Y \mid X_{i}))$ is the residual. The total effect sensitivity index $S_{T_{i}}$ is an extension for higher order coupling terms of the first-order sensitivity. It measures the total effect including the first- and higher order effects of factor X_i, and can be defined as follows:

$$ \begin{array}{@{}rcl@{}} S_{T_{i}} &=& \frac{E_{X_{\sim i}}(V_{X_{i}}(Y \mid X_{\sim i} ))}{V(Y)}\\ &=& 1-\frac{V_{X_{\sim i}}(E_{X_{i}}(Y\mid X_{\sim i}))}{V(Y)}, \quad \sum\limits_{i=1}^{n} S_{Ti} \geq 1. \end{array} $$

(16)

For more details about these methods, the reader can refer to Sobol (1993), Saltelli et al. (2008), Zhang et al. (2015), and Marzban and Lahmer (2016). The sensitivity analysis is conducted on the previously built Kriging model.

2.5 Optimization

2.5.1 Single objective optimization

Once the response surface from the Kriging model is obtained, an optimization algorithm is applied to find the global optimal point in each function separately, as well as considering the multi-objective case. The functions to be optimized are the static wind coefficients introduced in the equations (1), (2), and (3).

Generally, the optimization problem is formulated by maximizing the cost function with respect to the design variables, which are in this case the geometric parameters that define the edges of the streamlined deck while considering a fixed lane width and a deck shape that is symmetrical about the y-axis. The constraints are defined here while considering all possible variations in the design variables and ensuring that the final design is not concave. The general formula is given as follows:

$$ \begin{array}{@{}rcl@{}} \min\limits_{x} && f(x),\\ \text{s.t} && g_{i}(x) \leq 0, \quad i=1,...,p, \end{array} $$

(17)

where g_i defines the p inequality constraint functions.

In literature, many methods are proposed within this framework such as penalty function method, Lagrange multiplier, and gradient projection method. In this work, the penalty function approach is implemented; then, the optimization problem becomes an unconstrained function since the constraints are added to the main objective function. The optimization problem becomes (Snyman and Wilke 2018):

$$ \begin{array}{@{}rcl@{}} \min\limits_{x} && f(x) + P(x),\\ \text{where:} && P(x) = \sum\limits_{j=1}^{p}{{\upbeta}_{j} \cdot {g^{2}_{j}}(x)}. \end{array} $$

(18)

The penalty parameters β_j are defined as follows:

$$ {\upbeta}_{j} = \left\{\begin{array}{ll} 0, & \text{if } g_{j}(x) \leq 0, \\ \rho >> 0, & \text{if } g_{j}(x)>0. \end{array}\right. $$

2.5.2 Multi-objective optimization

Optimizing the fitted functions of the wind coefficients simultaneously leads to a multi-objective optimization problem. The functions can, in most cases, be conflicting, which means that no single solution can optimize simultaneously each objective. The results are presented in a Pareto front graph, which contains scatter points of Pareto optimal solutions (Madetoja et al. 2008). All Pareto optimal solutions are considered to be equally valid. The check of the final optimal solution needs to be done by considering additional criteria or based on an expert’s decision.

In this paper, the weighted sum method (Stanimirovic et al. 2011; Kim and De Weck 2004; Eichfelder 2009) is implemented to compute the Pareto optimal points for the multi-objective function. Its concept is based on adding the objective functions with weights (Marler and Arora 2010). Mathematically, the relation is presented as follows:

$$ \begin{array}{@{}rcl@{}} \min\limits_{X} && \sum\limits_{i=1}^{k}{w_{i} f_{i}(X)}, \\ \text{with} && w_{i} > 0; \quad \sum\limits_{i=1}^{k}{w_{i}}=1. \end{array} $$

(19)

2.5.3 Particle swarm optimization method

The particle swarm optimization (PSO) is used in this work to solve the optimization problems in equations (18) and (19). This method was developed by Eberhart and Kennedy (1995) and is derived from two concepts: the flocking of birds or the schooling of fish and the evolutionary computation such as stochastic algorithms. PSO is initialized with a group of random particles, where each particle i is represented by its position x_i and velocity v_i in the search space. In every iteration, each particle adjusts its trajectory according to its own previous best position (local best pbest_i) and the best previous position attained by any particle in the population (global best gbest) (Oliveira et al. 2017; Yang and Karamanoglu 2013). The particles update their positions through a process that incorporates a velocity, formulated as follows (Rini et al. 2011; Parsopoulos and Vrahatis 2002):

$$ \begin{array}{@{}rcl@{}} x_{i}(t+1) & = &x_{i}(t) + v_{i}(t+1),\\ v_{i}(t+1) & = &\omega \cdot v_{i}(t) + c_{1} \cdot r_{1} \left( \text{pbest}_{i}(t)-x_{i}(t)\right) \\&&+ c_{2} \cdot r_{2} \left( \text{gbest}(t) -x_{i}(t) \right), \end{array} $$

(20)

where r₁ and r₂ are random numbers within [0,1], ω is the inertial coefficient, selected as unit in the baseline particle swarm optimization, but an improvement of the algorithm is found when ω ≈ [0.5,0.9] (Martinez and Cao 2018). c₁ and c₂ are learning parameters or acceleration constants which proved suitable with a value of 2 (Yang and Karamanoglu 2013).

3 Framework and results

3.1 Description of the strategy

The present work proposes a novel methodology aiming to find the optimal shape of streamlined bridge decks based on a meta-modeling approach. The concept is to find the optimal shape of streamlined cross-section by minimizing the functions of wind coefficients obtained after Kriging approximation.

Generally, shape optimization allows the modification of the boundaries, so that the final design improves the aerodynamic performance. The first step is the selection of the design variables that represent the changeable geometry and has to be done prior to sampling. Six corner points define the layout of the streamlined bridge deck cross-section (see Fig. 2), and each point i has two coordinates (in x- and y-directions, x_i and y_i). Considering the symmetry of the section with respect to y-axis and while taking the lane width as a fixed parameter, we have five design variables that define the geometry layout of the deck section. These five geometric parameters are considered variables within fixed intervals, so that the resulting cross-section is not concave. Defining X = (x₁,y₁,x₂,y₂,x₃,y₃)^T as the vector that contains all the design variables, and by fixing the design variable x₁ = − 15 as the coordinate of a lane’s width of 30 m, the optimization problem is presented as follows:

$$ \begin{array}{@{}rcl@{}} \underset{x}{{\min}} &&\left( C_{L}(\mathbf{X}), C_{D}(\mathbf{X}), C_{M}(\mathbf{X}) \right)^{T},\\ \text{s.t.} && 1 \leq y_{1} \leq 1.8, \\ && -16.5 \leq x_{2} \leq x_{1}, \\ && 0 \leq y_{2} \leq y_{1} - 0.33, \\ && x_{1} \leq x_{3} \leq 0, \\ && -3.2 \leq y_{3} \leq -1. \end{array} $$

(21)

Figure 2 shows the variation of the corner points within pre-defined geometric intervals. The two designs show the schematic layout of the section obtained from the upper and the lower geometric limits of the design variables defined in this work.

Two approaches are considered in this paper for aerodynamic optimization: direct approach while considering zero degree angle of attack and an advanced approach where the aerodynamic coefficients are evaluated at different wind angles of attack varying from − 6 to + 6^∘ for each geometry sample. The first approach is simple and requires less simulations, and it is subjected to the assumptions of wind acting at 0^∘. However, the advanced approach requires more parameters in the simulations, and it is more probable to occur since it considers wind acting at different angles.

In this work, the Latin hypercube sampling (LHS) is implemented during the sampling process where the positions of the design variables, defined by the geometric coordinates, are modified in each sample within a fixed interval. Five hundred samples of cross-section geometry (see Fig. 2) are generated. No correlation is assumed on the generation of these samples.

After sampling, simulations are conducted using CFD solver to obtain the static wind coefficients (drag, lift, and moment). In the direct approach, the obtained static wind coefficients, evaluated from each sample of zero angle of attack and defined by C_L,0, C_D,0, and C_M,0 for the lift, drag, and moment respectively, are taken directly as the outputs to build the Kriging models for each case. However, in the advanced approach, the static wind coefficients of each sample are obtained at the angles of attack defined in the range from − 6 to + 6^∘ with a stepsize 2^∘. Therefore, simple regression fit of the static wind coefficients with respect to the angles of attack is made. The curve fitting function of the lift and moment is a linear function and it is a parabolic function in the case of drag. The slopes of the lift and moment are then evaluated in each sample, and denoted by $C^{\prime }_{L,\text {fit}}$ and $C^{\prime }_{M,\text {fit}}$. In the case of drag, the minimum drag value of the fitted parabolic function is evaluated instead and denoted by $C^{\min \limits }_{D,\text {fit}}$.

These coefficients, evaluated in both approaches, are then used as outputs to build the Kriging approximation functions. The approximation of the Kriging models is started by selecting 100 samples out of the generated 500 samples. The selected samples do not present any correlation. Cross-validation process is introduced, where the 100 samples are partitioned into 10 sets with equal size. The model is fit using all the samples except the first subset which is used to test the model. The predicted residual error sum of squares (PRESS), and the coefficient of prognosis (CoP) were both evaluated with the first held-out samples. Assuming that the CoP value obtained from the first iteration in cross-validation process is not large enough, the same operation is then repeated for each fold where the model with highest value of CoP is selected. This process is then repeated 10 times. However, the model is updated while adding each time 100 samples. This addition leads to an improvement of the CoP value regarding the previously retained value obtained from less samples. Therefore, in the flowchart (see Fig. 3), the quality of the model is checked in a nested loop inside the cross-validation process, and a global loop regarding the addition of new samples. Generally, the number of samples is important for modeling. As long as the number of samples is sufficiently large, we can have a good estimate of the model since it increases its accuracy. The common method to find an optimal number of samples is by increasing the number of samples in each stage and calculating in parallel the error between the data and the fitted model. The aim is to have a small error and when the error value is not decreasing further by increasing the samples; the number of samples is considered sufficient. However, this aspect is beyond the scope of this paper. The outline of this work is presented in the flow chart (Fig. 3).

Fig. 3

Flow chart for the proposed strategy

3.2 Numerical simulations for the choice of the model

Kriging approximation is conducted to build a model of the static wind coefficients. The results of the CoP are presented in Table 1.

Table 1 Results of the CoP evaluated from Kriging

Even though the CoP has some distance to 1, it is assumed to give reasonable good approximations for the underlying computational fluid dynamic model.

3.2.1 Sensitivity analysis

The first-order and total sensitivity analysis of the objective functions of the static wind coefficients are computed for both approaches and the results are shown in Fig. 4.

Fig. 4

First-order and total-order sensitivity indices of the Kriging surrogate models of the static wind coefficients: direct approach (left), advanced approach (right)

It is observed from the first-order and total-order sensitivity indices that the variables x₃ and y₃ are most significant in comparison to the other variables. Visualizing the response surfaces for problems with dimensions higher than three is difficult. Therefore, considering the results of the sensitivity analysis, the Kriging surrogate models are presented with regards to the two variables x₃ and y₁. The results of the response surfaces obtained by Kriging are shown in Fig. 5.

Fig. 5

Kriging surrogate models of the single wind coefficient functions: direct approach (left), advanced approach (right)

3.2.2 Kriging surrogate models

Outliers are observed in Fig. 5b and d. This is one of the problems of the CFD simulations. They represent failed or unfinished simulations, and they were not used to build the response surface. The high variance observed in Fig. 5a arises due to highly complex and nonlinear behavior of the model, also due to the numerical uncertainty of the CFD simulations.

3.3 Single objective optimization

3.3.1 Optimized shapes

Applying the penalty method, the geometry constraints are added to each fitted function. The particle swarm optimization method has been implemented to find the optimized shape for the three cases. Defining $C^{\text {opt}}_{L,0}$, $C^{\text {opt}}_{D,0}$, and $C^{\text {opt}}_{M,0}$ as the wind coefficients of lift, drag, and moment of the optimized shape in direct approach, and $C^{\prime , \text {opt}}_{L,\text {fit}}$, $C^{\min \limits , \text {opt}}_{D,\text {fit}}$, and $C^{\prime , \text {opt}}_{M,\text {fit}}$ for advanced approach; the final optimized shapes are plotted in Fig. 6.

Fig. 6

Optimized single objective shapes of the static wind coefficients. a $C^{\text {opt}}_{L,0}$ and $C^{\prime , \text {opt}}_{L,\text {fit}}$, b $C^{\text {opt}}_{D,0}$ and $C^{\min \limits , \text {opt}}_{D,\text {fit}}$, c $C^{\text {opt}}_{M,0}$ and $C^{\prime , \text {opt}}_{M,\text {fit}}$

The optimal cross-sections obtained after minimizing the static wind coefficients, such as lift, drag, and moment, can be presented respectively as semi-bluff deck, quasi streamlined deck, and bluff deck. The reader can refer to the work presented by Bruno et al. (2002) regarding the classification of the bridge deck sections. The two first shapes, obtained respectively after minimizing the lift and drag coefficient, influence the circulation of the flow in perpendicular and parallel directions, as they divert the incoming flow and reduce the formation of the vortices on the leading and trailing edges. Those shapes are extensively implemented for long-span bridges. The third case, presented as an outcome of neglecting the lift and drag effects in the optimization and considering solely the effects of the torsional moment, has a deep cross-section and involves unsteady flow that reaches along the side surface and gets separated at the wind-ward sharp edges. This leads to the generation of larger sinusoidal lift forces. Therefore, this kind of cross-section is prone to vortex shedding excitation. Interpretation regarding the circulation of the wind flow in such sections is presented in details by Wardlaw (2012).

3.3.2 Validation of the optimal shapes

After obtaining the optimized geometry for each case of the single objective, we evaluate the variation of wind coefficients with respect to the angles of attack for the two approaches. All the calculations are based on sampling for the interval of wind angle attack from − 6^∘ to + 6^∘. However, for the validation of the optimized shapes, static simulations are performed for each optimal shape in the interval from [− 10^∘, + 10^∘]. The slopes of the coefficients are also calculated while fitting a linear function for each case. Figure 7 shows the results of variation of wind coefficients with respect to the angles of attack for the two approaches.

Fig. 7

Static wind coefficients from CFD in the optimized shape profiles: direct approach (left), advanced approach (right). a, b Based on the optimized single objective of the lift; c, d based on the optimized single objective of the drag; e, f based on the optimized single objective of the moment

Tables 2 and 3 present the results for 0^∘ angle and slopes of the optimized wind coefficients obtained from direct and advanced approaches, evaluated from Fig. 7.

Table 2 Wind coefficients at α = 0^∘ and slopes of the optimized wind coefficients from the direct approach

Table 3 Wind coefficients at α = 0^∘ and slopes of the optimized wind coefficients from the advanced approach

The slopes of wind coefficients are good indicators of the aerodynamic instability. The effective slope of the lift curve is an important parameter in the buffeting phenomena of a streamlined deck. Experience shows that lower values of lift slopes tend to have lower buffeting responses. Also, the slopes of the lift and the moment can be used to evaluate gust loads and corresponding stresses.

It can be observed from the Tables 2 and 3. that the lift slope for both approaches in lift and drag functions is negative, indicating stability in the optimized shapes of these two cases with respect to buffeting instability. In the case of the moment function, the lift slope is negative in the advanced approach and in the direct approach has a low positive value (0.054), so the stability of the optimized moment shape is also ensured.

3.3.3 Performance check of the optimal shapes

The aerodynamic derivatives are computed from the CFD simulations, and Fig. 8 shows the aerodynamic derivatives $H_{1}^{*}$, $A_{2}^{*}$, and $A_{3}^{*}$ in function of v_r (see equation (9)).

Fig. 8

Aerodynamic derivatives $H_{1}^{*}$, $A_{2}^{*}$ and $A_{3}^{*}$ for the optimized sections: direct approach (left), advanced approach (right)

The derivative $H_{1}^{*}$ represents the aerodynamic damping due to vertical motion. A negative value of $H_{1}^{*}$ indicates positive aerodynamic damping and vice versa.

It is observed from these two approaches that the aerodynamic derivative $H_{1}^{*}$ is negative for the whole range of reduced speed v_r. This means that the obtained deck cross-section has a stable single degree of freedom (SDOF) behavior against vertical instability. The aerodynamic derivative $A_{2}^{*}$ is related to the SDOF torsional instability. From the plots, the torsional damping flutter derivative $A_{2}^{*}$ for the case of the optimal moment cross-section shows a tendency to reverse sign over a certain range of v_r. This behavior shows that the moment optimal shape is unstable with respect to the torsional flutter. In comparison with the two other shapes, the obtained moment optimal cross-section has a shallow shape and is specified by approximately equal upper and lower surfaces of the deck. Therefore, torsional flutter occurs, and this section has to be avoided. The other two cases of the optimal shapes for drag and lift are stable.

For the calculation of flutter limit, structural properties of the Lillebaelt Bridge deck cross-section are used (Abbas 2016). The section has a mass m = 11,667 kg/m, mass moment of inertia I = 1,017,778 kg m²/m, bending frequency f_h = 0.156 Hz, torsional frequency f_α = 0.5 Hz, and damping ratio for heave and pitch ξ_h = ξ_α = 0.01. The Lillebaelt Bridge is considered as reference for structural properties since it has also a streamlined cross-section.

The evaluation of the ratio β_f (see equation (4)) for the optimal shape reflects that the cases lift and drag in the direct approach are stable since their values are larger than one. In Table 4, the moment coefficient has the lowest value of β_f in both approaches, which confirms the previous results of the aerodynamic derivatives. This section is aerodynamically unstable.

Table 4 Predicted flutter limit U_cr, theoretical flat plate flutter limit U_cr,FP and β_f ratio for the candidate sections selected after optimization.

3.4 Multi-objective optimization MOO

3.4.1 Pareto front solutions

When dealing with multi-objective optimization, the aim is to optimize simultaneously the three objectives. Referring to the weighted sum approach which is based on varying the weighted coefficients in each iteration of optimization, it results in a solution called Pareto optimal where each point is a solution of a different weighted combination of the objective functions. In this step, a stochastic algorithm was utilized based on the particle swarm optimization method. By reducing the variation size of the weights, the optimization process becomes more expensive and requires larger runtime. The results presented in Fig. 9 are obtained by taking 0.02 as the variation in weighting factors during the optimization.

Fig. 9

Resulting 2D projection of sampled Pareto surface after filtering: direct approach (left), advanced approach (right)

The Pareto front consists of all non-dominated points; thus, the dominated points should be eliminated from the solution set. To achieve this, Pareto filters are introduced. The concept of Pareto filter consists on comparing every solution with the other solutions within the solution set and filtering out the points that are dominated. In this work, a filtering method developed by Parizi (2016) is implemented. When dealing with a multi-objective problem, there is no solution in the Pareto front that can be better than the others, since often the improvement of an objective can only be achieved at the expenses of worsening at least one other criteria. So, the decision-maker needs to be supported by additional criterion for making a particular choice. It is the responsibility of the decision-maker to confront the choice by adding some preference criteria. Several methods can be used to select the best solution. The 2D projection of derived Pareto samples often forms an L-shaped curve when two criteria are in conflict, called also Pareto front. This can be visualized from the cases (a), (b), and (f), and partly (c) in Fig. 9. For cases (d) and (e), strong conflicts are not visible.

Selecting the final solution from the L-curve is usually made by the decision-maker, since it requires making a trade-off between all the obtained Pareto solutions, where increasing one function may lead to the reduction of the others.

3.4.2 Selection of the optimal designs

Contrary to the previous work of checking the performance of the single objective function, which is considered as one special case of multi-objective optimization, checking the performance of the different solutions obtained after a multi-objective solution leads to the concept of validating the final optimal design that fulfills the required structural criteria. As the step lengths of the weights become more refined, a large number of solutions are obtained. Due to the trade-offs that exist between the objectives, several equally optimal solutions exist. Checking the stability of all the solutions after muti-objective optimization is not practical. Therefore, in this paper, the work is limited to some special cases and the efficiency of these models is checked.

The studied cases are taken when the three wind coefficients are equally contributing to the final multi-objective function, and the cases where one of the wind coefficients has no effect while the other two are equally contributing. This selection provides a good understanding of the contribution of each coefficient while disregarding its effect. W1, presenting the case where the three static wind coefficients (lift, drag, moment) are equally contributing, is the most probable case that can be selected by the decision-maker if no additional criterion is considered. Although the weight ratios are equal in the three wind coefficients, both approaches yield to different shapes. W2, W3, and W4 present the cases where, alternately, one of the static wind coefficients is neglected. This choice is preferable to test the individual effect of each coefficient (Fig. 10).

Fig. 10

Optimized shapes for the different cases of multi-objective optimization. a case 1: W₁ = [1/3,1/3,1/3], b case 2: W₂ = [1/2,1/2,0], c case 3: W₃ = [1/2,0,1/2], d case 4: W₄ = [0,1/2,1/2]

As observed previously in the case W1, both approaches give also different optimized shapes. In the advanced approach, the obtained cross-section presents a narrow bottom. Aerodynamically, the shapes obtained from this approach are more efficient as they divert the incoming flows of the wind around the bridge deck and prohibit the formation of large vortices on the leading and trailing edges. Selecting the best design from the four cases is not an easy task, as the decision-making depends on the detailed aerodynamic analysis. To cover this aspect, aeroelastic stability analysis is considered in the Section 3.4.3.

3.4.3 Performance check of the optimal designs (obtained by MOO)

Since the performance of the single optimized sections was checked previously, Fig. 11 present the variation of the aerodynamic derivatives of heave and pitch motions for the four selected cases.

Fig. 11

Aerodynamic derivatives for heave $H_{1}^{*}$ and pitch ($A_{2}^{*}$, $A_{3}^{*}$) motions: direct approach (left), advanced approach (right)

In Fig. 11, $A_{2}^{*}$ represents the torsional aerodynamic damping effect and is considered the most important flutter derivative. From the previous plots, it is observed that the aerodynamic derivatives $H_{1}^{*}$ and $A_{2}^{*}$ remain negative over the range of the reduced wind speed v_r for the four selected cases. This means that the selected sections are stable with respect to vertical and torsional flutter.

In the direct approach with 0^∘ angle of attack, case 3 has larger absolute values of $H_{1}^{*}$ and $A_{2}^{*}$ in comparison to the other cases. In the advanced approach, case 2 has larger absolute values of $H_{1}^{*}$ and case 3 has larger absolute values of $A_{2}^{*}$. All the cases have a positive value of $A_{3}^{*}$ representing a negative torsional aerodynamic stiffness effect. Case 3 has a slightly higher value of $A_{3}^{*}$ in both approaches. This means that the case 3 is more likely to present coupled mode motion in comparison to the other cases. The critical situation may occur by the coupling of heave and pitch motions leading to a classic flutter instability. For this reason, it is important to check the aeroelastic instability of the coupled vertical and torsional flutter of those sections.

The coupled stability is validated by solving an eigenvalue problem using all the eight aerodynamic derivatives and the equation of motion for the 2 DOF system by coupling both pitch and heave modes. The four cases are stable for the coupled vertical and torsional flutter.

Another criterion for validating the performance of the optimized shapes is to evaluate the critical flutter wind speed from an eigenvalue analysis. The results of β_f for both approaches are summarized in the Table 5.

Table 5 β_f for the candidates after multi-objective optimization

From the results shown in Tables 4 and 5, the streamlined decks show critical velocity close to the theoretical flat plate flutter limit.

From Table 5, the calculation of the ratio β_f gives values larger than one in most cases, except in the advanced approach for the case 3. This means that the three cases, W₁, W₂, and W₄, have larger flutter limits in comparison to the case W₃. It is also observed that the direct approach gives different shapes for the four cases, despite the variation of the weights in the different cases. However, the optimal shapes obtained by the advanced approach are very similar.

By considering the shape of the selected four cases, and after conducting the performance check, the designer may select case W4 from the advanced approach as the best case since it has higher flutter limit comparing to the other three cases. Besides, the advanced approach is more general than the direct approach as the wind is considered from different angles of attack for the calculation of the static wind coefficients.

4 Conclusion

This paper presents a novel framework on generating optimal aerodynamic shapes of bridge cross-section based on response surface, where Kriging approximation is used to build the surrogate models of the static wind coefficients. Two main aspects are presented: single objective optimization while applying the penalty method, so the constrained optimization problem is transferred into an unconstrained optimization problem; the multi-objective optimization, where the objective functions are transferred into a single objective function after applying the weighted sum method. The optimal designs are obtained by minimizing the mean of the aerodynamic coefficients in the direct approach, and the slopes of lift and moment coefficients and the minimum of the drag coefficient in the advanced approach. The performance of the optimal designs of bridge cross-sections was checked against the aerodynamic instabilities, mainly flutter.

The paper focuses exclusively on the optimization of streamlined deck sections, commonly used in long-span bridges. This type of deck is, generally, susceptible to aeroelastic instabilities. The optimization based on single objective shows strongly different designs. However, multi-objective optimization leads to very similar cross-section designs in the advanced approach. Moreover, the latter shows higher performances and are aerodynamically more efficient, as the edges avoid formation of large vortices. It was also observed that the aspect ratio, which is the width to depth ratio, has a significant influence on the aerodynamic behavior, where deeper cross-sections show lower resistance against flutter. Therefore, avoiding this type of section is primordial.

The framework presented in this paper is equally applicable to trapezoidal cross-sections which are more common in short- to medium-span bridges. Further work can be viewed as to combine the full buffeting analysis with the presented opimization strategy.