A hybrid self-adjusted single-loop approach for reliability-based design optimization

Abstract

Single-loop approach (SLA) exhibits higher efficiency than both double-loop and decoupled approaches for solving reliability-based design optimization (RBDO) problems. However, SLA sometimes suffers from the non-convergence difficulty during the most probable point (MPP) search process. In this paper, a hybrid self-adjusted single-loop approach (HS-SLA) with high stability and efficiency is proposed. Firstly, a new oscillating judgment criterion is firstly proposed to precisely detect the oscillation of iterative points in standard normal space. Then, a self-adjusted updating strategy is established to dynamically adjust the control factor of modified chaos control (MCC) method during the iterative process. Moreover, an adaptive modified chaos control (AMCC) method is developed to search for MPP efficiently by selecting MCC or advanced mean value method automatically based on the proposed oscillating judgment criterion. Finally, through integrating the developed AMCC into SLA, the hybrid self-adjusted single-loop approach is proposed to achieve stable convergence and enhance the computational efficiency of SLA for complex RBDO problems. The high efficiency of AMCC is demonstrated by five nonlinear performance functions for MPP search. Additionally, five representative RBDO examples indicate that the proposed HS-SLA can improve the efficiency, stability, and accuracy of SLA.

1 Introduction

There exist various kinds of uncertainties in practical engineering structures, such as material properties, geometric dimension, manufacturing process, and external loads. Reliability-based design optimization (RBDO) provides a powerful and systematic tool for optimum design of structures with considering these uncertainties, and the designs of RBDO are more reliable than those of traditional deterministic structural optimization. Generally, RBDO methods can be divided into three categories (Aoues and Chateauneuf 2010; Valdebenito and Schueller 2010): double-loop approaches, decoupled approaches, and single-loop approaches.

For double-loop approaches, two different ways can be applied to evaluate the probability constraints: reliability index approach (RIA) (Lee et al. 2002) and performance measure approach (PMA) (Tu et al. 1999). Actually, PMA always exhibits much higher efficiency and stability than RIA to solve RBDO problems (Lee et al. 2002; Youn and Choi 2004). For PMA, the inner reliability analysis loop aims to search for the most probable point (MPP). The advanced mean value (AMV) method (Wu et al. 1990) is popularly utilized to search for MPP owing to its simplicity and efficiency. However, AMV generates numerical instability such as divergence, periodic oscillation, bifurcation, and even chaos when locating the MPP for concave or highly nonlinear performance functions (Du et al. 2004; Youn et al. 2003). Later, several improved iterative algorithms were suggested to overcome the non-convergence of AMV when searching for MPP, such as conjugate mean value (CMV) method, hybrid mean value (HMV) method (Youn et al. 2003), enhanced hybrid mean value method (Youn et al. 2005b), conjugate gradient analysis method (Ezzati et al. 2015), and step length adjustment iterative algorithm (Yi and Zhu 2016). From the perspective of chaotic dynamics, Yang and Yi (2009) proposed the chaos control (CC) method to address the non-convergence issue of AMV based on stability transformation method (STM) (Pingel et al. 2004; Schmelcher and Diakonos 1997). To improve the efficiency of CC, modified chaos control (MCC) method (Meng et al. 2015) was developed by extending the iterative point to the target reliability surface in every iterative step. However, the chaos control factor has a great influence on the computational efficiency of MCC (Li et al. 2015; Meng et al. 2015; Meng et al. 2018), in which the control factor remains constant. Thereafter, some researches concentrate on the automatic determination of control factor during the iterative process of MPP search based on MCC. These methods include adaptive chaos control method (Li et al. 2015), relaxed mean value approach (Keshtegar and Lee 2016), enhanced chaos control method (Hao et al. 2017) which is related with the non-probabilistic RBDO (Meng et al. 2018; Meng and Zhou 2018; Meng et al. 2019), self-adaptive modified chaos control method (Keshtegar et al. 2017), hybrid self-adjusted mean value (HSMV) method (Keshtegar and Hao 2017), modified mean value method (Keshtegar 2017), hybrid descent mean value (HDMV) method (Keshtegar and Hao 2018c), enriched self-adjusted mean value (ESMV) method (Keshtegar and Hao 2018b), and dynamical accelerated chaos control (DCC) method (Keshtegar and Chakraborty 2018). Although these enhanced versions can enhance the efficiency of MPP search to a certain extent, the computational cost of double-loop approaches is still large for RBDO problems with highly nonlinear performance functions.

To improve the computational efficiency of double-loop approaches, decoupled approaches convert the original RBDO problem into a series of deterministic optimization problems by separating the inner reliability analysis loop from the external deterministic optimization loop. Representative decoupled approaches mainly include sequential optimization and reliability assessment (SORA) (Du and Chen 2004), sequential approximate programming approach (Cheng et al. 2006), and direct decoupling approach (Zou and Mahadevan 2006). Later, some improvements were also reported based on the concept of SORA, such as adaptive decoupling approach (Chen et al. 2013), approximate sequential optimization and reliability assessment (Yi et al. 2016), general RBDO decoupling approach (Torii et al. 2016), and probabilistic feasible region approach (Chen et al. 2018). The computational efficiency of SORA is also enhanced by using convex linearization (Cho and Lee 2011) and hybrid chaos control (HCC) method (Meng et al. 2015). In general, SORA is a widely utilized decoupled approach to solve RBDO problems (Aoues and Chateauneuf 2010), whereas its efficiency needs to be improved.

In single-loop approaches, the Karush-Kuhn-Tucker (KKT) optimality conditions of the inner reliability loops are employed to approximate probabilistic constraints with equivalent deterministic constraints, which can avoid the repeated MPP search process in reliability analysis. Hence, the efficiency of single-loop approaches is greatly improved than double-loop approaches for solving RBDO problems. Typically, the single-loop single vector (SLSV) method (Chen et al. 1997) firstly attempted to convert the double-loop RBDO problem to a true single-loop problem. Liang et al. (2008) proposed single-loop approach (SLA) to improve the efficiency of SLSV. A complete single-loop approach (Shan and Wang 2008) was developed on the basis of reliable design space to eliminate the reliability analysis process and achieve higher efficiency and accuracy. Jeong and Park (2017) introduced single-loop single vector method using the conjugate gradient to enhance the convergence capability and accuracy of SLSV. Although SLA is a promising strategy for linear and moderate nonlinear RBDO problems, it yields numerical instability and non-convergence solutions for highly nonlinear problems (Aoues and Chateauneuf 2010). To overcome this problem, Jiang et al. (2017) suggested the adaptive hybrid single-loop method to adaptively select the approximate MPP or accurate MPP which is located by the developed iterative control strategy. Keshtegar and Hao (2018a) developed the enhanced single-loop method based on single-loop approach and the hybrid enhanced chaos control method. Meng et al. (2018) proposed chaotic single-loop approach (CSLA) to realize convergence control of iterative algorithm of MPP search in SLA based on chaotic dynamics theory. Moreover, Zhou et al. (2018) suggested a two-phase approach which is an enhanced version of SLA based on sequential approximation. To improve the efficiency and stability of SLA, Meng and Keshtegar (2019) proposed adaptive conjugate single-loop approach based on the conjugate gradient vector with a dynamical conjugate scalar factor.

To combine two of these three different types of RBDO methods mentioned above is a new tendency to make full use of respective advantages of different RBDO methods in recent years. These hybrid methods contain adaptive-loop method (Youn 2007), adaptive hybrid approach (Li et al. 2015), semi-single-loop method (Lim and Lee 2016), etc. However, the numerical efficiency and stability of RBDO algorithms for large reliability index and highly nonlinear problems are still expected to enhance further.

In this paper, an adaptive modified chaos control (AMCC) method is firstly developed to search for MPP efficiently by selecting modified chaos control method or advanced mean value method automatically, based on the proposed oscillating judgment criterion of iterative point and self-adjusted control factor. Then, a hybrid self-adjusted single-loop approach (HS-SLA) is proposed by integrating the developed AMCC into SLA, in order to achieve stable convergence and enhance the computational efficiency of SLA for RBDO problems with highly nonlinear performance functions. Finally, five representative examples are tested and compared for RBDO algorithms to illustrate the high efficiency and stability of the proposed HS-SLA.

2 Reliability-based design optimization and methods of MPP search

2.1 Basic RBDO formulation

A typical RBDO problem is formulated as follows (Jiang et al. 2017; Youn et al. 2003; Youn et al. 2005b):

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern0.7em \mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}\\ {}\min \kern0.8000001em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{p}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em P\left({g}_i\left(\mathbf{d},\mathbf{X},\mathbf{P}\right)\le 0\right)\ge {R}_i,\kern0.6em i=1,2,...,{n}_g\\ {}\kern2.2em {\mathbf{d}}^L\le \mathbf{d}\le {\mathbf{d}}^U,\kern0.8000001em {\boldsymbol{\upmu}}_{\mathbf{X}}^L\kern0.4em \le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^U\kern0.1em \end{array}} $$

(1)

where d denotes deterministic design variable vector with lower bound d^L and upper bound d^U, X, and P represent random design variable vector and random parameter vector, respectively. μ_X and μ_P indicate the means of X and P, respectively. $\kern0.2em {\boldsymbol{\upmu}}_{\mathbf{X}}^L\kern0.3em$ and ${\boldsymbol{\upmu}}_{\mathbf{X}}^U\kern0.1em$ are the lower bound and upper bound of μ_X.f(d, μ_X, μ_P) means the objective function. The performance function g_i(d, X_i, P_i) ≤ 0 represents the safe region. n_g refers to the number of probabilistic constraints. The probabilistic constraint P(g_i(d, X, P) ≤ 0) ≥ R_i represents that the probability of satisfying the i-th performance function should not be less than the target reliability ${R}_i=\Phi \left({\beta}_i^{\mathrm{t}}\right)$, where ${\beta}_i^{\mathrm{t}}$ indicates the target reliability index of the i-th constraint and Φ(·) is the standard normal cumulative distribution function.

2.2 Performance measure approach

In PMA (Tu et al. 1999; Youn et al. 2003), the performance measure function is employed to replace the RBDO probabilistic constraint in (1). The RBDO model based on PMA can be formulated as:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern0.7em \mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}\\ {}\min \kern0.8000001em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{p}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em {g}_i\left(\mathbf{d},\mathbf{X},\mathbf{P}\right)\le 0,\kern0.6em i=1,2,...,{n}_g\\ {}\kern2em {\mathbf{d}}^L\le \mathbf{d}\le {\mathbf{d}}^U,\kern0.8000001em {\boldsymbol{\upmu}}_{\mathbf{X}}^L\kern0.4em \le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^U\kern0.2em \end{array}} $$

(2)

In the inverse reliability analysis of PMA, the random design variables are transformed from the original space (X-apace) into the standard normal space (U-space) through Rosenblatt transformation or Nataf transformation (U = T (X), U = T (P)). Then, the performance function is expressed as g_i (d, X, P) = g_i (T⁻¹ (U)) = G_i (U), which can be calculated by the following optimization problem in U-space (Youn et al. 2003):

$$ {\displaystyle \begin{array}{l}\min \kern0.8000001em G\left(\mathbf{U}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1.4em \left\Vert \mathbf{U}\right\Vert ={\beta}^{\mathrm{t}}\end{array}} $$

(3)

The optimal solution in (3) is defined as the most probable point on the target reliability surface.

2.2.1 Chaos control method

Owing to the simplicity and efficiency, the advanced mean value method (Wu et al. 1990) is popularly applied to search for the MPP by solving the optimization problem in (3) as follows:

$$ {\mathbf{u}}^{k+1}={\beta}^{\mathrm{t}}{\mathbf{n}}^k,\kern0.5em {\mathbf{n}}^k=-\frac{\nabla_{\mathbf{U}}g\left(\mathbf{d},{\mathbf{u}}^k\right)}{\left\Vert {\nabla}_{\mathbf{U}}g\left(\mathbf{d},{\mathbf{u}}^k\right)\right\Vert } $$

(4)

where ∇_Ug(u^k) is the gradient vector of performance function at the k-th iterative point u^k in U-space, and n^k is the normalized steepest descent direction.

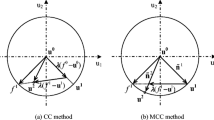
Although AMV is efficient for solving convex performance functions, it has difficulties in iterative convergence when the MPP is searched for concave or highly nonlinear performance functions (Du et al. 2004; Youn et al. 2003). As illustrated in Fig. 1a, AMV generates period-2 oscillation which constructs a diamond by the four points: the origin u⁰, two adjacent iterative points u^k and u^k + 1 at the round, and the intersecting point of the two negative gradient direction vectors n^k and n^k + 1. Introducing the chaotic dynamics theory, Yang and Yi (2009) proposed the chaos control method, shown in Fig. 1b, to control the non-convergence phenomenon of AMV based on stability transformation method (Pingel et al. 2004; Schmelcher and Diakonos 1997) with solid mathematical basis as follows:

$$ {\displaystyle \begin{array}{l}{\mathbf{u}}^{k+1}={\mathbf{u}}^k+\lambda \mathbf{C}\left(\mathbf{f}\left({\mathbf{u}}^k\right)-{\mathbf{u}}^k\right)\\ {}\mathbf{f}\left({\mathbf{u}}^k\right)=-{\beta}^{\mathrm{t}}\frac{\nabla_{\mathbf{U}}g\left(\mathbf{d},{\mathbf{u}}^k\right)}{\left\Vert {\nabla}_{\mathbf{U}}g\left(\mathbf{d},{\mathbf{u}}^k\right)\right\Vert}\end{array}} $$

(5)

where λ is the control factor ranging from 0 to 1 (i.e., λ∈(0,1)), and C is the n × n dimensional involutory matrix (namely, C² = I, only one element in each row and each column in this matrix is 1 or − 1, and the others are 0).

Fig. 1

MPP search for different methods. a Period-2 oscillation of AMV method. b CC method. c MCC method

2.2.2 Modified chaos control method

However, the efficiency of CC is limited due to excessively reducing every step size of the AMV method (Li et al. 2015; Meng et al. 2015). Accordingly, the modified chaos control method (Meng et al. 2015) indicated in Fig. 1c was proposed to enhance the convergence speed of CC by extending the iterative point to the target reliability surface in every iterative step. The iterative formula of MCC is written as:

$$ {\displaystyle \begin{array}{l}{\mathbf{u}}^{k+1}={\beta}^{\mathrm{t}}\frac{\tilde{\mathbf{n}}\left({\mathbf{u}}^{k+1}\right)}{\left\Vert \tilde{\mathbf{n}}\left({\mathbf{u}}^{k+1}\right)\right\Vert}\\ {}\tilde{\mathbf{n}}\left({\mathbf{u}}^{k+1}\right)={\mathbf{u}}^k+\lambda \mathbf{C}\left(\mathbf{f}\left({\mathbf{u}}^k\right)-{\mathbf{u}}^k\right)\\ {}\mathbf{f}\left({\mathbf{u}}^k\right)=-{\beta}^{\mathrm{t}}\frac{\nabla_{\mathbf{U}}g\left(\mathbf{d},{\mathbf{u}}^k\right)}{\left\Vert {\nabla}_{\mathbf{U}}g\left(\mathbf{d},{\mathbf{u}}^k\right)\right\Vert}\end{array}} $$

(6)

As observed in references (Li et al. 2015; Meng et al. 2015; Meng et al. 2018), the control factor λ has a significant influence on the computational efficiency of both CC and MCC.

2.3 Single-loop approach

In SLA (Liang et al. 2008), the probabilistic optimization problem is converted into a deterministic optimization problem by using KKT optimality conditions, and it avoids the repeated MPP search process in reliability analysis. The standard SLA is expressed as:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern0.7em \mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}\\ {}\min \kern0.7em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em {g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^k,{\mathbf{P}}_i^k\right)\le 0,\kern0.6em i=1,2,...,{n}_g\\ {}\kern2.2em {\mathbf{d}}^L\le \mathbf{d}\le {\mathbf{d}}^U,\kern0.8000001em {\boldsymbol{\upmu}}_{\mathbf{X}}^L\kern0.4em \le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^U\kern0.1em \\ {}\mathrm{where}\\ {}{\mathbf{X}}_i^k={\boldsymbol{\upmu}}_{\mathbf{X}}^k-{\alpha}_{\mathbf{X}i}^k{\sigma}_{\mathbf{X}}{\beta}_i^{\mathrm{t}},{\mathbf{P}}_i^k={\boldsymbol{\upmu}}_{\mathbf{P}}-{\alpha}_{\mathbf{P}i}^k{\sigma}_{\mathbf{P}}{\beta}_i^{\mathrm{t}}\\ {}{\alpha}_{\mathbf{X}i}^k={\sigma}_{\mathbf{X}}{\nabla}_{\mathbf{X}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)/\left\Vert {\sigma}_{\mathbf{X}}{\nabla}_{\mathbf{X}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)\right\Vert \\ {}{\alpha}_{\mathbf{p}i}^k={\sigma}_{\mathbf{p}}{\nabla}_{\mathbf{p}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)/\left\Vert {\sigma}_{\mathbf{p}}{\nabla}_{\mathbf{p}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)\right\Vert \end{array}} $$

(7)

In (7), ${\beta}_i^{\mathrm{t}}$ indicates the target reliability index of the i-th constraint. d means the vector of deterministic design variables with lower bound d^L and upper bound d^U. ${\mathbf{X}}_i^k$ and ${\mathrm{P}}_i^k$ represent the k-th approximate MPPs of random design variable vector X and random parameter vector P in X-space for the i-th performance function, respectively. During the outer deterministic optimization process, the random design variable mean μ_X is updated while the random parameter mean μ_P keeps unchanged. ${\alpha}_{\mathbf{X}i}^k$ and ${\alpha}_{\mathbf{P}i}^k$ represent the normalized gradient vector of the i-th constraint g_i(·) to X and P, respectively. For non-normally distributed random variables, Rosenblatt transformation or Nataf transformation can be applied to transform the original random space into the standard normal space. Despite the fact that SLA is highly efficient, it encounters difficulties in converging to accurate results for highly nonlinear performance functions.

3 Oscillating judgment criteria

Generally, correctly identifying the oscillation of iterative points during the iterative process exerts a remarkable influence on the efficiency of MPP search. Two common oscillating judgment criteria, i.e., criterion 1 and criterion 2, have been widely used to judge the oscillation of iterative points. However, both criterion 1 and criterion 2 cannot correctly and completely identify the oscillation of iterative points. In this section, a new oscillating judgment criterion 3 is developed to precisely detect the oscillation of the iterative points during the iterative process of MPP search.

3.1 Criterion 1

For hybrid mean value method (Youn et al. 2003), the type of performance function is defined by

$$ {\displaystyle \begin{array}{l}\kern0.3em {\varsigma}^{k+1}=\left({\mathbf{n}}^{k+1}-{\mathbf{n}}^k\right)\cdotp \left({\mathbf{n}}^k-{\mathbf{n}}^{k-1}\right)\\ {}\operatorname{sign}\left({\varsigma}^{k+1}\right)>0:\kern0.3em \mathrm{convex}\kern0.4em \mathrm{function}\\ {}\kern5.099998em \le 0:\kern0.3em \mathrm{concave}\kern0.4em \mathrm{function}\end{array}} $$

(8)

In (8),  ς^k + 1is the index for identifying the performance function type at the k + 1th step, n^k stands for the normalized steepest descent direction for a performance function at u^k, and sign(·) is a symbolic function. Criterion 1 is actually an angle condition. The basic idea of HMV is to first identify the performance function type according to criterion 1 in (8), and then adaptively select advanced mean value method or conjugate mean value method to search for MPP: if the performance function is convex, AMV is used to update the next iterative point. Otherwise, CMV is adopted for concave performance function. HMV is suitable for convex and weakly nonlinear concave performance function. Nevertheless, it converges slowly or even fails to converge for highly nonlinear concave function.

To combine respective advantages of different MPP search methods, some researches (Li et al. 2015; Meng et al. 2015) adaptively selected appropriate methods to control oscillation by judging the oscillation of iterative points based on criterion 1. Figure 2a and b exhibit the relationship between performance function type and oscillation of iterative points based on criterion 1. For convex performance function, the corresponding iterative points gradually converge (Fig. 2a); the iterative points corresponding to concave performance function appear to oscillate (Fig. 2b). However, for the case of Fig. 2c, the criterion 1 is invalid: although the performance function is convex, the corresponding iterative points gradually diverge. Therefore, criterion 1 cannot correctly and completely judge the oscillation of iterative points.

Fig. 2

Relationship between performance function type and oscillation of iterative points. a Convex type (convergence). b Concave type (oscillation). c Convex type (divergence)

3.2 Criterion 2

Based on the variation of oscillation amplitude of random variables in U-space, which is also considered as sufficient descent condition, criterion 2 in (9) is applied to judge the oscillation of iterative points, and then appropriate methods are adaptively chosen to search for MPP in references (Keshtegar and Hao 2018c; Yi and Zhu 2016):

$$ \left\Vert {\mathbf{u}}^{k+2}-{\mathbf{u}}^{k+1}\right\Vert \le \left\Vert {\mathbf{u}}^{k+1}-{\mathbf{u}}^k\right\Vert \kern0.1em $$

(9)

If the oscillation amplitude of iterative points in U-space decreases, the iterative points gradually converge (Fig. 3a), and the original method is maintained to update the next iterative points. Otherwise, if the oscillation amplitude increases, divergence or oscillation occurs at the iterative points (Fig. 3b), and a certain strategy is adopted to control the non-convergence of the random variables in the iterative process. However, criterion 2 fails to determine the oscillation of iterative points in Fig. 3c. Although the oscillation amplitude decreases little by little, the corresponding iterative points oscillate rather than converge. Therefore, criterion 2 cannot completely judge the oscillation of iterative points.

Fig. 3

Relationship between oscillation amplitude variation and oscillation of iterative points in U-space. a Decreases (convergence). b Increases (non-convergence). c Decreases (oscillation)

3.3 Criterion 3

To overcome the respective disadvantages of criterion 1 and criterion 2 described above, a new oscillating judgment criterion 3 is proposed to correctly detect oscillation of iterative points in U-space by combining criterion 1 and criterion 2:

$$ \Big\{{\displaystyle \begin{array}{l}{\varsigma}^{k+1}=\left({\mathbf{n}}^{k+1}-{\mathbf{n}}^k\right)\cdotp \left({\mathbf{n}}^k-{\mathbf{n}}^{k-1}\right)>0\\ {}\kern0.1em \left\Vert {\mathbf{u}}^{k+2}-{\mathbf{u}}^{k+1}\right\Vert \le \left\Vert {\mathbf{u}}^{k+1}-{\mathbf{u}}^k\right\Vert \end{array}} $$

(10)

Iterative points will gradually converge only if the two conditions of (10), i.e., angle condition and sufficient descent condition, are simultaneously satisfied (Fig. 4a). Otherwise, they fail to converge, and divergence or oscillation will occur (Fig. 4b–d). On the one hand, the criterion 3 proposed in this paper can detect the oscillation of iterative points. The convergence in Fig. 4a can be all detected by criterion 1, criterion 2, and criterion 3. For the case of Fig. 4b, all the above three oscillation criteria can judge the divergence of the iterative point. On the other hand, the proposed criterion 3 can overcome the drawbacks of both criterion 1 and criterion 2. For Fig. 4c, the iterative point is regarded as convergence with using criterion 1, while the iterative point is viewed as divergence via criterion 3, which is consistent with the fact that the iterative point diverges. For Fig. 4d, the iterative point is considered as convergence with using criterion 2. Nevertheless, the iterative point actually oscillates which is the same as the result judged by using criterion 3. Therefore, the proposed criterion 3 can precisely detect the oscillation of iterative points in U-space, and provide a better judgment criterion for selecting appropriate approaches to search for MPP. Consequently, the efficiency of MPP search is improved.

Fig. 4

Relationship between the satisfaction of criterion 3 and oscillation of iterative points in U-space. a Satisfy (convergence). b Dissatisfy (divergence). c Dissatisfy (divergence). d Dissatisfy (oscillation)

4 Hybrid self-adjusted single-loop approach

4.1 Self-adjusted updating strategy for chaos control factor

Chaos control factor λ^k has a remarkable influence on the computational efficiency of CC and MCC when searching for MPP. Therefore, it is of great significance to propose a proper updating strategy for λ^k to improve the convergence rate of MPP search. In this work, a new self-adjusted updating strategy is proposed to dynamically adjust the control factor during the iterative process as follows:

$$ {\lambda}^k=\frac{\lambda^{k-1}}{1+P\left(1-{\lambda}^{k-1}\right)}\kern0.1em $$

(11)

where P is a parameter (0.10 ≤ P ≤ 1.00). Figure 5 shows the iterative histories of self-adjusted control factor for different P. It can be seen that P has a great influence on the change of λ^k during the iterative process, and thus affects the convergence rate of MPP search. In order to prevent the slow convergence rate caused by too small control factor, the minimum value of λ^k is taken as λ_min = 0.25 and P is 0.40 for all the following RBDO numerical examples. Obviously, the iterative formula of proposed self-adjusted control factor is based on the previous iterative information and is simpler than those of methods such as HDMV, ESMV, DCC, and HSMV. Besides, the self-adjusted control factor is combined with the oscillating judgment criterion 3 in AMCC to achieve control of unstable solutions for highly nonlinear performance functions, and can improve the efficiency of MPP search with stable convergence.

Fig. 5

Iterative histories of chaos control factor λ^k for different P

4.2 Adaptive modified chaos control method for MPP search

Although AMV is efficient to search for MPP for convex performance functions, it has convergence difficulties for both concave and highly nonlinear performance functions. MCC performs well for concave or highly nonlinear performance functions. Nevertheless, the computational efficiency of MCC is greatly influenced by the control factor. Based on the above developed oscillating judgment criterion 3 in (10) and self-adjusted updating strategy for control factor in (11), an adaptive modified chaos control method is proposed to search for MPP in U-space. The iterative formula of AMCC is written as:

$$ {\displaystyle \begin{array}{l}{\mathbf{u}}_{\mathrm{AMCC}}^{k+1}=\Big\{\begin{array}{l}{\mathbf{u}}_{\mathrm{AMV}}^{k+1},\kern0.3em \mathrm{criterion}\kern0.3em 3\kern0.3em \mathrm{is}\kern0.3em \mathrm{satisfied}\\ {}{\mathbf{u}}_{\mathrm{MCC}}^{k+1},\kern0.3em \mathrm{criterion}\kern0.3em 3\kern0.3em \mathrm{is}\kern0.3em \mathrm{not}\kern0.3em \mathrm{satisfied}\end{array}\\ {}\mathrm{where}\kern1.7em {\mathbf{u}}_{\mathrm{MCC}}^{k+1}={\beta}^{\mathrm{t}}\frac{{\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}}{\left\Vert {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}\right\Vert}\\ {}\kern4.599998em {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}={\mathbf{u}}_{\mathrm{AMCC}}^k+{\lambda}^k\mathbf{C}\left({\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right)\end{array}} $$

(12)

The basic idea of AMCC is that modified chaos control method or advanced mean value method is automatically selected to control the iterative direction of the next MPP in the light of the oscillation of iterative points. If the current iterative point does not satisfy the oscillating judgment criterion 3, which means the current iterative point fails to converge, the control factor λ^k of MCC needs to be dynamically updated based on the proposed self-adjusted updating strategy in (11), and then MCC is adopted to control the iterative oscillation. Otherwise, if the iterative point in U-space satisfies the oscillating judgment criterion 3, which means the iterative point does not oscillate. In other words, the control factor λ^k needs not to be updated and remains unchanged, so AMV is used to update the next iterative point. The framework of proposed AMCC method to search for MPP is plotted in Fig. 6. The proposed AMCC method can provide stable results and achieve global convergence for MPP search. The corresponding proof for C = I is presented as follows:

Fig. 6

Framework of AMCC to search for MPP

Firstly, it is assumed that the iterative points hold the angle condition and sufficient descent condition simultaneously at each iteration (Fig. 4a), i.e., the criterion 3 is satisfied as $\left({\mathbf{n}}_{\mathrm{AMV}}^k-{\mathbf{n}}_{\mathrm{AMCC}}^{k-1}\right)\cdotp \left({\mathbf{n}}_{\mathrm{AMCC}}^{k-1}-{\mathbf{n}}_{\mathrm{AMCC}}^{k-2}\right)>0$ and $\left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert \le \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^k-{\mathbf{u}}_{\mathrm{AMCC}}^{k-1}\right\Vert$. Therefore, AMV is adopted to update the new iterative points as ${\mathbf{u}}_{\mathrm{AMCC}}^{k+1}={\mathbf{u}}_{\mathrm{AMV}}^{k+1}$. Then, we have

$$ {\displaystyle \begin{array}{l}\left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^2-{\mathbf{u}}_{\mathrm{AMCC}}^1\right\Vert \le \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^1-{\mathbf{u}}_{\mathrm{AMCC}}^0\right\Vert ={\beta}^{\mathrm{t}}\\ {}\left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^2-{\mathbf{u}}_{\mathrm{AMCC}}^1\right\Vert ={t}_1\left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^1-{\mathbf{u}}_{\mathrm{AMCC}}^0\right\Vert ={t}_1\kern0.2em {\beta}^{\mathrm{t}},\kern0.3em 0\le {t}_1\le 1\kern0.1em \\ {}\cdots \\ {}\left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert ={t}_k{t}_{k-1}\cdots {t}_1\kern0.2em \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^1-{\mathbf{u}}_{\mathrm{AMCC}}^0\right\Vert ={\beta}^{\mathrm{t}}\prod \limits_{i=1}^k{t}_i,\kern0.4em 0\le {t}_1,{t}_2,\cdots {t}_k\le 1\end{array}} $$

It can be concluded that $\underset{k\to \infty }{\lim}\prod \limits_{i=1}^k{t}_i\approx 0$ and $\underset{k\to \infty }{\lim}\left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert \approx 0$. Therefore, ${\mathbf{u}}_{\mathrm{AMCC}}^{k+1}\approx {\mathbf{u}}_{\mathrm{AMCC}}^k$.

Secondly, if the iterative points only satisfy the sufficient descent condition but not angle condition (Fig. 4d), i.e., $\left({\mathbf{n}}_{\mathrm{AMV}}^k-{\mathbf{n}}_{\mathrm{AMCC}}^{k-1}\right)\cdotp \left({\mathbf{n}}_{\mathrm{AMCC}}^{k-1}-{\mathbf{n}}_{\mathrm{AMCC}}^{k-2}\right)\le 0$ and $\left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert \le \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^k-{\mathbf{u}}_{\mathrm{AMCC}}^{k-1}\right\Vert$, MCC is applied to update the new iterative points. From (12), we have

$$ {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k={\lambda}^k\left({\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right) $$

Since 0 < λ^k < 1, then $\left\Vert {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert <\left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert$. Thus,

$$ \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert <\left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert \le \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^k-{\mathbf{u}}_{\mathrm{AMCC}}^{k-1}\right\Vert $$

$$ {\displaystyle \begin{array}{l}\left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert ={p}_k{p}_{k-1}\cdots {p}_1\kern0.2em \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^1-{\mathbf{u}}_{\mathrm{AMCC}}^0\right\Vert ={\beta}^{\mathrm{t}}\prod \limits_{i=1}^k{p}_i,\kern0.4em 0\le {p}_1,{p}_2,\cdots {p}_k\le 1\\ {}\left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert ={q}_k{q}_{k-1}\cdots {q}_1\kern0.2em \left\Vert {\mathbf{u}}_{\mathrm{AMCC}}^1-{\mathbf{u}}_{\mathrm{AMCC}}^0\right\Vert ={\beta}^{\mathrm{t}}\prod \limits_{i=1}^k{q}_i,\kern0.4em 0<{q}_1,{q}_2,\cdots {q}_k<1\\ {}\mathrm{where}\kern0.4em 0<{q}_i<{p}_i\le 1,\kern0.3em i=1,2,\cdots, k\end{array}} $$

Clearly, $\prod \limits_{i=1}^k{q}_i\to 0$ is attained more quickly than $\prod \limits_{i=1}^k{p}_i\to 0$ for k → ∞, then, we have ${\mathbf{u}}_{\mathrm{AMCC}}^{k+1}\approx {\mathbf{u}}_{\mathrm{AMCC}}^k$. Therefore, AMCC can converge more quickly than AMV used only in Fig. 4d by reducing the oscillating amplitude of iterative points.

Finally, if the iterative points do not satisfy the sufficient descent condition, the new iterative points are computed by MCC in (12) no matter whether the angle condition is satisfied or not (Fig. 4b, c). We can obtain ${\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k={\lambda}^k\left({\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right)$. Since ${\left({\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right)}^{\mathrm{T}}\left({\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right)={\lambda}^k{\left({\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right)}^{\mathrm{T}}\left({\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right)$, the following formulas are derived

$$ {\left\Vert {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert}^2\le {\lambda}^k\left\Vert {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert \cdotp \left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert $$

$$ \frac{\left\Vert {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert }{\kern0.1em \left\Vert {\mathbf{u}}_{\mathrm{AMV}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert}\le {\lambda}^k $$

The proposed control factor is λ^k ≈ 0 when k → ∞ as illustrated by Fig. 5 and (11), which means that $\left\Vert {\tilde{\mathbf{u}}}_{\mathrm{MCC}}^{k+1}-{\mathbf{u}}_{\mathrm{AMCC}}^k\right\Vert \approx 0$ when k → ∞. Thus, ${\mathbf{u}}_{\mathrm{MCC}}^{k+1}\approx {\mathbf{u}}_{\mathrm{AMCC}}^k$. Consequently, a fixed point is captured as ${\mathbf{u}}_{\mathrm{AMCC}}^{k+1}\approx {\mathbf{u}}_{\mathrm{AMCC}}^k$ for k → ∞. To sum up, AMCC can achieve stable iterative solutions and realize global convergence.

To verify the efficiency of AMCC, the oscillating judgment criterion 3 is replaced with criterion 1 and criterion 2 to obtain algorithms of AMCC1 and AMCC2, respectively. Four mathematical examples and a high dimensional engineering reliability problem (i.e., the velocity problem of the door in a vehicle side impact for Example 5) for reliability analysis are selected to demonstrate the efficiency of AMCC compared with AMV, HMV, CC, HCC, AMCC1, and AMCC2. For the CC and HCC, C = I and λ = 0.10 are adopted. The convergence criterion is set as || x^k + 1 – x^k || / || x^k + 1 || ≤ 10⁻⁶ and the initial value is u⁰ = (0, 0) for all those methods.

Example 1 (Youn et al. 2003)

$$ {G}_1\left(\mathbf{x}\right)=-\exp \left({x}_1-7\right)-{x}_2+10,\kern0.7em {x}_i\sim N\left(6.0,{0.8}^2\right),\kern0.6em i=1,2,\kern0.7em {\beta}^{\mathrm{t}}=3.0 $$

Example 2 (Yang and Yi 2009)

$$ {G}_2\left(\mathbf{x}\right)=0.3{x}_1^2{x}_2-{x}_2+0.8{x}_1+1,\kern0.7em {x}_1\sim N\left(1.2,{0.42}^2\right),\kern0.7em {x}_2\sim N\left(1.0,{0.42}^2\right),\kern0.7em {\beta}^{\mathrm{t}}=6.0 $$

Example 3 (Yang and Yi 2009)

$$ {G}_3\left(\mathbf{x}\right)={x}_1^3+{x}_1^2{x}_2+{x}_2^3-18,\kern0.7em {x}_1\sim N\left(10,{5}^2\right),\kern0.7em {x}_2\sim N\left(9.9,{5}^2\right),\kern0.7em {\beta}^{\mathrm{t}}=3.0 $$

Example 4 (Yang and Yi 2009)

$$ {G}_4\left(\mathbf{x}\right)={x}_1^3+{x}_2^3-18,\kern0.7em {x}_1\sim N\left(10,{5}^2\right),\kern0.7em {x}_2\sim N\left(9.9,{5}^2\right),\kern0.7em {\beta}^{\mathrm{t}}=3.0 $$

Example 5 (Yang and Yi 2009; Youn et al. 2005a)

$$ {\displaystyle \begin{array}{l}{G}_5\left(\mathbf{x}\right)=-0.75+0.489{x}_3{x}_7+0.843{x}_5{x}_6-0.0432{x}_9{x}_{10}+0.0556{x}_9{x}_{11}+0.000786{x}_{11}^2\\ {}{x}_i\sim N\left(1.0,{0.05}^2\right),i=1\sim 7,\\ {}{x}_i\sim N\left(0.3,{0.006}^2\right),i=8,9,\\ {}{x}_i\sim N\left(0.0,{10.0}^2\right),i=10,11;\kern0.6em {\beta}^{\mathrm{t}}=3.0\end{array}} $$

The iterative results of performance function values at the MPP and required iterative numbers in the parentheses for different methods are listed in Table 1. It is observed that there is no oscillation for convex performance function G₁(x) in the iterative process of MPP search. As a result, AMV, HMV, HCC, AMCC1, AMCC2, and AMCC only utilize the AMV to search for MPP, and same iterative numbers are obtained for all these methods, while the iterative number of CC is the most. Additionally, AMV fails to converge for the remaining four performance functions. The AMV iterations searching for MPP for G₂(x) and G₅(x) generate period-18 and period-2 solutions, respectively, while the iterative solutions for G₃(x) and G₄(x) are in chaos with intrinsic randomness. Although HMV and CC can control the non-convergence of G₂(x), G₄(x), and G₅(x), they exhibit lower efficiency compared to AMCC. For concave and highly nonlinear performance functions G₂(x) and G₃(x) and the high dimensional performance function G₅(x), AMCC1 based on criterion 1 has difficulty in converging to the corresponding MPPs. For concave performance function G₄(x), AMCC2 based on criterion 2 needs more iterative numbers than AMCC1 and AMCC. However, AMCC converges more efficiently than both AMCC1 and AMCC2 for the four performance functions G₂(x), G₃(x), G₄(x), and G₅(x).

Table 1 Iterative results of MPP for different methods

It should be pointed out that, for the adaptive modified chaos control method, other involutory matrices except C = I can also be taken to control the non-convergence of inverse reliability computation such as periodic solution and chaos. For example, the MPP of G₂(x) is captured after 22 iterations by AMCC when C = C₁ = [1 0; 0–1]. For G₃(x), the MPP is obtained after 14 iterations by AMCC when C = C₂ = [0–1; − 1 0] with the same results as C = I. For simplicity, however, the involutory matrix C is usually taken as identity matrix (i.e., C = I) for various modified MPP search methods based on chaos feedback control.

4.3 Flowchart and procedure of HS-SLA

Combine the developed adaptive modified chaos control method in subsection 4.2 with single-loop approach, an efficient hybrid self-adjusted single-loop approach is proposed to achieve stable convergence and enhance the computational efficiency of SLA for complex RBDO problems. The optimization formulation of HS-SLA is written as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\;\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}\\ {}\min\;f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em {g}_i\left({\mathbf{d}}^k,{T}^{-1}\left({\mathbf{u}}_{\mathbf{X}i}^k\right),{T}^{-1}\left({\mathbf{u}}_{\mathbf{P}i}^k\right)\right)\le 0,i=1,2,...,{n}_g\\ {}\kern2em {\mathbf{d}}^L\le \mathbf{d}\le {\mathbf{d}}^U,{\boldsymbol{\upmu}}_{\mathbf{X}}^L\le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^U\kern0.1em \\ {}\mathrm{where}\kern0.5em \\ {}\mathrm{for}\ \mathrm{AMV}:{\mathbf{u}}_{\mathbf{X}i}^k={\tilde{\mathbf{u}}}_{\mathbf{X}i}^k,{\mathbf{u}}_{\mathbf{P}i}^k={\tilde{\mathbf{u}}}_{\mathbf{P}i}^k\\ {}\mathrm{for}\ \mathrm{MCC}:{\mathbf{u}}_{\mathbf{X}i}^k={\beta}_i^{\mathrm{t}}\frac{{\mathbf{u}}_{\mathbf{X}i}^{k-1}+{\lambda}_i^{k-1}\mathbf{C}\left({\tilde{\mathbf{u}}}_{\mathrm{X}i}^k-{\mathbf{u}}_{\mathrm{X}i}^{k-1}\right)}{\left\Vert {\mathbf{u}}_{\mathrm{X}i}^{k-1}+{\lambda}_i^{k-1}\mathbf{C}\left({\tilde{\mathbf{u}}}_{\mathbf{X}i}^k-{\mathbf{u}}_{\mathrm{X}i}^{k-1}\right)\right\Vert },{\mathbf{u}}_{\mathbf{P}i}^k={\beta}_i^{\mathrm{t}}\frac{{\mathbf{u}}_{\mathbf{P}i}^{k-1}+{\lambda}_i^{k-1}\mathbf{C}\left({\tilde{\mathbf{u}}}_{\mathbf{P}i}^k-{\mathbf{u}}_{\mathrm{P}i}^{k-1}\right)}{\left\Vert {\mathbf{u}}_{\mathrm{P}i}^{k-1}+{\lambda}_i^{k-1}\mathbf{C}\left({\tilde{\mathbf{u}}}_{\mathrm{P}i}^k-{\mathbf{u}}_{\mathrm{P}i}^{k-1}\right)\right\Vert}\\ {}{\tilde{\mathbf{u}}}_{\mathbf{X}i}^k=T\left({\mathbf{X}}_i^k\right),{\tilde{\mathbf{u}}}_{\mathrm{P}i}^k=T\left({\mathbf{P}}_i^k\right)\\ {}{\mathbf{X}}_i^k={\boldsymbol{\upmu}}_{\mathbf{X}}^k-{\alpha}_{\mathrm{X}i}^k{\sigma}_{\mathrm{X}}{\beta}_i^{\mathrm{t}},{\alpha}_{\mathbf{X}i}^k={\sigma}_{\mathrm{X}}{\nabla}_{\mathrm{X}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)/\left\Vert {\sigma}_{\mathrm{X}}{\nabla}_{\mathrm{X}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)\right\Vert \\ {}{\mathbf{P}}_i^k={\boldsymbol{\upmu}}_{\mathrm{P}}-{\alpha}_{\mathrm{P}i}^k{\sigma}_{\mathrm{P}}{\beta}_i^{\mathrm{t}},{\alpha}_{\mathbf{p}i}^k={\sigma}_{\mathrm{p}}{\nabla}_{\mathrm{p}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)/\left\Vert {\sigma}_{\mathrm{p}}{\nabla}_{\mathrm{p}}{g}_i\left({\mathbf{d}}^k,{\mathbf{X}}_i^{k-1},{\mathbf{P}}_i^{k-1}\right)\right\Vert \end{array}} $$

(13)

where ${\mathbf{u}}_{\mathbf{X}i}^k$ and ${\mathbf{u}}_{\mathbf{P}i}^k$ are the k-th approximate MPPs of random design variable vector X and random parameter vector P in U-space for the i-th performance function, respectively. The chaos control factor is updated by the self-adjusted updating strategy in (11) and the initial value is set as 0.50 for each performance function, i.e.,${\lambda}_i^0=0.5$. The new self-adjusted updating strategy in (11) provides an appropriate control factor, and the iterative search direction vectors are dynamically adjusted based on the proposed oscillating judgment criterion 3 in AMCC for MPP search. These measures contribute to the proposed HS-SLA achieving high computational accuracy for solving RBDO problems.

Figure 7 shows the flowchart of HS-SLA, and its procedure is summarized as follows:

• (1) Initialize ${\mathbf{X}}_i^0=\kern0.3em {\boldsymbol{\upmu}}_{\mathbf{X}}^0$ and ${\mathbf{P}}_i^0=\kern0.3em {\boldsymbol{\upmu}}_{\mathbf{P}}$.

• (2) Utilize AMCC to adaptively select AMV or MCC to update the next MPP: when the iterative point in U-space satisfies the oscillating judgment criterion 3 or k < 3, AMV is used to update the next iterative point (${\mathbf{u}}_{\mathbf{X}i}^{k+1}$,${\mathbf{u}}_{\mathbf{P}i}^{k+1}$). Otherwise, if the current iterative point does not satisfy the oscillating judgment criterion 3 and k ≥ 3, the control factors are dynamically updated based on the proposed self-adjusted updating strategy in (11), and MCC is then adopted to control the oscillation and calculate the next MPP (${\mathbf{u}}_{\mathbf{X}i}^{k+1}$,${\mathbf{u}}_{\mathbf{P}i}^{k+1}$).

• (3) Perform the deterministic optimization to update the random design variable means ${\boldsymbol{\upmu}}_{\mathbf{X}}^{k+1}$using optimization algorithm such as the method of moving asymptotes.

• (4) Check if the convergence criterion $\left\Vert {\boldsymbol{\upmu}}_{\mathbf{X}}^{k+1}-{\boldsymbol{\upmu}}_{\mathbf{X}}^k\right\Vert /\left\Vert {\boldsymbol{\upmu}}_{\mathbf{X}}^{k+1}\right\Vert \le \varepsilon ={10}^{-4}$is satisfied. If it is satisfied, then stop. Otherwise, set k = k + 1, and go to step (2) to continue iterative calculation until convergence.

Fig. 7

Flowchart of the hybrid self-adjusted single-loop approach for RBDO problems

5 Numerical examples for RBDO problems

In this section, the efficiency and stability of the proposed HS-SLA are compared with the other approaches such as RIA, PMA, SORA, SLA, and CSLA by five nonlinear RBDO problems. The convergence criterion of these RBDO approaches is ||d^k + 1 – d^k||/||d^k + 1|| ≤ ε = 10⁻⁴.

5.1 Weakly nonlinear mathematical Example 1

This RBDO problem (Cho and Lee 2011; Youn and Choi 2004) contains three weakly nonlinear performance functions and two random variables which obey the Gumbel distribution. The standard deviations of the two random variables are both 0.3, and their mean values are selected as design variables. The initial values of the design variables are d⁰ = [5.0, 5.0]. Two different target reliability indexes, i.e., β^t = 3.0 and β^t = 4.0, are considered to investigate their effect on the efficiency and stability of the proposed HS-SLA. This RBDO example is formulated as

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern2.1em \mathbf{d}=\left[{d}_1,{d}_2\right]\\ {}\mathit{\min}\kern2.1em f\left(\mathbf{d}\right)={d}_1+{d}_2\\ {}\mathrm{s}.\mathrm{t}.\kern2.45em P\left[{g}_j\left(\mathbf{X}\right)\le 0\right]\ge \Phi \left({\beta}^{\mathrm{t}}\right),\kern0.6em j=1,2,3\end{array}} $$

$$ {\displaystyle \begin{array}{l}\mathrm{where}\kern0.75em {g}_1\left(\mathbf{X}\right)=1-\frac{X_1^2{X}_2}{20},\\ {}\kern3.1em {g}_2\left(\mathbf{X}\right)=1-\frac{{\left({X}_1+{X}_2-5\right)}^2}{30}-\frac{{\left({X}_1-{X}_2-12\right)}^2}{120},\\ {}\kern3.1em {g}_3\left(\mathbf{X}\right)=1-\frac{80}{\left({X}_1^2+8{X}_2+5\right)},\\ {}\kern3.2em 0\le {d}_i\le 10,\kern0.4em \mathrm{for}\kern0.4em i=1,2,\\ {}\kern3.1em {\mathbf{d}}^0=\left[5.0,5.0\right]\end{array}} $$

The optimal results of different approaches are tabulated in Table 2 for β^t = 3.0 and Table 3 for β^t = 4.0. In these two Tables and the following Tables, Iters denote the number of outer optimal iterations, and F-evals represent the sum of the number of performance function and objective function evaluations and the number of their gradient function evaluations. F-evals are used to measure the computational efficiency of different RBDO approaches. The optimal results of RIA, PMA, SORA, SLA, and CSLA for β^t = 3.0 and β^t = 4.0 are extracted from the reference (Meng et al. 2018).

Table 2 RBDO results of Example 1 for β^t = 3.0

Table 3 RBDO results of Example 1 for β^t = 4.0

As presented in Table 2, all RBDO approaches except RIA can successfully converge, and the results are consistent with those of the reference (Aoues and Chateauneuf 2010) for β^t = 3.0. The number of function evaluations of SORA is less than that of PMA in that SORA decouples the reliability analysis loop from the optimization loop. By converting the probabilistic optimization problem into a deterministic optimization problem, SLA exhibits much higher efficiency compared to PMA and SORA. CSLA improves the efficiency of SLA, because it can control the oscillation of iterative points in U-space and improve the iterative convergence by adopting the chaos control theory. Additionally, the proposed HS-SLA is capable of precisely judging the oscillation of iterative points in U-space through a more reasonable oscillating judgment criterion. As a result, less computational effort for HS-SLA is required to converge to the optimum compared to both SLA and CSLA.

The optimal results of different approaches for β^t = 4.0 are summarized in Table 3. Similar results of RBDO approaches except SORA and SLA for β^t = 4.0 can be obtained as those for β^t = 3.0. RIA fails to converge for the two target reliability indexes. For large reliability index, more computational efforts of PMA and SORA are needed and a lack of accuracy for SORA is also simultaneously observed. Despite the high efficiency, SLA has difficulties in converging to the correct optimum for large target reliability index. However, large reliability index has less effect on CSLA and HS-SLA. Both CSLA and HS-SLA can converge to the correct optimum, and the number of function evaluations of HS-SLA is less than CSLA. Therefore, SLA exhibits some weakness in terms of stability, while the stability of HS-SLA remains unchanged with the increase of target reliability index. Moreover, HS-SLA can also improve the accuracy of SLA for both β^t = 3.0 and β^t = 4.0.

To test whether the target reliability of the probabilistic constraints is satisfied, Monte Carlo simulation (MCS) with ten million samples is applied to evaluate the reliability index of the probabilistic constraints at the optimum. In Table 2, ${\beta}_j^{\mathrm{MCS}}$ stands for the reliability index of the j-th probabilistic constraint at the optimum. As shown in Table 2 for β^t = 3.0, the first and second probabilistic constraints (g₁ and g₂) are active, while the third one (g₃) is inactive and the corresponding reliability index is infinite. All the RBDO approaches can satisfy the target reliability index at the optimum.

For β^t = 4.0, all the probabilistic constraints of RBDO approaches except SORA and SLA satisfy the target reliability at the optimum listed in Table 3. RIA cannot converge to the optimum. Although SORA can obtain an optimized design, the reliability index of the second probability constraint g₂ is smaller than the target reliability index, which means g₂ is violated. The reliability index of SLA for the second probability constraint g₂ at the optimum is only 1.6003 which is much smaller than the target reliability index. Therefore, the optimized solution of SLA cannot satisfy the target reliability index of the second probability constraint.

5.2 Highly nonlinear mathematical Example 2

This mathematical problem (Meng et al. 2018; Youn et al. 2005b) contains three highly nonlinear performance functions. There are two random variables which are statistically independent and follow the normal distribution X_i ~ N (d_i, 0.3²), i = 1, 2. The design variables are the means of the two random variables. Three different initial points, i.e., d⁰ = [1, 1], d⁰ = [5, 5], and d⁰ = [15, 15], are chosen to verify the stability of the proposed HS-SLA. The target reliability index is β^t = 3.0. The RBDO example is formulated as

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern1.45em \mathbf{d}=\left[{d}_1,{d}_2\right]\\ {}\mathit{\min}\kern1.75em f\left(\mathbf{d}\right)=-\frac{{\left({d}_1+{d}_2-10\right)}^2}{30}-\frac{{\left({d}_1-{d}_2+10\right)}^2}{120}\\ {}\mathrm{s}.\mathrm{t}.\kern2.35em P\left[{g}_j\left(\mathbf{X}\right)\le 0\right]\ge \Phi \left({\beta}_j^{\mathrm{t}}\right),\kern0.6em j=1,2,3\end{array}} $$

$$ {\displaystyle \begin{array}{l}\mathrm{where}\kern0.75em {g}_1\left(\mathbf{X}\right)=1-\frac{X_1^2{X}_2}{20},\\ {}\kern3.3em {g}_2\left(\mathbf{X}\right)={\left(Y-6\right)}^2+{\left(Y-6\right)}^3-0.6{\left(Y-6\right)}^4+Z-1,\\ {}\kern3.2em {g}_3\left(\mathbf{X}\right)=1-\frac{80}{\left({X}_1^2+8{X}_2+5\right)},\\ {}\kern3.25em Y=0.9063{X}_1+0.4226{X}_2,\kern0.3em Z=0.4226{X}_1-0.9063{X}_2,\\ {}\kern3.15em {\beta}_1^{\mathrm{t}}={\beta}_2^{\mathrm{t}}={\beta}_3^{\mathrm{t}}={\beta}^{\mathrm{t}}=3.0,\\ {}\kern3.25em 0\le {d}_i\le 20,\kern0.4em {X}_i\sim N\left({d}_i,{0.3}^2\right),\mathrm{for}\kern0.2em i=1,2\kern0.1em \end{array}} $$

The RBDO results of three different initial points are listed in Tables 4, 5, and 6, respectively. All RBDO approaches can converge to the optimum except RIA and SLA, which are consistent with the reference (Meng et al. 2018). As observed in these tables, SORA is considerably more efficient than PMA for all the three different initial points. SLA generates period-2 solution during the iterative process due to the second highly nonlinear performance function g₂. CSLA converges to the correct optimum by controlling the oscillation and the corresponding numbers of function evaluations are much less than those of SORA. Based on the developed reasonable oscillating judgment criterion 3 and self-adjusted control factor, the proposed HS-SLA can control the periodic oscillation of SLA. Consequently, HS-SLA improves the efficiency and stability of SLA. Furthermore, HS-SLA shows higher convergence rate than CSLA for all the three different initial points.

Table 4 RBDO results of Example 2 for d⁰ = [1, 1]

Table 5 RBDO results of Example 2 for d⁰ = [5, 5]

Table 6 RBDO results of Example 2 for d⁰ = [15, 15]

As illustrated in Tables 4, 5, and 6, PMA and SORA are sensitive to the initial point. PMA and SORA require less computational effort when the initial point lies in the vicinity of the optimum. In contrast, when the initial point is far from the optimum, the numbers of function evaluations required by PMA and SORA substantially increase. However, different initial points have less influence on the computational efficiency and stability of CSLA and HS-SLA, and thus less computational cost for CSLA and HS-SLA is needed.

In Tables 4, 5, and 6, the reliability indexes for three different initial points at the optimum are evaluated by MCS with ten million samples. Same conclusions can be drawn for all three different initial points. The first and second probability constraints (g₁ and g₂) are active, while the third one is inactive. The probabilistic constraints except RIA and SLA can meet the target reliability at the optimum. Moreover, iterative histories of objective function for CSLA and HS-SLA with three initial points for Example 2 are presented in Fig. 8. Overall, HS-SLA converges to the correct objective function more quickly than CSLA. Moreover, the iterative processes of MPPs and control factors of three performance functions by HS-SLA with d⁰ = [5, 5] are listed in Table 7. Only the iterative point in U-space cannot meet the oscillating judgment criterion 3 in (10) and presents non-convergence, the corresponding control factor λ^k is automatically updated by (11). As the iterative number increases, the oscillation amplitude of every iterative step decreases and the control factor gradually decreases.

Fig. 8

Iterative histories of objective function for CSLA and HS-SLA with three different initial points for Example 2. a d⁰ = [1, 1]. b d⁰ = [5, 5]. c d⁰ = [15, 15]

Table 7 Iterative processes of MPPs and control factors of HS-SLA for Example 2 with d⁰ = [5, 5]

To further verify the efficiency and stability of HS-SLA, ten initial values of design variables are randomly generated in the interval [0, 20], and the RBDO results of CSLA and HS-SLA are listed in Tables 8 and 9. It is indicated that both CSLA and HS-SLA can converge to the optimum when choosing the random initial points, and HS-SLA is more efficient and accurate than CSLA. Moreover, the MCS results of CSLA and HS-SLA are similar: the first and second probability constraints are active while the third one is inactive, and all the probability constraints of CSLA and HS-SLA satisfy the target reliability.

Table 8 RBDO results of Example 2 for CSLA with ten random initial values

Table 9 RBDO results of Example 2 for HS-SLA with ten random initial values

5.3 Welded beam structure

A welded beam structure (Lee and Lee 2005) in Fig. 9 is considered. There are four random design variables and five probability constraints. The objective of this RBDO problem is to minimize the welding cost with the target reliability index β^t = 3.0. The design variables are depth and length of welding, and height and thickness of the beam. Each design variable follows a statistically independent normal distribution. The probabilistic constraints are related to shear stress, bending stress, bucking, and displacement behaviors. The system parameters are listed in Table 10. The RBDO model of the welded beam is expressed as:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern1.85em \mathbf{d}=\left[{d}_1,{d}_2,{d}_3,{d}_4\right]\\ {}\mathit{\min}\kern1.9em f\left(\mathbf{d},\mathbf{z}\right)={c}_1{d}_1^2{d}_2+{c}_2{d}_3{d}_4\left({z}_2+{d}_2\right)\\ {}\mathrm{s}.\mathrm{t}.\kern2.45em P\left[{g}_j\left(\mathbf{X},\mathbf{z}\right)\le 0\right]\ge \Phi \left({\beta}_j^{\mathrm{t}}\right),\kern0.6em j=1,2,\cdots, 5\kern4.699997em \\ {}\mathrm{where}\kern0.75em {g}_1\left(\mathbf{X},\mathbf{z}\right)=\tau \left(\mathbf{X},\mathbf{z}\right)/{z}_6-1,\kern0.5em {g}_2\left(\mathbf{X},\mathbf{z}\right)=\sigma \left(\mathbf{X},\mathbf{z}\right)/{z}_7-1,\kern0.5em \\ {}\kern3.799999em {g}_3\left(\mathbf{X},\mathbf{z}\right)={X}_1/{X}_4-1,\kern2.1em {g}_4\left(\mathbf{X},\mathbf{z}\right)=\delta \left(\mathbf{X},\mathbf{z}\right)/{z}_5-1,\\ {}\kern3.25em {g}_5\left(\mathbf{X},\mathbf{z}\right)=1-{P}_c\left(\mathbf{X},\mathbf{z}\right)/{z}_1,\\ {}\kern3.25em \tau \left(\mathbf{X},\mathbf{z}\right)={\left\{t{\left(\mathbf{X},\mathbf{z}\right)}^2+2t\left(\mathbf{X},\mathbf{z}\right) tt\left(\mathbf{X},\mathbf{z}\right){X}_2/\left(2R\left(\mathbf{X}\right)\right)+ tt{\left(\mathbf{X},\mathbf{z}\right)}^2\right\}}^{1/2},\\ {}\kern3.25em t\left(\mathbf{X},\mathbf{z}\right)={z}_1/\left(\sqrt{2}{X}_1{X}_2\right),\kern0.4em tt\left(\mathbf{X},\mathbf{z}\right)=M\left(\mathbf{X},\mathbf{z}\right)R\left(\mathbf{X}\right)/J\left(\mathbf{X}\right),\end{array}} $$

$$ {\displaystyle \begin{array}{l}M\left(\mathbf{X},\mathbf{z}\right)={z}_1\left({z}_2+{X}_2/2\right),R\left(\mathbf{X}\right)=\sqrt{X_2^2+{\left({X}_1+{X}_3\right)}^2}/2,\\ {}J\left(\mathbf{X}\right)=\sqrt{2}{X}_1{X}_2\left\{{X}_2^2/12+{\left({X}_1+{X}_3\right)}^2/4\right\},\\ {}\sigma \left(\mathbf{X},\mathbf{z}\right)=\frac{6{z}_1{z}_2}{X_3^2{X}_4},\delta \left(\mathbf{X},\mathbf{z}\right)=\frac{4{z}_1{z}_2^3}{z_3{X}_3^3{X}_4},\\ {}{P}_c\left(\mathbf{X},\mathbf{z}\right)=\frac{4.013{X}_3{X}_4^3\sqrt{z_3{z}_4}}{6{z}_2^2}\left(1-\frac{X_3}{4{z}_2}\sqrt{\frac{z_3}{z_4}}\right),\\ {}{\beta}_1^{\mathrm{t}}={\beta}_2^{\mathrm{t}}=\cdots ={\beta}_5^{\mathrm{t}}={\beta}^{\mathrm{t}}=3.0,\\ {}3.175\le {d}_1\le 50.8,0\le {d}_2\le 254,0\le {d}_3\le 254,0\le {d}_4\le 50.8,\\ {}{X}_i\sim N\left({d}_i,{0.1693}^2\right)\kern0.32em \mathrm{for}\kern0.2em i=1,2,\\ {}{X}_i\sim N\left({d}_i,{0.0107}^2\right)\kern0.32em \mathrm{for}\kern0.2em i=3,4,\\ {}{\mathbf{d}}^0=\left[6.208,157.82,210.62,6.208\right]\end{array}} $$

Fig. 9

A welded beam structure

Table 10 System parameters for the welded beam structure

The result of deterministic optimization is set as the initial design point, i.e., d⁰ = [6.208, 157.82, 210.62, 6.208]. The optimal results of different RBDO approaches for the welded beam structure are given in Table 11. As illustrated from Table 11, the optimized results of these RBDO approaches except RIA are in agreement with those in reference (Li et al. 2015). SLA improves the efficiency of PMA and SORA. HS-SLA is more efficient than SLA and CSLA. Table 12 gives the evaluation of probabilistic constraints for welded beam structure by MCS with ten million samples at the optimum. For all RBDO approaches except RIA, g₁, g₂, g₃, and g₅ are active constraints while g₄ is inactive constraint. All the probability constraints of different RBDO approaches except RIA satisfy the target reliability at the optimum.

Table 11 RBDO results of the welded beam structure

Table 12 Evaluation of probabilistic constraints at the optimum for the welded beam structure by MCS

5.4 A speed reducer

Figure 10 is a speed reducer (Lee and Lee 2005; Meng et al. 2018) which is used to rotate the engine and propeller with efficient velocity in light plane. There are seven random variables and 11 probability constraints. To minimize the weight is the objective function of this RBDO problem. The probability constraints are related to bending and contact stress, longitudinal displacement, stress of the shaft, and geometry. Seven design variables are gear width (X₁), teeth module (X₂), number of teeth in the pinion (X₃), distance between bearings (X₄, X₅), and axis diameter (X₆, X₇). All random design variables are statistically independent and obey lognormal distribution with a standard deviation of 0.005. The RBDO model of the speed reducer is formulated as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern1.95em \mathbf{d}=\left[{d}_1,{d}_2,{d}_3,{d}_4,{d}_5,{d}_6,{d}_7\right]\\ {}\mathit{\min}\kern2em f\left(\mathbf{d}\right)=0.7854{d}_1{d}_2^2\left(3.3333{d}_3^2+14.9334{d}_3-43.0934\right)-1.508{d}_1\left({d}_6^2+{d}_7^2\right)\\ {}\kern7.699995em +7.477\left({d}_6^3+{d}_7^3\right)+0.7854\left({d}_4{d}_6^2+{d}_5{d}_7^2\right)\\ {}\mathrm{s}.\mathrm{t}.\kern2.6em P\left[{g}_j\left(\mathbf{X}\right)\le 0\right]\ge \Phi \left({\beta}_j^{\mathrm{t}}\right),\kern0.6em j=1,2,\cdots, 11\kern4.699997em \end{array}} $$

$$ {\displaystyle \begin{array}{l}\mathrm{where}\kern0.75em {g}_1\left(\mathbf{X}\right)=\frac{27}{X_1{X}_2^2{X}_3}-1,\kern1.1em {g}_2\left(\mathbf{X}\right)=\frac{397.5}{X_1{X}_2^2{X}_3^2}-1,\kern0.7em \\ {}\kern3.799999em {g}_3\left(\mathbf{X}\right)=\frac{1.93{X}_4^3}{X_2{X}_3{X}_6^4}-1,\kern0.8000001em {g}_4\left(\mathbf{X}\right)=\frac{1.93{X}_5^3}{X_2{X}_3{X}_7^4}-1,\kern1em \\ {}\kern3.799999em {g}_5\left(\mathbf{X}\right)=\sqrt{{\left(745{X}_4/\left({X}_2{X}_3\right)\right)}^2+16.9\times {10}^6}/\left(0.1{X}_6^3\right)-1100,\\ {}\kern3.799999em {g}_6\left(\mathbf{X}\right)=\sqrt{{\left(745{X}_5/\left({X}_2{X}_3\right)\right)}^2+157.5\times {10}^6}/\left(0.1{X}_7^3\right)-850,\kern0.8000001em \\ {}\kern3.799999em {g}_7\left(\mathbf{X}\right)={X}_2{X}_3-40,\kern0.4em {g}_8\left(\mathbf{X}\right)=5-{X}_1/{X}_2,\kern1em {g}_9\left(\mathbf{X}\right)={X}_1/{X}_2-12,\kern1.1em \\ {}\kern3.699999em {g}_{10}\left(\mathbf{X}\right)=\left(1.5{X}_6+1.9\right)/{X}_4-1,\kern0.6em {g}_{11}\left(\mathbf{X}\right)=\left(1.1{X}_7+1.9\right)/{X}_5-1,\\ {}\kern3.799999em {\beta}_1^{\mathrm{t}}={\beta}_2^{\mathrm{t}}=\cdots ={\beta}_{11}^{\mathrm{t}}={\beta}^{\mathrm{t}}=3.0,\\ {}\kern3.799999em 2.6\le {d}_1\le 3.6,\kern0.8000001em 0.7\le {d}_2\le 0.8,\kern0.8000001em 17\le {d}_3\le 28,\kern0.8000001em 7.3\le {d}_4\le 8.3,\\ {}\kern3.799999em 7.3\le {d}_5\le 8.3,\kern0.8000001em 2.9\le {d}_6\le 3.9,\kern0.7em 5.0\le {d}_7\le 5.5\kern0.1em \\ {}\kern3.799999em {X}_i\sim LN\left({d}_i,{0.005}^2\right)\kern0.3em ,\kern0.5em \mathrm{for}\kern0.3em i=1,2,\cdots, 7,\\ {}\kern3.799999em {\mathbf{d}}^0=\left[3.50,0.70,17.0,7.30,7.72,3.35,5.29\right]\end{array}} $$

Fig. 10

A speed reducer

The optimal results of different approaches for the speed reducer are listed in Table 13. As observed in Table 13, all these RBDO approaches converge to the same optimum as shown in the literature (Meng et al. 2018). Compared to the double-loop approaches (i.e., RIA and PMA) and the decoupled approach (i.e., SORA), SLA, CSLA, and HS-SLA can improve the RBDO efficiency for this problem owing to the single-loop strategy. The proposed HS-SLA requires less computational effort than both SLA and CSLA for this example. Table 14 exhibits the reliability indexes of each probabilistic constraint calculated by MCS with ten million samples at the optimum. Same conclusions can be drawn for all different approaches. The four probability constraints of g₅, g₆, g₈, and g₁₁ are active, while the remaining seven are inactive. All the probabilistic constraints satisfy the target reliability at the optimum.

Table 13 RBDO results of the speed reducer in Example 4

Table 14 Evaluation of probabilistic constraints at the optimum for the speed reducer by MCS

5.5 High dimensional RBDO problem

To verify the applicability of HS-SLA to high dimensional RBDO problem, the last mathematical example is the Hock and Schittkowski problem no.113 (Lee and Lee 2005), which has ten random design variables and eight probability constraints. All design variables follow independent normal distribution with a standard deviation of 0.02. The description of this example is formulated as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern1.2em \mathbf{d}=\left[{d}_1,{d}_2,{d}_3,{d}_4,{d}_5,{d}_6,{d}_7,{d}_8,{d}_9,{d}_{10}\right]\\ {}\mathit{\min}\kern1.3em f\left(\mathbf{d}\right)={d}_1^2+{d}_2^2+{d}_1{d}_2-14{d}_1-16{d}_2+{\left({d}_3-10\right)}^2+4{\left({d}_4-5\right)}^2+{\left({d}_5-3\right)}^2\\ {}\kern7.799995em +2{\left({d}_6-1\right)}^2+5{d}_7^2+7{\left({d}_8-11\right)}^2+2{\left({d}_9-10\right)}^2+{\left({d}_{10}-7\right)}^2+45\\ {}\mathrm{s}.\mathrm{t}.\kern1.9em P\left[{g}_j\left(\mathbf{X}\right)\le 0\right]\ge \Phi \left({\beta}_j^{\mathrm{t}}\right),\kern0.6em j=1,2,\cdots, 8\kern4.699997em \end{array}} $$

$$ {\displaystyle \begin{array}{l}\kern0.1em \mathrm{where}\kern3.699999em \\ {}\kern3.299999em {g}_1\left(\mathbf{X}\right)=\frac{4{X}_1+5{X}_2-3{X}_7+9{X}_8}{105}-1,\kern0.3em \\ {}\kern3.299999em {g}_2\left(\mathbf{X}\right)=10{X}_1-8{X}_2-17{X}_7+2{X}_8,\\ {}\kern3.299999em {g}_3\left(\mathbf{X}\right)=\frac{-8{X}_1+2{X}_2+5{X}_9-2{X}_{10}}{12}-1,\\ {}\kern3.199999em {g}_4\left(\mathbf{X}\right)=\frac{3{\left({X}_1-2\right)}^2+4{\left({X}_2-3\right)}^2+2{X}_3^2-7{X}_4}{120}-1,\\ {}\kern3.299999em {g}_5\left(\mathbf{X}\right)=\frac{5{X}_1^2+8{X}_2+{\left({X}_3-6\right)}^2-2{X}_4}{40}-1,\\ {}\kern3.199999em {g}_6\left(\mathbf{X}\right)=\frac{0.5{\left({X}_1-8\right)}^2+2{\left({X}_2-4\right)}^2+3{X}_5^2-{X}_6}{30}-1,\\ {}\kern3.299999em {g}_7\left(\mathbf{X}\right)={X}_1^2+2{\left({X}_2-2\right)}^2-2{X}_1{X}_2+14{X}_5-6{X}_6,\kern0.4em \\ {}\kern3.299999em {g}_8\left(\mathbf{X}\right)=-3{X}_1+6{X}_2+12{\left({X}_9-8\right)}^2-7{X}_{10},\\ {}\kern3.299999em {\beta}_1^{\mathrm{t}}={\beta}_2^{\mathrm{t}}=\cdots ={\beta}_8^{\mathrm{t}}={\beta}^{\mathrm{t}}=3.0,\\ {}\kern3.299999em 0\le {d}_i\le 10,{x}_i\sim N\left({d}_i,{0.02}^2\right),\kern0.5em \mathrm{for}\kern0.3em i=1,2,\cdots, 10\\ {}\kern3.299999em {\mathbf{d}}^0=\left[2.17,2.36,8.77,5.10,0.99,1.43,1.32,9.83,8.28,8.38\right]\end{array}} $$

The optimal result obtained from deterministic optimization (Lee and Lee 2005) is taken as the initial design point, i.e., d⁰ = [2.17, 2.36, 8.77, 5.10, 0.99, 1.43, 1.32, 9.83, 8.28, 8.38]. The optimal results of different RBDO approaches tabulated in Table 15 are close to those from the reference (Cho and Lee 2011). As seen in Table 15, the number of function evaluations of SLA is less than RIA, PMA, and SORA, and CSLA improves the efficiency of SLA. Furthermore, less computational effort for HS-SLA is required to converge to the optimum compared to both SLA and CSLA. Therefore, the computational efficiency of HS-SLA is the highest. The reliability indexes of each probabilistic constraint calculated by MCS with 10 million samples at the optimum are given in Table 16. Same conclusions can be made for all different approaches. Two probability constraints (g₆ and g₈) are inactive, while the remaining six are active. All the probabilistic constraints satisfy the target reliability at the optimum. HS-SLA is more efficient and stable for this high dimensional RBDO problem.

Table 15 RBDO results of the Hock and Schittkowski problem no.113 in Example 5

Table 16 Evaluation of probabilistic constraints at the optimum by MCS in Example 5

6 Conclusions

Despite the high efficiency of single-loop approach, SLA has difficulties to find the correct optimum for RBDO problem with large target reliability index and highly nonlinear performance functions. In this paper, a new oscillating judgment criterion of iterative point and self-adjusted updating strategy for control factor are investigated firstly. Then, an adaptive modified chaos control method is suggested to automatically select the MPP search formulas between MCC method and AMV method based on the oscillation of the iterative points. Moreover, an efficient hybrid self-adjusted single-loop approach is proposed by integrating the developed AMCC into SLA. Five mathematical examples for reliability analysis are presented to demonstrate the high efficiency of AMCC to search for MPP. Finally, five representative RBDO examples are tested to demonstrate the high efficiency and stability of the proposed HS-SLA. Some conclusions can be drawn as follows.

• (1) For RBDO problems with large reliability index and highly nonlinear performance functions, SLA has difficulties in terms of iterative convergence. However, the stability of HS-SLA remains unchanged and HS-SLA are more efficient than other RBDO approaches.

• (2) Both PMA and SORA are very sensitive to the initial point, while CSLA and HS-SLA are insensitive to the choice of initial point.

• (3) HS-SLA is more efficient and stable for high dimensional RBDO problems. Consequently, HS-SLA can improve the efficiency, accuracy, and stability of SLA. Moreover, HS-SLA is more efficient and stable than other approaches for RBDO problems with highly nonlinear performance function. In the future, the research will focus on the application of the proposed HS-SLA for large-scale structural design.

7 Replication of results

Data will be made available on request.