Multi-information source constrained Bayesian optimization

Abstract

Design decisions for complex systems often can be made or informed by a variety of information sources. When optimizing such a system, the evaluation of a quantity of interest is typically required at many different input configurations. For systems with expensive to evaluate available information sources, the optimization task can potentially be computationally prohibitive using traditional techniques. This paper presents an information-economic approach to the constrained optimization of a system with multiple available information sources. The approach rigorously quantifies the correlation between the discrepancies of different information sources, which enables the overcoming of information source bias. All information is exploited efficiently by fusing newly acquired information with that previously evaluated. Independent decision-makings are achieved by developing a two-step look-ahead utility policy and an information gain policy for objective function and constraints respectively. The approach is demonstrated on a one-dimensional example test problem and an aerodynamic design problem, where it is shown to perform well in comparison to traditional multi-information source techniques.

1 Introduction

Design decisions for complex engineered systems are increasingly being informed by queries to multiple sources of information. These information sources may consist of variable fidelity models, expert opinions, historical data, or newly conducted physical experiments. Our aim here is to create a systematic procedure for enabling the efficient exploitation of all available information sources. The context we focus on is constrained optimization problems with expensive to evaluate information sources. For such problems, traditional optimization strategies, such as the employment of gradient-based algorithms or heuristic techniques can be inappropriate. This can be, for example, due to sheer expense in the case of heuristics, and the need to calculate finite differences of say an experimental information source in the case of gradient-based algorithms, where resources often would not be spent on queries in such close proximity in input space. Given such considerations, the approach we propose for multi-information source optimization focuses on Bayesian global optimization strategies, where query points are selected based on expected contribution to such quality metrics as information gained regarding a constraint or expected improvement in an objective. Such a strategy enables the natural fusion of information from multiple sources, which we exploit here to ensure that all available information can be used for the optimization task at hand.

Our work builds generally on concepts from multifidelity optimization, where several different computational models are available for a given task. One common approach in multifidelity optimization is to treat the models as a hierarchy and replace or calibrate low-fidelity information with high-fidelity results (Alexandrov et al. 2000; Jones et al. 1998; Booker et al. 1999; Jones 2001; Sasena et al. 2002; Ghoreishi and Allaire 2018a). Trust region methods are used to approximate the high-fidelity model for optimizing an objective function when the derivatives of the objective are available. In refs. Alexandrov et al. (1998) and Alexandrov et al. (2001), a trust region-based model-management method is employed in which the gradients of the low-fidelity objective function and constraints are scaled or shifted to match those of a high-fidelity model. ref. March and Willcox (2012) presents a convergent multifidelity optimization algorithm using the trust region method that does not require the high-fidelity derivatives, and considers hierarchies between the low and high-fidelity models. In ref. Huang et al. (2006), a multifidelity sequential kriging optimization method is proposed which uses the expected improvement as a measure to determine the next design point and the level of fidelity model to evaluate, and the autoregressive assumption is used to build the multifidelity model based on hierarchical relationships among the information sources. In practice, the fidelity of information sources can vary over the design space. Therefore, the assumption of hierarchical relationship among the information sources might not be practical, and all the available data from different information sources need to be fused to take into account all potential information any given source may bring to bear on the optimization problem.

There are several techniques used in practice for achieving the fusion of information from multiple information sources. Among them are the adjustment factors approach (Mosleh and Apostolakis 1986; Reinert and Apostolakis 2006; Riley et al. 2011), Bayesian model averaging (Leamer 1978; Madigan and Raftery 1994; Draper 1995; Hoeting et al. 1999) which believe that each model has some probability of being true and the fused estimate is a weighted average of the available models. The other available techniques are fusion under known correlation (Geisser 1965; Morris 1977; Winkler 1981a; Ghoreishi and Allaire 2018b; Ghoreishi et al. 2018), and covariance intersection method Julier and Uhlmann (1997, 2001). Covariance intersection algorithm has a tendency to discard lower fidelity information sources to achieve the most conservative estimate possible in cases with scalar quantities of interest. It requires that the information source with the highest fidelity be used for the fused estimate. While using the high-fidelity model at all points in the design space leads to a reduction in uncertainty due to model inadequacy, this approach leads to a loss of information provided by the low-fidelity models that could be used to better estimate the model output if the correlation coefficients were known. Accounting for correlation is critical in information fusion. Aggressive approaches, such as assuming each model is independent from all others, are often incorrect, and can lead to potentially serious misconceptions regarding confidence in quantity of interest estimates.

In this work, we propose a method for the constrained optimization of a quantity of interest where multiple information sources, which are generally expensive to evaluate, are available for approximating the quantity of interest and constraints. To enable informed querying of information sources and to account for each source’s discrepancy, we construct Gaussian processes for each source using available evaluations from a given source and that source’s discrepancy information. Following standard practice for the fusion of normally distributed data (Winkler 1981b), we create fused Gaussian processes for the objective function and constraints, that contain all currently available information from each information source. A novel aspect of this work is the use of fusion techniques that support the rigorous incorporation of correlation both within information sources in terms of information source estimates, and between information sources in terms of information source estimate errors. This latter aspect enables the mitigation of bias among information sources. Specifically, traditional fusion techniques estimate a quantity of interest as a weighted average of information source estimates. This average always resides within the extremes of the information source estimates. That is, if all information sources are biased in the same direction with respect to a quantity of interest, traditional fusion techniques cannot overcome this bias and will produce a similarly biased estimate. Our work employs a novel model reification technique described in detail in ref. Thomison and Allaire (2017), that overcomes this limitation in the fused Gaussian processes.

By constructing the fused Gaussian processes, the next design to evaluate and the information source to query for the objective function are determined based on our proposed two-step look-ahead policy. This policy is achieved by sequential augmentation process and the knowledge gradient policy as a one-step look-ahead policy to maximize (or minimize) an objective (Scott et al. 2011; Frazier et al. 2008; Imani et al. 2018; Powell and Ryzhov 2012; Frazier et al. 2009). Notice that our proposed two-step look-ahead policy goes beyond the existing Bayesian optimization techniques which only take the next step into account for decision-making process. The next design to evaluate and the information source to query for the constraints are determined based on our proposed information gain policy achieved by sequential augmentation process and the Kullback-Leibler divergence. This is the novel aspect of our methodology that decision-making for querying from constraint information sources is independent of objective function decision-making, and the constraint information sources can be queried at different design locations than the objective information source during the same optimization iteration, and involve entirely separate information sources than those of the objective. The proposed method yields several benefits summarized as follows

• Incorporation of correlations both within and between information sources;

• Direct decision-making on the fused model regarding which information source to query next and where to query it;

• A two-step look-ahead policy and an information gain policy for sequential objective function and constraints decision-making;

• Independent decision-making for querying from constraints and objective function information sources.

Our proposed multi-information source optimization approach is applied to optimize a one-dimensional example test problem and an aerodynamic design example, and the results are compared with a traditional multi-information source optimization method presented in ref. Lam et al. (2015) which is currently the state of the art in constrained Bayesian optimization. It is shown that our proposed method results in higher quality solutions for the demonstrations presented, particularly in the case of a limited budget available for querying.

The rest of the paper is organized as follows. Section 2 describes the problem we aim to address in this work. Section 3 presents our approach in detail. In Section 4, the approach is applied to a one-dimensional test function and an aerodynamic example problem and the results are discussed. Finally, conclusions are drawn and future work opportunities are described in Section 5.

2 Problem statement

We consider the problem of optimizing a quantity of interest subject to m inequality constraints, where multiple sources of information are available for both the objective and constraints. A mathematical statement of the problem is formulated as

$$\begin{array}{@{}rcl@{}} {\mathbf{x}}^{*} &=& \underset{\mathbf{x} \in \chi}{\text{argmax}}~f(\mathbf{x})\\ & &\text{s.t.} \quad g_{j}(\mathbf{x}) \leq 0, \quad j = 1,2,\dots, m, \end{array} $$

(1)

where f is the real-world objective function, g_j, where j = 1,2,…,m, are the m real-world constraints, and x is a set of design variables in the vector space χ. In the optimization process, the real-world objective function and the real-world constraints must be estimated at each iteration.

For this estimation task, often several information sources, such as numerical simulation models, experiments, expert opinions, etc., are available. These sources have varying fidelities, or approximation accuracies over the design space, and varying computational costs. The approach we describe here enables the exploitation of all available sources of information, in an information-economic sense, that balances the cost and associated fidelity of each information source when choosing how to estimate the quantity of interest and the constraints. In our formulation, the core issue is how to manage dynamic querying to choose what new information sources to sample and with what input, at each step of the overall decision process. The choice of next design point to query must be based on how much a sample tells us about the design goal at hand and if that sample is expected to satisfy the current constraints. This choice must trade off the costs associated with a particular information source query and the utility or information gained by executing the query.

Here, we assume we have available some set of information sources, f_i(x), where i ∈{1,2,…,S}, that can be used to estimate the quantity of interest, f(x), at design point x. In order to predict the output of each information source at locations that have not yet been queried, an intermediate surrogate is constructed for each information source using Gaussian processes (Rasmussen and Williams 2006). These surrogates are denoted by f_{GP, i}(x). We consider the prior distributions of the information sources modeled by Gaussian processes as

$$ f_{GP,i}(\mathbf{x}) \sim \mathcal{GP}\left( \textbf{0}, k_{i}(\mathbf{x},\mathbf{x})\right), $$

(2)

where k_i(x, x) is a real-valued kernel function over the input space. For the kernel function, we consider the commonly used squared exponential covariance function, which is specified as

$$ k_{i}(\mathbf{x},\mathbf{x^{\prime}}) = {\sigma_{s}^{2}} \exp\left( - \sum\limits_{h = 1}^{d} \frac {(x_{h}-x^{\prime}_{h})^{2}}{2{l_{h}^{2}}}\right), $$

(3)

where d is the dimension of the input space, ${\sigma _{s}^{2}}$ is the signal variance, and l_h, where h = 1,2,…,d, is the characteristic length-scale that indicates the correlation between the points within dimension h. The parameters ${\sigma _{s}^{2}}$ and l_h associated with each information source can be estimated via maximum likelihood. Assuming we have available N_i evaluations of information source i denoted by $\{\mathbf {X}_{N_{i}}, \mathbf {y}_{N_{i}}\}$, where $\mathbf {X}_{N_{i}} = (\mathbf {x}_{1,i}, \ldots , \mathbf {x}_{N_{i},i})$ represents the N_i input samples to information source i and $\mathbf {y}_{N_{i}} = \left (f_{i}(\mathbf {x}_{1,i}), \ldots , f_{i}(\mathbf {x}_{N_{i},i})\right )$ represents the corresponding outputs from information source i, the posterior distribution of information source i at design point x is given as

$$ f_{GP,i}(\mathbf{x}) \mid \mathbf{X}_{N_{i}}, \mathbf{y}_{N_{i}} \sim \mathcal{N}\left( \mu_{i}(\mathbf{x}),\sigma_{GP,i}^{2}(\mathbf{x})\right), $$

(4)

where

$$\begin{array}{@{}rcl@{}} \mu_{i}(\mathbf{x}) &=& K_{i}(\mathbf{X}_{N_{i}},\mathbf{x})^{T}[K_{i}(\mathbf{X}_{N_{i}},\mathbf{X}_{N_{i}})+\sigma^{2}_{n,i}I]^{-1} \mathbf{y}_{N_{i}},\\ \sigma_{GP,i}^{2} (\mathbf{x}) &=& k_{i}(\mathbf{x},\mathbf{x}) - K_{i}(\mathbf{X}_{N_{i}},\mathbf{x})^{T}\\ &&\qquad [K_{i}(\mathbf{X}_{N_{i}},\mathbf{X}_{N_{i}})+\sigma^{2}_{n,i}I]^{-1}K_{i}(\mathbf{X}_{N_{i}},\mathbf{x}), \end{array} $$

(5)

where $K_{i}(\mathbf {X}_{N_{i}},\mathbf {X}_{N_{i}})$ is the N_i × N_i matrix whose m, n entry is $k_{i}(\mathbf {x}_{m,i}, \mathbf {x}_{n,i})$, and $K_{i}(\mathbf {X}_{N_{i}}, \mathbf {x})$ is the N_i × 1 vector whose m^th entry is k_i(x_{m, i},x) for information source i. Note that here we have included the term $\sigma ^{2}_{n,i}$, which can be used to model observation error for information sources based on experiments and can also be used to guard against numerical ill-conditioning.

To these Gaussian process surrogates, in order to estimate the fused value as will be discussed in Section 3, we further quantify the uncertainty of each information source with respect to the true quantity of interest by adding a term associated with the fidelity of the information source. Specifically, we quantify the total variance which captures both the variance associated with the Gaussian process representation and the quantified variance associated with the fidelity of the information source over the input space, as

$$ {\sigma_{i}^{2}}(\mathbf{x}) = \sigma_{GP,i}^{2} (\mathbf{x}) + \sigma_{f,i}^{2}(\mathbf{x}), $$

(6)

where $\sigma _{f,i}^{2}(\mathbf {x})$ is the fidelity variance of information source i that has been estimated from, for example, expert opinion or available real-world data. Here, we estimate the fidelity variance of each information source by computing the error values which are the absolute difference between the available data from the true quantity of interest and the information source. A Gaussian process is then performed using the square of these error values as training points to estimate the fidelity variance over the input space as mean of the Gaussian process. Figure 1 shows a depiction of total variance for an information source represented by Gaussian process.

Fig. 1

A depiction of total variance, which includes both the variance associated with the Gaussian process and variance associated with the fidelity of the information source

Our approach to information sources that can be used to evaluate any of the m constraints in Problem (1) follows that of our approach to the objective based information sources. For any given constraint, g_j, where j ∈{1,2,…,m}, we have available some set of information sources, g_{i, j}(x), where i ∈{1,2,...,G_j}, that can be used to estimate the quantity of interest, g_j(x), at the design point x. Following the same approach taken for the objective information sources, we quantify the total variance of the i th information source of the j th constraint as

$$ \sigma^{2}_{i,j}(\mathbf{x}) = \sigma^{2}_{GP,i,j}(\mathbf{x}) + \sigma^{2}_{g_{j},i}(\mathbf{x}). $$

(7)

where $\sigma ^{2}_{GP,i,j}(\mathbf {x})$ is the variance associated with the Gaussian process representation of g_{i, j} and $\sigma ^{2}_{g_{j},i}(\mathbf {x})$ is the quantified fidelity variance of the information source.

3 Approach

This section describes our multi-information source constrained Bayesian optimization approach. We first present how we fuse the knowledge from information sources, and construct fused Gaussian processes for the objective function and the m constraints, required for finding the solution for the maximization problem in (1). Then, we present our proposed strategies for choosing the next design points and information sources of objective function and constraints to query. We conclude this section with a complete algorithm for implementing our approach.

3.1 Fusion of information sources

A fundamental claim in this work is that any information source can provide potentially useful information to a given task at hand. That is, information sources are not assumed to be hierarchical and the goal is not to just optimize whatever is deemed the highest fidelity source. Indeed, according to (6) and (7), the discrepancy of an information source can vary over its domain. Thus, a strict hierarchy of information source fidelity is an unlikely and restrictive assumption.

To take into account all potential information any given source may bring to bear on the optimization problem (i.e., objective or constraint information at a given input), we fuse our information sources following standard practice for the fusion of normally distributed data (Winkler 1981b), since our information sources are represented as Gaussian processes. According to the method of Winkler, the fused mean and variance at point x can be computed as Winkler (1981b)

$$ \mu_{\text{Wink}}(\mathbf{x})=\frac{\mathbf{e}^{T} \tilde{\Sigma}(\mathbf{x})^{-1} \boldsymbol{\mu}(\mathbf{x})}{\mathbf{e}^{T} \tilde{\Sigma}(\mathbf{x})^{-1} \mathbf{e}}, $$

(8)

$$ \sigma^{2}_{\text{Wink}}(\mathbf{x})= \frac{1}{\mathbf{e}^{T} \tilde{\Sigma}(\mathbf{x})^{-1} \mathbf{e}}, $$

(9)

where e = [1,…,1]^⊤, μ(x) = [μ₁(x),…,μ_S(x)]^⊤ contains the mean values of S models at point x, and $\tilde {\Sigma }(\mathbf {x})$ is the covariance matrix between the models given as

$$ \tilde{\Sigma}(\mathbf{x})= \left[\begin{array}{lllll} {\sigma_{1}^{2}}(\mathbf{x})&\cdots&\rho_{1S}(\mathbf{x})\sigma_{1}(\mathbf{x})\sigma_{S}(\mathbf{x})\\ \rho_{12}(\mathbf{x})\sigma_{1}(\mathbf{x})\sigma_{2}(\mathbf{x})&\cdots&\rho_{2S}(\mathbf{x})\sigma_{2}(\mathbf{x})\sigma_{S}(\mathbf{x})\\ \vdots& \ddots&\vdots\\ \rho_{1S}(\mathbf{x})\sigma_{1}(\mathbf{x})\sigma_{S}(\mathbf{x})&\cdots&{\sigma_{S}^{2}}(\mathbf{x}) \end{array}\right], $$

(10)

where ${\sigma _{i}^{2}}(\mathbf {x})$ is the total variance of model i at point x and ρ_ij(x) is the correlation coefficient between the deviations of information sources i and j at point x.

To estimate the correlations between the model deviations, we use the reification process defined in Allaire and Willcox (2012) and Thomison and Allaire (2017), which refers to the process of treating each model, in turn, as ground truth. Following this process, the correlation between the errors is computed as follows

$$ {\rho}_{ij}(\mathbf{x}) = \frac{{\sigma_{j}^{2}}(\mathbf{x})}{{\sigma_{i}^{2}}(\mathbf{x}) + {\sigma_{j}^{2}}(\mathbf{x})} \tilde{\rho}_{ij}(\mathbf{x}) + \frac{{\sigma_{i}^{2}}(\mathbf{x})}{{\sigma_{i}^{2}}(\mathbf{x})+{\sigma_{j}^{2}}(\mathbf{x})} \tilde{\rho}_{ji}(\mathbf{x}), $$

(11)

where ${\sigma _{i}^{2}}(\mathbf {x})$ and ${\sigma _{j}^{2}}(\mathbf {x})$ are the total variances of information sources i and j at point x, and $\tilde {\rho }_{ij}(\mathbf {x})$ and $\tilde {\rho }_{ji}(\mathbf {x})$ are computed by reifying models i and j respectively as

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{ij}(\mathbf{x}) &=& \frac{\sigma_{i}(\mathbf{x})}{\sqrt{\left( \mu_{i}(\mathbf{x})-\mu_{j}(\mathbf{x})\right)^{2} + {\sigma_{i}^{2}}(\mathbf{x})}},\\ \tilde{\rho}_{ji}(\mathbf{x}) &=& \frac{\sigma_{j}(\mathbf{x})}{\sqrt{\left( \mu_{j}(\mathbf{x})-\mu_{i}(\mathbf{x})\right)^{2} + {\sigma_{j}^{2}}(\mathbf{x})}}, \end{array} $$

(12)

where μ_i(x) and μ_j(x) are the mean values of models i and j, respectively at design point x. Note that the correlation between the errors in (11) is the variance-weighted average of the two correlation coefficients in (12). The detailed process of estimating the correlation between the errors of two models can be found in Allaire and Willcox (2012) and Thomison and Allaire (2017).

To imbue the fused model with the complete learned information, we construct a fused Gaussian process (which also accounts for correlation between design points). To accomplish this, we construct the Gaussian process from a finite set of samples $\mathbf {x}_{1:N_{f}}\subset \chi$. Let $\boldsymbol {\mu }_{\text {Wink}}(\mathbf {x}_{1:N_{f}})$ and ${\Sigma }(\mathbf {x}_{1:N_{f}}) = diag\left (\sigma ^{2}_{\text {Wink}}(\mathbf {x_{1}}), \dots , \sigma ^{2}_{\text {Wink}}(\mathbf {x}_{N_{f}})\right )$ be the vector of fused means and a diagonal matrix containing the fused variances at $\mathbf {x}_{1:N_{f}}$ obtained according to (8) and (9) respectively. Considering the squared exponential covariance function (other options could be employed) and obtaining the hyperparameters via maximum likelihood, we construct the fused Gaussian process. The posterior predictive distribution of fused estimate at any set of samples X in the design space can be obtained as

$$ \hat{f}^{\text{fused}}(\mathbf{X}) \sim \mathcal{N}(\boldsymbol{\mu}^{\text{fused}}(\mathbf{X}), {\Sigma}^{\text{fused}}(\mathbf{X})), $$

(13)

where

$$\begin{array}{@{}rcl@{}} \boldsymbol{\mu}^{\text{fused}}(\mathbf{X}) &=& K(\mathbf{x}_{1:N_{f}},\mathbf{X})^{T}[K(\mathbf{x}_{1:N_{f}},\mathbf{x}_{1:N_{f}})+{\Sigma}(\mathbf{x}_{1:N_{f}})]^{-1}\\ &&\qquad \boldsymbol{\mu}_{\text{Wink}}(\mathbf{x}_{1:N_{f}}),\\ {\Sigma}^{\text{fused}}(\mathbf{X}) &=& K(\mathbf{X},\mathbf{X}) - K(\mathbf{x}_{1:N_{f}},\mathbf{X})^{T}[K(\mathbf{x}_{1:N_{f}},\mathbf{x}_{1:N_{f}})+\\ &&\qquad {\Sigma}(\mathbf{x}_{1:N_{f}})]^{-1} K(\mathbf{x}_{1:N_{f}},\mathbf{X}). \end{array} $$

(14)

Fused Gaussian processes are also constructed for each of the constraints to predict the feasibility of the design to evaluate. This approach follows that of the approach taken above for the fused Gaussian process of the objective function.

3.2 Two-step look-ahead utility function for objective function query

Equipped with fused Gaussian processes for the objective and each constraint, the next step of our methodology for solving (1) is identification of the next design point location to query and with which information source to execute the query. The design point to evaluate is based on the fused Gaussian processes of the objective function and constraints. This choice must trade off the goals of learning or exploring the fused model of objective function and maximizing or exploiting this function. Further, this choice must eventually be feasible with respect to the fused constraint models. We denote the feasible design space by χ_feas where χ_feas ⊂ χ.

To determine the next design point and information source to query, we generate Latin hypercube samples in the input design space as alternatives denoted as X_alt. Among these alternatives, we seek to identify a set of feasible design points, as determined by dynamically updated constraints described below. From this feasible set denoted by X_feas, we seek to determine which design point and which information source to query that design point will lead to the maximum utility in the fused Gaussian process of the objective function with minimum cost of query. This utility is also described below.

We define a two-step look-ahead policy as the utility function which is able to consider both our current best design given a potential query result and the ability we would have, armed with this potential query, to find an even better design on the next query. In our proposed method, unlike most Bayesian optimization techniques which are developed based on a one-step look-ahead procedure, a two-step look-ahead optimization is achieved.

Let (x_1:N,y_1:N) be the design points and the corresponding objective values, and i_1:N be the indices of the queried information sources of the objective function up to time step N. We define the utility obtained by querying the design point x ∈X_feas from information source i as

$$\begin{array}{@{}rcl@{}} U_{\mathbf{x},i} &=& \mathbb{E}\left[\max\limits_{\mathbf{x}^{\prime} \in \chi_{\text{feas}}} \mu^{\text{fused}}(\mathbf{x}^{\prime})+ \max\limits_{\mathbf{x}^{\prime\prime} \in \chi_{\text{feas}}} EI_{\mathbf{x},i}\left.(\mathbf{x}^{\prime\prime})\right|\right.\\ && \qquad \left. \mathbf{x}_{1:N}, y_{1:N}, i_{1:N}, \mathbf{x}_{N + 1} = \mathbf{x}, i_{N + 1} = i\right] , \end{array} $$

(15)

where EI_{x, i}(x^″) is the one-step look-ahead expected increase in the maximum of the fused Gaussian process given x_N+ 1 = x and i_N+ 1 = i as

$$\begin{array}{@{}rcl@{}} EI_{\mathbf{x},i}(\mathbf{x}^{\prime\prime}) &=& \mathbb{E}\left[\max\limits_{\mathbf{x}^{\prime} \in \chi_{\text{feas}}} \mu^{\text{fused}}(\mathbf{x}^{\prime})\mid \mathbf{x}_{N + 2} = \mathbf{x}^{\prime\prime}\right]\\ && \quad -\max\limits_{\mathbf{x}^{\prime} \in \chi_{\text{feas}}} \mu^{\text{fused}}(\mathbf{x}^{\prime}). \end{array} $$

(16)

The exact computation of (15) is not possible. Thus in this paper, we provide a Monte Carlo technique for its approximation. For a given point x at information source i, the objective function values are normally distributed based on the mean and variance of the corresponding Gaussian process. Drawing N_q independent samples from this normal distribution as ${f_{i}^{q}}(\mathbf {x})\sim \mathcal {N}\left (\mu _{i}(\mathbf {x}),\sigma _{GP,i}^{2}(\mathbf {x})\right ), q = 1, \dots , N_{q}$, results in the following approximation of (15)

$$\begin{array}{@{}rcl@{}} U_{\mathbf{x},i} \approx \frac{1}{N_{q}}\sum\limits_{q = 1}^{N_{q}}\left( \max\limits_{\mathbf{x}^{\prime} \in \chi_{\text{feas}}} \mu_{\mathbf{x},i}^{\text{fused},q}(\mathbf{x}^{\prime})\right.\\ \qquad \quad \left. + \max\limits_{\mathbf{x}^{\prime\prime} \in \chi_{\text{feas}}}EI^{q}_{\mathbf{x},i}(\mathbf{x}^{\prime\prime})\right), \end{array} $$

(17)

where $\mu _{\mathbf {x},i}^{\text {fused},q}(\mathbf {x}^{\prime })$ denotes the mean of the fused Gaussian process upon temporarily augmenting $(\mathbf {x},{f_{i}^{q}}(\mathbf {x}))$, one at a time, to the available samples of information source i, and $EI^{q}_{\mathbf {x},i}(\mathbf {x}^{\prime \prime })$ is the one-step look-ahead expected increase in the maximum of the fused Gaussian process upon augmentation of query $(\mathbf {x},{f_{i}^{q}}(\mathbf {x}))$ to information source i. Note that for each generated sample, q = 1,…,N_q, the previously added sample is removed and the next new sample is augmented, then the Gaussian process of information source i and as a result, the fused Gaussian process of the objective function are updated temporarily. We compute the second term in (17) by the Knowledge Gradient (KG) approach over the temporary fused Gaussian process in a closed form solution (Frazier et al. 2008; Powell and Ryzhov 2012; Frazier et al. 2009). Letting $S^{N + 1}_{\mathbf {x}^{\prime \prime }} = \mathbb {E}[\hat {f}^{\text {fused}}(\mathbf {x}^{\prime \prime })\mid \mathbf {x}_{1:N}, y_{1:N}, i_{1:N}, \mathbf {x}_{N + 1}=\mathbf {x}, y_{N + 1}={f_{i}^{q}}(\mathbf {x}),$i_N+ 1 = i] be the knowledge state, the value of being at state S^N+ 1 is defined as $V^{N}(S^{N + 1})=\max \limits _{\mathbf {x}^{\prime \prime } \in \chi } S^{N + 1}_{\mathbf {x}^{\prime \prime }}$. The knowledge gradient which is a measure of expected increase in the maximum of the objective function, if the design point x^″ would be queried at the next time step, can be defined as

$$\nu_{\mathbf{x}^{\prime\prime}}^{KG,N + 1}=\mathbb{E}[V^{N + 2}\left( S^{N + 2}(\mathbf{x}^{\prime\prime})\right)-V^{N + 1}(S^{N + 1}) \mid S^{N + 1}], $$

where the expectation is taken over the stochasticity in the posterior distribution of the fused model representing the objective function at design point x^″.

The utility is evaluated for all feasible, as feasibility will be discussed in the following subsections, alternatives and all information sources. By denoting C_{x, i} as the cost of querying information source i of the objective function at design point x, we find the query (i_N+ 1,x_N+ 1) that maximizes the utility per unit cost, given by

$$ (i_{N + 1},\mathbf{x}_{N + 1}) =\underset{i \in [1, \dots, S], \mathbf{x} \in \mathbf{X}_{feas}}{\text{argmax}} \frac{U_{\mathbf{x},i}}{C_{\mathbf{x},i}}. $$

(18)

Figure 2 shows a depiction of computation of our proposed two-step look-ahead utility function for choosing the next query for an objective function with two information sources. The left column shows the Gaussian processes of the two information sources and the fused Gaussian process constructed from these information sources. The right column shows the temporary Gaussian processes of information source 1 and the fused model after augmenting the query (x, q) to information source 1 (i = 1). The terms of the two-step look-ahead utility function are shown on the temporary fused Gaussian process.

Fig. 2

A depiction of computing our proposed two-step look-ahead utility function for choosing the next design and information source of objective function to query

3.3 Information gain policy for constraints query

We propose to use the information gain for selection of the next design point and information source of the constraints to query. In order to measure the information gain, we use the Kullback-Leibler (KL) divergence (Kullback and Leibler 1951; Ghoreishi and Allaire 2016, 2017; Ghoreishi 2016) which is a criterion for evaluating the difference between two probability distributions P and Q with densities p(x) and q(x), defined as

$$ D_{K\!L}(P \parallel Q) = {\int}^{+\infty}_{-\infty} p(x) \log \frac{p(x)}{q(x)} dx. $$

(19)

Latin hypercube sampling is again used for generating alternatives denoted as X_g in the design space. For a given point x at information source i of constraint g_j, the constraint values are normally distributed based on the mean and variance of the corresponding Gaussian process. By drawing N_r independent samples from this normal distribution denoted by $g_{i,j}^{r}(\mathbf {x}), r = 1, \dots , N_{r}$, and temporarily augmenting each sample, one at a time, to the available samples of the corresponding information source, the Gaussian process of information source i and consequently, the fused Gaussian process of constraint g_j are temporarily updated. We denote the temporary fused Gaussian process of constraint g_j after augmenting sample $(\mathbf {x},g_{i,j}^{r}(\mathbf {x}))$ to information source i by $\hat {g}_{\mathbf {x},i,{j}}^{\text {fused},r}$, and the current actual fused Gaussian process before augmenting any sample by $\hat {g}_{j}^{\text {fused}}$. We repeat this process for all N_r generated samples. Then, we compute the Information Gain (IG) for the potential query of design point x at information source i of constraint g_j which is the average Kullback-Leibler divergence between the current and the temporary Gaussian processes over the design space as

$$ {IG}_{\mathbf{x},i}^{j} = \frac{1}{N_{r}} \sum\limits_{r = 1}^{N_{r}} \sum\limits_{s = 1}^{N_{s}} D_{K\!L}\left( \hat{g}_{\mathbf{x},i,{j}}^{\text{fused},r}(\mathbf{x}^{\prime}_{s}) \parallel \hat{g}_{j}^{\text{fused}}(\mathbf{x}^{\prime}_{s})\right) , $$

(20)

where the Kullback-Leibler divergence over the design space of two Gaussian processes is approximated by Monte Carlo technique at N_s samples $\mathbf {x}^{\prime }_{s} \in \chi$. The information gain is then evaluated for all the alternatives and all the information sources of constraint g_j. By denoting $C_{\mathbf {x},i}^{j}$ as the cost of querying information source i of constraint g_j at design x, we find the query $(i_{N + 1}^{j},\mathbf {x}_{N + 1}^{j})$ that maximizes the information gain per unit cost, given by

$$ (i_{N + 1}^{j},\mathbf{x}_{N + 1}^{j}) =\underset{i \in [1, \dots, G_{j}], \mathbf{x} \in \mathbf{X}_{g}}{\text{argmax}}~\frac{{IG}_{\mathbf{x},i}^{j}}{C_{\mathbf{x},i}^{j}}. $$

(21)

3.4 Feasibility of a design point

The specifics of our constraint handling methodology are as follows. The value of fused constraint g_j at a design point x is estimated to be distributed normally with mean $\mu ^{\text {fused}}_{j}(\mathbf {x})$ and standard deviation $\sigma ^{\text {fused}}_{j}(\mathbf {x})$, according to the fused Gaussian process representation of that constraint. In the first iterations of the approach, since the constraints are not learned, we aim to avoid over-restricting the search space and to involve the infeasible samples in the search process to explore the information they might carry. We achieve this by considering the fused standard deviation of constraints at each design point in addition to the fused mean value of the constraints at that point. Therefore, the design point x must satisfy

$$ \mu^{\text{fused}}_{j}(\mathbf{x})-3\sigma^{\text{fused}}_{j}(\mathbf{x}) \leq 0, \quad j = 1,\dots, m. $$

(22)

In this strategy, variances are large in the first iterations, which helps the methodology to explore the design space, and as the process goes on, the fused Gaussian processes of the constraints are updated, which results in decreases in the value of their respective variances. This reduces the possibility of an infeasible sample to be selected. Here, a practitioner can control the level of acceptability in terms of constraint violation by modifying the coefficient of $\sigma ^{\text {fused}}_{j}(\mathbf {x})$ in (22) as deemed appropriate. It should be noted that in the final step for returning the optimal solution, only the fused means of the constraints are considered for determining the feasibility of the design points, as will be discussed in the next subsection. Figure 3 shows this strategy that the feasible region shrinks and gets closer to the true feasible region after one query.

Fig. 3

A depiction of our constraint handling strategy that the feasible region shrinks and gets closer to the true feasible region after one query

3.5 Multi-information source constrained Bayesian optimization approach

Our complete proposed multi-information source constrained Bayesian optimization approach is presented in Fig. 4. In our proposed approach, the first step is constructing a Gaussian process for each information source of the objective function and all the constraints based on their available data. These information sources are combined together and the fused Gaussian processes of the objective function and constraints are constructed as discussed in Section 3.1. The next design points and information sources to query are selected based on our proposed two-step look-ahead utility function for the objective function and the information gain measurement for the constraints. After querying the selected design points from the selected information sources, the corresponding Gaussian processes are updated. Therefore, the mean, variance, and correlation coefficient values are also updated, resulting in new fused Gaussian processes of the objective function and constraints based on the Gaussian processes of the information sources learned so far in the process and their learned correlations. This process repeats until a termination criterion, such as exhaustion of the querying budget, is met.

Fig. 4

A depiction of our proposed multi-information source constrained Bayesian optimization approach

Finally, the feasible design point with maximum fused mean of the objective function is selected as the optimum solution of (1), as

$$\begin{array}{@{}rcl@{}} {\mathbf{x}}^{*} &=& \underset{\mathbf{x} \in \chi_{\text{feas}}}{\text{argmax}} \mu^{\text{fused}}(\mathbf{x}),\\ \chi_{\text{feas}} &:=& \{\mathbf{x}\mid \mu^{\text{fused}}_{j}(\mathbf{x}) \leq 0, \quad j = 1, \dots, m\}. \end{array} $$

(23)

In order to find the best approximation to the optimum solution, we discretize the design space. This discretization must be sufficiently fine to ensure a good approximation of the continuous design space solution. Then, the values of the predicted mean of the objective function and the constraints are computed at each point according to (8). Among all the feasible points, the point that has the maximum function value is selected as the optimum solution. We note here, that alternatively, we could also optimize the fused objective function subject to the fused constraint functions using standard gradient-based techniques on the mean functions of the processes.

4 Application and results

In this section, we present the key features of our multi-information source constrained Bayesian optimization approach on two demonstrations. The first case is an analytical problem with one-dimensional input and output, and the second demonstration is the minimization of the drag coefficient of a NACA 0012 airfoil subject to a constraint on the lift coefficient.

4.1 One-dimensional problem

The first example is maximization of a one-dimensional constrained function shown in Fig. 5 and defined as

$$\begin{array}{@{}rcl@{}} x^{*} &=& \underset{\mathbf{x} \in [0 1.2]}{\text{argmax}} -(1.4-3x) \sin(18x)\\ &&\text{s.t.} \quad x^{2}-1.2 \leq 0. \end{array} $$

(24)

Fig. 5

One-dimensional optimization problem of (24)

The feasible optimal solution for this problem is (x^∗,f(x^∗)) = (1.0954,1.4388). We consider two information sources of f₁(x) and f₂(x) for the objective function, with constant discrepancies of $\sigma ^{2}_{f,1} = 0.04$ and $\sigma ^{2}_{f,2} = 0.2$, and evaluation costs of C₁ = 25 and C₂ = 20, given as

$$\begin{array}{@{}rcl@{}} &f_{1}(x) = -(1.6-3x) \sin(18x),\\ &f_{2}(x) = -(1.8-3x) \sin(18x + 0.1). \end{array} $$

(25)

We note that in our methodology, two Gaussian processes are constructed for these two information sources based on their available data and $\sigma ^{2}_{f,1}$ and $\sigma ^{2}_{f,2}$ are added to the uncertainty associated with the Gaussian processes to obtain the total uncertainties.

Two information sources, denoted as g_1,1(x) and g_2,1(x), are considered for the constraint. These sources have constant discrepancies of $\sigma ^{2}_{g_{1},1} = {5 \times 10^{-6}}$ and $\sigma ^{2}_{g_{1},2} = 0.002$, and evaluation costs of ${C_{1}^{1}} = 10$ and ${C_{2}^{1}} = 5$, given as

$$\begin{array}{@{}rcl@{}} &g_{1,1}(x) = (x - 0.001)^{2} - 1.2,\\ &g_{2,1}(x) = (x + 0.02)^{2} - 1.2. \end{array} $$

(26)

We note that the constant discrepancies used in this example are not restrictions of the work. In the next application problem, the discrepancies are permitted to vary over the design space.

Figure 6 shows the Gaussian processes of the two objective information sources, the fused objective function, and the fused constraint function. We note that owing to the constant discrepancies, we can refer specifically to the information sources as low fidelity and high fidelity, where high fidelity refers to the source with lower discrepancy. The fused models shown in the figure represent what has been learned after applying our methodology with a computational budget limited to 450 and 20 Latin hypercube samples as alternatives. The red solid lines show the true function f(x) and the true constraint g(x), and the black solid lines show the learned mean functions of the Gaussian processes. It is shown that after querying six samples from the high-fidelity model and nine samples from the low-fidelity model of objective function, the fused model provides a reasonable estimate of the true objective function and the feasible optimal solution.

Fig. 6

The learned low-fidelity, high-fidelity, and fused objective functions and fused constraint after applying our approach on optimization problem of (24-26)

In order to asses the performance of our approach, we compare our methodology with a standard multi-information source optimization method presented in ref. Lam et al. (2015). We refer to this method as the MF algorithm. This algorithm is the state of art in constrained Bayesian optimization and has been used as a benchmark for many Bayesian optimization techniques (Wang 2017; Poloczek et al. 2017; Peherstorfer et al. 2016; Chaudhuri et al. 2018; Kandasamy et al. 2017). In ref. Lam et al. (2015), each information source has a separate Gaussian process, and predictions are obtained by fusing the information via the method presented in ref. Winkler (1981b) without considering the correlation between the information sources. In this algorithm, the acquisition function selects the point to sample and the information source to query separately. The next design to evaluate is selected by applying the expected improvement function on the multifidelity surrogate, and the next information source of objective function to query is chosen based on a heuristic that aims to balance information gain and cost of query. It should be noted that there is no decision-making with regards to the information sources used for constraints in the MF algorithm. In the MF algorithm, it is assumed that the constraint information source is identical to the objective function information source and the query is based on that of the objective.

Table 1 represents the expectation and variance of the design points obtained by our proposed approach and the MF algorithm, as well as the expectation and variance of the objective function at these points over 100 independent replications of the simulations for two different cost values for information sources and budget of 1000 as the stopping criterion. As can be seen, in the case of C₁ = 20,C₂ = 20 in which the cost of the first information source is lower, better results are obtained in the fixed budget as more samples can be queried from the information sources in comparison to C₁ = 25,C₂ = 20. Figure 7 shows the average maximum function values obtained by our approach and MF algorithm for different budgets.

Table 1 Expectation and variance of the results obtained by our proposed approach and the MF Algorithm (Lam et al. 2015) over 100 replications of the simulations of optimization problem in (24–26) for two different cost values for information sources and budget of 1000 as the stopping criterion. The feasible optimal solution is (x^∗,f(x^∗)) = (1.0954,1.4388)

Fig. 7

The average maximum function value obtained by our proposed approach and the MF Algorithm (Lam et al. 2015) over 100 independent replications of the simulations of the optimization problem in (24–26) for different budgets as the stopping criterion

As can be seen, our approach improves on the work of ref. Lam et al. (2015), as the expectations of the obtained results are closer to the true optimal values and the variances of the estimations are lower. This is due to the fact that our methodology allows for the rigorous exploitation of correlations between information sources and across the design space. This results in reduced uncertainty by querying one new design sample, even if it is queried from an information source with lower fidelity. Thus, we obtain more accurate estimates of the true objective function and also constraint from each sample. Furthermore, allowing for separate decision-making with regards to the constraints adds flexibility to our approach that can also be exploited for efficiency gains. With regards to the exploitation of correlation, we note here that the value of the low-fidelity information source at the true optimum is 1.2240 and the value of the high-fidelity information source is 1.2862 at the same location. The true objective function value at that point is 1.4388. As can be seen from the table, the estimated objective function value is greater than either information source using our fusion-based approach built with model reification. This is not the case for the MF algorithm, which has no means for overcoming bias. Finally, it should be mentioned that the higher performance of the proposed method comes with higher computational cost. Indeed, our proposed method constructs |X_feas|× N_q × S more Gaussian processes for each query in comparison to the MF algorithm, while these computations are negligible in comparison to the actual experiments’ costs. Notice that the computation involved for each query due to the need for multiple Gaussian processes by the proposed method can be done in parallel.

4.2 NACA 0012 drag coefficient with lift coefficient constraints

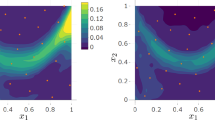
The second demonstration of our multi-information source constrained Bayesian optimization approach is a two- dimensional constrained aerodynamic design example. The airfoil of interest is the NACA 0012, a common validation airfoil (JJ Thibert et al. 1979; Rumsey 2014). In this demonstration, we consider two information sources for the objective and constraint. The sources are the computational fluid dynamics programs XFOIL (Drela 1989) and SU2 (Palacios et al. 2013). Figure 8 shows an example output of the two simulators that illustrates the difference in fidelity levels. XFOIL is a solver for the design and analysis of airfoils in the subsonic regime. It combines a panel method with the Karman-Tsien compressibility correction for the potential flow with a two-equation boundary layer model. This causes XFOIL to overestimate lift and underestimate drag (Barrett and Ning 2016). SU2 uses a finite volume scheme and Reynolds-averaged Navier-Stokes (RANS) method with the Spalart-Allmaras turbulence model, which allows SU2 to be significantly more accurate than XFOIL in the more turbulent flow regimes at higher values of Mach number and angle of attack.

Fig. 8

Example outputs of NACA 0012 airfoil from XFOIL and SU2

In this problem, we are particularly concerned with finding the Mach number M and angle of attack α that minimize the coefficient of drag C_D of a NACA 0012 airfoil subject to maintaining a minimum coefficient of lift C_L

$$\begin{array}{@{}rcl@{}} {\mathbf{x}}^{*} &=& \underset{\mathbf{x} \in \chi}{\text{argmax}} - C_{D} (\mathbf{x}) \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} &&\text{s.t.} \quad 0.4 - C_{L} (\mathbf{x}) \leq 0, \end{array} $$

(28)

where x^∗ = (M^∗,α^∗). The design space is χ = I_M × I_α with I_M = [0.15 0.75] and I_α = [− 2.2 13.3]. To validate our approach, wind tunnel data from NASA and AGARD are used to construct true models using spline interpolation to determine values between the given data points. The true models of the objective and the constraint constructed from the wind tunnel data, as well as a contour plot of objective and constraint are shown in Fig. 9.

Fig. 9

Optimization problem of (28)

These data are also used to estimate the model discrepancy at all points in the design space by taking the difference between the true model and the simulator, XFOIL or SU2. The differences at all available samples are used as training data for a Gaussian process regression. We set the evaluation costs of the objective information sources to be C₁ = 100 and C₂ = 70, and for information sources of the constraint, we set the evaluation costs to be $C_{g_{11}} = 50$ and $C_{g_{21}} = 20$. The number of Latin hypercube samples as alternatives is set to 100.

Figures 10 and 11 show the Gaussian processes and contour plots of XFOIL and SU2 coefficient of drag obtained by our proposed approach and the MF Algorithm respectively. As can be seen, in our proposed approach by querying 61 samples from SU2 and 56 samples from XFOIL, the regions around the optimal solution of both information sources are well explored, and the optimal solutions of the learned surrogates of the information sources are close to the optimal design points of the real information sources. However, in the MF algorithm, 8 and 131 samples are queried from the SU2 and XFOIL information sources respectively and the Gaussian process of SU2 is not properly explored, therefore the optimal solution is far from the true value.solution is far from the true value.

Fig. 10

Gaussian processes and contour plots of XFOIL and SU2 coefficient of drag obtained by our proposed approach

Fig. 11

Gaussian processes and contour plots of XFOIL and SU2 coefficient of drag obtained by MF Algorithm

Table 2 represents averaged results and their variances obtained by our approach and the MF algorithm for a computational budget limited to 100,000. The expected results are averaged over 1000 replications of the simulations. The true models used to validate the method and estimate the model discrepancies are the full set of real-world NACA 0012 wind tunnel data, which include 68 data points for objective (C_D) and 64 data points for constraint (C_L) throughout the design space. The feasible optimal design point and the corresponding coefficient of drag for the true model are x^∗ = (0.6574,3.0132) and C_D^∗ = 0.0064 respectively. It is clear that our proposed methodology outperforms the MF Algorithm by obtaining the lower expected objective value, which is closer to the optimal solution obtained from the true model. Furthermore, our approach obtained expected design points closer to the true feasible design points with lower variances. We emphasize here that our approach is developed to best approximate the true optimum design and objective and not to identify the optimal point on the highest fidelity model. In this case, as in the previous demonstration, the fusion of our information sources, with the incorporation of model reification, enabled a more accurate estimate of the true optimal point, which could not have been achieved with either model in isolation, or with traditional fusion techniques.

Table 2 Expectation and variance of the results obtained by our proposed approach and MF Algorithm (Lam et al. 2015) over 1000 replications of the simulations of optimization problem in (28). True optimal values are x^∗ = (0.6574,3.0132) and C_D^∗ = 0.0064

5 Conclusion

This paper has presented an approach to perform constrained optimization of expensive to evaluate functions when different information sources with varying fidelities and evaluation costs are available for the objective function and constraints. This is achieved by estimating the correlation between the information sources and fusing the information obtained from each information source to construct the fused Gaussian processes. Then, the cost of querying and a two-step look-ahead utility function obtained from the fusion process and the knowledge gradient policy, are incorporated to identify the next design and objective information source to query. The approach also considers the trade off between cost and information gain as quantified by the Kullback-Leibler divergence for identifying design points and information sources for constraint handling. The proposed strategy samples the design space by balancing exploration and exploitation tasks both between and within the available information sources to efficiently move sequentially toward the true, real-world optimum of a constrained objective function. We demonstrated our approach on the constrained optimization of a one-dimensional example test problem and an aerodynamic design problem. With these demonstrations, it has been shown that the proposed approach estimates well feasible optimal values of the objective in an efficient decision-theoretic manner.