Robust design optimization of laminated plates under uncertain bounded buckling loads

Abstract

In this paper, a new systematic approach is suggested for better exploration of given uncertain buckling loads in the problem of optimal designs of hybrid symmetric laminated composites. Laminated composites are made up of 16-layered carbon-epoxy, glass-epoxy, and hybrid carbon-glass plies with discrete ply angles as design variables. In the analysis, the ply angles and the type of constituents in the laminates are varied, and one source of uncertainty, namely, uncertainty in buckling load is incorporated. In order to form nested optimization, a new improved rank-based version of Quantum-inspired Evolutionary Algorithm (QEA) is proposed and different versions of QEA and Genetic Algorithm (GA) are utilized. Using anti-optimization approach, the worst case biaxial compressive loading is obtained by Golden Section Search (GSS) method and the buckling load capacity is maximized. Numerical results of the optimal configurations are obtained under several bi-axial loading cases, panel aspect ratios, and materials. The results are investigated from different perspectives and sensitivity analyses are performed.

1 Introduction

In recent decades, laminated composites received considerable attention from many scientists as potentially promising alternatives to traditional structures, owing to their remarkable characteristics such as high stiffness, specific strength, and light weight. The design of laminated composites deals with different parameters, like dimension, fiber orientation, number of plies, stacking sequence, and the type of constituents in hybrid laminates; and optimal selection of these parameters to achieve the desired mechanical performance.

In the past few decades, significant research has been conducted to examine the design problem of composite structures. Fukunaga et al. (1995) presented an approach for optimal configurations of symmetrically laminated plates to maximize buckling loads. In this paper, the Automated Design Synthesis (ADS) method had been used as the optimizer and four lamination parameters were considered as the design variables. Based on the flexural lamination parameter technique, Liu et al. (2004) investigated a continuous variable optimization approach for maximization of the buckling loads of unstiffened composite panels. The results obtained from a combinatorial design of the stacking sequence via a Genetic Algorithm had been compared in relation with the solutions of the flexural lamination parameter method. In another study, Liu et al. (2015) have addressed a lamination parameter-based approach seeking the weight and mechanical performance optimization of blended composite panels. Comprehensive reviews on the classification and comparison of optimization methods for the problem of lay-up selection of the laminated composite structures have been presented in Ghiasi et al. (2010, 2009). Among the various classifications described in these reviews, four of them are outlined as follows: (1) an approach proposed by Venkataraman and Haftka (1999), in which the procedure was categorized into two single laminate and stiffened plate design; (2) Abrate (1994), in which the problems were classified according to their objective functions; (3) Fang and Springer (1993), that used four categories for the designing approach, i.e., analytical approaches, enumeration procedures, heuristic methods, and nonlinear programming; and (4) Setoodeh et al. (2006) that considered two approaches for the design of composite structures, namely constant stiffness with the aim of obtaining optimum stacking sequence for material distribution and variable stiffness over the domain of the structure.

The term “hybrid” encompasses all laminated composites with more than one type of constituent as the matrix and reinforcement phases. Development of hybrid laminated composites led to improvements in terms of principal features, for example, improvements in performance, flexibility, weight, and cost (Reis et al. 2007). Several studies can be found on the optimal design of hybrid laminated composites in the literature. Huang and Haftka (2005) optimized the fiber orientations near a hole in a single layer of a multilayered composite laminate for increased strength using gradient-based and genetic algorithms. Lee et al. (2013) incorporated variable critical load cases (bending, shear and torsion) within the design optimization problem of hybrid (fiber–metal) composite structures (HCS). Kalantari et al. (2017) investigated the design problem of carbon-glass/epoxy hybrid composite laminates in the presence of three different uncertainty sources, including uncertainties in lamina thickness, fiber orientation, and matrix voids. In their work, the conflicting objectives were considered as material cost and density, where minimum flexural strength was chosen as a constraint. Adali et al. (2003) compared the optimal stacking configuration of constant thickness symmetric hybrid laminates for both robust and deterministic buckling load cases. They observed that the stacking sequence designed for a deterministic load case differs considerably from that of a robust laminate designed by taking the load uncertainties into account. Recently, Akmar et al. (2017)discussed the probabilistic optimization of hybrid laminated composites from two different points of view. Firstly, in the fine scale, weave pattern was considered as the design variable of single-ply Representative Volume Element (RVE), in the presence of four uncertain microscopic parameters, namely, yarn spacing, yarn width, yarn height, and misalignment in yarn angle. In the second problem, Ant Colony Optimization (ACO) was utilized in the problem of stacking sequence design of hybrid laminated composites. Al₂O₃/Al was considered as the inner laminate plies while (SiC/Al) was used for the outer plies.

The present study is a continuation of the previous work (Kaveh et al. 2018), in which the Biogeography-Based Optimization (BBO) algorithm has been utilized to determine the optimal stacking sequence of hybrid laminates under deterministic conditions. The objective of the present paper is finding the optimum designs of hybrid symmetrically laminated composites to maximize the biaxial buckling load when they are subjected to a domain of bounded uncertain loading. As suggested in Elishakoff et al. (1994), a two-level design approach using anti-optimization is conducted to deal with the uncertain loads. Thus the critical buckling load factor λ_cb is maximized under the worst condition of loading.

In the past, the stacking sequence optimization problem was solved by classical gradient-based methods. The deficiencies of the methods in dealing with non-convex spaces and discrete variables led to their limited success (Soremekun et al. 2001). During the recent decades, different metaheuristic algorithms have been established as the most promising and effective tools for dealing with optimal design problems (Çarbaş and Saka 2012; Saka and Erdal 2009; Tejani et al. 2016; Kaveh 2017a,b). These iterative algorithms are commonly inspired by natural phenomena including biology, ethology, or even physical processes (Hussain et al. 2018). Evolutionary algorithms (EAs) are the most well-known metaheuristics that mimic the evolutionary process in nature to improve the initial solutions over consecutive generations. For example, the Genetic Algorithm (GA) (Goldberg and Holland 1988) that is inspired by the “natural selection theory” of Darwin, utilizes the selection and mutation as the search operators, or Quantum-inspired Evolutionary Algorithm (QEA) (Han and Kim 2002) which follows concepts from quantum computing such as Q-bits, superposition, quantum gates, and quantum measurement. Their outstanding features including simplicity of implementation, being gradient-free, compatibility with discrete variables, and finding near global optimal solutions have made them popular tools for optimization. It should be noted that one of the challenges in the implementation of evolutionary algorithms is the difficulty in determination of algorithm-specific parameters, such as crossover and mutation rates of GA. Finding the ideal parameters is a time-consuming task, and the inappropriate parameter setting may damage the performance of the algorithms. For instance, de Almeida (2016) demonstrated that the harmony memory size (HMS), harmony memory consideration rate (HMCR), and pitch adjusting rate (PAR) have an apparent effect on the reliability of the Harmony Search Algorithm (HSA) for optimizing the laminated composites. From this point of view, the parameter-less algorithms like QEA are at an advantage, which needs only the general parameters. Moreover, QEA is a binary-coded algorithm which makes it suitable for studying the stacking sequence problem with discrete variables. So here, an improved version of Quantum-Inspired Evolutionary Algorithm (QEA) is proposed and along with two other versions, are applied for solving the optimal design problem of hybrid laminated composites, for the first time in literature. Furthermore, two versions of a Genetic Algorithm (GA) are implemented for comparison. The Golden-Section Search (GSS) method is employed as the anti-optimizer for comparison of the results with those of Adali et al. (2003).

The rest of the paper is elucidated through the following sections. In Section 2, a description of the optimization and anti-optimization procedures are presented. In Section 3, the theoretical framework of the problem is provided. Section 4 defines the objective function of the problem, the numerical results, and investigations. Finally, Section 5 contains some concluding remarks.

2 Optimization and anti-optimization methods

Since the laminated composites experience varying loads, they must be designed in such a way to withstand and meet the design requirements. Here, the aim of the optimal robust design is maximizing the capacity of laminated composites when they are encountered with the worst case of aforementioned uncertain condition (Adali et al. 2003). Therefore, here the stacking sequence is optimized by a metaheuristic algorithm and the worst loading condition is found by an anti-optimizer. In the following, the utilized algorithms are reviewed.

2.1 Quantum-inspired evolutionary algorithm (QEA)

Quantum-inspired evolutionary algorithm (QEA) is a well-known quantum computing-inspired optimization algorithm, proposed by Han and Kim (2002). The basic information and concepts about quantum computing, steps of QEA, and its different versions are given in following.

2.1.1 The basics of quantum computing

The common classical computers require the data to be encoded into bits, where they always represent one of two definite states “0” or “1”. While quantum computers use Q-bits as unit of quantum information, which can be in the “0” state, “1”state, or in superposition of these states (Hey 1999). Thus, the state of a Q-bit is represented as follows:

$$ \mid \left.\varPsi \right\rangle =\alpha \mid \left.0\right\rangle +\beta \mid \left.1\right\rangle $$

(1)

where α and β are complex numbers, and ∣.⟩ stands for state of the system. The values of |α|² and |β|² represent the probability of “0” and “1” states, respectively. It is clear that according to the probability axioms, the following equation holds:

$$ {\alpha}^2+{\beta}^2=1 $$

(2)

In QEA, the information unit is Q-bit which is shown in the following equation:

$$ q=\left[\begin{array}{c}\alpha \\ {}\beta \end{array}\right] $$

(3)

In order to transfer more quantum information, the Q-bits join together and create an individual. A string of m Q-bit contains the information of 2^m states, which shows the efficiency of this representation. A two-Q-bit individual is defined as:

$$ q=\left[\begin{array}{c}{\alpha}_1\\ {}{\beta}_1\end{array}\kern0.5em \begin{array}{c}{\alpha}_2\\ {}{\beta}_2\end{array}\right] $$

(4)

This individual represents the state of the system as:

$$ \mid \left.\varPsi \right\rangle ={\left|{\alpha}_1\right|}^2.{\left|{\alpha}_2\right|}^2\left.|00\right\rangle +{\left|{\alpha}_1\right|}^2.{\left|{\beta}_2\right|}^2\left.|01\right\rangle +{\left|{\beta}_1\right|}^2.{\left|{\alpha}_2\right|}^2\left.|10\right\rangle +{\left|{\beta}_1\right|}^2.{\left|{\beta}_2\right|}^2\left.|11\right\rangle $$

(5)

(5) means that, for instance, the probability of | 10⟩ state is |β₁|². |α₂|².

2.1.2 Steps of the QEA

QEA as an evolutionary algorithm having population of individuals. The population of n individuals at generation t is defined as:

$$ Q(t)=\left\{{q_1}^t,{q_2}^t,\dots, {q_n}^t\right\} $$

(6)

where ${q}_i^t$is the ith individual in the tth generation. The steps of QEA are provided in the subsequent sections.

Initialization

At the first step, with the assumption that the probabilities of all the solutions are equal, Q(t) is initialized. Hence, both α² and β² are equal to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ resulting in $\raisebox{1ex}{$\sqrt{2}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ for α and β.

Observation

Since QEA is working on a classical computer, so the quantum states do not collapse into a single state. The binary solutions (P(t)) are made by observing the states of Q(t) and using a probabilistic approach. For this purpose, a uniform random parameter within (0, 1) is generated for each Q-bit. If the random number is less than α², the corresponding binary bit is 0, otherwise it is 1.

Evaluation

Considering the binary solutions which are created for each individual, they are evaluated using the objective function. The obtained values are associated to the corresponding solutions.

Saving

The solutions, which have higher quality, can help the algorithm by searching their neighborhood and increase the convergence rate of the algorithm (Kaveh and Dadras 2017). In this regard, the best solutions among B(t − 1) and P(t) are selected and stored into B(t).

Migration

Two main models of migration are suggested, local migration and global migration. In local migration, the ${b}_j^t$, which is the better one of two neighboring solutions is copied in B(t), while in global migration b is copied to all solutions in B(t).

Updating

In iterative optimization algorithms, the new solutions are usually generated according to the previous ones. In QEA, the Q-gate is defined as the updating operator. The Q-bits can be represented as the components of a point on unit circle as illustrated in Fig. 1. A suitable tool for updating the points on the circle to new position is rotation around the center by a definite degree, as given in (7). Hence, the rotation gate is utilized as the basic Q-gate:

Fig. 1

Quantum rotation gate (Q-gate).

$$ U\left(\Delta {\theta}_i\right)=\left[\begin{array}{cc}\mathit{\cos}\left(\Delta {\theta}_i\right)& -\mathit{\sin}\left(\Delta {\theta}_i\right)\\ {}\mathit{\sin}\left(\Delta {\theta}_i\right)& \kern0.75em \mathit{\cos}\left(\Delta {\theta}_i\right)\end{array}\right] $$

(7)

where ∆θ is the rotation angle of each Q-bit, which are defined according to Table 1. (In Fig. 1 the θs are replaced by the radian and; if q is not located in the first/third quadrant, negative values will be used for θs).

Table 1 ∆θ_i look-up table for maximization

Termination

Different criteria can be considered as the termination condition. Here, when the number of generations reaches a predefined maximum number, the algorithm breaks and reports the best solution found so far.

To clarify the structure of QEA, it is schematically demonstrated in Fig. 2 and the pseudo code of the QEA follows.

Fig. 2

Overall configuration for the QEA algorithm

The pseudo code of QEA

2.1.3 QEA-H _ϵ gate

This version of QEA follows the procedure mentioned above, excluding the updating step. In QEA-H_ϵ gate, an extended version of Rotation gate is utilized which is called H_ϵ. This gate is defined as follows:

[α^′, β^′]^T = H_ε(α, β, ∆θ), where for $\left[{\alpha}_i^{\prime \prime }\ {\beta}_i^{\prime \prime}\right]=R\left(\alpha, \beta, \Delta \theta \right)$:

$$ \mathrm{if}\ {\left|{\alpha_i}^{\prime \prime}\right|}^2\le \varepsilon\ \mathrm{and}\ {\left|{\beta_i}^{\prime \prime}\right|}^2\ge 1-\varepsilon \to {\left[{\alpha}_i^{\prime }\ {\beta}_i^{\prime}\right]}^T={\left[\sqrt{\epsilon }\ \sqrt{1-\epsilon}\right]}^T $$

$$ \mathrm{if}\ {\left|{\alpha_i}^{\prime \prime}\right|}^2\ge 1-\varepsilon\ \mathrm{and}\ {\left|{\beta_i}^{\prime \prime}\right|}^2\ge \varepsilon \to {\left[{\alpha}_i^{\prime }\ {\beta}_i^{\prime}\right]}^T={\left[\sqrt{1-\epsilon }\ \sqrt{\epsilon}\right]}^T $$

$$ \mathrm{otherwise}\ {\left[{\alpha}_i^{\prime }\ {\beta}_i^{\prime}\right]}^T={\left[{\alpha}_i^{\prime \prime }\ {\beta}_i^{\prime \prime}\right]}^T $$

where 0 < ε ≪ 1, here ε is assumed as 0.0075; R stands for rotation gate which was defind in (7). This gate is depicted in Fig. 3.

Fig. 3

H_ϵ gate for a condition iii and b conditions i and ii

2.1.4 QEA-iRotation gate

In the basic version of QEA, a constant value (0.01π) is utilized as the step size. In this paper, a rank-based dynamic mechanism is proposed. As given in Table 1, the new version utilizes the rank of individuals to update Q-bits. The parameter d is calculated as follows:

$$ {d}_i= dmin+\frac{dmax- dmin}{nPop-1}\left({r}_i-1\right) $$

(8)

where r_i and nPop stand for the rank of ith particle and the number of populations, respectively. dmax and dmin are respectively assumed as 0.05π and 0.001π. According to this equation, around the better populations are exploited slightly, while the updating of inferior individuals is performed by larger steps. This improved QEA is called as “QEA-iRotation gate”.

2.2 The genetic algorithm

GA is one of the most commonly used evolutionary optimization algorithm which is inspired by theory of Darwin from biological evolutions and survival of the fittest. The GA developed by Holland (1992), involves a selection mechanism, such as Roulette wheel selection or Tournament selection (Sivanandam and Deepa 2007) and genetic operators such as crossover and mutation (Kaveh and Ilchi Ghazaan 2015). The main goal of the Genetic Algorithm is to produce a new population (child or offspring), that has been improved with reference to the previous population (parents), through the use of genetic operators and selection mechanisms. The Genetic Algorithm can be categorized into two major binary (or integer) GA and real (or continuous) GA types. In this paper, the discrete stacking sequence problem is studied, therefore the binary version is employed and in the following sections, steps of the Binary Genetic Algorithm (Arora 2017) are outlined.

2.2.1 Initialization

In the first step, primary population (chromosomes) is randomly generated. Each chromosome comprises of a set of genes (variables) and each gene can contain one or more genomes with digits of 0 or 1. The components of population in GA method are illustrated in Fig. 4. In this paper, four states (ply angles) are considered for each design variable, due to binary encoding, thus the variables contain two genomes.

Fig. 4

Components of population in the GA method

2.2.2 Evaluation

The fitness values of the chromosomes are determined using the objective function, which is defined in the next sections.

2.2.3 Selection

Different selection methods have been proposed to determine the parents for the next generation. Here, Roulette wheel selection and Tournament selection techniques are employed. In Roulette wheel, the chromosomes are selected with a probability proportional to their fitness value, while in Tournament selection, a few groups are made randomly, and their best chromosomes are selected. For more details, the reader may refer to Goldberg and Deb (1991) and Sivanandam and Deepa (2008).

2.2.4 Crossover

Each pair selected in the previous step, reproduces two children. Here, three most well-known crossover operators, including one point, two point, and uniform random crossover are utilized to reproduce the children. It should be mentioned that 80% of the GA’s population is generated by crossover.

2.2.5 Mutation

This step mimics the biological mutation and tries to maintain genetic diversity. Up to this stage, a few numbers of individuals are randomly selected and some of their genes are replaced by a random value. Here, 20% of the population is mutated and only one gene of each chromosome is exposed to mutation. These values are determined based on a trial and error process to get the best performance.

2.2.6 Elitism

In order to survive, the best chromosomes are evaluated and nPop number of the best elite chromosomes are considered as the next generation.

2.2.7 Termination

The procedure mentioned in the previous steps continues in succession until the employed stopping criterion is met. Here, the number of objective function evaluations (NFE) are limited to a predefined number.

The flowchart of the GA is illustrated in Fig. 5.

Fig. 5

Flowchart of a general GA algorithm

2.3 Anti-optimization problem

Elishakoff et al. (1994) conducted one of the earliest works on the robust design of structures under bounded uncertainty in loads. Lombardi and Haftka (1998) applied the anti-optimization technique to the problem of structural optimization in the presence of uncertainty in loading conditions. Anti-optimization is about exploring an uncertain domain for the worst case. The GSS algorithm is a simple and real-coded optimization algorithm. As explained in the following, it is very fast and suitable for single-variable problems (Arora 2017), so the worst case values of the continuous uncertain domains can be easily obtained in the searching interval with this algorithm. It is used to find the extremum by reducing the width of the search intervals, consecutively.

2.3.1 Golden section search (GSS)

This scheme is one of the numerical optimization techniques in the class of variable interval-reducing methods (Arora 2017). Unlike equal-interval search method, in the variable interval-reducing methods, the uncertain increment reduces systematically according to the associated technique. In the GSS method, the increment is varied in each step. The increment of the previous step (δ) is multiplied by a constant value known as the Golden Ratio (φ) which is defined in (9).

$$ \varphi =\left(1+\sqrt{5}\right)/2 $$

(9)

Once the new uncertainty interval is less than a certain amount, the termination condition is satisfied. The steps of this method for a minimization one-dimensional (single-variable) problem are provided in the following:

• Step 1: For an interval of [a, b], evaluate the objective function for

$$ c=a+\frac{b-a}{\varphi } $$

(10)

and

$$ d=d-\frac{b-a}{\varphi}\kern0.5em $$

(11)

• Step 2: If f(c) > f(d), move the interval to [c, b], otherwise, move the interval to [a, c].

• Step 3: If the stopping criteria is satisfied, stop, and report the solution, otherwise, come back to step 1 for a new round of minimization.

3 Theoretical framework and problem formulation

3.1 Theoretical framework

Based on the classical laminated plate theory (CLPT), the governing equation of buckling for a symmetric N layer laminate can be expressed as (Reddy 2004):

$$ {D}_{11}\frac{\partial^4w}{\partial {x}^4}+4{D}_{16}\frac{\partial^4w}{\partial {x}^3\partial y}+2\left({D}_{12}+2{D}_{66}\right)\frac{\partial^4w}{\partial {x}^2\partial {y}^2}+4{D}_{26}\frac{\partial^4w}{\partial x\partial {y}^3}+{D}_{22}\frac{\partial^4w}{\partial {y}^4}+\lambda \left({N}_x\frac{\partial^2w}{\partial {x}^2}+{N}_y\frac{\partial^2w}{\partial {y}^2}\right)=0 $$

(12)

In (12), w is the deflection in the z direction, and h is the total thickness of the laminate. In addition, D_ij stands for the bending stiffness coefficients, and can be expressed by (13)

$$ {D}_{ij}={\int}_{-\frac{h}{2}}^{\frac{h}{2}}{\overline{Q}}_{ij}\left({z}^2\right) dz=\sum \limits_{k=1}^N{\int}_{z_k}^{z_{k+1}}{\overline{Q}}_{ij}^{(k)}\left({z}^2\right) dz=\frac{1}{3}\sum \limits_{K=1}^N{\overline{Q}}_{ij}^{(k)}\left({z}_{k+1}^3-{z}_k^3\right) $$

(13)

where ${\overline{Q}}_{ij}^{(k)}$ represents the transformed reduced stiffness of this layer, which is expressed by:

$$ {\overline{Q}}_{ij}^{(k)}={\left[T\right]}^{-1}\left[Q\right]{\left({\left[T\right]}^{-1}\right)}^T. $$

(14)

The coefficients of the reduced stiffness matrix ([Q]) can be stated as the following equation:

$$ \left[Q\right]=\left[\begin{array}{ccc}{Q}_{11}& {Q}_{12}& 0\\ {}{Q}_{12}& {Q}_{22}& 0\\ {}0& 0& {Q}_{66}\end{array}\right];=\frac{E_1}{1-{\upsilon}_{12}{\upsilon}_{21}},{Q}_{12}=\frac{\upsilon_{12}{E}_2}{1-{\upsilon}_{12}{\upsilon}_{21}}=\frac{\upsilon_{21}{E}_1}{1-{\upsilon}_{12}{\upsilon}_{21}},{Q}_{22}=\frac{E_2}{1-{\upsilon}_{12}{\upsilon}_{21}},{Q}_{66}={G}_{12}. $$

(15)

In the above equation, E₁, E₂, and G₁₂are longitudinal Young’s modulus, transverse Young’s modulus, and shear modulus, respectively and υ₁₂ and υ₂₁ are Poisson’s ratios. Further, the transformation matrix [T] can be calculated by:

$$ \left[T\right]=\left[\begin{array}{ccc}{C}^2& {S}^2& 2 CS\\ {}{S}^2& {C}^2& -2 CS\\ {}- CS& CS& {C}^2-{S}^2\end{array}\right];C= Cos\left(\theta \right),S= Sin\left(\theta \right). $$

(16)

For simply supported edges, the boundary conditions are stated as:

$$ w=0,{M}_x=0\kern0.5em \mathrm{at}\;x=0,a $$

(17)

$$ w=0,{M}_y=0\kern0.5em \mathrm{at}\;y=0,b $$

(18)

Considering the governing equation expressed in (12) and the boundary conditions in (17) and (18), the following value of the critical buckling load multiplier λ_cb of biaxial compression case is obtained (Haftka and Gürdal 2012; Reddy 2004):

$$ {\lambda}_b\left(m,n\right)={\pi}^2\left[\frac{m^4{D}_{11}+2\left({D}_{12}+{D}_{66}\right){(rmn)}^2+{(rn)}^4{D}_{22}}{(am)^2{N}_x+{\left(\mathit{\operatorname{ran}}\right)}^2{N}_y}\right] $$

(19)

where length and width of the plate are denoted by a and b, respectively. r = a/b is the aspect ratio, and bending stiffness matrix coefficients are indicated by D_ij. Different mode shapes can be obtained by inserting different values of m and n associated with the transverse displacement patterns. Here, the smallest of λ_b(1, 1), λ_b(1, 2), λ_b(2, 1), and λ_b(2, 2) is taken as the critical buckling load. The results given by Nemeth (1986) indicate that when the following constraints are satisfied, D₁₆ and D₂₆ terms are insignificant

$$ \delta =\frac{D_{16}}{{\left({D_{11}}^3{D}_{22}\right)}^{-\frac{1}{4}}}\le 0.2, $$

(20)

$$ \gamma =\frac{D_{26}}{{\left({D}_{11}{D_{22}}^3\right)}^{-\frac{1}{4}}}\le 0.2 $$

(21)

In computations, the satisfaction of the above constraints is ensured. Therefore the mentioned terms do not arise in (19).

4 Problem definition and numerical results

Studying the performance of laminated composite under buckling loads, as one of the most frequent causes of failure in laminated composites, is fairly crucial. In the presence of unavoidable uncertainty in buckling loads, mitigating the influences of such uncertainty is the only existing choice.

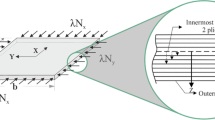
In Fig. 6, the schematic illustration of the geometry of this simply supported composite plate, subjected to an in-plane compressive load, is demonstrated. In order to compare and verify the validity of the results, the problem conditions are in accordance with those of Adali et al. (2003). It is assumed that the plate is symmetric, balanced, and comprised of 16 layers, made of hybrid carbon-glass, carbon-epoxy, and glass-epoxy plies. Due to the symmetry of the plates, the number of design variables is reduced from 16 to 8. Material properties of carbon–glass/epoxy laminates are given in Table 2. The optimization problem can be defined as the maximization of the critical buckling load factor λ_cb as the objective function, which can be formulated as follows (Adali et al. 2003):

Fig. 6

Schematic configuration of a multilayered sandwich panel: a Geometry of the laminated plate and applied loads, b sequence of plies

Table 2 Material properties of carbon–glass/epoxy laminates

$$ \operatorname{Maximize}:{\lambda}_{cb}\left(\theta \right)={\pi}^2\left[\frac{m^4{D}_{11}+2\left({\mathrm{D}}_{12}+{D}_{66}\right){(rmn)}^2+{(rn)}^4{D}_{22}}{(am)^2{N}_x+{\left(\mathit{\operatorname{ran}}\right)}^2{N}_y}\right] $$

(22)

where θ is the vector of design variables, containing the fiber ply angle of laminates. Besides, λ_cb can be found using combinations of m and n that yield the lowest buckling load. In binary implementation for discrete ply angles, stacks with θ = 0^°, + 45^°, − 45^°, and 90^° are converted to binary numbers 00, 01, 10, and 11, respectively. It should be noted that, the achieved optimal sequences are in the standard order of outermost lamina to innermost one (see Fig. 6b).

In many conditions, precise probabilistic data on uncertainty in buckling loads of laminated composites are not available a priori; however, these can be bounded to a defined set. These bounded domains that are denoted by U_p; (p = 1, 2, …, ∞), can be defined by:

$$ {U}_p=\left\{\left({N}_x,{N}_y\right)|{N}_x\ge 0,{N}_y\ge 0,{N}_x^p+{N}_y^p\le 1\ \right\} $$

(23)

Based on the value of exponent p, distinct shapes for uncertain domains are obtained. As illustrated in Fig. 7, p = 1 and p = 2 stand for triangular and circular domains, respectively. For a given p, the minimum value of buckling load factor is determined by solving the following anti-optimization problem:

Fig. 7

Domains of uncertainty: a triangular, b circular

$$ \lambda \left({\theta}_K;{N}^{\ast}\right)=\underset{N\epsilon {U}_p}{\min}\lambda \left({\theta}_K;N\right) $$

(24)

In the level of anti-optimization, N = (N_x, N_y) ∈ U_p are considered as the design variables corresponding to the lowest buckling capacity (worst case).

The results are presented for both triangular domain U₁, and circular domain U₂. As illustrated in Fig. 6, in the case of hybrid carbon–glass/epoxy laminate, glass–epoxy layers are considered as the inner plies of the plate, and carbon–epoxy layers are the outer plies. Moreover, an equal number of plies are assumed for both of them. It is assumed that the plate has the original width of b = 1 m (a = br), and total thickness of H = 0.1 m. It should be noted that, N_x and N_y are in kN/m.

Considering different materials and loading domains, six cases are examined, where each set includes ten experiments for different panel aspect ratios. The introduced optimization algorithms are independently run 30 times for each of the problems, and the number of objective function evaluations (NFE) is limited to 5000 as the stopping criteria (Kaveh et al. 2018). The optimal buckling loads obtained for the examples along with the results of Adali et al. (2003) are presented in Tables 3, 4 and 5. For the sake of brevity, the optimal orientations are provided in Tables 6–11 of the online Appendix. The results are investigated from different aspects in the following sections.

Table 3 Buckling loads obtained for the glass-epoxy plate exposed to uncertain loads

Table 4 Buckling loads obtained for the carbon-epoxy plate exposed to uncertain loads

Table 5 Buckling loads obtained for the carbon-glass/epoxy plate exposed to uncertain loads

4.1 A comparison of the effect of different materials

For comparison, the bar chart of the values of optimal buckling factors is illustrated in Figs. 8 and 9. As it can be seen, in both types of the loading domains (U₁ and U₂), the carbon-epoxy plate has maximum robust buckling load capacity among the examined materials and glass-epoxy plate has the minimum buckling load. The ratios of buckling capacity of plates constructed with different materials are shown in Fig. 10. As it can be seen in Fig. 10, the capacity ratio of carbon/glass to carbon-epoxy is almost constant and equal to 90%, while this ratio for carbon/glass to glass-epoxy varies from 361 to 431%. The effect of aspect ratios is investigated in the next section.

Fig. 8

Optimal values of the buckling factors for the case of U₁ loading domain

Fig. 9

Optimal values of buckling factors for the case of U₂ loading domain

Fig. 10

The ratios of buckling capacity of the plates for both loading domains

4.2 An investigation on the effect of aspect ratio

As provided in Tables 3, 4 and 5 and illustrated in Figs. 8 and 9, by increasing the aspect ratio, the buckling capacity of plates decrease. Moreover, it is observed that the more the aspect ratios increase, the capacity reduction rates decrease. For instance, by increasing the aspect ratio from 0.2 to 0.4, the carbon-epoxy plate has a capacity reduction of 74%, while by changing the aspect ratio from 1.8 to 0.4, this ratio is fallen by only 1%. According to Fig. 10, the capacity ratio of carbon/glass to glass/epoxy, rises in side aspect ratios and it is sensitive to the type of loading domain.

4.3 An investigation on the effect of loading domain

Ratios of the buckling capacity subjected to circular domain (U₂) to those of subjected to triangular domain (U₁), are plotted in Fig. 11. This figure shows a V-shape behavior. In case that $\frac{a}{b}=0.2$, the capacities of all materials for both loading domains are almost equal, while in other cases, the capacities corresponding to U₁ are higher than those of U₂.

Fig. 11

The ratios of the results of U₂ loading domain to U₁

When$\kern0.5em \frac{a}{b}=0.8,1,1.2,\kern0.5em \mathrm{and}\ 1.4$, the ratios for different materials are almost equal. The minimum ratio is 70.7% which corresponds to $\frac{a}{b}=1$ (square plate), and by moving away from this particular aspect ratio, the capacity ratios are increased.

4.4 A comparison among performance of the different optimization algorithms

Examining the primary statistical results showed that there is no meaningful difference between the utilized algorithms, and all the meta-heuristics strongly have found the global optima (see Tables 3, 4 and 5; 6–11). In order to find the algorithms which converged to the solution faster than the rest, their status were studied, when they have passed half of the path (2500 NFE). The average percent of independent runs which converged to the global optima are given in Table 6, and the best results are written in bold font. As indicated in Table 6, the optimum result can be found by all of the algorithms in this NFE, when$\frac{a}{b}=0.8,1,1.2,\mathrm{and}\ 1.4$. This event may imply that the global optima in the mentioned aspect ratios are more accessible than others. This point can be confirmed by the results of Adali et al. (2003), in which, the Golden Section Search method has obtained the same buckling capacity of the present paper, while in other ratios it is trapped to local optima. It can be also seen from Table 6, that the proposed improved QEA algorithm obtained the best performance for lower aspect ratios ($\frac{a}{b}=0.2,0.4,\mathrm{and}\ 0.6$), while in higher aspect ratios ($\frac{a}{b}=1.6,1.8,\mathrm{and}\ 2$) the situation is different. According to Table 6, the improved QEA obtained the best result in 13 cases, which are equal to or higher than those of other compared algorithms. The GA-Roulette wheel also has suitable performance, but it must be noted that a further parameter setting task was performed to tune its internal parameters while QEA do not have any internal parameter and it can be implemented as a black-box optimizer, so this is another strength feature of this method.

Table 6 The average percent of convergence to global optima in half of the optimization procedure for different cases

5 Conclusions

The optimal robust arrangements for the stacking sequence of multilayered composites, under different loading conditions, were derived. For the first time, various versions of the QEA were employed for optimization of composite laminates. Moreover, a rank-based dynamical version of QEA was proposed. In order to verify and demonstrate the performance of the proposed algorithm, Roulette wheel, and Tournament selection, as two highly practical mechanisms were implemented in the well-known Genetic algorithm. The studied panels were made of 16-layered carbon-glass, glass-epoxy, and hybrid laminates with carbon-glass and glass-epoxy plies. Two distinct domains of loading conditions were considered as the sources of uncertainty. An anti-optimization process was embedded to find the worst case loading for robust design. The numerical results were examined from different perspectives, including the effect of the utilized materials, plate aspect ratios, and performance of the algorithms. As it can be seen from Figs. 8 and 9, carbon-epoxy plates, especially at lower aspect ratios, have the highest buckling capacity. It was observed in Fig. 11, that circular loading domain resulted in lower buckling loads, especially when the plate is square. According to Table 6, the optimal solutions of near square plates were more accessible than those of other aspect ratios. As provided in Tables 4 and 5, the utilized metaheuristics obtained higher or equal results in comparison with those of Adali et al. (2003). As discussed in Section 4.4, the proposed QEA generally converged faster than other algorithms. In contrary with the GA, the QEA do not have any internal parameter and it can be implemented as a black-box optimizer. Further investigations and sensitivity analyses were provided in Section 4.