Energy-minimum optimization of the intelligent excavating process for large cable shovel through trajectory planning

Abstract

Large cable shovel (LCS) is a complex engineering machine which is widely used in the open pit mine. It is characterized by low efficiency, high maintenance cost, and high energy consumption if manipulated by an inexperienced operator. To address these challenges, intelligentization could be a feasible solution. In this work, an intelligent excavation system is put forward and the corresponding energy-minimum optimization through trajectory planning of the optimal excavation is developed to realize the intelligentization of the LCS. Firstly, the excavating resistance acting on the dipper is modeled and the corresponding forces are analyzed. Then, by establishing the kinetics and dynamic models of the excavating process, the point to point (PTP) trajectory planning method is developed by setting the objective to minimize the energy consumption per unite volume material. Polynomial curves in different degrees are used in the PTP planning method and the optimal one is compared with the conventional S-curve in terms of the excavating performance. To explore the advantage of the proposed intelligent system and the corresponding trajectory planning based energy-minimum optimization method, four types of ore piles with different pile angles are compared with respect to the excavating performance. Results show that the larger the pile angle is, the later the maximum hoist power and crowd power will appear. Further, the effects on the excavating performance from different ore piles with complex terrains, including the flat type, concave type, convex type, and concave-convex type, are also studied in the numerical experiments. It is found that the trajectory based energy-minimum optimization method for the intelligent LCS can significantly save excavation energy as well as keep sufficient fill factor.

1 Introduction

Large cable shovels (LCSs) are large-scale engineering machine used to excavate the blasted material, such as the stripping coal and the oil sands, and load the material onto the mining dump truck for transportation in an open pit mine. From the viewpoint of design, large cable shovel is generally thought to be of high efficiency, wide operating range, strong environmental adaptability, and low maintenance cost. However, this is usually not the truth during the practical mining, because the large size and complex ore pile condition often lead to either low fill factor (the fill factor is defined as the ratio of the actual loading volume of the dipper to the maximum loadable volume after one excavation cycle) or overload and thus inefficient or even risky excavation, though the LCS is manipulated by a skilled operator. The inappropriate excavation then leads to enormous economic loss, such as the extra electric energy and the rapid wear of the dipper teeth. For this reason, an intelligent excavation system and optimal trajectory optimization are desired to ensure the excavation more efficient and energy saving.

Currently, there is a significant amount of work that has been performed for the intelligent excavation and/or design optimization of the excavating process of cable shovels from the viewpoint of structure optimization or optimal control strategy.

For example, many literatures have focused on the intelligent excavation of the LCS. Dunbabin and Corke (2006) set up a laser mapping system on the cable shovel to obtain the terrain mapping of the material surface and adopt the crowd retract procedure to modify the excavating trajectory to realize the intelligent excavation for cable shovel. The results showed that the system can run reliably. Awuah-Offei and Frimpong (2006) developed the spatial dynamics of the dipper geometry and modeled the loaded material weight using the ordinary differential equations for the intelligent cable shovel, finding that the model can parameterize shovel excavation schemes for optimum production performance. Frimpong et al. (2005) proposed an intelligent shovel excavation technology by bringing in both the linear and angular motions of dipper handle and dipper and obtained better results in the high-efficiency excavation for the cable shovel. Frimpong and Hu (2008) then advanced this intelligent excavation technology by addressing the dynamic requirements of the cable shovel using the Newton-Euler techniques and found that this method can successfully predict optimum path trajectories, dynamic velocities and acceleration profiles.

For the design optimization of the excavating process of cable shovels from the viewpoint of structure optimization or optimal control strategy, Awuah-Offei and Frimpong (2007, 2011) modeled the excavating process of the cable shovel and took the dynamic payload into account to find the optimal dipper handle and hoist rope speeds for given initial conditions. Results show that the optimal operating conditions yield a better efficiency than the non-optimal conventional operation. Wei et al. (2011) proposed a new medium-tool interaction model and built a new three-DOF excavating mechanism for the cable shovel, finding that the cable shovel with three-DOF excavating mechanism is more flexible and efficient. Wei and Gao (2012) also studied the optimal trajectory of the new three-DOF excavating mechanism with two crowd driving systems (two dipper handles) and one hoist driving system, which is different from the two-DOF one with only one crowd driving system but more energy-efficient. Stavropoulou et al. (2013) simulated the excavating process by means of a kinematical shovel model, a dynamic payload model, and a cutting resistance model. Results showed that the specific energy of cutting exhibits a size effect. Rasuli et al. (2014) developed a detailed dynamic model of the cable shovel and experimentally verified the model by showing precise dynamic payload estimation. Denman et al. (2010) achieved the near-minimum time control on the swing drive of an electric mining shovel. Hua et al. (2012) put forward a new constraints expression and handling based method to perform the structural optimization of an excavator boom. Patel and Prajapati (2013) optimized the structure and shape of the backhoe excavator attachment using Finite Element Analysis (FEA) approach by trial and error method. Özgen et al. (2008) performed the shape optimization of excavator booms automatically by using Genetic Algorithm method that is embedded in developed computer software. Results showed that the final weight had been decreased by 5% and maximum stress had been improved by 10%. Sui et al. (2012) established a multi-objective optimization model to find the optimal structural parameters for the working device of the LCS, finding that the LCS’s performance has been greatly improved.

Although so much work has been done to improve the performance of the cable shovel with respect to the control and structure parameters, there are still some inevitable challenges, for example the human errors, which is the main reason leading to the inefficient excavating trajectory. As investigated by Patnayak et al. (2008), 25% variability in hoist power consumption and 50% variability in productivity was noted between different operators. Therefore, the demand of an advanced intelligent excavation system and trajectory optimization technique, which makes the LCS efficiently and economically excavate, is urgent.

The remaining of the paper is organized as follows. Section 2 discusses the structural compositions and the working mechanism of the intelligent LCS. Section 3 develops the excavating resistance model and builds the dynamical model for the excavating process. Section 4 builds the optimal control and trajectory planing model using the point to point method for the whole excavating circle. In Section 5, the optimal control problem is modeled, and the optimization results are obtained and discussed. Section 6 simulates the actual working conditions and conduct the numerical experiments for the trajectory planning method of the intelligent LCS. Section 7 provides the concluding remarks and future work.

2 Intelligent excavation system (IES)

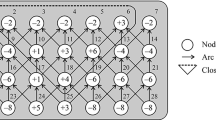
As an extremely large and complex multidisciplinary system, the LCS must coordinate the activities of every sub-system and/or component concertedly while processing the excavating tasks. The conventional LCS without the intelligent excavation system, is usually composed of three major parts, including the upper assembly, the lower assembly, and the attachments, as illustrated in Fig. 1. Among them, the attachments, including the dipper handle, hoist ropes, dipper, boom point sheaves, etc., are the main operating mechanism that directly contacts the material to complete the excavating tasks. The upper assembly contains an electromechanical system, which is composed of two hoist motors and one crowd motor. For the lower assembly, the most important functional component is the crawler. A complete excavating cycle has four activities: propel, swing, hoist and crowd/retract. The hoist mechanism and crowd mechanism synergistically drive the dipper to excavate the material from the bottom up. After loading up, the dipper arrives the dumping height, swings to the top of the mining truck, and then dumps the material down. Then, the LCS swings to the next working point and lays the empty dipper down to the bottom by the cooperative work of the hoist and crowd mechanisms.

Fig. 1

The scheme of the intelligent LCS

As can be seen, the final excavating trajectory is deter-mined directly by the crowd and hoist, namely the speeds of the crowd and hoist motors. However, the large scale machine itself and the complex terrain as well as the unpredictable excavating resistance make the optimal excavating trajectory planning rather difficult, such that the conventional LCS usually does not work under optimal conditions, and 50% variability in productivity was noted between different operators (Patnayak et al. 2008). To reduce human’s uncertainty or undesirable influence and make the best of LCS, an intelligent excavation system (IES) installed on the carbody, is proposed in this work, as illustrated in Figs. 1 and 2. The compositions of the IES include a 3D scanner, a power sensor, a proximity detector, a displacement detector, and a wireless transceiver, etc., which are connected wirelessly with the computing sys-tem through wireless network. From Fig. 2, the numbers from 1 to 11 denote the data flow orders for the arrows between different devices. The data collected from different detectors is first transmitted to the CPU and Storage device for excavating planning, and then goes back to the Control device for the actuator working. The detail processes are presented in the following part.

Fig. 2

IES installed on the body of the LCS

Figure 3 illustrates the intelligent excavating process of the LCS. At the beginning of the excavating process, the IES receives excavating planning, such as the expected payload volume. Then the 3D scanner starts to scan the ore pile to pick up the surface information. Based on the surface information and the pre-defined material properties, the central process unit (CPU) performs the optimization of the excavating trajectory using a set of mechanical and dynamic equations. The output optimization results consist of two aspects, the position when the LCS initially located and the optimal excavating trajectory, respectively. The output optimization results include the position when the LCS should be located and the optimal excavating trajectory, thus the proximity detector and the displacement detector start to identify whether the LCS currently locates in the appropriate position first. If not, the controller and lower assembly execute the repositioning of the LCS. Then the LCS starts the excavation from the right location and feeds back some relevant information collected by the sensors, such as the power sensor, the proximity detector, and the displacement detector, to the CPU for recording. After each operation cycle, the IES identifies whether the whole excavating planning has been completed. If not, then go on excavating, otherwise, stop to prepare for the next excavation planning. In addition to these intelligent functions, the IES possesses the capacity of self-learning, which makes it be able to accumulate the excavating experience through mining the “big data” produced during a long-term operation, and verify and amend the empirical or analytical equations used a priori. In theory, the intelligent excavation with IES can eliminate the empirical errors and rapidly fulfill a task with minimum energy consumption as long as the optimal excavating trajectory is obtained exactly. So the rest of this paper mainly focuses on this issue to find the optimal excavating trajectory, namely the optimal control speeds of the crowd and hoist motors, to achieve the optimal excavation for the intelligent LCS.

Fig. 3

The flow chart of the intelligent excavating process

3 Modeling of the LCS

3.1 Excavating resistance

To optimize the excavating trajectory, the accurate prediction of excavating resistance is crucial. Due to the large size of the LCS, many factors, such as the interactions between the shovel dipper and the ore pile, the gravities of material loaded into the dipper, and the self-weight of dipper handle and the dipper, play non-negligible roles on the excavating resistance.

Up to now, many empirical equations have been developed to deal with the resistance prediction of the complex excavating process (Dexter et al. 2007; Takahashi et al. 1998). Nevertheless, most of these models assume or simplify the dynamic excavation as steady process, and thus cannot take into account the effect of time-varying dipper penetration and excavating speed. In this work, a dynamic prediction model of the excavating resistance based on the method of trial wedges proposed by McKyes (1985) is established for the LCS. Figure 4 shows the resistance analysis of the dipper while excavating. F₁ denotes the tangential cutting resistance; F₂ denotes the normal cutting resistance; F₃ is the friction caused by the normal cutting resistance F₂; and G denotes the gravity of the material loaded in the dipper.

Fig. 4

Force analysis of the excavating process

The tangential cutting resistance, F₁, as formulated in (1), can be further decomposed into three parts, including the bottom resistance F₁₁, the velocity induced resistance F₁₂, and the resistance caused by the extrusion from the two sides of the dipper F₁₃.

$$ F_{1}=F_{11}+F_{12}+F_{13} $$

(1)

For F₁₁, it can be obtained as follows (McKyes 1985):

$$ \left\{ \begin{array}{lr} F_{11}=\omega (\gamma gd^{2}N_{\gamma}+cdN_{c}+\gamma \upsilon^{2}dN_{a}) & \\ N_{\gamma}= 0.5(\cot \beta+ \cot \rho)/E_{N}& \\ N_{c}=[1+\cot\rho \cot(\rho+\varphi)]/E_{N}\\ N_{a}=[\tan\rho+\cot(\rho+\varphi)]/[1+\tan\rho\cot\beta/E_{N}] &\\ E_{N}=\cos(\beta+\delta)+\sin(\beta+\delta)\cot(\rho+\varphi)&\\ \rho=(\pi-\varphi)& \end{array}\right. $$

(2)

where, ω is the dipper width, γ is the material density, d is the excavating depth, c is the material cohesion, υ is the speed of the dipper teeth, β is the excavating angle, ρ is the dip angle of the slip surface, φ is the internal friction angle of the material, and δ is the mechanical-soil friction angle.

F₁₂ and F₁₃ can be obtained through (3) (Wei et al. 2011) and (4) (McKyes 1985):

$$ F_{12}= \frac{\omega d \upsilon^{2}\gamma [\tan\rho \sin(\rho+\varphi)+\cos(\rho+\varphi)]}{\sin(\beta+\delta+\rho+\varphi)(1+\tan\rho\cot\beta)} $$

(3)

$$ F_{13}= \frac{2 d^{3}\gamma(\cot\beta+\cot\rho)\sin(\beta\,+\,\delta)\sqrt{\cot^{2}\rho\,+\,\cot\beta\cot\rho}}{3\omega \sin(\beta+\rho+\varphi+\delta)} $$

(4)

The normal cutting force, F₂, perpendicular to the speed of the dipper teeth, is produced by the extrusion reaction between the dipper and the material, so it can be derived in terms of the corresponding material properties of the dipper and material. As mentioned above, the cable shovel is usually used to excavate the blasted material in the open pit mine, so the normal cutting resistance F₂ for the blasting material can be obtained by (Wei et al. 2011)

$$ F_{2}= \frac{F_{1}\tan\delta}{1-\tau \tan\delta} $$

(5)

where τ is the proportionality coefficient and usually among $0.3\sim 0.45$, so F₃ can be cast as (Wei et al. 2011)

$$ F_{3}= \mu F_{2} $$

(6)

where $\mu =\tan \delta$.

It should be noted that the material loaded into the dipper accumulates continuously all the time during the dipper cutting through the ore pile, so the loaded material mass, the rotational inertia, and the centroid of the dipper-material system change continuously. It can be seen that an accurate estimation of the loaded material mass comes to be a crucial issue in the trajectory planning of the intelligent LCS. An instantaneous excavating status is illustrated in Fig. 5, where the material surface (y_m) and the excavating trajectory (y_t) are predefined. By assuming the material to be homogeneous, the current loaded volume of the material can be described as the product of the dipper width and the area of the quadrangle $\widehat {ABCD}$, which is equal to the area of $\widehat {OBC}$. So, at any time instant during a excavating process, the current loaded volume, V _c, can be obtained using the integral:

$$ V_{c}(x)=\omega\cdot{{\int}_{x_{t_{in}}}^{x}}(y_{m}(x)-y_{t}(x))dx $$

(7)

where, $x_{t_{in}}$ is the initial horizontal position when the dipper cuts into the ore pile. Then the gravity of the material loaded in the dipper, G, can be calculated as

$$ G=\gamma V_{c}(x) $$

(8)

Note that, the gravity of loaded material becomes constant if dipper teeth overtops the material surface.

Fig. 5

The instantaneous loading volume of the excavating process

3.2 Dynamic analysis

The development of the IES requires kinematics and dynamic models of the shovel operating modes to describe the evolution of the excavator motion with time (Frimpong and Hu 2008). As described in Section 2, the excavating activities of the dipper are actuated simultaneously by the hoist and crowd motors. In this paper, the speeds of the crowd and hoist motors are set to be the two control parameters, based on which the dynamic analysis of the LCS is performed as follows.

While excavating, there are two types of motions simultaneously carried out for the dipper handle, the rectilinear motion in the direction parallel with the major axes of the dipper handle and the circular motion around the axis of the crowd gear, respectively. Based on the motion characteristics, a polar coordinate system is established to describe the dynamic system, as illustrated in Fig. 6, where the axis of the crowd gear, O, is set to be the origin, the stretching length of the dipper handle is set to be the polar diameter (r), and the angle between the vertical direction and the axes of dipper handle is set to be the independent variable (ψ). So the lagrange equation of this system can be written as

$$ \left\{\begin{array}{lr} \displaystyle\frac{d}{dt} \frac{\partial E}{\partial \dot r}- \frac{\partial E}{\partial r}= F_{h} & \\ \displaystyle\frac{d}{dt} \frac{\partial E}{\partial \dot \psi}- \frac{\partial E}{\partial \psi}= F_{\psi} & \end{array} \right. $$

(9)

where E is the total kinetic energy of the system, including the translational kinetic energy and the rotational kinetic energy; F_h is the radial force, namely the force acting on the dipper handle in the direction of the major axis; and F_ψ is the circumferential force. In this paper, the mass of the dipper handle is set to follow the uniform distribution in the axial direction and the dipper is simplified to be the regular shape, then the dynamic equation can be obtained as (10) and (11).

$$\begin{array}{@{}rcl@{}} (m_{h}\,+\,m_{d}\,+\,m_{m})\ddot r\!&=&\!F_{h}\,+\,(m_{d}g\,+\,m_{h}g\,+\,m_{m}g)\cos \psi\\ &&\!-F_{n}\,-\,F_{r}\cos\pi \,+\,m_{h}\dot\psi^{2}r- \frac{1}{2}m_{h}l_{h}\dot\psi^{2}\\ &&\!+(m_{d}+m_{m})\dot\psi^{2}+\frac{1}{2}(m_{d}+m_{m})l_{d}\dot\psi^{2}\\ \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} && \!\!\!\left[\left( r^{2}\,-\,l_{h}r\,+\,\frac{1}{3}{l_{h}^{2}}\right)\!m_{h}\,+\,\left( \!r^{2}+l_{d}+\frac{1}{3}{l_{d}^{2}}\right)\!(m_{d}\,+\,m_{m})\right]\ddot \psi\\ &&\quad = F_{h}r\sin\pi\,-\,F_{t}(l_{d}\,+\,r)\,-\,(m_{d}\,+\,m_{m})g\sin\psi\left( \!\frac{l_{d}}{2}\,+\,r\right)\\ &&\qquad -m_{h}g\sin\psi \left( r-\frac{l_{h}}{2}\right) \end{array} $$

(11)

where m_h are the mass of the dipper handle; m_d is the mass of the dipper; m_m is the current mass of the loaded material in the dipper; l_h are the length of the dipper handle; l_d is the length of the dipper; F_r is the tensile force provided by the hoist ropes; F_n is the normal excavating resistance acting on the dipper teeth; F_t is the tangential excavating resistance acting on the dipper teeth; and π is the angle between the hoist ropes and the dipper handle. Then the speeds of the hoist ropes and the dipper handle, namely the hoist motor speed and the crowd motor speed, can be obtained from (12) and (13):

$$ v_{handle}= \frac{d h_{h}}{dt} $$

(12)

$$ v_{rope}= \frac{d S_{rope}}{dt} $$

(13)

where S_rope is the length of the hoist rope.

Fig. 6

The polar coordinate system built in the dynamic analysis

4 Trajectory planning of the intelligent excavating process

4.1 Trajectory planning using the point to point method

Currently, many different trajectory optimization methods corresponding to specific equipments, such as the mechanical arm and the artificial earth satellite, have been proposed. For example, Dong and Lee (2015) developed a numerical model of the levelluffing crane (LLC) to optimize the loading/unloading trajectory, based on which the strength-based deterministic optimization (DO) is used to minimize the weight of a double rocker. Dufour et al. (2015) used the pseudo-spectral approach to optimize the trajectory of a sub-orbital spaceplane and then conducted a trajectory driven multi-disciplinary design optimization (MDO) for a sub-orbital spaceplane by taking into account the aerodynamics, the structure, and the optimal control. Du et al. (2015) developed a single-layer optimization model to find the optimal trajectory of the hatch door of the airliner ARJ21-700. Currently, the conventional S-curve trajectory planning method, which is used to establish the trapezoidal control strategy, is adopted for most of the engineering machines to complete the functional motions. Nevertheless, the S-curve has not been certified to be the optimal trajectory planning method, so some other trajectory planning methods should inevitably be proposed and the corresponding superiority should also be certified. In this paper, the point to point (PTP) trajectory planning, proposed by Huang et al. (2012), which has been successfully applied to many practical engineering (Hsu et al. 2014; Fung and Cheng 2014), is adopted. The PTP trajectory is designed on the basis of a high-degree polynomial, which is able to satisfy desired constraints of position, velocity, and acceleration at the start and end points (Huang et al. 2012).

In PTP method, the trajectory curve is set to be an n-degree polynomial function

$$ s(t)=a_{n}t^{n}+a_{n-1}t^{n-1}+{\cdots} +a_{3}t^{3}+a_{2}t^{2}+a_{1}t+a_{0} $$

(14)

where a_n (n is the positive integer) denotes the polynomial coefficient, and the coefficient of the highest degree is not equal to 0. Subsequently, some essential constraints can be deduced based on the initial and final conditions of the optimal control problems. It should be noted that the number of the constraints limits the highest degree n of the polynomial.

The optimization objective of this paper is to find the optimal excavating trajectory for the intelligent LCS to realize the minimum energy consumption while rapid excavation. Dipper handle and hoist rope speeds are the key measures of operator practices (Awuah-Offei and Frimpong 2011). In another word, it is to find the optimal speeds of the motors and the optimal trajectory of the dipper to achieve the minimum energy consumption while rapid excavation. In this paper, two directional trajectories are defined to describe the overall trajectory of the dipper: the x-axis directional trajectory and the y-axis directional trajectory, respectively. The corresponding Cartesian coordinate system is illustrated in Fig. 7, where the origin is the bottom of the ore pile. So the excavating trajectory of the intelligent LCS can be calculated as (15):

$$ \left\{ \begin{array}{lr} s_{x}(t)=a_{x_{n}}t^{n}+a_{x_{n-1}}t^{n-1}+{\cdots} +a_{x_{2}}t^{2}+a_{x_{1}}t+a_{x_{0}} & \\ s_{y}(t)=a_{y_{n}}t^{n}+a_{y_{n-1}}t^{n-1}+{\cdots} +a_{y_{2}}t^{2}+a_{y_{1}}t+a_{y_{0}}& \end{array}\right. $$

(15)

Fig. 7

The Cartesian coordinate system built to describe the excavating trajectory

The initial and final states of the excavating activities are illustrated in Table 1, where the sign “$\bigodot$” means the value to be optimized. The hoist and crowd motors drive the dipper to excavate the material from the bottom to the top with both the initial and final speeds being zero ($v_{i_{x,y}}= 0$, $v_{f_{x,y}}= 0$). In order to ensure the excavation smooth and stable, the initial and final accelerated speeds should also be zero ($a_{i_{x,y}}= 0$, $a_{f_{x,y}}= 0$). For the initial location of the dipper teeth, it is set to be the origin of the coordinate system as illustrated in Fig. 7. It should be noted that 𝜃_i could not be constant in order to guarantee a good result when excavating different types of material, that is the distance between the shovel carbody and the ore pile should be varied. The final time instant t_f and the final location of the dipper teeth ($s_{x_{f}}, \;s_{y_{f}}$) also vary and will be determined by objective/constraint functions.

Table 1 Initial and final states of the excavating activities

On the basis of the analysis above, the essential constraints for the trajectory planning of the intelligent LCS in this study can be described as

$$ \left\{\begin{array}{lr} s_{i_{x}}=\bigodot & \\ v_{i_{x}}= 0& \\ a_{i_{x}}= 0& \end{array}\right. $$

(16)

$$ \left\{ \begin{array}{lr} s_{i_{y}}=\bigodot& \\ v_{i_{y}}= 0& \\ a_{i_{y}}= 0& \end{array}\right. $$

(17)

Combining (15)–(17), the following equations can be obtained:

$$ \left\{\begin{array}{ll} \!a_{x_{0}}\!=&0 \\ \!a_{x_{1}}\!=&0 \\ \!a_{x_{2}}\!=&0\\ \!a_{x_{3}}\!=&\frac{10s_{x_{f}}}{{t_{f}^{3}}} \,-\,{t_{f}^{3}}a_{x_{6}}\,-\,3{t_{f}^{4}}a_{x_{7}}\,-\,6{t_{f}^{5}}a_{x_{8}}\,-\,10{t_{f}^{6}}a_{x_{9}}-\cdots\\ &-(0.5n^{2}-4.5n + 10)t_{f}^{(n-3)}a_{x_{n}} \\ \!a_{x_{4}}\!=&-\frac{15s_{x_{f}}}{{t_{f}^{4}}} \,+\,3{t_{f}^{2}}a_{x_{6}}\,+\,8{t_{f}^{3}}a_{x_{7}}\,+\,15{t_{f}^{4}}a_{x_{8}}\,+\,24{t_{f}^{5}}a_{x_{9}}\!+\cdots\\ &+(n^{2}-8n + 15)t_{f}^{(n-4)}a_{x_{n}} \\ \!a_{x_{5}}\!=&\frac{6s_{x_{f}}}{{t_{f}^{5}}} \,-\,3t_{f}a_{x_{6}}\,-\,6{t_{f}^{2}}a_{x_{7}}\,-\,10{t_{f}^{3}}a_{x_{8}}\,-\,15{t_{f}^{4}}a_{x_{9}}-\cdots\\ &-(0.5n^{2}-3.5n + 6)t_{f}^{(n-5)}a_{x_{n}} \end{array}\right. $$

(18)

$$ \left\{\begin{array}{ll} \!a_{y_{0}}=&0 \\ \!a_{y_{1}}=&0\\ \!a_{y_{2}}=&0 \\ \!a_{y_{3}}=&\frac{10s_{y_{f}}}{{t_{f}^{3}}} \,-\,{t_{f}^{3}}a_{y_{6}}\,-\,3{t_{f}^{4}}a_{y_{7}}\,-\,6{t_{f}^{5}}a_{y_{8}}\,-\,10{t_{f}^{6}}a_{y_{9}}-\cdots\\&-(0.5n^{2}-4.5n + 10)t_{f}^{(n-3)}a_{y_{n}} \\ \!a_{y_{4}}=&-\frac{15s_{y_{f}}}{{t_{f}^{4}}} \,+\,3{t_{f}^{2}}a_{y_{6}}\,+\,8{t_{f}^{3}}a_{y_{7}}\,+\,15{t_{f}^{4}}a_{y_{8}}\,+\,24{t_{f}^{5}}a_{y_{9}}\!+\cdots\\&+(n^{2}-8n + 15)t_{f}^{(n-4)}a_{y_{n}} \\ \!a_{y_{5}}=&\frac{6s_{y_{f}}}{{t_{f}^{5}}} \,-\,3t_{f}a_{y_{6}}\,-\,6{t_{f}^{2}}a_{y_{7}}\,-\,10{t_{f}^{3}}a_{y_{8}}\,-\,15{t_{f}^{4}}a_{y_{9}}\!-\cdots\\&-(0.5n^{2}-3.5n + 6)t_{f}^{(n-5)}a_{y_{n}} \end{array}\right. $$

(19)

In the PTP trajectory planning method, the total time is discretized into small segments or intervals such that

$$ t_{0}=t_{1}<t_{2}<\cdots<t_{n}=t_{f} $$

(20)

where, t₀ is the initial time and t_f is the final mission time. Based this discretization, the speed and accelerated speed at any instant can be cast. Thus, the optimal control problem is transformed into a general nonlinear optimization problem trying to find the optimal coefficients of the n-degree polynomial and the final location of dipper teeth ($s_{x_{f}}, \;s_{y_{f}}$).

4.2 Objective function

As mentioned in Section 4.1, this paper aims to find the optimal speeds of the hoist and crowd motors and the optimal trajectory of the dipper to achieve the minimum energy consumption. Note that, the total energy consumption of the intelligent LCS is directly determined by the fill factor. The larger the fill factor is, the more energy will be consumed by the intelligent LCS. So the pure energy consumption is inappropriate to be set as the sole and ultimate indicator for the LCS. In this paper, two demands, to minimize the energy consumption of a single excavating cycle and to maximize the fill factor of the dipper, are combined together as the sole objective function:

$$ f=\frac{E_{total}}{V_{p}} $$

(21)

where E_total denotes the total energy consumption and V _p denotes the actual dipper loading volume of material. The total energy consumed by the LCS to excavate the material is completely provided by three motors (two hoist motors and one crowd motor), so the total energy consumption can be formulated as (22):

$$ E_{total}= 2E_{r}+E_{h} $$

(22)

where, E_r denotes the output energy of the hoist motors and E_h denotes the output energy of the crowd motor. The total energy consumed by any single motor can be obtained using (23):

$$ E_{single}={\int}_{t_{i}}^{t_{f}}F(t)v(t)dt $$

(23)

where, F(t) denotes the force output from the single motor and v(t) denotes the linear speed of the motor.

5 Numerical simulation and results

5.1 Optimization model establishment

As analyzed in Section 4.1, searching the optimal s(t), v(t), and a(t) of the dynamic system is equivalent to searching the optimal n-degree polynomial coefficients, so $a_{x_{6\sim n}}$ and $b_{x_{6\sim n}}$ are selected to be the design variables. In the practical excavation, the initial angle 𝜃_i, which determines the initial distance between the LCS and the material pile, potentially influence on the excavating performance of the LCS through affecting the shape of the excavating trajectory. For the excavating endpoint, the LCS should work together with the mining truck to complete the dumping motion, so it is essential to take into account the final location of the dipper teeth ($s_{x_{f}}, \;s_{y_{f}}$) in order to avoid the interference between different devices. In addition, a smaller time consumption means a higher excavating efficiency and productivity, so the final time t_f is also taken into account in this PTP trajectory planning. Based on all above, the dependent optimization variables in this paper are selected as illustrated in (24)

$$ \mathbf{x} = [a_{x_{6}}, a_{x_{7}}, \cdots, a_{x_{n}}, a_{y_{6}}, a_{y_{7}}, \cdots, a_{y_{n}}, t_{f}, s_{x_{f}}, s_{y_{f}}, \theta_{i}] $$

(24)

Usually, in the practical mining the LCS dumps the material onto the mining trucks, which requires a lowest height and a smallest horizontal distance for the final location of the dipper teeth. Based on the practical engineering, the lowest height and the smallest horizontal distance are set to be 10 and 11 m, respectively. In addition, due to the maximum length of the dipper handle and the maximum height of the boom, the upper boundaries of the final location $s_{x_{f}}$ and $s_{y_{f}}$ are both set to be 15 m. In order to ensure the working efficiency of the LCS, the final time instant t_f should also be scheduled within reasonable range. In this paper, the bound of t_f is set to $5\sim 12$ s. Based on the physical characteristics and performance requirements of the LCS, 𝜃_i is set to be $15.00^{\circ } \sim 45.00^{\circ }$. And the polynomial coefficients are set to range from negative infinite to positive infinite as listed in Table 2.

Table 2 Upper and lower bounds of design variables

In addition, in order to avoid underload or overload, the minimum and maximum fill factor for each cycle is set to be 90 and 110% of the nominal loading capacity, respectively, which means that the loading volume V _p should be in the range of $0.9V_{\max }\sim 1.1V_{\max }$ (m³). The stretching length of the dipper handle r should be less than the maximum length of the dipper handle, namely r ≤ l_h. In order to make the control process stable and reliable, the control speeds of the dipper handle and the hoist ropes are limited to be greater than 0, namely v_h ≥ 0 and v_r ≥ 0. Given the motor dynamic characteristics, as an example illustrated in Fig. 8a, the instantaneous power and/or torque of any motor should be less than the maximum allowable power and/or torque the corresponding motor can provide, namely $P_{h,r}\leq P_{h,r_{\max }}$ and/or $T_{h,r}\leq T_{h,r_{\max }}$, where P and T continually vary with respect to the motor speeds while excavating. Besides the physical and performance constraints, some auxiliary constraints are also added to insure a reasonable and practicable trajectory. For example the final location of the dipper teeth should be above the material surface, namely $s_{y_{f}}>h_{m_{f}}$, where $h_{m_{f}}$ is the corresponding material height at the final moment. To insure that the dipper teeth excavate into the ore pile successfully, the initial derivative of the excavating trajectory should be less than the initial slope of the ore pile, namely $\left (\frac {ds}{dt}\right )_{i}<\tan \kappa$, where κ is the pile angle of the ore pile.

Fig. 8

The characteristic curves of the hoist and crowd motors

So the overall optimization formulation can be written as follows:

$$ \left\{\begin{array}{rl} \text{ find} \quad & \mathbf{x}\\ \min \quad& f=\frac{E_{total}}{V_{p}}\\ \text{s.t.} \quad&g_{i}\leq 0 \quad (i = 1,\;2,\;3,\;4,\;5,\;6,\;7,\;8,\;9) \end{array}\right. $$

(25)

where

$$ \left\{\begin{array}{lr} g_{1}=r- l_{h}\\ g_{2}=-v_{h} & \\ g_{3}=-v_{r} & \\ g_{4}=P_{h}- P_{h_{\max}}& \\ g_{5}=P_{r}- P_{r_{\max}} & \\ g_{6}=h_{m_{f}}-s_{y_{f}} &\\ g_{7}=\left( \frac{ds}{dt}\right)_{i}-\tan \kappa &\\ g_{8}=V_{p}-1.1V_{\max} &\\ g_{9}= 0.9V_{\max}-V_{p} & \end{array}\right. $$

(26)

In this paper, the LCS with a dipper payload of 55 m³ is taken as a case. The rated power of the hoist motor is 2500 kW with the rated rotational speed being 650 r/min and the rated power of the crowd motor is 950 kW with the rated rotational speed being 600 r/min. The efficiency of the motors are all 0.9 and the transmission ratios of the hoist and crowd driving systems are 51.06 and 39.60, respectively. The corresponding characteristic curves of the hoist and crowd motors are illustrated in Fig. 8, where the motors are able to keep constant torque in the low-speed region and constant power in the high-speed region. The initial values of some important parameters are listed in Table 3 and the corresponding explanations are illustrated in Fig. 9. The Non-Dominated Sorting Genetic Algorithm II (NSGA-II) (Deb et al. 2002) is implemented in this paper to perform the optimization, and the sample size and the generations are set to be 100 and 60, respectively.

Table 3 The initial values of some important parameters

Fig. 9

The corresponding structure explanation of the LCS

5.2 Determination of the optimal degree of the polynomial

Theoretically, higher order polynomials contain all the curve types that the lower order polynomials can present and may lead to a better representation for the excavating trajectory, however, this increasing order of the polynomials may introduce more design variables into the optimization process, which may cause expensive computation. In addition, from our numerical experiments, the magnitude orders of the optimal polynomial coefficients vary greatly with the orders of polynomials used in the trajectory planning. In this situation, the truncation errors may occur more likely due to the limit of the search algorithm when the orders of polynomials are higher. Thus, the obtained excavating trajectory from the polynomials with a higher order may be not necessarily better than that obtained from the polynomials with a lower order. It conforms to the results and statement of Fung and Cheng (2014): a higher degree of the polynomial will not necessarily show significant energy-saving in the absolute input electrical energy during the trajectory planning. So the comparisons among 6 to 11 degrees of polynomials are performed to find the optimal degree of the polynomial for the trajectory optimization in this paper. In the comparison, the initial and final locations are both set to be the same and the material surface angle is uniformly set to be 40^∘ for all the different degrees of polynomials. The final optimal coefficients of the polynomials with 6 to 11 degree in x and y directions are listed in Table 4. It is observed that the magnitudes of all the polynomial coefficients are very small, the reason of which is that the n th power of the time is extremely large. Figure 10 shows the comparisons of the optimal trajectories among the 6 to 11 degree polynomials for the intelligent LCS. It is obviously found that the optimal trajectories with 6 degree to 11 degree have different tendencies. Detailedly, there is a common intersection in the middle position for the 6 trajectories and the vertical orders of the trajectories are inverse in the left and right sides of the intersection. The comparisons of the trajectory profiles among the 6 to 11 degree polynomials is illustrated in Fig. 11, from which it can be seen that the control parameters and some critical performance indicators also have different tendencies.

Table 4 The coefficients of polynomials with different degrees in two directions

Fig. 10

Comparisons of the optimal trajectories regarding 6 to 11 degree polynomials

Fig. 11

Comparisons of the optimal control regarding 6 to 11 degree polynomial trajectory planning methods

As defined the objective function to be the energy consumption per volume of the material, it is also set to be the selection metric for the optimal maximum degree of the polynomial. Figure 12 shows the loading capacity and energy consumption per volume of the 6 different degrees of polynomials. It can be seen that the optimal loading capacities of all the trajectories meet the minimum requirement as 90% of the fill factor and achieve the maximum value of 50 m³ as well. From Fig. 12b, the 6-degree polynomial trajectory achieves the minimum energy consumption per volume of 0.1615 kW/m³ with a relatively large loading volume. Based on the analysis above, the optimal maximum degree of the polynomial for the trajectory planning of the intelligent LCS is selected to be 6.

Fig. 12

Comparisons of the optimization results regarding 6 to 11 degree polynomial trajectory planning methods

5.3 Comparisons between the PTP and the S-curve trajectory plannings

Currently, in the practical mining engineering the S-curve is most widely used as the control curve of the hoist and crowd motors for the manual LCS. As mentioned in Section 1, the human errors are inevitable and irregular for the conventional operation of the manual LCS, which results in the fact that it’s meaningless to compare a non-optimal S-curve with the proposed method. In this work, we assume that an highly skillful operator is manipulating the LCS, and thus the optimal S-curve can be obtained for the comparison. If the proposed PTP method has a better performance than the so-called S-curve method, it can be concluded that the proposed 6-degree polynomial PTP method is more practicable for the intelligent LCS than the conventional S-curve method no matter if the LCS is manual or intelligent. In this paper, the expression of the adopted S-curve is (Wikipedia 2017):

$$ s(t)=\frac {a_{1}}{a_{2}+a_{3}e^{a_{4}t+a_{5}}} $$

(27)

where, a_i’s are the parameters determining the shape of S-curve.

By setting all the initial locations to be the same, the comparison of the optimal excavating trajectories between the 6-degree polynomial and S-curve methods are illustrated in Fig. 13. From Fig. 13, the excavating trajectory of the 6-degree polynomial is smoother than the S-curve. It is observed that the trajectory based on the 6-degree polynomial performs a shallower cut through the ore pile than that based on the S-curve. As listed in Table 5, for the optimal energy consumption per volume of material driven by the S-curve method is 0.1733 kW/m³, which is greater than that (0.1615 kW/m³) driven by the 6-degree polynomial trajectory planning method. In another word, the 6-degree polynomial PTP trajectory planning method can save 6.81% energy compared to the S-curve method under the same working condition. This is also in agreement with the findings of Patnayak et al. (2008): a deep cut through an ore pile generally results in higher power consumption than a shallow cut. The main reason is that a shallow cut through the ore pile can generate a relative small excavating resistance and a slow gravity accumulation while excavating. Figure 14 shows the comparisons of the trajectory profiles between the 6-degree polynomial and the S-curve methods.

Fig. 13

Comparisons of the optimal trajectories between the 6 degree polynomial and S-curve planning methods

Table 5 The comparison between the 6-degree polynomial and the S-curve trajectory planning methods

Fig. 14

Comparisons of the optimal control between the 6-degree polynomial and the S-curve trajectory planning methods

6 Numerical experiments on actual working conditions

6.1 Performance comparison among different pile angles

In order to verify the availability of the proposed method, the optimized control strategy for various pile angles (35^∘, 40^∘, 45^∘, and 50^∘) is investigated. The optimization results are shown in Table 6. It shows that the optimized loading capacities of all the four scenarios do meet the requirement of 90% fill factor. The energy consumption is reasonably low and the excavating cycles can ensure the working efficiency. It is found that larger t_f and 𝜃_i are of help to save energy as the pile angle increases. For the final location of the dipper teeth, it becomes closer to the machine body with the pile angle increasing. The detail excavating processes are shown in Fig. 15, where the dash-dotted lines denote the material surfaces, the solid lines denote the optimal excavating trajectories, and the circles denote the axes of crowd gears. For the dashed lines, they describe the initial polar radius and 𝜃_i. As shown from Fig. 15, 𝜃_i is very close to 15^∘ when the pile angle is 35^∘, which means that the LCS should stand much closer to the ore pile while excavating the pile with a small pile angle. On the contrary, it should stand farther while excavating pile with a large pile angle. Figure 16 illustrates the control parameters and some important performance indicators during the excavation. The hoist motor and crowd motor speeds are both 0 at the initial and the end moment, which ensures the stability of the excavating process and avoids the extra energy consumption. From Fig. 16b, it is found that the maximum crowd motor speed will increase when the pile angle increases. Figure 16c and d reflect that the intelligent LCS should stretch out the dipper handle longer when excavating the ore pile with a smaller pile angle. In addition, the stretching length of the dipper handle almost remains unchanged within the first and last few seconds, namely doing the approximate circular motion, especially in the situation with large pile angle. It can be seen from Fig. 16e that the initial tension needed to start the excavation becomes larger and the time when the tension reaches the maximum value becomes later as the pile angle increases. From Fig. 16f, the initial thrust needed to start the excavating activity become smaller with the pile angle increasing. For the power consumed by the intelligent LCS as shown in Fig. 16g and h, the larger the pile angle is, the later the maximum hoist power and crowd power will appear. It is also observed that the maximum hoist powers with respect to all the four pile angles reach the upper bound of the hoist motor being 2250 kW, while none of the crowd powers reaches the upper bound. Therefore, more powerful hoist motor is desirable if a high performance of the LCS is required.

Table 6 The optimization results of the four types of excavating scenarios with respect to different pile angles

Fig. 15

The optimal trajectories of the excavating tasks with different pile angles

Fig. 16

Comparisons the four different excavating scenarios regarding different pile angles

6.2 Performance verification on actual working pile surface

In the practical excavation, the slope of the ore piles usually can not remain absolutely straight and smooth due to the random distribution of ore blocks. From an overall visual angle of the material pile, its slope usually presents many different random forms, such as the concave, the convex, and the wave-like shape, which are all macroscopic fluctuations. Relatively, some small fluctuations which are formed by the local aggregation of the material, defined as the microscopic fluctuations, simultaneously exist on the macroscopic fluctuations. So the actual terrain is very complex as shown in Fig. 17, where the ore pile roughly stacks along the theoretical pile angle from bottom to top with many local ups and downs. Thus, both the macroscopic and microscopic fluctuations are taken into account in this paper to simulate a more realistic terrain to verify the efficiency and reliability of the PTP trajectory planning method for the LCS. At the first stage of the intelligent excavation as mentioned in Section 2, the intelligent LCS uses the 3D scanner to extract a series of coordinates for constructing the mathematical models of the corresponding pending surface. As illustrated in Fig. 17, the i th set of coordinate points is obtained from the i th excavating task and each set differs greatly from that of another, which requires the intelligent LCS to recognize the terrains of ore pile accurately and makes excavating decisions rapidly. In this paper, in order to simulate the types of the actual pile surface as many as possible, four different scenarios with microscopic fluctuations are compared and analyzed: the flat type, the concave type, the convex type, and the concave-convex type, all of which stack along the same pile angle being 40^∘.

Fig. 17

The actual material surface with fluctuant terrains

Figure 18 shows the excavating task of the ore pile surface with different types of fluctuations. It is found that the PTP trajectory planning method can find the best trajectories for all of the scenarios. As the baseline scenario, the excavating task of the ore pile surface with the flat fluctuations is shown in Fig. 18a, where the optimal 𝜃_i is 18.02^∘. Figure 18b shows the optimal trajectory of the excavating task with respect to the concave type of fluctuations. It is found that the trajectory of this scenario cuts more deeply into the theoretical ore surface than that of the flat type and 𝜃_i is also small with the value being 15.00 ^∘. That is to say that the LCS should be close to the ore pile while excavating the ore pile with concave fluctuations to ensure a high fill factor. The excavating task of the ore surface with convex fluctuations is shown in Fig. 18c, where the optimal trajectory cuts into the theoretical ore pile more shallowly than that of the baseline and concave scenario. In this convex scenario, 𝜃_i is 21.01^∘ meaning that the LCS should keep a reasonable distance away from the ore pile to avoid the overload. For the concave-convex type as shown in Fig. 18d, the optimal trajectory is very similar to the baseline scenario but with a bigger 𝜃_i being 19.24^∘, which is the result of automatic optimization. For the concave scenario, if the concavity of the pile surface continues to increase as illustrated in Fig. 19, there will be no optimal results for the excavating trajectory even with the smallest 𝜃_i. For this situation, two methods can be undertaken: i) step forward toward the ore pile to insure the fill factor requirement, and ii) crank down the fill factor requirement.

Fig. 18

Comparisons the four different excavating scenarios with respect to different types of fluctuations

Fig. 19

The material surface with a large concavity

The history of the control parameters and some important time-dependent parameters of the four scenarios are illustrated in Figs. 20, 21, 22 and 23, where the subscript “h” denotes the dipper handle and the subscript “r” denotes the hoist ropes. From Figs. 20a, 21a, 22a and 23a, it is observed that all the crowd speeds of the four scenarios reach the maximum values the crowd motor can provide, however, with different appearing time instants. The same situation happens to the hoist speeds of the four scenarios. As can be seen from Fig. 16e–h, the forces and powers optimized and simulated using the ideally straight pile surface are all smooth during the entire time domain of excavation. Comparatively, it is observed from Figs. 20–23 that the forces and powers present some saltations when using the actual material surfaces with both the macroscopic and microscopic fluctuations. As analyzed, the macroscopic fluctuations, such as the flat scenario and the concave scenario, influence the overall trend of the forces and powers during the time domain. For the saltations of the forces and powers, it is caused by the microscopic fluctuations of the pile surfaces. Ultimately, the reason of such trend and saltations of forces and powers is the time-varying instantaneous excavating depth during the excavating time domain. It is concluded that the forces and powers simulated using the actual material surfaces are more real than that using the theoretical material surface by showing some actual saltations. The amplitude and density of the force and power saltations are determined by the flatness of the material surface. Figures 20–23 also show that the forces and powers needed by the four scenarios are almost the same, the reason of which is the limitation of the maximum allowable output power of the hoist and crowd motors.

Fig. 20

The history of the speed, force, and power in the flat scenario

Fig. 21

The history of the speed, force, and power in the concave scenario

Fig. 22

The history of the speed, force, and power in the convex scenario

Fig. 23

The history of the speed, force, and power in the concave-convex scenario

Table 7 shows the optimization results of the four scenarios with respect to different types of fluctuations. It is found that the smaller the dipper penetration is, the faster the LCS can complete an excavating cycle and the flat type of the ore surface consumes the lowest power to complete the excavating task among all the scenarios. All the results meet the requirements of the practical engineering, so the PTP trajectory planning method performed for the intelligent LCS is flexible and reliable in the practical mining engineering.

Table 7 The optimization results of the four types of excavating scenarios with respect to different types of fluctuations

7 Conclusion

A energy-minimum optimization through point to point (PTP) trajectory planing of the intelligent excavating process for Large Cable Shovel (LCS) was developed in this paper. By building the excavating resistance model of the excavating process, the force analysis of the dipper was performed. The excavating activity of the LCS was decomposed into two directions: the rectilinear motion parallel with the major axes of dipper handle and the circular motion perpendicular to the major axes of the dipper handle, respectively. Then based on the force analysis, the dynamic equations of the excavating process were established as well. By comparing different degrees of the polynomial trajectory planning methods, the 6-degree polynomial is selected as the optimal PTP trajectory planning method. Also, the 6-degree polynomial trajectory planning method is demonstrated to be better than the conventional S-curve method on the aspect of the excavating performance. To explore some potential laws of the optimal control strategy and excavating process, the comparisons between different excavating scenarios with respect to different pile angles were conducted. Results showed that the larger the pile angle is, the later the maximum hoist power and crowd power will appear. The actual pile surfaces with different types of large scale and small scale fluctuations were taken into account in the numerical experiments for the optimal control of the intelligent excavating of the LCS. It was found that the flat type needs the lowest power to complete the excavating task among all the types. It can be seen that the energy-minimum trajectory planning optimization model built in this paper for the intelligent excavating process of the LCS is flexible and available.

As a complex engineering machine, the LCS is composed of many complex structural components, including the dipper handle, the boom, and the dipper. All the corresponding structure parameters have great influences on the control strategy and the machine performance. For the future work, it is planed that the structure parameters will be also taken into account and the optimization process should simultaneously deal with the control and structure parameters. In addition, the power source of the cable shovel is provided by the electric motors, the efficiency of which is set to be a flat constant rate of 0.9 in this paper, but actually it is a function of input (electric) power and shaft speed (Guzzella et al. 2007). So the future work will also take this time-varying motor efficiency into account.