1 Introduction

Flow machines are a wide field of knowledge. They are widely used in industry through devices such as hydraulic turbines and pumps. Most part of these devices work with Newtonian fluids, however, there are some specific devices dedicated to work with non-Newtonian fluids, such as blood pumps. Blood pumps can be found in circulatory extracorporeal devices and ventricular assist devices (VADs) (Osaki et al. 2008). Thus, this work will focus on blood pump design, more specifically radial pumps.

The main function of a blood pump is to have a suitable hydraulic performance while maintaining good haematological compatibility to avoid hemolysis (release of hemoglobin from red blood cells) and thrombosis (clotting). Numerical simulations can provide very precise information about the behaviour of fluid flow in non-newtonian fluid machines, such as blood pumps, thus helping engineers to get a comprehensive performance evaluation of a particular design (Jafarzadeh et al. 2011), Cheah et al. (2007). The work of Behbahani et al. (2009) presents a review that focuses on the CFD-based design strategies applied to improve the blood flow in blood pumps and other blood-handling devices. Both simulation methods for blood flow and blood damage models are reviewed. In addition, the rheology of blood and some constitutive models that endeavour to represent the complex flow behaviour of blood are also described (Behbahani et al. 2009).

However, the challenge of improving the performance of these non-Newtonian fluid machines requires the solution of an inverse-based design optimization problem, in which an oriented search must be conducted to obtain the optimized design. This can be achieved by using optimization techniques which can increase the performance. The design optimization strategy for blood pumps was first presented by Antaki et al. (1995), however, many obstacles made its application difficult. According to Antaki et al. (1995), the main challenges are lack of improved models to describe the blood flow, a better description of the relationship between the characteristics of macroscopic and microscopic blood flow, and appropriate automatic algorithms for implementing the shape changes in response to computed flow characteristics. We can also cite the work of da Silva et al. (2007a) and da Silva et al. (2007b) who conducted the size optimization of viscous micropumps. In their work the constitutive law of the non-Newtonian fluid is approximated by a power law model.

Topology optimization method distributes fluid or solid in a design domain to extremize a defined objective function subjected to some constraints. The topology optimization method (TOM) for fluids was introduced by Borrvall and Petersson (Borrvall and Petersson 2003) who optimized the channel flow in a 2D Brinkman medium to minimize the dissipated power. The flow modeling is restricted to the incompressible Stokes flow, neglecting the influence of inertia. In order to relax the optimization problem from an integer (black-white) problem where either fluid or solid property is allowed in an element, a porous flow model is introduced with a continuous (gray) permeability design variable for each element. This leads to a design problem where the flow and (almost) non-flow regions are developed by allowing interpolation between the upper and lower values of the permeability (Gersborg-Hansen 2003; 2007). Following, many authors have applied topology optimization to design fluid devices (Andreasen et al. 2009; Deng et al. 2012; Kreissl et al. 2010; Okkels and Bruus 2007) and Deng et al. (2013a), Deng et al. (2013b) studied the topology optimization of steady and unsteady Navier-Stokes flows considering body forces, such as, Coriolis and Centrifugal forces. Other interesting work (Evgrafov A. 2015) presents a locally cubically convergent algorithm for topology optimization of Stokes flows based on a Chebyshev’s iteration globalized with Armijo linesearch.

The topology optimization method applied to flow machines has been recently studied in the work of Romero and Silva (2014), by considering Navier-Stokes flow with the addition of a rotating reference system, arising the effects of Centrifugal force and Coriolis force. In their work, different configurations are obtained for the machine rotor, by exploring the influence of the initial domain and the effects of changes in the boundary conditions, however, only Newtonian fluids are considered. As a result non-intuitive geometries, that differ from traditional configurations, are obtained.

All optimization studies cited above consider Newtonian fluids. However many fluids in chemical and biomedical applications are non-Newtonian fluids, being blood the most relevant. The effects of non-Newtonian fluid properties on biomedical design optimization problems are of considerable interest. For example Abraham et al. (2005) studied shape optimization of an arterial bypass and Pingen and Maute (2010), studied non-Newtonian effect on the layout and geometry of flow channels by using topology optimization approach. For non-Newtonian flow phenomena they use the Carreau-Yasuda (C-Y) model and the flow is modeled with the single-relaxation hydrodynamic Lattice Boltzmann method. Other works which may be mentioned in topology optimization for non-Newtonian fluids applied to the blood flow are Hyun et al. (2014) and Zhang and Liu (2015). They have studied the two dimensional design of the arterial bypass based in topology optimization method constrained by the steady incompressible non-Newtonian flow. Further, optimal shape design of rotary blood pump under non-Newtonian flow consideration has been studied by Antaki et al. (1995).

Previous works cited above related to blood pump design show that the rotor is the pump component that mainly influences pump hydraulic performance and its haematological conditions. The criteria for the flow characteristics when designing artificial heart components are (1) to minimize damage in the blood (hemolysis) and (2) to prevent blood clotting (thrombosis). It is well known that damage of the blood is directly related to the high shear stress and exposure times experienced by blood cells. Furthermore, the existence of stagnation and recirculation regions has shown to have a strong correlation with the onset of coagulation and deposition of blood components within a prosthetic device. A well known problem related to flow in blood pump is caused by recirculation and stagnation of blood within the device, which leads to the formation of clots. It is not clear how to express this phenomenon mathematically. Possibly by minimizing the mean square residence time of blood within the device over several cycles would be a suitable strategy. Since low vorticity is equivalent to poor circulation in the device it can be related to a lower probability for the separation and recirculation flow (Tavoularis et al. 2003). In this sense, some works (Antaki et al. 1995; Ghattas et al. 1995) have suggested to use vorticity as an objective function to optimize the haematological conditions of a blood pump. Thus, objective functions involving vorticity and energy dissipation mechanisms are reasonable choices to reduce recirculation and hence thrombosis. However, the shear stress functions are directly related to hemolysis of the blood (Ghattas et al. 1995) and we show that the decrease of vorticity also contributes to the decrease of shear stress functions, thus, decreasing the hemolysis. Therefore, to improve the haematological conditions, we propose to minimize the vorticity and energy dissipation.

As other works related to modeling of non-Newtonian fluids, we can mention the work of Zhang et al. (2016) who studied a roller type viscous micropumps design problem using a level set based topology optimization method and the work of Chen (2016) who presents a review about a topology optimization of microfluidics.

Thus, the combination of advanced numerical techniques as computational fluid dynamic and topology optimization can be an efficient tool to improve the geometry of non-Newtonian flow machines such as blood pumps to obtain significant enhancement of pump hydraulic performance and its haematological conditions. The optimization of hydraulic performance for a pump can be achieved by minimizing flow dissipative energy and power consumption. Regarding haematological conditions, we show that an improvement can be achieved by minimizing the energy dissipation and the vorticity in the rotor. Thus, in this work, topology optimization techniques are applied for designing the rotor pump such that the energy dissipation, vorticity, and power consumption are minimized by considering the design of rotor of radial flow machines operating with non-Newtonian fluid and laminar flow, aiming blood pump applications. A modified Cross model is adopted for the non-Newtonian fluid modeling. The rotor or impeller optimization is obtained by optimizing the channel shape between two of its blades. Moreover, the numerical analysis in this study is applied to predict the flow field between two blades of a rotor without considering the influence of the volute. Thus, the final rotors may have solid shapes between channels instead of thin blades. This gives more flexibility for the channel design allowing novel rotor designs. If a thin blade is imposed, by controlling the thickness of the solid region, for example, channels may need to have parallel faces which may limit the channel design. A general multi-objective is defined by involving the minimization of the energy dissipation, the minimization of vorticity, and minimization of power consumption. The steady state Navier-Stokes equation and the derived continuous adjoint equations are solved through the standard finite element method by using Taylor-Hood element and considering non-Newtonian fluid. In the flow problem, we assume that the design domain is filled with some idealized porous material of spatially varying permeability. Solid wall and fluid correspond to the limits of very low and very high permeability, respectively. In the final design there should preferably be no regions with intermediate permeability because only the 0 or 1 values in the final design have physical meaning.

To solve the optimization problem, we apply an iterative algorithm based on the method of moving asymptotes (MMA) (Svanberg 1987). Two-dimensional (2D) numerical examples are presented to illustrate this methodology aiming blood pump applications. A comparison among designs obtained by considering Newtonian and non-Newtonian fluid is included. Finally, it is verified that an improvement of the hemolysis index can be achieved by minimizing the vorticity in the rotor.

This paper is organized as follows: the continuous model of incompressible Navier-Stokes flow considering non-Newtonian fluid is briefly stated in Section 2; the continuous formulation of the topology optimization fluid problem and objective functions are derived in Section 3; the numerical implementation of the optimization method, the formulation of finite element method for fluid problem, and sensitivity analysis are discussed in Section 4; numerical examples are presented in Section 5. Finally, some conclusions are inferred in Section 6.

2 Equilibrium equations

2.1 Navier-Stokes equations for incompressible fluids

The flow considered in this work is assumed to be laminar with low Reynolds number. Furthermore, the flow velocity is small compared with the speed of sound, which causes a negligible compressibility, whereby the flow is modelled as incompressible. Equations of motion for a fluid are the Navier-Stokes equations (White Frank 2007)

$$\begin{array}{@{}rcl@{}} \displaystyle \rho \frac{D \textbf{u}}{ D \, t} = \nabla \cdot \boldsymbol{\sigma} + \rho \textbf{f}, \end{array} $$
(1)

where u is the velocity field, σ is the stress tensor and ρ is the mass density constant throughout the domain.

The incompressibility imposed on mass conservation yields the continuity equation

$$\begin{array}{@{}rcl@{}} \displaystyle \nabla \cdot \textbf{u} = 0. \end{array} $$
(2)

The stress tensor σ is given by

$$ \boldsymbol{\sigma}(\textbf{u},p) = - p \textbf{I} + \boldsymbol{\tau}, $$
(3)

where I denotes the identity tensor, p is the pressure and τ is the viscosity stress tensor, and

$$ \boldsymbol{\tau}(\textbf{u},\eta) = 2 \eta \textbf{D}(\textbf{u}), \qquad \textbf{D}(\textbf{u}) = \frac{1}{2} \left( \nabla \textbf{u} + \nabla \textbf{u}^{T} \right), $$
(4)

where η is the dynamic viscosity. For a Newtonian fluid η is a constant, whereas in the case of a generalized non-Newtonian fluid, we incorporate the shear thinning behavior of blood, as expressed by the modified Cross model:

$$ \eta (\dot \gamma) = \eta_{\infty} + (\eta_{0} - \eta_{\infty}) \left[ 1 + (\lambda \dot \gamma)^{b} \right]^{-a}, $$
(5)

where for parallel shear flows, the shear rate (\(\dot \gamma \)) is given by

$$ \dot \gamma = \left( 2 \textbf{D}({\textbf{u}}) : \textbf{D}(\textbf{u}) \right)^{1/2} . $$
(6)

Here, \(\eta _{\infty } \) and η 0 are the infinite shear viscosity and the zero shear viscosity, respectively, which combined with the parameters λ, a, and b, are applied to adjust the model to a particular fluid or material.

Considering 2D flow, the shear rate can be expressed as

$$ \dot \gamma = \left[ 2 \left( \frac{\partial u_{1}}{\partial x_{1}}\right)^{2} + 2 \left( \frac{\partial u_{2}}{\partial x_{2}}\right)^{2} + \left( \frac{\partial u_{1}}{\partial x_{2}} + \frac{\partial u_{2}}{\partial x_{1}} \right)^{2} \right]^{1/2}. $$
(7)

where u 1 and u 2 are the velocity components in the direction of the coordinates x 1 and x 2, respectively.

The laminar flow condition is verified by calculating the Reynolds number, according to the usual definition of the Reynolds number for centrifugal pumps

$$ Re = \frac{R^{2} \omega_{0}}{\nu}, $$
(8)

where R is a length scale (here the impeller radius), ω 0 the angular velocity and ν kinematic viscosity. The laminar flow occurs for R e<105.

2.1.1 Radial flow pump

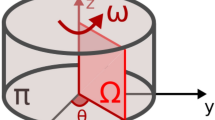
For radial flow pump modeling, we have to deal with systems in rotation, and we must be able to describe the flow in relation to the rotating reference system (Kundu Pijush and Cohen Ira 2002). We consider that the system is in rotational stable motion with constant angular velocity ω around an axis which coincides with the axis of the coordinate z of fixed frame (inertial frame). u is defined as the relative velocity field of the rotating system, which is measured in a rotating reference frame, r is the vector perpendicular to the axis of rotation, and ω = ω 0 e 3 (see Fig. 1). Thus, the inertial acceleration is equal to the acceleration measured in a rotating system, plus the Coriolis acceleration 2ω×u and the centripetal acceleration ω×ω×r. Therefore, Coriolis and centripetal accelerations are calculated by considering the rotating reference frame. (Romero and Silva 2014)

Fig. 1
figure 1

Profile geometry of the radial impeller blades. r = x 1 e 1 + x 2 e 2: position vector, u: absolute velocity, u r relative velocity and ω×r frame velocity

Full size image

Finally, for a domain Ω, following Borrvall and Petersson (2003), an absorption term κ(α)u is introduced into the Navier-Stokes steady state equation as a source term, given rise to the Brinkman model with a convection term, where κ is the inverse permeability and α is the variable design, and thus, we obtain the following final equation that describes the flow field (Romero and Silva 2014).

$$\begin{array}{@{}rcl@{}} \displaystyle \rho \nabla \textbf{u} \cdot \textbf{u} = & - \nabla p + \eta(\dot \gamma) \nabla \cdot (\nabla \textbf{u} + \nabla \textbf{u}^{T}) + \rho \textbf{f}\\ & - 2\rho \, \boldsymbol{\omega} \times \textbf{u} - \rho\, \boldsymbol{\omega} \times \boldsymbol{\omega} \times \textbf{r} - \kappa(\alpha ) \textbf{u}, \end{array} $$
(9)

3 Topology Optimization problem formulation

The fluid topology optimization considers equations that govern the flow in a porous medium to model the flow field. In this case the absorption term defines solid and fluid distribution in the domain. Topology optimization method considers that the coefficient of absorption is space dependent κ(x) and optimizes the absorption term.

3.1 Material model

A porosity field is defined to optimize the paths of fluid through the field. The regions with very high permeability can be regarded as pure fluid, while virtually no fluid can penetrate porous regions with low permeability. These regions of low permeability are interpreted as regions of solid (Borrvall and Petersson 2003; Gersborg-Hansen 2003; 2007). Thus, the absorption term defines the distribution of material in the design domain.

The absorption coefficient κ can be considered as material interpolation scheme, which interpolates between a small flow rate (porous κ≫1) and a high flow rate or undisturbed flow (κ=0). α is the spatially varying design variable field. This α field is determined by the optimization algorithm. The choice of interpolation function \( \alpha \rightarrow \kappa (\alpha ) \), makes the design variable α to assume values between 0 and 1. The idea is to choose function κ such a way that intermediate values of κ can be avoided. Therefore, the following convex interpolation function is adopted which is a function of the parameter q, (Borrvall and Petersson 2003)

$$ \kappa(\textbf{x}) = \kappa(\bar \alpha(\textbf{x})) = \kappa_{max} +(\kappa_{min}-\kappa_{max}) \alpha_{i} \frac{1+q}{\alpha_{i} +q}, \quad $$
(10)

where i=1,...,n u m e l, and numel is the total number of elements, and

$$ \frac{\partial \kappa(\alpha)}{\partial \alpha_{i}} = (\kappa_{min}-\kappa_{max}) (1+q) \frac{ q}{(\alpha_{i} +q)^{2}}, $$
(11)

with κ∈[κ m i n ,κ m a x ] and x∈Ω i , q is a parameter that controls the convexity of κ (Borrvall and Petersson 2003). Thus, for \( q \rightarrow \infty \), \(\kappa \rightarrow \kappa _{max} +(\kappa _{min} - \kappa _{max}) \alpha _{i}\) is a linear function. The optimization process seeks 0−1 values for the design variable (α i ≈0 or α i ≈1), as an intermediate value would not have a physical meaning, that is, when \(\alpha _{i} \approx 1 \Rightarrow \kappa = \kappa _{min} = 0\), represents a viscous flow with a free flow without restriction while on the other hand \(\alpha _{i} \approx 0 \Rightarrow \kappa = \kappa _{max}\) represents the flow in porous media, with a restricted flow. Ideally, impermeable solid walls can be represented with \(\kappa _{max}= \infty \), however to avoid numerical problems κ m a x is chosen as a finite value, for this work κ m a x =10000 (Olesen et al. 2006).

3.2 Topology optimization problem

The optimization problem in this work has the following formulation

$$ \left. \begin{array}{cc} \text{ min} c(\textbf{z}(\alpha),\alpha) \\ \alpha \\ \text{such that}: & \\ &\textbf{r}(\textbf{z}(\alpha),\alpha) = 0 \\ &\textbf{g}(\textbf{z}(\alpha),\alpha) \leq 0 \\ &\alpha_{min} \leq \alpha \leq \alpha_{max} \end{array} \right\} $$
(12)

The defined multi-objective function c(z(α),α) includes the minimization of energy dissipation, minimization of the vorticity, and the minimization of power consumption. The objective function is a function of two types of variables, the design variable α and the state variable z. The mathematical system r(z,α)=0 define the state problem, and g(z,α)≤0 represent mechanical constraints on the variables.

A volume constraint is defined to limit the amount of fluid and thus, driving the porosity distribution towards the upper or lower bounds. It is prescribed that, at most, a given fraction of the design domain f|Ω|, is allowed to be occupied by fluid, and the remainder must be solid, thus

$$ {\int}_{\Omega} \alpha d {\Omega} \leq f| {\Omega} |, $$
(13)

where f is the prescribed volume fraction, a constant between 0 and 1.

3.3 Multi-Objective function

To improve pump hydraulic performance and its haematological conditions three objective functions are considered in the optimization problem according to the following definitions:

  • Energy dissipation: The expression proposed by Borrvall and Petersson (2003), for the dissipation of energy for the fluidic problem is given by

    $$ \boldsymbol{\Phi}={\int}_{\Omega} \left[\frac{1}{2} \mu \left( \nabla \textbf{u} + \nabla \textbf{u}^{T} \right) : \left( \nabla \textbf{u} + \nabla \textbf{u}^{T} \right) + \kappa (\textbf{x}) \textbf{u}^{2} \right] d {\Omega}, $$
    (14)

    This objective function is valid in many applications, and specially important in applications where the energy available for pumping the fluid is restricted, requiring a good performance of the channel in which the fluid flows. It also contributes to decrease thrombosis and hemolysis, as discussed in Section 1.

  • Vorticity: Vorticity is a measure of the circulation and rotation of a fluid, and is twice the average shear rate of a fluid element. In this work, the vorticity is measured in a least-square sense through the functional given by Tavoularis et al. (2003), Berggren Martin (1998), Abraham et al. (2004) and Quarteroni and Rozza (2003)

    $$ J (\textbf{u} ) = {\int}_{\Omega} |\nabla \times \textbf{u} |^{2} d {\Omega} = {\int}_{\Omega} \left( \frac{\partial u_{2}}{\partial x_{1}} - \frac{\partial u_{1}}{\partial x_{2}} \right)^{2} d {\Omega}. $$
    (15)

    As discussed in Section 1, it also contributes to decrease thrombosis and hemolysis, thus, improving the haematological conditions.

  • Pump power: Reducing power consumption is important for pumps, mainly blood pumps in VADs since implantable devices depend on external energy sources. The rate of power on a flow machine rotor is given by the dot product of the rotor angular velocity(ω), and the applied torque (T e ),

    $$ \dot W = \boldmath{\omega} \cdot \textbf{T}_{e}. $$
    (16)

    Since the angular velocity is constant, for simplicity, the torque, instead of power, is considered as objective function. The body force contribution may be neglected due to symmetry and considering that the mass flow in the inlet domain is normal to the boundary, the total torque for steady flow will be equal to the integral of the boundary outlet flow, i.e. (Fox Robert and McDonald Alan 1985),

    $$\begin{array}{@{}rcl@{}} \textbf{T}_{e} &=& {\int}_{{\Gamma}_{e}} \rho(\textbf{r} \times \textbf{u} ) \textbf{u} \cdot \textbf{n} d{\Gamma} + {\int}_{{\Gamma}_{e}} \rho(\textbf{r} \times \boldsymbol{\omega} \times \textbf{r}) \textbf{u} \cdot \textbf{n} d{\Gamma}\\ &=& {\textbf{T}}_{r} + \textbf{T}_{t}= T_{r} \textbf{e}_{3} + T_{t} \textbf{e}_{3}. \end{array} $$
    (17)

    where T r is the torque due to the relative flow out and T t the torque due to the rotational movement of the reference system.

    These three objective functions are combined to define a multi-objective function (Romero and Silva 2014)

    $$ {\Psi} = w_{e} log({\Phi}) + w_{v} log(J) + w_{t} log(T_{e}), $$
    (18)

    where Ψ is the multi-objective function, Φ is the viscous dissipation term, J is the vorticity and T e is the torque. w e , w v and w t are the weighting coefficients associated with energy dissipation, vorticity, and torque, respectively. They allow the control of the influence of energy dissipation, vorticity, and torque term, respectively. It is considered that w e + w v + w t =1.0. The logarithmic function is applied to smooth the differences in magnitude of the various objective functions involved.

    These functions (energy dissipation, vorticity, and power) contain information about the flow properties and their connections with the change in rotor geometry.

3.4 Hemolysis Index

Hemolysis is one of the most important performance parameters of blood pumps. The measure of hemolysis, is a reliable indicator of the overall blood damage. Hemolysis is measured in terms of the concentration of the free hemoglobin in blood stream, or plasma free hemoglobin (p f H b). The hemolysis index (H) can be calculated from measurements of plasma free hemoglobin and is defined as the change in plasma free hemoglobin (Δp f H b) as a percentage of the total hemoglobin (H b) (Fraser et al. 2010):

$$ H = \frac{\Delta pfHb}{Hb} \times 100 $$
(19)

Giersiepen et al. (1990) developed a correlation for steady-shear hemolysis at short time scales, which is based on experimental results relevant to flow in a VAD. Under constant, uniform shear stress, as found, for example, in a Couette device, a power-law function has been proposed to represent the relationship of hemolysis index with the shear stress (σ) and exposure time (Δt):

$$ H = C \sigma^{\beta} {\Delta} t^{\delta} $$
(20)

where C, δ and β are constants, C=1.21×10−5, δ=0.747 and β=2.004 (Fraser et al. 2010). Bludszuweit (1995) proposed a representative instantaneous scalar stress parameter called equivalent shear stress, obtained from the six components of the complete stress tensor that can be used to estimate σ. Thus, the equivalent shear stress, σ I , is calculated from the shear stress components, σ i j , by using the following equation:

$$\begin{array}{@{}rcl@{}} \sigma_{I} &=& \left[ \frac{1}{6} \left( (\sigma_{11} - \sigma_{22} )^{2} +(\sigma_{22} - \sigma_{33} )^{2} + (\sigma_{33} - \sigma_{11} )^{2} \right)\right.\\ &&+\left. \left( \sigma_{12}^{2} + \sigma_{23}^{2} + \sigma_{31}^{2} \right) \right]^{\frac{1}{2}} \end{array} $$
(21)

The principal methods for estimating hemolysis in devices by using computational fluid dynamics have been developed considering: Eulerian methods (Zhang and Liu 2015), which integrate shear stress and residence time over every mesh element; and Lagrangian methods, which estimate hemolysis on a small section of a streamline and integrate this along the whole line (André and Farinas Marie-Isabelle 2004). The mean residence time is found by tracing stream-lines from the inlet plane through the device to the outlet plane and finding the mean time taken by a particle to reach the outlet through these streamlines.

Thus, Arora et al. (2004) present a method to predict hemolysis based on a scalar measure of the instantaneous shear stress τ, i.e., a scalar quantity derived from the instantaneous deviatoric stress tensor

$$ \tau = \sqrt{\frac{1}{2} {\boldsymbol{\tau} : \boldsymbol{\tau}}} $$
(22)

where τ = η(∇ u + ∇ u T). This method of computing hemolysis is called “stress-based” and the quantity τ is called “scalar shear stress” by authors (Arora et al. 2004). The work of Antaki et al. (1995) also proposes that the design optimization of blood-wetted components can be achieved by minimizing shear stress, and to reach this goal, they have defined an objective function given by.

$$ f = {\int}_{\Omega} \tau d V $$
(23)

However, hemolysis becomes important in high shear stress flow. Thus, for a steady flow, by assuming that a hemolysis rate is caused by the spatial distribution of shear stress only, the following hemolysis index is defined by Montevecchi et al. (1995):

$$ I = \frac{{\int}_{\Omega} \tau^{2.4} d V}{Q} $$
(24)

where Q is the flow rate.

Thus, only for qualitative comparison analysis we will evaluate the hemolysis index by proposing an expression based on (24) and (23), being defined by:

$$ I = {\int}_{\Omega} \tau^{2.4} d V $$
(25)

where τ is given by (22).

4 Numerical implementation of optimization problem

4.1 Finite element modeling of radial flow machines

The integral expressions of the weak formulation of the flow problem in porous media, steady state, considering a rotating reference system is given by Romero and Silva (2014)

$$ R_{c} = {\int}_{\Omega} (\nabla \cdot \textbf{u} ) M d {\Omega} = 0, $$
(26)
$$\begin{array}{@{}rcl@{}} R_{m} &=& {\int}_{\Omega} (\rho \textbf{u} \cdot\nabla \textbf{u})\cdot \textbf{w} d {\Omega} + {\int}_{\Omega}\kappa(\textbf{x}) \textbf{w} \cdot \textbf{u}d {\Omega} \\ &&+ {\int}_{\Omega} \textbf{T}:{\nabla \textbf{w}}d {\Omega} \, \\ && + {\int}_{\Omega} \textbf{w}\left[2 \rho(\boldsymbol{\omega} \times \textbf{u} ) + \rho \, \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \textbf{r} ) d {\Omega}\right] \, \\ && -{\int}_{\Omega} \textbf{b} \cdot \textbf{w}d {\Omega} - {\int}_{\Gamma} (\textbf{T} \cdot\textbf{n})\cdot \textbf{w}d {\Gamma} = 0, \end{array} $$
(27)

where w and M are weighting functions, w is vector, and M is scalar, which will be equated in the weak form Galerkin finite element models, to the interpolation functions used for u and p, respectively. They have the following correspondence w≈Ψ and M≈χ i (see Reddy and Gartling (2010)).

The weighting function ϕ i associated with the momentum equations is bi-quadratic, and χ i related with the continuity equation is linear (Fig. 2), and T is the stress tensor.

Fig. 2
figure 2

Finite element nodes that express a the velocity, b pressure, and c design variable in a quadrilateral element

Full size image

To implement the finite element method, these equations are solved by using Taylor-Hood elements, where the fluid velocity and the pressure are quadratically and linearly interpolated, respectively (Romero and Silva 2014). The design variable is constant inside the element (Fig. 2).

For a given quadrilateral Q, the velocity field u=[u 1 u 2]T and pressure p are approximated by linear combination of the basis function in the form

$$\begin{array}{@{}rcl@{}} u_{1}(\textbf{x}) &=& \sum\limits_{j=1}^{n} \phi_{j}(\textbf{x}) {u_{j}^{1}}=\boldsymbol{\Psi}^{T}\textbf{u}_{1};\\ \, \,u_{2}(\textbf{x} ) &=& \sum\limits_{j=1}^{n} \phi_{j}(\textbf{x}) {u_{j}^{2}}=\boldsymbol{\Psi}^{T}\textbf{u}_{2}; \, \, \\ p(\textbf{x} ) &=& \sum\limits_{j=1}^{m} \chi_{j}(\textbf{x}) p_{j}=\boldsymbol{\chi}^{T}\textbf{p}; \end{array} $$
(28)

where u 1,u 2, and p are vectors with the nodal values of the approximated solution for the velocity field and pressure defined in the weak formulation of the finite element method.

By replacing the approximation of pressure and velocity fields obtained through finite element interpolation functions, we obtain the algebraic equations of the finite element method. For the two-dimensional case, the algebraic system of equations may be represented by

$$\begin{array}{@{}rcl@{}} &&\left[ \begin{array}{lll} \textbf{K}_{\kappa} & 0 & 0 \\ 0 & {K}_{\kappa} & 0 \\ 0 & 0 & 0 \end{array} \right] \left\{\begin{array}{l} \textbf{u}_{1} \\ \textbf{u}_{2} \\ \textbf{p} \end{array} \right\} \\ && +\left[ \begin{array}{lcl} \textbf{C}_{1}(u_{1}) + C_{2}(u_{2}) & 0 & 0\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 &C_{1}(u_{1})+ C_{2}(u_{2}) & 0 \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 & 0 & 0 \end{array} \right] \left\{\begin{array}{l} \textbf{u}_{1} \\ \textbf{u}_{2} \\ \textbf{p} \end{array} \right\} \\ &&+ \left[ \begin{array}{lll} 2\textbf{K}_{11}(\textbf{U}) + \textbf{K}_{22}(\textbf{u}) & \textbf{K}_{12}(\textbf{u}) & -\textbf{Q}_{1} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\textbf{K}_{21}(\textbf{U}) & \textbf{K}_{11}(\textbf{u}) + 2 \textbf{K}_{22}(\textbf{u}) & -\textbf{Q}_{2} \\ \qquad\quad -\textbf{Q}_{1}^{T} & -\textbf{Q}_{2}^{T} & 0 \end{array} \right] \left\{\begin{array}{l} \textbf{u}_{1} \\ \textbf{u}_{2} \\ \textbf{p} \end{array} \right\} \\ && +\left[\begin{array}{lll} 0 & \textbf{K}_{r} & 0 \\ -\textbf{K}_{r} & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] \left\{\begin{array}{l} \textbf{u}_{1} \\ \textbf{u}_{2} \\ \textbf{p} \end{array} \right\}= \left\{\begin{array}{l} \textbf{f}_{1} \\ \textbf{f}_{2} \\ \textbf{0} \end{array} \right\}\,, \end{array} $$
(29)

where U=[u 1 u 2]T, and u 1,u 2 are vectors with the nodal values of velocity in the x 1 and x 2 direction respectively. The matrix coefficients are defined as

$$\begin{array}{@{}rcl@{}} \textbf{K}_{\kappa} &=& {\int}_{{\Omega}^{e}} \kappa \boldsymbol{\Psi} \boldsymbol{\Psi}^{T} d {\Omega}; \\ \textbf{C}_{j}(u_{j}) &=& {\int}_{{\Omega}^{e}} \rho_{0} \boldsymbol{\Psi} (\boldsymbol{\Psi}^{T} \textbf{u}_{j}) \frac{\partial \boldsymbol{\Psi}^{T}}{\partial x_{j}} d {\Omega}\\ \textbf{K}_{ij} &=& {\int}_{{\Omega}^{e}} \eta(\textbf{U}) \frac{\partial \boldsymbol{\Psi}}{\partial x_{j}} \frac{\partial \boldsymbol{\Psi}^{T}}{\partial x_{i}} d {\Omega};\\ \textbf{Q}_{i} &=& {\int}_{{\Omega}^{e}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{i}} \chi^{T} d {\Omega}, \quad i,j=1,2; \\ \textbf{K}_{r} &=& {\int}_{{\Omega}^{e}} 2 \omega_{0} \boldsymbol{\Psi} \boldsymbol{\Psi}^{T} d {\Omega}; \\ \textbf{f}_{i} &=& {\int}_{{\Omega}^{e}} \rho \boldsymbol{\Psi}f_{i} d {\Omega} + {\int}_{{\Omega}^{e}} \rho {\omega_{0}^{2}} \boldsymbol{\Psi} x_{i} d {\Omega} + \left\{ \oint_{{\Gamma}^{e}} h_{i} \boldsymbol{\Psi} ds \right\}\,, \\ \end{array} $$
(30)

being κ = κ(α i ). The matrix K κ can also be defined as

$$ \textbf{K}_{\kappa} = \kappa \textbf{K}_{m} \quad \text{ where;} \quad \textbf{K}_{m} = {\int}_{{\Omega}^{e}} \boldsymbol{\Psi} \boldsymbol{\Psi}^{T} d {\Omega}\, , $$
(31)

These equations are essentially the same for newtonian or non-newtonian fluids. The overall system is non-symmetrical and non-linear due to the contribution of C (u), the convective term, which is non-symmetrical and non-linear. Therefore, for solving the system, an appropriate procedure such as Newton method is applied. The matrix K κ is symmetric and comes from the absorption term. All nonlinearities of (29) are not explicitly accounted for in defining the Jacobian derivative matrix, i.e. the matrix dependent viscosity. The complexity of dealing with all nonlinearity properties with such rigorous way would be prohibitive and often unjustified. These nonlinearities are usually soft enough not to affect the convergence of the Newton algorithm. Therefore, a strict formulation for the Jacobian matrix is applied only to advective terms which are highly non-linear (Reddy and Gartling 2010). The velocity field and pressure are the state variables of the problem, and they are defined in a compact form based on discrete residual (29) as

$$ \textbf{r} (\textbf{z}(\kappa), \kappa) = 0, $$
(32)

where z is a vector that contains all state variables z=[u 1 u 2 p]T, and it is shown that r and state variables z implicitly depend on the material model κ. Based on the discrete finite element formulation, the definitions of energy dissipation, vorticity, and power consumption are presented ahead.

4.2 Energy dissipation

The energy dissipation given by (14) can be expressed in discrete form by Romero and Silva (2014)

$$ \boldsymbol{\Phi} = \frac{1}{2} \textbf{U}^{T} (\bar{\textbf{K}}_{d} (\textbf{U}) + \bar{\textbf{K}}_{\kappa} )\textbf{U} = \frac{1}{2} {\textbf{z}}^{\textbf{T}} \textbf{C}(\textbf{U}) \textbf{z}, $$
(33)

where

$$ \textbf{C}(\textbf{U})\equiv \left[ \begin{array}{ll} \bar{\textbf{K}}_{d} (\textbf{U}) + \bar{\textbf{K}}_{\kappa} & 0 \\ \qquad0 & 0 \end{array} \right] . $$
(34)

The matrix C(U) is symmetric because \(\bar {\textbf {K}}_{d} (\textbf {U}) + \bar {\textbf {K}}_{\kappa }\) is symmetric. \(\bar {\textbf {K}}_{d} (\textbf {U})\) and \(\bar {\textbf {K}}_{\kappa } \) are given by

$$ \bar{\textbf{K}}_{d} (\textbf{U}) = \left[\begin{array}{ll} 2\textbf{K}_{11}(\textbf{U}) + \textbf{K}_{22}(\textbf{U}) & \textbf{K}_{12}(\textbf{U})\\ \textbf{K}_{21}(\textbf{U}) & \textbf{K}_{11}(\textbf{U}) + 2 \textbf{K}_{22}(\textbf{U}) \end{array} \right], $$
(35)
$$ \bar{\textbf{K}}_{\kappa} = \left[ \begin{array}{ll} \textbf{K}_{\kappa} & 0 \\ 0 &\textbf{K}_{\kappa} \end{array} \right], $$
(36)

where the matrices K i j are defined in (30).

4.3 Vorticity

The numerical integration of functional of vorticity ((15)) gives

$$ J (\textbf{u} ) = \sum\limits_{e=1}^{ne} {\int}_{{\Omega}_{e}} \left( \frac{\partial u_{2}}{\partial x_{1}} - \frac{\partial u_{1}}{\partial x_{2}} \right)^{2} d {\Omega} =\sum\limits_{e=1}^{ne} \textbf{U}^{T} \textbf{M}_{v} \textbf{U}, $$
(37)

where ne is the total number of elements, and the local matrix M v obtained from (37) is defined as Romero and Silva (2014)

$$ \textbf{M}_{v} = \left[\begin{array}{ll} \textbf{M}^{11}_{v} \textbf{M}^{12}_{v} \\ \textbf{M}^{21}_{v} \textbf{M}^{22}_{v}\end{array} \right], $$
(38)

where

$$\begin{array}{@{}rcl@{}} {\textbf{M}}^{11}_{v} &=& {\int}_{{\Omega}_{e}} \left( \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}} \frac{\partial \boldsymbol{\Psi}^{T}}{\partial x_{2}} \right) d {\Omega}; \textbf{M}^{12}_{v} =- {\int}_{{\Omega}_{e}} \left( \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}} \frac{\partial \boldsymbol{\Psi}^{T}}{\partial x_{1}} \right)\\ &&\times d {\Omega};\\ \textbf{M}^{21}_{v} &=& - {\int}_{{\Omega}_{e}} \left( \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}} \frac{\partial \boldsymbol{\Psi}^{T}}{\partial x_{2}} \right) d {\Omega}; \textbf{M}^{22}_{v} ={\int}_{{\Omega}_{e}} \left( \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}} \frac{\partial {\boldsymbol{\Psi}}^{T}}{\partial x_{1}} \right)\\ &&\times d {\Omega}. \end{array} $$
(39)

where Ψ=[ϕ 1,...,ϕ n ]T and n is the number of local nodes.

4.4 Pump torque

The absolute value of torque defined by (17), is defined in terms of the components of the velocity and position vectors. Thus

$$ \textbf{T}_{e} = \sum\limits_{e=1}^{nbc} \left( {T^{e}_{r}} \textbf{e}_{3} + {T^{e}_{t}} \textbf{e}_{3} \right). $$
(40)

where nbc is the number of elements in the outlet.

The torque \( {T^{e}_{r}}\) per element can be expressed by Romero and Silva (2014)

$$ {T^{e}_{r}} = \textbf{U}^{T} \textbf{M}_{r} \textbf{U}, $$
(41)

The local matrix M r is not symmetric, and is defined as Romero and Silva (2014)

$$ \textbf{M}_{r} = \left[\begin{array}{ll} \textbf{M}^{11}_{r} & \textbf{M}^{12}_{r} \\ \textbf{M}^{21}_{r} & \textbf{M}^{22}_{r} \end{array} \right], $$
(42)

where

$$ \begin{array}{ll} {M^{11}_{r}}_{ij} \,=\, \,-\,{\int}_{-1}^{1} \rho \left( \phi_{i} x_{2} \frac{d x_{2}}{d \gamma} \phi_{j} \right) d \gamma\!;\! \qquad &{M^{12}_{r}}_{ij} \,=\, {\int}_{\,-\,1}^{1} \rho \left( \phi_{i} x_{2} \frac{d x_{1}}{d \gamma} \phi_{j} \right) d \gamma; \\ {M^{21}_{r}}_{ij} \,=\, {\int}_{-1}^{1} \rho \left( \phi_{i} x_{1} \frac{d x_{2}}{d \gamma} \phi_{j} \right) d \gamma; & {M^{22}_{r}}_{ij} \,=\, -\!{\int}_{\,-\,1}^{1} \rho \left( \phi_{i} x_{1} \frac{d x_{1}}{d \gamma} \phi_{j} \right) d \gamma, \end{array} ; $$
(43)

where i,j=1,...,n b and nb is the number of nodes in the local contour elements, and γ is a local coordinate.

The torque integral \({T^{e}_{t}}\) per element can be expressed by Romero and Silva (2014)

$$ {T^{e}_{t}} = -{\int}_{-1}^{1} \rho \, \omega_{0} (\textbf{r} \cdot \textbf{r}) \left( u_{1} \frac{\partial x_{2}}{\partial \gamma} - u_{2} \frac{\partial x_{1}}{\partial \gamma} \right) d\gamma = \textbf{V}^{T} \textbf{U}, $$
(44)

where V=[V 1 V 2]T, and

$$\begin{array}{@{}rcl@{}} {V^{1}_{i}} &=& -{\int}_{-1}^{1} \rho \, \omega_{0}\left( ({x_{1}^{2}} + {x_{2}^{2}}) \frac{d x_{2}}{d \gamma} \phi_{i} \right) d \gamma; \, \, {V^{2}_{i}}\\ &=& {\int}_{-1}^{1} \rho \, \omega_{0} \left( ({x_{1}^{2}} + {x_{2}^{2}}) \frac{d x_{1}}{d \gamma} \phi_{i} \right) d \gamma, \end{array} $$
(45)

where i=1,...,n b

4.5 Sensitivity analysis through adjoint method

The topology optimization problem is implemented by using the gradient optimization method through an iterative process. The mathematical programming, is a process that depends on the information of the gradients of the objective function and constraints to guide the optimization and to obtain optimal value.

The gradient of multi-objective function, is given by

$$ \frac{d\, {\Psi}}{d \,\alpha_{i}} = w_{e} \frac{1}{\Phi} \frac{d\, {\Phi}}{d \,\alpha_{i}} + w_{v} \frac{1}{J} \frac{d\, J}{d \,\alpha_{i}} + w_{t} \frac{1}{T_{e}} \frac{d\, T_{e}}{d \,\alpha_{i}}. $$
(46)

The calculation of sensitivities \(\frac {d\, {\Phi }}{d \,\alpha _{i}}\), \(\frac {d\, J}{d \,\alpha _{i}}\), and \(\frac {d\, T_{e}}{d \,\alpha _{i}}\) is briefly described ahead.

From the FEM equilibrium equation system the term \(\frac {d \textbf {z}}{d \alpha _{i}} \) can be obtained. Thus, from (29), the residual vector is given by

$$ \textbf{R} = \textbf{K}_{G} \textbf{z} - \textbf{F}, $$
(47)

where

$$ \textbf{K}_{G} =\left[ \begin{array}{ll} \textbf{C(U)} + \textbf{K(U)} & -\textbf{Q} \\ -\textbf{Q}^{T}& 0 \end{array} \right]; \quad \textbf{z} = \left[ \begin{array}{l} \textbf{U} \\ \textbf{p} \end{array} \right]; \textbf{F} =\left[ \begin{array}{l} \textbf{f} \\ \textbf{0} \end{array} \right], $$
(48)

where U and p are vectors with the nodal values of velocity and pressure of the finite element method approximate solution.

By differentiating ((47)) with respect to design variable (α) it is obtained

$$ \frac{d \textbf{R}}{d \alpha_{i}} = \frac{\partial \textbf{R}}{\partial \textbf{z}} \frac{d \textbf{z}}{d \alpha_{i}} + \frac{\partial \textbf{R}}{\partial \alpha_{i}} =0, $$
(49)

where \(\frac {\partial \textbf {R}}{\partial \textbf {z}} = \textbf {J}\), is the Jacobian matrix resulting from the application of Newton’s method to the solution of nonlinear system.

Thereby,

$$ \textbf{J} \frac{d \textbf{z}}{d \alpha_{i}} = -\frac{\partial \textbf{R}} {\partial \alpha_{i}}= - \frac{\partial \textbf{K}_{G}}{\partial \alpha_{i}} \,\textbf{z} +\frac{\partial \textbf{F}} {\partial \alpha_{i}} = \textbf{r}_{i}. $$
(50)

From (50), we have

$$ \frac{d \textbf{z}}{d \alpha_{i}} = \textbf{J}^{-1} \textbf{r}_{i}. $$
(51)

As shown, the gradient of multi-objective function, given by (46), depends on information of the gradients of each single objective function, which in turn depends on the solution of the adjoint equation associated with each objective function, which are energy dissipation, vorticity, and torque. These derivations can be found in detail in Romero and Silva (2014). The three adjoint problems can be combined and only one adjoint equation associated with the multi-objective function needs to be solved. Thus, by deriving and substituting (33), and (37), and finally (41), (44) into (46), it is obtained (Romero and Silva 2014):

$$\begin{array}{@{}rcl@{}} \frac{d\, {\Psi}}{d \,\alpha_{i}} &= & \frac{w_{e}}{\phi} \left[\frac{1}{2} \textbf{z}^{T} \frac{\partial \textbf{C(U)}}{\partial \alpha_{i}} \textbf{z} + \textbf{z}^{T}\textbf{C(U)} \frac{d \textbf{z}}{d \alpha_{i}} \right] \\ &&+ \frac{ w_{v}}{ J} \textbf{U}^{T} (\textbf{M}_{v} + \textbf{M}_{v}^{T}) \frac{d \textbf{U}}{d \alpha_{i}}\, \, \\ &&+ \frac{ w_{t}} {T_{e}} \left[ \textbf{U}^{T} (\textbf{M}_{r} + \textbf{M}_{r}^{T}) + \textbf{V}^{T} \right] \frac{d \textbf{U}}{d \alpha_{i}} , \end{array} $$
(52)

From de FEM equilibrium system,

$$ \textbf{U} = \textbf{L}^{T} \textbf{z} \Rightarrow \frac{d \textbf{U}}{d \alpha_{i}} = \textbf{L}^{T} \frac{d \textbf{z}}{d \alpha_{i}} $$
(53)

replacing (51) and (53) into (52) and packing (Romero and Silva 2014)

$$\begin{array}{@{}rcl@{}} \frac{d\, {\Psi}}{d \,\alpha_{i}} \!&=&\! \frac{1}{2}\frac{w_{e}}{\phi} \textbf{z}^{T} \frac{\partial \textbf{C(U)}}{\partial \alpha_{i}} \textbf{z} \, \\ && +\left[\frac{w_{e}}{\phi}\textbf{z}^{T}\textbf{C(U)} \,+\, \frac{ w_{v}}{ J} \textbf{U}^{T} (\textbf{M}_{v} \,+\, \textbf{M}_{v}^{T}) \textbf{L}^{T}\right.\\ &&\quad\quad +\!\left. \frac{ w_{t}} {T_{e}} \left( \textbf{U}^{T} (\textbf{M}_{r} \,+\, \textbf{M}_{r}^{T}) \,+\, \textbf{V}^{T} \right) \textbf{L}^{T} \right] \textbf{J}^{-\!1} \textbf{r}_{i}, \end{array} $$
(54)

finally

$$\frac{d\, {\Psi}}{d \,\alpha_{i}} =\frac{1}{2}\frac{w_{e}}{\phi} \textbf{z}^{T} \frac{\partial \textbf{C(U)}}{\partial \alpha_{i}} \textbf{z} + \textbf{S}_{t}^{T} \textbf{r}_{i}, $$
(55)

where S t is obtained from the solution of the system (Romero and Silva 2014):

$$\begin{array}{@{}rcl@{}} \textbf{J}^{T} \textbf{S}_{t} &=& \left[ \frac{ w_{e}}{\Phi} \textbf{C(U)}\textbf{z}+ \frac{ w_{v}}{ J} \textbf{L}(\textbf{M}_{v} + \textbf{M}_{v}^{T}) \textbf{U}\right.\\ &&\left.+\frac{ w_{t}} {T_{e}} \textbf{L}\left[ (\textbf{M}_{r} + \textbf{M}_{r}^{T}) \textbf{U} + \textbf{V} \right] \right]. \end{array} $$
(56)

This system is independent of the derivative with respect to design variable, so it is solved once per iteration of the optimization process. Because the system is dependent on the previous velocity field U, and the residual vector R is assumed to be zero, this system is solved by considering velocities resulting from the Newton converged process.

In (55), the vector r i , given by (50), is calculated for each element i in the domain, and J, is the Jacobian matrix resulting from the application of Newton’s method to the solution of nonlinear system.

4.6 Sensitivity of energy dissipation

The sensitivity of \(\frac {\partial \textbf {C(U)}}{\partial \alpha _{i}}\) can be computed as a sum of the gradients of \( \bar {\textbf {K}}_{d}(\textbf {U})\) and \( \bar {\textbf {K}}_{\kappa }\) with respect to the design variable, thus

$$ \frac{\partial {\textbf{C}(U)}}{\partial \alpha_{i}} =\left[\begin{array}{ll} \frac{\partial \bar{\textbf{K}}_{d} (\textbf{U})}{\partial \alpha_{i}}+\frac{\partial \bar{\textbf{K}}_{k}}{\partial \alpha_{i}}\,0\\ \qquad 0 \qquad\quad\,\, 0\\ \end{array} \right] $$
(57)

where

$$ \frac{\partial \bar{\textbf{K}_{d}} (\textbf{U})} {\partial \alpha_{i}} \,=\,\frac{\partial} {\partial \alpha_{i}} \left[\begin{array}{ll} 2{\textbf{K}}_{11}(\textbf{U}) \,+\, \textbf{K}_{22}(\textbf{u}) & \textbf{K}_{12}(\textbf{U})\\ \textbf{K}_{21}(\textbf{U}) & \textbf{K}_{11}(\textbf{U}) + 2 \textbf{K}_{22}(\textbf{u}) \end{array} \right], $$
(58)

and

$$ \frac{ \partial \bar{\textbf{K}}_{\kappa}}{\partial \alpha_{i}} = \frac{ \partial \kappa(\alpha)} { \partial \alpha_{i}}\left[\begin{array}{ll} \textbf{K}_{m} & 0 \\ 0 &\textbf{K}_{m} \end{array} \right], $$
(59)

\(\frac { \partial \kappa (\alpha )} { \partial \alpha _{i}} \) is given by (11).

In this case

$$ \frac{\partial \textbf{K}_{ij}}{\partial \alpha_{l}} = {\int}_{{\Omega}^{e}} \frac{\partial \eta(\textbf{U})}{\partial \textbf{u}} \frac{ \partial \textbf{U}}{\partial \alpha_{l}}\frac{\partial \boldsymbol{\Psi}}{\partial x_{j}} \frac{\partial \boldsymbol{\Psi}^{T}}{\partial x_{i}} d {\Omega}; $$
(60)

and \(\frac {\partial \eta (\textbf {U})}{\partial \textbf {U}}\) is given by (61).

4.6.1 Sensitivity of viscosity

Since non-Newtonian viscosity is dependent on shear rate which is dependent on the velocity, it is necessary to calculate the sensitivity of viscosity with respect to velocity. Thus, differentiating (5) with respect to velocity vector

$$ \frac{\partial \eta(\dot \gamma)}{\partial \textbf{U}} = \frac{\partial \eta(\dot \gamma)}{\partial \dot \gamma} \frac{\partial \dot \gamma} {\partial \textbf{U}} $$
(61)

where

$$ \frac{\partial \eta(\dot \gamma)}{\partial \dot \gamma} = (n-1)\lambda (\mu_{0} - \mu_{\infty})[ 1 + (\lambda \dot \gamma)^{a} ]^{\frac{ n-1}{a}-1} \, (\lambda \dot \gamma)^{a-1} $$
(62)

Since the implementation of non-Newtonian viscosity is considered as a continuous model to be used in FEM, the viscosity value at each integration point is required. Thus \(\eta (\dot \gamma ) \) is expressed as a diagonal matrix with the viscosity values associated with each integration point on the main diagonal. From (7),

$$ \frac{\partial \dot \gamma}{\partial \textbf{u}_{1}}= {\dot \gamma}^{-1} \left[ 2 \frac{\partial u_{1}}{\partial x_{1}} \frac{\partial {\Psi}}{\partial x_{1}} + \left( \frac{\partial u_{1}}{\partial x_{2}} + \frac{\partial u_{2}}{\partial x_{1}} \right)\frac{\partial {\Psi}}{\partial x_{2}} \right] $$
(63)
$$ \frac{\partial \dot \gamma}{\partial \textbf{u}_{2}}= {\dot \gamma}^{-1} \left[ 2 \frac{\partial u_{2}}{\partial x_{2}} \frac{\partial {\Psi}}{\partial x_{2}} + \left( \frac{\partial u_{1}}{\partial x_{2}} + \frac{\partial u_{2}}{\partial x_{1}} \right) \frac{\partial {\Psi}}{\partial x_{1}} \right] $$
(64)

by substituting equations (28) and grouping terms,

$$ \frac{\partial \dot \gamma}{\partial \textbf{U}} = {\dot \gamma}^{-1}\textbf{M}_{g} \textbf{U} $$
(65)

where

$$ \textbf{M}_{g} = \left[\begin{array}{ll} 2 \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}}^{T} + \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}}^{T} & \,\,\,\,\qquad \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}}^{T} \\ \,\,\,\,\qquad\frac{\partial \boldsymbol{\Psi}}{\partial x_{1}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}}^{T} & 2 \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{2}}^{T} + \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}} \frac{\partial \boldsymbol{\Psi}}{\partial x_{1}}^{T} \end{array} \right] $$
(66)

When the modified Cross model is used, η depends on u, thus, the evaluation of finite element jacobians and computation of sensitivity of the energy dissipative would require to compute the derivative of η with respect to u. However, in this case we have dropped these derivatives. This leads to an inexactness in the jacobian and sensitivity calculations which, may affect the finite element convergence and optimization process. Besides, we have found that the performance of numerical process is satisfactory, and therefore, we choose to avoid the additional implementation effort required to compute the exact jacobian and sensitivity (Abraham et al. 2005).

4.7 Optimization algorithm

The procedure for iterative optimization includes the following steps (see Fig. 3a) The Navier-Stokes equations are solved by considering the given initial value of the design variable, (b) adjoint equations are solved based on the numerical solution of the Navier-Stokes, (c) the sensitivities of the objective function and constraints are calculated (see next section), (d) a design variable is updated by the method of moving asymptotes (MMA) (Svanberg 1987). The above steps are implemented iteratively until the stopping criteria are satisfied. In the above procedure, the Navier-Stokes equations and the corresponding adjoint problem are solved by using the finite element method which is implemented in the Matlab system.

Fig. 3
figure 3

Flowchart of the topology optimization algorithm

Full size image

The volume constraint is given by

$$ \sum\limits_{i=1}^{ne} \alpha_{i}a_{i} \leq fV^{*}, $$
(67)

with a i being the area of the element i, 0<f≤1 is a fraction coefficient and V ∗ is the total volume to be considered.

The stopping criteria is given by

$$ || \alpha^{k} - \alpha^{k-1} ||_{\infty} \ll 1\times 10^{-3}, $$
(68)

where k is the iteration number.

5 Numerical examples

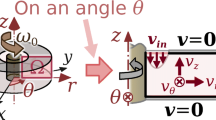
In the numerical examples, the goal is to predict the flow field between two rotor blades of a radial pump, without considering the influence of the volute (Romero and Silva 2014). Thus, only a segment of the impeller pump is modeled using a two-dimensional model as shown in Fig. 1. It is proposed to optimize the existing channel between two blades as a result of topology optimization, by considering the multi-objective function (46) involving viscous dissipation, power (through the torque), and vorticity functions and by evaluating the values of these functions in the final design. Newtonian and non-Newtonian fluids are considered.

The topology optimization determines the shape of the channel and the optimized position of the outlet channel for pump design, since these positions are unknown a priori. The radial velocity profiles are assumed to be uniform at inlet and the flow cross-sectional area is assumed to be constant along the radius. Therefore, the computational domain has the geometry shown in Fig. 4a. The position of the inlets and outlets of optimized channel will be located on the boundary Γ1 and Γ3, respectively. The initial mesh for both computational domains is shown in Fig. 4b. The boundary conditions adopted for pump design are |u|=1 in Γ1,u = 0 in Γ2, and p=0 in Γ3. The dimensions used are R 1=0.4 and R 2=1.0. The computational domain Ω is discretized into 4000 elements unless specified other number.

Fig. 4
figure 4

a Design domain with boundary conditions for pump design; b The initial mesh for the computational domain (4000 elements)

Full size image

In all examples, the density ρ and the viscosity μ for Newtonian model are adopted equal to 1058 K g/m 3 and 0.0035 P a s, respectively. For non-Newtonian model the viscosity is defined by using the modified Cross model defined in section (2.1). Following (Abraham et al. 2005), a suitable choice for the model of human blood is η 0=1.6×10−1 P a s, \(\eta _{\infty } = 3.5 \times 10^{-3} Pa \, s\), a=1.23, b=0.64 and λ=8.2s. Unless specified other values, computational results are obtained for angular velocity equal to 1000 r p m clockwise.

In Section 5.1, a comparative study is made between the use of non-Newtonian viscosity and Newtonian viscosity as a model template, evaluating the influence of the choice of the viscosity over the final optimized topology.

From Section 5.2 to Section 5.3, a comparative study about how the variation of certain parameters affects the final topology for a pump design is presented. Thus, in Section 5.2, the influence of initial guess for the design variable is analyzed. In Section 5.3, a comparative study on how the variation of multi-objective function weighting values affect the final topology of pump channel is presented. Finally, in section 5.4, the influence of angular velocity value on the topology results is analyzed. The value of hemolysis index (25) for these results is calculated, and its relation with vorticity values is analyzed.

5.1 Influence of Newtonian and non-Newtonian flow models

In this section, it is illustrated the ability of topology optimization to identify design with conceptually different channel pump layout under Newtonian and non-Newtonian flows models. In this study, only the minimization of the energy dissipation is considered by varying the angular velocity. The coefficients w e , w v , and w t are equal to 1, 0, and 0, respectively, for all results in this example. The topology optimization results are presented in Fig. 5. They show that at low rpm (<700 r p m) the optimized Newtonian and non-Newtonian design topologies differ significantly, considering the shape and the outlet channel position. At large rpm, for both Newtonian and non-Newtonian optimization, the shape and outlet channel position results are similar. Fig. 6 shows the topology for the entire rotor at (500 r p m).

Fig. 5
figure 5

Comparison of optimized topologies obtained by considering the minimization of energy dissipation only for Newtonian and non-Newtonian flows modes: 500 r p m a Newtonian; b non-Newtonian; 600 r p m c Newtonian; d non-Newtonian; 700 r p m e Newtonian; f non-Newtonian; 800 r p m g Newtonian; h non-Newtonian; 900 r p m i Newtonian; j non-Newtonian; 1000 r p m k Newtonian; l non-Newtonian

Full size image
Fig. 6
figure 6

Optimized topology of entire rotor for 500 r p m a Newtonian; b non-Newtonian

Full size image

5.2 Influence of initial guess for non-Newtonian flow models

For comparison purposes, it will be considered as reference, traditional channel geometries, such as, straight blades, inclined straight blades, curved blades and involute curved blades (Romero and Silva 2014). In the curved blades the radius of curvature is constant along the blade, however in the involute blade the radius of curvature varies along the blade as described in (Stepanoff 1957). Table 1 presents the values for energy dissipation, vorticity, power, and hemolysis index (25) for these reference channel shapes for non-Newtonian flow. From Table 1, it is noticed that the hemolysis index value I follows the vorticity value behaviour, that is, low and high values of I correspond to low and high values of vorticity.

Table 1 Results for reference channels with different geometries ω=1000 r p m for non-Newtonian flow models
Full size table

Figures 7, 8 and 9, show the relative velocity, vorticity field and scalar shear stress for these reference traditional radial pump configurations such as straight blades, inclined curved blades and involute blades. Scalar shear stress is calculated through (22).

Fig. 7
figure 7

Relative velocity field for following topologies: a straight blades; b curved blades; c involute curved blades

Full size image
Fig. 8
figure 8

Vorticity field for following topologies: a straight blades; b curved blades; c involute curved blades

Full size image
Fig. 9
figure 9

Scalar shear stress field for following topologies: a straight blades; b curved blades; c involute curved blades

Full size image

In this section, only the minimization of energy dissipation is considered as a comparative example by varying the initial guess for the design variables. It is considered as the initial guess α i =0.99 (this implies that the design variables for all elements of the extended domain are initialized with the value of 0.99), straight blades, and blade-shaped involute. In the latter two cases, design variables are initialized to create a channel formed by straight and involute blades shape, respectively.

Topology optimization results are presented in Figs. 10, 11, and 12 together with corresponding relative velocity field, vorticity field, and scalar shear stress field. From these results and Table 2, it can be seen how the choice of the initial guess for the design variable affects the final optimized topology, i.e., the final topology is dependent on the initial guess, as expected. In Figs. 11 and 12 which correspond to the initial guess of straight and involute blades, respectively, it is observed a double channel topology, similar to the configuration proposed by Golcu et al. (2006). Essentially, it proposes to consider blade splitters between two blades, to obtain an increase of efficiency.

Fig. 10
figure 10

Optimized topology obtained by minimizing the energy dissipation only for initial guess α i =0.99 (ω=1000 r p m): a optimized topology channel; b optimized topology of entire rotor; c Velocity field; d pressure field; e vorticity field; f scalar shear stress field

Full size image
Fig. 11
figure 11

Optimized topology obtained by minimizing the energy dissipation only by considering straight blades as initial guess (ω=1000 r p m): a optimized topology channel; b optimized topology of entire rotor c Velocity field; d pressure field; e vorticity field; f scalar shear stress field

Full size image
Fig. 12
figure 12

Optimized topology obtained by minimizing the energy dissipation only by considering involute blades as initial guess (w e =1.0) (ω=1000 r p m): a optimized topology channel; b optimized topology of entire rotor c Velocity field; d pressure field; e vorticity field; f scalar shear stress field

Full size image
Table 2 Results obtained by minimizing the energy dissipation for different initial guess of design variables with non-Newtonian model. ω=1000 r p m
Full size table

From Table 2, the results considering the straight blades as initial guess, generate lower energy dissipation. This happens due to the fact that the fluid particles have a shortest path between the rotor inlet and outlet. In addition, it is noticed that the hemolysis index values I follows quite close to the vorticity values behaviour. In the case of the results obtained by considering the straight and involute blade initial guess, their vorticity values are very close, so are the hemolysis index values.

5.3 Multi-objective optimization

In this section, the results are obtained by considering different values of weight coefficients w e ,w v , and w t . The topology optimization results are presented from Figs. 13, 14, 15, 16, 17, 18 and 19. As seen in Table 3, when solving the problem of optimizing a multi-objective function (to minimize) energy dissipation function and vorticity function or energy dissipation function and power function, the values obtained for energy dissipation function are higher when compared with energy dissipation results obtained for the optimization problem considering energy dissipation as a single function (see Table 2), as expected. However, vorticity function and power function are minimized. From Table 3, it is noticed that high and low values of vorticity corresponds to high and low values of hemolysis index, thus, the hemolysis index values I follows quite close to the vorticity values behaviour showing that the minimization of hemolysis index can be achieved by minimizing vorticity.

Fig. 13
figure 13

Optimized topology obtained by minimizing the energy dissipation and vorticity considering involute blade as initial guess. w e =0.5, w v =0.5, and w t =0.0. a optimized topology channel; b optimized topology of entire rotor c Velocity field; d pressure field; e vorticity field; f scalar shear stress field

Full size image
Fig. 14
figure 14

Optimized topology obtained by minimizing the energy dissipation and vorticity considering α i =0.99 as initial guess. w e =0.5, w v =0.5, and w t =0.0. a optimized topology channel; b optimized topology of entire rotor; c Velocity field; d pressure field; e vorticity field; f scalar shear stress field

Full size image
Fig. 15
figure 15

Optimized topology obtained by minimizing the energy dissipation and power considering α i =0.99 as initial guess. w e =0.5,w v =0.0, and w t =0.5. a optimized topology channel; b optimized topology of entire rotor; c Velocity field; d pressure field; e vorticity field; f scalar shear stress field

Full size image
Fig. 16
figure 16

Optimized topology obtained by minimizing the energy dissipation and vorticity considering α i =0.99 as initial guess. and w e =0.5, w v =0.5 and w t =0.0a optimized topology channel; b Velocity field

Full size image
Fig. 17
figure 17

Optimized topology obtained by minimizing the energy dissipation and vorticity considering α i =0.99 as initial guess. and w e =0.25, w v =0.75 and w t =0.0a optimized topology channel; b Velocity field; c Vorticity field; d scalar shear stress field

Full size image
Fig. 18
figure 18

Optimized topology obtained by minimizing the vorticity considering α i =0.99 as initial guess. and w e =0.0, w v =1.0 and w t =0.0a optimized topology channel; b Velocity field; c Vorticity field; d scalar shear stress field

Full size image
Fig. 19
figure 19

Optimized topology obtained by minimizing the power only considering α i =0.99 as initial guess. and w t =1.0. a optimized topology channel; b Velocity field; c Vorticity field; d scalar shear stress field

Full size image
Table 3 Results obtained by minimizing the energy dissipation, vorticity and power with non-Newtonian model
Full size table

5.4 Influence of the angular velocity on the optimum topology

In this example it is shown how the angular velocity affects the optimized topology. Topology optimization results and corresponding topologies of entire rotors are shown in Fig.s 20 and 21, respectively. As seen in Fig. 20, the angular position between the inlet and the outlet of the channel increases as the angular velocity increases.

Fig. 20
figure 20

Optimized topology channel obtained by minimizing the energy dissipation and vorticity (w e =0.5; w v =0.5; w t =0.0) for a non-Newtonian fluid varying the angular velocity: a ω=1000 r p m; b ω=2000 r p m; c ω=3000 r p m; d ω=4000 r p m

Full size image
Fig. 21
figure 21

Corresponding optimized topology of the entire rotor obtained by minimizing the energy dissipation and vorticity (w e =0.5; w v =0.5; w t =0.0) for a non-Newtonian fluid varying the angular velocity: a ω=1000 r p m; b ω=2000 r p m; c ω=3000 r p m; d ω=4000 r p m

Full size image

6 Conclusions

A novel method based on topology optimization for designing radial pump rotors aiming at non-Newtonian flow application has been proposed. The method is investigated for Newtonian and non-Newtonian flow with low and moderate Reynolds numbers by considering blood pump applications. The modified Cross constitutive model was selected for the non-Newtonian fluid. The problem is posed as optimizing the channel between the blades of pump rotors.

In order to improve the pumping performance necessary for a VADs, energy dissipation, the vorticity, and the power consumption are considered as objective functions. For a VADs it is also important to reduce the hemolysis, which is related with the shear stress, and stagnation points. We have verified that the reduction of the vorticity contributes to the reduction of the hemolysis index, improving pump haematological conditions.

The influence of fluid type (Newtonian and Non-Newtonian), initial guess, weighting coefficients, and angular velocity values for the flow are analyzed. The results for Newtonian and Non-Newtonian fluid-type differ for low Reynold number only, as expected. The optimized results are strongly influenced by initial guess as well as the angular velocity value. The multi-objective function could successfully provide a way to obtain different designs by weighting the contribution of the three defined objective functions. All these examples indicate that the method has a high potential to find optimized design of blood flow machine rotors.

As future work, authors suggest to consider a more complete flow model which includes high Reynolds number, turbulence models suitable for systems in rotation. Although a two-dimensional model represents quite closely the rotor flow behaviour of a centrifugal pump, a three-dimensional model would be more realistic and practical. It is also important to study how the housing affects the rotor flow.